2015清华大学自主招生试题(含答案)
2015年各高校自主招生考试试题

2015年各高校自主招生考试试题北京大学今年北大自招太过亲民,遇到这样的自招题你敢想?一句周杰伦《青花瓷》里的歌词,问描述的是什么?答案有“青花瓷”、“青花盆”和“青花瓶”,你觉得选什么呢……北大语文试题只有一道题目,要求根据孟子《生于忧患死于安乐》和庄子《人间世》这两个材料,写一篇文章。
英语有阅读材料涉及美国白人警察枪杀黑人、贵州省一教育基金会受“郭美美事件”影响遭遇零捐助等时事热点。
面试部分考题:1.用一条长度一定的的绳子围成一个n边形,怎样围才能使围出的的n边形面积最大?2.后轮驱动的车辆,起动和刹车时,分别是车头翘起还是车尾翘起?判断并说明理由。
3.如何看待微信在人际交往中的作用?4.如何看待欧洲历史上的分与合?5.北京和张家口联合申办冬奥会面临哪些机遇和挑战?6.请用三个词概括中国传统文化,并谈谈中国文化如何真正“走出去”。
7.怎么看待追求财富导致雾霾的说法8.请谈一下动物迁徙的意义?9.谈谈你对嘀嘀打车与专车经营的看法。
10.你认为的文学阅读的最高境界是什么?11.请谈有教无类与因材施教的关系。
12.请谈你对国企高管限薪令的看法。
13.有人提议将网络战归为武力冲突,谈谈你的看法。
14.谈谈你对亚投行的看法。
15.有人提议在基础教育阶段实施男女分开管理,即开办男校和女校,谈谈你的看法。
16.谈一谈信仰、义务、责任的关系。
17.爱因斯坦说:“简单是科学追求的伟大目标。
”谈谈你的看法。
18.请你设计一下中国的养老体系?19.你如何看待就医不要钱这种理想设计?20.谈一谈你对批判性思维和惯性思维的关系的理解。
21.谈一谈你所认识的经济全球化下中国的粮食问题。
22.谈一谈自我意识?23.有人说在全球化背景下我国粮食安全已经不是一个问题,你怎么看?24.你对“绿水金山就是真金白银”有何看法?25.你对“贫富分化是经济发展必然现象”有何看法?26.谈一谈你对自主招生的看法。
时事热点——中国传媒大学今年中国传媒大学的自招面试,考生被问的最多的就是时政和社会热点,真不愧为传媒大学。
清华大学自主招生考试精彩试题(语文+数学+化学+物理)

2010清华大学自主招生考试试题(语文+数学+化学+物理)分两天1月1日上午9:00-12:00 中英文综合 200分下午2:00-3:30 数学 100分下午4:00-5:30 物理 100分1月2日上午9:00-12:00 理科综合 300分,数学物理化学各100分中英文综合题型分值第一部分英语基础(40分)单选词汇(1分×10)单元语法与词汇(1分×10)完形填空(1分×20)第二部分英语阅读(2分×20=40分)共8篇左右,每篇后2至3个单选题。
内容基本为美国文化政治第三部分中文(94分)4篇文章,后面分5大题:每篇的阅读理解题,第五大题为新词解释与作文第四部分中英文综合应用(26分)给一段文言文,翻译成中文(6分),用英文概括大意并评论(20分)第一部分英语基础(略)第二部分英语阅读(略)第三部分中文(全)白居易的粉丝李国文中国文学,一直有大众化和小众化的分野。
唐代的白居易,则是最能代表中国文学大众化的典型诗人。
白居易,生于公元772年(唐代宗大历七年),终于公元846年(唐武宗会昌六年),活了74岁。
经历顺宗、宪宗、穆宗、敬宗、文宗、武宗六朝。
无论当时,无论后世,谈及这位诗人,离不开以下三点:一,他在诗坛领袖群伦,推动潮流的地位;二,他在朝野引起轰动,遐迩知名的程度;三,作为诗人,他在当时中国人之大多数心目中的无与伦比的尊崇,非同凡响的声望,他的粉丝,可以说是举国上下,遍地皆是,大江南北,无处不在,这也许是最值得大书而特书的中国文学的“白居易现象”。
他的朋友元稹为他的诗集《白氏长庆集》序中,这样写道:“二十年间,禁省、观寺、邮候、墙壁之上无不书,王公、妾妇、马走之口无不道。
缮写模勒,炫卖于市井中,或持之以交酒茗者,处处皆是。
”明人胡震享的《唐音癸签》一书中引《丰年录》:“开成中,物价至贱,村路卖鱼肉者,俗人买以胡绡半尺,士大夫买以乐天诗。
”白居易的一首诗,竟可以换来一条胖头鱼,一方五花肉,我估计当代诗人的作品,怕难以卖出这样的高价来。
2015年各高校自主招生考试试题综述

2015年各高校自主招生考试试题回忆录一、北京大学今年北大自招太过亲民,遇到这样的自招题你敢想?一句周杰伦《青花瓷》里的歌词,问描述的是什么?答案有“青花瓷”、“青花盆”和“青花瓶”,你觉得选什么呢……北大语文试题只有一道题目,要求根据孟子《生于忧患死于安乐》和庄子《人间世》这两个材料,写一篇文章。
英语有阅读材料涉及美国白人警察枪杀黑人、贵州省一教育基金会受“郭美美事件”影响遭遇零捐助等时事热点。
面试部分考题:1.用一条长度一定的的绳子围成一个n边形,怎样围才能使围出的的n边形面积最大?2.后轮驱动的车辆,起动和刹车时,分别是车头翘起还是车尾翘起?判断并说明理由。
3.如何看待微信在人际交往中的作用?4.如何看待欧洲历史上的分与合?5.北京和张家口联合申办冬奥会面临哪些机遇和挑战?6.请用三个词概括中国传统文化,并谈谈中国文化如何真正“走出去”。
7.怎么看待追求财富导致雾霾的说法8.请谈一下动物迁徙的意义?9.谈谈你对嘀嘀打车与专车经营的看法。
10.你认为的文学阅读的最高境界是什么?11.请谈有教无类与因材施教的关系。
12.请谈你对国企高管限薪令的看法。
13.有人提议将网络战归为武力冲突,谈谈你的看法。
14.谈谈你对亚投行的看法。
15.有人提议在基础教育阶段实施男女分开管理,即开办男校和女校,谈谈你的看法。
16.谈一谈信仰、义务、责任的关系。
17.爱因斯坦说:“简单是科学追求的伟大目标。
”谈谈你的看法。
18.请你设计一下中国的养老体系?19.你如何看待就医不要钱这种理想设计?20.谈一谈你对批判性思维和惯性思维的关系的理解。
21.谈一谈你所认识的经济全球化下中国的粮食问题。
22.谈一谈自我意识?23.有人说在全球化背景下我国粮食安全已经不是一个问题,你怎么看?24.你对“绿水金山就是真金白银”有何看法?25.你对“贫富分化是经济发展必然现象”有何看法?26.谈一谈你对自主招生的看法。
二、2015年北京大学自主招生“博雅人才培养计划”部分面试题1.北京申办冬奥会有哪些机遇和挑战2.如何治理雾霾,有何建议3.中国传统文化将如何走出去4.微信在人际交往中的作用5.欧洲历史上的分与合6.如何看待中国申请冬奥会面试分为两个阶段,第二阶段为一对一考察理科生需在45分钟内,尝试解答一道物理题和一道数学题,然后分别接受一名物理考官和一名数学考官的一对一考察。
清华大学自主招生笔试面试真题

清华大学自主招生笔试面试真题自主招生考试中,笔试和面试是考生和家长最为关注的,而每年都有关于自主招生脑洞大开的题目,大家很好奇自主招生考试都考什么?下面是清华大学自主招生部分笔试面试真题,仅供参考。
笔试题型:理科:数学30题,物理20题,化学18题,一共68题,180分钟合在一起考的。
文科:数学35题,语文12题,历史20题。
众多考生表示,本次数学试题较易,物理难度较大,化学正常。
刘震介绍,今年,清华自主选拔的初试依旧采取机考形式,全部为客观选择题,直接在计算机上做答。
根据去年的探索经验,机考不仅能保证阅卷及时准确,而且也大大降低了纸质试卷作弊的可能性,分发和回收考卷更为安全高效。
文科综合文史类笔试试题:考题有明清时的自然经济瓦解、抗日战争、诗词等内容,不是考知识点记忆,主要考查阅读面、逻辑思维深度等,数学与逻辑难度较大。
今年的语文试题对语文基础知识与运用能力提出了更高要求,材料多出自社会热点或经典著作,注重对知识联系实际、学以致用能力的考查;注重考查对经典或常识的精准理解,注重对独立思考与批判思维的考查。
化学试题成为新考查内容今年化学成为新考查内容。
刘震表示,新增化学试题注重对学科基础内容的考查、综合多模块内容、加强化学学科的应用性、创新试题的设问模式,充分体现化学学科的学术价值,考查了考生的基础知识、综合能力、科学素养和创新精神,关注环境问题,讨论产生酸雨的原因及危害、食品中的增塑剂与人体健康等社会焦点问题。
物理试题注重基本概念的准确理解和灵活运用。
通过采用单选和多选题随机编排的方式,来考查学生构建正确、合理的物理模型,综合运用物理知识分析、解决实际问题的能力,同时增加了能力考查的区分度。
除了定量的分析和计算外,试题还设置了部分内容来考查学生运用物理学基本原理来定性和半定量分析问题的能力。
化学:涉及空气污染的比较多,还有大学的有机化学,如:哪些气体会导致空气污染,测出其中含量?地球的臭氧含量以及造成大气污染的元素?;化学有一道是高考原题。
清华大学2015年自主招生数学试题及答案解析
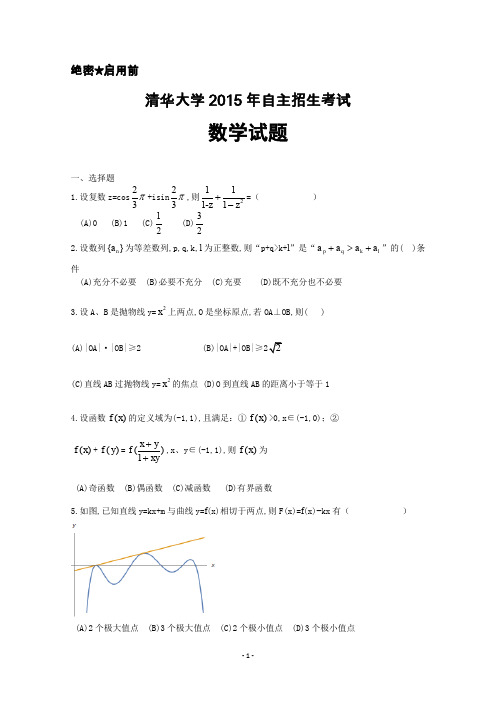
绝密★启用前清华大学2015年自主招生考试数学试题一、选择题1.设复数z=cos 23π+isin 23π,则2111-1z z +-=( ) (A)0 (B)1 (C)12 (D)32 2.设数列{}n a 为等差数列,p,q,k,l 为正整数,则“p+q>k+l ”是“p q k l a a a a +>+”的( )条件(A)充分不必要 (B)必要不充分 (C)充要 (D)既不充分也不必要3.设A 、B 是抛物线y=2x 上两点,O 是坐标原点,若OA ⊥OB,则( )(A)|OA|·|OB|≥2 (B)|OA|+|OB|≥(C)直线AB 过抛物线y=2x 的焦点 (D)O 到直线AB 的距离小于等于1 4.设函数()f x 的定义域为(-1,1),且满足:①()f x >0,x ∈(-1,0);②()f x +()f y =()1x y f xy++,x 、y ∈(-1,1),则()f x 为 (A)奇函数 (B)偶函数 (C)减函数 (D)有界函数5.如图,已知直线y=kx+m 与曲线y=f (x)相切于两点,则F(x)=f (x)−kx 有( )(A)2个极大值点 (B)3个极大值点 (C)2个极小值点 (D)3个极小值点6.△ABC 的三边分别为a 、b 、c .若c=2,∠C=3π,且sinC+sin(B −A)−2sin2A=0,则有( )(A)b=2a (B)△ABC 的周长为 (C)△ABC (D)△ABC 的外接圆半径为7.设函数2()(3)x f x x e =-,则( )(A)()f x 有极小值,但无最小值 (B) ()f x 有极大值,但无最大值(C)若方程()f x =b 恰有一个实根,则b>36e (D)若方程()f x =b 恰有三个不同实根,则0<b<36e 8.已知A={(x,y)∣222x y r +=},B={(x,y)∣222()()x a y b r -+-=,已知A∩B={(11,x y ),(22,x y )},则( )(A)0<22a b +<22r (B)1212()(y )0a x x b y -+-=(C)12x x +=a ,12y y +=b (D)22a b +=1122ax by +9.已知非负实数x,y,z 满足22244x y z +++2z=3,则5x+4y+3z 的最小值为( )(A)1 (B)2 (C)3 (D)410.设数列{n a }的前n 项和为n S ,若对任意正整数n,总存在正整数m,使得n S =m a ,则( )(A ){n a }可能为等差数列 (B ){n a }可能为等比数列(C ){n a }的任意一项均可写成{n a }的两项之差(D)对任意正整数n,总存在正整数m,使得n a =m S11.运动会上,有6名选手参加100米比赛,观众甲猜测:4道或5道的选手得第一名;观众乙猜测:3道的选手不可能得第一名;观众丙猜测:1,2,6道选手中的一位获得第一名;观众丁猜测:4,5,6道的选手都不可能获得第一名.比赛后发现没有并列名次,且甲、乙、丙、丁中只有1人猜对比赛结果,此人是( )(A)甲 (B)乙 (C)丙 (D)丁12.长方体ABCD −1111A B C D 中,AB=2,AD=A 1A =1,则A 到平面1A BD 的距离为( )。
清华大学自主招生试题 数学 Word版含解析

一、选择题1.设复数z=cos 23π+isin 23π,则2111-1z z +-=( ) (A)0 (B)1 (C)12 (D)322.设数列{}n a 为等差数列,p,q,k,l 为正整数,则“p+q>k+l ”是“p q k l a a a a +>+”的( )条件(A)充分不必要 (B)必要不充分 (C)充要 (D)既不充分也不必要 3.设A 、B 是抛物线y=2x 上两点,O 是坐标原点,若OA ⊥OB,则( )(A)|OA|·|OB|≥2 (B)|OA|+|OB|≥22(C)直线AB 过抛物线y=2x 的焦点 (D)O 到直线AB 的距离小于等于14.设函数()f x 的定义域为(-1,1),且满足:①()f x >0,x ∈(-1,0);②()f x +()f y =()1x yf xy++,x 、y ∈(-1,1),则()f x 为 (A)奇函数 (B)偶函数 (C)减函数 (D)有界函数5.如图,已知直线y=kx+m 与曲线y=f (x)相切于两点,则F(x)=f (x)−kx 有( )(A)2个极大值点 (B)3个极大值点 (C)2个极小值点 (D)3个极小值点 6.△ABC 的三边分别为a 、b 、c .若c=2,∠C=3π,且sinC+sin(B −A)−2sin2A=0,则有( ) (A)b=2a (B)△ABC 的周长为3 (C)△ABC 的面积为33(D)△ABC 的外接圆半径为337.设函数2()(3)xf x x e =-,则( )(A)()f x 有极小值,但无最小值 (B) ()f x 有极大值,但无最大值 (C)若方程()f x =b 恰有一个实根,则b>36e(D)若方程()f x =b 恰有三个不同实根,则0<b<36e 8.已知A={(x,y)∣222x y r +=},B={(x,y)∣222()()x a y b r -+-=,已知A∩B={(11,x y ),(22,x y )},则( )(A)0<22a b +<22r (B)1212()(y )0a x x b y -+-= (C)12x x +=a ,12y y +=b (D)22a b +=1122ax by +9.已知非负实数x,y,z 满足22244x y z +++2z=3,则5x+4y+3z 的最小值为( ) (A)1 (B)2 (C)3 (D)410.设数列{n a }的前n 项和为n S ,若对任意正整数n ,总存在正整数m ,使得n S =m a ,则( )(A ){n a }可能为等差数列 (B ){n a }可能为等比数列(C ){n a }的任意一项均可写成{n a }的两项之差(D)对任意正整数n ,总存在正整数m ,使得n a =m S11.运动会上,有6名选手参加100米比赛,观众甲猜测:4道或5道的选手得第一名;观众乙猜测:3道的选手不可能得第一名;观众丙猜测:1,2,6道选手中的一位获得第一名;观众丁猜测:4,5,6道的选手都不可能获得第一名.比赛后发现没有并列名次,且甲、乙、丙、丁中只有1人猜对比赛结果,此人是( ) (A)甲 (B)乙 (C)丙 (D)丁12.长方体ABCD −1111A B C D 中,AB=2,AD=A 1A =1,则A 到平面1A BD 的距离为( )(A)13 (B)23(C)22 (D)6313.设不等式组||||22(1)x y y k x +≤⎧⎨+≤+⎩所表示的区域为D ,其面积为S ,则( )(A)若S=4,则k 的值唯一 (B)若S=12,则k 的值有2个(C)若D 为三角形,则0<k ≤23(D)若D 为五边形,则k>4 14.△ABC 的三边长是2,3,4,其外心为O ,则OA AB OB BC OC CA ⋅+⋅+⋅=( ) (A)0 (B)−15 (C)−212(D)−29215.设随机事件A 与B 互相独立,且P(B)=0.5,P(A −B)=0.2,则( )(A)P(A)=0.4 (B)P(B −A)=0.3 (C)P(AB)=0.2 (D)P(A+B)=0.916.过△ABC 的重心作直线将△ABC 分成两部分,则这两部分的面积之比的( ) (A)最小值为34 (B)最小值为45 (C)最大值为43 (D 最大值为5417.从正15边形的顶点中选出3个构成钝角三角形,则不同的选法有( )(A)105种 (B)225种 (C)315种 (D)420种18.已知存在实数r ,使得圆周222x y r +=上恰好有n 个整点,则n 可以等于( ) (A)4 (B)6 (C)8 (D)12 19.设复数z 满足2|z|≤|z −1|,则( ) (A)|z|的最大值为1 (B)|z|的最小值为13 (C)z 的虚部的最大值为23(D)z 的实部的最大值为1320.设m,n 是大于零的实数,a =(mcosα,msinα),b =(ncosβ,nsinβ),其中α,β∈[0,2π)α,β∈[0,2π).定义向量12a =(2m α2m α),12b =(2n β2n β),记θ=α−β,则( )(A)12a ·12a =a (B)1122a b ⋅=2mn θ(C)112222||44a b mn θ-≥(D)112222||44a b mn θ+≥21.设数列{n a }满足:1a =6,13n n n a a n++=,则( ) (A)∀n ∈N ∗,n a <3(1)n + (B)∀n ∈N ∗,n a ≠2015 (C)∃n ∈N ∗,n a 为完全平方数 (D)∃n ∈N ∗, n a 为完全立方数 22.在极坐标系中,下列方程表示的图形是椭圆的有( ) (A )ρ=1cos sin θθ+ (B )ρ=12sin θ+ (C )ρ=12cos θ- (D )ρ=112sin θ+23.设函数2sin ()1xf x x x π=-+,则( )(A )()f x ≤43(B)|()f x |≤5|x| (C)曲线y=()f x 存在对称轴 (D)曲线y=()f x 存在对称中心24.△ABC 的三边分别为a ,b,c ,若△ABC 为锐角三角形,则( ) (A)sinA>cosB (B)tanA>cotB (C)222a b c +> (D)333a b c +>25.设函数()f x 的定义域是(−1,1),若(0)f =(0)f '=1,则存在实数δ∈(0,1),使得( ) (A)()f x >0,x ∈(−δ,δ) (B)()f x 在(−δ,δ)上单调递增 (C)()f x >1,x ∈(0,δ) (D)()f x >1,x ∈(−δ,0)26.在直角坐标系中,已知A(−1,0),B(1,0).若对于y 轴上的任意n 个不同的点k P (k=1,2,…,n),总存在两个不同的点i P ,j P ,使得|sin ∠A i P B −sin ∠A j P B|≤13,则n 的最小值为( )(A)3 (B)4 (C)5 (D)627.设非负实数x,y 满足2x+y=1,则22x y + )(A)最小值为45 (B)最小值为25(C)最大值为1 (D)最大值为12328.对于50个黑球和49个白球的任意排列(从左到右排成一行),则( )(A)存在一个黑球,它右侧的白球和黑球一样多 (B)存在一个白球,它右侧的白球和黑球一样多(C)存在一个黑球,它右侧的白球比黑球少一个 (D)存在一个白球,它右侧的白球比黑球少一个29.从1,2,3,4,5中挑出三个不同数字组成五位数,其中有两个数字各用两次,例如12231,则能得到的不同的五位数有( ) (A)300个 (B)450个 (C)900个 (D)1800个30.设曲线L 的方程为42242(22)(2)y x y x x +++-=0,则( ) (A)L 是轴对称图形 (B)L 是中心对称图形 (C)L ⊂{(x,y)∣22x y +≤1} (D)L ⊂{(x,y)∣−12≤y ≤12} ##Answer## 1.【解析】2111-1z z +-=211-zz z zz z +-=11-z z z z +-=22cos sin 1332221-cos sin 2sin 333i i i πππππ-+--=212sin 2sincos333i πππ-⋅-22cos()sin()333(cossin )22i i ππππ-+-+ =cos 0sin 02sin [cos()sin()]366i i πππ+-+-77)sin()]663i ππ-+- 31sin )6623i i ππ+=1,选B2.【简解】 ()p q k l a a a a +-+=[(p+q)-(k+l)]d ,与公差d 的符号有关,选D3.【解析】设A(211,x x ),B(222,x x ),OA OB ⋅=1212(1)x x x x +=0⇒211x x =-答案(A),||||OA OB ⋅2211221111(1)(1)x x x x ++2121111x x +++11122||||x x +⋅=2,正确;答案(B),|OA|+|OB|≥2||||OA OB ⋅22,正确;答案(C),直线AB 的斜率为222121x x x x --=21x x +=111x x - 方程为y-21x =(111x x -)(x-1x ),焦点(0,14)不满足方程,错误;答案(D),原点到直线AB :(111x x -)x-y+1=0的距离2111()1x x -+1,正确。
[精选]近年北大清华自主招生试题(化学)资料
![[精选]近年北大清华自主招生试题(化学)资料](https://img.taocdn.com/s3/m/8078f0482af90242a895e5de.png)
北京大学2015自主招生化学试题1填充题(1)在NaCl的溶液里有Mg2+(NaOH),SO42-(BaCl2),Ca2+(Na2CO3)等杂质离子,括号中是除杂的试剂,加入试剂的顺序为(2)电解熔融LiCl,得到Li和Cl2。
将1mol•L-1LiCl的溶液加热蒸干,得到固体,电解熔融固体,阳极出的并不是Cl2,为什么?(3)Ag为什么能置换出HI(aq)和H2S(aq)中的氢?(4)给一个物质的结构简式,写出合成尼龙-6的方程式(5)给单体结构简式,写出三聚的结构简式(三聚氰胺)。
写出由尿素合成三聚氰胺的方程式(6)给出NaCl的溶解热,Na变成离子的能量变化及Cl变成离子的能量变化,问根据数据能得出什么?(7)已知NH4A(A为酸根)受热分解是质子转移,若A为氧化性酸根,分解时还有氧化还原反应。
试写出NH4NO2,NH4Cr2O7,NH4MnO4分解的方程式2 简答题(1)将足量的Zn加入1mol•L-1的HCl和HAc溶液中。
试解释释氢气的速率不同,释氢气的量不同(2)向Na2S,Na2CO3溶液中通入SO2以制备Na2S2O3•5H2O,1.通入一段时间后,生成沉淀,2.继续通入SO2,沉淀逐渐消失直至溶液澄清,3.再通入SO2,又生成沉淀,此时,加热浓缩冷却结晶过滤,得到Na2S2O3•5H2O。
1写出各步反应的方程2原溶液中Na2S,Na2CO3的物质的量之比为多少时,适合生成Na2S2O3•5H2O(3)向Na2HPO4溶液中滴加AgNO3,生成黄色沉淀。
已知Ag3PO4和Ag2HPO4沉淀均为黄色,试用(普通)实验方法检验出沉淀的成分(4)1写出H2O的结构简式2写出H2O作为溶剂的特点3写出有H2O参加的两种不同类型反应的化学方程式北京大学2014年自主招生试题1.Ca在空气中燃烧的固体产物溶于水,放热,放出有臭味的气体,写出方程式。
2.同样浓度下,醋酸和氨水的电离程度相同,但氢氧化铝可以完全溶于醋酸,却不能溶于氨水,问这能说明氢氧化铝的什么性质?3.和水一样,酯也可以在氨中发生氨解反应,写出RCOOR'的氨解反应方程式。
近年北大清华自主招生试题(化学)

1填充题(1)在NaCl的溶液里有Mg2+(NaOH),SO42-(BaCl2),Ca2+(Na2CO3)等杂质离子,括号中是除杂的试剂,加入试剂的顺序为(2)电解熔融LiCl,得到Li和Cl2。
将1mol•L-1LiCl的溶液加热蒸干,得到固体,电解熔融固体,阳极出的并不是Cl2,为什么?(3)Ag为什么能置换出HI(aq)和H2S(aq)中的氢?(4)给一个物质的结构简式,写出合成尼龙-6的方程式(5)给单体结构简式,写出三聚的结构简式(三聚氰胺)。
写出由尿素合成三聚氰胺的方程式(6)给出NaCl的溶解热,Na变成离子的能量变化及Cl变成离子的能量变化,问根据数据能得出什么?(7)已知NH4A(A为酸根)受热分解是质子转移,若A为氧化性酸根,分解时还有氧化还原反应。
试写出NH4NO2,NH4Cr2O7,NH4MnO4分解的方程式2 简答题(1)将足量的Zn加入1mol•L-1的HCl和HAc溶液中。
试解释释氢气的速率不同,释氢气的量不同(2)向Na2S,Na2CO3溶液中通入SO2以制备Na2S2O3•5H2O,1.通入一段时间后,生成沉淀,2.继续通入SO2,沉淀逐渐消失直至溶液澄清,3.再通入SO2,又生成沉淀,此时,加热浓缩冷却结晶过滤,得到Na2S2O3•5H2O。
1写出各步反应的方程2原溶液中Na2S,Na2CO3的物质的量之比为多少时,适合生成Na2S2O3•5H2O(3)向Na2HPO4溶液中滴加AgNO3,生成黄色沉淀。
已知Ag3PO4和Ag2HPO4沉淀均为黄色,试用(普通)实验方法检验出沉淀的成分(4)1写出H2O的结构简式2写出H2O作为溶剂的特点3写出有H2O参加的两种不同类型反应的化学方程式1.Ca在空气中燃烧的固体产物溶于水,放热,放出有臭味的气体,写出方程式。
2.同样浓度下,醋酸和氨水的电离程度相同,但氢氧化铝可以完全溶于醋酸,却不能溶于氨水,问这能说明氢氧化铝的什么性质?3.和水一样,酯也可以在氨中发生氨解反应,写出RCOOR'的氨解反应方程式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题1.设复数z=cos 23π+isin 23π,则2111-1z z +-=( ) (A)0 (B)1 (C)12 (D)322.设数列{}n a 为等差数列,p,q,k,l 为正整数,则“p+q>k+l ”是“p q k l a a a a +>+”的( )条件 (A)充分不必要 (B)必要不充分 (C)充要 (D)既不充分也不必要3.设A 、B 是抛物线y=2x 上两点,O 是坐标原点,若OA ⊥OB,则( )(A)|OA|·|OB|≥2 (B)|OA|+|OB|≥22(C)直线AB 过抛物线y=2x 的焦点 (D)O 到直线AB 的距离小于等于14.设函数()f x 的定义域为(-1,1),且满足:①()f x >0,x ∈(-1,0);②()f x +()f y =()1x yf xy++,x 、y ∈(-1,1),则()f x 为(A)奇函数 (B)偶函数 (C)减函数 (D)有界函数5.如图,已知直线y=kx+m 与曲线y=f (x)相切于两点,则F(x)=f (x)−kx 有( )(A)2个极大值点 (B)3个极大值点 (C)2个极小值点 (D)3个极小值点 6.△ABC 的三边分别为a 、b 、c .若c=2,∠C=3π,且sinC+sin(B −A)−2sin2A=0,则有( ) (A)b=2a (B)△ABC 的周长为3△ABC 23(D)△ABC 237.设函数2()(3)xf x x e =-,则( )(A)()f x 有极小值,但无最小值 (B) ()f x 有极大值,但无最大值 (C)若方程()f x =b 恰有一个实根,则b>36e (D)若方程()f x =b 恰有三个不同实根,则0<b<36e8.已知A={(x,y)∣222x y r +=},B={(x,y)∣222()()x a y b r -+-=,已知A∩B={(11,x y ),(22,x y )},则( )(A)0<22a b +<22r (B)1212()(y )0a x x b y -+-= (C)12x x +=a ,12y y +=b (D)22a b +=1122ax by +9.已知非负实数x,y,z 满足22244x y z +++2z=3,则5x+4y+3z 的最小值为( ) (A)1 (B)2 (C)3 (D)410.设数列{n a }的前n 项和为n S ,若对任意正整数n ,总存在正整数m ,使得n S =m a ,则( ) (A ){n a }可能为等差数列 (B ){n a }可能为等比数列(C ){n a }的任意一项均可写成{n a }的两项之差(D)对任意正整数n ,总存在正整数m ,使得n a =m S 11.运动会上,有6名选手参加100米比赛,观众甲猜测:4道或5道的选手得第一名;观众乙猜测:3道的选手不可能得第一名;观众丙猜测:1,2,6道选手中的一位获得第一名;观众丁猜测:4,5,6道的选手都不可能获得第一名.比赛后发现没有并列名次,且甲、乙、丙、丁中只有1人猜对比赛结果,此人是( )(A)甲 (B)乙 (C)丙 (D)丁12.长方体ABCD −1111A B C D 中,AB=2,AD=A 1A =1,则A 到平面1A BD 的距离为( )(A)13 (B)23(C)2 (D)313.设不等式组||||22(1)x y y k x +≤⎧⎨+≤+⎩所表示的区域为D ,其面积为S ,则( )(A)若S=4,则k 的值唯一 (B)若S=12,则k 的值有2个 (C)若D 为三角形,则0<k ≤23(D)若D 为五边形,则k>4 14.△ABC 的三边长是2,3,4,其外心为O ,则OA AB OB BC OC CA ⋅+⋅+⋅=( ) (A)0 (B)−15 (C)−212(D)−29215.设随机事件A 与B 互相独立,且P(B)=0.5,P(A −B)=0.2,则( )(A)P(A)=0.4 (B)P(B −A)=0.3 (C)P(AB)=0.2 (D)P(A+B)=0.916.过△ABC 的重心作直线将△ABC 分成两部分,则这两部分的面积之比的( ) (A)最小值为34 (B)最小值为45 (C)最大值为43 (D 最大值为5417.从正15边形的顶点中选出3个构成钝角三角形,则不同的选法有( )(A)105种 (B)225种 (C)315种 (D)420种18.已知存在实数r ,使得圆周222x y r +=上恰好有n 个整点,则n 可以等于( )(A)4 (B)6 (C)8 (D)12 19.设复数z 满足2|z|≤|z −1|,则( ) (A)|z|的最大值为1 (B)|z|的最小值为13 (C)z 的虚部的最大值为23 (D)z 的实部的最大值为1320.设m,n 是大于零的实数,a =(mcosα,msinα),b =(ncosβ,nsinβ),其中α,β∈[0,2π)α,β∈[0,2π).定义向量12a =(2α2α),12b =(2β2β),记θ=α−β,则( )(A)12a ·12a =a (B)1122a b ⋅=2θ(C)112222||44a b mn θ-≥ (D)112222||44a b mn θ+≥21.设数列{n a }满足:1a =6,13n n n a a n++=,则( ) (A)∀n ∈N ∗,n a <3(1)n + (B)∀n ∈N ∗,n a ≠2015 (C)∃n ∈N ∗,n a 为完全平方数 (D)∃n ∈N ∗, n a 为完全立方数 22.在极坐标系中,下列方程表示的图形是椭圆的有( )(A )ρ=1cos sin θθ+ (B )ρ=12sin θ+ (C )ρ=12cos θ- (D )ρ=112sin θ+23.设函数2sin ()1xf x x x π=-+,则( )(A )()f x ≤43(B)|()f x |≤5|x| (C)曲线y=()f x 存在对称轴 (D)曲线y=()f x 存在对称中心24.△ABC 的三边分别为a ,b,c ,若△ABC 为锐角三角形,则( )(A)sinA>cosB (B)tanA>cotB (C)222a b c +> (D)333a b c +>25.设函数()f x 的定义域是(−1,1),若(0)f =(0)f '=1,则存在实数δ∈(0,1),使得( ) (A)()f x >0,x ∈(−δ,δ) (B)()f x 在(−δ,δ)上单调递增 (C)()f x >1,x ∈(0,δ) (D)()f x >1,x ∈(−δ,0)26.在直角坐标系中,已知A(−1,0),B(1,0).若对于y 轴上的任意n 个不同的点k P (k=1,2,…,n),总存在两个不同的点i P ,j P ,使得|sin ∠A i P B −sin ∠A j P B|≤13,则n 的最小值为( ) (A)3 (B)4 (C)5 (D)627.设非负实数x,y 满足2x+y=1,则的( )(A)最小值为45 (B)最小值为25(C)最大值为1 (D)28.对于50个黑球和49个白球的任意排列(从左到右排成一行),则( )(A)存在一个黑球,它右侧的白球和黑球一样多 (B)存在一个白球,它右侧的白球和黑球一样多 (C)存在一个黑球,它右侧的白球比黑球少一个 (D)存在一个白球,它右侧的白球比黑球少一个 29.从1,2,3,4,5中挑出三个不同数字组成五位数,其中有两个数字各用两次,例如12231,则能得到的不同的五位数有( )(A)300个 (B)450个 (C)900个 (D)1800个30.设曲线L 的方程为42242(22)(2)y x y x x +++-=0,则( ) (A)L 是轴对称图形 (B)L 是中心对称图形 (C)L ⊂{(x,y)∣22x y +≤1} (D)L ⊂{(x,y)∣−12≤y ≤12} ##Answer##1.【解析】 2111-1z z +-=211-zz z zz z +-=11-z z z z +-=22cos sin 1332221-cos sin 2sin 333i i i πππππ-+-- =212sin 2sincos333i πππ-⋅-22cos()sin()33sin )22i i ππππ-+-+ =cos 0sin 02sin [cos()sin()]366i i πππ+-+-77)sin()]66i ππ-+-1sin )6622i i ππ++-=1,选B2.【简解】 ()p q k l a a a a +-+=[(p+q)-(k+l)]d ,与公差d 的符号有关,选D3.【解析】设A(211,x x ),B(222,x x ),OA OB ⋅=1212(1)x x x x +=0⇒211x x =-答案(A),||||OA OB ⋅=≥=2,正确;答案(B),|OA|+|OB|≥,正确;答案(C),直线AB 的斜率为222121x x x x --=21x x +=111x x - 方程为y-21x =(111x x -)(x-1x ),焦点(0,14)不满足方程,错误;答案(D),原点到直线AB :(111x x -)x-y+1=0的距离≤1,正确。
选ABD4.【解析】x=y=0⇒(0)f =0,y=-x ⇒()()f x f x -=-,()f x 为奇函数,(A)正确;()f x ≡0,(B)错误;12x x <,1()f x -2()f x =1()f x +2()f x -=12121x x f x x ⎛⎫- ⎪-⎝⎭>0⇒1()f x >2()f x ⇒()f x ↓,(C)正确;()f x =-tan2x π满足已知条件,但无界,(D)错误。
选A,C 5.【简解】将直线平移知:斜率为k 的直线,与曲线y=()f x 至多有五个公共点,其中在此直线先下方后上方的两个区间,先上方后下方的三个区间,故()F x 有三个极大值点,两个极小值点。
选BC6.【解析】2R=sin c C =43⇒R=233,D 正确; 又sinC+sin(B-A)=sin(B+A)+sin(B-A)=2sinBcosA=2sin2A=4sinAcosA ⇒cosA=0或sinB=2sinA ⇒A=2π或b=2a ; A=2π时,b=233, a =433,周长为2+3,面积为233;b=2a 时,2c =222cos a b ab C +-⇒a =233,B=2π,同样有周长为2+3,面积为233。
