长春工业大学物理答案光刚体c 3-5
长春工业大学物理答案光稳恒磁场c8-11

练习八 电流的磁场(一)1.一无限长直导线abcde 弯成图8-1所示的形状,中部bcd 是半径为R 、对圆心O 张角为1200的圆弧,当通以电流I 时,O 处磁感应强度的在大小B=RI06336μππ+-,方向为垂直纸面向里2.如图8-2所示,均匀磁场的磁感应强度为B =0.2T ,方向沿x 轴正方向,则通过abod 面的磁通量为_________,通过befo 面的磁通量为__________,通过aefd 面的磁通量为_______。
3.(2)两个载有相等电流I的圆圈,半径均为R,一个水平放置,另一个竖直放置,如图8-3所示,则圆心处磁感应强度的大小为:4.(4)如图8-4所示,在无限长载流导线附近作一球形闭合曲面S,当面S向长直导线靠近的过程中,穿过S的磁通量Φ及面上任一点P的磁感应强度大小B的变化为:(1)Φ增大,B增大;(2)Φ不变,B不变;(3)Φ增大,B不变;(4)Φ不变,B增大。
5.(1)磁场的高斯定理说明了下面的哪些叙述是正确的?a 穿入闭合曲面的磁感应线条数必然等于穿出的磁感应线条数;b 穿入闭合曲面的磁感应线条数不等于穿出的磁感应线条数;c 一根磁感应线可以终止在闭合曲面内;d 一根磁感应线可以完全处于闭合曲面内。
(1)ad ; (2)ac ; (3)cd ; (4)ab 。
6.真空中的两根无限长直载流通导线L 1和L 2相互平行放置,I 1=20A ,I 2=10A ,如图所示,A 、B 两点与两导线共面,a=0.05m 。
求:(1)A 、B 两点处的磁感应强度B 1和B 2;(2)磁感应强度为零的位置。
解:以×为正,(1)7042010104102.122--⨯=⨯⨯=+=πμπμπμT a I a I B A T aI a I B B 520101033.1232-⨯=-⋅=πμπμ (2)经过分析,磁感应强度为零的点应该在L 2的下方,假设到L 2的距离为xma x xI a x I 1.022)2(202010==++⋅-=πμπμ7.两平行长直导线相距d=40cm,通过导线的电流I1=I2=20A,电流流向如图所示。
高二物理3-5试卷含答案

高二物理月考试卷一、单项选择题(每题只有一个正确选项,每题4分)1.关于物体的动量,下列说法中正确的是 ( ). A .物体的动量越大,其惯性也越大 B .同一物体的动量越大,其速度一定越大 C .物体的加速度不变,其动量一定不变 D .运动物体在任一时刻的动量方向一定是该时刻的位移方向2.在光电效应实验中,用单色光照射某种金属表面,有光电子逸出,则光电子的最大初动能取决于入射光的 ( ). A .频率 B .强度 C .照射时间 D .光子数目3.有一束紫外线照射某金属时不能产生光电效应,可能使该金属产生光电效应的措施是 ( ). A .改用频率更小的紫外线照射 B .改用频率更大X 射线照射 C .改用强度更大的原紫外线照射 D .延长原紫外线的照射时间 4.A 球的质量是m ,B 球的质量是2m ,它们在光滑的水平面上以相同的动量运动.B 在前,A 在后,发生正碰后,A 球仍朝原方向运动,但其速率是原来的一半,碰后两球的速率比vA ′∶vB ′为 ( ). A .1∶2 B .1∶3 C .2∶1 D .2∶35.质量为m 1、m 2的两物体,分别受到不同的恒力F 1、F 2的作用,由静止开始运动,下列说法正确的是 ( ).A .若在相同位移内它们动量变化相同,则F 1F 2=m 1m 2B .若在相同位移内它们动能变化相同,则F 1F 2= m 2m 1C .若在相同时间内它们动能变化相同,则F 1F 2=m 2m 1D .若在相同时间内它们动能变化相同,则F 1F 2= m 1m 26.质量为m 、速度为v 的A 球与质量为3m 的静止B 球发生正碰.碰撞可能是弹性的,也可能是非弹性的,因此,碰撞后B 球的速度可能有不同的值.碰撞后B 球的速度大小可能是 ( ). A .0.6v B .0.4v C .0.2v D .v7.如图1-3所示,一铁块压着一纸条放在水平桌面上,当以速度v 抽出纸条后,铁块掉在地上的P 点.若以2v 速度抽出纸条,则铁块落地点为 ( ).A .仍在P 点B .在P 点左边C .在P 点右边不远处D .在P 点右边原水平位移的两倍处8.载人气球原静止于高h 的空中,气球质量为M ,人的质量为m 。
长春工业大学物理化学考试题及答案
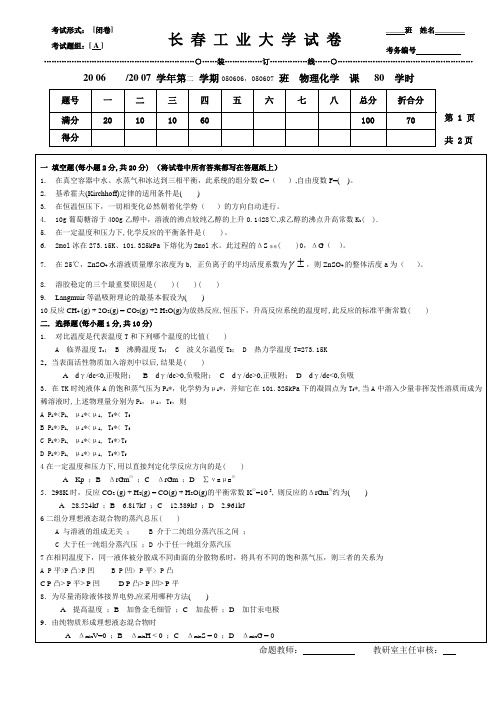
)
波义尔温度 TB; D
2.当表面活性物质加入溶剂中以后,结果是( A dγ /dc<0,正吸附;
B dγ /dc>0,负吸附; C dγ /dc>0,正吸附; D dγ /dc<0,负吸
3.在 TK 时纯液体 A 的饱和蒸气压为 PA*,化学势为μ A*,并知它在 101.325kPa 下的凝固点为 Tf*,当 A 中溶入少量非挥发性溶质而成为 稀溶液时,上述物理量分别为 PA,μ A,Tf,则 A PA*<PA, μ A*<μ A, Tf*< Tf B PA*>PA, μ A*<μ A, Tf*< Tf C PA*>PA, μ A*<μ A, Tf*>Tf D PA*>PA, μ A*>μ A, Tf*>Tf 4 在一定温度和压力下,用以直接判定化学反应方向的是( A Kp ;B Δ rGm ;C
-1
。
⊙
)
⊙
Δ rGm ;D
∑ν Bμ
B
⊙ ⊙
5.298K 时,反应 CO2 (g) + H2(g) = CO(g) + H2O(g)的平衡常数 K =10-5, 则反应的Δ rGm 约为( A 28.524kJ ;B 6.817kJ ;C 6 二组分理想液态混合物的蒸汽总压( A 与溶液的组成无关 ; 12.389kJ ;D 2.961kJ )
考试形式: [闭卷] 考试题组:[ A ]
长 春 工 业 大 学 试 卷
/20 07 学年第二 学期 050606,050607 班
二 10 三 10 四 60 五 六
_____班 考务编号
姓名________
……………………………………………………○……装……………订……………线……○………………………………………………
长春工业大学大一物理习题册详解答案

(2) 写出 t=2 秒时刻质点的位置矢量, 并计算第 2 秒内的平均 速度量值; x(2)=4, y(2)=11 所以 x(1)=2, y(1)=17 所以 所以
3.初速度为 v0 5i 4 j (m/s) ,质量为 m=0.05kg 的质点, 受到冲量 I 2.5i 2 j (Ns) 的作用, 则质点的末速度 (矢 量)为 。
dx 2t 4 dt 当 v 0时,t 2, 解:v 当 t 0时,v 4, 所以v t图像:
2.质点沿半径 R=0.01 米的圆周运动,其运动方程 =2+4t 3,、 t 分别以弧度和秒计。则 t=2 秒时,其切向加速度量值 at = ; 法向加速度量值 a n = ; 当 a t=a/2 (a 为总加速度量值) 时, = 。 6.在离水面高为 h 米的岸边,有人用绳拉船靠岸,船在离岸边 s 米处, 当人以 v0 米/秒的速率收绳时, 试求船的速度、 加速度。
1 1 2 A J 2 J0 2 2
0
3 g 2L
7.设质量为 M 长为 l 的均匀直棒,可绕垂直于杆的上端的水平 轴无摩擦地转动。它原来静止在平衡位置上,现有一质量 m=M/3 的弹性小球水平飞来,正好碰在杆的下端。相碰后,使 杆从平衡位置摆动到最大位置max=60处,如图所示。求:
3.(2)物体沿一闭合路径运动,经t 时间后回到出发点 A,如 图所示,初速度 v1 ,末速度 v2 ,且 | v1 || v2 | ,则在t 时间 内其平均速度 v 与平均加速度 a 分别为: Nhomakorabea
7.质点沿直线运动,初速度 v0,加速度 为正常数,求: (1)质点完全静止所需的时间;
水被抽到地面,势能的增加量为: E P mgh Vgh 2.45 10 6 J
大学物理物理c答案

大学物理答案及评分标准(C 卷)一、填空题:1、2m/s -6m/s2、是:保守力做功跟路径无关。
3、ωJ 和221ωJ 4、导体内场强处处为零 5、取向极化和位移极化 6、304r r l Id B d ⨯⋅=μπ 7、M RT 2和M RT 38、R 25和R 23 9、开尔文表述是:不可能从单一的热源吸收热量使之完全变成有用功而不引起其他的变化。
10、频率相同、振动方向相同、位相差恒定。
二、选择题:1、(B )2、(D )3、(B )4、(A )5(A )三、判断题:1.(×) 2.(×) 3. (×) 4. (×) 5. (×) 6. (√) 7. (×) 8. (×) 9. (×)10. (√)四、解答题:1. 解:(1)根据题意:Kv a -=, 所以Kv dt dv -=,分离变量后,Kdt vdv -=,.................................(1分) 积分得,⎰⎰-=t v v Kdt v dv 00,所以有Kt e v t v -=0)(;....................... (3分) 同理,可以求得)1(00Kt e K v x x ---=。
......................................... (1分) (2)根据题意,Kx a =所以, dx Kx dx dtdv ⋅=⋅,积分得⎰⎰=x x v v Kxdx vdv 00;............. (1分) 所以有:)(202202x x K v v -+=.............................................(4分)2. 解:设导体平板的面积为S , 各面的电荷面密度分别为1σ、 2σ、3σ、4σ,根据电荷守恒的条件:A Q S S =+21σσ (1)B Q S S =+43σσ(2)---------------------------- (2分)在金属板内取如图所示的高斯面,根据高斯定理有:032=+σσ (3)---------------------------- (3分)根据场强叠加原理,金属板内某点P 的场强为零:40302012222εσεσεσεσ-+=p E -----------------(3分) 联立求解得:SQ Q B A 241+==σσ SQ Q B A 232-=-=σσ----------------------(2分) 3. 解:由于同轴电缆导体内的电流均匀分布,其磁场轴对称分布。
大学物理c的试题及答案

大学物理c的试题及答案一、选择题(每题2分,共20分)1. 下列哪个选项是牛顿第一定律的描述?A. 物体在没有外力作用下,总保持静止或匀速直线运动状态B. 物体的加速度与作用力成正比,与质量成反比C. 物体的加速度与作用力成正比,与质量成正比D. 物体在任何情况下都保持静止或匀速直线运动状态答案:A2. 光在真空中的传播速度是多少?A. 299,792,458 m/sB. 299,792,458 km/sC. 299,792,458 km/hD. 299,792,458 m/h答案:A3. 以下哪个是电场强度的定义?A. 电场力与电荷的比值B. 电荷与电场力的比值C. 电场力与电场强度的比值D. 电场强度与电荷的比值答案:A4. 根据热力学第一定律,系统内能的增加等于系统吸收的热量与对外做的功之和。
A. 正确B. 错误答案:A5. 电磁波的频率与波长的关系是?A. 频率与波长成正比B. 频率与波长成反比C. 频率与波长无关D. 频率与波长成正比,但只在特定条件下成立答案:B6. 根据麦克斯韦方程组,变化的磁场会产生什么?A. 变化的电场B. 恒定的电场C. 恒定的磁场D. 没有影响答案:A7. 欧姆定律描述的是电流、电压和电阻之间的关系,其表达式为?A. I = V/RB. I = R/VC. V = I * RD. R = V/I答案:A8. 以下哪个选项是描述波的干涉现象?A. 两个波相遇时,振幅相加B. 两个波相遇时,振幅相减C. 两个波相遇时,振幅不变D. 两个波相遇时,振幅消失答案:A9. 根据量子力学,电子在原子中的运动状态是由什么决定的?A. 电子的电荷B. 电子的质量C. 电子的能级D. 电子的动量答案:C10. 根据相对论,当物体的速度接近光速时,其质量会如何变化?A. 质量不变B. 质量增加C. 质量减少D. 质量消失答案:B二、填空题(每题2分,共20分)1. 根据牛顿第二定律,物体的加速度与作用力成_______,与物体的质量成_______。
刚体考试题及答案

刚体考试题及答案一、选择题(每题2分,共20分)1. 刚体的转动惯量是关于旋转轴的()。
A. 常数B. 函数C. 随机变量D. 无规律变化答案:A2. 刚体绕固定轴的转动惯量I与质量M和半径r的关系是()。
A. I = Mr^2B. I = 2MrC. I = MrD. I = 1/2Mr^2答案:D3. 刚体的平移运动和转动运动的合成是()。
A. 平移运动B. 转动运动C. 螺旋运动D. 不确定答案:C4. 刚体的角速度和线速度的关系是()。
A. 线速度是角速度的两倍B. 线速度是角速度的一半C. 线速度与角速度成正比D. 线速度与角速度无关答案:C5. 刚体的角动量守恒的条件是()。
A. 外力矩为零B. 外力为零C. 外力矩和外力都为零D. 外力矩和外力都不为零答案:A6. 刚体的动能与()有关。
A. 质量B. 速度C. 转动惯量D. 所有以上因素答案:D7. 刚体的角加速度与()有关。
A. 外力矩B. 转动惯量C. 角速度D. 所有以上因素答案:A8. 刚体的进动角速度与()有关。
A. 外力矩B. 转动惯量C. 角速度D. 所有以上因素答案:D9. 刚体的章动周期与()有关。
A. 转动惯量B. 外力矩C. 角速度D. 所有以上因素答案:A10. 刚体的自由振动的周期与()有关。
A. 转动惯量B. 外力矩C. 角速度D. 所有以上因素答案:A二、填空题(每题2分,共20分)1. 刚体的转动惯量是关于旋转轴的________。
答案:常数2. 刚体绕固定轴的转动惯量I与质量M和半径r的关系是I = ________。
答案:1/2Mr^23. 刚体的平移运动和转动运动的合成是________。
答案:螺旋运动4. 刚体的角速度和线速度的关系是线速度与角速度________。
5. 刚体的角动量守恒的条件是外力矩________。
答案:为零6. 刚体的动能与________有关。
答案:所有以上因素7. 刚体的角加速度与________有关。
刚体答案

n
2 J 0 3R 02 / 16 πg 4M
4、解:根据牛顿运动定律和转动定律列方程 对物体: 对滑轮: 运动学关系: 将①、②、③式联立得
mg-T =ma TR = J a=R
① ② ③
a=mg / (m+
∵ ∴
1 M) 2
T
R M
T a mg
v 0=0,
1 v =at=mgt / (m+ M) 2
① ②
=15 rad /s,t=10 s, =32rad , 0.99 rad /s2
3、解:在 r 处的宽度为 dr 的环带面积上摩擦力矩为
dM
总摩擦力矩 故平板角加速度
mgmgR 0 3
=M /J
设停止前转数为 n,则转角 = 2n 2 由 0 2 4 Mn / J 可得
a=r
解上述 5 个联立方程得:
a
T=11mg / 8
8、解:将杆与两小球视为一刚体,水平飞来小球与刚体视为一系统.由角动量守恒得
v 2l 2l m 0 J (逆时针为正向) 3 2 3 2l l 又 J m( ) 2 2m( ) 2 3 3 3v 将②代入①得 0 2l mv 0
则人对与地固联的转轴的角速度为
① ②
9、解:(1) 设当人以速率 v 沿相对圆盘转动相反的方向走动时,圆盘对地的绕轴角速度为,
v 2v 1R R 2
设盘的质量为 M,则人的质量为 M / 10,有:
①
人与盘视为系统,所受对转轴合外力矩为零,系统的角动量守恒.
2 2 1 2 M 1 R 1 MR 2 M 1 R MR ② 0 2 10 2 2 10 2 2v 将①式代入②式得: 0 ③ 21R
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
练习三刚体的定轴转动(一)1.一个转动的轮子由于轴承摩擦力矩的作用,其转动角速度渐渐变慢,第一秒末的角速度是起始角速度ω0的0.8倍。
若摩擦力矩不变,第二秒末角速度为(用ω0表示);该轮子在静止之前共转了转。
2.一个可视为质点的小球和两根长均为l的细棒刚性连接成如图3-2所示的形状,假定小球和细棒的质量均为m,那么,该装置绕过O点的OZ轴转动的转动惯量为。
3.(1)两个匀质圆盘A、B的密度分别为ρA和ρB,且ρA>ρB。
质量和厚度相同。
两圆盘的旋转轴均通过盘心并垂直于盘面,则它们的转动惯量的关系是:(1)I A<I B;(2)I A=I B;(3)I A>I B;(4)不能判断。
分析:m相等,ρA>ρB,V A小,厚度相等,R A小,J=1/2mR2,所以J A小4.(3)一力矩M作用于飞轮上,飞轮的角加速度为β1,如撤去这一力矩,飞轮的角加速度为-β2,则该飞轮的转动惯量为:5.(3)如图,A 与B 是两个质量相同的小球,A 球用一根不能伸长的绳子拴着,B 球用橡皮筋拴着,把它们拉到水平位置,放手后两小球到达竖直位置时绳长相等,则此时两球的线速度(1)B A V V =; (2)B A V V <;(3)B A V V >; (4)无法判断。
6.(4)一质量为60kg 的人站在一质量为60kg 、半径为l m 的匀质圆盘的边缘,圆盘可绕与盘面相垂直的中心竖直轴无摩擦地转动。
系统原来是静止的,后来人沿圆盘边缘走动,当人相对圆盘的走动速度为2m/s 时,圆盘角速度大小为 :(1) 1rad/s ; (2) 2rad/s ;(3)2/3rad/s ; (4)4/3rad/s 。
解:角动量守恒7. 如图3-7所示,物体1和2的质量分别为1m 与2m ,滑轮的转动惯量为J ,半径为r 。
(1)如物体2与桌面间的摩擦系数为μ,求系统的加速度a 及绳中的张力1T 和2T (设绳子与滑轮间无相对滑动,滑轮与转轴无摩擦);(2)如物体2与桌面间为光滑接触,求系统的加速度a 及绳中的张力1T 和2T 。
图3-7Jr m r m Jg m gr m m gr m m T Jr m r m Jg m gr m m gr m m T J r m r m gr m gr m a J r m r m gr m gr m ++++=++++=++-=++-=22212221221222211221221122212221222121,μμμμμαJr m r m gr m m T J r m r m Jg m gr m m T Jr m r m gr m a ++=+++=++=22212212222112211222121,0)2(时:=当μ8.一长为2l ,质量为3m 的细棒的两端粘有质量分别为2m 和m 的物体(如图3-8所示),此杆可绕中心O 轴在铅直平面内转动。
先使其在水平位置,然后静止释放。
求:(1)此刚体的转动惯量;(2)水平位置时的杆的角加速度;(3)通过铅直位置时杆的角速度。
(1)此刚体的转动惯量;解: 222242)2)(3(121mL mL mL L m J =++= (2)水平位置时的杆的角加速度; 解:M=J α, M=2mgL-mgL L g 4=α (3)通过铅直位置时杆的角速度。
解:机械能守恒:0+0=mgL-2mgL+1/2J ω2L g 2/=ω练习四 刚体的定轴转动(二)1.用一条皮带将两个轮子A 和B 连接起来,轮与皮带间无相对滑动,B 轮的半径是A 轮半径的3倍。
(1)如果两轮具有相同的角动量,则A 、B 两轮转动惯量的比值为 ;(2)如果两轮具有相同的转动动能,则A 、B 两轮转动惯量的比值为 。
2.某滑冰者转动的角速度原为ω0,转动惯量为I 0,当他收拢双臂后,转动惯量减少了1/4。
这时他转动的角速度为 ;他若不收拢双臂,而被另一个滑冰者作用,角速度变为02ωω=,则另一滑冰者对他施加力矩所作的功A 为 。
解:3.银河系有一可视为球体的天体,由于引力凝聚,体积不断收缩。
设它经过一万年体积收缩了1%,而质量保持不变。
则它的自转周期将 3 ;其转动动能将 1 。
(1)增大; (2)不变; (3)减小。
4.(3)一子弹水平射入一木棒后一同上摆。
在上摆的过程中,以子弹和木棒为系统,则总角动量、总动量及总机械能是否守恒?结论是:(1)三量均不守恒; (2)三量均守恒;(3)只有总机械能守恒;(4)只有总动量不守恒。
5.(4)如图4-2,一轻绳跨过两个质量均为m,半径均为R的匀质圆盘状定滑轮。
绳的两端分别系着质量分别为m和2m的重物。
不计滑轮转轴的摩擦。
将系统由静止释放,且绳与两滑轮间均无相对滑动,则两滑轮之间绳的张力为:(1)mg;(2)3mg/2;(3)2mg;(4)11mg/8。
6.一质量为m,长为l的均匀细棒,放在水平桌面上,可绕杆的一端转动,如图6-5所示,初始时刻杆的角速度为ω0。
设杆与桌面的摩擦系数为μ,求:(1)杆所受的摩擦力矩;(2)当杆转过90︒时,摩擦力矩所作的功和杆的转动角速度ω。
解:⎰-==2/04πμπθmgl d M A f L g J J A 23212120202πμωωωω-=∴-=7.设质量为M 长为l 的均匀直棒,可绕垂直于杆的上端的水平轴无摩擦地转动。
它原来静止在平衡位置上,现有一质量m =M/3的弹性小球水平飞来,正好碰在杆的下端。
相碰后,使杆从平衡位置摆动到最大位置θmax =60︒处,如图4-7所示。
求:(1)设为弹性碰撞,试计算小球初速度v 0的值; 解:碰撞前后,E k 守恒: 2222203/12/12/12/1mLML J J mv mv ==+=ω 碰撞前后,L 守恒:ωJ mvL L mv +=0棒上升,E 守恒: 2,0,2)60cos 1(212102gL v v L g L mg J o ===-=ωω三式联立,解得:(2)碰撞过程中小球受到多大的冲量。
解: gL mv mv I 2210-=-=练习五刚体的定轴转动(三)1.如图5-1所示,均匀细棒长为l,质量为M,下端无摩擦地铰在水平面上的O点。
当杆受到微扰从竖直位置倒至水平面上时,顶端A点的速度为:。
2.如图5-2所示,半径为R,质量为m的匀质圆盘可绕水平固定轴转动。
现以一轻绳绕在轮边缘,绳的下端挂一质量为m的物体,圆盘从静止开始转动后,它转过的角度和时间的关系为。
3.(1)长为L的均匀细杆OM绕水平O轴在竖直面内自由转动,今使细杆OM从水平位置开始自由下摆,在细杆摆动到铅直位置的过程中,其角速度ω,角加速度β如何变化?(1)ω增大,β减小;(2)ω减小,β减小;(3)ω增大,β增大;(4)ω减小,β增大。
↓===↑=+-=JmgL L mg M J JmgL J L mg L mg 2sin ,sin 2cos ,21)cos 1(222θβθβθωωθ守恒:在下降过程中,机械能4(3)人造地球卫星绕地球作椭圆运动,地球在椭圆的一个焦点上,卫星的动量P ,角动量L 及卫星与地球所组成的系统的机械能E 是否守恒?(1)P 不守恒,L 不守恒,E 不守恒;(2)P 守恒,L 不守恒,E 不守恒;(3)P 不守恒,L 守恒,E 守恒;(4)P 守恒,L 守恒,E 守恒;(5)P 不守恒,L 守恒,E 不守恒;分析:万有引力是保守力,机械能守恒;是有心力,角动量守恒万有引力是卫星所受的外力,不为0,所以动量不守恒5.(3)如图5-5所示,A 、B 为两个相同绕着轻绳的定滑轮,A 滑轮挂一质量为M 的物体,B 滑轮受拉力F ,而且F=Mg ,设A,B 两滑轮的角加速度分别为A β和B β,不计滑轮轴的摩擦,则有(1)A β=B β; (2) A β>B β ;(3)A β<B β; (4)开始A β=B β以后A β<B β。
图5-5 BA A AB AB MR J MgRR a J MgR J TR J FR B MaT Mg M A βββββββ<+======-所以:滑轮:2::,6.如图5-6所示,B 的质量m 2足够大,使其能在重力作用下运动,设A 的质量为m 1与斜面间的摩擦系数为μ,轴承摩擦不计,绳不可伸长,质量为M 的滑轮可视为均匀圆盘,求物体B 由静止下落的高度h 时的速度。
A :A A A a m mg mg T =--θθμsin cosB :B a m T g m 222=-轮:αJ R T R T =-12R a a B A α== ah v ah v v 22202==-7.如图5-7所示,把细杆OM 由水平位置静止释放,杆摆至铅直位置时刚好与静止在光滑水平桌面上质量为m 的小球相碰,设杆的质量与小球的质量相同,碰撞又是弹性的,求碰撞后小球的速度。
L g ml J J mgl 331,212122=→==ωω 碰撞前后:(1)L 守恒:mvL J J+='ωω(2)E 守恒: 22221'2121mv J J +=ωω (1)(2)联立消去 gL v 3'=得ω。
