历年高考数学试题
2024年高中数学高考试卷(3篇)

数学(理科)考试时间:150分钟满分:150分一、选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1. 设函数$f(x) = \frac{x^2 - 4}{x - 2}$,则$f(x)$的定义域为()A. $(-\infty, -2) \cup (2, +\infty)$B. $(-\infty, -2) \cup (2, +\infty) \cup \{2\}$C. $(-\infty, 2) \cup (2, +\infty)$D. $(-\infty, 2) \cup (2, +\infty) \cup \{-2\}$2. 已知向量$\vec{a} = (1, 2)$,$\vec{b} = (2, 3)$,则$\vec{a} \cdot\vec{b}$的值为()A. 7B. 5C. 1D. -13. 函数$y = \log_2(x + 1)$的图像与直线$y = 2x + 1$的图像有()A. 1个交点B. 2个交点C. 3个交点D. 无交点4. 在等差数列$\{a_n\}$中,若$a_1 = 2$,$a_5 = 10$,则该数列的公差为()A. 1C. 3D. 45. 若不等式$2x - 3 < 5x + 2$的解集为$x > -1$,则实数$k$的值为()A. -1B. 0C. 1D. 26. 已知函数$y = x^3 - 3x$,若$x_1$,$x_2$,$x_3$是方程$y = 0$的三个根,则$x_1 + x_2 + x_3$的值为()A. 0B. 1C. -1D. 37. 在直角坐标系中,点$A(1, 2)$关于直线$y = x$的对称点为()A. $(2, 1)$B. $(1, 2)$C. $(-2, -1)$D. $(-1, -2)$8. 若复数$z = a + bi$(其中$a$,$b$为实数)满足$|z - 3i| = |z + 3i|$,则实数$a$的值为()A. 0B. 3C. -3D. 不存在9. 已知平面直角坐标系中,点$P(2, 3)$,点$Q$在直线$y = x + 1$上,则点$PQ$的长度最小值为()A. 1B. $\sqrt{2}$C. 2D. $\sqrt{5}$10. 在三角形ABC中,$A = 60^\circ$,$b = 2$,$c = 3$,则边$a$的长度为()A. $\sqrt{3}$B. $\sqrt{6}$C. $\sqrt{7}$D. $\sqrt{8}$11. 若复数$z$满足$|z - 1| = |z + 1|$,则复数$z$的几何意义为()A. 复数$z$对应的点在实轴上B. 复数$z$对应的点在虚轴上C. 复数$z$对应的点在单位圆上D. 复数$z$对应的点在直线$y = x$上12. 已知函数$f(x) = \frac{x^2 - 4}{x - 2}$,则$f(2)$的值为()A. 2B. -2C. 4D. 无意义二、填空题(本大题共6小题,每小题5分,共30分。
高考数学历年真题及答案详解

高考数学历年真题及答案详解一、选择题1. 题目描述:在平面直角坐标系中,点A(-3, 4)关于y轴的对称点是()。
A. (3, -4)B. (-3, -4)C. (-3, 4)D. (3, 4)答案解析:点关于y轴对称即x取相反数,所以答案为A.(3, -4)。
2. 题目描述:已知函数 f(x) = 2^(2x-3),则当 x = 1 时,f(x) 的值是()。
A. 1B. 2C. 4D. 8答案解析:将x=1代入函数中,即f(1) = 2^(2*1-3),化简得f(1)= 2^(-1) = 1/2,所以答案为A. 1。
二、填空题1. 题目描述:已知三角形ABC中,∠B = 90°,AC = 5 cm,BC =12 cm,求AB的长度。
答案解析:根据勾股定理,AB^2 + BC^2 = AC^2,代入已知数据得AB^2 + 12^2 = 5^2,化简得AB^2 = 25 - 144 = -119,由于长度不能为负数,所以不存在满足要求的三角形ABC。
2. 题目描述:若a1, a2, a3为等差数列的前三项,且满足a1 + a3 = 18,a2 - a3 = 4,求a1, a2和a3的值。
答案解析:由等差数列的性质可知,a2 = (a1 + a3) / 2,代入已知数据得a2 = 9.5,将a2带入a2 - a3 = 4解得a3 = 5.5,再将a3带入a1 +a3 = 18解得a1 = 12.5,所以a1 = 12.5,a2 = 9.5,a3 = 5.5。
三、解答题1. 题目描述:设函数f(x) = cos(x + 1) - sin(x - 1),求f(x)的单调递增区间。
答案解析:对f(x)求导得f'(x) = -sin(x + 1) - cos(x - 1),令f'(x) = 0,解方程得x = 1/4 (4πn + 3π/2) - 1,其中n为整数。
通过二阶导数的符号判断可知,当x < -1或x > -3/4 + 4πn,f(x)单调递增;当-3/4 + 4πn < x< -1,f(x)单调递减。
历年(2019-2024)全国高考数学真题分类(事件与概率)汇编(附答案)

历年(2019-2024)全国高考数学真题分类(事件与概率)汇编考点01 古典概率一、单选题1.(2024∙全国甲卷∙高考真题)甲、乙、丙、丁四人排成一列,则丙不在排头,且甲或乙在排尾的概率是()A.14B.13C.12D.232.(2023∙全国乙卷∙高考真题)某学校举办作文比赛,共6个主题,每位参赛同学从中随机抽取一个主题准备作文,则甲、乙两位参赛同学抽到不同主题概率为()A.56B.23C.12D.133.(2023∙全国甲卷∙高考真题)某校文艺部有4名学生,其中高一、高二年级各2名.从这4名学生中随机选2名组织校文艺汇演,则这2名学生来自不同年级的概率为()A.16B.13C.12D.234.(2022∙全国甲卷∙高考真题)从分别写有1,2,3,4,5,6的6张卡片中无放回随机抽取2张,则抽到的2张卡片上的数字之积是4的倍数的概率为()A.15B.13C.25D.235.(2022∙全国新Ⅰ卷∙高考真题)从2至8的7个整数中随机取2个不同的数,则这2个数互质的概率为()A.16B.13C.12D.236.(2021∙全国甲卷∙高考真题)将3个1和2个0随机排成一行,则2个0不相邻的概率为() A.0.3 B.0.5 C.0.6 D.0.87.(2019∙全国∙高考真题)两位男同学和两位女同学随机排成一列,则两位女同学相邻的概率是A.16B.14C.13D.128.(2019∙全国∙高考真题)生物实验室有5只兔子,其中只有3只测量过某项指标,若从这5只兔子中随机取出3只,则恰有2只测量过该指标的概率为A.23 B.35C.25D.15二、填空题21.(2024∙全国新Ⅰ卷∙高考真题)甲、乙两人各有四张卡片,每张卡片上标有一个数字,甲的卡片上分别标有数字1,3,5,7,乙的卡片上分别标有数字2,4,6,8,两人进行四轮比赛,在每轮比赛中,两人各自从自己持有的卡片中随机选一张,并比较所选卡片上数字的大小,数字大的人得1分,数字小的人得0分,然后各自弃置此轮所选的卡片(弃置的卡片在此后的轮次中不能使用).则四轮比赛后,甲的总得分不小于2的概率为 .22.(2024∙全国甲卷∙高考真题)有6个相同的球,分别标有数字1、2、3、4、5、6,从中无放回地随机取3次,每次取1个球.记m 为前两次取出的球上数字的平均值,n 为取出的三个球上数字的平均值,则m 与n 之差的绝对值不大于12的概率为 .23.(2024∙全国新Ⅱ卷∙高考真题)在如图的4×4的方格表中选4个方格,要求每行和每列均恰有一个方格被选中,则共有 种选法,在所有符合上述要求的选法中,选中方格中的4个数之和的最大值是 .24.(2023∙天津∙高考真题)把若干个黑球和白球(这些球除颜色外无其它差异)放进三个空箱子中,三个箱子中的球数之比为5:4:6.且其中的黑球比例依次为40%,25%,50%.若从每个箱子中各随机摸出一球,则三个球都是黑球的概率为 ;若把所有球放在一起,随机摸出一球,则该球是白球的概率为 . 25.(2022∙浙江∙高考真题)现有7张卡片,分别写上数字1,2,2,3,4,5,6.从这7张卡片中随机抽取3张,记所抽取卡片上数字的最小值为ξ,则(2)P ξ== ,()E ξ= .26.(2022∙全国甲卷∙高考真题)从正方体的8个顶点中任选4个,则这4个点在同一个平面的概率为 . 27.(2022∙全国乙卷∙高考真题)从甲、乙等5名同学中随机选3名参加社区服务工作,则甲、乙都入选的概率为 .28.(2021∙浙江∙高考真题)袋中有4个红球m 个黄球,n 个绿球.现从中任取两个球,记取出的红球数为ξ,若取出的两个球都是红球的概率为16,一红一黄的概率为13,则m n -= ,()E ξ= .29.(2020∙江苏∙高考真题)将一颗质地均匀的正方体骰子先后抛掷2次,观察向上的点数,则点数和为5的概率是 .30.(2019∙江苏∙高考真题)从3名男同学和2名女同学中任选2名同学参加志愿者服务,则选出的2名同学中至少有1名女同学的概率是 .考点02 条件概率1.(2024∙天津∙高考真题),,,,A B C D E 五种活动,甲、乙都要选择三个活动参加.甲选到A 的概率为 ;已知乙选了A 活动,他再选择B 活动的概率为 .2.(2023∙全国甲卷∙高考真题)某地的中学生中有60%的同学爱好滑冰,50%的同学爱好滑雪,70%的同学爱好滑冰或爱好滑雪.在该地的中学生中随机调查一位同学,若该同学爱好滑雪,则该同学也爱好滑冰的概率为( ) A .0.8B .0.6C .0.5D .0.43.(2022∙天津∙高考真题)52张扑克牌,没有大小王,无放回地抽取两次,则两次都抽到A 的概率为 ;已知第一次抽到的是A ,则第二次抽取A 的概率为考点03 全概率公式与贝叶斯公式1.(2024∙上海∙高考真题)某校举办科学竞技比赛,有、、A B C 3种题库,A 题库有5000道题,B 题库有4000道题,C 题库有3000道题.小申已完成所有题,他A 题库的正确率是0.92,B 题库的正确率是0.86,C 题库的正确率是0.72.现他从所有的题中随机选一题,正确率是 .2.(2023∙全国新Ⅰ卷∙高考真题)甲、乙两人投篮,每次由其中一人投篮,规则如下:若命中则此人继续投篮,若末命中则换为对方投篮.无论之前投篮情况如何,甲每次投篮的命中率均为0.6,乙每次投篮的命中率均为0.8.由抽签确定第1次投篮的人选,第1次投篮的人是甲、乙的概率各为0.5. (1)求第2次投篮的人是乙的概率; (2)求第i 次投篮的人是甲的概率;(3)已知:若随机变量i X 服从两点分布,且()()110,1,2,,i i i P X P X q i n ==-===⋅⋅⋅,则11n n i i i i E X q ==⎛⎫= ⎪⎝⎭∑∑.记前n 次(即从第1次到第n 次投篮)中甲投篮的次数为Y ,求()E Y .考点04 正态分布指定区间的概率1.(2024∙全国新Ⅰ卷∙高考真题)(多选)随着“一带一路”国际合作的深入,某茶叶种植区多措并举推动茶叶出口.为了解推动出口后的亩收入(单位:万元)情况,从该种植区抽取样本,得到推动出口后亩收入的样本均值 2.1x =,样本方差20.01s =,已知该种植区以往的亩收入X 服从正态分布()21.8,0.1N ,假设推动出口后的亩收入Y 服从正态分布()2,N x s ,则( )(若随机变量Z 服从正态分布()2,N μσ,()0.8413P Z μσ<+≈)A .(2)0.2P X >>B .(2)0.5P X ><C .(2)0.5P Y >>D .(2)0.8P Y ><2.(2022∙全国新Ⅱ卷∙高考真题)已知随机变量X 服从正态分布()22,N σ,且(2 2.5)0.36P X <≤=,则( 2.5)P X >= .3.(2021∙全国新Ⅱ卷∙高考真题)某物理量的测量结果服从正态分布()210,N σ,下列结论中不正确的是( ) A .σ越小,该物理量在一次测量中在(9.9,10.1)的概率越大 B .该物理量在一次测量中大于10的概率为0.5C .该物理量在一次测量中小于9.99与大于10.01的概率相等D .该物理量在一次测量中落在(9.9,10.2)与落在(10,10.3)的概率相等参考答案考点01 古典概率一、单选题 1.(2024∙全国甲卷∙高考真题)甲、乙、丙、丁四人排成一列,则丙不在排头,且甲或乙在排尾的概率是( ) A .14 B .13C .12D .23【答案】B【详细分析】解法一:画出树状图,结合古典概型概率公式即可求解.解法二:分类讨论甲乙的位置,结合得到符合条件的情况,然后根据古典概型计算公式进行求解. 【答案详解】解法一:画出树状图,如图,由树状图可得,甲、乙、丙、丁四人排成一列,共有24种排法, 其中丙不在排头,且甲或乙在排尾的排法共有8种, 故所求概率81=243P =. 解法二:当甲排在排尾,乙排第一位,丙有2种排法,丁就1种,共2种; 当甲排在排尾,乙排第二位或第三位,丙有1种排法,丁就1种,共2种;于是甲排在排尾共4种方法,同理乙排在排尾共4种方法,于是共8种排法符合题意;基本事件总数显然是44A 24=,根据古典概型的计算公式,丙不在排头,甲或乙在排尾的概率为81243=. 故选:B2.(2023∙全国乙卷∙高考真题)某学校举办作文比赛,共6个主题,每位参赛同学从中随机抽取一个主题准备作文,则甲、乙两位参赛同学抽到不同主题概率为( )6323【答案】A【详细分析】对6个主题编号,利用列举列出甲、乙抽取的所有结果,并求出抽到不同主题的结果,再利用古典概率求解作答.【答案详解】用1,2,3,4,5,6表示6个主题,甲、乙二人每人抽取1个主题的所有结果如下表:甲 1234 5 61 (1,1) (1,2) (1,3) (1,4)(1,5) (1,6) 2 (2,1)(2,2) (2,3) (2,4) (2,5) (2,6) 3 (3,1) (3,2) (3,3)(3,4) (3,5)(3,6) 4 (4,1)(4,2) (4,3) (4,4) (4,5) (4,6) 5 (5,1) (5,2) (5,3)(5,4) (5,5) (5,6) 6(6,1)(6,2)(6,3)(6,4)(6,5)(6,6)共有36个不同结果,它们等可能,其中甲乙抽到相同结果有(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),共6个, 因此甲、乙两位参赛同学抽到不同主题的结果有30个,概率305366P ==. 故选:A3.(2023∙全国甲卷∙高考真题)某校文艺部有4名学生,其中高一、高二年级各2名.从这4名学生中随机选2名组织校文艺汇演,则这2名学生来自不同年级的概率为( )A .16B .13C .12D .23【答案】D【详细分析】利用古典概率的概率公式,结合组合的知识即可得解.【答案详解】依题意,从这4名学生中随机选2名组织校文艺汇演,总的基本事件有24C 6=件, 其中这2名学生来自不同年级的基本事件有1122C C 4=,所以这2名学生来自不同年级的概率为4263=. 故选:D.4.(2022∙全国甲卷∙高考真题)从分别写有1,2,3,4,5,6的6张卡片中无放回随机抽取2张,则抽到的2张卡片上的数字之积是4的倍数的概率为( )5353【答案】C【详细分析】方法一:先列举出所有情况,再从中挑出数字之积是4的倍数的情况,由古典概型求概率即可.【答案详解】[方法一]:【最优解】无序 从6张卡片中无放回抽取2张,共有()()()()()()()()()()()()()()()1,2,1,3,1,4,1,5,1,6,2,3,2,4,2,5,2,6,3,4,3,5,3,6,4,5,4,6,5,615种情况,其中数字之积为4的倍数的有()()()()()()1,4,2,4,2,6,3,4,4,5,4,66种情况,故概率为62155=. [方法二]:有序从6张卡片中无放回抽取2张,共有()()()()()()()()()()()()()()()1,2,1,3,1,4,1,5,1,6,2,3,2,4,2,5,2,6,3,4,3,5,3,6,4,5,4,6,5,6,(2,1),(3,1),(4,1),(5,1),(6,1),(3,2),(4,2),(5,2),(6,2),(4,3),(5,3),(6,3),(5,4),(6,4),(6,5)30种情况,其中数字之积为4的倍数有(1,4),(2,4),(2,6),(3,4),(4,1),(4,2),(4,3),(4,5),(4,6),(5,4),(6,2),(6,4)12种情况,故概率为122305=. 故选:C.【整体点评】方法一:将抽出的卡片看成一个组合,再利用古典概型的概率公式解出,是该题的最优解; 方法二:将抽出的卡片看成一个排列,再利用古典概型的概率公式解出;5.(2022∙全国新Ⅰ卷∙高考真题)从2至8的7个整数中随机取2个不同的数,则这2个数互质的概率为( )A .16B .13C .12D .23【答案】D【详细分析】由古典概型概率公式结合组合、列举法即可得解.【答案详解】从2至8的7个整数中随机取2个不同的数,共有27C 21=种不同的取法,若两数不互质,不同的取法有:()()()()()()()2,4,2,6,2,8,3,6,4,6,4,8,6,8,共7种, 故所求概率2172213P -==. 故选:D.6.(2021∙全国甲卷∙高考真题)将3个1和2个0随机排成一行,则2个0不相邻的概率为( ) A .0.3 B .0.5C .0.6D .0.8【答案】C【详细分析】利用古典概型的概率公式可求概率.【答案详解】解:将3个1和2个0随机排成一行,可以是:00111,01011,01101,01110,10011,10101,10110,11001,11010,11100,共10种排法,其中2个0不相邻的排列方法为:01011,01101,01110,10101,10110,11010,共6种方法,故2个0不相邻的概率为6=0.610, 故选:C.7.(2019∙全国∙高考真题)两位男同学和两位女同学随机排成一列,则两位女同学相邻的概率是A .16B .14 C .13D .12【答案】D【解析】男女生人数相同可利用整体发详细分析出两位女生相邻的概率,进而得解.【答案详解】两位男同学和两位女同学排成一列,因为男生和女生人数相等,两位女生相邻与不相邻的排法种数相同,所以两位女生相邻与不相邻的概率均是12.故选D .【名师点评】本题考查常见背景中的古典概型,渗透了数学建模和数学运算素养.采取等同法,利用等价转化的思想解题.8.(2019∙全国∙高考真题)生物实验室有5只兔子,其中只有3只测量过某项指标,若从这5只兔子中随机取出3只,则恰有2只测量过该指标的概率为 A .23B .35C .25D .15【答案】B【详细分析】本题首先用列举法写出所有基本事件,从中确定符合条件的基本事件数,应用古典概率的计算公式求解.【答案详解】设其中做过测试的3只兔子为,,a b c ,剩余的2只为,A B ,则从这5只中任取3只的所有取法有{,,},{,,},{,,},{,,},{,,},{,,}a b c a b A a b B a c A a c B a A B ,{,c,},{,c,},{b,,},{c,,}b A b B A B A B 共10种.其中恰有2只做过测试的取法有{,,},{,,},{,,},{,,},a b A a b B a c A a c B {,c,},{,c,}b A b B 共6种, 所以恰有2只做过测试的概率为63105,选B . 【名师点评】本题主要考查古典概率的求解,题目较易,注重了基础知识、基本计算能力的考查.应用列举法写出所有基本事件过程中易于出现遗漏或重复,将兔子标注字母,利用“树图法”,可最大限度的避免出错.二、填空题 21.(2024∙全国新Ⅰ卷∙高考真题)甲、乙两人各有四张卡片,每张卡片上标有一个数字,甲的卡片上分别标有数字1,3,5,7,乙的卡片上分别标有数字2,4,6,8,两人进行四轮比赛,在每轮比赛中,两人各自从自己持有的卡片中随机选一张,并比较所选卡片上数字的大小,数字大的人得1分,数字小的人得0分,然后各自弃置此轮所选的卡片(弃置的卡片在此后的轮次中不能使用).则四轮比赛后,甲的总得分不小于2的概率为 . 【答案】12/0.5 【详细分析】将每局的得分分别作为随机变量,然后详细分析其和随机变量即可. 【答案详解】设甲在四轮游戏中的得分分别为1234,,,X X X X ,四轮的总得分为X .对于任意一轮,甲乙两人在该轮出示每张牌的概率都均等,其中使得甲获胜的出牌组合有六种,从而甲在该轮获胜的概率()631448k P X ===⨯,所以()()31,2,3,48k E X k ==. 从而()()()441234113382k k k E X E X X X X E X ===+++===∑∑.记()()0,1,2,3k p P X k k ===.如果甲得0分,则组合方式是唯一的:必定是甲出1,3,5,7分别对应乙出2,4,6,8,所以04411A 24p ==; 如果甲得3分,则组合方式也是唯一的:必定是甲出1,3,5,7分别对应乙出8,2,4,6,所以34411A 24p ==. 而X 的所有可能取值是0,1,2,3,故01231p p p p +++=,()1233232p p p E X ++==. 所以121112p p ++=,1213282p p ++=,两式相减即得211242p +=,故2312p p +=.所以甲的总得分不小于2的概率为2312p p +=. 故答案为:12.【名师点评】关键点名师点评:本题的关键在于将问题转化为随机变量问题,利用期望的可加性得到等量关系,从而避免繁琐的列举.22.(2024∙全国甲卷∙高考真题)有6个相同的球,分别标有数字1、2、3、4、5、6,从中无放回地随机取3次,每次取1个球.记m 为前两次取出的球上数字的平均值,n 为取出的三个球上数字的平均值,则m 与n 之差的绝对值不大于12的概率为 . 【答案】715【详细分析】根据排列可求基本事件的总数,设前两个球的号码为,a b ,第三个球的号码为c ,则323a b c a b +-≤≤++,就c 的不同取值分类讨论后可求随机事件的概率.【答案详解】从6个不同的球中不放回地抽取3次,共有36A 120=种,设前两个球的号码为,a b ,第三个球的号码为c ,则1322a b c a b +++-≤, 故2()3c a b -+≤,故32()3c a b -≤-+≤, 故323a b c a b +-≤≤++,若1c =,则5a b +≤,则(),a b 为:()()2,3,3,2,故有2种, 若2c =,则17a b ≤+≤,则(),a b 为:()()()()()1,3,1,4,1,5,1,6,3,4,()()()()()3,1,4,1,5,1,6,1,4,3,故有10种,当3c =,则39a b ≤+≤,则(),a b 为:()()()()()()()()1,2,1,4,1,5,1,6,2,4,2,5,2,6,4,5, ()()()()()()()()2,1,4,1,5,1,6,1,4,2,5,2,6,2,5,4,故有16种,当4c =,则511a b ≤+≤,同理有16种, 当5c =,则713a b ≤+≤,同理有10种, 当6c =,则915a b ≤+≤,同理有2种, 共m 与n 的差的绝对值不超过12时不同的抽取方法总数为()22101656++=, 故所求概率为56712015=. 故答案为:71523.(2024∙全国新Ⅱ卷∙高考真题)在如图的4×4的方格表中选4个方格,要求每行和每列均恰有一个方格被选中,则共有 种选法,在所有符合上述要求的选法中,选中方格中的4个数之和的最大值是 .【答案】 24 112【详细分析】由题意可知第一、二、三、四列分别有4、3、2、1个方格可选;利用列举法写出所有的可能结果,即可求解.【答案详解】由题意知,选4个方格,每行和每列均恰有一个方格被选中, 则第一列有4个方格可选,第二列有3个方格可选,第三列有2个方格可选,第四列有1个方格可选, 所以共有432124⨯⨯⨯=种选法;每种选法可标记为(,,,)a b c d ,ab c d ,,,分别表示第一、二、三、四列的数字, 则所有的可能结果为:(11,22,33,44),(11,22,34,43),(11,22,33,44),(11,22,34,42),(11,24,33,43),(11,24,33,42), (12,21,33,44),(12,21,34,43),(12,22,31,44),(12,22,34,40),(12,24,31,43),(12,24,33,40), (13,21,33,44),(13,21,34,42),(13,22,31,44),(13,22,34,40),(13,24,31,42),(13,24,33,40), (15,21,33,43),(15,21,33,42),(15,22,31,43),(15,22,33,40),(15,22,31,42),(15,22,33,40),所以选中的方格中,(15,21,33,43)的4个数之和最大,为152********+++=. 故答案为:24;112【名师点评】关键点名师点评:解决本题的关键是确定第一、二、三、四列分别有4、3、2、1个方格可选,利用列举法写出所有的可能结果.24.(2023∙天津∙高考真题)把若干个黑球和白球(这些球除颜色外无其它差异)放进三个空箱子中,三个箱子中的球数之比为5:4:6.且其中的黑球比例依次为40%,25%,50%.若从每个箱子中各随机摸出一球,则三个球都是黑球的概率为 ;若把所有球放在一起,随机摸出一球,则该球是白球的概率为 . 【答案】 0.0535/0.6 【详细分析】先根据题意求出各盒中白球,黑球的数量,再根据概率的乘法公式可求出第一空; 根据古典概型的概率公式可求出第二个空.【答案详解】设甲、乙、丙三个盒子中的球的个数分别为5,4,6n n n ,所以总数为15n , 所以甲盒中黑球个数为40%52n n ⨯=,白球个数为3n ; 乙盒中黑球个数为25%4n n ⨯=,白球个数为3n ; 丙盒中黑球个数为50%63n n ⨯=,白球个数为3n ;记“从三个盒子中各取一个球,取到的球都是黑球”为事件A ,所以,()0.40.250.50.05P A =⨯⨯=;记“将三个盒子混合后取出一个球,是白球”为事件B , 黑球总共有236n n n n ++=个,白球共有9n 个, 所以,()93155n P B n ==. 故答案为:0.05;35.25.(2022∙浙江∙高考真题)现有7张卡片,分别写上数字1,2,2,3,4,5,6.从这7张卡片中随机抽取3张,记所抽取卡片上数字的最小值为ξ,则(2)P ξ== ,()E ξ= . 【答案】1635,127/517【详细分析】利用古典概型概率公式求(2)P ξ=,由条件求ξ分布列,再由期望公式求其期望.【答案详解】从写有数字1,2,2,3,4,5,6的7张卡片中任取3张共有37C 种取法,其中所抽取的卡片上的数字的最小值为2的取法有112424C C C +种,所以11242437C C C 16(2)C 35P ξ+===, 由已知可得ξ的取值有1,2,3,4,2637C 15(1)C 35P ξ===,16(2)35P ξ==,,()()233377C 31134C 35C 35P P ξξ======所以15163112()1234353535357E ξ=⨯+⨯+⨯+⨯=, 故答案为:1635,127. 26.(2022∙全国甲卷∙高考真题)从正方体的8个顶点中任选4个,则这4个点在同一个平面的概率为 . 【答案】635. 【详细分析】根据古典概型的概率公式即可求出.【答案详解】从正方体的8个顶点中任取4个,有48C 70n ==个结果,这4个点在同一个平面的有6612m =+=个,故所求概率1267035m P n ===. 故答案为:635. 27.(2022∙全国乙卷∙高考真题)从甲、乙等5名同学中随机选3名参加社区服务工作,则甲、乙都入选的概率为 . 【答案】310/0.3 【详细分析】根据古典概型计算即可【答案详解】解法一:设这5名同学分别为甲,乙,1,2,3,从5名同学中随机选3名,有:(甲,乙,1),(甲,乙,2),(甲,乙,3),(甲,1,2),(甲,1,3),(甲,2,3),(乙,1,2),(乙,1,3),(乙,2,3),(1,2,3),共10种选法; 其中,甲、乙都入选的选法有3种,故所求概率310P =. 故答案为:310. 解法二:从5名同学中随机选3名的方法数为35C 10=甲、乙都入选的方法数为13C 3=,所以甲、乙都入选的概率310P =故答案为:31028.(2021∙浙江∙高考真题)袋中有4个红球m 个黄球,n 个绿球.现从中任取两个球,记取出的红球数为ξ,若取出的两个球都是红球的概率为16,一红一黄的概率为13,则m n -= ,()E ξ= .【答案】 189【详细分析】根据古典概型的概率公式即可列式求得,m n 的值,再根据随机变量ξ的分布列即可求出()E ξ. 【答案详解】2244224461(2)366m n m n m n C P C CCξ++++++====⇒=,所以49m n ++=, ()P 一红一黄114244133693m m n C C m m m C ++⋅====⇒=, 所以2n =, 则1m n -=.由于11245522991455105(2),(1),(0)63693618C C C P P P C C ξξξ⋅⨯========== 155158()2106918399E ξ∴=⨯+⨯+⨯=+=.故答案为:1;89.29.(2020∙江苏∙高考真题)将一颗质地均匀的正方体骰子先后抛掷2次,观察向上的点数,则点数和为5的概率是 . 【答案】19【详细分析】分别求出基本事件总数,点数和为5的种数,再根据概率公式解答即可. 【答案详解】根据题意可得基本事件数总为6636⨯=个. 点数和为5的基本事件有()1,4,()4,1,()2,3,()3,2共4个.∴出现向上的点数和为5的概率为41369P ==. 故答案为:19.【名师点评】本题考查概率的求法,考查古典概型、列举法等基础知识,考查运算求解能力,是基础题. 30.(2019∙江苏∙高考真题)从3名男同学和2名女同学中任选2名同学参加志愿者服务,则选出的2名同学中至少有1名女同学的概率是 . 【答案】710. 【详细分析】先求事件的总数,再求选出的2名同学中至少有1名女同学的事件数,最后根据古典概型的概率计算公式得出答案.【答案详解】从3名男同学和2名女同学中任选2名同学参加志愿服务,共有2510C =种情况.若选出的2名学生恰有1名女生,有11326C C=种情况,若选出的2名学生都是女生,有221C=种情况,所以所求的概率为617 1010 +=.【名师点评】计数原理是高考考查的重点内容,考查的形式有两种,一是独立考查,二是与古典概型结合考查,由于古典概型概率的计算比较明确,所以,计算正确基本事件总数是解题的重要一环.在处理问题的过程中,应注意审清题意,明确“分类”“分步”,根据顺序有无,明确“排列”“组合”.考点02 条件概率1.(2024∙天津∙高考真题),,,,A B C D E五种活动,甲、乙都要选择三个活动参加.甲选到A的概率为;已知乙选了A活动,他再选择B活动的概率为.【答案】 3512【详细分析】结合列举法或组合公式和概率公式可求甲选到A的概率;采用列举法或者条件概率公式可求乙选了A活动,他再选择B活动的概率.【答案详解】解法一:列举法从五个活动中选三个的情况有:,,,,,,,,,ABC ABD ABE ACD ACE ADE BCD BCE BDE CDE,共10种情况,其中甲选到A有6种可能性:,,,,,ABC ABD ABE ACD ACE ADE,则甲选到A得概率为:63105P==;乙选A活动有6种可能性:,,,,,ABC ABD ABE ACD ACE ADE, 其中再选则B有3种可能性:,,ABC ABD ABE,故乙选了A活动,他再选择B活动的概率为31 = 62.解法二:设甲、乙选到A为事件M,乙选到B为事件N,则甲选到A的概率为()2435C3 C5P M==;乙选了A活动,他再选择B活动的概率为()()()133524351C2CCP MN CP N MP M===故答案为:35;122.(2023∙全国甲卷∙高考真题)某地的中学生中有60%的同学爱好滑冰,50%的同学爱好滑雪,70%的同学爱好滑冰或爱好滑雪.在该地的中学生中随机调查一位同学,若该同学爱好滑雪,则该同学也爱好滑冰的概率为( ) A .0.8 B .0.6C .0.5D .0.4【答案】A【详细分析】先算出同时爱好两项的概率,利用条件概率的知识求解. 【答案详解】同时爱好两项的概率为0.50.60.70.4+-=, 记“该同学爱好滑雪”为事件A ,记“该同学爱好滑冰”为事件B , 则()0.5,()0.4P A P AB ==,所以()0.4()0.8()0.5P AB P B A P A ===∣. 故选:A .3.(2022∙天津∙高考真题)52张扑克牌,没有大小王,无放回地抽取两次,则两次都抽到A 的概率为 ;已知第一次抽到的是A ,则第二次抽取A 的概率为 【答案】1221 117【详细分析】由题意结合概率的乘法公式可得两次都抽到A 的概率,再由条件概率的公式即可求得在第一次抽到A 的条件下,第二次抽到A 的概率.【答案详解】由题意,设第一次抽到A 的事件为B ,第二次抽到A 的事件为C ,则()()()()1431411221,(),|1525122152131713BC P BC P B P C B P B P =⨯======. 故答案为:1221;117.考点03 全概率公式与贝叶斯公式1.(2024∙上海∙高考真题)某校举办科学竞技比赛,有、、A B C 3种题库,A 题库有5000道题,B 题库有4000道题,C 题库有3000道题.小申已完成所有题,他A 题库的正确率是0.92,B 题库的正确率是0.86,C 题库的正确率是0.72.现他从所有的题中随机选一题,正确率是 .【答案】0.85【详细分析】求出各题库所占比,根据全概率公式即可得到答案. 【答案详解】由题意知,,,A B C 题库的比例为:5:4:3, 各占比分别为543,,121212, 则根据全概率公式知所求正确率5430.920.860.720.85121212p =⨯+⨯+⨯=.故答案为:0.85.(附加)2.(2023∙全国新Ⅰ卷∙高考真题)甲、乙两人投篮,每次由其中一人投篮,规则如下:若命中则此人继续投篮,若末命中则换为对方投篮.无论之前投篮情况如何,甲每次投篮的命中率均为0.6,乙每次投篮的命中率均为0.8.由抽签确定第1次投篮的人选,第1次投篮的人是甲、乙的概率各为0.5. (1)求第2次投篮的人是乙的概率; (2)求第i 次投篮的人是甲的概率;(3)已知:若随机变量i X 服从两点分布,且()()110,1,2,,i i i P X P X q i n ==-===⋅⋅⋅,则11n n i i i i E X q ==⎛⎫= ⎪⎝⎭∑∑.记前n 次(即从第1次到第n 次投篮)中甲投篮的次数为Y ,求()E Y . 【答案】(1)0.6(2)1121653i -⎛⎫⨯+ ⎪⎝⎭(3)52()11853nnE Y ⎡⎤⎛⎫=-+⎢⎥ ⎪⎝⎭⎢⎥⎣⎦【详细分析】(1)根据全概率公式即可求出;(2)设()i i P A p =,由题意可得10.40.2i i p p +=+,根据数列知识,构造等比数列即可解出; (3)先求出两点分布的期望,再根据题中的结论以及等比数列的求和公式即可求出. 【答案详解】(1)记“第i 次投篮的人是甲”为事件i A ,“第i 次投篮的人是乙”为事件i B , 所以,()()()()()()()21212121121||P B P A B P B B P A P B A P B P B B =+=+ ()0.510.60.50.80.6=⨯-+⨯=.(2)设()i i P A p =,依题可知,()1i i P B p =-,则()()()()()()()11111||i i i i i i i i i i i P A P A A P B A P A P A A P B P A B +++++=+=+,即()()10.610.810.40.2i i i i p p p p +=+-⨯-=+, 构造等比数列{}i p λ+, 设()125i i p p λλ++=+,解得13λ=-,则1121353i i p p +⎛⎫-=- ⎪⎝⎭, 又11111,236p p =-=,所以13i p ⎧⎫-⎨⎩⎭是首项为16,公比为25的等比数列,即11112121,365653i i i i p p --⎛⎫⎛⎫-=⨯=⨯+ ⎪ ⎪⎝⎭⎝⎭. (3)因为1121653i i p -⎛⎫=⨯+ ⎪⎝⎭,1,2,,i n =⋅⋅⋅,所以当*N n ∈时,()122115251263185315nn n n n E Y p p p ⎛⎫- ⎪⎡⎤⎛⎫⎝⎭=+++=⨯+=-+⎢⎥ ⎪⎝⎭⎢⎥⎣⎦- ,故52()11853nnE Y ⎡⎤⎛⎫=-+⎢⎥ ⎪⎝⎭⎢⎥⎣⎦. 【名师点评】本题第一问直接考查全概率公式的应用,后两问的解题关键是根据题意找到递推式,然后根据数列的基本知识求解.考点04 正态分布指定区间的概率1.(2024∙全国新Ⅰ卷∙高考真题)(多选)随着“一带一路”国际合作的深入,某茶叶种植区多措并举推动茶叶出口.为了解推动出口后的亩收入(单位:万元)情况,从该种植区抽取样本,得到推动出口后亩收入的样本均值 2.1x =,样本方差20.01s =,已知该种植区以往的亩收入X 服从正态分布()21.8,0.1N ,假设推动出口后的亩收入Y 服从正态分布()2,N x s ,则( )(若随机变量Z 服从正态分布()2,N μσ,()0.8413P Z μσ<+≈)A .(2)0.2P X >>B .(2)0.5P X ><C .(2)0.5P Y >>D .(2)0.8P Y ><【答案】BC【详细分析】根据正态分布的3σ原则以及正态分布的对称性即可解出. 【答案详解】依题可知,22.1,0.01x s ==,所以()2.1,0.1Y N ,故()()()2 2.10.1 2.10.10.84130.5P Y P Y P Y >=>-=<+≈>,C 正确,D 错误; 因为()1.8,0.1X N ,所以()()2 1.820.1P X P X >=>+⨯,因为()1.80.10.8413P X <+≈,所以()1.80.110.84130.15870.2P X >+≈-=<, 而()()()2 1.820.1 1.80.10.2P X P X P X >=>+⨯<>+<,B 正确,A 错误, 故选:BC .2.(2022∙全国新Ⅱ卷∙高考真题)已知随机变量X 服从正态分布()22,N σ,且(2 2.5)0.36P X <≤=,则( 2.5)P X >= .【答案】0.14/750. 【详细分析】根据正态分布曲线的性质即可解出.【答案详解】因为()22,X N σ ,所以()()220.5P X P X <=>=,因此()()()2.522 2.50.50.360.14P X P X P X >=>-<≤=-=.故答案为:0.14.3.(2021∙全国新Ⅱ卷∙高考真题)某物理量的测量结果服从正态分布()210,N σ,下列结论中不正确的是( ) A .σ越小,该物理量在一次测量中在(9.9,10.1)的概率越大 B .该物理量在一次测量中大于10的概率为0.5C .该物理量在一次测量中小于9.99与大于10.01的概率相等D .该物理量在一次测量中落在(9.9,10.2)与落在(10,10.3)的概率相等【答案】D【详细分析】由正态分布密度曲线的特征逐项判断即可得解.【答案详解】对于A ,2σ为数据的方差,所以σ越小,数据在10μ=附近越集中,所以测量结果落在()9.9,10.1内的概率越大,故A 正确;对于B ,由正态分布密度曲线的对称性可知该物理量一次测量大于10的概率为0.5,故B 正确;对于C ,由正态分布密度曲线的对称性可知该物理量一次测量结果大于10.01的概率与小于9.99的概率相等,故C 正确;对于D ,因为该物理量一次测量结果落在()9.9,10.0的概率与落在()10.2,10.3的概率不同,所以一次测量结果落在()9.9,10.2的概率与落在()10,10.3的概率不同,故D 错误. 故选:D.。
中国历届高考数学试卷

一、1977年高考数学试卷1977年是我国恢复高考的第一年,数学试卷如下:1. (1)求函数y=2x-1在x=2时的函数值。
(2)已知等差数列的前三项分别为2,5,8,求该数列的通项公式。
2. (1)若三角形ABC的三边长分别为a,b,c,且a=3,b=4,c=5,求该三角形的面积。
(2)已知函数y=x^2-4x+4,求该函数的顶点坐标。
二、1980年高考数学试卷1980年高考数学试卷如下:1. (1)已知等差数列的前三项分别为3,5,7,求该数列的通项公式。
(2)若等比数列的首项为2,公比为3,求该数列的前5项。
2. (1)已知圆的方程为x^2+y^2=4,求该圆的面积。
(2)若函数y=3x-2,求该函数在x=1时的导数。
三、1990年高考数学试卷1990年高考数学试卷如下:1. (1)已知等差数列的前三项分别为1,4,7,求该数列的通项公式。
(2)若等比数列的首项为1,公比为2,求该数列的前4项。
2. (1)已知圆的方程为x^2+y^2=9,求该圆的半径。
(2)若函数y=e^x,求该函数在x=0时的导数。
四、2000年高考数学试卷2000年高考数学试卷如下:1. (1)已知等差数列的前三项分别为2,5,8,求该数列的通项公式。
(2)若等比数列的首项为1,公比为3,求该数列的前5项。
2. (1)已知圆的方程为x^2+y^2=16,求该圆的面积。
(2)若函数y=lnx,求该函数在x=1时的导数。
五、2010年高考数学试卷2010年高考数学试卷如下:1. (1)已知等差数列的前三项分别为3,6,9,求该数列的通项公式。
(2)若等比数列的首项为2,公比为4,求该数列的前4项。
2. (1)已知圆的方程为x^2+y^2=25,求该圆的半径。
(2)若函数y=sinx,求该函数在x=π/2时的导数。
通过以上历届高考数学试卷,我们可以看出高考数学试卷的题型和难度逐年递增,考察的知识点也越来越广泛。
考生在备考过程中,需要掌握基础知识,提高解题能力,才能在高考中取得优异成绩。
历年(2019-2024)全国高考数学真题分类(统计与数字特征)汇编(附答案)
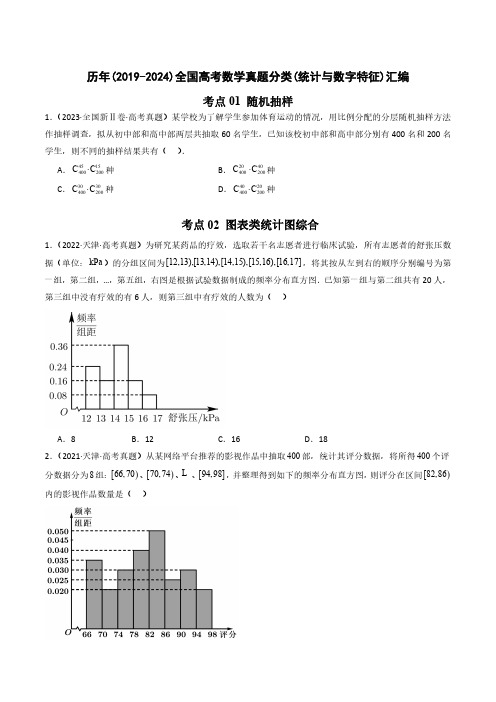
历年(2019-2024)全国高考数学真题分类(统计与数字特征)汇编考点01 随机抽样1.(2023∙全国新Ⅱ卷∙高考真题)某学校为了解学生参加体育运动的情况,用比例分配的分层随机抽样方法作抽样调查,拟从初中部和高中部两层共抽取60名学生,已知该校初中部和高中部分别有400名和200名学生,则不同的抽样结果共有( ).A .4515400200C C ⋅种B .2040400200C C ⋅种 C .3030400200C C ⋅种D .4020400200C C ⋅种考点02 图表类统计图综合1.(2022∙天津∙高考真题)为研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa )的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,…,第五组,右图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )A .8B .12C .16D .182.(2021∙天津∙高考真题)从某网络平台推荐的影视作品中抽取400部,统计其评分数据,将所得400个评分数据分为8组:[)66,70、[)70,74、L 、[]94,98,并整理得到如下的频率分布直方图,则评分在区间[)82,86内的影视作品数量是( )A.20 B.40 C.64 D.804.(2021∙全国甲卷∙高考真题)为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:根据此频率分布直方图,下面结论中不正确的是()A.该地农户家庭年收入低于4.5万元的农户比率估计为6%B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%C.估计该地农户家庭年收入的平均值不超过6.5万元D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间5.(2020∙全国新Ⅱ卷∙高考真题)(多选)我国新冠肺炎疫情进入常态化,各地有序推进复工复产,下面是某地连续11天复工复产指数折线图,下列说法正确的是A.这11天复工指数和复产指数均逐日增加;B.这11天期间,复产指数增量大于复工指数的增量;C.第3天至第11天复工复产指数均超过80%;D.第9天至第11天复产指数增量大于复工指数的增量;5.(2020∙天津∙高考真题)从一批零件中抽取80个,测量其直径(单位:mm),将所得数据分为9组:[)[)[)[],并整理得到如下频率分布直方图,则在被抽取的零件中,5.31,5.33,5.33,5.35,,5.45,5.47,5.47,5.49直径落在区间[5.43,5.47)内的个数为()A.10 B.18 C.20 D.36考点03 样本的数字特征一、单选题1.(2024∙全国新Ⅱ卷∙高考真题)某农业研究部门在面积相等的100块稻田上种植一种新型水稻,得到各块稻田的亩产量(单位:kg)并整理如下表亩产[900,950) [950,1000) [1000,1050) [1050,1100) [1100,1150) [1150,1200) 量频数 6 12 18 30 24 10根据表中数据,下列结论中正确的是()A.100块稻田亩产量的中位数小于1050kgB.100块稻田中亩产量低于1100kg的稻田所占比例超过80%C.100块稻田亩产量的极差介于200kg至300kg之间D.100块稻田亩产量的平均值介于900kg至1000kg之间2.(2022∙全国乙卷∙高考真题)分别统计了甲、乙两位同学16周的各周课外体育运动时长(单位:h),得如下茎叶图:则下列结论中错误的是()A.甲同学周课外体育运动时长的样本中位数为7.4B.乙同学周课外体育运动时长的样本平均数大于8C .甲同学周课外体育运动时长大于8的概率的估计值大于0.4D .乙同学周课外体育运动时长大于8的概率的估计值大于0.63.(2022∙全国甲卷∙高考真题)某社区通过公益讲座以普及社区居民的垃圾分类知识.为了解讲座效果,随机抽取10位社区居民,让他们在讲座前和讲座后各回答一份垃圾分类知识问卷,这10位社区居民在讲座前和讲座后问卷答题的正确率如下图:则( )A .讲座前问卷答题的正确率的中位数小于70%B .讲座后问卷答题的正确率的平均数大于85%C .讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差D .讲座后问卷答题的正确率的极差大于讲座前正确率的极差4.(2020∙全国∙高考真题)在一组样本数据中,1,2,3,4出现的频率分别为1234,,,p p p p ,且411i i p ==∑,则下面四种情形中,对应样本的标准差最大的一组是( )A .14230.1,0.4p p p p ====B .14230.4,0.1p p p p ====C .14230.2,0.3p p p p ====D .14230.3,0.2p p p p ====5.(2020∙全国∙高考真题)设一组样本数据x 1,x 2,…,xn 的方差为0.01,则数据10x 1,10x 2,…,10xn 的方差为( )A .0.01B .0.1C .1D .106.(2019∙全国∙高考真题)演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是A .中位数B .平均数C .方差D .极差二、多选题9.(2023∙全国新Ⅰ卷∙高考真题)有一组样本数据126,,,x x x ⋅⋅⋅,其中1x 是最小值,6x 是最大值,则( ) A .2345,,,x x x x 的平均数等于126,,,x x x ⋅⋅⋅的平均数B .2345,,,x x x x 的中位数等于126,,,x x x ⋅⋅⋅的中位数C .2345,,,x x x x 的标准差不小于126,,,x x x ⋅⋅⋅的标准差D .2345,,,x x x x 的极差不大于126,,,x x x ⋅⋅⋅的极差10.(2021∙全国新Ⅱ卷∙高考真题)下列统计量中,能度量样本12,,,n x x x 的离散程度的是( )A .样本12,,,n x x x 的标准差B .样本12,,,n x x x 的中位数C .样本12,,,n x x x 的极差D .样本12,,,n x x x 的平均数11.(2021∙全国新Ⅰ卷∙高考真题)有一组样本数据1x ,2x ,…,n x ,由这组数据得到新样本数据1y ,2y ,…,n y ,其中i i y x c =+(1,2,,),i n c =⋅⋅⋅为非零常数,则( )A .两组样本数据的样本平均数相同B .两组样本数据的样本中位数相同C .两组样本数据的样本标准差相同D .两组样本数据的样本极差相同三、填空题12.(2020∙江苏∙高考真题)已知一组数据4,2,3,5,6a a -的平均数为4,则a 的值是 .13.(2019∙江苏∙高考真题)已知一组数据6,7,8,8,9,10,则该组数据的方差是 .考点04 变量间的相关关系1.(2024∙天津∙高考真题)下列图中,线性相关性系数最大的是( )A .B .C .D .2.(2023∙天津∙高考真题)鸢是鹰科的一种鸟,《诗经∙大雅∙旱麓》曰:“鸢飞戾天,鱼跃余渊”. 鸢尾花因花瓣形如鸢尾而得名,寓意鹏程万里、前途无量.通过随机抽样,收集了若干朵某品种鸢尾花的花萼长度和花瓣长度(单位:cm ),绘制散点图如图所示,计算得样本相关系数为0.8642r =,利用最小二乘法求得相应的经验回归方程为 0.75010.6105y x =+,根据以上信息,如下判断正确的为( )A .花瓣长度和花萼长度不存在相关关系B .花瓣长度和花萼长度负相关C .花萼长度为7cm 的该品种鸢尾花的花瓣长度的平均值为5.8612cmD .若从样本中抽取一部分,则这部分的相关系数一定是0.86423.(2020∙全国∙高考真题)某校一个课外学习小组为研究某作物种子的发芽率y 和温度x (单位:°C )的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(,)(1,2,,20)i i x y i = 得到下面的散点图:由此散点图,在10°C 至40°C 之间,下面四个回归方程类型中最适宜作为发芽率y 和温度x 的回归方程类型的是( )A .y a bx =+B .2y a bx =+C .e x y a b =+D .ln y a b x =+参考答案考点01 随机抽样1.(2023∙全国新Ⅱ卷∙高考真题)某学校为了解学生参加体育运动的情况,用比例分配的分层随机抽样方法作抽样调查,拟从初中部和高中部两层共抽取60名学生,已知该校初中部和高中部分别有400名和200名学生,则不同的抽样结果共有( ).A .4515400200C C ⋅种B .2040400200C C ⋅种 C .3030400200C C ⋅种 D .4020400200C C ⋅种【答案】D【详细分析】利用分层抽样的原理和组合公式即可得到答案. 【答案详解】根据分层抽样的定义知初中部共抽取4006040600⨯=人,高中部共抽取2006020600⨯=, 根据组合公式和分步计数原理则不同的抽样结果共有4020400200C C ⋅种.故选:D.考点02 图表类统计图综合1.(2022∙天津∙高考真题)为研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa )的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,…,第五组,右图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )A .8B .12C .16D .18【答案】B 【详细分析】结合已知条件和频率分布直方图求出志愿者的总人数,进而求出第三组的总人数,从而可以求得结果. 【答案详解】志愿者的总人数为20(0.240.16)1+⨯=50, 所以第三组人数为50×0.36=18,有疗效的人数为18-6=12.故选:B.2.(2021∙天津∙高考真题)从某网络平台推荐的影视作品中抽取400部,统计其评分数据,将所得400个评分数据分为8组:[)66,70、[)70,74、L 、[]94,98,并整理得到如下的频率分布直方图,则评分在区间[)82,86内的影视作品数量是( )A .20B .40C .64D .80【答案】D 【详细分析】利用频率分布直方图可计算出评分在区间[)82,86内的影视作品数量.【答案详解】由频率分布直方图可知,评分在区间[)82,86内的影视作品数量为4000.05480⨯⨯=.故选:D.4.(2021∙全国甲卷∙高考真题)为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:根据此频率分布直方图,下面结论中不正确的是( )A .该地农户家庭年收入低于4.5万元的农户比率估计为6%B .该地农户家庭年收入不低于10.5万元的农户比率估计为10%C .估计该地农户家庭年收入的平均值不超过6.5万元D .估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间【答案】C【详细分析】根据直方图的意义直接计算相应范围内的频率,即可判定ABD,以各组的中间值作为代表乘以相应的频率,然后求和即得到样本的平均数的估计值,也就是总体平均值的估计值,计算后即可判定C.【答案详解】因为频率直方图中的组距为1,所以各组的直方图的高度等于频率.样本频率直方图中的频率即可作为总体的相应比率的估计值.该地农户家庭年收入低于4.5万元的农户的比率估计值为0.020.040.066%+==,故A 正确;该地农户家庭年收入不低于10.5万元的农户比率估计值为0.040.0230.1010%+⨯==,故B 正确;该地农户家庭年收入介于4.5万元至8.5万元之间的比例估计值为0.100.140.2020.6464%50%++⨯==>,故D 正确;该地农户家庭年收入的平均值的估计值为30.0240.0450.1060.1470.2080.2090.10100.10110.04120.02130.02140.027.68⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯=(万元),超过6.5万元,故C 错误.综上,给出结论中不正确的是C.故选:C.【名师点评】本题考查利用样本频率直方图估计总体频率和平均值,属基础题,样本的频率可作为总体的频率的估计值,样本的平均值的估计值是各组的中间值乘以其相应频率然后求和所得值,可以作为总体的平均值的估计值.注意各组的频率等于⨯频率组距组距. 5.(2020∙全国新Ⅱ卷∙高考真题)(多选)我国新冠肺炎疫情进入常态化,各地有序推进复工复产,下面是某地连续11天复工复产指数折线图,下列说法正确的是A .这11天复工指数和复产指数均逐日增加;B .这11天期间,复产指数增量大于复工指数的增量;C .第3天至第11天复工复产指数均超过80%;D .第9天至第11天复产指数增量大于复工指数的增量;【答案】CD【详细分析】注意到折线图中有递减部分,可判定A 错误;注意考查第1天和第11天的复工复产指数的差的大小,可判定B 错误;根据图象,结合复工复产指数的意义和增量的意义可以判定CD 正确.【答案详解】由图可知,第1天到第2天复工指数减少,第7天到第8天复工指数减少,第10天到第11复工指数减少,第8天到第9天复产指数减少,故A 错误;由图可知,第一天的复产指标与复工指标的差大于第11天的复产指标与复工指标的差,所以这11天期间,复产指数增量小于复工指数的增量,故B 错误;由图可知,第3天至第11天复工复产指数均超过80%,故C 正确;由图可知,第9天至第11天复产指数增量大于复工指数的增量,故D 正确;【名师点评】本题考查折线图表示的函数的认知与理解,考查理解能力,识图能力,推理能力,难点在于指数增量的理解与观测,属中档题.5.(2020∙天津∙高考真题)从一批零件中抽取80个,测量其直径(单位:mm ),将所得数据分为9组:[)[)[)[]5.31,5.33,5.33,5.35,,5.45,5.47,5.47,5.49 ,并整理得到如下频率分布直方图,则在被抽取的零件中,直径落在区间[5.43,5.47)内的个数为( )A .10B .18C .20D .36【答案】B 【详细分析】根据直方图确定直径落在区间[)5.43,5.47之间的零件频率,然后结合样本总数计算其个数即可. 【答案详解】根据直方图,直径落在区间[)5.43,5.47之间的零件频率为:()6.25 5.000.020.225+⨯=, 则区间[)5.43,5.47内零件的个数为:800.22518⨯=.故选:B.【名师点评】本题主要考查频率分布直方图的计算与实际应用,属于中等题.考点03 样本的数字特征一、单选题1.(2024∙全国新Ⅱ卷∙高考真题)某农业研究部门在面积相等的100块稻田上种植一种新型水稻,得到各块稻田的亩产量(单位:kg )并整理如下表 亩产量[900,950) [950,1000) [1000,1050) [1050,1100) [1100,1150) [1150,1200) 频数 6 12 18 30 24 10 根据表中数据,下列结论中正确的是( )A .100块稻田亩产量的中位数小于1050kgB .100块稻田中亩产量低于1100kg 的稻田所占比例超过80%C .100块稻田亩产量的极差介于200kg 至300kg 之间D .100块稻田亩产量的平均值介于900kg 至1000kg 之间【答案】C【详细分析】计算出前三段频数即可判断A ;计算出低于1100kg 的频数,再计算比例即可判断B ;根据极差计算方法即可判断C ;根据平均值计算公式即可判断D.【答案详解】对于 A, 根据频数分布表可知, 612183650++=<,所以亩产量的中位数不小于 1050kg , 故 A 错误;对于B ,亩产量不低于1100kg 的频数为341024=+,所以低于1100kg 的稻田占比为1003466%100-=,故B 错误; 对于C ,稻田亩产量的极差最大为1200900300-=,最小为1150950200-=,故C 正确;对于D ,由频数分布表可得,平均值为1(692512975181025301075241125101175)1067100⨯⨯+⨯+⨯+⨯+⨯+⨯=,故D 错误. 故选;C.2.(2022∙全国乙卷∙高考真题)分别统计了甲、乙两位同学16周的各周课外体育运动时长(单位:h ),得如下茎叶图:则下列结论中错误的是( )A .甲同学周课外体育运动时长的样本中位数为7.4B .乙同学周课外体育运动时长的样本平均数大于8C .甲同学周课外体育运动时长大于8的概率的估计值大于0.4D .乙同学周课外体育运动时长大于8的概率的估计值大于0.6【答案】C【详细分析】结合茎叶图、中位数、平均数、古典概型等知识确定正确答案.【答案详解】对于A 选项,甲同学周课外体育运动时长的样本中位数为7.37.57.42+=,A 选项结论正确.对于B 选项,乙同学课外体育运动时长的样本平均数为:6.37.47.68.18.28.28.58.68.68.68.69.09.29.39.810.18.50625816+++++++++++++++=>, B 选项结论正确.对于C 选项,甲同学周课外体育运动时长大于8的概率的估计值60.3750.416=<, C 选项结论错误.对于D 选项,乙同学周课外体育运动时长大于8的概率的估计值130.81250.616=>, D 选项结论正确.故选:C3.(2022∙全国甲卷∙高考真题)某社区通过公益讲座以普及社区居民的垃圾分类知识.为了解讲座效果,随机抽取10位社区居民,让他们在讲座前和讲座后各回答一份垃圾分类知识问卷,这10位社区居民在讲座前和讲座后问卷答题的正确率如下图:则( )A .讲座前问卷答题的正确率的中位数小于70%B .讲座后问卷答题的正确率的平均数大于85%C .讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差D .讲座后问卷答题的正确率的极差大于讲座前正确率的极差【答案】B【详细分析】由图表信息,结合中位数、平均数、标准差、极差的概念,逐项判断即可得解. 【答案详解】讲座前中位数为70%75%70%2+>,所以A 错; 讲座后问卷答题的正确率只有一个是80%,4个85%,剩下全部大于等于90%,所以讲座后问卷答题的正确率的平均数大于85%,所以B 对;讲座前问卷答题的正确率更加分散,所以讲座前问卷答题的正确率的标准差大于讲座后正确率的标准差,所以C 错;讲座后问卷答题的正确率的极差为100%80%20%-=,讲座前问卷答题的正确率的极差为95%60%35%20%-=>,所以D 错.故选:B.4.(2020∙全国∙高考真题)在一组样本数据中,1,2,3,4出现的频率分别为1234,,,p p p p ,且411i i p ==∑,则下面四种情形中,对应样本的标准差最大的一组是( )A .14230.1,0.4p p p p ====B .14230.4,0.1p p p p ====C .14230.2,0.3p p p p ====D .14230.3,0.2p p p p ====【答案】B【详细分析】计算出四个选项中对应数据的平均数和方差,由此可得出标准差最大的一组.【答案详解】对于A 选项,该组数据的平均数为()()140.1230.4 2.5A x =+⨯++⨯=,方差为()()()()222221 2.50.12 2.50.43 2.50.44 2.50.10.65A s =-⨯+-⨯+-⨯+-⨯=; 对于B 选项,该组数据的平均数为()()140.4230.1 2.5B x =+⨯++⨯=,方差为()()()()222221 2.50.42 2.50.13 2.50.14 2.50.4 1.85B s =-⨯+-⨯+-⨯+-⨯=; 对于C 选项,该组数据的平均数为()()140.2230.3 2.5C x =+⨯++⨯=,方差为()()()()222221 2.50.22 2.50.33 2.50.34 2.50.2 1.05C s =-⨯+-⨯+-⨯+-⨯=; 对于D 选项,该组数据的平均数为()()140.3230.2 2.5D x =+⨯++⨯=,方差为()()()()222221 2.50.32 2.50.23 2.50.24 2.50.3 1.45D s =-⨯+-⨯+-⨯+-⨯=. 因此,B 选项这一组的标准差最大.故选:B.【名师点评】本题考查标准差的大小比较,考查方差公式的应用,考查计算能力,属于基础题. 5.(2020∙全国∙高考真题)设一组样本数据x 1,x 2,…,xn 的方差为0.01,则数据10x 1,10x 2,…,10xn 的方差为( )A .0.01B .0.1C .1D .10【答案】C【详细分析】根据新数据与原数据关系确定方差关系,即得结果. 【答案详解】因为数据(1,2,,)i ax b i n +=L ,的方差是数据(1,2,,)i x i n =L ,的方差的2a 倍, 所以所求数据方差为2100.01=1⨯故选:C【名师点评】本题考查方差,考查基本详细分析求解能力,属基础题.6.(2019∙全国∙高考真题)演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是A .中位数B .平均数C .方差D .极差【答案】A【详细分析】可不用动笔,直接得到答案,亦可采用特殊数据,特值法筛选答案.【答案详解】设9位评委评分按从小到大排列为123489x x x x x x ≤≤≤≤≤ .则①原始中位数为5x ,去掉最低分1x ,最高分9x ,后剩余2348x x x x ≤≤≤ ,中位数仍为5x ,∴A 正确. ②原始平均数1234891()9x x x x x x x =+++++ ,后来平均数234817x x x x x '=+++ () 平均数受极端值影响较大,∴x 与x '不一定相同,B 不正确 ③()()()222219119S x x x x x x ⎡⎤=-+-++-⎣⎦ ()()()222223817s x x x x x x ⎡⎤'=-'+-'++-'⎢⎥⎣⎦ 由②易知,C 不正确. ④原极差91=x -x ,后来极差82=x -x 可能相等可能变小,D 不正确.【名师点评】本题旨在考查学生对中位数、平均数、方差、极差本质的理解.考点04 变量间的相关关系1.(2024∙天津∙高考真题)下列图中,线性相关性系数最大的是( )A .B .C .D .【答案】A【详细分析】由点的分布特征可直接判断【答案详解】观察4幅图可知,A 图散点分布比较集中,且大体接近某一条直线,线性回归模型拟合效果比较好,呈现明显的正相关,r 值相比于其他3图更接近1.故选:A2.(2023∙天津∙高考真题)鸢是鹰科的一种鸟,《诗经∙大雅∙旱麓》曰:“鸢飞戾天,鱼跃余渊”. 鸢尾花因花瓣形如鸢尾而得名,寓意鹏程万里、前途无量.通过随机抽样,收集了若干朵某品种鸢尾花的花萼长度和花瓣长度(单位:cm ),绘制散点图如图所示,计算得样本相关系数为0.8642r =,利用最小二乘法求得相应的经验回归方程为 0.75010.6105y x =+,根据以上信息,如下判断正确的为( )A .花瓣长度和花萼长度不存在相关关系B .花瓣长度和花萼长度负相关C .花萼长度为7cm 的该品种鸢尾花的花瓣长度的平均值为5.8612cmD .若从样本中抽取一部分,则这部分的相关系数一定是0.8642【答案】C【详细分析】根据散点图的特点及经验回归方程可判断ABC 选项,根据相关系数的定义可以判断D 选项.【答案详解】根据散点的集中程度可知,花瓣长度和花萼长度有相关性,A 选项错误散点的分布是从左下到右上,从而花瓣长度和花萼长度呈现正相关性,B 选项错误,把7x =代入 0.75010.6105y x =+可得 5.8612cm y =,C 选项正确;由于0.8642r =是全部数据的相关系数,取出来一部分数据,相关性可能变强,可能变弱,即取出的数据的相关系数不一定是0.8642,D 选项错误故选:C3.(2020∙全国∙高考真题)某校一个课外学习小组为研究某作物种子的发芽率y 和温度x (单位:°C )的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(,)(1,2,,20)i i x y i = 得到下面的散点图:由此散点图,在10°C 至40°C 之间,下面四个回归方程类型中最适宜作为发芽率y 和温度x 的回归方程类型的是( )A .y a bx =+B .2y a bx =+C .e x y a b =+D .ln y a b x =+ 【答案】D【详细分析】根据散点图的分布可选择合适的函数模型.【答案详解】由散点图分布可知,散点图分布在一个对数函数的图象附近, 因此,最适合作为发芽率y 和温度x 的回归方程类型的是ln y a b x =+. 故选:D.【名师点评】本题考查函数模型的选择,主要观察散点图的分布,属于基础题.。
高考数学试题140道及答案

高考数学试题140道及答案一、选择题(本题共8小题,每小题5分,共40分)1. 若函数f(x) = x^2 - 4x + 3的零点为x1和x2,则x1 + x2的值为:A. 2B. 3C. 4D. 5答案:B2. 已知向量a = (3, -1),向量b = (2, 2),则向量a与向量b的点积为:A. 4B. 5C. 6D. 7答案:A3. 若sin(α) = 1/2,则cos(2α)的值为:A. 1/2B. -1/2C. 0D. -1答案:B4. 已知数列{an}为等差数列,且a1 = 2,a3 = 6,则数列的公差d为:A. 1B. 2C. 3D. 4答案:B5. 函数y = ln(x)的导数为:A. 1/xB. xC. x^2D. 1/x^2答案:A6. 已知抛物线y = x^2 - 4x + 4的顶点坐标为:A. (2, 0)B. (-2, 0)C. (2, 4)D. (-2, 4)答案:A7. 已知双曲线x^2/a^2 - y^2/b^2 = 1的焦点在x轴上,且a = 2,则b的值为:A. 2B. 3C. 4D. 5答案:B8. 已知圆的方程为(x - 1)^2 + (y - 2)^2 = 9,圆心到直线x + y - 3 = 0的距离为:A. 1B. 2C. 3D. 4答案:C二、填空题(本题共6小题,每小题5分,共30分)9. 已知函数f(x) = x^3 - 3x^2 + 2,求f'(x) = _______。
答案:3x^2 - 6x10. 已知三角形ABC的边长分别为a = 3,b = 4,c = 5,求三角形的面积S = _______。
答案:611. 已知等比数列{bn}的首项b1 = 2,公比q = 3,求第n项bn = _______。
答案:2 * 3^(n-1)12. 已知直线l的方程为y = 2x + 1,求直线l与x轴的交点坐标为(_______,_______)。
历年高考数学真题(全国卷整理版)完整版完整版

参考公式:如果事件 A、B互斥,那么球的表面积公式P( A B) P( A) P(B)S 4R2如果事件 A、B相互独立,那么其中 R表示球的半径P(A B) P( A) P(B)球的体积公式如果事件 A 在一次试验中发生的概率是p ,那么V3R3n 次独立重复试验中事件 A 恰好发生k次的概率4其中 R 表示球的半径P n (k ) C n k p k (1 p)n k (k 0,1,2, n)普通高等学校招生全国统一考试一、选择题13i 1、复数i =1A 2+I B2-I C 1+2i D 1- 2i2、已知集合 A ={1.3.m },B={1,m} ,A B = A, 则 m=A0或3 B 0或3C1或3 D 1或33椭圆的中心在原点,焦距为 4 一条准线为 x=-4 ,则该椭圆的方程为A x2y2=1Bx2y2=1 16++12128C x2y2=1Dx2y28+12+=1 444已知正四棱柱ABCD- A 1B 1C1D1中,AB=2 ,CC1= 2 2 E 为 CC1的中点,则直线 AC 1与平面 BED 的距离为A2B3C2D1(5)已知等差数列{a n} 的前 n 项和为 S n, a5=5, S5=15,则数列的前100项和为10099(C)99101(A)(B)(D)100101101100(6)△ ABC 中, AB 边的高为 CD ,若a· b=0, |a|=1, |b|=2,则(A)(B)(C)(D)3(7)已知α为第二象限角,sinα+ sinβ =3,则 cos2α = 5555--(C) 9(D)3(A)3(B)9(8)已知 F1、 F2 为双曲线 C: x2-y2=2的左、右焦点,点P 在 C 上, |PF1|=|2PF2|,则 cos ∠F1PF2=1334(A) 4(B)5(C)4(D)51(9)已知 x=ln π, y=log52 ,z=e2,则(A)x < y< z(B)z<x<y(C)z < y< x(D)y < z< x(10) 已知函数y= x2-3x+c 的图像与 x 恰有两个公共点,则c=(A )-2 或 2 (B)-9 或 3 (C)-1 或 1 (D)-3 或 1(11)将字母 a,a,b,b,c,c,排成三行两列,要求每行的字母互不相同,梅列的字母也互不相同,则不同的排列方法共有(A)12 种( B)18 种( C)24 种( D)36 种7(12)正方形 ABCD 的边长为1,点 E 在边 AB 上,点 F 在边 BC 上, AE = BF =3。
(word完整版)历年高考数学真题(全国卷整理版)43964.doc

实用文档参考公式:如果事件 A、B互斥,那么P( A B) P( A)P( B)如果事件 A、B相互独立,那么P(AgB)P( A)gP( B)如果事件 A 在一次试验中发生的概率是p ,那么n 次独立重复试验中事件 A 恰好发生 k 次的概率P n (k ) C n k p k (1 p)n k (k 0,1,2,⋯n) 球的表面积公式S 4R2其中 R 表示球的半径球的体积公式V 3 R34其中 R表示球的半径普通高等学校招生全国统一考试一、选择题1、复数 1 3i =1 iA 2+IB 2-IC 1+2iD 1- 2i2、已知集合 A= {1.3. m },B={1,m} ,A U B=A, 则 m=A 0 或3B 0 或 3C 1或3D 1 或 33 椭圆的中心在原点,焦距为4 一条准线为 x=-4 ,则该椭圆的方程为A x2 + y2 =1B x2 + y2 =116 12 12 8C x2 + y2 =1D x2 + y2 =18 4 12 44 已知正四棱柱ABCD- A1B1C1D1中, AB=2, CC= 2 2 E 为 CC的中点,则直线AC与平面1 1 1 BED的距离为A 2B 3C 2D 1(5)已知等差数列{a n} 的前 n 项和为 S n,a5=5, S5=15,则数列的前100项和为(A) 100(B)99(C)99(D)101 101101100100(6)△ ABC中, AB边的高为 CD,若a· b=0, |a|=1 , |b|=2 ,则(A)( B)(C)(D)3(7)已知α为第二象限角, sin α+ sin β =3,则 cos2α =555 5--9(D) 3(A) 3 (B ) 9 (C)(8)已知 F1、 F2 为双曲线 C : x2 -y 2 =2 的左、右焦点,点 P 在 C 上, |PF1|=|2PF2| ,则 cos ∠ F1PF2=1 334(A) 4( B ) 5(C)4(D)51( 9)已知 x=ln π, y=log52 , z=e 2,则 (A)x < y < z ( B ) z < x <y (C)z < y < x (D)y< z < x(10) 已知函数 y = x2 -3x+c 的图像与 x 恰有两个公共点,则 c =(A ) -2 或 2 ( B ) -9 或 3 (C ) -1 或 1 ( D )-3 或 1( 11)将字母 a,a,b,b,c,c, 排成三行两列,要求每行的字母互不相同,梅列的字母也互不相同,则不同的排列方法共有( A ) 12 种( B ) 18 种( C ) 24 种( D ) 36 种7(12)正方形 ABCD 的边长为 1,点 E 在边 AB 上,点 F 在边 BC 上, AE = BF = 3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
历年高考数学试题
命题与逻辑
一.选择题,在每小题给出的四个选择题只有一项是符合题目要求的。
1.设集合A 、B 是全集U 的两个子集,则A B ⊂是()U C A B U ⋃=的( )
(A )充分不必要条件(B )必要不充分条件(C )冲要条件(D )既不充分也不必要条件
2.对任意实数a ,b ,c ,给出下列命题:
①“b a =”是“bc ac =”充要条件;
②“5+a 是无理数”是“a 是无理数”的充要条件;
③“a >b ”是“a 2>b 2”的充分条件;
④“a <5”是“a <3”的必要条件.其中真命题的个数是( )
A .1
B .2
C .3
D .4
3.设α、β为两个不同的平面,l 、m 为两条不同的直线,且βα⊂⊂m l ,. 有如下两个命题:①若m l //,//则βα;②若.,βα⊥⊥则m l 那么( )
A .①是真命题,②是假命题
B .①是假命题,②是真命题
C .①②都是真命题
D .①②都是假命题
4.已知m 、n 是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列四个命题: ①若βαβα//,,则⊥⊥m m ;
②若βααβγα//,,则⊥⊥;
③若βαβα//,//,,则n m n m ⊂⊂;
④若m 、n 是异面直线,βααββα//,//,,//,则n n m m ⊂
⊂ 其中真命题是( )
A .①和②
B .①和③
C .③和④
D .①和④ 5.“m =2
1”是“直线(m +2)x +3my +1=0与直线(m -2)x +(m +2)y -3=0相互垂直”的 (A )充分必要条件 (B )充分而不必要条件 (C )必要而不充分条件 (D )既不充分也不必要条件
6.“a =b ”是“直线相切与圆2)()(222=++-+=b y a x x y ”的( )
A .充分不必要条件
B .必要不充分条件
C .充分必要条件
D .既不充分又不必要条件
7.已知直线m 、n 与平面βα,,给出下列三个命题:
①若;//,//,//n m n m 则αα
②若;,,//m n n m ⊥⊥则αα
③若.,//,βαβα⊥⊥则m m
其中真命题的个数是( )
A .0
B .1
C .2
D .3
8.已知α、β均为锐角,若q p q p 是则,2:),sin(sin :πβαβαα<
++<的 ( ) A .充分而不必要条件 B .必要而不充分条件 C .充要条件 D .既不充分也不必要条件
9.已知直线m 、n 与平面α、β,给出下列三个命题:
①若m//α,n//α,则m//n ;
②若m//α,n ⊥α,则n ⊥m ;
③若m ⊥α,m//β,则α⊥β.
其中真命题的个数是( )
A .0
B .1
C .2
D .3
10.已知q p ab q a p 是则,0:,0:≠≠的( )
A .充分不必要条件
B .必要不充分条件
C .充要条件
D .既不充分也不必要条件
11.在△ABC 中,设命题,sin sin sin :A
c C b B a p ==命题q:△ABC 是等边三角形,那么命题p 是命题q 的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分又不必要条件
12.已知βα,均为锐角,若q p q p 是则,2:),sin(sin :π
βαβαα<++<的 ( )
A .充分而不必要条件
B .必要而不充分条件
C .充要条件
D .既不充分也不必要条件
13.“m =2
1”是“直线(m +2)x +3my +1=0与直线(m -2)x +(m +2)y -3=0相互垂直”的 (A )充分必要条件 (B )充分而不必要条件 (C )必要而不充分条件 (D )既不充分也不必要条件
14.条件甲:“a >1”是条件乙:“a a >”的[答]( )
(A)既不充分也不必要条件 (B) 充要条件 (C) 充分不必要条件 (D)必要不充分条件
15.“1=a ”是“函数||)(a x x f -=在区间),1[+∞上为增函数”的
A .充分不必要条件
B .必要不充分条件
C .充要条件
D .既不充分也不必要条件
16.给出下列四个命题:
①垂直于同一直线的两条直线互相平行.
②垂直于同一平面的两个平面互相平行.
③若直线12,l l 与同一平面所成的角相等,则12,l l 互相平行.
④若直线12,l l 是异面直线,则与12,l l 都相交的两条直线是异面直线.
其中假命题的个数是( )
A.1
B.2
C.3
D.4
17.设p :x 2
-x -20>0,q :212
--x x <0,则p 是q 的 (A )充分不必要条件 (B )必要不充分条件 (C )充要条件 (D )既不充分也不必要条件
18.若空间中有四个点,则“这四个点中有三点在同一直线上”是“这四个点在同一平面上”的( )
(A )充分非必要条件;(B )必要非充分条件;(C )充要条件;(D )非充分非必要条件.
19.如图,平面中两条直线1l 和2l 相交于点O ,对于平面上任意一点M ,若p 、q 分别是M 到直线1l 和2l 的距离,
则称有序非负实数对(p ,q )是点M 的“距离坐标”.已知常数p ≥0,q ≥0,给出下列命题: ①若p =q =0,则“距离坐标”为(0,0)的点有且仅有1个;
②若pq =0,且p +q ≠0,则“距离坐标”为(p ,q )的点有且仅有2个;
③若pq ≠0,则“距离坐标”为(p ,q )的点有且仅有4个.
上述命题中,正确命题的个数是( )
(A )0; (B )1; (C )2; (D )3.
20.“a >b >c ”是“ab <2
2
2b a +”的 (A)充分而不必要条件 (B)必要而不充分条件 (C)充分必要条件 (D)既不允分也不必要条件
21.设,a R ∈b ,已知命题:p a b =;命题2
22:22a b a b q ++⎛⎫≤ ⎪⎝⎭,则p 是q 成立的( ) A .必要不充分条件 B .充分不必要条件C .充分必要条件 D .既不充分也不必要条件
22.对于平面α和共面的直线m 、,n 下列命题中真命题是
(A )若,,m m n α⊥⊥则n α∥ (B )若m αα∥,n ∥,则m ∥n
(C )若,m n αα⊂∥,则m ∥n (D )若m 、n 与α所成的角相等,则m ∥n
23.关于直线m 、n 与平面α、β,有下列四个命题:
①βα//,//n m 且βα//,则n m //; ②βα⊥⊥n m ,且βα⊥,则n m ⊥;
③βα//,n m ⊥且βα//,则n m ⊥; ④βα⊥n m ,//且βα⊥,则n m //.
其中真命题的序号是:
A. ①、②
B. ③、④
C. ①、④
D. ②、③
24.有限集合S 中元素个数记作card ()S ,设A 、B 都为有限集合,给出下列命题:
①φ=B A 的充要条件是card ()B A = card ()A + card ()B ;
②B A ⊆的必要条件是card ()≤A card ()B ;
③B A ⊄的充分条件是card ()≤A card ()B ;
④B A =的充要条件是card ()=A card ()B .
其中真命题的序号是
A. ③、④
B. ①、②
C. ①、④
D. ②、③
25.关于x 的方程()011222=+---k x x ,给出下列四个命题:
①存在实数k ,使得方程恰有2个不同的实根;
②存在实数k ,使得方程恰有4个不同的实根;
③存在实数k ,使得方程恰有5个不同的实根;
④存在实数k ,使得方程恰有8个不同的实根.
其中假命题的个数是
A. 0
B. 1
C. 2
D. 3
26."等式sin(α+γ)=sin2β成立"是"α、β、γ成等差数列"的( ) 1l 2l O
M (p ,q )。
