2019-2020年高考数学大题专题练习——立体几何(一)
精编新版2020高考数学《立体几何初步》专题完整考题(含答案)
2019年高中数学单元测试卷立体几何初步学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．已知正四棱柱1111ABCD A B C D -中12AA AB =,则CD 与平面1BDC 所成角的正弦值等于（ ）A ．23B ．3C ．3D ．13（2013年普通高等学校招生统一考试大纲版数学（理）WORD 版含答案（已校对））2．分别和两条异面直线都相交的两条直线的位置关系是---------------------------------------（ ）(A)异面 (B)相交 (C)平行 (D)异面或相3．已知定直线a ，直线b 同时满足条件：①a b 、异面；②a b 、所成的角为定值α；③a b 、的距离为定值d ，则这样的直线b 有------------------------------------------------------------------（ ）(A) 1条 (B) 2条 (C)4条 (D)无数二、填空题4． 下列四个命题：①若αα⊂b a ,//，则b a //， ②若αα//,//b a ，则b a //③若α⊂b b a ,//，则α//a ， ④若b a a //,//α，则α//b 或α⊂b其中为真命题的序号有 ．（填上所有真命题的序号）5．两条异面直线的所成角的取值范围是_________________6．在两个互相垂直的平面的交线,l A B A C B D 上有两点和和分别在两个平面内且垂直于交线,l 如果AC=3cm,AB =4cm,BD=5cm,那么CD=7．已知l 是一条直线，,αβ是两个不同的平面. 若从“①l α⊥；②//l β；③αβ⊥”中选取两个作为条件，另一个作为结论，试写出一个你认为正确的命题 ▲ .（请用代号表示）8．正三棱锥ABC P -高为2，侧棱与底面成045角，则点A 到侧面PBC 的距离是9．现剪切一块边长为4的正方形铁板，制作成一个母线长为4的圆锥V 的侧面，那么，当剪切掉作废的铁板面积最小时，圆锥V 的体积为 ．10．已知集合{M P =|P 是棱长为1的正方体1111ABCD A B C D -表面上的点，且}AP =，则集合M 中所有点的轨迹的长度是___▲___.11．一个六棱柱的底面是正六边形，其侧棱垂直底面．已知该六棱柱的顶点都在同一个球面 上，且该六棱柱的高为3，底面周长为3，那么这个球的体积为________．解析：∵正六棱柱的底面周长为3，∴正六棱柱的底面边长为12. 又正六棱柱的高为3，∴正六棱柱的过中心的对角线长为(3)2＋1＝2.∴正六棱柱的外接球半径为1.∴V 球＝43π.12．如图，在正方体1111ABCD A B C D -中，1A B 与1B C 所成的角为----------------------------------------------------------------（ ）(A) 30 (B) 45 (C) 60 (D) 9013．若一个长方体的长、宽、高分别为3、2、1，则它的外接球的表面积是 ▲ .14．已知m ，n 是不重合的两条直线，α，β是不重合的两个平面．下列命题：①若α⊥β，m ⊥α，则m ∥β； ②若m ⊥α，m ⊥β，则α∥β；③若m ∥α，m ⊥n ，则n ⊥α； ④若m ∥α，m ⊂β，则α∥β．其中所有真命题的序号是 ▲ ．答案: ②15．如图,在三棱柱ABC C B A -111中,F E D ，，分别是1AA AC AB ，，的中点,设三棱锥ADE F -的体积为1V ,三棱柱ABC C B A -111的体积为2V ,则=21:V V ____________.（2013年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD 版含附加题））16．已知直线,l m ，平面,αβ，且l α⊥，m β⊂，给出下列四个命题：①若l m ⊥，则α∥β；②若α∥β，则l m ⊥；③若l ∥m ，则αβ⊥；④若αβ⊥，则l ∥m ；其中为真命题的序号是_______.17．,,a b c 表示直线，M 表示平面，给出下列四个命题：①若//,//a M b M ，则//a b ； ②若b ⊂M ，a ∥b ，则a ∥M ；③若,a c b c ⊥⊥，则a ∥b ； ④若a ⊥M ，b ⊥M ，则a ∥b ．其中正确命题的序号是________（请将你认为正确的结论的序号都填上）．18．已知l ，m ，n 是三条不同的直线，γβα,, 是三个不同的平面，下列命题： ①若l ∥m ，n ⊥m ，则n ⊥l ； ②若l ∥m ，m ⊂α，则l ∥α；③若l ⊂α，m ⊂β，α∥β，则l ∥m ；④若α⊥γ，β⊥γ，α∩β=l ，则l ⊥γ。
最新精选2020高考数学《立体几何初步》专题完整考题(含参考答案)
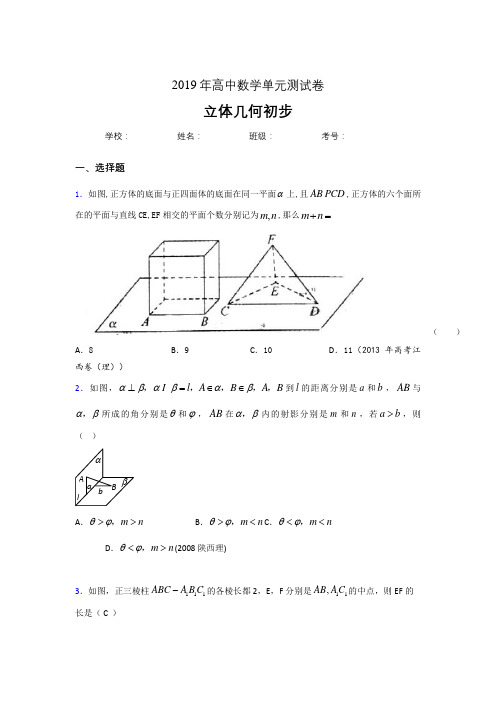
2019年高中数学单元测试卷立体几何初步学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．如图,正方体的底面与正四面体的底面在同一平面α上,且AB CD ,正方体的六个面所在的平面与直线CE,EF 相交的平面个数分别记为,m n ,那么m n +=（ ）A ．8B ．9C ．10D ．11（2013年高考江西卷（理）） 2．如图，l A B A B αβαβαβ⊥=∈∈，，，，，到l 的距离分别是a 和b ，AB 与αβ，所成的角分别是θ和ϕ，AB 在αβ，内的射影分别是m 和n ，若a b >，则（ ）A ．m n θϕ>>，B ．m n θϕ><，C ．m n θϕ<<，D ．m n θϕ<>，(2008陕西理)3．如图，正三棱柱111ABC A B C -的各棱长都2，E ，F 分别是11,AB A C 的中点，则EF 的长是（ C ）A Ba bl αβC1C(2006浙江文)4．连结球面上两点的线段称为球的弦．半径为4的球的两条弦AB 、CD 的长度分别等于27、43，M 、N 分别为AB 、CD 的中点，每条弦的两端都在球面上运动，有下列四个命题：①弦AB 、CD 可能相交于点M ②弦AB 、CD 可能相交于点N ③MN 的最大值为5 ④MN 的最小值为l 其中真命题的个数为A ．1个B ．2个C ．3个D ．4个(2008江西理)5．在正方体1111ABCD A B C D -中,,E F 分别为棱11,AA CC 的中点,则在空间中与三条直线11,,A D EF CD 都相交的直线( )A.不存在B.有且只有两条C.有且只有三条D.有无数条(2008辽宁理) 6．已知a 、b 、c 是直线，β是平面，给出下列命题：①若c a c b b a //,,则⊥⊥； ②若c a c b b a ⊥⊥则,,//； ③若b a b a //,,//则ββ⊂；④若a 与b 异面，且ββ与则b a ,//相交；⑤若a 与b 异面，则至多有一条直线与a ，b 都垂直. 其中真命题的个数是（ ） A ．1B ．2C ．3D ．4(2005湖北文)7．空间四边形ABCD 中，A B B C C D 、、的中点分别是P Q R 、、，且2,,3P Q Q P R ==，那么异面直线AC 和BD 所成的角是________________8．若点E F G H 、、、顺次为空间四边形ABCD 四边AB BC CD DA 、、、的中点，且3,4EG FH ==，则22AC BD +等于---------------------------------------------------------------（ ）(A) 25 (B) 50 (C) 100 (D) 209．如图，点,,E F G 分别是四面体ABCD 的棱,,BC CD DA 的中点，此四面体中与过,,E F G 的截面平行的棱的条数有（ ）A ．0条B ．1条C ．2条D ．3条二、填空题10．若,,l m n 是三条互不相同的空间直线，,αβ是两个不重合的平面， 则下列命题中为真命题的是 ▲ (填所有正确答案的序号)． ①若//,,,l n αβαβ⊂⊂则//l n ； ②若,,l αβα⊥⊂则l β⊥； ③若,,l n m n ⊥⊥则//l m ； ④若,//,l l αβ⊥则αβ⊥．11．Rt ABC ∆在平面α内的射影是111A B C ∆，设直角边AB α，则111A B C ∆的形状是 三角形．12．已知圆锥的底面半径为2cm ，高为1cm ，则圆锥的侧面积是 2cm ． 13．如图，在正三棱锥A BCD -中，底面BCD ∆的边长为，点,E F 分别是CD 和AD 的中点，且EF BF ⊥，则正三棱锥A BCD -的外接球的表面积为 ▲ .第11题14．圆柱形容器内盛有高度为3cm 的水，若放入三个相同的球（球的半径与圆柱的底面半径相同）后，水恰好淹没最上面的球（如图所示），则球的半径是____cm.15．在正四棱柱ABCD —A 1B 1C 1D 1中，AA 1=2AB ，E 为AA 1中点，则异面直线BE 与CD 1所成角的余弦值为__ ____。
最新精编2020高考数学《立体几何初步》专题完整题(含参考答案)
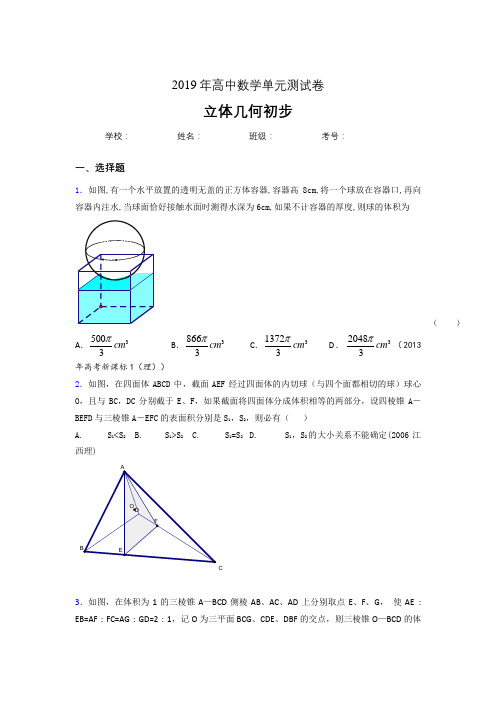
2019年高中数学单元测试卷立体几何初步学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为（ ）A ．35003cm π B ．38663cm π C ．313723cm πD ．320483cm π（2013年高考新课标1（理））2．如图，在四面体ABCD 中，截面AEF 经过四面体的内切球（与四个面都相切的球）球心O ，且与BC ，DC 分别截于E 、F ，如果截面将四面体分成体积相等的两部分，设四棱锥A －BEFD 与三棱锥A －EFC 的表面积分别是S 1，S 2，则必有（ ） A. S 1<S 2 B. S 1>S 2 C. S 1=S 2 D. S 1，S 2的大小关系不能确定(2006江西理)C3．如图，在体积为1的三棱锥A —BCD 侧棱AB 、AC 、AD 上分别取点E 、F 、G ， 使AE : EB=AF : FC=AG : GD=2 : 1，记O 为三平面BCG 、CDE 、DBF 的交点，则三棱锥O —BCD 的体积等于 （ ）CDB 1A 1A ．91B ．81 C ． 71 D ．41(2005重庆理)4．已知a b c 、、是直线，α是平面，b 、c ≠⊂α，则“⊥a 平面α”是“b a ⊥且c a ⊥”的…………………………………………………………………………………………（ ） A ．充要条件． B ．充分非必要条件． C ．必要非充分条件． D ．非充分非必要条件．5．若3sin (0)52x x π=--<<，则tan x =_____________.二、填空题6．已知正三棱锥P －ABC ，点P ，A ，B ，C PA ，PB ，PC 两两相互垂直，则三棱锥P －ABC 的体积为 ．7．如图，在正方体ABCD －A 1B 1C 1D 1中，二面角B AC B --1的正切值 为 ．8．已知a 、b 是不同的直线，α、β、γ是不同的平面，给出下列命题： ①若α∥β，a ⊂α，则a ∥β ； ②若a 、b 与α所成角相等，则a ∥b ； ③若α⊥β、β⊥γ，则α∥γ； ④若a ⊥α, a ⊥β，则α∥β 其中正确的命题的序号是 .9．正方体1111ABCD A B C D -的体对角线1AC 与面对角线BD 所成角为 ． 10． a ，b ，c 是空间中互不重合的三条直线，下面给出五个命题： ①若a ∥b ，b ∥c ，则a ∥c ； ②若a ⊥b ，b ⊥c ，则a ∥c ；③若a 与b 相交，b 与c 相交，则a 与c 相交； ④若a ⊂平面α，b ⊂平面β，则a ，b 一定是异面直线； 上述命题中正确的是________(只填序号)．11．已知球O 的半径为3，则球O 的表面积为 ．12．设,a b 是两条不同直线，,αβ是两个不同平面，给出下列四个命题：①若,,a b a α⊥⊥ b α⊄，则//b α；②若//,a ααβ⊥，则a β⊥；③若,a βαβ⊥⊥，则//a α或a α⊂；④若,,a b a b αβ⊥⊥⊥则αβ⊥．其中正确的命题是_____ ____（请把所有正确命题的序号都填上）．13．如图，在透明塑料制成的长方体ABCD - A 1B 1C 1D 1容器内灌进一些水，将容器底面一边BC 固定于地面上，再将容器倾斜，随着倾斜度的不同，有下列三个说法：①水的形状始终呈棱柱形状；②水面四边形EFGH 的面积不改变；③当E ∈AA 1时，AE + BF 是定值．其中正确说法是 ．14．设,m n 是两条不同的直线，,αβ是两个不同的平面，下列正确命题序号是 ▲ ．(1)若m ∥α,n ∥α,则m ∥n ， (2)若,m m n α⊥⊥则//n α(3)若m α⊥，n β⊥且m n ⊥，则αβ⊥；(4)若β⊂m ，βα//，则α//m15． 设平面,,βα直线b a ,，集合{}{}垂直的平面与，垂直的平面与βα==B A ，{}垂直的直线与a M =，{}垂直的直线与b N =，给出下列命题：①若∅≠B A ，则;//βα ②若βα//，则B A =；③若b a ,为异面直线，则∅=N M ；④若b a ,相交，则;N M = 其中不正确的命题序号是___ ★ ．（1），（3），（4） 16．如图，在四棱锥P －ABCD 中，PA ⊥底面ABCD ， 底面各边都相等，M 是PC 上的一个动点，当点M 满足 时，平面M BD ⊥平面PCD ．17．关于直角AOB ∠在平面α内的射影有如下判断：①可能是0的角；②可能是锐角；③可能是直角；④可能是钝角；⑤可能是180的角。
精编2020高考数学《立体几何初步》专题完整考题(含参考答案)
2019年高中数学单元测试卷立体几何初步学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．设四面体的六条棱的长分别为和a 且长为a 的棱异面,则a 的取值范围是（ ）A ．B ．C ．D ．（2012重庆文）2．设γβα、、、为平面，l n m 、、为直线，则β⊥m 的一个充分条件是( ) A ． l m l ⊥=⋂⊥,,βαβαB ． γβγαγα⊥⊥=⋂,,mC ． αγβγα⊥⊥⊥m ,,D ． αβα⊥⊥⊥m n n ,,（2005天津）3．有一塔形几何体由若干个正方体构成，构成方式如图所示，上层正方体下底面的四个顶点是下层正方体上底面各连接中点，已知最底层正方体的棱长为2，且该塔形的表面积（含最底层正方体的底面面积）超过39，则该塔形中正方体的个数至少是 （ ）A ．4B ．5C ．6D ．7(2005重庆文)4．若二面角l αβ--为1200，直线m α⊥，则β所在平面内的直线与m 所成角的取值范围是（ ）（A ）0(0,90] （B ）[300，600] （C ）[600，900] （D ）[300，900] (2004安徽春季理7） 5．1．一条直线和直线外的三点所能确定的平面的个数是-------------------------------------------（ ）(A) 1或3个 (B) 1或4个 (C) 1个、3个或4个 (D) 1个、2个或46．若干个棱长为2、3、5的长方体，依相同方向拼成棱长为90的正方体，则正方体的一条对角线贯穿的小长方体的个数是（ ） A ．64 B ．66C ．68D ．70二、填空题7．下列命题中正确命题的个数是①一条直线和另一条直线平行，那么它和经过另一条直线的任何平面平行；②一条直线平行于一个平面，则这条直线与这个平面内所有直线都没有公共点，因此这条直线与这个平面内的所有直线都平行；③若直线与平面不平行，则直线与平面内任一直线都不平行；④与一平面内无数条直线都平行的直线必与此平面平行。
【精品】2019届高三数学年复习专题--立体几何专题训练附参考答案
1 【精品】2019届高三数学年复习专题--立体几何专题训练附参考答案一、解答题 1.如图所示，在四棱锥P-ABCD 中，底面ABCD 是棱长为2的正方形，侧面PAD 为正三角形，且面PAD ⊥面ABCD ，E 、F 分别为棱AB 、PC 的中点． （1）求证：EF ∥平面PAD ； （2）求三棱锥B-EFC 的体积； （3）求二面角P-EC-D 的正切值．2.如图，三棱柱ABF-DCE 中，∠ABC=120°，BC=2CD ，AD=AF ，AF ⊥平面ABCD ．（Ⅰ）求证：BD ⊥EC ；（Ⅱ）若AB=1，求四棱锥B-ADEF 的体积．3.正方体ABCD-A 1B 1C 1D 1，AA 1=2，E 为棱CC 1的中点． （1）求证：B 1D 1⊥AE ；（2）求三棱锥A-BDE 的体积．4.如图，四棱锥P-ABCD 中，底面ABCD 是矩形，平面PAD ⊥底面ABCD ，且△PAD 是边长为2的等边三角形，PC= ，M 在PC 上，且PA ∥面MBD ． （1）求证：M 是PC 的中点； （2）求多面体PABMD 的体积．25.已知四棱锥P-ABCD ，底面ABCD 为菱形，∠ABC=60°，△PAB 是等边三角形，AB=2，PC= ，AB 的中点为E.（1）证明：PE ⊥平面ABCD ； （2）求三棱锥D-PBC 的体积．6.一块边长为10cm 的正方形铁块按如图所示的阴影部分裁下，然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器．（1）试把容器的容积V 表示为x 的函数.（2）若x =6，求图2的主视图的面积.7.如图，矩形ABCD 中，BC=2，AB=1，PA ⊥平面ABCD ，BE ∥PA ，BE=PA ，F 为PA 的中点．（1）求证：PC ∥平面BDF ．（2）记四棱锥C-PABE 的体积为V 1，三棱锥P-ACD 的体积为V 2，求的值．8.如图，直三棱柱ABC-A 1B 1C 1中，D ，E 分别是AB ，BB 1的中点，AA 1=AC=CB=2，AB=2 ．（Ⅰ）证明：BC 1∥平面A 1CD ；（Ⅱ）求锐二面角D-A 1C-E 的余弦值．9.如图，在四棱锥P-ABCD中，底面ABCD是菱形，∠DAB=60°，PD⊥平面ABCD，PD=AD=1，点E、F分别为AB和PC的中点，连接EF、BF．（1）求证：直线EF∥平面PAD；（2）求三棱锥F-PBE的体积．10.如图，梯形FDCG，DC∥FG，过点D，C作DA⊥FG，CB⊥FG，垂足分别为A，B，且DA=AB=2．现将△DAF沿DA，△CBG沿CB翻折，使得点F，G重合，记为E，且点B在面AEC的射影在线段EC上．（Ⅰ）求证：AE⊥EB；（Ⅱ）设=λ，是否存在λ，使二面角B-AC-E的余弦值为？若存在，求λ的值；若不存在，说明理由．11.在四边形ABCD中，对角线AC，BD垂直相交于点O，且OA=OB=OD=4，OC=3．将△BCD沿BD折到△BED的位置，使得二面角E-BD-A的大小为90°（如图）．已知Q为EO的中点，点P在线段AB 上，且．（Ⅰ）证明：直线PQ∥平面ADE；（Ⅱ）求直线BD与平面ADE所成角θ的正弦值．12.如图，四棱锥P-ABCD是底面边长为1的正方形，PD⊥BC，PD=1，PC=．（Ⅰ）求证：PD⊥面ABCD；（Ⅱ）求二面角A-PB-D的大小．3413.如图在三棱锥A-BCD 中，侧面ABD 、ACD 是全等的直角三角形，AD 是公共的斜边，且AD= ，BD=CD=1，另一个侧面是正三角形. （1）求证：AD ⊥BC ；（2）求二面角B-AC-D 的余弦值； （3）点E 在直线AC 上，当直线ED 与平面BCD 成30°角若时，求点C 到平面BDE 的距离．14.如图所示，在边长为 的正方形ABCD 中，以A 为圆心画一个扇形，以O 为圆心画一个圆，M ，N ，K 为切点，以扇形为圆锥的侧面，以圆O 为圆锥底面，围成一个圆锥，求圆锥的全面积与体积．15.如图，在四棱锥P-ABCD 中，PA ⊥平面ABCD ，∠ABC=∠BAD=90°，AD=AP=4，AB=BC=2，M 为PC 的中点，点N 在线段AD 上．（I ）点N 为线段AD 的中点时，求证：直线PA ∥BMN ； （II ）若直线MN 与平面PBC 所成角的正弦值为，求平面PBC 与平面BMN 所成角θ的余弦值．16.如图，在正方体ABCD-A 1B 1C 1D 1中，E 是CC 1的中点，求证： （1）AC 1⊥BD ；（2）AC 1∥平面BDE ．17.如图，棱长为1的正方体ABCD-A 1B 1C 1D 1中， （1）求证：AC ⊥平面B 1D 1DB ； （2）求三棱锥B-CD 1B 1的体积．18.在四棱锥P-ABCD中，平面PAD⊥平面ABCD，∠APD=90°，PA=PD=AB=a，ABCD是矩形，E是PD的中点．（1）求证：PB∥平面AEC（2）求证：PB⊥AC．19.如图，已知平面ADC∥平面A1B1C1，B为线段AD的中点，△ABC≈△A1B1C1，四边形ABB1A1为正方形，平面AA1C1C丄平面ADB1A1，A1C1=A1A，∠C1A1A=，M为棱A1C1的中点．（I）若N为线段DC1上的点，且直线MN∥平面ADB1A1，试确定点N的位置；（Ⅱ）求平面MAD与平面CC1D所成的锐二面角的余弦值．20.如图，三棱柱ABC-A1B1C1中，D为AA1的中点，E为BC的中点．（1）求证：直线AE∥平面BDC1；（2）若三棱柱 ABC-A1B1C1是正三棱柱，AB=2，AA1=4，求平面BDC1与平面ABC所成二面角的正弦值．21.如图所示，已知长方体ABCD中，AB=4，AD=2，M为DC的中点．将△ADM沿AM折起，使得AD⊥BM．（1）求证：平面ADM⊥平面ABCM；（2）若点E为线段DB的中点，求点E到平面DMC的距离．5622.如图所示，在正方体ABCD-A 1B 1C 1D 1中，E 是棱DD 1的中点． （1）若正方体的棱长为1，求三棱锥B 1-A 1BE 的体积；（2）在棱C 1D 1上是否存在一点F ，使B 1F ∥面A 1BE ？若存在，试确定点F 的位置，并证明你的结论．23.如图，三棱柱ABC-A 1B 1C 1中，BC ⊥平面AA 1C 1C ，BC=CA=AA 1=2，∠CAA 1=60°．（1）求证：AC 1⊥A 1B ；（2）求直线A 1B 与平面BAC 1所成角的正弦值．24.在图所示的几何体中，底面ABCD 为正方形，PD ⊥平面ABCD ，EC ∥PD ，且PD=AD=2EC=2，N 为线段PB 的中点． （1）证明：NE ⊥平面PBD ； （2）求四棱锥B-CEPD 的体积．25.已知梯形ABCD 中AD ∥BC ，∠ABC=∠BAD=，AB=BC=2AD=4，E 、F 分别是AB 、CD 上的点，EF ∥BC ，AE=x ．沿EF 将梯形AEFD 翻折，使平面AEFD ⊥平面EBCF （如图）．G 是BC 的中点．（1）当x =2时，求证：BD ⊥EG ；（2）当x 变化时，求三棱锥D-BCF 体积的最大值．26.如图，长方体ABCD-A 1B 1C 1D 1中，AB=16，BC=10，AA 1=8，点E ，F 分别在A 1B 1，D 1C 1上，A 1E=D 1F=4，过点E ，F 的平面α与此长方体的面相交，交线围成一个正方形．（1）在图中画出这个正方形（不必说明画法和理由）； （2）求直线AF 与平面α所成角的正弦值．727.在如图所示的多面体ABCDEF 中，四边形ABCD 为正方形，底面ABFE 为直角梯形，∠ABF 为直角， ，，平面ABCD ⊥平面ABFE ． （1）求证：DB ⊥EC ；（2）若AE=AB ，求二面角C-EF-B 的余弦值．28.如图，四棱锥P-ABCD 中，AD ⊥平面PAB ，AP ⊥AB ． （1）求证：CD ⊥AP ； （2）若CD ⊥PD ，求证：CD ∥平面PAB ．29.如图所示，四棱锥P-ABCD 的侧面PAD 是边长为2的正三角形，底面ABCD 是∠ABC=60°的菱形，M 为PC 的中点，PC= ．（Ⅰ）求证：PC ⊥AD ；（Ⅱ）求三棱锥M-PAB 的体积．30.如图，在四棱锥P-ABCD 中，底面ABCD 是平行四边形，∠ADC=45°，AD=AC=2，O 为AC 的中点，PO ⊥平面ABCD 且PO=6，M 为BD的中点．（1）证明：AD ⊥平面PAC ； （2）求直线AM 与平面ABCD 所成角的正切值．31.如图，多面体EF-ABCD 中，ABCD 是正方形，AC 、BD 相交于O ，EF ∥AC ，点E 在AC 上的射影恰好是线段AO 的中点． （Ⅰ）求证：BD ⊥平面ACF ；（Ⅱ）若直线AE 与平面ABCD 所成的角为60°，求平面DEF 与平面ABCD 所成角的正弦值．32.如图，三棱锥P-ABC 中，平面PAC ⊥平面ABC ，∠BCA=90°，且BC=CA=2，PC=PA ．（1）求证：PA ⊥BC ；8 （2）当PC 的值为多少时，满足PA ⊥平面PBC ？并求出此时该三棱锥P-ABC 的体积．33.如图，直三棱柱ABC-A 1B 1C 1中，AA 1=AB ，AB ⊥BC ，且N 是A 1B 的中点．（1）求证：直线AN ⊥平面A 1BC ；（2）若M 在线段BC 1上，且MN ∥平面A 1B 1C 1，求证：M 是BC 1的中点．34.．如图所示，在长方体ABCD-A 1B 1C 1D 1中，AB=AD=1，AA 1=2，点P 为DD 1的中点． （1）求证：直线BD 1∥平面PAC （2）求证：平面PAC ⊥平面BDD 1B 1．35.如图，在四棱锥P-ABCD 中，底面ABCD 为直角梯形，AD ∥BC ，∠ADC=90°，平面PAD ⊥底面ABCD ，Q 为AD 的中点，M 是棱PC 上的点，PA=PD=2，BC=AD=1，CD= ． （1）求证：平面MQB ⊥平面PAD ； （2）若二面角M-BQ-C 大小的为60°，求QM 的长．36.如 图，正方体ABCD-A 1B 1C 1D 1的棱长为2，E 、F 、G 分别为 AB 、BB 1、B 1C 1 的中点． （1）求证：A 1D ⊥FG ；（2）求二面角 A 1-DE-A 的正切值．37.四棱锥P-ABCD 的直观图与三视图如图，PC ⊥面ABCD（1）画出四棱锥P-ABCD 的侧视图（标注长度） （2）求三棱锥A-PBD的9 体积．38.如图，长方体ABCD-A 1B 1C 1D 1中，AB=AD=1，AA 1=2，点P 为棱DD 1上一点．（1）求证：平面PAC ⊥平面BDD 1B 1；（2）若P 是棱DD 1的中点，求CP 与平面BDD 1B 1所成的角大小．39.如图，四棱锥P-ABCD 中，PA ⊥底面ABCD ，AB ∥CD ，AD=CD=1，∠BAD=120°，PA= ，∠ACB=90°，M 是线段PD 上的一点（不包括端点）．（Ⅰ）求证：BC ⊥平面PAC ； （Ⅱ）求二面角D-PC-A 的正切值； （Ⅲ）试确定点M 的位置，使直线MA 与平面PCD 所成角θ的正弦值为．40.已知四棱锥P-ABCD 中，AD=2BC ，且AD ∥BC ，点M ，N 分别是PB ，PD 中点，平面MNC 交PA 于Q ． （1）证明：NC ∥平面PAB（2）试确定Q 点的位置，并证明你的结论．41.一个正三棱柱的三视图如图所示，求这个三棱柱的表面积和体10 积．42.如图，四棱锥P-ABCD 的底面是正方形，侧棱PA ⊥底面ABCD ，E 是PA 的中点． （Ⅰ）求证：PC ∥平面BDE ； （Ⅱ）证明：BD ⊥CE ．43.如图所示，在正方体ABCD-A 1B 1C 1D 1中，E 、G 、H 分别是BC 、C 1D 1、AA 1、的中点．（Ⅰ）求异面直线D 1H 与A 1B 所成角的余弦值（Ⅱ）求证：EG ∥平面BB 1D 1D ．44.如图所示，在四棱锥P-ABCD 中，AB ∥CD ，AB ⊥AD ，AB=AD=AP=2CD=2，M 是棱PB 上一点． （Ⅰ）若BM=2MP ，求证：PD ∥平面MAC ； （Ⅱ）若平面PAB ⊥平面ABCD ，平面PAD ⊥平面ABCD ，求证：PA ⊥平面ABCD ；（Ⅲ）在（Ⅱ）的条件下，若二面角B-AC-M 的余弦值为，求 的值．45.如图，已知在侧棱垂直于底面的三棱柱ABC-A 1B 1C 1中，AC=3，AB=5，BC=4，AA 1=4点D 是AB 的中点． （1）求证：AC 1∥平面B 1DC ；11 （2）求三棱锥A 1-B 1CD 的体积．46.如图，以正四棱锥V-ABCD 的底面中心O 为坐标原点建立空间直角坐标系O-xyz ，其中O x ∥BC ，O y ∥AB ，E 为VC 中点，正四棱锥的底面边长为2a ，高为h ，且有cos ＜， ＞=-． （1）求的值；（2）求二面角B-VC-D 的余弦值．47.如图1，四边形ABCD 为直角梯形，AD ∥BC ，AD ⊥AB ，AD=1，BC=2，E 为CD 上一点，F 为BE 的中点，且DE=1，EC=2，现将梯形沿BE 折叠（如图2），使平面BCE ⊥ABED ．（1）求证：平面ACE ⊥平面BCE ；（2）能否在边AB 上找到一点P （端点除外）使平面ACE 与平面PCF 所成角的余弦值为？若存在，试确定点P 的位置，若不存在，请说明理由．48.如图，三棱柱ABC-A 1B 1C 1中，侧面ACC 1A 1⊥侧面ABB 1A 1，∠B 1A 1A=∠C 1A 1A=60°，AA 1=AC=4，AB=1． （Ⅰ）求证：A 1B 1⊥B 1C 1；（Ⅱ）求三棱锥ABC-A 1B 1C 1的侧面积．49.在四棱锥中P-ABCD ，底面ABCD 是正方形，侧面PAD ⊥底面ABCD ，且PA=PD=AD 、E 、F ，分别为PC 、BD 的中点． （1）求证：EF ∥平面PAD ；（2）若AB=2，求三棱锥E-DFC 的体积．1250.如图，四棱锥P-ABCD 中，△PAD 为正三角形，AB ∥CD ，AB=2CD ，∠BAD=90°，PA ⊥CD ，E 为棱PB 的中点 （Ⅰ）求证：平面PAB ⊥平面CDE ；（Ⅱ）若直线PC 与平面PAD 所成角为45°，求二面角A-DE-C 的余弦值．51.如图，在边长为2的正方形ABCD 中，点E ，F 分别是AB ，BC 的中点，将△AED ，△DCF 分别沿DE ，DF 折起，使A ，C 两点重合于P ．（Ⅰ）求证：平面PBD ⊥平面BFDE ； （Ⅱ）求四棱锥P-BFDE 的体积．【答案】1.（1）证明：取PD 中点G ，连结GF 、AG ，∵GF 为△PDC 的中位线，∴GF ∥CD 且， 又AE ∥CD 且，∴GF ∥AE 且GF=AE ，13 ∴EFGA 是平行四边形，则EF ∥AG ， 又EF ⊄面PAD ，AG ⊂面PAD ， ∴EF ∥面PAD ；（2）解：取AD 中点O ，连结PO ，∵面PAD ⊥面ABCD ，△PAD 为正三角形，∴PO ⊥面ABCD ，且 ， 又PC 为面ABCD 斜线，F 为PC 中点，∴F 到面ABCD 距离，故；（3）解：连OB 交CE 于M ，可得R t △EBC ≌R t △OAB ， ∴∠MEB=∠AOB ，则∠MEB+∠MBE=90°，即OM ⊥EC ．连PM ，又由（2）知PO ⊥EC ，可得EC ⊥平面POM ，则PM ⊥EC ， 即∠PMO 是二面角P-EC-D 的平面角，在R t △EBC 中，，∴， ∴，即二面角P-EC-D的正切值为．2.（Ⅰ）证明：三棱柱ABF-DCE 中，AF ⊥平面ABCD ．∴DE ∥AF ，ED ⊥平面ABCD ，∵BD ⊂平面ABCD ，∴ED ⊥BD ， 又ABCD 是平行四边形，∠ABC=120°，故∠BCD=60°． ∵BC=2CD ，故∠BDC=90°．故BD ⊥CD ． ∵ED∩CD=D ，∴BD ⊥平面ECD ． ∵EC ⊂平面ECD ， ∴BD ⊥EC ；（Ⅱ）解：由BC=2CD ，可得AD=2AB ，∵AB=1，∴AD=2，作BH ⊥AD于H ，∵AF ⊥平面ABCD ，∴BH ⊥平面ADEF ，又∠ABC=120°， ∴BH=，∴．3.解：（1）证明：连接BD ，则BD ∥B 1D 1， ∵ABCD 是正方形，∴AC ⊥BD ． ∵CE ⊥面ABCD ， ∴CE ⊥BD ． 又AC∩CE=C ， ∴BD ⊥面ACE ． ∵AE ⊂面ACE ， ∴BD ⊥AE ，∴B 1D 1⊥AE ．-----------（6分）（2）S △ABD =2 △．-----------（12分） 4.证明：（1）连AC 交BD 于E ，连ME ．14∵ABCD 是矩形，∴E 是AC 中点．又PA ∥面MBD ，且ME 是面PAC 与面MDB 的交线， ∴PA ∥ME ，∴M 是PC 的中点． 解：（2）取AD 中点O ，连OC ．则PO ⊥AD ， 由平面PAD ⊥底面ABCD ，得PO ⊥面ABCD ，∴ ， ，∴ ， ∴ ， ，∴．5.证明：（1）由题可知PE ⊥AB ，CE ⊥AB ． ∵AB=2，∴PE=CE= ．又∵PC= ，∴PE 2+EC 2=PC 2， ∴∠PEC=90°，即PE ⊥CE ． 又∵AB ，CE ⊂平面ABCD ， ∴PE ⊥平面ABCD ；解：（2）S △BCD =×22×sin 120°= ，PE= ． 由（1）知：PE ⊥平面ABCD ，V P-BCD =•S △BCD •PE=1．∵V D-PBC =V P-BCD ，∴三棱锥D-PBC 的体积为1． 6.解：（1）设所截等腰三角形的底边边长为x cm ． 在R t △EOF 中，EF=5cm ，OF=x cm ，所以EO=． 于是V=x 2（cm 3）．依题意函数的定义域为{x |0＜x ＜10}．（2）主视图为等腰三角形，腰长为斜高，底边长=AB=6，底边上的高为四棱锥的高=EO==4，S==12（cm 2）7.（1）证明：连结BF ，连接BD 交AC 与点O ，连OF ， 依题得O 为AC 中点，又F 为PA 的中点， 所以OF 为△PAC 中位线，所以OF ∥PC因为OF ⊂平面BDF ，PC ⊄平面BDF 所以PC ∥平面BDF ． ∴V 1=梯形 =（2）解：设BE=a ，则PA=2BE=2a ， V 2=△ =（a +2a ）×1×2=a ． =． ∴．8.解：（Ⅰ）连结AC 1，交A 1C 于点O ，连结DO ，则O 为AC 1的中点，因为D 为AB 的中点，所以OD ∥BC 1，又因为OD ⊂平面A 1CD ，BC 1⊄平面A 1CD ，∴BC 1∥平面A 1CD…（4分） （Ⅱ）由 ， ，可知AC ⊥BC ，以C 为坐标原点，方向为x 轴正方向， 方向为y轴正。
精编新版2020高考数学《立体几何初步》专题完整版考核题(含参考答案)
2019年高中数学单元测试卷立体几何初步学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．设三棱柱ABC-A 1B 1C 1的体积是V ，P .Q 分别是侧棱AA 1上的点，且PA=QC 1，则四棱锥B-APQC 的体积为（ ）A.V 61 B.V 41 C.V 31 D.V 21 (2005全国3理)2．α、β是两个不同的平面，m 、n 是平面α及β之外的两条不同直线, 给出四个论断：① m ⊥ n ②α⊥β ③ m ⊥β ④ n ⊥α以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题：___________________.二、填空题3．已知圆柱的底面半径为1，母线长与底面的直径相等，则该圆柱的表面积为 ▲ ． 4． 如图，已知一个多面体的平面展开图由一边长为1的正方体和4个边长为1的正三角形组成，则该多面体的体积是 ．5．如图，在四棱锥P ABCD -中，PA ⊥底面ABCD ，底面各边都相等，M 是PC 上的一动点，当点M 满足 时，平面MBD ⊥平面PCD ．(只需写出一种情形)6．在正方体1111D C B A ABCD -中，与1AD 平行的表面的对角线有 条7．设a b 、是两条不同的直线，α、β是两个不同的平面，则下列四个命题 ①若,a b a α⊥⊥，则//b α， ②若,a βαβ⊥⊥，则//a α, ③若βαβα⊥⊥则,,//a a ④若,,a b a b αβ⊥⊥⊥，则αβ⊥,其中正确的命题序号是 ▲ ．ABCD PM8．在矩形ABCD中，AB = 4，BC = 3，沿AC将矩形ABCD折成一个直二面角B-AC-D，则折后BD=．9．在直四棱柱ABCD-A1B1C1D1中，当底面四边形ABCD满足条件时，有A1C⊥B1D1（注：填上你认为正确的一种即可，不必考虑所有可能的情形）.10．如果a,b是异面直线，P是不在a,b上的任意一点，下列四个结论：（1）过P一定可作直线L与a , b都相交；（2）过P一定可作直线L与a , b都垂直；（3）过P一定可作平面α与a , b都平行；（4）过P一定可作直线L与a , b都平行，其中正确的结论有个11．下列命题中：(1）、平行于同一直线的两个平面平行；(2）、平行于同一平面的两个平面平行；(3）、垂直于同一直线的两直线平行；(4）、垂直于同一平面的两直线平行.其中正确的个数有三、解答题12．如图,在长方体ABCD-A1B1C1D1中,AB=2,AD=1,A1A=1,证明直线BC1平行于平面DA1C,并求直线BC1到平面D1AC的距离.（2013年高考上海卷（理））C11A13．如图，以长方体ABCD-A1B1C1D1的顶点A、C及另两个顶点为顶点构造四面体．（1）若该四面体的四个面都是直角三角形，试写出一个这样的四面体（不要求证明）；（2）我们将四面体中两条无公共端点的棱叫做对棱，若该四面体的任一对对棱垂直，试写出一个这样的四面体（不要求证明）；（3）若该四面体的任一对对棱相等，试写出一个这样的四面体（不要求证明），并计算它的体积与长方体的体积的比．A BC DD1A1C1B114．如图,在长方体1111D C B A ABCD -中,11==AD AA ,2=AB ,E 、F 分别 为11C D 、11D A 的中点．(1）求证：⊥DE 平面BCE ； (2）求证：//AF 平面BDE ．(3）能否在面C C BB 11内找一点G,使AF DG ⊥若能,请找出所有可能的位置并证明,若不能,请说明理由.15．如图，ABC ∆的AB 边交平面α于D ，BC 边交平面α于E 。
精编新版2020高考数学《立体几何初步》专题完整题(含参考答案)
2019年高中数学单元测试卷立体几何初步学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．如图，AB 是平面α的斜线段．．．，A 为斜足，若点P 在平面α内运动，使得ABP △的面积为定值，则动点P 的轨迹是（ ）A ．圆B ．椭圆C ．一条直线D ．两条平行直线(2008浙江理)2．给出下列四个命题：①垂直于同一直线的两条直线互相平行 ②垂直于同一平面的两个平面互相平行③若直线12l l ，与同一平面所成的角相等，则12l l ，互相平行 ④若直线12l l ，是异面直线，则与12l l ，都相交的两条直线是异面直线 其中假命题的个数是（D ） Ａ．1 Ｂ．2Ｃ．3Ｄ．4(2006辽宁文)3．设m 、n 是两条不同的直线，,,αβγ是三个不同的平面，给出下列四个命题： ①若，，则 ②若，，，则③若，，则 ④若αγ⊥，βγ⊥，则//αβ其中正确命题的序号是 A ①和② B ②和③ C ③和④D ①和④AB Pα（第10题）4．已知平面βα,和直线，给出条件：①α//m ；②α⊥m ；③α⊂m ；④βα⊥；⑤βα//.（i ）当满足条件 时，有β//m ；（ii ）当满足条件 时，有β⊥m . （填所选条件的序号）(2005湖南文15)5．下列四个结论：⑴两条直线都和同一个平面平行，则这两条直线平行。
⑵两条直线没有公共点，则这两条直线平行。
⑶两条直线都和第三条直线垂直，则这两条直线平行。
⑷一条直线和一个平面内无数条直线没有公共点，则这条直线和这个平面平行。
其中正确的个数为A 0B 1C 2D 36．在ABC ∆中，︒=∠90ACB ,AB=8,︒=∠60BAC ,PC ⊥面ABC ，PC ＝4，M 是AB 边上的一动点，则PM 的最小值为（ ） A ．72 B ．7 C ．19 D ．57．线a 、b 和平面α，下面推论错误的是 A.b a ⊥⇒⎭⎬⎫⊆⊥ααb a B αα⊥⇒⎭⎬⎫⊥b b // a aC ααα⊆⇒⎭⎬⎫⊥⊥a //a b b a 或D b //a b //a ⇒⎭⎬⎫⊆αα8．平面α与平面β平行的一个充分条件是----------------------------------------------------------（ ） (A)α内有两条直线与β平行 (B)α内有无数条直线与β平行 (C)α内任一直线与β平行 (D)αβ、都平行于同一直线 二、填空题9．已知l 、m 、n 是直线，a 、b 、g 是平面，下列命题中为真命题是 ① 若//m l ，且m a ⊥，则l a ⊥； ② 若//m l ，且//m a ，则//l a ； ③ 若l a b =，m b g =，n g a =，则////l m n ；④ 若m a g =，l bg =，且//a b ，则//m l ．10．线段AB 在平面α内，则直线AB 与平面α的位置关系是_________． 11．如图，在正方体ABCD －A 1B 1C 1D 1中，M 是DD 1的中点， 则下列结论正确的是 ▲ （填序号） ①线段A 1M 与B 1C 所在直线为异面直线； ②对角线BD 1⊥平面AB 1C ； ③平面AMC ⊥平面AB 1C ； ④直线A 1M//平面AB 1C.12．设直线n 和平面α，不管直线n 和平面α的位置关系如何，在平面α内总存在直线m ，使得它与直线n ▲ ;(在“平行”、 “相交”、 “异面”、 “垂直”中选择一个填空)13．设m ，n 是两条不同的直线，α，β是两个不同的平面，给出下列命题： （1）若βα//，β⊂m ，α⊂n ，则n m //； （2）若βα//，β⊥m ，α//n ，则n m ⊥； （3）若βα⊥，α⊥m ，β//n ，则n m //； （4）若βα⊥，α⊥m ，β⊥n ，则n m ⊥. 上面命题中，所有真命题的序号为 .14．如图，在棱长为2的正方体ABCD —A 1B 1C 1D 1中，E ，F 分别是棱AB ，BC 中点，则三棱锥B —B 1EF 的体积为 。
精编2020高考数学《立体几何初步》专题完整考题(含答案)
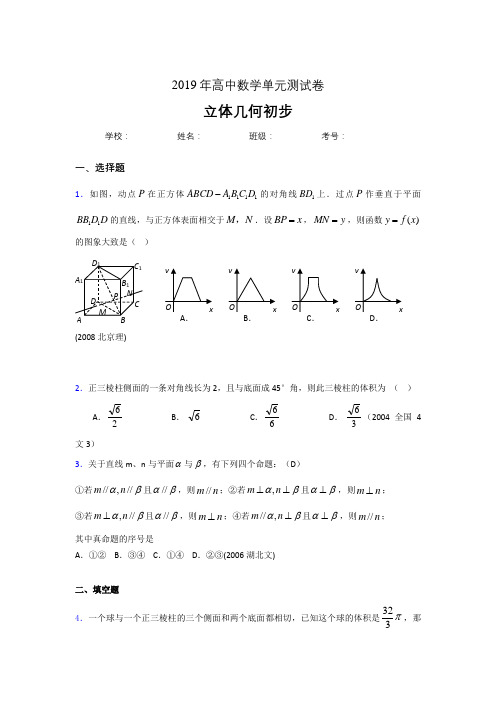
2019年高中数学单元测试卷立体几何初步学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．如图，动点P 在正方体1111ABCD A B C D -的对角线1BD 上．过点P 作垂直于平面11BB D D 的直线，与正方体表面相交于M N ，．设BP x =，MN y =，则函数()y f x =的图象大致是（ ）(2008北京理)2．正三棱柱侧面的一条对角线长为2，且与底面成45°角，则此三棱柱的体积为 （ ）A ．26 B ． 6C ．66 D ．36（2004全国4文3）3．关于直线m 、n 与平面α与β，有下列四个命题：（D ）①若//,//m n αβ且//αβ，则//m n ；②若,m n αβ⊥⊥且αβ⊥，则m n ⊥； ③若,//m n αβ⊥且//αβ，则m n ⊥；④若//,m n αβ⊥且αβ⊥，则//m n ； 其中真命题的序号是A ．①②B ．③④C ．①④D ．②③(2006湖北文)二、填空题4．一个球与一个正三棱柱的三个侧面和两个底面都相切，已知这个球的体积是323π，那么这个三棱柱的体积是ACD MN P A 1B 1C 1D 1 A ．B ．C ．D ．5．如图，在三棱锥ABC P -中，⊥PA 底面ABC ，90=∠ABC ，1===BC AB PA ，则PC 与底面ABC 所成角的正切值．．．为 .6．如图，正方体的平面展开图，在这个正方体中，①BM 与ED 平行；②CN 与BE 是异面直线；③CN 与BM 成60°的角；④DM 与BN 垂直。
其中正确．．的序号．．是____________；7．体积为8的一个正方体，其表面积与球O 的表面积相等，则球O 的体积等于________．8．已知正三棱锥的底面边长是6，侧棱与底面所成角为60°，则此三棱锥的体积为 ▲ .9．已知直线b a ,和平面α，若αα⊥⊥b a ,，则a 与b 的位置关系是 ． 10．正方体1111ABCD A B C D -中，与对角线1AC 异面的棱有 条.11．在棱长为4的正方体1111ABCD A B C D -中，E 、F 分别为棱1AA 、11D C 上的动点，点PABC（第8题）EG 为正方形11B BCC 的中心. 则空间四边形AEFG 在该正方体各个面上的正投影构成的图形中，面积的最大值为 ▲ . 关键字：投影；正方体；求最值12．设,l m 为两条不同的直线，,αβ为两个不同的平面，下列命题中正确的是 ．（填序号）①若,//,,l m αβαβ⊥⊥则l m ⊥； ②若//,,,l m m l αβ⊥⊥则//αβ； ③若//,//,//,l m αβαβ则//l m ； ④若,,,,m l l m αβαββ⊥=⊂⊥则l α⊥．13．在正三棱锥P －ABC 中，D ，E 分别是AB ，BC 的中点，有下列三个结论： ① AC ⊥PB ； ② AC ∥平面PDE ； ③ AB ⊥平面PDE 。
2019--2020年高考数学试题分类汇编立体几何及答案详解
2019--2020年高考数学试题分类汇编立体几何一、选择题.1、（2019年高考全国I 卷理科12）已知三棱锥P −ABC 的四个顶点在球O 的球面上，P A =PB =PC ，△ABC 是边长为2的正三角形，E ，F 分别是P A ，AB 的中点，∠CEF =90°，则球O 的体积为A ．68πB ．64πC ．62πD ．6π 答案：D解析：如图，三棱锥ABC P -为正三棱锥，不妨设a PC PB PA 2||||||===，底面外接圆半径为r ，由题意可得3||,||==CF a EF .在PAC ∆中，由余弦定理可得aa a a PAC 21222444cos 22=⨯⨯-+=∠， 所以在EAC ∆中22124||222+=⨯⨯⨯-+=a aa a a EC 又︒=∠90CEF ，根据勾股定理可得222||||||CF EF EC =+，即2||=PC 在直角POC ∆中，332||=OC ,36||||22=-=r PC OP 由正三棱锥外接球半径公式可得26||2||222=+=OP OP r R ，故体积为π6 2、（2019年高考全国II 卷文理科7）设α，β为两个平面，则α∥β的充要条件是 A ．α内有无数条直线与β平行B ．α内有两条相交直线与β平行C ．α，β平行于同一条直线D ．α，β垂直于同一平面答案：B解析：由“判定定理:如果一个平面内有两条相交直线分别与另一个平面内两条相交直线平行,那么这两个平面平行”可知答案选B3、（2019年高考全国II 卷文理科16）．中国有悠久的金石文化，印信是金石文化的代表之一．印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”（图1）.半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美．图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1．则该半正多面体共有________个面，其棱长为_________．（本题第一空2分，第二空3分．） 答案：A解析：(1)上层8个,中层8个,下层8个上下底各1个(2)设棱长为a ,如图作出该几何体的截面,1,21=-=CE a CD 又△CDE 为等腰直角三角形,则a a =-⨯212，解得12-=a .则棱长为12- 4、（2019年高考全国III 卷文理科8）如图，点N 为正方形ABCD 的中心，△ECD 为正三角形，平面ECD ⊥平面ABCD ，M 是线段ED 的中点，则A ．BM =EN ，且直线BM 、EN 是相交直线B ．BM ≠EN ，且直线BM ，EN 是相交直线C ．BM =EN ，且直线BM 、EN 是异面直线D ．BM ≠EN ，且直线BM ，EN 是异面直线答案：B解析：建系如图)23,0,23(),0,11,1(),3,0,1(),0,2,0(M N E B 所以7)023()20()023(||222=-+-+-=BM , 2)300()01()11(||222=-+-+-=EN又因为BN BE BM +=21 所以B 、M 、E 、N 四点共面。
2019-2020年高考数学大题专题练习——立体几何(一)
2019-2020年高考数学大题专题练习——立体几何（一）1.如图所示，四棱锥P ABCD 中，底面ABCD 为正方形，⊥PD 平面ABCD ，2PD AB ，点,,E F G 分别为,,PC PD BC 的中点.(1)求证：EF PA ⊥；(2)求二面角D FG E 的余弦值.2.如图所示，该几何体是由一个直角三棱柱ADE BCF 和一个正四棱锥P ABCD 组合而成，AF AD ⊥，2AEAD .(1)证明：平面⊥PAD 平面ABFE ；(2)求正四棱锥P ABCD 的高h ，使得二面角C AF P 的余弦值是223.3.四棱锥P ABCD-中，侧面PDC是边长为2的正三角形，且与底面垂直，底面ABCD是面积为ADC∠为锐角，M为PB的中点．（Ⅰ）求证：PD∥面ACM．（Ⅱ）求证：PA⊥CD．（Ⅲ）求三棱锥P ABCD-的体积．4.如图，四棱锥S ABCD-满足SA⊥面ABCD，90DAB ABC∠=∠=︒．SA AB BC a===，2AD a=．（Ⅰ）求证：面SAB⊥面SAD．（Ⅱ）求证：CD⊥面SAC．SB A DMC BAPD5.在四棱锥P ABCD -中，底面ABCD 为矩形，测棱PD ⊥底面ABCD ，PD DC =，点E 是BC 的中点，作EF PB ⊥交PB 于F ． （Ⅰ）求证：平面PCD ⊥平面PBC ． （Ⅱ）求证：PB ⊥平面EFD ．6.在直棱柱111ABC A B C -中，已知AB AC ⊥，设1AB 中点为D ，1A C 中点为E ． （Ⅰ）求证：DE ∥平面11BCC B ． （Ⅱ）求证：平面11ABB A ⊥平面11ACC A ．E DABC C 1B 1A 1DAB CEF P7.在四棱锥P ABCD -中，PA ⊥平面ABCD ，//AB CD ，AB AD ⊥，PA PB =，::2:2:1AB AD CD =.（1）证明BD PC ⊥；（2）求二面角A PC D --的余弦值；（3）设点Q 为线段PD 上一点，且直线AQ 平面PAC 所成角的正弦值为23，求PQ PD的值.8.在正方体1111ABCD A B C D -中，O 是AC 的中点，E 是线段D 1O 上一点，且D 1E ＝λEO . （1）若λ=1，求异面直线DE 与CD 1所成角的余弦值； （2）若λ=2，求证：平面CDE ⊥平面CD 1O .9.如图，在四棱锥P ABCD -中，底面ABCD 是平行四边形，135BCD =︒∠，侧面PAB ⊥底面ABCD ，90BAP =︒∠，2AB AC PA ===，E ，F 分别为BC ，AD 的中点，点M 在线段PD 上．（Ⅰ）求证：EF ⊥平面PAC ．（Ⅱ）若M 为PD 的中点，求证：ME ∥平面PAB ． （Ⅲ）如果直线ME 与平面PBC 所成的角和直线ME 与平面ABCD 所在的角相等，求PMPD的值．10.如图，在三棱柱111ABC A B C -，1AA ⊥底面ABC ，AB AC ⊥，1AC AB AA ==，E ，F 分别是棱BC ，1A A 的中点，G 为棱1CC 上的一点，且1C F ∥平面AEG ． （1）求1CGCC 的值． （2）求证：1EG AC ⊥． （3）求二面角1A AG E --的余弦值．A 1B 1C 1G F AB CEM F E CBAPD11.如图，在四棱锥P ABCD -中，PB ⊥底面ABCD ，底面ABCD 为梯形，AD BC ∥，AD AB ⊥，且3PB AB AD ===，1BC =．（Ⅰ）若点F 为PD 上一点且13PF PD =，证明：CF ∥平面PAB ．（Ⅱ）求二面角B PD A --的大小． （Ⅲ）在线段PD 上是否存在一点M ，使得CM PA ⊥？若存在，求出PM 的长；若不存在，说明理由．12.如图，在四棱锥E ABCD -中，平面EAD ⊥平面ABCD ，CD AB ∥，BC CD ⊥，EA ED ⊥，4AB =，2BC CD EA ED ====．Ⅰ证明：BD AE ⊥．Ⅱ求平面ADE 和平面CDE 所成角（锐角）的余弦值．DABCEPF DBCA13.己知四棱锥P ABCD -中，PA ⊥平面ABCD ，底面ABCD 是菱形，且2PA AB ==．60ABC ∠=︒，BC 、PD 的中点分别为E ，F ．（Ⅰ）求证BC PE ⊥．（Ⅱ）求二面角F AC D --的余弦值．（Ⅲ）在线段AB 上是否存在一点G ，使得AF 平行于平面PCG ？若存在，指出G 在AB 上的位置并给予证明，若不存在，请说明理由．14.如图，ABCD 是边长为3的正方形，DE ⊥平面ABCD ，AF DE ∥，3DE AF =，BE 与平面ABCD 所成角为60︒．（Ⅰ）求证：AC ⊥平面BDE ． （Ⅱ）求二面角F BE D --的余弦值．（Ⅲ）设点M 线段BD 上一个动点，试确定点M 的位置，使得AM ∥平面BEF ，并证明你的结论．DDABCEF15.如图，PA ⊥面ABC ，AB BC ⊥，22AB PA BC ===，M 为PB 的中点． （Ⅰ）求证：AM ⊥平面PBC ． （Ⅱ）求二面角A PC B --的余弦值． （Ⅲ）在线段PC 上是否存在点D ，使得BD AC ⊥，若存在，求出PDPC的值，若不存在，说明理由．16.如图所示，在四棱锥P -ABCD 中，AB ⊥平面,//,PAD AB CD E 是PB 的中点,2,5,3,2AHPD PA AB AD HD===== . （1）证明：PH ⊥平面ABCD ；（2）若F 是CD 上的点，且23FC FD ==，求二面角B EF C --的正弦值.MDABCP17.如图，DC ⊥平面ABC ，//EB DC ，22AC BC EB DC ====，120ACB ∠=︒，Q为AB 的中点．（Ⅰ）证明：CQ ⊥平面ABE ； （Ⅱ）求多面体ACED 的体积； （Ⅲ）求二面角A -DE -B 的正切值．18.如图1 ,在△ABC 中，AB =BC =2, ∠B =90°,D 为BC 边上一点，以边AC 为对角线做平行四边形ADCE ，沿AC 将△ACE 折起，使得平面ACE ⊥平面ABC ,如图2.(1)在图 2中，设M 为AC 的中点，求证:BM 丄AE ； (2)在图2中，当DE 最小时，求二面角A -DE -C 的平面角.19.如图所示，在已知三棱柱ABF -DCE 中，90ADE ∠=︒，60ABC ∠=︒，2AB AD AF ==，平面ABCD ⊥平面ADEF ，点M在线段BE 上，点G 是线段AD 的中点．（1）试确定点M 的位置，使得AF ∥平面GMC ； （2）求直线BG 与平面GCE 所成角的正弦值．20.已知在四棱锥P -ABCD 中，底面ABCD 是菱形，AC =AB ，P A ⊥平面ABCD ，E ，F 分别是AB ，PD 的中点.（Ⅰ）求证：AF ∥平面PCE ；（Ⅱ）若22AB AP ==，求平面P AD 与平面PCE 所成锐二面角的余弦值.21.如图，五面体P ABCD 中，CD ⊥平面P AD ，ABCD 为直角梯形，,2BCD PD BC CD π∠===1,2AD AP PD =⊥. （1）若E 为AP 的中点，求证：BE ∥平面PCD ； （2）求二面角P -AB-C 的余弦值.22.如图（1）所示，已知四边形SBCD 是由Rt △SAB 和直角梯形ABCD 拼接而成的，其中90SAB SDC ∠=∠=︒.且点A 为线段SD 的中点，21AD DC ==，2AB =.现将△SAB沿AB 进行翻折，使得二面角S -AB -C 的大小为90°，得到图形如图（2）所示，连接SC ，点E ，F 分别在线段SB ，SC 上. （Ⅰ）证明：BD AF ⊥；（Ⅱ）若三棱锥B -AEC 的体积为四棱锥S -ABCD 体积的25，求点E 到平面ABCD 的距离.23.四棱锥S-ABCD中，AD∥BC，,BC CD⊥060SDA SDC∠=∠=，AD DC=1122BC SD==，E为SD的中点.（1）求证：平面AEC⊥平面ABCD；（2）求BC与平面CDE所成角的余弦值.24.已知三棱锥P-ABC，底面ABC是以B为直角顶点的等腰直角三角形，P A⊥AC，BA=BC=P A=2，二面角P-AC-B的大小为120°.（1）求直线PC与平面ABC所成角的大小；（2）求二面角P-BC-A的正切值.25.如图，在四棱锥P -ABCD 中，平面P AD ⊥平面ABCD ，090=∠=∠BCD ABC ，AB CB DC PD PA 21====，E 是PB 的中点， （Ⅰ）求证：EC ∥平面APD ；（Ⅱ）求BP 与平面ABCD 所成的角的正切值； （Ⅲ）求二面角P -AB -D 的余弦值.26.四棱锥P ﹣ABCD 的底面ABCD 为边长为2的正方形，P A =2，PB =PD =22，E ，F ，G ，H 分别为棱P A ，PB ，AD ，CD 的中点．（1）求CD 与平面CFG 所成角的正弦值；（2）探究棱PD 上是否存在点M ，使得平面CFG ⊥平面MEH ，若存在，求出PDPM的值；若不存在，请说明理由．试卷答案1以点D 为坐标原点，建立如图所示的空间直角坐标系D xyz ，则 0,0,0D ，0,2,0A ，2,0,0C，0,0,2P ，1,0,1E ，0,0,1F ，2,1,0G .(1)∵0,2,2PA ，1,0,0EF，则0PA EF ，∴PA EF .(2)易知0,0,1DF，2,11FG， 设平面DFG 的法向量111,,m x y z ，则m DF m FG ，即1111020z x yz ，令11x ，则1,2,0m 是平面DFG 的一个法向量，同理可得0,1,1n 是平面EFG 的一个法向量，∴210cos ,552m n m nm n， 由图可知二面角D FG E 为钝角， ∴二面角D FG E 的余弦值为105.2.(1)证明：直三棱柱ADE BCF 中，AB 平面ADE ，所以：AB AD ，又AD AF ，所以：AD平面ABFE ，AD 平面PAD ，所以：平面PAD 平面ABFE .(2)由(1)AD平面ABFE ，以A 为原点，,,AB AE AD 方向为,,x y z 轴建立空间直角坐标系A xyz ，设正四棱锥P ABCD 的高h ，2AE AD ，则0,0,0A ，2,2,0F ，2,0,2C ，1,,1P h . 2,2,0AF，2,0,2AC，1,,1APh .设平面ACF 的一个法向量111,,m x y z ，则：1111220220m AF x y n ACx z ，取11x ，则111y z ，所以：1,1,1m .设平面AFP 的一个法向量222,,n x y z ，则222222200n AF x y n APx hy z ，取21x ，则21y ，21z h ，所以：1,1,1n h ，二面角C AF P 的余弦值是223，所以：211122cos ,3321m n h m n m nh ， 解得：1h .3.E ODPABC M（Ⅰ）证明：连结AC 交BD 于O ，则O 是BD 中点， ∵在PBD △中，O 是BD 的中点，M 是PB 的中点， ∴PD MO ∥，又PD ⊄平面ACM ，MO ⊂平面ACM ，∴PD ∥平面ACM ．（Ⅱ）证明：作PE CD ⊥，则E 为CD 中点，连结AE ， ∵底面ABCD 是菱形，边长为2，面积为，∴11sin 222sin 222S AD DC ADC ADC =⨯⨯⨯∠⨯=⨯⨯∠⨯=∴sin ADC ∠，60ADC ∠=︒， ∴ACD △是等边三角形， ∴CD AE ⊥， 又∵CD PE ⊥， ∴CD ⊥平面PAE ， ∴CD PA ⊥．（Ⅲ）11233P ABCD ABCD V S PE -=⨯=⨯．4.DABCSE（1）证明：∵SA ⊥平面ABCD ，AB ⊂平面ABCD ， ∴AB SA ⊥， 又∵90BAD ∠=︒， ∴AB AD ⊥， ∵SA AD A =， ∴AB ⊥平面SAD ， 又AB ⊂平面SAB ， ∴平面SAB ⊥平面SAD ． （Ⅱ）证明：取AD 中点为E ，∵90DAB ABC ∠=∠=︒，2AD a =，BC a =，E 是AD 中点， ∴ABCE ∠是矩形，CE AB a ==，DE a =，∴CD =，在ACD △中，AC，CD =，2AD a =， ∴222AC CD AD +=， 即CD AC ⊥，又∵SA ⊥平面ABCD ，CD ⊂平面ABCD ， ∴CD SA ⊥， ∴CD ⊥平面PAC ． 5.P F ECB AD（Ⅰ）证明：∵PD ⊥底面ABCD ，BC ⊂平面ABCD ， ∴PD BC ⊥，又∵底面ABCD 为矩形， ∴BC CD ⊥， ∴BC ⊥平面PCD ， ∵BC ⊂平面PBC ， ∴平面PCD ⊥平面PBC ．（Ⅱ）证明：∵PD DC =，E 是PC 中点， ∴DE PC ⊥，又平面PCD ⊥平面PBC ，平面PCD 平面PBC PC =， ∴DE ⊥平面PBC ， ∴DE PB ⊥， 又∵EF PB ⊥，EF DE E =，∴PB ⊥平面EFD ．6.E A 1B 1C 1CBAD（Ⅰ）证明：连结1A B ， ∵D 是1AB 的中点， ∴D 是1A B 的中点，∵在1A BC △中，D 是1A B 的中点，E 是1A C 的中点， ∴DE BC ∥，又DE ⊄平面11BCC B ，BC ⊂平面11BCC B ， ∴DE ∥平面11BCC B ．（Ⅱ）证明：∵111ABC A B C -是直棱柱， ∴1AA ⊥平面ABC ， ∴1AA AB ⊥， 又AB AC ⊥， ∴AB ⊥平面11ACC A ， ∵AB ⊂平面11ABB A ， ∴平面11ABB A ⊥平面11ACC A ．7.以A 为坐标原点，建立空间直角坐标系(2,0,0)B，D ，(0,0,2)P，C（1）(BD =-，(1,2)PC =-， ∵0BD PC •=∴BD PC ⊥（2）(1,AC =，(0,0,2)AP =，平面PAC 的法向量为(2,1,0)m =-(0,2)DP =，(1,0,0)AP =，平面DPC 的法向量为(0,2,1)n =--.2cos ,3m n m n m n•==•，二面角B PC D --的余弦值为3.（3）∵AQ AP PQ AP tPD =+=+，[]0,1t ∈ ∴(0,0,2)(0,2,2)(0,2,22)AQ t t t =+-=- 设θ为直线AQ 与平面PAC 所成的角2sin cos ,3AQ m AQ m AQ mθ•===• 2222223684332(22)tt t t t t =⇒=-++-，解得2t =（舍）或23. 所以，23PQ PD =即为所求.8.解:(1)不妨设正方体的棱长为1，以DA ,DC ,1DD 为单位正交基底建立如图所示的空间直角坐标系D xyz -． 则A (1，0，0)，()11022O ，，，()010C ，，，D 1(0，0，1)， E ()111442，，， 于是，.由cos＝＝.所以异面直线AE 与CD 1所成角的余弦值为36. （2）设平面CD 1O 的向量为m =(x 1，y 1，z 1)，由m ·CO ＝0，m ·1CD ＝0 得 取x 1＝1，得y 1＝z 1＝1，即m =(1，1，1) .由D 1E ＝λEO ，则E ，.又设平面CDE 的法向量为n ＝(x 2，y 2，z 2)，由n ·CD ＝0，n ·DE ＝0. 得取x 2=2，得z 2＝－λ，即n ＝(－2，0，λ) .因为平面CDE ⊥平面CD 1F ，所以m ·n ＝0，得λ＝2．9.（Ⅰ）证明：在平行四边形ABCD 中， ∵AB AC =，135BCD =︒∠，45ABC =︒∠， ∴AB AC ⊥，∵E ，F 分别为BC ，AD 的中点， ∴EF AB ∥，∴EF AC ⊥，∵侧面PAB ⊥底面ABCD ，且90BAP =︒∠， ∴PA ⊥底面ABCD ，∴PA EF ⊥， 又∵PAAC A =，PA ⊂平面PAC ，AC ⊂平面PAC ，∴EF ⊥平面PAC ．（Ⅱ）证明：∵M 为PD 的中点，F 为AD 的中点， ∴MF PA ∥，又∵MF ⊄平面PAB ，PA ⊂平面PAB ， ∴MF ∥平面PAB ，同理，得EF ∥平面PAB ， 又∵MFEF F =，MF ⊂平面M EF ，EF ⊂平面M EF ，∴平面MEF ∥平面PAB ，又∵ME ⊂平面M EF ， ∴ME ∥平面PAB ．（Ⅲ）解：∵PA ⊥底面ABCD ，AB AC ⊥，∴AP ，AB ，AC 两两垂直，故以AB ，AC ，AP 分别为x 轴，y 轴和z 轴建立如图空间直角坐标系，则(0,0,0)A ，(2,0,0)B ，(0,2,0)C ，(0,0,2)P ，(2,2,0)D -，(1,1,0)E ， 所以(2,0,2)PB =-，(2,2,2)PD =--，(2,2,0)BC =-， 设([0,1])PMPDλλ=∈，则(2,2,2)PM λλλ=--， ∴(2,2,22)M λλλ--，(12,12,22)ME λλλ=+--， 易得平面ABCD 的法向量(0,0,1)m =， 设平面PBC 的法向量为(,,z)n x y =，则：n BC n PB ⎧⋅=⎪⎨⋅=⎪⎩，即220220x y x z -+=⎧⎨-=⎩，令1x =，得(1,1,1)n =， ∴直线ME 与平面PBC 所成的角和此直线与平面ABCD 所成的角相等， ∴|cos ,||cos ,|ME m ME n <>=<>，即||||||||||||ME m ME n ME m ME n ⋅⋅=⋅⋅，∴|21|λ-=，解得λ=或λ=（舍去），故PM PD ．D10.（1）∵1C F ∥平面AEG ，又1C F ⊂平面11ACC A ，平面11ACC A 平面AEG AG =，∴1C F AG ∥，∵F 为1AA 的点，且侧面11ACC A 为平行四边形， ∴G 为1CC 中点， ∴112CG CC =． （2）证明：∵1AA ⊥底面ABC ，1AA AB ⊥，1AA AC ⊥， 又AB AC ⊥，如图，以A 为原点建立空间直角坐标系A xyz -，设2AB =，则由1AB AC AA ==可得(2,0,0)C ，(0,2,0)B ，1(2,0,2)C ，1(0,0,2)A ， ∵E ，G 分别是BC ，1CC 的中点，∴(1,1,0)E ，(2,0,1)G ， ∴1(1,1,1)(2,0,2)0EG CA ⋅=-⋅-=， ∴1EG CA ⊥， ∴1EG AC ⊥． （3）设平面AEG 的法向量为(,,)n x y z =，则：0n AE n AG ⎧⋅=⎪⎨⋅=⎪⎩，即020x y x z +=⎧⎨+=⎩，令1x =，则1y =-，2z =-， ∴(1,1,2)n =--，由已知可得平面1A AG 的法向量(0,1,0)m =， ∴6cos ,6||||n m n m n m ⋅<>==-⋅由题意知二面角1A AG E --为钝角， ∴二面角1A AG E --的余弦值为．111.（Ⅰ）证明：过点F 作FH AD ∥， 交PA 于H ，连结BH ，如图所示，∵13PF PD =，∴13HF AD BC ==，又FH AD ∥，AD BC ∥，HF BC ∥， ∴四边形BCFH 为平行四边形， ∴CF BH ∥，又BH ⊄平面PAB ，CF ⊄平面PAB ， ∴CF ∥平面PAB ．z D（Ⅱ）解：∵梯形ABCD 中，AD BC ∥，AD AB ⊥， ∴BC AB ⊥， ∵PB ⊥平面ABCD ， ∴PB AB ⊥，PB BC ⊥，∴如图，以B 为原点，BC ，BA ，BP 所在直线为x ，y ，z 轴建立空间直角坐标系， 则(1,0,0)C ，(3,0,0)D ，(0,3,0)A ，(0,0,3)P ，设平面BPD 的一个法向量为(,,)n x y z =， 平面APD 的一个法向量为(,,)m a b c =， ∵(3,3,3)PD =-，(0,0,3)BP =，∴00PD n BP n ⎧⋅=⎪⎨⋅=⎪⎩，即333030x y z z +-=⎧⎨=⎩，令1x =得(1,1,0)n =-，同理可得(0,1,1)m =， ∴1cos ,2||||n m n m n m ⋅<>==-⋅，∵二面角B PD A --为锐角， ∴二面角B PD A --为π3． （Ⅲ）假设存在点M 满足题意，设(3,3,3)PM PD λλλλ=-， ∴(13,3,33)CM CP PD λλλλ=+=-+-，∵(0,3,3)PA =-，∴93(33)0PA CM λλ⋅=+-=，解得12λ=，∴PD 上存在点M 使得CM PA ⊥，且12PM PD =．12.Ⅰ∵BC CD ⊥，2BC CD ==，∴BD =，同理EA ED ⊥，2EA ED ==，∴AD =，又∵4AB =，∴由勾股定理可知222BD AD AB +=，BD AD ⊥， 又∵平面EAD ⊥平面ABCD ，平面EAD 平面ABCD AD =，BD ⊂平面ABCD ，∴BD ⊥平面AED ， 又∵AE ⊂平面AED ， ∴BD AE ⊥．Ⅱ解：取AD 的中点O ，连结OE ，则OE AD ⊥， ∵平面EAD ⊥平面ABCD ，平面EAD 平面ABCD AD =，∴OE ⊥平面ABCD ，取AB 的中点F ，连结DF BD ∥，以O 为原点，建立如图所示的空间直角坐标系O xyz -，则(D ，(C -，E ，(DC =-，(2,0,DE =， 设平面CDE 的法向量为(,,)n x y z =，则00DC n DE n ⎧⋅=⎪⎨⋅=⎪⎩即00x z x y +=⎧⎨-+=⎩，令1x =，则1z =-，1y =，∴平面CDE 的法向量(1,1,1)n =-， 又平面ADE 的一个法向量为1(0,1,0)n =， 设平面ADE 和平面CDE 所成角（锐角）为θ， 则1113cos |cos ,|3||||nn n n n n θ⋅=<>==⋅，∴平面ADE 和平面CDE． C13.（1）证明：连结AE ，PE ．∵PA ⊥平面ABCD ，BC ⊂平面ABCD ， ∴PA BC ⊥．又∵底面ABCD 是菱形，AB BC =，60ABC ∠=︒， ∴ABC △是正三角形． ∵E 是BC 的中点， ∴AE BC ⊥．又∵PA AE A =，PA ⊂平面PAE ，PE ⊂平面PAE ，∴BC ⊥平面PAE ， ∴BC PE ⊥．（2）由（1）得AE BC ⊥，由BC AD ∥可得AE AD ⊥． 又∵PA ⊥底面ABCD ，∴PA AE ⊥，PA AD ⊥．∴以A 为原点，分别以AE ，AD ，AP 为x 轴，y 轴，z 轴建立空间直角坐标系A xyz -，如图所示，则(0,0,0)A，E ，(0,2,0)D ，(0,0,2)P，1,0)B -，C ，(0,1,1)F ．∵PA ⊥平面ABCD ，∴平面ABCD 的法向量为(0,0,2)AP =． 又∵(3,1,0)AC =，(0,1,1)AF =． 设平面ACF 的一个法向量(,,)n x y z =，则：AC n AF n ⎧⋅=⎪⎨⋅=⎪⎩，即00y y z +==⎪⎩+，令1x =，则y =z ，∴(1,3,n =-． ∴21cos ,7||||AP n AP n AP n ⋅==． ∵二面角F AC D --是锐角， ∴二面角F AC D -- （3）G 是线段AB 上的一点，设(01)AG t AB t =≤≤． ∵(3,1,0)AB =-，∴,,0)G t -． 又∵(3,1,2)PC =-，(3,,2)PG t t =--． 设平面PCG 的一个法向量为(,,)n x y z =，则：1100PC n PGn ⎧⋅=⎪⎨⋅=⎪⎩，即1111112020yz ty z-=--=+，∴1()n t t =-+， ∵AF ∥平面PCG ，∴AF n ⊥，0AF n ⋅=1)0t -=， 解得12t =． 故线段AB 上存在一点G ，使得AF 平行于平面PCG ，G 是AB 中点．14.（1）证明：∵DE ⊥平面ABCD ，AC ⊂平面ABCD ， ∴DE AC ⊥． ∵ABCD 是正方形， ∴AC BD ⊥． 又DEBD D =，∴AC ⊥平面BDE ．（2）∵DA ，DC ，DE 两两重叠，∴建立空间直角坐标系D xyz -如图所示．∵BE 与平面ABCD 所成角为60︒，即60DBE ∠=︒，∴EDDB． 由3AD =，可知DZ =AF ，则(3,0,0)A，F，E ，(3,3,0)B ，(0,3,0)C ．∴(0,BF =-，(3,0,EF =-， 设平面BEF 的法向量为(,,)n x y z =，则00n BF n EF ⎧⋅=⎪⎨⋅=⎪⎩，即3030y x ⎧-=⎪⎨-=⎪⎩，令z (4,2,6)n =． ∵AC ⊥平面BDE ，∴CA 为平面BDE 的一个法向量，(3,3,0)CA =-，∴cos ,||||32n CA n CA n CA ⋅==．∵二面角F BE D --为锐角， ∴二面角F BE D -- （3）点M 线段BD 上一个动点，设(,,0)M t t ，则(3,,0)AM t t =-．∵AM ∥平面BEF ，∴0AM n ⋅=，即4(3)20t t -+=，解得2t =，此时，点M 坐标为(2,2,0)，13BM BD =，符合题意．15.（1）证明：∵PA ⊥平面ABC ，BC ⊂平面ABC ， ∴PA BC ⊥．∵BC AB ⊥，PA AB A =， ∴BC ⊥平面PAB ． 又AM ⊂平面PAB ， ∴AM BC ⊥．∵PA AB =，M 为PB 的中点， ∴AM PB ⊥． 又∵PBBC B =，∴AM ⊥平面PBC ．（2）如图，在平面ABC 内作AZ BC ∥，则AP ，AB ，AZ 两两垂直，建立空间直角坐标系A xyz -．则(0,0,0)A ，(2,0,0)P ，(0,2,0)B ，(0,2,1)C ，(1,1,0)M ． (2,0,0)AP =，(0,2,1)AC =，(1,1,0)AM =．设平面APC 的法向量为(,,)n x y z =，则：0n AP n AC ⎧⋅=⎪⎨⋅=⎪⎩，即020x y z =⎧⎨+=⎩，令1y =，则2z =-． ∴(0,1,2)n =-．由（1）可知(1,1,0)AM =为平面PBC 的一个法向量，∴cos||||5AM nn AMAM n⋅⋅==∵二面角A PC B--为锐角，∴二面角A PC B--．（3）证明：设(,,)D v wμ是线段PC上一点，且PD PCλ=，(01)λ≤≤，即(2,,)(2,2,1)v wμλ-=-，∴22μλ=-，2vλ=，wλ=．∴(22,22,)BDλλλ=--．由0BD AC⋅=，得4[0,1]5λ=∈，∴线段PC上存在点D，使得BD AC⊥，此时45PDPCλ==．16.解：（1）证明：因为AB⊥平面PAD，所以PH AB⊥，因为3,2AHADHD==，所以2,1AH HD==，设PH x=，由余弦定可得，22221cos22x HD PH xPHDx HD x+--∠==⋅22221cos24x HA PH xPHAx HA x+--∠==⋅因为cos cosPHD PHA∠=-∠，故1PH x==，所以PH AD⊥，因为AD AB A=，故PH⊥平面ABCD.（2）以H为原点，以,,HA HP HP所在的直线分别为,,x y z轴，建立空间直角坐标系，则3139(2,3,0),(0,0,1),(1,,),(1,,0),(1,,0)2222B P E F C--，所以可得，3311(3,,0),(1,,),(2,0,),(0,3,0)2222BF BE EF FC=--=--=-=，设平面BEF的法向量(,,)n x y z=，则有：33002(1,2,4)30022x yBF nnzBE n x y⎧--=⎪⎧⋅=⎪⎪⇒⇒=-⎨⎨⋅=⎪⎪⎩--+=⎪⎩，设平面EFC的法向量(,,)m x y z=，则有：020(1,0,4)2030z EF m x m FC m y ⎧⎧⋅=--=⎪⎪⇒⇒=-⎨⎨⋅=⎪⎪⎩=⎩，故17cos ,21n m n m n m⋅===⋅设二面角B EF C --的平面角为θ ，则sin 21θ=.17.解（Ⅰ）证明：∵DC ⊥平面ABC ，//BE DC ∴BE ⊥平面ABC ∴CQ BE ⊥ ①又∵2AC BC ==，点Q 为AB 边中点 ∴CQ AB ⊥ ②AB BE B =故由①②得CQ ⊥平面ABE（Ⅱ）过点A 作AM BC ⊥交BC 延长线于点M ∵,AM BC AM BE ⊥⊥ ∴AM ⊥平面BEDC ∴13A CED CDE V S AM -∆=sin33AM AC π==11212CDE S ∆=⨯⨯= ∴113A CED V -=⨯= （Ⅲ）延长ED 交BC 延长线于S ，过点M 作MQ ES ⊥于Q ，连结AQ 由（Ⅱ）可得：AQM ∠为A DE B --的平面角∵1//2CD BC ∴2SC CB == ∴SE ==1MC MS ==∵SQM ∆∽SBE ∆∴QM SM BE SE=∴1225QM=即55QM=∴3tan1555AMAQMQM∠===18.（1）证明：∵在中，，∴当为的中点时，∵平面平面，平面，平面平面∴平面∵平面∴（2）如图，分别以射线，的方向为，轴的正方向，建立空间直角坐标系设，则，，，∵，，平面平面∴∴当且仅当时，最小，此时，设，平面，则，即∴令，可得，，则有∴∴观察可得二面角的平面角19.（1）取FE 的中点P ，连接CP 交BE 于点M ，M 点即为所求的点． 连接PG ，∵G 是AD 的中点，P 是FE 的中点，∴//PG AF ， 又PG ⊂平面MGC ，AF ⊄平面MGC ，所以直线//AF 平面MGC ， ∵//PE AD ，//AD BC ，∴//PE BC ，∴2BM BCME PE==， 故点M 为线段BE 上靠近点E 的三等分点． （2）不妨设2AD =，由（1）知PG AD ⊥， 又平面ADEF ⊥平面ABCD ，平面ADEF平面ABCD AD =，PG ⊂平面ADEF ，∴PG ⊥平面ABCD ．故PG GD ⊥，PG GC ⊥，以G 为坐标原点，GC ，GD ，GP 分别为x ，y ，z 轴建立空间直角坐标系G xyz -，∵60ABC ∠=︒，2AB AD AF ==，∴ADC ∆为正三角形，3GC =，∴(0,0,0)G ，3,0,0)C ，(0,1,0)D ，(0,1,1)E ，∴(0,1,1)GE =，(3,0,0)GC =，设平面CEG 的一个法向量1(,,)n x y z =，则由10n GE ⋅=，10n GC ⋅=可得0,30,y z x +=⎧⎪⎨=⎪⎩令1y =，则1(0,1,1)n =-，∵(3,1,0)CD =-BA =，且(0,1,0)A -，故3,2,0)B -，故(3,2,0)BG =-， 故直线BG 与平面GCE 所成角的正弦值为11||14sin 7||||n BG n BG θ⋅==⋅．20.（Ⅰ）取PC 中点H ，连接、EH FH .∵E 为AB 的中点，ABCD 是菱形，∴//AE CD ，且12AE CD =，又F 为PD 的中点，H 为PC 的中点，∴//FH CD ，且12FH CD =，∴//AE FH ，且AE FH =，则四边形AEHF 是平行四边形，∴//AF EH .又AF ⊄平面PCE ，EH ⊂面PCE ，∴//AF 平面PCE .（Ⅱ）取BC 的中点为O ，∵ABCD 是菱形，AC AB =，∴AO BC ⊥，以A 为原点，,,AO AD AP 所在直线分别为,,z x y 轴，建立空间直角坐标系A xyz -，则)()()3,1,0,3,1,0,0,2,0BCD -，)()313,0,0,0,0,1,,02OP E ⎫-⎪⎪⎝⎭，∴()333,1,1,,,022PC EC ⎛⎫=-= ⎪ ⎪⎝⎭，()3,0,0AO =，设平面的法向量为()1,,n x y z =，则1100n PC n EC ⎧⋅=⎪⎨⋅=⎪⎩，即3033022x y z x y ⎧+-=⎪+=⎪⎩，令1y =-，则3,2x z ==，∴平面PCE 的一个法向量为)13,1,2n =-，又平面PAD 的一个法向量为()21,0,0n =.∴12121236cos ,|n ||n |4314n n n n ⋅<>===⋅++.即平面PAD 与平面PCE 621.解：（1）证明：取PD 的中点F ，连接,EF CF ， 因为,E F 分别是,PA PD 的中点，所以//EF AD 且12EF AD =， 因为1,//2BC AB BC AD =，所以//EF BC 且EF BC =，所以//BE CF , 又BE ⊄平面,PCD CF ⊂平面PCD ，所以//BE 平面PCD .（2）以P 为坐标原点，,PD PA 所在直线分别为x 轴和y 轴，建立如图所示的空间直角坐标系，不妨设1BC =，则13(0,0,0),3,0),(1,0,0),(1,0,1),(2P A D C B ， 13(0,3,0),(,1),(1,3,0)2PA AB AD ==-=-,设平面PAB 的一个法向量为(,,)n x y z =，则30013002n PA yn AB x z ⎧=⎧⋅=⎪⎪⇒⎨⎨⋅=+=⎪⎪⎩⎩， 令2x =，得(2,0,1)n =-， 同理可求平面ABD 的一个法向量为6(3,3,0)cos ,55n m m n m n m⋅=⇒===⨯，平面ABD 和平面ABC 为同一个平面， 所以二面角P AB C --.22.解：（Ⅰ）证明：因为二面角S AB C --的大小为90°，则SA AD ⊥， 又SA AB ⊥，故SA ⊥平面ABCD ，又BD ⊂平面ABCD ，所以SA BD ⊥； 在直角梯形ABCD 中，90BAD ADC ∠=∠=︒，21AD CD ==，2AB =， 所以1tan tan 2ABD CAD ∠=∠=，又90DAC BAC ∠+∠=︒， 所以90ABD BAC ∠+∠=︒，即AC BD ⊥； 又ACSA A =，故BD ⊥平面SAC ，因为AF ⊂平面SAC ，故BD AF ⊥.（Ⅱ）设点E 到平面ABCD 的距离为h ，因为B ABC E ABC V V --=，且25E ABC S ABCD V V --=，故511215*********ABCD S ABCD E ABCABC S SAV V S h h --∆⨯⋅⨯===⋅⨯⨯⨯梯形，故12h =，做点E 到平面ABCD 的距离为12.23.（1）E 为SD 的中点，01,602AD DC SD SDA SDC ==∠=∠=.ED EC AD DC ∴===设O 为AC 的中点，连接,EO DO 则EO AC ⊥//,AD BC BC CD ⊥ .AD BC ∴⊥又OD OA OC ==EOC EOD ∴∆≅∆ 从而EO OD ⊥AC ABCD = DO ⊂面ABCD 0AC DO =EO ∴⊥面ABCD EO ⊂面AEC∴面EAC ⊥面ABCD ………………6分（2）设F 为CD 的中点,连接OF EF 、,则OF 平行且等于12AD AD ∥BC EF ∴∥BC不难得出CD ⊥面OEF （EO CD ⊥ FO CD ⊥）∴面ECD ⊥面OEFOF 在面ECD 射影为EF ，EFO ∠的大小为BC 与面ECD 改成角的大小设AD a =，则2aOF =32EF a = 3os OF c EFO EF <== 即BC 与ECD 3（亦可以建系完成） ………………12分24.解（Ⅰ）过点P 作PO ⊥底面ABC ，垂足为O ， 连接AO 、CO ，则∠PCO 为所求线面角，,AC PA ⊥,AC PO PA PO P ⊥⋂=且，AC ∴⊥平面PAO .则∠P AO 为二面角P -AC -B 平面角的补角∴∠ 60=PAO ，又23PA =∴，，1sin 2PO PCO CO ∠== 030PCO ∴∠=，直线PC 与面ABC 所成角的大小为30°.（Ⅱ）过O 作OE BC ⊥于点E ,连接PE ，则PEO ∠为二面角P -BC -A 的平面角，AC ⊥平面PAO ,AC OA ⊥045AOE ∠=,设OE 与CA 相交于F 22OE EF FO ∴=+=+在PEO ∆中，3436tan 7222POPEO EO-∠===+则二面角P -BC -A 的正切值为4367-.25.解：（Ⅰ）如图，取PA 中点F ，连接FD EF ,，E 是BP 的中点，AB EF // 且AB EF 21=，又AB DC AB DC 21,//= ∴∴DC EF //四边形EFDC 是平行四边形，故得//EC FD又⊄EC 平面⊂FD PAD ,平面PAD//EC ∴平面ADE（Ⅱ）取AD 中点H ,连接PH ,因为PD PA =，所以AD PH ⊥平面⊥PAD 平面ABCD 于AD ，⊥∴PH 面ABCD ，HB ∴是PB 在平面ABCD 内的射影 PBH ∠∴是PB 与平面ABCD 所成角四边形ABCD 中，090=∠=∠BCD ABC ∴四边形ABCD 是直角梯形AB CB DC 21== 设a AB 2=，则a BD 2=在ABD ∆中，易得a AD DBA 2,450=∴=∠.22212222a a a DH PD PH =-=-=又22224AB a AD BD ==+ABD ∆∴是等腰直角三角形，090=∠ADBa a a DB DH HB 2102212222=+=+=∴ ∴ 在PHB Rt ∆中，5521022tan ===∠a aHB PH PBH（Ⅲ）在平面ABCD 内过点H 作AB 的垂线交AB 于G 点，连接PG ,则HG 是PG 在平面ABCD 上的射影，故AB PG ⊥，所以PGH ∠是二面角D AB P --的平面角， 由a HA a AB 22,2==，又a HG HAB 21450=∴=∠ 在PHG Rt ∆中，22122tan ===∠a aHG PH PGH ∴ 二面角D AB P --的余弦值大小为.3326.（1）∵四棱锥P ﹣ABCD 的底面ABCD 为边长为2的正方形，PA=2，PB=PD=2，∴PA 2+AB 2=PB 2，PA 2+AD 2=PD 2， ∴PA ⊥AB ，PA ⊥AD ，∴以A 为原点，AB 为x 轴，AD 为y 轴，AP 为z 轴， 建立空间直角坐标系，∵E ，F ，G ，H 分别为棱PA ，PB ，AD ，CD 的中点． ∴C （2，2，0），D （0，2，0），B （2，0，0）， P （0，0，2），F （1，0，1），G （0，1，0）， =（﹣2，0，0），=（﹣1，﹣2，1），=（﹣2，﹣1，0），设平面CFG 的法向量=（x ，y ，z ）， 则，取x=1，得=（1，﹣2，﹣3），设CD与平面CFG所成角为θ，则sinθ=|cos＜＞|===．∴CD与平面CFG所成角的正弦值为．（2）假设棱PD上是否存在点M（a，b，c），且，（0≤λ≤1），使得平面CFG⊥平面MEH，则（a，b，c﹣2）=（0，2λ，﹣2λ），∴a=0，b=2λ，c=2﹣2λ，即M（0，2λ，2﹣2λ），E（0，0，1），H（1，2，0），=（1，2，﹣1），=（0，2λ，1﹣2λ），设平面MEH的法向量=（x，y，z），则，取y=1，得=（，1，），平面CFG的法向量=（1，﹣2，﹣3），∵平面CFG⊥平面MEH，∴=﹣2﹣=0，解得∈[0，1]．∴棱PD上存在点M，使得平面CFG⊥平面MEH，此时=．。
专题01 立体几何部分(解析版)-2020年江苏高考数学试卷名师分析与预测
专题一 立体几何部分一、近几年江苏高考1、（1）（2019江苏卷）如图，长方体1111ABCD A B C D -的体积是120，E 为1CC 的中点，则三棱锥E -BCD 的体积是_____.【答案】10.【解析】因为长方体1111ABCD A B C D -的体积为120， 所以1120AB BC CC ⋅⋅=，因为E 为1CC 的中点， 所以112CE CC =，由长方体的性质知1CC ⊥底面ABCD ， 所以CE 是三棱锥E BCD -的底面BCD 上的高， 所以三棱锥E BCD -的体积1132V AB BC CE =⨯⋅⋅=111111201032212AB BC CC =⨯⋅⋅=⨯=. （2）（2019江苏卷）.如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ．求证：（1）A 1B 1∥平面DEC 1；（2）BE ⊥C 1E ． 【解析】（1）因为D ，E 分别为BC ，AC 的中点，所以ED∥AB.在直三棱柱ABC-A1B1C1中，AB∥A1B1，所以A1B1∥ED.又因为ED⊂平面DEC1，A1B1 平面DEC1，所以A1B1∥平面DEC1.（2）因为AB=BC，E为AC的中点，所以BE⊥AC.因为三棱柱ABC-A1B1C1是直棱柱，所以CC1⊥平面ABC.又因为BE⊂平面ABC，所以CC1⊥BE.因为C1C⊂平面A1ACC1，AC⊂平面A1ACC1，C1C∩AC=C，所以BE⊥平面A1ACC1.因为C1E⊂平面A1ACC1，所以BE⊥C1E.2、（1）（2018江苏卷）如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为________．【答案】【解析】分析：解决本类题目的关键是准确理解几何体的定义，真正把握几何体的结构特征，可以根据条件构建几何模型，在几何模型中进行判断；求一些不规则几何体的体积时，常用割补法转化成已知体积公式的几何体进行解决．先分析组合体的构成，再确定锥体的高，最后利用锥体体积公式求结果.详解：由图可知，该多面体为两个全等正四棱锥的组合体，正四棱锥的高为1，底面正方形的边长等于，所以该多面体的体积为（2）（2018江苏卷）在平行六面体中，．求证：（1）；（2）．【解析】分析：（1）先根据平行六面体得线线平行，再根据线面平行判定定理得结论；（2）先根据条件得菱形ABB1A1，再根据菱形对角线相互垂直，以及已知垂直条件，利用线面垂直判定定理得线面垂直，最后根据面面垂直判定定理得结论.详解：证明：（1）在平行六面体ABCD-A1B1C1D1中，AB∥A1B1．因为AB平面A1B1C，A1B1平面A1B1C，所以AB∥平面A1B1C．（2）在平行六面体ABCD-A1B1C1D1中，四边形ABB1A1为平行四边形．又因为AA1=AB，所以四边形ABB1A1为菱形，因此AB1⊥A1B．又因为AB1⊥B1C1，BC∥B1C1，所以AB1⊥BC．又因为A1B∩BC=B，A1B平面A1BC，BC平面A1BC，所以AB1⊥平面A1BC．因为AB 1平面ABB 1A 1，所以平面ABB 1A 1⊥平面A 1BC ．3、（1）（2017江苏卷）如图，圆柱O 1O 2内有一个球O ，该球与圆柱的上、下底面及母线均相切．记圆柱O 1O 2的体积为V 1，球O 的体积为V 2，则V 1V 2的值是________．【答案】 32【解析】设球的半径为R ，则圆柱的底面半径为R ，高为h ＝2R .因为V 1＝πR 2h ＝2πR 3，V 2＝4πR 33，所以V 1V 2＝32. （2）（2017江苏卷）如图，在三棱锥ABCD 中，AB ⊥AD ，BC ⊥BD ，平面ABD ⊥平面BCD ，点E ，F (E 与A ，D 不重合)分别在棱AD ，BD 上，且EF ⊥AD . 求证：(1) EF ∥平面ABC ； (2) AD ⊥AC .证明：(1) 在平面ABD内，因为AB⊥AD，EF⊥AD，所以EF∥AB.又因为EF⊄平面ABC，AB⊂平面ABC，所以EF∥平面ABC.(2) 因为平面ABD⊥平面BCD，平面ABD∩平面BCD＝BD，BC⊂平面BCD，BC⊥BD，所以BC⊥平面ABD. 因为AD⊂平面ABD，所以BC⊥AD.又AB⊥AD，BC∩AB＝B，AB⊂平面ABC，BC⊂平面ABC，所以AD⊥平面ABC.又因为AC⊂平面ABC，所以AD⊥AC.4、（1）（2016江苏卷）现需要设计一个仓库，它由上下两部分组成，上部的形状是正四棱锥P A1B1C1D1，下部的形状是正四棱柱ABCDA1B1C1D1(如图所示)，并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍．(1) 若AB＝6 m，PO1＝2 m，则仓库的容积是多少？(2) 若正四棱锥的侧棱长为6 m，则当PO1为多少时，仓库的容积最大？【答案】 (1) 由PO 1＝2知O 1O ＝4PO 1＝8. 因为A 1B 1＝AB ＝6，所以正四棱锥P A 1B 1C 1D 1的体积 V 锥＝13·A 1B 21·PO 1＝13×62×2＝24(m 3)； 正四棱柱ABCDA 1B 1C 1D 1的体积 V 柱＝AB 2·O 1O ＝62×8＝288(m 3)．所以仓库的容积V ＝V 锥＋V 柱＝24＋288＝312(m 3)．(2) 设A 1B 1＝a (m)，PO 1＝h (m)，则0<h <6，O 1O ＝4h .连结O 1B 1.因为在Rt △PO 1B 1中，O 1B 21＋PO 21＝PB 21， 所以⎝⎛⎭⎫2a 22＋h 2＝36，即a 2＝2(36－h 2)， 于是仓库的容积V ＝V 柱＋V 锥＝a 2·4h ＋13a 2·h ＝133a 2h ＝263(36h －h 3)，0<h <6，从而V ′＝263(36－3h 2)＝26(12－h 2)．令V ′＝0，得h ＝23或h ＝－23(舍)． 当0<h <23时，V ′>0，V 是单调增函数； 当23<h <6时，V ′<0，V 是单调减函数． 故h ＝23时，V 取得极大值，也是最大值．因此，当PO1＝2 3 m时，仓库的容积最大．（2）（2016江苏卷）如图，在直三棱柱ABCA1B1C1中，D，E分别为AB，BC的中点，点F在侧棱B1B上，且B1D⊥A1F，A1C1⊥A1B1.求证：(1) 直线DE∥平面A1C1F；(2) 平面B1DE⊥平面A1C1F.解析：(1) 在直三棱柱ABCA1B1C1中，A1C1∥AC.在△ABC中，因为D，E分别为AB，BC的中点，所以DE∥AC，于是DE∥A1C1.又因为DE⊄平面A1C1F，A1C1⊂平面A1C1F，所以直线DE∥平面A1C1F.(2) 在直三棱柱ABCA1B1C1中，A1A⊥平面A1B1C1.因为A1C1⊂平面A1B1C1，所以A1A⊥A1C1.又因为A1C1⊥A1B1，A1A⊂平面ABB1A1，A1B1⊂平面ABB1A1，A1A∩A1B1＝A1，所以A1C1⊥平面ABB1A1.因为B1D⊂平面ABB1A1，所以A1C1⊥B1D.又因为B1D⊥A1F，A1C1⊂平面A1C1F，A1F⊂平面A1C1F，A1C1∩A1F＝A1，所以B1D⊥平面A1C1F.因为直线B1D⊂平面B1DE，所以平面B1DE⊥平面A1C1F.5、（1）（2015江苏卷）现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2、高为8的圆柱各一个．若将它们重新制作成总体积与高均保持不变，但底面半径相同的新的圆锥与圆柱各一个，则新的底面半径为________．【答案】7【解析】设新的底面半径为r ，则13π×52×4＋π×22×8＝13πr 2×4＋πr 2×8，解得r ＝7.（2）（2015江苏卷）如图，在直三棱柱ABCA 1B 1C 1中，已知AC ⊥BC ，BC ＝CC 1.设AB 1的中点为D ，B 1C ∩BC 1＝E .求证：(1) DE ∥平面AA 1C 1C ； (2) BC 1⊥AB 1.(1) 由题意知，E 为B 1C 的中点， 又D 为AB 1的中点，因此DE ∥AC .又因为DE ⊄平面AA 1C 1C ，AC ⊂平面AA 1C 1C ， 所以DE ∥平面AA 1C 1C .(2) 因为棱柱ABCA 1B 1C 1是直三棱柱， 所以CC 1⊥平面ABC .因为AC ⊂平面ABC ，所以AC ⊥CC 1.又因为AC ⊥BC ，CC 1⊂平面BCC 1B 1，BC ⊂平面BCC 1B 1，BC ∩CC 1＝C ，所以AC ⊥平面BCC 1B 1. 又因为BC 1⊂平面BCC 1B 1，所以BC 1⊥AC .因为BC ＝CC 1，所以矩形BCC 1B 1是正方形，因此BC 1⊥B 1C . 因为AC ，B 1C ⊂平面B 1AC ，AC ∩B 1C ＝C ，所以BC 1⊥平面B 1AC . 又因为AB 1⊂平面B 1AC ，所以BC 1⊥AB 1.二、近几年高考试卷分析从近五年江苏高考数学来看体现了以下几个方面：1、从题型来看主要以一个填空，一个解答；（2016年填空题中没有考查体积，体积的考查体现在应用题中）；2、从知识点考查的内容来看主要以填空题是关于体积的计算，解答题设置了2问，第一问考查了平行，主要时候以线面平行，使用的方法还是以中位线为主。
2019-2020高考数学(理)复习试题汇编 第八章 立体几何 含解析
r 3 ，所以1 222R3a 3 ， V 4 （.第八章 立体几何第一节 空间几何体及其表面积和体积题型 85 空间几何体的表面积与体积1.（2017 江苏 6）如图所示，在圆柱 O O 内有一个球 O ，该球与圆柱的上、下面及母线均1 2相切．记圆柱 O 1O 2 的体积为V 1 ，球 O 的体积为V 2 ，则O 2OO 1VV1 的值是 ．21.解析 设球 O 的半径为 r ，由题意V1r 2 2r ，V24 3V V23 3．故填 ．2．2017 天津理 10）已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18 ，则这个球的体积为.2.解析 设正方体的边长为 a ，则 6a 218 a 23 .外接球直径为正方体的体对角线，所以4 27 9πR 3π π 33 8 23.（2107 全国 1 卷理科 16）如图所示，圆形纸片的圆心为 O ，半径为5 cm ，该纸片上的等边三角形 ABC 的中心为 O .D ， E ， F 为圆 O 上的点，△DBC ，△ECA ，△FAB 分别是以 BC ， CA ， AB 为底边的等腰三角形.沿虚线剪开后，分别以 BC ， CA ， AB 为折痕折起 △DBC ， △ECA ， △FAB ，使得 D ， E ， F 重合，得到三棱锥.当 △ABC 的边长变化时，所得三棱锥体积（单位： c m 3）的最大值为_______.EAFOBC1h = DG - OG = 25 - 10x + x - x = 25 - 10x ， △S ABC = 2 3x ⋅ 3x ⋅ 12⋅ h = 3x 2 25 - 10x = 3 25x 4 - 10x 5 .令 f (x ) = 25x 4 - 10 x 5 ， x ∈ 0, ⎪ ， 1 ⎛ 5 ⎫ f (x ) 在 (0,2 )上单调递增，在 2, ⎪ 上单调递减.故 f (x )≤ f (2) = 80 ，则A ． πB ． 3π r = 12 - ⎪ =3.解析 由题意，联结 OD ，交 BC 于点 G ，如图所示，则 O D ⊥ BC ， OG =3 BC ，6即 OG 的长度与 BC 的长度成正比.设 OG = x ，则 BC = 2 3x ， DG = 5 - x ，三棱锥的高2 2 2 2 =3 3x 2 ，则 V =3 △S ABC ⎝ 2 ⎭f ' (x ) = 100 x 3- 50 x 4，令 f ' (x ) > 0 ，即 x 4- 2x 3< 0 ， x < 2 ，当 f ' (x ) < 0 ，得 2 < x < 52，所以⎛ 5 ⎫⎝ 2 ⎭V ≤ 3 ⨯ 80 = 4 15 ，所以体积的最大值为 4 15 cm 3.题型 86 旋转体的表面积、体积及球面距离4.（2107 全国 3 卷理科 8）已知圆柱的高为 1，它的两个底面的圆周在直径为 2 的同一个球的球面上，则该圆柱的体积为（）.4C ． π 2D ．π44．解析 如图所示，由题可知球心在圆柱体的中心处，圆柱体上、下底面圆的半径⎛ 1 ⎫2⎝ 2 ⎭3 2 ，则圆柱体的体积V = πr 2h = 3π4 .故选B.题型87 几何体的外接球与内切球S=⨯(π⨯12)⨯3=232S= 2⨯1⨯⎪⨯3=1，所以几何体体积，三棱锥体积为22第二节空间几何体的直观图与三视图题型88斜二测画法与直观图——暂无题型89空间几何体的三视图5.某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm3）是（）. A.π2π3π3π+1 B.+3 C.+1 D.222+35.解析由三视图可知，直观图是由半个圆锥与一个三棱锥构成，半圆锥体积为111π1⎛1⎫3⎝2⎭S=S+S=π+1．故选A．126.（2017全国1卷理科7）某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯形的面积之和为（）.A.10B.12C.14D.16= V = V - V = π ⋅ 32 ⋅10 - ⋅ π ⋅ 32 ⋅ 6 = 63π .故选 B.2 上 26. 解析 由三视图可画出立体图，如图所示，该多面体只有两个相同的梯形的面，S = (2 + 4)⨯ 2 ÷ 2 = 6 ， S 梯全梯 6 ⨯ 2 = 12 .故选 B.7.（2107 全国 2 卷理科 4）如图所示，网格纸上小正方形的边长为 1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分所得，则该几何体的体积为（ ）.A ． 90πB ． 63πC ． 42πD ． 36π7．解析 该几何体可视为一个完整的圆柱减去一个高为 6 的圆柱的一半，如图所示．1 1总6468.（2017 北京理 7）某四棱锥的三视图如图所示，则该四棱锥的最长棱的长度为（）.A. 3 2B. 2 3C. 2 2D.29.解析该几何体的体积为V=1π⨯12⨯1⨯2+2⨯1⨯1=+2．8.解析几何体四棱锥如图所示，最长棱为正方体的体对角线，即l=22+22+22=23.故选B.19.（2017山东理13）由一个长方体和两个圆柱体构成的几何体的三视图如图所示，则该4几何体的体积为.π42第三节空间点、直线、平面之间的位置关系题型90证明“点共面”“线共面”“点共线”或“线共点”——暂无题型91截面问题——暂无10.（2017江苏18）如图所示，水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm，容器Ⅰ的底面对角线AC的长为107cm，容器Ⅱ的两底面对角线EG，C G()=30，从而s in∠MAC=3.记AC=107，A M=40，所以MC=402-1071111故PQ1=12，从而AP=PQ sin∠MACE G的长分别为14cm和62cm．分别在容器Ⅰ和容器Ⅱ中注入水，水深均为12cm．现11有一根玻璃棒l，其长度为40cm（容器厚度、玻璃棒粗细均忽略不计）.（1）将l放在容器Ⅰ中，l的一端置于点A处，另一端置于侧棱CC1上，求l没入水中部分的长度；（2）将l放在容器Ⅱ中，l的一端置于点E处，另一端置于侧棱GG1上，求l没入水中部分的长度．D1C1H1G1A1B1O1E1F1DH OA B E F容器Ⅰ容器Ⅱ10.解析（1）由正棱柱的定义，C C⊥平面ABCD，所以平面A ACC⊥平面ABCD，111CC⊥AC．1记玻璃棒的另一端落在CC1上点M处，如图所示为截面A1ACC1的平面图形．因为24AM与水面的交点为P，过点P作PQ1⊥AC，Q1为垂足，则PQ1⊥平面ABCD，1111=16．答：玻璃棒l没入水中部分的长度为16cm．= + ∠KGG ⎪ = cos ∠KGG = ． 设 ∠EGG = α ， ∠ENG = β ，则 sin α = sin⎝ 2 1 ⎭5 < α < π ，所以 cos α = - 因为 0 < β < πsin α cos β + cos α sin β = 4 ⨯ + - ⎪⨯ = ．222A 1AC 1 MP 1Q 1 C问(1)（2）如图所示为截面 E 1EGG 1 的平面图形， O ， O 1 是正棱台两底面的中心．由正棱台的定义，OO 1 ⊥ 平面 EFGH ，所以平面 E 1EGG 1 ⊥ 平面 EFGH ，O 1O ⊥ EG ．同理，平面 E 1EGG 1 ⊥ 平面 E 1F 1G 1H 1 ， O 1O ⊥ E 1G 1 ．记玻璃棒的另一端落在 GG 1 上点 N 处．过 G 作 GK ⊥ E 1G 1 ， K 为垂足，则 GK = OO 1 = 32 ．因为 EG 14 ， E 1G 1 = 62 ，所以 KG 1 = 62 - 142= 24 ，从而 GG = 1KG 2 + GK 2 = 242 + 322 = 40 ．1⎛π ⎫ 4 1 1因为π3． 2 5在 △ENG 中，由正弦定理可得40 14 7= ，解得 sin β = ． sin α sin β 2524，所以 cos β =， 225于是 sin ∠NEG = sin (π- α - β ) = sin (α + β )=24 ⎛ 3 ⎫ 7 35 25 ⎝ 5 ⎭ 25 5记 EN 与水面的交点为 P ，过 P 作 P Q 2 ⊥ EG ， Q 2 为垂足，则 P 2Q 2 ⊥ 平面 EFGH ，故 P 2Q 2 = 12 ，从而 EP =PQsin ∠NEG( )= 30 ， PQ AC = 10 7 ， A M = 40 ，所以 C M = 402 - 10 7 CM AM 30 40 1= 20 ．2 22答：玻璃棒 l 没入水中部分的长度为 20 cm ．E 1O 1KG 1NP 2E O G Q 2问(2)评注 此题本质上考查解三角形的知识，但在这样的大背景下构造的应用题让学生有畏惧之感，且该应用题的实际应用性也不强．也有学生第（1）问采用相似法解决，解法如下：21 1= 12 ，所以由 △ AP Q 1△∽ A CM ， PQ AP 12 AP1 1 = 1 ，即 = 1 ，解得 AP = 16 ． 1答：玻璃棒 l 没入水中部分的长度为16 cm ．题型 92 异面直线的判定——暂无第四节 直线、平面平行的判定与性质题型 93 证明空间中直线、平面的平行关系11.（2107 浙江 19（1））如图所示，已知四棱锥 P - ABCD ， △P AD 是以 AD 为斜边的等腰直角三角形， BC //AD ， CD ⊥ AD ， PC = AD = 2DC = 2CB ， E 为 PD 的中点.（1）证明： C E // 平面 PAB .PEA DB C11.解析 （1）如图所示，设 P A DE 的中点为 F ，联结 EF ， FB .因为E，F分别为PD，P A的中点，所以EF//AD，且EF=12 AD.又因为BC//AD，BC=12AD，所以EF//BC，且EF=BC，所以四边形BCEF为平行四边形，所以C E//BF，又BF⊂平面P AB，所以CE//平面P AB.PFH Q EANDB M C12.（2017江苏15）如图所示，在三棱锥A-BCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E,F（E与A,D不重合）分别在棱AD,BD上，且EF⊥AD．求证：（1）EF∥平面ABC；（2）AD⊥AC．AEB F DC12.解析（1）在平面ABD内，因为AB⊥AD，EF⊥AD，且点E与点A不重合，所以EF//AB.又因为EF⊄平面ABC，AB⊂平面ABC，所以EF//平面ABC.（2）因为平面ABD⊥平面BCD，平面ABD平面BCD=BD，BC⊂平面BCD，BC⊥BD，所以BC⊥平面ABD.因为AD⊂平面ABD，所以BC⊥AD.又AB⊥AD，BC AB=B，AB⊂平面ABC，BC⊂平面ABC，所以AD⊥平面ABC.又因为AC⊂平面ABC，所以AD⊥AC.13.（2017全国2卷理科19）如图所示，在四棱锥P-ABCD中，侧面P AD为等边三角形且垂直于底面ABCD，AB=BC=（1）求证：直线C E//平面P AB；12AD，∠BAD=∠ABC=90o，E是PD的中点.=PMEADBC13．解析 （1）令 P A 的中点为 F ，联结 EF ， BF ，如图所示．因为点E ， F 为 PD ， P A1的中点，所以 E F 为 △P AD 的中位线，所以EF // AD ．又因为∠BAD = ∠ABC = 90︒ ，所以=2BC ∥AD ．又因为 AB = BC = 12 1AD ，所以 BC // = 2 AD ，于是 EF // BC ．从而四边形 BCEF 为平行四边形，所以 CE ∥BF ．又因为 BF ⊂ 面P AB ，所以 CE ∥ 平面 PAB .zPFMEBAxCOM 'D y题型 94 与平行有关的开放性、探究性问题第五节 直线、平面垂直的判定与性质题型 95 证明空间中直线、平面的垂直关系14.（2017 江苏 15）如图所示，在三棱锥 A - BCD 中，AB ⊥ AD ，BC ⊥ BD ，平面 ABD ⊥平面 BCD ， 点 E, F （ E 与 A, D 不重合）分别在棱 AD , BD 上，且 EF ⊥ AD ．求证：（1） EF ∥平面 ABC ；（2） AD ⊥ AC ．ABEF DC14.解析（1）在平面ABD内，因为AB⊥AD，EF⊥AD，且点E与点A不重合，所以EF//AB.又因为EF⊄平面ABC，AB⊂平面ABC，所以EF//平面ABC.（2）因为平面ABD⊥平面BCD，平面ABD平面BCD=BD，BC⊂平面BCD，BC⊥BD，所以BC⊥平面ABD.因为AD⊂平面ABD，所以BC⊥AD.又AB⊥AD，BC AB=B，AB⊂平面ABC，BC⊂平面ABC，所以AD⊥平面ABC.又因为AC⊂平面ABC，所以AD⊥AC.15.（2017全国1卷理科18（1））如图所示，在四棱锥P-ABCD中，AB//CD，且∠BAP=∠CDP=90.(1)求证：平面P AB⊥平面P AD；PD CA B15.解析（1）证明：因为∠BAP=∠CDP=90，所以P A⊥AB，PD⊥CD.又因为AB∥CD，所以PD⊥AB.又因为PD P A=P，PD，P A⊂平面P AD，所以AB⊥平面P AD.又AB⊂平面P AB，所以平面P AB⊥平面P AD.16.（2017全国3卷理科19（1））如图所示，四面体ABCD△中，ABC是正三角形，△ACD 是直角三角形，∠ABD=∠CBD，AB=BD．（1）求证：平面ACD⊥平面ABC；由 ⎨BD = BD，得 △ A BD ≥? CBD ，所以 AD = CD ，即 △ A CD 为等腰直角三角形，⎪∠ABD = ∠DBC， OB = ， 夹角或其补角（异面线所成角为 0 ， ⎥ ）.可知 MN = AB = ， NP = BC = ，取 BC 的中点 Q ，联结 PQ, MQ , PM ，则可知 △PQM 为直角三角形．PQ = 1 ，MQ = AC .π⎤ 2 ⎦ 1 116．解析 ⑴如图所示，取 AC 的中点为 O ，联结 BO ， DO .因为 △ABC 为等边三角形，所以 BO ⊥ AC ， AB = BC .⎧ AB = BC ⎪ ⎩从而 ∠ADC 为直角.又 O 为底边 AC 中点，所以 DO ⊥ AC .令 AB = a ，则 AB = AC = BC = BD = a ，易得 OD =a 3a 2 2所以 OD2 + OB2 = BD2 ，从而由勾股定理的逆定理可得 ∠DOB = π2 ，即 OD ⊥ OB .⎧OD ⊥ AC ⎪OD ⊥ OB ⎪⎪由 ⎨ AC OB = O ，所以 OD ⊥ 平面 ABC .⎪ AC ⊂ 平面ABC ⎪⎪⎩OB ⊂ 平面ABC又因为 OD ⊂ 平面 ADC ，由面面垂直的判定定理可得平面 ADC ⊥ 平面 ABC .DEC OBA题型 96 与垂直有关的开放性、探索性问题——暂无第六节 空间向量与立体几何题型 97 空间向量及其运算题型 98 空间角的计算17.（2017 全国 2 卷理科 10）已知直三棱柱 ABC - A B C 中， ∠ABC = 120 ， AB = 2 ，1 1 1BC = CC = 1，则异面直线 AB 与 BC 所成角的余弦值为（）.1 11A ．3215 10 B ． C ． D ．5 53317．解析设 M ，N ，P 分别为 AB ，BB ，B C 的中点，则 AB 和 BC 的夹角为 MN 和 NP11 111⎛ 1 5 1 2 ⎝ 2 2 2 212A⋅B c⋅o B sC∠=4A+B1-C⨯2⨯2⋅ -1⎪=222-AC=7，则MQ=7，则在△MQP中，MP=MQ2+PQ2=⎪+ ⎪- 2⎪⎭2⎪⎭2⎪⎭MN2+NP2-PM2在△PMN中，cos∠PNM==⎝2⋅MN⋅NP又异面直线所成角为 0，⎥，则其余弦值为．故选C.π⎤2⎦在△ABC中，A C=A B+B2C⎛1⎫⎝2⎭，7即1122.⎛1⎝5⎛5⎫2⎛2⎫2⎛11⎫2⎝⎝522⋅⋅22=-10.518.（2107山东理17）如图所示，几何体是圆柱的一部分，它是由矩形ABCD（及其内部）以AB边所在直线为旋转轴旋转120得到的，G是DF的中点.（1）设P是CE上的一点，且AP⊥BE，求∠CBP的大小；（2）当AB=3，AD=2，求二面角E-AG-C的大小.18.解析（1）因为AP⊥BE，AB⊥BE，AB，AP⊂平面ABP，AB AP=A，所以BE⊥平面ABP.又BP⊂平面ABP，所以BE⊥BP.又∠EBC=120︒，所以∠CBP=30︒.（2）以B为坐标原点，分别以B E，BP，BA所在的直线为x，y，z轴，建立如图所示的空间直角坐标系.13⎪m⋅AG=0⎪x+3y=0⎪⎪由⎨，可得⎨2⎪n⋅C G=0⎪2x+3z=0⎪⎪从而cos m,n=m⋅nm⋅n2，易知二面角zAF GDExBPCy由题意得A(0,0,3)，E(2,0,0)，G(1,3,3)，C(-1,3,0)，则AE=(2,0,-3)，AG=(1,3,0)，CG=(2,0,3).设m=(x1,y1,z1)是平面AEG的一个法向量，⎧m⋅AE=0⎧2x1-3z1=0由⎨，可得⎨，11取z1=2，可得平面AEG的一个法向量m=(3,-3,2).设n=(x2,y2,z2)是平面ACG的一个法向量，⎧n⋅AG=0⎧x+3y=0222，取z2=-2，可得平面ACG的一个法向量n=(3,-3,-2).=1E-AG-C为锐角.因此所求的角为60︒.19.（2017江苏22）如图所示，在平行六面体ABCD-A B C D中，AA⊥平面ABCD，11111且AB=AD=2，AA=3，∠BAD=120︒．1（1）求异面直线A1B与AC1所成角的余弦值；（2）求二面角B-A1D-A的正弦值．{ }则 cos A 1B, AC 1 = (3, -1,- 3 )⋅ (3,1, 3)1 =- ． A B AC = )A 1D 1B 1C 1ADBC19.解析 在平面 ABCD 内，过点 A 作 AE ⊥ AD ，交 BC 于点 E ．因为 AA 1 ⊥ 平面 ABCD ，所以 AA 1 ⊥ AE ， AA 1 ⊥ AD ．如图所示，以 AE , AD , AA 1 为正交基底，建立空间直角坐标系 A - xyz ．zA 1D 1B 1C 1AD yBECx因为 AB = AD = 2 ， AA = 3 ， ∠BAD = 120︒ ．1则 A (0,0,0 ) ，B (3, -1,0 )，D (0,2,0 ) ，E ( 3,0,0 )， A (0,0, 3 )，C( 3,1, 3 )．1 1（1） A B =1( 3, -1,- 3 )， AC = ( 3,1, 3 )，1A B ⋅ AC1 1 1 1 7 7因此异面直线 A 1B 与 AC 1 所成角的余弦值为 1 7．（2）平面 A 1DA 的一个法向量为 AE = (3,0,0 )．设 m = (x, y , z ) 为平面 BA 1D 的一个法向量，又 A 1B = (3, -1,- 3 )， BD =(-3,3,0 ，⎧⎪m ⋅ A B= 0 ⎧ 3x - y - 3z = 0 则 ⎨ ，即 ⎨ ．( )⎩ ⎩ ⋅ 3因此二面角 B - A 1D - A 的正弦值为 7 )0 0 2 0 0 2 01 ⎪m ⋅ BD = 0 ⎪- 3x + 3 y = 0不妨取 x = 3 ，则 y = 3 ， z = 2 ，所以 m = 3, 3,2 为平面 BA 1D 的一个法向量.从而 cos AE , m =AE ⋅ m AE m =(3,0,0 ) (3, 3 ⨯ 43,2 )= 34，设二面角 B - A 1D - A 的大小为θ ，则 cos θ = 4 ．因为 θ ∈ [0, π] ，所以 sin θ = 1 - cos 2θ =74．4．20. （ 2017 全 国 1 卷 理 科 18 ） 如 图 所 示 ， 在 四 棱 锥 P - ABCD 中 ， AB //CD ， 且∠BAP = ∠CDP = 90 .(1)求证：平面 P AB ⊥ 平面 P AD ；(2)若 P A = PD = AB = DC ， ∠APD = 90 ，求二面角 A - PB - C 的余弦值.PDCAB20. 解析 （1）证明：因为 ∠BAP = ∠CDP = 90 ，所以 P A ⊥ AB ， PD ⊥ CD .又因为 AB ∥ CD ，所以 PD ⊥ AB .又因为 PDP A = P ， PD ， P A ⊂ 平面 P AD ，所以 AB ⊥平面 P AD .又 AB ⊂ 平面 P AB ，所以平面 P AB ⊥ 平面 P AD .（2）取 AD 的中点 O ， BC 的中点 E ，联结 PO ， OE ，因为 AB ∥CD ，所以四边形 ABCD为平行四边形，所以 OE ∥AB .由（1）知， AB ⊥ 平面 P AD ，所以 OE ⊥ 平面 P AD .又 PO ，AD ⊂ 平面 P AD ，所以 OE ⊥ PO ， OE ⊥ AD .又因为 P A = PD ，所以 PO ⊥ AD ，从而 PO ，OE ， AD 两两垂直.以 O 为坐标原点，建立如图所示的空间直角坐标系O - xyz ，设 P A = 2 ，所以 D (- 2 ， ， )， B ( 2 ， ， )， P (0 ，， 2 )， C (-2 ， ， ，)0-2-00⎪⎪⎩⎩()()PD⋅n=所以PD=(-2，，2)，PB=(2，，2)，BC=(-2设n=(x,y,z)为平面PBC的一个法向量，2，，.⎧n⋅PB=0⎧2x+2y-2z=0由⎨，得⎨⎪n⋅BC=0⎪-22x=0.令y=1，则z=2，x=0，可得平面PBC的一个法向量n=0,1,2.因为∠APD=90︒，所以PD⊥P A，又知AB⊥平面P AD，PD⊂平面P AD，所以PD⊥AB，又P A AB=A，所以PD⊥平面P AB.即PD是平面P AB的一个法向量，PD=-2,0,-2，从而cos PD,n=PD⋅n-223=-33.由图知二面角A-PB-C为钝角，所以它的余弦值为-33.21.（2017全国2卷理科19）如图所示，在四棱锥P-ABCD中，侧面P AD为等边三角形且垂直于底面ABCD，AB=BC=12AD，∠BAD=∠ABC=90o，E是PD的中点.（1）求证：直线C E//平面PAB；（2）点M在棱PC上，且直线BM与底面ABCD所成的锐角为45，求二面角M-AB-D的余弦值.PM EA DB C21．解析（1）令P A的中点为F，联结EF，BF，如图所示．因为点E，F为PD，P A=2=( )0 0 - 0 - 0 0 0 1 0 0 3 3 设 MM ' = a ， CM ' = a ， OM ' = 1 - a ．所以 M ' 1 - 3 a ，0 ，0 ⎪ ．3 a 2 + 1 = a ⇒ a = M ' 1 - ，0 ，0 ⎪⎪ ， M 1 - 2 ，0 ， 2 ，1， ⎪ ， AM = 1 - 22 ⎪⎭ ， AB = (1，0 ，0) ． 2 ⎪⎭ ⎫ ⎛ ⎛ 211的中点，所以 E F 为 △P AD 的中位线，所以EF // AD ．又因为∠BAD = ∠ABC = 90︒ ，所以BC ∥AD ．又因为 AB = BC = 1 21AD ，所以 BC // =2 AD ，于是 EF // BC ．从而四边形 BCEF 为平行四边形，所以 CE ∥BF ．又因为 BF ⊂ 面P AB ，所以 CE ∥ 平面 PAB .（2）以 AD 的中点 O 为坐标原点，建立如图所示的空间直角坐标系．设 AB = BC = 1 ，则O (0 ，， ) ， A (0 ， 1， ) ， B (1， 1， ) ， C (1， ，) ， D (0 ，，) ， P 0 ，， 3 ．点 M 在底面 ABCD 上的投影为 M ' ，所以 MM ' ⊥ BM ' ，联结 BM ' ．因为 ∠MBM ' = 45 ，所以△MBM ' 为等腰直角三角形．因为 △POC 为直角三角形，OC =33OP ，所以 ∠PCO = 60 ．⎛ 3 ⎫ 3 3 ⎝ ⎭⎛ 3 ⎫2 1 6BM ' = 3 a ⎪ + 12 + 02 = 2 ⎝ ⎭．从而 OM ' = 1 - 3 2 a = 1 -3 2．所以 ⎛ 2 2 6 ⎫ 2 6 ⎫ ⎝ ⎭ ⎝ ⎝设平面 ABM 的法向量 m = (0 ，y ，z ) ，则 m ⋅ AM = y +6 z = 0 ，所以m = (0 ，- 6 ，2) ，111易知平面 ABD 的一个法向量为 n = (0 ，0 ，1) ，从而 cos m ,n = m ⋅ n 10= ．故二面角m ⋅ n 5M - AB - D 的余弦值为 105．zPFMEBAxCOM 'D y22.（2017 全国 3 卷理科 19）如图所示，四面体 ABCD 中，△ A BC 是正三角形，△ ACD是直角三角形，∠ABD = ∠CBD ， AB = BD ．（1）求证：平面 ACD ⊥ 平面 ABC ；（2）过 AC 的平面交 BD 于点 E ，若平面 AEC 把四面体 ABCD 分成体积相等的两部分，由⎨BD=BD，得△A BD≥?CBD，所以AD=CD，即△A CD为等腰直角三角形，⎪∠ABD=∠DBC，OB=，⎛a⎫⎛a⎫建立空间直角坐标系，则O(0,0,0)，A ,0,0⎪，D 0,0,⎪，B 0,2,0⎪，E 0,4a,⎪⎪，⎛2⎭AE=-,,⎪⎪，AD= -,0,⎝244⎭⎪，OA= ,0,0⎪.求二面角D–AE–C的余弦值．22．解析⑴如图所示，取AC的中点为O，联结BO，DO.因为△ABC为等边三角形，所以BO⊥AC，AB=BC.⎧AB=BC⎪⎩从而∠ADC为直角.又O为底边AC中点，所以DO⊥AC.令AB=a，则AB=AC=BC=BD=a，易得OD=a3a 22所以OD2+OB2=BD2，从而由勾股定理的逆定理可得∠DOB=π2，即OD⊥OB.⎧OD⊥AC⎪OD⊥OB⎪⎪由⎨AC OB=O，所以OD⊥平面ABC.⎪AC⊂平面ABC⎪⎪⎩OB⊂平面ABC又因为OD⊂平面ADC，由面面垂直的判定定理可得平面ADC⊥平面ABC.DECOBA⑵由题意可知VD-ACE =VB-ACE，即B，D到平面ACE的距离相等，即点E为BD的中点.以O为坐标原点，OA为x轴正方向，OB为y轴正方向，OD为z轴正方向，设AC=a，⎛3a⎫3a⎫⎝2⎭⎝⎝⎭⎝4⎭易得⎛a3a a⎫⎛a a⎫⎛a⎫⎝22⎭⎝2⎭设平面AED的法向量为n1=(x1,y1,z1)，平面AEC的法向量为n2=(x2,y2,z2)，⎪⎩AD⋅n=0(3,1,3)；⎧⎪⎨AE⋅n则⎨，取n=⎪⎩OA⋅n=0()⎧⎪AE⋅n=0=012121，取n=0,1,-3.2设二面角D-AE-C为θ，易知θ为锐角，则cosθ=zDECOn⋅n12n⋅n12B y7=.7xA23.（2017北京理16）如图所示，在四棱锥P-ABCD中，底面ABCD为正方形，平面P AD⊥平面ABCD，点M在线段PB上，PD//平面MAC，P A=PD=（1）求证：M为PB的中点；（2）求二面角B-PD-A的大小；（3）求直线MC与平面BDP所成角的正弦值．6，AB=4．23.解析（1）设AC,BD的交点为E，联结ME.因为PD∥平面MAC，平面MAC平面PBD=ME，所以PD∥ME.因为ABCD是正方形，所以E为BD的中点，所以M为PB的中点.PMA BD E C（2）取AD的中点O，联结O P，OE.因为P A=PD，所以OP⊥AD.又因为平面P AD⊥平面ABCD，且OP⊂平面P AD，所以OP⊥平面ABCD.因为OE⊂平面ABCD，所以OP⊥OE.⎪⎪⎩⎩M -1,2,⎪⎪，C(2,4,0)，MC=(3,2,-).设直线MC与平面BDP所成角为α，则sinα=cos<n,MC>=n⋅MC因为ABCD是正方形，所以O E⊥AD.如图所示，建立空间直角坐标系O-xyz，则P(0,0,2)，D(2,0,0)，B(-2,4,0)，BD=(4,-4,0)，PD=(2,0,-2).⎧n⋅BD=0⎧4x-4y=0设平面BDP的法向量为n=(x,y,z)，则⎨，即⎨⎪n⋅PD=0⎪2x-2z=0令x=1，则y=1，z=2，于是n=(1,1,2)..平面P AD的法向量为p=(0,1,0)，所以cos<n,p>=n⋅p1=. |n||p|2由题知二面角B-PD-A为锐角，所以它的大小为zPM π3.A BD OECyx⎛2⎫2（3）由（1）知⎝2⎭2所以直线MC与平面BDP所成角的正弦值为26.9n MC=269.24.（2017天津理17）如图所示，在三棱锥P-ABC中，P A⊥底面ABC，∠BAC=90.点D，E，N分别为棱P A，PC，BC的中点，M是线段AD的中点，P A=AC=4，AB=2.（1）求证：MN//平面BDE；（2）求二面角C-EM-N的正弦值；（3）已知点H在棱P A上，且直线NH与直线BE所成角的余弦值为721，求线段AH的0 0) 0 0) 4 0) 0 4) 0 2) 2 2) 0 1) 2 0) ⎪ ⎪⎩ n ⋅ MN = 0 ⎪ 因此有 cos n 1, n 2 = n⋅ n415 | n || n | 2121PDMAEBNC24.解析 如图所示，以 A 为坐标原点，{AB, AC, AP }为基底，建立如图所示的空间直角坐标系，依题意可得 A(0，， ， B(2，， ， C (0，， ， P(0，， ， D(0，， ， E (0，， ，M (0，， ， N (1，， ．zPDMEB ACxNy（1）证明： DE = (0, 2,0 )， DB = (2,0, -2 ) .设 n = ( x , y , z) 为平面 BDE 的一个法向量，⎧n ⋅ DE = 0 ⎧2 y = 0 则 ⎨ ，即 ⎨ ，不妨设 z = 1 ，可得 n = (1,0,1) .⎪⎩n ⋅ DB = 0⎩2 x - 2 z = 0又 MN = (1,2, -1) ，可得 MN ⋅ n = 0 ，因为 MN ⊄ 平面 BDE ，所以 MN // 平面 BDE ．（2）易知 n = (1,0,0) 为平面 CEM 的一个法向量.设 n = ( x , y , z) 为平面 EMN 的一个法向12⎧n ⋅ EM = 0量，则 ⎨ 2 2⎧-2 y - z = 0 ，因为 EM = (0, -2, -1) ， MN = (1,2, -1) ，所以 ⎨⎩ x + 2 y - z = 0 .不妨设 y = 1 ，可得 n = (-4,1,-2) .21 2 =- ，于是 sin n , n =1 21 2.所以二面角 C - EM - N 的正弦值为 1521.由已知得 cos NH , BE = | NH ⋅ BE | 解得 h = 8 0 h（3）依题意，设 AH = h (0剟h 4 ) ，则 H （0， ， ），进而可得 NH = (-1,-2, h) ，BE = (-2,2,2) .| 2h - 2 | 7= = ，整理得10h 2 - 21h + 8 = 0 ，| NH || BE | h 2 + 5 ⨯ 2 3 2118 1或 h = .所以线段 AH 的长为 或 .5 2 5 225.（2107 浙江 19）如图所示，已知四棱锥P - ABCD ，△P AD 是以 AD 为斜边的等腰直角三角形， BC //AD ， CD ⊥ AD ， PC = AD = 2DC = 2CB ， E 为 PD 的中点.（1）证明： C E // 平面 P AB ；（2）求直线 CE 与平面 PBC 所成角的正弦值.PEA DB C25.解析 （1）如图所示，设 P A DE 的中点为 F ，联结 EF ， FB .1因为 E ， F 分别为 PD ， P A 的中点，所以 EF //AD ，且 EF = AD .2又因为 BC //AD ， BC = 1 2AD ，所以 EF //BC ，且 EF =BC ，所以四边形 BCEF 为平行四边形，所以 C E //BF ，又 BF ⊂ 平面 P AB ，所以 CE // 平面 P AB .PFH QEANDBM C（2）分别取 BC ， AD 的中点为 M ， N .联结 PN 交 EF 于点 Q ，联结 MQ .因为 E ，F ，N 分别是 PD ，P A ，AD 的中点，所以 Q 为 EF 的中点，在平行四边形 BCEF 中， MQ //CE .由 △P AD 为等腰直角三角形，得 PN ⊥ AD .-BC在Rt△MQH中，QH=1Q，R分别为AB，BC，CA上的点，AP=PB，==2，分别记二面角D–PR–Q，由DC⊥AD，N是AD的中点，所以ND=12AD=BC，且DN∥BC,所以四边形BCDN 是平行四边形，所以B N∥CD，所以B N⊥AD.又BN PN=N,所以AD⊥平面PBN，由BC//AD，得BC⊥平面PBN，又BC⊂平面PBC，所以平面PBC⊥平面PBN.过点Q作PB的垂线，垂足为H，联结MH.MH是MQ在平面PBC上的射影，所以∠QMH是直线CE与平面PBC所成的角.设CD=1.在△PCD中，由PC=2，CD=1，PD=2，由余弦定理得C E=2，又BC⊥平面PBN，PB⊂平面PBN，所以BC⊥PB.在△PBN中，由PN=BN=1，PB=PC22=3，QH⊥PB,Q为PN的中点，得QH=14.2，MQ=2，所以sin∠QMH=，48所以直线C E与平面PBC所成角的正弦值是28.26．（2107浙江9）如图所示，已知正四面体D–ABC（所有棱长均相等的三棱锥），P，BQ CRQC RAD–PQ–R，D–QR–P的平面角为α，β，γ，则（）.A．γ<α<βC．α<β<γB．α<γ<βD．β<γ<α26.解析如图所示，设点D在底面ABC内的射影为O，判断O到PR，P Q，QR的距离，O到哪条线段的距离越小，对应的二面角就越大.显然有α,β,γ均为锐角．P为三等分点，O到△PQR三边的距离相等．动态研究问题：P111P，所以O到QR的距离不变，O到PQ的距离减少，O到PR的距离变大．所以α<γ<β．设AB'与直线a所成夹角为α∈⎢0,⎥，则cosα=(cosθ,sinθ,-1)⋅(0,1,0)sinθ∈⎢0,⎥，⎣2⎦⎡所以α∈⎢,⎥，故③正确，④错误．CQ R OA P P1B题型99空间距离的计算——暂无题型100与空间角、空间距离有关的开放性、探索性问题——暂无27.（2017全国3卷理科16）a，b为空间中两条互相垂直的直线，等腰直角三角形ABC的直角边AC所在的直线与a，b都垂直，斜边AB以直线AC为旋转轴旋转，有下列结论：①当直线AB与a成60角时，AB与b成30角；②当直线AB与a成60角时，AB与b成60角；③直线AB与a所成角的最小值为45；④直线AB与a所成角的最小值为60；其中正确的是________.（填写所有正确结论的编号）.27．解析由题意知，a，b，AC三条直线两两相互垂直，作出图像如图所示．不妨设图中所示的正方体的边长为1，故AC=1，AB=2，边AB以直线AC为旋转轴旋转，则点A 保持不变，点B的运动轨迹是以C为圆心，1为半径的圆．以C为坐标原点，以CD为x轴正方向，CB为y轴正方向，CA为z轴正方向，建立空间直角坐标系．则D(1,0,0)，A(0,0,1)，直线a的方向单位向量a=(0,1,0)，a=1．B点起始坐标为(0,1,0)，直线b的方向单位向量b=(1,0,0)，b=1．设B点在运动过程中的坐标B'(cosθ,sinθ,0)，其中θ为B'C与CD的夹角，θ∈[0,2π).那么AB'在运动过程中的向量AB'=(cosθ,sinθ,-1)，AB'=2．⎡π⎤⎣2⎦a AB'=22⎤2⎡ππ⎤⎣42⎦cos β = AB ' ⋅ b ．从而 cos β = cos θ = ． 因为 β ∈ ⎢0, ⎥ ，所以 β = ，此时 AB ' 与 b 的夹角为 60︒ ．所以②正确，①错误．故填② ③.π设 AB ' 与直线 b 所成夹角为 β ∈[0, ] ，2b AB ' = (- cos θ ,sin θ ,1) ⋅ (1,0,0) b AB ' = 2 2cos θ .当 AB ' 与直线 a 夹角为 60︒ 时，即 α = π 3，sin θ = 2 cos α = 2 cos π 3 =2 2．因为 cos 2 θ + sin 2 θ = 1，所以 cos θ =2 2 1 2 2 2⎡ π ⎤ π ⎣ 2 ⎦3zAyC(O)a Bθ B 'b D x28.（2017 天津理 17）如图所示，在三棱锥P - ABC 中， P A ⊥ 底面 ABC ， ∠BAC = 90 .点 D ，E ，N 分别为棱 P A ， PC ， BC 的中点， M 是线段 AD 的中点， P A = AC = 4 ，AB = 2 .（1）求证： MN // 平面 BDE ；（2）求二面角 C - EM - N 的正弦值；（3）已知点 H 在棱 P A 上，且直线 NH 与直线 BE 所成角的余弦值为长.P D EM ABNC7 21，求线段 AH 的0 0) 0 0) 4 0) 0 4) 0 2) 2 2) 0 1) 2 0) 则 ⎨，即 ⎨ ，不妨设 z = 1 ，可得 n = (1,0,1) . ⎪⎩n ⋅ DB = 02 x - 2 z = 0 ⎪ ⎪⎩n ⋅ MN = 0 ，因为 EM = (0, -2, -1) ， MN = (1,2, -1) ，所以 ⎨x + 2 y - z = 0 ⎪ 因此有 cos n , n = n⋅ n 4 15| n || n | 21 21 1 2由已知得 cos NH , BE = | NH ⋅ BE | 解得 h = 8 0 h28.解析 如图所示，以 A 为坐标原点，{AB, AC, AP }为基底，建立如图所示的空间直角坐标系，依题意可得 A(0，， ， B(2，， ， C (0，， ， P(0，， ， D(0，， ， E (0，， ，M (0，， ， N (1，， ．zPDMEB ACxNy（1）证明： DE = (0, 2,0 )， DB = (2,0, -2 ) .设 n = ( x , y , z) 为平面 BDE 的一个法向量，⎧n ⋅ DE = 0 ⎧2 y = 0 ⎩又 MN = (1,2, -1) ，可得 MN ⋅ n = 0 ，因为 MN ⊄ 平面 BDE ，所以 MN // 平面 BDE ．（2）易知 n = (1,0,0) 为平面 CEM 的一个法向量.设 n = ( x , y , z) 为平面 EMN 的一个法向12量，⎧n ⋅ EM = 0则 ⎨ 2 2⎧-2 y - z = 0 ⎩ .不妨设 y = 1 ，可得 n = (-4,1,-2) .21 2 =- ，于是 sin n , n = 1 2 12.所以二面角 C - EM - N 的正弦值为 1521.（3）依题意，设 AH = h (0剟h 4 ) ，则 H （0， ， ），进而可得 NH = (-1,-2, h) ，BE = (-2,2,2) .| 2h - 2 | 7= = ，整理得10h 2 - 21h + 8 = 0 ，| NH || BE | h 2 + 5 ⨯ 2 3 211 8 1或 h = .所以线段 AH 的长为 或 .5 2 5 2题型101立体几何中的最值问题探究与扩展——暂无。
2019_2020学年高中数学第一章立体几何初步1.1.3.1圆柱、圆锥、圆台练习(含解析)新人教B版必修2
第1课时圆柱、圆锥、圆台A．直线绕定直线旋转形成柱面B．半圆绕定直线旋转形成球体C．有两个面互相平行，其余四个面都是等腰梯形的六面体是棱台D．圆柱的任意两条母线所在的直线是相互平行的答案 D解析两直线平行时，直线绕定直线旋转才形成柱面，故A错误；半圆以直径所在直线为轴旋转才形成球体，故B错误；C不符合棱台的定义．所以应选D．2．下列命题正确的是( )A．梯形绕一边所在直线旋转得到的旋转体是圆台B．夹在圆柱的两个平行截面间的几何体是圆柱C．棱锥截去一个小棱锥后剩余部分是棱台D．圆锥截去一个小圆锥后剩余部分是圆台答案 D解析绕梯形的一边所在直线旋转得到的旋转体也可能是组合体．当夹在圆柱的两个平行截面不与圆柱的底面平行时，不是圆柱．用与棱锥的底面不平行的平面截去一个小棱锥后，剩余部分不是棱台．圆锥是直角三角形绕其一条直角边所在的直线旋转而成的，圆锥截去一个小圆锥后剩余部分是圆台．A．10 B．20C．30 D．40答案 B解析如图轴截面为矩形，所以面积为(2＋2)×5＝20．4．下列说法中，不正确的是 ( ) A ．圆桂的侧面展开图是一个矩形 B ．圆锥中过轴的截面是一个等腰三角形C ．等腰直角三角形绕它的一条边所在的直线旋转一周形成的曲面围成的几何体是圆锥D ．圆台中平行于底面的截面是圆面 答案 C解析 等腰直角三角形绕它的一条直角边所在的直线旋转一周才能形成圆锥，此处必须说明是绕它的一条直角边所在的直线．若换成直角三角形的斜边，则旋转后产生的几何体不是圆锥，而是两个圆锥的组合体，且这两个圆锥同底．5．圆台的一个底面周长是另一个底面周长的3倍，轴截面的面积为392 cm 2，母线与轴的夹角为45°，求这个圆台的高、母线长和底面半径．解 圆台的轴截面如图所示，根据题意可设圆台的上、下底面半径分别为x cm 和3x cm ，即A′O′＝x cm ，AO ＝3x cm(O′，O 分别为上、下底面圆心)，过A′作AB 的垂线，垂足为点D ．在Rt△AA′D 中，∠AA′D＝45°，AD ＝AO －A′O′＝2x cm ， 所以A′D＝AD ＝2x cm ，又S 轴截面＝12(A′B′＋AB)·A′D＝12×(2x＋6x)×2x＝392 (cm 2)，所以x ＝7．综上，圆台的高OO′＝14 cm ，母线长AA′＝2OO′＝14 2 cm ，上、下底面的半径分别为7 cm 和21 cm ．一、选择题1．下列命题正确的个数为( )①圆柱的轴是过圆柱上、下底面圆的圆心的直线；②圆柱的母线是连接圆柱上底面上一点和下底面上一点的直线；③矩形的任意一条边所在直线都可以作为轴，其他边绕其旋转形成圆柱；④矩形绕任何一条直线旋转，都可以围成圆柱．A ．1B ．2C ．3D ．4 答案 B解析 根据圆柱的定义可知命题①③正确，命题②④错误．2．一个圆锥的母线长为2，圆锥的轴截面的面积为3，则母线与轴的夹角为( ) A ．30° B．60°C ．30°或60° D．60°或75° 答案 C解析 设圆锥的高为h ，则底面圆的半径为4－h 2，由题意，得S ＝12h×24－h 2＝3，平方整理得h 4－4h 2＋3＝0，解得h 2＝1或h 2＝3，∴h＝1或h ＝3．母线与轴的夹角为30°或60°．3．上、下底面面积分别为36π和49π，母线长为5的圆台，其两底面之间的距离为( ) A ．4 B ．3 2 C ．2 3 D ．2 6 答案 D解析 设圆台的母线为l ，高为h ，上、下两底面圆的半径分别为r ，R ，则满足关系式l 2＝h 2＋(R －r)2，根据题意可得h ＝26，即两底面之间的距离为26．4．“两底面直径之差等于母线长”的圆台( ) A ．是不存在的B ．其母线与高线必成60°角C ．其母线与高线必成30°角D ．其母线与高线所成的角不是定值 答案 C解析 设圆台上、下底面半径分别为r 1，r 2，母线长为l ，则由题意可得2r 2－2r 1＝l ，∴r 2－r 1l ＝12， 再设母线与高线所成的角为θ，∴sinθ＝12，θ＝30°．5．用平行于圆锥底面的平面截圆锥，所得截面面积与底面面积的比为1∶3，则截面把圆锥的母线分为上下两段的比是( )A ．1∶3B ．1∶9C ．1∶ 3D ．(1＋3)∶2 答案 D解析 圆锥的上底面半径与下底面半径之比为1∶3，故截去小圆锥的母线与大圆锥的母线之比为1∶3，截面把圆锥的母线分为上下两段的比是1∶(3－1)＝(1＋3)∶2．二、填空题6．圆锥轴截面的顶角为120°，过顶点的截面三角形的最大面积为2，则圆锥的母线长为________．答案 2解析 对于该圆锥，过顶点的截面三角形中面积最大的三角形为等腰直角三角形，其腰为母线，所以母线长为2．7．用一张(6×10) cm 2的矩形硬纸卷成圆柱的侧面，则圆柱轴截面的面积等于________，轴截面的周长等于________．答案60π cm 212＋20π cm 或20＋12πcm 解析 若圆柱的母线长为6，则底面直径为10π，轴截面的面积为60π cm 2，周长为⎝ ⎛⎭⎪⎫12＋20πcm ；若圆柱的母线长为10，则底面直径为6π，轴截面的面积为60π cm 2，周长为⎝⎛⎭⎪⎫20＋12π cm ．8．给出下列命题：①圆柱的母线与它的轴可以不平行；②圆锥的顶点、圆锥底面圆周上任意一点及底面圆的圆心三点的连线都可以构成直角三角形；③在圆台的上、下两底面圆周上各取一点，则这两点的连线是圆台的母线；④圆柱的任意两条母线所在的直线是互相平行的．其中正确的是________．答案②④解析由圆柱、圆锥、圆台的定义及母线的性质可知②④正确，①③错误．三、解答题9．轴截面为正方形的圆柱叫做等边圆柱，已知某等边圆柱的轴截面面积为16 cm2，求其底面周长和高．解如图所示，作出等边圆柱的轴截面ABCD，由题意知，四边形ABCD为正方形，设圆柱的底面半径为r，则AB＝AD＝2r．由题意可得轴截面的面积S＝AB×AD＝2r×2r＝4r2＝16，解得r＝2．所以其底面周长C＝2πr＝2π×2＝4π(cm)，高h＝2r＝4(cm)．10．如图所示，已知圆锥SO中，底面半径r＝1，母线长l＝4，M为母线SA上的一个点，且SM＝x，从点M拉一根绳子，围绕圆锥侧面转到点A．求：(1)绳子的最短长度的平方f(x)；(2)绳子最短时，顶点到绳子的最短距离；(3)f(x)的最大值．解将圆锥的侧面沿SA展开在平面上，如图所示，则该图为扇形，且弧AA′的长度L 就是圆O的周长，∴L＝2πr＝2π．∴∠ASM＝L2πl×360°＝2π2π×4×360°＝90°．(1)由题意知绳子长度的最小值为展开图中的AM，其值为AM＝x2＋16(0≤x≤4)．∴f(x)＝AM 2＝x 2＋16(0≤x≤4)．(2)绳子最短时，在展开图中作SR⊥AM，垂足为R ，则SR 的长度为顶点S 到绳子的最短距离，在△SAM 中，∵S △SAM ＝12SA·SM＝12AM·SR，∴SR＝SA·SM AM ＝4xx 2＋16(0≤x≤4)，即绳子最短时，顶点到绳子的最短距离为4xx 2＋16(0≤x≤4)． (3)∵f(x)＝x 2＋16(0≤x≤4)是增函数， ∴f(x)的最大值为f(4)＝32．。
2019高考数学大题专题练习立体几何一.doc
2019-2020 年高考数学大题专题练习——立体几何（一）1.如图所示，四棱锥P - ABCD 中，底面 ABCD 为正方形，PD平面ABCD，PD = AB = 2 ，点E, F , G分别为PC, PD , BC的中点.(1) 求证：PA EF ；(2) 求二面角D - FG - E的余弦值 .2.如图所示，该几何体是由一个直角三棱柱ADE - BCF 和一个正四棱锥P - ABCD 组合而成， AD AF ，AE = AD = 2.(1) 证明：平面 PAD 平面ABFE；(2) 求正四棱锥 P - ABCD 的高 h ，使得二面角 C - AF - P 的余弦值是22 .33.四棱锥P ABCD 中，侧面 PDC 是边长为 2 的正三角形，且与底面垂直，底面ABCD 是面积为 2 3 的菱形，ADC 为锐角， M 为 PB 的中点．P（Ⅰ）求证： PD ∥面ACM．M（Ⅱ）求证： PA CD ．（Ⅲ）求三棱锥 P ABCD 的体积． C BD A4.如图，四棱锥S ABCD 满足 SA面ABCD，DAB ABC 90 ． SA AB BC a ，AD2a ．（Ⅰ）求证：面SAB面SAD．（Ⅱ）求证：CD面SAC．SA DBC5.在四棱锥P ABCD中，底面ABCD为矩形，测棱 PD 底面 ABCD ， PDDC，点 E 是BC 的中点，作EF PB 交 PB 于 F ．P（Ⅰ ）求证：平面 PCD 平面 PBC ．F E（Ⅱ）求证：PB 平面 EFD ．D CA B6.在直棱柱ABC A1B1C1 中，已知AB AC ，设AB1中点为 D ，A1C中点为 E ．（Ⅰ）求证： DE ∥平面 BCC1 B1．（Ⅱ ）求证：平面ABB1 A1平面 ACC1 A1．AB CD EA1B1C 17.在四棱锥P ABCD 中， PA平面ABCD，AB // CD，AB AD ， PA PB ，AB : AD : CD 2 : 2 :1 .（1）证明BD PC ；（2）求二面角 A PC D 的余弦值；（3）设点Q为线段PD上一点，且直线AQ 平面PAC所成角的正弦值为2，求PQ的值 . 3PD8.在正方体ABCD A1 B1C1D1中， O 是 AC 的中点， E 是线段 D1O 上一点，且D1E＝λEO. （1）若λ=1，求异面直线 DE 与 CD1所成角的余弦值；（2）若λ=2，求证：平面 CDE⊥平面 CD 1O.9.如图，在四棱锥 P ABCD 中，底面 ABCD 是平行四边形， ∠BCD 135 ，侧面 PAB ⊥底面 ABCD ， ∠ BAP 90 ， AB AC PA 2 ， E ， F 分别为 BC ， AD 的中点，点 M 在线段 PD 上．（Ⅰ）求证： EF ⊥ 平面 PAC ．P（Ⅱ）若 M 为 PD 的中点，求证：ME ∥ 平面 PAB ．M（Ⅲ）如果直线 ME 与平面 PBC 所成的角和直线 ME 与ADF平面 ABCD 所在的角相等，求PM的值．BECPD10.如图，在三棱柱ABC A 1B 1C1，AA1⊥底面 ABC ， AB ⊥ AC ，AC AB AA1， E ， F 分别是棱BC，A 1 A的中点，G为棱CC 1上的一点，且C 1F∥平面 AEG ．C 1A 1（ 1 ）求 CG的值．CC 1GB1F2 ）求证： EG ⊥ AC 1（ ．（ 3）求二面角 A 1 AG E 的余弦值．CAEB11.如图，在四棱锥P ABCD 中，PB⊥底面 ABCD ，底面 ABCD 为梯形， AD ∥ BC ，AD⊥ AB ，且PB AB AD 3 ， BC 1 ．（Ⅰ ）若点 F 为 PD 上一点且PF 1PD ，证明： CF ∥平面PAB．3（Ⅱ）求二面角 B PD A 的大小．（Ⅲ ）在线段 PD 上是否存在一点M ，使得CM ⊥ PA ？若存在，求出PM 的长；若不存在，说明PF理由．A DB C12.如图，在四棱锥 E ABCD 中，平面EAD⊥平面 ABCD ， CD ∥ AB ， BC ⊥ CD ，EA⊥ ED ， AB 4 ，BC CD EA ED 2．Ⅰ证明： BD ⊥ AE ．Ⅱ求平面 ADE 和平面CDE所成角（锐角）的余弦值．EDCAB13.己知四棱锥P ABCD 中， PA 平面 ABCD ，底面ABCD 是菱形，且 PA AB 2 ．ABC 60 ， BC 、PPD 的中点分别为 E ， F ． F（Ⅰ）求证 BC PE ．A（Ⅱ）求二面角 F AC D 的余弦值． D （Ⅲ）在线段 AB 上是否存在一点G ，使得 AF 平行于B E C平面 PCG ？若存在，指出 G 在 AB 上的位置并给予证明，若不存在，请说明理由．E14.如图，ABCD是边长为3的正方形，DE 平面 ABCD ，AF∥DE ， DE 3AF ， BE 与平面 ABCD 所成角为 60 ．（Ⅰ）求证： AC 平面 BDE ．（Ⅱ）求二面角 F BE D 的余弦值．FD C （Ⅲ ）设点M线段BD上一个动点，试确定点M 的位置，使得 AM ∥平面 BEF ，并证明你的结论． A B15.如图，PA面 ABC ， AB BC ，CAB PA 2BC 2 ，M为PB的中点． D（Ⅰ ）求证： AM 平面 PBC ．AB（Ⅱ）求二面角 A PC B 的余弦值．MP（Ⅲ）在线段 PC 上是否存在点D，使得BD AC ，若存在，求出PD 的值，若不存在，说明理由．PC16.如图所示，在四棱锥P-ABCD 中， AB⊥平面PAD , AB / /CD , E是 PB 的中点 ,PD 2, PA5, AB AD 3, AH2 . HD（1）证明： PH⊥平面 ABCD ；（2）若 F 是 CD 上的点，且FC 2FD 3，求二面角B EF C的正弦值 .17.如图， DC ⊥平面 ABC，EB / / DC，AC BC EB 2DC 2 ，ACB 120 ，Q为 AB 的中点．（Ⅰ）证明： CQ⊥平面 ABE ；（Ⅱ）求多面体ACED 的体积；（Ⅲ）求二面角A-DE-B 的正切值．18.如图 1 , 在△ ABC 中， AB=BC=2, ∠ B=90 °,D 为 BC 边上一点，以边 AC 为对角线做平行四边形 ADCE ，沿 AC 将△ACE 折起，使得平面 ACE ⊥平面 ABC,如图 2.(1)在图 2 中，设 M 为 AC 的中点，求证 :BM 丄 AE；(2) 在图 2 中，当 DE 最小时，求二面角 A -DE -C 的平面角 .19.如图所示，在已知三棱柱ABF -DCE 中，ADE 90 ，ABC 60 ，AB AD 2 AF ，平面ABCD⊥平面ADEF，点M在线段 BE 上，点 G 是线段 AD 的中点．（1）试确定点 M 的位置，使得 AF ∥平面 GMC ；（2）求直线 BG 与平面 GCE 所成角的正弦值．20.已知在四棱锥P-ABCD 中，底面ABCD 是菱形， AC=AB， PA⊥平面 ABCD ，E， F 分别是AB，PD 的中点 .（Ⅰ）求证： AF ∥平面 PCE；（Ⅱ）若 AB 2 AP 2 ，求平面PAD与平面PCE所成锐二面角的余弦值.21.如图，五面体PABCD 中， CD ⊥平面 PAD ， ABCD 为直角梯形，BCD, PD BC CD 1 AD, AP PD .2 2（1）若 E 为 AP 的中点，求证： BE∥平面 PCD ；（2）求二面角 P-AB-C 的余弦值 .22.如图（ 1）所示，已知四边形SBCD 是由 Rt △ SAB 和直角梯形ABCD 拼接而成的，其中SAB SDC 90 .且点A为线段SD 的中点，AD 2DC 1 ， AB 2 .现将△SAB 沿AB 进行翻折，使得二面角 S-AB-C 的大小为 90°，得到图形如图（ 2）所示，连接 SC，点 E，F 分别在线段 SB，SC 上 .（Ⅰ）证明：BD AF ；（Ⅱ）若三棱锥B-AEC 的体积为四棱锥S-ABCD 体积的2，求点 E 到平面 ABCD 的距离 . 523. 四棱锥S-ABCD 中，AD∥ BC ，BC CD, SDA SDC 600 ，AD DC 1 1BC SD ，E为SD的中点.2 2（1）求证：平面 AEC⊥平面 ABCD ；（2）求 BC 与平面 CDE 所成角的余弦值 .24.已知三棱锥P-ABC，底面 ABC 是以 B 为直角顶点的等腰直角三角形，PA⊥ AC， BA =BC =PA=2，二面角P-AC-B 的大小为 120°.（1）求直线 PC 与平面 ABC 所成角的大小；（2）求二面角 P-BC-A 的正切值 .25.如图，在四棱锥P-ABCD 中，平面PAD ⊥平面ABCD ，ABC BCD 900， PA PD DC CB 1 AB ，E是PB的中点，2（Ⅰ）求证： EC∥平面 APD ；（Ⅱ）求 BP 与平面 ABCD 所成的角的正切值；（Ⅲ）求二面角P-AB-D 的余弦值 .26.四棱锥 P﹣ ABCD 的底面 ABCD 为边长为 2 的正方形， PA=2， PB=PD =2 2 ，E，F，G，H分别为棱PA， PB， AD ，CD 的中点．（1）求 CD 与平面 CFG 所成角的正弦值；（2）探究棱 PD 上是否存在点 M，使得平面 CFG⊥平面 MEH ，若存在，求出PM的值；PD若不存在，请说明理由．试卷答案1以点 D 为坐标原点，建立如图所示的空间直角坐标系 D - xyz ，则D (0,0,0 ) ， A (0,2,0 )， C (- 2,0,0 ) ， P (0,0,2 ) ， E (- 1,0,1) ， F (0,0,1) ， G (- 2,1,0).uuuruuur(1) ∵ PA = (0,2, - 2) ， EF = (1,0,0 ) ，uuur uuur 0 ， ∴ PA ^ EF .则 PA?EF uuur uuur (2) 易知 DF = (0,0,1 )， FG = (- 2,1- 1) ，ur设平面 DFG 的法向量 m = (x 1 , y 1, z 1) ，ur uuurìì = 0m?DF?则，即 ，íur uuurí0 - 2x?m?FG令 x 1 = 1 ，则 m = (1,2,0 ) 是平面 DFG 的一个法向量， r同理可得 n = (0,1,1) 是平面 EFG 的一个法向量，ur r2 10 ur r m ×n∴ cos < m, n >= urr ==，m × 5′ 25n由图可知二面角 D - FG - E 为钝角，∴二面角 D - FG - E 的余弦值为10 -.52.(1) 证明：直三棱柱 ADE - BCF 中， AB ^ 平面 ADE ，所以： AB ^ AD ，又 AD ^ AF ，所以： AD ^ 平面 ABFE ， AD ì平面 PAD ，所以：平面 PAD ^ 平面 ABFE .(2) 由 (1) AD ^ 平面 ABFE ，以 A 为原点， AB, AE , AD 方向为 x, y, z 轴建立空间直角坐标系A - xyz ，设正四棱锥 P - ABCD 的高 h ， AE = AD = 2 ， 则 A (0,0,0 ) ， F (2,2,0 ) ， C (2,0,2 ) ， P (1,- h,1). uuur uuur uuurAF = (2,2,0) ， AC = (2,0, 2) ， AP = (1,- h,1) .ur设平面 ACF 的一个法向量 m = (x 1 , y 1 , z 1 )，ur uuurì= 0urm? AF 2x 1 + 2 y 1uuurr()n ? AC 2 x 1 + 2 z 1 = 0r uuurrì( x 2 , y 2 , z 2)?n ? AF 2 x 2 + 2 y 2 = 0，设平面 AFP 的一个法向量 n =，则 íruuur?n ? AP x 2 - hy 2 + z 2 = 0r取 x 2 = 1 ，则 y 2 = - 1 ， z 2 = - 1 - h ，所以： n = (1,- 1,- 1- h ) ，ur rur r二面角 C - AF - P 的余弦值是2 2m?n=，所以： cos < m, n >= urr 3m n解得： h = 1.1 1 +1 + h23 2 + (h +1)= 2 2，33.PMC BEODA（Ⅰ ）证明：连结 AC 交 BD 于 O ，则 O 是 BD 中点，∵在 △PBD 中， O 是 BD 的中点， M 是 PB 的中点，∴ PD ∥MO ，又 PD平面 ACM ， MO 平面 ACM ，∴PD∥平面 ACM ．（Ⅱ ）证明：作PE ⊥ CD ，则E为CD中点，连结AE ，∵底面 ABCD 是菱形，边长为 2 ，面积为 2 3，∴ S 1 AD DC sin ADC 2 1 2 2sin ADC 2 2 3 ，2 2∴sin ADC 3 ，ADC 60 ，2∴ △ ACD 是等边三角形，∴CD⊥ AE ，又∵ CD ⊥ PE ，∴CD⊥平面 PAE ，∴CD ⊥ PA ．（Ⅲ ） V P ABCD 1S ABCD PE 1 2 3 3 2 ．3 34.SA EDB C（ 1 ）证明：∵ SA⊥平面 ABCD ， AB平面ABCD，∴AB ⊥ SA，又∵ BAD 90 ，∴AB⊥ AD ，∵SAI AD A ，∴AB⊥平面 SAD，又 AB 平面 SAB，∴平面 SAB⊥平面SAD．（Ⅱ ）证明：取 AD 中点为 E ，∵DAB ABC 90 ， AD 2a ， BC a ， E 是 AD 中点，∴ABCE 是矩形， CE AB a ， DE a ，∴ CD 2a ，在△ACD 中，AC 2a ， CD 2a ，AD 2a ，∴ AC 2 CD 2 AD 2 ，即CD⊥ AC ，又∵ SA⊥平面 ABCD ， CD平面ABCD，∴CD⊥ SA，∴CD ⊥平面PAC．5.PEFCDA B（Ⅰ）证明：∵ PD底面ABCD，BC平面ABCD，∴PD BC ，又∵底面 ABCD 为矩形，∴BC CD ，∴BC 平面 PCD ，∵ BC平面PBC，∴平面 PCD平面PBC．（Ⅱ ）证明：∵ PD DC ， E 是 PC 中点，∴ DE PC ，又平面 PCD平面PBC，平面PCD I平面PBC PC ，∴DE 平面PBC，∴DE PB ，又∵ EF PB ， EF I DE E ，∴PB 平面 EFD ．6.ABCDEA 1B 1C1（Ⅰ ）证明：连结 A 1 B ，∵ D 是 AB 1 的中点，∴ D 是 A 1B 的中点，∵在 △ A 1 BC 中， D 是 A 1 B 的中点， E 是 A 1 C 的中点， ∴ DE ∥ BC ，又 DE平面 BCC 1 B 1 ， BC 平面 BCC 1B 1 ，∴ DE ∥平面 BCC 1B 1 ．（Ⅱ ）证明： ∵ ABC A 1 B 1C 1 是直棱柱，∴ AA 1 平面 ABC ， ∴ AA 1 AB ， 又 ABAC ，∴ AB 平面 ACC 1 A 1 ， ∵ AB 平面 ABB 1 A 1 ，∴平面 ABB 1 A 1 平面 ACC 1 A 1 ．以 为坐标原点，建立空间直角坐标系 B(2,0,0) ， D (0, 2,0) ，P(0,0,2) ，7. AC (1, 2,0)uuur uuur (1, 2, 2) ，（1） BD ( 2, 2,0) ， PCuuur uuur∵ BD ? PC 0 ∴ BD PCuuur(1,uuur ur( 2, 1,0) （2） AC 2,0) ， AP (0,0, 2) ，平面 PAC 的法向量为 muuuruuurr 2, 1) .DP (0,2, 2) ， AP (1,0,0) ，平面 DPC 的法向量为 n (0,ur rur r2 2 m ?ncos m,nurr，二面角 BPC D 的余弦值为.m ? n 33uuur uuur uuur uuur uuur0,1（3） ∵ AQ AP PQ AP tPD ， tuuur (0,0, 2) t(0, 2, 2) (0, 2t, 22t )∴ AQ 设 为直线 AQ 与平面 PAC 所成的角uuur uruuur urAQ ? m2sincos AQ, muuurur3AQ ? m3 2t 22t2t)22 3t2 6t28t4 ，解得 t 2 （舍）或2.(2 33所以，PQ2 即为所求 .PD38.解 :(1) 不妨设正方体的棱长为1，以 DA , DC , DD 1为单位正交基底建立如图所示的空间直角坐标系D xyz ．则 A(1， 0，0) ， O12 ，12，0 ， C 0，1，0 ， D 1(0， 0， 1)，E1，1 ，1，4 4 2 于是，.由 cos＝ ＝ .所以异面直线 AE 与 CD 1 所成角的余弦值为3 .6（2）设平面 CDuuur uuuur ＝0 1111CO ＝ 0， m · O 的向量为m=(x ， y ， z )，由 m ·得取 x 1 ＝ 1，得 y 1＝ z 1＝ 1，即 由 D 1E ＝λEO ，则 E又设平面 CDE 的法向量为n ＝ (x 2，y 2， z 2)，由 m=(1 ，1， 1) .，.n ·＝ 0， n · ＝ 0.CD DE得取 x 2=2 ，得 z 2＝－ λ，即 n ＝ (－ 2，0， λ ) .因为平面 CDE ⊥ 平面 CD 1F ，所以 m ·n ＝0，得 λ＝2．9.（ Ⅰ ）证明：在平行四边形 ABCD 中，∵ AB AC ， ∠ BCD 135 ， ∠ ABC 45 ，∴ AB ⊥ AC ， ∵ E ， F 分别为 BC ， AD 的中点，∴ EF ∥ AB ， ∴ EF ⊥ AC ，∵侧面 PAB ⊥ 底面 ABCD ，且 ∠ BAP90 ，∴ PA ⊥ 底面 ABCD ， ∴ PA ⊥ EF ，又∵ PA I ACA ， PA 平面 PAC ， AC 平面 PAC ，∴ EF ⊥ 平面 PAC ．（Ⅱ ）证明： ∵ M 为 PD 的中点， F 为 AD 的中点，∴ MF ∥ PA ，又 ∵ MF平面 PAB ， PA 平面 PAB ，∴ MF ∥ 平面 PAB ，同理，得 EF ∥ 平面 PAB ，又∵ MF I EFF ， MF 平面 MEF ， EF 平面 MEF ，∴平面MEF ∥ 平面PAB ，又 ∵ME平面MEF，∴ ME ∥ 平面 PAB ．（Ⅲ ）解： ∵ PA ⊥ 底面 ABCD ， AB ⊥ AC ，∴ AP ， AB ， AC 两两垂直，故以AB ， AC ， AP 分别为 x 轴， y 轴和 z 轴建立如图空间直角坐标系，则 A(0,0,0) ， B(2,0,0) ， C(0,2,0) ， P(0,0,2) ， D( 2,2,0) ， E(1,1,0) ，uuur (2,0,uuur ( 2,2,uuur ( 2,2,0) ，所以 PB 2) ， PD 2) ， BC 设 PM(uuuur( 2 ,2 ,2 ) ， [0,1]) ，则 PM PDuuur∴ M ( 2 ,2 ,2 (1 2 ,1 2 ,2 2) ，2 ) ， MEur(0,0,1) ，易得平面 ABCD 的法向量 mr ( x, y,z)设平面 PBC 的法向量为 n ，则：r uuur 0 2x 2 y 0rn BC(1,1,1)，r uuur ，即 2x 2 z 0 ，令 x 1，得 nn PB 0∴直线 ME 与平面 PBC 所成的角和此直线与平面 ABCD 所成的角相等，uuur ur uuur ruuuur ur uuuur r ∴ | cos| ME m | | ME n | ME , m | | cos ME , n |，即 uuur ur uuur r ， | ME | | m | | ME | | n | ∴ | 21| 2 ，解得33 或 33（舍去），322故PM 3 3 ．PD 2z PMAF Dx BC yE10.（ 1） ∵ C 1F ∥ 平面 AEG ，又 C 1F 平面 ACC 1 A 1 ，平面 ACC 1 A 1 I 平面 AEG AG ，∴ C 1 F ∥ AG ，∵ F 为 AA 1 的点，且侧面 ACC 1 A 1 为平行四边形，∴ G 为 CC 1 中点，∴CG 1 ． CC 1 2（ 2 ）证明： ∵ AA 1 ⊥ 底面 ABC ， AA 1 ⊥ AB ， AA 1 ⊥ AC ，又 AB ⊥ AC ，如图，以 A 为原点建立空间直角坐标系A xyz ，设 AB 2 ，则由 ABACAA 1 可得 C(2,0,0) ， B(0,2,0) ， C 1 (2,0,2) ， A 1 (0,0,2) ，∵ E ， G 分别是 BC ， CC 1 的中点， ∴ E(1,1,0) ， G(2,0,1) ，uuur uuur (1, 1,1) ( 2,0,2) 0 ， ∴ EG CA 1uuur uuur ∴EG ⊥ CA 1 ， ∴ EG ⊥ AC ．1r ( x, y, z) ，则：（ 3）设平面 AEG 的法向量为 n r uuur 0 x y 0n AE1 ，则 y 1 ， z2 ， r uuur ，即 2 x z ，令 x n AG 0 0 r (1, 1, 2) ， ∴ nur由已知可得平面 A 1 AG 的法向量 m (0,1,0) ，r ur r ur 6∴ cos n mn, m r ur ，| n | | m | 6 由题意知二面角 A 1 AG E 为钝角，∴二面角 A 1 AG E 的余弦值为6 ．z C1A1G B 1Fx C AEBy11.（Ⅰ ）证明：过点 F 作 FH ∥ AD ，交 PA 于 H ，连结 BH ，如图所示，∵ PF 1 PD ，3∴ HF 1 AD BC ，3又FH ∥ AD ，AD∥BC，HF∥BC，∴四边形 BCFH 为平行四边形，∴ CF ∥ BH ，又 BH平面PAB，CF平面PAB，∴ CF ∥平面PAB．zPHFyA DxB C（Ⅱ）解：∵梯形 ABCD 中， AD ∥ BC ，AD⊥AB，∴BC ⊥ AB ，∵PB⊥平面ABCD，∴ PB⊥ AB ，PB⊥BC，∴如图，以 B 为原点，BC， BA ， BP所在直线为x ，y， z 轴建立空间直角坐标系，则 C(1,0,0) ， D (3,0,0) ， A(0,3,0) ， P(0,0,3) ，设平面 BPD 的一个法向量为 r ( x, y, z) ，n平面 APD 的一个法向量为 ur(a, b,c) ，muuur (3,3, uuur ∵ PD 3) ， BP (0,0,3) ，uuur r 0 3x 3 y 3z 0PD n∴ uuur r 0 ，即 3z 0 ，BP nr ur (0,1,1) ，令 x 1 得 n (1, 1,0) ，同理可得 mr ur r ur 1∴ cos n m ，n, m r ur 2| n | | m | ∵二面角 B PD A 为锐角，∴二面角 B PD A 为 π．3uuuur uuur3 ) ，（Ⅲ ）假设存在点 M 满足题意，设 PM PD (3 ,3 , uuuur uuur uuur ( 1 3 ,3 ,3 3 ) ， ∴ CM CP PDuuur (0,3,uuur uuuur 93(33) 0 ，解得1 ∵ PA 3) ， ∴ PA CM，2∴ PD 上存在点 M 使得 CM ⊥ PA ，且 PM1 3 3 2PD．212.Ⅰ∵ BC ⊥ CD ， BCCD 2 ，∴ BD 2 2 ，同理 EA ⊥ ED ， EA ED2 ， ∴AD 2 2，又∵ AB 4 ， ∴ 由勾股定理可知 BD 2AD 2AB 2， BD ⊥ AD ，又∵ 平面 EAD ⊥ 平面 ABCD ，平面 EAD I 平面 ABCD AD ， BD 平面 ABCD ，∴ BD ⊥ 平面 AED ， 又∵ AE 平面 AED ， ∴ BD ⊥ AE ．Ⅱ解：取 AD 的中点 O ，连结 OE ，则 OE ⊥ AD ，∵平面 EAD ⊥ 平面 ABCD ，平面 EAD I 平面 ABCDAD ，∴ OE ⊥ 平面 ABCD ，取 AB 的中点 F ，连结 DF ∥ BD ，以 O 为原点，建立如图所示的空间直角坐标系 O xyz ，则 D( 2,0,0) ， C ( 2 2, 2,0) ， E(0,0,uuur uuur( 2,0, 2) ，2) ， DC (2, 2,0) ， DE r ( x, y, z) ，设平面 CDE 的法向量为 nuuur r 0x z 0DC n ，令 x 1 ，则 z 1， y 1 ，则 uuurr 0 即x y 0 DEnr (1,1, 1) ，∴平面 CDE 的法向量 n 又平面ADE 的一个法向量为 r1(0,1,0) ，n设平面 ADE 和平面 CDE 所成角（锐角）为，r rr r则 cos| cos|rnn r3 ，1| n | | n 1 | 3∴平面 ADE 和平面 CDE 所成角（锐角）的余弦值为3 ．3zDCAOxFBy13.zPFAD yB E Cx（ 1 ）证明：连结 AE ， PE ．∵ PA 平面 ABCD ， BC 平面 ABCD ，∴ PA BC ．又∵ 底面 ABCD 是菱形， AB BC ， ABC 60 ，∴ △ABC 是正三角形．∵ E 是 BC 的中点，∴ AEBC ．又∵ PA I AEA ， PA 平面 PAE ， PE 平面 PAE ，∴ BC 平面 PAE ，∴ BC PE ．（ 2 ）由（ 1）得 AEBC ，由 BC ∥ AD 可得 AEAD ．又∵ PA 底面 ABCD ，∴ PA AE ， PA AD ．∴以 A 为原点，分别以 AE ， AD ， AP 为 x 轴， y 轴， z 轴建立空间直角坐标系 A xyz ，如图所示，则 A(0,0,0) ， E( 3,0,0) ， D (0,2,0) ， P(0,0,2) ， B( 3, 1,0) ， C ( 3,1,0) ， F (0,1,1) ．∵ PA 平面 ABCD ，uuur (0,0,2) ．∴平面 ABCD 的法向量为 AP uuur ( uuur(0,1,1) ．又∵ AC 3,1,0) ， AF 设平面 ACF 的一个法向量 r( x, y, z) ，则： n uuur r 03x y 0AC n ，令 x 1 ，则 y 3 ， z3 ，uuur r 0 ，即 0AF n y + zr∴ n (1, 3,uuur r ∴ cos AP, n3) ．uuur r AP n uuur r| AP || n |21 ．7∵二面角 F AC D 是锐角，∴二面角 FAC D 的余弦值为 21 ．7uuur uuur（ 3） G 是线段 AB 上的一点，设 AG t AB (0 ≤ t ≤ 1) ． uuur 3, 1,0) ， ∴ G( 3t , t,0) ． ∵ AB (uuur ( 3,1, uuur( 3t, t , 2) ．又∵ PC 2) ， PGr设平面 PCG 的一个法向量为 n ( x, y, z) ，则：uuur ur 0 3 x 1 + y 1 2z 1 0 urPC n 13(t 1), 3t ) ， uuur ur，即 3tx ty 2 z 0 ， ∴ n 1 (t +1, PG 10 n 1 1 1PCGuuur r uuur r 1) + 3t 0 ， ∵平面 ， ∴ AF n ， AF n 0 ，即 3( tAF ∥解得 t1 ．2故线段 AB 上存在一点 G ，使得 AF 平行于平面 PCG ， G 是 AB 中点．14.（ 1 ）证明： ∵ DE平面 ABCD ， AC 平面 ABCD ，∴ DE AC ．∵ ABCD 是正方形，∴ AC BD ．又 DE I BDD ，∴ AC 平面 BDE ．（ 2 ） ∵ DA ， DC ， DE 两两重叠， ∴ 建立空间直角坐标系 Dxyz 如图所示．zEFDCyA Bx∵ BE 与平面 ABCD 所成角为 60 ，即 DBE 60 ，∴ ED3 ．DB由 AD 3 ，可知 DZ 3 16 ， AF6 ，则 A(3,0,0) ， F (3,0, 6) ， E(0,0,3 6) ，B(3,3,0) ， C (0,3,0) ． uuur (0, 3, uuur (3,0, 2 6) ，∴ BF 6) ， EF r ( x, y, z) ，则设平面 BEF 的法向量为 nr uuur 0 3 y 6 z 0rn BFr uuur ，即 3x 2 6 z ，令 z 6 ，则 n (4,2, 6) ．n EF 0 0∵ AC 平面 BDE ，uuur uuur(3, 3,0) ， ∴ CA 为平面 BDE 的一个法向量，CAr uuur r uuur613 n CA∴ cos n, CA r uuuur26．|n ||CA | 3 2 13∵二面角 F BE D 为锐角，∴二面角 FBE D 的余弦值为13 ． 13uuuuruuuur r0 ，解得t 2 ，∵ AM ∥平面BEF，∴ AM n 0 ，即 4(t 3) 2t此时，点 M 坐标为(2,2,0) ， BM 1BD ，符合题意．315.zCDAByMPx（ 1 ）证明：∵ PA平面ABC，BC平面ABC，∴PA BC ．∵ BC AB ，PAI AB A ，∴ BC平面PAB．又 AM平面PAB，∴AM BC ．∵ PA AB ， M 为 PB 的中点，∴AM PB ．又∵ PB I BC B ，∴ AM平面PBC．（ 2 ）如图，在平面ABC 内作AZ∥BC，则AP，AB，AZ两两垂直，建立空间直角坐标系A xyz ．则 A(0,0,0) ， P(2,0,0) ， B(0,2,0) ， C (0,2,1) ， M (1,1,0)．uuur uuur uuuur(1,1,0) ．AP (2,0,0) ， AC (0,2,1) ， AMr( x, y, z) ，则：设平面 APC 的法向量为 nr uuur0 x 0n AP，令 y 1，则z 2．r uuur ，即2 y z 0n AC 0r(0,1, 2) ．∴ nuuuur(1,1,0) 为平面 PBC 的一个法向量，由（ 1）可知AMr uuuuruuuurr 1 10AM n．∴ cos nAMuuuurr5 2 10| AM || n | ∵二面角 A PC B 为锐角，∴二面角 A PC B 的余弦值为 10 ．10 uuur uuur（ 3）证明：设 D (≤ 1) ，, v, w) 是线段 PC 上一点，且 PDPC ， (0 ≤ 即 ( 2,v, w) ( 2,2,1) ， ∴ 2 2 ， v2 ， w．uuur (2 2 ,2 2,) ．∴ BDuuur uuur 0，得4由BD AC[0,1] ，5∴线段 PC 上存在点 D ，使得 BDAC ，此时PD4 ．PC516.解：（ 1）证明：因为 AB 平面 PAD ，所以 PHAB ，因为 AD3,AH2 ，所以 AH 2, HD1，HD设 PHx ，由余弦定可得，cos PHDx 2HD 2 PH 2x 21 cos PHA x2 HA 2 PH 2 x 2 12x HD 2x2x HA 4x因为 cos PHD cos PHA ，故 PH x1 ，所以 PHAD ，因为 AD I AB A ，故 PH 平面 ABCD .（2）以 H 为原点，以 HA, HP , HP 所在的直线分别为 x, y, z 轴，建立空间直角坐标系，则 B(2,3,0), P(0,0,1), E(1,3 , 1), F ( 1, 3 ,0), C ( 1, 9,0) ，2 222uuur ( 3, 3uuur ( 3 1 uuur (1 uuur，所以可得， BF,0), BE 1, , ), EF 2,0, ), FC (0,3,0)r 2 2 2 2( x, y, z) ，设平面 BEF 的法向量 nuuur r3x 3BF n 0 yr则有：2( 1,2, 4) ，uuur r3 z nBE nx 0y22ur(x, y, z) ，设平面 EFC 的法向量 muuur ur z 0 urEF m 0 2x21,0, 4) ，则有： uuur urm (FC m 3y 0r urr ur 1717n m故 cos n,mrur21 17 ,n m 21设二面角 BEF C 的平面角为，则 sin 2 21.2117.解（ Ⅰ）证明： ∵ DC平面 ABC ， BE / /DC∴ BE 平面 ABC∴ CQ BE ①又∵ ACBC 2，点 Q 为 AB 边中点∴ CQ AB ②AB I BE B故由 ①② 得 CQ平面 ABE（Ⅱ ）过点 A 作 AMBC 交 BC 延长线于点 M∵ AMBC , AM BE∴ AM 平面 BEDC∴V A CED1S CDE gAM3AM AC gsin33 ， S CDE11 2 12∴VA CED1 1 333 3（Ⅲ ）延长 ED 交 BC 延长线于 S ，过点 M 作 MQ ES 于 Q ，连结 AQ由（ Ⅱ ）可得：AQM 为 A DE B 的平面角∵ CD // 1BC2∴ SC CB 2∴ SE BE 2 SB 2 2 5MC MS 1∵ SQM ∽SBE∴ QM SM BE SE∴ QM 15 即 QM 52 2 5∴ tan AQM AM 315 QM 5518.（ 1）证明：∵在中，，∴当为的中点时，∵平面平面，平面，平面平面∴平面∵平面∴（2）如图，分别以射线，的方向为，轴的正方向，建立空间直角坐标系设，则，，，∵，，平面平面∴∴当且仅当时，最小，此时，设， 平面 ，则 ，即∴令，可得 ， ，则有∴∴观察可得二面角的平面角19.（ 1）取 FE 的中点 P ，连接 CP 交 BE 于点 M ， M 点即为所求的点． 连接 PG ，∵ G 是 AD 的中点， P 是 FE 的中点， ∴ PG / / AF ，又 PG平面 MGC ， AF平面 MGC ，所以直线 AF / / 平面 MGC ，∵ PE / / AD ， AD / / BC ， ∴ PE / / BC ， ∴BMBC 2 ，MEPE故点 M 为线段 BE 上靠近点 E 的三等分点． （2）不妨设 AD 2 ，由（ 1）知 PG AD ，又平面 ADEF平面 ABCD ，平面 ADEF I 平面 ABCDAD ，PG平面 ADEF ， ∴ PG 平面 ABCD ．故 PGGD ， PG GC ，以 G 为坐标原点， GC ， GD ， GP 分别为 x ， y ， z 轴建立空间直角坐标系 G xyz ，∵ ABC60 ， AB AD 2 AF ，∴ ADC 为正三角形， GC3 ，∴ G(0,0,0) ， C ( 3,0,0) ， D (0,1,0) uuuruuur 3,0,0) ，， E(0,1,1) ， ∴ GE (0,1,1) ， GC ( urur uuur ur uuur y z 0, 设平面 CEG 的一个法向量 n 1 ( x, y, z) ，则由 n 1 GE 0 ， n 1 GC 0 可得3x0,ur令 y 1，则 n 1 (0,1, 1)，uuuruuur 1,0) ，故 B( 3, uuur 3, 2,0) ，∵ CD ( 3,1,0)BA ，且 A(0, 2,0) ，故 BG (ur uuur故直线 BG 与平面 GCE 所成角的正弦值为| n 1 BG |sinuruuur| n 1 | | BG |14 ．720.（Ⅰ）取PC中点H，连接EH、FH .∵E为AB的中点，ABCD 是菱形，∴ AE / /CD ，且AE 1CD ，又F为PD的中点，H为PC的中点，∴FH / /CD，2且FH 1FH ，则四边形 AEHF 是平行四边形，CD ，∴AE / / FH，且AE2∴ AF / / EH .又 AF 平面 PCE ， EH 面 PCE ，∴ AF / / 平面 PCE .（Ⅱ ）取 BC 的中点为 O ，∵ ABCD 是菱形， AC AB ，∴AO BC ，以 A 为原点，AO, AD , AP 所在直线分别为x, y,z 轴，建立空间直角坐标系 A xyz，则B 3, 1,0 ,C 3,1,0 ,D 0,2,0 ， O 3,0,0 , P 0,0,1 ,E 3 1，, ,02 2uuur3,1, uuur 3 3 uuur3,0,0 ，设平面的法向量为∴ PC 1 , EC , ,0 ， AO2 2uuur3x y z 0n1 PC 0n1 ，令 y 1 ，则 x 3, z 2 ，x, y, z ，则uuur ，即3 x 3 yn1 EC 0 02 2∴平面 PCE 的一个法向量为n1 3, 1,2 ，又平面 PAD 的一个法向量为n2 1,0,0 .∴cos n1 , n2n1 n2 3 6| n1 | | n2 | 3 1 4 .即平面PAD与平面46PCE 所成锐二面角的余弦值为.421.解：（ 1）证明：取PD 的中点 F ，连接 EF ,CF ，因为 E, F 分别是 PA, PD 的中点，所以EF / / AD 且 EF1AD ，2因为 BC 1AB, BC / / AD ，所以 EF / / BC 且 EF BC ，所以 BE / /CF ,2又 BE平面 PCD ,CF平面 PCD ，所以 BE / / 平面 PCD .（ 2）以 P 为坐标原点， PD , PA 所在直线分别为 x 轴和 y 轴，建立如图所示的空间直角坐标系，不妨设 BC 1，则 P(0,0,0), A(0, 3,0), D (1,0,0), C (1,0,1), B( 1,3 ,1) ，2 2uuuruuur 13uuur3,0) ,PA(0, 3,0), AB(2 ,1), AD (1,2rr uuur3y 0( x, y, z) ，则 n PA设平面 PAB 的一个法向量为 nr uuur1 x 3 y ，n AB z 0r22令 x 1) ， 2，得 n (2,0,同理可求平面 ABD 的一个法向量为urr ur r urn m 6 15 m (3, 3,0)cos n, mr ur5 12，n m5平面 ABD 和平面 ABC 为同一个平面，所以二面角 PAB C 的余弦值为15 .522.解：（ Ⅰ ）证明：因为二面角S AB C 的大小为 90°，则 SA AD ， 又 SA AB ，故 SA 平面 ABCD ，又 BD 平面 ABCD ，所以 SABD ；在直角梯形 ABCD 中， BADADC90 ， AD 2CD 1 ， AB 2 ，所以 tan ABDtan CAD1DACBAC 90 ，，又2所以 ABDBAC 90 ，即 ACBD ；又 AC I SA A ，故 BD 平面 SAC ，因为AF 平面 SAC ，故 BD AF .（Ⅱ ）设点 E 到平面 ABCD 的距离为 h ，因为 V B ABCVE ABC2 VE ABC，且，VS ABCD515 12VS ABCDS 梯形 ABCD SA1 523故11，V E ABCh1 h2S ABC232故 h1，做点 E 到平面 ABCD 的距离为1.2223. （ ）Q E 为 SD 的中点， AD DC1SD, SDASDC 60012ED EC AD DC.设 O 为 AC 的中点，连接 EO, DO 则 EOACQ AD // BC, BC CDADBC.又 OD OA OCEOCEOD 从而 EO OD Q AC ABCD DO 面 ABCDAC I DOEO 面 ABCD Q EO 面 AEC面 EAC面ABCD 6 分（2）设F为CD的中点 ,连接OF、EF ,则OF平行且等于1AD 2Q AD ∥ BC EF ∥ BC不难得出 CD 面 OEF （ Q EO CD FO CD ）面ECD 面 OEFOF 在面 ECD 射影为 EF ，EFO 的大小为 BC 与面 ECD 改成角的大小设 AD a ，则OF aEF 3 a 2 2c osOF 3 EFO3EF即 BC 与 ECD 改成角的余弦值为3 12分.（亦可以建系完成）324.解（Ⅰ）过点 P 作 PO⊥底面 ABC ，垂足为O，连接 AO、 CO，则∠PCO为所求线面角，Q AC PA, AC PO ,且 PA PO P ，AC 平面 PAO .则∠PAO为二面角P-AC-B平面角的补角∴∠ PAO 60 ，又Q PA 2，PO= 3 ， sinPO 1 PCO2COPCO 300，直线PC与面ABC所成角的大小为30°.（Ⅱ ）过 O 作 OE BC 于点 E ,连接 PE ，则PEO 为二面角P-BC-A的平面角，Q AC 平面 PAO , AC OA AOE 450 ,设 OE 与 CA 相交于 F OE EF FO 22, 2在 PO3 4 36 PEO 中， tan PEO2 7EO22则二面角 P-BC -A 的正切值为4 36 .725.解：（ Ⅰ ）如图，取PA 中点 F ，连接 EF , FD ，E 是 BP 的中点，EF // AB 且 EF1AB ，又 DC // AB , DC 1 AB22EF //DC四边形 EFDC 是平行四边形，故得 EC / / FD又EC 平面 PAD , FD 平面 PADEC // 平面 ADE（Ⅱ ）取 AD 中点 H ,连接 PH ,因为 PAPD ，所以 PH AD平面 PAD平面 ABCD 于 AD ，PH面 ABCD ，HB 是 PB 在平面 ABCD 内的射影PBH 是 PB 与平面 ABCD 所成角四边形 ABCD 中，ABCBCD 900四边形 ABCD 是直角梯形DC CB1AB2设 AB2a ，则 BD2a在 ABD 中，易得 DBA 450 ,AD 2aPH PD 2 DH 2 a2 1 a2 2 a.2 2又BD 2 AD 2 4a2 AB 2ABD 是等腰直角三角形，ADB 90 0 HB DH 2 DB 2 1 a2 2a2 10 a2 2PH 2 a5在 Rt PHB 中，tan PBH 2HB 510 a2（Ⅲ ）在平面 ABCD 内过点 H 作 AB 的垂线交 AB 于 G 点，连接 PG ,则 HG 是 PG 在平面 ABCD 上的射影，故PG AB ，所以PGH 是二面角 P AB D 的平面角，由 AB a HA 2 a ，又HAB 45 0 12 2PH 2 a在 Rt PHG 中， tan PGH 2 2HG 1 a2二面角 P AB D 的余弦值大小为 3 .326.（ 1）∵四棱锥 P﹣ ABCD 的底面 ABCD 为边长为 2 的正方形， PA=2， PB=PD=2，∴PA2+AB 2=PB 2，PA2+AD 2=PD2，∴PA⊥ AB ，PA⊥ AD ，∴以 A 为原点， AB 为 x 轴， AD 为 y 轴， AP 为 z 轴，建立空间直角坐标系，∵E， F， G，H 分别为棱PA，PB ，AD ， CD 的中点．∴C（ 2，2， 0）， D （0， 2， 0）， B （2， 0， 0），P（ 0， 0，2）， F（ 1， 0， 1）， G（ 0， 1，0），=（﹣ 2， 0， 0），=（﹣ 1，﹣ 2，1），=（﹣ 2，﹣ 1， 0），设平面 CFG 的法向量=（ x， y， z），则，取 x=1，得=（ 1，﹣ 2，﹣ 3），设CD与平面CFG所成角为θ，则 sin θ=|cos＜＞ |= = = ．∴CD 与平面 CFG 所成角的正弦值为．（2）假设棱 PD 上是否存在点 M （ a， b， c），且，（ 0≤λ≤1），使得平面CFG⊥平面 MEH ，则（ a， b，c﹣ 2） =（ 0， 2λ，﹣ 2λ），∴ a=0，b=2λ， c=2﹣ 2λ，即 M （ 0，2λ， 2﹣2λ），E（ 0， 0， 1）， H （ 1，2， 0），=（ 1， 2，﹣ 1），=（ 0， 2λ，1﹣ 2λ），设平面 MEH 的法向量=（ x，y， z），则，取 y=1，得=（， 1，），平面 CFG 的法向量 =（ 1，﹣ 2，﹣ 3），∵平面 CFG⊥平面 MEH ，∴= ﹣ 2﹣=0，解得∈ [0， 1]．∴棱 PD 上存在点 M ，使得平面CFG ⊥平面 MEH ，此时=．。
高考数学专题—立体几何(空间向量求空间角与空间距离)
高考数学专题——立体几何（空间向量求角与距离）一、空间向量常考形式与计算方法设直线l,m 的方向向量分别为l ⃗,m ⃗⃗⃗⃗，平面α,β的法向量分别为n ⃗⃗1,n 2⃗⃗⃗⃗⃗. （1）线线角：（正负问题）：用向量算取绝对值（因为线线角只能是锐角）直线l,m 所成的角为θ，则0≤θ≤π2，计算方法：cos θ=l⃗⋅m ⃗⃗⃗⃗|l⃗|⋅|m ⃗⃗⃗⃗|； （2）线面角：正常考你正弦值，因为算出来的是角的余角的余弦值 非正常考你余弦值，需要再算一步。
直线l 与平面α所成的角为θ，则0≤θ≤π2，计算方法：sin θ=|l ⃗⋅n 1⃗⃗⃗⃗⃗⃗||l⃗|⋅|n ⃗⃗|； (3)二面角：同进同出为补角；一进一出为原角。
注意：考试从图中观察，若为钝角就取负值，若为锐角就取正值。
平面α,β所成的二面角为θ，则0≤θ≤π，如图①，AB ，CD 是二面角α－l －β的两个面内与棱l 垂直的直线，则二面角的大小θ＝⟨AB⃗⃗⃗⃗⃗⃗,CD ⃗⃗⃗⃗⃗⃗⟩．如图②③，n ⃗⃗1,n 2⃗⃗⃗⃗⃗分别是二面角α－l －β的两个半平面α，β的法向量，则二面角的大小θ满足|cos θ|＝|n⃗⃗1⋅n 2⃗⃗⃗⃗⃗⃗|n⃗⃗1|⋅|n2⃗⃗⃗⃗⃗⃗||，二面角的平面角大小是向量n 1与n 2的夹角(或其补角)． (4)空间距离额计算：通常包含点到平面距离，异面直线间距离。
二、空间向量基本步骤空间向量求余弦值或正弦值四步法（1）建系：三垂直，尽量多点在轴上；左右下建系，建成墙角系；锥体顶点在轴上；对称面建系。
一定要注明怎样建成的坐标系（2）写点坐标（3）写向量：向量最好在面上或者轴上（可简化计算量） （4）法向量的简化计算直线的方向向量和平面的法向量（1）直线的方向向量就是指和这条直线平行(或共线)的向量，记作，显然一条直线的方向向量可以有无数个.（2）若直线l ⊥α，则该直线的方向向量即为该平面的法向量，平面的法向量记作，有无数多个，任意两个都是共线向量.平面法向量的求法：设平面的法向量为α⃗=(x,y,z ).在平面内找出（或求出）两个不共线的向量a ⃗=(x 1,y 1,z 1)，b ⃗⃗=(x 2,y 2,z 2)，根据定义建立方程组，得到{α⃗×a ⃗=0α⃗×b ⃗⃗=0，通过赋值，取其中一组解，得到平面的法向量.三、空间向量求距离向量方法求异面直线距离：先求两异面直线的公共法向量，再求两异面直线上任意两点的连结线段在公共法向量上的射影长。
2019-2020年高中数学高考复习《立体几何大题》习题附详细解析
2019-2020年高中数学高考复习《立体几何大题》习题附详细解析1．长方体1111D C B A ABCD -中，1==BC AB ，21=AA ，E 是侧棱1BB 中点（Ⅰ）求直线1AA 与平面E AC 1所成角的大小（Ⅱ）求二面角B AC E --1的大小（Ⅲ）求三棱锥11C AD E -的体积2. 如图，在正三棱柱ABC-A 1B 1C 1中，底面边长是2，D 是棱BC 的中点，点M 在棱BB 1上，且BM=31B 1M ，又CM ⊥AC 1. （Ⅰ）求证：A 1B//平面AC 1D （Ⅱ）求三棱锥B 1-ADC 1体积.3.如图，四面体ABCD 中，O 、E 分别是BD 、BC的中点，2,CA CB CD BD AB AD ===== （I ）求证：AO ⊥平面BCD（II ）求异面直线AB 与CD 所成角余弦值的大小（III ）求点E 到平面ACD 的距离ABMDEOC4.已知四棱锥P—ABCD的底面是正方形，PA⊥底面ABCD．异面直线PB与CD所成的角为45°．求：（1）二面角B—PC—D的大小（2）直线PB与平面PCD所成角大小5.四棱锥P—ABCD中，PA⊥ABCD，四边形ABCD是矩形. E、F分别是AB、PD的中点.若PA=AD=3，CD=6. （I）求证：AF//平面PCE（II）求点F到平面PCE的距离；（III）求直线FC与平面PCE所成角的大小6.已知在四棱锥P-ABCD中，底面ABCD是边长为4的正方形，△PAD是正三角形，平面PAD ⊥平面ABCD，E、F、G分别是PA、PB、BC的中点（I）求证：EF 平面PAD（II）求平面EFG与平面ABCD所成锐二面角的大小立体几何大题答案1．长方体1111D C B A ABCD -中，1==BC AB ，21=AA ，E 是侧棱1BB 中点（Ⅰ）求直线1AA 与平面E AC 1所成角的大小（Ⅱ）求二面角B AC E --1的大小（Ⅲ）求三棱锥11C AD E -的体积答案：（I ）arcsin，距离与面33AEC )(1515arccos)(3311D III II 61V 11AEC -D = 2.如图，在正三棱柱ABC-A 1B 1C 1中，底面边长是2，D 是棱BC 的中点，点M 在棱BB 1上，且BM=31B 1M ，又CM ⊥AC 1. （Ⅰ）求证：A 1B//平面AC 1D （Ⅱ）求三棱锥B 1-ADC 1体积.答案：提示：)1(连接C A 1,交1AC 于点,E 连接DE ,则DE 是BC A 1∆的中位线，B A DE 1//,又111ADC B A ,ADC 面面⊄⊂DE ,D AC //11面B A ∴.)2(在正三棱锥111C B A ABC -中，BC 是D 的中点，则11B BCC 面⊥AD ,从而MC AD ⊥,又1AC CM⊥,则1ADC CM 和面内的两条相交直线1AC AD,都垂直，1ADC MC 面⊥∴,于是1DC CM⊥,则1CDC ∠与MCB ∠互余，则1tan CDC ∠与MCB ∠tan 互为倒数，易得221=AA ， 连结D B 1，∴2211=∆D C B S ,D C B 11面⊥AD , ∴三棱锥11ADC -B 的体积为362.方法2：以D 为坐标原点，DA DC ,为x y,轴，建立空间直角坐标系，设hBB =1，则)0,0,0(D ,)0,0,1(-B ,)0,0,1(C ,)0,3,0(A ,),0,1(1h B -，),0,1(1h C ， ),3,0(1h A ，)4,0,1(hM -，→B A 1),3,1(h ---=，),3,1(),0,3,0(1h A C AD --=-=→→，设平面D AC 1的法向量),,(z y x n=→，则⎪⎩⎪⎨⎧=⋅=⋅→→→→010n A C n AD )1,0,(-=⇒→h n ，→→⊥n B A 1 ∴D AC //11面B A)2(),3,1(),4,0,2(1h AC h CM -=-=→→，1AC CM ⊥,=⋅→→1AC CM 0422=+-h，22=∴h .平面D AC 1的法向量为)1,0,22(-=→n ，)22,3,1(1-=→A B 点)22,0,1(1-B 到平面D AC 1的距离3241=⋅=→→→nd nA B，233=∴∆ADC S . 3623242333111=⨯⨯=∴-ADC B V .3.如图，四面体ABCD 中，O 、E 分别是BD 、BC的中点，2,CA CB CD BD AB AD ===== （I ）求证：AO ⊥平面BCD（II ）求异面直线AB 与CD 所成角余弦值的大小（III ）求点E 到平面ACD 的距离．答案：方法一： （I ）证明：连结OC ,,.BO DO AB AD AO BD ==∴⊥,,.BO DO BC CD CO BD ==∴⊥ 在AOC ∆中，由已知可得1,AO CO == 而2,AC =222,AO CO AC ∴+=90,oAOC ∴∠=即.AO OC⊥,BD OC O = AO ∴⊥平面BCD（II ）解：取AC 的中点M ，连结OM 、ME 、OE ，由E 为BC 的中点知ME ∥AB,OE ∥DC∴直线OE 与EM 所成的锐角就是异面直线AB 与CD 所成的角在OME ∆中，111,22EM AB OE DC ====OM 是直角AOC ∆斜边AC 上的中线，11,2OM AC ∴== cos OEM ∴∠= ∴异面直线AB 与CD 所成角的大小为（III ）解：设点E 到平面ACD 的距离为.h,11....33E ACD A CDE ACD CDE V V h S AO S --∆∆=∴= 在ACD ∆中，2,CA CD AD ===12ACD S ∆∴=而211,22CDE AO S ∆===1.CDEACDAO S h S ∆∆∴=∴点E 到平面ACD方法二： （I ）同方法一.（II ）解：以O 为原点，如图建立空间直角坐标系，则(1,0,0),(1,0,0),B D -1(0,0,1),((1,0,1),(1,2C A E BA CD =-=- .2cos ,BA CD BA CD BA CD ∴<>==∴异面直线AB 与CD 所成角的大小为（III ）解：设平面ACD的法向量为(,,),n x y z =则.(,,).(1,0,1)0,.(,,1)0,n AD x y z n AC x y z ⎧=--=⎪⎨=-=⎪⎩0,0.x z z +=⎧∴-= ABMDEOCy令1,y =得(3,1,n =-是平面ACD 的一个法向量。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2019-2020年高考数学大题专题练习——立体几何（一）1.如图所示，四棱锥中，底面为正方形，平面，P ABCD -ABCD ⊥PD ABCD ，点分别为的中点.2PD AB ==,,E F G ,,PC PD BC (1)求证：；EF PA ⊥(2)求二面角的余弦值.D FGE --2.如图所示，该几何体是由一个直角三棱柱和一个正四棱锥组合而ADE BCF -P ABCD -成，，.AF AD ⊥2AE AD ==(1)证明：平面平面；⊥PAD ABFE (2)求正四棱锥的高，使得二面角P ABCD-h C AF P --3.四棱锥中，侧面是边长为2的正三角形，且与底面垂直，底面是面积P ABCD -PDC ABCD 为的菱形，为锐角，为的中点．ADC ∠M PB （Ⅰ）求证：∥面．PD ACM （Ⅱ）求证：．PA ⊥CD （Ⅲ）求三棱锥的体积．P ABCD -4.如图，四棱锥满足面，．，S ABCD -SA ⊥ABCD 90DAB ABC ∠=∠=︒SA AB BC a ===．2AD a =（Ⅰ）求证：面面．SAB ⊥SAD （Ⅱ）求证：面．CD ⊥SAC SCBA DMC BAPD5.在四棱锥中，底面为矩形，测棱底面，，点是P ABCD -ABCD PD ⊥ABCD PD DC =E 的中点，作交于．BC EF PB ⊥PB F （Ⅰ）求证：平面平面．PCD ⊥PBC （Ⅱ）求证：平面．PB ⊥EFD 6.在直棱柱中，已知，设中点为，中点为．111ABC A B C -AB AC ⊥1AB D 1A C E （Ⅰ）求证：平面．DE ∥11BCC B （Ⅱ）求证：平面平面．11ABB A ⊥11ACC A E DABC C 1B 1A 1D ABCEF P7.在四棱锥中，平面，，，，P ABCD -PA ⊥ABCD //AB CD AB AD ⊥PA PB =.::2:AB AD CD =（1）证明；BD PC ⊥（2）求二面角的余弦值；A PC D --（3）设点为线段上一点，且直线平面所Q PD AQ PAC，求的值.PQ PD8.在正方体中，O 是AC 的中点，E 是线段D 1O 上一点，且D 1E ＝λEO .1111ABCD A B C D -（1）若λ=1，求异面直线DE 与CD 1所成角的余弦值；（2）若λ=2，求证：平面CDE ⊥平面CD 1O .9.如图，在四棱锥中，底面是平行四边形，，侧面P ABCD -ABCD 135BCD =︒∠PAB ⊥底面，，，，ABCD 90BAP =︒∠2AB AC PA ===E F 分别为，的中点，点在线段上．BC AD M PD （Ⅰ）求证：平面．EF ⊥PAC （Ⅱ）若为的中点，求证：平面．M PD ME ∥PAB （Ⅲ）如果直线与平面所成的角和直线与ME PBC ME 平面所在的角相等，求的值．ABCD PMPD10.如图，在三棱柱，底面，，，，分别111ABC A B C -1AA ⊥ABC AB AC ⊥1AC AB AA ==E F 是棱，的中点，为棱上的一点，且平BC 1A A G 1CC 1C F ∥面．AEG （）求的值．11CGCC （）求证：．21EG A C ⊥（）求二面角的余弦值．31A AG E --A 1B 1C 1G F AB CEM FE CBA PD11.如图，在四棱锥中，底面，底面为梯形，，P ABCD -PB ⊥ABCD ABCD AD BC ∥，且，．AD AB ⊥3PB AB AD ===1BC =（Ⅰ）若点为上一点且，证明：平面．F PD 13PF PD=CF ∥PAB （Ⅱ）求二面角的大小．B PD A --（Ⅲ）在线段上是否存在一点，使得PD M CM PA ⊥若存在，求出的长；若不存在，说明理由．PM 12.如图，在四棱锥中，平面平面，，，E ABCD -EAD ⊥ABCD CD AB ∥BC CD ⊥，，．EA ED ⊥4AB =2BC CD EA ED ====Ⅰ证明：．BD AE ⊥Ⅱ求平面和平面所成角（锐角）的余弦值．ADE CDE DABCEPFDBCA13.己知四棱锥中，平面，底面P ABCD -PA ⊥ABCD 是菱形，且．，、ABCD 2PA AB ==60ABC ∠=︒BC 的中点分别为，．PD E F （Ⅰ）求证．BC PE ⊥（Ⅱ）求二面角的余弦值．F AC D --（Ⅲ）在线段上是否存在一点，使得平行于AB G AF 平面？若存在，指出在上的位置并给予证明，若不存在，请说明理由．PCG G AB14.如图，是边长为的正方形，平面，ABCD 3DE ⊥ABCD ，，与平面所成角为．AF DE ∥3DE AF =BE ABCD 60︒（Ⅰ）求证：平面．AC ⊥BDE （Ⅱ）求二面角的余弦值．F BE D --（Ⅲ）设点线段上一个动点，试确定点的位置，M BD M 使得平面，并证明你的结论．AM ∥BEF D DABCEF15.如图，面，，PA ⊥ABC AB BC ⊥，为的中点．22AB PA BC ===M PB （Ⅰ）求证：平面．AM ⊥PBC （Ⅱ）求二面角的余弦值．A PCB --（Ⅲ）在线段上是否存在点，使得PCD BD AC ⊥，若存在，求出的值，若不存在，说明理由．PDPC 16.如图所示，在四棱锥P -ABCD 中，AB ⊥平面是PB 的中点,,//,PAD AB CD E .2,3,2AHPD PA AB AD HD=====（1）证明：PH ⊥平面ABCD ；（2）若F 是CD 上的点，且，求二面角的正弦值.23FC FD ==B EF C --MDABCP17.如图，DC ⊥平面ABC ，，//EB DC ，，Q22AC BC EB DC ====120ACB ∠=︒为AB 的中点．（Ⅰ）证明：CQ ⊥平面ABE ；（Ⅱ）求多面体ACED 的体积；（Ⅲ）求二面角A -DE -B 的正切值．18.如图1,在△ABC 中，AB =BC =2,∠B =90°,D 为BC 边上一点，以边AC 为对角线做平行四边形ADCE ，沿AC 将△ACE 折起，使得平面ACE ⊥平面ABC ,如图2.(1)在图 2中，设M 为AC 的中点，求证:BM 丄AE ；(2)在图2中，当DE 最小时，求二面角A -DE -C 的平面角.19.如图所示，在已知三棱柱ABF -DCE 中，，，90ADE ∠=︒60ABC ∠=︒2AB AD AF==，平面ABCD ⊥平面ADEF ，点M 在线段BE 上，点G 是线段AD 的中点．（1）试确定点M 的位置，使得AF ∥平面GMC ；（2）求直线BG 与平面GCE 所成角的正弦值．20.已知在四棱锥P -ABCD 中，底面ABCD 是菱形，AC =AB ，PA ⊥平面ABCD ，E ，F 分别是AB ，PD 的中点.（Ⅰ）求证：AF ∥平面PCE ；（Ⅱ）若，求平面PAD 与平面PCE 所成锐二面角的余弦值.22AB AP ==21.如图，五面体PABCD 中，CD ⊥平面PAD ，ABCD 为直角梯形，,2BCD PD BC CD π∠===1,2AD AP PD =⊥.（1）若E 为AP 的中点，求证：BE ∥平面PCD ；（2）求二面角P -AB-C 的余弦值.22.如图（1）所示，已知四边形SBCD 是由Rt △SAB 和直角梯形ABCD 拼接而成的，其中.且点A 为线段SD 的中点，，.现将△SAB 沿AB90SAB SDC ∠=∠=︒21AD DC ==2AB =进行翻折，使得二面角S -AB -C 的大小为90°，得到图形如图（2）所示，连接SC ，点E ，F 分别在线段SB ，SC 上.（Ⅰ）证明：；BD AF ⊥（Ⅱ）若三棱锥B -AEC 的体积为四棱锥S -ABCD 体积的，求点E 到平面ABCD的距离.2523.四棱锥S -ABCD 中，AD ∥BC ，,BC CD ⊥060SDA SDC ∠=∠=，，E 为SD 的中点.AD DC =1122BC SD ==（1）求证：平面AEC ⊥平面ABCD ；（2）求BC 与平面CDE 所成角的余弦值.24.已知三棱锥P -ABC ，底面ABC 是以B 为直角顶点的等腰直角三角形，PA ⊥AC ，BA =BC =PA =2，二面角P -AC -B 的大小为120°.（1）求直线PC 与平面ABC 所成角的大小；（2）求二面角P -BC -A 的正切值.25.如图，在四棱锥P -ABCD 中，平面PAD ⊥平面ABCD ，090=∠=∠BCD ABC ，，E 是PB 的中点，AB CB DC PD PA 21====（Ⅰ）求证：EC ∥平面APD ；（Ⅱ）求BP 与平面ABCD 所成的角的正切值；（Ⅲ）求二面角P -AB -D 的余弦值.26.四棱锥P ﹣ABCD 的底面ABCD 为边长为2的正方形，PA =2，PB =PD =2，E ，F ，G ，H 分别为棱PA ，PB 2，AD ，CD 的中点．（1）求CD 与平面CFG 所成角的正弦值；（2）探究棱PD 上是否存在点M ，使得平面CFG ⊥平面MEH ，若存在，求出的值；若PDPM不存在，请说明理由．t试卷答案1以点为坐标原点，建立如图所示的空间直角坐标系，则D Dxyz -，，，，，，.()0,0,0D ()0,2,0A ()2,0,0C -()0,0,2P ()1,0,1E -()0,0,1F ()2,1,0G -(1)∵，，()0,2,2PA =- ()1,0,0EF =则，∴.0PA EF ×=PA EF ^(2)易知，，()0,0,1DF = ()2,11FG =--设平面的法向量，DFG ()111,,m x y z =则，即，00m DF m FG ì×=ïíï×=î 1111020z x y z ì=ïí-+-=ïî令，则是平面的一个法向量，11x =()1,2,0m =DFG 同理可得是平面的一个法向量，()0,1,1n =EFG ∴，cos ,m n m n m n×<>==×由图可知二面角为钝角，D FG E --∴二面角的余弦值为D FG E ---2.(1)证明：直三棱柱ADE BCF -中，AB ^平面ADE ，所以：AB AD ^，又AD AF ^，所以：AD ^平面ABFE ，AD Ì平面PAD ，所以：平面PAD ^平面ABFE .(2)由(1)AD ^平面ABFE ，以A 为原点，,,AB AE AD 方向为,,x y z 轴建立空间直角坐标系an dAl l t h A xyz -，设正四棱锥P ABCD -的高h ，2AE AD ==，则()0,0,0A ，()2,2,0F ，()2,0,2C ，()1,,1P h -.()2,2,0AF = ，()2,0,2AC = ，()1,,1AP h =-.设平面ACF 的一个法向量()111,,m x y z =，则：1111220220m AF x y n AC x z ì×=+=ïíï×=+=î ，取11x =，则111y z ==-，所以：()1,1,1m =-- .设平面AFP 的一个法向量()222,,n x y z = ，则22222220n AF x y n AP x hy z ì×=+=ïíï×=-+=î，取21x =，则21y =-，21z h =--，所以：()1,1,1n h =---，二面角C AF P --cos ,m n m n m n ×<>==，解得：1h =.3.E ODPABCM（Ⅰ）证明：连结交于，则是中点，AC BD O O BD ∵在中，是的中点，是的中点，PBD ∥O BD M PB ∴，PD MO ∥又平面，平面，PD ⊄ACM MO ⊂ACM ∴平面．PD ∥ACM（Ⅱ）证明：作，则为中点，连结，PE CD ∥E CD AE ∵底面是菱形，边长为，面积为，ABCD 2∴，11sin 222sin 222S AD DC ADC ADC =⨯⨯⨯∠⨯=⨯⨯∠⨯=∴，，sinADC ∠60ADC ∠=︒∴是等边三角形，ACD ∥∴，CD AE ∥又∵，CD PE ∥∴平面，CD ∥PAE ∴．CD PA ∥（Ⅲ）．11233P ABCD ABCD V S PE -=⨯=⨯=4.DABCSE（）证明：∵平面，平面，1SA ∥ABCD AB ⊂ABCD ∴，AB SA ∥又∵，90BAD ∠=︒∴，AB AD ∥∵，SA AD A = ∴平面，AB ∥SAD 又平面，AB ⊂SAB ∴平面平面．SAB ∥SAD （Ⅱ）证明：取中点为，AD E ∵，，，是中点，90DAB ABC ∠=∠=︒2AD a =BC a =E AD ∴是矩形，，，ABCE ∠CE AB a ==DE a =∴，CD =在中，，，，ACD∥AC=CD =2AD a =∴，222AC CD AD +=即，CD AC ∥又∵平面，平面，SA ∥ABCD CD ⊂ABCD ∴，CD SA ∥∴平面．CD ∥PAC 5.PFECBAD （Ⅰ）证明：∵底面，平面，PD ⊥ABCD BC ⊂ABCD ∴，PD BC ⊥又∵底面为矩形，ABCD ∴，BC CD ⊥∴平面，BC ⊥PCD ∵平面，BC ⊂PBC ∴平面平面．PCD ⊥PBC （Ⅱ）证明：∵，是中点，PD DC =E PC ∴，DE PC ⊥又平面平面，平面平面，PCD ⊥PBC PCD PBC PC =∴平面，DE ⊥PBC ∴，DE PB ⊥又∵，，EF PB ⊥EF DE E = ∴平面．PB ⊥EFD 6.E A1B 1C 1CBAD （Ⅰ）证明：连结，1A B ∵是的中点，D 1AB ∴是的中点，D 1A B ∵在中，是的中点，是的中点，1A BC ∥D 1A B E 1A C ∴，DE BC ∥又平面，平面，DE⊄11BCC B BC ⊂11BCC B ∴平面．DE ∥11BCC B （Ⅱ）证明：∵是直棱柱，111ABC A B C -∴平面，1AA ⊥ABC ∴，1AA AB ⊥又，AB AC ⊥∴平面，AB ⊥11ACC A ∵平面，AB ⊂11ABB A ∴平面平面．11ABB A ⊥11ACC A 7.以A 为坐标原点，建立空间直角坐标系(2,0,0)B ，D ，(0,0,2)P ，C （1）(BD =- ，2)PC =-，∵0BD PC ∙=∴BD PC⊥（2）AC = ，(0,0,2)AP = ，平面PAC 的法向量为1,0)m =-(0,2)DP = ，(1,0,0)AP = ，平面DPC 的法向量为(0,1)n =-.cos ,m n m n m n∙==∙，二面角B PC D --.g（3）∵AQ AP PQ AP tPD =+=+，[]0,1t ∈∴(0,0,2)2),22)AQ t t =+-=-设θ为直线AQ 与平面PAC 所成的角sin cos ,AQ m AQ m AQ mθ∙===∙223684t t t =⇒=-+，解得2t =（舍）或23.所以，23PQ PD =即为所求.8.解:(1)不妨设正方体的棱长为1，以,,DADC 1DD 为单位正交基底建立如图所示的空间直角坐标系．D xyz -则A (1，0，0)，，，D 1(0，0，1)，()11022O ，，()010C ，，E ， ()111442，，于是，.由cos ＝＝.所以异面直线AE 与CD 1. （2）设平面CD 1O 的向量为m =(x 1，y 1，z 1)，由m ·＝0，m ·＝0CO1CD 得取x 1＝1，得y 1＝z 1＝1，即m =(1，1，1) .由D 1E ＝λEO ，则E，.又设平面CDE 的法向量为n ＝(x 2，y 2，z 2)，由n ·＝0，n ·＝0.CD DE 得取x 2=2，得z 2＝－λ，即n ＝(－2，0，λ) .因为平面CDE ⊥平面CD 1F ，所以m ·n ＝0，得λ＝2．9.（Ⅰ）证明：在平行四边形中，ABCD ∵，，，AB AC =135BCD =︒∠45ABC =︒∠∴，∵，分别为，的中点，AB AC ⊥E F BC AD ∴，∴，EF AB ∥EF AC ⊥∵侧面底面，且，PAB ⊥ABCD 90BAP =︒∠∴底面，∴，PA ⊥ABCD PA EF ⊥又∵，平面，平面，PA AC A = PA ⊂PAC AC ⊂PAC ∴平面．EF ⊥PAC （Ⅱ）证明：∵为的中点，为的中点，M PD F AD ∴，又∵平面，平面，MF PA ∥MF ⊄PAB PA ⊂PAB ∴平面，同理，得平面，MF ∥PAB EF ∥PAB 又∵，平面，平面，MF EF F = MF ⊂MEF EF ⊂MEF ∴平面平面，又∵平面，MEF ∥PAB ME ⊂MEF ∴平面．ME ∥PAB （Ⅲ）解：∵底面，，PA ⊥ABCD AB AC ⊥∴，，两两垂直，故以，，分别为轴，轴和轴建立如图空间AP AB AC AB AC AP x y z 直角坐标系，则，，，，，，(0,0,0)A (2,0,0)B (0,2,0)C (0,0,2)P (2,2,0)D -(1,1,0)E 所以，，，(2,0,2)PB =- (2,2,2)PD =--(2,2,0)BC =- 设，则，([0,1])PMPDλλ=∈(2,2,2)PM λλλ=-- ∴，，(2,2,22)M λλλ--(12,12,22)ME λλλ=+--易得平面的法向量，ABCD (0,0,1)m =设平面的法向量为，则：PBC (,,z)n x y =，即，令，得，00n BC n PB ⎧⋅=⎪⎨⋅=⎪⎩ 220220x y x z -+=⎧⎨-=⎩1x =(1,1,1)n = ∴直线与平面所成的角和此直线与平面所成的角相等，ME PBC ABCD ∴，即，|cos ,||cos ,|ME m ME n <>=<> ||||||||||||ME m ME n ME m ME n ⋅⋅=⋅⋅∴（舍去），|2λ-λ=λ=故．PM PD=D10.（）∵平面，又平面，平面平面，11C F ∥AEG 1C F ⊂11ACC A 11ACC A AEG AG =∴，1C F AG ∥∵为的点，且侧面为平行四边形，F 1AA 11ACC A ∴为中点，G 1CC ∴．112CG CC =（）证明：∵底面，，，21AA ⊥ABC 1AA AB ⊥1AA AC ⊥又，如图，以为原点建立空间直角坐标系，AB AC ⊥A A xyz -设，则由可得，，，，2AB =1AB AC AA ==(2,0,0)C (0,2,0)B 1(2,0,2)C 1(0,0,2)A ∵，分别是，的中点，∴，，E G BC 1CC (1,1,0)E (2,0,1)G ∴，1(1,1,1)(2,0,2)0EG CA ⋅=-⋅-=∴，1EG CA ⊥∴．1EG A C ⊥（）设平面的法向量为，则：3AEG (,,)n x y z =，即，令，则，，00n AE n AG ⎧⋅=⎪⎨⋅=⎪⎩ 020x y x z +=⎧⎨+=⎩1x =1y =-2z =-∴，(1,1,2)n =-- 由已知可得平面的法向量，1A AG (0,1,0)m =∴，cos ,||||n m n m n m ⋅<>==⋅由题意知二面角为钝角，1A AG E --∴二面角的余弦值为．1A AG E --111.（Ⅰ）证明：过点作，F FH AD ∥交于，连结，如图所示，PA H BH ∵，13PF PD=∴，13HF AD BC ==又，，，FH AD ∥AD BC ∥HF BC ∥∴四边形为平行四边形，BCFH ∴，CF BH ∥又平面，平面，BH ⊄PAB CF ⊄PAB ∴平面．CF ∥PAB D（Ⅱ）解：∵梯形中，，，ABCD AD BC ∥AD AB ⊥∴，BC AB ⊥∵平面，PB ⊥ABCD ∴，，PB AB ⊥PB BC ⊥∴如图，以为原点，，，B BC BA BP所在直线为，，轴建立空间直角坐标系，x y z 则，，，，(1,0,0)C (3,0,0)D (0,3,0)A (0,0,3)P 设平面的一个法向量为，BPD (,,)n x y z = 平面的一个法向量为，APD (,,)m a b c = ∵，，(3,3,3)PD =- (0,0,3)BP = ∴，即，00PD n BP n ⎧⋅=⎪⎨⋅=⎪⎩ 333030x y z z +-=⎧⎨=⎩令得，同理可得，1x =(1,1,0)n =- (0,1,1)m = ∴，1cos ,2||||n m n m n m ⋅<>==-⋅∵二面角为锐角，B PD A --∴二面角为．B PD A --π3（Ⅲ）假设存在点满足题意，设，M (3,3,3)PM PD λλλλ=-∴，(13,3,33)CM CP PD λλλλ=+=-+- ∵，∴，解得，(0,3,3)PA =- 93(33)0PA CM λλ⋅=+-= 12λ=∴上存在点使得，且．PD M CMPA ⊥12PM PD ==12.Ⅰ∵，，∴，BC CD ⊥2BC CD ==BD =同理，，∴，EA ED ⊥2EA ED ==AD =又∵，∴由勾股定理可知，，4AB =222BD AD AB +=BD AD ⊥又∵平面平面，平面平面，平面，EAD ⊥ABCD EAD ABCD AD =BD ⊂ABCD ∴平面，BD ⊥AED 又∵平面，AE ⊂AED ∴．BD AE ⊥Ⅱ解：取的中点，连结，则，AD O OE OE AD ⊥∵平面平面，平面平面，EAD ⊥ABCD EAD ABCD AD =∴平面，OE ⊥ABCD取的中点，连结，AB F DF BD ∥以为原点，建立如图所示的空间直角坐标系，O O xyz -则，，，，，(D (C -E (DC = DE =设平面的法向量为，CDE (,,)n x y z =则即，令，则，，00DC n DE n ⎧⋅=⎪⎨⋅=⎪⎩ 00x z x y +=⎧⎨-+=⎩1x =1z =-1y =∴平面的法向量，CDE (1,1,1)n =- 又平面的一个法向量为，ADE 1(0,1,0)n = 设平面和平面所成角（锐角）为，ADE CDE θ则，111cos |cos ,|||||n n n n n n θ⋅=<>==⋅∴平面和平面．ADE CDE C13.（）证明：连结，．1AE PE ∵平面，平面，PA ⊥ABCD BC ⊂ABCD∴．PA BC ⊥又∵底面是菱形，，，ABCD AB BC =60ABC ∠=︒∴是正三角形．ABC ∥∵是的中点，E BC ∴．AE BC ⊥又∵，平面，平面，PA AE A = PA ⊂PAE PE ⊂PAE ∴平面，BC ⊥PAE∴．BC PE ⊥（）由（）得，由可得．21AE BC ⊥BC AD ∥AE AD ⊥又∵底面，∴，．PA ⊥ABCD PA AE ⊥PA AD ⊥∴以为原点，分别以，，为轴，轴，轴建立空间直角坐标系，A AEAD AP x y zA xyz -如图所示，则，，，，，，(0,0,0)A E (0,2,0)D (0,0,2)P 1,0)B -C ．(0,1,1)F ∵平面，PA ⊥ABCD ∴平面的法向量为．ABCD (0,0,2)AP =又∵，．AC = (0,1,1)AF =设平面的一个法向量，则：ACF (,,)n x y z =，即，令，则，，0AC n AF n ⎧⋅=⎪⎨⋅=⎪⎩00y y z +==⎪⎩+1x =y =z =∴．(1,n =∴．cos ,||||AP n AP n AP n ⋅==∵二面角是锐角，F AC D --∴二面角F AC D --（）是线段上的一点，设．3G AB (01)AG t AB t =≤≤∵，∴．1,0)AB =-,,0)G t -又∵，．2)PC =- ,,2)PG t =--设平面的一个法向量为，则：PCG (,,)n x y z =，即，∴，1100PC n PG n ⎧⋅=⎪⎨⋅=⎪⎩1111112020y z ty z -=--=+1()n t t =- +∵平面，∴，，AF ∥PCG AF n ⊥ 0AF n ⋅=1)0t -=解得．12t=故线段上存在一点，使得平行于平面，是中点．AB G AF PCGG AB14.（）证明：∵平面，平面，1DE⊥ABCD AC⊂ABCD∴．DE AC⊥∵是正方形，ABCD∴．AC BD⊥又，DE BDD=∴平面．AC⊥BDE（）∵，，两两重叠，∴建立空间直角坐标系如图所示．2DA DC DE D xyz-∵与平面所成角为，即，BE ABCD60︒60DBE∠=︒∴．EDDB=由，可知，，则，，，3AD=DZ=AF=(3,0,0)A F E(3,3,0)B，．(0,3,0)C∴，，(0,BF=-(3,0,EF=-设平面的法向量为，则BEF(,,)n x y z=，即，令．n BFn EF⎧⋅=⎪⎨⋅=⎪⎩3030yx⎧-+=⎪⎨-=⎪⎩z n=∵平面，AC⊥BDE∴为平面的一个法向量，，CABDE(3,3,0)CA=-∴．cos ,||||n CA n CA n CA ⋅===∵二面角为锐角，F BE D --∴二面角F BE D --（）点线段上一个动点，设，则．3M BD (,,0)M t t (3,,0)AM t t =-∵平面，∴，即，解得，AM ∥BEF 0AM n ⋅=4(3)20t t -+=2t =此时，点坐标为，，符合题意．M (2,2,0)13BM BD=15.（）证明：∵平面，平面，1PA ⊥ABC BC ⊂ABC ∴．PA BC ⊥∵，，BC AB ⊥PA AB A = ∴平面．BC ⊥PAB 又平面，AM ⊂PAB ∴．AM BC ⊥∵，为的中点，PA AB =M PB ∴．AM PB ⊥又∵，PB BC B = ∴平面．AM ⊥PBC （）如图，在平面内作，则，，两两垂直，建立空间直角坐标2ABC AZ BC ∥AP AB AZ 系．则，，，，．A xyz -(0,0,0)A (2,0,0)P (0,2,0)B (0,2,1)C (1,1,0)M ，，．(2,0,0)AP = (0,2,1)AC = (1,1,0)AM =设平面的法向量为，则：APC (,,)n x y z = ，即，令，则．00n AP n AC ⎧⋅=⎪⎨⋅=⎪⎩020x y z =⎧⎨+=⎩1y =2z =-∴．(0,1,2)n =- 由（）可知为平面的一个法向量，1(1,1,0)AM = PBC ∴．cos ||||AM n n AM AM n ⋅⋅==∵二面角为锐角，A PCB --∴二面角．A PCB --（）证明：设是线段上一点，且，，3(,,)D v w μPC PD PC λ=(01)λ≤≤即，(2,,)(2,2,1)v w μλ-=-∴，，．22μλ=-2v λ=w λ=∴．(22,22,)BD λλλ=--由，得，0BD AC ⋅= 4[0,1]5λ=∈∴线段上存在点，使得，此时．PC D BD AC ⊥45PD PCλ==16.解：（1）证明：因为平面，所以，AB ⊥PAD PH AB ⊥因为，所以，3,2AHAD HD==2,1AH HD ==设，由余弦定可得，PH x = 22221cos 22x HD PH x PHD x HD x +--∠==⋅22221cos 24x HA PH x PHA x HA x+--∠==⋅因为，故，cos cos PHD PHA ∠=-∠1PH x ==所以，因为，故平面.PH AD ⊥AD AB A = PH ⊥ABCD （2）以为原点，以所在的直线分别为 轴，建立空间直角坐标系，H ,,HA HP HP ,,x y z 则，3139(2,3,0),(0,0,1),(1,,(1,,0),(1,,0)2222B P E FC --所以可得，，3311(3,,0),(1,,),(2,0,(0,3,0)2222BF BE EF FC =--=--=-=设平面的法向量，BEF (,,)n x y z =则有：，33002(1,2,4)30022x y BF n n z BE n x y ⎧--=⎪⎧⋅=⎪⎪⇒⇒=-⎨⎨⋅=⎪⎪⎩--+=⎪⎩设平面的法向量，EFC (,,)m x y z =则有：，020(1,0,4)2030z EF m x m FC m y ⎧⎧⋅=--=⎪⎪⇒⇒=-⎨⎨⋅=⎪⎪⎩=⎩故cos ,n m n m n m⋅===⋅设二面角的平面角为 ，则B EF C --θsin θ=17.解（Ⅰ）证明：∵平面，DC ⊥ABC //BE DC∴平面BE ⊥ABC ∴ ①CQ BE ⊥又∵，点为边中点2AC BC ==Q AB ∴ ②CQ AB ⊥AB BE B=I 故由①②得平面CQ ⊥ABE（Ⅱ）过点作交延长线于点A AM BC ⊥BC M ∵,AM BC AM BE ⊥⊥∴平面AM ⊥BEDC ∴13A CED CDE V S AM -∆=g sin3AM AC π==g 11212CDE S ∆=⨯⨯=∴113A CEDV -=⨯=（Ⅲ）延长交延长线于，过点作于，连结ED BC S M MQ ES ⊥Q AQ 由（Ⅱ）可得：为的平面角AQM ∠A DE B --∵1//2CD BC ∴2SC CB ==∴SE ==1MC MS ==∵∽SQM ∆SBE ∆∴QM SMBE SE=∴即2QM=QM =∴tan AMAQM QM∠===18.（1）证明：∵在中，，∴当为的中点时，∵平面平面，平面，平面平面∴平面∵平面∴（2）如图，分别以射线，的方向为，轴的正方向，建立空间直角坐标系设，则，，，∵，，平面平面∴∴当且仅当时，最小，此时，设，平面，则，即∴令，可得，，则有∴∴观察可得二面角的平面角19.（1）取FE 的中点P ，连接CP 交BE 于点M ，M 点即为所求的点．连接PG ，∵G 是AD 的中点，P 是FE 的中点，∴//PG AF ，又PG ⊂平面MGC ，AF ⊄平面MGC ，所以直线//AF 平面MGC ，∵//PE AD ，//AD BC ，∴//PE BC ，∴2BM BCME PE==，故点M 为线段BE 上靠近点E 的三等分点．（2）不妨设2AD =，由（1）知PG AD ⊥，又平面ADEF ⊥平面ABCD ，平面ADEF 平面ABCD AD =，PG ⊂平面ADEF ，∴PG ⊥平面ABCD ．故PG GD ⊥，PG GC ⊥，以G 为坐标原点，GC ，GD ，GP 分别为x ，y ，z 轴建立空间直角坐标系G xyz -，∵60ABC ∠=︒，2AB AD AF ==，∴ADC ∆为正三角形，GC =，∴(0,0,0)G，C ，(0,1,0)D ，(0,1,1)E ，∴(0,1,1)GE =，GC =，设平面CEG的一个法向量1(,,)n x y z=，则由1n GE⋅=，1n GC⋅=可得0,0,yz+=⎧⎪=令1y=，则1(0,1,1)n=-，∵(CD=BA=，且(0,1,0)A-，故2,0)B-，故(2,0)BG=，故直线BG与平面GCE所成角的正弦值为11||sin||||n BGn BGθ⋅==⋅．20.（Ⅰ）取PC中点H，连接、EH FH.∵E为AB的中点，ABCD是菱形，∴//AE CD，且12AE CD=，又F为PD的中点，H为PC的中点，∴//FH CD，且12FH CD=，∴//AE FH，且AE FH=，则四边形AEHF是平行四边形，∴//AF EH.又AF⊄平面PCE，EH⊂面PCE，∴//AF平面PCE.（Ⅱ）取BC的中点为O，∵ABCD是菱形，AC AB=，∴AO BC⊥，以A为原点，,,AO AD AP所在直线分别为,,zx y轴，建立空间直角坐标系A xyz-，则))()1,0,,0,2,0B C D-，)()1,0,0,1,,02O P E⎫-⎪⎪⎭，∴)31,,02PC EC⎫=-=⎪⎪⎭，)AO=，设平面的法向量为()1,,n x y z=，则11n PCn EC⎧⋅=⎪⎨⋅=⎪⎩，即y zx y+-=+=，令1y=-，则2x z==，∴平面PCE的一个法向量为)11,2n=-，又平面PAD的一个法向量为()21,0,0n=.∴121212cos,|n||n|n nn n⋅<>===⋅即平面PAD与平面PCE所成锐二面角的in21.解：（1）证明：取的中点，连接，PD F,EF CF因为分别是的中点，所以且，,E F,PA PD//EF AD12EF AD=因为，所以且，所以,1,//2BC AB BC AD=//EF BC EF BC=//BE CF又平面平面，所以平面.BE⊄,PCD CF⊂PCD//BE PCD（2）以为坐标原点，所在直线分别为轴和轴，建立如图所示的空间直角坐P,PD PA x y标系，不妨设，1BC=则，1(0,0,0),(1,0,0),(1,0,1),(2P A D C B,1((1,2PA AB AD===设平面的一个法向量为，则，PAB(,,)n x y z=1002n PAn AB x z=⎧⋅=⎪⇒⎨⎨⋅==⎪⎪⎩⎩令，得，2x=(2,0,1)n=-同理可求平面的一个法向量为ABDcos,n mm n mn m⋅=⇒===平面和平面为同一个平面，ABD ABC所以二面角.P AB C--22.解：（Ⅰ）证明：因为二面角的大小为90°，则，S AB C--SA AD⊥又，故平面，又平面，所以；SA AB⊥SA⊥ABCD BD⊂ABCD SA BD⊥在直角梯形中，，，，ABCD90BAD ADC∠=∠=︒21AD CD==2AB=所以，又，1tan tan2ABD CAD∠=∠=90DAC BAC∠+∠=︒所以，即；90ABD BAC∠+∠=︒AC BD⊥又，故平面，AC SA A=I BD⊥SAC因为平面，故.AF⊂SAC BD AF⊥（Ⅱ）设点到平面的距离为，因为，且，E ABCD hB ABC E ABCV V--=25E ABCS ABCDVV--=故，511215321122132ABCDS ABCDE ABCABCS SAVV S h h--∆⨯⋅⨯===⋅⨯⨯⨯∥∥故，做点到平面的距离为.12h=E ABCD1223.（1）为的中点，ESD01,602AD DC SD SDA SDC==∠=∠=.ED EC AD DC∴===设为的中点，连接则O AC,EO DO EO AC⊥//,AD BC BC CD⊥.AD BC∴⊥又OD OA OC==从而EOC EOD∴∆≅∆EO OD⊥面AC ABCD=DO⊂ABCD0AC DO=面面EO∴⊥ABCD EO⊂AEC面面………………6分∴EAC ⊥ABCD （2）设为的中点,连接,则平行且等于F CD OF EF 、OF 12AD ∥∥AD BC EF ∴BC不难得出面（ ）CD ⊥OEF EO CD ⊥ FO CD ⊥面面∴ECD ⊥OEF在面射影为，的大小为与面改成角的大小OF ECD EF EFO ∠BC ECD 设，则 AD a =2aOF =EF =os OF c EFO EF <==即与.（亦可以建系完成） ………………12分BC ECD 24.解（Ⅰ）过点P 作PO ⊥底面ABC ，垂足为O ，连接AO 、CO ，则∠为所求线面角，PCO ，,AC PA ⊥ ,AC PO PA PO P ⊥⋂=且平面.则∠PAO 为二面角P -AC -B 平面角的补角AC ∴⊥PAO ∴∠，又， 60=PAO 2PA =∴，P O = 1sin 2PO PCO CO ∠==，直线PC 与面ABC 所成角的大小为30°.030PCO ∴∠=（Ⅱ）过作于点,连接，则为二面角P -BC -A 的平面角，O OE BC ⊥E PE PEO ∠平面,,AC ⊥ PAO AC OA ⊥045AOE ∠=设与相交于OE CA F 2OE EF FO ∴=+=+a在中，PEO ∆tan POPEO EO∠===则二面角P -BC -A 25.解：（Ⅰ）如图，取中点，连接，PA F FD EF ,是的中点，E BP 且，又AB EF // AB EF 21=AB DC AB DC 21,//= 四边形是平行四边形，故得∴∴DC EF //EFDC //EC FD又平面平面⊄EC ⊂FD PAD ,PAD平面//EC ∴ADE（Ⅱ）取中点,连接,因为，所以AD H PH PD PA =ADPH ⊥ 平面平面于， ⊥PAD ABCD AD 面，⊥∴PH ABCD 是在平面内的射影HB ∴PB ABCD 是与平面所成角PBH ∠∴PB ABCD 四边形中， ABCD 090=∠=∠BCD ABC 四边形是直角梯形∴ABCD AB CB DC 21==设，则a AB 2=aBD 2=在中，易得ABD ∆aAD DBA 2,450=∴=∠.22212222a a a DH PD PH =-=-=又22224ABa AD BD ==+ 是等腰直角三角形，ABD ∆∴090=∠ADB a a a DB DH HB 2102212222=+=+=∴ 在中，∴PHB Rt ∆5521022tan ===∠a aHB PH PBH （Ⅲ）在平面内过点作的垂线交于点，连接,则是在平ABCD H AB AB G PG HG PG 面上的射影，故，所以是二面角的平面角，ABCD AB PG ⊥PGH ∠D AB P --由，又a HA a AB 22,2==aHG HAB 21450=∴=∠在中，PHG Rt ∆22122tan ===∠a aHG PHPGH 二面角的余弦值大小为∴D AB P --.3326.（1）∵四棱锥P ﹣ABCD 的底面ABCD 为边长为2的正方形，PA=2，PB=PD=2，∴PA 2+AB 2=PB 2，PA 2+AD 2=PD 2，∴PA ⊥AB ，PA ⊥AD ，∴以A 为原点，AB 为x 轴，AD 为y 轴，AP 为z 轴，建立空间直角坐标系，∵E ，F ，G ，H 分别为棱PA ，PB ，AD ，CD 的中点．∴C （2，2，0），D （0，2，0），B （2，0，0），P （0，0，2），F （1，0，1），G （0，1，0），=（﹣2，0，0），=（﹣1，﹣2，1），=（﹣2，﹣1，0），设平面CFG 的法向量=（x ，y ，z ），则，取x=1，得=（1，﹣2，﹣3），设CD与平面CFG所成角为θ，则sinθ=|cos＜＞|===．∴CD与平面CFG 所成角的正弦值为．（2）假设棱PD上是否存在点M（a，b，c），且，（0≤λ≤1），使得平面CFG⊥平面MEH，则（a，b，c﹣2）=（0，2λ，﹣2λ），∴a=0，b=2λ，c=2﹣2λ，即M（0，2λ，2﹣2λ），E（0，0，1），H（1，2，0），=（1，2，﹣1），=（0，2λ，1﹣2λ），设平面MEH 的法向量=（x，y，z），则，取y=1，得=（，1，），平面CFG 的法向量=（1，﹣2，﹣3），∵平面CFG⊥平面MEH，∴=﹣2﹣=0，解得∈[0，1]．∴棱PD上存在点M，使得平面CFG⊥平面MEH ，此时=．。