第01章习题分析与解答
电子技术第1章课后答案

第1章半导体存器件1。
1 在如图1.4所示的各个电路中,已知直流电压V,电阻kΩ,二极管的正向压降为0.7V,求U o。
图1.4 习题1.1的图分析U o的值与二极管的工作状态有关,所以必须先判断二极管是导通还是截止。
若二极管两端电压为正向偏置则导通,可将其等效为一个0.7V的恒压源;若二极管两端电压为反向偏置则截止,则可将其视为开路。
解对图1。
4(a)所示电路,由于V,二极管VD承受正向电压,处于导通状态,故:(V)对图1.4(b)所示电路,由于V,二极管VD承受反向电压截止,故:(V)对图1.4(c)所示电路,由于V,二极管VD承受正向电压导通,故:(V)1.2 在如图1.5所示的各个电路中,已知输入电压V,二极管的正向压降可忽略不计,试分别画出各电路的输入电压u i和输出电压u o的波形.分析在u i和5V电源作用下,分析出在哪个时间段内二极管正向导通,哪个时间段内二极管反向截止。
在忽略正向压降的情况下,正向导通时可视为短路,截止时可视为开路,由此可画出各电路的输入、输出电压的波形。
图1。
5 习题1.2的图解对图1。
5(a)所示电路,输出电压u o为:u i≥5V时二极管VD承受正向电压导通,U D=0,u o=5V;u i〈5V时二极管VD承受反向电压截止,电阻R中无电流,u R=0,u o=u i。
输入电压u i和输出电压u o的波形如图1.6(a)所示。
图1。
6 习题1.2解答用图对图1。
5(b)所示电路,输出电压u o为:u i≥5V时二极管VD承受正向电压导通,U D=0,u o= u i;u i〈5V时二极管VD承受反向电压截止,电阻R中无电流,u R=0,u o=5V。
输入电压u i和输出电压u o的波形如图1。
6(b)所示。
对图1。
5(c)所示电路,输出电压u o为:u i≥5V时二极管VD承受反向电压截止,电阻R中无电流,u R=0,u o= u i;u i〈5V时二极管VD承受正向电压导通,U D=0,u o=5V。
第1章 电路及其分析方法习题与解答

题 1-23 图 B.12V C.2.25V B 基本题 1-24 电路如题 1-24a 和 b 图所示,试计算 a、b 两端的电阻 A.6
0V
(a) 题 1-24 图
(b)
解:图( a ) Rab = 2 + 16 //(12 // 12 + 10) = 10Ω,图(b) Rab = 6 // 6 + 6 // 6 + 12 // 0 = 6Ω 1-25 求题 1-25a 和 b 图所示电路中的电压 U、电流 I。
题 1-38 图
解: (a)原图标 a,b (b) 求 U0 的图 (c)求 R0 的图 (d)等效回路 由图(b):∵I2=I1+2,(4+4)I1+(3+6)I2=0∴I1=-18/13(A), I2=8/13(A) U0 =4 I1+3I2=4×(-8/13)+3×8/13=-8/13(V) 由图(c):R0 =(4+6)//(4+3)=70/17(Ω) 由图(d):I=(4+U0)/( R0 +4)=(4-8/13)/( 70/17 +4)=374/897(A)
叠加原理:
代值,有
⎧ I1 + I 2 + I 3 = 0 ⎪ ⎨5I 2 + 110 = 10 I1 + 110 ⎪10 I = 15 I + 110 3 ⎩ 1
第1章
电路及其分析方法习题解答
7
原电路
()E1 单独作用
' 1
(b) E2 单独作用
' ⎧ KCL对上面结点,有:I + I 2 + I 3' = 0 ⎪ ' ' 对(a)图: ⎨ KVL对左边回路,有:I 2 R2 + E1 = I1 R1 ⎪ ' ' ⎩ KVL对右边回路,有:I1 R1 = I 3 R3 + E1 ' ' = −6( A),I 3 = −2( A) ∴ I1' = 8( A),I 2
《电子电路基础》习题解答第1章

第一章习题解答题1.1 电路如题图1.1所示,试判断图中二极管是导通还是截止,并求出AO两端的电压UAO。
设二极管是理想的。
解:分析:二极管在外加正偏电压时是导通,外加反偏电压时截止。
正偏时硅管的导通压降为0.6~0.8V 。
锗管的导通压降为0.2~0.3V 。
理想情况分析时正向导通压降为零,相当于短路;反偏时由于反向电流很小,理想情况下认为截止电阻无穷大,相当于开路。
分析二极管在电路中的工作状态的基本方法为“开路法”,即:先假设二极管所在支路断开,然后计算二极管的阳极(P 端)与阴极(N 端)的电位差。
若该电位差大于二极管的导通压降,该二极管处于正偏而导通,其二端的电压为二极管的导通压降;如果该电位差小于导通压降,该二极管处于反偏而截止。
如果电路中存在两个以上的二极管,由于每个二极管的开路时的电位差不等,以正向电压较大者优先导通,其二端电压为二极管导通压降,然后再用上述“开路法”法判断其余二极管的工作状态。
一般情况下,对于电路中有多个二极管的工作状态判断为:对于阴极(N 端)连在一起的电路,只有阳极(P 端)电位最高的处于导通状态;对于阳极(P 端)连在一起的二极管,只有阴极(N 端)电位最低的可能导通。
图(a )中,当假设二极管的VD 开路时,其阳极(P 端)电位P U 为-6V ,阴极(N 端)电位N U 为-12V 。
VD 处于正偏而导通,实际压降为二极管的导通压降。
理想情况为零,相当于短路。
所以V U AO 6-=;图(b )中,断开VD 时,阳极电位V U P 15-=,阴极的电位V U N 12-=, ∵ N PUU < ∴ VD 处于反偏而截止∴ VU AO 12-=; 图(c ),断开VD1,VD2时∵ V U P 01= V U N 121-= 11N P U U > V U P 152-= V U N 122-= 22N P U U<∴ VD1处于正偏导通,VD2处于反偏而截止V U AO 0=;或,∵ VD1,VD2的阴极连在一起∴ 阳极电位高的VD1就先导通,则A 点的电位V U AO 0=,而 A N P U UV U =<-=2215∴ VD2处于反偏而截止 图(d ),断开VD1、VD2,∵ V U P 121-= V U N 01= 11N P U U < V U P 122-= VU N 62-= 22N P U U <;∴ VD1、VD2均处于反偏而截止。
第一章 误差分析与误差的传播习题及解答

四、解答题 1. 设 x>0,x*的相对误差为 δ,求 f(x)=ln x 的误差限。
解:求 lnx 的误差极限就是求 f(x)=lnx 的误差限,由公式有
已知 x*的相对误差 满足
,而
,故
即
2. 下列各数
都是经过四舍五入得到的近似值,试指出它们有几
位有效数字,并给出其误差限与相对误差限。 解:直接根据定义和式(1.2.2)(1.2.3)则得
第一章 误差分析与误差的传播
一、判断题: 1.舍入误差是模型准确值与用数值方法求得的准确值产生的误差。 ( )
x2 2. 用 1- 2 近似表示 cosx 产生舍入误差。
( )
3. 任给实数 a 及向量 x ,则 || ax || a || x ||。
()
二、填空题:
1.设
x*
2.40315 是真值
5. 计算下列矩阵的范数:
1)
,求
2)
,求
3)
,求
解:1)
2)
3)
1 0 1
6.
求矩阵
A
0
1
0
的谱半径.
2 0 2
1 0 1
解 I A 0 1 0 1 3
4分
2 0 2
矩阵 A 的特征值为 1 0, 2 1, 3 3
8分
所以谱半径 A max0,1,3 3
7. 证明向量 X 的范数满足不等式
和
。( 2.7183 和 8.0000)
12. 、
,则 A 的谱半径
=
,A 的
=
( 11.计算
)
取
,利用( )式计算误差最小。
四个选项:
解:
三、选择题
固体物理第一二章习题解答讲解学习
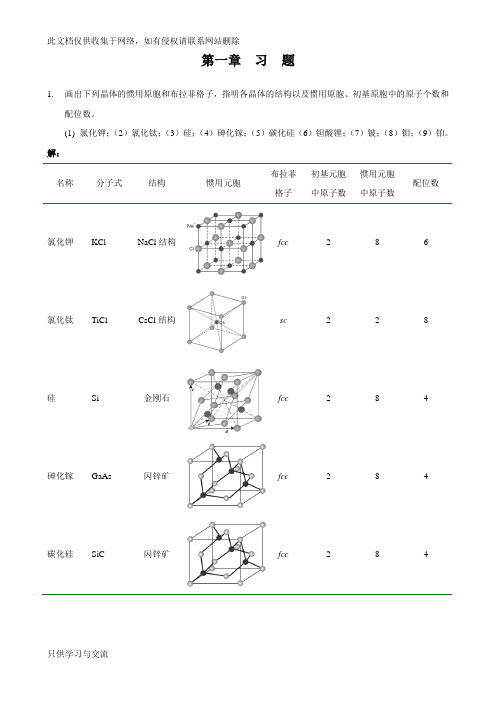
第一章习题1.画出下列晶体的惯用原胞和布拉菲格子,指明各晶体的结构以及惯用原胞、初基原胞中的原子个数和配位数。
(1)氯化钾;(2)氯化钛;(3)硅;(4)砷化镓;(5)碳化硅(6)钽酸锂;(7)铍;(8)钼;(9)铂。
解:名称分子式结构惯用元胞布拉菲格子初基元胞中原子数惯用元胞中原子数配位数氯化钾KCl NaCl结构fcc 2 8 6 氯化钛TiCl CsCl结构sc 2 2 8 硅Si 金刚石fcc 2 8 4 砷化镓GaAs 闪锌矿fcc 2 8 4 碳化硅SiC 闪锌矿fcc 2 8 4钽酸锂LiTaO 3钙钛矿sc552、6、12O 、Ta 、Li铍Behcp简单六角2612钼 Mo bccbcc 1 2 8铂 Pt fccfcc 1 4 122. 试证明:理想六角密堆积结构的128 1.6333c a ⎛⎫== ⎪⎝⎭。
如果实际的ca值比这个数值大得多,可以把晶体视为由原子密排平面所组成,这些面是疏松堆垛的。
证明:如右图所示,六角层内最近邻原子间距为a ,而相邻两层的最近邻原子间距为:212243⎪⎪⎭⎫ ⎝⎛+=c a d 。
当d =a 时构成理想密堆积结构,此时有:212243⎪⎪⎭⎫ ⎝⎛+=c a a ,由此解出:633.13821=⎪⎭⎫⎝⎛=a c 。
若633.1>ac时,则表示原子平面的层间距较理想结构的层间距大, 因此层间堆积不够紧密。
3. 画出立方晶系中的下列晶向和晶面:[101]、[110]、[112]、[121]、(110)、(211)、(111)、(112)。
解:4. 考虑指数为(100)和(001)的面,其晶格属于面心立方,且指数指的是立方惯用原胞。
若采用初基原胞基矢坐标系为轴,这些面的指数是多少?解:如右图所示:在立方惯用原胞中的(100)晶面,在初基原胞基矢坐标系中,在1a 、2a 、3a 三个基矢坐标上的截距为()2,,2∞,则晶面指数为(101)。
电子科技大学-数值分析答案-钟尔杰

| x n +1 − 7 |=
而xn具有n位有效数,故
所以
| x n +1 − 7 |≤
由此得xn+1的误差限
1 2 7
| x n − 7 |2 ≤
1 × × 10 2− 2 n 2 7 4
1
| x n +1 − 7 |≤
1 × 10 1− 2 n 2
故,xn+1是 7 的具有 2n位有效数字的近似值。 三、问题 1.假定 a0,b0是非负实数且a0≠b0,按如下递推公式
∑ [ai ∑ b j ]
i =1 j =1
n,仍为( n + 2 ) ( n – 1) / 2。 ,算法输出 11 试构造一个算法,对输入的数据 x0,x1,x2,……,xn,以及x(均为实数) 为 ( x –x0) ( x –x1) ( x –x2)……( x –xn) 的计算结果。 解 算法如下: 第一步:输入x;x0,x1,x2,……,xn,M Å (x – x0 );k Å 0; 第二步:M Å M×(x – x0 );k Å k+1; 第三步:判断,若 k ≤ n,则转第二步;否则输出 M,结束。 12 利用级数公式
4
π 1 dx = arctan 1 = 可以计算出无理数π 的值。将定积分表示为积分和 2 4 1+ x
R
H
∫
1
0
xn dx ( n = 1,2,…,20) 的递推 5+ x
关系,并研究递推算法的数值稳定性。 6.计算两个多项式Pn(x)和Qm(x)的乘积多项式Tn+m(x)的方法称为向量的卷积方法。设
第一章 习题解答与问题
一、习题解答 1 设 x>0,x 的相对误差限为 δ,求 ln x 的误差。 解:设 x的准确值为x*,则有 ( | x – x* | /|x*| ) ≤ δ 所以 e(ln x)=| ln x – ln x* | =| x – x* | ×| (ln x)’|x=ξ·≈ ( | x – x* | / | x*| ) ≤ δ 另解: e(ln x)=| ln x – ln x* | =| ln (x / x*) | = | ln (( x – x* + x*)/ x*) | = | ln (( x – x* )/ x* + 1) |≤( | x – x* | /|x*| ) ≤ δ 2 设 x = – 2.18 和 y = 2.1200 都是由准确值经四舍五入而得到的近似值。求绝对误差限 ε( x ) 和 ε( y ) 。 解:| e(x) | = |e(– 2.18)|≤ 0.005,| e(y) | = |e( 2.1200)|≤ 0.00005,所以 ε( x )=0.005, ε( y ) = 0.00005。 3 下近似值的绝对误差限都是 0.005,问各近似值有几位有效数字 x1=1.38,x2= –0.0312,x3= 0.00086 解:根据有效数字定义,绝对误差限不超过末位数半个单位。由题设知,x1,x2, x3有效 数末位数均为小数点后第二位。故x1具有三位有效数字,x2具有一位有效数字,x3具有零位 有效数字。 4 已知近似数 x 有两位有效数字,试求其相对误差限。 解:| er(x) | ≤ 5 × 10– 2 。 5 设 y0 = 28,按递推公式 yn = yn-1 –
心里统计课后习题1-6章习题解答

统计学参考答案第01章习题解答1. 随机变量:某一变量在实验、调查和观测之前,不能预知其数值的变量。
随机变量的特点是:离散性、变异性、规律性。
总体(population)又叫“母体”,是指具有某一种特征的一类事物的全体。
个体亦称“单位”、“样品”,统计学术语,统计学术语指总体中的每一个单位、样品或成员。
是统计调查、试验或观测的最基本对象,是构成样本、总体的最小单元。
在心理学研究中,个体根据研究目的的不同,可以是人,也可以是人在某种实验条件下的某个反应,或每个实验结果、每个数据。
在总体中按照一定的规则抽取的部分个体,称为总体的一个样本(sample)。
根据样本容量(通常以30为界线)的大小,可区分为大样本和小样本。
根据两样本来自的两总体是相关还是独立,可分为相关样本和独立样本。
次数:某一随机事件在某一类别中出现的数据多少,亦称频数(frequency)。
频率:某一事件发生的次数与总事件的比率。
概率(probability):某随机事件在某一总体中出现的比率。
表示样本的数字特征的量叫统计量。
如描述数据集中趋势的一些统计指标称为平均数;描述一组数据离散程度的统计指标称为标准差。
表示总体的数字特征的量叫参数。
如反应总体集中情况的统计指标称为总体平均数;反应总体离散程度的统计指标称为标准差。
观测值(observation):实验、调查和观测某些个体在某一变量上的具体的数值,即为观测值。
2. 何谓心理与教育统计学?学习它有何意义?心理与教育统计学是专门研究如何搜集、整理、分析在心理教育方面由实验和调查所获得的数据资料,并如何根据这些数字所传递的信息,进行科学推论找出客观规律的一门学科。
它是应用数理统计学的一个分支,是心理与教育研究中的科学工具。
意义:(1)研究心理与教育现象变化的统计规律;(2)为心理与教育研究提供科学的依据;(3)促进量化研究的发展……3.选用统计方法有哪几个步骤?(1)实验或调查设计是否合理,即所获得的数据是否适合用统计方法去处理,正确将其数量化是应用统计方法的起步,如果对数量化的过程及其意义没有了解,将一些不着边际的数据加以统计处理是毫无意义的;(2)要分析实验或调查数据的类型,不同数据类型所使用的统计方法有很大差别,针对不同的数据类型选用与之相应的统计方法至关重要;(3)要分析数据的分布规律,看数据是正态分布还是非正态分布,方差是否已知,以及是大样本数据还是小样本数据。
数值分析第四版课后习题答案

第一章习题解答1、 在下列各对数中,x 是精确值 a 的近似值。
3.14,7/100)4(143.0,7/1)2(0031.0,1000/)3(1.3,)1(========x a x a x a x a ππ试估计x 的绝对误差和相对误差。
解:(1)0132.00416.01.3≈=≈−=−=aee x a e r π (2)0011.00143.0143.07/1≈=≈−=−=a ee x a e r (3)0127.000004.00031.01000/≈=≈−=−=aee x a e r π (4)001.00143.03.147/100≈=≈−=−=aee x a e r2、已知四个数:001.0,25.134,0250.0,3.264321====x x x x 。
试估计各近似数的有效位数和误差限,并估计运算3211x x x =μ和1431/x x x =μ的相对误差限。
解:21111121101901.0,1021,3,10263.06.23−−⨯≈=⨯==⨯==x x x x n x r δδδ22214212102.0,1021,3,10250.00250.0−−−⨯≈=⨯==⨯==x x x x n x r δδδ 43332333103724.0,1021,5,1013425.025.134−−⨯≈=⨯==⨯==x x x x n x r δδδ 5.0,1021,1,101.0001.04443424==⨯==⨯==−−x x x x n x r δδδ 由相对误差限公式:i r ini n in ni i ir x x fx x f x x x f x x f u δδδ∂∂=∂∂=∑∑==1111),,(),,()(所以有:232123113211103938.0)(1)(−⨯≈++=x x x x x x x x x r δδδμμδ4971.0)(1)(4133141214311≈++−=x x x x x x x x x x r δδδμμδ 3、设精确数a>0,x 是a的近似值,x 的相对误差限是0.2,求㏑x 的相对误差限。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章质点运动学习题解答1-1质点作曲线运动,在时刻质点的位矢为,速度为,速率为,在至时间内的位移为, 路程为, 位矢大小的变化量为( 或称),平均速度为,平均速率为.(1) 根据上述情况,则必有( B )习题1-1图(A)(B) ,当时有(C) ,当时有(D) ,当时有(2) 根据上述情况,则必有( C )(A) ,(B) ,(C) ,(D) ,1-2一运动质点在某瞬时位于位矢的端点处,对其速度的大小有四种意见,即(1);(2);(3);(4).下述判断正确的是( D )(A) 只有(1)(2)正确(B) 只有(2)正确(C) 只有(2)(3)正确(D) 只有(3)(4)正确1-3质点作曲线运动,表示位置矢量,表示速度,表示加速度,表示路程,表示切向加速度.对下列表达式,即(1);(2) ;(3) ;(4) 。
下述判断正确的是( D )(A) 只有(1)、(2)是对的(B) 只有(3)、(4)是对的(C) 只有(2)是对的(D) 只有(3)是对的1-4一个质点在做圆周运动时,则有( B )(A) 切向加速度一定改变,法向加速度也改变 (B) 切向加速度可能不变,法向加速度一定改变 (C) 切向加速度可能不变,法向加速度不变 (D) 切向加速度一定改变,法向加速度不变 1-5 一质点沿轴运动,其坐标与时间的关系为,则该质点速度方向沿轴正向的时间区间为( A )。
(A) (B) (C) (D)1-6 质点的运动方程为,则质点在秒时到原点的距离为m ,速度矢量为m/s 。
1-7 一质点做半径为、周期为的匀速率圆周运动,试问经过四分之一周期的时间间隔内,质点所发生的位移的大小是( ),走过的路程是( )。
1-8 已知质点以初速度、加速度作直线运动(),则速度与时间的关系式为()。
1-9 一质点沿半径米的圆周运动,其所走路程与时间的关系为,则在秒时速率为(),切向加速度的值为()。
1-10 飞机驾驶员想往正北方向航行,而风以的速度由东向西刮来,如果飞机的航速(在静止空气中的速率),试问驾驶员应取什么航向?飞机相对于地面的速率为多少?试用矢量图说明。
解:设下标A 指飞机,F 指空气,E 指地面。
由题可知:v FE =60 km/h 正西方向。
v AF =180 km/h 方向未知v AE 大小未知, 正北方向 由相对速度关系有:FE AF AE υυυϖϖϖ+=AE υϖ、AF υϖ、FE υϖ构成直角三角形,可得:习题1-11图00410 20 2 6()()h km FE AF AE /17022=-=υυυϖϖϖ;()014.19==-AE FE tg υυθ1-11 如图,一人用绳拉一辆位于高出地面的平台上的小车在水平地面上奔跑,已知人的速度u 为恒量,绳端与小车的高度差为h 。
设人在滑轮正下方时开始计时,求t 时刻小车的速度和加速度。
分析:根据图可知绳的变化与人运动的时间有关。
在任何时刻t,绳、人距离墙的距离和高度h 满足:2222l t u h =+由于绳长对时间一阶导数就是小车的速率,因此可对上式进行求导得到速度(速率),速度求导得到加速度。
解:由2222l t u h =+可求出()22ut h l +=。
上式对时间求一阶导数:()222ut h t u dtdl+==υ上式再求导:1-12 一质点沿轴方向作直线运动,其速度与时间的关系如习题图1-12所示.设时,.试根据已知的图,画出图以及图。
分析 根据加速度的定义可知,在直线运动中v -t 曲线的斜率为加速度的大小(图中AB 、CD 段斜率为定值,即匀变速直线运动;而线段BC 的斜率为0,加速度为零,即匀速直线运动).加速度为恒量,在a -t 图上是平行于t 轴的直线,由v -t 图中求出各段的斜率,即可作出a -t 图线.又由速度的定义可知,x -t 曲线的斜率为速度的大小.因此,匀速直线运动所对应的x -t 图应是一直线,而匀变速直线运动所对应的x –t 图为t 的二次曲线.根据各段时间内的运动方程x =x (t ),求出不同时刻t 的位置x ,采用描数据点的方法,可作出x -t 图.解 将曲线分为AB 、BC 、CD 三个过程,它们对应的加速度值分别为20 4 1 10 10 202 6AB CD 习题1-12图2s m 20-⋅=--=AB AB AB t t a v v (匀加速直线运动)0=BC a (匀速直线运动) 2s m 10-⋅-=--=CD CD CD t t a v v (匀减速直线运动)根据上述结果即可作出质点的a -t 图[图(B)].在匀变速直线运动中,有2021t t x x ++=v由此,可计算在0~2s和4~6s时间间隔内各时刻的位置分别为用描数据点的作图方法,由表中数据可作0~2s和4~6s时间内的x -t 图.在2~4s时间内, 质点是作1s m 20-⋅=v 的匀速直线运动, 其x -t 图是斜率k =20的一段直线[图(c)].1-13 一质点P 沿半径R =3.0m 的圆周作匀速率运动,运动一周所需时间为20.0s ,设t =0时,质点位于O 点。
按习题1-13(a )图中所示Oxy 坐标系,求(1) 质点P 在任意时刻的位矢;(2)5 s 时的速度和加速度。
分析 该题属于运动学的第一类问题,即已知运动方程r =r (t )求质点运动的一切信息(如位置矢量、位移、速度、加速度).在确定运动方程时,若取以点(0,3)为原点的O′x′y′坐标系,并采用参数方程x′=x′(t )和y′=y′(t )来表示圆周运动是比较方便的.然后,运用坐标变换x =x 0 +x ′和y =y 0 +y ′,将所得参数方程转换至Oxy 坐标系中,即得Oxy 坐标系中质点P 在任意时刻的位矢.采用对运动方程求导的方法可得速度和加速度.解 (1) 如图(B)所示,在O′x′y′坐标系中,因t Tθπ2=,则质点P 的参数方程为 t T R x π2sin =', t TR y π2cos -='坐标变换后,在O x y 坐标系中有t T R x x π2sin='=, R t TR y y y +-=+'=π2cos 0 则质点P 的位矢方程为习题1-13图j i r ⎪⎭⎫ ⎝⎛+-+=R t T R t T R π2cos π2sinj i )]π1.0(cos 1[3)π1.0(sin 3t t -+=(2) 5s时的速度和加速度分别为j j i r )s m π3.0(π2sin π2π2cos π2d d 1-⋅=+==t TT R t T T R t v 1-14 一质点在半径为R 的圆周上以恒定的速率运动,质点由位置A 运动到位置B,OA 和OB 所对的圆心角为Δθ。
(1)试证位置A 和B 之间的平均加速度为;(2) 当Δθ分别等于90°、30°、10°和1°时,平均加速度各为多少?并对结果加以讨论。
分析 瞬时加速度和平均加速度的物理含义不同,它们分别表示为td d v=a 和tΔΔv=a .在匀速率圆周运动中,它们的大小分别为R a n 2v =,t a ΔΔv = ,式中|Δv |可由图(B)中的几何关系得到,而Δt 可由转过的角度Δθ 求出.由计算结果能清楚地看到两者之间的关系,即瞬时加速度是平均加速度在Δt →0 时的极限值.解 (1) 由图(b)可看到Δv =v 2 -v 1 ,故θΔcos 2Δ212221v v v v -+=v)Δcos 1(2θ-=v而vv θR s t ΔΔΔ==所以θR θt a Δ)cos Δ1(2ΔΔ2v -==v (2) 将Δθ=90°,30°,10°,1°分别代入上式, 得R a 219003.0v ≈,R a 229886.0v ≈R a 239987.0v ≈,Ra 24000.1v ≈以上结果表明,当Δθ→0 时,匀速率圆周运动的平均加速度趋近于一极限值,该值即为法(a )(b )习题1-14图向加速度R2v .1-15 一质点在半径为0.10m 的圆周上运动,其角位置为,式中θ的单位为rad ,t的单位为s 。
(1) 求在t =2.0s 时质点的法向加速度和切向加速度。
(2) 当切向加速度的大小恰等于总加速度大小的一半时,θ值为多少? (3) t 为多少时,法向加速度和切向加速度的值相等?解:(1) 由题意,得则质点的切向加速度和法向加速度分别为则 t =2.0s 时,切向加速度和法向加速度分别为(2) 由题意知 由 ,可得将式(1)、(2) 代入上式得此时角位置为(3) 要使 ,且 ;可得到414424Rt Rt =,最后 2d 12d t t θω==d 24d t t ωα==(1)RtR a t 24==α(2)42144Rt R a n ==ω2240.1 2.0 4.8m s α-==⨯⨯=⋅t a R 22220.1(12 2.0)230.4m s ω-==⨯⨯=⋅n a R 222n t ta a a a +==22nt a a =3324 3.15rad t θ=+=3213=t Rt R a t 24==αn t a a =42144Rt R a n ==ω0.55st =。
