2016希望杯复赛四年级试题答案解析
4四年级希望杯答案及过程

四年级希望杯1、计算:19×75+23×25=【答案】2000【考点】四则运算【解析】原式=1425+575=20002、定义新运算:a△b=(a+b)×b,a□b=a×b+b,如:1△4=(1+4)×4,1□4=1×4+4按从左到右的顺序计算:1△2□3=【答案】21【考点】定义新运算【解析】1△2=(1+2)×3=6,6□3=6×3+3=213、abc是三位数,若a是奇数,且abc是3的倍数,则abc最小是【答案】111【考点】数论【解析】a为奇数,且要求最小,则a=1,b=0又要求为3的倍数,则a+b+c为3的倍数,所以c=24、三个连续的自然数的乘积是120,它们的和是【答案】15【考点】分解质因数【解析】120=2×2×2×3×5=4×5×6,则他们三个数的和为155、已知x,y是大于0的自然数,且x+y=150。
若x是3的倍数,y是5的倍数,则(x,y)的不同取值有对【答案】9【考点】数论【方法】由题意得,x,y为3和5的公倍数才符合要求,公倍数有15、30、45、60、75、90、105、120、135则共有9对不同取值6、如果8×(2+1÷x)=18,则x=【答案】4【考点】解方程【解析】等式两边分别除以8,得2+1÷x=2.25,再等式两边分别减去2得1÷x=0.25,则x=47、观察以下的一列数:11,17,23,29,35,……若从第n个数开始,每个数都大于2017,则n=【答案】336【考点】等差数列【解析】等差数列中,项数=(末项-首项)÷公差+1,则n最小为(2017-11)÷6+1,则n=3368、图1由20个方格组成,其中含有A的正方形有个【答案】13【考点】图形计算【解析】含有A的正方形边长为1的有1个,边长为2的有4个,边长为3的有6个,边长为4的有2个,共有1+4+6+2=13个9、图2由12个面积为1的方格组成,则图中和阴影梯形面积相同的长方形有个【答案】10【考点】图形计算【过程】由题意可知阴影部分面积为3,则面积为3的长方形竖着排列有4个,横着排列有6个,则面积为3的长方形共有4+6=10个10、某学习小组数学成绩的统计图如图3,该小组的平均成绩是分【答案】90【考点】平均数问题【解析】平均成绩为(6×85+3×89+5×95+1×98)÷(6+3+5+1)=9011、今年,小军5岁,爸爸31岁,再过年,爸爸的年龄是小军的3倍【答案】8【考点】年龄问题【解析】年龄差为31-5=26(岁),且年龄差不变,当爸爸年龄是小军年龄的3倍时,则差了2倍,则小军的年龄为26÷2=13岁,则13-5=8岁12、10个连续的自然数从大到小排列,若最后6个数的和比钱4个数的和的2倍大15,则这10个数中最小的数是【答案】6【考点】数论【解析】由题意,我们只知道这10个数是连续的,那我们可以用符号来表示最小的数字(如△),那么其它的9个数字就是△+1,△+2,△+3,……,△+913、如图4,把一个边长是5cm的正方形纸片沿虚线分为5个长方形,然后按照箭头标记的方向和长度移动其中的4个长方形,则所得图形的周长是 cm【答案】40【考点】巧算周长【解析】按照要求平移后周长增加了,增加的部分为每两层中间相隔的部分,从上往下第一层与第二层之间分别增加2+2=4,第二层与第三层之间分别增加2+1=3,第三层与第四层之间分别增加1+1=2,第四层与第五层之间分别增加1+0=1,则平移后不规则图形周长为4×5+4×2+3×2+2×2+1×2=4014、在一个长方形内画3个圆,这个长方形最多可被分为部分【答案】15【考点】图形计数【解析】想要分成的部分最多,则要求三个圆分别相交且和长方形的四条边分别相切,则共分成15部分15、2017年3月19日是星期日,据此推算,2017年9月1日是星期【答案】五【考点】周期问题【解析】3月19号到9月1号共12+30+31+30+31+31+1=166天,166÷6=23……5,则9曰1号为星期五16、观察7=5×1+2,12=5×2+2,17=5×3+2,这里,7,12,17被叫做“3个相邻的被5除余2的数”,若有3个相邻的被5除余2的数的和等于336,则其中最小的数是【答案】107【考点】数论【方法】由题意知,336÷5=67……1,因为3个连续被5除余2的数,则这三个数中共有67-1=66个5,又知3个数为连续数,则分别有21、22、23个5,所以最小的数为21×+2=10717、甲,乙,两人分别从A,B两地同时出发,相向而行,甲到达A,B中点C时,乙距C 点还有240米,乙到达C点时,甲已经超过C点360米,则两人在D点相遇时,CD的距离是米【答案】144【方法】行程问题【解析】由题意知相同时间内,乙走240米,甲走360米,即乙跑2米,甲跑3米。
四年级希望杯奥数试卷【含答案】

四年级希望杯奥数试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 下列哪个数字是偶数?A. 3B. 4C. 5D. 62. 一个正方形的四条边长相等,那么它的周长是?A. 边长的两倍B. 边长的三倍C. 边长的四倍D. 边长的五倍3. 下列哪个数字是质数?A. 12B. 17C. 20D. 214. 1千米等于多少米?A. 100米B. 1000米C. 10,000米D. 100,000米5. 下列哪个图形是三维图形?A. 正方形B. 圆形C. 立方体D. 三角形二、判断题(每题1分,共5分)1. 1+1=3 ()2. 长方形是一种特殊的正方形。
()3. 0是最小的自然数。
()4. 圆的周长等于直径的两倍。
()5. 任何数乘以0都等于0。
()三、填空题(每题1分,共5分)1. 1+2+3+4+5=_____2. 一个长方形的长是10厘米,宽是5厘米,那么它的面积是____平方厘米。
3. 100的因数有____个。
4. 9是____的倍数。
5. 一个正方体的体积是27立方厘米,那么它的边长是____厘米。
四、简答题(每题2分,共10分)1. 请列举出前五个质数。
2. 请解释什么是因数和倍数。
3. 请简述平行四边形的特征。
4. 请解释什么是周长和面积。
5. 请列举出三种不同的三维图形。
五、应用题(每题2分,共10分)1. 一个长方形的长是8厘米,宽是4厘米,求它的周长和面积。
2. 一个数加上20后等于30,这个数是多少?3. 一个正方形的周长是24厘米,求它的边长。
4. 两个数相乘等于18,这两个数可能是什么?5. 一个立方体的体积是64立方厘米,求它的边长。
六、分析题(每题5分,共10分)1. 小明有10个苹果,他吃了一些后,还剩下6个苹果。
请问他吃了多少个苹果?2. 一个长方形的长是10厘米,宽是5厘米,求它的对角线长度。
七、实践操作题(每题5分,共10分)1. 请用纸和剪刀制作一个正方形。
小学四年级希望杯历年数学竞赛试题与答案1-14届(最新全套完整版)
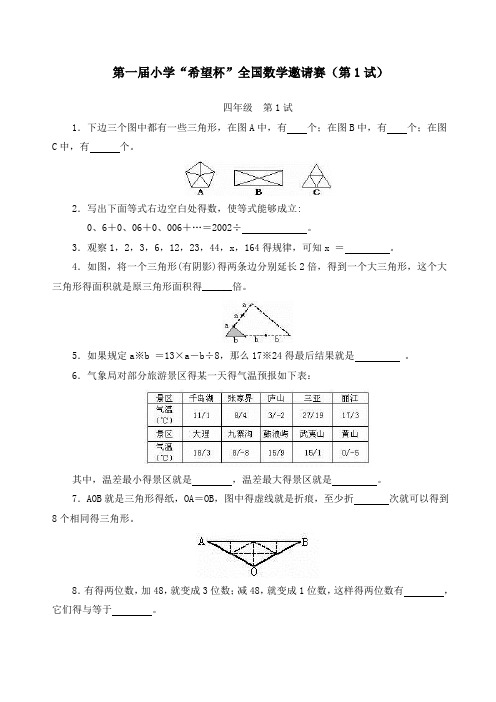
第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处得数,使等式能够成立:0、6+0、06+0、006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164得规律,可知x =。
4.如图,将一个三角形(有阴影)得两条边分别延长2倍,得到一个大三角形,这个大三角形得面积就是原三角形面积得______倍。
5.如果规定a※b =13×a-b÷8,那么17※24得最后结果就是。
6.气象局对部分旅游景区得某一天得气温预报如下表:其中,温差最小得景区就是,温差最大得景区就是。
7.AOB就是三角形得纸,OA=OB,图中得虚线就是折痕,至少折次就可以得到8个相同得三角形。
8.有得两位数,加48,就变成3位数;减48,就变成1位数,这样得两位数有,它们得与等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组得书一样多,得到拥护,于就是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组得书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002与 b=20022003×2003中,较大得数就是,它比较小得数大。
12.小明得家离学校2千米,小光得家离学校3千米,小明与小光得家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人得话只有一句就是真话。
会开车得就是。
14.为了支援西部,1班班长小明与2班班长小光带了同样多得钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
【通用】全国四年级希望杯数学竞赛全部试题与答案
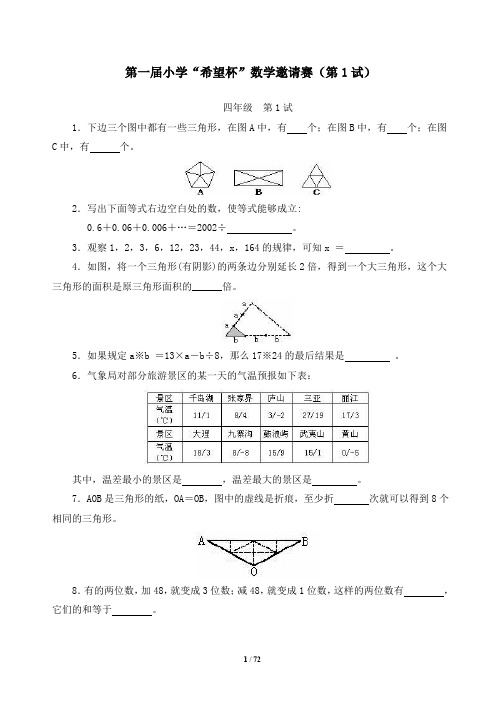
第一届小学“希望杯”数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
四年级希望杯奥数试卷【含答案】

四年级希望杯奥数试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 下列哪个数字是偶数?A. 3B. 4C. 5D. 62. 一个正方形的四条边长相等,那么它的周长是?A. 边长的两倍B. 边长的三倍C. 边长的四倍D. 边长的五倍3. 下列哪个数字是质数?A. 12B. 13C. 15D. 184. 一个长方形的长是10厘米,宽是5厘米,那么它的面积是?A. 50平方厘米B. 60平方厘米C. 70平方厘米D. 80平方厘米5. 下列哪个数字是最大的两位数?A. 90B. 91C. 92D. 93二、判断题(每题1分,共5分)1. 1+1=3 ()2. 9乘以9等于81 ()3. 2加2等于4 ()4. 10减去5等于7 ()5. 8除以2等于4 ()三、填空题(每题1分,共5分)1. 5加5等于______。
2. 20减去10等于______。
3. 6乘以6等于______。
4. 49除以7等于______。
5. 100减去25等于______。
四、简答题(每题2分,共10分)1. 请写出5个两位数。
2. 请写出5个三位数。
3. 请写出5个两位数的和。
4. 请写出5个两位数的差。
5. 请写出5个两位数的积。
五、应用题(每题2分,共10分)1. 小明有10个苹果,他吃掉了3个,还剩下几个苹果?2. 小红有20个糖果,她给了小华5个糖果,还剩下几个糖果?3. 一个长方形的长是8厘米,宽是4厘米,求这个长方形的面积。
4. 一个正方形的边长是6厘米,求这个正方形的周长。
5. 两个数的和是15,其中一个数是7,另一个数是多少?六、分析题(每题5分,共10分)1. 请用两种方法计算24加36的和。
2. 请用两种方法计算56减去28的差。
七、实践操作题(每题5分,共10分)1. 请用纸和剪刀剪出一个正方形,边长为10厘米,然后计算这个正方形的面积。
2. 请用纸和剪刀剪出一个长方形,长为12厘米,宽为8厘米,然后计算这个长方形的周长。
第十四届小学四年级“希望杯”全国数学邀请赛试题及答案

第十四届小学“希望杯”全国数学邀请赛四年级第1试试题2016年3月20日上午8:30至10:00以下每题6分,共120分。
1、计算:25×259÷(37÷8)= .2、若9个连续偶数的和是2016,则这些数中,最小的是.3、有110张相同得长方形纸片,长比宽多10厘米,将这些纸片如图1无重合摆放,可以摆成长是2750厘米的长方形,将这些纸片如图2无重合摆放,可以摆成长是厘米的长方形。
4、甲、乙、丙3人一起购买学习用品,已知甲和乙共支付了67元,乙和丙共支付了64元,甲和丙共支付了63元,那么,甲支付了元。
5、图3由5×4个边长为1的小正方形组成,其中阴影部分的面积是。
6、一个工厂电表的示数是52222千瓦,若干天后,电表的示数(五位数)又出现4个相同的数码,那么该工厂在这些天内至少又用了千瓦的电.7、已知碳素笔每支1元8角,笔记本每个3元5角,文具盒每个4元2角,晶晶买这三种文具刚好用了20元,则她买了个笔记本。
8、一个除法算式,若被除数比除数大2016,商是15,余数是0,则被除数是。
9、若一个长方形的长减少3厘米、宽增加2厘米,得到一个和原长方形面积相等的正方形,则长方形的周长是厘米。
10、已知a,b,c都是质数,若a×b+b×c=119,则a+b+c= .11、王华每星期二、六学书法,已知2016年的元旦是星期五,那么在2016年8月,王华学书法的天数是。
12、一个四位数A,将四位数的各位上的数字(均不为0)重新排列得到的最大数比A大7668,得到的最小数比A小594,则A= 。
a2016能被12整除,则这样的六位数有个。
13、若六位数b14、3堆桃子的个数分别是93,70,63,一只猴子在3堆桃子间搬运,已知猴子每次最多可以搬5个桃子,并且在从一堆搬到另一堆的途中会吃掉1个,当3堆桃子个数相等时,猴子至少吃掉了个桃子。
15、在1到100这100个数中,被2,3,5除都有非零的余数,且余数彼此不等的数有个。
小学四年级希望杯历年数学竞赛试题与答案1-14届(最新全套完整版)

第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
2016希望杯复赛四年级试题答案解析

2016年第14届四年级希望杯复赛解析一、填空题(每小题5分,共60分)1、计算:2016×2014-2013×2015+2012×2015-2013×2016=_______. 【答案】1【解析】()()11 2015 -120162012-20132015-2013-201420162016×2013-2015×2012+2015×2013-2014×2016=⨯⨯=⨯⨯=2、60的不同约数(1除外)的个数是_______.【答案】11【解析】60=1×60 =2×30 =3×20 =4×15 =5×12 =6×10.60的约数(1除外)有:2、3、4、5、6、10、12、15、20、30、60,共11个。
3、今年丹丹4岁,丹丹的爸爸28岁,a年后,爸爸的年龄是丹丹年龄的3倍,则a的值是_______.【答案】8【解析】年龄问题。
关键是年龄差不变。
年龄差为28 – 4=24(岁)当爸爸年龄是丹丹年龄的3倍时,两人的年龄差仍为24岁。
所以,a年后丹丹的年龄为24÷(3-1)=12(岁)a=12-4=8(年)4、已知a 比c 大2,则三位自然数abc 与 cba 的差是_______. 【答案】198【解析】abc -cba =1001010010a b c c b ++--a - ()100()a c a c =--- =2002-198=5、正方形A 的边长是10,若正方形B,C 的边长都是自然数,且B,C 的面积和等于A 的面积,则B 和C 的边长的和是_______. 【答案】14【解析】B,C 的面积和等于A 的面积,即B,C 的面积和是10×10=100,则b 2+c 2=100,且b ,c 皆为自然数,一试便知为6和8,B 和C 的边长的和是6+8=14.6、已知9个数的平均数是9,如果把其中一个数改为9后,这9个数的平均数变为8,那么这个被改动的数原来是_________. 【答案】18【解析】平均数=总和÷总个数平均数由9变为8,减少了9-8=1;总数减少了1×9=9;所以原来的数为9+9=18.7、如图I ,水平相邻和竖直相邻的两个格点间的距离都是1,则图中阴影部分的面积是_______. 【答案】17【解析】根据毕克定理,正方形格点图算面积: 面积=内部点+边界点÷2-1 内部点:8个边界点:20个所以面积:8+20÷2-1=178、两个数的和是363,用较大的数除以较小的数得商16余6,则这两个数中较大的是_______.【答案】342=根据和倍问题【解析】较大数减去6之后是较小数的16倍,且它们的和为3636-357的基本公式:较小数=和÷(倍数+1),较小数=357÷(16+1)=21,所以较大数:363-21=3429、如图2,阴影部分是一个边长为6厘米的正方形,在它的四周有四个长方形,若四个长方形的周长和是92厘米,则四个长方形的面积的和是__________平方厘米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年第14届四年级希望杯复赛解析
一、填空题(每小题5分,共60分)
1、计算:2016×2014-2013×2015+2012×2015-2013×2016=_______. 【答案】1
【解析】
()()
1
1 2015 -1
2016
2012
-
2013
2015
-
2013
-
2014
2016
2016
×
2013
-
2015
×
2012
+
2015
×
2013
-
2014
×
2016
=
⨯⨯
=
⨯⨯
=
2、60的不同约数(1除外)的个数是_______.
【答案】11
【解析】60=1×60 =2×30 =3×20 =4×15 =5×12 =6×10.
60的约数(1除外)有:2、3、4、5、6、10、12、15、20、30、60,共11个。
3、今年丹丹4岁,丹丹的爸爸28岁,a年后,爸爸的年龄是丹丹年龄的3倍,则a的值是_______.
【答案】8
【解析】年龄问题。
关键是年龄差不变。
年龄差为28 – 4=24(岁)
当爸爸年龄是丹丹年龄的3倍时,两人的年龄差仍为24岁。
所以,a年后丹丹的年龄为24÷(3-1)=12(岁)
a=12-4=8(年)
4、已知a 比c 大2,则三位自然数abc 与 cba 的差是_______.
【答案】198 【解析】abc -cba =1001010010a b c c b ++--a - ()100()a c a c =--- =2002-
198=
5、正方形A 的边长是10,若正方形B,C 的边长都是自然数,且B,C 的面积和等于A 的面积,则B 和C 的边长的和是_______.
【答案】14
【解析】B,C 的面积和等于A 的面积,即B,C 的面积和是10×10=100,则b 2+c 2=100,且b ,c 皆为自然数,一试便知为6和8,B 和C 的边长的和是6+8=14.
6、已知9个数的平均数是9,如果把其中一个数改为9后,这9个数的平均数变为8,那么这个被改动的数原来是_________.
【答案】18
【解析】平均数=总和÷总个数
平均数由9变为8,减少了9-8=1;总数减少了1×9=9;所以原来的数为9+9=18.
7、如图I ,水平相邻和竖直相邻的两个格点间的距离都是1,则图中阴影部分的面积是_______.
【答案】17
【解析】根据毕克定理,正方形格点图算面积:
面积=内部点+边界点÷2-1
内部点:8个
边界点:20个
所以面积:8+20÷2-1=17
8、两个数的和是363,用较大的数除以较小的数得商16余6,则这两个数中较大的是
_______.
【答案】342
=根据和倍问题【解析】较大数减去6之后是较小数的16倍,且它们的和为3636-357
的基本公式:较小数=和÷(倍数+1),较小数=357÷(16+1)=21,所以较大
数:363-21=342
9、如图2,阴影部分是一个边长为6厘米的正方形,在它的四周有四个长方形,若四个长方形的周长和是92厘米,则四个长方形的面积的和是__________
平方厘米。
【答案】132
【解析】四个长方形都有一条长为6厘米的边
所以四个长方形另外一条边的和为
92÷2-6×4=22(厘米)
把四个长方形拼在一起,根据面积不变
面积:6×22=132(平方厘米)
15a b 4x 12y
d c
10、有一根长240厘米的木棒,先从左端开始每隔7厘米划一条线,再从右端开始每隔6厘米划一条线,并且从划线处截断木棒,则所截得得小木棒中,长度是3厘米的木棒有_______根
【答案】12
【解析】240刚好能被6整除,所以“从右端开始每隔6厘米划一条线”等价于“从左端开始每隔6厘米划一条线”,6跟7的最小公倍数为42,所以每42厘米一个周期。
分析一个周期的截口长度:端点,6米,7厘米,12厘米,14厘米,18厘米,21厘米,24厘米,28厘米,30厘米,35厘米,36厘米,42厘米。
)
21-18=3(厘米),24-21=3(厘米)所以一个周期有2段3厘米的木棒。
240÷42=5(组)……30(厘米)
5组里面共有5×2=10(段)
余下的30厘米中,还有2段3厘米的。
故共有10+2=12段3厘米的木棒。
11、在图3的9个方格中,每行每列以及每条对角线上三个数的和都相等,则x +y +a +b +c +d=_______。
【答案】68
【解析】
根据15+4=12+y ,可以得出,y=15+4-12=7.
根据2y=4+a ,可以得出,2×7=4+a, a=10.
根据2×15=12+d,可以得出,d=2×15-12=18.
根据2x =a+d =10+18,可以得出x=14
幻和=15+4+14 =33,则c =33÷3 =11.
b=33-11-14=8.
所以,x+y+a+b+c+d=14+7+10+8+11+18 =68.
或11×9-15-4-12=68
12、甲、乙两人分别从A、B两地同时出发,相向而行,4小时可相遇;若两人的时速都增加3千米,则出发后3小时30分可相遇,A、B两地相距________千米。
【答案】168
【解析】方法一:比例法
3小时30分为3.5小时,原来和现在的时间比为4:3.5=8:7;路程不变,速度与时间成反比,速度比为7:8,两人的时速都增加3千米,速度和增加3×2=6千米,原来的速度和:6÷(8-7)×7=42(千米/时),路程为42×4=168(千米)
方法二:方程
不妨设原来的速度和为x千米/时
4x=3.5(x+3×2)
X=42
路程为42×4=168(千米)
二、解答题(每小题15分,共60分)(每题都要写出推算过程)
13、如图4,用正方形a,b,c,d,e拼成一个长30
厘米,宽是22厘米的长方形,求正方形e的面积。
【解析】
a+b=22
a+b+c=30
所以c=8厘米
2c+e=22
所以e=6厘米
所以正方形e的面积是:6×6=36(平方厘米)
14、有两块地,平均亩产粮食675千克,其中第一块地是5亩,亩产粮食705千克,如果第二块地亩产粮食650千克,那么,第二块地有多少亩?
【解析】第一块地总共比平均少:(705-675)×5=150(千克)
所以第二块地比平均多150千克
第二块地的亩数:150÷(675-650)=6(亩)
15、4个连续的自然数,从小到大依次是11的倍数、7的倍数、5的倍数、3的倍数,求这4个自然数的和的最小值。
【解析】方法一:设这4个连续的自然数为a、a+1、a+2、a+3.
根据题意,a+3是3的倍数,所以,a也是3的倍数,而a是11的倍数,则a是33的倍数。
又因为第三个数a+2是5的倍数,个位为0或者5,
则第一个数a的个位应该为3或者8.
又a是33的倍数,
a最小为33×1=33,后面的数为34、35、36,而34不是7的倍数,排除。
a可以为33×6=168,后面的数为169、170、171,而169不是7的倍数,排除。
a可以为33×11=363,后面的数为364、365、366,验证,符合。
所以,这4个自然数的和的最小值是363+364+365+366=1458.
方法二:设这4个自然数分别为11a、11a+1、11a+2、11a+3.
11a+1是7的倍数,那么11a÷7余6,则a÷7余5.
11a+2是5的倍数,那么11a÷5余3,则a÷5余3.
11a+3是3的倍数,那么11a÷3无余数,则a÷3无余数.
符合条件的a最小为5×7-2=33.则11a=11×33=363.
这4个自然数为363、364、365、366.
所以和的最小值363+364+365+366=1458.
16、有6个密封的盒子,分别装有红球、白球和黑球,每个盒子里只有一种颜色的球,且球的个数分别是15,16,18,19,20,31,已知黑球的个数是红球个数的两倍,装白球的盒子只有1个,问:
(1)装有15个球的盒子里装的是什么颜色的球?
(2)有多少个盒子里装的是黑球?
【解析】(1)所有球的个数:15+16+18+19+20+31=119(个)
黑球的个数是红球的2倍,黑球加红球的个数是红球的(2+1=3)倍
119÷3=39 (2)
根据余数的可加可减性,白球的个数除以3也是余2,白球的个数只能是20 黑球和红球共:119-20=99(个)
红球:99÷3=33(个)只能是15+18=33(个)
答:装有15个球的盒子里装的是红球。
(2)还剩下16,19,31的盒子里装的是黑球,即有3个盒子
答:有3个盒子里装的是黑球。
