同济大学钢结构基本原理第七章作业答案
钢结构基本基础原理课后习题集标准答案完全版

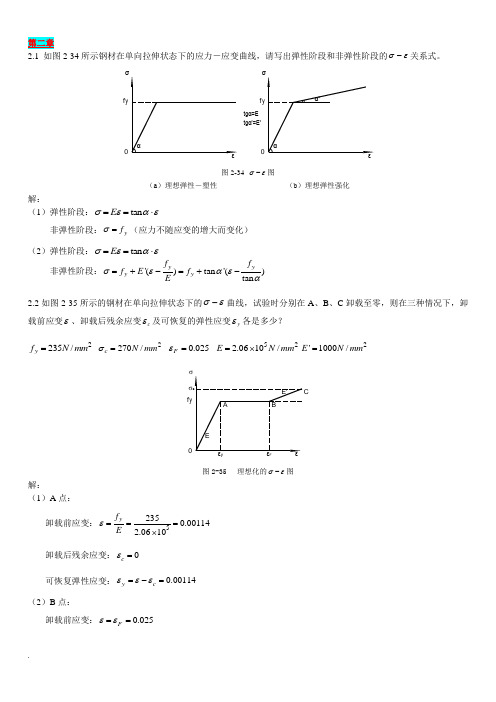
第二章2.1如图2-34所示钢材在单向拉伸状态下的应力一应变曲线,请写出弹性阶段和非弹性阶 段的 关系式。
解:(1)弹性阶段:E tan非弹性阶段: f y (应力不随应变的增大而变化) (2)弹性阶段:E tan f yf y 非弹性阶段:f y E'(」)f y tan '( ・) Etan(b )理想弹性强化图(2) B 点:卸载前应变: F 0.025卸载后残余应变:c0.02386E可恢复弹性应变:y c0.00114(3) C 点:c f y卸载前应变: F0.025 0.035 0.06E'卸载后残余应变:c c0.05869E可恢复弹性应变: yc0.001312.3试述钢材在单轴反复应力作用下,钢材的 曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材曲线与反复应力大小和作用时间关系:当构件反复力| | fy 时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材曲线基本无变化;当I I fy 时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连 续进行,钢2.2如图2-35所示的钢材在单向拉伸状态下的 曲线,试验时分别在 A 、 B 、C 卸载至零,则在三种情况下, 卸载前应变、卸载后残余应变c 及可恢复的弹性应变y 各是多少?2f y 235N/mm 22270 N / mm 2F0.025 E2.06 105N/mm 2 E' 1000N/mm 2解: (1)A 点:卸载前应变:f y E2350.001142.06 105卸载后残余应变:可恢复弹性应变:0.00114图图2-35 理想化的 C材曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢材曲线会相对更高而更短。
另外,载一定作用力下,作用时间越快,钢材强度会提高、而变形能力减弱,钢材曲线也会更高而更短。
同济大学钢结构基本原理课后习题答案完全版

第二章如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan yyy y f f f E f E σεαεα=+-=+-如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少? 2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610yf E ε===⨯卸载后残余应变:0c ε= 可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f E εε=-= 可恢复弹性应变:0.00114y c εεε=-=(3)C 点:卸载前应变:0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变:0.05869c c E σεε=-= 可恢复弹性应变:0.00131y c εεε=-=试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢结构基本原理(第二版)习题参考解答第七章

7.1 一压弯构件长15m ,两端在截面两主轴方向均为铰接,承受轴心压力1000N kN =,中央截面有集中力150F kN =。
构件三分点处有两个平面外支承点(图7-21)。
钢材强度设计值为2310/N mm 。
按所给荷载,试设计截面尺寸(按工字形截面考虑)。
解:选定截面如下图示:图1 工字形截面尺寸下面进行截面验算:(1)截面特性计算()23002026502021420540A mm =⨯⨯+-⨯⨯=339411300650286610 1.45101212x I mm =⨯⨯-⨯⨯=⨯ 63/325 4.4810x x W I mm ==⨯337411220300610149.01101212y I mm =⨯⨯⨯+⨯⨯=⨯ 53/150 6.0110y y W I mm ==⨯266.2x i mm ==66.2y i m m = (2)截面强度验算36226100010562.510172.3/310/20540 4.4810x M N N mm f N mm A W σ⨯⨯=+=+=<=⨯ 满足。
(3)弯矩作用平面内稳定验算 长细比1500056.3266.2x λ== 按b 类构件查附表4-4,56.368.2,查得0.761x ϕ=。
2257222.061020540' 1.20101.1 1.156.3EX x EA N N ππλ⨯⨯⨯===⨯⋅⨯ 弯矩作用平面内无端弯矩但有一个跨中集中荷载作用:371000101.00.2 1.00.20.981.2010 1.1mx EX N N β⨯=-⨯=-⨯=⨯⨯, 取截面塑性发展系数 1.05x γ= 363611000100.98562.5100.7612054010001010.8 1.05 4.481010.8' 1.2010mx x x x x EX M N A N W N βϕγ⨯⨯⨯+=+⨯⎛⎫⎛⎫⨯-⨯⨯⨯-⨯ ⎪ ⎪ ⎪⨯⎝⎭⎝⎭ 22189.54/310/N mm f N mm =<= ,满足。
钢结构基本原理课后习题答案完全版

2。
1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式.tgα'=E'f y 0f y 0tgα=E 图2—34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2。
2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσF图2—35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε==卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
同济大学钢结构基本原理课后习题答案完全

第二章如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan yyy y f f f E f E σεαεα=+-=+-如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少? 2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610yf E ε===⨯卸载后残余应变:0c ε= 可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f E εε=-= 可恢复弹性应变:0.00114y c εεε=-=(3)C 点:卸载前应变:0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变:0.05869c c E σεε=-= 可恢复弹性应变:0.00131y c εεε=-=试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
同济大学钢结构基本原理(沈祖炎)课后习题答案

同济大学钢结构基本原理(沈祖炎)课后习题答案完全版第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f 0f 0tgα=E 图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f 0σF图2-35 理想化的σε-图解:(1)A 点:卸载前应变:2350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
(完整版)钢结构基本原理课后习题与答案完全版
2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσ图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε==卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢结构基本原理课后习题集答案解析(第二版)

第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσF图2-35 理想化的σε-图解:(1)A 点: 卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=(2)B 点: 卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y2
fy
tx 0.65 0.35M 2 / M1
0.825
tx 0 . 6 5
37.5 0 .35 75
Mx N tx y Af d bWx f d
1150 103 0.825 75 106 1.0 0.723 18320 310 0.944 3340.2 103 310 0.280 0.063 0.343 1.0
V1 74.57 52.73kN 2cos 2cos 450 l 180 102.64 斜缀条长细比: i cos 450 2.48
一个斜缀条受力: N1 为 b 类截面,查表得 0.538 。 折减系数: 0
图 7-23
习题 7.4
答:查表求得 I63a 截面特性如下: 面积: A0
154.59cm2 ,b = 176mm
94004cm4 , i1 y 24.66cm ;
对强轴惯性矩及回转半径为: I1 y 对弱轴惯性矩及回转半径为: I1x L125 10 截面特性如下: 面积: A 24.373cm
2
0.965 0.300
2 2
4 ]
2
0.682
构件无横向荷载作用: βmx =0.65+0.35(M2/M1)=1
2 EA 2 2.06 105 18320 N Ex 7515.3kN x2 70.42
N x Af d
mx M xWx1 1 0.8
2
1702.4cm4 , i1x 3.32cm 。
回转半径(弱轴)为: iy 0
2.48cm 。
则整个截面的截面特性为:
A 154.59 2 309.18cm2
I x 2 1702.4 154.59 902 2507762.8cm4
2507762.8 25382.2cm3 17.6 90 2 2507762.8 W 27864cm3 对受压边截面模量: x1 90
max
N M h0 1150 103 75 106 230 83.43N / mm2 3 An Wnx h 18320 3340.2 10 250 N M h0 1150 103 75 106 230 42.12 N / mm2 3 An Wnx h 18320 3340.2 10 250
故中间段平面外稳定满足要求。 验算边段面外稳定: (由于两边段尺寸相同,下边段压力较大,故只 算下边段) 构件无横向荷载作用:
tx 0.65 0.35M 2 / M1
tx 0.65
Mx N tx y Af d bWx f d
1150 103 0.65 37.5 106 1.0 0.723 18320 310 0.944 3340.2 103 310 0.280 0.025 0.305 1.0
Wx
ix
Ix
A
2507762.8 90.06cm 309.18
x
lox
ix
2930 32.53 90.06
ox x2 27
A 309.18 32.532 27 35.07 Ax 2 24.373
为 b 类截面,查表得 x
0.918 。
' Ex
N Wx1 1 x ' N Ex 1.0M x 2500 103 0.918 30918 0.918 2500 27864 103 1 46472.33 f d 205
得: M x
N x A
mx M x
1 2
[0.965 0.300 2
2
0.965 0.300
2 2
4 ]
2
0.7463
构件无横向荷载作用:βmx =0.65+0.35(M2/M1)
mx 0.65 0.35
' Ex
80 0.4167 120
2 EA 2 2.06 105 10960 N 4047.84kN 1.1x2 70.742
3096.9kNm
2)平面外整体稳定验算:
平面外整体稳定验算,将转变为单肢在弯矩作用平面外的稳定计算。
(3)单肢稳定 取e
Mx N
90 e N; 180 90 e N 另一侧轴力为: N 2 N N1 180 l1x 180 54.2 单肢弯矩平面内长细比: 1x i1x 3.32
答: 结构 M 图, N 图如上图所示, 其内力为: Mmax=120kNm, N=800kN。 1. 截面性质:
A 320 12 2 37610 10960mm2
Ix
320 403763 315363413mm4
Wx
315363413 1576817mm3 200
故腹板局部稳定满足要求。
7.3
一压弯构件的受力支承及截面如图 7-23 所示(平面内为两端铰
支支承) 。设材料为 Q 235 f y 235N / mm2 ,计算其截面强度和弯矩 作用平面内的稳定性。
工字型梁截面图
图 7-23
习题 7.3
习题 7.3
M 图(kNm)
习题 7.3
N 图(kN)
故两边段段平面外稳定满足要求。
(4)局部稳定 按不允许板件发生局部失稳的准则进行校核 1)外伸翼缘板
b 320 12 235 235 7.7 15 15 12.4 t 2 20 fy 345
故翼缘板局部稳定满足要求 2)腹板 取弯矩值最大即距地面 10m 处截面进行验算( λmax ):
N f ' d N Ex
1150 103 0.682 18320 310
0.65 75 106 0.8 1150 1.1 1.05 3340.2 103 1 310 7515.3 0.297 0.052 0.349 1.0
故面内稳定满足条件。
4.平面外稳定验算
Iy
iy
320 20 2 460 12 10929 10 mm 12
3 3 4
1
4
Iy
A
10929 104
18320
77mm
1.0 5 103 y 64.9 77
y
y
fy
E
64.9
310 0.8018 2.06 105
(1) 强度
Mx N Mx 2500 103 f d 205 A Wx 0.918 30918 25382.2 103
得: M x
3150.97kNm
(2)整体稳定 1)平面内整体稳定验算:
2 EA 2 2.06 105 30918 N 46472.33kN 2 1.1ox 1.1 35.072
故平面内稳定内满足要求。
7.4
某压弯缀条式格构构件,截面如图 7-24 所示,构件平面内外计算长 度 lox 29.3m,loy 18.2m。 已知轴压力(含自重)N =2500kN,问可 以承受的最大偏心弯矩 Mx 为多少。设钢材牌号为 Q235,N 与 Mx 均 为设计值,钢材强度设计值取 205N/mm2。
N x A
mx M xWx1 1 0.8
N ' N Ex
800 103 0.7463 10960
0.65 75 106 0.8 800 1.05 1576817 1 4047.84 97.8 35.87 133.67 N / mm 2 f d 215 N / mm 2
则偏向侧单肢轴力为: N1 为 b 类截面,查表得 1x
0.838 。
单肢弯矩平面外长细比: 1 y
l1 y
i1 y
1820 73.8 24.66
由于
b 176 0.28 0.8 h 630
故为 a 类截面,查表得 1 y
0.819 1x 。
N1 90 e 2500 103 f d 205 1 y A0 180 0.819 15459
得: e 96.875cm
M x N e 2500 0.96875 2421.88kNm
(4)缀条稳定 因斜缀条长于横缀条,且前者的计算内力大于后者,故只需验算斜缀 条。
由于弯矩沿柱轴向不变,则
V 柱段计算剪力:
Af d 85
fy 235
30918 205 235 74.57kN 85 235
钢结构基本原理第七章作业
7.2
一压弯构件长 15m,两端在截面两主轴方向均为铰接,承受轴心压力 N=1000kN,高度 10m 处作用力 F=150kN,沿构件轴线方向,且有 750mm 偏心距。构件三分点处有两个平面外支承点(图 7-22) 。钢材 强度设计值为 310N/mm2。按所给荷载,设计截面尺寸(按工字型截 面考虑) 。
图 7-22
习题 7.2
M 图(kNm)
N 图(kN)
答:结构 M 图,N 图如上图所示。10 米高度处内力最大,对其进行 验算。其内力为:M=75kNm,N=1150kN。 选用焊接截面如下图所示,取翼缘焰切边。
习题 7.2 设计工字型截面
1. 截面性质:
An ' A 320 20 2 460 12 18320mm2
I nx I x
320 500 12
