实验三-时域及频域采样定理
数字信号处理实验报告 3

数字信号处理实验报告姓名:班级:通信学号:实验名称:频域抽样定理验证实验类型:验证试验指导教师:实习日期:2013.频域采样定理验证实验一. 实验目的:1. 加深对离散序列频域抽样定理的理解2.了解由频谱通过IFFT 计算连续时间信号的方法3.掌握用MATLAB 语言进行频域抽样与恢复时程序的编写方法 4、用MATLAB 语言将X(k)恢复为X(z)及X(e jw )。
二. 实验原理:1、1、频域采样定理: 如果序列x(n)的长度为M ,频域抽样点数为N ,则只有当频域采样点数N ≥M 时,才有x N (n)=IDFT[X(k)]=x(n),即可由频域采样X(k)无失真的恢复原序列 x(n)。
2、用X(k)表示X(z)的内插公式:∑-=-----=10111)(1)(N k kNNzWz k X Nz X内插函数: zWzkNNN z 1k111)(-----=ϕ频域内插公式:∑-=-=10)2()()(N K j k Nk X e X πωϕω频域内插函数:e N j N N )21()2sin()2sin(1)(--=ωωωωϕ三. 实验任务与步骤:实验一:长度为26的三角形序列x(n)如图(b)所示,编写MATLAB 程序验证频域抽样定理。
实验二:已知一个时间序列的频谱为X(e jw )=2+4e -jw +6e -j2w +4e -j3w +2e -j4w分别取频域抽样点数N为3、5和10,用IPPT计算并求出其时间序列x(n),用图形显示各时间序列。
由此讨论原时域信号不失真地由频域抽样恢复的条件。
实验三:由X32(k)恢复X(z)和X(e jw)。
四.实验结论与分析:实验一:源程序:M=26;N=32;n=0:M; %产生M长三角波序列x(n)xa=0:floor(M/2);xb= ceil(M/2)-1:-1:0; xn=[xa,xb];Xk=fft(xn,512); %1024点FFT[x(n)], 用于近似序列x(n)的TFX32k=fft(xn,32); %32点FFT[x(n)]x32n=ifft(X32k); %32点IFFT[X32(k)]得到x32(n)X16k=X32k(1:2:N); %隔点抽取X32k得到X16(K)x16n=ifft(X16k,N/2); %16点IFFT[X16(k)]得到x16(n)subplot(3,2,2);stem(n,xn,'.');box ontitle('(b) 三角波序列x(n)');xlabel('n');ylabel('x(n)');axis([0,32,0,20])k=0:511;wk=2*k/512;subplot(3,2,1);plot(wk,abs(Xk));title('(a)FT[x(n)]');xlabel('\omega/\pi');ylabel('|X(e^j^\omega)|');axis([0,1,0,200])k=0:N/2-1;subplot(3,2,3);stem(k,abs(X16k),'.');box ontitle('(c) 16点频域');xlabel('k');ylabel('|X_1_6(k)|');axis([0,8,0,200])n1=0:N/2-1;subplot(3,2,4);stem(n1,x16n,'.');box ontitle('(d) 16点IDFT[X_1_6(k)]');xlabel('n');ylabel('x_1_6(n)');axis([0,32,0,20])k=0:N-1;subplot(3,2,5);stem(k,abs(X32k),'.');box ontitle('(e) 32点频域采样');xlabel('k');ylabel('|X_3_2(k)|');axis([0,16,0,200])n1=0:N-1;subplot(3,2,6);stem(n1,x32n,'.');box ontitle('(f) 32点IDFT[X_3_2(k)]');xlabel('n');ylabel('x_3_2(n)');axis([0,32,0,20])结果如下所示:实验一分析:序列x(n)的长度M=26,由图中可以看出,当采样点数N=16<M时,x16(n)确实等于原三角序列x(n)以16为周期的周期延拓序列的主值序列。
实验三(时域抽样与频域抽样)

时域抽样与频域抽样
一、实验目的
1. 加深理解连续时间信号的离散化过程中的数学概念和物 理概念,掌握时域抽样定理(奈奎斯特采样定理)的基 本内容。 2. 加深对时域取样后信号频谱变化的认识。掌握由抽样序 列重建原连续信号的基本原理与实现方法,理解其工程 概念。 3. 加深理解频谱离散化过程中的数学概念和物理概念,掌 握频域抽样定理的基本内容。
二. 实验原理——时域抽样
1、时域抽样概述
时域抽样定理给出了连续信号抽样过程中信 号不失真的约束条件:信号抽样频率 fs 大于等于2 倍的信号最高频率fm,即 fs 2fm。
时域抽样先把连续信号 x(t)变成适合数字系统 处理的离散信号x[k];然后根据抽样后的离散信号 x[k]恢复原始连续时间信号x(t)完成信号重建。
0
0.01
0.02
0.03
三. 程序示例——频域抽样
2.已知序列 x [ k ] {1, 1, 1; k 0,1,2} 对其频谱X(ej)进行抽样, 分别取N=2,3,10,观察频域抽样造成的混叠现象。
x=[1,1,1]; P=256; omega=[0:P-1]*2*pi/P; X0=1+exp(-j*omega)+exp(-2*j*omega); N=input('Type in N= '); omegam=[0:N-1]*2*pi/N; Xm=1+exp(-j*omegam)+exp(-2*j*omegam); subplot(2,1,1); plot(omega./pi,abs(X0)); xlabel('Omega/PI'); hold on stem(omegam./pi,abs(Xm),'r','o'); hold off x1=[zeros(1,2*N) x zeros(1,2*N)]; x2=[zeros(1,N) x zeros(1,3*N)]; x3=[x zeros(1,4*N)]; x4=[zeros(1,3*N) x zeros(1,N)]; x5=[zeros(1,4*N) x]; xx=x1+x2+x3+x4+x5; k=-2*N:2*N+length(x)-1; subplot(2,1,2); stem(k,x1); hold on subplot(2,1,2); stem(k,xx,'r','*'); hold off
实验三 时域采样与频域采样
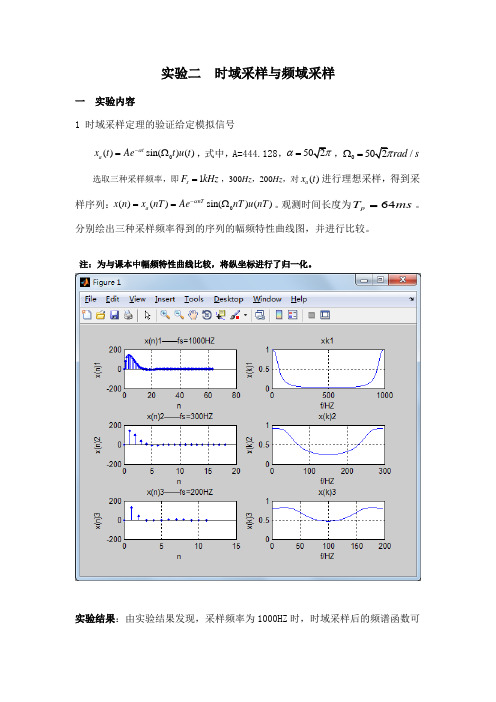
实验二 时域采样与频域采样一 实验内容1 时域采样定理的验证给定模拟信号0()sin()()t a x t Ae t u t α-=Ω,式中,A=444.128,α=,0/rad s Ω=选取三种采样频率,即1s F kH z =,300Hz ,200Hz ,对()a x t 进行理想采样,得到采样序列:0()()sin()()nT a x n x nT Ae nT u nT α-==Ω。
观测时间长度为64p T m s =。
分别绘出三种采样频率得到的序列的幅频特性曲线图,并进行比较。
注:为与课本中幅频特性曲线比较,将纵坐标进行了归一化。
实验结果:由实验结果发现,采样频率为1000HZ 时,时域采样后的频谱函数可以较好的表现出原模拟信号的幅频特性,且是原幅频特性的周期延拓。
当采样频率为300HZ和200HZ时,其频谱函数与原幅频特性相比,有较大的误差,且在fs/2的位置误差最大。
实验分析:理想采样信号的频谱是原模拟信号的频谱沿频率轴,每间隔采样角频率2*pi*fs重复出现一次,并叠加形成的周期函数,所以只有当采样角频率2*pi*fs大于等于原模拟信号的角频率时才不会发生混叠。
2 频域采样定理的验证给定信号:1013()271426n nx n n nothers+≤≤⎧⎪=-≤≤⎨⎪⎩,对()x n的频谱函数()jX eω在[0,2π]上分别等间隔采样16点和32点,得到16()X k和32()X k,再分别对16()X k和32()X k进行IDFT,得到16()x n和32()x n。
分别画出()jX eω、16()X k和32()X k的幅度谱,并绘图显示()x n、16()x n和32()x n的波形,进行对比和分析。
实验结论:由上图分析知,频域采样32点时,其逆变换得到的xn32能较好的还原xn,只是尾部多了几个0而已,而对于频域采样16点时,逆变换之后已经产生较大的误差,不能等效为xn。
DSP实验时域采样与频域采样

实验二时域采样与频域采样一. 实验目的时域采样理论与频域采样理论是数字信号处理中的重要理论。
要求掌握模拟信号采样前后频谱的变化,以及如何选择采样频率才能使采样后的信号不丢失信息;要求掌握频率域采样会引起时域周期化的概念,以及频率域采样定理及其对频域采样点数选择的指导作用。
二. 实验原理与方法时域采样定理的要点是:1) 对模拟信号)(t x a 以间隔T 进行时域等间隔理想采样,形成的采样信号的频谱)(ˆΩj X是原模拟信号频谱()a X j Ω以采样角频率s Ω(T s/2π=Ω)为周期进行周期延拓。
公式为:)](ˆ[)(ˆt xFT j X a a =Ω )(1∑∞-∞=Ω-Ω=n s a jn j X T 2) 采样频率s Ω必须大于等于模拟信号最高频率的两倍以上,才能使采样信号的频谱不产生频谱混叠。
利用计算机计算上式并不方便,下面我们导出另外一个公式,以便用计算机上进行实验。
理想采样信号)(ˆt xa 和模拟信号)(t x a 之间的关系为: ∑∞-∞=-=n a a nT t t x t x)()()(ˆδ 对上式进行傅立叶变换,得到:dt e nT t t x j X t j n a a Ω-∞∞-∞-∞=⎰∑-=Ω])()([)(ˆδ dt e nT t t x t j n a Ω-∞-∞=∞∞-∑⎰-)()( δ=在上式的积分号内只有当nT t =时,才有非零值,因此:∑∞-∞=Ω-=Ωn nT j aae nT xj X )()(ˆ上式中,在数值上)(nT x a =)(n x ,再将T Ω=ω代入,得到:∑∞-∞=-=Ωn nj aen x j X ω)()(ˆ上式的右边就是序列的傅立叶变换)(ωj eX ,即T j a e X j X Ω==Ωωω)()(ˆ上式说明理想采样信号的傅立叶变换可用相应的采样序列的傅立叶变换得到,只要将自变量ω用T Ω代替即可。
频域采样定理的要点是:1.) 对信号x(n)的频谱函数X(ej ω)在[0,2π]上等间隔采样N 点,得到2()(), 0,1,2,,1j N k NX k X e k N ωπω===-则N 点IDFT[()N X k ]得到的序列就是原序列x(n)以N 为周期进行周期延拓后的主值区序列,公式为:()IDFT[()][()]()N N N N i x n X k x n iN R n ∞=-∞==+∑2.) 由上式可知,频域采样点数N 必须大于等于时域离散信号的长度M(即N ≥M),才能使时域不产生混叠,则N 点IDFT[()N X k ]得到的序列()N x n 就是原序列x(n),即()N x n =x(n)。
时域采样与频域采样

备注:(1)、按照要求独立完成实验内容。
(2)、实验结束后,把电子版实验报告按要求格式改名(例:09号_张三_实验七.doc )后,实验室统一刻盘留档。
实验四 时域采样与频域采样一、实验目的时域采样理论与频域采样理论是数字信号处理中的重要理论。
掌握模拟信号采样前后频谱的变化,以及如何选择采样频率才能使采样前后的信号不丢失信息;要求掌握频率域采样会引起时域周期化的概念,以及频率域采样定理及其对采样点数选择的指导作用。
二、实验原理在数字信号处理的应用中,只要涉及时域或者频域采样,都必须服从这两个采样理论的要点。
时域采样原理和频域采样原理,得到一个有用的结论,这两个采样理论具有对偶性:“时域采样频谱周期延拓,频域采样时域信号周期延拓”。
因此放在一起进行实验。
三、实验内容(包括代码与产生的图形及结果分析)1. 给定模拟信号如下:xa(t)=Ae -αt sin(Ω0t)u(t)式中, A=444.128,α=50 π,Ω0=50 π rad/s ,将这些参数带入上式中,对x a (t进行傅里叶变换,它的幅频特性曲线如图1所示。
现用DFT(FFT)求该模拟信号的幅频特性,以验证时域采样理论。
按照xa(t)的幅频特性曲线,选取三种采样频率,即Fs=1 kHz ,300 Hz ,200 Hz 。
观测时间选Tp=64 ms 。
要求: 编写实验程序,计算x 1(n)、 x 2(n)和x 3(n)的幅度特性,并绘图显示。
观察分析频谱混叠失真。
close all;clear all;clc;22图1 x a (t)的幅频特性曲线Tp=64/1000; %观察时间Tp=64毫秒%产生M长采样序列x(n)% Fs=1000;T=1/Fs;Fs=1000;T=1/Fs;M=Tp*Fs;n=0:M-1;A=444.128;alph=pi*50*2^0.5;omega=pi*50*2^0.5;xnt=A*exp(-alph*n*T).*sin(omega*n*T);Xk=T*fft(xnt,M); %M点FFT[xnt)]subplot(3,2,1);n=0:length(xnt)-1;stem(n,xnt,'.');xlabel('n');ylabel('yn');axis([0,n(end),min(xnt),1.2*max(xnt)]);%绘图box on;title('(a) Fs=1000Hz');k=0:M-1;fk=k/Tp;subplot(3,2,2);plot(fk,abs(Xk));title('(a) T*FT[xa(nT)],Fs=1000Hz'); xlabel('f(Hz)');ylabel('幅度');axis([0,Fs,0,1.2*max(abs(Xk))])%========================% Fs=300Hz;T=1/Fs;Fs=300;T=1/Fs;M=Tp*Fs;n=0:M-1;A=444.128;alph=pi*50*2^0.5;omega=pi*50*2^0.5;xnt=A*exp(-alph*n*T).*sin(omega*n*T);Xk=T*fft(xnt,M); %M点FFT[xnt)]subplot(3,2,3);n=0:length(xnt)-1;stem(n,xnt,'.');xlabel('n');ylabel('yn');axis([0,n(end),min(xnt),1.2*max(xnt)]);%绘图box on;title('(a) Fs=300Hz');k=0:M-1;fk=k/Tp;subplot(3,2,4);plot(fk,abs(Xk));title('(a) T*FT[xa(nT)],Fs=300Hz');xlabel('f(Hz)');ylabel('幅度');axis([0,Fs,0,1.2*max(abs(Xk))])%========================% Fs=200Hz;T=1/Fs;Fs=200;T=1/Fs;M=Tp*Fs;n=0:M-1;A=444.128;alph=pi*50*2^0.5;omega=pi*50*2^0.5;xnt=A*exp(-alph*n*T).*sin(omega*n*T);Xk=T*fft(xnt,M); %M 点FFT[xnt)]subplot(3,2,5);n=0:length(xnt)-1;stem(n,xnt,'.');xlabel('n');ylabel('yn');axis([0,n(end),min(xnt),1.2*max(xnt)]);%绘图box on;title('(a) Fs=200Hz');k=0:M-1;fk=k/Tp;subplot(3,2,6);plot(fk,abs(Xk));title('(a) T*FT[xa(nT)],Fs=200Hz');xlabel('f(Hz)');ylabel('幅度');axis([0,Fs,0,1.2*max(abs(Xk))])2. 频域采样理论的验证。
时域采样与频域采样

实验二:时域采样与频域采样一、实验目的:时域采样理论与频域采样理论是数字信号处理中的重要理论。
要求掌握模拟信号采样前后频谱的变化,以及如何选择采样频率才能使采样后的信号不丢失信息;要求掌握频率域采样会引起时域周期化的概念,以及频率域采样定理及其对频域采样点数选择的指导作用。
二、实验原理与方法:1、时域采样定理的要点:1)对模拟信号)(t x a 以间隔T 进行时域等间隔理想采样,形成的采样信号的频谱)(ˆΩj X 是原模拟信号频谱()a X j Ω以采样角频率s Ω(T s /2π=Ω)为周期进行周期延拓。
公式为:)](ˆ[)(ˆt x FT j X a a=Ω )(1∑∞-∞=Ω-Ω=n s a jn j X T 2)采样频率s Ω必须大于等于模拟信号最高频率的两倍以上,才能使采样信号的 频谱不产生频谱混叠。
利用计算机计算上式并不方便,下面我们导出另外一个公式,以便用计算机上进行实验。
理想采样信号)(ˆt xa 和模拟信号)(t x a 之间的关系为 ∑∞-∞=-=n a a nT t t x t x)()()(ˆδ 对上式进行傅立叶变换,得到:dt e nT t t x j X t j n a a Ω-∞∞-∞-∞=⎰∑-=Ω])()([)(ˆδdt e nT t t x t j n a Ω-∞-∞=∞∞-∑⎰-)()( δ=在上式的积分号内只有当nT t =时,才有非零值,因此∑∞-∞=Ω-=Ωn nT j aae nT xj X )()(ˆ上式中,在数值上)(nT x a =)(n x ,再将T Ω=ω代入,得到:∑∞-∞=-=Ωn nj aen x j X ω)()(ˆ上式的右边就是序列的傅立叶变换)(ωj e X ,即T j a e X j X Ω==Ωωω)()(ˆ 上式说明理想采样信号的傅立叶变换可用相应的采样序列的傅立叶变换得到,只要将自变量ω用T Ω代替即可。
2、频域采样定理的要点:a) 对信号x(n)的频谱函数X(e j ω)在[0,2π]上等间隔采样N 点,得到2()() , 0,1,2,,1j N k NX k X e k N ωπω===-则N 点IDFT[()N X k ]得到的序列就是原序列x(n)以N 为周期进行周期延拓后的主值区序列,公式为:()IDFT[()][()]()N N N N i x n X k x n iN R n ∞=-∞==+∑b) 由上式可知,频域采样点数N 必须大于等于时域离散信号的长度M(即N≥M),才能使时域不产生混叠,则N 点IDFT[()N X k ]得到的序列()N x n 就是原序列x(n),即()N x n =x(n)。
频域取样定理
2
t
时域抽样
时分复用
屏域抽样
频分复用
s
1
T s (t )
s
t
T s
f t
s
t t
m
m
T T 2T
s s
s
t t T
m m
s
2T s
t
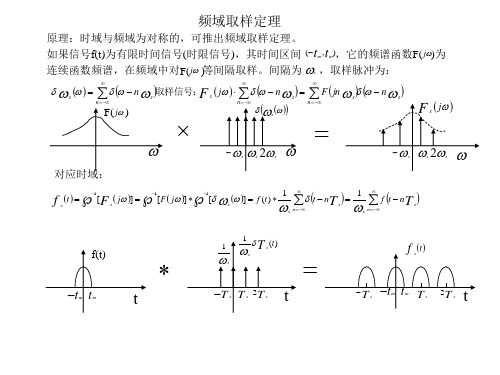
即当频域取样的周期 s ,T s 2 t m时在时域中信号 f s t不重叠。 Ts 可用矩形脉冲低选通信号,恢复原信号,如图。 2 s 频域采样定理:时域信号必须为有限时间信号;频域抽样周期 Ts , 只有当 T s 2t m时,才 可恢复原信号。
s
n
n 取样信号: F j n F jn n
s s n
F( j )
对应时域:
1 1
s
1
s
Hale Waihona Puke sn s
s
2
如果信号ft为有限时间信号时限信号其时间区间它的频谱函数f连续函数频谱在频域中对等间隔取样
频域取样定理
原理:时域与频域为对称的,可推出频域取样定理。 如果信号f(t)为有限时间信号(时限信号),其时间区间 (t m , t m),它的频谱函数F( j)为 连续函数频谱,在频域中对F( j ) 等间隔取样。间隔为 s ,取样脉冲为:
s
s
1
s n
1
s n
F j
s
s
2
s
s
f s t [ F s j ] [F j ] [ s ]
时、频域采样定理的验证
实验二时、频域采样定理的验证
实验目的
掌握时域采样定理,频域采样定理。
掌握模拟信号采样前后频谱的变化,以及如何选择采样频率才能使采样后的信号不丢失信息;掌握频域采样会引起时域周期化,以及频域采样定理及其对频域采样点数选择的指导作用。
实验内容
1.时域采样理论
的验证
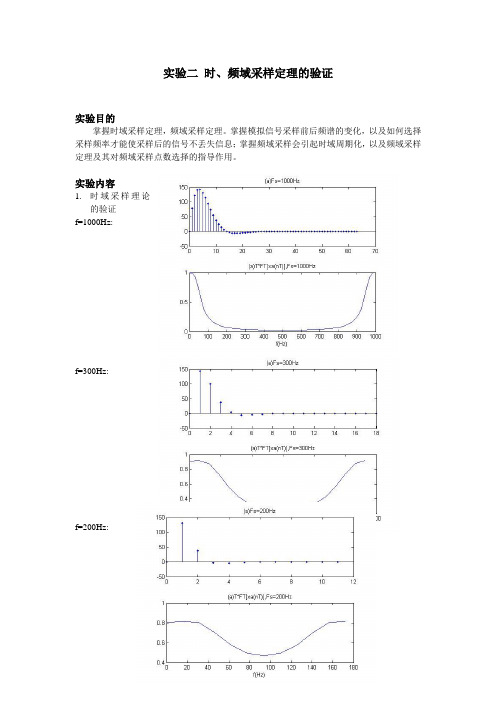
f=1000Hz:
f=300Hz:
f=200Hz:
2.频域采样理论的验证
实验小结
通过本次实验,我巩固了信号在matlab中的运算表示方法、图形输出函数(plot、stem),同时会用软件求fft和ifft,由此验证了时域采样定理,频域采样定理。
通过观察不同平率的模拟信号采样,采样频率如果过低会导致丢失信息;通过频域采样发现它会引起时域周期化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广州大学学生实验报告开课学院及实验室:电子楼317 ﻩ2013年月日n)以N为周期进行周期延拓后的主值区序列,--三、实验用MATL AB函数介绍1. fft功能:一维快速傅立叶变换(FFT)。
Xk=fft(x n,N):采用FFT 算法计算序列向量x n的N点DFT ,缺省N 时,fft 函数自动按xn 的长度计算xn 的DFT 。
当N 为2的整数次幂时,ff t按基2算法计算,否则用混合基算法。
2. i ff t功能:一维快速逆傅立叶变换(IFFT)。
调用格式:与f ft 相同。
四、实验内容和步骤 (一) 时域采样定理实验1. 给定模拟信号如下:0()sin()()at a x t Ae t u t -=Ω假设式中A=444.128,250π=a , 2500π=Ωrad /s ,将这些参数代入上式中,对()a x t 进行傅立叶变换,得到()a X j Ω,画出它的幅频特性()~a X jf f,如图3.1所示。
根据该曲线可以选择采样频率。
图3.1()a x t 的幅频特性曲线实验过程及原始数据: clf ;A=444.128;a=50*pi *sqrt(2);w0=50*pi *sqrt (2); fs=1000; %采样频率1000HZ T =1/fs;n=0:0.05*fs -1; %产生的长度区间nx t=A*exp(-a*n*T).*sin(w0*n*T); %产生采样序列xt(n) f =f ft(xt,l eng th(n)); %采样序列xt(n)的FFT 变换 k1=0:le ng th (f)-1;fk1=k1/0.05; %设置xt(n)的频谱的横坐标的取值 subplot (1,2,1)st em(n,xt,'.') %xt 离散图 tit le('(a)fs=1000Hz');xlab el ('n ');ylab el('x(n )'); subplot (1,2,2) plot(fk1,ab s(f))title('(a ) FT[x(nT)],Fs =1000Hz '); xlabel('f(H z)');ylabel('幅度')2. 按照选定的采样频率对模拟信号进行采样,得到时域离散信号()x n :0()()sin()()anT a x n x nT Ae nT u nT ==Ω这里给定采样频率如下:1s f kHz =,300Hz ,200Hz 。
分别用这些采样频率形成时域离散信号,按顺序分别用1()x n 、2()x n 、3()x n 表示。
选择观测时间50p T ms=。
实验过程及原始数据: c lf;A=444.128;a=50*sqrt(2)*pi;w0=50*sqrt(2)*p i; Tp=50/1000;F1=1000;F2=300;F3=200; T1=1/F1;T2=1/F 2;T3=1/F 3;n1=0:0.5: T p*F1-1;n2=0:0.5:T p*F2-1;n3=0:0.5:T p*F3-1; x1=A*exp (-a*n1*T1).*s in (w0*n 1*T 1);x2=A*exp (-a*n2*T 2).*sin(w0*n 2*T2); x3=A*exp (-a*n3*T3).*sin(w 0*n3*T3); f1=fft (x 1,length (n1)); f2=fft(x2,len gth(n2)); f3=fft(x3,l eng th(n3)); k 1=0:length (f1)-1;f k1=k1/Tp; k2=0:length(f2)-1;fk2=k2/Tp; k3=0:le ng th(f3)-1;--fk3=k3/Tp; sub plot(3,2,1) stem(n1,x1,'.') title('(a)Fs =1000Hz');xlabe l('n');ylabe l('x1(n)'); sub plot(3,2,3) stem(n2,x2,'.') tit le('(b)Fs=300Hz');xlab el('n');yl abel('x2(n)'); subpl ot(3,2,5) stem(n3,x 3,'.') ti tle('(c)Fs=200Hz');xlabel ('n');yla bel ('x 3(n )'); su bplot (3,2,2) pl ot(fk 1,abs(f1))tit le('(a) FT[x a(nT)]的频谱特性,Fs=1000Hz'); xlabe l('f(Hz)');ylabel('幅度') subpl ot (3,2,4) pl ot(fk2,a bs(f2))titl e('(b) F T[xa(nT)] 的频谱特性,Fs=300Hz'); xlab el('f(Hz)');yl abe l('幅度') subp lot(3,2,6) plot(fk3,ab s(f3))ti tle('(c ) F T[xa(nT )] 的频谱特性,F s=200Hz '); xlabel('f(H z)');ylab el('幅度')3. 计算()x n 的傅立叶变换()jwX e : 100()[()]sin()i in anT jwj ni n X e FT x n AenT eω--===Ω∑ (3.6)式中,1,2,3i =,分别对应三种采样频率的情况123111(,,)1000300200T s T s T s ===。
采样点数用下式计算:pi i T n T =(3.7)(3.6)式中,ω是连续变量。
为用计算机进行数值计算,改用下式计算:100()[()]sin()i ki k n jw anT jw n M i n X eDFT x n Ae nT e --===Ω∑ (3.8)式中,2k kM πω=,0,1,2,3...k =,1M -;64M =。
可以调用MATLA B函数fft 计算3.8式。
4. 打印三种采样频率的幅度曲线()~k jw kX e w ,0,1,2,3...k =,1M -;64M =。
f=inp ut('f= '); %输入取样频率f=1000 T =1/f;n=0:50/(1000*T);M=64;%设置信号有关参数 A=444.128; a=50*sq rt(2.0);w0=50*sqrt (2.0)*pi; xn=A*ex p(-a*n*T).*sin(w0*n*T); % 产生x(n)Xk=f ft(xn,1024); %1024 点FF T[x (n)],用于近似序列 x(n)的FT X64k=fft(xn,M); %FF T[x(n)]x 64n=ifft(X64k ); %64 点IFFT[X64(k)] 得到64(n) subpl ot(2,2,1);ste m(n,x n,'.');grid ;box on title ('(a) x1(n)');xlab el('n');y label ('x 1(n)'); k=0:M -1;s ubplo t(2,2,2);stem (k,abs(X 64k ),'.');grid; t itle('(b) 64 点频域采样 输入取样频率f=1000'); xlab el('k');ylabel('|X 64(k)|'); k =0:1023;wk =2*k/1024;sub plot (2,2,3);plot(wk,abs(Xk ));gr id;ti tle('(c)FT[x 1(n)]');xlabel('\o mega/\pi ');ylabel('|X (e^j ^\ome ga)|'); n1=0:M-1;su bplo t(2,2,4);ste m(n 1,x64n,'.');grid ;box o n titl e('(d ) 64 点')ifft(X64(k));xla be l('n');y lab el('x64(n)'); f=input('f= '); % 输入取样频率f=300 T=1/f;n=0:50/(1000*T);M=64;%设置信号有关参数A=444.128; a=50*sqrt(2.0);w0=50*sqrt (2.0)*pi; x n=A*exp(-a*n*T).*s in(w0*n*T); % 产生x(n) X k=f ft(xn,1024); %1024 点F FT[x(n)], 用于近似序列x(n)的F TX64k=fft (xn,M); %F FT[x(n)]x64n =if ft(X64k); %64点 IFFT[X64(k)]得到 x64(n) subplot (2,2,1);stem (n ,xn,'.');g rid ;ti tle('(a) x2(n)');xlabe l('n ');ylab el('x2(n)'); k=0:M -1;subplot(2,2,2);st em(k,abs (X 64k),'.');gr id;box o ntit le('(b) 64 点频域采样输入取样频率f=300'); xlabel('k');yla bel('|X64(k)|'); k=0:1023;wk=2*k/1024;subplot(2,2,3);plot(wk ,abs(X k));grid;title ('(c )F T[x2(n)]');xlabel ('\ome ga/\pi');ylabel('|X (e^j^\ome ga)|');n1=0:M-1;s ubplot(2,2,4);s te m(n1,x64n,'.');g rid;box on titl e('(d) 64 点IFF T[X64(k)]');-- xlabel('n');ylabel('x64(n)');f=input('f= ');% 输入取样频率f=200T=1/f;n=0:50/(1000*T);M=64; %设置信号有关参数A=444.128; a=50*sqrt(2.0);w0=50*sqrt(2.0)*pi;xn=A*exp(-a*n*T).*sin(w0*n*T); %产生 x(n)Xk=fft(xn,1024);%1024 点FFT[x(n)],用于近似序列x(n)的FTX64k=fft(xn,M);%FFT[x(n)]x64n=ifft(X64k); %64 点IFFT[X64(k)]得到x64(n)subplot(2,2,1);stem(n,xn,'.');grid;boxontitle('(a)x3(n)');xlabel('n');ylabel('x3(n)');k=0:M-1;subplot(2,2,2);stem(k,abs(X64k),'.');grid;title('(b) 64点频域采样输入取样频率f=200');xlabel('k');ylabel('|X64(k)|');k=0:1023;wk=2*k/1024;subplot(2,2,3);plot(wk,abs(Xk));grid;title('(c)FT[x3(n)]');xlabel('\omega/\pi');ylabel('|X(e^j^\omega)|');n1=0:M-1;subplot(2,2,4);stem(n1,x64n,'.');grid;box ontitle('(d) 64 µã')ifft(X64(k));xlabel('n');ylabel('x64(n)');采样频率fs=1000采样频率fs=300采样频率fs=200 (二)频域采样定理实验给定信号如下:⎪⎩⎪⎨⎧≤≤-≤≤+=其它261427131)(nnnnnx编写程序分别对频谱函数()FT[()]jX e x nω=在区间]2,0[π上等间隔采样32和16点,得到)()(1632kXkX和:32232()() , 0,1,2,31jkX k X e kωπω===16216()() , 0,1,2,15jkX k X e kωπω===再分别对)()(1632kXkX和进行32点和16点IFFT,得到)()(1632nxnx和:323232()IFFT[()] ,0,1,2,,31x n X k n==161616()IFFT[()] ,0,1,2,,15x n X k n==分别画出()jX eω、)()(1632kXkX和的幅度谱,并绘图显示x(n)、)()(1632nxnx和的波形,进行对比和分析,验证总结频域采样理论。
