三角函数定义及其三角函数公式大全
三角函数公式大全及记忆口诀

三角函数公式大全及记忆口诀一、正弦函数(sine function)公式:1. 正弦函数的定义:在直角三角形中,正弦函数是对边与斜边之比,表示为sinθ。
2. 正弦函数的基本关系式:sinθ = 对边 / 斜边3. 弦函数的平方和恒等式:sin²θ + cos²θ = 1二、余弦函数(cosine function)公式:1. 余弦函数的定义:在直角三角形中,余弦函数是邻边与斜边之比,表示为cosθ。
2. 余弦函数的基本关系式:cosθ = 邻边 / 斜边3. 弦函数与余弦函数的关系:cosθ = sin(90° - θ)三、正切函数(tangent function)公式:1. 正切函数的定义:在直角三角形中,正切函数是对边与邻边之比,表示为tanθ。
2. 正切函数的基本关系式:tanθ = 对边 / 邻边3. 弦函数与正切函数的关系:tanθ = sinθ / cosθ四、余切函数(cotangent function)公式:1. 余切函数的定义:在直角三角形中,余切函数是邻边与对边之比,表示为cotθ。
2. 余切函数的基本关系式:cotθ = 邻边 / 对边3. 弦函数与余切函数的关系:cotθ = 1 / tanθ = cosθ / sinθ五、正割函数(secant function)公式:1. 正割函数的定义:在直角三角形中,正割函数是斜边与邻边之比,表示为secθ。
2. 正割函数的基本关系式:secθ = 斜边 / 邻边= 1 / cosθ六、余割函数(cosecant function)公式:1. 余割函数的定义:在直角三角形中,余割函数是斜边与对边之比,表示为cscθ。
2. 余割函数的基本关系式:cscθ = 斜边 / 对边= 1 / sinθ七、和差公式:1. 正弦函数和差公式:sin(θ±φ) = sinθcosφ ± cosθsinφ2. 余弦函数和差公式:cos(θ±φ) = cosθcosφ ∓ sinθsinφ3. 正切函数和差公式:tan(θ±φ) = (tanθ ± tanφ) / (1 ∓tanθtanφ)八、倍角公式:1. 正弦函数倍角公式:sin2θ = 2sinθcosθ2. 余弦函数倍角公式:cos2θ = cos²θ - sin²θ = 2cos²θ - 1= 1 - 2sin²θ3. 正切函数倍角公式:tan2θ = (2tanθ) / (1 - tan²θ)九、半角公式:1. 正弦函数半角公式:sin(θ/2) = ±√[(1 - cosθ) / 2]2. 余弦函数半角公式:cos(θ/2) = ±√[(1 + cosθ) / 2]3. 正切函数半角公式:tan(θ/2) = ±√[(1 - cosθ) / (1 +cosθ)]十、和差化积公式:1. 正弦函数和差化积公式:sinθ ± sinφ = 2sin[(θ ±φ)/2]cos[(θ ∓ φ)/2]2. 余弦函数和差化积公式:cosθ + cosφ = 2cos[(θ +φ)/2]cos[(θ - φ)/2]3. 正切函数和差化积公式:tanθ ± tanφ = sin(θ ± φ) /cosθcosφ以上是三角函数的常用公式。
三角函数公式大全_三角函数公式完整版

三角函数公式大全_三角函数公式完整版三角函数是高等数学中的基本内容之一,它研究的是角的函数关系。
三角函数在几何、物理、工程等领域中广泛应用,具有重要的理论和实际意义。
在这篇文章中,我们将介绍三角函数的基本概念、性质和常用的公式。
1.弧度制和角度制在三角函数中,我们常用的角度单位有弧度制和角度制。
弧度制是通过半径等于1的圆上的一段弧长来定义的。
角度制是通过一个完整的圆(360度)被分成的部分来定义的。
两者之间的转换关系如下:弧度制=角度制×π/180角度制=弧度制×180/π2.三角函数的定义在直角三角形中,我们可以定义三角函数:正弦函数sinθ、余弦函数cosθ、正切函数tanθ、余切函数cotθ、正割函数secθ和余割函数cscθ。
对于一个角θ:sinθ = 对边/斜边cosθ = 邻边/斜边tanθ = 对边/邻边cotθ = 邻边/对边secθ = 斜边/邻边cscθ = 斜边/对边3.基本三角函数的关系正弦函数与余弦函数是最基本的三角函数。
它们之间有一定的关系:sin²θ + cos²θ = 1tanθ = sinθ/cosθcotθ = cosθ/sinθsecθ = 1/cosθcscθ = 1/sinθ4.基本三角函数的性质正弦函数和余弦函数的取值范围是[-1,1];正切函数和余切函数的定义域是除去所有使得余弦函数为零的x,其他的实数集;正割函数和余割函数的定义域是除去所有使得正弦函数为零的x,其他的实数集。
5.三角函数的周期性与奇偶性正弦函数和余弦函数都是周期函数,其周期为2π(或360度)。
正弦函数是奇函数,满足sin(-θ) = -sinθ,即对于任意的角度θ,有sin(θ + π) = -sinθ。
余弦函数是偶函数,满足cos(-θ) = cosθ,即对于任意的角度θ,有cos(θ + π) = cosθ。
6.三角函数的诱导公式通过使用三角函数的定义和相关的三角恒等式,我们可以得到一系列的诱导公式:sin(π - θ) = sinθ cos(π - θ) = -cosθ tan(π - θ) = -tanθsin(θ + π) = -sinθ cos(θ + π) = -cosθ tan(θ + π) = tanθsin(π/2 - θ) = cosθ cos(π/2 - θ) = sinθ tan(π/2- θ) = 1/tanθsin(π/2 + θ) = cosθ cos(π/2 + θ) = -sinθ tan(π/2 + θ) = -1/tanθ7.三角函数的和差公式三角函数的和差公式是在两个角的三角函数之间建立关系的公式,它们包括正弦函数、余弦函数和正切函数的和差公式:sin(α + β) = sinαcosβ + cosαsinβsin(α - β) = sinαcosβ - cosαsinβcos(α + β)= cosαcosβ - sinαsinβcos(α - β) = cosαcosβ + sinαsinβtan(α + β) = (tanα + tanβ) / (1 - tanαtanβ)tan(α - β) = (tanα - tanβ) / (1 + tanαtanβ)8.三角函数的倍角公式三角函数的倍角公式是表达一个角的二倍和三倍的三角函数的公式,它们包括正弦函数、余弦函数和正切函数的倍角公式:sin2θ = 2sinθcosθcos2θ = cos²θ - sin²θtan2θ= (2tanθ) / (1 - tan²θ)sin3θ = 3sinθ - 4sin³θcos3θ = 4cos³θ - 3cosθtan3θ = (3tanθ - tan³θ) / (1 - 3tan²θ)9.三角函数的半角公式三角函数的半角公式是表达一个角的一半的三角函数的公式,它们包括正弦函数、余弦函数和正切函数的半角公式:sin(θ/2) = ±√[(1 - cosθ)/2]cos(θ/2) = ±√[(1 + cosθ)/2]tan(θ/2) = ±√[(1 - cosθ)/(1 + cosθ)]10.三角函数的积化和差公式三角函数的积化和差公式是在两个角的三角函数之间建立关系的公式,它们包括正弦函数和余弦函数的积化和差公式:sinαsinβ = (1/2)[cos(α - β) - cos(α + β)]cosαcosβ = (1/2)[cos(α - β) + cos(α + β)]sinαcosβ = (1/2)[sin(α + β) + sin(α - β)]sinαcosβ = (1/2)[sin(α + β) - sin(α - β)]这些公式只是三角函数的一小部分,但它们是最常用和最基础的公式。
三角函数常用公式表格

三角函数常用公式表格三角函数是数学中一个重要的分支,在几何、物理、工程等众多领域都有着广泛的应用。
为了方便学习和使用,我们将常见的三角函数公式整理成一个表格,并对每个公式进行详细的解释。
一、基本三角函数定义1、正弦函数(Sine Function):sin(θ) =对边/斜边2、余弦函数(Cosine Function):cos(θ) =邻边/斜边3、正切函数(Tangent Function):tan(θ) =对边/邻边二、同角三角函数基本关系1、平方关系:sin²(θ) +cos²(θ) = 1这意味着对于任何角度θ,正弦的平方加上余弦的平方总是等于1。
2、商数关系:tan(θ) =sin(θ) /cos(θ)只要余弦不为零,正切就等于正弦除以余弦。
三、诱导公式1、sin(θ) =sin(θ)2、cos(θ) =cos(θ)3、sin(π θ) =sin(θ)4、cos(π θ) =cos(θ)5、sin(π +θ) =sin(θ)6、cos(π +θ) =cos(θ)诱导公式可以帮助我们将不同象限的角度的三角函数值进行转化。
四、和差角公式1、sin(α +β) =sin(α)cos(β) +cos(α)sin(β)2、sin(α β) =sin(α)cos(β) cos(α)sin(β)3、cos(α +β) =cos(α)cos(β) sin(α)sin(β)4、cos(α β) =cos(α)cos(β) +sin(α)sin(β)这些公式在求解三角函数的和差运算时非常有用。
五、二倍角公式1、sin(2θ) =2sin(θ)cos(θ)2、cos(2θ) =cos²(θ) sin²(θ) =2cos²(θ) 1 =1 2sin²(θ)3、tan(2θ) =2tan(θ) /(1 tan²(θ))二倍角公式常用于将角度加倍时的三角函数计算。
(完整版)三角函数常用公式表
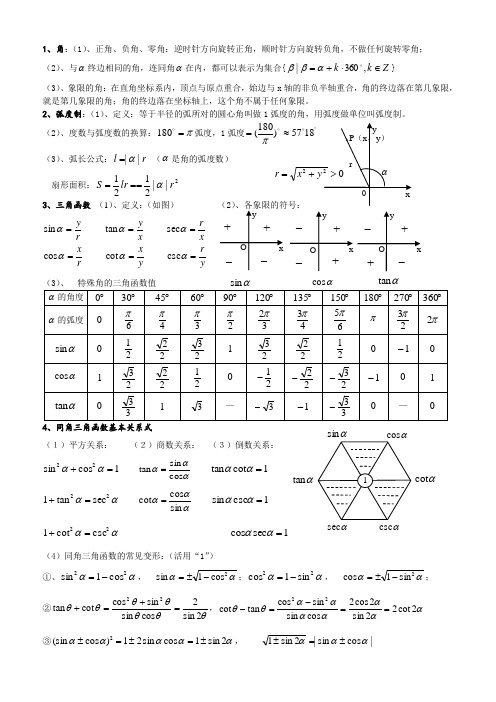
1、角:(1)、正角、负角、零角:逆时针方向旋转正角,顺时针方向旋转负角,不做任何旋转零角; (2)、与α终边相同的角,连同角α在内,都可以表示为集合{Z k k ∈⋅+=,360|αββ}(3)、象限的角:在直角坐标系内,顶点与原点重合,始边与x 轴的非负半轴重合,角的终边落在第几象限,就是第几象限的角;角的终边落在坐标轴上,这个角不属于任何象限。
2、弧度制:(1)、定义:等于半径的弧所对的圆心角叫做1弧度的角,用弧度做单位叫弧度制。
(2)、度数与弧度数的换算:π=180弧度,1弧度)180( =π(3)、弧长公式:r l ||α= (α是角的弧度数)扇形面积:2||2121r lr S α===3、三角函数 (1)、定义:(如图) (2)yry x r x xrx y r y ======ααααααcsc cot cos sec tan sin 4、同角三角函数基本关系式(1)平方关系: (2)商数关系: (3)倒数关系:1cos sin 22=+αα αααcos sin tan = 1cot tan =αα αα22sec tan 1=+ αααsin cos cot =1csc sin =αα αα22csc cot 1=+ 1sec cos =αα(4)同角三角函数的常见变形:(活用“1”) ①、αα22cos 1sin-=, αα2cos 1sin -±=;αα22sin 1cos -=, αα2sin 1cos -±=;②θθθθθθθ2sin 2cos sin sin cos cot tan 22=+=+,αααααααθθ2cot 22sin 2cos 2cos sin sin cos tan cot 22==-=-③ααααα2sin 1cos sin 21)cos (sin 2±=±=±, |cos sin |2sin 1ααα±=±xy+ +_ _O xy++__ Oαtanxy+ +__O=r αsec αsinαtan αcotcsc5、诱导公式:(奇变偶不变,符号看象限)公式一: ααααααtan )360tan(cos )360cos(sin )360sin(=︒⋅+=︒⋅+=︒⋅+k k k公式二: 公式三: 公式四: 公式五:ααααααtan )180tan(cos )180cos(sin )180sin(-=-︒-=-︒=-︒ ααααααtan )180tan(cos )180cos(sin )180sin(=+︒-=+︒-=+︒ ααααααtan )tan(cos )cos(sin )sin(-=-=--=- ααααααtan )360tan(cos )360cos(sin )360sin(-=-︒=-︒-=-︒ 补充:ααπααπααπcot )2tan(sin )2cos(cos )2sin(=-=-=- ααπααπααπcot )2tan(sin )2cos(cos )2sin(-=+-=+=+ ααπααπααπcot )23tan(sin )23cos(cos )23sin(=--=--=- ααπααπααπcot )23tan(sin )23cos(cos )23sin(-=+=+-=+6、两角和与差的正弦、余弦、正切 7 .辅角公式 ⎪⎪⎭⎫ ⎝⎛++++=+x b a b x b a a b a xb x a cos sin cos sin 222222 )sin()sin cos cos (sin 2222ϕϕϕ+⋅+=⋅+⋅+=x b a x x b a(其中ϕ称为辅助角,ϕ的终边过点),(b a ,ab =ϕtan ) (多用于研究性质) 8、二倍角公式:(1)、α2S : αααcos sin 22sin = (2)、降次公式:(多用于研究性质) α2C : ααα22sin cos 2cos -= ααα2sin 21cos sin =1cos 2sin 2122-=-=αα 212cos 2122cos 1sin 2+-=-=αααα2T : ααα2tan 1tan 22tan -= 212cos 2122cos 1cos 2+=+=ααα (3)、二倍角公式的常用变形:①、|sin |22cos 1αα=-, |cos |22cos 1αα=+;②、|sin |2cos 2121αα=-, |cos |2cos 2121αα=+③22sin 1cos sin 21cos sin 22244ααααα-=-=+; ααα2cos sin cos 44=-;④半角:2cos 12sin αα-±=,2cos 12cos αα+±=,αααcos 1cos 12tan +-±=ααααcos 1sin sin cos 1+=-=9、三角函数的图象性质 (1)、函数的周期性:①、定义:对于函数f (x ),若存在一个非零常数T ,当x 取定义域内的每一个值时,都有:f (x +T )= f (x ),那么函数f (x )叫周期函数,非零常数T 叫这个函数的周期;②、如果函数f (x )的所有周期中存在一个最小的正数,这个最小的正数叫f (x )的最小正周期。
三角函数公式(最全)

5 、幂级数
c0+c1x+c2x2+...+cnxn+...=
∑cnxn (n=0.. ∞)
c0+c1(x-a)+c2(x-a)2+...+cn(x-a)n+...=
90 ° -(60 ° -a)]sin[-90
° +(60 ° +a)] =-4cosacos(6
a)[-cos(60
° +a)] =4cosacos(60
° -a)cos(60
上述两式相比可得: tan3a=tana · tan(60 ° +a)
· tan(60 ° -a)
6、四倍角公式
sin4a=-4*[cosa*sina*(2*sina^2-1)] cos4a=1+(-8*cosa^2+8*cosa^4) tan4a=(4*tana-4*tana^3)/(1-6*tana^2+tana^4)
1
三角函数公式
一、定义公式
锐角三角函数 任意角三角函数
正弦( sin ) 余弦( cos ) 正切( tan 或 tg ) 余切( cot 或 ctg ) 正割( sec ) 余割( csc) 正弦( sin ) 余弦( cos ) 正切( tan 或 tg ) 余切( cot 或 ctg ) 正割( sec ) 余割( csc)
在任意△ ABC 中,角 A 、 B 、 C 所对的边长分别为 a 、 b 、 c , 三角形 外接圆的半径为 R.则有:
三角函数公式大全

三角函数公式大全1.三角函数的基本定义:- 正弦函数:sinθ = 对边/斜边- 余弦函数:cosθ = 邻边/斜边- 正切函数:tanθ = 对边/邻边- 余切函数:cotθ = 1/tanθ- 正割函数:secθ = 1/cosθ- 余割函数:cscθ = 1/sinθ2.三角函数的周期性:- 正弦函数的周期为2π:sin(θ+2π) = sinθ- 余弦函数的周期为2π:cos(θ+2π) = cosθ- 正切函数的周期为π:tan(θ+π) = tanθ3.三角函数的平方和差公式:- 正弦函数的平方和差公式:sin(A±B) = sinAcosB ± cosAsinB - 余弦函数的平方和差公式:cos(A±B) = cosAcosB ∓ sinAsinB - 正切函数的平方和差公式:tan(A±B) = (tanA ± tanB)/(1 ∓tanAtanB)4.三角函数的倍角公式:- 正弦函数的倍角公式:sin2θ = 2sinθcosθ- 余弦函数的倍角公式:cos2θ = cos²θ - sin²θ- 正切函数的倍角公式:tan2θ = (2tanθ)/(1 - tan²θ)5.三角函数的半角公式:- 正弦函数的半角公式:sin(θ/2) = ±√((1 - cosθ)/2)- 余弦函数的半角公式:cos(θ/2) = ±√((1 + cosθ)/2)- 正切函数的半角公式:tan(θ/2) = ±√((1 - cosθ)/(1 +cosθ))6.三角函数的和差化积公式:- 正弦函数的和差化积公式:sinA + sinB = 2sin((A+B)/2)cos((A-B)/2)- 余弦函数的和差化积公式:cosA + cosB = 2cos((A+B)/2)cos((A-B)/2)- 正弦函数的差化积公式:sinA - sinB = 2cos((A+B)/2)sin((A-B)/2)- 余弦函数的差化积公式:cosA - cosB = 2sin((A+B)/2)sin((A-B)/2)7.其他重要公式:- 三角函数的平方公式:sin²θ + cos²θ = 1- 三角函数的倒数公式:sin(π/2 - θ) = cosθ,cos(π/2 - θ) = sinθ,tan(π/2 - θ) = cotθ- 三角函数的和差化差公式:cos(A-B) = cosAcosB + sinAsinB,cos(A+B) = cosAcosB - sinAsinB这些是三角函数中一些重要的公式,对于理解和应用三角函数有很大的帮助。
三角函数定义及三角函数公式大全

三角函数定义及三角函数公式大全三角函数是数学中一类重要的函数,主要用于描述和分析三角形以及周期性现象。
三角函数的定义涵盖了正弦函数、余弦函数、正切函数、余切函数、割函数和余割函数等,它们在数学和物理等领域都有广泛的应用。
下面将对每个三角函数的定义及其公式进行详细介绍。
1. 正弦函数(sine function):正弦函数是一个周期性函数,在单位圆上定义。
它的定义域是所有实数,值域是[-1, 1]。
通常用sin(x)或者sinθ来表示,其中θ为角度值。
正弦函数的公式为:sin(x) = sinθ = y/r = 对边/斜边2. 余弦函数(cosine function):余弦函数同样也是一个周期性函数,也在单位圆上定义。
它的定义域是所有实数,值域也是[-1, 1]。
通常用cos(x)或者cosθ来表示。
余弦函数的公式为:cos(x) = cosθ = x/r = 邻边/斜边3. 正切函数(tangent function):正切函数是一个无界函数,定义于所有实数上。
它的定义域是除了π/2 + kπ(k=0,1,2,...)外的所有实数,值域是(-∞, ∞)。
正切函数通常用tan(x)或者ta nθ来表示。
正切函数的公式为:tan(x) = tanθ = y/x = 对边/邻边4. 余切函数(cotangent function):余切函数也是一个无界函数,定义于所有实数上。
它的定义域是除了kπ(k=0,1,2,...)外的所有实数,值域也是(-∞, ∞)。
余切函数通常用cot(x)或者cotθ来表示。
余切函数的公式为:cot(x) = cotθ = x/y = 邻边/对边5. 割函数(secant function):割函数是一个无界函数,在余弦函数的基础上定义。
它的定义域是除了π/2 + kπ(k=0,1,2,...)外的所有实数,值域是(-∞, -1]∪[1, ∞)。
割函数通常用sec(x)或者secθ来表示。
三角函数公式大全及其推导方法

三角函数公式大全及其推导1. 三角函数的定义由此,我们定义:如Figure I, 在ΔABC 中sin () cos () tan ()11 cot ()tan 11 sec ()cos 11 csc ()sin b c ac ba ab b ac a a cc b b cθθθθθθθθθθθθθθθ∠=∠=∠=∠===∠===∠===对边的正弦值:斜边邻边的余弦值:斜边对边的正切值:邻边邻边的余切值:对边斜边的正割值:邻边斜边的余割值:对边 备注:当用一个字母或希腊字母表示角时,可略写∠符号,但用三个子母表示时,不能省略。
在本文中,我们只研究sin 、cos 、tan 。
2. 额外的定义222222sin (sin )cos (cos )tan (tan )θθθθθθ===A c b θC a B Figure I3. 简便计算公式22sin cos cos(90)cos sin sin(90)111tan tan tan(90)sin cos 1bA c cA b b a a A bθθθθθθθθ===-∠===-∠====-∠+= 证明:2222222222901sin sin 1sin cos 1ABC ABC a b c a b c cB A θθ∆∠=∴+=∴+=∴+=∴+=在中,证完222222sin tan cos sin cos 1tan 1cos cos cos b b c a a cθθθθθθθθθ===+=+=4. 任意三角形的面积公式如Figure II ,Ca b hd eB c A Figure II121sin 21sin ()2ABC S ah ab C ac B ∆===两边和其夹角正弦的乘积 5. 余弦定理:任意三角形一角的余弦等于两邻边的平方和减对边的平方之差与两邻边积的两倍之比。
证明: 如Figure II,2222222222222222222222(cos )(sin )2cos cos sin =2cos (cos sin )2cos cos 22b d h a c B c B a ac B c B c Ba ac B c B B a c ac Bb ac a c b B ac ac=+=-+=-++-++=+---+-⇒==-证完6. 海伦公式 证明: 如Figure II ,1sin 212121212ABC S ab C ∆========()()()()()()()222222222222222222=2ABC a b c c a b c b a b c a a b c a b c c a b c b a b c a a b ca b c a b c a b c a b c a b c a b c s S s s a s b s c ∆++-++-++-++=⨯⨯⨯++-++-++-++=⨯⨯⨯++++++++⎛⎫⎛⎫⎛⎫=--- ⎪⎪⎪⎝⎭⎝⎭⎝⎭++=---设:7. 正弦定理如 Figure III ,c 为ΔABC 外接圆的直径,sin 2 sin a A cac r r ABC A =∴==∆(为的外接圆半径)同理:, sin sin 2sin sin sin b c c c B Ca b c r A B C ==∴===A cO B a C Figure III8. 加法定理(1) 两角差的余弦如 Figure IV ,AOC BOC AOB αβαβ∠=∠∠=∠∠=∠-∠令AO=BO=r点A 的横坐标为cos A x r α= 点A 的纵坐标为sin A y r α= 点B 的横坐标为cos B x r β= 点B 的纵坐标为sin B y r β=()()()()()()22222222222222222222222222sin sin cos cos sin sin 2sin sin cos cos 2cos cos sin sin 2sin sin cos cos 2cos cos sin cos sin cos 2sin sin 2cos cos 112s A B A B AB y y x x r r r r r r r r r r r r r αββααβαβαβαβαβαβαβαβααββαβαβ=-+-=-+-=+-++-=+-++-=+++--=+-()()()22in sin cos cos 22sin sin cos cos 21sin sin cos cos r r αβαβαβαβαβαβ+⎡⎤⎣⎦=-+⎡⎤⎣⎦=-+⎡⎤⎣⎦y AB OC x β (α-β) α Figure IV由余弦公式可得:()()()()2222222222cos 2cos 22cos 22cos 21cos AB AC BC AC BC ACBr r r r r r r r αβαβαβαβ=+-⋅∠=++⋅-=+-=--⎡⎤⎣⎦=--⎡⎤⎣⎦综上得:()cos sin sin cos cos αβαβαβ-=+ (2) 两角和的余弦 ()()()()cos cos sin sin cos cos sin sin cos cos cos cos sin sin αβαβαβαβαβαβαβαβ+=--⎡⎤⎣⎦=-+-=-+=-(3) 两角和的正弦()()()()()sin cos 90cos 90sin 90sin cos 90cos cos sin sin cos αβαβαβαβαβαβαβ+=︒-+⎡⎤⎣⎦=︒--⎡⎤⎣⎦=︒-+︒-=+(4) 两角差的正弦 ()()()()sin sin cos sin sin cos cos sin sin cos sin cos cos sin αβαβαβαβαβαβαβαβ-=+-⎡⎤⎣⎦=-+-=-+=-(5) 两角和的正切()()()sin tan cos cos sin sin cos cos cos sin sin cos sin sin cos cos cos cos cos sin sin cos cos sin sin cos cos sin sin 1cos cos tan tan 1tan tan αβαβαβαβαβαβαβαβαβαβαβαβαββαβααβαβαβαβ++=++=-+=-+=-+=-(6) 两角差的正切()()()()tan tan tan tan 1tan tan tan tan 1tan tan αβαβαβαβαβαβ-=+-⎡⎤⎣⎦+-=---=+9. 两倍角公式()()()()()()()222222222222sin 2sin sin cos sin cos 2sin cos cos 2cos cos cos sin sin cos sin 12sin 2cos 1sin 2tan 2cos 22sin cos cos sin 2sin cos cos cos sin cos 2sin cos sin 1cos 2tan 1ta αααααααααααααααααααααααααααααααααααααα=+=+==+=-=-=-=-==-=-=-=-2n α10. 积化和差公式()()()()1sin cos 2sin cos 21sin cos sin cos cos sin cos sin 21sin sin 2αβαβαβαβαβαβαβαβ==++-=++-⎡⎤⎣⎦()()()()()()()()1cos cos 2cos cos 21cos cos cos cos sin sin sin sin 21cos cos 21sin sin 2sin sin 21sin sin sin sin cos cos cos cos 21cos cos 2αβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβ==++-=++-⎡⎤⎣⎦==++-=+--⎡⎤⎣⎦ 11. 和差化积公式(1)设:A=α+β, B=α-β,()()()()sin sin sin sin sin cos cos sin sin cos cos sin 2sin cos 2sin cos 222sin cos 22sin sin sin sin sin cos cos sin sin cos cos sin 2cos si A B A B A B A B αβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβα+=++-=++-=++-+--⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭+-⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭-=+--=+-+=n 2cos sin 222cos sin 22A B A B βαβαβαβαβ++-+-+⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭+-⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭(2)设:cos sin αα==∵22cos sin 1αα+=()()sin sin cos cos sin sin cos sin sin b a θθθθαθαθαθ+=+=+=+12. 其他常用公式()()()()()()()()()()()()()()000sin 360sin cos 360cos tan 360tan sin 90cos cos 90sin 1tan 90tan sin 90cos cos 90sin 1tan 90tan sin 90cos cos 90sin 1tan 90tan sin 180sin cos 180cos n n n θθθθθθθθθθθθθθθθθθθθθθθθθθθ+⨯=+⨯=+⨯=︒-=︒-=︒-=︒+=︒+=-︒+=--︒=--︒=-︒=-︒-=︒-=-()()()()()()()()tan 180tan sin 180sin cos 180cos tan 180tan sin sin cos cos tan tan tan 2190 1cos 1cos 11sin 1sin 1n θθθθθθθθθθθθθθθθθθθ︒-=-±︒=-±︒=-±︒=-=--=-=-+⨯︒⎡⎤⎣⎦-≤≤⇒≤-≤≤⇒≤不存在在计算机中,三角函数的算法是这样的,其中x 用弧度计算()()1357210246sin 1!3!5!7!21!cos 0!2!4!6!2!n n nn x x x x x x n x x x x x x n +=∞=∞=-+-+=+=-+-+=∑∑推导公式:(a+b+c)/(sinA+sinB+sinC)=2R(其中,R为外接圆半径) 由正弦定理有a/sinA=b/sinB=c/sinC=2R所以a=2R*sinAb=2R*sinBc=2R*sinC加起来a+b+c=2R*(sinA+sinB+sinC)带入(a+b+c)/(sinA+sinB+sinC)=2R*(sinA+sinB+sinC)/(sinA+sinB+sinC)=2R 两角和公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-cosAsinBcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)cot(A+B)=(cotAcotB-1)/(cotB+cotA)cot(A-B)=(cotAcotB+1)/(cotB-cotA)倍角公式Sin2A=2SinA?CosA对数的性质及推导用^表示乘方,用log(a)(b)表示以a为底,b的对数*表示乘号,/表示除号定义式:若a^n=b(a>0且a≠1)则n=log(a)(b)基本性质:1.a^(log(a)(b))=b2.log(a)(MN)=log(a)(M)+log(a)(N);3.log(a)(M/N)=log(a)(M)-log(a)(N);4.log(a)(M^n)=nlog(a)(M)推导1.这个就不用推了吧,直接由定义式可得(把定义式中的[n=log(a)(b)]带入a^n=b)2.MN=M*N由基本性质1(换掉M和N)a^[log(a)(MN)]=a^[log(a)(M)]*a^[log(a)(N)]由指数的性质a^[log(a)(MN)]=a^{[log(a)(M)]+[log(a)(N)]}又因为指数函数是单调函数,所以log(a)(MN)=log(a)(M)+log(a)(N)3.与2类似处理MN=M/N由基本性质1(换掉M和N)a^[log(a)(M/N)]=a^[log(a)(M)]/a^[log(a)(N)]由指数的性质a^[log(a)(M/N)]=a^{[log(a)(M)]-[log(a)(N)]}又因为指数函数是单调函数,所以4.与2类似处理M^n=M^n由基本性质1(换掉M)a^[log(a)(M^n)]={a^[log(a)(M)]}^n由指数的性质a^[log(a)(M^n)]=a^{[log(a)(M)]*n}又因为指数函数是单调函数,所以log(a)(M^n)=nlog(a)(M)其他性质:性质一:换底公式log(a)(N)=log(b)(N)/log(b)(a)推导如下N=a^[log(a)(N)]a=b^[log(b)(a)]综合两式可得N={b^[log(b)(a)]}^[log(a)(N)]=b^{[log(a)(N)]*[log(b)(a)]}又因为N=b^[log(b)(N)]所以b^[log(b)(N)]=b^{[log(a)(N)]*[log(b)(a)]}所以log(b)(N)=[log(a)(N)]*[log(b)(a)]{这步不明白或有疑问看上面的} 所以log(a)(N)=log(b)(N)/log(b)(a)性质二:(不知道什么名字)推导如下由换底公式[lnx是log(e)(x),e称作自然对数的底]log(a^n)(b^m)=ln(a^n)/ln(b^n)由基本性质4可得log(a^n)(b^m)=[n*ln(a)]/[m*ln(b)]=(m/n)*{[ln(a)]/[ln(b)]}再由换底公式log(a^n)(b^m)=m/n*[log(a)(b)]--------------------------------------------(性质及推导完)公式三:log(a)(b)=1/log(b)(a)证明如下:由换底公式log(a)(b)=log(b)(b)/log(b)(a)----取以b为底的对数,log(b)(b)=1=1/log(b)(a)还可变形得:log(a)(b)*log(b)(a)=1平方关系:sin^2(α)+cos^2(α)=1tan^2(α)+1=sec^2(α)c ot^2(α)+1=csc^2(α)·商的关系:tanα=sinα/cosαcotα=cosα/sinα·倒数关系:tanα·cotα=1sinα·cscα=1cosα·secα=1万能公式:sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]常用的诱导公式有以下几组:公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanαsin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanα(以上k∈Z)一般的最常用公式有:Sin(A+B)=SinA*CosB+SinB*CosASin(A-B)=SinA*CosB-SinB*CosACos(A+B)=CosA*CosB-SinA*SinBCos(A-B)=CosA*CosB+SinA*SinBTan(A+B)=(TanA+TanB)/(1-TanA*TanB) Tan(A-B)=(TanA-TanB)/(1+TanA*TanB) 平方关系:sin^2(α)+cos^2(α)=1tan^2(α)+1=sec^2(α)cot^2(α)+1=csc^2(α)·积的关系:sinα=tanα*cosαcosα=cotα*sinαtanα=sinα*secαcotα=cosα*cscαsecα=tanα*cscαcscα=secα*cotα·倒数关系:tanα·cotα=1sinα·cscα=1cosα·secα=1直角三角形ABC中,角A的正弦值就等于角A的对边比斜边,余弦等于角A的邻边比斜边正切等于对边比邻边,三角函数恒等变形公式·两角和与差的三角函数:cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)·辅助角公式:Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t),其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)·倍角公式:sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)tan(2α)=2tanα/[1-tan^2(α)]·三倍角公式:sin(3α)=3sinα-4sin^3(α)cos(3α)=4cos^3(α)-3cosα·半角公式:sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα·降幂公式sin^2(α)=(1-cos(2α))/2=versin(2α)/2cos^2(α)=(1+cos(2α))/2=vercos(2α)/2tan^2(α)=(1-cos(2α))/(1+cos(2α))·万能公式:sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]·积化和差公式:sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·和差化积公式:sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·其他:sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*( n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*( n-1)/n]=0以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0部分高等内容·高等代数中三角函数的指数表示(由泰勒级数易得):sinx=[e^(ix)-e^(-ix)]/(2i)cosx=[e^(ix)+e^(-ix)]/2tanx=[e^(ix)-e^(-ix)]/[ie^(ix)+ie^(-ix)]泰勒展开有无穷级数,e^z=exp(z)=1+z/1!+z^2/2!+z^3/3!+z^4/4!+…+z^n/n!+…此时三角函数定义域已推广至整个复数集。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
⒗最简单的三角方程
方程 sin x a
cos x a
tgx a
a 1 a 1 a 1 a 1
方程的解集
x | x 2k arcsin a, k Z
x | x k 1k arcsin a, k Z
x | x 2k arccos a, k Z
诀:函数名不变,符号看象限)
⑵ 、 、 3 、 3 的三角函数值,等于 的异名函数
2
2
2
2
..
值,前面加上一个把 看成锐角时原函数值的符号。(口诀:函数名改
变,符号看象限)
四、和角公式和差角公式
sin( ) sin cos cos sin sin( ) sin cos cos sin cos( ) cos cos sin sin cos( ) cos cos sin sin
它的余角的正弦值。由A B 90
得B 90 A sin A cosB
cos A sin B
B
sin A cos(90 A)
斜边 c
对 a边
b
cos A sin(90 A) A
邻边 C
4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于
它的余角的正切值 由A B 90
而减小。 7、正切、余切的增减性: 当 0°< <90°时,tan 随 的增大而增大,cot 随 的增大而
减小。
1、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未 知的边和角。依据:①边的关系: a2 b2 c2 ;②角的关系:A+B=90°; ③边角关系:三角函数的定义。(注意:尽量避免使用中间数据和除法)
l
3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位 角。如图 3,OA、OB、OC、OD 的方向角分别是:45°、135°、225°。
4、指北或指南方向线与目标方向 线所成的小于 90°的水平角,叫做 方向角。如图 4,OA、OB、OC、OD 的方向角分别是:北偏东 30°(东北方 向) , 南偏东 45°(东南方向), 南偏西 60°(西南方向), 北偏西 60°(西北方向)。 sin(α+β)=sinαcosβ+cosαsinβ sin(α-β)=sinαcosβ-cosαsinβ cos(α+β)=cosαcosβ-sinαsinβ cos(α-β)=cosαcosβ+sinαsinβ
⑤ cos x sin ctg
⑥
r
csc r 1 ctg sec y sin
⑵倒数关系: sin csc cos sec tg ctg 1
⑶平方关系: sin2 cos2 sec2 tg2 csc2 ctg2 1
⑷ a sin b cos a2 b2 sin( ) (其中辅助角 与点(a,b)在同一
2
cos cos 1 cos( ) cos( ) sin sin 1 cos( ) cos
2
2
⒕和差化积公式:
① sin
sin
2 sin
cos
2
2
③ cos cos 2 cos cos
2
2
② sin
sin
2 cos
sin
2
2
④ cos cos 2 sin sin
tan( ) tan tan 1 tan tan
tan( ) tan tan 1 tan tan
五、二倍角公式
sin 2 2sin cos cos2 cos2 sin2 2cos2 1 1 2sin2 … ()
tan 2
2 tan 1 tan2
二倍角的余弦公式 () 有以下常用变形:(规律:降幂扩角,升幂缩
象限
2 2 3 2 3 2
sin con tg
ctg
+ cos + sin + ctg + tg
+ cos - sin - ctg - tg
- cos - sin + ctg + tg
- cos + sin - ctg - tg
三角函数值等于 的异名三 角函数值,前面加上一个把 看作锐角时,原三角函数 值的符号;即:函数名改变,
商数关系: tan sin , cot cos 。
cos
sin
平方关系: sin2 cos2 1,1 tan2 sec2 ,1 cot2 csc2 。
三、诱导公式
⑴ 2k (k Z) 、 、 、 、 2 的三角函数值,等于 ..
的同名函数值,前面加上一个把 看成锐角时原函数值的符号。(口
x | x 2k arccos a, k Z
x | x k arctga, k Z
ctgx a
x | x k arcctga, k Z
三角公式汇总 2
一、任意角的三角函数
.. 在角 的终边上任取一点 P(x, y) ,记: r x2 y2 ,
正弦: sin y 余弦: cos x
- - + 2 - 2k +
- sin + sin - sin - sin
+ sin
+ cos - cos - cos + cos
+ cos
- tg - tg + tg - tg
+ tg
ctg
- ctg - ctg + ctg - ctg + ctg
三角函数值等于 的同名三角 函数值,前面加上一个把 看 作锐角时,原三角函数值的符 号;即:函数名不变,符号看
2
2
⒖反三角函数:
名称 反正弦函数
反余弦函数 反正切函数
arcsin x 1,1增
y arccosx 1,1减
y arctgx R 增
y arcctgx R 减
值域
2
,
2
0,
,
2 2
0,
性质 arcsin(-x) -arcsinx 奇
arccos(x) arccosx arctg(-x) - arctgx 奇
2、应用举例: (1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
铅垂线
视线
仰角 水平线 俯角
视线
h
i h:l
α
l
(2)坡面的铅直高度 h 和水平宽度 l 的比叫做坡度(坡比)。用字母 i 表 示,即 i h 。坡度一般写成1: m 的形式,如 i 1:5 等。
l
把坡面与水平面的夹角记作 (叫做坡角),那么 i h tan 。
i). tgA tgB tgC tgA tgB tgC ⒑二倍角公式:(含万能公式)
ii). tg A tg B tg A tg C tg B tg C 1 22 22 22
① sin 2
2 sin
cos
2tg 1 tg2
② cos 2
cos2
sin2
2 cos2
11
2 sin2
r
r
正切: tan y 余切: cot x
x
y
正割: sec r 余割: csc r
x
y
注:我们还可以用单位圆中的有向线段表示任意角的三角函数:如 ..
图,与单位圆有关的有向线段 MP 、 OM 、 AT 分别叫做角 的正弦线、余
弦线、正切线。
二、同角三角函数的基本关系式
倒数关系: sin csc 1, cos sec 1, tan cot 1。
角)
1 cos2 2cos2 1 sin 2 (sin cos)2
1 cos2 2sin2 1 sin 2 (sin cos)2
③ tg3
3tg tg3 1 3tg 2
tg tg(60 ) tg(60 )
⒓半角公式:(符号的选择由 所在的象限确定) 2
① sin 1 cos
2
2
④ cos2 1 cos
2
2
② sin2 1 cos
2
2
⑤1 cos 2 sin2 2
③ cos 1 cos
符号看象限
⒐和差角公式
① sin( ) sin cos cos sin ② cos( ) cos cos sin sin
③
tg(
)
tg 1 tg
tg tg
④ tg tg tg( )(1 tg tg )
⑤ tg( ) tg tg tg tg tg tg 其中当 A+B+C=π 时,有: 1 tg tg tg tg tg tg
2
2
⑥1 cos 2 cos2 2
⑦ 1 sin (cos sin )2 cos sin
22
22
⑧ tg 1 cos sin 1 cos 2 1 cos 1 cos sin
⒔积化和差公式:
sin cos 1 sin( ) sin( )
2
cos sin 1 sin( ) sin( )
可换成∠B):
定义
正 弦
sin
A
A的对边 斜边
余 弦
cos
A
A的邻边 斜边
正 切
tan
A
A的对边 A的邻边
余 切
cot
A
A的邻边 A的对边
表达式
sin A a c
cos A b c
tan A a b
cot A b a
取值范围
0 sin A 1 (∠A 为锐
角)
0 cosA 1 (∠A 为锐
三角函数定义及其三角 函数公式大全
Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】
