计量经济学第四章 多元线性回归模型
合集下载
计量经济学课程第4章(多元回归分析)
Page 2
§4.1 多元线性回归模型的两个例子
一、例题1：CD生产函数
Qt AKt 1 Lt 2 et
这是一个非线性函数，但取对数可以转变为一个 对参数线性的模型
ln Qt 0 1 ln Kt 2 ln Lt t
t ~ iid(0, 2 )
注意：“线性”的含义是指方程对参数而言是线 性的
R 2 1 RSS /(N K 1) TSS /(N 1)
调整思想： 对 R2 进行自由度调整。
Page 20
基本统计量TSS、RSS、ESS的自由度：
1.
TSS的自由度为N-1。基于样本容量N，TSS
N i1
(Yi
Y
)2
因为线性约束 Y 1 N
Y N
i1 i
而损失一个自由度。
分布的多个独立统计量平方加总，所得到的新统计量就服从
2 分布。
《计量经济学》，高教出版社2011年6月，王少平、杨继生、欧阳志刚等编著
Page 23
双侧检验
概 率 密 度
概率1－
0
2 1 / 2
2 /2
图4.3.1
2
（N-K-1）的双侧临界值
双侧检验：统计值如果落入两尾中的任何一个则拒绝原假设
《计量经济学》，高教出版社2011年6月，王少平、杨继生、欧阳志刚等编著
Page 24
单侧检验
概 率 密 度
概率 概率
0
2 1
2
图4.3.2 （2 N-K-1）的单侧临界值
H0：
2
2，
0
HA :
2
2 0
§4.1 多元线性回归模型的两个例子
一、例题1：CD生产函数
Qt AKt 1 Lt 2 et
这是一个非线性函数，但取对数可以转变为一个 对参数线性的模型
ln Qt 0 1 ln Kt 2 ln Lt t
t ~ iid(0, 2 )
注意：“线性”的含义是指方程对参数而言是线 性的
R 2 1 RSS /(N K 1) TSS /(N 1)
调整思想： 对 R2 进行自由度调整。
Page 20
基本统计量TSS、RSS、ESS的自由度：
1.
TSS的自由度为N-1。基于样本容量N，TSS
N i1
(Yi
Y
)2
因为线性约束 Y 1 N
Y N
i1 i
而损失一个自由度。
分布的多个独立统计量平方加总，所得到的新统计量就服从
2 分布。
《计量经济学》，高教出版社2011年6月，王少平、杨继生、欧阳志刚等编著
Page 23
双侧检验
概 率 密 度
概率1－
0
2 1 / 2
2 /2
图4.3.1
2
（N-K-1）的双侧临界值
双侧检验：统计值如果落入两尾中的任何一个则拒绝原假设
《计量经济学》，高教出版社2011年6月，王少平、杨继生、欧阳志刚等编著
Page 24
单侧检验
概 率 密 度
概率 概率
0
2 1
2
图4.3.2 （2 N-K-1）的单侧临界值
H0：
2
2，
0
HA :
2
2 0
多元线性回归的计算模型
多元线性回归的计算模型多元线性回归模型的数学表示可以表示为：Y=β0+β1X1+β2X2+...+βkXk+ε，其中Y表示因变量，Xi表示第i个自变量，βi表示第i个自变量的回归系数（即自变量对因变量的影响），ε表示误差项。
1.每个自变量与因变量之间是线性关系。
2.自变量之间相互独立，即不存在多重共线性。
3.误差项ε服从正态分布。
4.误差项ε具有同方差性，即方差相等。
5.误差项ε之间相互独立。
为了估计多元线性回归模型的回归系数，常常使用最小二乘法。
最小二乘法的目标是使得由回归方程预测的值与实际值之间的残差平方和最小化。
具体步骤如下：1.收集数据。
需要收集因变量和多个自变量的数据，并确保数据之间的正确对应关系。
2.建立模型。
根据实际问题和理论知识，确定多元线性回归模型的形式。
3.估计回归系数。
利用最小二乘法估计回归系数，使得预测值与实际值之间的残差平方和最小化。
4.假设检验。
对模型的回归系数进行假设检验，判断自变量对因变量是否显著。
5. 模型评价。
使用统计指标如决定系数（R2）、调整决定系数（adjusted R2）、标准误差（standard error）等对模型进行评价。
6.模型应用与预测。
通过多元线性回归模型，可以对新的自变量值进行预测，并进行决策和提出建议。
多元线性回归模型的计算可以利用统计软件进行，例如R、Python中的statsmodels库、scikit-learn库等。
这些软件包提供了多元线性回归模型的函数和方法，可以方便地进行模型的估计和评价。
在计算过程中，需要注意检验模型的假设前提是否满足，如果不满足可能会影响到模型的可靠性和解释性。
总而言之，多元线性回归模型是一种常用的预测模型，可以分析多个自变量对因变量的影响。
通过最小二乘法估计回归系数，并进行假设检验和模型评价，可以得到一个可靠的模型，并进行预测和决策。
计量经济学-多元回归PPT课件
. 28
F与t的关系（一元回归模型）
Y i B 1 B 2X 2 u
检验统计:t 量 b2 b2
b2 x2
sb2 ˆ / x2
e2
n2
t2
b22 x 2 e2
yˆ 2 / 1 e2
F
n2
n .2
29
. 5
4.3 多元回归参数的估计
Y i B 1 B 2 X 2 i B 3 X 3 i u i
最小二乘准则： 真实值与拟合值的离差平方和最小。
e n
n
2
i
Yi
2
Yˆi
i1
i1
n
2
Yi b1b2 X2i b3 X3i
i1
. 6
回归系数的OLS估计量
b1Yb2X2b3X3 b2x2i yx i2 2 i xx 3 23 2 ii (x 3 x i2 yiix3 i)x 22ix3i
-------------------------------------------------------------------------------------
y Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------------------------------------------------------------------------------
educ: 受教育的年数 exper: 工作经历 tenure: 现任职务的任期 当一个人在同一企业多待一年，对工资的影响？
. 19
多元回归的拟合优度R2
多元相关系数（复相关系数）： R 2 ✓ 度量因变量Y与所有解释变量的线性相关程度。 简单相关系数r： ✓ 度量因变量Y与解释变量Xi的线性相关程度。 ✓ 一元回归模型的r2=相关系数r的平方
计量经济学-多元线性回归模型
多元线性回归模型的表达式
Y=β0+β1X1+β2X2+...+βkXk+ε，其中Y为因变 量，X1, X2,..., Xk为自变量，β0, β1,..., βk为回归 系数，ε为随机误差项。
多元线性回归模型的假设条件
包括线性关系假设、误差项独立同分布假设、无 多重共线性假设等。
研究目的与意义
研究目的
政策与其他因素的交互作用
多元线性回归模型可以引入交互项，分析政策与其他因素（如技 术进步、国际贸易等）的交互作用，更全面地评估政策效应。
实例分析：基于多元线性回归模型的实证分析
实例一
预测某国GDP增长率：收集该国历史数据，包括GDP、投资、消费、出口等变量，建立 多元线性回归模型进行预测，并根据预测结果提出政策建议。
最小二乘法原理
最小二乘法是一种数学优化技术，用 于找到最佳函数匹配数据。
残差是观测值与预测值之间的差，即 e=y−(β0+β1x1+⋯+βkxk)e = y (beta_0 + beta_1 x_1 + cdots + beta_k x_k)e=y−(β0+β1x1+⋯+βkxk)。
在多元线性回归中，最小二乘法的目 标是使残差平方和最小。
t检验
用于检验单个解释变量对被解释变量的影响 是否显著。
F检验
用于检验所有解释变量对被解释变量的联合 影响是否显著。
拟合优度检验
通过计算可决系数（R-squared）等指标， 评估模型对数据的拟合程度。
残差诊断
检查残差是否满足独立同分布等假设，以验 证模型的合理性。
04
多元线性回归模型的检验与 诊断
Y=β0+β1X1+β2X2+...+βkXk+ε，其中Y为因变 量，X1, X2,..., Xk为自变量，β0, β1,..., βk为回归 系数，ε为随机误差项。
多元线性回归模型的假设条件
包括线性关系假设、误差项独立同分布假设、无 多重共线性假设等。
研究目的与意义
研究目的
政策与其他因素的交互作用
多元线性回归模型可以引入交互项，分析政策与其他因素（如技 术进步、国际贸易等）的交互作用，更全面地评估政策效应。
实例分析：基于多元线性回归模型的实证分析
实例一
预测某国GDP增长率：收集该国历史数据，包括GDP、投资、消费、出口等变量，建立 多元线性回归模型进行预测，并根据预测结果提出政策建议。
最小二乘法原理
最小二乘法是一种数学优化技术，用 于找到最佳函数匹配数据。
残差是观测值与预测值之间的差，即 e=y−(β0+β1x1+⋯+βkxk)e = y (beta_0 + beta_1 x_1 + cdots + beta_k x_k)e=y−(β0+β1x1+⋯+βkxk)。
在多元线性回归中，最小二乘法的目 标是使残差平方和最小。
t检验
用于检验单个解释变量对被解释变量的影响 是否显著。
F检验
用于检验所有解释变量对被解释变量的联合 影响是否显著。
拟合优度检验
通过计算可决系数（R-squared）等指标， 评估模型对数据的拟合程度。
残差诊断
检查残差是否满足独立同分布等假设，以验 证模型的合理性。
04
多元线性回归模型的检验与 诊断
计量经济学(庞浩主编)第四章练习题参考解答
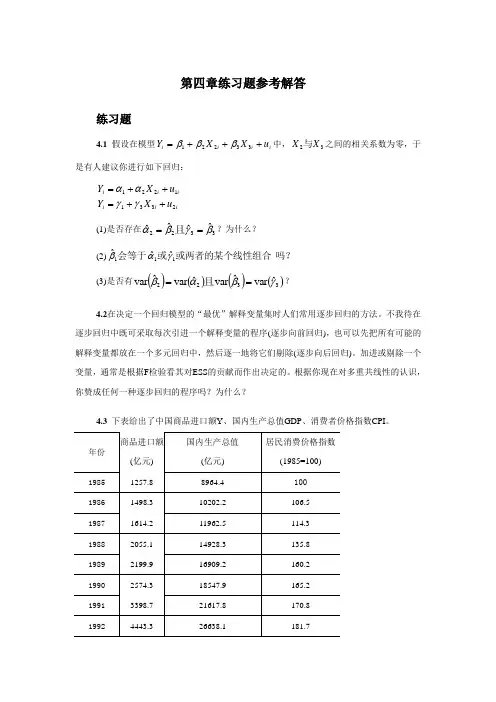
第四章练习题参考解答练习题4.1 假设在模型i i i i u X X Y +++=33221βββ中，32X X 与之间的相关系数为零，于是有人建议你进行如下回归：ii i i i i u X Y u X Y 23311221++=++=γγαα(1)是否存在3322ˆˆˆˆβγβα==且？为什么？ (2)吗？或两者的某个线性组合或会等于111ˆˆˆγαβ (3)是否有()()()()3322ˆvar ˆvar ˆvar ˆvar γβαβ==且？ 4.2在决定一个回归模型的“最优”解释变量集时人们常用逐步回归的方法。
不我待在逐步回归中既可采取每次引进一个解释变量的程序(逐步向前回归)，也可以先把所有可能的解释变量都放在一个多元回归中，然后逐一地将它们剔除(逐步向后回归)。
加进或剔除一个变量，通常是根据F 检验看其对ESS 的贡献而作出决定的。
根据你现在对多重共线性的认识，你赞成任何一种逐步回归的程序吗？为什么？4.3 下表给出了中国商品进口额Y 、国内生产总值GDP 、消费者价格指数CPI 。
资料来源：《中国统计年鉴》，中国统计出版社2000年、20XX 年。
请考虑下列模型：i t t t u CPI GDP Y ++=ln ln ln 321βββ＋ (1)利用表中数据估计此模型的参数。
(2)你认为数据中有多重共线性吗？ (3)进行以下回归：it t i t t i t t v CPI C C GDP v CPI B B Y v GDP A A Y 321221121ln ln ln ln ln ln ++=+=+=＋＋根据这些回归你能对数据中多重共线性的性质说些什么？(4)假设数据有多重共线性，但32ˆˆββ和在5%水平上个别地显著，并且总的F 检验也是显著的。
对这样的情形，我们是否应考虑共线性的问题？4.4 自己找一个经济问题来建立多元线性回归模型，怎样选择变量和构造解释变量数据矩阵X 才可能避免多重共线性的出现？4.5 克莱因与戈德伯格曾用1921-1950年(1942-1944年战争期间略去)美国国内消费Y 和工资收入X1、非工资—非农业收入X2、农业收入X3的时间序列资料，利用OLSE 估计得出了下列回归方程：37.107 95.0 (1.09) (0.66) (0.17) (8.92) 3121.02452.01059.1133.8ˆ2==+++=F R X X X Y (括号中的数据为相应参数估计量的标准误)。
计量经济学多元线性回归ppt课件
回归中因运算近似而导致的误差会比较大。
Beta系数
有时，我们会看见“规范化系数〞或“Beta系数 〞，这些称号有着特殊的意义
运用Beta系数是由于有时我们把y和各个x交换为 规范化版本——也就是，减去均值后除以规范离 差。
系数反映对于一单位x的规范离差的y的规范离差。
Beta系数
样本回归方程的标准形式是
多元回归分析 Multiple Regression Analysis
y = b0 + b1x1 + b2x2 + . . . bkxk + u
4.进一步的问题
本章大纲
数据的测度单位换算对OLS统计量的影响 对函数方式的进一步讨论 拟合优度和回归元选择的进一步讨论 预测和残差分析
课堂提纲PacksFa NhomakorabeaincIntercept
Observations R-squared SSR SER
Table 6.1
(1) bwght
(2)bwghtlbs
-0.4634 (0.0916) --
0.0927 (0.0292) 116.794 (1.049) 8 0.0298 557,485.51 20.063
定义：
y i y 2 to su to a s m flqu Sa S总 rT es平 y ˆi y 2expslu o am sifq nu e Sa d S r解 E es释
u ˆi2 ressiu d om su fqau S la S r残 R es 差平
SST= SSE + SSR
现 在 ， bˆ j 与 ˆ j的 关 系 如 何 ？
Beta系数
可以看到
yˆi
ˆ y
Beta系数
有时，我们会看见“规范化系数〞或“Beta系数 〞，这些称号有着特殊的意义
运用Beta系数是由于有时我们把y和各个x交换为 规范化版本——也就是，减去均值后除以规范离 差。
系数反映对于一单位x的规范离差的y的规范离差。
Beta系数
样本回归方程的标准形式是
多元回归分析 Multiple Regression Analysis
y = b0 + b1x1 + b2x2 + . . . bkxk + u
4.进一步的问题
本章大纲
数据的测度单位换算对OLS统计量的影响 对函数方式的进一步讨论 拟合优度和回归元选择的进一步讨论 预测和残差分析
课堂提纲PacksFa NhomakorabeaincIntercept
Observations R-squared SSR SER
Table 6.1
(1) bwght
(2)bwghtlbs
-0.4634 (0.0916) --
0.0927 (0.0292) 116.794 (1.049) 8 0.0298 557,485.51 20.063
定义：
y i y 2 to su to a s m flqu Sa S总 rT es平 y ˆi y 2expslu o am sifq nu e Sa d S r解 E es释
u ˆi2 ressiu d om su fqau S la S r残 R es 差平
SST= SSE + SSR
现 在 ， bˆ j 与 ˆ j的 关 系 如 何 ？
Beta系数
可以看到
yˆi
ˆ y
第四章 多元线性回归模型(计量经济学,潘省初)
Y1 β 0 β 1 X 11 β 2 X 21 β 3 X 31 ... β K X K 1 u1 Y2 β 0 β 1 X 12 β 2 X 22 β 3 X 32 ... β K X K 2 u2 ...... Yn β 0 β 1 X 1n β 2 X 2 n β 3 X 3n ... β K X Kn un
ˆ 116.7 0.112 X 0.739 P Y (9.6) (0.003) (0.114)
R 2 0.99
Y和X的计量单位为10亿美元 (按1972不变价格计算).
食品价格平减指数 P 100，（ 1972 100） 总消费支出价格平减指数
3
多元线性回归模型中斜率系数的含义
上述假设条件可用矩阵表示为以下四个条件：
9
(1) E(u)=0 (2)
由于
E (uu) 2 I n
u1 u2 uu u1 u2 ... u n
2
u12 u1u2 ...... u1un 2 u2u1 u2 ...... u2un ... un ................................. 2 unu1 unu2 ...... un
一．假设条件 （1）E(ut)=0, t=1,2,…,n （2）E(ui uj)=0, i≠j （3）E(ut2)=σ2, t=1,2,…,n （4）Xjt是非随机量， j=1,2, … k
t=1,2, … n
8
除上面4条外，在多个解释变量的情况下，还有 两个条件需要满足： （5）（K+1）< n; 即观测值的数目要大于待估计的参数的个数 （要有足够数量的数据来拟合回归线）。 （6）各解释变量之间不存在严格的线性关系。
计量经济学 )多元线性回归模型的统计检验
i i
ˆ) 0 X i1 (Yi Y i
ˆ) 0 X i 2 (Yi Y i
… X (Y Y ˆ) 0 ik i i
所以 从而
ˆ )(Y ˆ Y ) 0 (Y Y
i i
ˆ ) 2 (Y ˆ Y )2 (Y Y ) (Y Y i i i i
解释的那部分离差的大小。
• 那么，TSS、ESS、RSS之间存在的如下关系：
总离差平方和 = 回归平方和 + 残差平方和
TSS
=
ESS
+
RSS
关于TSS=ESS+ RSS的证明过程（教材P73） 证明： 将TSS，即总离差平方和进行分解：
ˆ ) (Y ˆ Y )) 2 TSS (Y Y ) 2 ((Y Y
• 拟合优度检验：检验模型对样本观测值的拟合 程度。
• 在一元回归模型中，拟合优度检验是通过构造 一个可以表征拟合程度的统计量R2来实现。
• 在多元回归模型中，也可以用该统计量来衡量 样本回归线对样本观测值的拟合程度。
总离差平方和、回归平方和及残差平方和
• 定义
TSS (Y Y ) 2
i
2 ˆ y i
y
2 i
1
yi
ei
2 2
检验模型的拟合优度。 R2叫做多重可决系数，也简称为可决系数或判定系数。
毫无疑问，R2越接近于1，模型的拟合优度越高。 但是在应用过程中人们发现，如果在模型中增加一个解释变量， 那么模型的回归平方和随之增大，从而R2也随之增大。 这就给人一个错觉：要使模型拟合得好，就必须增加解释变量。 所以，用来检验拟合优度的统计量必须能够防止这种倾向。
说 明
ˆ) 0 X i1 (Yi Y i
ˆ) 0 X i 2 (Yi Y i
… X (Y Y ˆ) 0 ik i i
所以 从而
ˆ )(Y ˆ Y ) 0 (Y Y
i i
ˆ ) 2 (Y ˆ Y )2 (Y Y ) (Y Y i i i i
解释的那部分离差的大小。
• 那么，TSS、ESS、RSS之间存在的如下关系：
总离差平方和 = 回归平方和 + 残差平方和
TSS
=
ESS
+
RSS
关于TSS=ESS+ RSS的证明过程（教材P73） 证明： 将TSS，即总离差平方和进行分解：
ˆ ) (Y ˆ Y )) 2 TSS (Y Y ) 2 ((Y Y
• 拟合优度检验：检验模型对样本观测值的拟合 程度。
• 在一元回归模型中，拟合优度检验是通过构造 一个可以表征拟合程度的统计量R2来实现。
• 在多元回归模型中，也可以用该统计量来衡量 样本回归线对样本观测值的拟合程度。
总离差平方和、回归平方和及残差平方和
• 定义
TSS (Y Y ) 2
i
2 ˆ y i
y
2 i
1
yi
ei
2 2
检验模型的拟合优度。 R2叫做多重可决系数，也简称为可决系数或判定系数。
毫无疑问，R2越接近于1，模型的拟合优度越高。 但是在应用过程中人们发现，如果在模型中增加一个解释变量， 那么模型的回归平方和随之增大，从而R2也随之增大。 这就给人一个错觉：要使模型拟合得好，就必须增加解释变量。 所以，用来检验拟合优度的统计量必须能够防止这种倾向。
说 明
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
K
=
(X' X)
β
1
X11
...
X
K1
1 ... 1 Y1
X12
...
X1n
Y2
... ... ... ...
XK2
...
X
Kn
Yn
X'
Y
即 (X' X)β X'Y
β(XX)1XY
15
三. 最小二乘估计量 β 的性质
我们的模型为 YXu
估计式为
Yˆ
Xβ
1．β 的均值
β(XX)1XY
因而 ˆ 是线性估计量。
23
现设 *为 的任意一个线性无偏估计量，即 * cY
其中 c 是一个(K+1)*n非随机元素矩阵。则
* c Y c (X u ) c X c u
E( *) E(c X cu) c X cE(u) cX
显然，若要 * 为无偏估计量，即 E(*) ，只有
问题是选择 ˆ0,ˆ1,....ˆ,k ，使得残差平方和最小。
残差为：
et Yt Y ˆt
Yt ˆ0ˆ1X1t ....ˆKXKt
12
要使残差平方和
S e t2 Y t ˆ 0 ˆ 1 X 1 t ... ˆ K X K t2
为最小，则应有：
S ˆ00 , S ˆ10 , ..., ˆ S K0
、 (6) 两 条 即矩阵X的秩 =（K+1)< n 当然，为了后面区间估计和假设检验的需要，还 要加上一条：
（5） u t ～ N(0,2) ，t=1,2,…n
11
二．最小二乘估计
我们的模型是： Y t 0 1 X 1 t 2 X 2 t . . . k X k t u t t=1,2,…n
E X X 1 X u u X X X 1
X X 1 X E u u X X X 1
X X 1 X 2 In X X X 1 X X 1X X X X 1 2
XX12
20
如前所述，我们得到的实际上不仅是β 的方差，而且是
一个方差-协方差矩阵，为了反映这一事实，我们用下面的 符号表示之：
......
......
β0
Xkt β1
Xkt X1t ......βK
XKt 2
XktYt
按矩阵形式，上述方程组可表示为：
14
n
X1t
...
XKt
X1t X1t 2
...
XKtX1t
...
XKt
β
0
...
...
...
X1t XKt
...
XKt2
β 1
..
β
与双变量线性模型相似， 2的无偏估计量是
ˆ2
et 2
n (K 1)
分母是 et2 的自由度，这是因为我们在估计
的过程中，失去了（K+1）个自由。
β0,β1,.
.β.k
4． 高斯-马尔科夫定理
对于 YXβu 以及标准假设条件（1）-（4），
普通最小二乘估计量是最佳线性无偏估计量（BLUE）
22
我们得到如下K+1个方程（即正规方程）：
13
β0 n
β1 X1t ......βK XKt Yt
β0 X1t β1 X1t2 ......βK X1t XKt X1tYt
β0 X2t β1 X2t X1t ......βK X2t XKt X2tYt
......
......
即 IDXI
因而有 DX 0
cc(XX)1XD(XX)1XD (XX)1XDX(XX)1D
(XX)1XX(XX)1(XX)1XD D X(XX)1D D
由 DX 0从而 XD 0，因此上式中间两项为0，我们有
cc(XX)1D D
26
因此
Var ( *) 2 c c
2 ( X X ) 1 D D
cX I ， I 为（K+1）阶单位矩阵。
24
* 的方差为：
Var ( * ) Var (c X cu)
Var (cu) c Var (u) c
2 cc
我们可将 c 写成 c(XX)1XD
从而将 的任意线性无偏估计量 * 与OLS估计量 ˆ 联系
起来。
25
由 cX I 可推出： (X X ) 1X XD XI
1
X
1
...
1
X 11 X 12 ... X 1n
... ... ... ...
X K1
X
K
2
...
X
Kn
0 1
2
,
...
K
u 1
u
u2
... un
注:转“矩阵代数基础”
7
第二节 多元线性回归模型的估计
多元线性回归模型的估计与双变量线性模型类似，仍采用 OLS法。当然，计算要复杂得多，通常要借助计算机。理论 推导需借助矩阵代数。下面给出普通最小二乘法应用于多元 线性回归模型的假设条件、估计结果及所得到的估计量的性 质。
YY YXβ
30
而
Y Y 2 Y 2 n Y 2 Y Y n Y 2
将上述结果代入R2的公式，得到：
R2 1 Ye2Y2
YY2 e2 YY2
YYnY2(YYYXˆ)
YYnY2
YX ˆ nY 2
YY nY 2
这就是决定系数 R2 的矩阵形式。
31
二．修正决定系数：R 2
残差平方和的一个特点是，每当模型增加一个解 释变量，并用改变后的模型重新进行估计，残差平 方和的值会减小。
在这个模型中，Y由X1、X2、X3、… XK所解释， 有K+1个未知参数β0、β1、β2、…βK 。
这里，“斜率”βj的含义是其它变量不变的情况 下，Xj改变一个单位对因变量所产生的影响。
2
例1： Y β 0 β 1X β 2P u
其中，Y=在食品上的总支出 X=个人可支配收入 P=食品价格指数
我们已在上一段中证明了无偏性，下面证明线性和最小方 差性。证明的路子与双变量模型中类似，只不过这里我们采 用矩阵和向量的形式。
由OLS估计量 ˆ 的公式
β(XX)1XY
可知, ˆ 可表示为一个矩阵和因变量观测值向量 Y 的乘积：
ˆ kY
其中 k(XX)1X 是一个 (K+1)*n 非随机元素矩阵。
17
2．β 的方差
为求Var( β )，我们考虑
Eβ ββ β
这是一个（K+1）*(K+1)矩阵，其主对角线上元素即
构成
Var(
β
)，非主对角线元素是相应的协方差，如
下所示：
18
β0β0
E
β1β1
...
β0β0
βKβK
β1β1
...
βKβK
V a(β r 0)
C
o(vβ1,β0)
...
3
多元线性回归模型中斜率系数的含义
上例中斜率系数的含义说明如下： 价格不变的情况下，个人可支配收入每上升10
亿美元（1个billion），食品消费支出增加1.12亿 元（0.112个 billion）。
收入不变的情况下，价格指数每上升一个点， 食品消费支出减少7.39亿元（0.739个billion）
第四章 多元线性回归模型
简单线性回归模型的推广
1
第一节 多元线性回归模型的概念
在许多实际问题中，我们所研究的因变量的变动 可能不仅与一个解释变量有关。因此，有必要考虑线 性模型的更一般形式，即多元线性回归模型：
Y t β 0 β 1 X 1 t β 2 X 2 t . .β k .X k t u t t=1,2,…,n
由此可以推论，决定系数是一个与解释变量的个 数有关的量：
解释变量个数增加 e2 减小 R2 增大
也就是说，人们总是可以通过增加模型中解释变量 的方法来增大 R2 的值。因此，用 R2 来作为拟合优 度的测度，不是十分令人满意的。
Y=α+βX + u
我们有
R2
1
e2 Y Y2
其中， e2 =残差平方和
28
对于多元线性模型
Y 01 X 1 . ..K X K u
我们可用同样的方法定义决定系数：
R2
解释变差 总变差1
e2 Y Y
2
或 R2 ESS1 RSS TSS TSS
为方便计算，我们也可以用矩阵形式表示R2
29
e 我们有：残差
Y Y
其中， Y X β
残差平方和：
et 2 ee
(Y Y)(Y Y) (YXβ)(YXβ)
(YβX)Y (Xβ)
Y Y β X Y Y X β β X X β
Y Y β X Y Y X β β X X (X X ) 1 X Y
Y Y β X Y Y X β β X Y
C
o(vβK,β0)
Co(vβ0,β1)
Va(β r1)
...
Co(vβK,β1)
... Co(vβ0,βK) ... Co(vβ1,βK)
...
...
...
Va(β r K)
下面推导此矩阵的计算公式.
19
由上一段的结果，我们有 因此
ββ(XX)1Xu
E β β β β E X X 1 X uX X 1 X u
一．假设条件 （1）E(ut)=0, t=1,2,…,n （2）E(ui uj)=0, i≠j （3）E(ut2)=σ2, t=1,2,…,n （4）Xjt是非随机量， j=1,2, … k