数列求和课件
合集下载
课件4:6.4 数列求和

若干项. ❖ (4)倒序相加法 ❖ 把数列分别正着写和倒着写再相加,即等差数列求和公式的
推导过程的推广. ❖ (5)错位相减法 ❖ 主要用于一个等差数列与一个等比数列对应项相乘所得的数
列的求和,即等比数列求和公式的推导过程的推广.
❖ (6)并项求和法
❖ 一个数列的前n项和中,可两两结合求解,则称之为并项求 和.形如an=(-1)nf(n)类型,可采用两项合并求解.
活学活用 2 (2015·黑龙江哈尔滨三模)已知数列{an}的各
项均为正数,前 n 项和为 Sn,且 Sn=ana2n+1,n∈N+.
(1)求证:数列{an}是等差数列;
(2)设 bn=21Sn,Tn=b1+b2+…+bn,求 Tn.
(1)证明:∵2Sn=a2n+an.
①
当 n=1 时,2a1=a21+a1,∵a1>0,∴a1=1.
第六章 数 列
6.4 数列求和
考纲要求
❖ 1.熟练掌握等差、等比数列的前n项和公式. ❖ 2.掌握非等差、等比数列求和的几种常见方法. ❖ 3.能在具体的问题情境中识别数列的等差关系或等比关系,并
能用相关知识解决相应的问题.
[要点梳理] 1.求数列的前 n 项和的方法 (1)公式法 ①等差数列的前 n 项和公式 Sn=na12+an=na1+nn2-1d.
即(an+an-1)(an-an-1-3)=0.
∵an+an-1>0,∴an-an-1=3(n≥2).
❖ 当a1=2时,a2=5,a6=17,此时a1,a2,a6不成等比数列, ∴a1≠2;
❖ 当a1=1时,a2=4,a6=16,此时a1,a2,a6成等比数列, ❖ ∴a1=1. ❖ ∴an=3n-2,bn=4n-1. ❖ (2)由(1)得 ❖ Tn=1×4n-1+4×4n-2+…+(3n-5)×41+(3n-2)×40,③ ❖ ∴4Tn=1×4n+4×4n-1+7×4n-2+…+(3n-2)×41. ④ ❖ 由④-③,得
《数列求和》课件

《数列求和》PPT课件
数列求和 PPT课件大纲
介绍
数列是数学中的重要概念,我们将探讨数列的定义和性质,以及数列求和的意义与公式
了解等差数列的定义和公式,能够根据公式计算等差数列的求和。
2
推导与应用
探究等差数列求和公式的推导过程,并学会利用公式解决实际问题。
3
实例演练
通过实例演练,加深对等差数列求和的理解和应用能力。
深入推导斯特林公式,掌握其原 理和推到过程。
应用示例
探索斯特林公式在数学和科学中 的实际应用,并解决相关问题。
零阶贝塞尔函数
1
定义与性质
学习零阶贝塞尔函数的定义和性质,了解其在数学和物理领域的重要作用。
2
公式推导
深入推导零阶贝塞尔函数的公式,掌握其基本原理。
3
应用案例
研究零阶贝塞尔函数在实际问题中的应用,加深对其应用场景的理解。
总结
数列求和在数学中具有重要的地位,掌握各种数列求和公式的区别和应用, 能够进一步拓展数列求和的研究方向。
等比数列求和
定义与公式
了解等比数列的定义和公式, 能够根据公式计算等比数列 的求和。
推导与应用
探究等比数列求和公式的推 导过程,并学会利用公式解 决实际问题。
实例演练
通过实例演练,加深对等比 数列求和的理解和应用能力。
斯特林公式
定义与定理
学习斯特林公式的定义和定理, 了解其在数学中的重要性。
推导过程
数列求和 PPT课件大纲
介绍
数列是数学中的重要概念,我们将探讨数列的定义和性质,以及数列求和的意义与公式
了解等差数列的定义和公式,能够根据公式计算等差数列的求和。
2
推导与应用
探究等差数列求和公式的推导过程,并学会利用公式解决实际问题。
3
实例演练
通过实例演练,加深对等差数列求和的理解和应用能力。
深入推导斯特林公式,掌握其原 理和推到过程。
应用示例
探索斯特林公式在数学和科学中 的实际应用,并解决相关问题。
零阶贝塞尔函数
1
定义与性质
学习零阶贝塞尔函数的定义和性质,了解其在数学和物理领域的重要作用。
2
公式推导
深入推导零阶贝塞尔函数的公式,掌握其基本原理。
3
应用案例
研究零阶贝塞尔函数在实际问题中的应用,加深对其应用场景的理解。
总结
数列求和在数学中具有重要的地位,掌握各种数列求和公式的区别和应用, 能够进一步拓展数列求和的研究方向。
等比数列求和
定义与公式
了解等比数列的定义和公式, 能够根据公式计算等比数列 的求和。
推导与应用
探究等比数列求和公式的推 导过程,并学会利用公式解 决实际问题。
实例演练
通过实例演练,加深对等比 数列求和的理解和应用能力。
斯特林公式
定义与定理
学习斯特林公式的定义和定理, 了解其在数学中的重要性。
推导过程
课件3:6.4 数列求和

(2)由(1)知a2n-11a2n+1=3-2n11-2n =12(2n1-3-2n1-1), 从而数列a2n-11a2n+1的前 n 项和为12(-11-11+11-13+… +2n1-3-2n1-1)=1-n2n.
三 错位相减法求和
【例 3】(2013·湖南)设 Sn 为数列{an}的前项和,已知 a1≠0,2an-a1=S1·Sn,n∈N*
【跟踪训练 2】 已知等差数列{an}的前 n 项和 Sn 满足 S3 =0,S5=-5.
(1)求{an}的通项公式; (2)求数列{a2n-11a2n+1}的前 n 项和.
解析:(1)设{an}的公差为 d, 则 Sn=na1+nn-2 1d. 由已知可得35aa11++31d0=d=0-5 ,解得ad1==-1 1 . 故{an}的通项公式为 an=2-n.
(2)因为 an=n,所以 a1=1,Sn=1+2+…+n=nn+2 1, 所以S1n=nn2+1=2(1n-n+1 1), 所以S11+S12+…+S1n
=2[(1-12)+(12-13)+…+(1n-n+1 1)] =2(1-n+1 1)=n2+n1.
【温馨提示】使用裂项相消法求和时,要注意正负项 相消时消去了哪些项,保留了哪些项,切不可漏写未被消 去的项,未被消去的项有前后对称的特点,实质上造成正 负相消是此法的根源与目的.
(1)证明:数列ann是等差数列; (2)设 bn=3n· an,求数列{bn}的前 n 项和 Sn.
解析:(1)证明:由已知可得na+n+11=ann+1, 即na+n+11-ann=1, 所以ann是以a11=1 为首项,1 为公差的等差数列.
(2)由(1)得ann=1+(n-1)·1=n,所以 an=n2. 从而 bn=n·3n. Sn=1×31+2×32+3×33+…+n·3n,① 3Sn=1×32+2×33+…+(n-1)·3n+n·3n+1.② ①-②得,-2Sn=31+32+…+3n-n·3n+1
第讲数列的求和精选课件

若一个数列是由等比数列或是等差数列组成,以 考查公式为主,可先分别求和,再将各部分合并,这就是我们说 的分组求和.
【互动探究】 1.(2019 年陕西)已知{an}是公差不为零的等差数列,a1=1,
且 a1,a3,a9 成等比数列. (1)求数列{an}的通项公式; (2)求数列{2 a n}的前 n 项和 Sn.
4.数列 112,214,318,…,n+21n,…的前 n 项和 Sn=______ __12_n_(n_+__1_)_+__1_-__21_n___.
5.数列{an}的通项公式 an=
1 n+
n+1,若前
n
项的和为
10,
则项数 n=___1_2_0___.
考点1 利用公式或分组法求和
例1:(2011 年重庆)设{an}是公比为正数的等比数列,a1=2, a3=a2+4.
数列求和常用的方法
1.公式法 (1)等差数列{an}的前
n
项和公式:Sn=nnaa1+ 12+nann2-,1d.
(2)等比数列{an}的前n项和Sn:①当q=1时,Sn=__n_a_1_;
a11-qn
a1-anq
②当 q≠1 时,Sn=____1_-__q___=____1_-__q__.
2.分组求和法 把一个数列分成几个可以直接求和的数列. 3.错位相减法 适用于一个等差数列和等比数列对应项相乘构成的数列求 和. 4.裂项相消法 有时把一个数列的通项公式分成两项差的形式,相加过程消 去中间项,只剩有限项再求和.
解析:(1)P1(-1,0),an=n-2,bn=2n-2. (2)f(n)=n2- n-2, 2,n为 n为奇偶数数,. 假设存在符合条件. ①若 k 为偶数,则 k+5 为奇数. 有 f(k+5)=k+3,f(k)=2k-2. 如果 f(k+5)=2f(k)-2,则 k+3=4k-6⇒k=3 与 k 为偶数矛 盾.故不符(舍去). ②若 k 为奇数,则 k+5 为偶数, 有 f(k+5)=2k+8,f(k)=k-2. ∴2k+8=2(k-2)-2 这样的 k 也不存在. 综上所述:不存在符合条件的 k.
【互动探究】 1.(2019 年陕西)已知{an}是公差不为零的等差数列,a1=1,
且 a1,a3,a9 成等比数列. (1)求数列{an}的通项公式; (2)求数列{2 a n}的前 n 项和 Sn.
4.数列 112,214,318,…,n+21n,…的前 n 项和 Sn=______ __12_n_(n_+__1_)_+__1_-__21_n___.
5.数列{an}的通项公式 an=
1 n+
n+1,若前
n
项的和为
10,
则项数 n=___1_2_0___.
考点1 利用公式或分组法求和
例1:(2011 年重庆)设{an}是公比为正数的等比数列,a1=2, a3=a2+4.
数列求和常用的方法
1.公式法 (1)等差数列{an}的前
n
项和公式:Sn=nnaa1+ 12+nann2-,1d.
(2)等比数列{an}的前n项和Sn:①当q=1时,Sn=__n_a_1_;
a11-qn
a1-anq
②当 q≠1 时,Sn=____1_-__q___=____1_-__q__.
2.分组求和法 把一个数列分成几个可以直接求和的数列. 3.错位相减法 适用于一个等差数列和等比数列对应项相乘构成的数列求 和. 4.裂项相消法 有时把一个数列的通项公式分成两项差的形式,相加过程消 去中间项,只剩有限项再求和.
解析:(1)P1(-1,0),an=n-2,bn=2n-2. (2)f(n)=n2- n-2, 2,n为 n为奇偶数数,. 假设存在符合条件. ①若 k 为偶数,则 k+5 为奇数. 有 f(k+5)=k+3,f(k)=2k-2. 如果 f(k+5)=2f(k)-2,则 k+3=4k-6⇒k=3 与 k 为偶数矛 盾.故不符(舍去). ②若 k 为奇数,则 k+5 为偶数, 有 f(k+5)=2k+8,f(k)=k-2. ∴2k+8=2(k-2)-2 这样的 k 也不存在. 综上所述:不存在符合条件的 k.
数列的求和优秀课件

aS a 2 a 3 a ( n 1 ) a n n
2 3 4
n
n 1
( 1 a ) S a a 1
a ( 1 a) na 若 a 1 , 则 S n 2 ( 1 a ) 1 a
1 1 1 a n n ( n 1 ) n n 1 1 1 1 1 a ( ) n ( 2 n 1 )( 2 n 1 ) 2 2 n 12 n 1
1 1 1 1 a [( )] n n ( n 1 )( n 2 )2 n ( n 1 )( n 1 )( n 2 )
常数),
且
的值; 的前n项的和 S
n
的
10.设数列 a n 满足
2 n 1
(Ⅰ)求数列 n a n 的通项; b b n (Ⅱ)设 求数列 n an
的前 n 项和 S
n
n a 3 a 3 a … 3a 1 2 3 n 3
aN
*
.
19、一个人的理想越崇高,生活越纯洁。 20、非淡泊无以明志,非宁静无以致远。 21、理想是反映美的心灵的眼睛。 22、人生最高之理想,在求达于真理。 便有了文明。 24、生当做人杰,死亦为鬼雄。 25、有理想的、充满社会利益的、具有明确目的生活是世界上最美好的和最有意义的生活。 26、人需要理想,但是需要人的符合自然的理想,而不是超自然的理想。 27、生活中没有理想的人,是可怜的。 28、在理想的最美好的世界中,一切都是为美好的目的而设的。 29、理想的人物不仅要在物质需要的满足上,还要在精神旨趣的满足上得到表现。 30、生活不能没有理想。应当有健康的理想,发自内心的理想,来自本国人民的理想。 31、理想是美好的,但没有意志,理想不过是瞬间即逝的彩
2025高考数学一轮复习-6.4-数列求和【课件】

【解析】 ∵an=nn1+1=1n-n+1 1 ∴数列{an}的前 n 项和 Sn=1-n+1 1=n+n 1 又 Sn=22001290,∴n=2019,故选 B.
易错易混 4.在数列{an}中,已知 an=n+11n+3(n∈N*),则{an}的前 n 项和 Sn=
_____12__56_-__n_+1__2_-__n_+1__3_ ______. 【解析】 ∵an=n+11n+3=12n+1 1-n+1 3, ∴Sn=1212-14+13-15+14-16+15-17+…+n+1 1-n+1 3 =1212+13-n+1 2-n+1 3 =1256-n+1 2-n+1 3.
第六章 数列
第四节 数列求和
课前双基巩固
——整合知识 夯实基础
『知识聚焦』 1.公式法 (1)等差数列{an}的前 n 项和 Sn=na12+an=na1+nn-2 1d. 推导方法:倒序相加法.
na1,q=1, (2)等比数列{an}的前 n 项和 Sn=a111--qqn,q≠1. 推导方法:乘公比, 错位相减法 .
6.若{log2an}是首项为 1,公差为 2 的等差数列,则数列{nan}的前 n 项和为 _S_n_=__2_+__6_n_9-__2__·4_n_.
【解析】 由题意可得 log2an=1+2(n-1)=2n-1, ∴an=22n-1=2·4n-1,∴nan=2n·4n-1, ∴数列{nan}的前 n 项和 Sn=2(1×40+2×41+3×42+…+n×4n-1), ∴12Sn=1×40+2×41+3×42+…+n×4n-1, ∴2Sn=1×41+2×42+3×43+…+n×4n,
课堂考点突破
——精析考题 提升能力
考点一 分组转化求和 【例 1】 已知数列{an}满足 a1=1,an+an-1=2n(n≥2,n∈N*). (1)记 bn=a2n,求数列{bn}的通项公式; (2)求数列{an}的前 n 项和 Sn.
易错易混 4.在数列{an}中,已知 an=n+11n+3(n∈N*),则{an}的前 n 项和 Sn=
_____12__56_-__n_+1__2_-__n_+1__3_ ______. 【解析】 ∵an=n+11n+3=12n+1 1-n+1 3, ∴Sn=1212-14+13-15+14-16+15-17+…+n+1 1-n+1 3 =1212+13-n+1 2-n+1 3 =1256-n+1 2-n+1 3.
第六章 数列
第四节 数列求和
课前双基巩固
——整合知识 夯实基础
『知识聚焦』 1.公式法 (1)等差数列{an}的前 n 项和 Sn=na12+an=na1+nn-2 1d. 推导方法:倒序相加法.
na1,q=1, (2)等比数列{an}的前 n 项和 Sn=a111--qqn,q≠1. 推导方法:乘公比, 错位相减法 .
6.若{log2an}是首项为 1,公差为 2 的等差数列,则数列{nan}的前 n 项和为 _S_n_=__2_+__6_n_9-__2__·4_n_.
【解析】 由题意可得 log2an=1+2(n-1)=2n-1, ∴an=22n-1=2·4n-1,∴nan=2n·4n-1, ∴数列{nan}的前 n 项和 Sn=2(1×40+2×41+3×42+…+n×4n-1), ∴12Sn=1×40+2×41+3×42+…+n×4n-1, ∴2Sn=1×41+2×42+3×43+…+n×4n,
课堂考点突破
——精析考题 提升能力
考点一 分组转化求和 【例 1】 已知数列{an}满足 a1=1,an+an-1=2n(n≥2,n∈N*). (1)记 bn=a2n,求数列{bn}的通项公式; (2)求数列{an}的前 n 项和 Sn.
第四节 数列求和 课件(共48张PPT)

-
1 n+3
)=
1 2
56-n+1 2-n+1 3. 答案:1256-n+1 2-n+1 3
考点1 分组转化法求和 [例1] (2020·焦作模拟)已知{an}为等差数列,且 a2=3,{an}前4项的和为16,数列{bn}满足b1=4,b4= 88,且数列{bn-an}为等比数列. (1)求数列{an}和{bn-an}的通项公式; (2
an=n(n1+k)型
[例2] (2020·中山七校联考)已知数列{an}为公差 不为0的等差数列,满足a1=5,且a2,a9,a30成等比数列.
(1)求{an}的通项公式; (2)若数列{bn}满足bn+1-bn=an(n∈N*),且b1=
3,求数列b1n的前n项和Tn.
1.裂项时常用的三种变形.
(1)n(n1+1)=n1-n+1 1.
(2)n(n1+2)=12n1-n+1 2.
(3)(2n-1)1(2n+1)=122n1-1-2n1+1.
(4)
1 n+
n+1=
n+1-
n.
2.应用裂项相消法时,应注意消项的规律具有对称 性,即前面剩第几项则后面剩倒数第几项.
3.在应用错位相减法求和时,若等比数列的公比为 参数,应分公比等于1和不等于1两种情况求解.
) B. 2 020-1
C. 2 021-1 D. 2 021+1
解析:由f(4)=2,可得4α=2,解得α=12,
则f(x)= x.
所以an=
1 f(n+1)+f(n)
=
1 n+1+
= n
n+1 -
n,
所以S2 020=a1+a2+a3+…+a2 020=( 2 - 1 )+ ( 3- 2)+( 4- 3)+…+( 2 021- 2 020)=
数列求和的几种方法课件ppt
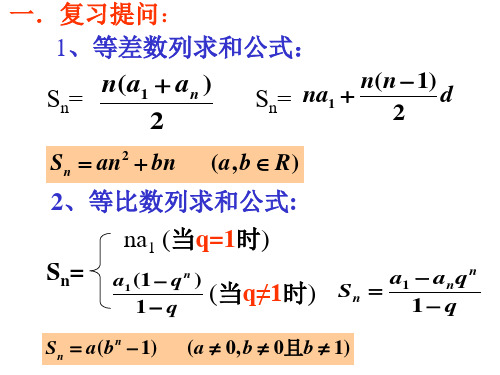
2、设法消去中间项:
(2)乘公比,错位相减(对“A·G”型);
(3)裂通项,交替相消
1、转化成等差、等比数列求和
(公式法、分组求和法、错位相减法、 裂(并)项法求和)
练习: 指出下列求和的方法:
合并项求和
特殊的数列,在求数列的和时,可将一些项放在一起先求和,然后再求Sn.
[例] 在各项均为正数的等比数列中,若
的值.
求和: (1)Sn=1+(3+4)+(5+6+7)+…+(2n-1+2n+ …+3n-2); (2)Sn=12-22+32-42+…+(-1)n-1·n2.
(1)一般应从通项入手,若无通项,先求通项,然后通过对通项变形,转化为适用特点的形式,从而求和.
数列求和的方法
(2)解决非等差、等比和,两种思路: ①转化的思想,即化为等差或等比数列. ②裂项相消法、错位相减法、倒序相加法等求和.
数列求和的常用方法:
(1) 拆项(对A±G型 如果拆项不明显,写出通项,如例2 )
na1+ d
n(n+1)(2n+1)
n2(n+1)2
倒序相加
令
例题1. 求和
(1)
[解Байду номын сангаас原式=
n(n+3)/2
(x≠1)
(x=1)
分析:原式=(1+2+3+…+n)+
我们把这种类型的数列称为“A+G”型。而求此类数列的和,一般是把数列的每一项分成两项,再分别利用等差和等比数列的求和公式求解。此方法称为分组求和法。
(2)乘公比,错位相减(对“A·G”型);
(3)裂通项,交替相消
1、转化成等差、等比数列求和
(公式法、分组求和法、错位相减法、 裂(并)项法求和)
练习: 指出下列求和的方法:
合并项求和
特殊的数列,在求数列的和时,可将一些项放在一起先求和,然后再求Sn.
[例] 在各项均为正数的等比数列中,若
的值.
求和: (1)Sn=1+(3+4)+(5+6+7)+…+(2n-1+2n+ …+3n-2); (2)Sn=12-22+32-42+…+(-1)n-1·n2.
(1)一般应从通项入手,若无通项,先求通项,然后通过对通项变形,转化为适用特点的形式,从而求和.
数列求和的方法
(2)解决非等差、等比和,两种思路: ①转化的思想,即化为等差或等比数列. ②裂项相消法、错位相减法、倒序相加法等求和.
数列求和的常用方法:
(1) 拆项(对A±G型 如果拆项不明显,写出通项,如例2 )
na1+ d
n(n+1)(2n+1)
n2(n+1)2
倒序相加
令
例题1. 求和
(1)
[解Байду номын сангаас原式=
n(n+3)/2
(x≠1)
(x=1)
分析:原式=(1+2+3+…+n)+
我们把这种类型的数列称为“A+G”型。而求此类数列的和,一般是把数列的每一项分成两项,再分别利用等差和等比数列的求和公式求解。此方法称为分组求和法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2n-1+22n-3+„+2)+2=22(n+1)-1.4分
1)+„+(a2-a1)]+a1=3(2
而a1=2,符合上式,所以数列{an}的通项公式为an=22n-1.6分
工具
第五章
数列
栏目导引
(2)由 bn=nan=n·2n-1 知 2 Sn=1· 2+2·3+3·5+„+n·2n 1, ①8 分 2 2 2 从而 22·n=1·3+2·5+3·7+„+n·2n 1.② 9 分 S 2 2 2 2 ①-②得(1-22)Sn=2+23+25+„+22n 1-n·2n 1,10 分 2 1 + 即 Sn= [(3n-1)22n 1+2].12 分 9
工具
第五章
数列
栏目导引
数列{an}中a1=3,已知点(an,an+1)在直线y=x+2上,
(1)求数列{an}的通项公式;
(2)若bn=an·n,求数列{bn}的前n项和Tn. 3 解析: (1)∵点(an,an+1)在直线y=x+2上, ∴an+1=an+2,即an+1-an=2. ∴数列{an}是以3为首项,2为公差的等差数列, ∴an=3+2(n-1)=2n+1.
数列
栏目导引
(本小题满分12分)(2010· 全国新课标卷)设数列{an}满足a1=2,an
22n-1. +1-an=3· (1)求数列{an}的通项公式; (2)令bn=nan,求数列{bn}的前n项和Sn. 【规范解答】 (1)由已知,当n≥1时,an+1=[(an+1-an)+(an-an-
1 =2n-2+ n-1. 2
工具
第五章
数列
栏目导引
1.一般地,如果数列{an}是等差数列,{bn}是等比数列,求数列
{an·n}的前n项和时,可采用错位相减法. b 2.用乘公比错位相减法求和时,应注意 (1)要善于识别题目类型,特别是等比数列公比为负数的情形; (2)在写出“Sn”与“qSn”的表达式时应特别注意将两式“错位项对 齐”以便下一步准确写出“Sn-qSn”的表达式.
答案: B
工具
第五章
数列
栏目导引
4.已知数列{an}的通项an=-5n+2,则其前n项和Sn=______.
解析: Sn=a1+a2+a3+„+an =-5(1+2+3+„+n)+2n -5nn+1 = +2n 2 -5n2-n = . 2
-5n2-n 答案: 2
工具
第五章
数列
栏目导引
1 1 1 5.数列 1,42,74,108,„前 10 项的和为________.
成立.
1 1 1 1 , 解析: (1)∵an= = =2 - 1+2+3+„+n nn+1 n n+1 2 1 1 1 1 1 1- +2 - +„+2 - ∴Sn=2 n n+1 2 2 3 1 2n Sn 2 = =21- ,∴bn= = (n∈N+). n+1 n+1 n n+1
工具
第五章
数列
栏目导引
1 1 2 2 4 - (2)证明:Cn=bn·n+1= b · = =4n+1 n+2 , n+1 n+2 n+1n+2 1 1 1 1 1 1 1 1 1 - =4 - <4× =2, ∴Tn=42-3+43-4+„+4 2 n+1 n+2 2 n+2
当n=4时,24-12-1=3>0,
∴2n-3n-1<0中n的最大值为3.
工具
第五章
数列
栏目导引
(2)Sn=a1+a2+„+an =(2+22+„+2n)-3(1+2+3+„+n)-n 21-2n nn+1 = -3· 2 -n 1-2 =2
n+1
n3n+5 - -2. 2
工具
第五章
数列
+1
工具
第五章
数列
栏目导引
1 1 数列通项形如 an= ,bn= 等可用此法.使 nn-1 2n-1+ 2n+1 用裂项法,要注意正负项相消时,消去了哪些项,保留了哪些项;你是 否注意到由于数列{an}中每一项 an 均裂成一正一负两项,所以互为相反 数的项合并为零后,所剩正数项与负数项的项数必是一样多的,切不可 漏写未被消去的项,未被消去的项有前后对称的特点.实质上,正负项 相消是此法的根源和目的.
对通项变形,转化为等差或等比或可求数列前n项和的数列来求之.
工具
第五章
数列
栏目导引
已知函数f(x)=2x-3x-1,点(n,an)在f(x)的图象上,an的前n项
和为Sn. (1)求使an<0的n的最大值. (2)求Sn. 解析: (1)依题意an=2n-3n-1, ∴an<0即2n-3n-1<0. 当n=3时,23-9-1=-2<0.
工具
第五章
数列
栏目导引
3 3 由①②得 a1=5,d=5, 3 3 3 ∴an=5+(n-1)×5=5n(n∈N+). n2+n+1 25 n2+n+1 (2)bn=3 3 =9· nn+1 n·n+1 5 5 1 25 1 , = 1+n- 9 n+1 ∴b1+b2+b3+„+b99 1 1 1 1 1 1 1 25 = 9 1+1-2+1+2-3+1+3-4+„+1+99-100 1 25 = 99+1-100 9 =275+2.75=277.75.
工具
第五章
数列
栏目导引
等差数列{an}是递增数列,前 n 项和为 Sn,且 a1,a3,a9 成等比 数列,S5=a52. (1)求数列{an}的通项公式; n2+n+1 (2)若数列{bn}满足 bn= ,求数列{bn}的前 99 项的和. an·n+1 a
解析: (1)设数列{an}的公差为 d(d>0), ∵a1,a3,a9 成等比数列,∴a32=a1a9, ∴(a1+2d)2=a1(a1+8d),∴d2=a1d, ∵d>0,∴a1=d,① 5×4 ∵S5=a52,∴5a1+ · d=(a1+4d)2② 2
第4课时
数列求和
工具
第五章
数列
栏目导引
工具
第五章
数列
栏目导引
求数列的前 n 项和的方法 1.公式法 (1)等差数列的前 n 项和公式 na1+an nn-1 na1+ d S n= = 2 2 (2)等比数列前 n 项和公式 ①当 q=1 时,Sn=na1; a11-qn a1-anq ②当 q≠1 时,Sn= = . 1-q 1-q
工具
第五章
数列
栏目导引
1.数列{(-1)n· n}的前2 010项的和S2 010为(
A.-2 010 C.2 010 B.-1 005 D.1 005
)
解析: S2 010=-1+2-3+4-5+„-2 009+2 010=(-1+2)+ (-3+4)+„+(-2 009+2 010)=1 005. 答案: D
工具
第五章
数列
栏目导引
(2)∵bn=an·n,∴bn=(2n+1)·n, 3 3 ∴Tn=3×3+5×32+7×33+„+(2n-1)·n-1+(2n+1)·n,① 3 3 ∴3Tn=3×32+5×33+„+(2n-1)·n+(2n+1)·n+1,② 3 3 由①-②得 -2Tn=3×3+2(32+33+„+3n)-(2n+1)·n 3 91-3n 1 + =9+2× -(2n+1)·n 1 3 1-3
即 Tn<2 对任意 n∈N+成立.
工具
第五章
数列
栏目导引
数列求和的方法
(1)一般的数列求和,应从通项入手,若无通项,先求通项,然后
通过对通项变形,转化为与特殊数列有关或具备某种方法适用特点的形 式,从而选择合适的方法求和. (2)数列求和的常见类型及方法 ①an=kn+b,利用等差数列前n项和公式直接求解; ②an=a·n-1,利用等比数列前n项和公式直接求解,但要注意对q q 分q=1与q≠1两种情况进行讨论;
栏目导引
【变式训练】
1 1 1 1+ + +„+ n-1 2 4 2
1 1 1 1. 求 和 Sn = 1 + 1+2 + 1+2+4 + „ +
解析: 和式中的第 k 项为: 1 1 1 ak=1+2+4+„+ k-1= 2
1k 1-2 1 =21-2k. 1 1- 2
第五章
数列
栏目导引
1 3.数列{an}的前 n 项和为 Sn,若 an= ,则 S5 等于( nn+1 A.1 5 B. 6 1 C. 6 1 D. 30
)
n+1-n 1 1 1 解析: an= = = - nn+1 nn+1 n n+1 ∴S5=a1+a2+a3+a4+a5 1 1 1 1 1 5 =1-2+2-3+„+5-6=6.
工具
第五章
数列
栏目导引
③an=bn+cn,数列{bn},{cn}是等比数列或等差数列,采用分组转 化法求{an}前n项和; ④an =bn·n ,{bn}是等差数列,{cn}是等比数列,采用错位相减法 c 求{an}前n项和;
⑤an=f(n)-f(n-1),采用裂项相消法求{an}前n项和;
⑥an-k+ak=cbn,可考虑倒序相加法求和;
.
工具
第五章
数列
栏目导引
2.分组转化法
把数列的每一项分成两项,使其转化为几个等差、等比数列,再求
解.
3.裂项相消法
把数列的通项拆成两项之差求和,正负相消剩下首尾若干项. 4.倒序相加法 把数列正着写和倒着写再相加(即等差数列求和公式的推导过程的 推广).
5.错位相减法
主要用于一个等差数列与一个等比数列对应项相乘所得的数列的求 和,即等比数列求和公式的推导过程的推广.
- +1
∴Tn=n·n 1. 3
+
工具
第五章
数列
栏目导引
【变式训练】 2.已知数列{an}满足:Sn=1-an(n∈N+),其中 Sn 为 数列{an}的前 n 项和. (1)试求{an}的通项公式; n (2)若数列{bn}满足:bn=a (n∈N+),试求{bn}的前 n 项和公式 Tn. n
1)+„+(a2-a1)]+a1=3(2
而a1=2,符合上式,所以数列{an}的通项公式为an=22n-1.6分
工具
第五章
数列
栏目导引
(2)由 bn=nan=n·2n-1 知 2 Sn=1· 2+2·3+3·5+„+n·2n 1, ①8 分 2 2 2 从而 22·n=1·3+2·5+3·7+„+n·2n 1.② 9 分 S 2 2 2 2 ①-②得(1-22)Sn=2+23+25+„+22n 1-n·2n 1,10 分 2 1 + 即 Sn= [(3n-1)22n 1+2].12 分 9
工具
第五章
数列
栏目导引
数列{an}中a1=3,已知点(an,an+1)在直线y=x+2上,
(1)求数列{an}的通项公式;
(2)若bn=an·n,求数列{bn}的前n项和Tn. 3 解析: (1)∵点(an,an+1)在直线y=x+2上, ∴an+1=an+2,即an+1-an=2. ∴数列{an}是以3为首项,2为公差的等差数列, ∴an=3+2(n-1)=2n+1.
数列
栏目导引
(本小题满分12分)(2010· 全国新课标卷)设数列{an}满足a1=2,an
22n-1. +1-an=3· (1)求数列{an}的通项公式; (2)令bn=nan,求数列{bn}的前n项和Sn. 【规范解答】 (1)由已知,当n≥1时,an+1=[(an+1-an)+(an-an-
1 =2n-2+ n-1. 2
工具
第五章
数列
栏目导引
1.一般地,如果数列{an}是等差数列,{bn}是等比数列,求数列
{an·n}的前n项和时,可采用错位相减法. b 2.用乘公比错位相减法求和时,应注意 (1)要善于识别题目类型,特别是等比数列公比为负数的情形; (2)在写出“Sn”与“qSn”的表达式时应特别注意将两式“错位项对 齐”以便下一步准确写出“Sn-qSn”的表达式.
答案: B
工具
第五章
数列
栏目导引
4.已知数列{an}的通项an=-5n+2,则其前n项和Sn=______.
解析: Sn=a1+a2+a3+„+an =-5(1+2+3+„+n)+2n -5nn+1 = +2n 2 -5n2-n = . 2
-5n2-n 答案: 2
工具
第五章
数列
栏目导引
1 1 1 5.数列 1,42,74,108,„前 10 项的和为________.
成立.
1 1 1 1 , 解析: (1)∵an= = =2 - 1+2+3+„+n nn+1 n n+1 2 1 1 1 1 1 1- +2 - +„+2 - ∴Sn=2 n n+1 2 2 3 1 2n Sn 2 = =21- ,∴bn= = (n∈N+). n+1 n+1 n n+1
工具
第五章
数列
栏目导引
1 1 2 2 4 - (2)证明:Cn=bn·n+1= b · = =4n+1 n+2 , n+1 n+2 n+1n+2 1 1 1 1 1 1 1 1 1 - =4 - <4× =2, ∴Tn=42-3+43-4+„+4 2 n+1 n+2 2 n+2
当n=4时,24-12-1=3>0,
∴2n-3n-1<0中n的最大值为3.
工具
第五章
数列
栏目导引
(2)Sn=a1+a2+„+an =(2+22+„+2n)-3(1+2+3+„+n)-n 21-2n nn+1 = -3· 2 -n 1-2 =2
n+1
n3n+5 - -2. 2
工具
第五章
数列
+1
工具
第五章
数列
栏目导引
1 1 数列通项形如 an= ,bn= 等可用此法.使 nn-1 2n-1+ 2n+1 用裂项法,要注意正负项相消时,消去了哪些项,保留了哪些项;你是 否注意到由于数列{an}中每一项 an 均裂成一正一负两项,所以互为相反 数的项合并为零后,所剩正数项与负数项的项数必是一样多的,切不可 漏写未被消去的项,未被消去的项有前后对称的特点.实质上,正负项 相消是此法的根源和目的.
对通项变形,转化为等差或等比或可求数列前n项和的数列来求之.
工具
第五章
数列
栏目导引
已知函数f(x)=2x-3x-1,点(n,an)在f(x)的图象上,an的前n项
和为Sn. (1)求使an<0的n的最大值. (2)求Sn. 解析: (1)依题意an=2n-3n-1, ∴an<0即2n-3n-1<0. 当n=3时,23-9-1=-2<0.
工具
第五章
数列
栏目导引
3 3 由①②得 a1=5,d=5, 3 3 3 ∴an=5+(n-1)×5=5n(n∈N+). n2+n+1 25 n2+n+1 (2)bn=3 3 =9· nn+1 n·n+1 5 5 1 25 1 , = 1+n- 9 n+1 ∴b1+b2+b3+„+b99 1 1 1 1 1 1 1 25 = 9 1+1-2+1+2-3+1+3-4+„+1+99-100 1 25 = 99+1-100 9 =275+2.75=277.75.
工具
第五章
数列
栏目导引
等差数列{an}是递增数列,前 n 项和为 Sn,且 a1,a3,a9 成等比 数列,S5=a52. (1)求数列{an}的通项公式; n2+n+1 (2)若数列{bn}满足 bn= ,求数列{bn}的前 99 项的和. an·n+1 a
解析: (1)设数列{an}的公差为 d(d>0), ∵a1,a3,a9 成等比数列,∴a32=a1a9, ∴(a1+2d)2=a1(a1+8d),∴d2=a1d, ∵d>0,∴a1=d,① 5×4 ∵S5=a52,∴5a1+ · d=(a1+4d)2② 2
第4课时
数列求和
工具
第五章
数列
栏目导引
工具
第五章
数列
栏目导引
求数列的前 n 项和的方法 1.公式法 (1)等差数列的前 n 项和公式 na1+an nn-1 na1+ d S n= = 2 2 (2)等比数列前 n 项和公式 ①当 q=1 时,Sn=na1; a11-qn a1-anq ②当 q≠1 时,Sn= = . 1-q 1-q
工具
第五章
数列
栏目导引
1.数列{(-1)n· n}的前2 010项的和S2 010为(
A.-2 010 C.2 010 B.-1 005 D.1 005
)
解析: S2 010=-1+2-3+4-5+„-2 009+2 010=(-1+2)+ (-3+4)+„+(-2 009+2 010)=1 005. 答案: D
工具
第五章
数列
栏目导引
(2)∵bn=an·n,∴bn=(2n+1)·n, 3 3 ∴Tn=3×3+5×32+7×33+„+(2n-1)·n-1+(2n+1)·n,① 3 3 ∴3Tn=3×32+5×33+„+(2n-1)·n+(2n+1)·n+1,② 3 3 由①-②得 -2Tn=3×3+2(32+33+„+3n)-(2n+1)·n 3 91-3n 1 + =9+2× -(2n+1)·n 1 3 1-3
即 Tn<2 对任意 n∈N+成立.
工具
第五章
数列
栏目导引
数列求和的方法
(1)一般的数列求和,应从通项入手,若无通项,先求通项,然后
通过对通项变形,转化为与特殊数列有关或具备某种方法适用特点的形 式,从而选择合适的方法求和. (2)数列求和的常见类型及方法 ①an=kn+b,利用等差数列前n项和公式直接求解; ②an=a·n-1,利用等比数列前n项和公式直接求解,但要注意对q q 分q=1与q≠1两种情况进行讨论;
栏目导引
【变式训练】
1 1 1 1+ + +„+ n-1 2 4 2
1 1 1 1. 求 和 Sn = 1 + 1+2 + 1+2+4 + „ +
解析: 和式中的第 k 项为: 1 1 1 ak=1+2+4+„+ k-1= 2
1k 1-2 1 =21-2k. 1 1- 2
第五章
数列
栏目导引
1 3.数列{an}的前 n 项和为 Sn,若 an= ,则 S5 等于( nn+1 A.1 5 B. 6 1 C. 6 1 D. 30
)
n+1-n 1 1 1 解析: an= = = - nn+1 nn+1 n n+1 ∴S5=a1+a2+a3+a4+a5 1 1 1 1 1 5 =1-2+2-3+„+5-6=6.
工具
第五章
数列
栏目导引
③an=bn+cn,数列{bn},{cn}是等比数列或等差数列,采用分组转 化法求{an}前n项和; ④an =bn·n ,{bn}是等差数列,{cn}是等比数列,采用错位相减法 c 求{an}前n项和;
⑤an=f(n)-f(n-1),采用裂项相消法求{an}前n项和;
⑥an-k+ak=cbn,可考虑倒序相加法求和;
.
工具
第五章
数列
栏目导引
2.分组转化法
把数列的每一项分成两项,使其转化为几个等差、等比数列,再求
解.
3.裂项相消法
把数列的通项拆成两项之差求和,正负相消剩下首尾若干项. 4.倒序相加法 把数列正着写和倒着写再相加(即等差数列求和公式的推导过程的 推广).
5.错位相减法
主要用于一个等差数列与一个等比数列对应项相乘所得的数列的求 和,即等比数列求和公式的推导过程的推广.
- +1
∴Tn=n·n 1. 3
+
工具
第五章
数列
栏目导引
【变式训练】 2.已知数列{an}满足:Sn=1-an(n∈N+),其中 Sn 为 数列{an}的前 n 项和. (1)试求{an}的通项公式; n (2)若数列{bn}满足:bn=a (n∈N+),试求{bn}的前 n 项和公式 Tn. n
