必修四三角函数和三角恒等变换知识点及题型分类汇总
必修4复习-三角恒等变换与三角函数的性质

答案:2
2.(2012· 唐山模拟)已知tan 2θ=-2 2,π<2θ<2π,化简 θ 2cos22-sin θ-1 2sin
π θ+ 4
=________.
1i s )2 xn 2 x2soc
求函数递 增区间.
略解:
1 cos2x 3 sin2x 2 2
(ni s π x2 ) 6 1
17
»感受三角变换的魅力
1n t 例4、 知t a 已n a , 7 角 , 求 2 . 1 , 并 且, 均 为 锐 3
-lg(1+sin 2x) sin x+cos x2 1+sin 2x =lg =lg =0. 1+sin 2x 1+sin 2x
[巧练模拟]——————(课堂突破保分题,分分必保!)
α 1 -tan2 1-cos 2α 1.(2012· 洛阳模拟)化简: α · sin 2α =________. tan2
4 答案:-3
cos α-sin α 5.已知α、β均为锐角,且tan β= , cos α+sin α 则tan(α+β)=__________. π 1-tan α 解析:tan β= =tan 4-α, 1+tan α
π ∵α、β为锐角,∴β=4-α, π ∴α+β=4,∴tan(α+β)=1.
答案:1
»感受三角变换的魅力
例3、函 求 数 值小 和值 最 解:y ni s yx i s n 3 c x的, so 周最 期大 . 1i s x 3oc x 3oc x 2(n s s 2 2
00三角函数、三角恒等变换、解三角形知识点归纳

T
P
A
Mo
x
P A
oM x
(Ⅱ) T
(Ⅰ)
y
T
y
M
A
o
x
P (Ⅲ)
MA
o
x
(Ⅳ) P T
由四个图看出:
当角 的终边不在坐标轴上时,有向线段 OM x, MP y ,于是有
sin y y y MP , cos x x x OM , tan y MP AT AT
r1
r1
x OM OA
B.方法与要点 一个口诀 1、诱导公式的记忆口诀为:奇变偶不变,符号看象限.
2、四种方法
在求值与化简时,常用方法有:
(1)弦切互化法:主要利用公式 tan α=sin α化成正、余弦. cos α
(2)和积转换法:利用(sin θ±cos θ)2=1±2sin θcos θ的关系进行变形、转化.
( sin cos 、 sin cos 、 sin cos 三个式子知一可求二)
第一象限角的集合为 k 360 k 360 90, k 第二象限角的集合为 k 360 90 k 360 180, k 第三象限角的集合为 k 360 180 k 360 270, k 第四象限角的集合为 k 360 270 k 360 360, k 终边在 x 轴上的角的集合为 k 180, k 终边在 y 轴上的角的集合为 k 180 90, k 终边在坐标轴上的角的集合为 k 90, k
三角函数知识点总结
一、任意角、弧度制及任意角的三角函数
1.任意角 (1)角的概念的推广 ①按旋转方向不同分为正角、负角、零角.
正角:按逆时针方向旋转形成的角 任意角负角:按顺时针方向旋转形成的角
零角:不作任何旋转形成的角
必修四(三角函数,平面向量,三角恒等变换)
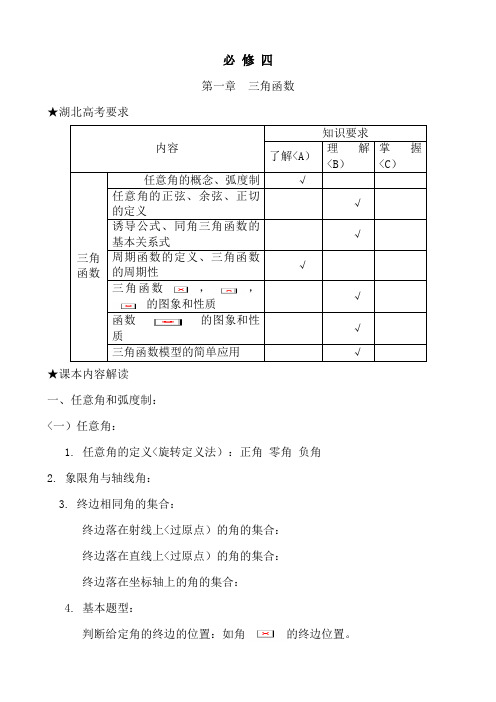
必修四第一章三角函数★湖北高考要求的图象和性质函数★课本内容解读一、任意角和弧度制:<一)任意角:1. 任意角的定义<旋转定义法):正角零角负角2. 象限角与轴线角:3. 终边相同角的集合:终边落在射线上<过原点)的角的集合:终边落在直线上<过原点)的角的集合:终边落在坐标轴上的角的集合:4. 基本题型:判断给定角的终边的位置:如角的终边位置。
在给定范围内找与已知角终边相同的角: 如在内找出终边与角相同的所有角。
<二)弧度制:1. 弧度制定义:把长度等于半径长的弧所对的圆心角叫做1弧度的角。
2.弧度数公式:3. 弧度与角度之间的互化:4. 之间特殊角的弧度数与角度数:5. 扇形的面积公式:,与结合后有三种形式6. 基本题型:角度数与弧度数的互化弧度数公式及扇形面积公式的应用二、任意角的三角函数:(一> 任意角的三角函数:1. 任意角的三角函数的定义:坐标定义法:2. 三个三角函数的符号<从定义出发):一全<正),二正弦<正),三正切<正),四余弦<正)3. 公式一:4.三个三角函数线:正弦线、余弦线、正切线5. 同角三角函数的基本关系:<变形)6.基本题型:利用定义求一些特殊角的三个三角函数值:如:求的正弦、余弦与正切值给出角终边上的点或其他信息求三个三角函数值:三角函数符号的应用:作出已知角的三角函数线:利用三角函数线比较三角函数值的大小与解简单的三角不等式:利用同角三角函数的基本关系进行简单的计算、化简与证明:<二)三角函数的诱导公式:1. 基本公式:公式一:与的三个三角函数值的关系:公式二:与的三个三角函数值的关系:公式三:与的三个三角函数值的关系:公式四:与的三个三角函数值的关系:以上公式特点:函数名不变,符号看象限公式五:与的正余弦的关系:公式六:与的正余弦的关系:以上公式特点:函数名改变,符号看象限对上述公式要求理解证明方法,牢记公式2. 基本题型:利用基本公式进行计算与化简三、三角函数的图像与性质1.正弦曲线、余弦曲线,五点作图法及换元五点法2.正弦函数、余弦函数和正切函数的图象与性质:当时,当;当时,.在在上在上是增函数.对称轴3. 函数的图象与性质:<1)图象:可用换元五点法或图像变换作图;<2)性质:用整体代换思想结合相应基本三角函数求解,主要包括以下几个方面:周期,最值<相应自变量的值),单调区间,对称轴方程及对称轴点坐标等。
必修四三角恒等变换题型归纳梳理

三角恒等变换题型归纳梳理一、知识点总结:1、同角三角函数的基本关系式 :①22sin cos 1θθ+=,②tan θ=θθcos sin , 2、正弦、余弦的诱导公式(奇变偶不变,符号看象限) 3、和角与差角公式sin()sin cos cos sin αβαβαβ±=± cos()cos cos sin sin αβαβαβ±=tan tan tan()1tan tan αβαβαβ±±=. ααααcos sin 21)cos (sin 2±=±ϕ由点(,)a b 的象限决定,tan baϕ=). 4、二倍角公式及降幂公式sin 2sin cos ααα=. 2222cos 2cos sin 2cos 112sin ααααα=-=-=-22tan tan 21tan ααα=-. 221cos 21cos 2sin ,cos 22αααα-+== 5、三角函数的周期公式函数sin()y x ωϕ=+, (A,ω,ϕ为常数,且A ≠0)的周期2||T πω=; 函数tan()y x ωϕ=+,,2x k k Z ππ≠+∈(A,ω,ϕ为常数,且A ≠0)的周期||T πω=. 二、重难点题型突破:1、两角和与差的余弦公式的应用cos()cos cos sin sin αβαβαβ±=例1.(1)(2019·山东高一期末)( )A B . C .D . 10208020cos cos cos sin ︒-︒︒=1212-【解析】由诱导公式,所以选择A (2).已知为锐角,为第三象限角,且,,则的值为( )A .B .C .D .【解析】为锐角,且,.为第三象限角,且,,.故选A. 【变式训练】(1)(2020·四川成都市·棠湖中学高一月考)cos80cos 200sin100sin340+=( )A .12B .2C .12-D【详解】()()()cos80cos 200sin100sin340cos80cos 18020sin 18080sin 36020+=++--()cos80cos 20sin80sin 20cos80cos 20sin80sin 20=--=-+()1cos 8020cos602=--=-=-.故选:C.(2)(2018·徐汇区·上海中学高三月考)1cos(2)9αβ-=-,2sin(2)3αβ-=,且α、02πβ⎛⎫∈ ⎪⎝⎭,,则()cos αβ+=________102080201020sin1020cos cos cos sin cos cos sin︒-︒︒=︒-︒︒1020sin1020cos(1020)cos302cos cos sin ︒-︒︒=︒+︒=︒=αβ12cos 13α=3sin 5β=-()cos αβ-6365-3365-63653365α12cos 13α=5sin 13α∴==β3sin 5β=-4cos 5β∴==-()12453cos cos cos sin sin 135135αβαβαβ⎛⎫⎛⎫∴-=+=⨯-+⨯- ⎪ ⎪⎝⎭⎝⎭6365=-【详解】由,0,2παβ⎛⎫∈ ⎪⎝⎭,可得:2,2παβπ⎛⎫-∈-⎪⎝⎭,2,2παβπ⎛⎫-∈- ⎪⎝⎭,又1cos(2)09αβ-=-<,2sin(2)03αβ-=>,所以2,2παβπ⎛⎫-∈ ⎪⎝⎭,20,2παβ⎛⎫-∈ ⎪⎝⎭,sin(2)αβ-=,cos(2)αβ-=,又因为(2)(2)αβαβαβ+=---,所以 ()[]cos cos (2)(2)αβαβαβ+=---cos(2)cos(2)sin(2)sin(2)αβαβαβαβ=--+--1293=-+=. 二、两角和与差的正弦公式的应用sin()sin cos cos sin αβαβαβ±=±例2.(1)(2021·江苏高一)sin11cos19cos11cos71︒︒+︒︒的值为( )A B .12C D 【详解】sin11cos19cos11cos71︒︒+︒︒sin11cos19cos11sin19=︒︒+︒︒()1sin 1119sin 302=︒+︒=︒=.故选:B. (2)(2020·湖南省平江县第一中学高三月考)若,αβ为锐角,且满足4cos 5α=,5cos()13αβ+=,则sin β的值为( )A .1665-B .3365C .5665D .6365【详解】因为,αβ为锐角,且4cos 5α=,5cos()13αβ+=, 所以312sin ,sin()513ααβ=+=,所以故sin sin[()]βαβα=+-124533313513565=⨯-⨯=,故选:B.【变式训练】.(1)(2020·全国高一课时练习)sin152sin 30cos15+=__.【详解】sin152sin 30sin152sin(4515)cos15cos15++-=sin15cos15sin151cos15+-==.答案为:1. (2)(2021·浙江宁波市·高一期末)已知35sin ,cos ,0,,,51322ππαβαβπ⎛⎫⎛⎫==-∈∈ ⎪ ⎪⎝⎭⎝⎭,则()sin αβ+=________.【详解】30,,sin 25παα⎛⎫∈= ⎪⎝⎭,则4cos 5α=,5,,cos 213πβπβ⎛⎫∈=- ⎪⎝⎭,则12sin 13β= ()3541233sin sin cos cos sin 51351365αβαβαβ⎛⎫+=+=⨯-+⨯= ⎪⎝⎭,故答案为:3365三、 两角和与差的正切公式的应用tan tan tan()1tan tan αβαβαβ±±=例3.(1)(2020·全国高一单元测试)已知角α的顶点与坐标原点O 重合,始边与x 轴的非负半轴重合,它的终边过点(3,4)P --,则tan 4πα⎛⎫+⎪⎝⎭的值为( ) A .247-B .7-C .247D .1731【详解】由题意,利用任意角的三角函数的定义可得44tan 33α-==-, 所以41tan 13tan 7441tan 13πααα++⎛⎫+===- ⎪-⎝⎭-.故选:B . (2).已知,,那么( )()2tan 5αβ+=1tan 44πβ⎛⎫-= ⎪⎝⎭tan 4πα⎛⎫+= ⎪⎝⎭A .B .C .D .【解析】因为,所以,故选:C【变式训练】(1)(2019·山东菏泽市·高一期中)已知α,β为锐角,3sin 5α=,12cos 13β=,则()tan αβ+的值为( )A .5633B .1663C .3356D .6316【详解】因为α,β为锐角,3sin 5α=,12cos 13β=,所以4cos 5α=,5sin 13β=.所以3tan 4α=,5tan 12β=. 所以()tan tan tan 1tan tan αβαβαβ++==-⋅5633.故选:A.(2)(2020·上海)()()()()1tan11tan 21tan31tan 44︒︒︒︒++++的值为( ). A .222B .232C .112D .122【详解】因为()tan1tan 44tan 45tan 14411tan1tan 44+=+==-,所以tan1tan 441tan1tan 44+=-,所以()()1tan11tan 441tan1tan 44tan1tan 44︒︒︒︒++=+++11tan1tan 44tan1tan 442︒=+-+=.同理:()()()()1tan 21tan 431tan31tan 42︒︒︒︒++=++()()1tan 221tan 232︒︒==++=所以,()()()()1tan11tan 21tan31tan 44︒︒︒︒++++13181322322518()44ππααββ⎛⎫+=+-- ⎪⎝⎭()()()tan tan 34tan tan 44221tan tan 4παββππααββπαββ⎛⎫+-- ⎪⎡⎤⎛⎫⎛⎫⎝⎭+=+--== ⎪ ⎪⎢⎥⎛⎫⎝⎭⎝⎭⎣⎦++- ⎪⎝⎭()()()()()()1tan11tan 441tan 21tan 431tan 221tan 23︒︒︒︒︒︒⎡⎤⎡⎤⎡⎤=++⋅++++⎣⎦⎣⎦⎣⎦222=.故选:A.四、二倍角公式的应用sin 2sin cos ααα=;2222cos 2cos sin 2cos 112sin ααααα=-=-=-22tan tan 21tan ααα=-;221cos 21cos 2sin ,cos 22αααα-+== 例4.(1)(2020·昆明市官渡区第一中学高一开学考试)已知cos 4πα⎛⎫+= ⎪⎝⎭,则sin 2α=( ) A .45B .25C .45±D .25±【详解】cos 4πα⎛⎫+= ⎪⎝⎭,24cos 2=2cos 1245ππαα⎛⎫⎛⎫∴++-=- ⎪ ⎪⎝⎭⎝⎭,即4sin 25α-=-, 所以4sin 25α=.故选:A . (2).(2020·黑龙江双鸭山市·双鸭山一中高一期末(文))已知tan 34πα⎛⎫+=⎪⎝⎭,则tan2α=( ) A .34-B .43-C .34D .43【详解】tantan 1tan 4tan 341tan 1tan tan 4παπααπαα++⎛⎫+=== ⎪-⎝⎭-,解得1tan 2α=, 因此,22122tan 42tan 21tan 3112ααα⨯===-⎛⎫- ⎪⎝⎭.故选:D 【变式训练】(1)(2020·新疆生产建设兵团第五师高级中学高一开学考试)已知α是锐角,1sin 233πα⎛⎫+= ⎪⎝⎭,则cos 12πα⎛⎫- ⎪⎝⎭的值是( )A .3B .3-C .3D .3-【详解】设12x πα=-,则12x πα=-,则1sin 2sin 2sin 2cos 2312323x x x ππππα⎡⎤⎛⎫⎛⎫⎛⎫+=-+=-== ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦, 02πα<<,5121212πππα∴-<-<,即51212x ππ-<<,所以,cos 0x >,21cos 22cos 13x x ∴=-=,22cos 3x ∴=,因此,cos 3x =.故选:A. (2)(2020·江西高三月考(文))已知3tan 65πα⎛⎫+=- ⎪⎝⎭,则sin 23πα⎛⎫+= ⎪⎝⎭( )A .817B .817-C .1517D .1517-【详解】设6παθ+=,则223παθ+=,3tan tan 65παθ⎛⎫+==- ⎪⎝⎭,2222sin cos 2tan 15sin 22sin cos cos sin 1tan 17θθθθθθθθθ∴====-++.故选:D. 五、辅助公式的应用例5.(1)(2020·恩施清江外国语学校高二期末)函数())cos()2f x x x ππ=-+-的单调增区间为( ) A .5[2,2],66k k k Z ππππ-++∈ B .2[2,2],33k k k Z ππππ-++∈ C .5[2,2],66k k k Z ππππ-++∈ D .2[2,2],33k k k Z ππππ-++∈【详解】())cos()2f x x x ππ=-+-cos x x =-2sin()6x π=-令22262k x k πππππ-+≤-≤+,解得:22233k x k ππππ-+≤≤+ 所以函数()f x 的单调递增区间为:2[2,2],33k k k Z ππππ-++∈,故选:D(2)(2020·全国高三专题练习(理))已知向量()sin cos a x x x =-,()sin ,cos b x x =,函数()f x a b =⋅.(1)求()f x 的单调递增区间;(2)当50,12x π⎡⎤∈⎢⎥⎣⎦时,求()f x 的值域.【详解】(1)向量()sin cos a x x x =-,()sin ,cos b x x =,()()222sin cos cos cos sin cos f x a b x x x x x x x x∴=⋅=+-=+-2cos 22sin 26x x x π⎛⎫=-=- ⎪⎝⎭,解不等式()222262k x k k Z πππππ-≤-≤+∈,得()63k x k k Z ππππ-≤≤+∈.因此,函数()y f x =的单调递增区间为(),63k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦; (2)当50,12x π⎡⎤∈⎢⎥⎣⎦时,22,663x πππ⎡⎤-∈-⎢⎥⎣⎦,则1sin 2126x π⎛⎫-≤-≤ ⎪⎝⎭,()12f x ∴-≤≤. 因此,函数()y f x =在区间50,12π⎡⎤⎢⎥⎣⎦上的值域为[]1,2-.【变式训练】(1)(2020·忻州实验中学校月考)函数21()sin cos )2f x x x x =+-最小正周期为( ) A .2B .1C .2πD .π【详解】21sin 21cos 21()sin cos )2222x x f x x x x +⎫=+-=+-⎪⎭1sin 22sin 2223x x x π⎛⎫=+=+ ⎪⎝⎭,22T ππ∴==.故选:D(2)(2020·邵阳市第二中学高三其他模拟(文))已知函数()sin (0)f x x x ωωω=>的图象关于直线8x π=对称,则ω的最小值为( )A .13B .23C .43D .83【详解】()sin 2sin 3f x x x x πωωω⎛⎫=+=+ ⎪⎝⎭,由于该函数的图象关于直线8x π=对称,则()832k k Z πππωπ+=+∈,得()483k k Z ω=+∈,0ω>,当0k =时,ω取得最小值43.故选:C. 三、课后训练1.(2020·莆田第七中学高二期中)sin 45cos15cos 45sin15⋅+⋅的值为( )A .B .12-C .12D .2【详解】3sin 45cos15cos 45sin15sin(4515)sin 60⋅+⋅=+==,故选:D.2.(2020·蚌埠第一中学高三期中)已知sin α=,()sin 10αβ-=-,,αβ均为锐角,角β等于( )A .5π12B .π3C .π4D .π6【详解】因为,αβ均为锐角,所以22ππαβ-<-<.又()sin αβ-=,所以()cos αβ-=.又sin α=,所以cos α=. 所以()()()sin sin sin cos cos sin βααβααβααβ⎡⎤=--=---⎣⎦=5105102⎛⎫=--= ⎪ ⎪⎝⎭.所以π4β=.故选:C . 3.(2020·全国高二)已知α、β为锐角,3cos 5α=,()1tan 3βα-=,则tan β=( ) A .139B .913C .3D .13【详解】α为锐角,则24sin 1cos 5αα,所以,sin 4tan cos 3ααα==, ()()()14tan tan 33tan tan 3141tan tan 133βααββααβαα+-+∴=-+===⎡⎤⎣⎦---⨯.故选:C. 4.(2020·广西桂林十八中高三月考(文))已知α22sin αα=,则cos2α等于( )A .23B .29C .13-D .49-【详解】因为cos 2sin ααα=,sin 0α≠,所以cos α=, 所以221cos22cos1133αα=-=-=-.故选:C. 5.(2020·林芝市第二高级中学高一期末)计算sin15sin30sin75的值等于()AB C .18D .14【详解】原式111sin15cos15sin30248===.故选C 6.(2021·全国高三专题练习)要得到函数2sin 2y x x =+-2sin 2y x =的图象( )A .向左平移3π个单位 B .向右平移3π个单位 C .向左平移6π个单位 D .向右平移6π个单位【详解】依题意2ππsin 22sin 22sin 236y x x x x ⎡⎤⎛⎫⎛⎫=+=+=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,故只需将函数2sin 2y x =的图象向左平移6π个单位.所以选C.7.(2020·邵阳市第二中学高三其他模拟(文))已知函数()sin (0)f x x x ωωω=+>的图象关于直线8x π=对称,则ω的最小值为( )A .13B .23C .43D .83【详解】()sin 2sin 3f x x x x πωωω⎛⎫=+=+ ⎪⎝⎭, 由于该函数的图象关于直线8x π=对称,则()832k k Z πππωπ+=+∈,得()483k k Z ω=+∈, 0ω>,当0k =时,ω取得最小值43.故选:C.8.(2020·杭州市西湖高级中学高一月考)在ABC ∆中,若()sin sin sin 2A B C C +-=,则ABC ∆的形状为( )A .等腰三角形B .直角三角形C .等腰直角三角形D .等腰三角形或直角三角形 【详解】()sin sin sin 2A B C C +-=,()()sin sin sin 2B C B C C ∴++-=,化简得sin cos sin cos B C C C =,即()cos sin sin 0C B C -=.cos 0C ∴=或sin sin 0B C -=,即2C π=或b c =.因此,ABC ∆为等腰三角形或直角三角形.故选:D.9.(2019·河北邢台市·邢台一中高一期末)已知()tan αβ1+=,()tan αβ7-=,则tan2β=______.【详解】()()()()()()tan tan 173tan2tan 1tan tan 1174αβαββαβαβαβαβ+---⎡⎤=+--===-⎣⎦++-+⨯,故答案为34- 10.(2020·浙江高一单元测试)已知15sin 17α=,5cos 13β=-,且 ,2παπ⎛⎫∈ ⎪⎝⎭,,2πβπ⎛⎫∈ ⎪⎝⎭,求cos()αβ+,sin()αβ-.【详解】∵15sin 17α=,∴ 8cos 17α==±,∵ ,2παπ⎛⎫∈ ⎪⎝⎭,∴ 8cos 17α=-,∵ 5cos 13β=-,∴ 12sin 13β==±,∵ ,2πβπ⎛⎫∈ ⎪⎝⎭,∴ 12sin 13β=, ∴ 851512cos()cos cos sin sin ()140()17131713221αβαβαβ+=-=-⨯---⨯=; 155812sin()sin cos cos sin ()()1713121227113αβαβαβ-=-=⨯---⨯=. 11.(2020·长沙市·湖南师大附中高二月考)设函数()ππsin sin 62f x x x ωω⎛⎫⎛⎫=-+- ⎪ ⎪⎝⎭⎝⎭,其中03ω<<,已知π06f ⎛⎫= ⎪⎝⎭. (1)求()f x 的最小正周期;(2)将函数()y f x =的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将整个图象向左平移π4个单位,得到函数()y g x =的图象,求()g x 在区间π3π,44⎡⎤-⎢⎥⎣⎦上的最小值.【详解】(1)因为()ππ1sin sin sin cos cos 6222f x x x x x x ωωωωω⎛⎫⎛⎫=-+-=-- ⎪ ⎪⎝⎭⎝⎭,所以()3cos 223f x x x x πωωω⎛⎫=-=- ⎪⎝⎭,因为π06f ⎛⎫= ⎪⎝⎭,所以0663f πππω⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭,所以,63k k Z ππωπ-=∈, 所以62,k k Z ω=+∈,又03ω<<,所以2ω=,所以22T ππ==;(2)因为()23f x x π⎛⎫=- ⎪⎝⎭,将()y f x =的图象上各点的横坐标伸长为原来的2倍(纵坐标不变)可得3y x π⎛⎫=- ⎪⎝⎭,将3y x π⎛⎫=- ⎪⎝⎭图象向左平移π4个单位可得()4312g x x x πππ⎡⎤⎛⎫⎛⎫=+-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,因为π3π,44x ⎡∈⎤-⎢⎥⎣⎦,所以π2π,1233x π⎛⎫⎡⎤-∈- ⎪⎢⎥⎝⎭⎣⎦,所以()min 332g x π⎛⎫=-=- ⎪⎝⎭,此时4πx =-, 所以()g x 的最小值为32-.12.(2020·天津南开区·南开中学高三月考)已知函数2()sin cos cos 22f x x x x x ⎛⎫=-+ ⎪ ⎪⎝⎭,x ∈R .(Ⅰ)求函数()f x 的最小正周期及单调递增区间;(Ⅱ)若α为锐角且7129f πα⎛⎫+=- ⎪⎝⎭,β满足()3cos 5αβ-=,求sin β.【详解】(Ⅰ)()22sin cos 22f x x x x x =-+1sin 2cos 222x x =+sin 23x π⎛⎫=+ ⎪⎝⎭. 所以()f x 的最小正周期T π=,令222232k x k πππππ-≤+≤+,k Z ∈,解得51212x k k ππππ-+≤≤,k Z ∈,所以函数()f x 的单调递增区间为5,1212k k ππππ⎡⎤-+⎢⎥⎣⎦,k Z ∈. (Ⅱ)由(Ⅰ)得7sin 2cos 21229f ππααα⎛⎫⎛⎫+=+==- ⎪ ⎪⎝⎭⎝⎭, 227cos 22cos 112sin 9ααα=-=-=-因为α为锐角,所以1cos 3α=,sin 3α=, 又因为()3cos 5αβ-=,所以()4sin 5αβ-=±,所以()()()sin sin sin cos cos sin βααβααβααβ=--=⋅--⋅-=⎡⎤⎣⎦。
必修4-第三章三角恒等变换-知识点详解

必修4 第三章三角恒等变换知识点详解3.1 两角和与差的正弦、余弦和正切公式1. 两角和与差的正弦、余弦、正切公式:()sin sin cos cos sin sin 22sin cos 令αβαβαβαβααα=±=±−−−→=βαβαβαsin sin cos cos )cos(-=+βαβαβαsin sin cos cos )cos(+=-βαβαβαsin cos cos sin )sin(+=+βαβαβαsin cos cos sin )sin(-=-2. 倍角公式:()()2222222cos cos cos sin sin cos 2cos sin 2cos 112sin tan tan 1+cos2tan cos 1tan tan 21cos2sin 22tan tan 21tan 令 = = αβαβαβαβααααααβααβααβααααα=±=−−−→=-↓=-=-±±=⇒-↓=-3. 正切变形公式tanα+tanβ=tan(α+β)(1-tanαtanβ)tanα-tanβ=tan(α-β)(1+tanαtanβ)3.2 简单的三角恒等变换三角函数的化简、计算、证明的恒等变形的基本思路是:一角二名三结构。
即首先观察角与角之间的关系,注意角的一些常用变式,角的变换是三角函数变换的核心!第二看函数名称之间的关系,通常“切化弦”;第三观察代数式的结构特点。
基本的技巧有:(1)巧变角(已知角与特殊角的变换、已知角与目标角的变换、角与其倍角的变换、两角与其和差角的变换. 如()()ααββαββ=+-=-+,2()()ααβαβ=++-,2()()αβαβα=+--,22αβαβ++=⋅,()()222αββααβ+=---等), (2)公式变形使用(tan tan αβ±()()tan 1tan tan αβαβ=±。
三角恒等变换和三角函数性质专题

知识梳理 1.正弦、余弦、正切函数图像与性质
函数
y=sinx
y=cosx
y=tanx
图像
定义域 值域 奇偶性 最小正周期
单调性
R
[-1,1] 奇函数 2π
在[-������+2kπ,������+2kπ](k∈Z)上递增.
2
2
在[������+2kπ,3������+2kπ](k∈Z)上递减
2
x=-������+2kπ,k∈Z时,y取得最小值-1
2
x=2kπ,k∈Z时,y取得最大值1. 无最值
x=π+2kπ,k∈Z时,y取得最小值-1
对称中心:(kπ,0)(k∈Z). 对称轴:x=������+kπ(k∈Z)
2
对称中心:(������+kπ,0)(k∈Z).
2
对称轴:x=kπ(k∈Z)
2
2
R [-1,1] 偶函数 2π
在[-π+2kπ,2kπ](k∈Z)上递增. 在[2kπ,π+2kπ](k∈Z)上递减
{x|x≠������+kπ,k∈Z}
2
R 奇函数 π
在 ( - ������ + kπ , ������ + kπ)(k ∈ Z)
2
2
上递增
最值 对称性
x=������+2kπ,k∈Z时,y取得最大值1.
例4.已知f ������
= sin
������
+
������ 6
+ sin
������
−
������ 6
+������������������������ + ������的最大值为1
必修4 数学 三角函数2——三角恒等变换
高中数学 必修4———三角恒等变换一、知识归纳1、两角和与差的正弦、余弦和正切公式:⑴()cos cos cos sin sin αβαβαβ-=+; ⑵()cos cos cos sin sin αβαβαβ+=-; ⑶()sin sin cos cos sin αβαβαβ-=-; ⑷()sin sin cos cos sin αβαβαβ+=+; ⑸()tan tan tan 1tan tan αβαβαβ--=+(()()tan tan tan 1tan tan αβαβαβ-=-+); ⑹()tan tan tan 1tan tan αβαβαβ++=-(()()tan tan tan 1tan tan αβαβαβ+=+-). 2、二倍角的正弦、余弦和正切公式:(1)sin 22sin cos ααα=. (2)21sin 2(sin cos )ααα±=± (3)2222cos2cos sin 2cos 112sin ααααα=-=-=-(2cos 21cos 2αα+=,21cos 2sin 2αα-=).(4)万能公式:a 、()sin cos αααϕA +B =+,其中tan ϕB =A . b 、22tan sin 21tan ααα=+;221tan cos 21tan ααα-=+;22tan tan 21tan ααα=- 【类型题】2.若ABC △的内角A 满足322sin =A ,则=+A A cos sin ( ) A .315 B .315- C .35 D .35- 3.函数1)12(sin )12(cos )(22-++-=ππx x x f 是( )A .奇函数B .偶函数C .奇函数且偶函数D .既不是奇函数也不是偶函数4.若412sin =α,且)24(ππα,∈,则ααsin cos -的值是( ) A .23 B .43 C .23- D .43- 5.已知31tan =α,21tan =β,则)2tan(βα+等于( ) A .34 B .3 C .31 D .2- 9.函数x x x f cos 3sin )(-=([]π,0∈x )的单调递增区间是 。
必修四三角函数和三角恒等变换知识点与题型分类总结
三角函数知识点总结1、任意角:正角: ;负角: ;零角: ;2、角α的顶点与 重合,角的始边与 重合,终边落在第几象限,则称α为第几象限角.第一象限角的集合为 第二象限角的集合为 第三象限角的集合为 第四象限角的集合为 终边在x 轴上的角的集合为 终边在y 轴上的角的集合为 终边在坐标轴上的角的集合为 3、与角α终边相同的角的集合为 4、已知α是第几象限角,确定()*n nα∈N 所在象限的方法:先把各象限均分n 等份,再从x 轴的正半轴的上方起,依次将各区域标上一、二、三、四,则α原来是第几象限对应的标号即为nα终边所落在的区域.5、 叫做1弧度.6、半径为r 的圆的圆心角α所对弧的长为l ,则角α的弧度数的绝对值是 .7、弧度制与角度制的换算公式:8、若扇形的圆心角为()αα为弧度制,半径为r ,弧长为l ,周长为C ,面积为S ,则l= .S=9、设α是一个任意大小的角,α的终边上任意一点P 的坐标是(),x y ,它与原点的距离是()220r r x y =+>,则sin y r α=,cos x r α=,()tan 0yx xα=≠. 10、三角函数在各象限的符号:第一象限全为正,第二象限正弦为正,第三象限正切为正,第四象限余弦为正. 11、三角函数线:.12、同角三角函数的基本关系:(1) ;(2) ;(3) 13、三角函数的诱导公式:()()1sin 2sin k παα+=,()cos 2cos k παα+=,()()tan 2tan k k παα+=∈Z . ()()2sin sin παα+=-,()cos cos παα+=-,()tan tan παα+=. ()()3sin sin αα-=-,()cos cos αα-=,()tan tan αα-=-.()()4sin sin παα-=,()cos cos παα-=-,()tan tan παα-=-.()5sin cos 2παα⎛⎫-=⎪⎝⎭,cos sin 2παα⎛⎫-= ⎪⎝⎭. ()6sin cos 2παα⎛⎫+= ⎪⎝⎭,cos sin 2παα⎛⎫+=- ⎪⎝⎭.口诀:奇变偶不变,符号看象限. 重要公式⑴()cos cos cos sin sin αβαβαβ-=+;⑵()cos cos cos sin sin αβαβαβ+=-; ⑶()sin sin cos cos sin αβαβαβ-=-;⑷()sin sin cos cos sin αβαβαβ+=+; ⑸()tan tan tan 1tan tan αβαβαβ--=+(()()tan tan tan 1tan tan αβαβαβ-=-+);⑹()tan tan tan 1tan tan αβαβαβ++=-(()()tan tan tan 1tan tan αβαβαβ+=+-).二倍角的正弦、余弦和正切公式: ⑴sin 22sin cos ααα=.(2)2222cos2cos sin 2cos 112sin ααααα=-=-=-(2cos 21cos 2αα+=,21cos 2sin 2αα-=).⑶22tan tan 21tan ααα=-.公式的变形:()βαβαβαtan tan 1)tan(tan tan μ•±=±,辅助角公式()22sin cos sin αααϕA +B =A +B +,其中tan ϕB =A. 14、函数sin y x =的图象平移变换变成函数()sin y x ωϕ=A +的图象. 15.函数()()sin 0,0y x ωϕω=A +A >>的性质:①振幅:A ;②周期:2πωT =;③频率:12f ωπ==T ;④相位:x ωϕ+;⑤初相:ϕ.16.图像正弦函数、余弦函数和正切函数的图象与性质:三角函数题型分类总结一.求值1、sin330︒= tan690° = o585sin =2、(1)(07全国Ⅰ) α是第四象限角,12cos 13α=,则sin α= (2)(09北京文)若4sin ,tan 05θθ=->,则cos θ= . (3)(09全国卷Ⅱ文)已知△ABC 中,12cot 5A =-,则cos A = . (4) α是第三象限角,21)sin(=-πα,则αcos = )25cos(απ+= 3、(1) (07陕西) 已知5sin ,5α=则44sin cos αα-= . (2)(04全国文)设(0,)2πα∈,若3sin 5α=,则2cos()4πα+= .(3)(06福建)已知3(,),sin ,25παπα∈=则tan()4πα+= 4(07重庆)下列各式中,值为23的是( ) (A )2sin15cos15︒︒ (B )︒-︒15sin 15cos 22(C )115sin 22-︒(D )︒+︒15cos 15sin 22 5. (1)(07福建) sin15cos75cos15sin105+oooo= (2)(06陕西)cos 43cos77sin 43cos167o o o o+= 。
人教版高中数学【必修四】[知识点整理及重点题型梳理]_三角恒等变换综合_基础
人教版高中数学必修四知识点梳理重点题型(常考知识点)巩固练习三角恒等变换综合【学习目标】1、会用向量的数量积推导出两角差的余弦公式.2、能利用两角差的余弦公式导出两角差的正弦、正切公式.3、能利用两角差的余弦公式导出两角和的正弦、余弦、正切公式,导出二倍角的正弦、余弦、正切公式,了解它们的内在联系.4、能运用上述公式进行简单的恒等变换(包括导出积化和差、和差化积、半角公式,但对这三组公式不要求记忆).【知识网络】【要点梳理】要点一:两角和、差的正、余弦、正切公式sin()±αβ= ①;cos()±=αβ ②; tan()±=αβ ③;要点诠释:1.公式的适用条件(定义域) :公式①、②对任意实数α,β都成立,这表明①、②是R 上的恒等式;公式③中,∈,且R αβk (k Z)2±≠+∈、、παβαβπ2.正向用公式①、②,能把和差角()±αβ的弦函数表示成单角α,β的弦函数;反向用,能把右边结构复杂的展开式化简为和差角()±αβ 的弦函数.公式③正向用是用单角的正切值表示和差角()±αβ的正切值化简.要点二:二倍角公式1. 在两角和的三角函数公式βαβαβαβα=+++中,当T C S ,,时,就可得到二倍角的三角函数公式222,,S C T ααα:sin 2α= 2()S α;cos2α= 2()C α; tan 2α= 2()T α.要点诠释:1.在公式22,S C αα中,角α没有限制,但公式2T αα中,只有当)(224Z k k k ∈+≠+≠ππαππα和时才成立;2. 余弦的二倍角公式有三种:ααα22sin cos 2cos -==1cos 22-α=α2sin 21-;解题对应根据不同函数名的需要,函数不同的形式,公式的双向应用分别起缩角升幂和扩角降幂的作用.3. 二倍角公式不仅限于2α和α的二倍的形式,其它如4α是2α的二倍,24αα是的二倍,332αα是的二倍等等,要熟悉这多种形式的两个角相对二倍关系,才能熟练地应用二倍角公式,这是灵活运用这些公式的关键.要点三:二倍角公式的推论升幂公式:21cos 22cos αα+=, 21c o s 22s i n αα-=降幂公式:ααα2sin 21cos sin =; 22cos 1sin 2αα-=;22cos 1cos 2αα+=.要点四:三角恒等变换的基本题型三角式的化简、求值、证明是三角恒等变换的基本题型: 1.三角函数式的化简(1)常用方法:①直接应用公式进行降次、消项;②切割化弦,异名化同名,异角化同角;③ 三角公式的逆用等.(2)化简要求:①能求出值的应求出值;②使三角函数种数尽量少;③使项数尽量少;④尽量使分母不含三角函数;⑤尽量使被开方数不含三角函数.2.三角函数的求值类型有三类(1)给角求值:一般所给出的角都是非特殊角,要观察所给角与特殊角间的关系,利用三角变换消去非特殊角,转化为求特殊角的三角函数值问题;(2)给值求值:给出某些角的三角函数式的值,求另外一些角的三角函数值,解题的关键在于“变角”,如2(),()()ααββααβαβ=+-=++-等,把所求角用含已知角的式子表示,求解时要注意角的范围的讨论;(3)给值求角:实质上转化为“给值求值”问题,由所得的所求角的函数值结合所求角的范围及函数的单调性求得角.3.三角等式的证明(1)三角恒等式的证题思路是根据等式两端的特征,通过三角恒等变换,应用化繁为简、左右同一等方法,使等式两端化“异”为“同”;(2)三角条件等式的证题思路是通过观察,发现已知条件和待证等式间的关系,采用代入法、消参法或分析法进行证明.【典型例题】类型一:正用公式 例1.已知2313sin ,,,cos ,,23232πααππββπ⎛⎫⎛⎫=-∈=∈ ⎪ ⎪⎝⎭⎝⎭. (1)求sin2α的值;(2)求()cos αβ-的值.【思路点拨】(1)由题意知,cos α=,然后利用二倍角公式求得sin 2α的值.(2)求得sin β=【答案】(12【解析】(1)23sin ,,,32πααπ⎛⎫=-∈ ⎪⎝⎭得cos 3α=-,2sin 22sin cos 23ααα⎛⎛⎫==⨯-⨯= ⎪ ⎝⎭⎝⎭(2)13cos ,,2,32πββπ⎛⎫=∈ ⎪⎝⎭得sin 3β=-()cos cos cos sin sin αβαβαβ∴-=+=1233⎛⎛⎫+-⨯ ⎪ ⎝⎭⎝⎭=9举一反三:【变式1】求值: sin15︒= ;sin 75︒= ;cos75︒=【答案】4 4 4【解析】sin15sin(6045)sin 60cos 45cos 60sin 454︒=︒-︒=︒︒-︒︒=,sin 75sin(3045)sin 30cos 45cos30sin 454︒=︒+︒=︒︒+︒︒=,cos 75cos(3045)cos30cos 45sin 30sin 45︒=︒+︒=︒︒-︒︒=. 【变式2】已知tan α和tan β是方程2260x x +-=的两个根,求tan()αβ+的值. 【答案】18-【解析】由韦达定理,得21tan tan -=β+α, 3tan tan -=β⋅α, ∴ 81tan tan 1tan tan )tan(-=β⋅α-β+α=β+α. 例2.已知2π<β<α<4π3,cos (α-β)=1312,sin (α+β)=-53,求sin2α的值. 【思路点拨】因为2()()ααβαβ=++-,分别求出αβ+和αβ-的正弦值和余弦值,利用两角和的正弦公式可求解. 【答案】5665- 【解析】∵432π<β<α<π,∴π<α+β<23π,0<α-β<4π ∵sin(α+β)=-53,cos(α-β)=1312,∴cos(α+β)=-54,sin(α-β)=135∴sin2α=sin[(α+β)+(α-β)]=6556-.【总结升华】(1)解题中应用了2()()ααβαβ=++-式子的变换,体现了灵活解决问题的能力,应着重体会,常见的变换技巧还有(),βαβα=+-2()()βαβαβ=+--, 2()αβαβα+=++等.(2)已知某一个(或两个)角的三角函数值,求另一个相关角的三角函数值,基本的解题策略是从“角的关系式”入手切入或突破.角的关系主要有互余(或互补)关系,和差(为特殊角)关系,倍半关系等.对于比较复杂的问题,则需要两种关系的混合运用.举一反三:【变式1】(2017 江苏海陵区月考)已知13sin )14αβα=-=,且02πβα<<<. (1)求tan2α的值;(2)求cosβ的值. 【思路点拨】(1)由已知利用同角三角函数基本关系式可求cosα,tanα,进而利用二倍角的正切函数公式可求tna2α的值.(2)由已知可求范围02πβα-<-<,利用同角三角函数基本关系式可求sin (β-α)的值,由β=(β-α)+α,利用两角和的余弦函数公式即可计算得解.【答案】(1)47-;(2)12【解析】(1)∵sin 7α=,且02πβα<<<.∴1sin cos ,tan 7cos αααα====∴22tan tan 21tan 47ααα==--. (2)∵13cos()14βα-=,且02πβα<<<.∴02πβα-<-<,可得:sin()14βα-==-∴1311cos cos()]cos()cos sin()sin (1471472ββααβααβαα=-+=---=⨯--⨯= 【变式2】已知4cos()cos 2.125212πππθ-=-<θ<πθ,且,求(+)的值【答案】50【解析】角的关系式:4)12(2122ππθπθ+-=+(和差与倍半的综合关系)∵4cos()1252ππθ-=-<θ<π,且,∴53)12sin(=-πθ∴2524)12cos()12sin(2)12(2sin -=--=-πθπθπθ2571)12(cos 2)12(2cos 2=--=-πθπθ ∴]4)12(2cos[.122cos ππθπθ+-=)+(=)]12(2sin )12(2[cos 22πθπθ---724()2252550=+=类型二:逆用公式 例3.求值:(1)sin 24cos36cos24cos54︒︒+︒︒;(2)1cos 212212ππ+; (3)01tan 751tan 75+-; 【思路点拨】 题目中涉及到的角并非特殊角,而从式子的结构出发应逆用和角公式等先化简再计算. (1)若将式中的cos54︒改写为sin36︒则恰为两角和的正弦; (2)中将其转化为特殊角的三角函数值,然后可以逆用公式; (3)利用tan 451︒=将1tan15+︒视为tan 45tan15︒+︒,将1tan15-︒视为1tan 45tan15-︒︒,则式子恰为两角和的正切.【答案】(1)2(2)2(3【解析】(1)原式=sin 24cos36cos 24sin 36sin(2436)︒︒+︒︒=︒+︒=;(2)原式=sin 30cos15cos30sin15sin(3015)2=︒︒+︒︒=︒+︒=;(3)原式0000000tan 45tan 75tan(4575)tan1201tan 45tan 75+==+==- 【总结升华】①把式中某函数作适当的转换之后,再逆用两角和(差)正(余)弦公式,二倍角公式等,即所谓“逆用公式”.②辅助角公式:sin cos )a b αααϕ+=+,其中角ϕ在公式变形过程中自然确定. 举一反三: 【变式1】求值:(1)sin164sin 224sin 254sin314⋅+⋅; (2)0000sin 20cos110cos160sin 70+; (3)sin347cos148sin 77cos58⋅+⋅ 【答案】(1)1/2(2)-1(3)1/2 【解析】(1)原式1sin16sin 44cos16cos 44cos(1644)2=-⋅+⋅=+=; (2)原式=0sin 20cos 70cos 20sin 70sin(2070)1--=-+=-;(3)原式=()2cos 77sin 58sin 77cos58sin 7758sin135+=+==【变式2】下列各式中,值为12的是( )A.cos15sin15︒︒B.22cos 112π-C.D. 2tan 22.51tan 22.5︒-︒【答案】D ;【解析】11cos15sin15sin 3024︒︒=︒=;22cos 1cos1262ππ-==;cos15=︒; 22tan 22.512tan 22.511tan 451tan 22.521tan 22.522︒︒=⋅=︒=-︒-︒. 例4. 求值:(1)cos36cos72︒︒;(2)πππ73cos 72cos 7cos【思路点拨】问题的特征是角存在倍角关系,且都是余弦的乘积.方法是分子分母(分母视为1)同乘以最小角的正弦.【答案】(1)1/4(2)1/8 【解析】(1)原式=000000000sin 36cos36cos 721sin 72cos 721sin1441sin 362sin 364sin 364=⨯=⨯=; (2)原式=πππππππ74cos 72cos 7cos )74cos(72cos 7cos-=-24sin cos cos cos 7777sin7224sin cos cos 7772sin78sin 7...8sin718πππππππππππ=-=-==-=-【总结升华】此种类型题比较特殊,特殊在:①余弦相乘;②后一个角是前一个角的2倍;③最大角的2倍与最小角的和与差是π.三个条件缺一不可.另外需要注意2的个数.应看到掌握了这些方法后可解决一类问题,若通过恰当的转化,转化成具有这种特征的结构,则可考虑采用这个方法.举一反三:【变式】求值:cos20cos40cos80︒︒︒【答案】18【解析】原式=2sin 20cos 20cos 40cos802sin 20︒︒︒︒︒=00000020sin 880cos 80sin 220sin 2280cos 40cos 40sin 2=⨯ =8120sin 8160sin 00=. 类型三:变用公式 例5.求值:(1)0tan 20tan 4020tan 40++;(2)00(1tan 2)(1tan 43)++【思路点拨】表示两个正切的和,可以“凑”公式的变形:tan tan tan tan (1tan tan )1tan tan αβαβαβαβ++=--tan()(1tan tan )αβαβ=+-.(1)中204060︒+︒=︒,又340tan 20tan 140tan 20tan )4020tan(00000=-+=+,变形:0000tan 20tan 40tan 20tan 40)+=-.【答案】(1(2)2 【解析】(1)原式000000tan(2040)(1tan 20tan 40)20tan 40=+-+000020tan 4020tan 40=+=(2)原式=01tan 2tan 43tan 2tan 43+++0000001tan(243)(1tan 2tan 43)tan 2tan 43=++-+000011tan 2tan 43tan 2tan 432=+-+=【总结升华】本题是利用了两角和正切公式的变形,找出tan tan ,tan tan αβαβ+与tan()αβ+三者间的关系,进行转化,即所谓“变用公式”解决问题;变用公式在一些解三角问题中起着重要作用,需灵活掌握.但它是以公式原型为基础,根据题目需要而采取的办法,如:tan 451︒=,22sin cos 1αα+=.举一反三:【变式1】(2015春 甘肃高台县期末)化简tan 70cos10201)︒︒︒-. 【答案】-1【解析】sin 70cos10tan 70cos10201)cos 70︒︒︒︒︒-=︒sin 70cos102sin(2030)cos70cos 20︒︒︒-︒=⋅︒︒2sin10cos10sin 70sin 20sin 701sin 20cos 20sin 20cos 20-︒︒︒-︒︒===-︒︒︒︒.例6. 化简:(1)sin 50(1)︒+︒;(2)222cos 12tan()sin ()44αππαα--+【思路点拨】(1)题中首先“化切为弦”,同时用好“50︒”和“40︒”的互余关系,注意逆用和角公式化简; (2)题初看有“化切为弦”,“降幂”等诸多想法,但首先应注意到2)4()4(παπαπ=++-这个关系. 【答案】(1)1(2)1 【解析】(1)原式0sin50(1=0sin50= =000000sin 30cos10cos30sin102sin50cos10+⋅000000000sin 402cos40sin 402sin50cos10cos10sin80cos101cos10cos10=⋅====(2)原式=2cos 22tan()sin [()]424απππαα---2cos 22sin()4cos ()4cos()4cos 22sin()cos()44cos 2cos 2cos 2sin(2)21απαπαπααππααααπαα=-⋅--=--==-=【总结升华】(1)三角变换所涉及的公式实际上正是研究了各种组合的角(如和差角,倍半角等)的三角函数与每一单角的三角函数关系.因而具体运用时,注意对问题所涉及的角度及角度关系进行观察.(2)三角变换中一般采用“降次”、“化弦”、“通分”的方法;在三角变换中经常用到降幂公式:21cos 2cos 2αα+=,21cos 2sin 2αα-=.举一反三: 【变式1】化简:(1)1sin10sin 80-; (2)01tan10cos50+【答案】(1)4(3【解析】(1)原式=1cos103sin104sin(3010)4sin10cos10sin10cos10sin 20---===;(2)原式=0001sin10cos50cos10+0001sin10sin 40sin80=+02cos40cos80sin80︒+︒= =380sin 10cos 30cos 280sin 20cos 60cos 240cos 00=︒︒︒=︒+︒. 类型四:三角函数知识的综合应用例7.(2015 广东江门一模)已知函数()sin f x x x ωω=的最小正周期为π,x ∈R ,ω>0是常数.(1)求ω的值;(2)若6()2125f θπ+=,(0,)2πθ∈,求sin2θ. 【思路点拨】(1)由两角和的正弦公式化简解析式可得()2sin()3f x x πω=+,由已知及周期公式即可求ω的值.(2)由已知及三角函数中的恒等变换应用可得6()2cos 2125f θπθ+==,可得cos θ,由(0,)2πθ∈,可得sin θ,sin2θ的值.【答案】(1)ω=2;(2)2425【解析】(1)∵()sin 2sin()3f x x x x πωωω=+=+,∵函数()sin f x x x ωω=+的最小正周期为π, ∴2T ππω==,解得:ω=2.(2)∵6()2sin[2()]2sin()2cos 212212325f θπθπππθθ+=++=+==, ∴3cos 5θ=,∵(0,)2πθ∈,∴4sin 5θ==, ∴3424sin 22sin cos 25525θθθ==⨯⨯=. 举一反三:精品文档 用心整理资料来源于网络 仅供免费交流使用 【变式1】已知向量a (cos sin ,sin )x x x ωωω=-a ,b(cos sin ,)x x x ωωω=--b ,设函数()f x a b λ=⋅+()x ∈R 的图象关于直线πx =对称,其中ω,λ为常数,且1(,1)2ω∈. (Ⅰ)求函数()f x 的最小正周期; (Ⅱ)若()y f x =的图象经过点π(,0)4,求函数()f x 在区间3π[0,]5上的取值范围. 【答案】(Ⅰ) 6π5(Ⅱ)[12- 【解析】(Ⅰ)因为22()sin cos cos f x x x x x ωωωωλ=-+⋅+cos 22x x ωωλ=-++π2sin(2)6x ωλ=-+. 由直线πx =是()y f x =图象的一条对称轴,可得πsin(2π)16ω-=±, 所以ππ2ππ()62k k ω-=+∈Z ,即1()23k k ω=+∈Z . 又1(,1)2ω∈,k ∈Z ,所以1k =,故56ω=. 所以()f x 的最小正周期是6π5. (Ⅱ)由()y f x =的图象过点π(,0)4,得π()04f =,即5πππ2sin()2sin 6264λ=-⨯-=-=,即λ=故5π()2sin()36f x x =-由3π05x ≤≤,有π5π5π6366x -≤-≤, 所以15πsin()1236x -≤-≤,得5π12sin()236x -- 故函数()f x 在3π[0,]5上的取值范围为[12-.。
数学必修四复习提纲——三角函数与三角恒等变换
yACB第一章 三角函数1、任意角:正角、零角、负角;与α终边相同的角表示为{}|2,k k Z ββαπ=+∈2、轴线角: 终边在x 轴上的角的集合:{}|,k k Z ββπ=∈; 终边在y 轴上的角的集合:|,2k k Z πββπ⎧⎫=+∈⎨⎬⎩⎭; 终边在坐标轴上的角的集合:|,2k k Z πββ⎧⎫=∈⎨⎬⎩⎭等;(见笔记)(提醒:终边相同的角不一定相等,相等的角终边一定相同) 3、象限角: 如第一象限角:|22,2k k k Z παπαπ⎧⎫<<+∈⎨⎬⎩⎭; 4、弧度制:弧长等于半径的圆弧所对的圆心角叫做1弧度的角; (提醒:一个式子中不能角度,弧度混用)换算:180°=π弧度; 1弧度= 0'18057.305718π⎛⎫≈≈ ⎪⎝⎭; 1°= 180π弧度 计算:角的大小α=l r ;弧长l = r α⋅,面积S = 12l r ⋅=212r α⋅=212l α。
5、任意角的三角函数:1)定义:角α终边上任意一点P(x ,y),则r )0r >,sin y rα=、cos x r α= 、tan y xα=。
提醒:如果点P 在单位圆上,即r=1,则sin ,cos ,tan yy x xααα===)特殊角的三角函数值(任意角均可由诱导公式化成特殊角)2)三角函数线: sin MP α= cos OM α= tan AT α=3)三角函数值符号:一全正、二正弦、三正切,四余弦sin αcos α tan α4)同角三角函数的基本关系: ①1cos sin 22=+αα ②sin tan +,cos 2k k Z απααπα⎛⎫=≠∈ ⎪⎝⎭5)三角函数的诱导公式:sin(2)sin cos(2)cos tan(2)tan k k k πααπααπαα+=+=+= x x x x xx t a n )t a n (c o s )c o s (s i n )s i n (-=--=-=-πππ x x x x xx t a n )t a n (c o s )c o s(s i n )s i n (-=-=--=- x x x x xx t a n )t a n (c o s )c o s (s i n )s i n (=+-=+-=+πππ提醒:求任意角的三角函数值一般步骤如下6、三角函数的图象和性质:cos()sin 2παα+=-sin()cos 2παα+=cos()sin 2παα-=sin()cos 2παα-=7、()sin y A x ωϕ=+的图像和性质:1)作图:①五点法:依次令x ωϕ+= 0 、2π、π、32π、2π ②变换作图法: (A>0,ω>0) (横向伸缩和左右平移变的都是系数为1的x )● 方法1:将y =sinx 的图像0,x ||0,x ||ϕϕϕϕ><−−−−−−−−→沿轴向左平移个单位沿轴向右平移个单位()sin y x ϕ=+ 1ω−−−−−−−−−→横坐标伸长或缩短为原来的倍()sin y x ωϕ=+ A −−−−−−−−−→纵坐标伸长或缩短为原来的倍()sin y A x ωϕ=+● 方法2:将y =sinx 的图像1ω−−−−−−−−−→横坐标伸长或缩短为原来的倍()sin y x ω=||0,x ||0,x ϕϕωϕϕω><−−−−−−−−−→沿轴向左平移个单位沿轴向右平移个单位()sin y x ωϕ=+A −−−−−−−−−→纵坐标伸长或缩短为原来的倍()sin y A x ωϕ=+2)振幅|A|;周期T = 2||πω ;频率f = 1T ;初相x ωϕ+;相位ϕ(A >0,ω>0)3)定义域 【练习19】函数的定义域是( )(答:B ) A 、B 、C 、D 、解析:由题意可得sinx ﹣≥0⇒sinx ≥,由单位圆可知, 又x∈(0,2π)∴函数的定义域是. 故选B .4)最值(先把ω化成正的) 【练习21】函数,当f (x )取得最小值时,x 的取值集合为( )(答:A ) A 、 B 、 C 、D 、解析:∵函数当 sin (﹣)=﹣1时函数取到最小值, ∴﹣=﹣+2k π,k∈Z 函数, ∴x=﹣+4k π,k∈Z,5)()sin y A x ωϕ=+的对称轴、对称中心①对称轴0x x =满足:0(Z)2x k k πωϕπ+=+∈;②对称轴中心0(,0)x 满足:0(Z)x k k ωϕπ+=∈6)单调区间(先把ω化成正的) 若A >0,增区间:令 22k ππ-+≤x ωϕ+≤22k ππ+ ,再解不等式减区间:令22k ππ+≤x ωϕ+≤322k ππ+,再解不等式 若A <0,反过来。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
必修四三角函数和三角恒等变换知识点及题型分类汇总————————————————————————————————作者:————————————————————————————————日期:23三角函数知识点总结1、任意角:正角: ;负角: ;零角: ;2、角α的顶点与 重合,角的始边与 重合,终边落在第几象限,则称α为第几象限角.第一象限角的集合为 第二象限角的集合为 第三象限角的集合为 第四象限角的集合为 终边在x 轴上的角的集合为 终边在y 轴上的角的集合为 终边在坐标轴上的角的集合为 3、与角α终边相同的角的集合为 4、已知α是第几象限角,确定()*n nα∈N 所在象限的方法:先把各象限均分n 等份,再从x 轴的正半轴的上方起,依次将各区域标上一、二、三、四,则α原来是第几象限对应的标号即为nα终边所落在的区域.5、 叫做1弧度.6、半径为r 的圆的圆心角α所对弧的长为l ,则角α的弧度数的绝对值是 .7、弧度制与角度制的换算公式:8、若扇形的圆心角为()αα为弧度制,半径为r ,弧长为l ,周长为C ,面积为S ,则l= .S=9、设α是一个任意大小的角,α的终边上任意一点P 的坐标是(),x y ,它与原点的距离是()220r r x y =+>,则sin y r α=,cos x r α=,()tan 0yx xα=≠. 10、三角函数在各象限的符号:第一象限全为正,第二象限正弦为正,第三象限正切为正,第四象限余弦为正. 11、三角函数线:.12、同角三角函数的基本关系:(1) ;(2) ;(3) 13、三角函数的诱导公式:()()1sin 2sin k παα+=,()cos 2cos k παα+=,()()tan 2tan k k παα+=∈Z . ()()2sin sin παα+=-,()cos cos παα+=-,()tan tan παα+=.4()()3sin sin αα-=-,()cos cos αα-=,()tan tan αα-=-. ()()4sin sin παα-=,()cos cos παα-=-,()tan tan παα-=-.()5sin cos 2παα⎛⎫-=⎪⎝⎭,cos sin 2παα⎛⎫-= ⎪⎝⎭. ()6sin cos 2παα⎛⎫+=⎪⎝⎭,cos sin 2παα⎛⎫+=- ⎪⎝⎭. 口诀:奇变偶不变,符号看象限. 重要公式⑴()cos cos cos sin sin αβαβαβ-=+;⑵()cos cos cos sin sin αβαβαβ+=-; ⑶()sin sin cos cos sin αβαβαβ-=-;⑷()sin sin cos cos sin αβαβαβ+=+; ⑸()tan tan tan 1tan tan αβαβαβ--=+(()()tan tan tan 1tan tan αβαβαβ-=-+);⑹()tan tan tan 1tan tan αβαβαβ++=-(()()tan tan tan 1tan tan αβαβαβ+=+-).二倍角的正弦、余弦和正切公式: ⑴sin 22sin cos ααα=.(2)2222cos2cos sin 2cos 112sin ααααα=-=-=-(2cos 21cos 2αα+=,21cos 2sin 2αα-=).⑶22tan tan 21tan ααα=-.公式的变形:()βαβαβαtan tan 1)tan(tan tan ∙±=±,辅助角公式()22sin cos sin αααϕA +B =A +B +,其中tan ϕB =A. 14、函数sin y x =的图象平移变换变成函数()sin y x ωϕ=A +的图象. 15.函数()()sin 0,0y x ωϕω=A +A >>的性质:①振幅:A;②周期:2πωT=;③频率:12fωπ==T;④相位:xωϕ+;⑤初相:ϕ.16.图像正弦函数、余弦函数和正切函数的图象与性质:56三角函数题型分类总结一.求值1、sin330︒= tan690° = o585sin =2、(1)(07全国Ⅰ) α是第四象限角,12cos 13α=,则sin α= (2)(09北京文)若4sin ,tan 05θθ=->,则cos θ= . (3)(09全国卷Ⅱ文)已知△ABC 中,12cot 5A =-,则cos A = . (4) α是第三象限角,21)sin(=-πα,则αcos = )25cos(απ+= 3、(1) (07陕西) 已知5sin ,5α=则44sin cos αα-= . (2)(04全国文)设(0,)2πα∈,若3sin 5α=,则2cos()4πα+= .(3)(06福建)已知3(,),sin ,25παπα∈=则tan()4πα+= 4(07重庆)下列各式中,值为23的是( ) (A )2sin15cos15︒︒ (B )︒-︒15sin 15cos 22(C )115sin 22-︒(D )︒+︒15cos 15sin 22 5. (1)(07福建) sin15cos75cos15sin105+= (2)(06陕西)cos 43cos77sin 43cos167oooo+= 。
(3)sin163sin 223sin 253sin313+= 。
6.(1) 若sin θ+cos θ=15,则sin 2θ= (2)已知3sin()45x π-=,则sin 2x 的值为(3) 若2tan =α ,则ααααcos sin cos sin -+=7. (08北京)若角α的终边经过点(12)P -,,则αcos = tan 2α=78.(07浙江)已知3cos()22πϕ+=,且||2πϕ<,则tan ϕ= 9.若cos 22π2sin 4αα=-⎛⎫- ⎪⎝⎭,则cos sin αα+= 10.(09重庆文)下列关系式中正确的是 ( )A .0sin11cos10sin168<< B .0sin168sin11cos10<< C .0sin11sin168cos10<< D .0sin168cos10sin11<< 11.已知53)2cos(=-πα,则αα22cos sin -的值为 ( )A .257B .2516-C .259D .257-12.已知sin θ=-1312,θ∈(-2π,0),则cos (θ-4π)的值为 ( )A .-2627B .2627C .-26217D .2621713.已知f (cosx )=cos3x ,则f (sin30( )A .1B .23C .0D .-1 14.已知sin x -sin y = -32,cos x -cos y = 32,且x ,y 为锐角,则tan(x -y )的值是 ( ) A .5142 B . -5142 C .±5142 D .28145± 15.已知tan160o =a ,则sin2000o 的值是 ( ) A.a 1+a 2 B.-a 1+a 2 C.11+a 2 D.-11+a 216.()2tan cot cos x x x += ( )(A)tan x (B)sin x (C)cos x (D)cot x 17.若02,sin 3cos απαα≤≤>,则α的取值范围是: ( )(A),32ππ⎛⎫⎪⎝⎭ (B),3ππ⎛⎫⎪⎝⎭ (C)4,33ππ⎛⎫ ⎪⎝⎭ (D)3,32ππ⎛⎫⎪⎝⎭18.已知cos (α-6π)+sin α=的值是则)67sin(,354πα- ( )8(A )-532 (B )532 (C)-54 (D) 5419.若,5sin 2cos -=+a a 则a tan = ( ) (A )21 (B )2 (C )21- (D )2- 20.0203sin 702cos 10--= A. 12B.22C. 2D.32二.最值1.(09福建)函数()sin cos f x x x =最小值是= 。
2.①(08全国二).函数x x x f cos sin )(-=的最大值为 。
②(08上海)函数f (x )=3sin x +sin(π2+x )的最大值是③(09江西)若函数()(13tan )cos f x x x =+,02x π≤<,则()f x 的最大值为3.(08海南)函数()cos 22sin f x x x =+的最小值为 最大值为 。
4.(09上海)函数22cos sin 2y x x =+的最小值是 . 5.(06年福建)已知函数()2sin (0)f x x ωω=>在区间,34ππ⎡⎤-⎢⎥⎣⎦上的最小值是2-,则ω的最小值等于6.(08辽宁)设02x π⎛⎫∈ ⎪⎝⎭,,则函数22sin 1sin 2x y x +=的最小值为 .7.函数f (x )=3sin x +sin(π2+x )的最大值是8.将函数x x y cos 3sin -=的图像向右平移了n 个单位,所得图像关于y 轴对称,则n 的最小正值是 A .6π7 B .3π C .6π D .2π 9.若动直线x a =与函数()sin f x x =和()cos g x x =的图像分别交于M N ,两点,则MN 的最大值为( ) A .1 B .2 C .3D .210.函数y=sin (2πx+θ)cos (2πx+θ)在x=2时有最大值,则θ的一个值是9( ) A .4π B .2πC .32π D .43π11.函数2()s i n3s i n c o s f x x x x =+在区间,42ππ⎡⎤⎢⎥⎣⎦上的最大值是( )A.1B.132+ C.32D.1+312.求函数2474sin cos 4cos 4cos y x x x x =-+-的最大值与最小值。
三.单调性1.(04天津)函数]),0[()26sin(2ππ∈-=x x y 为增函数的区间是 ( ).A. ]3,0[πB. ]127,12[ππC. ]65,3[ππ D. ],65[ππ 2.函数sin y x =的一个单调增区间是 ( )A .ππ⎛⎫- ⎪44⎝⎭,B .3ππ⎛⎫ ⎪44⎝⎭,C .3π⎛⎫π ⎪2⎝⎭,D .32π⎛⎫π⎪2⎝⎭, 3.函数()sin 3cos ([,0])f x x x x π=-∈-的单调递增区间是 ( ) A .5[,]6ππ--B .5[,]66ππ--C .[,0]3π-D .[,0]6π- 4.(07天津卷) 设函数()sin ()3f x x x π⎛⎫=+∈ ⎪⎝⎭R ,则()f x ( ) A .在区间2736ππ⎡⎤⎢⎥⎣⎦,上是增函数B .在区间2π⎡⎤-π-⎢⎥⎣⎦,上是减函数 C .在区间34ππ⎡⎤⎢⎥⎣⎦,上是增函数D .在区间536ππ⎡⎤⎢⎥⎣⎦,上是减函数5.函数22cos y x =的一个单调增区间是 ( ) A .(,)44ππ-B .(0,)2πC .3(,)44ππD .(,)2ππ6.若函数f (x)同时具有以下两个性质:①f (x)是偶函数,②对任意实数x ,都有f (x +4π)= f (x -4π),则f (x)的解析式可以是( )A .f (x)=cosxB .f (x)=cos(2x 2π+) C .f (x)=sin(4x 2π+) D .f (x) =cos6x10四.周期性1.(07江苏卷)下列函数中,周期为2π的是 ( ) A .sin 2x y = B .sin 2y x = C .cos 4xy = D .cos 4y x =2.(08江苏)()cos 6f x x πω⎛⎫=-⎪⎝⎭的最小正周期为5π,其中0ω>,则ω= 3.(04全国)函数|2sin |xy =的最小正周期是( ).4.(1)(04北京)函数x x x f cos sin )(=的最小正周期是 .(2)(04江苏)函数)(1cos 22R x x y ∈+=的最小正周期为( ). 5.(1)函数()sin 2cos2f x x x =-的最小正周期是(2)(09江西文)函数()(13tan )cos f x x x =+的最小正周期为 (3). (08广东)函数()(sin cos )sin f x x x x =-的最小正周期是 . (4)(04年北京卷.理9)函数x x x x f cos sin 322cos )(-=的最小正周期是 . 6.(09年广东文)函数1)4(cos 22--=πx y 是 ( )A .最小正周期为π的奇函数 B. 最小正周期为π的偶函数 C. 最小正周期为2π的奇函数 D. 最小正周期为2π的偶函数7.(浙江卷2)函数2(sin cos )1y x x =++的最小正周期是 .8.函数21()cos (0)3f x x w w =->的周期与函数()tan 2xg x =的周期相等,则w 等于( )(A )2 (B )1 (C )12 ( D )14五.对称性1.(08安徽)函数sin(2)3y x π=+图像的对称轴方程可能是 ( )A .6x π=-B .12x π=-C .6x π=D .12x π=2.下列函数中,图象关于直线3π=x 对称的是 ( )A )32sin(π-=x y B )62sin(π-=x y C )62sin(π+=x y D )62sin(π+=x y3.(07福建)函数πsin 23y x ⎛⎫=+⎪⎝⎭的图象 ( ) A.关于点π03⎛⎫ ⎪⎝⎭,对称B.关于直线π4x =对称 C.关于点π04⎛⎫ ⎪⎝⎭,对称 D.关于直线π3x =对称 4.(09全国)如果函数3cos(2)y x φ=+的图像关于点4(,0)3π中心对称,那么φ的最小值为 ( ) (A)6π (B) 4π (C) 3π (D) 2π5.已知函数y=2sinwx 的图象与直线y+2=0的相邻两个公共点之间的距离为32π,则w 的值为( )A .3 B .23 C .32D .31六.图象平移与变换1.(08福建)函数y =cos x (x ∈R)的图象向左平移2π个单位后,得到函数y=g(x )的图象,则g(x )的解析式为2.(08天津)把函数sin y x =(x R ∈)的图象上所有点向左平行移动3π个单位长度,再把所得图象上所有点的横坐标缩短到原来的12倍(纵坐标不变),得到的图象所表示的函数是 3.(09山东)将函数sin 2y x =的图象向左平移4π个单位, 再向上平移1个单位,所得图象的函数解析式是4.(09湖南)将函数y=sinx 的图象向左平移ϕ(0 ≤ϕ<2π)的单位后,得到函数y=sin ()6x π-的图象,则ϕ等于 5.要得到函数)42sin(π-=x y 的图象,需将函数x y 2sin =的图象向 平移 个单位6 (2)(全国一8)为得到函数πcos 23y x ⎛⎫=+ ⎪⎝⎭的图像,只需将函数sin 2y x =的图像 向 平移 个单位 (3)为了得到函数)62sin(π-=x y 的图象,可以将函数x y 2cos =的图象向 平移个单位长度7.(2009天津卷文)已知函数)0,)(4sin()(>∈+=w R x wx x f π的最小正周期为π,将)(x f y =的图像向左平移||ϕ个单位长度,所得图像关于y 轴对称,则ϕ的一个值是A2π B 83π C 4π D 8π8.将函数 y = 3 cos x -sin x 的图象向左平移 m (m > 0)个单位,所得到的图象关于 y 轴对称,则 m 的最小正值是 ( )A. π6B. π3 C. 2π3 D. 5π611.将函数y=f (x )sinx 的图象向右平移4π个单位,再作关于x 轴的对称曲线,得到函数y=1-2sin 2x 的图象,则f (x)是( )A .cosx B .2cosx C .Sinx D .2sinx 七.图象1.(07宁夏、海南卷)函数πsin 23y x ⎛⎫=- ⎪⎝⎭在区间ππ2⎡⎤⎢⎥⎣⎦,的简图是 ( )2(浙江卷7)在同一平面直角坐标系中,函数])20[)(232cos(ππ,∈+=x x y 的图象和直线21=y 的交点个数是(A )0 (B )1 (C )2 (D )43.已知函数y=2sin(ωx+φ)(ω>0)在区间[0,2π]的图像如下:那么ω=( )A. 1B. 2C. 1/2D. 1/3 4.(2006年四川卷)下列函数中,图象的一部分如右图所示的是 ( )(A )sin 6y x π⎛⎫=+⎪⎝⎭(B )sin 26y x π⎛⎫=-⎪⎝⎭yx 11- 2π-3π-O 6ππ yx11- 2π-3π-O 6ππ y x1 1-2π-3πO 6π-πy xπ 2π-6π-1 O 1- 3πABCD(C )cos 43y x π⎛⎫=-⎪⎝⎭ (D )cos 26y x π⎛⎫=-⎪⎝⎭5.(2009江苏卷)函数sin()y A x ωϕ=+(,,A ωϕ为常数,0,0A ω>>)在闭区间[,0]π-上的图象如图所示,则ω= .6.(2009宁夏海南卷文)已知函数()2sin()f x x ωφ=+的图像如图所示,则712f π⎛⎫=⎪⎝⎭。
