最小均方LMS算法
LMS算法及改进

LMS算法及改进LMS(Last Mean Square)算法是最小均方差算法的一种,主要用于解决线性系统的参数估计问题。
它通过对样本数据进行迭代处理,不断调整参数的数值,使得模型的预测值与实际观测值的均方差最小。
1.初始化参数:开始时,先给定参数的初始估计值,通常可以将其初始化为0或一个较小的随机数。
2.数据输入:将样本数据输入到算法中。
3.计算预测值:根据当前的参数估计值,计算系统的输出值,即模型的预测值。
4.计算误差:将预测值与实际观测值进行比较,得到误差的值。
5.更新参数:根据误差的值,调整参数的估计值,使得误差越来越小。
通常采用梯度下降的方法来更新参数,即不断地按照误差的负梯度方向更新参数。
6.重复迭代:重复进行步骤3~5,直到参数的估计值收敛,或达到最大迭代次数。
1. Normalized LMS算法:为了提高收敛速度和稳定性,引入了归一化因子来调整步长。
归一化因子可以根据当前误差的方差来自适应地调整步长,从而避免了大步长时参数估计值的剧烈波动。
2. Leaky LMS算法:该算法通过引入衰减因子,将过去的误差对当前的参数估计值的贡献进行衰减。
这样可以减小误差的影响,提高了算法的稳定性和鲁棒性。
3. Recursive Least Squares(RLS)算法:RLS算法是LMS算法的一种改进,它通过引入协方差矩阵和递归更新方法,提高了算法的收敛速度和鲁棒性。
相比于LMS算法,RLS算法在计算复杂度上更高,但在应对非平稳环境时具有更好的性能。
除上述改进算法外,还有很多其他的改进算法被提出,如Affine Projection(AP)算法、Variable Step Size(VSS)算法等。
这些改进算法在不同的应用场景下都具有独特的优势。
总之,LMS算法是一种经典的最小均方差算法,广泛应用于线性系统的参数估计问题。
然而,由于其自身的局限性,研究者们提出了一系列的改进算法,如Normalized LMS算法、Leaky LMS算法和RLS算法等,以提高算法的性能。
第三章最小均方(LMS)算法

E{| e(n) |2} E{e(n)e* (n)} E{| d (n) |2} w H rxd (w H rxd )* w H R xxw
E{| d (n) |2} 2 Re{w H rxd } w H R xxw
rxd (0)
rxd
E{x(n)d * (n)}
rxd (1)
x(n)
xT
(n)w*
i 1
e(n) d (n) y(n) d (n) w H x(n)
rxx (i) E{x(n)x* (n i)} rxx (i) rx*x (i) rxd (i) E{x(n)d * (n i)} rdx (i) rd*x (i)
f (w) E{| e(n) |2}
2 11
2 22
1
v'12
v'
2 2
1
(C1 / 1) (C2 / 2 )
1 均方误差椭圆
的长轴正比于
min
短轴正比于 1 max
§3.3 最陡下降法 3.3.1 最陡下降法的递推公式
=E{| d (n) |2} 2 Re{w H rxd } w H R xxw
w 2R xxw 2rxd
v(n) (I 2QΛQ1)n v(0) [Q(I 2Λ)Q1]n v(0)
正交原理
w=w E{| e2 (n) |} 0 e(n) d (n) w H x(n)
e er je j d dr jd j x xr jx j w w r jw j
| e |2 er2 e2j
[dr
(w
T r
x
r
wTj x
j
)]2
[d
j
(wTr x
j
matlab 最小均方误差(lms)算法

matlab 最小均方误差(lms)算法The least mean squares (LMS) algorithm in MATLAB is a widely used adaptive filter algorithm that aims to minimize the mean square error between the desired signal and the output of the filter. MATLAB provides convenient tools and functions for implementing and optimizing LMS algorithms, making it a popular choice for researchers and engineers working in signal processing and system identification.MATLAB中的最小均方误差(LMS)算法是一种广泛使用的自适应滤波器算法,旨在最小化期望信号与滤波器输出之间的均方误差。
MATLAB提供了方便的工具和函数,用于实现和优化LMS算法,使其成为信号处理和系统辨识领域的研究人员和工程师的首选。
One of the key advantages of using the LMS algorithm in MATLAB is its simplicity and efficiency. With just a few lines of code, users can implement an LMS filter and start optimizing it for their specific application. This ease of use makes MATLAB a popular choice for beginners and experts alike who are looking to quickly prototype and test adaptive filter solutions.在MATLAB中使用LMS算法的一个重要优势是其简单性和高效性。
最小均方(LMS)算法

第3章最小均方(LMS)算法最小均方算法即LMS算法是B.widrow和Hoff于1960年提出的:由于实现简单且对信号统计特性变化具有稳健件,LMS算法获得了极广泛的应用。
LMS算法是基于最小均方误差准则(MMSE)的维纳滤波器和最陡下降法提出的。
本章将进—步时论最小均方误差滤波器和针对这种滤波器的最陡下降法,并在此基础上详细讨论LMS算法。
LMS算法的缺点在于当输人信号的自相关关矩阵的特征值分散时,其收敛件变差。
为了克服这问题并进一步简化LMs算法,学者们进行广长期研究并提出了不少改进算法,本章将对这些算法进行讨论。
最小均方误差滤波器最小均方误差滤波器的推导第2章2.2节已对均于图1.2的最小均力误差滤波器作了概述。
本分将针对时域滤波情况进一步讨论最小均方误差滤波器。
为便于讨论,I.5国内外MIMO技术研究现状虽然MIMO无线通信技术源于天线分集技术与智能天线技术,但是MIMO系统在无需增加频谱与发射功率下就可以获得令人振奋的容量与可靠性提升,它引发了大量的理论研究与外场实验。
自从1995年Telatar推导出多天线高斯信道容量['6}, 1996年Foschini提出BLAST算法[72]与1998年Tarokh等提出空时编码[(4]以来,MIMO无线通信技术的研究如雨后春笋般涌现[(73-300]。
至2004年底,IEEE数据库收录该领域的研究论文己达数千篇(http://ieeexplore. ieee. org/},它们包含了MIMO无线通信技术的理论研究到实验验证以及商用化的各个方面。
目前,国际上很多科研院校与商业机构都争相对MIMO通信技术进行深入研究,MIMO技术正以前所未有的速度向前发展[85]。
这里列举一些国内外在研究MIMO 通信技术方面最具有代表性的机构与个人,以洞察MIMO技术的研究现状与发展动态。
A T&T Bell Lab是多天线技术研究的倡导者,其研究员I. E. Telatar ,G.J.Foschini、M.J.Gans,GD.Golden, R.A.V alenzuela, P.W.Wolniansky、D-S.Shiu,J.M.Kahn, J.Ling, J.C.Liberti,Jr.等长期从事MIMO技术研究[68,84],其第一个空时方案就是著名的BLAST结构[[74一,S,lzz],其开创性的研究包括【5,72-76,88】等]lproject/blastl] o J.H.Winters等还公布了一些研究与测试结果[ 19,64,96,180,279,282,283,285,286,306]。
语音降噪--LMS算法

语音降噪–LMS算法语音降噪是指通过技术手段将语音信号中的噪声成分去除,提高语音信号的清晰度和准确性的一种方法。
LMS(最小均方算法)是一种常见的语音降噪算法,下文将介绍该算法的原理和实现方式。
算法原理LMS算法基于自适应线性滤波理论,通过估计噪声信号与语音信号在某个时刻的相关性来进行降噪处理。
该算法的基本流程如下:1.获取含有噪声的语音信号:通常采用麦克风捕捉环境语音信号,或从音频文件中读取。
2.前置处理:对原始语音信号进行增益处理、预加重等前置处理,便于后续滤波处理。
3.滤波处理:将语音信号输入自适应滤波器中,通过不断调整滤波器的权值,使得滤波器的输出尽可能的接近于原始语音信号,并最小化滤波器输出和实际语音信号的均方误差。
4.降噪处理:将滤波器的输出减去噪声信号的预测。
算法实现LMS算法的实现可以用MATLAB编程完成,以下是其中的关键步骤:1.读取音频数据:可以用MATLAB的audioread函数直接读取本地音频文件,或使用麦克风捕捉环境语音信号。
2.进行前置处理:可以使用MATLAB的filter函数进行卷积滤波,或手动计算并应用增益、预加重等处理。
3.自适应滤波器的初始化:通常使用MATLAB的zeros函数初始化自适应滤波器的权重向量。
4.滤波处理:在MATLAB中可以使用filter函数实现自适应滤波器的滤波过程,并使用LMS算法对滤波器的权重进行调整。
5.噪声预测:通过估计语音信号和噪声信号的相关性得到噪声估计值,从而实现降噪处理。
LMS算法是一种常用的语音降噪算法,其本质是自适应滤波,通过在线调整滤波器的权重来最小化其输出与实际语音信号的均方误差,从而实现降噪处理。
对于语音处理领域的从业者来说,掌握LMS算法的原理和实现方法是必不可少的。
最小均方算法(lms)的原理

最小均方算法(lms)的原理
最小均方算法(LMS)是一种用于信号处理和自适应滤波的算法,它是一种迭代算法,
用于最小化预测误差的均方值。
在该算法中,滤波器的系数会根据输入信号实时地调整,
以使得滤波器的输出能够尽可能地接近期望输出。
LMS算法的核心理念是通过不断迭代,不断的调整滤波器的系数,使其能够最大限度
地降低误差。
该算法首先需要确定一组初始系数,并计算出当前的滤波器输出以及误差。
然后,根据误差的大小和方向来调整滤波器的系数,并重复这个过程,直到误差的均方值
达到最小。
这个过程的数学原理可以用一个简单的公式来表示:
w(n+1) = w(n) + µe(n)X(n)
其中, w(n)是当前滤波器的系数,µ是一个可调节的步长参数,e(n)是当前的误差,
X(n)是输入数据的向量。
在该算法中,步长参数µ的大小对LMS算法的性能有重要的影响。
如果其选择过大,
会导致算法不稳定,收敛到一个错误的值;而如果µ的值过小,则算法收敛速度慢。
此外,在使用LMS算法时,还需要进行一些预处理。
比如,在对输入信号进行滤波时,通常需要进行预加重处理,以便在高频段上增强信号的弱化部分。
同时,在为滤波器确定
初始系数时,还需要利用一些特定的算法来进行优化,以使得滤波器的性能能够得到进一
步的提升。
5.4最小均方算法

uv
uv
uv
w(n 1) w(n) 2e(n)x N (n)
问题:
能否由任意起始位置w(0)经迭代最终收敛到最优解w*
跟最速梯度法权向量的收敛性有何区别?
uvT uv Q e(n) d(n) w (n)xN (n)
uvT uv d(n) xN (n)w(n)
uv
uv
w(n 1) w(n) 2
页页
2 1(1 k22 ) 3 4 (1 k22 )
k2
[RX
(2)
1 i 1
a1 (i ) RX
(2
i)]/
1
1 3
则 2 3 4 (11 9) 2 3
2
k3 [RX (3) a2 (i)RX (3 i)] / 2
i 1
[ 1 4
a2 (1)RX
(2)
a2 (2)RX
(1)] /
c(2)
4.58
所以,ARMA(2,1)模型的系统函数为
1 0.57z1 H1(z) 1 2.93z1 2.59z2
X
第第
2. 已知平稳随机信号x(n)的自相关函数值:
1177 页页
R(0) 1, R(1) 0.5, R(2) 0.5, R(3) 0.25,
现用AR(3)模型估计它的功率谱,设模型参
i 1 p
1 ai zi
i 1
p
q
差分方程: x(n) ai x(n i) Gbi(n i)
i 1
i0
功率谱:
q
2
1 bie ji
Sx
(e
j
)
G 2
2
i 1 p
1 aie ji
i 1
matlab的LMS算法
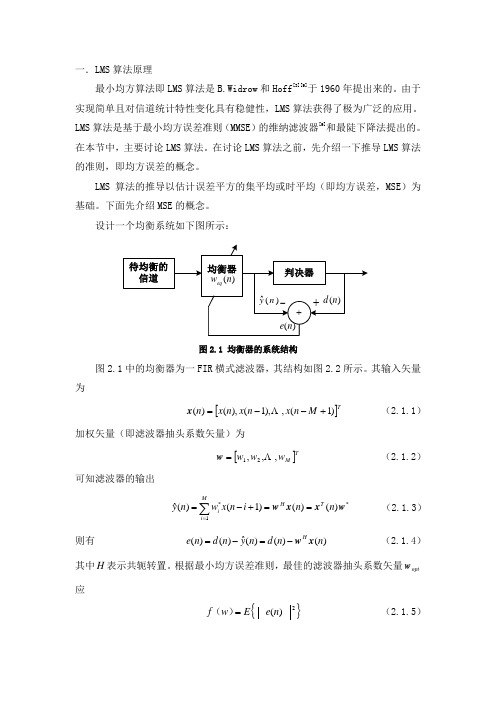
一.LMS 算法原理最小均方算法即LMS 算法是B.Widrow 和Hoff [3][9]于1960年提出来的。
由于实现简单且对信道统计特性变化具有稳健性,LMS 算法获得了极为广泛的应用。
LMS 算法是基于最小均方误差准则(MMSE )的维纳滤波器[9]和最陡下降法提出的。
在本节中,主要讨论LMS 算法。
在讨论LMS 算法之前,先介绍一下推导LMS 算法的准则,即均方误差的概念。
LMS 算法的推导以估计误差平方的集平均或时平均(即均方误差,MSE )为基础。
下面先介绍MSE 的概念。
设计一个均衡系统如下图所示:待均衡的信道均衡器)(n w eq 判决器++)(n d -)(n e )(ˆn y图2.1 均衡器的系统结构图2.1中的均衡器为一FIR 横式滤波器,其结构如图2.2所示。
其输入矢量为[]TM n x n x n x n )1(,),1(),()(+--= x (2.1.1)加权矢量(即滤波器抽头系数矢量)为[]TM w w w ,,,21 =w (2.1.2)可知滤波器的输出*1*)()()1()(ˆw x x w n n i n x w n y T H Mi i ==+-=∑= (2.1.3)则有 )()()(ˆ)()(n n d n y n d n e H x w -=-= (2.1.4) 其中H 表示共轭转置。
根据最小均方误差准则,最佳的滤波器抽头系数矢量opt w 应{}2)(n e Ew f =)( (2.1.5)使得性能函数—均方误差[9]为最小。
式(2.1.5)称为均方误差性能函数。
+1w 2w Mw )(n x )1(-n x )1(+-M n x 1-z1-z1-z线性组合器)(ˆn y图2.2 时域FIR 横式滤波器在指定的信道条件下,)(w f 为各滤波器抽头系数的函数。
现在来研究系统处于平稳状态时的情况。
将式(2.1.4)代入式(2.1.5)可得{}{})()()(*2n e n e E n e Ew f ==)({}w R w r w r w xxHxdHxdHn d E +--=*2)()( {}{}w R w r w xxHxdHn d E +-=Re 2)(2(2.1.6)其中xd r 表示)(n d 和)(n x 的互相关矢量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正交原理
w=w E{| e2 (n) |} 0 e(n) d (n) w H x(n)
e er je j d dr jd j x xr jx j w w r jw j
| e |2 er2 e2j
[dr
(w
T r
x
r
wTj x
j
)]2
wopt=R-xx1rxd
E{|
d
(n)
|2
}
wH opt
rxd
min
E{| d(n)
|2} 2 Re{woHptrxd }
wH opt
R
xx
wopt
E{|
d (n)
|2}
wH opt
R
xx
w
opt
正规方程的解
(1) 直接矩阵求逆算法(DMI算法)或采样矩阵求逆(SMI)算法。 (2) 最陡下降法(加权系数的递推)----最小均方算法即LMS算法 (3) Levinson-Durbin算法(加权系数的递推)利用矩阵的埃尔米特 和Toeplitz性质
E{x(n i)e* (n)} 0 i 0,1,, M 1
根据正交原理推正规方程
0 E{x(n)e*(n)} E{x(n)[d *(n) xH (n)wopt ]}
E{x(n)d *(n)} E{x(n)xH (n)}wopt
R xxw rxd
§3.2 关于均方误差性能函数的进一步讨论 3.2.1 均方误差性能函数的各种表达式
[d
j
(wTr x
j
wTj xr )]2
w | e |2 wr | e |2 jw j | e |2 2xe*
w E{| e(n) |2} E{w | e(n) |2} E{2e* (n)x(n)} 0
E{x(n)e* (n)} 0 E{p(n)q* (n)} 0
i 1
qi ' QH qi [q1, , qi , , qM ]H qi [0, ,1, 0]T
3.2.2 几何意义
w
w1 w2
w opt
wopt1 wopt 2
v
w w opt
v1 v2
'
R xx
rxx (0)
rxx
(1)
rxx (1)
rxx (0) rxx (0) 0
图3.2 均方误差性能面
图3.3 等均方误差椭圆族
min vT R xx v C vT R xxv C1
v' v' C QT
R
xxQ
Λ
1
0
0
2
v'T Λv ' C1
2 11
rxx (i) E{x(n)x* (n i)} rxx (i) rx*x (i) rxd (i) E{x(n)d * (n i)} rdx (i) rd*x (i)
f (w) E{| e(n) |2}
E{| e(n) |2} E{e(n)e* (n)} E{| d (n) |2} w H rxd (w H rxd )* w H R xxw
rxx (1) rxx (0)
rxx (M 1)
rxx (M 2)
(1)是埃米尔特矩阵
R
H xx
R xx
rxx (1 M ) rxx (2 M )
rxx (0)
(2)是正定的或半正定的。
v H R xxv E{v H x(n)x H (n)v} E{| x H (n)v |2} 0
E{| d (n) |2} 2 Re{w H rxd } w H R xxw
rxd (0)
rxd
E{x(n)d * (n)}
rxd (1)
rxd (1 M )
rxx (0)
R xx
E{x(n)x H (n)}
rxx (1)
w opt
R
r 1
xx xd
min
E{e2 (n)}min
E{d
2
(n)}
wH opt
rxd
w(n 1) w(n) w
w(n 1) w(n) [2R xxw(n) 2rxd ]
(3)具有Toeplitz性质,即其任意对角线上的元素相等。
最佳解---维纳解
E{| d (n) |2} 2 Re{w H rxd } w H R xxw
f (w) E{| e(n) |2} w w E{e2 (n)} 0
(正规方程) R xx w opt=rxd
Q H Q I, Q H Q1 Q H R xxQ Λ R xx QΛQH QΛQ1
Λ Diag(1, 2 , M ) =min vH QΛQH v
v' Q H v [v1 ',, vM ']T
v Qv'
min v'H Λv ' min M i vi' 2
=min+(w wopt )H Rxx (w wopt )
v w w opt = min+v H R xx v
R xxqi
iqi
i 1,2,, M
qiH q j
1 0
i j i j
q11 q1M
Q
q1,,q M
Fra bibliotekqM1 qMM
2 22
1
v'12 v'22 1
(C1 / 1) (C2 / 2 )
1 均方误差椭圆
的长轴正比于
min
短轴正比于 1 max
§3.3 最陡下降法 3.3.1 最陡下降法的递推公式
=E{| d (n) |2} 2 Re{w H rxd } w H R xxw
w 2R xxw 2rxd
w [w1 , w2 ,..., wM ]T
x(n) [x1(n), x2 (n),..., xM (n)]T [x(n), x(n 1),..., x(n M 1)]T
y(n)
M
wi* x(n i
1)
wH
x(n)
xT
(n)w*
i 1
e(n) d (n) y(n) d (n) w H x(n)
