三视图练习题大全
三视图习题50道(含答案)
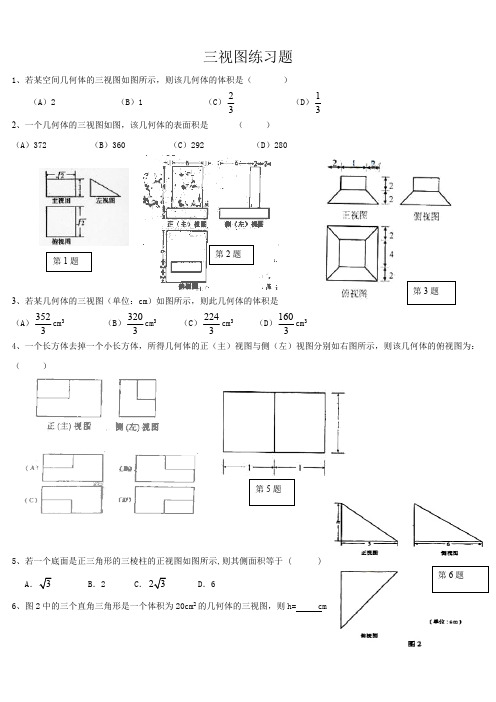
三视图练习题1、若某空间几何体的三视图如图所示,则该几何体的体积是()(A)2(B)1(C)23(D)132、一个几何体的三视图如图,该几何体的表面积是()(A)372 (B)360 (C)292 (D)2803、若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是(A)3523cm3(B)3203cm3 (C)2243cm3(D)1603cm34、一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如右图所示,则该几何体的俯视图为:()5、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于 ( )AB.2 C..66、图2中的三个直角三角形是一个体积为20cm2的几何体的三视图,则h= cm第2题第5题7、一个几何体的三视图如图所示,则这个几何体的体积为 。
8、如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.9、如图1,△ ABC 为正三角形,AA '//BB ' //CC ' , CC ' ⊥平面ABC 且3AA '=32BB '=CC '=AB,则多面体△ABC -A B C '''的正视图(也称主视图)是( )10、一空间几何体的三视图如图所示,则该几何体的体积为( ).A.2π+B. 4π+C. 2π+D. 4π11、上图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )A .B .C .D .9π10π11π12π第7题侧(左)视图正(主)视图俯视图俯视图正(主)视图侧(左)视图12、一个棱锥的三视图如图,则该棱锥的全面积(单位:c 2m )为 ()(A )(B )(C )(D )13、若某几何体的三视图(单位:cm )如图所示,则此几何体的体积是 3cm .14、设某几何体的三视图如上图所示。
三视图练习题含答案
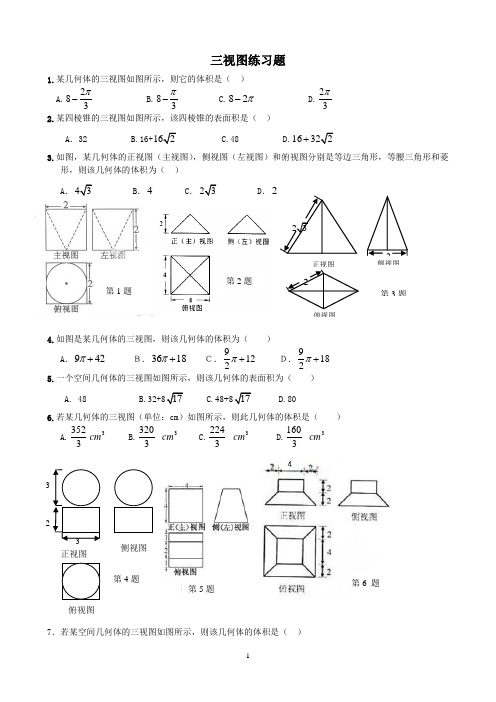
23正视图侧视图2俯视图2第3题三视图练习题1.某几何体的三视图如图所示,则它的体积是( ) A.283π-B.83π-C.π28-D.23π 2.某四棱锥的三视图如图所示,该四棱锥的表面积是( )A .32 B.16+162 C.48 D.16322+3.如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等边三角形,等腰三角形和菱形,则该几何体的体积为( ) A .43 B .4 C .23 D .24.如图是某几何体的三视图,则该几何体的体积为( )A .942π+ B.3618π+ C.9122π+ D.9182π+ 5.一个空间几何体的三视图如图所示,则该几何体的表面积为( )A. 48B.32+817C.48+817D.806.若某几何体的三视图(单位:cm )如图所示,则此几何体的体积是( ) A.35233cm B.3203 3cm C.2243 3cm D.16033cm7.若某空间几何体的三视图如图所示,则该几何体的体积是( )3 32正视图侧视图俯视图第4题第5题第1题 第2题第6 题A.2B.1C.23D.138.某几何体的三视图如图所示,则该几何体的体积为( )A.π816+B. π88+C. π1616+D. π168+ 9. 某四棱台的三视图如图所示,则该四棱台的体积是( ) A.4 B.314 C.316D.610. 某三棱锥的三视图如图所示,已知该三视图中正视图和俯视图均为边长为2的正三角形,侧视图为如图所示的直角三角形,则该三棱锥的体积为( ) A .1 B .3 C .4D .511. 一个几何体的三视图如图所示,则这个几何体的体积为( )A .(8)36π+ B .(82)36π+ C .(6)36π+ D .(92)36π+12.某几何体的底面为正方形,其三视图如图所示,则该几何体的体积等于( )A .1B .2C .3D .413.某几何体的三视图如图所示,则其体积为______.14.若某几何体的三视图(单位:cm )如图所示,则此几何体的体积等于______3cm . 15.某几何体的三视图如图所示,则该几何体的体积是______.第7题第8题第9题第10题3122第11题 211俯视图正视图13第12题16.已知某三棱锥的三视图(单位:cm )如图所示,则该三棱锥的体积是 17.一个空间几何体的三视图如图所示,则这个空间几何体的体积是 .18.如图所示,一个三棱锥的三视图是三个直角三角形,则该三棱锥外接球的表面积为19.若某空间几何体的三视图如下图所示,则该几何体的表面积是_______________.20.一个正方体的内切球与它的外接球的体积比是( ).A .1∶33B .1∶22C .1∶383D .1∶4221.已知球面上A 、B 、C 三点的截面和球心的距离都是球半径的一半,且AB =BC =CA =2,则球表面积是( ) A.π964 B. π38 C. π4 D. π91622. P 、A 、B 、C 是球O 面上的四点,且PA 、PB 、PC 的两两垂直,PA=PB=PC=9,则球心O 到截面ABC 的距离为23.半径为5的球被一个平面所截,截面面积为16π,则球心到截面的距离为 ( ) A. 4 B.3 C.2.5 D. 224.表面积为3π的圆锥,它的侧面展开图是一个半圆,则该圆锥的底面直径为________.第17题 24 3正视图 侧视图 俯视图第18题 第15题第14题第13题第16题 第19题25. 当圆锥的侧面积与底面积的比值是2时,圆锥的轴截面的顶角等于 26.一平面截一球得到直径是6的圆面,球心到这个平面的距离是4,则该球的体积为 27.一个正四面体的棱长为2,四个顶点在同一个球面上,则此球的表面积为 28.已知一个三棱锥ABC P -的三条侧棱PC PB PA ,,两两垂直,且长度分别为2,3,4,则 该棱锥的外接球的表面积为29.已知用斜二测画法得到的正方形的直观图的面积为218,则原来正方形的面积为 30.正三棱锥的高为1,底面边长为62,正三棱锥内有一个球与其四个面相切.求该棱锥的表面积与体积,内切球的半径.31. 在球心同侧有相距cm 9的两个平行截面,它们的面积分别为249cm π和2400cm π.求球的表面积.32. 球面上有三点A 、B 、C 组成这个球的一个截面的内接三角形三个顶点,其中18=AB ,24=BC 、30=AC ,球心到这个截面的距离为球半径的一半,求球的表面积.答案1.A2.B3.C4.D5.C6.B7.B8.A9.B 10.A 11.A 12.A 13.3π 14.24 15.1616-π 16.1 17.67π 18.29π 19. 20+8220.A 21.A 22.233 23.B 24. 2 25.︒9026.3500π 27.π628.π29 29.72 30. 3629+32 26-31.2500π 32.π1200。
三视图练习题含答案

23正视图侧视图2俯视图2第3题三视图练习题1.某几何体的三视图如图所示,则它的体积是( ) A.283π-B.83π-C.π28-D.23π2.某四棱锥的三视图如图所示,该四棱锥的表面积是( )A .32 B.16+162 C.48 D.16322+3.如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等边三角形,等腰三角形和菱形,则该几何体的体积为( ) A .43 B .4C .23 D .24.如图是某几何体的三视图,则该几何体的体积为( )A .942π+ B.3618π+C.9122π+D.9182π+ 5.一个空间几何体的三视图如图所示,则该几何体的表面积为( ) A. 48 B.32+817C.48+817D.806.若某几何体的三视图(单位:cm )如图所示,则此几何体的体积是( ) A.35233cm B.32033cm C.22433cm D.16033cm3 32正视图侧视图俯视图第4题第5题第1题 第2题第6 题7.若某空间几何体的三视图如图所示,则该几何体的体积是( ) A.2B.1C.23D.138.某几何体的三视图如图所示,则该几何体的体积为( ) A.π816+ B.π88+ C.π1616+ D.π168+9. 某四棱台的三视图如图所示,则该四棱台的体积是( ) A.4 B.314 C.316D.610. 某三棱锥的三视图如图所示,已知该三视图中正视图和俯视图均为边长为2的正三角形,侧视图为如图所示的直角三角形,则该三棱锥的体积为( ) A .1B .3C .4D .511. 一个几何体的三视图如图所示,则这个几何体的体积为( )A .(8)36π+B .(82)36π+C .(6)36π+D .(92)36π+ 12.某几何体的底面为正方形,其三视图如图所示,则该几何体的体积等于( )A .1B .2C .3D .4第7题第8题第9题第10题3122第11题 211俯视图正视图13第12题13.某几何体的三视图如图所示,则其体积为______.14.若某几何体的三视图(单位:cm )如图所示,则此几何体的体积等于______3cm . 15.某几何体的三视图如图所示,则该几何体的体积是______.16.已知某三棱锥的三视图(单位:cm )如图所示,则该三棱锥的体积是 17.一个空间几何体的三视图如图所示,则这个空间几何体的体积是.18.如图所示,一个三棱锥的三视图是三个直角三角形,则该三棱锥外接球的表面积为19.若某空间几何体的三视图如下图所示,则该几何体的表面积是_______________.20.一个正方体的内切球与它的外接球的体积比是( ).A .1∶33B .1∶22C .1∶383 D .1∶4221.已知球面上A 、B 、C 三点的截面和球心的距离都是球半径的一半,且AB =BC =CA =2,则球表面积是( )A.π964 B. π38C. π4D. π916第17题 24 3正视图 侧视图 俯视图第18题 第15题第14题第13题第16题 第19题22. P 、A 、B 、C 是球O 面上的四点,且PA 、PB 、PC 的两两垂直,PA=PB=PC=9,则球心O 到截面ABC 的距离为23.半径为5的球被一个平面所截,截面面积为16π,则球心到截面的距离为 ( ) A.4 B.3 C.2.5 D.224.表面积为3π的圆锥,它的侧面展开图是一个半圆,则该圆锥的底面直径为________. 25.答案1.A2.B3.C4.D5.C6.B7.B8.A9.B 10.A 11.A 12.A 13.3π 14.24 15.1616-π 16.1 17.67π 18.29π 19. 20+8220.A 21.A 22.233 23.B 24. 2 25.︒9026.3500π 27.π628.π29 29.72 30. 3629+3226-31.2500π 32.π1200。
机械制图-三视图练习
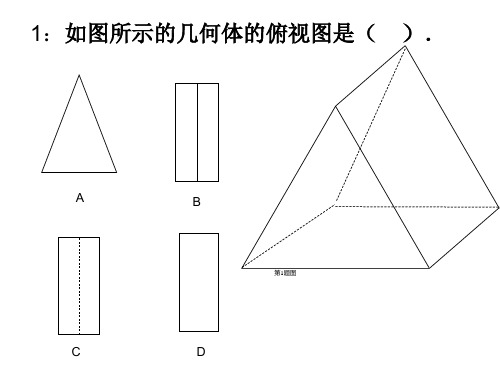
A
B
C.
D
A.圆锥 柱
主视图
左视图
C.长方体 俯视图 D. 球体
23. 如图,空心圆柱的左视图是( )
B.圆
24. 如图所示的几何体的俯视图是 () 25. 如图所示的几何体的正视图是( )
(第6题图)
A.
B.
C.
D.
26. 如图,是由两个相同的小正方体和一个圆锥 体组成的立体图形,其俯视图是( )
A.
B.
12. 如图所示的物体的俯视图是( )
13. 由5个相同的正方体搭成的几何体如图所示, 则它的左视图是( )
主视方向
A.
B.
C.
D.
14. 下列四个几何体中,主视图是三角形的是( )
15. 如图所示的物体由两个紧靠在一起的圆柱体组 成,它的主视图是( )
16. 如图,下列水平放置的几何体中,主视图不是 长方形的是( )
9:骰子是一种特A 别的数字B 立方体C ,它符D 合 规则:相对两面的点数之和总是7.下面四 幅图中可以折成符合规则的骰子的是 ()
10:画下面几何体的三视图
从上面看
主视图
从左面看
左视图
从正面看
俯视图
11:由一些大小相同的小正方体组成的几何体的主 视图和俯视图
(1)请你画出这个几何体的一种左视图;
B.5 D.3
19. 将两个大小完全相同的杯子(如图甲)叠放在一起( 如图乙),则图乙中实物的俯视图是( ).
20. 如图3,是由四个相同的小正方形组成的立体 图形,它的左视图是( )
图3
主视方
A
B
C
D
向
21. 下列所给的几何体中,主视图是三角形的是( )
小学三视图练习题

小学三视图练习题### 小学三视图练习题一、选择题1. 下列哪个选项是正确的主视图?A. 从物体的左侧观察得到的视图B. 从物体的右侧观察得到的视图C. 从物体的正面观察得到的视图D. 从物体的背面观察得到的视图2. 侧视图是从哪个方向观察物体得到的?A. 正面B. 背面C. 左侧D. 右侧3. 俯视图是从哪个方向观察物体得到的?A. 从物体的上方B. 从物体的下方C. 从物体的侧面D. 从物体的正面二、填空题4. 观察一个长方体的三视图,主视图显示的是长方体的______面和______面。
5. 当物体被放置在水平面上时,其______视图通常显示物体的底部。
三、判断题6. 三视图包括主视图、侧视图和俯视图。
()7. 所有物体的主视图都是从物体的正面观察得到的。
()四、简答题8. 请简述什么是三视图,并说明它们各自的特点。
五、绘图题9. 根据题目提供的长方体的三视图,绘制出该长方体的立体图。
六、应用题10. 假设你有一个正方体的盒子,其边长为10厘米。
请根据正方体的三视图,计算出正方体的体积。
七、实践题11. 请用纸板制作一个简单的立方体,并从三个不同的方向观察它,记录下你观察到的三视图。
八、分析题12. 观察一个圆柱体的三视图,分析并描述主视图、侧视图和俯视图所展示的圆柱体的特征。
九、综合题13. 假设你面前有一个由多个几何体组成的复杂物体,请尝试从三个不同的方向观察它,并绘制出相应的三视图。
十、创新题14. 设计一个简单的几何体,并为其绘制三视图。
在设计时,考虑如何通过三视图来最有效地传达该几何体的形状和尺寸。
请根据上述题目进行作答,注意审题并合理运用三视图的相关知识。
祝你练习愉快!。
三视图习题50道(含答案)

word 格式三视图练习题则该几何体的体积是()(D)()(D ) 280第3题(单位cm ) 16033(D) 所得几何体的正则该几何体的俯视图为()1 3第5题(A) 2(主)视图与侧(左)视图分别如右图所示(B ) 1(C ) 292第1题(B ) 3603、若某几何体的三视图 如图所示,则此几何体的体积是 1、若某空间几何体的三视图如图所示—cm 34、一个长方体去掉一个小长方体 2、一个几何体的三视图如图,该几何体的表面积是(B ) 320cm 3“,f=L23(A ) 352cm 3 33r — 1111I ___J第2题1'1-T P5、 若一个底面是正三角形的三棱柱的正视图如图所示,则其侧.面积等于(A . . 3B . 2C . 2 3D . 66、 图2中的三个直角三角形是一个体积为20cm 2的几何体的三视图,则h=7、 一个几何体的三视图如图所示 ,则这个几何体的体积为 _____________AA // BB // CC , CC 丄平面 ABC3且3 AA = 3 BB = CC =AB,则多面体△ ABC - ABC 的正视图(也称主视图)是()8、如图,网格纸的小正方形的边长是1 ,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为9、如图1 , △ ABC 为正三角形,)S 2a.俯视图正(主)视图侧(左)视图A. 9 nB. 10 nC. 11 n D . 12 n10、一空间几何体的三视图如图所示,则该几何体的体积为().A.2 2.3B. 4 2 . 3侧(左)视图C. 2D. 4第11题第10题11、上图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是12、一个棱锥的三视图如图,则该棱锥的全面积(单位:c m2)为(A) 48+12 . 2 (B) 48+24 . 2 ( C) 36+12 2 (D)36+24 213、若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是cm3第12题正视图侧视图俯视图15题14、设某几何体的三视图如上图所示。
三视图练习题(含答案)
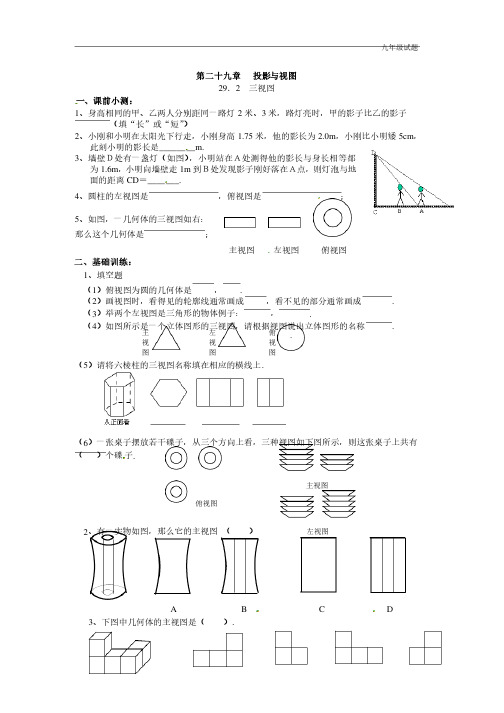
第二十九章投影与视图29.2 三视图一、课前小测:1、身高相同的甲、乙两人分别距同一路灯2米、3米,路灯亮时,甲的影子比乙的影子(填“长”或“短”)2、小刚和小明在太阳光下行走,小刚身高1.75米,他的影长为2.0m ,小刚比小明矮5cm ,此刻小明的影长是________m.3、墙壁D处有一盏灯(如图),小明站在A处测得他的影长与身长相等都为1.6m ,小明向墙壁走1m 到B处发现影子刚好落在A点,到B处发现影子刚好落在A点,则灯泡与地则灯泡与地面的距离CD =_______.4、圆柱的左视图是,俯视图是;5、如图,一几何体的三视图如右:那么这个几何体是;主视图左视图俯视图二、基础训练:1、填空题(1)俯视图为圆的几何体是,.(2)画视图时,看得见的轮廓线通常画成,看不见的部分通常画成. (3)举两个左视图是三角形的物体例子:,.(4)如图所示是一个立体图形的三视图,请根据视图说出立体图形的名称.(5)请将六棱柱的三视图名称填在相应的横线上.(6)一张桌子摆放若干碟子,从三个方向上看,三种视图如下图所示,则这张桌子上共有()个碟子.2、有一实物如图,那么它的主视图()AB C D 3、下图中几何体的主视图是(). 俯视图主视图左视图主视图左视图俯视图俯视图主(正)视图左视图(A) (B) (C ) (D)4、若干桶方便面摆放在桌子上,实物图片左边所给的是它的三视图,则这一堆方便面共有(有( ) (A )5桶 (B ) 6桶(C )9桶 (D )12桶5、水平放置的正方体的六面分别用“前面、后面、上面、下面、左面、右面”表示,如图是一个正方体的表面展开图,若图中“2”在正方体的前面,则这个正方体的后面是方体的前面,则这个正方体的后面是 ( ) ( )A .OB O B.. 6C 6 C.快.快.快D D D.乐.乐.乐三、综合训练:1.小明从正面观察下图所示的两个物体,看到的是(.小明从正面观察下图所示的两个物体,看到的是( )2、右图是由一些完全相同的小立方块搭成的几何体的三种视图,那么搭成这个几何体所用的小立方块的个数是(的小立方块的个数是( )A 5个B 6个C 7个D 8个3、如果用□表示1个立方体,用表示两个立方体叠加,用■表示三个立方体叠加,那么下面右图由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是 ( )4、下面是空心圆柱在指定方向上的视图,正确的是…(、下面是空心圆柱在指定方向上的视图,正确的是…( )B AC D正面 A B C D (A) (B) (C) (D)5、画出下面实物的三视图:实物的三视图:第二十九章 投影与视图29.2 三视图三视图 参考答案:考答案: 课前小测:课前小测:1、短、短2、35723、15644、矩形,圆、矩形,圆5、空心圆柱、空心圆柱 二、基础训练:二、基础训练:1、(1)球,圆柱体;(2)实线,虚线;(3)圆锥,正四棱锥,倒放的正三棱柱等;(4)圆锥;(5)俯视图,正视图,左视图;(6)12.2、A ;3、C4、B5、B三、综合训练:三、综合训练:1、C2、D3、B ;4、A ;5、题图:图:主视图左视图俯视图。
三视图习题加解析

三视图典型例题加解析一、选择题1如图,在下列四个几何体中,其三视图(正视图、侧视图、俯视图)中有且仅有两个相同的是( )A .②③④B .①②③C .①③④D .①②④解析:①的三个视图都是边长为1的正方形;②的俯视图是圆,正视图、侧视图都是边长为1的正方形;③的俯视图是一个圆及其圆心,正视图、侧视图是相同的等腰三角形;④的俯视图是边长为1的正方形,正视图、侧视图是相同的矩形.A2、平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为( )A.6π B .43π C .46πD .63π解析:利用截面圆的性质先求得球的半径长. 如图,设截面圆的圆心为O ′,M 为截面圆上任一点, 则OO ′=2,O ′M =1,∴OM =(2)2+1=3,即球的半径为3, ∴V =43π(3)3=43π.3.若一个几何体的三视图如图所示,则此几何体的体积为( )A.112 B .5 C.92D .4解析:三视图还原为实物图,利用六棱柱体积公式求解.由三视图可知,此几何体为直六棱柱,且底面的面积为4,高为1,则体积V =Sh =4.D4.一个几何体的三视图如图所示,则这个几何体的表面积为( )A .6+ 5B .6+2 5C .8+ 5D .8+2 5解析:由三视图知,该几何体是一个底面为直角三角形的直棱柱,其表面积等于2×(12×1×2)+(2×12+22+1×2+2×2)=8+25,选D.5.如图,正方体ABCD -A ′B ′C ′D ′的棱长为4,动点E 、F 在棱AB 上,且EF =2,动点Q 在棱D ′C ′上,则三棱锥A ′EFQ 的体积( )A .与点E 、F 位置有关B .与点Q 位置有关C .与点E 、F 、Q 位置都有关D .与点E 、F 、Q 位置均无关,是定值解析:因为V A ′-EFQ =V Q -A ′EF =13×(12×2×4)×4=163,故三棱锥A ′-EFQ 的体积与点E 、F 、Q 的位置均无关,是定值.6.一个几何体的三视图如图所示,则该几何体的表面积为________.解析:将三视图还原为直观图后求解.根据三视图可知几何体是一个长方体挖去一个圆柱,所以S =2×(4+3+12)+2π-2π=38.7.某商店门口标识墩的直观图以及正视图和俯视图如图所示,墩的上半部分是正四棱锥P -EFGH ,下半部分是长方体ABCD -EFGH .(1)请画出该标识墩的侧视图; (2)求该标识墩的体积.解析:(1)由于墩的上半部分是正四棱锥P -EFGH ,下半部分是长方形ABCD -EFGH ,故其侧视图与正视图全等.该标识墩的侧视图如图所示.(2)由三视图易得,长方体与正四棱锥的底面均是边长为40 cm 的正方形,长方体的高为20 cm ,正四棱锥的高为60 cm.故该标识墩的体积V =V P -EFGH +V ABCD -EFGH =13×40×40×60+40×40×20=64 000(cm 3).8.已知某几何体的直观图和三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.(1)若M 为CB 的中点,证明:MA ∥平面CNB 1; (2)求这个几何体的体积.解析:(1)证明:取CB 1的中点P ,连接MP ,NP .因为M 为CB 的中点,所以MP ∥BB 1,且MP =12BB 1.由三视图可知,四边形ABB 1N 为直角梯形,AN ∥BB 1且AN =12BB 1,则MP ∥AN 且MP =AN ,所以四边形ANPM 为平行四边形,所以AM ∥NP .又因为AM ⊄平面 CNB 1,NP ⊂平面CNB 1,所以AM ∥平面CNB 1. (2)因为该几何体的正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,所以BC ⊥BA ,BC ⊥B 1B .又BB 1与BA 相交于点B ,连接BN ,所以BC ⊥平面ABB 1N ,所以BC 为三棱锥C -ABN 的高.取BB 1的中点Q ,连接QN ,因为四边形ABB 1N 是直角梯形且AN =12BB 1=4,所以四边形ABQN 为正方形,所以NQ ⊥BB 1,又BC ⊥平面ABB 1N ,NQ ⊂平面ABB 1N ,所以BC ⊥NQ ,又BC 与BB 1相交于点B ,所以NQ ⊥平面C 1B 1BC ,所以NQ 为四棱锥N -CBB 1C 1的高.所以该几何体的体积V =V C -ABN +VN -CBB 1C 1 =13CB ·S △ABN +13NQ ·S 四边形BCC 1B 1 =13×4×12×4×4+13×4×4×8=1603.9.给出如下四个命题:①棱柱的侧面都是平行四边形;②棱锥的侧面为三角形,且所有侧面都有一个共同的公共点;③多面体至少有四个面;④棱台的侧棱所在直线均相交于同一点.其中正确的命题个数有( ) A .1个 B .2个 C .3个 D .4个【解】D .10.圆锥底面半径为1cm,其中有一个内接正方体,求这个内接正方体的棱长.【解】分析:画出轴截面图,设正方体的棱长为x ,利用相似列关系求解. 过圆锥的顶点S 和正方体底面的一条对角线CD 作圆锥的截面,得圆锥的轴截面SEF ,正方体对角面CDD 1C 1,如图所示. 设正方体棱长为x ,则CC 1=x ,C 1D1=. 作SO ⊥EF 于O ,则SO =OE =1,1~ECC EOS ∆∆, ∴11CC EC SO EO ==.11∴ x =, cm 11.如图,正四棱锥P ABCD -底面的四个顶点,,,A B C D 在球O 的同一个大圆上,点P 在球面上,如果163P ABCD V -=,则球O 的表面积是A. 4πB. 8πC. 12π D. 16π【解】如图,正四棱锥P ABCD -底面的四个顶点,,,A B C D在球O 的同一个大圆上,点P在球面上,PO 与平面ABCD 垂直,是棱锥的高,PO =R ,22ABCD S R =,163P ABCD V -=,所以2116233R R ⋅⋅=,解得R =2,则球O 的表面积是16π,选D. 12求球的表面积和体积.【解】分析:作出轴截面,利用勾股定理求解.作轴截面如图所示,CC '=AC == 设球半径为R ,则222R OC CC '=+229=+= ∴3R =,∴2436S R ππ==球,34363V R ππ==球.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三视图练习题大全1、若某空间几何体的三视图如图所示,则该几何体的体积是2112、一个几何体的三视图如图,该几何体的表面积是72609803一个长方体去掉一个小长方体,所得几何体的正视图与侧视图则该几何体的俯视图为:4、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于...A.C..65、图2中的三个直角三角形是一个体积为20cm的几何体的三视图,则h= cm、一个几何体的三视图如图所示,则这个几何体的体积为。
、如图,网格纸的小正方形的边长是1,则这个几何体的体积为。
129、一空间几何体的三视图如图所示,则该几何体的体积为.A.2??B.??C.?? 俯视图正视图侧视图D.??3正视图侧视图俯视图10、上图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是A.9πB.10π C.11π D.12π11、已知某个几何体的三视图如下,根据图中标出的尺寸,可得这个几何体的体积是A.4000380003cm B.cm C.2000cm3D.4000cm333B.2π C.3π D.4π12、一个几何体的三视图如上图所示,其中正视图与侧视图都是边长为2的正三角形,则这个几何体的侧面积为A.13、如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积为A.32π B.16π C.12πD.8π14、下图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是A.9πB.10πC.11π D.12π15、右图是一个多面体的三视图,则其全面积为正视图侧视俯视图2ABCD616、如图所示,一个空间几何体的正视图和侧视图都是底为1,高为2的矩形,俯视图是一个圆,那么这个几何体的表面积为A.2? B.5?C.4?D.5?217、一个几何体的三视图及其尺寸如图所示,则该几何体的侧面积为_ ______cm2.18、如果一个几何体的三视图如图所示, 则此几何体的表面积是A. AB?6C6D424. 如图所示,一个空间几何体的正视图和侧视图都是底为1,高为2的矩形,俯视图是一个圆,那么这个几何体的表面积为5?C.4? D.5?A.2? B.25.如果一个几何体的三视图如图所示, 则此几何体的表面积是A. 如图所示,则该几何体的侧面积为_______cm2.22左视侧视图俯视俯视图4三视图练习题1.如图是某几何体的三视图,则此几何体的体积是 A.3B.10C.7D.1802.一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是A、球B、三棱锥C、正方体D、圆柱3.如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是A、9πB、10πC、11πD、12π4.有一个几何体的三视图及其尺寸如图,则该几何体的表面积及体积为A.24?cm2,12?cm3B. 15?cm2,12?cm32C.4?cm,36?cm3D.以上都不正确5.如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.A. B. CD.6.一空间几何体的三视图如图所示,则该几何体的体积为. A. 1B. CD.7.若某空间几何体的三视图如图所示,则该几何体的体积是 A.??B. C.1D.??8.某几何体的正视图如图所示,则该几何体的俯视图不可能的是9.已知某个几何体的三视图如图,根据图中标出的尺寸,可得这个几何体的体积是cm3.A.8?? C.12??2?32?D.12?3B.8?10.已知正六棱柱的底面边长和侧棱长均为2cm,其三视图中的俯视图如图所示,则其左视图的面积是122238cm cm22侧视图主视图11.右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是A.6πB.7π C.8πD.9π俯视图12.如图是一个几何体的三视图,若它的体积是a=A.1 B.13.已知某几何体的三视图如图所示,其中正视图、侧视图都是等腰直角三角形,则这个几何体的体积是 A.cm B.14.如图,水平放置的三棱柱ABC-A1B1C1中,侧棱AA1⊥平面A1B1C1,其正视图是边长为a的正方形.俯视图是边长为a的正三角形,则该三棱柱的侧视图的面积为A.a2B.正视图2,则该几何体的表面积是俯视图A.20+3π B.24+3πC.20+4π D.24+4π16.如图为一个几何体的三视图,其中俯视图为正三角形,A1B1=2,AA1=4,则该几何体的表面积为A11A.+B.4+C.4+2D.2AC正视图侧视图俯视图17.图1是设某几何体的三视图,则该几何体的体积为 A.9??42B.36??1C.??1 D.??18929218.已知某几何体的三视图如图所示,根据图中标注的尺寸可得该几何体的体积是正视图123cm3348C.cm3D.cm333A.cmB.俯视图图119.已知几何体其三视图,若图中圆半径为1,等腰三角形腰为3,则该几何体表面积为A.6π B.5π C.4π D.3π20.若一个正三棱柱的三视图如下图所示,则这个正三棱柱的高和底面边长分别为A.2, B.2, C.4,2D.2,4正视图左视图俯视图1.1.5三视图课程学习目标[课程目标]目标重点:正投影与三视图的画法与应用, 目标难点:三视图的画法以及应用学法关键1.画三视图时,可以把垂直投影面的视线想象成平行光线从不同的方向射向几何体,体会可见的轮廓线的投影就是所要画出的视图,画出的三视图要检验是否符合.长对正、高平齐、宽相等.的基本特征.2.由三视图想象几何体时也要根据.长对正、高平齐、宽相等.的基本特征,想象视图中每部分对应的实物的形象,特别注意几何体中与投影面垂直或平行的线及面的位置研习教材重难点研习点1 正投影1.定义:在物体的平行投影中,如果投射线与投射面垂直,则称这样的平行投影为正投影.. 正投影的性质:①直线或线段的平行投影仍是直线或线段;②平行直线的平行投影是平行或重合的直线;③平行于投影面的线段,它的投影与这条线段平行且等长;④与投影面平行的平面图形,它的投影与这个图形全等;⑤在同一直线或平行直线上,两条线段平行投影的比等于这两条线段的比;⑥垂直于投影面的直线或线段的正投影是点;⑦垂直于投影面的平面图形的正投影是直线或直线的一部分.研习点三视图1. 水平投射面:一个投射面水平放置,叫做水平投射面.. 俯视图:投射到水平投射面内的图形叫做俯视图.3. 直立投射面:一个投射面放置在正前方,这个投射面叫做直立投射面.. 主视图:投射到直立投射面内的图形叫做主视图.5. 侧立投射面:和直立、水平两个投射面都垂直的投射面叫做侧立投射面.. 左视图:投射到侧立投射面内的图形叫做左视图.7. 三视图:将空间图形向水平投射面、直立投射面、侧立投射面作正投影,然后把这三个投影按一定的布局放在一个平面内,这样构成的图形叫做空间图形的三视图.研习点3.三视图的画法要求:三视图的主视图、俯视图、左视图分别是人从物体的正前方、正上方、正左方看到的物体轮廓线的正投影组成的平面图形;一个物体的三视图的排列规则是:俯视图放在主视图的下面,长度与主视图一样,左视图放在主视图的右面,高度与主视图一样,宽度与俯视图的宽度一样;记忆口诀:长对正,高平齐,宽相等;主左一样高,主俯一样长,俯、左一样宽。
在视图中,被挡住的轮廓线画成虚线,尺寸线用细实线标出;d表示直径,R表示半径;单位不注明时按mm计.研习点4.常见的简单几何体的三视图对于一些常见的简单组合体的三视图,一定要认真观察,先认识它的基本结构,然后再画它的三视图.圆柱的主视图和左视图都是矩形,俯视图是圆;圆锥的主视图和左视图都是等腰三角形,俯视图是圆和圆心;圆台的主视图和左视图都是等腰梯形,俯视图是两个同心圆;球的主视图、左视图和俯视图都是圆;探究解题新思路基础拓展型题型1.画出三视图例1.画出如图所示的水管三叉接头的三视图。
三视图的画法关键是分清观察者的方向,从正面、侧面、上面三个方向去观察图形,然后画出三视图。
解:所得三视图如图所示:三视图的训练有助于培养空间想象能力和解决实际问题的能力. 三视图是用两两相互垂直的三个平面作为投影面,把物体放在这个空间内,分别向三个平面进行正投影,然后将水平投影绕水平面和正面的交线向下转90°,将侧面投影绕侧面和正面的交线向右转90°,就得到了三视图,这就是投影面的展开推平.1.画出如图所示正四棱锥的三视图。
小结:在画三视图时,可以把垂直投影面的视线想象成平行光线从不同的方向射向物体,体会可见的轮廓线的投影就是所要画出的视图. 要检验画出的三视图是否符合. 长对正,高平齐,宽相等.的基本特征.2. 下图所示的是一些立体图形的三视图,请说出立体图形的名称答案:该立体图形为长方体。
该立体图为圆锥。
小结:由三视图想象几何体时也要根据“长对正,高平齐,宽相等”的基本特征,想象视图中每部分对应的实物部分的形象,特别要注意几何体中与投影面垂直或平行的线及面的位置。
2. 物体实物图如右图所示,下面可以作为其俯视图和左视图的是综合创新型例. 在图1和图2中,图是由图中实物画出的主视图和俯视图,你认为正确吗?如果不正确,请指出错误并改正,然后分别画出它们的左视图图1中,图由两个长方体组合而成,主视图正确;俯视图错误,俯视图应该画出不可视轮廓线;左视图轮廓是一个矩形,有一条可视的交线图2中,图是由一个圆柱和一个正六棱柱组合后以中心轴为轴线挖去一个细圆柱构成的组合体,主视图和俯视图都不正确,主视图上面的矩形中缺少两条不可视轮廓线;俯视图中缺少中间小圆柱形成的轮廓线;左视图的轮廓是上下两个矩形叠放在一起,上面的矩形中有两条不可视轮廓线,下面的矩形中有一条可视轮廓线图1中,主视图正确,俯视图不正确,俯视图和左视图应如图3所示:图2中,主视图和俯视图都不正确,几何体的三视图形状应如图4所示:画简单的组合体的三视图时应注意以下问题:确定主视、俯视、左视的方向,同一物体放置的位置不同,所画的三视图可能不同. 看清简单组合体是由哪几个基本几何体生成的,并注意它们的生成方式,特别是它们的交线位置.要检验画出的三视图是否符合.长对正,高平齐,宽相等.的基本特征. 特别注意几何体中与投影面垂直或平行的线及面的位置3. 如左下图所示是物体的实物图,A、B、C、D 四个选项对应的图形中为它的一个俯视图的是4. 如图,正方体ABCD-A1B1C1D1中,E、F分别是AA1,C1D1的中点,G是正方形BCC1B1的中心,则空间四边形AEFG 在该正方体各面上的正投影不可能是如图,一个封闭的立方体,在它的六个面上各标出A,B,C,D,E,F这六个字母,现放成下面三种不同的位置,所看见的表面上的字母已标明,则字母A,B,C对面的字母分别是练习1.已知右图中的三个直角三角形是一个几何体的三视图,那么这个几何体的体积等于 A.30B.20侧视图正视图。
