实用回归分析小论文
回归分析论文

因变量: 财政收入 y 1415.884=-.645X1+-.264X2+-.452X3+-.002X4+.637X5+-.008X6 t=.598 -3.684 -1.266 -.798 -.074 4.903 -.967
四、检验及修正 1.经济意义检验 从上表中可以看出, 各指标符号与先验信息有点出入, 所估计结果与经济原理向悖,说明观测数据具有多重 共线性等问题,但仍具有经济意义。 2.统计推断检验 从回归结果可以看出,模型的拟合优度非常好 (������ 2 =0.996),F 统计量的值在给定显著性水平 α=0.05 的情况下也较显著,t 统计值均不显著,由直观判定法 得知自变量的回归系数所带正负号与定性分析结果违 背。说明观测值变量之间存在多重共线的影响使其 t 值不显著。 3.基本假定检验 1)多重共线性检验 ①检验:由 F=122.712 > F0.05 (5,18)=2.64(显著性水平 α=0.05) 表明模型从整体上看粮食产量与解释变量间 线形关系显著。 这里采用“简单相关系数矩阵法”对其进行检验
.999
**
1
.867
**
.997
**
.495
*
显 著 性 ( 双 .000 侧) N 21
.000
.000
.000
.022
21
21
21
21
21
人口数 x4
Pearson 关性
相 .909
**
.872
**
.867
**
1
.892
**
.576
**
显 著 性 ( 双 .000 侧) N 21
.000
实用回归分析论文(SPSS实验结果)

我国农民人均生活收入及消费支出分析学院:理学院班级:统计1001班:于海龙中国农民人均生活收入及消费支出简要分析论文摘要:通过本学期对实用回归分析课程的学习,对于一些实际问题作出以下分析。
实用回归分析中的方法在经济、管理、医学及心理学等方面的研究起着很重要的作用,在我国的国民经济问题中,增加农民收入是我国扩大需与真正走向共同富裕的关键,通过运用SPSS 软件分析方法对我国农民的收入及消费支出进行了各种细致分析, 以便能够更好地了解我国农村居民的收入结构和消费结构与消费行为等。
关键词:农民生活收入消费支出多元线性回归分析正文:一、农民人均生活收入及消费支出分析近年来,全国上下认真贯彻落实科学发展观,以农业增产、农民增收为目的,加大各项惠农政策措施落实力度,多措并举做好农村劳动力转移就业工作,克服金融危机和严重干旱等自然灾害带来的不利影响,使全市农村经济保持了稳定发展的良好态势,农民现金收入持续增长,生活消费水平继续提高。
我国是一个农业大国,至今仍有9亿农村人口,占全国人口总数的70%,农民是我国最大的群体,农村消费能力的提升直接关系到国民经济的全局。
从农村市场看,中国有近六成人口生活在农村。
农村城镇化的进程对经济增长的带动作用是非常明显的,世界上还没有哪个国家有规模如此巨大的城镇化。
农村居民的收入虽然低于城市居民,但是基数巨大,且农村人口的收入也在稳定增长。
随着经济的发展,我国农民的收入水平和消费水平的结构也发生了很大变化,农民生活水平的提高和消费的增加对于实现国民经济又好又快发展、正确处理好需和外需的关系至关重要。
但从总体来看,农民消费水平仍然较低,调查显示有的地区都不及城市居民人均消费支出的三分之一。
而且消费结构不合理,局限于食品类等生存基本需求品,消费在衣着装饰等方面的极少。
而影响农民消费水平的根本原因是农民的收入。
农民生活消费支出主要包括食品、衣着、医疗卫生、教育文化、家庭设备、交通等方面,本文只挑选了四种典型的消费支出作为代表来分析农村居民的消费结构。
回归分析法论文

回归分析方法在数据处理中的应用摘要:回归分析方法是处理变量间相关关系的有力工具[1]。
回归分析模型目前已应用于生活中的各个方面.并在实际应用中证实了其准确性和可行性。
正因为回归分析方法应用范围广、效果好,因此如何进行回归分析就变得至关重要。
本文通过一个实例介绍了如何使用EXCEL 进行回归分析,从而实现生活中数据的有效处理。
关键词:数据处理回归分析应用举例1 引言随着社会的发展,生活中很多问题交叉、重叠,涉及到众多复杂相关的可变因素,解决的难度日益加大[2]。
解决这些问题需要多学科的融合,其中数学方法在这些问题的分析预测中起到了重要作用。
随着计算机的发展.使用数学方法更加准确高效,大大推进了其在生活中的应用。
回归分析是一种处理变量间相关关系的数理统计方法[3].它能够科学地寻求事件规律并预测其发展趋势,回归分析模型目前已应用于生活中各个方面。
2 回归分析回归分析法,是在掌握大量观察数据的基础上,利用烽理统计方法建立因变量与自变量之间的回归关系函数表达式(称回归方程式)。
回归分析中,当研究的因果关系只涉及因变量和一个自变量时,叫做一元回归分析;当研究的因果关系涉及因变量和两个或两个以上自变量时,叫做多元回归分析。
此外,回归分析中,又依据描述自变量与因变量之间因果关系的函数表达式是线性的还是非线性的,分为线性回归分析和非线性回归分析[4]。
通常线性回归分析法是最基本的分析方法,遇到非线性回归问题可以借助数学手段化为线性回归问题处理。
回归分析法是定量预测方法之一。
它依据事物内部因素变化的因果关系来预测事物未来的发展趋势。
由于它依据的是事物内部的发展规律,因此这种方法比较精确。
回归分析是统计分析中应用最为广泛的一个分支,它起源于19 世纪高斯的最小二乘法[5]。
根据回归分析方法得出的数学表达式称为回归方程,它可能是直线,也可能是曲线。
对于某一个试验项目,通过实验数据所得出的相关图,可以直观地发现各个状态量并不都落在一条直线上,而是在直线上上下波动,呈现出线性相关的趋势。
1应用回归分析论文

JISHOU UNIVERSITY之阿布丰王创作本科生课程论文题目:粮食总产量的影响因素分析课程名称:应用回归分析所属学院:专业年级:学生姓名:学号:完成时间:2015 年12月23日目录摘要:----------------------------------------------- 1 关键词:-------------------------------------------- 1一、引言--------------------------------------------- 1二、模型设定及数据准备----------------------------- 1三、回归模型建立------------------------------------ 21.模型设定---------------------------------------- 22、估计参数--------------------------------------- 3四、模型检验----------------------------------------- 41、经济意义检验--------------------------------- 42、统计检验--------------------------------------- 43、回归模型检验----------------------------------- 4(1)多重共线性检验 --------------------------- 4(2)逐步回归5(3)异方差检验 ------------------------------ 7(4)自相关检验 ------------------------------ 8五、模型的确定--------------------------------------- 9六、结论--------------------------------------------- 9 参考文献9附录------------------------------------------------ 10粮食总产量的影响因素分析摘要:目前,我国70%人口为农村人口,农业生产的发展直接关系广大农民生活的提高,直接关系到国家经济建设目标的实现。
实用回归分析论文

实用回归分析论文回归分析是一种广泛应用于研究和预测变量关系的统计方法。
它可以用来探索自变量与因变量之间的关系,并根据这些关系进行预测。
本篇论文旨在利用SPSS软件进行回归分析,并解释实验结果。
为了说明回归分析的实用性,本论文以一个假设为例进行讨论。
假设我们想研究其中一种健康饮食对人体血糖水平的影响。
我们能够搜集到500名参与者的相关数据,包括他们的饮食习惯和血糖水平。
在SPSS软件中,我们可以采用多元线性回归模型来探索自变量(饮食习惯)与因变量(血糖水平)之间的关系。
首先,我们需要将数据输入SPSS软件,并进行数据清洗和处理,确保数据的准确性和可靠性。
接下来,我们可以使用回归模型来进行实验结果的分析。
在SPSS软件中,我们可以选择"回归"选项,并指定因变量和自变量。
在这个示例中,我们将血糖水平作为因变量,饮食习惯作为自变量。
SPSS软件会给出回归模型的结果。
其中最重要的指标是相关系数和显著性水平。
相关系数用来衡量自变量与因变量之间的线性关系的强度,取值范围在-1到+1之间。
显著性水平可以告诉我们这个自变量对因变量的解释力是否显著。
通常,显著性水平小于0.05表示相关关系是显著的。
在这个案例中,回归分析的结果显示饮食习惯与血糖水平之间存在显著相关性(相关系数为0.4,显著性水平为0.01)。
这意味着饮食习惯对于解释血糖水平的变异有统计学意义。
我们可以通过这一结果来推测具体的饮食习惯与血糖水平之间的关系,进一步指导实际生活中的健康饮食选择。
此外,在SPSS软件中,我们还可以进行其他的回归分析,如逐步回归和多重回归。
这些方法可以帮助我们确定最佳的自变量组合,以及对因变量的解释力。
逐步回归可用于选择最有意义的自变量,而多重回归可以进一步探索多个自变量对因变量的解释力。
总结起来,回归分析是一种实用的统计方法,可以用来研究和预测变量之间的关系。
使用SPSS软件进行回归分析,可以对实验结果进行详细的解释和推断,从而指导实际生活中的决策和行动。
实用回归分析论文(SPSS实验结果)

实用回归分析论文(SPSS实验结果)由于没有具体的数据或研究题目,以下仅为回归分析论文的一般模板。
1. 研究背景和目的:介绍本次研究的背景和目的。
描述相关文献对该领域的研究情况,指出知识空白和研究的必要性。
例如:本研究旨在探讨X变量与Y变量之间的关系,并研究其他可能因素对此关系的影响。
回归分析被广泛应用于社会科学、经济学和医学等领域,但在某些情况下,该方法可能被错误地应用或解读。
因此,本研究旨在提供更多有关回归分析的实用性信息,以便更好地应用于实际研究中。
2. 变量选择和数据收集:介绍所选的独立变量、因变量以及可能的干扰因素。
描述数据收集的方法和样本的特点,阐述数据的统计学特征。
例如:本研究选择了X1、X2和X3作为独立变量,Y作为因变量。
在探究X和Y之间的关系时,本研究考虑了干扰因素A和B。
数据收集采用了问卷调查的方法,样本为100位大学生。
调查数据的统计学特征如下:均值、标准差、最大值和最小值。
3. 回归模型:描述所使用的回归模型及其假设。
根据假设,说明如何进行统计分析。
例如:本研究选择了多元线性回归模型。
假设独立变量与因变量之间存在线性关系,且同时考虑了干扰因素的影响。
在此假设下,通过进行多元线性回归分析,得出具体的回归方程。
使用SPSS软件进行统计分析,通过显著性检验和模型拟合程度来验证上述假设。
4. 实验结果:解释回归分析结果,如拟合程度、系数的显著性、变量的解释等。
根据结果,提供对研究目的的回答,对假说进行证明或推翻。
例如:本研究得到的回归方程为Y = a + b1*X1 + b2*X2 + b3*X3 +c1*A + c2*B。
通过F检验,得出回归模型的显著性水平P<0.01,表明回归模型解释了数据的一定程度。
通过系数显著性检验,得出X1、X3和B对Y变量具有显著影响,而其余变量影响不显著。
对于X1、X3和B,本研究解释了其对Y变量的具体贡献,分析了研究问题的深层含义。
5. 结论和建议:总结研究结论,说明其对实践和理论的贡献,并提出未来研究的方向。
实用回归分析小论文
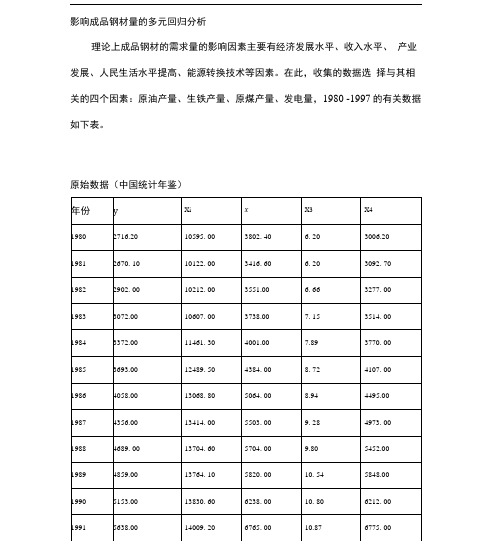
影响成品钢材量的多元回归分析理论上成品钢材的需求量的影响因素主要有经济发展水平、收入水平、产业发展、人民生活水平提高、能源转换技术等因素。
在此,收集的数据选择与其相关的四个因素:原油产量、生铁产量、原煤产量、发电量,1980 -1997的有关数据如下表。
原始数据(中国统计年鉴)将中国成品钢材的需求量设为y,作为被解释变量,而原油产量生铁产 量X2、原煤产量対、发电量X4作为解释变量,通过建立这些经济变量的线性 模型来研究影响成品钢材需求量的原因。
模型的设定二参数估计设因变量y 与自变量Xi 、X2、X3、X4的一般线性回归模型为0 + iXi2X2 3X34X4是随机变量,通常满足o ; Var ()=a.因变量:成品钢材(万吨)再用SPSS做回归线性,根据系数表得岀回归方程为:$ 170. 287 0. 041% 0. 554X2 17. 818x3 0. 389x t再做回归预测,得出如下截图:¥XI k2 x3 [)(4 PREJ RES 12716. 203802. 40 e. so 3006. 20 2e?S. 0S76G -182.837662G70. 1010122. 0C 3416. 60 G. 20 3092. 70 2736. 53110 -60. 431102902. 0010212. 00 3651.00 6. 66 3277. 00 2072,91514 29 19ZaG3072. 0010607. 00 3738. 00 7J5 3514.00 3043. 62443 28 375573372. 0011461. 30 4001.00 A89 3770. 00 3240. 51684 131. 484163693 0012489,50 4384. 00 3 72 4107.00 3526,63541 1B6. 3&459 4056. 0013068. 0C 50B4. 00 8.94 4495 00 4C2£. 56ei9 31 433814356. 0013414. 00 5503. 00 9.28 4973. 00 A4 35.52677 -79. 526774689. 0013704. 6C 5704. 00 9.80 5452. 00 4712.05819 ■ 23.058194059. 00137E4 W 582C. 00 10 54 5346. 00 4914.91371 -55.613715153. 0013630. 60 623B. CD IQ. BO 621200 5250.70360 -127.703S05638. 0014009. 20 5765. 00 1187 6775. 00 5733. 194656E97 0Q14209. 70 7599. 03 11. 16 7539 00 6623. 64790 173. 3K21D 771E. 0014623 00 9739. 00 11 51 8395. 00 7474. 00431 241.196608482 0014608, 20 3741,00 12. 40 0281. 00 S3 56.43425 126. 656769979. 8015004. 94 10529. 27 1361 10070. 30 9051. 44M -81. 64200933S. 0215733. 39 107Z2. 50 13. 97 10013. 10 9421. 11147 -63. 091479978. 931607J 14 11511. 41 1373 11355.63 10059. 53741 -80. 60741 16225 86 12044. 54 1367 12334. 69 10P27. 33875 ■17453. 00 12445. 96 14. 54 13457. 00 11323. 07164故当原油产量为16225. 86万吨,生铁产量为12044. 54万吨,原煤产量为13. 87万吨以及发电量为12334. 89亿千瓦时时,成品钢材量预测值为10727. 33875万吨;当原油产量为17453万吨,生铁产量为12445. 96万吨,原煤产量为14. 54万吨以及发电量为13457亿千瓦时时,成品钢材量预测值为10727. 33875万吨。
实用回归分析范文

实用回归分析范文回归分析是一种常用的统计分析方法,用于探索两个或多个变量之间的关系。
通过回归分析,我们可以预测一个因变量(依赖变量)如何随着一个或多个自变量(独立变量)的变化而变化。
回归分析可以帮助我们了解变量之间的关系,并进行预测和决策。
首先,我们需要收集相关变量的数据。
例如,我们想要了解一个人的体重如何与其身高和性别相关,我们需要收集一组样本,其中包括每个人的身高、体重和性别。
接下来,我们将构建一个回归模型来描述因变量(体重)如何受到自变量(身高和性别)的影响。
常用的回归模型包括线性回归模型和非线性回归模型。
线性回归模型假设因变量与自变量之间存在一个线性关系,而非线性回归模型假设它们之间存在一个非线性关系。
构建回归模型后,我们将评估模型的准确性和可靠性。
通常采用最小二乘法来估计模型参数,并计算残差来衡量模型的拟合程度。
如果残差具有随机性、接近正态分布并且没有明显的模式,那么我们可以认为模型是可靠的。
同时,我们还可以计算拟合优度指标(如R方值)来评估模型的解释能力。
在评估模型之后,我们可以使用模型进行预测和推断。
通过输入自变量的值,我们可以根据回归模型预测因变量的值。
同时,我们还可以使用模型的参数估计值来进行统计推断,比如计算置信区间和假设检验。
最后,我们需要解释回归模型的结果。
我们可以通过分析模型的参数和对应的显著性水平,来判断自变量对因变量的影响是否显著。
同时,我们还可以通过散点图、回归方程式和拟合线来直观地展示变量之间的关系。
总之,实用回归分析是一种强大的工具,可以帮助我们了解变量之间的关系,并进行预测和决策。
通过适当的数据收集、模型建立和结果解释,回归分析可以为实际问题的解决提供有力支持。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
影响成品钢材量的多元回归分析
理论上成品钢材的需求量的影响因素主要有经济发展水平、收入水平、产业发展、人民生活水平提高、能源转换技术等因素。
在此,收集的数据选择与其相关的四个因素:原油产量、生铁产量、原煤产量、发电量,1980 —1997的有关数据如下表。
原始数据(中国统计年鉴)
将中国成品钢材的需求量设为y,作为被解释变量,而原油产量x i、生铁产
量X2、原煤产量X3、发电量X4作为解释变量,通过建立这些经济变量的线性
模型来研究影响成品钢材需求量的原因。
模型的设定
设因变量y与自变量X i、X2、X3、X4的一般线性回归模型为
0 + i X i 2X2 3X3 4X4
是随机变量,通常满足0 ;Var()=
二参数估计
a
a.因变量成品钢材(万吨)
再用spss做回归线性,根据系数表得出回归方程为:
$ 170.287 0.041% 0.554X2 17.818x3 0.389x4
再做回归预测,得出如下截图:
¥X1k2x3)(4PREJ RES_1
2716.203802.40 e.so3006.202e?S.0S76G-182.83766
2G70.1010122.0C3416.60G.203092.702736.53110-60.43110
2902.0010212.003651.00 6.663277.002072,9151429 19ZaG
3072.0010607.003738.007J53514.003043.6244328 37557
3372.0011461.304001.00A893770.003240.51684131.48416
3693 0012489,504384.00 3 724107.003526,635411B6.3&459
4056.0013O68.0C50B4.008.944495 004C2£.56ei931 43381
4356.0013414.005503.009.284973.00A4 35.52677-79.52677
4689.00137O4.6C5704.009.805452.004712.05819■23.05819
4059.00137E4 W582C.0010 545346.004914.91371-55.61371
5153.0013630.60623B.CD1Q.B06212005250.70360-127.703S0
5638.0014009.205765.0011876775.005733.19465
6E97 0Q14209.707599.0311.167539 006623.64790173.3K21D
771E.0014623 009739.0011 518395.007474.00431241.19660
8482 0014608,203741,0012.400281.00S3 56.43425126.65676
9979.8015004.9410529.27136110070.309051.44M-81.64200
933S.0215733.391O7Z2.5O13.9710013.109421.11147-63.09147
9978.931607J 1411511.41137311355.6310059.53741-80.60741 -16225 8612044.54136712334.6910P27.33875■
17453.0012445.9614.5413457.0011323.07164
故当原油产量为16225.86万吨,生铁产量为12044.54万吨,原煤产量为13.87万吨以及发电量为12334.89亿千瓦时时,成品钢材量预测值为10727.33875万吨;当原油产量为17453万吨,生铁产量为12445.96万吨,原煤产量为14.54万吨以及发电量为13457亿
千瓦时时,成品钢材量预测值为10727.33875万吨。
三回归方程检验
由相关系数表看出,因变量与各个自变量的相关系数都很高,都在
0.9以上,说明变量间的线性相关程度很高,适合做多元线性回归模型。
b
a. 预测变量:(常量),发电量(亿千瓦时)原油(万吨),原煤(万吨)生铁(万吨)
b. 因变量:成品钢材(万吨)
由R2 =0.997以及调整之后的R2 =0.997知,模型对样本观测数据的拟合度很
b
a. 预测变量:(常量),发电量(亿千瓦时)原油(万吨),原煤(万吨)生铁(万吨)
b. 因变量:成品钢材(万吨)
由F=1296.001 P值=0.000< =0.05,故拒绝原假设,认为自变量联合起来对因变量有显著影响,通过F检验。
系数a
a.因变量:成品钢材(万吨)
因为t3 =-0.154 P值=0.880远远大于=0.05,故接受原假设,认为X3对因变
量y没有显著影响,故应剔除X3。
用后退法剔除变量后,再做回归线性,得如下表:
原油(万吨),生铁(万吨)
a
a.因变量:成品钢材(万吨)
b. 预测变量:(常量),发电量(亿千瓦时)
c. 预测变量:(常量),发电量(亿千瓦时)
d. 因变量:成品钢材(万吨)
预测变量:(常量),发电量(亿千瓦
时)
,原油(万吨),原煤(万吨),生铁(万吨)。
a. Anova d
最后剔除X i、X3两个自变量,得出新的回归方程为:
$ 309.403 0.59% 0.311x4
F=2718.023 P值=0.000 故拒绝原假设,通过F检验
四基本假定检验
1、异方差检验
等级相关系数检验
做abs(e)与x的等级相关系数,得出表如下
在置信度(双测)为时,相关性是显著的
由表中P值全大于0.01,故接受原假设,模型中不存在异方差
2、自相关检验
b
a. 预测变量:(常量),发电量(亿千瓦时)原油(万吨),原煤(万吨)生铁(万吨)
b. 因变量:成品钢材(万吨)
DW=0.992 n=18 k=5,查表得出d i 0.82,d u 1.87,故DW 落入无法确定的领域。
自相关性不明显,由此也看出DW检验的局限性。
3、多重共线性
a
a.因变量成品钢材(万吨)
a
a.因变量:成品钢材(万吨)
因为VIF中有两个远远的大于10,故模型存在严重的多重共线性。
由共线性诊断表中数
据得出,X2、X3、X4之间存在多重共线性。
故先剔除变量X4,再做线性回归,得出表如下:
a
a.因变量:成品钢材(万吨)
a
a.因变量:成品钢材(万吨)
由于模型中仍然存在多重共线性,故继续剔除VIF最大的变量X3,再做线性回归,
得出表如下
系数a
a.因变量:成品钢材(万吨)
a
a.因变量:成品钢材(万吨)
a
a.因变量:成品钢材(万吨)
由于剔除变量X3后,VIF值都小于10,故多重共线性得以消除,得出新的回归方程:$ 282.131 0.017x10.92X2
4、异常值和强影响值
残差统计量
a.因变量:成品钢材(万吨)
因为p/n=4/18=0.22 表中ch, =0.644>0.44 故关于x 异常。
