07土木位移法求解计算题_及答案_
电大《土木工程力学》(本)历届试题及答案

1。
用位移法计算图示各结构,基本未知量是两个的结构为(A ).2。
用力法计算超静定结构时,基本未知量是(D多余未知力)。
3。
图示结构杆件BA的B端转动刚度为( B 3 )。
4。
用力矩分配法计算结构得到一个收敛的结果,是因为( D ).A。
分配系数小于1 B。
分配结点之间传递系数小于1C。
结点上有外力矩作用 D. A 和B 同时满足5。
反映结构动力特性的重要物理参数是( B自振频率)。
6. 用力矩分配法计算超静定结构时,刚结点的不平衡力矩等于( B附加刚臂中的约束反力矩)。
7。
影响线的纵坐标是( D指定截面的某一量值)。
8. 受弯杆件截面内力有( D弯矩剪力轴力)。
9. 不考虑杆件的轴向变形,竖向杆件的E I = 常数。
下图所示体系的振动自由度为( A 1 ). 10。
力法典型方程是( B 多余约束处的位移协调条件).三、(10分)21。
作图示静定结构的弯矩图.四、(16分)22。
用力法计算图示结构并作弯矩图,EI=常数。
解:典型方程五、(14分)23.用位移法计算图示刚架,列出典型方程,求出系数项及自由项。
解:典型方程1。
图示对称结构作用反对荷载,EI=常数,对称轴穿过的AB杆件内力满足(D)2。
机动法作静定梁弯矩影响线应用的原理是( C刚体虚功原理 ).3.结构不考虑阻尼时的自振频率为,考虑阻尼时的自振频率为,则( C )4.图示结构中,除横梁外,各杆件EI=常数。
不考虑杆件的轴向变形,则体系振动的自由度数为(A 1)。
5.位移法典型方程是根据( D附加约束的平衡条件)列出的.6.图示a、b两体系的自振频率与的关系为( B ).7.图示对称结构作用反对称荷载,杆件EI为常量,利用对称性简化后的一半结构为( A )。
8.用位移法求解图示结构时,基本未知量的个数是( B 3 )。
9.简支梁A支座竖向反力影响线纵坐标的物理意义是 ( D ).A.A支座竖向反力 B.P=1在截面K的位置C.P=1在截面A的位置 D.A、B同时满足10.力法典型方程中的系数项表示基本结构在( A荷载作用下产生的方向的位移 )。
位移法例题

精品文档第 7章位移法习题7-1:用位移法计算图示超静定梁,画出弯矩图,杆件EI 为常数。
qF PEI B EIA CL L/2L/2题7-1图7-2:用位移法计算图示刚架,画出弯矩图,杆件EI 为常数。
A3m4kN/m2kN.mBD3mC3m题7-2图7-3:用位移法计算图示刚架,画出弯矩图,杆件EI 为常数。
B DEIq EI EIH2A C2 L2题7-3图7-4:用位移法计算图示超静定梁,画出弯矩图。
M2EI B EIA CL L.题7-4图7-5:用位移法计算图示刚架,画出弯矩图,杆件EI 为常数。
10kN/m2kNC ED4mA B4m2m题7-5图7-6:用位移法计算图示排架,画出弯矩图。
A B C 10kNEA=∞EA =∞3.5m EI EI EID E F4m4m题7-6图7-7:用典型方程法计算7-2 题,画出弯矩图。
7-8:用典型方程法计算7-3 题,画出弯矩图。
7-9:用典型方程法计算7-5 题,画出弯矩图。
7-10:用典型方程法计算图示桁架,求出方程中的系数和自由项。
B10kN4mEA EAA CEA4m题 7-10 图7-11:用典型方程法计算图示刚架,求出方程中的系数和自由项。
.10kNA BEI EICEI4mD E FEI4m4m题 7-11 图7-12:用位移法计算图示结构,杆件EI 为常数(只需做到建立好位移法方程即可)。
A4m10kN/mB FD4mC E4m2m题 7-12 图7-13:用位移法计算图示结构,并画出弯矩图。
A EA=∞BLEI qF2EI EEIEI LC DL题 7-13 图7-14:用位移法计算图示结构,并画出弯矩图。
.EEILMC DF PEI EI LA BL/2L题 7-14 图7-15:用位移法计算图示刚架, 画出弯矩图。
AEI LMBEIEI LCL题 7-15 图7-16:用位移法计算图示结构,并画出弯矩图。
EIEI EIaqEIqEI E A EI aa a题 7-16 图7-17:用位移法计算图示结构,并绘弯矩图,所有杆件的EI 均相同。
结构力学-第7章-位移法习题答案
1 2
ql
1 12
ql 2
/ l
7 12
ql
由位移法方程得出:
r11Z1
R1 p
0
Z1
7ql 4 348EI
作出最终 M 图
7-9 试不经计算迅速画出图示结构的弯矩图形。
(a)
B
θA A
(b)
C B
yB
B′
A
C
题 7-9 图 7-10 试计算图示有剪力静定杆的刚架,并绘出 M 图。
13EI l
, r12
r21
3EI l2
r22
18EI l2
R1 p
1 16
ql 2 , R2 p
ql
代入,解得
Z1
66 3600
ql3 EI
,
Z2
211 3600
ql 4 EI
(4)求最终弯矩图
(e)
50kN·m
80kN·m 10kN·m 20kN
A 2EI B EI C
EI
(b)
B
3EI
C
EI
EI
A
D
Δ l
l
解:(1)求 M1, M 2 , M 3, M p 图。
(2)由图可知:
r11
16i, r12
r21
6i, r23
r32
6i l
, r22
16i, r33
24i l
R1 p
0, R2 p
位移法习题答案

位移法习题答案位移法的基本步骤包括:1. 选择位移函数:根据结构的边界条件和对称性,选择合适的位移函数。
2. 建立位移矩阵:将位移函数表示为位移矩阵的形式。
3. 应用位移边界条件:根据结构的固定边界条件,确定位移矩阵中的未知数。
4. 计算内力:利用位移矩阵和结构的几何关系,计算出结构的内力。
5. 验证位移法结果:通过比较位移法的结果与其他方法(如力法)的结果,验证位移法的准确性。
例题:考虑一个简支梁,长度为L,受集中力P作用于中点。
使用位移法求解梁的弯矩和剪力分布。
解答:首先,我们假设梁的位移函数为:\[ w(x) = \frac{Px(L-x)}{2EI} \]其中,\( w(x) \) 是梁在x位置的位移,\( E \) 是材料的弹性模量,\( I \) 是截面惯性矩。
接下来,根据位移函数,我们可以计算梁的弯矩和剪力:\[ M(x) = -EI \frac{d^2w}{dx^2} \]\[ V(x) = -EI \frac{dw}{dx} \]应用位移边界条件,我们可以确定位移函数中的未知数。
对于简支梁,位移在支点处为零,即:\[ w(0) = w(L) = 0 \]将位移函数代入上述条件,我们可以验证假设的位移函数满足边界条件。
最后,代入位移函数到弯矩和剪力的表达式中,我们可以得到:\[ M(x) = -\frac{P}{2} \left( \frac{L^2}{4} - x^2 \right) \]\[ V(x) = -\frac{P}{2} \left( L - 2x \right) \]通过上述计算,我们得到了梁在任意位置的弯矩和剪力分布。
结论:位移法是一种有效的结构分析方法,它通过位移函数来求解结构的内力和位移。
通过本题的解答,我们可以看到位移法在求解简支梁问题中的应用。
请注意,上述内容是一个示例答案,具体的习题答案会根据具体的题目而有所不同。
在实际应用中,需要根据具体的结构和受力情况来选择合适的位移函数和计算方法。
结构力学位移法题及答案
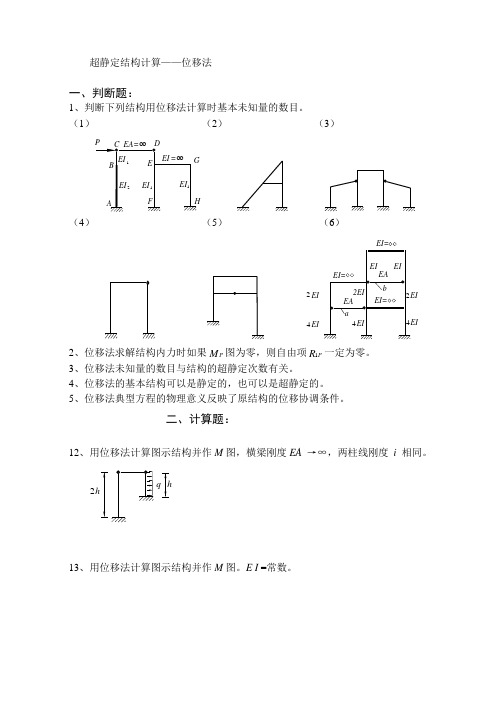
超静定结构计算——位移法一、判断题:1、判断下列结构用位移法计算时基本未知量的数目。
(1) (2) (3)(4) (5) (6)EIEIEIEI 2EI EI EIEIEAEA ab EI=EI=EI=244422、位移法求解结构内力时如果P M 图为零,则自由项1P R 一定为零。
3、位移法未知量的数目与结构的超静定次数有关。
4、位移法的基本结构可以是静定的,也可以是超静定的。
5、位移法典型方程的物理意义反映了原结构的位移协调条件。
二、计算题:12、用位移法计算图示结构并作M 图,横梁刚度EA →∞,两柱线刚度 i 相同。
213、用位移法计算图示结构并作M 图。
E I =常数。
lll /2l /214、求对应的荷载集度q 。
图示结构横梁刚度无限大。
已知柱顶的水平位移为 ()5123/()EI →。
12m12m8mq15、用位移法计算图示结构并作M 图。
EI =常数。
ll ll16、用位移法计算图示结构,求出未知量,各杆EI 相同。
4m19、用位移法计算图示结构并作M 图。
qll20、用位移法计算图示结构并作M 图。
各杆EI =常数,q = 20kN/m 。
6m6m23、用位移法计算图示结构并作M 图。
EI =常数。
ll 224、用位移法计算图示结构并作M 图。
EI =常数。
q29、用位移法计算图示结构并作M 图。
设各杆的EI 相同。
qql l /2/232、用位移法作图示结构M 图。
E I =常数。
qql l/2l /2l36、用位移法计算图示对称刚架并作M 图。
各杆EI =常数。
l l38、用位移法计算图示结构并作M 图。
EI =常数。
ql l l l42、用位移法计算图示结构并作M 图。
2m 2m43、用位移法计算图示结构并作M 图。
EI =常数。
lllql48、已知B 点的位移∆,求P 。
ll/2/2A∆51、用位移法计算图示结构并作M 图。
q超静定结构计算——位移法(参考答案)1、(1)、4; (2)、4; (3)、9; (4)、5; (5)、7;(6)、7。
位移法—位移法的典型方程和计算实例(建筑力学)

i
18.94kN m
i
2
i
3.158
M CD 6i
18.95kN m
i
3 21.05
M BD i
20 35.79kN m
4
i
作M图,如图示
位移法
位移法计算步骤归纳如下
(1)确定基本未知量。在原结构上加入附加约束,得到
衡条件求出杆端剪力。
M
B
FQAB
M
A
0
2.5 4 2 20
kN 0
4
0
FQBA
2.5 4 2 20
kN 10kN
4
位移法
同理,取杆件BC,由平衡条件得
FQCB FQBC 10kN
取杆件BD,由平衡条件得
FQDB FQBD 7.5kN
1.5i1 0.9375i 2 15 0
1
3.16
i
2
21.05
i
位移法
(6)作M图
利用叠加公式 M M1Z1 M 2 Z 2 M 计算杆端弯矩
3.158 3 21.05
M AC 2i
i
25.26kN m
i
2
i
3.158 3 21.05
k211 k22 2 F2 0
位移法
(3)求系数和自由项
k11=4i +6 i=10 i
k12= -1.5 i =k21
k12= -1.5 i
k22 0.75i 0.1875 i 0.9375 i
位移法
F1 0
土木工程力学(本)位移法计算题答案新(往年考题)----
1. 用位移法计算图示刚架,求出系数项及自由项。
EI =常数。
(15分)解:(1)基本未知量这个刚架基本未知量只有一个结点B 的角位移1∆。
(2)基本体系在B 点施加附加刚臂,约束B 点的转动,得到基本体系。
Δ1(3)位移法方程01111=+∆P F k(4)计算系数和自由项令EI i =,作1M 图2=11k 11i作P M 图24由0=∑B M ,得=P F 1m kN ⋅-21⑸解方程组,求出=∆1i1121 2.用位移法计算图示刚架,求出系数项和自由项。
(15分)解:(1)基本未知量这个刚架基本未知量只有一个结点B 的角位移1∆。
(2)基本体系在B 点施加附加刚臂,约束B 点的转动,得到基本体系。
(3)位移法方程01111=+∆P F k(4)计算系数和自由项令lEIi =,作1M 图=12得=11k 12i作P M 图P得=P F 18Pl3用位移法计算图示刚架,求出系数项及自由项。
EI =常数。
(15分)解:(1)基本未知量这个刚架基本未知量只有一个结点B 的角位移1∆。
(2)基本体系在B 点施加附加刚臂,约束B 点的转动,得到基本体系。
(3)位移法方程 01111=+∆P F k(4)计算系数和自由项令lEI i =,作1M 图得=11k8i作PM图得4、用位移法计算图示刚架,求出系数项和自由项。
l l / 2 l / 2解:(1)基本未知量这个刚架基本未知量只有一个结点角位移1∆。
(2)基本体系在刚结点施加附加刚臂,约束B点的转动,得到基本体系。
基本体系(3)位移法方程01111=+∆P F k(4)计算系数和自由项令l EIi =,作1M 图 得=11k 12i 作P M 图 得=P F 18Pl F P F P5、用位移法计算图示刚架,求出系数项及自由项。
EI =常数。
2m2m 4m4m(1)基本未知量这个刚架基本未知量只有一个结点角位移1∆。
(2)基本体系在刚结点施加附加刚臂,约束结点的转动,得到基本体系。
土木工程力学形考四题库
土木工程力学形考四题库1.位移法基本方程中的自由项代表荷载在基本体系作用下产生的第i个附加约束中的约束反力和第j个附加约束中的约束反力。
答案:C。
2.在图示刚架中,只有AB、BE杆产生弯矩。
答案:D。
3.求解图示结构时,基本未知量的个数是10.答案:B。
4.下图所示结构的位移法基本未知量数目为3.答案:B。
5.图示结构位移法方程中的系数为8.答案:D。
6.如果要使图示节点A的转角为5,应在节点A施加的力偶M为5.答案:C。
7.图示连续梁中AB杆B端的弯矩等于0.答案:C。
8.力矩分配法的直接对象是杆端弯矩。
答案:A。
9.用力矩分配法计算结构得到一个收敛的结果,是因为分配系数小于1.答案:A。
10.下图所示连续梁,欲使A端发生单位转动,需在A端施加的力矩为8.答案:D。
11.图示超静定结构结点角位移的个数是3.答案:B。
12.用位移法计算超静定结构时,其基本未知量为结点位移。
答案:D。
13.下图所示三根梁的EI、杆长相同,它们的固定端的弯矩之间的关系是(2)、(3)的固定端弯矩相同。
答案:C。
14.图示结构位移法方程中的自由项为-2.答案:B。
15.图示结构杆件BC的B端转动刚度为8.答案:D。
16.汇交于一刚结点的各杆端弯矩分配系数之和等于1.答案:A。
17.等截面直杆的弯矩传递系数C与远端支承有关。
答案:C。
18.分配弯矩是A端转动时产生的A端弯矩。
答案:B。
19.在位移法计算中规定正的杆端弯矩是绕杆端顺时针转动。
答案:A。
20.位移法典型方程实质上是一个线性方程组。
答案:A。
1.位移法解超静定结构的基本未知量个数与以下哪个因素有关?(A)A。
结构的形式B。
多余约束的数目C。
结点数D。
杆件数2.下图所示的超静定结构结点角位移的个数是?(C)A。
2B。
3C。
4D。
53.下列哪个条件与杆件的传递弯矩有关?(D)A。
分配弯矩B。
传递系数C。
分配系数D。
同时满足以上条件4.下图所示的刚架MAD的弯矩为多少?(A)A。
位移法例题
r21=- 24i/l 2
0
6i/l 6i/l
r12= -24i/l 2
r12
Z2=1
-12i/l 2 -12i/l 2 12i/l 2
-12i/l 2 -12i/l 2 r22=48i/l 2 12i/l 2
r22
6i/l
M 2图
FP
说明:水平杆的M图没画,并不是其M=0,而 是EI无穷大的杆能平衡任何弯矩。
R1P FP
R1P=-FP
0 0 0 0 0
FP
R2P FP MP图
R2P=-FP
0
作用在结点上的外力相当于 支座,故杆件无弯矩。 解得
3FP l 2 Z1 = 24i FP l 2 Z2 = 12i
FPl /4 FPl /4 FPl / 2
FPl / 2
M图
(4) 利用叠加法作出弯矩图
例4:用位移法计算图示结构 ,并作弯矩图.EI= 常数. 4:
l
A l
D
(同济大学,2004年考研题)
Z1 = 1
B 4i A 4i 2i l
C 2i l D
Z2 = 1
6i/l
2i/l
B
C
4i/l
M1 图
A
6i/l
D
l
M2 图
l
Z1 = −ql / ( 84i )
2
Z 2 = ql / ( 3i )
3
M 图(× ql )
2
例2: 位移法求解图示结构。
P
P /2
l A EA = B
Z1
l
l
P
l
注意: M 1图和 M P图的正确作图
例3:用位移法作图示结构的 M 图。EI=常数.
电大《土木工程力学》(本)历届试题及答案
1.用位移法计算图示各结构,基本未知量是两个的结构为(A )。
2.用力法计算超静定结构时,基本未知量是(D 多余未知力)。
3.图示结构杆件BA 的B 端转动刚度BA S 为(B3)。
4.用力矩分配法计算结构得到一个收敛的结果,是因为(D )。
B 附22.用力法计算图示结构并作弯矩图,EI=常数。
解:典型方程011111=∆+=∆Px δ五、(14分)23.用位移法计算图示刚架,列出典型方程,求出系数项及自由项。
解:典型方程01111=+∆P F k1.图示对称结构作用反对荷载,EI=常数,对称轴穿过的AB 杆件内力满足(D 0,0,0===N Q F F M )2.机动法作静定梁弯矩影响线应用的原理是(C 刚体虚功原理)。
3.结构不考虑阻尼时的自振频率为ω,考虑阻尼时的自振频率为D ω,则(C D ωω )4)。
7。
表示正确,以×表示错误)二、判断题(将判断结果填入括弧,以√表示正确,以×表示错误。
每小题3分,共30分)11.基本附属型结构力的传递顺序是:从附属部分到基本部分。
(√)12.结构由于弱阻尼其自由振动不会衰减。
(×)13.当AB 杆件刚度系数i S AB 3 时,杆件的B 端为固定支座。
(×)14.温度变化时静定结构中的杆件发生变形。
(√)15.图(a)对称结构受对称荷载作用,利用对称性可简化为图(b)来计算。
(√)16.结构的自振频率与干扰力无关。
(√)(√)形。
(15.(√)18.静定结构剪力影响线是由直线段组成的。
(√)19.反映结构动力特性的参数是振动质点的数目。
(×)20.力矩分配法只适用于连续梁的计算。
(×)1.图示为刚架的虚设力状态,按此力状态及位移计算公式可求出A处的水平位移。
(√)2.图示结构用位移法求解,基本未知量的数目是2。
(×)3.力法典型方程是根据平衡条件得到的。
(×)4.对称结构在反对称荷载作用下,对称轴穿过的截面只有反对称的内力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、试用位移法计算图示刚架,并绘出其弯矩图。
(EI =常数) (22’)
2m 2m 2m 2m 2m 2m
解:利用对称性,基本系可取为(3分)
R 1
F
以刚结点B 处的角位移1ϕ为基本未知量,典型方程为(2分)
1110R if k F ϕ+=
单位弯矩图和荷载弯矩图分别为(2
个图,每个3分,)
11ϕ=作用下的1M F M
115k EI =, 12R f F =-
所以可得10.4/EI ϕ= 最后的内力和内力图按11F M M M ϕ=+可得
3、试用位移法计算图示刚架,并绘出其弯矩图。
已知各杆EI 相同。
(22’)
A 6m 3m
3m 3m 3m
解:利用对称性,基本系可取为(3分)
F R 1
A
以刚结点B 处的角位移1ϕ为基本未知量,典型方程为(2分)
1110R if k F ϕ+=
单位弯矩图和荷载弯矩图分别为(2个图,每个3分,)
11ϕ=作用下的1M F M 115/3k EI =, 1420R f F =
所以可得1252/EI ϕ=-
最后的内力和内力图按11F M M M ϕ=+可得。
