高一数学平面向量知识点及典型例题解析
第4讲 平面向量万能建系法5种常见题型(解析版) 高一数学讲义(新人教2019)必修二
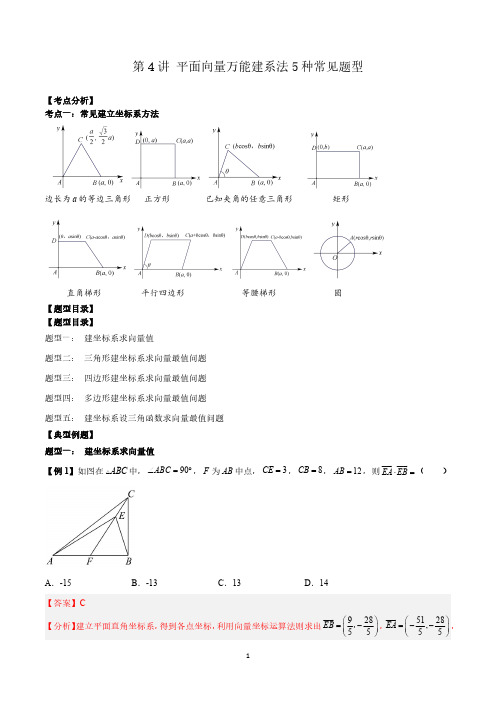
第4讲平面向量万能建系法5种常见题型【考点分析】考点一：常见建立坐标系方法边长为a 的等边三角形正方形已知夹角的任意三角形矩形直角梯形平行四边形等腰梯形圆【题型目录】【题型目录】题型一：建坐标系求向量值题型二：三角形建坐标系求向量最值问题题型三：四边形建坐标系求向量最值问题题型四：多边形建坐标系求向量最值问题题型五：建坐标系设三角函数求向量最值问题【典型例题】题型一：建坐标系求向量值【例1】如图在ABC 中，90ABC ∠=︒，F 为AB 中点，3CE =，8CB =，12AB =，则EA EB ⋅= （）A ．-15B ．-13C ．13D ．14则()120A -，，(00)B ，，(08)C ，，(60)F -，，又3CE =，8CB =，12AB =，则2210CF CB BF =+=，即310CE FC =，即710FE FC =，则()77601010BE BF FE BF FC +==+=-+ ，()(776,81010EA EF FA CF FA =+=+=--+- 【例2】已知正方形ABCD 的边长为2，以CD 为边作正三角形CDE ，使得,A E 位于直线CD 的两侧，则AC AE →→⋅的值为（）A ．6-B ．6-C ．6+D ．6+【答案】D 【分析】建立平面直角坐标系，利用向量的坐标运算求解.【详解】以A 为坐标原点，以,AB AD 为,x y 轴非负半轴，建立平面直角坐标系，如图，由正三角形CDE 及正方形ABCD ()()2,2,1,23C E +，所以()()2,21,23AC AE →→⋅=⋅+=故选：D【例3】如图甲所示，古代中国的太极八卦图是以同圆内的圆心为界，画出相等的两个阴阳鱼.其平面图形记为图乙中的正八边形ABCDEFGH ，其中2OA =，则以下结论错误的是（）A 0OE OG ++=B ．OA OD ⋅=-C ．4AG EH +=D ．AO 在OH 方向上的投影向量为2OH - 【答案】C【分析】选择合适的位置建立平面直角坐标系，写出相应点的坐标，逐项验证即可.【详解】由题意，分别以,HD BF 所在直线为,x y 轴，建立平面直角坐标系，如图所示：在正八边形ABCDEFGH 中，由AOB BOC COD DOE ∠=∠=∠=∠360458GOH HOA =∠=∠== 过A 作AM HD OM AM⊥⇒=因为2OA =，所以OM AM ==所以(2,2),(0,2),(2,A B E ---【例4】《九章算术》中有一个“引葭赴岸”问题：“今有池方一丈，葭生其中央，出水一尺．引葭赴岸，适与岸齐．问水深、葭长各几何？”其大意为现有水池1丈见方（即1CE =丈10=尺），芦苇生长在水池的中央，长出水面部分的长度为1尺．将芦苇向池岸牵引，牵引至恰巧与水岸齐接的位置（如图所示）．试问水深、芦苇的长度各是多少？若将芦苇,AB AC 均视为线段，在芦苇移动的过程中，设其长度不变，则AC DE ⋅=（）．A ．90平方尺B ．92平方尺C ．94平方尺D ．98平方尺【答案】C 【分析】设AB x =（尺），利用勾股定理可构造方程求得AB ，以A 为坐标原点可建立平面直角坐标系，利用平面向量数量积的坐标运算可求得结果.【详解】设AB x =（尺），则1AC x =+（尺），5AD = （尺），()22251x x ∴+=+，解得：12x =．以A 为坐标原点，建立如图所示的平面直角坐标系（单位：尺），则()0,0A ，()5,0D ，()5,12C ，()5,12E -，()5,12AC ∴= ，()10,12DE =- ，5014494AC DE ∴⋅=-+= （平方尺）．故选：C.【例5】已知正方形ABCD 的边长为2，点P 满足1()2AP AB AC =+ ，则||PD = _________；PB PD ⋅= _________．【答案】(1).(2).1-【解析】以点A 为坐标原点，AB 、AD 所在直线分别为x 、y 轴建立如下图所示的平面直角坐标系，则点()0,0A 、()2,0B 、()2,2C 、()0,2D ，()()()()1112,02,22,1222AP AB AC =+=+= ，则点()2,1P ，()2,1PD ∴=- ，()0,1PB =- ，因此，PD == ()021(1)1PB PD ⋅=⨯-+⨯-=- .【题型专练】1．已知矩形ABCD 中，4AB =uuu r ，2AD = ，3DM MC = ，BP PC = ，则AM AP ⋅= （）A ．6B ．10C ．14D ．38【答案】C 【分析】以B 为原点，,BA BC 分别为,x y 轴建立平面直角坐标系，由条件得出点,P M 的坐标，进而得出向量,AP AM uuu r uuur的坐标，从而得出向量的数量积.【详解】以B 为原点，,BA BC 分别为,x y 轴建立平面直角坐标系.则()0,4A ,()2,4,D ()2,0C 由BP PC = ，则()1,0P ,由3DM MC = ，则()2,1M 所以()1,4AP =-uuu r ,()2,3AM =-uuur 所以()()124314AM AP ⋅=⨯+-⨯-=uuur uuu r 故选：C。
平面向量知识点总结、经典例题及解析、高考题50道及答案
）））））））第五章 平面向量【考纲说明】1、理解平面向量的概念和几何表示，理解两个向量相等及共线的含义，掌握向量的加、减、数乘运算及其几何意义，会用坐标表示。
2、了解平面向量的基本定理，掌握平面向量的坐标运算。
3、掌握数量积的坐标表达式，会进行平面向量数量积的运算，会用向量方法解决简单的平面几何问题、力学问题与其他一些实际问题。
【知识梳理】一、 向量的基本概念与线性运算 1 向量的概念：（1）向量：既有大小又有方向的量，记作AB ；向量的大小即向量的模（长度），记作|AB | 向量不能比较大小，但向量的模可以比较大小．（2）零向量：长度为0的向量，记为0 ，其方向是任意的，0与任意向量平行（3）单位向量：模为1个单位长度的向量常用e 表示．（4）平行向量（共线向量）：方向相同或相反的非零向量，记作a ∥b平行向量也称为共线向量（5）相等向量：长度相等且方向相同的向量相等向量经过平移后总可以重合，记为b a= 大小相等，方向相同),(),(2211y x y x =⎩⎨⎧==⇔2121y y x x（6）相反向量：与a 长度相等、方向相反的向量，叫做a的相反向量记作a-,零向量的相反向量仍是零向量若a 、b是互为相反向量，则a =b -,b =a -,a +b =2 向量的线性运算：（1）向量的加法：求两个向量和的运算叫做向量的加法 向量加法满足交换律与结合律；向量加法有“三角形法则”与“平行四边形法则” ．（2）向量的减法 ：求向量a 加上b 的相反向量的运算叫做a 与b的差．向量的减法有三角形法则，b a -可以表示为从b 的终点指向a 的终点的向量（a 、b有共同起点）（3）向量的数乘运算：求实数λ与向量a 的积的运算，记作λa．①a a⋅=λλ；②当0>λ时，λa 的方向与a 的方向相同；当0<λ时，λa 的方向与a的方向相反； 当0=λ时，0 =a λ，方向是任意的③数乘向量满足交换律、结合律与分配律3. 两个向量共线定理：向量b 与非零向量a共线⇔有且只有一个实数λ，使得b =λ向量b 与非零向量a共线⇔有两个均不是零的实数λ、μ，使得0a b λμ+=．二、平面向量的基本定理与坐标表示 1 平面向量的基本定理：如果21,e e 是一个平面内的两个不共线向量，那么对这一平面内的任一向量a，有且只有一对实数21,λλ使：2211e e a λλ+=，其中不共线的向量21,e e叫做表示这一平面内所有向量的一组基底2. 平面向量的坐标表示：（1）在直角坐标系中，分别取与x 轴、y 轴方向相同的两个单位向量,i j 作为基底 由平面向量的基本定理知，该平面内的任一向量a 可表示成a xi yj =+，由于a 与数对(x,y)是一一对应的，因此把(x,y)叫做向量a 的坐标，记作a =(x,y)，其中x 叫作a 在x 轴上的坐标，y 叫做在y 轴上的坐标显然0=（0,0），(1,0)i =，(0,1)j =． （2）设OA xi y j =+.则向量OA 的坐标(x,y)就是终点A 的坐标，即若OA =(x,y)，则A 点的坐标为(x,y)，反之亦成立（O 是坐标原点）． 3 平面向量的坐标运算：（1）若()()1122,,,a x y b x y ==，则()1212,a b x x y y ±=±±． （2）若()()2211,,,y x B y x A ，则()2121,AB x x y y =--，1(AB x =（3）若a =(x,y)，则λa =(λx,λy)．（4）若()()1122,,,a x y b x y ==，则1221//0a b x y x y ⇔-=． （5）若()()1122,,,a x y b x y ==，则1212a b x x y y ⋅=⋅+⋅． 三、平面向量的数量积 1 两个向量的数量积：已知两个非零向量a 与b ，它们的夹角为θ，a ·b 等于a 的长度与b 在a 方向上的投影的乘积叫做a 与b 的数量积（或内积），即a ·b =︱a ︱·︱b ︱cos θ，规定00a ⋅=2 向量的投影：︱b ︱cos θ=||a ba ⋅∈R ，称为向量b 在a 方向上的投影 投影的绝对值称为射影 3 向量的模与平方的关系：22||a a a a ⋅==4 乘法公式成立：()()2222a b a b a b a b +⋅-=-=-； ()2222a b a a b b±=±⋅+222a a b b =±⋅+．5 平面向量数量积的运算律：①交换律成立：a b b a ⋅=⋅．②对实数的结合律成立：()()()()a b a b a b R λλλλ⋅=⋅=⋅∈．③分配律成立：()a b c a c b c ±⋅=⋅±⋅()c a b =⋅±； 特别注意：①结合律不成立：()()a b c a b c ⋅⋅≠⋅⋅．②消去律不成立a b a c⋅=⋅不能得到b c =．③a b ⋅=0不能得到a =0或b =06 两个向量的数量积的坐标运算：已知两个向量1122(,),(,)a x y b x y ==，则a ·b =1212x x y y + 7 向量的夹角：已知两个非零向量a 与b ，作OA =a , OB =b ,则∠AOB=θ （001800≤≤θ）叫做向量a 与b 的夹角cos θ=cos ,a b a b a b⋅<>=⋅=当且仅当两个非零向量a 与b 同方向时，θ=00，当且仅当a 与b 反方向时θ=1800，同时0与其它任何非零向量之间不谈夹角这一问题8 垂直：如果a 与b 的夹角为900则称a 与b 垂直，记作a ⊥ba ⊥b ⇔a ·b＝O ⇔2121=+y y x x【经典例题】【例1】（2010全国Ⅱ，8）△ABC 中，点D 在边AB 上，CD 平分∠ACB ，若CB a =，ECBA CA b =，1,2a b ==，则CD = （ ）（A ）1233a b + （B ）2133a b + （C ）3455a b + （D ）4355a b + 【答案】B ．【解析】由角平分线的性质得2AD DB =,即有22()()33AD CB CA a b =-=-．从而221()333CD CA AD b a b a b =+=+-=+．故选B ．【例2】（2009北京，2）已知向量a 、b 不共线，c k =a +b (k ∈R ),d =a -b ,如果c //d ， 那么 （ ） A ．1k =且c 与d 同向 B ．1k =且c 与d 反向 C ．1k =-且c 与d 同向 D ．1k =-且c 与d 反向 【答案】D ．【解析】取a ()1,0=，b ()0,1=，若1k =，则c =a +b ()1,1=，d =a -b ()1,1=-， 显然，a 与b 不平行，排除A 、B ．若1k =-，则c =-a +b ()1,1=-，d =-a +b ()1,1=--， 即c //d 且c 与d 反向，排除C ，故选D ．【例3】（2009湖南卷文）如图，D ，E ，F 分别是∆ABC 的边AB ，BC ，CA 的中点，则( ) A ．0AD BE CF ++= B ．0BD CF DF -+=C ．0AD CE CF +-= D ．0BD BE FC --= 【答案】A ． 【解析】,,AD DB AD BE DB BE DE FC =∴+=+==得0AD BE CF ++=．或0AD BE CF AD DF CF AF CF ++=++=+=．【例4】（2009宁夏海南卷文）已知()()3,2,1,0a b =-=-，向量a b λ+与2a b -垂直，则实数λ的值为( )A.17-B.17C.16-D.16【答案】A ．【解析】向量a b λ+＝（－3λ－1，2λ），2a b -＝（－1,2），因为两个向量垂直，故有（－3λ－1，2λ）×（－1,2）＝0，即3λ＋1＋4λ＝0，解得：λ＝17-，故选A ． 【例5】（2009全国卷Ⅰ文）设非零向量a 、b 、c 满足c b a c b a =+==|,|||||，则>=<b a , （ ）A ．150° B.120° C.60° D.30° 【答案】B ．【解析】由向量加法的平行四边形法则，知a 、b 可构成菱形的两条相邻边，且a 、b 为起点处的对角线长等于菱形的边长，故选择B ．【例6】（2009安徽卷文）在平行四边形ABCD 中，E 和F 分别是边CD 和BC 的中点，或=+，其中，R ，则+= _________．【答案】43． 【解析】设BC b =、BA a =则12AF b a =- ,12AE b a =- ,AC b a =- 代入条件得2433u u λλ==∴+=． 【例7】（2009辽宁卷文）在平面直角坐标系xoy 中，四边形ABCD 的边AB ∥DC,AD ∥BC,已知点A(－2，0)，B （6，8），C(8,6),则D 点的坐标为___________． 【答案】(0,－2)．【解析】平行四边形ABCD 中,OB OD OA OC +=+ ∴OD OA OC OB =+-＝(－2,0)＋(8,6)－(6,8)＝(0,－2) 即D 点坐标为(0,－2)．【例8】（2012江苏）如图,在矩形ABCD 中,22AB BC ==，，点E 为 BC 的中点，点F 在边CD 上,若2AB AF =,则AE BF 的值是___．【答案】2．【解析】由2AB AF =,得cos 2ABAF FAB ∠=,由矩形的性质,得cos =AF FAB DF ∠．∵2AB =，∴22DF ⋅=，∴1DF =∴21CF =-．记AE BF 和之间的夹角为,AEB FBC θαβ∠=∠=，，则θαβ=+． 又∵2BC =，点E 为BC 的中点，∴1BE =． ∴()()=cos =cos =cos cos sin sin AE BF AEBF AEBF AE BF θαβαβαβ+-()=cos cos sin sin =122212AE BF AE BF BE BC AB CF αβαβ--=⨯--=.本题也可建立以, AB AD 为坐标轴的直角坐标系,求出各点坐标后求解．【例9】(2009湖南卷理)在ABC ∆，已知2233AB AC AB AC BC ⋅=⋅=，求角A ，B ，C 的大小． 【答案】2,,663A B C πππ===． 【解析】解：设,,BC a AC b AB c ===由23AB AC AB AC ⋅=⋅得2cos 3bc A bc =，所以3cos 2A = 又(0,),A π∈因此6A π=由233AB AC BC ⋅=得23bc a =，于是23sin sin 3sin 4C B A ⋅=-所以53sin sin()64C C π⋅-=，133sin (cos sin )224C C C ⋅+=，因此 22sin cos 23sin 3,sin 23cos 20C C C C C ⋅+=-=，既sin(2)03C π-=由A=6π知506C π<<，所以3π-，4233C ππ-<，从而20,3C π-=或2,3C ππ-=，既,6C π=或2,3C π=故2,,,636A B C πππ===或2,,663A B C πππ===． 【课堂练习】一、选择题1.（2012辽宁理）已知两个非零向量a ,b 满足|a +b |=|a -b |,则下面结论正确的是（ ）A ．a ∥bB ．a ⊥bC ．{0,1,3}D ．a +b =a -b2. (2009年广东卷文)已知平面向量a =,1x （），b =2,x x （－），则向量+a b ( )A. 平行于x 轴B. 平行于第一、三象限的角平分线C. 平行于y 轴D. 平行于第二、四象限的角平分线3.（2012天津文）在ABC ∆中,90A ∠=︒,1AB =,AC=2,设点,P Q 满足,(1),AP AB AQ AC R λλλ==-∈.若2BQ CP ⋅=-,则λ=( )（ ）A ．13 B ．23C ．43D ．2 4.（2009浙江卷理）设向量a ，b 满足：||3=a ，||4=b ，0⋅=a b ．以a ，b ，-a b 的模为边长构成三角形，则它的边与半径为1的圆的公共点个数最多为 ( )A ．3 B.4 C ．5D ．65.（2012重庆理）设,x y ∈R,向量()()()4,2,,1,1,-===c y b x a ,且c b c a //,⊥,则a b += （）A B C ．D ．106. （2009浙江卷文）已知向量(1,2)=a ，(2,3)=-b ．若向量c 满足()//+c a b ，()⊥+c a b ，则c =（ ）A ．77(,)93B ．77(,)39--C ．77(,)39D ．77(,)93--7．（2012浙江理）设a ,b 是两个非零向量.（ ）A ．若|a +b |=|a |-|b |,则a ⊥bB ．若a ⊥b ,则|a +b |=|a |-|b |C ．若|a +b |=|a |-|b |,则存在实数λ,使得a =λbD ．若存在实数λ,使得a =λb ,则|a +b |=|a |-|b |8.（2009全国卷Ⅰ理）设a 、b 、c 是单位向量，且a ·b ＝0，则()()a c b c -•-的最 小值为( )A.2- 2C.1-D.19.（2012天津理）已知△ABC 为等边三角形,=2AB ,设点P,Q 满足=AP AB λ,=(1)AQ AC λ-,R λ∈,若3=2BQ CP ⋅-,则=λ （ ）A ．12 B ．12± C ．12± D ．32-±10.（2009全国卷Ⅱ理）已知向量()2,1,10,||a a b a b =⋅=+=||b =( )A.B. C. 5 D. 2511.（2012大纲理）ABC ∆中,AB 边上的高为CD ,若,,0,||1,||2CB a CA b a b a b ==⋅===,则AD =（ ）A ．1133a b -B ．2233a b - C ．3355a b - D ．4455a b - 12.（2008湖南）设D 、E 、F 分别是△ABC 的三边BC 、CA 、AB 上的点，且2,DC BD =2,CE EA =2,AF FB =则AD BE CF ++与BC( )A. 反向平行B. 同向平行C. 互相垂直D. 既不平行也不垂直13.（2008广东）在平行四边形ABCD 中，AC 与BD 交于点O E ，是线段OD 的中点，AE 的延长线与CD 交于点F ．若AC =a ，BD =b ，则AF =（ ）A ．1142+a b B ．2133+a b C ．1124+a bD ．1233+a b 14.（2007湖北）设(43)=，a ，a 在b 上的投影为522，b 在x 轴上的投影为2，且||14≤b ，则b 为（ ）A ．(214)，B ．227⎛⎫- ⎪⎝⎭，C ．227⎛⎫- ⎪⎝⎭，D ．(28)，15.（2012安徽理）在平面直角坐标系中,(0,0),(6,8)O P ,将向量OP 按逆时针旋转34π后,得向量OQ 则点Q 的坐标是 （ ） A ．(72,2)-- B ．(72,2)- C ．(46,2)-- D ．(46,2)-二、填空题16.（2012浙江文）在△ABC 中,M 是BC 的中点,AM=3,BC=10,则AB AC ⋅=________.17.（2009安徽卷理）给定两个长度为1的平面向量OA 和OB ，它们的夹角为120o.如图所示，点C 在以O 为圆心的圆弧AB 上变动. 若,OC xOA yOB =+其中,x y R ∈,则x y + 的最大值是________.18.（2012上海文）在知形ABCD 中,边AB 、AD 的长分别为2、1. 若M 、N 分别是边BC 、CD 上的点,且满足||||||||CD CN BC BM =,则AN AM ⋅的取值范围是_________ .19.（2012课标文）已知向量a ,b 夹角为045,且|a |=1,|2-a b |=10,则|b |=_______. 20.（2012湖南文）如图4,在平行四边形ABCD 中 ,AP ⊥BD,垂足为P,3AP =且APAC = _____.A DBCP21.（2012湖北文）已知向量(1,0),(1,1)a b ==,则(Ⅰ)与2a b +同向的单位向量的坐标表示为____________; (Ⅱ)向量3b a -与向量a 夹角的余弦值为____________.22.（2012北京文）已知正方形ABCD 的边长为1,点E 是AB 边上的动点,则DE CB ⋅的值为________. 23.（2012安徽文）设向量(1,2),(1,1),(2,)a m b m c m ==+=,若()a c +⊥b ,则a =_____.24.（2012江苏）如图,在矩形ABCD 中,22AB BC ==，，点E 为BC 的中点,点F 在边CD上,若2AB AF =,则AE BF 的值是___.25.（2012安徽理）若平面向量,a b 满足:23a b -≤;则a b 的最小值是_____三、解答题26. (2009年广东卷文)（已知向量)2,(sin -=θa 与)cos ,1(θ=b 互相垂直，其中)2,0(πθ∈（1）求θsin 和θcos 的值（2）若ϕϕθcos 53)cos(5=-，<<ϕ02π,求ϕcos 的值 27.（2009上海卷文）已知ΔABC 的角A 、B 、C 所对的边分别是a 、b 、c ，设向量(,)m a b =， (sin ,sin )n B A =，(2,2)p b a =-- .（1） 若m //n ，求证：ΔABC 为等腰三角形； （2） 若m ⊥p ，边长c = 2，角C =3π，求ΔABC 的面积 . 28. 已知A 、B 、C 分别为ABC △的三边a 、b 、c 所对的角，向量)sin ,(sin B A m =，)cos ,(cos A B n =，且C n m 2sin =⋅.（Ⅰ）求角C 的大小；（Ⅱ）若A sin ，C sin ，B sin 成等差数列，且18)(=-⋅AC AB CA ，求边c 的长.【课后作业】一、选择题1.（2009辽宁卷理）平面向量a 与b 的夹角为060，(2,0)a =，1b = 则2a b +=( )A.B. C. 4 D. 22.（2009宁夏海南卷理）已知O ，N ，P 在ABC ∆所在平面内，且,0OA OB OC NA NB NC ==++=，且PA PB PB PC PC PA •=•=•，则点O ，N ，P 依次是ABC ∆的( )A. 重心 外心 垂心B. 重心 外心 内心C. 外心 重心 垂心D. 外心 重心 内心3.（2008安徽）在平行四边形ABCD 中，AC 为一条对角线，若(2,4)AB =，(1,3)AC =,则BD =（ ）A ． （－2，－4）B ．（－3，－5）C ．（3，5）D ．（2，4）4.（2008浙江）已知a ，b 是平面内两个互相垂直的单位向量，若向量c 满足0)()(=-⋅-c b c a ,则c 的最大值是( )A. 1B. 2C.2 D.225.（2007海南、宁夏）已知平面向量(11)(11)==-，，，a b ，则向量1322-=a b（ ） A ．(21)--， B ．(21)-，C ．(10)-，D ．(12)，6.（2007湖南）设，a b 是非零向量，若函数()()()f x x x =+-a b a b 的图象是一条直线，则必有（ ）A ．⊥a bB ．∥a bC ．||||=a bD ．||||≠a b7. （2007天津）设两个向量22(2cos )λλα=+-，a 和sin 2m m α⎛⎫=+ ⎪⎝⎭，b ，其中mλα，，为实数．若2=a b ，则mλ的取值范围是 （ ） A ．[-6，1]B ．[48]，C ．（-6，1]D ．[-1，6]8. 在ABC BC AB ABC ∆︒︒=︒︒=∆则已知向量中),27cos 2,63cos 2(),72cos ,18(cos ,的面积等于（ ） A ．22 B ．42 C ．23 D ．29. 已知平面向量(3,1),(,3),//,a b x a b x ==-则等于 （ ）A ．9B ．1C ．－1D ．－910. 已知a 、b 是不共线的AB a b λ=+AC a b μ=+(,)R λμ∈，则A 、B 、C 三点共线的充要条件是：（ ）A ．1λμ+=B ．1λμ-=C ．1λμ=-D ．1λμ=二、填空题11. 设向量2,3,19,AB AC AB AC CAB ==+=∠=则_________.12. 若向量,2,2,()a b a b a b a ==-⊥ 满足，则向量b a 与的夹角等于 .13. 已知平面上的向量PA 、PB 满足224PA PB +=,2AB =，设向量2PC PA PB =+，则PC 的最小值是 .14.（2008江苏）a ，b 的夹角为120︒，1a =，3b = 则5a b -= ． 15. （2007安徽）在四面体O ABC -中，OA OB OC D ===，，，a b c 为BC 的中点，E 为AD 的中点，则OE = （用，，a b c 表示）．16.（2007北京）已知向量2411()()，，，a =b =．若向量()λ⊥b a +b ，则实数λ的值是 .17. 已知向量(cos15,sin15)a =，(sin15,cos15)b =--，则a b |+|的值为 .18.（2007广东）若向量a 、b 满足b a b a 与,1==的夹角为120°，则b a b a ··+＝ .三、解答题19.（2009湖南卷文）已知向量(sin ,cos 2sin ),(1,2).a b θθθ=-=（1）若//a b ，求tan θ的值；（2）若||||,0,a b θπ=<<求θ的值。
高一数学平面向量的概念及几何运算试题答案及解析
高一数学平面向量的概念及几何运算试题答案及解析1.下列说法正确的是（）.A．方向相同或相反的向量是平行向量B．零向量是C．长度相等的向量叫做相等向量D．共线向量是在一条直线上的向量【答案】B【解析】选项A:方向相同或相反的非零向量是平行向量；选项C：方向相同且长度相等的向量叫相等向量；选项D：共线向量所在直线可能重合，也可能平行；故选B.【考点】平面向量的有关概念.2.已知点A(－1,5)和向量,则点B的坐标为.【答案】（5,14）【解析】设B（m，n），∵点A（-1，5），∴=（m+1，n-5），∵由已知得，∴m+1=6且n-5=9，解之得m=5，n=14．即点B的坐标为（5，14）故答案为：（5，14）.【考点】平面向量的坐标运算．3.已知均为单位向量,它们的夹角为，那么（）A．B．C．D．4【答案】C【解析】因为且，所以，所以，因此，选C.【考点】1.平面向量的模；2．平面向量的数量积.4.在平行四边形ABCD中，下列结论中错误的是A．B．C．D．0【答案】C【解析】根据题意，由于向量的大小和方向相等就是相等向量，故成立，对于B，由于,对于D，，故排除法. 应该是,选C.【考点】向量的加减法点评：主要是考查了向量的加减法是运算，属于基础题。
5..【答案】【解析】【考点】向量加减法点评：利用相反向量可将向量减法运算转化为加法运算，向量加法运算首尾相接最终结果是由起点指向终点的向量6.以下说法错误的是（）A．零向量与任一非零向量平行B．零向量与单位向量的模不相等C．平行向量方向相同D．平行向量一定是共线向量【答案】C【解析】平行向量的方向相同或相反，所以，说法错误的是“平行向量方向相同”，选C。
【考点】本题主要考查向量的基础知识。
点评：简单题，确定说法错误的选项，应将各选项逐一考察。
7.下列命题正确的是A．若·=·，则=B．若，则·="0"C．若//，//，则//D．若与是单位向量，则·=1【答案】B【解析】解：因为选项A中不能约分，选项B中，两边平方可知成立，选项C中，当为零向量时不成立，选项D中，夹角不定，因此数量积结果不定，选B8.定义平面向量之间的一种运算“”如下：对任意的向量，令，给出下面四个判断：①若与共线，则；②若与垂直，则；③；④.其中正确的有（写出所有正确的序号）.【答案】①④【解析】①若,则,即,正确.②由①知错.③错.④,正确.9.已知O,A,B是平面上的三个点，直线AB上有一点C，满足,则（）A．B．C．D．【答案】B【解析】解：因为\选B10.如图，在平行四边形中，已知，，，为的中点，则【答案】【解析】解：因为运用平面向量的基本定理可知，,结合向量的数量积公式得到结论为11.下列各说法中，其中错误的个数为⑴向量的长度与向量的长度相等⑵平行向量就是向量所在直线平行⑶⑷ (5)A．2个B．3个C．4个D．5个【答案】C【解析】选C （1）正确(2)因为平行向量是向量所在直线平行或重合，所以此命题错误；（3）若向量,本命题是错误命题.（4）没有说明是非零向量，所以此命题也是错误的.（5）若再加上,才成立.因而此命题也是错误的.故错误命题共有四个.12.已知下列命题：①若向量∥，∥，则∥；②若＞，则＞；③若，则=或=；④在△中，若，则△是钝角三角形；⑤. 其中正确命题的个数是（）.A．0B．1C．2D．3【答案】A【解析】时①不正确；向量不能比较大小，②不正确；，③不正确；为锐角，不能判断△的形状，④不正确；，⑤不正确.13.已知平面向量，则向量（）A．B．C．D．【答案】D【解析】本题考查向量的坐标运算.若则.故选D14.已知四边形是菱形，点在对角线上（不包括），则（）A．B．C．D．【答案】A【解析】设，其中，则。
高中平面向量知识点详细归纳总结(附带练习)
向量的概念一、高考要求：理解有向线段及向量的有关概念,掌握求向量和与差的三角形法则和平行四边形法则,掌握向量加法的交换律和结合律.二、知识要点：1. 有向线段:具有方向的线段叫做有向线段,在有向线段的终点处画上箭头表示它的方向.以A 为始点,B 为终点的有向线段记作AB ,注意:始点一定要写在前面,已知AB ,线段AB 的长度叫做有向线段AB 的长(或模),AB 的长度记作AB ||.有向线段包含三个要素:始点、方向和长度.2. 向量:具有大小和方向的量叫做向量,只有大小和方向的向量叫做自由向量.在本章中说到向量,如不特别说明,指的都是自由向量.一个向量可用有向线段来表示,有向线段的长度表示向量的大小,有向线段的方向表示向量的方向.用有向线段AB 表示向量时,我们就说向量AB .另外,在印刷时常用黑体小写字母a 、b 、c 、…等表示向量;手写时可写作带箭头的小写字母a 、b 、c 、…等.与向量有关的概念有:(1) 相等向量:同向且等长的有向线段表示同一向量或相等的向量.向量a 和b 同向且等长,即a 和b 相等,记作a =b .(2) 零向量:长度等于零的向量叫做零向量,记作0.零向量的方向不确定.(3) 位置向量:任给一定点O 和向量a ,过点O 作有向线段OA a =,则点A 相对于点O 的位置被向量a 所唯一确定,这时向量a 又常叫做点A 相对于点O 的位置向量.(4) 相反向量:与向量a 等长且方向相反的向量叫做向量a 的相反向量,记作a -.显然,()0a a +-=.(5) 单位向量:长度等于1的向量,叫做单位向量,记作e .与向量a 同方向的单位向量通常记作0a ,容易看出:0a a a =│ │. (6) 共线向量(平行向量):如果表示一些向量的有向线段所在的直线互相平行或重合,即这些向量的方向相同或相反,则称这些向量为共线向量(或平行向量).向量a 平行于向量b ,记作a ∥b .零向量与任一个向量共线(平行).三、典型例题：例:在四边形ABCD 中,如果AB DC =且AB BC =│ │ │ │ ,那么四边形ABCD 是哪种四边形? 四、归纳小结：1. 用位置向量可确定一点相对于另一点的位置,这是用向量研究几何的依据.2. 共线向量(平行向量)可能有下列情况: (1)有一个为零向量;(2)两个都为零向量;(3)方向相同,模相等(即相等向量);(4)方向相同,模不等;(5)方向相反,模相等;(6)方向相反,模不等.五、基础知识训练：（一）选择题：1. 下列命题中: (1)向量只含有大小和方向两个要素. (2)只有大小和方向而无特定的位置的向量叫自由向量. (3)同向且等长的有向线段表示同一向量或相等的向量. (4)点A 相对于点B 的位置向量是BA . 正确的个数是( )A.1个B.2个C.3个D.4个2. 设O 是正△ABC 的中心,则向量,,AO OB OC 是( )A.有相同起点的向量B.平行向量C.模相等的向量D.相等向量3. a b =的充要条件是( )A.a b =│ │ │ │ B.a b =│ │ │ │ 且a b ∥ []l C.a b ∥ D.a b =│ │ │ │ 且a 与b 同向 4. AA BB ''=是四边形ABB A ''是平行四边形的( )A.充分条件B.必要条件C.充要条件D.既非充分又非必要条件5. 依据下列条件,能判断四边形ABCD 是菱形的是( )A.AD BC =B.AD BC ∥且AB CD ∥C.AB DC =且AB AD =│ │ │ │ D.AB DC =且AD BC = 6. 下列关于零向量的说法中,错误的是( )A.零向量没有方向B.零向量的长度为0C.零向量与任一向量平行D.零向量的方向任意7. 设与已知向量a 等长且方向相反的向量为b ,则它们的和向量a b +等于( )A.0B.0C.2aD.2b（二）填空题：8. 下列说法中: (1)AB 与BA 的长度相等 (2)长度不等且方向相反的两个向量不一定共线 (3)两个有共同起点且相等的向量,终点必相同(4)长度相等的两个向量必共线。
平面向量知识点+例题+练习+答案
五、平面向量1．向量的概念①向量 既有大小又有方向的量。
向量的大小即向量的模（长度），记作|AB |即向量的大小，记作｜a |。
向量不能比较大小，但向量的模可以比较大小。
向量表示方法：（1）几何表示法：用带箭头的有向线段表示，如AB ，注意起点在前，终点在后；（2）符号表示法：用一个小写的英文字母来表示，如a ，b ，c 等；（3）坐标表示法：在平面内建立直角坐标系，以与x 轴、y 轴方向相同的两个单位向量i ，j 为基底，则平面内的任一向量a 可表示为(),a xi y j x y =+=，称(),x y 为向量a 的坐标，a ＝(),x y 叫做向量a 的坐标表示。
如果向量的起点在原点，那么向量的坐标与向量的终点坐标相同。
向量和数量的区别：向量常用有向线段来表示，注意不能说向量就是有向线段，为什么？（向量可以平移）。
如已知A （1,2），B （4,2），则把向量AB 按向量a ＝（－1,3）平移后得到的向量是_____（答：（3,0））②零向量长度为0的向量，记为0 ，其方向是任意的，0 与任意向量平行零向量a ＝0 ⇔｜a ｜＝0。
由于0的方向是任意的，且规定0平行于任何向量，故在有关向量平行（共线）的问题中务必看清楚是否有“非零向量”这个条件。
（注意与0的区别）③单位向量 模为1个单位长度的向量，向量0a 为单位向量⇔｜0a ｜＝1。
(与AB 共线的单位向量是||AB AB ±)；④平行向量（共线向量）方向相同或相反的非零向量。
任意一组平行向量都可以移到同一直线上，方向相同或相反的向量，称为平行向量，记作a ∥b ，规定零向量和任何向量平行。
由于向量可以进行任意的平移(即自由向量)，平行向量总可以平移到同一直线上，故平行向量也称为共线向量。
提醒：①相等向量一定是共线向量，但共线向量不一定相等；②两个向量平行与与两条直线平行是不同的两个概念：两个向量平行包含两个向量共线, 但两条直线平行不包含两条直线重合；③平行向量无传递性！（因为有0)；④三点A B C 、、共线⇔ AB AC 、共线；数学中研究的向量是自由向量，只有大小、方向两个要素，起点可以任意选取，现在必须区分清楚共线向量中的“共线”与几何中的“共线”、的含义，要理解好平行向量中的“平行”与几何中的“平行”是不一样的。
(精选试题附答案)高中数学第六章平面向量及其应用知识点总结归纳
(名师选题)（精选试题附答案）高中数学第六章平面向量及其应用知识点总结归纳单选题1、△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知a sin A －b sin B =4c sin C ，cos A =－14，则bc = A ．6B ．5C ．4D ．3 答案：A分析：利用余弦定理推论得出a ，b ，c 关系，在结合正弦定理边角互换列出方程，解出结果. 详解：由已知及正弦定理可得a 2−b 2=4c 2，由余弦定理推论可得 −14=cosA =b 2+c 2−a 22bc , ∴c 2−4c 22bc=−14 , ∴3c 2b =14 , ∴b c =32×4=6，故选A ．小提示：本题考查正弦定理及余弦定理推论的应用．2、已知向量a ⃑，b ⃑⃑满足|a ⃑|=√3，|b ⃑⃑|=2，且a ⃑⊥(a ⃑−b ⃑⃑)，则a ⃑与b ⃑⃑的夹角为（ ） A ．30°B ．60°C ．120°D ．150° 答案：A分析：利用数量积的定义，即可求解.解：a ⃑⊥(a ⃑−b ⃑⃑),所以a ⃑⋅(a ⃑−b⃑⃑)=0,即|a →|2−|a →||b →|cos <a →,b →>=0， 解得cos <a →,b →>=√32,又因为向量夹角的范围为[0°,180°]，则a ⃑与b ⃑⃑的夹角为30°，故选：A.3、向量PA ⃑⃑⃑⃑⃑⃑=(k,12)，PB ⃑⃑⃑⃑⃑⃑=(4,5)，PC ⃑⃑⃑⃑⃑⃑=(10,k)．若A,B,C 三点共线，则k 的值为（ ） A ．−2B ．1C ．−2或11D ．2或−11答案：C分析：求得BA⃑⃑⃑⃑⃑⃑，CA ⃑⃑⃑⃑⃑⃑，利用向量共线的充要条件，可得关于k 的方程，求解即可. 解：由题可得：BA⃑⃑⃑⃑⃑⃑=PA ⃑⃑⃑⃑⃑⃑−PB ⃑⃑⃑⃑⃑⃑=(k,12)−(4,5)=(k −4,7)， CA⃑⃑⃑⃑⃑⃑=PA ⃑⃑⃑⃑⃑⃑−PC ⃑⃑⃑⃑⃑⃑=(k,12)−(10,k )=(k −10,12−k ). 因为A,B,C 三点共线，所以BA ⃑⃑⃑⃑⃑⃑∥CA ⃑⃑⃑⃑⃑⃑，所以(k −4)(12−k )−7(k −10)=0，整理得k 2−9k −22=0，解得k =−2或k =11. 故选：C.4、在△ABC 中，已知B =120°，AC =√19，AB =2，则BC =（ ） A ．1B ．√2C ．√5D ．3 答案：D分析：利用余弦定理得到关于BC 长度的方程，解方程即可求得边长. 设AB =c,AC =b,BC =a ，结合余弦定理：b 2=a 2+c 2−2accosB 可得：19=a 2+4−2×a ×c ×cos120∘， 即：a 2+2a −15=0，解得：a =3（a =−5舍去）， 故BC =3. 故选：D.小提示：利用余弦定理及其推论解三角形的类型： (1)已知三角形的三条边求三个角；(2)已知三角形的两边及其夹角求第三边及两角； (3)已知三角形的两边与其中一边的对角，解三角形．5、魏晋时刘徽撰写的《海岛算经》是有关测量的数学著作，其中第一题是测海岛的高．如图，点E ，H ，G 在水平线AC 上，DE 和FG 是两个垂直于水平面且等高的测量标杆的高度，称为“表高”，EG 称为“表距”，GC 和EH 都称为“表目距”，GC 与EH 的差称为“表目距的差”则海岛的高AB =（ ）A．表高×表距表目距的差+表高B．表高×表距表目距的差−表高C．表高×表距表目距的差+表距D．表高×表距表目距的差−表距答案：A分析：利用平面相似的有关知识以及合分比性质即可解出．如图所示：由平面相似可知，DEAB =EHAH,FGAB=CGAC，而DE=FG，所以DE AB =EHAH=CGAC=CG−EHAC−AH=CG−EHCH，而CH=CE−EH=CG−EH+EG，即AB=CG−EH+EGCG−EH ×DE=EG×DECG−EH+DE＝表高×表距表目距的差+表高．故选：A.小提示：本题解题关键是通过相似建立比例式，围绕所求目标进行转化即可解出．6、已知向量a⃑=(−1,m)，b⃑⃑=(2,4)，若a⃑与b⃑⃑共线，则m=（）A．−1B．1C．−2D．2答案：C分析：根据平面向量共线坐标表示可得答案.由题意得2m=−4，即m=−2.故选：C7、在正方形ABCD 中，BC ⃑⃑⃑⃑⃑⃑−DC ⃑⃑⃑⃑⃑⃑+AB ⃑⃑⃑⃑⃑⃑=（ ） A ．BD ⃑⃑⃑⃑⃑⃑⃑B ．DB ⃑⃑⃑⃑⃑⃑⃑C ．AD ⃑⃑⃑⃑⃑⃑D ．DA ⃑⃑⃑⃑⃑⃑ 答案：C分析：根据平面向量加减运算法则计算可得.解：BC ⃑⃑⃑⃑⃑⃑−DC ⃑⃑⃑⃑⃑⃑+AB ⃑⃑⃑⃑⃑⃑=BC ⃑⃑⃑⃑⃑⃑+CD ⃑⃑⃑⃑⃑⃑+AB ⃑⃑⃑⃑⃑⃑=BD ⃑⃑⃑⃑⃑⃑⃑+AB ⃑⃑⃑⃑⃑⃑=AD ⃑⃑⃑⃑⃑⃑. 故选：C.8、已知边长为1的正方形ABCD ，设AB ⃑⃑⃑⃑⃑⃑=a ⃑，AD ⃑⃑⃑⃑⃑⃑=b ⃑⃑，AC ⃑⃑⃑⃑⃑⃑=c ⃑，则|a ⃑−b ⃑⃑+c ⃑|=（ ） A ．1B ．2C ．3D ．4 答案：B分析：根据向量加法的平行四边形法则，结合正方形的性质可得答案. 因为ABCD 是边长为1的正方形，AB ⃑⃑⃑⃑⃑⃑=a ⃑,AD ⃑⃑⃑⃑⃑⃑=b ⃑⃑,AC ⃑⃑⃑⃑⃑⃑=c ⃑， 所以a ⃑−b ⃑⃑+c ⃑=AB ⃑⃑⃑⃑⃑⃑−AD ⃑⃑⃑⃑⃑⃑+AC ⃑⃑⃑⃑⃑⃑=AB ⃑⃑⃑⃑⃑⃑−AD ⃑⃑⃑⃑⃑⃑+(AB ⃑⃑⃑⃑⃑⃑+AD ⃑⃑⃑⃑⃑⃑)=2AB ⃑⃑⃑⃑⃑⃑ 又|AB ⃑⃑⃑⃑⃑⃑|=1，所以|a ⃑−b ⃑⃑+c ⃑|=|2AB ⃑⃑⃑⃑⃑⃑|=2 故选：B9、已知非零平面向量a ⃗，b ⃑⃗，c ⃗，下列结论中正确的是（ ） （1）若a ⃗⋅c ⃗=b ⃑⃗⋅c ⃗，则a ⃗=b ⃑⃗；（2）若|a ⃗+b ⃑⃗|=|a ⃗|+|b ⃑⃗|，则a ⃗//b⃑⃗ （3）若|a ⃗+b ⃑⃗|=|a ⃗−b ⃑⃗|，则a ⃗⊥b ⃑⃗（4）若(a ⃗+b ⃑⃗)⋅(a ⃗−b ⃑⃗)=0，则a ⃗=b ⃑⃗或a ⃗=−b ⃑⃗ A ．（1）（2）B ．（2）（3）C ．（3）（4）D ．（2）（3）（4） 答案：B解析：根据向量的数量积运算，以及向量模的计算公式，逐项判断，即可得出结果. 已知非零平面向量a ⃗，b ⃑⃗，c ⃗，（1）若a⃗⋅c⃗=b⃑⃗⋅c⃗，则(a⃗−b⃑⃗)⋅c⃗=0，所以a⃗=b⃑⃗或(a⃗−b⃑⃗)⊥c⃗，即（1）错；（2）若|a⃗+b⃑⃗|=|a⃗|+|b⃑⃗|，则a⃗与b⃑⃗同向，所以a⃗//b⃑⃗，即（2）正确；（3）若|a⃗+b⃑⃗|=|a⃗−b⃑⃗|，则|a⃗|2+|b⃑⃗|2+2a⃗⋅b⃑⃗=|a⃗|2+|b⃑⃗|2−2a⃗⋅b⃑⃗，所以2a⃗⋅b⃑⃗=0，则a⃗⊥b⃑⃗；即（3）正确；（4）若(a⃗+b⃑⃗)⋅(a⃗−b⃑⃗)=0，则|a⃗|2−|b⃑⃗|2=0，所以|a⃗|=|b⃑⃗|，不能得出向量共线，故（4）错；故选：B.小提示：本题主要考查向量数量积的运算，考查向量有关的判定，属于基础题型.10、已知不共线的平面向量a⃗,b⃑⃗,c⃗两两所成的角相等，且|a⃗|=1,|b⃑⃗|=4,|a⃗+b⃑⃗+c⃗|=√7，则|c⃗|=（）A．√2B．2C．3D．2或3答案：D分析：先求出θ=2π3，转化|a⃗+b⃑⃗+c⃗|=√(a⃗+b⃑⃗+c⃗)2=√7，列方程即可求出.由不共线的平面向量a⃗，b⃑⃑，c⃑两两所成的角相等，可设为θ，则θ=2π3.设|c⃑|=m.因为|a⃗|=1，|b⃑⃗|=4，|a⃗+b⃑⃗+c⃗|=√7，所以|a⃗+b⃑⃗+c⃗|2=7，即a⃗2+2a⃗⋅b⃑⃗+b⃑⃗2+2b⃑⃗⋅c⃗+2a⃗⋅c⃗+c⃗2=7，所以12+2×1×4cos2π3+42+2×4×mcos2π3+2×1×mcos2π3+m2=7即m2−5m+6=0，解得：m=2或3.所以|c⃑|=2或3故选：D填空题11、已知向量a⃑=(3,1),b⃑⃑=(1,0),c⃑=a⃑+kb⃑⃑．若a⃑⊥c⃑，则k=________．答案：−103.分析：利用向量的坐标运算法则求得向量c⃗的坐标，利用向量的数量积为零求得k的值∵a ⃗=(3,1),b ⃑⃗=(1,0),∴c ⃗=a ⃗+kb ⃑⃗=(3+k,1), ∵a ⃗⊥c ⃗,∴a ⃗⋅c ⃗=3(3+k )+1×1=0，解得k =−103, 所以答案是：−103.小提示：本题考查平面向量的坐标运算，平面向量垂直的条件，属基础题，利用平面向量p ⃗=(x 1,y 1),q ⃗=(x 2,y 2)垂直的充分必要条件是其数量积x 1x 2+y 1y 2=0.12、若向量a →=(1，1)与向量b →=(1，x )的夹角为锐角，则x 的取值范围是___________. 答案：(−1,1)∪(1,+∞)解析：设向量a →与向量b →的夹角为θ，由cosθ=a⃑⃗⋅b ⃑⃗|a⃑⃗||b ⃑⃗|=√2×√1+x 2,.设向量a →与向量b →的夹角为θ，则cosθ=a⃑⃗⋅b ⃑⃗|a⃑⃗||b ⃑⃗|=√2×√1+x 2因为夹角为锐角， 所以0<cos θ<1，即 0<√2×√1+x 2<1，所以x >−1 且(1+x)2<2(1+x 2), 解得 −1<x <1 或 x >1， 所以答案是：(−1,1)∪(1,+∞)13、已知向量a ⃗,b ⃑⃗的夹角为120°，|a ⃗|=2,|b ⃑⃗|=1，若(a ⃗+3b ⃑⃗)⊥(2a ⃗+λb ⃑⃗)，则实数λ=___________. 答案：−1分析：由(a ⃗+3b ⃑⃗)⊥(2a ⃗+λb ⃑⃗)，可得(a ⃗+3b ⃑⃗)⋅(2a ⃗+λb ⃑⃗)=0，化简后结已知条件可求得答案 解：因为向量a ⃗,b ⃑⃗的夹角为120°，|a ⃗|=2,|b ⃑⃗|=1，且(a ⃗+3b ⃑⃗)⊥(2a ⃗+λb ⃑⃗)， 所以(a ⃗+3b ⃑⃗)⋅(2a ⃗+λb ⃑⃗)=0，即2a ⃗2+(6+λ)a ⃗⋅b ⃑⃗+3λb ⃑⃗2=0， 所以8+(6+λ)×2×1×(−12)+3λ=0，解得λ=−1， 所以答案是：−114、已知点A (3,−4)与B (−1,2)，点P 在直线AB 上，且|AP ⃑⃑⃑⃑⃑⃑|=|PB ⃑⃑⃑⃑⃑⃑|，则点P 的坐标为________． 答案：(1,−1)分析：根据模长相等关系可确定P 为线段AB 中点，由中点坐标公式计算得到结果. ∵P 在直线AB 上，且|AP⃑⃑⃑⃑⃑⃑|=|PB ⃑⃑⃑⃑⃑⃑|，∴P 为线段AB 中点， 又A (3,−4)，B (−1,2)，∴P (1,−1). 所以答案是：(1,−1).15、已知|b ⃑⃑|=3，向量a ⃑在向量b ⃑⃑上的投影向量为2b ⃑⃑，则a ⃑·b ⃑⃑＝____________. 答案：18解析：由题意向量a ⃑在向量b ⃑⃑上的投影向量为2b ⃑⃑，分析可得|a ⃑|cos <a ⃑,b ⃑⃑>=2|b ⃑⃑|，代入公式，即可得答案. 因为向量a ⃑在向量b ⃑⃑上的投影向量为2b ⃑⃑，则可得|a ⃑|cos <a ⃑,b ⃑⃑>=2|b ⃑⃑|， 所以a ⃑·b ⃑⃑=|a ⃑||b ⃑⃑|cos <a ⃑,b ⃑⃑>=2|b ⃑⃑|·|b ⃑⃑|=2|b ⃑⃑|2=18， 所以答案是：18.小提示：本题考查向量投影的应用，考查分析理解的能力，属基础题. 解答题16、已知函数f (x )=2cosxsin (x +π6).（1）求f (x )的最小正周期及f (x )在区间[−π6,π4]上的最大值（2）在锐角△ABC 中，f （A 2）=32，且a =√3，求b +c 取值范围.答案：（1）最小正周期为π，最大值32；（2）(3,2√3].分析：（1）先利用三角恒等变换对函数进行化简，进而通过三角函数的图像和性质的应用得到答案； （2）利用正弦定理进行边化角，然后借助三角恒等变换进行化简，最后通过三角函数的图像和性质的应用求出结果.（1）f(x)=2cosx ⋅(sinx ⋅√32+cosx ⋅12) =√32sin2x +1+cos2x2=sin(2x +π6)+12，所以f (x )的最小正周期为π.因为−π6≤x ≤π4，所以−π6≤2x +π6≤2π3于是，当2x +π6=π2，即x =π6时，f (x )取得最大值32（2）在△ABC 中，A +B +C =πf(A2)=sin(A +π6)+12=32，∴sin(A +π6)=1，A ∈(0,π2),∴A +π6∈(π6,23π)，∴A +π6=π2,∴A =π3.由正弦定理asinA=b sinB=c sinC=2，∴b =2sinB,c =2sinC ，∴b +c =2sinB +2sinC =2sinB +2sin (A +B )=2sinB +2sin (π3+B)=2sinB +√3cosB +sinB =3sinB +√3cosB =2√3sin(B +π6)，∵{0<B <π20<C <π2⇒{0<B <π20<23π−B <π2⇒π6<B <π2，∴B +π6∈(π3,2π3)，∴sin(B +π6)∈(√32,1]， ∴b +c =2√3sin(B +π6)∈(3,2√3].17、平面内给定三个向量a ⃗=(3,2)，b ⃑⃗=(−1,2)，c ⃗=(4,1). （1）求满足a ⃗=mb ⃑⃗−nc ⃗的实数m ，n ； （2）若(a ⃗+kc ⃗)//(2b ⃑⃗−a ⃗)，求实数k 的值. 答案：（1）m =59，n =−89；（2）k =−1613.分析：（1）依题意求出mb ⃑⃗−nc ⃗的坐标，再根据向量相等得到方程组，解得即可； （2）首先求出a ⃗+kc ⃗与2b ⃑⃗−a ⃗的坐标，再根据向量共线的坐标表示计算可得； 解：（1）因为a ⃗=(3,2)，b ⃑⃗=(−1,2)，c ⃗=(4,1)，且a ⃗=mb ⃑⃗−nc ⃗ (3，2)=a ⃗=mb ⃑⃗−nc ⃗=m(−1，2)−n(4，1)=(−m −4n ，2m −n).∴ {−m −4n =32m −n =2，解得m =59，n =−89.（2）a ⃗+kc ⃗=(3，2)+k(4，1)=(3+4k ，2+k). 2b ⃑⃗−a ⃗=2(−1，2)−(3，2)=(−5，2). ∴−5(2+k)−2(3+4k)=0，解得k =−1613.18、如图，已知ΔABC 中，D 为BC 的中点，AE =12EC ，AD ，BE 交于点F ，设AC ⃑⃑⃑⃑⃑⃑=a ⃑，AD ⃑⃑⃑⃑⃑⃑=b⃑⃑．（1）用a ⃑,b ⃑⃑分别表示向量AB ⃑⃑⃑⃑⃑⃑，EB ⃑⃑⃑⃑⃑⃑； （2）若AF⃑⃑⃑⃑⃑⃑=tAD ⃑⃑⃑⃑⃑⃑，求实数t 的值． 答案：（1）AB ⃑⃑⃑⃑⃑⃑=2b ⃑⃑−a ⃑，EB ⃑⃑⃑⃑⃑⃑=−43a ⃑+2b⃑⃑；（2）t =12． 解析：（1）根据向量线性运算，结合线段关系，即可用a ⃑,b ⃑⃑分别表示向量AB ⃑⃑⃑⃑⃑⃑，EB ⃑⃑⃑⃑⃑⃑； （2）用a ⃑,b ⃑⃑分别表示向量FB ⃑⃑⃑⃑⃑⃑，EB⃑⃑⃑⃑⃑⃑，由平面向量共线基本定理，即可求得t 的值. （1）由题意，D 为BC 的中点，AE =12EC ，可得AE ⃑⃑⃑⃑⃑⃑=13AC ⃑⃑⃑⃑⃑⃑，AC ⃑⃑⃑⃑⃑⃑=a ⃑，AD ⃑⃑⃑⃑⃑⃑=b ⃑⃑． ∵AB ⃑⃑⃑⃑⃑⃑+AC ⃑⃑⃑⃑⃑⃑=2AD ⃑⃑⃑⃑⃑⃑， ∴AB ⃑⃑⃑⃑⃑⃑=2b ⃑⃑−a ⃑， ∴EB ⃑⃑⃑⃑⃑⃑=AB ⃑⃑⃑⃑⃑⃑–AE⃑⃑⃑⃑⃑⃑ =2b ⃑⃑−a ⃑−13a ⃑=−43a ⃑+2b⃑⃑ （2）∵AF ⃑⃑⃑⃑⃑⃑=tAD ⃑⃑⃑⃑⃑⃑=tb ⃑⃑， ∴FB ⃑⃑⃑⃑⃑⃑=AB ⃑⃑⃑⃑⃑⃑–AF ⃑⃑⃑⃑⃑⃑ =−a ⃑+(2−t )b⃑⃑∵EB ⃑⃑⃑⃑⃑⃑=−43a ⃑+2b ⃑⃑，FB ⃑⃑⃑⃑⃑⃑，EB⃑⃑⃑⃑⃑⃑共线， 由平面向量共线基本定理可知满足−1−43=2−t 2，解得t =12．小提示：本题考查了平面向量的线性运算，平面向量共线基本定理的应用，属于基础题. 19、在△ABC 中，角A 、B 、C 的对边分别为a ，b ，c.已知a =√6,b =2c,cosA =−14. (1)求c 的值； (2)求sinB 的值； (3)求sin(2A −B)的值. 答案：(1)c =1(2)sinB =√104(3)sin(2A −B)=√108分析：（1）根据余弦定理a 2=b 2+c 2−2bccosA 以及b =2c 解方程组即可求出； （2）由（1）可求出b =2，再根据正弦定理即可解出；（3）先根据二倍角公式求出sin2A,cos2A ，再根据两角差的正弦公式即可求出．（1）因为a 2=b 2+c 2−2bccosA ，即6=b 2+c 2+12bc ，而b =2c ，代入得6=4c 2+c 2+c 2，解得：c =1． （2）由（1）可求出b =2，而0<A <π，所以sinA =√1−cos 2A =√154，又a sinA=b sinB ，所以sinB =bsinA a=2×√154√6=√104． （3）因为cosA =−14，所以π2<A <π，故0<B <π2，又sinA =√1−cos 2A =√154， 所以sin2A =2sinAcosA =2×(−14)×√154=−√158，cos2A =2cos 2A −1=2×116−1=−78，而sinB =√104，所以cosB =√1−sin 2B =√64， 故sin(2A −B)=sin2AcosB −cos2AsinB =(−√158)×√64+78×√104=√108．。
第6讲 平面向量等和线定理求系数和问题(解析版) 高一数学讲义(新人教2019)必修二
第6讲平面向量等和线定理求系数和问题【考点分析】考点一：平面向量等和线问题①平面向量共线定理则,,A B C 三点共线，O 为直线外一点，则OA OB OC λμ=+ 且1λμ+=⇔,,A B C 三点共线。
②平面向量等和线问题如图：B A ,两点共线，若O 为直线AB 外一点，MN 为与AB平行的直线，若k =，点P 为MN 上一点，若OB OA OP μλ+=，则k =+μλ。
证明如下：因为MN 与AB平行，所以k ==，所以ON kOB OM k OA 1,1==，所以ON k OM k OB OA OP μλμλ+=+=，因为P N M ,,三点共线，所以1=+kk μλ，所以k =+μλ③利用等和线解题的步骤第一步：确定系数和为1的直线；第二步：平移该直线，结合题目给出动点范围，分析在何处取得最值；第三步：从长度比，点的位置的角度计算最值。
【典型例题】题型一：平面向量等和线求系数和问题【例1】如图，在矩形ABCD 中，1AB =，2AD =，动点P 在以点C 为圆心且与BD 相切的圆上，若满足AP mAB nAD =+ ，则n m +的最大值为（）A ．3B ．22C ．5D ．2【答案】A【解析】法一：如图：以A 为原点，以AB ，AD 所在的直线为x ，y 轴建立如图所示的坐标系，则(0,0)A ，(1,0)B ，(0,2)D ，(1,2)C ， 动点P 在以点C 为圆心且与BD 相切的圆上，设圆的半径为r ，2BC = ，1CD =，22215BD ∴+=∴1122BC CD BD r = ，5r ∴=∴圆的方程为224(1)(2)5x y -+-=，设点P 的坐标为25(15θ+252)5θ+， AP AB AD λμ=+ ，25(15θ∴+，25sin 2)(15θλ+=，0)(0μ+，2)(λ=，2)μ，∴2515θλ+=，5225θμ+=，2552sin()255λμθθθϕ∴+=++=++，其中tan 2ϕ=，∵1)sin(1≤+≤-ϕθ，∴31≤+≤μλ，故λμ+的最大值为3，故选A ．法二：由等和线性质知：APAP AD AN n m 1==+，所以当1P 在如图所示位置时，n m +取得最大值，33==+rr n m 【例2】如图，边长为2的等边三角形的外接圆为圆O ，P 为圆O 上任一点，若AP xAB yAC =+ ，则22x y+的最大值为（）A ．83B ．2C ．43D ．1【答案】A【详解】作BC 的平行线与圆相交于点P ，与直线AB 相交于点E ，与直线AC 相交于点F ，设AP AE AF λμ=+ ，则1λμ+=，∵BC//EF ，∴设AE AF k AB AC ==，则4[0,]3k ∈∴,AE k AB AF k AC == ，AP AE AF k AB k AC λμλμ=+=+ ∴,x k y kλμ==∴22x y=+8223k k λμ+=≤（）故选：A.【例3】在ABC 中，M 为BC 边上任意一点，N 为线段AM 上任意一点，若AN AB AC λμ=+ （λ，μ∈R ），则λμ+的取值范围是（）A ．10,3⎡⎤⎢⎥⎣⎦B ．11,32⎡⎤⎢⎥⎣⎦C ．[0,1]D ．[1,2]【答案】C【解析】【分析】设AN t AM = ，()01t ≤≤，当0=t 时，可得0λμ==，从而有0λμ+=；当01t <≤时，有B A A M AC t tλμ=+ ，根据M 、B 、C 三点共线，可得1t tl m +=，进而可得(]0,1t λμ+=∈，从而即可求解.【详解】解：由题意，设AN t AM = ，()01t ≤≤，当0=t 时，0AN = ，所以0AB AC λμ+= ，所以0λμ==，从而有0λμ+=；当01t <≤时，因为AN AB AC λμ=+ （λ，μ∈R ），所以B t A A A M C λμ=+ ，即B A A M AC t tλμ=+ ，因为M 、B 、C 三点共线，所以1t t l m +=，即(]0,1t λμ+=∈.综上，λμ+的取值范围是[0,1].故选：C.【例4】如图，已知点P 在由射线OD 、线段OA ，线段BA 的延长线所围成的平面区域内（包括边界），且OD与BA 平行，若OP xOB yOA =+ ，当12x =-时，y 的取值范围是（）A ．[]0,1B ．1,12⎡⎤-⎢⎥⎣⎦C ．13,22⎡⎤-⎢⎣⎦D ．13,22⎡⎤⎢⎥⎣⎦【答案】D【解析】【分析】根据向量加法的平行四边形法则，OP 为平行四边形的对角线，该四边形应是以OA 与OB 的反向延长线为两邻边，当12x =-时，要使P 点落在指定区域内，即P 点应落在EF 上，得到y 的取值范围.【详解】∵//OD AB ，OP xOA yOB =+uuu r uur uuu r ，由向量加法的平行四边形法则，OP 为平行四边形的对角线，该四边形应是以OA 与OB 的反向延长线为两邻边，∴当12x =-时，要使P 点落在指定区域内，即P 点应落在EF 上，13,22CE OA CF OA ==，∴y 的取值范围为1322⎡⎤⎢⎥⎣⎦，.故选：D.【例5】在扇形OAB 中，60AOB ∠=，C 为弧AB 上的一动点，若OC xOA yOB =+ ，则3x y +的取值范围是_________．【答案】[]1,3【解析】【分析】以O 为原点，,OA OB 分别为x ，y 轴正方向建立平面直角坐标系.向量坐标化进行坐标运算，利用三角函数求出3x y +的取值范围.【详解】以O 为原点，,OA OB 分别为x ，y 轴正方向建立平面直角坐标系.则()11,0,22OA OB ⎛== ⎝⎭.不妨设()cos ,sin ,03OC πθθθ⎛⎫=≤≤ ⎪⎝⎭ .因为OC xOA yOB =+，所以1cos 2sin 2x y y θθ⎧=+⎪⎪⎨⎪=⎪⎩，解得：cos sin 33x y θθθ⎧=-⎪⎪⎨⎪=⎪⎩，所以s 3co 3in x y θθ-+=.因为cos y θ=在0,3πθ⎡⎤∈⎢⎥⎣⎦上单调递减，sin y θ=-在0,3πθ⎡⎤∈⎢⎣⎦上单调递减，所以s 3co 3in 3x y θθ-+=在0,3πθ⎡⎤∈⎢⎥⎣⎦上单调递减.所以当0θ=时33x y +=最大；当3πθ=时cos sin 1333332x y ππ===+最小.所以3x y +的取值范围是[]1,3.故答案为：[]1,3.【题型专练】1.在直角ABC 中，AB AC ⊥，2AB AC ==，以BC 为直径的半圆上有一点M （包括端点），若AM AB AC λμ=+ ，则λμ+的最大值为（）A ．4BC ．2D【答案】C【解析】【分析】建立平面直角坐标系，利用坐标表示M ，结合三角函数最值的求法，求得λμ+的最大值.【详解】依题意在直角ABC 中，AB AC ⊥，2AB AC ==，以A 为原点建立如图所示平面直角坐标系，()()0,2,2,0C B ，设D 是BC 的中点，则()1,1D .。
高一数学平面向量知识点及典型例题解析
高一数学 第八章 平面向量第一讲 向量的概念与线性运算 一．【要点精讲】 1．向量的概念①向量：既有大小又有方向的量。
几何表示法AB ，a ；坐标表示法),(y x j y i x a =+= 。
向量的模（长度），记作|AB |.即向量的大小，记作｜a|。
向量不能比较大小，但向量的模可以比较大小.②零向量：长度为0的向量，记为0，其方向是任意的，规定0平行于任何向量。
（与0的区别） ③单位向量｜a｜＝1。
④平行向量（共线向量）方向相同或相反的非零向量，记作a ∥b⑤相等向量记为b a=。
大小相等，方向相同),(),(2211y x y x =⎩⎨⎧==⇔2121y y x x 2．向量的运算（1）向量加法：求两个向量和的运算叫做向量的加法.如图，已知向量a ，b ，在平面内任取一点A ，作AB =a ，BC =b ，则向量叫做a 与b的和，记作a+b ，即 a+b AB BC AC =+=特殊情况：(1)BBabba +AABC C)2()3(向量加法的三角形法则可推广至多个向量相加：AB BC CD PQ QR AR +++++=，但这时必须“首尾相连”。
②向量减法： 同一个图中画出a b a b +-、要点:向量加法的“三角形法则”与“平行四边形法则”（1）用平行四边形法则时，两个已知向量是要共始点的，和向量是始点与已知向量的始点重合的那条对角线，而差向量是另一条对角线，方向是从减向量指向被减向量。
（2） 三角形法则的特点是“首尾相接”，由第一个向量的起点指向最后一个向量的终点的有向线段就表示这些向量的和；差向量是从减向量的终点指向被减向量的终点. （3）实数与向量的积3．两个向量共线定理：向量b 与非零向量a共线⇔有且只有一个实数λ，使得b =a λ。
二．【典例解析】题型一： 向量及与向量相关的基本概念概念 例1判断下列各命题是否正确(1)零向量没有方向 (2)ba ==则 (3)单位向量都相等 (4) 向量就是有向线段(5)两相等向量若共起点,则终点也相同 (6)若b a =，c b =，则c a =；(7)若b a //，c b //，则c a// (8) b a =的充要条件是||||b a =且b a //；(9) 若四边形ABCD 是平行四边形,则DA BC CD B ==,A练习. (四川省成都市一诊)在四边形ABCD 中，“AB →＝2DC →”是“四边形ABCD 为梯形”的 A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分也不必要条件题型二: 考查加法、减法运算及相关运算律 例2 化简)()(BD AC CD AB ---=练习1.下列命题中正确的是 A ．OA OB AB -= B ．0AB BA +=C ．00AB ⋅=D ．AB BC CD AD ++=2.化简AC -BD +CD -AB 得 A ．AB B ．DA C ． D ．03．如图，D 、E 、F 分别是△ABC 的边AB 、BC 、CA 的中点，则( )A.AD →＋BE →＋CF →＝0B.BD →－CF →＋DF →＝0C.AD →＋CE →－CF →＝0D.BD →－BE →－FC →＝0题型三: 结合图型考查向量加、减法例3在ABC ∆所在的平面上有一点P ，满足PA PB PC AB ++=，则PBC ∆与ABC ∆的面积之比是( )A ．13B ．12C ．23D ．34例4重心、垂心、外心性质练习: 1．如图，在ΔABC 中，D 、E 为边AB 的两个三等分点，CA →=3a ，CB → =2b ，求CD → ，CE → ． 2已知a b a b+-=求证a b ⊥3若O 为ABC ∆的内心，且满足()(2)0OB OC OB OC OA -⋅+-=，则ABC ∆的形状为（ ）A.等腰三角形B.正三角形C.直角三角形D.钝角三角形4．已知O 、A 、B 是平面上的三个点，直线AB 上有一点C ，满足2AC →＋CB →＝0，则OC →＝( ) A ．2OA →－OB → B ．－OA →＋2OB →C.23OA →－13OB → D ．－13OA →＋23OB → 5．已知平面上不共线的四点O ，A ，B ，C .若OA →－3OB →＋2OC →＝0，则|AB →||BC →|等于________．6．已知平面内有一点P 及一个△ABC ，若PA →＋PB →＋PC →＝AB →，则( )A ．点P 在△ABC 外部B ．点P 在线段AB 上C ．点P 在线段BC 上D ．点P 在线段AC 上ABDE7．在△ABC 中，已知D 是AB 边上一点，若AD →＝2DB →，CD →＝13CA →＋λCB →，则λ等于( ) A.23 B.13 C ．－13 D ．－23 题型四: 三点共线问题例 4 设21,e e 是不共线的向量,已知向量2121212,3,2e e e e e k e -=+=+=,若A,B,D 三点共线,求k 的值例5已知A 、B 、C 、P 为平面内四点， A 、B 、C 三点在一条直线上 PC → =mPA → +nPB →，求证： m+n=1．练习：1．已知：2121212 ,B),(3e e e +=-=+=，则下列关系一定成立的是（ ）A 、A ，B ，C 三点共线 B 、A ，B ，D 三点共线 C 、C ，A ，D 三点共线 D 、B ，C ，D 三点共线2．(原创题)设a ，b 是两个不共线的向量，若AB →＝2a ＋k b ，CB →＝a ＋b ，CD →＝2a －b ，且A ，B ，D 三点共线，则实数k 的值等于________．第2讲 平面向量的基本定理与坐标表示 一．【要点精讲】1．平面向量的基本定理如果21,e e 是一个平面内的两个不共线向量，那么对这一平面内的任一向量a ，有且只有一对实数21,λλ使：2211e e a λλ+=其中不共线的向量21,e e 叫做表示这一平面内所有向量的一组基底. 2．平面向量的坐标表示如图，在直角坐标系内，我们分别取与x 轴、y 轴方向相同的_单位向量_ i 、j 作为基底a ，有且只有一对实数x 、y ，BC AOM D使得a xi yj =+…………○1，把),(y x 叫做向量a 的（直角）坐标，记作(,)a x y =…………○2其中x 叫做a 在x 轴上的坐标，y 叫做a 在y 轴上的坐标，○2式叫做向量的坐标表示与a 相等的向量的坐标也为,(y x 特别地，(1,0)i =，(0,1)j =，0(0,0)=特别提醒：设yj xi +=，则向量的坐标),(y x 就是点A 的坐标；反过来，点A 的坐标),(y x 也就是向量的坐标在平面直角坐标系内，每一个平面向量都是可以用一对实数唯一表示3．平面向量的坐标运算（1）若11(,)a x y =，22(,)b x y =，则a b +=1212(,)x x y y ++，a b -= 1212(,)x x y y --（2） 若),(11y x A ，),(22y x B ，则AB = （3）若(,)a x y =和实数λ，则a λ=(,)x y λλ4．向量平行的充要条件的坐标表示：设a=(x 1, y 1) ，b =(x 2, y 2) 其中b ≠aa ∥b (b≠)的充要条件是12210x y x y -=二．【典例解析】题型一. 利用一组基底表示平面内的任一向量[例1] 在△OAB 中，21,41==，AD 与BC 交于点M ，设OA =a ，OB =b ，用a ,b 表示OM .练习:1．若已知1e 、2e 是平面上的一组基底，则下列各组向量中不能作为基底的一组是 ( ) A ．1e 与—2e B ．31e 与22e C ．1e ＋2e 与1e —2e D ．1e 与21e 2．在平行四边形ABCD 中，E 和F 分别是边CD 和BC 的中点，若AC →＝λAE →＋μAF →，其中λ、μ∈R ，则λ＋μ＝________.题型二: 向量加、减、数乘的坐标运算 例 3 已知A （—2,4）、B （3,—1）、C （—3,—4）且3=,2=,求点M 、N 的坐标及向量的坐标.练习:1. (2008年高考辽宁卷)已知四边形ABCD 的三个顶点A (0,2)，B (－1，－2)，C (3,1)，且BC →＝2AD →，则顶点D 的坐标为( )A ．(2，72)B ．(2，－12) C ．(3,2) D ．(1,3)2．若M(3, -2) N(-5, -1) 且 12MP =MN , 求P 点的坐标；3．若M(3, -2) N(-5, -1)，点P 在MN 的延长线上，且 12MP MN =,求P 点的坐标；4.(2009年广东卷文)已知平面向量a =,1x （） ，b =2,x x （－）， 则向量+a b ( )A 平行于x 轴B.平行于第一、三象限的角平分线C.平行于y 轴D.平行于第二、四象限的角平分线5．在三角形ABC 中，已知A (2,3)，B (8，－4)，点G (2，－1)在中线AD 上，且AG →＝2GD →， 则点C 的坐标是( )A ．(－4,2)B ．(－4，－2)C ．(4，－2)D ．(4,2)6．设向量a ＝(1，－3)，b ＝(－2,4)，c ＝(－1，－2)，若表示向量4a 、4b －2c 、2(a －c )、d 的有向线段首尾相接能构成四边形，则向量d 为( )A ．(2,6)B ．(－2,6)C ．(2，－6)D ．(－2，－6)7．已知A (7,1)、B (1,4)，直线y ＝12ax 与线段AB 交于C ，且AC →＝2CB →，则实数a 等于( ) A ．2 B ．1 C.45 D.53 题型三: 平行、共线问题例4已知向量(1sin ,1)θ=-a ，1(,1sin )2θ=+b ，若a ∥b ，则锐角θ等于（ ）A ．30︒B ． 45︒C ．60︒D ．75︒例5．（2009北京卷文）已知向量(1,0),(0,1),(),a b c ka b k R d a b ===+∈=-， 如果//c d 那么( )A ．1k =且c 与d 同向B ．1k =且c 与d 反向C ．1k =-且c 与d 同向D ．1k =-且c 与d 反向练习：1．若向量a=(-1,x)与b =(-x, 2)共线且方向相同，求x2．已知点O(0，0)，A(1，2)，B(4，5)及AB t OA OP +=，求(1)t 为何值时，P 在x 轴上？P 在y 轴上？P 在第二象限。
6.1 平面向量的概念 (精讲)(原卷版)
6.1平面向量的概念 (精讲）6.1.1向量的实际背景与概念6.1.2向量的几何表示6.1.3相等向量与共线向量目录一、必备知识分层透析二、重点题型分类研究题型1：向量的有关概念题型2：向量的几何表示角度1：向量的模角度2：零向量与单位向量题型3：相等向量与共线向量角度1：相等向量角度2：平行向量（共线向量）一、必备知识分层透析知识点1：向量的概念（1）向量在数学中,我们把既有大小又有方向的量叫做向量.①我们所学的向量是自由向量,即只有大小和方向,而无特定的位置,这样的向量可以作任意平移.②向量与向量之间不能比较大小.（2）数量只有大小没有方向的量称为数量,如年龄、身高、长度、面积体积、质量等（3）向量与数量的区别①向量与数量的区别:向量有方向,而数量没有方向；数量与数量之间可以比较大小,而向量与向量之间不能比较大小②向量与矢量:数学中的向量是从物理中的矢量(如位移、力、加速度、速度等)中抽象出来的,但在这里我们仅考虑它的大小及方向；而物理中的这些量,既同时具备大小和方向这两个属性,还具有其他属性(如“力”就是由大小方向、作用点所决定的).知识点2：向量的几何表示(1)有向线段具有方向的线段叫做有向线段①有向线段:具有方向的线段叫做有向线段,其方向是由起点指向终点.以A为起点、B为终AB. 表点的有向线段记作AB(如图所示),线段AB的长度也叫做有向线段的长度,记作||示有向线段时,起点一定要写在终点的前面,上面标上箭头.②有向线段的三个要素:起点、方向、长度.知道了有向线段的起点、方向、长度,它的终点就唯一确定了.（2）向量的表示①几何表示:向量可以用有向线段表示,有向线段的长度表示向量的大小,有向线段的方向表示向量的方向.②字母表示:向量可以用字母a,b,c,…表示（3）向量的模AB.向量AB的大小称为向量AB的长度(或称模),记作||（4）两种特殊的向量零向量:长度为0的向量叫做零向量,记作0.单位向量:长度等于1个单位长度的向量,叫做单位向量①若用有向线段表示零向量,则其终点与起点重合.与0的区别与联系,0是一个向量|0|；书写时0表示零向量方向相同或相反的非零向量叫做平行向量.向量a 与b 平行,记作a b .规定:零向量与任意即对于任意向量a ,都有0a .长度相等且方向相同的向量叫做相等向量.向量a 与b 相等,记作a b =.两个向量相等必须具备的条件是长度相等,方向相同因为向量完全由它的方向和模确定,故任意两个相等的非零向量与有向线段的起点无关.）共线向量任一组平行向量都可以平移到同一条直线上共线向量所在直线平行或重合,如果两个向量所在的直线平行或重合·高一课时练习）下列四个命题正确的是（ ）．若a 与b 不共线，则a 与b 都是非零向量．两个相等的向量起点、方向、长度必须都．（2022·全国·高一专题练习）下列命题中，正确的是||||a b =，则a b =．若a b =，则||||a b = ||||a b >，则a b > ||0a =，则0a = ．（2022·全国·高一假期作业）有下列命题：①两个相等向量，若它们的起点相同，则终点也相同；②若||a b |=|，则a b =； ③若AB DC =，则四边形ABCD 是平行四边形；m n =，n k =，则m k =；⑤若//a b ，//b c ，则//a c ； ⑥有向线段就是向．（2022·高一课时练习）下列说法正确的是（．向量AB与向量BA的长度相等例题2．（BD=________.例题3．（·全国·高一专题练习）若在一个边长为的正三角形所对应的有向线段为AD（其中则向量AD的模的最小值为高一专题练习）如果一架飞机向东飞行200 km，再向南飞行机飞行的路程为s，位移为a，那么（a aa a不能比大小2022·高一课时练习）已知在边长为ABCD中，∠，则BD=2022·高一课时练习）已知圆O的周长是，AB是圆O的直径，是圆周上一点，π=⊥CD=___________.,CD角度2：零向量与单位向量典型例题．向量就是有向线段>，则a b||||a b>．（2022秋·新疆巴音郭楞·高一校考阶段练习）下列说法正确的是（e=．单位向量均相等．单位向量1．零向量与任意向量平行．若向量a，b满足||||a b=，则a b=±．（2022秋·广东东莞·高一校联考期中）下列说法错误的是（．若0a =，则0a =．零向量是没有方向的 ．（多选）（2022春·广东佛山向量的说法正确的是（ ）．单位向量：模为1的向量例题1．（2022春·广东揭阳·中，AB DC =，则下列向量相等的是（．AD 与CB．OC 与OA ．AC 与DB D ．DO OB =例题2．（2022·全国·高三专题练习）“a b =”是“||||a b =”的（ ．充分非必要条件B ．必要非充分条件 ．充分必要条件 D ．既非充分又非必要条件例题3．（多选）（2022·高一课时练习）下列说法中错误的是（ ）||||a b =，则a b = B ．若a b ≠，则||||a b ≠||||a b =，则a 与b 可能共线||||a b ≠，则a 一定不与b 共线(1)分别写出与AO 、BO 相等的向量；写出与AO 共线的向量；写出与AO 的模相等的向量；写出与AO 的夹角为90︒的向量；向量AO 与CO 是否相等？（多选）（2022秋·浙江嘉兴若非零向量a ，b ，下列命题正确的是．若a b =，则a b =．若a b =，则a b = ．若//a b ，则a b = ．若a b =，则//a b．（多选）（2022秋·山东菏泽高一统考期中）设点O 是平行四边形ABCD 点，则下列结论正确的是（ ）．AO OC = B ．AO BO = ．AO BO = D ．AB 与CD 共线 ．（2022·高一课时练习）如图所示，在平行四边形ABCD 中，E ，F 分别是CD ，AB 中点.(1)写出与向量FC 共线的向量；(2)求证：BE FD =.4．（2022·全国·高三专题练习）在平行四边形ABCD 中，E ，F 分别为边AD 、BC 的中点，如图．(1)写出与向量FC 共线的向量；(2)求证：BE FD =．角度2：平行向量（共线向量）典型例题例题1．（2022春·河南·高三校联考阶段练习）已知,,,A B C D 为平面上四点，则“向量AB CD ∥”是“直线AB CD ”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件例题2．（2022秋·上海杨浦·高一复旦附中校考期中）①加速度是向量；②若//a b 且//b c ，则//a c ；③若AB CD =，则直线AB 与直线CD 平行．上面说法中正确的有（ ）个．A ．0B ．1C ．2D ．3同类题型演练1．（2022秋·湖北·高一校联考期中）“//b a ”是“a b =”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件2．（2022秋·上海浦东新·高一校考期末）命题：若//,//a b b c ，则//a c ，则命题为_______（填写：真命题或假命题）3．（2022·高一课时练习）已知命题“若//a b ，//b c ，则//a c ”是假命题，则b =__________.。
高一平面向量知识点及典例
高一平面向量知识点及典例平面向量是高一数学学习中的重要内容，它不仅在数学中有着广泛的应用，还在物理、工程等领域发挥着重要作用。
本文将介绍高一平面向量的基本概念、性质和典型例题，希望能帮助同学们更好地理解和应用平面向量。
一、平面向量的概念平面向量是由大小和方向共同确定的有向线段，通常用大写字母表示。
平面向量AB可以记作→AB，其中A称为起点，B称为终点。
平面向量还可以用坐标表示，例如向量→AB可以表示为AB的坐标 (x, y)。
二、平面向量的性质1. 平面向量的加法与减法给定两个平面向量→AB和→CD，可以进行向量的加法和减法运算。
向量加法的结果是一个新的向量→EF，满足→EF = →AB +→CD；向量减法的结果是一个新的向量→GH，满足→GH =→AB - →CD。
2. 平面向量的数量积平面向量→AB和→CD的数量积记作→AB·→CD，表示两个向量的数量积等于向量→AB的模长乘以向量→CD在→AB上的投影长度。
若→AB·→CD = 0，则称向量→AB与→CD垂直。
3. 平面向量的数量积性质平面向量的数量积具有以下性质：交换律（→AB·→CD =→CD·→AB）、分配律（→AB·(→CD +→EF) = →AB·→CD +→AB·→EF）以及数量积与平移无关等。
三、平面向量的典型例题1. 例题一已知向量→AB = (3, 4)，→CD = (5, -2)，求→AB +→CD的坐标。
解：向量→AB +→CD的坐标为(3+5, 4+(-2)) = (8, 2)。
2. 例题二设向量→AB = (2, -3)，→CD = (4, 1)，求→AB·→CD的值。
解：→AB·→CD = (2*4)+(-3*1) = 5。
3. 例题三如图所示，在△ABC中，向量→AB = (2, 3)，向量→BC = (4, 1)，求向量→AC的坐标。
高中数学必修二 专题02 平面向量的基本定理、坐标运算及数量积(重难点突破)(含答案)
专题02 平面向量的基本定理、坐标运算及数量积一、考情分析二、题型分析(一) 平面向量的基本定理与坐标表示知识点1 平面向量基本定理如果e 1，e 2是同一平面内的两个不共线向量，那么对于这一平面内的任意向量a ，有且只有一对实数λ1，λ2，使a ＝λ1e 1＋λ2e 2，其中e 1，e 2是一组基底．例1．（1）.（2019·四川雅安中学高一月考）以下四组向量能作为基底的是（ ）A ．B ．C ．D ．12(1,2),(2,4)e e ==12(3,1),(1,3)e e =-=-12(2,1),(2,1)e e ==--121(,0),(3,0)2e e ==【答案】B【解析】对于，与共线，不能作为基底；对于，与不共线，能作为基底；对于，与共线，不能作为基底；对于，与共线，不能作为基底，故选B. （2）.（2019·江西高一期末）设是平面内的一组基底,则下面四组向量中,能作为基底的是（ ）A ．与B ．与C ．与D ．与 【答案】C【解析】由是平面内的一组基底，所以和不共线，对应选项A ：，所以这2个向量共线，不能作为基底；对应选项B ：，所以这2个向量共线，不能作为基底； 对应选项D ：，所以这2个向量共线，不能作为基底； 对应选项C ：与不共线，能作为基底.故选：C ．A 114220,e ⨯-⨯=∴2eB ()()1331180,e ⨯--⨯-=≠∴2eC ()()121120,e ⨯--⨯-=∴2eD 110030,2e ⨯-⨯=∴2e 12,e e 21e e -12e e -1223e e +1246e e --12e e +12e e -121128e e -+1214e e -12,e e 1e 2e 21e e -()12e e =--1223e e +()121462e e =---121128e e -+121124e e ⎛⎫=-- ⎪⎝⎭12e e +12e e -（3）.（2020·内蒙古高三月考）在正方形中，点为内切圆的圆心，若，则的值为（ ）A ．B ．C ．D ．【答案】D【解析】连并延长到与相交于点，设正方形的边长为1，则，设内切圆的半径为，则，可得. 设内切圆在边上的切点为，则，有，，故. 故选：DABCD O ABC ∆AO xAB yAD =+xy 1434-1412OB AC HABCD 122BH BD ==ABC ∆r)1BH OH OB r r =+=+==r =ABC ∆AB E ()1AO AE EO r AB r AD=+=-+22222112222AB AD AB AD ⎛⎛⎫-=-+=+- ⎪⎪⎝⎭⎝⎭x =1y =-11222xy ⎛⎫=-= ⎪ ⎪⎝⎭【变式训练1】．（2020·北京高三开学考试）在平行四边形ABCD 中，，，，则 .（用表示） 【答案】 【解析】如图：＝－＝＋2＝＋＝－＋(－)＝－＋ ＝.故本题答案为. 【变式训练2】．（2020·辽宁高考模拟）在中，，，若，则（ ）A ．B ．C ．D ．【答案】D【解析】因为，所以点是的中点，又因为，所以点是的中点，所以有：，因此1AB e =2AC e =14NC AC =12BM MC =MN =12,e e 1225312e e -+MN CN CM CN BM CN 23BC 14AC 23AC AB 214e 212()3e e -1225312e e -+1225312e e -+ABC ∆2AB AC AD +=0AE DE +=EB xAB y AC =+3y x =3x y =3y x =-3x y =-2AB AC AD +=D BC 0AE DE +=E AD 11131()22244BE BA AE AB AD AB AB AC AB AC =+=-+=-+⨯+=-+，故本题选D. 31,344x y x y =-=⇒=-(二) 平面向量的坐标运算知识点2 平面向量的坐标运算(1)若a ＝(x 1，y 1)，b ＝(x 2，y 2)(b ≠0)，则a±b ＝(x 1±x 2，y 1±y 2)．(2)若A (x 1，y 1)，B (x 2，y 2)，则AB →＝(x 2－x 1，y 2－y 1)． (3)若a ＝(x ，y )，λ∈R ，则λa ＝(λx ，λy )．(4)a ·b ＝x 1x 2＋y 1y 2.(5)|a |＝x 21＋y 21.若A (x 1，y 1)，B (x 2，y 2)，则|AB →|＝（x 1－x 2）2＋（y 1－y 2）2.例2．（1）.（2020·福建高三月考）已知，若，则的坐标为（ ）A ．B ．C ．D ． 【答案】D【解析】设,因为,所以.所以,所以, 解得: ,.所以.故选D. （2）.（2019·湖南高一期末）已知，，则（ ） A ．2 BC ．4 D．【答案】C 【解析】由题得=（0,4）所以．故选：C(5,2),(4,3)a b =-=--230a b c -+=c 8(1,)3138(,)33-134(,)33134(,)33--(,)c x y =230a b c -+=(5,2)2(4,3)3(,)(0,0)x y ----+=(583,263)(0,0)x y ++-++=1330,430x y +=+=133x 43y =-134(,)33c =--()0,1A -()0,3B ||AB =AB ||04AB =+=【变式训练1】.（2020·湖北高一期中）已知向量，向量.（1）求向量的坐标；（2）当为何值时，向量与向量共线.【答案】（1）（2）【解析】（1）（2），∵与共线，∴∴【变式训练2】.（2018·上海市嘉定区封浜高级中学高二期中）已知，为坐标原点.(1) 求向量的坐标及；(2) 若，求与同向的单位向量的坐标． 【答案】(1) ，；（2）.【解析】 （1）,.（2）,, 与同向的单位向量. ()1,2a =()3,2b =-2a b -k ka b +2a b -()7,2-12k =-()()()21,223,27,2a b -=--=-()()()1,23,23,22ka b k k k +=+-=-+()()()21,223,27,2a b -=--=-ka b +2a b -()()72223k k +=--12k =-(3,4),(5,10)A B ---O AB AB OC OA OB =+OC ()8,6AB =-10AB =21010OC n OC ⎛==- ⎝⎭()8,6AB =-2810AB ∴==()()()3,45,102,14OC OA OB =+=--+-=-22OC ==∴OC 21010OC n OC ⎛==- ⎝⎭(三) 平面向量的数量积知识点3．平面向量数量积1．平面向量数量积的有关概念(1)向量的夹角：已知两个非零向量a 和b ，记OA→＝a ，OB →＝b ，则∠AOB ＝θ(0°≤θ≤180°)叫作向量a 与b 的夹角．(2)数量积的定义：已知两个非零向量a 和b ，它们的夹角为θ，则数量|a ||b |cos θ叫作a 与b 的数量积，记作a ·b ，即a ·b ＝|a ||b |cos θ.规定：0·a ＝0.(3)数量积的几何意义：数量积a ·b 等于a 的模|a |与b 在a 的方向上的投影|b |cos θ的乘积．2．平面向量数量积的性质设a ，b 都是非零向量，e 是与b 方向相同的单位向量，θ是a 与e 的夹角，则(1)e·a ＝a·e ＝|a|cos θ.(2)当a 与b 同向时，a·b ＝|a||b|；当a 与b 反向时，a·b ＝－|a||b|.特别地，a·a ＝|a|2或|a|＝a ·a .(3)cos θ＝a·b |a||b|.(4)|a·b|≤|a||b|.3．平面向量数量积的坐标表示设a ＝(x 1，y 1)，b ＝(x 2，y 2)，a ，b 的夹角为θ，则(1)a ·b ＝x 1x 2＋y 1y 2.(2)|a |＝x 21＋y 21.若A (x 1，y 1)，B (x 2，y 2)，则|AB →|＝（x 1－x 2）2＋（y 1－y 2）2.(3)cos θ＝x 1x 2＋y 1y 2x 21＋y 21·x 22＋y 22.(4)a ⊥b ⇔a ·b ＝0⇔x 1x 2＋y 1y 2＝0.例3．（1）（2020·浙江高一期末）已知向量，，则__________，与方向相反的单位向量__________.【解析】依题意，故与方向相反的单位向量为. （2）.（2019·全国高考真题）已知=(2,3)，=(3，t )，=1，则= A ．-3B ．-2C ．2D ．3 【答案】C 【解析】 由，，得，则，．故选C【变式训练1】.（2019·安徽高三月考（理））已知，，均为单位向量，与的夹角为，则的最大值为( ) ()3,4a =()1,2b =-2a b +=a c =34,55⎛⎫-- ⎪⎝⎭()21,8a b +=2218a b +=+=a c ()()()3,43,434,5553,4a a -----⎛⎫===-- ⎪---⎝⎭AB AC ||BC AB BC ⋅(1,3)BC AC AB t =-=-211BC ==3t =(1,0)BC =(2,3)(1,0)21302AB BC ==⨯+⨯=a b c a b 60()(2)c a c b +⋅-A ．BC ．2D ． 3【答案】B 【解析】设与的夹角为，因为，，所以，所以，所以.故选：B ．【变式训练2】.（2020·四川高一月考）已知，若，则实数=__________；=__________. 【答案】0 0【解析】∵，∴，∵，∴，解得． 故答案为．【变式训练3】.（2019·江苏高考真题）如图，在中，D 是BC 的中点，E 在边AB 上，BE =2EA ，AD 与CE 交于点.若，则的值是_____. 32c 2a b -θ222|2|443a b a a b b -=-⋅+=|2|3a b -=2()(2)(2)21|||2|cos 1c a c b cc a b a b c a b θ+⋅-=+⋅--⋅=+⋅--()(2)3cos c a c b θ+⋅-=max =cos 1θ=()()1,3,1,2a b ==-0a b λμ+=λμ()()1,3,1,2a b ==-()()()1,31,2,32a b λμλμλμλμ+=+-=+-0a b λμ+=0320λμλμ+=⎧⎨-=⎩0λμ=⎧⎨=⎩0,0λμ==ABC O 6AB AC AO EC ⋅=⋅ABAC. 【解析】如图，过点D 作DF //CE ，交AB 于点F ，由BE =2EA ，D 为BC 中点，知BF =FE =EA ,AO =OD .， 得即故. 【变式训练4】.（2020·浙江高一期中）已知为单位向量，. （1）求；（2）求与的夹角的余弦值；()()()3632AO EC AD AC AE AB AC AC AE =-=+-()223131123233AB AC AC AB AB AC AB AC AB AC ⎛⎫⎛⎫=+-=-+- ⎪ ⎪⎝⎭⎝⎭22223211323322AB AC AB AC AB AC AB AC AB AC ⎛⎫=-+=-+= ⎪⎝⎭2213,22AB AC =3,AB AC =AB AC=,a b 12a b ⋅=2a b +2a b +b θ【答案】（1；（2）.【解析】由题得； 由题得与的夹角的余弦值为故答案为：（1；（2.7222=4++4=5+4a b a b a b +⋅⋅2a b +b θ(2)2cos |2|||7a b b a b a b b θ+⋅⋅====+(四) 平面向量的应用（平行与垂直）知识点1 平面向量的平行与垂直若a ＝(x 1，y 1)，b ＝(x 2，y 2)(b ≠0)，则a±b ＝(x 1±x 2，y 1±y 2)．(1)如果a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a ∥b 的充要条件为x 1y 2－x 2y 1＝0.a ∥b 的充要条件不能表示成x 1x 2＝y 1y 2，因为x 2，y 2有可能等于0.判断三点是否共线，先求每两点对应的向量，然后再按两向量共线进行判定．(2)如果a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a ⊥b ⇔a ·b ＝0⇔x 1x 2＋y 1y 2＝0.x 1y 2－x 2y 1＝0与x 1x 2＋y 1y 2＝0不同，前者是两向量a ＝(x 1，y 1)，b ＝(x 2，y 2)共线的充要条件，后者是它们垂直的充要条件．例4．(1)（2020·江西高一期末）已知向量，，若，则（ ）A ．B ．C ．D ．【答案】D 【解析】向量，，且，，解得. 故选：D.(2)．(多选题)已知向量a =(2，1)，b =(1，﹣1)，c =(m ﹣2，﹣n )，其中m ，n 均为正数，且(a b -)∥c ，下列说法正确的是（ ）A ．a 与b 的夹角为钝角()1,a m =()2,5b =//a b m =152-25-52()1,a m =()2,5b =//a b 25m ∴=52m =B ．向量a 在bC ．2m +n =4D ．mn 的最大值为2 【答案】CD对于A ，向量a =(2，1)，b =(1，﹣1)，则2110a b ⋅=-=>，则,a b 的夹角为锐角，错误；对于B ，向量a =(2，1)，b =(1，﹣1)，则向量a 在b 方向上的投影为22a b b⋅=，错误； 对于C ，向量a =(2，1)，b =(1，﹣1)，则a b -= (1，2)，若(a b -)∥c ，则(﹣n )=2(m ﹣2)，变形可得2m +n =4，正确；对于D ，由C 的结论，2m +n =4，而m ，n 均为正数，则有mn 12= (2m •n )12≤ (22m n +)2=2，即mn 的最大值为2，正确； 故选：CD.【变式训练1】（2020·浙江高一期中）已知向量满足.若，则 _______； ______.【答案】【解析】因为，所以（1）×m 4=0,所以m= 4.所以故答案为：(1). (2).【变式训练2】．（2020广东高一期末）已知， ;(1) 若，求的值；,a b (1,2),(2,)a b m =-=//a b m =||b =4-//a b ---2||=2+b =（4-)cos ,1(),sin ,1(θθ==b aR ∈θ)0,2(=+b a θθθcos sin 2sin 2+（2）若，，求的值.【答案】（1）（2） 【解析】（1），∴， ……1分∴ ； ……3分∴. ……7分（2）， ……8分∴，两边平方得， ……10分 ，且， ∴∴， ……12分 ∴. ……分)51,0(=-b a(,2)θππ∈θθcos sin +12-75-)cos ,1(),sin ,1(θθ==b a)0,2()cos sin ,2(=+=+θθb asin cos 0,tan 1θθθ+=∴=-1tan tan 2tan cos sin cos sin 2sin cos sin 2sin 222222++=++=+θθθθθθθθθθθ21-=)51,0()cos sin ,0(=-=-θθb a51cos sin =-θθ2512cos sin =θθ(,2)θππ∈02512cos sin >=θθ⎪⎭⎫⎝⎛∈ππθ23,0cos sin <+θθ57cos sin 21cos sin -=+-=+θθθθ14。
高中数学平面向量知识点与典型例题总结（师）
高中数学平面向量知识点与典型例题总结（师）《数学》必会基础题型——《平面向量》【基本概念与公式】【任何时候写向量时都要带箭头】1.向量：既有大小又有方向的量。
记作：AB 或a 。
2.向量的模：向量的大小（或长度），记作：||AB 或||a 。
3.单位向量：长度为1的向量。
若e 是单位向量，则||1e =。
4.零向量：长度为0的向量。
记作：0。
【0方向是任意的，且与任意向量平行】5.平行向量（共线向量）：方向相同或相反的向量。
6.相等向量：长度和方向都相同的向量。
7.相反向量：长度相等，方向相反的向量。
AB BA =-。
8.三角形法则：AB BC AC +=；AB BC CD DE AE +++=；AB AC CB -=（指向被减数）9.平行四边形法则：以,a b 为临边的平行四边形的两条对角线分别为a b +，a b -。
10.共线定理：//a b a b λ=?。
当0λ>时，a b 与同向；当0λ<时，a b 与反向。
11.基底：任意不共线的两个向量称为一组基底。
12.向量的模：若(,)a x y =，则2||a x y =+，22||a a =，2||()a ba b +=+13.数量积与夹角公式：||||cos a b a b θ?=?； cos ||||a b a b θ?=? 14.平行与垂直：1221//a b a b x y x y λ?=?=；121200a b a b x x y y ⊥??=?+=题型1.基本概念判断正误：（1）共线向量就是在同一条直线上的向量。
（2）若两个向量不相等，则它们的终点不可能是同一点。
（3）与已知向量共线的单位向量是唯一的。
（4）四边形ABCD 是平行四边形的条件是AB CD =。
（5）若AB CD =，则A 、B 、C 、D 四点构成平行四边形。
（6）因为向量就是有向线段，所以数轴是向量。
（7）若a 与b 共线， b 与c 共线，则a 与c 共线。
高一数学平面向量 PPT课件 图文
a－3b=(1, 2)－3(－3, 2)= (10, －4)
(ka+b)∥(a－3b)
－4(k－3)－10(2k+2)=0
K=－ 1
3
∵
ka+b=
10 3
,
4 3
=－
1 3
(a－3b)
∴它们反向
例2
思考:
此题还有没有其它解法?
分析 要证A、B、D三点共线，可证 AB=λBD关键是找到λ
解： ∵BD=BC+CD= 2a + 8b+ 3(a b)=a+5b
∴AB=2 BD
AB∥ BD
且AB与BD有公共点B
∴ A、B、D 三点共线
例3
知识结构
平面向量小 复习
知识要点 例题解析 巩固练习
课外作业
练习5 已知a=（1，0），b=（1，1），c =（－1，0） 求λ和μ，使 c =λa +μb.
新课标人教版课件系列
《高中数学》
必修4
2.6《平面向量-复习》
平面向量复习
知识结构 要点复习 例题解析
巩固练习
制作：曾毅 审校：王伟
知识结构
平面向量 复习
知识要点 例题解析 巩固练习
课外作业
表示 向量的三种表示
平
三角形法则
面
向量加法与减法
向
平行四边形法则
量
向量平行的充要条件
运算 实数与向量的积
知识Байду номын сангаас点 例题解析 巩固练习
课外作业
(完整版)高中数学平面向量讲义
平面向量 (学生专用 )专题六平面向量一. 基本知识【1】向量的基本看法与基本运算（1）向量的基本看法：①向量：既有大小又有方向的量向量不能够比较大小，但向量的模能够比较大小．②零向量：长度为0 的向量，记为0 ，其方向是任意的，0 与任意向量平行③单位向量：模为 1 个单位长度的向量④平行向量（共线向量）：方向相同或相反的非零向量⑤相等向量：长度相等且方向相同的向量uuur r uuur r r uuur uuur uuur（2）向量的加法：设AB a, BC b ，则a+ b = AB BC = AC① 0 a a 0 a ；②向量加法满足交换律与结合律；uuur uuur uuur uuur uuur uuurAB BC CD L PQ QR AR ，但这时必定“首尾相连”．（3）向量的减法：①相反向量：与 a 长度相等、方向相反的向量，叫做 a 的相反向量②向量减法：向量 a 加上b的相反向量叫做 a 与b的差，③作图法： a b 能够表示为从 b 的终点指向a的终点的向量（ a 、b有共同起点）（4）实数与向量的积：实数λ与向量a的积是一个向量，记作λa，它的长度与方向规定以下：（Ⅰ）a a ；（Ⅱ）当0 时，λ a 的方向与 a 的方向相同；当0 时，λa 的方向与 a 的方向相反；当0 时，a0 ，方向是任意的（5）两个向量共线定理：向量b与非零向量 a 共线有且只有一个实数，使得b= a （6）平面向量的基本定理：若是e1, e2是一个平面内的两个不共线向量，那么对这一平面内的任向来量 a ，有且只有一对实数 1 ,2使：a1e12e2，其中不共线的向量e1 , e2叫做表示这一平面内所有向量的一组基底【2】平面向量的坐标表示第1页（1） 平面向量的坐标表示 ：平面内的任向来量rr r rr 。
a 可表示成 axi yj ，记作 a =(x,y) （2）平面向量的坐标运算：rrr rx 1 x 2 , y 1 y 2①若 ax 1 , y 1 , bx 2 , y 2 ，则 a buuur②若 A x 1 , y 1 , B x 2 , y 2 ，则 AB x 2 x 1 , y 2 y 1r =(x,y) ，则 r x, y)③若 a a =(r r r r x 1 y 2 x 2 y 1 0④若 ax 1 , y 1 , b x 2 , y 2 ，则 a // b r r r r y 1 y 2⑤若 a x 1 , y 1 , b x 2 , y 2 ，则 a b x 1 x 2r r y 1 y 2⑥若 a b ，则 x 1 x 2【3】平面向量的数量积（1）两个向量的数量积：已知两个非零向量r rr r r rr ra 与b ，它们的夹角为 ，则 a · b =︱ a ︱·︱ b ︱ cos 叫做 a 与 b 的数量积（或内积）r r规定 0 arr rrr= a b（2）向量的投影： ︱ b ︱ cosr ∈ R ，称为向量 b 在 a 方向上的投影 投影的绝对值称| a |为射影（3）数量积的几何意义：r r r r ra ·b 等于 a 的长度与 b 在 a 方向上的投影的乘积（4）向量的模与平方的关系：r r r 2 r 2 a a a | a |（5）乘法公式成立：r r rrr 2 r 2 r 2 r 2 r r 2 r 2r r r 2r 2 r r r 2a b a ba b ab ； a ba 2ab ba2a b b（6）平面向量数量积的运算律：①交换律成立：rrr r a bb a②对实数的结合律成立： r r r r r r Ra ba b a b③分配律成立：r r r r r r r r r r a b c a cb c c a b第 2页特别注意：（ 1）结合律不成立：r r r r r r ab c a b c ；r rrrr r （ 2）消去律不成立 a ba c 不能够获取b c（rr=0r r r r3） a b 不能够获取 a =0 或 b=0（7）两个向量的数量积的坐标运算：rrrry 1 y 2已知两个向量 a ( x 1, y 1), b ( x 2 , y 2 ) ，则 a · b= x 1 x 2r r uuur r uuur r （ 8 ） 向 量 的 夹 角 ： 已 知 两 个 非 零 向 量 a 与 b ， 作 OA = a ,OB = b , 则 ∠ AOB= （0 0180 0 ） 叫做 向量r 与 r 的夹角abr r r rx 1 x 2 y 1 y 2a ? bcos= cosa ,br r = 2222a ? bx 1y 1x 2y 2当且仅当两个非零向量rrr rra 与b 同方向时， θ =0 ，当且仅当 a 与 b 反方向时θ=180 ，同时 0 与其他任何非零向量之间不谈夹角这一问题r r 0则称 r r r r （9）垂直 ：若是 a 与 b 的夹角为 90 a 与 b 垂直，记作 a ⊥ b（ 10）两个非零向量垂直的充要条件： a ⊥ ba ·b ＝ Ox xy y20 平面向量1 21数量积的性质二. 例题解析【模块一】向量的基本运算【例 1】给出以下六个命题：①两个向量相等，则它们的起点相同，终点相同；rr r r ②若 a b ，则 ab ③在平行四边形 ABCD 中必然有uuur uuurAB DC ；ur r r ur ur ur r r r r r r④若 m n, n p ，则 m p ； ⑤若 a // b ， b // c , 则 a // cr r r r r r r⑥任向来量与它的相反以下不相等. ⑦已知向量 a 0 ，且 a b 0 ，则 b 0r r r r r r r r r r r r⑧ a b 的充要条件是 a b 且 a // b ；⑨若 a 与 b 方向相同，且 a b ，则 ab ；⑩由于零向量的方向不确定，故零向量不与任意向量平行； 其中正确的命题的序号是第 3页r rr r ruur【例 2】已知向量 a, b 夹角为 45 ，且 a 1, 2a b10 ；求 b 的值 .uur uur r rr r【变式 1】若 a 2 ， b 3 ， a b3 求 a b 的值 .【变式 2】设向量 a ， b 满足 | a|=|b |=1 及 | 3a-2 b|=3 ，求 | 3a+b| 的值r r r rrr r r【例 3】已知向量 a 、 b 的夹角为 60o ， |a| 3， | b |2 ，若 (3a 5b) (ma b) ，求 m 的值.rrr r r r【例 4】若向量 a1,2 ， b1, 1 求 2a b 与 a b 的夹角 .【 变 式】 设 x, y R, 向 量 a x,1 ,b 1, y , c2, 4 , 且 a c,b // c, 则 a b_______（）A ． 5B ． 10C ． 2 5D ． 10【例 5】已知两个非零向量r rr r rra,b 满足 a ba b ，则以下结论必然正确的选项是（ ）r r r rr r DA a // bB a b Ca br r r r a b a b【变式 1】设 a , b 是两个非零向量 . （）A ．若 | a +b |=| a |-| b |, 则 a ⊥ bB ．若 a ⊥b , 则| a +b |=| a |-| b |C ．若 | a +b |=| a |-| b |, 则存在实数 λ, 使得 a =λbD ．若存在实数 λ, 使得 a =λb , 则| a +b |=| a |-| b |第 4页r r r r r r【变式 2】若平面向量a, b满足 : 2a b 3 ;则 agb 的最小值是_____【例 6】设0,rcosr13 2， a,sin ，b,22r r r r （1）证明 a b a b ；（2）r r r r的值 .当 2a b a2b时求角r rr ra b）【例 7】设a、b都是非零向量 , 以下四个条件中 , 使r r成立的充足条件是（| a ||b |r r r r r r r rr r A．a b B．a // b C．a 2b D．a // b且| a | | b |【模块二】向量与平面几何【例 1】在△ ABC中， A 90o AB 1, ACuuur uuur 2 ,设P、Q满足 AP AB ，uuur1uuurRuuur uuur2 ，则AQ AC ，BQ CP=（）A 1B2C4D2 333第5页AB2uuur uuur uuur uuur 【变式 1】已知△ ABC为等边三角形，设 P、Q满足AP AB AQ 1AC，，uuur uuur 3，则R BQ CP=（）2A 1B12C 1 10D 3 2 2222uuur uuur【例 2】在△ ABC中 ,AB=2,AC=3,ABgBC = 1则 BC ___ .（）A．3B．7C．2 2D．23uuur uuur uuur【变式 1】若向量BA2,3 , CA4,7 ,则 BC（）A．2, 4B．2,4C．6,10D．6, 10【例 3 】若等边ABC 的边长为2 3 ，平面内一点M 满足CM 1CB2CA ,则63MA? MB________.第6页平面向量 (学生专用 )uuur r uuur r r r r r2 ,则【例 4】ABC 中, AB 边上的高为 CD ,若CB a,CA b, a b0,| a |1,|b | uuurAD（）A．1r1rB．2r2rC．3r3rD．4r4r a b a b a b5a b 3333555uuur3【例5】在平面直角坐标系中,O (0,0), P(6,8) ,将向量 OP按逆时针旋转后 , 得向量4 uuurOQ ，则点 Q 的坐标是（）A．( 7 2,2) B． (72,2)C．( 4 6, 2)D．( 46, 2)uuur uuur【例 6】在ABC中, M是 BC的中点, AM=3, BC=10,则AB AC =______________.【例 7】在平行四边形中, ∠A= 3, 边、的长分别为2、1.若、分别是边、ABCD AB AD M N BC CD上的点,且满足| BM|| CN | ,则AM AN 的取值范围是_________ .| BC || CD |,【例 8】如图 ,在矩形 ABCD 中, AB 2 ，BC2，点E为 BC 的中点,点F在边 CD uuur uuur uuur uuur上, 若AB g AF 2 ,则 AE g BF 的值是____.第7页平面向量 (学生专用 )9 】已知正方形ABCD 的边长为1, 点 E 是 AB 边上的动点uuur uuur【例, 则DE CB的值为uuur uuur________; DE DC 的最大值为________.【例 10】已知直角梯形ABCD 中，AD// BC ,ADC 900, AD2, BC 1 , P 是腰uuur uuurDC 上的动点，则PA3PB 的最小值为___________uuur uuur uuur【例 11】如图，在VABC中，AD AB , BC 3 BD ,AD 1 ,uuur uuur3.则 AC gAD【例 12】 (15)uuur uuur1uuur1uuur3uuur 在四边形 ABCD中，AB = DC =（ 1，1），uuur BA uuur BC uuur BD ，BA BC BD则四边形ABCD的面积是第8页平面向量 (学生专用 ) uuur uuur【例 13】在VABC中，若AB2,3 , AC 6, 4 ，则 VABC 面积为【例 14】（ 2012 年河北二模）在VABC中，AB 边上的中线CD=6 ，点 P 为 CD 上（与 C,D ）uuur uuur uuur不重合的一个动点，则PA PB .PC的最小值是A 2B 0C -9D -18第9页。
高一数学平面向量知识点及典型例题解析汇报
高一数学 第八章 平面向量第一讲 向量的概念与线性运算 一．【要点精讲】 1．向量的概念①向量：既有大小又有方向的量。
几何表示法AB ，a ；坐标表示法),(y x j y i x a =+= 。
向量的模（长度），记作|AB |.即向量的大小，记作｜a|。
向量不能比较大小，但向量的模可以比较大小.②零向量：长度为0的向量，记为0，其方向是任意的，规定0平行于任何向量。
（与0的区别） ③单位向量｜a｜＝1。
④平行向量（共线向量）方向相同或相反的非零向量，记作a ∥b⑤相等向量记为b a=。
大小相等，方向相同),(),(2211y x y x =⎩⎨⎧==⇔2121y y x x 2．向量的运算（1）向量加法：求两个向量和的运算叫做向量的加法.如图，已知向量a ，b ，在平面内任取一点A ，作AB =a ，BC =b ，则向量叫做a 与b的和，记作a+b ，即 a+b AB BC AC =+=特殊情况：(1)BBabba +AABC C)2()3(向量加法的三角形法则可推广至多个向量相加：AB BC CD PQ QR AR +++++=，但这时必须“首尾相连”。
②向量减法： 同一个图中画出a b a b +-、要点:向量加法的“三角形法则”与“平行四边形法则”（1）用平行四边形法则时，两个已知向量是要共始点的，和向量是始点与已知向量的始点重合的那条对角线，而差向量是另一条对角线，方向是从减向量指向被减向量。
（2） 三角形法则的特点是“首尾相接”，由第一个向量的起点指向最后一个向量的终点的有向线段就表示这些向量的和；差向量是从减向量的终点指向被减向量的终点. （3）实数与向量的积3．两个向量共线定理：向量b 与非零向量a共线⇔有且只有一个实数λ，使得b =a λ。
二．【典例解析】题型一： 向量及与向量相关的基本概念概念 例1判断下列各命题是否正确(1)零向量没有方向 (2)==则 (3)单位向量都相等 (4) 向量就是有向线段(5)两相等向量若共起点,则终点也相同 (6)若b a =，c b =，则c a =；(7)若b a //，c b //，则c a // (8) b a =的充要条件是||||b a =且b a //；(9) 若四边形ABCD 是平行四边形,则DA BC CD B ==,A练习. (四川省成都市一诊)在四边形ABCD 中，“AB →＝2DC →”是“四边形ABCD 为梯形”的 A 、充分不必要条件 B 、必要不充分条件 C 、充要条件 D 、既不充分也不必要条件题型二: 考查加法、减法运算及相关运算律 例2 化简)()(---=练习1.下列命题中正确的是 A ．OA OB AB -= B ．0AB BA +=C ．00AB ⋅=D ．AB BC CD AD ++=2.化简AC -BD +CD -AB 得A ．AB B ．C ．D ．3．如图，D 、E 、F 分别是△ABC 的边AB 、BC 、CA 的中点，则( ) A.AD →＋BE →＋CF →＝0 B.BD →－CF →＋DF →＝0 C.AD →＋CE →－CF →＝0 D.BD →－BE →－FC →＝0题型三: 结合图型考查向量加、减法例3在ABC ∆所在的平面上有一点P ，满足PA PB PC AB ++=，则PBC ∆与ABC ∆的面积之比是( )A ．13B ．12C ．23D ．34例4重心、垂心、外心性质练习: 1．如图，在ΔABC 中，D 、E 为边AB 的两个三等分点，CA →=3a ，CB → =2b ，求CD → ，CE → ． 2已知a b a b+-=求证a b ⊥3若O 为ABC ∆的内心，且满足()(2)0OB OC OB OC OA -⋅+-=，则ABC ∆的形状为（ ）A.等腰三角形B.正三角形C.直角三角形D.钝角三角形4．已知O 、A 、B 是平面上的三个点，直线AB 上有一点C ，满足2AC →＋CB →＝0，则OC →＝( ) A ．2OA →－OB → B ．－OA →＋2OB →C.23OA →－13OB → D ．－13OA →＋23OB →ABDE5．已知平面上不共线的四点O ，A ，B ，C .若OA →－3OB →＋2OC →＝0，则|AB →||BC →|等于________．6．已知平面内有一点P 及一个△ABC ，若PA →＋PB →＋PC →＝AB →，则( )A ．点P 在△ABC 外部B ．点P 在线段AB 上C ．点P 在线段BC 上D ．点P 在线段AC 上7．在△ABC 中，已知D 是AB 边上一点，若AD →＝2DB →，CD →＝13CA →＋λCB →，则λ等于( )A.23B.13 C ．－13 D ．－23 题型四: 三点共线问题例 4 设21,e e 是不共线的向量,已知向量2121212,3,2e e e e e k e -=+=+=,若A,B,D 三点共线,求k 的值例5已知A 、B 、C 、P 为平面内四点， A 、B 、C 三点在一条直线上 PC → =mPA → +nPB → ，求证： m+n=1．练习：1．已知：2121212 ,B),(3e e e +=-=+=，则下列关系一定成立的是（ ）A 、A ，B ，C 三点共线 B 、A ，B ，D 三点共线 C 、C ，A ，D 三点共线 D 、B ，C ，D 三点共线2．(原创题)设a ，b 是两个不共线的向量，若AB →＝2a ＋k b ，CB →＝a ＋b ，CD →＝2a －b ，且A ，B ，D 三点共线，则实数k 的值等于________．第2讲 平面向量的基本定理与坐标表示 一．【要点精讲】1．平面向量的基本定理如果21,e e 是一个平面内的两个不共线向量，那么对这一平面内的任一向量a ，有且只有一对BC AOM D实数21,λλ使：2211e e a λλ+=其中不共线的向量21,e e叫做表示这一平面内所有向量的一组基底.2．平面向量的坐标表示如图，在直角坐标系内，我们分别取与x 轴、y 轴方向相同的_单位向量_ i 、j 作为基底任作一个向量a ，有且只有一对实数x 、y ，使得a xi yj =+…………○1，把),(y x 叫做向量a 的（直角）坐标，记作(,)a x y =…………○2其中x 叫做a 在x 轴上的坐标，y 叫做a 在y 轴上的坐标，○2式叫做向量的坐标表示与a 相等的向量的坐标也为,(y x 特别地，(1,0)i =，(0,1)j =，0(0,0)=特别提醒：设yj xi +=，则向量的坐标),(y x 就是点A 的坐标；反过来，点A 的坐标),(y x 也就是向量的坐标因此，在平面直角坐标系内，每一个平面向量都是可以用一对实数唯一表示3．平面向量的坐标运算（1）若11(,)a x y =，22(,)b x y =，则a b +=1212(,)x x y y ++，a b -= 1212(,)x x y y --（2） 若),(11y x A ，),(22y x B ，则AB = （3）若(,)a x y =和实数λ，则a λ=(,)x y λλ4．向量平行的充要条件的坐标表示：设a=(x 1, y 1) ，b =(x 2, y 2) 其中b ≠aa ∥b (b≠)的充要条件是12210x y x y -=二．【典例解析】题型一. 利用一组基底表示平面内的任一向量[例1] 在△OAB 中，21,41==，AD 与BC 交于点M ，设OA =a ，OB =b ，用a ,b 表示OM .练习:1．若已知1e 、2e 是平面上的一组基底，则下列各组向量中不能作为基底的一组是 ( )A ．1e 与—2eB ．31e 与22eC ．1e ＋2e 与1e —2eD ．1e 与21e 2．在平行四边形ABCD 中，E 和F 分别是边CD 和BC 的中点，若AC →＝λAE →＋μAF →，其中λ、μ∈R ，则λ＋μ＝________.题型二: 向量加、减、数乘的坐标运算 例 3 已知A （—2,4）、B （3,—1）、C （—3,—4）且CA CM 3=,CB CN 2=,求点M 、N 的坐标及向量MN 的坐标.练习:1. (2008年高考辽宁卷)已知四边形ABCD 的三个顶点A (0,2)，B (－1，－2)，C (3,1)，且BC →＝2AD →，则顶点D 的坐标为( )A ．(2，72)B ．(2，－12) C ．(3,2) D ．(1,3)2．若M(3, -2) N(-5, -1) 且 12MP =MN , 求P 点的坐标；3．若M(3, -2) N(-5, -1)，点P 在MN 的延长线上，且 12MP MN =,求P 点的坐标；4.(2009年广东卷文)已知平面向量a =,1x （） ，b =2,x x （－）， 则向量+a b ( )A 平行于x 轴B.平行于第一、三象限的角平分线C.平行于y 轴D.平行于第二、四象限的角平分线5．在三角形ABC 中，已知A (2,3)，B (8，－4)，点G (2，－1)在中线AD 上，且AG →＝2GD →， 则点C 的坐标是( )A ．(－4,2)B ．(－4，－2)C ．(4，－2)D ．(4,2)6．设向量a ＝(1，－3)，b ＝(－2,4)，c ＝(－1，－2)，若表示向量4a 、4b －2c 、2(a －c )、d 的有向线段首尾相接能构成四边形，则向量d 为( )A ．(2,6)B ．(－2,6)C ．(2，－6)D ．(－2，－6)7．已知A (7,1)、B (1,4)，直线y ＝12ax 与线段AB 交于C ，且AC →＝2CB →，则实数a 等于( )A ．2B ．1 C.45 D.53题型三: 平行、共线问题例4已知向量(1sin ,1)θ=-a ，1(,1sin )2θ=+b ，若a ∥b ，则锐角θ等于（ ）A ．30︒B ． 45︒C ．60︒D ．75︒例5．（2009北京卷文）已知向量(1,0),(0,1),(),a b c ka b k R d a b ===+∈=-， 如果//c d 那么( )A ．1k =且c 与d 同向B ．1k =且c 与d 反向C ．1k =-且c 与d 同向D ．1k =-且c 与d 反向练习：1．若向量a=(-1,x)与b =(-x, 2)共线且方向相同，求x2．已知点O(0，0)，A(1，2)，B(4，5)及AB t OA OP +=，求(1)t 为何值时，P 在x 轴上？P 在y 轴上？P 在第二象限。
高一 平面向量基本定理及坐标表示知识点+例题+练习 含答案
1．平面向量基本定理如果e 1、e 2是同一平面内两个不共线的向量，那么对于这一平面内的任一向量a ，有且只有一对实数λ1、λ2，使a ＝λ1e 1＋λ2e 2.其中，不共线的向量e 1、e 2叫做表示这一平面内所有向量的一组基底． 2．平面向量的坐标运算(1)向量加法、减法、数乘及向量的模 设a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a ＋b ＝(x 1＋x 2，y 1＋y 2)，a －b ＝(x 1－x 2，y 1－y 2)，λa ＝(λx 1，λy 1)，|a |＝x 21＋y 21. (2)向量坐标的求法①若向量的起点是坐标原点，则终点坐标即为向量的坐标．②设A (x 1，y 1)，B (x 2，y 2)，则AB →＝(x 2－x 1，y 2－y 1)，|AB →|＝(x 2－x 1)2＋(y 2－y 1)2. 3．平面向量共线的坐标表示设向量a ＝(x 1，y 1)，b ＝(x 2，y 2) (a ≠0)，如果a ∥b ，那么x 1y 2－x 2y 1＝0；反过来，如果x 1y 2－x 2y 1＝0，那么a ∥b . 【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”) (1)平面内的任何两个向量都可以作为一组基底．( × )(2)若a ，b 不共线，且λ1a ＋μ1b ＝λ2a ＋μ2b ，则λ1＝λ2，μ1＝μ2.( √ )(3)平面向量的基底不唯一，只要基底确定后，平面内的任何一个向量都可被这组基底唯一表示．( √ )(4)若a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a ∥b 的充要条件可表示成x 1x 2＝y 1y 2.( × )(5)当向量的起点在坐标原点时，向量的坐标就是向量终点的坐标．( √ )1．设e 1，e 2是平面内一组基底，那么下列说法正确的是________(填序号)． ①若实数λ1，λ2使λ1e 1＋λ2e 2＝0，则λ1＝λ2＝0；②空间内任一向量a 可以表示为a ＝λ1e 1＋λ2e 2(λ1，λ2为实数)； ③对实数λ1，λ2，λ1e 1＋λ2e 2不一定在该平面内；④对平面内任一向量a ，使a ＝λ1e 1＋λ2e 2的实数λ1，λ2有无数对． 答案 ①2．在△ABC 中，点D 在BC 边上，且CD →＝2DB →，CD →＝rAB →＋sAC →，则r ＋s ＝________. 答案 0解析 因为CD →＝2DB →，所以CD →＝23CB →＝23(AB →－AC →)＝23AB →－23AC →，则r ＋s ＝23＋⎝⎛⎭⎫－23＝0. 3．在▱ABCD 中，AC 为一条对角线，AB →＝(2,4)，AC →＝(1,3)，则向量BD →的坐标为__________． 答案 (－3，－5)解析 ∵AB →＋BC →＝AC →，∴BC →＝AC →－AB →＝(－1，－1)， ∴BD →＝AD →－AB →＝BC →－AB →＝(－3，－5)．4．设0＜θ＜π2，向量a ＝(sin 2θ，cos θ)，b ＝(cos θ，1)，若a ∥b ，则tan θ＝________.答案 12解析 ∵a ∥b ，∴sin 2θ×1－cos 2 θ＝0， ∴2sin θcos θ－cos 2 θ＝0，∵0＜θ＜π2，∴cos θ＞0，∴2sin θ＝cos θ，∴tan θ＝12.5．(教材改编)已知▱ABCD 的顶点A (－1，－2)，B (3，－1)，C (5,6)，则顶点D 的坐标为________． 答案 (1,5)解析 设D (x ，y )，则由AB →＝DC →，得(4,1)＝(5－x,6－y )，即⎩⎪⎨⎪⎧ 4＝5－x ，1＝6－y ，解得⎩⎪⎨⎪⎧x ＝1，y ＝5.题型一 平面向量基本定理的应用例1 (1)在梯形ABCD 中，AB ∥CD ，AB ＝2CD ，M ，N 分别为CD ，BC 的中点，若AB →＝λAM →＋μAN →，则λ＋μ＝________.(2)如图，在△ABC 中，AN →＝13NC →，P 是BN 上的一点，若AP →＝mAB →＋211AC →，则实数m 的值为________． 答案 (1)45 (2)311解析 (1)因为AB →＝AN →＋NB →＝AN →＋CN →＝AN →＋(CA →＋AN →)＝2AN →＋CM →＋MA →＝2AN →－14AB →－AM →，所以AB →＝85AN →－45AM →，所以λ＋μ＝45.(2)设BP →＝kBN →，k ∈R . 因为AP →＝AB →＋BP →＝AB →＋kBN → ＝AB →＋k (AN →－AB →)＝AB →＋k (14AC →－AB →)＝(1－k )AB →＋k 4AC →，且AP →＝mAB →＋211AC →，所以1－k ＝m ，k 4＝211，解得k ＝811，m ＝311.思维升华 (1)应用平面向量基本定理表示向量的实质是利用平行四边形法则或三角形法则进行向量的加、减或数乘运算．(2)用向量基本定理解决问题的一般思路是先选择一组基底，并运用该基底将条件和结论表示成向量的形式，再通过向量的运算来解决．(1)在平行四边形ABCD 中，AB →＝e 1，AC →＝e 2，NC →＝14AC →，BM →＝12MC →，则MN →＝________.(用e 1，e 2表示)(2)如图，已知点G 是△ABC 的重心，过G 作直线与AB ，AC 两边分别交于M ，N 两点，且AM →＝xAB →，AN →＝yAC →，则xy x ＋y的值为________．答案 (1)－23e 1＋512e 2 (2)13解析 (1)如图，MN →＝CN →－CM →＝CN →＋2BM →＝CN →＋23BC →＝－14AC →＋23(AC →－AB →)＝－14e 2＋23(e 2－e 1)＝－23e 1＋512e 2.(2)易知AG →＝13AB →＋13AC →，MN →＝－xAB →＋yAC →，故MG →＝⎝⎛⎭⎫13－x AB →＋13AC →.由于MG →与MN →共线，所以⎝⎛⎭⎫13－x y ＝－13x ， 即xy ＝13(x ＋y )，因此xy x ＋y ＝13.题型二 平面向量的坐标运算例2 (1)已知a ＝(5，－2)，b ＝(－4，－3)，若a －2b ＋3c ＝0，则c ＝________. (2)已知点A (1,3)，B (4，－1)，则与向量A B →同方向的单位向量为__________． 答案 (1)⎝⎛⎭⎫－133，－43 (2)⎝⎛⎭⎫35，－45 解析 (1)由已知3c ＝－a ＋2b ＝(－5,2)＋(－8，－6)＝(－13，－4)．所以c ＝⎝⎛⎭⎫－133，－43. (2)A B →＝O B →－O A →＝(4，－1)－(1,3)＝(3，－4)， ∴与A B →同方向的单位向量为A B→|A B →|＝⎝⎛⎭⎫35，－45. 思维升华 向量的坐标运算主要是利用加、减、数乘运算法则进行计算．若已知有向线段两端点的坐标，则应先求出向量的坐标，解题过程中要注意方程思想的运用及正确使用运算法则．(1)已知点A (－1,5)和向量a ＝(2,3)，若AB →＝3a ，则点B 的坐标为__________．(2)在△ABC 中，点P 在BC 上，且BP →＝2PC →，点Q 是AC 的中点，若P A →＝(4,3)，PQ →＝(1,5)，则BC →＝________.答案 (1)(5,14) (2)(－6,21)解析 (1)设点B 的坐标为(x ，y )，则AB →＝(x ＋1，y －5)．由AB →＝3a ，得⎩⎪⎨⎪⎧ x ＋1＝6，y －5＝9，解得⎩⎪⎨⎪⎧x ＝5，y ＝14.(2)BC →＝3PC →＝3(2PQ →－P A →)＝6PQ →－3P A →＝(6,30)－(12,9)＝(－6,21)．题型三 向量共线的坐标表示命题点1 利用向量共线求向量或点的坐标例3 (1)已知平面向量a ＝(1,2)，b ＝(－2，m )，且a ∥b ，则2a ＋3b ＝________.(2)已知梯形ABCD ，其中AB ∥CD ，且DC ＝2AB ，三个顶点A (1,2)，B (2,1)，C (4,2)，则点D 的坐标为________． 答案 (1)(－4，－8) (2)(2,4)解析 (1)由a ＝(1,2)，b ＝(－2，m )，且a ∥b ， 得1×m ＝2×(－2)，即m ＝－4. 从而b ＝(－2，－4)，那么2a ＋3b ＝2(1,2)＋3(－2，－4)＝(－4，－8)． (2)∵在梯形ABCD 中，AB ∥CD ，DC ＝2AB ， ∴DC →＝2AB →.设点D 的坐标为(x ，y )，则DC →＝(4,2)－(x ，y )＝(4－x,2－y )， AB →＝(2,1)－(1,2)＝(1，－1)，∴(4－x,2－y )＝2(1，－1)，即(4－x,2－y )＝(2，－2)，∴⎩⎪⎨⎪⎧ 4－x ＝2，2－y ＝－2，解得⎩⎪⎨⎪⎧x ＝2，y ＝4，故点D 的坐标为(2,4)． 命题点2 利用向量共线求参数例4 若三点A (1，－5)，B (a ，－2)，C (－2，－1)共线，则实数a 的值为________． 答案 －54解析 AB →＝(a －1,3)，AC →＝(－3,4)，根据题意AB →∥AC →，∴4(a －1)＝3×(－3)，即4a ＝－5， ∴a ＝－54.命题点3 求交点坐标例5 已知点A (4,0)，B (4,4)，C (2,6)，则AC 与OB 的交点P 的坐标为________． 答案 (3,3)解析 方法一 由O ，P ，B 三点共线，可设OP →＝λOB →＝(4λ，4λ)，则AP →＝OP →－OA →＝(4λ－4,4λ)． 又AC →＝OC →－OA →＝(－2,6)，由AP →与AC →共线，得(4λ－4)×6－4λ×(－2)＝0，解得λ＝34，所以OP→＝34OB →＝(3,3)，所以点P 的坐标为(3,3)． 方法二 设点P (x ，y )，则OP →＝(x ，y )，因为OB →＝(4,4)，且OP →与OB →共线，所以x 4＝y 4，即x ＝y .又AP →＝(x －4，y )，AC →＝(－2,6)，且AP →与AC →共线， 所以(x －4)×6－y ×(－2)＝0，解得x ＝y ＝3， 所以点P 的坐标为(3,3)．思维升华 平面向量共线的坐标表示问题的常见类型及解题策略(1)利用两向量共线求参数．如果已知两向量共线，求某些参数的取值时，利用“若a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a ∥b 的充要条件是x 1y 2＝x 2y 1”解题比较方便．(2)利用两向量共线的条件求向量坐标．一般地，在求与一个已知向量a 共线的向量时，可设所求向量为λa (λ∈R )，然后结合其他条件列出关于λ的方程，求出λ的值后代入λa 即可得到所求的向量．(3)三点共线问题．A ，B ，C 三点共线等价于AB →与AC →共线．设OA →＝(－2,4)，OB →＝(－a,2)，OC →＝(b,0)，a >0，b >0，O 为坐标原点，若A ，B ，C 三点共线，则1a ＋1b 的最小值为________．答案3＋222解析 由题意得AB →＝(－a ＋2，－2)，AC →＝(b ＋2，－4)， 又AB →∥AC →，所以(－a ＋2，－2)＝λ(b ＋2，－4)，即⎩⎪⎨⎪⎧－a ＋2＝λ(b ＋2)，－2＝－4λ，整理得2a ＋b ＝2， 所以1a ＋1b ＝12(2a ＋b )(1a ＋1b )＝12(3＋2a b ＋b a )≥12(3＋22a b ·b a )＝3＋222(当且仅当b ＝2a 时，等号成立)．11．解析法(坐标法)在向量中的应用典例 (14分)给定两个长度为1的平面向量OA →和OB →，它们的夹角为2π3.如图所示，点C 在以O 为圆心的AB 上运动．若OC →＝xOA →＋yOB →，其中x ，y ∈R ，求x ＋y 的最大值．思维点拨 可以建立平面直角坐标系，将向量坐标化，求出点A ，B 的坐标，用三角函数表示出点C 的坐标，最后转化为三角函数求最值． 规范解答解 以O 为坐标原点，OA →所在的直线为x 轴建立平面直角坐标系，如图所示，则A (1,0)，B (－12，32)．[4分]设∠AOC ＝α(α∈[0，2π3])，则C (cos α，sin α)，由OC →＝xOA →＋yOB →，得⎩⎨⎧cos α＝x －12y ，sin α＝32y ，所以x ＝cos α＋33sin α，y ＝233sin α，[8分] 所以x ＋y ＝cos α＋3sin α＝2sin(α＋π6)，[11分]又α∈[0，2π3]，所以当α＝π3时，x ＋y 取得最大值2.[14分]温馨提醒 本题首先通过建立平面直角坐标系，引入向量的坐标运算，然后用三角函数的知识求出x ＋y 的最大值．引入向量的坐标运算使得本题比较容易解决，体现了解析法(坐标法)解决问题的优势，凸显出了向量的代数特征，为用代数的方法研究向量问题奠定了基础．[方法与技巧]1．平面向量基本定理的本质是运用向量加法的平行四边形法则，将向量进行分解． 向量的坐标表示的本质是向量的代数表示，其中坐标运算法则是运算的关键． 2．根据向量共线可以证明点共线；利用两向量共线也可以求点的坐标或参数值． [失误与防范]1．要区分点的坐标和向量的坐标，向量坐标中包含向量大小和方向两种信息；两个向量共线有方向相同、相反两种情况．2．若a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a ∥b 的充要条件不能表示成x 1x 2＝y 1y 2，因为x 2，y 2有可能等于0，所以应表示为x 1y 2－x 2y 1＝0.A 组 专项基础训练 (时间：40分钟)1.如图，设O 是平行四边形ABCD 两对角线的交点，给出下列向量组： ①AD →与AB →；②DA →与BC →；③CA →与DC →；④OD →与OB →.其中可作为该平面内其他向量的基底的是________． 答案 ①③解析 ①中AD →，AB →不共线；③中CA →，DC →不共线．2．已知平面向量a ＝(1,1)，b ＝(1，－1)，则向量12a －32b ＝________.答案 (－1,2)解析 12a ＝(12，12)，32b ＝(32，－32)，故12a －32b ＝(－1,2)． 3．已知a ＝(1,1)，b ＝(1，－1)，c ＝(－1,2)，则c ＝________. 答案 12a －32b解析 设c ＝λa ＋μb ，∴(－1,2)＝λ(1,1)＋μ(1，－1)，∴⎩⎪⎨⎪⎧－1＝λ＋μ，2＝λ－μ，∴⎩⎨⎧λ＝12，μ＝－32，∴c ＝12a －32b .4．已知向量a ＝(1,2)，b ＝(1,0)，c ＝(3,4)．若λ为实数，(a ＋λb )∥c ，则λ＝________. 答案 12解析 ∵a ＋λb ＝(1＋λ，2)，c ＝(3,4)， 且(a ＋λb )∥c ，∴1＋λ3＝24，∴λ＝12.5．已知|OA →|＝1，|OB →|＝3，OA →·OB →＝0，点C 在∠AOB 内，且OC →与OA →的夹角为30°，设OC →＝mOA →＋nOB →(m ，n ∈R )，则m n 的值为________．答案 3解析 ∵OA →·OB →＝0，∴OA →⊥OB →，以OA 为x 轴，OB 为y 轴建立直角坐标系，OA →＝(1,0)，OB →＝(0，3)，OC →＝mOA →＋nOB →＝(m ，3n )．∵tan 30°＝3n m ＝33，∴m ＝3n ，即mn＝3. 6．已知A (7,1)，B (1,4)，直线y ＝12ax 与线段AB 交于点C ，且AC →＝2CB →，则实数a ＝________.答案 2解析 设C (x ，y )，则AC →＝(x －7，y －1)，CB →＝(1－x,4－y )，∵AC →＝2CB →，∴⎩⎪⎨⎪⎧ x －7＝2(1－x )，y －1＝2(4－y )，解得⎩⎪⎨⎪⎧x ＝3，y ＝3.∴C (3,3)．又∵C 在直线y ＝12ax 上，∴3＝12a ·3，∴a ＝2.7．已知点A (－1,2)，B (2,8)，AC →＝13AB →，DA →＝－13BA →，则CD →的坐标为________．答案 (－2，－4)解析 设点C ，D 的坐标分别为(x 1，y 1)，(x 2，y 2)． 由题意得AC →＝(x 1＋1，y 1－2)，AB →＝(3,6)， DA →＝(－1－x 2,2－y 2)，BA →＝(－3，－6)． 因为AC →＝13AB →，DA →＝－13BA →，所以有⎩⎪⎨⎪⎧ x 1＋1＝1，y 1－2＝2和⎩⎪⎨⎪⎧－1－x 2＝1，2－y 2＝2.解得⎩⎪⎨⎪⎧ x 1＝0，y 1＝4和⎩⎪⎨⎪⎧x 2＝－2，y 2＝0.所以点C ，D 的坐标分别为(0,4)，(－2,0)， 从而CD →＝(－2，－4)．8．已知向量OA →＝(3，－4)，OB →＝(0，－3)，OC →＝(5－m ，－3－m )，若点A ，B ，C 能构成三角形，则实数m 满足的条件是________． 答案 m ≠54解析 由题意得AB →＝(－3,1)，AC →＝(2－m,1－m )，若A ，B ，C 能构成三角形，则AB →，AC →不共线，则－3×(1－m )≠1×(2－m )，解得m ≠54. 9．已知A (1,1)，B (3，－1)，C (a ，b )．(1)若A ，B ，C 三点共线，求a ，b 的关系式；(2)若AC →＝2AB →，求点C 的坐标．解 (1)由已知得AB →＝(2，－2)，AC →＝(a －1，b －1)，∵A ，B ，C 三点共线，∴AB →∥AC →.∴2(b －1)＋2(a －1)＝0，即a ＋b ＝2.(2)∵AC →＝2AB →，∴(a －1，b －1)＝2(2，－2)．∴⎩⎪⎨⎪⎧ a －1＝4，b －1＝－4，解得⎩⎪⎨⎪⎧a ＝5，b ＝－3.∴点C 的坐标为(5，－3)．10．已知点O 为坐标原点，A (0,2)，B (4,6)，OM →＝t 1OA →＋t 2AB →.(1)求点M 在第二或第三象限的充要条件；(2)求证：当t 1＝1时，不论t 2为何实数，A ，B ，M 三点共线．(1)解 OM →＝t 1OA →＋t 2AB →＝t 1(0,2)＋t 2(4,4)＝(4t 2,2t 1＋4t 2)． 当点M 在第二或第三象限时，有⎩⎪⎨⎪⎧4t 2＜0，2t 1＋4t 2≠0， 故所求的充要条件为t 2＜0且t 1＋2t 2≠0.(2)证明 当t 1＝1时，由(1)知OM →＝(4t 2,4t 2＋2)．∵AB →＝OB →－OA →＝(4,4)，AM →＝OM →－OA →＝(4t 2,4t 2)＝t 2(4,4)＝t 2AB →，∴AM →与AB →共线，又有公共点A ，∴A ，B ，M 三点共线．B 组 专项能力提升(时间：15分钟)11．在△ABC 中，点P 是AB 上的一点，且CP →＝23CA →＋13CB →，Q 是BC 的中点，AQ 与CP 的交点为M ，又CM →＝tCP →，则t 的值为________．答案 34解析 ∵CP →＝23CA →＋13CB →， ∴3CP →＝2CA →＋CB →，即2CP →－2CA →＝CB →－CP →.∴2AP →＝PB →，因此P 为AB 的一个三等分点．∵A ，M ，Q 三点共线，∴CM →＝xCQ →＋(1－x )CA →＝x 2CB →＋(x －1)AC → (0<x <1)． ∵CB →＝AB →－AC →，∴CM →＝x 2AB →＋⎝⎛⎭⎫x 2－1AC →. ∵CP →＝CA →－P A →＝－AC →＋13AB →， 且CM →＝tCP →(0<t <1)，∴x 2AB →＋⎝⎛⎭⎫x 2－1AC →＝t ⎝⎛⎭⎫－AC →＋13AB →. ∴x 2＝t 3且x 2－1＝－t ，解得t ＝34. 12．已知向量a ＝(1,2)，b ＝(0,1)，设u ＝a ＋k b ，v ＝2a －b ，若u ∥v ，则实数k 的值为________．答案 －12解析 ∵u ＝(1,2)＋k (0,1)＝(1,2＋k )，v ＝(2,4)－(0,1)＝(2,3)，又u ∥v ，∴1×3＝2(2＋k )，得k ＝－12. 13．已知向量a ＝(1,1)，b ＝(1，－1)，c ＝(2cos α，2sin α)(α∈R )，实数m ，n 满足m a ＋n b ＝c ，则(m －3)2＋n 2的最大值为________．答案 16解析 由m a ＋n b ＝c ，可得⎩⎪⎨⎪⎧m ＋n ＝2cos α，m －n ＝2sin α，故(m ＋n )2＋(m －n )2＝2，即m 2＋n 2＝1，故点M (m ，n )在单位圆上，则点P (3,0)到点M 的距离的最大值为OP ＋1＝3＋1＝4，故(m －3)2＋n 2的最大值为42＝16.14．已知△ABC 和点M 满足MA →＋MB →＋MC →＝0.若存在实数m ，使得AB →＋AC →＝mAM →成立，则m ＝________.答案 3解析 ∵MA →＋MB →＋MC →＝0，∴M 为△ABC 的重心．如图所示，连结AM 并延长交BC 于D ，则D 为BC 的中点．∴AM →＝23AD →. 又AD →＝12(AB →＋AC →)， ∴AM →＝13(AB →＋AC →)， 即AB →＋AC →＝3AM →，∴m ＝3.15．如图所示，A ，B ，C 是圆O 上的三点，线段CO 的延长线与BA 的延长线交于圆O 外的一点D ，若OC →＝mOA →＋nOB →，则m ＋n 的取值范围是________．答案 (－1,0)解析 由题意得，OC →＝kOD →(k ＜0)，又|k |＝|OC →||OD →|＜1，∴－1＜k ＜0. 又∵B ，A ，D 三点共线，∴OD →＝λOA →＋(1－λ)OB →，∴mOA →＋nOB →＝kλOA →＋k (1－λ)OB →，∴m ＝kλ，n ＝k (1－λ)，∴m ＋n ＝k ，从而m ＋n ∈(－1,0)．。
高一数学向量知识点以及典型例题
平面向量知识点回顾一、 向量的概念（1）向量的基本要素：大小和方向.（2）向量的表示：几何表示法AB ；字母表示：a ；坐标表示法(,)x i y j x y α→→=⋅+⋅=. （3）向量的长度：即向量的大小，记作2a x y =+（4）特殊的向量：零向量a ＝O｜a ｜＝O . 单位向量a 为单位向量｜a ｜＝1.（5）相等的向量：大小相等，方向相同12112212(,)(,)x x x y x y y y =⎧=⇔⎨=⎩（6） 相反向量：0a b b a a b =−⇔=−⇔+=（7）平行向量(共线向量)：方向相同或相反的向量，称为平行向量.记作a ∥b .平行向量也称为共线向量.二、向量的运算法则（1）加法a b b a +=+()()a b c a b c ++=++AB BC AC +=注：向量的加法口诀：首尾相连，首连尾，方向指向末向量。
（2）减法()a b a b −=+− （减法可以变成加法来计算，因此加法的相关运算法则减法也适用）AB BA =− OB OA AB −=注：向量的减法口诀：首首相连，尾连尾，方向指向被减向量。
（3）数乘()()a a λμλμ=()a a a λμλμ+=+()a b a b λλλ+=+//a b a b λ⇔=注：1.a λ是一个向量,满足:a a λλ=；2.λ>0时, a λ与a 同向; λ<0时, a λ与a 异向; λ=0时,0a λ=.（4）数量积a b b a ⋅=⋅()()()a b a b a b λλλ⋅=⋅=⋅()a b c a c b c +⋅=⋅+⋅()22a a =a b a b ⋅≤注：1.a b ⋅是一个数；2.00a b ==或时，0a b ⋅=；3. 00a b ≠≠且时，()cos ,,a b a b a b θθ⋅=是之间的夹角三、向量的直角坐标系运算法则 ()11,a x y =，()22,b x y =（1） 加法()1212,a b x x y y +=++（2） 减法()1212,a b x x y y −=−−（3） 数乘()11,a x y λλλ=（4） 数量积1212a b x x y y ⋅=+21a x y =+四、重要的定理以及公式（应用）（1）平面向量基本定理1e ，2e 是同一平面内两个不共线的向量，那么，对于这个平面内任一向量，有且仅有一对实数12,λλ，使112a e e λλ=+.注：1.我们把不是共线的1e ，2e 叫做表示这一平面内所有向量的一组基底；2.基底不是唯一的，关键是不是共线；3.由定理可以将平面内任一a 在给出基底1e ，2e 的条件下进行分解；4.基底给定时，分解形式是唯一的，12,λλ是被a 、1e ，2e 唯一确定的数量。
高一向量知识点总结及例题
高一向量知识点总结及例题一、向量的概念1. 向量的定义：有向线段叫做向量向量的定义：具有大小和方向的量称为向量2. 向量的表示：一般用小写英文字母加上上方有箭头的符号表示向量，如a→（读作“a矢”）表示一个向量3. 特殊向量：零向量，单位向量零向量：方向任意，但模长为零的向量称为零向量，用0→表示单位向量：模长为1的向量称为单位向量4. 向量的性质：平行向量，共线向量二、向量的运算1. 向量的加法：平行四边形法则平行四边形法则：以向量的起点为顶点，则向量和为以这些向量为对角线的平行四边形的对角线。
2. 向量的减法：a-b=a+(-b)为a的负向量3. 向量的数乘：数c与向量a的积c倍c→4. 向量的夹角：若两向量a→和b→不共线，那么定义a→与b→的夹角α为0°≤α≤180°5. 向量的数量积：a•b=|a|•|b|•cosα6. 向量的数量积性质：（1）交换律：a•b=b•a（2）数量积的分配律：a•(b+c)=a•b+a•c（3）数量积的数乘结合律：(ca)•b=c(a•b)（4）|a•b|=|a|•|b|•cosα三、向量的坐标表示1，平面直角坐标系中的向量：（x1,y1）和（x2,y2）两点的向量为向量（x2-x1，y2-y1）2，向量的坐标与分解3，向量的坐标方向四、向量的应用1. 向量的应用：力，速度，位移2. 大小及方向的确定3. 用向量平行四边形的基本性质判定四边形的形状4. 向量的共线和共面例题：例1. 设向量a=(3,5)和向量b=(-2,4)，求向量a-b和向量b-a的坐标。
解：a-b=a+(-b)=（3,5）+(-2,-4) =(3-(-2),5-4)=(5,1)同理，b-a=b+(-a)=(-2,4)+(3,5)=(-2-3,4-5)=(-5,-1)例2：设a和b是非零向量，若|a•b|=|a|•|b|，则a、b的夹角取值为（）。
A. 45°B. 90°C. 135°D. 180°解：|a•b|=|a|•|b|cosα ，|a•b|=|a|•|b|时，cosα=1，所以α=0°。
高一数学第2讲 平面向量(知识点串讲)(解析版)
第2讲 平面向量（知识点串讲）知识整合1．向量的有关概念(1)向量：既有大小又有方向的量叫做向量，向量的大小叫做向量的长度(或模). (2)零向量：长度为0的向量，其方向是任意的． (3)单位向量：长度等于1个单位的向量．(4)平行向量：方向相同或相反的非零向量．平行向量又叫共线向量.规定：0与任一向量平行. (5)相等向量：长度相等且方向相同的向量． (6)相反向量：长度相等且方向相反的向量．例1、判断下列结论的正误(正确的打“√”，错误的打“×”) (1)向量不能比较大小，但向量的模可以比较大小．( ) (2)BA →＝OA →－OB →.( )(3)向量AB →与向量CD →是共线向量，则A ，B ，C ，D 四点在一条直线上．( )(4)已知a ，b 是两个非零向量，当a ，b 共线时，一定有b ＝λa (λ为常数)，反之也成立．( ) 【答案】 (1)√ (2)√ (3)× (4)√ [跟踪训练]1、有下列命题：①两个相等向量，它们的起点相同，终点也相同；②若|a |＝|b |，则a ＝b ；③若|AB →|＝|DC →|，则四边形ABCD 是平行四边形；④若m ＝n ，n ＝k ，则m ＝k ；⑤若a ∥b ，b ∥c ，则a ∥c ；⑥有向线段就是向量，向量就是有向线段．其中，假命题的个数是( )A ．2B ．3C ．4D ．5【答案】C [对于①，两个相等向量，它们的起点相同，终点也相同，①正确；对于②，若|a |＝|b |，方向不确定，则a ，b 不一定相等，∴②错误；对于③，若|AB →|＝|DC →|，AB →，DC →不一定相等，∴四边形ABCD 不一定是平行四边形，③错误；对于④，若m ＝n ，n ＝k ，则m ＝k ，④正确；对于⑤，若a ∥b ，b ∥c ，当b ＝0时，a ∥c 不一定成立，∴⑤错误；对于⑥，有向线段不是向量，向量可以用有向线段表示，∴⑥错误．综上，假命题是②③⑤⑥，共4个．] 知识整合2．向量的线性运算如果e 1，e 2是同一平面内的两个不共线向量，那么对于这一平面内的任意向量a ，有且只有一对实数λ1，λ2，使a ＝λ1e 1＋λ2e 2.其中，不共线的向量e 1，e 2叫做表示这一平面内所有向量的一组基底.例2、(2019·山东东营检测)如图所示，BC →＝3CD →，O 在线段CD 上，且O 不与端点C ，D 重合，若AO →＝mAB →＋(1－m )AC →，则实数m 的取值范围为________.【答案】⎝⎛⎭⎫－13，0 [设CO →＝kBC →，则k ∈⎝⎛⎭⎫0，13， ∴AO →＝AC →＋CO →＝AC →＋kBC →＝AC →＋k (AC →－AB →)＝(1＋k )AC →－kAB →. 又AO →＝mAB →＋(1－m )AC →，∴m ＝－k . ∵k ∈⎝⎛⎭⎫0，13，∴m ∈⎝⎛⎭⎫－13，0.] [跟踪训练]2、(2019·山东潍坊调研)如图，在平行四边形ABCD 中，AC ，BD 相交于点O ，E 为线段AO 的中点．若BE →＝λBA →＋μBD →(λ，μ∈R )，则λ＋μ等于( )A ．1B ．34C ．23D ．12【答案】B [∵E 为线段AO 的中点，∴BE →＝12BA →＋12BO →＝12BA →＋12⎝⎛⎭⎫12BD →＝12BA →＋14BD →＝λBA →＋μBD →，∴λ＋μ＝12＋14＝34.] 知识整合4．共线向量定理向量a (a ≠0)与b 共线，当且仅当有唯一一个实数λ，使b ＝λa .(1)一般地，首尾顺次相接的多个向量的和等于从第一个向量起点指向最后一个向量终点的向量，即A 1A 2→＋A 2A 3→＋A 3A 4→＋…＋A n －1A n ＝A 1A n →，特别地，一个封闭图形，首尾连接而成的向量和为零向量．(2)若P 为线段AB 的中点，O 为平面内任一点，则OP →＝12(OA →＋OB →)．(3)OA →＝λOB →＋μOC →(λ，μ为实数)，若点A ，B ，C 共线，则λ＋μ＝1.例3、(2019·山东青州月考)已知O 为△ABC 内一点，且2AO →＝OB →＋OC →，AD →＝tAC →，若B ，O ，D 三点共线，则t 的值为( )A ．14B ．13C ．12D ．23【答案】B [设线段BC 的中点为M ， 则OB →＋OC →＝2OM →.因为2AO →＝OB →＋OC →，所以AO →＝OM →， 则AO →＝12AM →＝14(AB →＋AC →)＝14⎝⎛⎭⎫AB →＋1t AD →＝14AB →＋14tAD →. 由B ，O ，D 三点共线，得14＋14t ＝1，解得t ＝13.][跟踪训练]3、设两个非零向量a 与b 不共线．(1)若AB →＝a ＋b ，BC →＝2a ＋8b ，CD →＝3(a －b )， 求证：A ，B ，D 三点共线；(2)试确定实数k ，使k a ＋b 和a ＋k b 共线．【答案】(1)证明 ∵AB →＝a ＋b ，BC →＝2a ＋8b ，CD →＝3(a －b )， ∴BD →＝BC →＋CD →＝2a ＋8b ＋3(a －b ) ＝2a ＋8b ＋3a －3b ＝5(a ＋b )＝5AB →，∴AB →，BD →共线．又∵它们有公共点B ，∴A ，B ，D 三点共线． (2)解 假设k a ＋b 与a ＋k b 共线， 则存在实数λ，使k a ＋b ＝λ(a ＋k b )， 即(k －λ)a ＝(λk －1)b .又a ，b 是两个不共线的非零向量， ∴k －λ＝λk －1＝0.消去λ，得k 2－1＝0，∴k ＝±1. 知识整合5．平面向量的坐标运算(1)向量的加法、减法、数乘向量及向量的模： 设a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a ＋b ＝(x 1＋x 2，y 1＋y 2)，a －b ＝(x 1－x 2，y 1－y 2)，λa ＝(λx 1，λy 1)，|a |＝x 21＋y 21. (2)向量坐标的求法：①若向量的起点是坐标原点，则终点坐标即为向量的坐标． ②设A (x 1，y 1)，B (x 2，y 2)，则AB →＝(x 2－x 1，y 2－y 1)， |AB →|＝x 2－x 12y 2－y 12.6．平面向量共线的坐标表示设a ＝(x 1，y 1)，b ＝(x 2，y 2)，其中b ≠0，则a ∥b ⇔x 1x 2＝y 1y 2.⇔x 1y 2－x 2y 1＝0.例4、(2019·山东潍坊检测)如图，正方形ABCD 中，E 为DC 的中点，若AE →＝λAB →＋μAC →，则λ＋μ的值为( )A ． 12B ．－12C ．1D ．－1【答案】A [法一：由题意得AE →＝AD →＋12AB →＝BC →＋AB →－12AB →＝AC →－12AB →，∴λ＝－12，μ＝1，∴λ＋μ＝12.法二：利用坐标法，以A 为坐标原点，AB 、AD 所在直线分别为x 轴，y 轴建立平面直角坐标系(图略)， 设正方形的边长为1，则A (0,0)，B (1,0)，C (1,1)，E ⎝⎛⎭⎫12， 1，∴AE →＝⎝⎛⎭⎫12， 1，AB →＝(1,0)，AC →＝(1,1)，则⎝⎛⎭⎫12， 1＝λ(1,0)＋μ(1,1)，∴λ＋μ＝12.][跟踪训练]4、(2019·山东青岛调研)已知向量a ＝(－1,1)，b ＝(3，m )，若a ∥(a ＋b )，则m ＝( ) A ．－2 B ．2 C ．3D ．－3【答案】D [向量a ＝(－1,1)，b ＝(3，m )，则a ＋b ＝(2，m ＋1)，a ∥(a ＋b )，则－(m ＋1)＝2，解得m ＝－3.] 知识整合7．向量的夹角已知两个非零向量a 和b ，作OA →＝a ，OB →＝b ，则∠AOB 就是向量a 与b 的夹角，向量夹角的范围是：[0，π].8．平面向量的数量积9．①交换律：a ·b ＝b ·a ；②数乘结合律：(λa )·b ＝λ(a ·b )＝a ·(λb )； ③分配律：a ·(b ＋c )＝a ·b ＋a ·c . (2)平面向量数量积运算的常用公式①(a ＋b )·(a －b )＝a 2－b 2. ②(a ＋b )2＝a 2＋2a ·b ＋b 2. ③(a －b )2＝a 2－2a ·b ＋b 2. 10．平面向量数量积的性质及其坐标表示设非零向量a ＝(x 1，y 1)，b ＝(x 2，y 2)，θ＝〈a ，b 〉.注：两个向量a ，b 的夹角为锐角⇔a ·b >0且a ，b 不共线；两个向量a ，b 的夹角为钝角⇔a ·b <0且a ，b 不共线．例5、(2018·天津卷)如图，在平面四边形ABCD 中，AB ⊥BC ，AD ⊥CD ，∠BAD ＝120°，AB ＝AD ＝1.若点E 为边CD 上的动点，则AE →·BE →的最小值为( )A ．2116B ．32C ．2516D ．3【答案】A [如图，以D 为坐标原点建立直角坐标系．连接AC ，由题意知∠CAD ＝∠CAB ＝60°，∠ACD ＝∠ACB ＝30°，则D (0,0)，A (1,0)，B ⎝⎛⎭⎫32，32，C (0，3)．设E (0，y )(0≤y ≤3)，则AE →＝(－1，y )，BE →＝⎝⎛⎭⎫－32，y －32，∴AE →·BE →＝32＋y 2－32y ＝⎝⎛⎭⎫y －342＋2116，∴当y ＝34时，AE →·BE →有最小值2116.] [跟踪训练]5、(2018·天津卷)在如图所示的平面图形中，已知OM ＝1，ON ＝2，∠MON ＝120°，BM →＝2MA →，CN →＝2NA →，则BC →·OM →的值为( )A ．－15B ．－9C ．－6D ．0【答案】C [如图，连接MN .∵BM →＝2MA →，CN →＝2NA →，∴AM AB ＝13＝AN AC ，∴MN ∥BC ，且MN BC ＝13，∴BC →＝3MN →＝3(ON →－OM →)， ∴BC →·OM →＝3(ON →·OM →－OM →2) ＝3(2×1×cos 120°－12)＝－6.]。
高中数学 第二章 平面向量 2.7 向量应用举例例题与探究(含解析)北师大版必修4-北师大版高一必修
2.7 向量应用举例典题精讲例1用向量法证明平行四边形两对角线的平方和等于四条边的平方和.思路分析：把平行四边形的边和对角线的长看成向量的长度，转化为证明向量长度之间的关系.基向量法和坐标法均可解决.答案：已知：四边形ABCD是平行四边形，求证：|AC|2＋|BD|2=2|AB|2＋2|AD|2.证法一：如图2-7-1所示，设AB=a, AD=b，∴AC=AB＋AD=a＋b，BD=AD-AB=b-a.图2-7-1∴|AC|2=（a+b）2=a2+2a·b+b2，|BD|2=（b-a）2=a2-2a·b＋b2.∴|AC|2＋|BD|2=2a2+2b2.又∵2|AB|2＋2|AD|2=2|OB|2＋2|OD|2=2a2+2b2，∴|AC|2＋|BD|2=2|AB|2＋2|AD|2,即平行四边形两对角线的平方和等于四条边的平方和.证法二：如图2-7-2所示，以A为原点，以AB所在直线为x轴，建立直角坐标系.设A（0，0）、D（a，b）、B（c，0），∴AC=AB＋AD图2-7-2=OB＋OD=（c,0）+(a，b)=(a+c,b)，BD=AD-AB=OD-OB=(a,b)-(c,0)=(a-c,b).∴|AC|2=（c+a）2+b2，|BD|2=（a-c）2+b2.∴|AC|2＋|BD|2=2a2+2c2+2b2.又∵2|AB|2＋2|AD|2=2|OB|2＋2|OD|2=2a2+2c2+2b2，∴|AC|2＋|BD|2=2|AB|2＋2|AD|2，即平行四边形两对角线的平方和等于四条边的平方和.绿色通道：1.向量法解决几何问题的步骤：①建立平面几何与向量的联系，用向量表示问题中涉及的几何元素，将平面几何问题转化为向量问题；②通过向量运算（有基向量法和坐标法两种），研究几何元素之间的关系；③把运算结果“翻译”成几何关系.这是用向量法解决平面几何问题的“三步曲”.又简称为：一建二算三译；也可说成为：捡便宜（建算译）.2.平面几何经常涉及距离、夹角的问题.而平面向量的运算,特别是数量积主要涉及向量的模及向量的夹角.因此,我们可以用向量方法解答几何问题.在具体问题中,先用向量表示相应的点、线段、夹角等几何元素,然后通过向量的运算,特别是数量积来研究点、线段等几何元素之间的关系,最后将结论转化为几何问题.变式训练如图2-7-3所示，AC、BD是梯形ABCD的对角线，BC＞AD，E、F分别为BD、AC的中点.试用向量证明：EF∥BC.图2-7-3 思路分析：证明EF ∥BC，转化为证明EF ∥BC，选择向量基底或建立坐标系均可解决. 证法一（基向量法）：设AB =a ，AD =b ，则有BD =AD -AB =b -a . ∵AD ∥BC ，∴存在实数λ＞1使BC =λAD =λb . ∵E 为BD 的中点，∴BE =21BD =21 (b -a ）. ∵F 为AC 的中点， ∴BF =BC +CF =BC +21CA =BC +21(BA -BC ）=21(BA +BC ）=21(BC -AB ）=21 (λb -a ）.∴EF =BF -BE =21 (λb -a ）-21 (b -a ）=（21λ-21）b . ∴EF =［（21λ-21）·λ1］BC . ∴EF ∥BC .EF ∥BC.证法二(坐标法)：如图2-7-4所示，以BC 为x 轴，以B 为原点建立平面直角坐标系.则B(0,0)，设A （a,b ）,D(c,b),C(d,0).图2-7-4∴E(2,2b c )，F(2,2b b a +). ∴EF =(2,2b b a +)-(2,2b c )=(0,2c d a -+)，BC =(d,0).∵2c d a -+×0-d×0=0. ∴EF ∥BC .∴EF ∥BC.例2如图2-7-5，一艘船从A 点出发以32km/h 的速度向垂直于对岸的方向行驶，同时河水的流速为2 km/h ，求船的实际航行速度的大小与方向（用与流速间的夹角表示）.图2-7-5 思路分析：船的实际航行速度是船的速度与水流速度的合速度，用平行四边形法则合成即可. 解：如图2-7-5所示，设AD =a 表示船垂直于对岸行驶的速度，AB =b 表示水流的速度，以AD 、AB 为邻边作平行四边形ABCD ，则AC 就是船的实际航行速度,即AC =a +b ， ∵|a |=32，|b |=2,a ·b =0，∴|AC |2=(a +b )2=a 2+2a ·b +b 2=16，即|AC |=4. ∵AC ·AB =（a +b ）·b =a ·b +b 2=4， ∴cos〈AC ,AB 〉21424||||=⨯=AB AC . 又∵0°≤〈AC ,AB 〉≤180°，∴〈AC ,AB 〉=60°,即船的实际航行速度的大小为4 km/h ，方向与水的流速间的夹角为60°.绿色通道： 用向量法解决物理问题的步骤：（类似于用向量方法解决平面几何问题的步骤） ①把物理问题中的量用向量来表示；②将物理问题转化为向量问题，通过向量运算解决数学问题；③把结果还原为物理问题.变式训练如图2-7-6所示，用两根绳子把重10 N 的物体W 吊在水平杆子AB 上，∠AC W=150°，∠BC W=120°,求A 和B 处所受力的大小.（忽略绳子的质量）思路分析：由于力和重量都是向量，求A 和B 处所受力的大小转化为求向量的模|CE |和|CF |.A 和B 处所受力的合力是10 N ，即物体W 的重量，用平行四边形法则解决.图2-7-6解：由题意，得四边形CEWF 是矩形， 则有CF +CE =CW ,CF ⊥CE |，CW |=10,∠FCW=60°.∴CF ·CE =0， ∴|CW |2=（CF +CE ）2=|CF |2+2CF ·CE +|CE |2. ∴|CF |2+|CE |2=100.① 又∵CF ·CE =0，〈CF ，CW 〉=60°，∴CF ·CW =CF ·（CF +CE ）=2CF +CF ·CE =2CF . ∴cos〈CF ，CW 〉||||CW CF 21||=CW . ∴|CF |=21|CW |=5,| CE |=35, 即A 和B 处所受力分别是35N 和5 N.例3（2006某某高三百校第二次考试卷，文9）O 是平面上一定点，A 、B 、C 是平面上不共线的三个点，动点P 满足OP =OA +λ(AB +AC ),λ∈［0，+∞),则P 的轨迹一定通过△A BC 的（ ） A.外心 B.垂心C.内心D.重心思路解析：OP =OA +λ(AB +AC )可以化为AP =λ(AB +AC ).所以AP ∥（AB +AC ）.又AB +AC 所在直线平分BC .所以AP 所在直线也平分BC .所以P 的轨迹一定通过△ABC答案：D绿色通道：判断图形的特点，主要从已知出发，利用向量运算的几何意义或由已知向量的关系判断出线线的位置关系或等量关系，从而对图形的特殊性作出判断.要作出准确判断，还要结合几何图形即数形结合.另外还要掌握三角形和特殊四边形的性质，例如三角形的四心（内心、外心、重心、垂心）的定义和性质，四边相等的四边形是菱形，对角线相等且相互平分的四边形是矩形等.变式训练1在四边形ABCD中,AB·BC=0,且AB=DC,则四边形ABCD是（）A.梯形B.菱形C.矩形D.正方形思路解析：由AB·BC=0，得AB⊥BC,又AB=DC,∴AB与DC平行且相等.从而四边形ABCD是矩形.答案：C变式训练2（2005全国高考卷Ⅰ，文12）点O是三角形ABC所在平面内的一点，满足OA·OB=OB·OC=OC·OA，则点O是△ABC的（）A.三个内角的角平分线的交点B.三条边的垂直平分线的交点C.三条中线的交点D.三条高的交点思路解析：由OA·OB=OB·OC，得OA·OB-OB·OC=0.∴OB·（OA-OC）=0，即OB·CA=0,∴OB⊥CA.同理可证OA⊥CB,OC⊥AB.∴OB⊥CA,OA⊥CB,OC⊥AB.答案：D问题探究问题1一位年轻的父亲将不会走路的小孩的两条胳膊悬空拎起，结果造成小孩胳臂受伤，试一试你能用向量知识加以解释吗？导思：这是日常生活中司空见惯的事情，解决这个题目的关键是首先建立数学模型，然后根据数学知识来解决，针对小孩的两条胳膊画出受力图形，然后通过胳膊受力分析，建立数学|F 1|=2cos 2||θG ,θ∈［0,π］来确定何种情景时，小孩的胳膊容易受伤.图2-7-7探究：设小孩的体重为G ，两胳膊受力分别为F 1，F 2，且F 1=F 2，两胳膊的夹角为θ,胳膊受力分析如图2-7-7（不计其他因素产生的力），不难建立向量模型：|F 1|=2cos 2||θG ，θ∈［0,π］，当θ=0时|F 1|=2||G ；当θ=3π2时，|F 1|=|G |；又2θ∈(0,2π)时，|F 1|单调递增，故当θ∈(0, 3π2)时，F 1∈(2||G ,|G |),当θ∈（3π2，π）时，|F 1|＞|G |.此时，悬空拎起小孩容易造成小孩受伤.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
高一数学 第八章 平面向量第一讲 向量的概念与线性运算 一．【要点精讲】 1．向量的概念①向量：既有大小又有方向的量。
几何表示法AB ，a ；坐标表示法),(y x j y i x a =+= 。
向量的模（长度），记作|AB |.即向量的大小，记作｜a|。
向量不能比较大小，但向量的模可以比较大小.②零向量：长度为0的向量，记为0，其方向是任意的，规定0平行于任何向量。
（与0的区别） ③单位向量｜a｜＝1。
④平行向量（共线向量）方向相同或相反的非零向量，记作a ∥b⑤相等向量记为b a=。
大小相等，方向相同),(),(2211y x y x =⎩⎨⎧==⇔2121y y x x 2．向量的运算（1）向量加法：求两个向量和的运算叫做向量的加法.如图，已知向量a ，b ，在平面内任取一点A ，作AB =a ，BC =b ，则向量AC 叫做a 与b的和，记作a+b ，即 a+b AB BC AC =+=特殊情况：abab a+bbaa+b(1)平行四边形法则三角形法则CBDCBAabbba +ba +AAB)2()3(向量加法的三角形法则可推广至多个向量相加：AB BC CD PQ QR AR +++++=，但这时必须“首尾相连”。
②向量减法： 同一个图中画出a b a b +-、要点:向量加法的“三角形法则”与“平行四边形法则”（1）用平行四边形法则时，两个已知向量是要共始点的，和向量是始点与已知向量的始点重合的那条对角线，而差向量是另一条对角线，方向是从减向量指向被减向量。
（2） 三角形法则的特点是“首尾相接”，由第一个向量的起点指向最后一个向量的终点的有向线段就表示这些向量的和；差向量是从减向量的终点指向被减向量的终点. （3）实数与向量的积3．两个向量共线定理：向量b 与非零向量a共线⇔有且只有一个实数λ，使得b =a λ。
二．【典例解析】题型一： 向量及与向量相关的基本概念概念 例1判断下列各命题是否正确(1)零向量没有方向 (2)b a ==则,(3)单位向量都相等 (4) 向量就是有向线段(5)两相等向量若共起点,则终点也相同 (6)若b a =，c b =，则c a =；(7)若b a //，c b //，则c a // (8) b a =的充要条件是||||b a =且b a //；(9) 若四边形ABCD 是平行四边形,则==,A练习. (四川省成都市一诊)在四边形ABCD 中，“AB →＝2DC →”是“四边形ABCD 为梯形”的 A 、充分不必要条件 B 、必要不充分条件 C 、充要条件 D 、既不充分也不必要条件题型二: 考查加法、减法运算及相关运算律 例2 化简)()(---=练习1.下列命题中正确的是 A ．OA OB AB -= B ．0AB BA +=C ．00AB ⋅=D ．AB BC CD AD ++=2.化简AC -BD +CD -AB 得 A ．AB B ． C ． D ．03．如图，D 、E 、F 分别是△ABC 的边AB 、BC 、CA 的中点，则( ) A.AD →＋BE →＋CF →＝0 B.BD →－CF →＋DF →＝0 C.AD →＋CE →－CF →＝0 D.BD →－BE →－FC →＝0题型三: 结合图型考查向量加、减法例3在ABC ∆所在的平面上有一点P ，满足PA PB PC AB ++=，则PBC ∆与ABC ∆的面积之比是( )A ．13B ．12C ．23D ．34例4重心、垂心、外心性质练习: 1．如图，在ΔABC 中，D 、E 为边AB 的两个三等分点，CA →=3a ，CB → =2b ，求CD → ，CE → ． 2已知a b a b+-=求证a b ⊥3若O 为ABC ∆的内心，且满足()(2)0OB OC OB OC OA -⋅+-=，则ABC ∆的形状为（ ）A.等腰三角形B.正三角形C.直角三角形D.钝角三角形4．已知O 、A 、B 是平面上的三个点，直线AB 上有一点C ，满足2AC →＋CB →＝0，则OC →＝( ) A ．2OA →－OB → B ．－OA →＋2OB →C.23OA →－13OB → D ．－13OA→＋23OB →ABCDE5．已知平面上不共线的四点O ，A ，B ，C .若OA →－3OB →＋2OC →＝0，则|AB →||BC →|等于________．6．已知平面内有一点P 及一个△ABC ，若PA →＋PB →＋PC →＝AB →，则( )A ．点P 在△ABC 外部B ．点P 在线段AB 上C ．点P 在线段BC 上D ．点P 在线段AC 上7．在△ABC 中，已知D 是AB 边上一点，若AD →＝2DB →，CD →＝13CA →＋λCB →，则λ等于( )A.23B.13 C ．－13 D ．－23 题型四: 三点共线问题例4 设21,e e 是不共线的向量,已知向量2121212,3,2e e CD e e CB e k e AB -=+=+=,若A,B,D 三点共线,求k 的值例5已知A 、B 、C 、P 为平面内四点， A 、B 、C 三点在一条直线上 PC → =mPA → +nPB → ，求证： m+n=1．练习：1．已知：2121212CD ,B C),(3e e e e e e AB +=-=+=，则下列关系一定成立的是（ ）A 、A ，B ，C 三点共线 B 、A ，B ，D 三点共线 C 、C ，A ，D 三点共线 D 、B ，C ，D 三点共线2．(原创题)设a ，b 是两个不共线的向量，若AB →＝2a ＋k b ，CB →＝a ＋b ，CD →＝2a －b ，且A ，B ，D 三点共线，则实数k 的值等于________．第2讲 平面向量的基本定理与坐标表示 一．【要点精讲】1．平面向量的基本定理可编辑BC AOM D如果21,e e 是一个平面内的两个不共线向量，那么对这一平面内的任一向量a ，有且只有一对实数21,λλ使：2211e e a λλ+=其中不共线的向量21,e e 叫做表示这一平面内所有向量的一组基底. 2．平面向量的坐标表示如图，在直角坐标系内，我们分别取与x 轴、y 轴方向相同的_单位向量_ i 、j 作为基底任作一个向量a ，有且只有一对实数x 、y ，使得a xi yj =+…………○1，把),(y x 叫做向量a 的（直角）坐标，记作(,)a x y =…………○2其中x 叫做a 在x 轴上的坐标，y 叫做a 在y 轴上的坐标，○2式叫做向量的坐标表示与a 相等的向量的坐标也为),(y x 特别地，(1,0)i =，(0,1)j =，0(0,0)= 特别提醒：设yj xi OA +=，则向量OA 的坐标),(y x 就是点A 的坐标；反过来，点A 的坐标),(y x 也就是向量OA 的坐标因此，在平面直角坐标系内，每一个平面向量都是可以用一对实数唯一表示3．平面向量的坐标运算（1）若11(,)a x y =，22(,)b x y =，则a b +=1212(,)x x y y ++，a b -= 1212(,)x x y y --（2） 若),(11y x A ，),(22y x B ，则AB = （3）若(,)a x y =和实数λ，则a λ=(,)x y λλ4．向量平行的充要条件的坐标表示：设a=(x 1, y 1) ，b =(x 2, y 2) 其中baa ∥b (b0)的充要条件是12210x y x y -=二．【典例解析】题型一. 利用一组基底表示平面内的任一向量[例1] 在△OAB 中，OB OD OA OC 21,41==，AD 与BC 交于点M ，设OA =a ，OB =b ，用a ,b 表示OM .练习:1．若已知1e 、2e 是平面上的一组基底，则下列各组向量中不能作为基底的一组是 ( ) A ．1e 与—2e B ．31e 与22e C ．1e ＋2e 与1e —2e D ．1e 与21e 2．在平行四边形ABCD 中，E 和F 分别是边CD 和BC 的中点，若AC →＝λAE →＋μAF →，其中λ、μ∈R ，则λ＋μ＝________.题型二: 向量加、减、数乘的坐标运算 例3 已知A （—2,4）、B （3,—1）、C （—3,—4）且CA CM 3=,CB CN 2=,求点M 、N 的坐标及向量MN 的坐标.练习:1. (2008年高考辽宁卷)已知四边形ABCD 的三个顶点A (0,2)，B (－1，－2)，C (3,1)，且BC →＝2AD →，则顶点D 的坐标为( )A ．(2，72)B ．(2，－12) C ．(3,2) D ．(1,3)2．若M(3, -2) N(-5, -1) 且 12MP =, 求P 点的坐标；3．若M(3, -2) N(-5, -1)，点P 在MN 的延长线上，且 12MP MN =,求P 点的坐标；4.(2009年广东卷文)已知平面向量a =,1x （） ，b =2,x x （－）， 则向量+a b ( )A 平行于x 轴B.平行于第一、三象限的角平分线C.平行于y 轴D.平行于第二、四象限的角平分线5．在三角形ABC 中，已知A (2,3)，B (8，－4)，点G (2，－1)在中线AD 上，且AG →＝2GD →， 则点C 的坐标是( )A ．(－4,2)B ．(－4，－2)C ．(4，－2)D ．(4,2)6．设向量a ＝(1，－3)，b ＝(－2,4)，c ＝(－1，－2)，若表示向量4a 、4b －2c 、2(a －c )、d 的有向线段首尾相接能构成四边形，则向量d 为( )A ．(2,6)B ．(－2,6)C ．(2，－6)D ．(－2，－6)7．已知A (7,1)、B (1,4)，直线y ＝12ax 与线段AB 交于C ，且AC →＝2CB →，则实数a 等于( )A ．2B ．1 C.45 D.53题型三: 平行、共线问题例4已知向量(1sin ,1)θ=-a ，1(,1sin )2θ=+b ，若a ∥b ，则锐角θ等于（ ）A ．30︒B ． 45︒C ．60︒D ．75︒例5．（2009北京卷文）已知向量(1,0),(0,1),(),a b c ka b k R d a b ===+∈=-， 如果//c d 那么( )A ．1k =且c 与d 同向B ．1k =且c 与d 反向C ．1k =-且c 与d 同向D ．1k =-且c 与d 反向练习：1．若向量a=(-1,x)与b =(-x, 2)共线且方向相同，求x2．已知点O(0，0)，A(1，2)，B(4，5)及AB t OA OP +=，求(1)t 为何值时，P 在x 轴上？P 在y 轴上？P 在第二象限。