有限元分析小论文
有限元论文(实用版)

基于ANSYS 的六角扳手有限元分析摘要:基于ANSYS 软件对六角螺栓扳手进行应力分析。
先通过选择单元类型、划分网格、施加边界进行分析;再者添加载荷,求解;最后得出结果,画出应力图,同时也找出结构最易破坏的位置。
关键词:六角扳手;有限元;应力云图;0 引言六角扳手不仅为轴提供支撑,还承受轴传递的各种载荷。
一个可靠的六角扳手对于减轻轴的偏心振动,保证机械设备的作业具有重要作用。
但由于六角扳手的形状复杂,传统的解析法在计算六角扳手的承载性能时存在较大误差。
故基于有限元分析软件ANSYS,对机械设备六角扳手的承载特性进行分析。
1 建立有限元模型六角扳手为左右对称结构,其三维视图和尺寸标注如图1。
六角扳手采用普通碳钢Q235,弹性模量E=2E11,泊松比u=0.3。
六角扳手承受主轴传递的竖直面载荷1500Mpa。
图1 六角扳手三维视图(单位:mm)1.1 选择单元类型图2 单元类型的选择进行任何有限元分析都必须选择合适的单元类型,单元类型决定附加的自由度,对于六角扳手,主要承受扭转,在设计过程中更关心的是其应力应变的变化情况,因此选用实体单元Quad 4node 42 和Brick 8node 45 进行结构离散。
SOLID45是三维20 节点四面体结构实体单元,在保证精度的同时,允许使用不规则的形状,适用于模拟曲线边界;每个节点有3 个自由度:节点X、Y 和Z 方向的位移,该单元具有空间的任意方向。
SOLID45单元还有可塑性、蠕动、应力刚化、大变形和大应变能力。
1.2 划分网格网格划分的过程就是结构离散化的过程,通常划分的单元越多越密集,就越能反映实际结构状况,计算精度越高,计算工作量越大,计算时间增长。
为兼顾计算精度和计算效率,采用自动划分与手动划分相结合的方法进行网格划分。
首先,利用软件对六角扳手自动划分网格,网格精度取SMRT6;然后根据扳手结构,网格精度选为LEVEL1。
经过网格加密以后共形成 448个单元和288个节点。
《防弹车门防弹性能有限元分析及其结构改进》范文

《防弹车门防弹性能有限元分析及其结构改进》篇一一、引言随着社会治安形势的日益严峻,汽车防弹技术的需求逐渐增加。
防弹车门作为汽车防弹技术的重要组成部分,其防弹性能的优劣直接关系到乘客的生命安全。
本文以有限元分析为手段,对防弹车门的防弹性能进行分析,并提出相应的结构改进措施,以提高其防弹性能。
二、防弹车门防弹性能有限元分析1. 有限元分析方法概述有限元分析是一种基于数学物理原理的数值分析方法,通过将连续的求解域离散成有限个单元,求解各单元的近似解,进而得到整个求解域的解。
在防弹车门防弹性能的分析中,有限元分析可以有效地模拟不同弹体对车门的冲击过程,为防弹车门的优化设计提供有力支持。
2. 防弹车门有限元模型的建立根据防弹车门的实际结构,建立精确的有限元模型。
模型中包括车门的钢板、防弹玻璃、防弹材料等部分,同时考虑各部分之间的连接关系。
在模型中设置合理的材料属性、接触关系和约束条件,以便进行后续的有限元分析。
3. 防弹性能的模拟与分析通过有限元分析软件,对不同弹体对车门的冲击过程进行模拟。
分析车门在不同冲击下的变形、应力分布和能量吸收等情况,评估车门的防弹性能。
同时,对车门的结构进行优化设计,以提高其防弹性能。
三、结构改进措施针对防弹车门在有限元分析中存在的问题,提出以下结构改进措施:1. 加强车门的钢板厚度和硬度,提高车门的抗冲击能力。
2. 优化车门的结构布局,合理分配各部分的材料和厚度,使车门在受到冲击时能够更好地吸收能量。
3. 采用新型的防弹材料和工艺,提高车门的防弹性能和耐用性。
4. 增强车门的密封性能,防止弹体碎片等物质侵入车内。
四、实验验证及效果评估为了验证结构改进措施的有效性,进行实验验证及效果评估。
在实验中,对改进前后的车门进行不同条件下的冲击测试,观察车门的变形、应力分布和能量吸收等情况。
同时,对比改进前后的防弹性能指标,评估结构改进措施的效果。
五、结论通过有限元分析和实验验证,本文提出的结构改进措施可以有效提高防弹车门的防弹性能。
有限元分析论文写作范文(专业推荐6篇)

有限元分析论文写作范文(专业推荐6篇)车架作为汽车的承载基体,安装着发动机、传动系、转向系、悬架、驾驶室、货厢等有关部件和总成,承受着传递给它的各种力和力矩。
车架工作状态比较复杂,无法用简单的数学方法对其进行准确的分析计算,而采用有限元方法可以对车架的静动态特性进行较为准确的分析,从而使车架设计从经验设计进入到科学设计阶段。
以下是我们为你准备的6篇有限元分析论文,希望对你有帮助。
有限元分析论文范文第一篇:油罐运输车的有限元分析及优化摘要:为验证油罐运输车的结构强度是否满足使用要求,运用有限元仿真分析方法分别建立其弯曲、扭转、紧急制动3种工况的模型并进行了最大应力分析。
结果显示,罐体结构的应力小于材料的屈服应力,在满足使用要求的基础上,采用尺寸优化分析方法减薄罐体的厚度可实现轻量化。
关键词:油罐运输车;有限元分析;尺寸优化伴随着世界经济持续发展,石油、天然气的需求逐步增加,油罐车作为短途运输交通工具发挥着重要的作用。
存在部分结构不合理和整车质量过重现象及潜在运输的危险性,同时使得运输成本增加。
因此基于CAD/CAE技术对整车进行结构分析与轻量化设计,可以提高产品的科技含量,为企业以后的生产提供设计指导。
1罐车有限元模型的建立1.1单元类型的选择罐体单元主要采用单元类型中的壳单元来划分网格,车架部分由于用梁单元不能分析应力集中问题,所以同样采用壳单元来划分车架网格,这样可以准确地得出分析结果。
罐体的单元选用四边形壳单元(QUAD4),在几何形状复杂的位置可以采用少量的三角形单元(TRIA3)来过渡,以满足总体网格质量的要求,通常要求三角形单元占总单元数的比例不超过5%【2】.罐体以及车架的单元全部为10mm尺寸单元。
1.2罐体与车架连接方式罐体与前后封头、罐体与防波板以及加强板与相应连接部件之间用节点耦合的方式模拟焊接。
大梁与副车架之间的连接采用ACM单元。
ACM单元模拟的是一种特殊的焊接方法(AreaContactMethod),不同于刚性单元结点连接的方法。
《铝合金轮毂的有限元分析》范文

《铝合金轮毂的有限元分析》篇一一、引言铝合金轮毂以其轻量化、耐腐蚀和良好的造型设计等特点,在现代汽车制造领域得到了广泛应用。
为了确保其设计、制造和使用的可靠性和安全性,有限元分析(FEA)技术被广泛应用于铝合金轮毂的力学性能评估。
本文将通过有限元分析的方法,对铝合金轮毂的力学性能进行深入研究。
二、铝合金轮毂的有限元模型建立1. 模型简化与假设在建立铝合金轮毂的有限元模型时,我们首先对实际结构进行适当的简化,忽略微小细节和次要因素。
同时,我们假设材料具有各向同性的特性,并遵循胡克定律。
2. 材料属性定义铝合金轮毂的材料属性包括弹性模量、泊松比、屈服强度等。
这些参数将直接影响有限元分析的准确性。
因此,在分析前需准确获取这些材料属性。
3. 网格划分网格划分是有限元分析的关键步骤。
我们采用合适的网格尺寸和类型,对铝合金轮毂进行网格划分,确保模型的准确性和计算效率。
三、铝合金轮毂的有限元分析方法1. 边界条件设定在有限元分析中,我们需要设定合理的边界条件,包括约束、载荷等。
这些边界条件将直接影响分析结果的准确性。
2. 静力学分析静力学分析是评估铝合金轮毂在静态载荷下的力学性能的重要手段。
我们通过施加力、压力等载荷,分析轮毂的应力分布、变形等情况。
3. 动力学分析动力学分析则用于评估铝合金轮毂在动态载荷下的力学性能。
我们通过模拟不同工况下的振动、冲击等动态载荷,分析轮毂的动态响应和疲劳寿命。
四、结果与讨论1. 静力学分析结果静力学分析结果显示,铝合金轮毂在承受静态载荷时,应力主要集中在轮辐与轮盘的连接处以及轮辐与轮毂边缘的过渡区域。
通过对比不同设计方案的应力分布情况,我们可以找出最优设计方案,以提高轮毂的承载能力和使用寿命。
2. 动力学分析结果动力学分析表明,铝合金轮毂在受到动态载荷时,会产生一定的振动和变形。
通过分析轮毂的动态响应和疲劳寿命,我们可以评估其在实际使用过程中的可靠性和安全性。
同时,我们还可以通过优化设计,降低轮毂的振动和疲劳损伤,提高其使用寿命。
有限元分析小论文

有限元分析小论文有限元分析是一种基于数值计算的工程分析方法,用于研究结构在外载荷作用下的应力、变形、振动等特性。
该方法通过将结构分割成有限个小元素,对每个小元素进行单独分析,再将各个小元素的结果组合起来得到整个结构的响应。
本文将从有限元分析的原理、应用和优缺点等方面进行论述。
有限元分析的原理是以连续体的离散为基础,将结构分割成很多小单元,每个小单元的物理特性可以通过有限个参数进行描述。
然后,根据力的平衡关系和物体运动学等基本理论,可以得到每个小单元的受力和运动情况。
最后,将所有小单元的受力和运动结果组合起来,得到整个结构的响应。
有限元分析在工程领域有广泛的应用。
首先,它可以用于研究结构在静态或动态加载下的应力和应变分布情况。
例如,在计算机辅助设计中,可以通过有限元分析预测结构在不同载荷下的变形情况,帮助工程师优化结构设计。
其次,有限元分析还可以用于模拟材料的行为和响应。
例如,在材料科学领域,可以通过有限元分析研究材料的强度、疲劳寿命等特性。
此外,有限元分析还可以用于求解流体力学、热传导等问题。
然而,有限元分析也存在一些局限性。
首先,该方法需要将结构分割成有限个小单元,因此分割的大小和形状会对结果产生影响。
如果分割不合理,可能导致结果不准确。
其次,有限元分析需要对结构的物理特性进行建模和输入,这对分析人员的经验要求较高。
最后,有限元分析的计算量较大,在分析大型结构时可能需要较长的计算时间。
综上所述,有限元分析是一种重要的工程分析方法,能够帮助工程师研究结构的响应和行为。
虽然该方法存在一些局限性,但它仍然是解决工程问题的一种有效工具。
随着计算机技术的不断发展,有限元分析的精度和效率也将进一步提高。
有限元分析实例范文

有限元分析实例范文假设我们正在设计一个桥梁结构,希望通过有限元分析来评估其受力情况和设计是否合理。
首先,我们需要将桥梁结构进行离散化,将其分为许多小的有限元单元。
每个有限元单元具有一定的材料性质和几何形状。
接下来,我们需要确定边界条件和加载条件。
例如,我们可以在桥梁两端设置固定边界条件,然后通过加载条件模拟车辆的载荷。
边界条件和加载条件的选择需要根据实际情况和设计要求来确定。
然后,我们需要选择适当的有限元模型和材料模型。
有限元模型选择的好坏将直接影响分析结果的准确性。
材料模型需要根据材料的弹性和塑性性质来选择合适的模型。
接下来,我们可以使用有限元软件将桥梁结构的离散化模型输入计算。
有限元软件将自动求解结构的受力平衡方程,并得出结构的应力和位移分布。
通过分析这些结果,我们可以评估桥梁结构的强度、刚度和稳定性等性能。
最后,根据有限元分析结果进行设计优化。
如果发现一些部分的应力过大,我们可以对设计进行调整,例如增加材料厚度或增加结构的增强筋。
通过不断优化设计,我们可以得到一个满足强度和刚度要求的桥梁结构。
需要注意的是,有限元分析只是工程设计中的一个工具,分析结果需要结合实际情况和工程经验来进行判断。
有限元分析的准确性也取决于离散化的精度、边界条件和材料模型等的选择。
总之,有限元分析是一种重要的工程分析方法,可以用于评估结构的受力情况和设计是否合理。
通过有限元分析,我们可以优化结构的设计,提高结构的性能和安全性。
希望以上例子对你对有限元分析有所了解。
土木工程学科有限元分析论文.doc

土木工程学科有限元分析论文采用大型有限元分析软件ABAQUS对本连接节点进行非线性有限元分析。
T型钢与方钢管采用Tie模拟焊接;T型钢与梁采用BoltForce通过调整螺栓长度模拟高强螺栓连接并实现预加载,考虑到栓帽与T型钢腹板、螺母与梁翼缘、梁翼缘与T型钢腹板的摩擦,摩擦系数选定为0.4。
T型钢、方钢管柱、H形钢梁和高强螺栓均采用实体单元实现。
模拟边界条件采用对柱底限制x、y和z方向的位移和x、z方向的转动,对柱顶限制x、y方向的线位移和x、z 方向的转角。
对梁端限制其平面外的转动。
BASE模型中对柱顶施加轴压比为0.2的轴向压力,对钢梁的悬臂端施加z方向位移控制的往复荷载[9]。
BASE模型的弯矩-转角滞回曲线如图3,滞回曲线呈现梭型,且稳定饱满,并随着梁端循环位移的不断增大,曲线整体刚度不断降低;梁端的极限承载力为74.361kN,极限承载力良好,对应梁端竖向位移为49.3mm;极限弯矩为89.2kN·m,极限转角为0.041rad,说明该节点具有较好的变形能力;耗能系数为2.09,说明耗能性能良好。
综上可以认为,BASE模型连接节点具有理想的抗震性能。
节点的最终破坏形式为两个T型钢腹板根部区域发生屈服破坏。
其中,能量耗散系数eC按最大荷载对应的滞回曲线所包围的面积来衡量,见图4所示。
BH250和BH300模型的弯矩-转角滞回曲线如图5与图6。
可见BH模型的滞回曲线趋势与BASE模型相似,呈现饱满的梭型[5]。
与BASE模型比照,BH250模型的初始转动刚度增加了6%,BH300的初始转动刚度增加了16%;BH250模型的极限承载力增加了30%,BH300模型的极限承载力增加了45%,说明梁高度变化对节点的极限承载力有相当大的影响,原因是在其他条件相同的情况下,随着梁高度的增加,梁上下翼缘承当的拉、压力相应减小,因此节点的承载力提高;BH250模型的耗能系数增加了6.6%,BH300模型的耗能系数增加了7.6%。
有限元分析设计论文
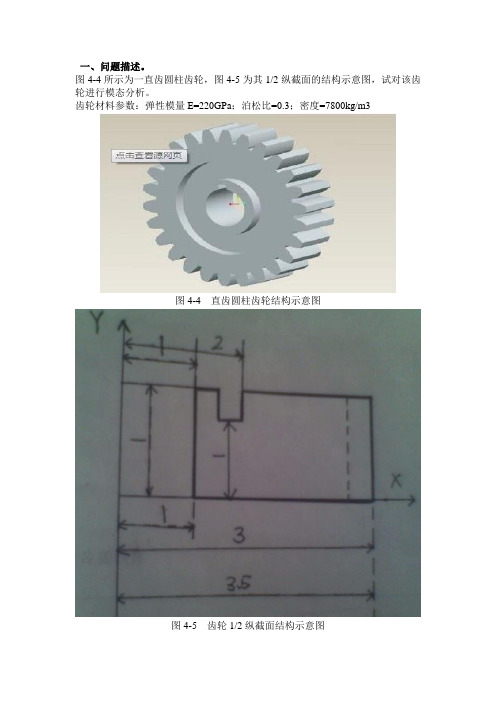
一、问题描述。
图4-4所示为一直齿圆柱齿轮,图4-5为其1/2纵截面的结构示意图,试对该齿轮进行模态分析。
齿轮材料参数:弹性模量E=220GPa;泊松比=0.3;密度=7800kg/m3图4-4 直齿圆柱齿轮结构示意图图4-5 齿轮1/2纵截面结构示意图二、单元类型的选择与设定(说明理由),材料属性指定。
该问题属于模态分析问题。
在分析过程中先建立其中一个轮齿的几何模型,再循环生成整体齿轮,选择SOLID90单元进行模态分析求解。
齿轮的模态分析需要创建三维实体模型,选择单元类型的时候一般选择实体模型Structural Solid来创建齿轮,单元类型选择对复杂形状具有较好的适应性的20节点的Brick 20node 95。
材料属性题目已指定:弹性模量E=220GPa,泊松比=0.3,密度=7800kg/m3。
1.定义工作文件名和工作标题。
1)选择Utility Menu︱File︱Change Jobname命令,出现Change Jobname对话框,在[/FILNAM]Enter new jobname输入栏中输入工作文件名EXERCISE1,单击OK按钮关闭该对话框。
2)选择Utility Menu︱File︱Change Title命令,出现Change Title对话框,在输入栏中输入MODAL ANALYSIS OF A GEAR,单击OK按钮关闭该对话框。
2.定义单元类型1)选择Main Menu︱Preprocessor︱Element Type︱Add/Edit/Delete命令,出现Element Types对话框,单击Add按钮,出现Library of Element Types对话框。
2)在Library of Element Types列表框中分别选择Structural Solid、Brick 20node 95,在Element type reference number输入栏中输入1,如图4-6所示,单击OK 按钮关闭该对话框。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形单元与矩形单元精细网格的计算精度比较
指导老师:
一、摘要
本论文研究的是三角形单元与矩形单元的精细网格的计算精度比较,通过ANSYS进行有限元法的程序实现,最后得出四边形网格的计算精度大于三角形网格的计算精度的结论。
二、提出问题
三角形单元与矩形单元的精细网格的计算比较
针对该问题,在ANSYS平台上,进行三角形单元与矩形单元的精细网格的划分,完成相应的力学分析。
(a)采用三角形单元的划分(b)采用四边形单元的划分
图1基于ANSYS平台的精细网格划分(每边划分10段)
三、解决过程
对该问题进行有限元分析的过程如下。
1 基于图形界面(GUI)的交互式操作(step by step)
(1) 进入ANSYS(设定工作目录和工作文件)
程序→ANSYS →ANSYS Interactive →Working directory(设置工作目录)→Initial jobname(设置工作文件名): TrussBridge →Press →Run →OK
(2) 设置计算类型
ANSYS Main Menu: Preferences… →Structural →OK
(3) 定义分析类型
ANSYS Main Menu: Preprocessor →Loads →Analysis Type →New Analysis→STATIC →OK
(4) 定义材料参数
ANSYS Main Menu: Preprocessor →Material Props →Material Models →Structural →Linear →Elastic →Isotropic →EX: 1(弹性模量), PRXY: 0.25(泊松比)→OK →鼠标点击该窗口右上角的“×”来关闭该窗口
(5)定义单元类型
ANSYS Main Menu: Preprocessor →Element Type →Add/Edit/Delete... →Add…→Structural Solid: Quad 4node 42 →OK(返回到Element Types窗口)→Close
(6)设置为带厚度的平面问题
ANSYS Main Menu: Preprocessor →Real Constants… →Add/Edit/Delete →Add →Type 1→
OK→Real Constant Set No: 1 (第1号实常数), THK: 1 (平面问题的厚度) →OK →Close
(7) 定义实常数以确定厚度
ANSYS Main Menu: Preprocessor →Real Constants…→Add…→Type 1 Plane42 →OK →Real Constants Set No: 1(第1号实常数), Thickness: 1(平面问题的厚度)→OK →Close (8) 构造模型
生成几何模型
ANSYS Main Menu: Preprocessor →Modeling →Create →Keypoints →In Active CS →Keypoint number:1,X,Y,Z Location in active CS:0,0,0 →Apply →(同样方式输入其余3个特征点坐标,分别为(1,0,0), (1,1,0), (0,1,0) )→OK
连接点生成面
ANSYS Main Menu: Preprocessor →Modeling →Create →Areas →Arbitrary →Through KPs →Min,Max,Inc:1,4,1 →OK
(9) 设定模型材料
ANSYS Main Menu: Preprocessor →Modeling →Create →Elements →Elem Attributes →MAT: 1 ,TYPE: 1 PLANE42 , REAL: 1 →OK
(10) 网格划分
ANSYS Utility Menu: Select →Entities →Sele lines →Sele All →OK
ANSYS Main Menu: Preprocessor →Meshing →Size Cntrls →ManualSize →Lines →All Lines→Element Sizes on All Seleceted Lines: NDIV: 10 (每一条线分为10段) ,SPACE: 1 →OK →ANSYS Main Menu:Preprocessor →Meshing →MeshTool →Mesh:Areas,Shape:Tri,mapped →Mesh →Pick ALL
(11) 模型加约束
ANSYS Utility Menu: Select →Everything
ANSYS Main Menu: Preprocessor →Loads →Define Loads →Apply →Structural →Displacement →On Keypoints→Min,Max,Inc:1 →OK →lab2:ALL DOF(约束1号特征点所有方向上的位移) →Apply →Min,Max,Inc:4 →OK →lab2:UX(约束4号特征点X方向上的位移) →OK
(12) 施加载荷
在2号特征点上施加负X方向的外载:
ANSYS Main Menu: Preprocessor →Loads →Define Loads →Apply →Structural →Force/Moment →On Keypoints →Min,Max,Inc:2 →OK →Direction of force/mom: FX , Force/moment value: -1 →Apply
在3号节点上施加X方向的外载:
ANSYS Main Menu: Preprocessor→Loads →Define Loads →Apply →Structural →Force/Moment→On Keypoints →Min,Max,Inc:3 →OK →Direction of force/mom: FX,Force/moment value: 1 →OK
(13) 计算分析
ANSYS Main Menu: Solution →Solve →Current LS →OK
(14) 结果显示
显示变形前后的位移:
ANSYS Main Menu: General Postproc →Plot Results →Deformed shape →Def + undeformed →OK
ANSYS Utility Menu: Parameters →Scalar Parameters →Selection下输入NB=NODE(1,0,0) →Accept →(以同样方式输入其余需要的结果参数表达式,分别为NB_UX=UX(NB);
NB_UY=UY(NB);NC=NODE(1,1,0);NC_UX=UX(NC) ;NC_UY=UY(NC);STR_ENGY= 0.5*(NB_UX*(-1)+ NC_UX*(1));POTE_ENGY=-0.5*(NB_UX*(-1)+ NC_UX*(1)) ) →Close ANSYS Utility Menu: List →Status →Parameters →All Parameters(显示所有计算结果)(15) 退出系统
ANSYS Utility Menu: File →Exit →Save Everything →OK
图二划分好的三角形网格
图三三角形网格的部分计算结果
图四三角形网格的displacement cart
四、数据结果
以下为计算结果:
采用三角形单元(每边分为10段)
NAME VALUE TYPE DIMENSIONS NB 2.00000000 SCALAR
NB_UX -9.56063701 SCALAR
NB_UY -9.36565959 SCALAR
NC 12.0000000 SCALAR
NC_UX 9.88621794 SCALAR
NC_UY -10.0535107 SCALAR
POTE_ENGY -9.72342747 SCALAR
STR_ENGY 9.72342747 SCALAR
采用四边形单元(每边分为10段)
NAME VALUE TYPE DIMENSIONS NB 2.00000000 SCALAR
NB_UX -12.6893715 SCALAR
NB_UY -12.6893715 SCALAR
NC 12.0000000 SCALAR
NC_UX 12.6893715 SCALAR
NC_UY -12.6893715 SCALAR POTE_ENGY -12.6893715 SCALAR
STR_ENGY 12.6893715 SCALAR
五、分析讨论
1、根据上面计算的POTE_ENGY参数,有以下的结果。
采用如图1(a)所示三角形单元网格划分计算得到的该系统的势能为
Π==U-W=9.72342747
采用如图1(b)所示矩形单元网格划分计算得到的该系统的势能为
Π==U-W=12.6893715
比较以上数据,易知矩形网格的计算精度较高。
2、有限元的程序实现需要大量算例练习才能熟练掌握,单纯做一到两个程序题是远远不够的。
3、Ansys是实现有限元法的强有力工具。
其比C++、Matlab编程操作更便捷。
