高二数学选修2-1空间向量试卷与答案
数学选修2-1空间向量与立体几何练习题含答案

24.已知向量 , ,若向量 与 共线,则 ________;若 ,则 ________.
25.在正方体 中:
(1)分别给出直线 , 的一个方向向量;
(2)分别给出平面 ,平面 ,平面 的一个法向量.
26.如图,边长为 的正方形 中, , 分别是边 , 上的点, .将 , 分别沿着 , 折起,使 , 重合于点 ,且二面角 为直二面角.
B
【考点】
平面的法向量
向量方法证明线、面的位置关系定理
直线的方向向量
【解析】
由已知可得: ,因此 ,再利用线面垂直的判定即可得出.
【解答】
解:∵直线 的方向向量为 ,
平面 的法向量 , ,
∴ ,
∴ .
故选 .
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
【考点】
空间直线的向量参数方程
直线的方向向量
【解析】
设直线 的一个方向向量为 ,运用向量垂直的条件:数量积为 ,化简可得所求向量.
【解答】
解:设直线 的一个方向向量为 ,
由两平面 与 分别以 与 为其法向量,
可得 , ,
可得 , ,
可设 ,则 , ,
可得 .
故答案为: .
16.
【答案】
【考点】
用空间向量求平面间的夹角
数学选修2-1空间向量与立体几何练习题含答案
学校:__________ 班级:__________ 姓名:__________ 考号:__________
1.已知 是空间的一组单位正交基底,而 是空间的另一组基底.若向量 在基底 下的坐标为 ,则向量 在基底 下的坐标为()
高中数学选修2-1 单元测试:空间向量及其应用word版含答案

空间向量及其应用单元测试1.(2017·江苏高考)如图,在平行六面体ABCD A 1B 1C 1D 1中,AA 1⊥平面ABCD ,且AB =AD =2,AA 1=3,∠BAD =120°.(1)求异面直线A 1B 与AC 1所成角的余弦值;(2)求二面角B A 1D A 的正弦值.解:在平面ABCD 内,过点A 作AE ⊥AD ,交BC 于点E .因为AA 1⊥平面ABCD ,所以AA 1⊥AE ,AA 1⊥AD .如图,以{AE ―→,AD ―→,AA 1―→}为正交基底,建立空间直角坐标系A xy .因为AB =AD =2, AA 1=3,∠BAD =120°,则A (0,0,0),B (3,-1,0),D (0,2,0),E (3,0,0),A 1(0,0,3),C 1(3,1,3). (1)A 1B ―→=(3,-1,-3),AC 1―→=(3,1,3). 则cos 〈A 1B ―→,AC 1―→〉=A 1B ―→·AC 1―→|A 1B ―→||AC 1―→|=3-1-37×7=-17. 因此异面直线A 1B 与AC 1所成角的余弦值为17. (2)可知平面A 1DA 的一个法向量为AE ―→=(3,0,0).设m =(x ,y , )为平面BA 1D 的一个法向量,又A 1B ―→=(3,-1,-3),BD ―→=(-3,3,0),则⎩⎪⎨⎪⎧ m ·A 1B ―→=0,m ·BD ―→=0,即⎩⎨⎧ 3x -y -3z =0,-3x +3y =0.不妨取x =3,则y =3, =2,所以m =(3,3,2)为平面BA 1D 的一个法向量, 从而cos 〈AE ―→,m 〉=AE ―→·m |AE ―→||m |=333×4=34. 设二面角B A 1D A 的大小为θ,则|cos θ|=34.因为θ∈[0,π],所以sin θ=1-cos 2θ=74. 因此二面角B A 1D A 的正弦值为74. 2.(2017·北京高考)如图,在四棱锥P ABCD 中,底面ABCD 为正方形,平面PAD ⊥平面ABCD ,点M 在线段PB 上,PD ∥平面MAC ,PA =PD =6,AB =4.(1)求证:M 为PB 的中点;(2)求二面角B PD A 的大小;(3)求直线MC 与平面BDP 所成角的正弦值.解:(1)证明:如图,设AC ,BD 的交点为E ,连接ME .因为PD ∥平面MAC ,平面MAC ∩平面PDB =ME ,所以PD ∥ME .因为底面ABCD 是正方形,所以E 为BD 的中点.所以M 为PB 的中点.(2)取AD 的中点O ,连接OP ,OE .因为PA =PD ,所以OP ⊥AD .又因为平面PAD ⊥平面ABCD ,平面PAD ∩平面ABCD =AD ,OP ⊂平面PAD ,所以OP ⊥平面ABCD .因为OE ⊂平面ABCD ,所以OP ⊥OE .因为底面ABCD 是正方形,所以OE ⊥AD .以O 为原点,以OD ―→,OE ―→,OP ―→为x 轴,y 轴, 轴的正方向建立如图所示的空间直角坐标系O xy ,则P (0,0,2),D (2,0,0),B (-2,4,0),BD ―→=(4,-4,0),PD ―→=(2,0,-2).设平面BDP 的一个法向量为n =(x ,y , ),则⎩⎪⎨⎪⎧ n ·BD ―→=0,n ·PD ―→=0,即⎩⎨⎧ 4x -4y =0,2x -2z =0.令x =1,得y =1, = 2.于是n =(1,1,2).又平面PAD 的一个法向量为p =(0,1,0),所以cos 〈n ,p 〉=n ·p |n ||p |=12.由题知二面角B PD A 为锐角,所以二面角B PD A 的大小为60°.(3)由题意知M ⎝ ⎛⎭⎪⎫-1,2,22,C (2,4,0), 则MC ―→=⎝⎛⎭⎪⎫3,2,-22. 设直线MC 与平面BDP 所成角为α,则sin α=|cos 〈n ,MC ―→〉|=|n ·MC ―→||n ||MC ―→|=269. 所以直线MC 与平面BDP 所成角的正弦值为269. 3.(2017·山东高考)如图,几何体是圆柱的一部分,它是由矩形ABCD (及其内部)以AB 边所在直线为旋转轴旋转120°得到的,G 是DF 的中点.(1)设P 是CE 上的一点,且AP ⊥BE ,求∠CBP 的大小;(2)当AB =3,AD =2时,求二面角E AG C 的大小.解:(1)因为AP ⊥BE ,AB ⊥BE , AB ,AP ⊂平面ABP ,AB ∩AP =A ,所以BE ⊥平面ABP .又BP ⊂平面ABP ,所以BE ⊥BP .又∠EBC =120°,所以∠CBP =30°.(2)以B 为坐标原点,分别以BE ,BP ,BA 所在的直线为x 轴,y 轴, 轴,建立如图所示的空间直角坐标系.由题意得A (0,0,3),E (2,0,0),G (1,3,3),C (-1,3,0),故AE ―→=(2,0,-3),AG ―→=(1,3,0),CG ―→=(2,0,3),设m =(x 1,y 1, 1)是平面AEG 的一个法向量.由⎩⎪⎨⎪⎧m ·AE ―→=0,m ·AG ―→=0,可得⎩⎨⎧ 2x 1-3z 1=0,x 1+3y 1=0. 取 1=2,可得平面AEG 的一个法向量m =(3,-3,2).设n =(x 2,y 2, 2)是平面ACG 的一个法向量.由⎩⎪⎨⎪⎧ n ·AG ―→=0,n ·CG ―→=0,可得⎩⎨⎧ x 2+3y 2=0,2x 2+3z 2=0.取 2=-2,可得平面ACG 的一个法向量n =(3,-3,-2).所以cos 〈m ,n 〉=m ·n |m |·|n |=9+3-44×4=12. 由图知二面角E AG C 为锐角,故所求二面角E AG C 的大小为60°.4.(2016·天津高考)如图,正方形ABCD 的中心为O ,四边形OBEF 为矩形,平面OBEF ⊥平面ABCD ,点G 为AB 的中点,AB =BE =2.(1)求证:EG ∥平面ADF ;(2)求二面角O EF C 的正弦值;(3)设H 为线段AF 上的点,且AH =23HF ,求直线BH 和平面CEF 所成角的正弦值. 解:依题意,OF ⊥平面ABCD ,如图,以O 为原点,分别以AD ―→,BA ―→,OF ―→的方向为x 轴,y 轴, 轴的正方向建立空间直角坐标系,依题意可得O (0,0,0),A (-1,1,0),B (-1,-1,0),C (1,-1,0),D (1,1,0),E (-1,-1,2),F (0,0,2),G (-1,0,0).(1)证明:依题意,AD ―→=(2,0,0),AF ―→=(1,-1,2).设n 1=(x 1,y 1, 1)为平面ADF 的法向量,则⎩⎪⎨⎪⎧ n 1·AD ―→=0,n 1·AF ―→=0,即⎩⎪⎨⎪⎧ 2x 1=0,x 1-y 1+2z 1=0,不妨取 1=1,可得n 1=(0,2,1).又EG ―→=(0,1,-2),可得EG ―→·n 1=0.又因为直线EG ⊄平面ADF ,所以EG ∥平面ADF .(2)易证OA ―→=(-1,1,0)为平面OEF 的一个法向量,依题意,EF ―→=(1,1,0),CF ―→=(-1,1,2).设n 2=(x 2,y 2, 2)为平面CEF 的法向量,则⎩⎪⎨⎪⎧ n 2·EF ―→=0,n 2·CF ―→=0,即⎩⎪⎨⎪⎧ x 2+y 2=0,-x 2+y 2+2z 2=0,不妨取x 2=1,可得n 2=(1,-1,1).因此有cos 〈OA ―→,n 2〉=OA ―→·n 2| OA ―→|·|n 2|=-63,于是sin 〈OA ―→,n 2〉=33. 所以,二面角O EF C 的正弦值为33. (3)由AH =23HF ,得AH =25AF . 因为AF ―→=(1,-1,2),所以AH ―→=25AF ―→=⎝ ⎛⎭⎪⎫25,-25,45, 进而有H ⎝ ⎛⎭⎪⎫-35,35,45, 从而BH ―→=⎝ ⎛⎭⎪⎫25,85,45. 因此cos 〈BH ―→,n 2〉=BH ―→·n 2|BH ―→|·|n 2|=-721. 所以直线BH 和平面CEF 所成角的正弦值为721.。
高二数学选修2-1空间向量试卷及答案
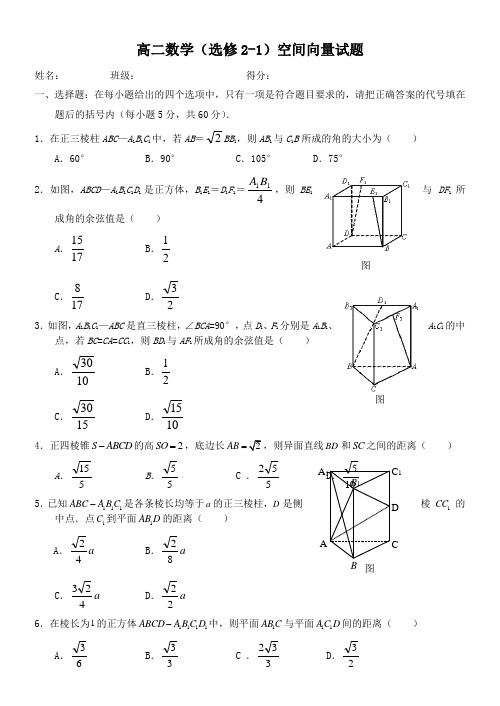
AA 1DCB B 1C 1图高二数学(选修2-1)空间向量试题姓名:_________班级:________ 得分:________一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共60分). 1.在正三棱柱ABC —A 1B 1C 1中,若AB =2BB 1,则AB 1与C 1B 所成的角的大小为( )A .60°B .90°C .105°D .75°2.如图,ABCD —A 1B 1C 1D 1是正方体,B 1E 1=D 1F 1=411B A ,则BE 1与DF 1所成角的余弦值是( )A .1715 B .21 C .178 D .23 3.如图,A 1B 1C 1—ABC 是直三棱柱,∠BCA =90°,点D 1、F 1分别是A 1B 1、A 1C 1的中点,若BC =CA =CC 1,则BD 1与AF 1所成角的余弦值是( )A .1030 B .21 C .1530 D .1015 4.正四棱锥S ABCD -的高2SO =,底边长2AB =,则异面直线BD 和SC 之间的距离( )A .515 B .55 C .552 D .105 5.已知111ABC A B C -是各条棱长均等于a 的正三棱柱,D 是侧棱1CC 的中点.点1C 到平面1AB D 的距离( )A .a 42 B .a 82 C .a 423 D .a 22 6.在棱长为1的正方体1111ABCD A B C D -中,则平面1AB C 与平面11A C D 间的距离( )A .63 B .33 C .332 D .23 图图7.在三棱锥P -ABC 中,AB ⊥BC ,AB =BC =21PA ,点O 、D 分别是AC 、PC 的中点,OP ⊥底面ABC ,则直线OD 与平面PBC 所成角的正弦值( )A .621B .338 C60210 D .302108.在直三棱柱111C B A ABC -中,底面是等腰直角三角形,90=∠ACB ,侧棱21=AA ,D ,E分别是1CC 与B A 1的中点,点E 在平面AB D 上的射影是ABD ∆的重心G .则B A 1与平面AB D 所成角的余弦值( )A .32 B .37C .23 D .73 9.正三棱柱111C B A ABC -的底面边长为3,侧棱3231=AA ,D 是C B 延长线上一点,且BC BD =,则二面角B AD B --1的大小( )A .3π B .6πC .65πD .32π10.正四棱柱1111D C B A ABCD -中,底面边长为22,侧棱长为4,E ,F 分别为棱AB ,CD 的中点,G BD EF =⋂.则三棱锥11EFD B -的体积V ( )A .66 B .3316 C .316D .1611.有以下命题:①如果向量b a ,与任何向量不能构成空间向量的一组基底,那么b a ,的关系是不共线; ②,,,O A B C 为空间四点,且向量OC OB OA ,,不构成空间的一个基底,则点,,,O A B C 一定共面;③已知向量c b a ,,是空间的一个基底,则向量c b a b a ,,-+也是空间的一个基底。
高中数学选修2-1 第三章《空间向量与立体几何》单元测试题(含答案)

这时Q ⎝ ⎛⎭⎪⎫43,43,83.答案:C二、填空题:本大题共4小题,每小题5分,共20分.13.若A (x,5-x,2x -1),B (1,x +2,2-x ),则当|AB →|取最小值时,x 的值等于________.解析:AB →=(1-x,2x -3,-3x +3),则 |AB →|=1-x2+2x -32+-3x +32=14x 2-32x +19=14⎝⎛⎭⎪⎫x -872+57,故当x =87时,|AB →|取最小值.答案:8714.正方体ABCD -A 1B 1C 1D 1中,直线BC 1与平面A 1BD 夹角的正弦值是________. 解析:如图,以DA 、DC 、DD 1分别为x 轴、y 轴、z 轴建立空间直角坐标系,设正方体的棱长为1,则A (1,0,0),B (1,1,0),C 1(0,1,1), 易证AC 1→是平面A 1BD 的一个法向量.AC 1→=(-1,1,1),BC 1→=(-1,0,1). cos 〈AC 1→,BC 1→〉=1+13×2=63. 所以BC 1与平面A 1BD 夹角的正弦值为63.答案:63设AC ∩BD =N ,连结NE ,则N ⎝ ⎛⎭⎪⎫22,22,0,E (0,0,1), ∴NE →=⎝ ⎛⎭⎪⎫-22,-22,1. 又A (2,2,0),M ⎝ ⎛⎭⎪⎫22,22,1, ∴AM →=⎝ ⎛⎭⎪⎫-22,-22,1. ∴NE →=AM →,且NE 与AM 不共线.∴NE ∥AM .又NE ⊂平面BED ,AM ⊄平面BDE ,∴AM ∥平面BDE .(2)设P (t ,t,0)(0≤t ≤2),则PF →=(2-t ,2-t,1),CD →=(2,0,0).又∵PF →与CD →所成的角为60°,|2-t ·2|2-t2+2-t 2+1·2=12, 解之得t =22,或t =322(舍去). 故点P 为AC 的中点.22.(本小题满分12分)如图,在圆锥PO 中,已知PO =2,⊙O 的直径AB =2,C 是AB 的中点,D 为AC 的中点.。
高二数学选修2-1第三章 空间向量与立体几何练习题及答案

第三章 空间向量与立体几何空间向量的数乘运算 测试题姓名:_________班级:________ 得分:_______ 1. 下列命题中不正确的命题个数是( )①若A 、B 、C 、D 是空间任意四点,则有AB +BC + CD +DA =0;②对空间任意点O 与不共线的三点A 、B 、C ,若OP =x OA +y OB +z OC (其中x 、y 、z ∈R ),则P 、A 、B 、C 四点共面;③若a 、b 共线,则a 与b 所在直线平行。
A .1B .2C .3D .42.设OABC 是四面体,G 1是△ABC 的重心,G 是OG 1上一点,且OG =3GG 1,若OG =x OA +y OB +z OC ,则(x ,y ,z )为( )A .(41,41,41) B .(43,43,43) C .(31,31,31) D .(32,32,32) 3.在平行六面体ABCD -EFGH 中,AG xAC y AF z AH =++,________.x y z ++=则4.已知四边形ABCD 中,AB =a -2c ,CD =5a +6b -8c ,对角线AC 、BD 的中点分别为E 、F ,则EF =_____________.5.已知矩形ABCD ,P 为平面ABCD 外一点,且P A ⊥平面ABCD ,M 、N 分别为PC 、PD 上的点,且M 分PC 成定比2,N 分PD 成定比1,求满足MN xAB y AD z AP =++的实数x 、y 、z 的值.§3.1.3空间向量的数量积运算1.已知正四棱柱1111ABCD A B C D -中,1AA =2AB ,E 为1AA 重点,则异面直线BE 与1CD 所形成角的余弦值为( ) A .1010 B . 15 C .31010 D . 352.如图,设A ,B ,C ,D 是空间不共面的四点,且满足0AB AC ⋅=,0AC AD ⋅=,0AB AD ⋅=,则△BCD 的形状是( )A .钝角三角形B .锐角三角形C .直角三角形D .不确定的_ C _ D _ A _ P_ N _ B_ M3.已知ABCD -A 1B 1C 1D 1 为正方体,则下列命题中错误的命题为__________.;221111111①(A A+A D +A B )=3(A B )()0;C ⋅-=1111②A A B A A 60;︒11向量与向量的夹角为AD A B ③ ⋅⋅11111立方体ABCD-A B C D 的体积为|AB AA AD |;④4.如图,已知:平行六面体ABCD -A 1B 1C 1D 1的底面ABCD 是菱形,且∠C 1CB =∠C 1CD =∠BCD =60° (1)证明:C 1C ⊥BD ; (2)当1CDCC 的值为多少时,能使A 1C ⊥平面C 1BD ?请给出证明. §3.1.4空间向量的正交分解及其坐标表示§3.1.5空间向量运算的坐标表示1.已知向量(2,2,3)OA =-,(,1,4)OB x y z =-,且平行四边形OACB 的对角线的中点坐标为M 31(0,,)22-,则(,,)x y z =( ) A .(2,4,1)--- B .(2,4,1)-- C .(2,4,1)-- D .(2,4,1)--2.已知(2,2,4)a =-,(1,1,2)b =-,(6,6,12)c =--,则向量、、a b c ( ) A .可构成直角三角形 B .可构成锐角三角形 C .可构成钝角三角形 D .不能构成三角形3.若两点的坐标是A (3cosα,3sinα,1),B (2cosθ,2sinθ,1),则|AB |的取值范围是( )A .[0,5]B .[1,5]C .(1,5)D .[1,25] 4.设点C (2a +1,a +1,2)在点P (2,0,0)、A (1,-3,2)、B (8,-1,4)确定的平面上,则a 的值为 . 5.如图,正三棱柱ABC -A 1B 1C 1的底边长为a ,侧棱长为2a .建立适当的坐标系,⑴写出A ,B ,A 1,B 1的坐标;⑵求AC 1与侧面ABB 1A 1所成的角.3.2立体几何中的向量方法1.到一定点(1,0,1)的距离小于或等于2的点的集合为( ) A .222{(,,)|(1)(1)4}x y z x y z -++-≤ B .222{(,,)|(1)(1)4}x y z x y z -++-= C .222{(,,)|(1)(1)2}x y z x y z -++-≤ D .222{(,,)|(1)(1)2}x y z x y z -++-=C 1 B 1 A 1B A2. 正方体ABCD —A 1B 1C 1D 1中,直线BC 1与平面A 1BD 所成角的余弦值为( ) A .42 B .32 C .33 D .23 3. 已知斜三棱柱111ABC A B C -,90BCA ∠=,2AC BC ==,1A 在底面ABC 上的射影恰为AC 的中点D ,又知11BA AC ⊥.(1)求证:1AC ⊥平面1A BC ; (2)求1C 到平面1A AB 的距离; (3)求二面角1A A B C --余弦值的大小.B 4. 如图,在直三棱柱111ABC A B C -中, AB =1,13AC AA ==,∠ABC =60°. (1)证明:1AB A C ⊥;(2)求二面角A —1A C —B 的大小.5. 如右图,四棱锥S-ABCD 的底面是正方形,每条侧棱的长都是底面边长的2倍,P 为侧棱S D 上的点. (1)求证:AC ⊥SD ;(2)若SD ⊥平面P AC ,求二面角P-AC-D 的大小 (3)在(2)的条件下,侧棱S C 上是否存在一点E , 使得BE ∥平面P AC .若存在,求S E :EC 的值; 若不存在,试说明理由.参考答案第三章 空间向量与立体几何3.1空间向量及其运算§3.1.1空间向量及其加减运算§3.1.2空间向量的数乘运算1.A2.A3.324.3a +3b -5c5.如图所示,取PC 的中点E ,连结NE ,则MN EN EM =-.∵1122EN CD BA ===12AB -,CBA C 1B 1 A1 D 1C 1B 1A 1DABC_ C_ D_ A_S_ F_ B_ P_ N_ EEN PM PE =-=211326PC PC PC -=,连结AC ,则PC AC AP AB AD AP =-=+- ∴11()26MN AB AB AD AP =--+-=211366AB AD AP --+,∴211,,366x y z =-=-=.§3.1.3空间向量的数量积运算1.C2.B3. ③④4.(1)设1,,CB a CD b CC c === ,则||||a b =,BD CD CB b a =-=- ,所以1()||||cos 60||||cos 600CC b a c b c a c b c a c ⋅=-⋅=⋅-⋅=︒-︒=BD ,11BD CC BD CC ∴⊥⊥即 ;(2)1,2,CD x CD CC ==1设则 2CC =x, 111,BD AA C C BD A C ⊥∴⊥ 面 ,11:0x AC CD ∴⋅= 只须求满足, 设1,,A A a AD b DC c ===,11,A C a b c C D a c =++=-,2211242()()6A C C D a b c a c a a b b c c xx ∴⋅=++⋅-=+⋅-⋅-=+-, 令24260x x+-=,则2320x x --=,解得1x =,或23x =-(舍去),111,.A C C BD ∴=⊥1CD时能使平面CC §3.1.4空间向量的正交分解及其坐标表示§3.1.5空间向量运算的坐标表示1.A2.D3.B4.165. (1)建系如图,则A (0,0,0) B (0,a ,0)A 1(0,0,2a ),C 1(-23a ,a 2,2a) (2)解法一:在所建的坐标系中,取A 1B 1的中点M , 于是M (0,a 2,2a),连结AM ,MC 1 则有1(,0,0)2MC =-(0,,0)AB a=,1)AA =, ∴10MC AB ⋅=,110MC AA ⋅=,所以,MC 1⊥平面ABB 1A 1.因此,AC 1与AM 所成的角就是AC 1与侧面ABB 1A 1所成的角.1(,)2a AC =-,(0,)2aAM =,A∴2194a AC AM ⋅=,而|13||3,||2AC a AM a ==,由cos<1,AC AM >=1132||||AC AM AC AM ⋅=,∴ <1,AC AM >=30°.∴AC 1与侧面ABB 1A 1所成的角为30°.3.2立体几何中的向量方法1.A2.C3.(1)如右图,取AB 的中点E ,则//DE BC ,因为BC AC ⊥, 所以DE AC ⊥,又1A D ⊥平面ABC , 以1,,DE DC DA 为,,x y z 轴建立空间坐标系, 则()0,1,0A -,()0,1,0C ,()2,1,0B ,()10,0,A t ,()10,2,C t ,()10,3,AC t =,()12,1,BA t =--,()2,0,0CB =,由10AC CB ⋅=,知1A C CB ⊥, 又11BA AC ⊥,从而1AC ⊥平面1A BC .(2)由1AC ⋅2130BA t =-+=,得3t = 设平面1A AB 的法向量为(),,n x y z =,(13AA =,()2,2,0AB =,所以130220n AA y z n AB x y ⎧⋅=+=⎪⎨⋅=+=⎪⎩,设1z =,则()3,3,1n =-, 所以点1C 到平面1A AB 的距离1AC n d n⋅==221. (3)再设平面1A BC 的法向量为(),,m x y z =,(10,3CA =-,()2,0,0CB =, 所以13020m CA y z m CB x ⎧⋅=-+=⎪⎨⋅==⎪⎩,设1z =,则()0,3,1m =, 故cos ,m n m n m n⋅<>==⋅77-,根据法向量的方向, 可知二面角1A A B C --7. 4.(1)三棱柱111ABC A B C -为直三棱柱,11AB AA AC AA ∴⊥⊥,,Rt ABC ∆,1,3,60AB AC ABC ==∠=︒,由正弦定理030ACB ∠=.090BAC ∴∠=AB AC ⊥即 .如右图,建立空间直角坐标系,则 1(0,0,0),(1,0,0)(0,3,0),(0,0,3)A B C A1(1,0,0),(0,3,3)AB AC ∴==, 110030(3)0AB AC ⋅=⨯+⨯+⨯-=, 1AB A C ∴⊥.(2) 如图可取(1,0,0)m AB ==为平面1AA C 的法向量, 设平面1A BC 的法向量为(,,)n l m n =, 则10,0,130BC n AC n BC ⋅=⋅==-又(,,), 303,330l m l m n m m n ⎧-+=⎪∴∴==⎨-=⎪⎩. 不妨取1,(3,1,1)m n ==则,22222231101015cos ,5(3)11100m n m n m n ⋅⨯+⨯+⨯<>===⋅++⋅++.1A AC BD ∴--15二面角的大小为arccos 5. 5. (1)连结BD ,设AC 交于BD 于O ,由题意知SO ABCD ⊥平面.以O 为坐标原点,OB OC OS ,,分别为x 轴、y 轴、z 轴正方向,建立坐标系O xyz -如右图.设底面边长为a ,则高62SO a =.于是 62(0,0,),(,0,0)22S a D a -,2(0,,0)2C a ,2(0,,0)2OC a =,26(,0,)2SD a =-,0OC SD ⋅= ,故OC SD ⊥.从而 AC SD ⊥. _ C_ A_S_ F_ BO(2)由题设知,平面PAC 的一个法向量(,0,)22DS a a =,平面DAC 的一个法向量002OS =(,,),设所求二面角为θ,则cos 2OS DS OS DSθ⋅==,得所求二面角的大小为30°. (3)在棱SC 上存在一点E 使//BE PAC 平面.由(2)知DS 是平面PAC 的一个法向量,且,0,),(0,,)2222DS a a CS a a ==-(.设,CE tCS = 则(,(1),)222BE BC CE BC tCS a t at =+=+=--,而 103BE DC t ⋅=⇔=.即当:2:1SE EC =时,BE DS ⊥.而BE 不在平面PAC 内,故//BE PAC 平面.(完)。
(典型题)高中数学高中数学选修2-1第二章《空间向量与立体几何》测试卷(含答案解析)

一、选择题1.如图,在三棱锥A BCD -中,平面ABC ⊥平面BCD ,BAC 与BCD △均为直角三角形,且90BAC BCD ∠=∠=︒,AB AC =,112CD BC==,点P 是线段AB 上的动点,若线段CD 上存在点Q ,使得异面直线PQ 与AD 成30的角,则线段PA 长的取值范围是( )A .20,⎛⎤ ⎥⎝⎦B .60,⎛⎤⎥ ⎝⎦C .(0,1]D .(0,2⎤⎦2.设动点P 在棱长为1的正方体1111ABCD A BC D -的对角线1BD 上,11D PD Bλ=,当APC ∠为锐角时,λ的取值范围是( )A .10,3⎡⎫⎪⎢⎣⎭B .10,2⎡⎫⎪⎢⎣⎭C .1,13⎛⎫ ⎪⎝⎭D .1,12⎛⎫ ⎪⎝⎭3.如图:在直棱柱111ABC A B C -中,1AA AB AC ==,AB AC ⊥,,,P Q M 分别是A 1B 1,BC,CC 1的中点,则直线PQ 与AM 所成的角是( )A .6π B .4π C .3π D .2π 4.如图,棱长为2的正方体1111ABCD A BC D -中,M 是棱1AA 的中点,点P 在侧面11ABB A 内,若1D P CM ⊥,则PBC ∆的面积的最小值为( )A .25B .5 C .45D .15.如图,在正方体1111ABCD A BC D -中,M 、N 分别是CD 、1CC 的中点,则异面直线1A M 与DN 所成角的大小是( )A .30B .45C .60D .906.如图,已知正三棱柱111ABC A B C -的棱长均为2,则异面直线1A B 与1BC 所成角的余弦值是( )A .3B.12C.14D.07.已知两平面的法向量分别为m=(0,1,0),n=(0,1,1),则两平面所成的二面角为()A.45°B.135°C.45°或135°D.90°8.已知正方体1111ABCD A BC D-的棱长为1,E为1BB的中点,则点C到平面11A D E的距离为A.5B.5C.5D.39.记动点P是棱长为1的正方体1111-ABCD A BC D的对角线1BD上一点,记11D PD Bλ=.当APC∠为钝角时,则λ的取值范围为( )A.(0,1)B.1(,1)3C.1(0,)3D.(1,3)10.在直三棱柱111ABC A B C-中,90ABC∠=︒,2AB=,11BC CC==,则异面直线1AB与1BC所成角的余弦值为()A.1010-B.1510-C.1010D.151011.如图,在直三棱柱111ABC A B C-中,1AB AC==,12BC AA==,点,E O分别是线段1,C C BC的中点,1113A F A A=,分别记二面角1F OB E--,1F OE B--,1F EB O--的平面角为,,αβγ,则下列结论正确的是()A .γβα>>B .αβγ>>C .αγβ>>D .γαβ>>12.在正三棱柱(底面是正三角形的直三棱柱)111ABC A B C -中,2AB =,E ,F 分别为11AC 和11A B 的中点,当AE 和BF 所成角的余弦值为710时,AE 与平面11BCC B 所成角的正弦值为( ) A .15 B .15 C .5 D .5 二、填空题13.设P ,A ,B ,C 是球O 表面上的四个点,PA ,PB ,PC 两两垂直,且1PA PB PC ===,则球O 的表面积为____________.14.空间四边形ABCD 的两条对棱AC 、BD 的长分别为5和4,则平行于两条对棱的截面四边形EFGH 在平移过程中,周长的取值范围是__________.15.如图所示,在正四棱柱1111ABCD A BC D -中,12AA =,1AB BC ==,动点P 、Q 分别在线段1C D 、AC 上,则线段PQ 长度的最小值是______.16.如图,平行六面体ABCD A B C D ''''-中,1,2,AB AD AA BAD BAA ===∠=∠''60DAA =='∠,则AC '的长为__________17.如图,已知平面α⊥平面β,A ,B 是平面α与平面β的交线上的两个定点,DA β⊂,CB β⊂,且DA AB ⊥,CB AB ⊥,4=AD ,8BC =,6AB =,在平面α内有一个动点P ,使得APD BPC ∠=∠,则PAB △的面积的最大值是______.18.在空间直角坐标系中,一点到三个坐标轴的距离都是1,则该点到原点的距离是________.19.正四棱柱1111ABCD A BC D -的底面边长为2,若1AC 与底面ABCD 所成角为60°,则11AC 和底面ABCD 的距离是________20.已知60︒ 的二面角的棱上有A ,B 两点,直线AC ,BD 分别在这个二面角的两个半平面内,且都垂直于AB ,已知1AB = ,2AC = ,3BD = ,则线段CD 的长为__________.三、解答题21.已知直角梯形SBCD 中,//SD BC .BC CD ⊥,336SD BC CD ===,过点B 作//BA CD 交SD 于A (如图1),沿AB 把SAB 折起,使得二面角S AB C --为直二面角,连接SC ,E 为棱SC 上任意一点(如图2).(1)求证:平面EBD ⊥平面SAC ;(2)在棱SC 上是否存在点E ,使得二面角E BD S --的余弦值为223?若存在,求出点E 的位置;若不存在,请说明理由.22.如图所示的多面体是由一个直平行六面体被平面AEFG 所截后得到的,其中60BAD ∠=︒,22AB AD ==,45BAE GAD ∠=∠=︒.(Ⅰ)求证:平面ADG ⊥平面BDG ; (Ⅱ)求直线BG 与平面AGFE 所成角的正弦值.23.如图,在四棱锥P ABCD -中,底面ABCD 是矩形,PA ⊥平面ABCD ,E 为PD 上的动点.(1)若//PB 平面AEC ,请确定点E 的位置,并说明理由.(2)设2AB AP ==,3AD =,若13PE PD =,求二面角P AC E --的正弦值.24.如图,在三棱柱111ABC A B C -中,侧面11ABB A 和11BCC B 都是正方形,平面11ABB A ⊥平面11BCC B ,,D E 分别为1BB ,AC 的中点.(1)求证://BE 平面1ACD . (2)求直线1B E 与平面1ACD 所成角的正弦值. 25.如图,已知三棱柱111ABC A B C -的底面是正三角形,侧面11BB C C 是矩形,,M N 分别为11,BC B C 的中点,P 为AM 上一点,过11B C 和P 的平面交AB 于E ,交AC 于F .(1)证明:平面111A AMN EB C F ⊥;(2)设O 为111A B C △的中心,若//AO 平面11EB C F ,且AO AB =,求直线1B E 与平面1A AMN 所成角的正弦值.26.如图,在四棱锥 P -ABCD 中,△PAB 为正三角形,四边形ABCD 为矩形,且平面PAB ⊥平面ABCD ,AB =2,PC =4(1)求证:平面PAB ⊥平面PAD(2)在线段PA 上是否存在一点N ,使得二面角A -BD -N 313N 的位置;若不存在,请说明理由【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】以C 为原点,CD 为x 轴,CB 为y 轴,过C 作平面BCD 的垂线为z 轴,建立空间直角坐标系,利用向量法能求出PA 长的取值范围. 【详解】如图,以C 为原点,CD 为x 轴,CB 为y 轴,过C 作平面BCD 的垂线为z 轴,建立空间直角坐标系,则()()()()0,0,0,0,1,1,0,2,0,1,0,0C A B D ,设(),0,0Q q ()01q ≤≤,设()0,,AP AB λλλ==-()01λ<≤,则()(,0,0)(0,1,1)(0,,)(,1,1)PQ CQ CA AP q q λλλλ=-+=---=---,(1,1,1)AD =--,异面直线PQ 与AD 成30的角,22||3cos30||||223PQ AD PQ AD q λ⋅∴===⋅++⋅, 22182516q q λ∴+=-+, 201,516[0,11]q q q ≤≤∴-+∈,即22182018211λλ⎧+≥⎨+≤⎩,解得22λ≤≤ 201,0λλ<≤∴<≤, 可得2||||22(0,1]PA AP λλ===∈. 故选:C.【点睛】利用向量求解空间角的关键在于“四破”:第一,破“建系关”,构建恰当的空间直角坐标系;第二,破“求坐标关”,准确求解相关点的坐标;第三,破“求法向量关”,求出平面的法向量;第四,破“应用公式关”.2.A解析:A 【分析】建立空间直角坐标系,APC ∠为锐角等价于cos 0PA PC APC PA PC⋅∠=>,即0PA PC ⋅>,根据向量数量积的坐标运算即可求解. 【详解】如图建立空间直角坐标系:则()1,0,0A ,()1,1,0B ,()0,1,0C ,()10,0,1D ,()11,1,1D B =-,()()111,1,1,,D P D B λλλλλ==-=-, ()11,01D A =-,()10,1,1D C =-,所以()()()111,01,,1,,1PA D A D P λλλλλλ=-=---=---,()()()110,1,1,,,1,1PC D C D P λλλλλλ=-=---=---,由APC ∠为锐角得cos 0PA PC APC PA PC⋅∠=>,即0PA PC ⋅>,所以()()22110λλλ--+->,即()()1310λλ-->,解得:103λ<<, 当0λ=时,点P 位于点1D 处,此时1APC ADC ∠=∠显然是锐角,符合题意, 所以103λ≤<, 故选:A 【点睛】关键点点睛:本题的关键点是APC ∠为锐角等价于cos 0PA PC APC PA PC⋅∠=>,即0PA PC ⋅>,还需利用11PA D A D P =-,11PC DC D P =-求出PA 、PC 的坐标,根据向量数量积的坐标运算即可求解.3.D解析:D 【分析】建立空间直角坐标系,结合直线的方向向量确定异面直线所成的角即可. 【详解】以点A 为坐标原点,建立如图所示的空间直角坐标系A xyz -, 设2AB =,则()()()()0,0,0,1,0,2,1,1,0,0,2,1A P Q M , 据此可得:()()0,1,2,0,2,1PQ AM =-=,0PQ AM ⋅=,故PQ AM ⊥,即直线PQ 与AM 所成的角是2π. 本题选择D 选项.【点睛】本题主要考查空间向量的应用,异面直线所成的角的求解等知识,意在考查学生的转化能力和计算求解能力.4.A解析:A 【分析】建立空间直角坐标系,设出P 点的坐标,利用1CM D P ⊥求得P 点坐标间的相互关系,写出三角形PBC 面积的表达式,利用二次函数的对称轴,求得面积的最小值.【详解】以1,,DA DC DD 分别为,,x y z 轴建立空间直角坐标系,依题意有()()()()12,0,1,0,2,0,0,0,2,2,,M C D P a b ,()()12,2,1,2,,2MC D P a b =--=-,由于1CM D P ⊥,故()()2,2,12,,24220a b a b --⋅-=-+-+=,解得22b a =-.根据正方体的性质可知,BC BP ⊥,故三角形PBC 为直角三角形,而()2,2,0B ,故()0,2,PB a b =--=PBC 的面积为(122BC PB ⨯⨯==126105a ==时,面积取得最小值为2655⎛⎫=⎝⎭,故选A. 【点睛】本小题主要考查空间两条直线相互垂直的坐标表示,考查三角形面积的最小值的求法,还考查了划归与转化的数学思想.属于中档题.空间两条直线相互垂直,那么两条直线的方向向量的数量积为零.对于两个参数求最值,可利用方程将其中一个参数转化为另一个参数,再结合函数最值相应的求法来求最值.5.D解析:D 【分析】可以建立空间直角坐标系,求出向量1A M 与DN 的夹角进而求出异面直线1A M 与DN 所成角. 【详解】解:以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系, 设正方体1111ABCD A BC D -中棱长为2, 则1(2,A 0,2),(0,M 1,0),(0,D 0,0),(0,N 2,1),1(2,AM =-1,2)-,(0,DN =2,1), 设异面直线1A M 与DN 所成角为θ, 则11cos 0A M DN A M DNθ⋅==⋅,90θ∴=.∴异面直线1A M 与DN 所成角的大小为90.故选D .【点睛】本题考查异面直线所成角的求法,考查正方体的结构特征,异面直线所成角等基础知识,是基础题.6.C解析:C 【分析】建立空间直角坐标系,结合空间向量的结论求解异面直线所成角的余弦值即可. 【详解】以AC 的中点O 为坐标原点,建立如图所示的空间直角坐标系O xyz -,则:()10,1,2A -,)3,0,0B,)13,0,2B ,()0,1,0C ,向量()13,1,2A B =-,()13,1,2B C =--,11cos ,A B BC <>1111A B B C A B B C⋅=⨯2222=⨯14=.本题选择C 选项.【点睛】本题主要考查异面直线所成的角的求解,空间向量的应用等知识,意在考查学生的转化能力和计算求解能力.7.C解析:C 【分析】先求出两个向量的夹角为,=45︒<>m n ,再转化为二面角的大小. 【详解】2cos ,212⋅<>===⨯⋅m n m n m n,即,=45︒<>m n , 所以两平面所成二面角为45°或180°-45°=135°. 答案:C 【点睛】本题考查了空间向量的夹角和二面角的求法,考查了计算能力和逻辑推理能力,属于基础题目.8.A【解析】分析:建立空间直角坐标系,结合题意得到点的坐标,然后利用空间向量求解点面距离即可.详解:如图所示,建立空间直角坐标系,则()10,0,1A ()10,1,1D,11,0,2E ⎛⎫⎪⎝⎭, 据此可得:()110,1,0A D =,111,0,2A E ⎛⎫=-⎪⎝⎭, 设平面11A D E 的法向量为()111,,m x y z =,则:1110102y x z =⎧⎪⎨-=⎪⎩, 据此可得平面11A D E 的一个法向量为()1,0,2m =,而()1,1,0C ,据此有:()11,1,1AC =-, 则点C 到平面11A D E 的距离为155AC m m⋅==. 本题选择A 选项.点睛:本题主要考查空间向量的应用,点面距离的求解等知识,意在考查学生的转化能力和计算求解能力.9.B解析:B 【分析】建立空间直角坐标系,利用∠APC 不是平角,可得∠APC 为钝角等价于cos ∠APC <0,即,从而可求λ的取值范围.由题设,建立如图所示的空间直角坐标系D-xyz ,则有A (1,0,0),B (1,1,0),C (0,1,0),1D (0,0,1) ∴ =(1,1,-1),∴ =(λ,λ,-λ),∴=+=(-λ,-λ,λ)+(1,0,-1)=(1-λ,-λ,λ-1) =+ =(-λ,-λ,λ)+(0,1,-1)=(-λ,1-λ,λ-1)显然∠APC 不是平角,所以∠APC 为钝角等价于cos ∠APC <0 ∴ 0PA PC ⋅<∴(1-λ)(-λ)+(-λ)(1-λ)+(λ-1)(λ-1)=(λ-1)(3λ-1)<0,得 <λ<1 因此,λ的取值范围是( ,1),故选B.点评:本题考查了用空间向量求直线间的夹角,一元二次不等式的解法,属于中档题.10.C解析:C 【分析】本题首先可以根据题意建立空间直角坐标系,然后根据2AB =以及11BC CC ==得出12,0,1AB 、()10,1,1BC =,最后根据1111cos θAB BC AB BC 即可得出结果.【详解】因为三棱柱111ABC A B C -是直三棱柱,且90ABC ∠=︒,所以可以以B 为原点、AB 为x 轴、BC 为y 轴、1BB 为z 轴构建空间直角坐标系, 如图:因为2AB =,11BC CC ==,所以()2,0,0A ,()10,0,1B ,()0,0,0B ,()10,1,1C , 故12,0,1AB ,()10,1,1BC =,设异面直线1AB 与1BC 所成角为θ, 则111110cos θ1052AB BC AB BC , 故选:C. 【点睛】本题考查异面直线所成角的求法,可借助空间向量来求解,能否合理的构建空间直角坐标系是解决本题的关键,考查计算能力,考查数形结合思想,是中档题.11.D解析:D 【分析】过点C 作//Cy AB ,以C 为原点,CA为x 轴,Cy 为y 轴,1CC 为z 轴,建立空间直角坐标系,利用向量法求解二面角的余弦值得答案. 【详解】解:因为1AB AC ==,1BC AA ==222AB AC BC +=,即AB AC ⊥ 过点C 作//Cy AB ,以C为原点,CA 为x 轴,Cy 为y 轴,1CC 为z 轴,建立空间直角坐标系, 则(1F ,0,1(2O ,12,0),(0E ,0,1(1B ,1,111(,22OB =,11(,22OE =--,11(,22OF =-,1EB =,EF=,设平面1OB E 的法向量(),,m x y z =,则111·02211·0222m OB x y m OE x y z ⎧=++=⎪⎪⎨⎪=--+=⎪⎩,取1x =,得()1,1,0m →=-,同理可求平面1OB F 的法向量(52,n =-,平面OEF 的法向量2(p =-,平面1EFB 的法向量2(,q =-. ∴461cos ||||m n m n α==434cos ||||m p m p β==,46cos ||||m q m q γ==. γαβ∴>>.故选:D .【点睛】本题考查二面角的大小的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,属于中档题.12.B解析:B 【分析】设1AA t =,以B 为原点,过B 作BC 的垂线为x 轴,BC 为y 轴,1BB 为z 轴,建立空间直角坐标系,由AE 和BF 所成角的余弦值为710,求出12t AA ==.由此能求出AE 与平面11BCC B 所成角α的正弦值. 【详解】设1AA t =,以B 为原点,过B 作BC 的垂线为x 轴,BC 为y 轴,1BB 为z 轴,建立空间直角坐标系,则3331(3,1,0),,,(0,0,0),,22A E t B F t ⎫⎫⎪⎪⎪⎪⎝⎭⎝⎭,3(AE =-,12,)t ,3(BF =12,)t , AE ∵和BF 所成角的余弦值为710,2221||||72|cos ,|10||||11t AE BF AE BF AE BF t t -∴<>===++, 解得2t =.∴3(AE =-,12,2), 平面11BCC B 的法向量(1,0,0)n =,AE ∴与平面11BCC B 所成角α的正弦值为:3||152sin ||||5AE n AE n α===. 故选:B .【点睛】本题考查线面角的正弦值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.二、填空题13.【分析】利用条件两两垂直且把三棱锥扩展为正方体球的直径即是正方体的体对角线长由球的表面积公式求解【详解】先把三棱锥扩展为正方体则正方体的体对角线的长为所以球的半径为所以球的表面积为【点睛】本题主要考 解析:3π【分析】利用条件PA ,PB ,PC 两两垂直,且1PA PB PC ===把三棱锥P ABC -扩展为正方体,球的直径即是正方体的体对角线长,由球的表面积公式求解. 【详解】先把三棱锥P ABC -3所以球的半径为32, 所以球的表面积为234π3π⨯=⎝⎭.【点睛】本题主要考查了球的体积公式:343V r π=球(其中r 为球的半径)及长方体的体对角线长公式:222l a b c =++,,a b c 分别是长方体的长、宽、高).14.【解析】如图所示设∴∴∴周长又∵∴周长的范围为故答案为: 解析:(8,10)【解析】 如图所示,设DH GHk DA AC==, ∴1AH EHk DA BD==-, ∴5GH k =,4(1)EH k =-, ∴周长82k =+. 又∵01k <<, ∴周长的范围为(8,10). 故答案为:(8,10).15.【分析】以点为坐标原点所在直线分别为轴建立空间直角坐标系利用空间向量法计算出异面直线的公垂线的长度即为所求【详解】由题意可知线段长度的最小值为异面直线的公垂线的长度如下图所示以点为坐标原点所在直线分解析:13【分析】以点D 为坐标原点,DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立空间直角坐标系,利用空间向量法计算出异面直线1C D 、AC 的公垂线的长度,即为所求. 【详解】由题意可知,线段PQ 长度的最小值为异面直线1C D 、AC 的公垂线的长度.如下图所示,以点D 为坐标原点,DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立空间直角坐标系,则点()1,0,0A 、()0,1,0C 、()10,1,2C 、()0,0,0D , 所以,()1,1,0AC =-,()10,1,2=DC ,()1,0,0DA =, 设向量(),,n x y z =满足n AC ⊥,1⊥n DC ,由题意可得1020n AC x y n DC y z ⎧⋅=-+=⎪⎨⋅=+=⎪⎩,解得2x y y z =⎧⎪⎨=-⎪⎩,取2y =,则2x =,1z =-,可得()2,2,1n =-, 因此,min23DA n PQn⋅==. 故答案为:23. 【点睛】关键点点睛:解本题的关键在于将PQ 长度的最小值转化为异面直线AC 、1C D 的距离,实际上就是求出两条异面直线的公垂线的长度,利用空间向量法求出两条异面直线间的距离,首先要求出两条异面直线公垂线的一个方向向量的坐标,再利用距离公式求解即可.16.【解析】所以【解析】22222||222AC AB BC CC AB BC CC AB BC BC CC AB CC =++=+++⋅+⋅'''⋅'+' 222000112211cos60221cos60212cos6011=+++⨯⨯⨯+⨯⨯⨯+⨯⨯⨯=所以11AC ='17.12【解析】解析:12 【解析】18.【解析】【分析】设出点的坐标根据题意列出方程组从而求得该点到原点的距离【详解】设该点的坐标因为点到三个坐标轴的距离都是1所以所以故该点到原点的距离为故填【点睛】本题主要考查了空间中点的坐标与应用空间【解析】 【分析】 设出点的坐标(,,)x y z ,根据题意列出方程组,从而求得该点到原点的距离. 【详解】设该点的坐标(,,)x y z因为点到三个坐标轴的距离都是1所以221x y +=,221y z +=,221x z +=,所以22232x y z ++=故该点到原点的距离为2226=2x y z ++, 故填6. 【点睛】本题主要考查了空间中点的坐标与应用,空间两点间的距离公式,属于中档题.19.【解析】分析:确定A1C1到底面ABCD 的距离为正四棱柱ABCD ﹣A1B1C1D1的高即可求得结论详解:∵正四棱柱ABCD ﹣A1B1C1D1∴平面ABCD ∥平面A1B1C1D1∵A1C1⊂平面A1B解析:26. 【解析】分析:确定A 1C 1到底面ABCD 的距离为正四棱柱ABCD ﹣A 1B 1C 1D 1的高,即可求得结论. 详解:∵正四棱柱ABCD ﹣A 1B 1C 1D 1, ∴平面ABCD ∥平面A 1B 1C 1D 1, ∵A 1C 1⊂平面A 1B 1C 1D 1, ∴A 1C 1∥平面ABCD∴A 1C 1到底面ABCD 的距离为正四棱柱ABCD ﹣A 1B 1C 1D 1的高∵正四棱柱ABCD ﹣A 1B 1C 1D 1的底面边长为2,AC 1与底面ABCD 成60°角, ∴A 1A=22tan60°=26 故答案为26.点睛:本题考查线面距离,确定A 1C 1到底面ABCD 的距离为正四棱柱ABCD ﹣A 1B 1C 1D 1的高是解题的关键.如果直线和已知的平面是平行的,可以将直线和平面的距离,转化为直线上一点到平面的距离.20.【解析】根据题意画图由空间向量法得到故答案为: 解析:22【解析】根据题意画图,由空间向量法得到()2222||2?·CD CA AB BD CA AB BD CA AB AB BD BDCA =++=+++++14===故答案为:三、解答题21.(1)证明见解析;(2)存在,点E 为棱SC 的中点. 【分析】(1)由翻折的性质结合二面角的定义可得SA AD ⊥,再由线面垂直的判定与性质可得SA BD ⊥,再结合平面几何的知识可得BD AC ⊥,进而可得BD ⊥平面SAC ,结合面面垂直的判定即可得证;(2)建立空间直角坐标系,表示点()2,2,44E λλλ-,由线面垂直的性质结合二面角的定义可得SOE ∠为二面角E BD S --的平面角,再由2cos OS OE SOE OS OE⋅∠==⋅可得解. 【详解】(1)证明:由翻折的性质可知:SA AB ⊥,AD AB ⊥, 所以SAD ∠为二面角S AB C --的平面角, 又因为二面角S AB C --为直二面角, 所以90SAD ∠=︒,即SA AD ⊥,又AB AD A ⋂=,所以SA ⊥平面ABCD ,所以SA BD ⊥, 由题意可知四边形ABCD 为正方形,所以BD AC ⊥, 又因为AC SA A ⋂=,所以BD ⊥平面SAC , 又BD ⊂平面EBD ,所以平面EBD ⊥平面SAC ; (2)存在;连接,OS OE ,以A 为原点,AB ,AD ,AS 的方向分别为x 轴,y 轴,z 轴正方向建立空间坐标系,如图,则()2,0,0B ,()0,2,0D ,()2,2,0C ,()0,0,4S ,又知点E 在线段SC 上, 设()2,2,4SE λSC λλλ==-(01λ≤≤),因此()2,2,44E λλλ-, 又因为()1,1,0O ,所以()1,1,4OS =--,()21,21,44OE λλλ=---, 由BD ⊥平面SAC 可得OE BD ⊥,OS BD ⊥, 所以SOE ∠为二面角E BD S --的平面角, 所以()()22121244422cos 3222144λλλOS OE SOE OS OEλλ-+-+-⋅∠===⋅⋅-+- 即29102244018λλλ-=-+,解得12λ=或92λ=,因为01λ≤≤,所以12λ=, 即棱SC 上存在点E ,使得二面角E BD S --的余弦值为23, 此时点E 为棱SC 的中点. 【点睛】 关键点点睛:(1)利用空间位置关系的判定与性质判定面面垂直;(2)由二面角的定义找到二面角的平面角,建立合适的空间直角坐标系,利用空间向量解决夹角问题.22.(Ⅰ)证明见解析;(Ⅱ)217【分析】(Ⅰ)证明:AD DB ⊥,GD DB ⊥,即可证明BD ⊥平面ADG ,从而得到平面ADG ⊥平面BDG ;(Ⅱ)建立空间直角坐标系,利用向量方法求直线GB 与平面AEFG 所成角的正弦值. 【详解】(Ⅰ)证明:在BAD 中,22AB AD ==,60BAD ∠=︒.由余弦定理2222cos60BD AD AB AB AD =+-︒,3BD =, 222AB AD DB =+,AD DB ∴⊥,在直平行六面体中,GD ⊥平面ABCD ,DB ⊂平面ABCD ,GD DB ∴⊥, 又ADGD D =,,AD DG ⊂平面ADGBD ∴⊥平面ADG .又因为BD ⊂平面BDG , 所以平面ADG ⊥平面BDG ;(Ⅱ)解:如图以D 为原点建立空间直角坐标系D xyz -,45BAE GAD ∠=∠=︒,22AB AD ==,(1A ∴,0,0),(0,3,0)B ,(0,3,2)E ,(0G ,0,1),(1,3,2)AE =-,(1,0,1)AG =-,(0,3,1)GB =-,设平面AEFG 的法向量(,,)n x y z =,·320·0n AE x y z n AG x z ⎧=-++=⎪⎨=-+=⎪⎩令1x =,得33y -=,1z =, ∴3(1,,1)n =-,设直线GB 和平面AEFG 的夹角为θ,∴21sin |cos ,|||7||||GB n GB n GB n θ=<>==, 所以直线GB 与平面AEFG 所成角的正弦值为21.【点睛】本题考查了立体几何中的面面垂直的判定和线面角的求解问题,意在考查学生的空间想象能力和逻辑推理能力;解答本题关键在于能利用直线与直线、直线与平面、平面与平面关系的相互转化,通过严密推理,同时对于立体几何中角的计算问题,往往可以利用空间向量法,通过求解平面的法向量,利用向量的夹角公式求解. 23.(1)点E 是PD 的中点,详见解析;(2)361. 【分析】(1)点E 是PD 的中点,连接BD 交AC 与点O ,连接OE ,由中位线定理得到//OE PB ,再利用线面平行的判定定理证明.(2)以A 为原点,以AB ,AD ,AP 分别为x ,y ,z 轴,建立空间直角坐标系,分别求得平面PAC 的一个法向量()111,,m x y z =,平面ACE 的一个法向量()222,,n x y z =,设二面角P AC E --为θ,由cos m n m nθ⋅=⋅求解.【详解】(1)点E 是PD 的中点,如图所示:连接BD 交AC 与点O ,连接OE , 所以//OE PB ,又PB ⊄平面AEC ,OE ⊂平面AEC , 所以//PB 平面AEC .(2)以A 为原点,以AB ,AD ,AP 分别为x ,y ,z 轴,建立空间直角坐标系,则()()()()40,0,2,0,0,0,2,3,0,0,3,0,0,1,3P A C D E ⎛⎫ ⎪⎝⎭,所以()()42,3,0,0,0,2,0,1,3AC AP AE ⎛⎫=== ⎪⎝⎭,设平面PAC 的一个法向量为()111,,m x y z =,则00m AC m AP ⎧⋅=⎨⋅=⎩,即 11123020x y z +=⎧⎨=⎩,令 1113,2,0x y z ==-=,则()3,2,0m =- 设平面ACE 的一个法向量为()222,,n x y z =,则00n AC n AE ⎧⋅=⎨⋅=⎩,即 2221230403x y y z +=⎧⎪⎨+=⎪⎩, 令 22233,2,2x y z ==-=,则33,2,2n ⎛⎫=- ⎪⎝⎭,设二面角P AC E --为θ, 所以213cos 61m n m nθ⋅==⋅,所以 22213361sin 1cos 161θθ⎛⎫=-- ⎪ ⎪⎝⎭. 【点睛】方法点睛:1、利用向量求异面直线所成的角的方法:设异面直线AC ,BD 的夹角为β,则cos β=AC BD AC BD⋅⋅.2、利用向量求线面角的方法:(1)分别求出斜线和它所在平面内的射影直线的方向向量,转化为求两个方向向量的夹角(或其补角);(2)通过平面的法向量来求,即求出斜线的方向向量与平面的法向量所夹的锐角,取其余角就是斜线和平面所成的角.3、利用向量求面面角的方法:就是分别求出二面角的两个面所在平面的法向量,然后通过两个平面的法向量的夹角得到二面角的大小,但要注意结合实际图形判断所求角是锐角还是钝角.24.(1)证明见解析;(2)23. 【分析】(1)取1AC 中点F ,证明四边形EFDB 为平行四边形,证出//BE DF ,即可证明//BE 平面1ACD ;(2)根据题意建立空间直角坐标系,写出点的坐标,求解平面1ACD 的 法向量,利用数量积的计算公式即可求出直线1B E 与平面1ACD 所成角的正弦值. 【详解】(1)证明:取1AC 中点F ,连接DF ,EF , ∵,E F 分别为1,AC AC 的中点,∴1//EF AA ,且112EF AA =,又四边形11ABB A 是正方形,∴11//BB AA 且11BB AA =, 即1//EF BB 且112EF BB =,又∵D 为1BB 中点,∴//EF BD 且EF BD =,所以四边形EFDB 为平行四边形,所以//BE DF ,又BE ⊄平面1ACD ,DF ⊂平面1ACD , 所以//BE 平面1ACD . (2)由题意,1,,BA BC BB 两两垂直,所以以B 为原点建立如图所示的空间直角坐标系,设12BA BC BB ===,则11(0,2,0),(1,0,1),(2,0,0),(0,1,0),(0,2,2)B E C D A . ,11(1,2,1),(2,1,0),(2,2,2)B E CD AC =-=-=-,设平面 1ACD 的法向量为(),,m x y z =,则100AC m CD m ⎧⋅=⎨⋅=⎩,即 222020x y z x y -++=⎧⎨-+=⎩,得()1,2,1m =-设直线1B E 与平面1ACD 所成角为θ, 1111412sin cos ,366B E m B E mB E mθ, 所以直线1B E 与平面1ACD 所成角的正弦值为23.【点睛】方法点睛:本题考查的是空间向量与立体几何的问题,(1)关于线面平行的证明,一般利用线面平行的判定定理证明,需要证明平行线,一般是找中位线或者平行四边形证明;(2)关于线面角的求解,一般利用空间向量的方法,需要求解平面的法向量,再代入数量积求解公式计算.25.(1)证明见解析;(210【分析】(1)证明EF ⊥平面1A AMN 即可得面面垂直;(2)求出BE 与EF 的夹角的余弦值,利用EF 是平面1A AMN 的法向量,易得线面角的正弦值. 【详解】(1)因为侧面11BB C C 是矩形,,M N 分别为11,BC B C 的中点,所以1BB BC ⊥,1//MN BB ,从而BC MN ⊥,又ABC 是正三角形,M 是BC 中点,所以AM BC ⊥,因为AM MN M ⋂=,,AM MN ⊂平面1A AMN ,所以BC ⊥平面1A AMN ,11//B C 平面ABC ,11BC ⊂平面11B C FE ,平面ABC 平面11B C FE EF =,所以11//B C EF ,而11//BC B C ,所以//EF BC ,所以EF ⊥平面1A AMN ,EF ⊂平面11B C FE ,所以平面111A AMN EB C F ⊥; (2)EFAM P =,连接PN ,//AO 平面11EB C F ,平面11EB C F平面1A AMN PN =,AO ⊂平面1A AMN ,所以//AO PN ,又由三棱柱的性质得//ON AP ,所以APNO 是平行四边形,所以AP NO =,O 是111A B C △的中心,则113ON A N =,所以11133AP A N AM ==, 所以13EF AP BC AM ==, 设3BC a =,则EF a =,3PN AO BC a ===,由三棱柱性质知四边形11B C FE 是等腰梯形,如图,11PN B C ⊥,作11EH B C ⊥于H ,则3EH PN a ==,又11(3)2B H a a a =-=, 所以110B E a =,111110cos 10B H EB C B E a ∠===. 由(1)知11B C 是平面1A AMN 的一个法向量,而11EB C ∠是1B E 与11B C 的夹角, 所以直线1B E 与平面1A AMN 所成角的正弦值等于1110cos EB C ∠=.【点睛】本题考查证明面面垂直,考查求直线与平面所成角.求直线与平面所成角的方法: (1)定义法:作出直线与平面所成的角(证明),然后解三角形得到角;(2)空间向量法,建立空间直角坐标系,求出平面的一个法向量,由直线的方向向量与平面法向量夹角的余弦值的绝对值得出线面角的正弦值.本题求线面角时,把两者结合,求出直线与平面的一个垂线的夹角的余弦值,从而得出线面角的正弦值,省略了建立空间直角坐标系,用推理代替了计算,也是一种求角的思路. 26.(1)证明见解析;(2)存在,点N 为AP 的中点. 【分析】(1)取AB 的中点O ,连接PO ,由面面垂直的性质得PO ⊥平面ABCD ,得出PO AD ⊥,从而说明AD ⊥平面PAB ,即可得证;(2)以O 为原点建立如图所示的空间直角坐标系,利用向量法可说明. 【详解】(1)证明:取AB 的中点O ,连接PO ,∵PAB △为正三角形,∴PO AB ⊥,又∵平面PAB ⊥平面ABCD ,且平面PAB ⋂平面ABCD AB =, ∴PO ⊥平面ABCD , 又AD ⊂平面ABCD ,∴PO AD ⊥, 又∵AD AB ⊥,AD PO ⊥,且PO AB O ⋂=, ∴AD ⊥平面PAB . 又∵AD ⊂平面PAD , ∴平面PAB ⊥平面PAD .(2)以O 为原点建立如图所示的空间直角坐标系,在直角PCB 中,4PC =,2PB =,∴23BC =, ∴(1,0,0),(1,0,0),(1,23,0)A B D -, 设AN AP λ=,则(1,0,3)N λλ-, 则()2,23,0BD =,()23BN λλ=-, 设平面BND 的一个法向量(,,)n x y z =,则·0·0n BD n BN ⎧=⎨=⎩,即()2230230x x z λλ⎧+=⎪⎨-=⎪⎩,令3x =,可得得23,1,1n λ⎛⎫=--⎪⎝⎭, 而平面ABD 的法向量(0,0,1)m =,由题意知:2113||||4n mn mλ-⋅==⋅⎛+1λ=-(舍)或12λ=,∴当点N为AP的中点时,二面角A BD N--的余弦值为13.【点睛】利用法向量求解空间线面角的关键在于“四破”:第一,破“建系关”,构建恰当的空间直角坐标系;第二,破“求坐标关”,准确求解相关点的坐标;第三,破“求法向量关”,求出平面的法向量;第四,破“应用公式关”.。
数学选修2-1空间向量及其运算练习题含答案

数学选修2-1空间向量及其运算练习题含答案学校:__________ 班级:__________ 姓名:__________ 考号:__________1. 在棱长为1的正方体ABCD −A 1B 1C 1D 1中,点E 为底面A 1B 1C 1D 1内一动点,则EA →⋅EC →的取值范围是( ) A.[12,1] B.[0,1] C.[−1,0]D.[−12,0]2. 已知向量a →=(3, 5, −1),b →=(2, 2, 3),c →=(1, −1, 2),则向量a →−b →+4c →的坐标为( ) A.(5, −1, 4) B.(5, 1, −4) C.(−5, 1, 4) D.(−5, −1, 4)3. 已知空间三点坐标分别为A (1,1,1),B (0,3,0),C (−2,−1,4),点P(−3,x,3)在平面ABC 内,则实数x 的值为( ) A.1 B.−2 C.0 D.−14. 如图,在四面体ABCD 中,设G 是CD 的中点,则AB →+12(BD →+BC →)等于( )A.AD →B.BG →C.CD →D.AG →5. 已知{a →, b →, c →}是空间的一组单位正交基底,而{a →−b →, c →, a →+b →}是空间的另一组基底.若向量p →在基底{a →, b →, c →}下的坐标为(6, 4, 2),则向量p →在基底{a →−b →, c →, a →+b →}下的坐标为( ) A.(1, 2, 5) B.(5, 2, 1) C.(1, 2, 3) D.(3, 2, 1)6. 若a →=(2, −3, 1),b →=(2, 0, 3),c →=(0, 2, 2),则a →⋅(b →+c →)=( ) A.4 B.15 C.7 D.37. 已知a →,b →是空间两个向量,若|a →|=|b →|=2,|a →−b →|=√7,则cos ⟨a →,b →⟩=( ) A.18B.14C.12D.18. 已知正方体ABCD −A 1B 1C 1D 1,点P ,Q 为线段B 1B ,AB 上的动点,下列命题正确的是( )A.(A 1A →+A 1D 1→+A 1B 1→)2=3A 1B 1→2B.A 1C →⋅(A 1B 1→−A 1A →)=0C.若AC 1→=xAB →+2yBC →+3zC 1C →,则x +y +z =75 D.对任意给定的点Q ,存在点P ,使得CP ⊥D 1Q9. 已知正四面体ABCD 的棱长为1,O 是该正四面体外接球球心,且AO →=xAB →+yAC →+zAD →,x ,y ,z ∈R ,则x +y +z =( ) A.34 B.13C.12D.1410. 下列命题正确的是( )A.a →|−|b →|<|a →+b →|是向量a →,b →不共线的充要条件B.在空间四边形ABCD 中,AB →⋅CD →+BC →⋅AD →+CA →⋅BD →=0 C.在棱长为1的正四面体ABCD 中,AB →⋅BC →=12D.设A ,B ,C 三点不共线,O 为平面ABC 外一点,若OP →=13OA →+23OB →+OC →则P ,A ,B ,C 四点共面11. 已知a →=(x, −2, 6),b →=(2, −1, 3),a → // b →,则x =________.12. 已知正方体ABCD −A 1B 1C 1D 1,点E ,F 分别是上底面A 1C 1和侧面CD 1的中心,求下列各式中的x ,y 的值:(1)AC 1→=x(AB →+BC →+CC 1→),则x =________;(2)AE →=AA 1→+xAB →+yAD →,则x =________,y =________;(3)AF →=AD →+xAB →+yAA 1→,则x =________,y =________.13. 在长方体ABCD −A 1B 1C 1D 1中,化简:DA →−DB →+B 1C →−B 1B →+A 1B 1→−A 1B →=________.14. 如图,在四边形ABCD 中,DC →=13AB →,E 为BC 的中点,且AE →=x ﹒AB →+y ⋅AD →,则3x −2y =________.15. 设点C(2a +1, a +1, 2)在点P(2, 0, 0),A(1, −3, 2),B(8, −1, 4)所确定的平面上,则a =________.16. 已知向量a →=(3,5,0),b →=(1,2,−1),则|a →−2b →|等于________.17. 已知点A(1, −2, 11)、B(4, 2, 3),C(6, −1, 4),则△ABC 中角C 的大小是________.18. 如图,在三棱锥D −ABC 中,已知AB =AD =2,BC =1,AC →⋅BD →=−3,则CD =________.19. 已知扇形AOB ,点C 在弧AB 上(异于A ,B 两点),线段AB 与OC 交与点M ,设OC →=tOA →+3tOB →(t ≠0),AM →=mAB →(m ≠0),则m =________.20. 设a →=(2, 2m −3, n +2),b →=(6, 2m −1, 4n −2),且a → // b →,则m +n =________.21. 已知点A(1, −2, 0)和a →=(−3, 4, 12),求点B 的坐标,使AB → // a →,且|AB|等于|a →|的2倍.22. 已知正方体ABCD −A ′B ′C ′D ′的边长为a . (1)求AC →⋅AA ′→; (2)求AC →⋅A ′C ′→;(3)求AC →⋅AC ′→.23. 已知向量a →=2e →1−3e →2,b→=2e →1+3e →2,其中e →1、e →2不共线,向量c →=2e →1−9e →2.问是否存在这样的实数λ、μ,使向量d→=λa →+μb →与c →共线?24. 已知向量a →,b →,c →分别平行于x 轴,y 轴,z 轴,他们的坐标各有什么特点?25. 已知向量a →=(−2, −1, 2),b →=(−1, 1, 2),c →=(x, 2, 2).(1)当|c →|=2√2时,若向量ka →+b →与c →垂直,求实数x 和k 的值;(2)若向量c →与向量a →,b →共面,求实数x 的值.26. 如图,在正四棱锥P −ABCD 中,底面ABCD 是边长为1的正方形,O 是AC 与BD 的交点,PO =1,M 是PC 的中点.(1)设AB →=a →,AD →=b →,AP →=c →,用a →,b →,c →表示向量BM →;(2)在如图的空间直角坐标系中,求向量BM →的坐标.27. 如图,在棱长为a 的正方体A 1B 1C 1D 1−ABCD 中,(1)作出面A 1BC 1与面ABCD 的交线l ,判断l 与直线A 1C 1位置关系,并给出证明;(2)证明B 1D ⊥面A 1BC 1;(3)求直线AC 到面A 1BC 1的距离;(4)若以A 为坐标原点,分别以AB ,AD ,AA 1所在的直线为x 轴、y 轴、z 轴,建立空间直角坐标系,试写出C ,C 1两点的坐标.28. 如图,在平行六面体ABCD −A 1B 1C 1D 1中,AB =5,AD =3,AA 1=4,∠DAB =90∘,∠BAA 1=∠DAA 1=60∘,E 是CC 1的中点,设AB →=a →,AD →=b →,AA 1→=c →.(1)用a →,b →,c →表示AE →;(2)求AE 的长?29. 设空间向量a →=(3, 5, −4),b →=(2, 1, 8).(1)计算2a →+3b →,3a →−2b →,a →⋅b →的值,并求a →与b →所成角的余弦值;(2)当λ、μ,满足什么条件时,使得λa →+μb →与z 轴垂直.30. 如图,在正方体ABCD −A 1B 1C 1D 1中,点E 是上底面A 1C 1 的中心,化简下列向量表达式,并在图中标出化简结果的向量.(1)AB →+BC →−C 1C →;(2)12AB →−12DA →−A 1A →.31. 已知长方体ABCD −A 1B 1C 1D 1,点E 、F 分别是上底面A 1B 1C 1D 1和面CC 1D 1D 的中心,求其中x ,y ,z 的值.(1)AC 1→=xAB →+yBC →+zCC 1→;(2)AE →=xAB →+yBC →+zCC 1→;(3)AF →=xBA →+yBC →+zC 1C →.32. 如图所示,在长方体体ABCD −A 1B 1C 1D 1中,O 为AC 的中点.(1)化简:A 1O →−12AB →−12AD →;(2)设E 是棱DD 1上的点,且DE →=23DD 1→,若EO →=xAB →+yAD →+zAA 1→,试求实数x ,y ,z 的值.33. 已知长方体ABCD −A 1B 1C 1D 1中,AB =AA 1=2,AD =4,E 为侧面AA 1B 1B 的中心,F 为A 1D 1的中点.求下列向量的数量积: (1)BC →⋅ED 1→;(2)BF →⋅AB 1→.34. 在平行六面体ABCD −A 1B 1C 1D 1中,AB =1,AD =2,AA 1=3,∠BAD =90∘,∠BAA 1=∠DAA 1=60∘.若AB →=a →,AD →=b →,AA 1→=c →(1)用基底{a →,b →,c →}表示向量BM →;(2)求向量AC 1→的长度.35. 如图,在三棱柱ABC −A 1B 1C 1中,侧面ACC 1A 1⊥底面ABC ,△A 1AC 为等边三角形,AC ⊥A 1B .(1)求证:AB =BC ;(2)若∠ABC =90∘,求A 1B 与平面BCC 1B 1所成角的正弦值.36. 三棱柱ABC −A 1B 1C 1中,M 、N 分别是A 1B 、B 1C 1上的点,且BM =2A 1M ,C 1N =2B 1N .设AB →=a →,AC →=b →,AA 1→=c →.(1)试用a →,b →,c →表示向量MN →;(2)若∠BAC =90∘,∠BAA 1=∠CAA 1=60∘,AB =AC =AA 1=1,求MN 的长.37. 已知六边形ABCDEF 的三对对边都互相平行,并且FC →=2AB →=2DE →,又设AB →=α→,BC →=β→,求CE →和CD →.38. 已知PA 垂直于正方形ABCD 所在平面,M ,N 分别是AB ,PC 的中点,并且PA =AD =1,求MN →,DC →的坐标.39. 若M 、A 、B 三点不共线,且存在实数λ1,λ2,使MC →=λ1MA →+λ2MB →,求证:A 、B 、C 三点共线的充要条件是λ1+λ2=1.40. 如图所示,在各个面都是平行四边形的四棱柱ABCD −A 1B 1C 1D 1中,P 是CA 1的中点,M 是CD 1的中点,N 是C 1D 1的中点,点Q 在CA 1上,且CQ:QA 1=4:1,设AB →=a ,AD →=b ,AA 1→=c ,用基底{a, b, c}表示以下向量:(1)AP →;(2)AM →;(3)AN →;(4)AQ →.参考答案与试题解析数学选修2-1空间向量及其运算练习题含答案一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 ) 1.【答案】 A【考点】 空间向量向量的概念与向量的模【解析】 此题暂无解析 【解答】解:如图,以D 为原点,以DA 所在的直线为x 轴,以DC 所在的直线为y 轴, 以DD 1 所在的直线为x 轴,建立空间直角坐标系,可得点A(1,0,0),C(0,1,0) 设点E 的坐标为(x,y,1),则0≤x ≤1,0≤y ≤1 ∴ EA →=(1,−x,−y −1), EC →=(−x,1−y,−1),EA →⋅EC →=−x(1−x)−y(1−y)+1=x 2−x +y 2−y +1=(x −12)2+(y −12)2+12. 由二次函数的性质可得,当x =y =12时,EA →⋅EC →.取得最小值12,当x =0或x =1,且y =0或y =1时,EA →⋅EC →取得最大值1, 因此EA →⋅EC →的取值范围是[12,1],故选A .2. 【答案】A【考点】空间向量运算的坐标表示【解析】直接利用空间向量的坐标运算求解即可.【解答】解:向量a →=(3, 5, −1),b →=(2, 2, 3),c →=(1, −1, 2),则向量a →−b →+4c →=(3, 5, −1)−(2, 2, 3)+4(1, −1, 2)=(5, −1, 4),故选:A .3.【答案】A【考点】空间向量的基本定理及其意义【解析】利用点P (−3,x ,3)在平面ABC 内,得到AP →=mAB →+nAC →,利用向量的坐标运算和空间向量基本定理求解即可.【解答】解:点P (−3,x ,3)在平面ABC 内,则AP →=mAB →+nAC →,即(−4,x −1,2)=m (−1,2,−1)+n (−3,−2,3),所以−4=−m −3n ,x −1=2m −2n ,2=−m +3n ,解得m =1,n =1,x =1,故选:A .4.【答案】D【考点】空间向量的加减法【解析】先求出则12(BD →+BC →)=BG →,根据向量的加法运算法则计算即可.【解答】解:∵ G 是CD 的中点,∴ AB →+12(BD →+BC →)=AB →+BG →=AG →,故选:D .5.【答案】A【考点】空间向量【解析】设向量p →在基底{a →−b →, c →, a →+b →}下的坐标为(x, y, z),由p →=6a →+4b →+2c →=x(a →−b →)+yc →+z(a →+b →),列出方程组,求出x ,y ,z 的值即可.【解答】解:设向量p →在基底{a →−b →, c →, a →+b →}下的坐标为(x, y, z),可得p →=6a →+4b →+2c →=x(a →−b →)+yc →+z(a →+b →),所以:{6=x +z4=−x +z 2=y∴ x =1,y =2,z =5故选:A .6.【答案】D【考点】空间向量的数量积运算空间向量运算的坐标表示【解析】先求出 b →+c →,再利用空间向量的数量积公式 a →=(x 1,y 1,z 1),b →=(x 2,y 2,z 2),a →⋅b →=x 1⋅x 2+y 1y 2+z 1z 2求出a →⋅(b →+c →).【解答】解:∵ b →=(2, 0, 3),c →=(0, 2, 2),∴ b →+c →=(2, 2, 5),∴ a →⋅(b →+c →)=2×2+(−3)×2+1×5=3,故选D .7.【答案】A【考点】空间向量的数乘运算【解析】此题暂无解析【解答】此题暂无解答8.【答案】A,B,D【考点】空间向量运算的坐标表示空间向量的数量积运算空间向量的加减法命题的真假判断与应用棱柱的结构特征【解析】此题暂无解析【解答】解:建立如图的空间直角坐标系,设正方体ABCD −A 1B 1C 1D 1的棱长为1,则A(0,0,1),C(1,1,1),A 1(0,0,0),B 1(0,1,0),C 1(1,1,0),D 1(1,0,0),所以A 1A →=(0,0,1),A 1D 1→=(1,0,0),A 1B 1→=(0,1,0),A 1C →=(1,1,1),AD →1=(1,0,−1), (A 1A →+A 1D 1→+A 1B 1→)2=(1,1,1)2=3=3A 1B 1→2,A 正确; A 1C →⋅(A 1B 1→−A 1A →)=(1,1,1)⋅(0,1,−1)=0,B 正确;AC 1→=AB →+BC →+CC 1→=AB →+BC →−C 1C →=xAB →+2yBC →+3zC 1C →,解得x =1,y =12,z =−13,则x +y +z =76,C 错误;当点P 与B 1重合时,CP ⊥AB 且CP ⊥AD 1,所以CP ⊥平面ABD 1,因为对于任意给定的点Q ,都有D 1Q ⊂平面ABD 1,所以对于任意给定的点Q ,存在点P ,使得D 1Q ⊥CP ,D 正确.故选ABD .9.【答案】A【考点】棱锥的结构特征空间向量的数乘运算空间向量【解析】 根据正四面体的性质求出棱锥的高,根据等体积法求出内切球的半径,建立坐标系,求出各向量的坐标,代入坐标运算即可解出.【解答】解:设正四面体的高为AM ,延长DM 交BC 于E ,则E 为BC 的中点.∴ DE =√32,DM =23DE =√33, ∴ AM =√AD 2−DM 2=√63, 设内切球半径为r,则V A−BCD =13S △BCD ⋅AM =4×13×S BCD ⋅r ,∴ r =AM4=√612,∴ OM =√612, 以M 为原点,建立如图所示的空间坐标系M −xyz ,则A (0,0,√63),B (12,−√36,0),C (−12,−√36,0), D (0,√33,0),O (0,0,√612) ∴ AO →=(0,0,−√64),AB →=(12,−√36,−√63), AC →=(−12,−√36,√63),AD →(0,√33,√63), AO →=xAB →+yAC →+zAD → { 12x −12y =0−√36x −√36y +√33z =0−√63x −√63y −√63z =−√64, 解得x =y =z =14. ∴ x +y +z =34. 故选A .10.【答案】B【考点】空间向量的基本定理及其意义空间向量的数量积运算共线向量与共面向量【解析】本题考查了空间向量的有关命题,根据向量共线,共面定理,向量数乘运算即可依次判断.【解答】解:若a →,b →为非零的同向向量,则|a →|−|b →|<|a →+b →|,故A 错;在空间四边形中,AB →⋅CD →+BC →⋅AD →+CA →⋅BD →=−BA →⋅(BD →−BC →)+BC →⋅(BD →−BA →)+BD →⋅(BA →−BC →)=−BA →⋅BD →+BA →⋅BC →+BC →⋅BD →−BC →⋅BA →+BD →⋅BA →−BD →⋅BC →=0,故B 正确;在棱长为1的四面体中,AB →⋅BC →=1⋅1⋅cos (π−∠ABC)=−cos ∠ABC ,不一定为12,故C 错;若A ,B ,C 三点不共线,P 与之共面,则OP →=tOA →+mOB →+nOC →,满足t +m +n =1, 而13+23+1≠1,故P ,A ,B ,C 不共面,故D 错误.故选B .二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )11.【答案】4【考点】共线向量与共面向量【解析】根据所给的两个向量的坐标和两个向量之间的平行关系,写出向量平行的坐标形式的充要条件,解方程即可.【解答】解:∵ a →=(2, −1, 3),b →=(2, −1, 3),a → // b →∴ x 2=−2−1=63∴ x =4故答案为:412.【答案】112,1212,12【考点】空间向量的数乘运算空间向量的加减法【解析】(1)根据向量加法的首尾相连法则求解;(2)由向量加法的三角形法则和四边形法则得AE →=AA 1→+A 1E →和A 1E →=12(A 1B 1→+A 1D 1→),再由向量相等求解;(3)由向量加法的三角形法则和四边形法则得AF →=AD →+DF →和DF →=12(DC →+DD 1→),再由向量相等求解.【解答】解:(1)根据向量加法的首尾相连法则,x =1;(2)由向量加法的三角形法则得,AE →=AA 1→+A 1E →,由四边形法则和向量相等得,A 1E →=12(A 1B 1→+A 1D 1→)=12(AB →+AD →); ∴ AE →=AA 1→+12AB →+12AD →,∴ x =y =12;(3)由向量加法的三角形法则得,AF →=AD →+DF →,由四边形法则和向量相等得,DF →=12(DC →+DD 1→)=12(AB →+AA 1→);∴ AF →=AD →+12AB →+12AA 1→,∴ x =y =12.13.【答案】BD 1→【考点】空间向量的加减法【解析】根据向量的加减的运算法则即可求出.【解答】解:长方体ABCD −A 1B 1C 1D 1中,如图,DA →−DB →+B 1C →−B 1B →+A 1B 1→−A 1B →=BA →+BC →+BB 1→=BD →+BB 1→=BD 1→, 故答案为:BD 1→,14.【答案】1【考点】向量的线性运算性质及几何意义【解析】利用向量共线定理和向量的三角形法则及其多边形法则即可得出.【解答】解:∵ E 为BC 的中点,∴ BE →=12BC →, 又BC →=BA →+AD →+DC →=−AB →+AD →+13AB →,∴ BE →=12(−23AB →+AD →)=−13AB →+12AD →,∴ AE →=AB →+BE →=AB →−13AB →+12AD →=23AB →+12AD →.而AE →=x ﹒AB →+y ⋅AD →,∴ x =23,y =12.∴ 3x −2y =2−1=1.故答案为:1.15.【答案】16【考点】共线向量与共面向量【解析】利用平面向量基本定理即可得出.【解答】解:由已知,得PA →=(−1, −3, 2),PB →=(6, −1, 4).设PC →=xPA →+yPB →(x ,y ∈R ),则(2a −1, a +1, 2)=x(−1,−3,2)+y(6,−1,4)=(−x +6y,−3x −y,2x +4y),所以{2a −1=−x +6y a +1=−3x −y 2=2x +4y ,解得{x =−7y =4a =16.故答案为:16.16.【答案】 √6【考点】空间向量运算的坐标表示空间向量的数乘运算空间向量的数量积运算【解析】本题考查空间向量的坐标运算及向量的模.【解答】解:a →−2b →=(3,5,0)−2(1,2,−1)=(1,1,2),所以|a →−2b →|=√1+1+4=√6故答案为:√6.17.【答案】90∘【考点】空间向量运算的坐标表示【解析】空间两点P 1(x 1, y 1, z 1),P 2(x 2, y 2, z 2),则P 1、P 2的距离:P 1P 2=√(x 1−x 2)2+(y 1−y 2)2+(z 1−z 2)2,根据这个公式可以计算出AC 、BC 的长度,再用两个向量的夹角公式,得到∠ACB 的余弦,从而得到角C 的大小【解答】解:∵ A(1, −2, 11)、B(4, 2, 3),C(6, −1, 4),∴ |AC →|=√(1−6)2+(−2+1)2+(11−4)2=√75|BC →|=√(4−6)2+(2+1)2+(3−4)2=√14又∵ CA →=(−5,−1,7),CB →=(−2,3,−1)∴ CA →⋅CB →=(−5)×(−2)+(−1)×3+7×(−1)=0可得cos ∠ACB =|CA|→|×|CB →|˙=0∵ ∠ACB ∈(0∘, 180∘)∴ ∠ACB =90∘故答案为90∘18.【答案】 √7【考点】空间向量的数量积运算【解析】用AB →,AD →表示BD →,根据已知条件列方程得出AC ,∠BAC ,∠DAC 的关系,使用等量代换计算CD 2=|AD →−AC →|2.【解答】解:设∠BAC =α,∠DAC =β,∵ |AC →−AB →|=BC →=1,∴ AC 2+AB 2−2AC ⋅AB cos α=1,即AC 2−4AC cos α=−3.∵ AC →⋅BD →=−3,∴ AC →⋅(AD →−AB →)=AC →⋅AD →−AC →⋅AB →=−3,即2AC cos β−2AC cos α=−3,∴ 2AC cos β=2AC cos α−3.∴ CD 2=(AD →−AC →)2=AD →2+AC →2−2AC →⋅AD →=4+AC 2−4AC cos β =4+AC 2−4AC cos α+6=7.∴ CD =√7.故答案为:√7.19.【答案】34【考点】向量的线性运算性质及几何意义【解析】根据条件及向量加法、减法,及数乘的几何意义及其运算便可得到OM →=(1−m)OA →+mOB →,从而有OC →=kOM →=k(1−m)OA →+kmOB →,由平面向量基本定理便得到{k(1−m)=t km =3t,解出m 即可. 【解答】解:如图,OM →=OA →+AM →=OA →+mAB →=OA →+m(OB →−OA →)=(1−m)OA →+mOB →;O ,M ,C 三点共线;∴ 存在实数k ,OC →=kOM →=k(1−m)OA →+mkOB →;又OC →=tOA →+3tOB →;∴ {k(1−m)=t mk =3t; 解得m =34.故答案为:34.20.【答案】10【考点】共线向量与共面向量【解析】利用向量平行的坐标之间的关系解答.【解答】解:∵ a →=(2, 2m −3, n +2),b →=(6, 2m −1, 4n −2),且a → // b →, ∴ 26=2m−32m−1=n+24n−2,解得m =2,n =8;∴ m +n =10;故答案为:10.三、 解答题 (本题共计 20 小题 ,每题 10 分 ,共计200分 ) 21.【答案】解:∵ AB → // a →,∴ 可设AB →=na →=(−3n, 4n, 12n),∵ |a →|=13,∴ |AB →|=|n|⋅|a →|=13|n|∵ |AB →|=2|a →|,13|n|=26,解得n =2或n =−2,当n =2时,OB →=OA →+AB →=(1, −2, 0)+(−6, 8, 24)=(−5, 6, 24), 当n =−2时,OB →=OA →+AB →=(1, −2, 0)+(6, −8, −24)=(7, −10, −24),故B 为(−5, 6, 24)或(7, −10, −24).【考点】空间向量的夹角与距离求解公式共线向量与共面向量【解析】设AB →=na →=(−3n, 4n, 12n),由|AB →|=2|a →|,得n =2或n =−2,由此利用OB →=OA →+AB →,能求出点B 的坐标.【解答】解:∵ AB → // a →,∴ 可设AB →=na →=(−3n, 4n, 12n),∵ |a →|=13,∴ |AB →|=|n|⋅|a →|=13|n|∵ |AB →|=2|a →|,13|n|=26,解得n =2或n =−2,当n =2时,OB →=OA →+AB →=(1, −2, 0)+(−6, 8, 24)=(−5, 6, 24), 当n =−2时,OB →=OA →+AB →=(1, −2, 0)+(6, −8, −24)=(7, −10, −24),故B 为(−5, 6, 24)或(7, −10, −24).22.【答案】解:(1)∵ AA ′⊥平面ABCD ,AC ⊂平面ABCD ,∴ AC ⊥AA ′,∴ AC →⋅AA ′→=0.(2)∵ AC // A ′C ′,∴ AC →⋅A ′C ′→=|AC →|⋅|A ′C ′→|⋅cos 0=√2a ⋅√2a =2a 2. (3)AC →⋅AC ′→=|AC →|⋅|AC ′→|cos ∠C ′AC=√2a ×√3a 2222√2a⋅√3a =2a 2.【考点】空间向量的数量积运算【解析】以D 为原点,DA 为x 轴,DC 为y 轴,DD′为z 轴,建立空间直角坐标系,利用向量法能求出结果.【解答】解:(1)∵ AA ′⊥平面ABCD ,AC ⊂平面ABCD ,∴ AC ⊥AA ′,∴ AC →⋅AA ′→=0.(2)∵ AC // A ′C ′,∴ AC →⋅A ′C ′→=|AC →|⋅|A ′C ′→|⋅cos 0=√2a ⋅√2a =2a 2. (3)AC →⋅AC ′→=|AC →|⋅|AC ′→|cos ∠C ′AC=√2a ×√3a 2222√2a⋅√3a =2a 2.23.【答案】 解:∵ d →=λ(2e →1−3e →2)+μ(2e →1+3e →2)=(2λ+2μ)e →1+(−3λ+3μ)e →2,若d →与c →共线,则存在实数k ≠0,使d →=kc →,即(2λ+2μ)e →1+(−3λ+3μ)e →2=2ke →1−9ke →2,由{2λ+2μ=2k −3λ+3μ=−9k 得λ=−2μ. 故存在这样的实数λ、μ,只要λ=−2μ,就能使d →与c →共线.【考点】向量的线性运算性质及几何意义【解析】先将向量a →、b →代入表示出向量d →,然后假设共线可得:应有实数k ,使d →=kc →.即可得到λ=−2μ的关系式,从而得到答案.【解答】解:∵ d →=λ(2e →1−3e →2)+μ(2e →1+3e →2)=(2λ+2μ)e →1+(−3λ+3μ)e →2,若d →与c →共线,则存在实数k ≠0,使d →=kc →,即(2λ+2μ)e →1+(−3λ+3μ)e →2=2ke →1−9ke →2,由{2λ+2μ=2k −3λ+3μ=−9k 得λ=−2μ. 故存在这样的实数λ、μ,只要λ=−2μ,就能使d →与c →共线.24.【答案】解:向量a →,b →,c →分别平行于x 轴,y 轴,z 轴,所以向量a →的横坐标不为0,横坐标为0,竖坐标为0;向量b →的横坐标为0,横坐标不为0,竖坐标为0;向量c →的横坐标为0,横坐标为0,竖坐标不为0;【考点】空间向量的正交分解及其坐标表示空间向量【解析】直接利用向量与坐标轴的关系,写出结果即可.【解答】解:向量a →,b →,c →分别平行于x 轴,y 轴,z 轴,所以向量a →的横坐标不为0,横坐标为0,竖坐标为0;向量b →的横坐标为0,横坐标不为0,竖坐标为0;向量c →的横坐标为0,横坐标为0,竖坐标不为0;25.【答案】解:(1)当|c →|=2√2时,√x 2+4+4=2√2,解得x =0,且向量ka →+b →=(−2k −1, 1−k, 2k +2).因为向量ka →+b →与c →垂直,所以(ka →+b →)⋅c →=0,即2(1−k)+2(2k +2)=0,解得k =−3,所以实数x 和k 的值分别为0和−3.(2)因为向量c →与向量a →,b →共面,所以设c →=λa →+μb →(λ,μ∈R),所以(x, 2, 2)=λ(−2, −1, 2)+μ(−1, 1, 2),所以{x =−2λ−μ,2=μ−λ,2=2λ+2μ,解得{x =−12,λ=−12,μ=32, 所以实数x 的值为−12.【考点】向量的线性运算性质及几何意义向量的数量积判断向量的共线与垂直空间向量的数量积运算共线向量与共面向量【解析】(Ⅰ)直接利用向量的垂直的充要条件的应用求出结果.(Ⅱ)直接利用共面向量基本定理的应用求出结果.【解答】解:(1)当|c →|=2√2时,√x 2+4+4=2√2,解得x =0,且向量ka →+b →=(−2k −1, 1−k, 2k +2).因为向量ka →+b →与c →垂直,所以(ka →+b →)⋅c →=0,即2(1−k)+2(2k +2)=0,解得k =−3,所以实数x 和k 的值分别为0和−3.(2)因为向量c →与向量a →,b →共面,所以设c →=λa →+μb →(λ,μ∈R),所以(x, 2, 2)=λ(−2, −1, 2)+μ(−1, 1, 2),所以{x =−2λ−μ,2=μ−λ,2=2λ+2μ,解得{x =−12,λ=−12,μ=32, 所以实数x 的值为−12.26.【答案】解:(1)∵ BM →=BC →+CM →,BC →=AD →,CM →=12CP →,CP →=AP →−AC →,AC →=AB →+AD →,∴ BM →=AD →+12(AP →−AC →)=AD →+12AP →−12(AB →+AD →) =12AD →+12AP →−12AB → =12b →+12c →−12a →.(2)a →=AB →=(1, 0, 0),b →=AD →=(0, 1, 0),∵ O(12,12,0),P(12,12,1).∴ c →=AP →=OP →−OA →=(0, 0, 1),∴ BM →=12b →+12c →−12a →=12(0, 1, 0)+12(0, 0, 1)−12(1, 0, 0)=(−12,12,12).【考点】空间向量的基本定理及其意义空间向量【解析】(1)利用向量的三角形法则可得:BM →=BC →+CM →,BC →=AD →,CM →=12CP →,CP →=AP →−AC →,AC →=AB →+AD →,代入化简即可得出.(2)由于a →=AB →=(1, 0, 0),b →=AD →=(0, 1, 0),c →=AP →=OP →−OA →=(0, 0, 1),代入即可得出.【解答】解:(1)∵ BM →=BC →+CM →,BC →=AD →,CM →=12CP →,CP →=AP →−AC →,AC →=AB →+AD →,∴ BM →=AD →+12(AP →−AC →)=AD →+12AP →−12(AB →+AD →) =12AD →+12AP →−12AB → =12b →+12c →−12a →.(2)a →=AB →=(1, 0, 0),b →=AD →=(0, 1, 0),∵ O(12,12,0),P(12,12,1).∴ c →=AP →=OP →−OA →=(0, 0, 1),∴ BM →=12b →+12c →−12a →=12(0, 1, 0)+12(0, 0, 1)−12(1, 0, 0) =(−12,12,12).27.【答案】(1)解:在平面ABCD 内过点B 作AC 的平行线BE ,∵ AC // A 1C 1,AC // BE ,∴ BE // A 1C 1,∴ 面A 1BC 1与面ABCD 的交线l 与BE 重合,即直线BE 就是所求的直线l .∵ BE // A 1C 1,l 与BE 重合,∴ l // A 1C 1.(2)证明:连接B 1D 1,∵ A 1B 1C 1D 1是正方形,∴ A 1C 1⊥B 1D 1,∵ A 1C 1⊥DD 1,∴ A 1C 1⊥面DBB 1D 1,∴ A 1C 1⊥B 1D .同理A 1B ⊥面ADC 1B 1,∴ A 1B ⊥B 1D ,∵ A 1C 1∩A 1B =A 1,∴ B 1D ⊥面A 1BC 1.(3)解:∵AC // A1C1,且AC在面A1BC1外,A1C1⊂面A1BC1,∴AC // 面A1BC1,∴直线AC到面A1BC1的距离即为点A到面A1BC1的距离,记为ℎ,在三棱锥中A−A1BC1中,V A_A1BC1=V C1−ABA1,∵正方体A1B1C1D1−ABCD棱长为a,∴V A−A1BC1=13⋅S△A1BC1⋅ℎ=13×12×(√2a)2×ℎ×sin60∘=√3a26ℎ,V C1−ABA1=13⋅S△ABA1⋅A1C1=13⋅12⋅a⋅a⋅√2a=√26a3,∵V A_A1BC1=V C1−ABA1,∴ℎ=√63a.(4)解:若以A为坐标原点,分别以AB,AD,AA1所在的直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系,∵正方体A1B1C1D1−ABCD的棱长为a,∴C(a, a, 0),C1(a, a, a).【考点】点、线、面间的距离计算柱体、锥体、台体的体积计算空间中直线与直线之间的位置关系空间向量的正交分解及其坐标表示【解析】(1)在平面ABCD内过点B作AC的平行线BE,由AC // A1C1,AC // BE,知BE // A1C1,故直线BE就是所求的直线l.且l // A1C1.(2)由A1C1⊥面DBB1D1,知A1C1⊥B1D.由A1B⊥面ADC1B1,知A1B⊥B1D,所以B1D⊥面A1BC1.(3)AC // A1C1,且AC在面A1BC1外,A1C1⊂面A1BC1,所以AC // 面A1BC1,直线AC到面A1BC1的距离即为点A到面A1BC1的距离,记为ℎ,由等积法能求出ℎ=√63a.(4)若以A为坐标原点,分别以AB,AD,AA1所在的直线为x轴、y轴、z轴,建立空间直角坐标系,能写出C,C1两点的坐标.【解答】(1)解:在平面ABCD内过点B作AC的平行线BE,∵AC // A1C1,AC // BE,∴BE // A1C1,∴面A1BC1与面ABCD的交线l与BE重合,即直线BE就是所求的直线l.∵BE // A1C1,l与BE重合,∴l // A1C1.(2)证明:连接B1D1,∵A1B1C1D1是正方形,∴A1C1⊥B1D1,∵A1C1⊥DD1,∴A1C1⊥面DBB1D1,∴A1C1⊥B1D.同理A1B⊥面ADC1B1,∴A1B⊥B1D,∵A1C1∩A1B=A1,∴B1D⊥面A1BC1.(3)解:∵AC // A1C1,且AC在面A1BC1外,A1C1⊂面A1BC1,∴AC // 面A1BC1,∴直线AC到面A1BC1的距离即为点A到面A1BC1的距离,记为ℎ,在三棱锥中A−A1BC1中,V A_A1BC1=V C1−ABA1,∵正方体A1B1C1D1−ABCD棱长为a,∴V A−A1BC1=13⋅S△A1BC1⋅ℎ=13×12×(√2a)2×ℎ×sin60∘=√3a26ℎ,V C1−ABA1=13⋅S△ABA1⋅A1C1=13⋅12⋅a⋅a⋅√2a=√26a3,∵V A_A1BC1=V C1−ABA1,∴ℎ=√63a.(4)解:若以A为坐标原点,分别以AB,AD,AA1所在的直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系,∵正方体A1B1C1D1−ABCD的棱长为a,∴C(a, a, 0),C1(a, a, a).28.【答案】解:(1)根据向量的三角形法则得到AE →=AB →+BC →+CE →=a →+b →+12c → (2)∵ |AE →|2=(a →+b →+12c →)2 =a →2+b →2+14c →2+2a →⋅b →+a →⋅c →+b →⋅c → =25+9+4+0+(20+12)⋅cos 60∘=54 ∴ |AE →|=3√6,即AE 的长为3√6.【考点】空间向量的基本定理及其意义空间向量的夹角与距离求解公式【解析】(1)根据向量的三角形法则把要表示的向量写成以几何体的棱为基底的向量的加法的形式,从向量的起点出发,沿着棱到终点.(2)根据上一问表示出的结果,把要求的向量两边平方,把得到平方式展开,得到已知向量的模长和数量积的关系,代入数据做出结果.【解答】解:(1)根据向量的三角形法则得到AE →=AB →+BC →+CE →=a →+b →+12c → (2)∵ |AE →|2=(a →+b →+12c →)2 =a →2+b →2+14c →2+2a →⋅b →+a →⋅c →+b →⋅c → =25+9+4+0+(20+12)⋅cos 60∘=54 ∴ |AE →|=3√6,即AE 的长为3√6.29.【答案】解:(1)∵ 空间向量a →=(3, 5, −4),b →=(2, 1, 8),∴ 2a →+3b →=(6, 10, −8)+(6, 3, 24)=(12, 13, 16),3a →−2b →=(9, 15, −12)−(4, 2, 16)=(5, 13, −28),a →⋅b →=6+5−32=−21,∴ a →与b →所成角的余弦值为:cos <a →,b →>=√9+25+16⋅√4+1+64=−7√138230. (2)z 轴的方向向量为(0, 0, 1),λa →+μb →=(3λ+2μ, 5λ+μ, −4λ+8μ),∵ λa →+μb →与z 轴垂直,则0⋅(3λ+2μ)+0⋅(5λ+μ)+(−4λ+8μ)=0,即8μ−4λ=0,∴ λ=2μ.∴ λ=2μ时,λa →+μb →与z 轴垂直.【考点】空间向量的数量积运算空间向量运算的坐标表示【解析】(1)利用空间向量坐标运算法则能求出2a →+3b →,3a →−2b →,a →⋅b →的值,并能求出a →与b →所成角的余弦值.(2)z 轴的方向向量为(0, 0, 1),λa →+μb →=(3λ+2μ, 5λ+μ, −4λ+8μ),由向量垂直的性质,能求出λ=2μ时,λa →+μb →与z 轴垂直.【解答】解:(1)∵ 空间向量a →=(3, 5, −4),b →=(2, 1, 8),∴ 2a →+3b →=(6, 10, −8)+(6, 3, 24)=(12, 13, 16),3a →−2b →=(9, 15, −12)−(4, 2, 16)=(5, 13, −28),a →⋅b →=6+5−32=−21,∴ a →与b →所成角的余弦值为:cos <a →,b →>=√9+25+16⋅√4+1+64=−7√138230. (2)z 轴的方向向量为(0, 0, 1),λa →+μb →=(3λ+2μ, 5λ+μ, −4λ+8μ),∵ λa →+μb →与z 轴垂直,则0⋅(3λ+2μ)+0⋅(5λ+μ)+(−4λ+8μ)=0,即8μ−4λ=0,∴ λ=2μ.∴ λ=2μ时,λa →+μb →与z 轴垂直.30.【答案】解:(1)AB →+BC →−C 1C →=AC →+CC 1→=AC 1→ ,AC 1→如图所示.(2)12AB →−12DA →−A 1A →=12(AB →+AD →)−A 1A →=12AC →+AA 1→=AE →,AE →如图所示.【考点】空间向量的加减法【解析】此题暂无解析【解答】解:(1)AB →+BC →−C 1C →=AC →+CC 1→=AC 1→, AC 1→如图所示.(2)12AB →−12DA →−A 1A →=12(AB →+AD →)−A 1A → =12AC →+AA 1→=AE →,AE →如图所示.31.【答案】解:(1)∵ 长方体ABCD −A 1B 1C 1D 1,点E 、F 分别是上底面A 1B 1C 1D 1和面CC 1D 1D 的中心,AC 1→=AB →+BC →+CC 1→=xAB →+yBC →+zCC 1→,∴ x =1,y =1,z =1.(2)AE →=AA 1→+A 1E →=12AB →+12BC →+CC 1→=xAB →+yBC →+zCC 1→,∴ x =12,y =12,z =1.(3)AF →=AD →+DF →=12AB →+BC →+12CC 1→=−12BA →+BC →+12CC 1→=xBA →+yBC →+zC 1C →, ∴ x =−12,y =1,z =12.【考点】空间向量的基本定理及其意义【解析】利用空间向量三角形法则结构长方体结构特征求解.【解答】解:(1)∵ 长方体ABCD −A 1B 1C 1D 1,点E 、F 分别是上底面A 1B 1C 1D 1和面CC 1D 1D 的中心,AC 1→=AB →+BC →+CC 1→=xAB →+yBC →+zCC 1→, ∴ x =1,y =1,z =1.(2)AE →=AA 1→+A 1E →=12AB →+12BC →+CC 1→=xAB →+yBC →+zCC 1→,∴ x =12,y =12,z =1.(3)AF →=AD →+DF →=12AB →+BC →+12CC 1→=−12BA →+BC →+12CC 1→=xBA →+yBC →+zC 1C →, ∴ x =−12,y =1,z =12.32.【答案】解:在长方体体ABCD −A 1B 1C 1D 1中,O 为AC 的中点;(1)A 1O →−12AB →−12AD →=A 1O →−12(AB →+AD →) =A 1O →−12AC → =A 1O →−AO →=A 1O →+OA →=A 1A →;(2)∵ E 是棱DD 1上的点,且DE →=23DD 1→,∴ OE →=OD →+DE →=12BD →+23DD 1→ =12(BA →+BC →)+23AA 1→ =12BA →+12BC →+23AA 1→ =−12AB →+12AD →+23AA 1→, ∴ EO →=−OE →=12AB →−12AD →−23AA 1→; 又EO →=xAB →+yAD →+zAA 1→,∴ x =12,y =−12,z =−23. 【考点】空间向量的基本定理及其意义空间向量的加减法【解析】根据题意,利用空间向量的线性运算法则,对(1)式进行化简,对(2)式进行线性表示即可.【解答】解:在长方体体ABCD −A 1B 1C 1D 1中,O 为AC 的中点;(1)A 1O →−12AB →−12AD →=A 1O →−12(AB →+AD →) =A 1O →−12AC → =A 1O →−AO →=A 1O →+OA →=A 1A →;(2)∵ E 是棱DD 1上的点,且DE →=23DD 1→, ∴ OE →=OD →+DE →=12BD →+23DD 1→ =12(BA →+BC →)+23AA 1→ =12BA →+12BC →+23AA 1→ =−12AB →+12AD →+23AA 1→,∴ EO →=−OE →=12AB →−12AD →−23AA 1→; 又EO →=xAB →+yAD →+zAA 1→,∴ x =12,y =−12,z =−23.33.【答案】解:(1)建立如图所示的空间直角坐标系,由题意可得A(0, 0, 0),B(2, 0, 0),C(2, 4, 0),E(1, 0, 1),B 1(2, 0, 2),D 1(0, 4, 2),F(0, 2, 2),可得BC →=(0, 4, 0),ED 1→=(−1, 4, 1),故BC →⋅ED 1→=0×(−1)+4×4+0×1=16.(2)可得BF →=(−2, 2, 2),AB 1→=(2, 0, 2),故BF →⋅AB 1→=−2×2+2×0+2×2=0.【考点】空间向量的数量积运算【解析】建立坐标系,由题意可得相关点的坐标,进而可得向量的坐标,由向量的坐标运算可得结果.【解答】解:(1)建立如图所示的空间直角坐标系,由题意可得A(0, 0, 0),B(2, 0, 0),C(2, 4, 0),E(1, 0, 1),B 1(2, 0, 2),D 1(0, 4, 2),F(0, 2, 2),可得BC →=(0, 4, 0),ED 1→=(−1, 4, 1),故BC →⋅ED 1→=0×(−1)+4×4+0×1=16.(2)可得BF →=(−2, 2, 2),AB 1→=(2, 0, 2),故BF →⋅AB 1→=−2×2+2×0+2×2=0.34.【答案】解:(1)由题意可得BM →=BB 1→+B 1M →=BB 1→+12B 1D 1→=BB 1→+12(A 1D 1→−A 1B 1→)=c →+12(b →−a →), 故BM →=−12a →+12b →+c →.------- (2)由条件得|a →|=1,|b →|=2,|c →|=3. a →⋅b →=0,a →⋅c →=32,b →⋅c →=3.------- AC 1→=a →+b →+c →.------故|AC →|=√(a →+b →+c →)2=√a →2+b →2+c →2+2a →⋅b →+2b →⋅c →+2a →⋅c →=√23.------ 【考点】空间向量的基本定理及其意义【解析】(1)利用两个向量的加减法的法则,以及其几何意义可得BM →=BB 1→+B 1M →=BB 1→+12(A 1D 1→−A 1B 1→),把已知的条件代入化简可得结果. (2)利用两个向量的数量积的定义求出基底中每个向量的模以及每两个向量的数量积,由|AC →|=√(a →+b →+c →)2=√a →2+b →2+c →2+2a →⋅b →+2b →⋅c →+2a →⋅c → 运算求得结果.【解答】解:(1)由题意可得BM →=BB 1→+B 1M →=BB 1→+12B 1D 1→=BB 1→+12(A 1D 1→−A 1B 1→)=c →+12(b →−a →),故BM →=−12a →+12b →+c →.-------(2)由条件得|a →|=1,|b →|=2,|c →|=3. a →⋅b →=0,a →⋅c →=32,b →⋅c →=3.------- AC 1→=a →+b →+c →.------故|AC →|=√(a →+b →+c →)2=√a →2+b →2+c →2+2a →⋅b →+2b →⋅c →+2a →⋅c →=√23.------ 35.【答案】(1)证明:如图,取AC 的中点O ,连接OA 1,OB .∵ 点O 为等边△A 1AC 边AC 的中点,∴ AC ⊥OA 1.∵ AC ⊥A 1B ,OA 1∩A 1B =A 1,OA 1⊂平面OA 1B ,A 1B ⊂平面OA 1B .∴ AC ⊥平面OA 1B ,又OB ⊂平面OA 1B ,∴ AC ⊥OB .∵ 点O 为AC 的中点,∴ AB =BC .(2)解:由(1)知,AB =BC , 又∠ABC =90∘ ,故△ABC 是以AC 为斜边的等腰直角三角形.∵ A 1O ⊥AC ,侧面ACC 1A 1⊥底面ABC ,面ACC 1A 1∩面ABC =AC ,∴ A 1O ⊥底面ABC以线段OB ,OC ,OA 1所在的直线分别为x 轴、y 轴、z 轴,建立如图所示的空间直角坐标系O −xyz ,设AC =2,则A(0,-1,0),A 1(0,0,√3),B(1,0,0),C(0,1,0).∴ BC →=(−1,1,0),BB →1=AA →1=(0,1,√3),A 1B →=(1,0,−√3).设平面BCC 1B 1的一个法向量n 0=(x 0,y 0,z 0),则由{n 0⋅BC →=0,n 0⋅BB 1→=0,得{−x 0+y 0=0,y 0+√3z 0=0,令y 0=√3,得x 0=√3,z 0=−1,∴ 平面BCC 1B 1的一个法向量为n 0=√3,√3,−1.设A 1B 与平面BCC 1B 1所成角为θ,则sin θ=cos ⟨n 0,A 1B⟩=|n 0⋅A 1B →||n 0||A 1B →|=√217.【考点】空间向量的正交分解及其坐标表示棱柱的结构特征【解析】此题暂无解析【解答】解:(1)证明:如图,取AC的中点O,连接OA1,OB.∵点O为等边△A1AC边AC的中点,∴AC⊥OA1.∵AC⊥A1B,OA1∩A1B=A1,OA1⊂平面OA1B,A1B⊂平面OA1B.∴AC⊥平面OA1B,又OB⊂平面OA1B,∴AC⊥OB.∵点O为AC的中点,∴AB=BC.(2)解:由(1)知,AB=BC,又∠ABC=90∘,故△ABC是以AC为斜边的等腰直角三角形.∵A1O⊥AC,侧面ACC1A1⊥底面ABC,面ACC1A1∩面ABC=AC,∴A1O⊥底面ABC以线段OB,OC,OA1所在的直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系O−xyz,设AC=2,则A(0,-1,0),A1(0,0,√3),B(1,0,0),C(0,1,0). ∴BC→=(−1,1,0),BB→1=AA→1=(0,1,√3),A 1B →=(1,0,−√3).设平面BCC 1B 1的一个法向量n 0=(x 0,y 0,z 0),则由{n 0⋅BC →=0,n 0⋅BB 1→=0,得{−x 0+y 0=0,y 0+√3z 0=0,令y 0=√3,得x 0=√3,z 0=−1,∴ 平面BCC 1B 1的一个法向量为n 0=√3,√3,−1.设A 1B 与平面BCC 1B 1所成角为θ,则sin θ=cos ⟨n 0,A 1B⟩=|n 0⋅A 1B →||n 0||A 1B →|=√217.36.【答案】解:(1)由图形知MN →=MA 1→+A 1B 1→+B 1N →=13BA 1→+AB →+13B 1C 1→=13(c →−a →)+a →+13(b →−a →)=13a →+13b →+13c →. (2)由题设条件∵ (a →+b →+c →)2=a →2+b →2+c →2+2a →⋅b →+2b →⋅c →+2a →⋅c →=1+1+1+0+2×1×1×12+2×1×1×12=5, ∴ |a →+b →+c →|=√5,|MN →|=13|a →+b →+c →=|√53. 【考点】空间向量的夹角与距离求解公式【解析】(1)由图形知MN →=MA 1→+A 1B 1→+B 1N →=13BA 1→+AB →+13B 1C 1→再用a →,b →,c →表示出来即可(2)求MN 的长,即求|MN →|=13|a →+b →+c →|,利用求向量模的方法,求|a →+b →+c →|即可求得MN 的长【解答】解:(1)由图形知MN →=MA 1→+A 1B 1→+B 1N →=13BA 1→+AB →+13B 1C 1→=13(c →−a →)+a →+13(b →−a →)=13a →+13b →+13c →. (2)由题设条件∵ (a →+b →+c →)2=a →2+b →2+c →2+2a →⋅b →+2b →⋅c →+2a →⋅c →=1+1+1+0+2×1×1×12+2×1×1×12=5,∴ |a →+b →+c →|=√5,|MN →|=13|a →+b →+c →=|√53. 37.【答案】解:如图,根据FC →=2AB →=2DE →知,AB // DE ,AB =DE ,AB // FC ,FC =2AB ; ∴ 四边形ABDE 为平行四边形,连接AD ,BE ,设交于O ;则O 点在线段FC 上;∴ OE →=BO →=BA →+BC →,CO →=BA →;∴ CE →=CO →+OE →=BA →+BA →+BC →=−2AB →+BC →=−2α→+β→; ∴ CD →=CE →+ED →=−2α→+β→+α→=−α→+β→.【考点】向量的线性运算性质及几何意义【解析】画出六边形,根据条件知AB // DE ,且AB =DE ,且AB // FC ,FC =2AB ,从而四边形ABDE 为平行四边形,连接对角线,交点O 应在FC 上.结合图形即可看出:OE →=BO →=BA →+BC →,CO →=BA →,从而可以得出CE →=−2α→+β→,而由CE →+ED →即可表示出CD →.【解答】解:如图,根据FC →=2AB →=2DE →知,AB // DE ,AB =DE ,AB // FC ,FC =2AB ; ∴ 四边形ABDE 为平行四边形,连接AD ,BE ,设交于O ;则O 点在线段FC 上;∴ OE →=BO →=BA →+BC →,CO →=BA →;∴ CE →=CO →+OE →=BA →+BA →+BC →=−2AB →+BC →=−2α→+β→;。
选修2-1空间向量与立体几何练习题及答案

选修2-1空间向量及立体几何练习题一、选择题(本大题共10个小题,每小题5分,共50分)1.(2013高密高二检测)已知a=(2x,1,3),b=(1,-2y,9),如果a 与b 为共线向量,则( C ) (A)x=1,y=1 (B)x=12,y=-12(C)x=16,y=-32(D)x=-16,y=32解析:∵a=(2x,1,3)与b=(1,-2y,9)共线,故有213129x y ==-, ∴x=16,y=-32.故选C. 2.(2013云南三明高二检测)已知a=3i+2j-k,b=i-j+2k,则5a 与3b 的数量积等于( A )(A)-15 (B)-5 (C)-3 (D)-1 解析:a=(3,2,-1),b=(1,-1,2), ∴5a ·3b=15a ·b=-15.故选A.3.若向量(1,0,z)与向量(2,1,2)的夹角的余弦值为,则z 等于( A )(A)0 (B)1 (C)-1 (D)2 解析:22331z =⨯+,22331z =+, 解得z=0, 故选A.4.(2013德州高二检测)空间直角坐标系中A(1,2,3),B(-1,0,5),C(3,0,4),D(4,1,3),则直线AB 与CD 的位置关系是( A ) (A)平行 (B)垂直 (C)相交但不垂直 (D)无法确定 解析:∵=(-2,-2,2),=(1,1,-1),=-2, ∴∥,又A,B,C,D 不共线, ∴AB ∥CD.5.在正方体ABCD A 1B 1C 1D 1中,B 1C 与对角面DD 1B 1B 所成角的大小为( B )(A)15° (B)30° (C)45° (D)60°解析:设正方体棱长为2,建立如图所示空间直角坐标系.则C(0,,0),B 1(,0,2), ∴=(-,,-2),又=(0,,0)是平面BB 1D 1D 的法向量. ·=2,且||=2,||=,∴cos<,12222=⨯. ∴B 1C 与平面BDD 1B 1的法向量夹角为60°, ∴B 1C 与平面BDD 1B 1的夹角为30°,故选B.6.已知平面α和平面β的法向量分别为m=(3,1,-5),n=(-6,-2,10),则( B )(A)α⊥β (B)α∥β(C)α与β相交但不垂直(D)以上都不对解析:∵n=-2(3,1,-5)=-2m,∴m∥n,∴α∥β.故选B.7.已知向量a=(1,x,1),b=(2,1,-1),a·b>0,则函数y=x2+4x-1的值域是( C )(A)(-∞,3) (B)(-∞,-3)(C)(-4,+∞) (D)(-∞,-4)解析:由于a·b=1×2+x-1=x+1>0,∴x>-1.∴y=x2+4x-1=(x+2)2-5在(-1,+∞)为增函数,所以y>(-1)2+4×(-1)-1=-4,即y∈(-4,+∞),故选C.8.(2013长春外国语学校高二检测)如图,在正方体ABCD A1B1C1D1中,下面结论错误的是( D )(A)BD∥平面CB1D1(B)AC1⊥BD(C)AC1⊥平面CB1D1(D)向量与的夹角为60°解析:以D为原点,DA、DC、DD1所在直线分别为x、y、z轴建立空间直角坐标系,不妨设正方体的棱长为1,则有D(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),A1(1,0,1),B1(1,1,1),C1(0,1,1),D1(0,0,1).=(-1,-1,0),=(-1,1,1),=(0,-1,1),=(-1,-1,0),=(1,0,1).对于选项A.由=知结论正确;对于选项B,由·=(-1,1,1)·(-1,-1,0)=0知结论正确;对于选项C,由选项B,易知AC1⊥B1D1,再由·=(-1,1,1)·(-1,0,-1)=0知结论正确;对于选项D,由cos<,>==-2,知结论不正确.29.正方体ABCD A1B1C1D1的棱长为1,O是底面A1B1C1D1的中心,则O到平面ABC1D1的距离为( B )(A)1(B)2(C)2(D)32解析:如图所示,建立空间直角坐标系,则A(1,0,0),C(0,1,0),B1(1,1,1),O12,12,1.∴=12,-12,-1,=(1,0,1).由于B1C⊥BC1,B1C⊥D1C1,∴B1C⊥平面ABC1D1,因此=n=(1,0,1)是平面ABC1D1的一个法向量, ∴点O到平面ABC1D1的距离d==122=24,故选B.10.已知O为坐标原点,=(1,2,3),=(2,1,2),=(1,1,2),点Q在直线OP上运动,则当·取得最小值时,点Q的坐标为( C )(A)12,34,13(B)12,32,34(C)43,43,83(D)43,43,73解析:设Q(x,y,z),∵Q在上,故有∥,∴x=λ,y=λ,z=2λ,则Q(λ,λ,2λ),∴=(1-λ,2-λ,3-2λ),=(2-λ,1-λ,2-2λ),∴·=6λ2-16λ+10=6(λ-43)2-23,当λ=43时,·取得最小值,此时Q43,43,83,故选C.二、填空题(本大题共4个小题,每小题5分,共20分)11.(2012北京高二模拟)已知a=(3λ,6,λ+6),b=(λ+1,3,2λ)为两平行平面的法向量,则λ= .解析:由题意知a ∥b,∴366132λλλλ+==+,解得λ=2. 答案:2 12.命题:①若a 与b 共线,b 与c 共线,则a 与c 共线; ②向量a 、b 、c 共面,则它们所在的直线也共面; ③若a 与b 共线,则存在惟一的实数λ,使b=λa; ④若A 、B 、C 三点不共线,O 是平面ABC 外一点,= 13+13+13,则点M 一定在平面ABC 上,且在△ABC 内部. 上述命题中的真命题是 .解析:当b=0时,①不正确;a,b,c 共面于平面α,a,b,c 所在直线可能异面,但都与平面α平行,所以②不正确;③不正确,a ∥b ⇔b=λa,但 a ≠0;由空间向量基本定理可知④正确. 答案:④13.(2012重庆高二上学期质量检测)空间四点O(0,0,0),A(0,0,3), B(0,3,0),C(3,0,0),O 点到平面ABC 的距离为 . 解析:设平面ABC 的一个法向量为n=(x,y,z),=(0,0,3),=(0,3,-3),=(3,0,-3), 则⇒,.y z x z =⎧⎨=⎩ ∴取n=(1,1,1) 故所求距离为d==.答案:14.(2012政和高二检测)如图,空间四边形OABC,点M,N分别为OA,BC 的中点,且=a,=b,=c,用a,b,c表示,则= .解析:=-=1 2(+)-12=-12a+12b+12c.答案:-12a+12b+12c三、解答题(本大题共4个小题,共50分)15.(本小题满分12分)已知矩形ABCD和矩形ADEF所在平面互相垂直,点M、N分别在对角线BD、AE上,且BM=13BD,AN=13AE,求证:MN∥平面CDE.证明:建立如图所示空间直角坐标系,设AB,AD,AF长分别为3a,3b,3c,则=++=(2a,0,-c).又平面CDE的一个法向量=(0,3b,0),由·=0,得到⊥.因为MN不在平面CDE内,所以NM∥平面CDE.16.(本小题满分12分)(2012浙江温州高二上学期期末联考)如图,在平行六面体ABCD A1B1C1D1中,AB=AD=AA1=1,∠BAD=60°,∠BAA1=∠DAA1=45°.(1)求||;(2)求证:BD⊥平面ACC1A1.(1)解:=++||2=(++)2=+++2(·+·+·)-2+2=2,=1+1+1+2-12∴|BD 1|=.(2)证明:=-,·=·(-)=0,则BD⊥AA1,又BD⊥AC,所以BD⊥平面ACC1A1.17.(本小题满分12分)(2013郴州高二检测)如图,在三棱柱ABC A1B1C1中,AA1⊥平面ABC,AC=3,BC=4,AB=5,AA1=4.(1)证明:AC ⊥BC 1;(2)求二面角C 1AB C 的余弦值大小.解:在三棱柱ABC A 1B 1C 1中,AA 1⊥平面ABC,AC=3,BC=4,AB=5,故AC,BC,CC 1两两垂直,建立空间直角坐标系(如图), 则C(0,0,0),A(3,0,0),C 1(0,0,4),B(0,4,0),B 1(0,4,4). (1)证明:=(-3,0,0), =(0,-4,4),∴·=0.故AC ⊥BC 1.(2)平面ABC 的一个法向量为m=(0,0,1),设平面C 1AB 的一个法向量为 n=(x,y,z), =(-3,0,4),=(-3,4,0),由得340,340,x z x y -+=⎧⎨-+=⎩ 令x=4,则y=3,z=3.∴n=(4,3,3), 故cos<m,n>=34=334.即二面角C 1AB C 的余弦值为33434.18.(本小题满分14分)(2011年高考北京卷)如图,在四棱锥P ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.(1)求证:BD⊥平面PAC;(2)若PA=AB,求PB与AC所成角的余弦值;(3)当平面PBC与平面PDC垂直时,求PA的长.(1)证明:∵PA⊥平面ABCD,∴PA⊥BD,∵底面ABCD为菱形,∴AC⊥BD,∵PA∩AC=A,∴BD⊥平面PAC.解:(2)设AC∩BD=O,∵∠BAD=60°,PA=AB=2,∴BO=1,AO=OC=,如图,以O为坐标原点,OB、OC所在直线为x,y轴,以过O点且垂直平面ABCD的直线为z轴,建立空间直角坐标系Oxyz,则:P(0,-,2),A(0,-,0),B(1,0,0),C(0,,0), ∴=(1,,-2),=(0,2,0),设PB 与AC 所成的角为θ,则cos θ=|cos<,>| =||=64. (3)由(2)知,=(-1,,0),设|PA|=t>0, 则P(0,-,t),∴=(-1,-,t),设平面PBC 的法向量为m=(x,y,z),则·m=0,·m=0, 即30,30,x y x y tz ⎧-+=⎪⎨--+=⎪⎩ 令y=,则x=3,z=6t, ∴m=3,,6t, 同理可得平面PDC 的法向量n=-3,,6t,∵平面PBC ⊥平面PDC,∴m ·n=0,即-6+236t =0, ∴t=,即|PA|=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二数学(选修2-1 )空间向量试题宝鸡铁一中司婷一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题 5 分,共 60 分).1.在正三棱柱ABC—A1B1C1中,若AB=2BB1,则 AB1与 C1B 所成的角的大小为()A. 60°B. 90°C. 105°D.75°2.如图,ABCD—A1B1C1D1是正方体,B1E1=D1F1=A1B1,则 BE1 4与 DF1所成角的余弦值是()A.15B.1172图8D.3C.2173.如图, 1 1 1—是直三棱柱,∠=90°,点1、 1 分别是 1 1、A B C ABC BCA D F A BA1C1的中点,若 BC=CA=CC1,则 BD1与 AF1所成角的余弦值是()A.C.30110B.230图1515D.104.正四棱锥S ABCD 的高 SO 2 ,底边长AB 2 ,则异面直线BD 和 SC 之间的距离().15.5C.2 5A5B55 5.已知ABC A1 B1 C1是各条棱长均等于 a 的正三棱柱, D 是侧棱 CC1的中点.点 C1到平面 AB1 D 的距离()A. 2 a B. 2 a48A 1D.5C110B1D A CB图C.32 a D. 2 a 426.在棱长为 1 的正方体ABCD A1 B1C1D1中,则平面 AB1C 与平面 A1 C1 D 间的距离()A.3B.3C.2 3D.363327.在三棱锥-中,⊥,==1,点、D 分别是、的中点,⊥底P ABC AB BC AB BC2PA O AC PC OP 面 ABC,则直线 OD与平面 PBC所成角的正弦值()A.21B.8 3C210 D .2106360308.在直三棱柱ABC A1B1C1中,底面是等腰直角三角形,ACB 90,侧棱 AA1 2 ,D,E 分别是CC1与A1B的中点,点 E 在平面AB D 上的射影是ABD 的重心G.则A1B 与平面 AB D所成角的余弦值()A.2B.7C.3D.3 33279.正三棱柱ABC A1 B1C1的底面边长为3,侧棱AA133 ,D是C B延长线上一点,2且 BD BC ,则二面角B1AD B 的大小()A.3B.6C.5D.26310.正四棱柱ABCD A1B1C1D1中,底面边长为 2 2 ,侧棱长为4, E,F 分别为棱AB,CD的中点,EF BD G .则三棱锥B1EFD1的体积V()A.6B.16 3C.16D.1663311.有以下命题:①如果向量 a, b 与任何向量不能构成空间向量的一组基底,那么a, b 的关系是不共线;② O , A, B,C 为空间四点,且向量OA, OB, OC不构成空间的一个基底,则点 O, A, B,C一定共面;③已知向量 a, b, c 是空间的一个基底,则向量 a b, a b, c 也是空间的一个基底。
其中正确的命题是: ()( A )①② ( B )①③ ( C )②③ ( D )①②③12. 如图:在平行六面体 ABCDA 1B 1C 1D 1 中, M 为 A 1C 1 与 B 1D 1 的交点。
若 AB a ,AD b , AA 1 c 则下列向量中与 BM 相等的向量是()D1C1M( A )1 a1b c(B) 1 a1b c222 2( C ) 1 a1b c( D ) 1a1b c2 222A1B1DCA B二、填空题:请把答案填在题中横线上(每小题 6 分,共 30 分).13.已知向量 a (0,1,1 ) , b(4,1,0) ,|a b |29 且0 ,则= ____________.14 .在正方体ABCD A 1 B 1C 1D 1 中, E 为 A 1B 1 的中点,则异面直线 D 1E 和 BC 1间的距离.15. 在棱长为 1 的正方体 ABCD A 1 B 1C 1D 1 中, E 、 F 分别是 A 1B 1 、 CD 的中点,求点 B 到 截面 AEC 1F 的距离 .16.已知棱长为 1 的正方体 AB CD -AB CD 中, E 、F 分别是 B C 和 CD 的中点,点 A 到平1 1 1 11 1 1 1 1面 D B EF 的距离.17.已知棱长为 1 的正方体 AB CD -A 1B 1C 1D 1 中, E 是 A 1B 1 的中点,求直线 A E 与平面 AB C 1D 1所成角的正弦值.三、解答题:解答应写出文字说明、证明过程或演算步骤(共 60 分).18.( 15 分)已知棱长为 1 的正方体 AB CD - A 1B 1C 1D 1,求平面 A 1B C 1 与平面 AB CD 所成的二面角的大小19.( 15 分)已知棱长为 1 的正方体 AB CD - A 1B 1C 1D 1 中, E 、 F 、 M 分别是 A 1C 1、A 1D 和B 1A 上任一点,求证:平面 A 1EF ∥平面 B 1MC .20.( 15 分)在四棱锥 P —ABCD 中,底面 ABCD 是一直角梯形, ∠ BAD =90°,AD ∥ BC ,AB =BC =a ,AD =2a ,且 PA ⊥底面 ABCD , PD 与底面成 30°角.( 1)若 AE ⊥ PD , E 为垂足,求证: BE ⊥ PD ;( 2)求异面直线 AE 与 CD 所成角的余弦值.21.( 15 分)已知棱长为 1 的正方体 A C 1, E 、 F 分别是 B 1C 1、 C 1D 的中点.( 1)求证: E 、 F 、 D 、 B 共面; ( 2)求点 A 1 到平面的 B DEF 的距离;( 3)求直线 A 1D 与平面 B DEF 所成的角.参考答案一、 1. C ; 2. A ; 3. B ;4. A ;5. A ; 6. C ; 7. A ; 8. B ; 9.D ; 10.B ; 11. A ;12. C ;二、 13. 314.26 15 . 6 16 .1; 17 .10335三、18. 解:如图建立空间直角坐标系,A 1C 1 =(- 1, 1,0), A 1B =( 0, 1,- 1)设 n 1 、 n 2 分别是平面 A BABz11D 1C 1由 n 1 A 1 B可解得 n =( 1 1 1A 11 , , )B 1n ACC1 1 1D易知 n 2 =( 0, 0, 1),AyBxn 1 n 23所以, cos n 1 , n 2 =n 1n 23所以平面 A 1B C 1 与平面 AB CD 所成的二面角大小为 a rccos3或- a rccos3 .3319.证明:如图建立空间直角坐标系,zD 1C1则 A1C1=(-1,1,0), B1 C =(-1,0,-1)EA 1B1A1D =(1,0,1),B1 A =(0,-1,-1)M yF设 A1E A1C1,A1 F A1D ,B1 M B1A(、、D CR ,且均不为0)A B x设 n1、 n2分别是平面A EF与平面B MC的法向量,11由n1 A1 E0可得n1A1C10即n1 A1C10n1 A1 F 0n1A1D 0n1 A1D 0解得:1n =(1,1,-1)由n2 B1 M0可得n2B1A 0即n2 B1 A 0n2 B1C 0n2 B1 C 0n2 B1C 0解得 n2=(-1,1,-1),所以 n1=- n2,n1∥ n2,所以平面 A1EF∥平面 B1MC.20.( 1)证明:∵PA⊥平面ABCD,∴PA⊥AB,又AB⊥AD.∴AB⊥平面PAD.又∵AE⊥PD,∴PD⊥平面 ABE,故 BE⊥ PD.( 2)解:以A 为原点,、、所在直线为坐标轴,建立空间直角坐标系,则点、AB AD APC D的坐标分别为(a, a,0),(0,2a,0).∵PA⊥平面 ABCD,∠ PDA是 PD与底面 ABCD所成的角,∴∠ PDA=30°.于是,在 Rt △AED中,由AD=2a,得AE=a.过E作EF⊥AD,垂足为F,在 Rt △AFE中,由AE=a,∠ EAF=60°,得 AF=a, EF=3a,∴ E(0,1a,3a)2222于是, AE{ 0, 1a,3a}, CD ={-a,a,0}2 2设AE 与 CD 的夹角为θ,则由AE CD 0 ( a)1a a3 a222cos θ =4|AE| |CD |( 1a) 2( 3 a) 2 ( a)2a2020222与 所成角的余弦值为2 . AECD421.解:( 1)略.( 2)如图,建立空间直角坐标系D —xyz ,则知 B ( 1, 1, 0), E( 1 ,1,1), F (0, 1,1).22设 n ( x, y, z)是平面 BDEF 的法向量 .由nDB, nDF ,DB(1,1,0), DF (0, 1,1)2 得nDB x y 0则xyn DF1 yz 0z 1y.22令 y1,得 n ( 1,1,1) .2设点 A 在平面 B DFE 上的射影为 H ,连结 A D ,知 A D 是平面 B DFE 的斜线段.111A D( 1,0, 1), AD n( 1)( 1)1 ( 1)( 1 ) 3 .12 2又 | A 1D| ( 1)2 O 2 ( 1)2 2 ,| n | ( 1)212 ( 1 ) 23 ,2 2A 1D n 32 cos A 1D, A 1H2 3 .| A 1D | | n |222| A 1 H | | A 1D | cos A 1D, A 1H2 21.2即点1到平面DFE 的距离为 1.AB( 3)由( 2)知, A H=1,又 A D=2 ,则△ A HD 为等腰直角三角形,111A 1 DH DA 1 H 45A 1 H平面 BDFE , HD 是 A 1 D 在平面 BDFE 上的射影 ,A 1 DH 就是直线 A 1 D 与平面 BDFE 所成的角 ,A 1 DH 45 .。
