图形计算器二次函数实例
几何画板二次函数案例

几何画板二次函数案例二次函数在几何画板中的应用非常广泛,下面我将为你提供一个案例,详细解释如何使用二次函数来构建一个几何图形。
案例:构建一个抛物线喷泉喷泉是一种常见的城市景观和装置,它通过一个喷水装置将水以特定的形式喷射出来,形成美丽的水柱。
在这个案例中,我们将使用二次函数来模拟喷泉的形状。
首先,让我们定义一个二次函数来描述喷泉的形状。
假设水柱的高度(h)是和喷射距离(x)相关的,我们可以使用以下二次函数来描述这种关系:h(x) = ax^2 + bx + c其中,a、b、c是需要确定的常数。
喷泉的形状通常是一个开口朝下的抛物线,所以a的值应该小于0。
接下来,我们将确定a、b和c的值。
为了简化问题,我们假设喷泉的最高高度是10米,并且喷射的最远距离是20米。
我们可以选择两个点来确定这个二次函数的值。
假设我们选择喷泉的两个关键点分别是(0,0)和(20,10)。
将这两个点带入二次函数的方程,我们可以得到以下两个方程:0=a*0^2+b*0+c=>c=010=a*20^2+b*20+0=>400a+20b=10通过解这个方程组,我们可以得到a和b的值。
解方程组可以得到a=-0.0125和b=0.25、所以二次函数的方程为:h(x)=-0.0125x^2+0.25x现在,我们可以使用这个二次函数来绘制喷泉的形状。
通过在几何画板上画出一系列点,然后使用平滑曲线连接这些点,我们可以得到整个喷泉的形状。
首先,我们选择几个x的值,例如x=0,2,4,...,20。
然后,我们使用二次函数计算对应的h(x)的值。
最后,在几何画板上画出这些点,并使用平滑曲线连接它们。
通过加入适当的颜色和细节,我们可以使这个几何图形更加真实和立体感。
我们还可以添加其他元素,如水柱顶部的喷雾效果。
通过调整二次函数的参数,我们可以自由地改变喷泉的形状和高度。
这使得几何画板成为优秀的工具,用于设计和模拟各种喷泉的形状,并选择出最佳的设计。
二次函数例子

二次函数例子
1. 哇塞,你知道投篮时篮球的轨迹吗?那其实就是一个二次函数的例子呀!当篮球被投出后,它的高度会先上升然后再下降,这不就和二次函数图像一模一样吗!
2. 嘿,想想公园里的喷泉,水喷上去又落下来的样子!那水的高度变化不就是二次函数的典型案例嘛,多有意思呀!
3. 哎呀,你有没有注意到秋千荡起来的弧度呀?一上一下的,这和二次函数多像啊,简直太神奇了!
4. 哇哦,每个月手机流量使用的情况其实也可以用二次函数来表示呢,开始用得少,中间猛用,然后又慢慢减少,可不是像二次函数图像一样嘛!
5. 你看那抛物线桥,多壮观啊!它的形状不正是二次函数在生活中的完美体现嘛,超酷的!
6. 嘿呀,烟花绽放的轨迹也是个二次函数呀!烟花升上去再炸开,那轨迹多美妙,绝对是二次函数的精彩呈现!
7. 哎呀,家里的吊灯摆动起来的轨迹也是二次函数呢,你好好想想,是不是很神奇呀!
我觉得二次函数真的是无处不在呀,在我们生活中好多地方都能看到它的影子,太有趣啦!。
生活中的二次函数例子5个

生活中的二次函数例子5个1.某种小商品的销量Y件与售价X元成一次函数关系。
某商场以每件4元的单价进了一批这种商品第一天以每件8元试销,结果售出60件,第二天以每件10元试销,结果售出50件。
(1)求销量Y与售价X的函数关系式。
(2)每件商品的售价定位多少元时,才能每天获得最大利润?每天的最大利润是多少元?2.某超市销售一种饮料,每瓶进价为9元,经市场调查表明,当售价在10元到14元之间(含10元,14元)浮动时,每瓶售价每增加0.5元,日均销量减少40瓶;当售价为每瓶12元时,日均销量为400瓶.问销售价格定为每瓶多少元时,所得日均毛利润(每瓶毛利润=每瓶售价-每瓶进价)最大?最大日均毛利润为多少元?3.某衬衣店将进价为30元的一种衬衣以40元售出,平均每月能售出600件调查表明:这种衬衣售价每上涨1元其销售量将减少10件.(1)写出月销售利润y(元)与售价x(元/件)之间的函数关系式;(2)当销售价定为45元时计算月销售量和销售利润;(3)衬衣店想在月销售量不少于300件的情况下,使月销售利润达到10 000元,销售价应定为多少?(4)当销售价定为多少元时会获得最大利润?求出最大利润.4.一家电子计算器专卖店每只进价13元,售价20元,多买优惠;凡是一次买10只以上的,每多买1只,所买的全部计算器每只就降低0.10元,例如,某人买20只计算器,于是每只降价0.10×(20﹣10)=1(元),因此,所买的全部20只计算器都按照每只19元计算,但是最低价为每只16元.(1)求一次至少买多少只,才能以最低价购买?(2)写出该专卖店当一次销售x(时,所获利润y(元)与x(只)之间的函数关系式,并写出自变量x的取值范围;(3)若店主一次卖的只数在10至50只之间,问一次卖多少只获得的利润最大?其最大利润为多少?5. 为了提高市民的宜居环境,某区规划修建一个文化广场(平面图形如图所示),其中四边形ABCD是矩形,分别以AB、BC、CD、DA边为直径向外作半圆,若整个广场的周长为628米,设矩形的边长AB=y米,BC=x 米.(注:取π=3.14)(1)试用含x的代数式表示y;(2)现计划在矩形ABCD区域上种植花草和铺设鹅卵石等,平均每平方米造价为428 元,在四个半圆的区域上种植草坪及铺设花岗岩,平均每平方米造价为400元;(3)设该工程的总造价为W元,求W关于x的函数关系式;(4)若该工程政府投入1千万元,问能否完成该工程的建设任务?若能,请列出设计方案,若不能,请说明理由?。
二次函数实际应用例题与解答,中考数学二次函数解决实际应用问题经典题型及答案解析

二次函数实际应用示例1.在排球家中,_队员站在边线发球,发球方向与边线垂直,球开始飞行时距地面1.9米,当球飞行距离为9米时达最大高度5.5米,已知球场长18米,问这样发球是否会直接把球打出边线?思路解析*先建立坐标系,如图,根据已知条件求出抛物线的解析式,再 求抛物线与x轴的交点坐标(横坐标为正),若这点的横坐标大于18,就可判断球出线.解:以发球员站立位置为原点,球运动的水平方向为x轴,建立直角坐标系伽图).由于其图象的顶点为(95执设二^函教关系式为y=a(x-9)、S.5(3丰0),由已知,这个函数的图象过(0,1.9),可以得到1.9=0(0-9)2+552解得a----7,45所以,所求二}欠函数的关系式是y=-M(x-9)2十5.5.45排球落在x轴上,则y=O,因此,-:(x・9)2+5.5=0.解方程,得*=9十半点0.1,X2=9-峪(负值,不合题意,舍去).所以,排球约在20」米远处落下,因为20.1>18,所以,这样发球会直接把球打出边线,2.某工厂大门是一抛物线型水泥建筑物,如图26.3-9所示,大门地面亮AB二4m,解:以队员甲投球站立位置为原点,球运动的水平方向为X轴,建立直角坐标系.由于球在空中的路径为抛物线,其图象的顶点为(4,4),设二}欠函数关系式为y=a(x-4)2-4(g0),由已知,这个函数的图象过(024),可以得到24=3(0-4)2+4.解得a=-0.1.所以所求二次函数的关系式是y=-0.1(x-4)2+4当x二7时,y=-0.1(x-4)2+4=3.1.因为3.1=3+0.1,0.1在篮球偏离球圈中心10cm以内.答:这个球能投中.综合•应用4.(2010安徽模拟)如图26.3-10,在平面直角坐标系中,二}欠函数y=ax2十c(a ")的图象过正方形ABO(:的三个顶点A、B、C,则ac的值是.思路解析:图中,正方形和抛物线都关于y轴对称,欲求ac的值,需求抛物线的解析式,点A、B、C都在抛物线上,它们的坐标跟正方形的边长有关,可设正方形的边长为2m「则A(0r2整m)、B(-皿阳7^所)、C(72w r把A、B的坐标值代入y=a*十c中,得a=四,c=2&,所以Imac=—X =2.2ni5.有一种螃蟹,从海上捕获后不放乔,最多只能存活两天,如果放养在塘内,可以延长存活时间,但每天也有一定数量的蟹死去,假设放养期内蟹的个体重量基本保持不变.现有一经销商,按市场价收购了这种;SB〔000千克放养在塘内,此时市场价为每千克30元.据测算,此后每千克活蟹的市场价每天可上升1元,但放养一天需各种费用400元,且平均每天还有10千克螯死去,假定死蟹均于当天全部售出,售价是每千克20元⑴设x天后每千克活蟹的市场价为P元,写出P关于x的函数关系式;(2)如果放养x天后将活蟹一次性出售,并记1000千克蟹的销售点颔Q元,写出Q关于x的函数关系式;⑶该经销商将这批蟹放弄多少天后出售,可获得最大利润(利润=销售总额-收购成本-费用)?最大利润是多少?思路解析:⑴市场价每天上升1元,则P=30+X;(2)销售总额为活蟹销售和死蟹销售两部分的和,活蟹数量每天减少10千克,死蟹数量跟放养天数成正比;(3)根据利润计算式表达,可没利润为w元,用函数瞄解决.答案:⑴P=30+x.(2)Q=(30+x)(1000-10x)+20-10x=-10x2+900x+30000.⑶设利润为w元,则w=(-10x2+900x+30000)-30-1000-400x=-10(x-Z5)2-»-6250.」.当x=25时,w有最大值,最大值为6250.答;经销商将这批蟹放养25天后出售,可获得最大?IJ润,6.将一条长为20cm的铁丝雪成两段,并以每一段铁丝的长度为周长做成f正方形.⑴要使这两个正方形的面积之和等于17cm2,那么这段铁丝磐成两段后的长:度分别是多少?(2)两个正方形的面积之和可能等于12cm?吗?若能,求出两段铁丝的长度;若不能,请说明理由.思路解析;用方程或函数考虑.设其中一段长为x cm,列出面积和的表达式,构成方程或函数,用它们的性质解决问题.方法一:⑴解:设剪成两段后其中一段为x cm,则另一段为(20-x)cm.由题意得(三沪+(竺1沪=17.4 4解得冶=16,x2=4.当为=16时,20-x=4;当x2=4时,20-x=16.答:这段铁丝雪成两段后的长度分别是16cm和4cm.(2)不能.理由是:(料牛)5.整理,得x<20x+104=0.•,A=b2-4ac=-16<0,.,此方程无配即不能雪成两段使得面积和为12新.方法二:剪成两段后其中一段为x cm,两个正方形面积的和为yen?.则y=弓尸+=;(x.10)2+12.5(0<x<20)・当y=17时,有上(乂-10)112.5=17.S解方程,得Xi=16,x2=4.当xi=16时,20*4;当X2二4时,20*16.答:这段铁丝剪成两段后的长度分别是16cm和4cm.(2)不能.理由是:函数y=|(x-10)2+1Z5中,a二;>0,当x=10时,函数有最小值,最小值88为12.5.•.・12v125,所以不能勇成两段使得面积和为12cm2.7.我市英山县某茶厂种植,春蕊牌“绿茶,由历任来市场销售行情知道,从每年的3月25日起的180天内,绿茶市场销售单价y(jt)与上市时间t庆)的关系可以近似地用如图①中的一条折线表示.绿茶的种植除了与气候、种植技术有关外,其种植的成本单价z齿)与上市时间t庆)的关系可以近似地用如图②的抛物肆图263-11①图26.3-11-②⑴写出图①中表示的市场销售单价y团)与上市时间t庆)(t>0)的函数关系式;(2)求出图②中表示的种梢成本单价z员)与上市时间t庆)(t>0)的函敬关系式;⑶认定市场销售单价减去种植成本单价为纯收益单价,问何时上市的绿茶纯收益单价缺?(说明:市场铠售单价和种植成本单价的单位:元/500克.)思路解析:从图形中得出相关数据,用分段函薮表示市场销售单价,种植成本是一E碰物线,再分别计算各时段的纯收益单价,匕咸得出结论.解:(1)①当0冬X三120时,y=-|x-b160;②当120<xE50时,y=80;2③当150UX式180时,y=±x-+20.5(2)设z=a(x・110)」20,N OC1把X=6O,y=W代入,^=a(60-110)120解得。
二次函数的应用案例总结

二次函数的应用案例总结二次函数是一种常见的数学函数形式,它的形式为:y = ax^2 + bx + c。
在现实生活中,二次函数可以用于解决各种问题,包括物理、经济、工程等领域。
本文将总结几个常见的二次函数应用案例,以展示二次函数的实际应用。
案例一:物体自由落体的高度模型假设一个物体从高处自由落体,忽略空气阻力,我们可以用二次函数来表示物体的高度与时间之间的关系。
设物体初始高度为H,加速度为g,时间为t。
根据物理定律,物体的高度可以表示为:h(t) = -0.5gt^2 + H。
这个二次函数模型可以帮助我们计算物体在任意时间点的高度,并可以用于预测物体何时落地。
案例二:销售收入和定价策略假设一个公司生产和销售某种产品,销售价格为p(单位:元),销售量为q(单位:件)。
二次函数可以用于建立销售收入与定价策略之间的模型。
设定售价的二次函数为:R(p) = -ap^2 + bp + c,其中a、b、c为常数。
我们可以通过分析二次函数的图像、求解极值等方法,确定最佳售价,以使得销售收入最大化。
案例三:桥梁设计中的弧线形状在桥梁设计中,常常需要确定桥梁的弧线形状,以使得车辆在桥上行驶时感到平稳。
二次函数可以用来描述桥梁的曲线形状。
设桥梁的弧线形状为y = ax^2 + bx,其中x表示桥梁长度的一半,y表示桥梁的高度。
通过调整参数a和b,可以得到不同形状的弧线,以满足设计要求。
案例四:市场需求和价格关系分析在经济学中,二次函数可以用于建立市场需求与价格之间的关系模型。
设市场需求量为D,价格为p。
根据经济理论,市场需求可以表示为:D(p) = ap^2 + bp + c,其中a、b、c为常数。
通过分析二次函数的图像、求解极值等方法,可以研究市场需求和价格之间的关系,得出不同价格下的市场需求量。
综上所述,二次函数在物理、经济、工程等领域中具有广泛的应用。
通过建立二次函数模型,我们可以更好地理解和解决各种实际问题。
二次函数的应用举例

二次函数的应用举例一、圆的方程在数学中,圆的方程可以通过二次函数来表示。
假设圆的圆心坐标为(h, k),半径为r,那么圆的方程可以写为:(x - h)² + (y - k)² = r²其中,(x, y)表示圆上的任意一点。
通过这个方程,我们可以得到圆上的所有点的坐标。
举例:假设有一个圆,圆心坐标为(2, 3),半径为4。
那么圆的方程可以写为:(x - 2)² + (y - 3)² = 16通过这个方程,我们可以求解出圆上的任意点的坐标。
二、抛物线抛物线是二次函数的一种特殊形式。
它可以用来模拟抛体在重力作用下的运动轨迹。
抛物线的方程可以写为:y = ax² + bx + c其中,a、b、c都是实数,而a不等于0。
抛物线的开口方向由a的正负号决定。
举例:假设有一个抛物线,方程为y = 2x² - 3x + 1。
我们可以通过这个方程来分析抛物线的特性。
1. 开口方向:由于a的值为正,所以该抛物线开口向上。
2. 顶点坐标:抛物线的顶点坐标可以通过公式计算得到。
公式为:x = -b / (2a)y = f(x) = a(x - h)² + k将a、b、c代入公式,可以计算出该抛物线的顶点坐标为:x = -(-3) / (2 * 2) = 3/4y = 2 * (3/4)² - 3 * (3/4) + 1 = 7/8所以该抛物线的顶点坐标为(3/4, 7/8)。
3. 对称轴:抛物线的对称轴垂直于x轴,并通过顶点。
所以这个抛物线的对称轴方程为x = 3/4。
通过这个抛物线的方程,我们可以确定它的基本特性,并进行更进一步的分析。
三、最优化问题二次函数还可以用来解决最优化问题,即在一定条件下寻找使某个函数值达到最大或最小的变量取值。
举例:假设有一个二次函数f(x) = 2x² + 3x - 5。
我们要找到使得函数f(x)取得最小值的x的取值。
九年级数学下册《二次函数的应用》优秀教学案例

(一)导入新课
在导入新课环节,我将结合学生的实际生活,提出以下问题:“同学们,你们在生活中遇到过抛物线运动吗?比如抛硬币、投篮等。这些现象与数学中的哪个知识点有关?”通过这个问题,引导学生回顾之前学过的抛物线知识,为新课的学习做好铺垫。
接着,我会展示一些与二次函数相关的图片和实例,如拱桥、卫星轨道等,让学生观察并思考这些图像的共同特点。在此基础上,引出本节课的主题——二次函数的应用,激发学生的好奇心和探究欲望。
小组合作是本章节教学的重要组成部分。我将根据学生的学习特点和兴趣,合理分组,使学生在合作交流中共同进步。在小组合作过程中,引导学生明确分工、相互协作,共同探讨二次函数的性质、图像以及应用问题。通过小组讨论、成果展示等形式,培养学生的团队协作能力和表达能力。
(四)反思与评价
在教学过程中,我将重视学生的反思与评价,让学生在反思中总结经验,不断提高。在每节课结束后,引导学生回顾所学内容,总结二次函数的性质、图像和应用方法,查找自己在学习过程中的不足之处,并进行针对性的改进。同时,开展多元化的评价方式,如自我评价、同伴评价、教师评价等,全面了解学生的学习情况,激发学生的学习积极性,促进学生的全面发展。此外,我还将关注学生的情感态度与价值观的培养,鼓励学生积极参与课堂活动,充分展示自己的个性特长,使学生在数学学习中获得成功的体验。
(三)学生小组讨论
在学生小组讨论环节,我会将学生分成若干小组,每组选出一名组长负责组织讨论。以下为讨论的主题和步骤:
1.各小组结合教材和实例,探讨二次函数在实际问题中的应用方法。
2.各小组分享自己在讨论过程中的发现和心得,相互交流、学习。
3.针对本节课的重点和难点,引导学生相互提问、解答,共同提高。
4.学会使用数学软件或图形计算器绘制二次函数图像,以便更好地理解二次函数的几何性质。
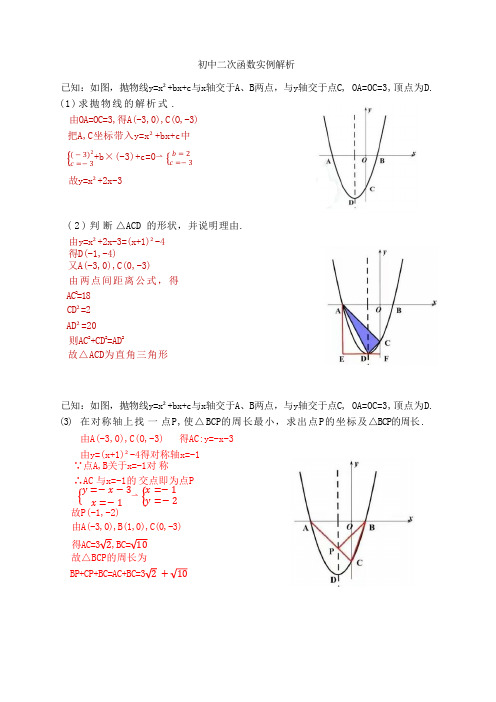
二次函数实例解析
初中二次函数实例解析已知:如图,抛物线y=x²+bx+c与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D.(1)求抛物线的解析式.由OA=OC=3,得A(-3,0),C(O,-3)把A,C坐标带入y=x²+bx+c中(−3)2=−3+b×(-3)+c=0⇀=2=−3故y=x²+2x-3(2)判断△ACD的形状,并说明理由.由y=x²+2x-3=(x+1)²-4得D(-1,-4)又A(-3,0),C(0,-3)由两点间距离公式,得AC2=18CD²=2AD²=20则AC2+CD2=AD2故△ACD为直角三角形已知:如图,抛物线y=x²+bx+c与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D.(3)在对称轴上找一点P,使△BCP的周长最小,求出点P的坐标及△BCP的周长.由A(-3,0),C(O,-3)得AC:y=-x-3由y=(x+1)²-4得对称轴x=-1∵点A,B关于x=-1对称∴AC与x=-1的交点即为点P=−−3=−1⇀=−1=−2故P(-1,-2)由A(-3,0),B(1,0),C(0,-3)得AC=32,BC=10故△BCP的周长为BP+CP+BC=AC+BC=32+10已知:如图,抛物线y=x²+bx+c与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D.(4)在直线AC下方的抛物线上有一点N,过点N作直线l//y轴,交AC 于点M,当点N 在什么位置时,线段MN 的长度最大,并求出最大值.设N(t,t²+2t-3)由AC:y=-x-3,则M(t,-t-3)则MN=y m -y n =-(t+32)2+94故当t=-32时,MN有最大值94此时N(-32,-154)(5)在直线AC下方的抛物线上是否存在一点N,使得△ACN 的面积最大,最大值为多少?过N作直线l//y 轴,交AC于M,交x轴于H作CP ⊥l于点P,则l⊥x轴S △ACN =S △AMN +S △CHN=12MN×|x a -x c |=32MN故当MN 取最大值时,△ACN面积最大(S △ACN )max =278已知:如图,抛物线y=x²+bx+c与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D.(6)在直线AC 下方的抛物线上是否存在一点P,使得P到直线AC的距离为2.若存在,求出点P的坐标;若不存在,请说明理由.在y轴上取点E(0,-5),作EF⊥AC,则CE=2又OA=OC,则∠OAC=∠OCA=∠ECF=45°,故EF=2过点E 作l/AC,则l上所有点到AC 的距离均为2由AC:y=-x-3,则l:y=-x-5联立=−−5=2+2−3得=−1=−4或=−2=−3故P(-1,-4)或(-2,-3)(7)在直线AC上是否存在一点P,使得BP+OP最小.若存在,求出点P的坐标,并求出最小值;若不存在,请说明理由.作B关于AC的对称点B’,连接BB'交AC于M,则PB=PB'连接OB',故OB'即为所求由AC:y=-x-3,OA=OC,则∠MAB=∠MBA=45°又A,B关于x=-1对称故M必在对称轴x=-1上,即M(-1,-2)由AB=4,得MA=MB=22,则MB'=MA=22故AB'=4且AB'⊥x轴,则B'(-3,-4)已知:如图抛物线y=x²+bx+c与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D. (8)在直线AC上是否存在一点P,使得BP+12AP最小,若存在,求出点P的坐标,并求出最小值;若不存在,请说明理由.如图,作直线l与AC夹角为30°,作PM⊥l,则BP+12AP=BP+PM作BN⊥l于点N,交AC于P此即为所求P点,BP+12AP最小值为BNBN=AB×sin75°=AB×sin(45°+30°)=4×(sin45°cos30°+cos45°sin30°)=4×(22×32+22×12)(9)点E是线段AC 上的一动点,点P是线段AB 上的一动点,PE//BC,是否存在这样的点P,使得△PEC的面积最大.若存在,求出点P的坐标,并求出△PEC 面积的最大值;若不存在,请说明理由.设P(t,0),AP=t+3,BP=1-t,AC:y=-x-3,BC:y=3x-3由PE//BC,设PE:y=3x+6则O=3t+6,解得b=-3t,即PE:y=3x-3t联立:=3K3=−K3得=3−34=−3−94即E(3K34,−3K94)S △PAE =12PA×|y E |=38(t+3)2S △PBC =12PB×OC=32(1-t)S △ABC =12AB×OC=6故S △PEC =S △ABC -S △PAE =-38(t+1)2+32当t=-1时S △PEC 取最大值32已知:如图,抛物线y=x²+bx+c与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D.(10)点P是直线AC 下方的抛物线的一个动点,作PE⊥x轴交AC 于点E,PF⊥AC 与点F,是否存在这样的点P,使得△PEF 周长的最大.若存在,求出点P 的坐标,并求出△PEF周长的最大值;若不存在,请说明理由.由OA=OC,得∠OAC=45°又PE⊥x轴,PF⊥AC,则∠PEF=∠EPF=45°故PE=2PF=2EF,则△PEF的周长为PE+PF+EF=(2+2)PF 故PF取最大值时即可(PF)max 92故△PEF周长最大值:94(2+1)(11)点E是对称轴上的一个动点,是否存在这样的点E,使得△ACE是等腰直角三角形。
