(课件)19.2.3 一次函数与方程、不等式
合集下载
19.2.3一次函数与方程、不等式ppt课件
2、通过下列这个函数图像能直接观察出哪个方程的
解是多少？
y
y
y=2x+3
3
2
ox
-3 o x
y=-2x-4
(1)答：2x+3=3，x=0 。 (2)答：2-x-4=2，x=-35 。
y 用函数观点看方程 一次函数与一元一次方程
y=2x−12
解kx+b=0
等价于哪两个问题?
O6
x
(1)可以转化为求一
的解，就是直线
B．方程 y=0时x的值
的解，就是一次函数
C．方程
的解，就是一次函数
当函数值为0时自变量的值
D．方程 轴交点的纵坐标
的解，就是直线
与x轴 当
与y
10
例1一个物体现在的速度是5m/s，其速度每秒增加2m/s，再 过几秒它的速度为17m/s？ （要求用两种方法解题）
解法1：设再过x秒物体的速度为17米/秒．列方程 2x+5=17．
右图中的两直线右图中的两直线ll的图象则可以看成的图象则可以看成方程组方程组y2x1yx435小东从a地出发以某一速度向b地前进同时小明从b地出发以另一速度向a地前进见下图图中的线段y分别表示小东小明离b地的距离km与所用时间h的关系
八年级 下册
19.2.3 一次函数与方程、不等式
1
• 学习目标： 1．认识一次函数与一元（二元）一次方程（组）、 一元一次不等式之间的联系．会用函数观点解释 方程和不等式及其解（解集）的意义； 2．经历用函数图象表示方程、不等式解的过程，进 一步体会“以形表示数，以数解释形”的数形结 合思想．
y
3x+6=0的解 其解为X=2
o2
x
一次函数与方程、不等式精选教学PPT课件
（3）请用函数的观点，说说你对一元一次方程有什么 新的认识；
（4）请用函数的观点，说说一次函数与一元一次不等 式的联系．
课后作业
作业：教科书第99～100页第8，10，11，13 题．
没有人能忽略这样一张脸孔：泪眼纷纷，呜咽声声，“求求，求求你们。”黑夜在颤抖，墨镜里，必藏着一双红肿、深陷、因其绝望而绝美的眼睛。 她叫苏珊,她说：“这原本是一个温良秋夜，她开车带着3岁和14个月大的两个孩子，行驶在静谧的公路上，忽然一个歹徒窜上车，持枪威逼她下车，带着她的孩子们，扬长而去。
结论推广到一般情形吗？
（1）3x+2＞2；（2）3x+2＜0；（3）3x+2＜-1．
不等式ax+b＞c的解集就是
使函数y =ax+b 的函数值大于c
的对应的自变量取值范围；
不等式ax+b＜c的解集就是
使函数y =ax+b 的函数值小于c 的对应的自变量取值范围．
-2
y 3 y =3x+2
2Байду номын сангаас1
-1 O -1
解决问题
二元一次方程与一次函数的关系
形
直线 y O
y =0.5x+15
x
点的坐标满 足的方程
点的坐标满足 以数对（x，y） 的函数关系 为坐标画点
一次函数
用方程
二元一次方程
数
y = 0.5x+15 观点看
y -0.5x =15
用函数观点看
二元一次方程
y = 0.5x+15
拓展问题
什么时刻，1 号气球的高度赶上2 号气球的高度？大 家会从数和形两方面分别加以研究吗？
二元一次方程 组的解就是相应的 两个一次函数图象 的交点坐标．
（4）请用函数的观点，说说一次函数与一元一次不等 式的联系．
课后作业
作业：教科书第99～100页第8，10，11，13 题．
没有人能忽略这样一张脸孔：泪眼纷纷，呜咽声声，“求求，求求你们。”黑夜在颤抖，墨镜里，必藏着一双红肿、深陷、因其绝望而绝美的眼睛。 她叫苏珊,她说：“这原本是一个温良秋夜，她开车带着3岁和14个月大的两个孩子，行驶在静谧的公路上，忽然一个歹徒窜上车，持枪威逼她下车，带着她的孩子们，扬长而去。
结论推广到一般情形吗？
（1）3x+2＞2；（2）3x+2＜0；（3）3x+2＜-1．
不等式ax+b＞c的解集就是
使函数y =ax+b 的函数值大于c
的对应的自变量取值范围；
不等式ax+b＜c的解集就是
使函数y =ax+b 的函数值小于c 的对应的自变量取值范围．
-2
y 3 y =3x+2
2Байду номын сангаас1
-1 O -1
解决问题
二元一次方程与一次函数的关系
形
直线 y O
y =0.5x+15
x
点的坐标满 足的方程
点的坐标满足 以数对（x，y） 的函数关系 为坐标画点
一次函数
用方程
二元一次方程
数
y = 0.5x+15 观点看
y -0.5x =15
用函数观点看
二元一次方程
y = 0.5x+15
拓展问题
什么时刻，1 号气球的高度赶上2 号气球的高度？大 家会从数和形两方面分别加以研究吗？
二元一次方程 组的解就是相应的 两个一次函数图象 的交点坐标．
19.2.3 一次函数与方程、不等式3ppt
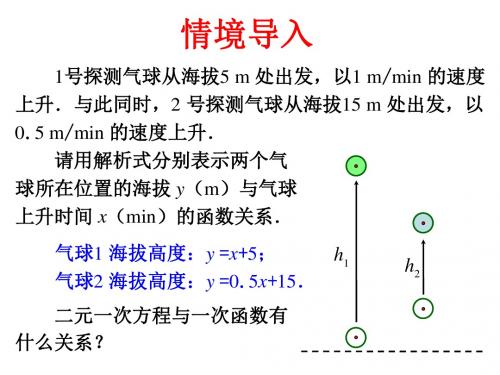
情境导入
什么时刻，1 号气球的高度赶上2 号气球的高度？ 我们能从数和形两方面分别加以研究吗？ 气球1 海拔高度：y =x+5 气球2 海拔高度：y =0.5x+15 从数的角度看： h1 h2
解方程组
y = x+ 5 ， y=0.5x+15.
解得
X=20， y=25.
19.2.3 一次函数与方程、 不等式
4.一家电信公司给顾客提供两种上网收费方
式：方式Ａ以每分钟0.1元的价格按上网时间
计费；方式Ｂ除收月租费20元外再以每分钟 0.05元的价格按上网时间计算．如何选择收 费方式能使上网者更合算？
【解析】设上网时间为x分，若按方式A，则收费y=0.1x元； 若按方式B，则收费y=0.05x+20元.
6分钟后比一比谁能正确解答问题
自学检测
1.已知一次函数y=3x+5与y=2x+b的图象交点为(-1，2)， y 3 x 5， 则方程组 y 2 x b 的解是_______,
2、求函数y=x+2和y=2x-3的交点坐标。
探究：一次函数与二元一次方程组的关系
(1)在同一直角坐标系中画出 3 8 y= x + 与 y = 2 x - 1的图象. 5 5 这个交点(1,1)是方程组
y1
B A P
x=1 y2＝－3x＋1，解得 y＝－2 ∴P(1，－2)，则点P到直线AB的距离为2.
1 5 5 ∴S△APB＝ 2 × 3 ×2＝ . 3
y2
课堂小结：
通过本课时的学习，需要我们握：
以二元一次方程的解为坐标的点都在相应的函数图象 上.反过来,一次函数图象上的点的坐标都适合相应的二元 一次方程.
19.2.3一次函数与方程、不等式(第2课时)课件
二、深入剖析，感悟新知
问题:1号探测气球从海拔5m处出发，以1m/min的速度 上升.与此同时，2号探测气球从海拔15m处出发，以 0.5m/min的速度上升.两个气球都上升了1h. （1）请用式子分别表示两个气球所在位置的海拔y （单位：m）关于上升时间x（单位：min）的函数关 系；
二、深入剖析，感悟新知
三、例题学习，提高认知
例2 如图，求直线l1与l2 的交点坐标.
y
分析：由函数图象可以求 直线l1与l2的解析式， 进而通过方程组求出交点坐标.
O x
四、随堂练习，巩固新知
1．教材第98页练习题． 2.已知一次函数y=3x+5与y=2x+b的图象交点为(-1，2)， y 3 x 5， 则方程组 y 2 x b 的解是_______,b的值为______.
y x 5， 元一次方程组 y 0.5 x 15 的解吗？为什么？
三、例题学习，提高认知
例1 当自变量x取何值时，函数y=2.5x+1和y=5x +17 的值相等？这个函数值是多少？
Zx`````xk
方法一 ：联立两个函数，得 2.5x+1=5x +17，解此方程； 方法二： 把两个函数转化为二元一次方程组，解方程组； 方法三： 画函数图象，求交点坐标.
Zxxk
二、深入剖析，感悟新知
思考：通过问题（2）、（3）的分析，我们能否概括 出二元一次方程的解和一次函数图象上的点的坐标之 间是什么关系？
Zxx```k
方程的解
一次函数图象上点的坐标
以二元一次方程的解为坐标的点，它都在其相应的 一次函数的图象上;一次函数图象上点的坐标，都 适合其相应的二元一次方程.
19.2.3一次函数与方程不等式的关系(3个课时)
19.2.3一次函数与一元一次方程学习目标：1、理解一次函数与一元一次方程的关系，会根据图象解决一元一次方程求解问题。
2、学习用函数的观点看待方程的方法，经历方程与函数关系问题的探究过程，学习用联系的观点看待数学问题。
学习重点：利用一次函数知识求一元一次方程的解。
学习难点：一次函数与一元一次方程的关系发现、归纳和应用。
学习过程：活动一、课前小测1、一次函数12+=x y ，当=x 时，3=y ；当=x 时，0=y ；当=x 时，1-=y 。
2、一次函数，12+=x y ，x 轴交点坐标为________；与y 轴交点坐标_________；图像经过_______象限，y 随x 的增大而______，图像与坐标轴所围成的三角形的面积是 。
活动二：观察分析，探究新知 1、自主探究(1)解方程2x+20=0(2)当自变量x 为何值时，函数y=2x+20的值为0？解：(1) 2x+20=0(2) 当y=0时 ，即思考：上面两个问题实际上是______问题．（3）画出函数y=2x+20的图象，并确定它与x 轴的交点坐标.（思考：直线y=2x+20与x 轴交点坐标为（____,_____），这说明方程2χ＋20＝0的解是x=_____）2、合作交流(小组交流答成共识,然后展示交流成果 )从“函数值”看，“解方程ax+b=0(a ，b 为常数， a ≠0)”与“求自变量 x 为何值时，一次函数y=ax+b 的值为0”有什么关系？从图象上看呢？求一元一次方程ax +b =0(a ，b 是常数，a ≠0)的解，从“函数值”看就是某个一次函数b ax y +=求一元一次方程ax +b =0(a , b 是常数，a ≠0)的解，从“函数图象”看就是直线b ax y +=与x 轴的交点的活动三、师生互动，运用新知1、根据下列图像，你能说出哪些一元一次方程的解？并直接写出相应方程的解？1、直线3+=x y 与y 轴的交点是（ ）A 、（0，3）B 、（0，1）C 、（3，0）D 、（1，0） 2、直线3+=kx y 与x 轴的交点是（1，0 ），则k 的值是（ ） A 、3 B 、2 C 、-2 D 、-3y=x-13600 OBt(分)S(米) A 153、直线y=x+3与x 轴的交点坐标为（ ， ），所以相应的方程x+3=0的解是x=4、直线y=3x+6与x 轴的交点的横坐标x 的值是方程2x+a=0的解，则a•的值是______5、弹簧的长度与所挂物体的质量的关系是一次函数，如图所示，请判断不挂物体时弹簧的长度是多少？活动五、课堂小结，巩固新知同学们，本节课你学到了那些重要的知识点或内容呢？请试着自己总结一下吧!活动六、作业1、有一个一次函数的图象，可心和黄瑶分别说出了它的两个特征． 可心：图象与x 轴交于点（6，0）。
19.2.3一次函数与方程不等式(2)ppt
y=2-x y=2x-1
思考：二元一次方程组与一次函数、直 线之间存在怎样的对应关系？
二元一次方程组
两个一次函数 两条直线
探究三：从函数的观点看解方程组
y
2
y=2x-1
1
x
0
12
-1
y=-x+2
这个二 元一次方程 组的解是图 象的什么？
归纳：
从“形”的角度看: 解方程组相当于确定两条直线的＿交＿点＿坐＿标。
标为(２，５) 。
2.若直线 y 2x 3 与 y 3x 2b
相交于直线 y x上同一点，则b的值是 .
3.如图，已知函数y＝3x＋b和y＝ax－3 的图象交于点P(－2，－5)，则根据图 象可得不等式3x＋b＞ax－3的解集是 ___________．
4Байду номын сангаас已知方程组
的解为
，则一次函数y=3x﹣3与y=﹣ x+3的交点
从“数”的角度看: 解方程组相当于考虑_自__变_量__为何值时， 两个_函__数_的__值__相等，以及这个函数值是何 值。
结
论:
❖ 求二元一次方程组的解实质上是求对应两条 直线的交点坐标;
❖ 反之,要确定两条直线的交点坐标就是求对应 二元一次方程组的解.
y
0
x
三、例题示范 运用新知
1.直线y=2x+1与直线y=3x-1的交点坐
P的坐标是 ___
5.如图，是用图象法解某二元 一次方程组的图象，则这个二 元一次方程组是（ ）
A
B
C
D
6.如图，直线y=kx+b经过 A（﹣1，1）和 B（﹣3,0)两 点，则不等式0＜kx+b＜-x的 解集为 .
一次函数与方程、不等式 (课件)
y
y=x+2
Y=x+2
y
2
o2
x
Yy==3-x3+6x+6
-3x+6=0的解 其解为X=2
-2
o
x
X+2=0的解
y
其解为X=-2
y=x-1
Y=x-1
o1
x
-1
X-1=0的解 其解为X=1
一元一次方程都可以转化为__k_x_+_b_=_0__ 的形式.
求方程kx+b=0的解
当一次函数y=kx+b的值为 0 时，求相应的_自__变__量__x
而这三个方程的解则分别对 应着此时自变量的值，即图 象上A，B，C三点的横坐 标．
分 析 从函数的角度看，解这三个方程
方程2x+1=3的解是： x=1 ； 方即程当 x=1时，函数y=2x+1的值为3，也就是 y=3 ；
方即程当2xx=+1- 12=时0的，解函是数：y=x2=x-+121；的值函为数0，也就是 y=0 ；
求直线y= ax+b 与 x 轴交点的横 坐标．
时间是一个常量，但对勤奋者来 说，却是一个“变量”，我们应当 在有限的时间内做出伟大的事业。
你的收获与平时的付出是成正比 的，一份耕耘，一份收获。相信自 己，只要付出，你一定会有收获！
的值.
求直线y=kx+b与 x轴 的交点的 横 坐标.
应用新知
例1 一个物体现在的速度是5米/秒，其速度每秒 增加2米，再过几秒它的速度为17米/秒？ 解法1：设再过x秒物体的速度为17米/秒．
列出方程 2x+5=17 解得x=6．
应用新知
人教初中数学八下 19.2.3《一次函数与方程、不等式》一次函数与一元一次不等式课件 【经典初中数学
1、先化简：把各个二次根式 都化为最简二次根式。
2、再观察：化简后的二次根 式的被开方数是否相同。
例题讲解
1、计算: (1 )1x 69x (2 ) 8 045 解：(1) 16x 9x (2) 80 45
4 x3 x (43) x
4 53 5 (43) 5
7 x
5
探究
2、计算:
(1)2 81 181 32
18a , 28, x2 4, 5x4 y ,
×× √
×
2
x2 y,
ab ,
3xy ,
1
2 5 3x
√
×√
×
如图，学校要砌一个正方形花坛，已知外 面的正方形边长为 cm，里2 面2的正方形的边 长为 cm，两个正方形2 的周长和为多少？
22
两个正方形的周长和为：
2
4(2 2 2)
8 24 2
若两个正方形的面积分别为 27cm2、12cm2，则两正方形的周长 和为多少？
1.求Y1和Y2与X的函数关系式
2.问拍这批照片到照相馆拍，费用省还是由学校自己拍费用省＝8x,Y2=4x+120
y
(2)由图象可知，当x=30 时，两家一样， Y=4x+120
当X>30时，照相馆省钱，
当X<30时，学校自己省钱.
0 30
x
24
25
教学反思：
5 63 2
3
4
下列解答是否正确？为什么？
(1)2 75 3 27 3 2 75 9 3 3 10 3 10 3 0
错在没有 按照二次根式 加减混算从左 向右依次进行 的运算顺序计 算。
( 2 ) 72 18 3 2 2
2、再观察：化简后的二次根 式的被开方数是否相同。
例题讲解
1、计算: (1 )1x 69x (2 ) 8 045 解：(1) 16x 9x (2) 80 45
4 x3 x (43) x
4 53 5 (43) 5
7 x
5
探究
2、计算:
(1)2 81 181 32
18a , 28, x2 4, 5x4 y ,
×× √
×
2
x2 y,
ab ,
3xy ,
1
2 5 3x
√
×√
×
如图，学校要砌一个正方形花坛，已知外 面的正方形边长为 cm，里2 面2的正方形的边 长为 cm，两个正方形2 的周长和为多少？
22
两个正方形的周长和为：
2
4(2 2 2)
8 24 2
若两个正方形的面积分别为 27cm2、12cm2，则两正方形的周长 和为多少？
1.求Y1和Y2与X的函数关系式
2.问拍这批照片到照相馆拍，费用省还是由学校自己拍费用省＝8x,Y2=4x+120
y
(2)由图象可知，当x=30 时，两家一样， Y=4x+120
当X>30时，照相馆省钱，
当X<30时，学校自己省钱.
0 30
x
24
25
教学反思：
5 63 2
3
4
下列解答是否正确？为什么？
(1)2 75 3 27 3 2 75 9 3 3 10 3 10 3 0
错在没有 按照二次根式 加减混算从左 向右依次进行 的运算顺序计 算。
( 2 ) 72 18 3 2 2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
湖北鸿鹄志文化传媒有限公司——助您成功
探究三、 1.当自变量x取何值时，函数y=2.5x+1和y=5x +17的值相等？这个函数值是多少？
方法一 ：联立两个函数，得 2.5x+1=5x +17，解 此方程； 方法二： 把两个函数转化为二元一次方程组，解 方程组； 方法三： 画函数图象，求交点坐标.
义务教育教科书（ RJ ）八年级数学下册
第十九章 一次函数 19.2 一次函数
湖北鸿鹄志文化传媒有限公司——助您成功
思考：
下面3个方程有什么共同点和不同点？你能从 函数的角度对解这3个方程进行解释吗？ （1）2x+1=3 (2) 2x+1=0 (3) 2x+1=-1
3
y=2x+1
-1
-1
1
湖北鸿鹄志文化传媒有限公司——助您成功
湖北鸿鹄志文化传媒有限公司——助您成功
2.如图，求直线l1与l2 的交点坐标.
y
分析：由函数图象可以求 直线l1与l2的解析式， 进而通过方程组求出交点坐标.
O x
湖北鸿鹄志文化传媒有限公司——助您成功
本节课你有什么收获？ 1.请用函数的观点，从数形两方面说说你对二元一 次方 程有什么新的理解； 2.请用函数观点，从数和形两个角度说说对二元一次方 程组的认识； 3.请用函数的观点，说说你对一元一次方程有什么新的 认识； 4.请用函数的观点，说说一次函数与一元一次不等式的 联系．
湖北鸿鹄志文化传媒有限公司——助您成功
分析： （1）气球上升时间x满足0≤x≤60 对于1号气球，y关于x的函数解析式为y=x+5 对于2号气球，y关于x的函数解析式为 y=0.5x+15 （2）在某个时刻两个气球位于同一高度，就 是说对于x的某个值（0≤x≤60），函数 y=x+5， y=0.5x+15有相同的值y.如能求出 这个x和y，则问题解决。
湖北鸿鹄志文化传媒有限公司——助您成功
人生像一杯茶，不会苦一辈子，但
总会苦一阵子。
湖北鸿鹄志文化传媒有限公司——助您成功
湖北鸿鹄志文化传媒有限公司——助您成功
4．某单位需要用车，准备和一个体车主或一国有出 租公司其中的一家签订合同，设汽车每月行驶xkm ，应付给个体车主的月租费是y元，付给出租车公 司的月租费是y元，y1，y2分别与x之间的函数关 系图象是如图所示的两条直线，• 观察图象，回答 下列问题： （1）每月行驶的路程在什么范围内时，租国有 出租车公司的出租车合算？ （2）每月行驶的路程等于多少时，租两家车的 费用相同？ （3）如果这个单位估计每月行驶的路程为2300km，• 那么这个单位租哪家的车合算？
湖北鸿鹄志文化传媒有限公司——助您成功
归纳：
所以 解一元一次不等式相当于在某个一次函数 y=ax+b的值大于0或小于0时，求自变量x的 取值范围。
湖北鸿鹄志文化传媒有限公司——助您成功
探究二、问题3：
1号探测气球从海拔5米处出发，以1m/min的速度上 升。与此同时，2号探测气球从海拔15米处出，以 0.5m/min的速度上升。两个气球都上升了1h. （1）用式子分别表示两个气球所在位置的海拔y（单 位：m）关于上升时间x(单位：min)的函数关系； （2）在某时刻两个气球能否位于同一高度？如果能， 这时气球上升了多少时间？位于什么高度？
这3个方程的等号左边都是2x+1,右边分别 是3，0，-1。这3个方程相当于在一次函数 y=2x+1的值分别为3，0，-1 时，求自变量x的值。所以 解一元一次方程相当于在某个 y=2x+1 一次函数y=ax+b的值 为0时，求自变量的值。
-1 -1
湖北鸿鹄志文化传媒有限公司——助您成功
探究．教材第98页练习题． 2.已知一次函数y=3x+5与y=2x+b的图象交点为(-1，2)， y 3x 5， 则方程组 y 2 x b 的解是_______,b的值为______.
湖北鸿鹄志文化传媒有限公司——助您成功
3．在同一坐标系中画出一次函数y1=-x+1与 y2=2x-2的图象，并根据图象回答下列问： （1）写出直线y1=-x+1与y2=2x-2的交点 P的坐标． （2）直接写出：当x取何值时y1>y2；y1<y2
湖北鸿鹄志文化传媒有限公司——助您成功
由此得方程组：
y=x+5 解得
y=0.5x+15 X=20
25
y=x+5 y=0.5x+15
20
y=25 也就是说，当上升20min时，两个气球 都位于25米的高度。
湖北鸿鹄志文化传媒有限公司——助您成功
归纳： 方程（组）与函数之间互相联系，从函数 的角度可以把它们统一起来。解决问题时，应 根据具体情况灵活地把它们结合起来考虑。
下面3个不等式有什么共同点和不同点？你能 从函数的角度对解这3个不等式进行解释吗？ （1）3x+2＞2 (2) 3x+2＜0 (3) 3x+2＜-1
y=3x+2 2
-1
。 。
-1 湖北鸿鹄志文化传媒有限公司——助您成功
归纳：
1、模仿前面“思考”的三个方程的总结进行 总结。 2、学生合作交流。 这3个不等式的不等号左边都是3x+2,右边分 别是大于2，小于0，小于-1。这3个不等式 相当于在一次函数y=3x+2的值分别为大于2 ，小于0，小于-1时，求自变量x的值。