模式匹配KMP算法实验步骤
模式匹配KMP算法研究报告

模式匹配的KMP算法研究学生姓名:黄飞指导老师:罗心摘要在计算机科学领域,串的模式匹配<以下简称为串匹配)算法一直都是研究焦点之一。
在拼写检查、语言翻译、数据压缩、搜索引擎、网络入侵检测、计算机病毒特征码匹配以及DNA序列匹配等应用中,都需要进行串匹配。
串匹配就是在主串中查找模式串的一个或所有出现。
在本文中主串表示为S=s1s2s3…sn,模式串表示为T=t1t2…tm。
串匹配从方式上可分为精确匹配、模糊匹配、并行匹配等,著名的匹配算法有BF算法、KMP算法、BM算法及一些改进算法。
本文主要在精确匹配方面对KMP算法进行了讨论并对它做一些改进以及利用改进的KMP来实现多次模式匹配。
关键字:模式匹配;主串;模式串;KMP算法Research and Analysis of KMP Pattern MatchingAlgorithmStudent:Huangfei Teacher:LuoxinAbstract In computer science,String pattern matching(Hereinafter referred to as the string matching>algorithmis always the focus of the study.In thespell check, language translation, data compression, search engine, thenetwork intrusion detection system, a computer virus signature matching DNAsequences and the application in the match,matched to string matching.String matching is in search of a string of pattern or all appear.In this paper, the string is S = s1s2s3... Sn, string pattern for T = t1t2... tm.String matching way can be divided from the accurate matching, fuzzy matching, parallel matching etc., the famous matching algorithms are KMP algorithm, BF algorithm, the algorithm and some BM algorithm.This paper in precise KMP algorithm for matching aspects are discussed and some improvement on it and using the improved KMP to realize the multiple pattern matching.Key words: pattern matching, The string。
kmp算法原理

kmp算法原理KMP算法(Knuth-Morris-Pratt算法)是一种用于快速搜索字符串中某个模式字符串出现位置的算法,由Knuth, Morris 和 Pratt于1977年提出。
KMP算法的工作方式如下:首先,给定一个主串S和一个模式串P,KMP算法的第一步就是先构造一个新的模式串P,其中的每一项存储着P中每一个字符前面由不同字符串组成的最长前缀和最长后缀相同的子串。
接着,在S中寻找P,它会从S的第一个字符开始,如果匹配上,就继续比较下一个字符,如果不匹配上,就根据P中相应位置上保存的信息跳到特定位置,接着再开始比较,如此不断循环下去,直到从S中找到P为止。
KMP算法的思路特别巧妙,比较效率很高,它的复杂度为O(m+n),其中m为主串的长度,n为模式串的长度。
它取代了以前的暴力搜索算法,极大地提高了程序的性能。
KMP算法的实现过程如下:(1)首先确定模式串P的每一个字符,构造模式串P的next数组:next[i]存储P中第i个字符之前最长相同前缀和后缀的长度(P中第i个字符之前最长相同前缀和后缀不包括第i个字符);(2)接着从S中的第一个字符开始比较P中的每一个字符,如果字符不匹配,则采用next数组中保存的信息跳到特定位置,而不是暴力比较,以此不断循环,直到从S中找到P为止。
KMP算法是由Don Knuth, Vaughan Pratt和James Morris在1977年提出的。
它的思想是利用之前遍历过的P的信息,跳过暴力比较,可以把字符串搜索时间从O(m×n)降低到O(m+n)。
KMP算法在很多领域有着重要的应用,如文本编辑,模式匹配,编译器设计与多项式字符串匹配等等,都是不可或缺的。
模式匹配KMP算法实验报告

实验四:KMP算法实验报告一、问题描述模式匹配两个串。
二、设计思想这种由D.E.Knuth,J.H.Morris和V.R.Pratt同时发现的改进的模式匹配算法简称为KM P算法。
注意到这是一个改进的算法,所以有必要把原来的模式匹配算法拿出来,其实理解的关键就在这里,一般的匹配算法:int Index(String S,String T,int pos)//参考《数据结构》中的程序{i=pos;j=1;//这里的串的第1个元素下标是1while(i<=S.Length && j<=T.Length){if(S[i]==T[j]){++i;++j;}else{i=i-j+2;j=1;}//**************(1)}if(j>T.Length) return i-T.Length;//匹配成功else return 0;}匹配的过程非常清晰,关键是当‘失配’的时候程序是如何处理的?为什么要回溯,看下面的例子:S:aaaaabababcaaa T:ababcaaaaabababcaaaababc.(.表示前一个已经失配)回溯的结果就是aaaaabababcaaaa.(babc)如果不回溯就是aaaaabababcaaaaba.bc这样就漏了一个可能匹配成功的情况aaaaabababcaaaababc这是由T串本身的性质决定的,是因为T串本身有前后'部分匹配'的性质。
如果T为a bcdef这样的,大没有回溯的必要。
改进的地方也就是这里,我们从T串本身出发,事先就找准了T自身前后部分匹配的位置,那就可以改进算法。
如果不用回溯,那T串下一个位置从哪里开始呢?还是上面那个例子,T为ababc,如果c失配,那就可以往前移到aba最后一个a的位置,像这样:...ababd...ababc->ababc这样i不用回溯,j跳到前2个位置,继续匹配的过程,这就是KMP算法所在。
实验六 串的模式匹配

⑵用KMP算法进行匹配。 (3)程序运行的结果要在屏幕上显示:
简单的朴素模式匹配算法中,模式串的位置、出现的次数。 模式串的next函数值。 说明:下课前请将源代码的.c(或.cpp) KMP算法的匹配位置。 文件以及.h文件打包后重命名为
“p6_姓名简拼_学号后三位”, 然后提交到教师机!
【实验内容】编写程序,实现顺序串的模式匹配算法。 【基本要求】在主程序中调用算法,输入一个主串和模式串, 在主串中检索模式串,显示模式串在主串中出现的次数和 位置。 ⑴用简单的朴素模式匹配算法计模式串出现 的次数; 从主串的任意给定位置检索模式串。
【实现提示】
要统计模式串在主串中出现的次数,可以先确定从
主串中第一个字符起,模式串的位置,然后再利用 指定位置的匹配算法找出其他匹配的位置; 利用一个数组来存放所有模式串出现的位置,然后 将这些位置依次打印输出。 串值在数组中存储时,是从数组的0号单元开始存 放的。注意修改教材中Next函数和KMP算法函数 中的变量! 至少包含以下头文件: #include <stdio.h> #include <string.h> #include <conio.h>
KMP算法计算next值和nextVal值
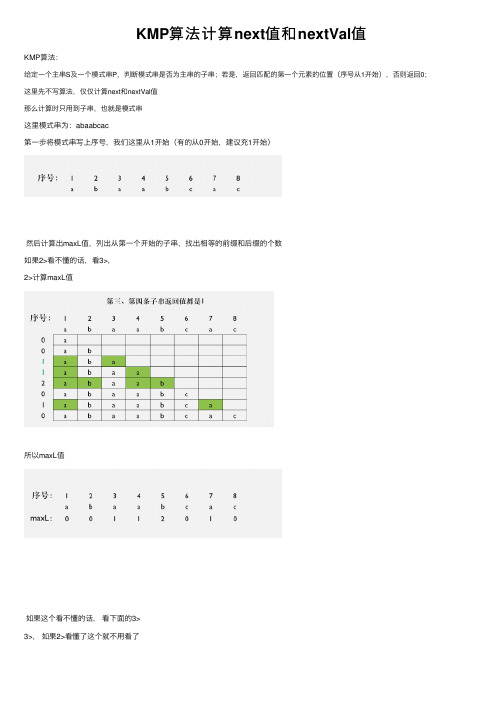
KMP算法计算next值和nextVal值
KMP算法:
给定⼀个主串S及⼀个模式串P,判断模式串是否为主串的⼦串;若是,返回匹配的第⼀个元素的位置(序号从1开始),否则返回0;这⾥先不写算法,仅仅计算next和nextVal值
那么计算时只⽤到⼦串,也就是模式串
这⾥模式串为:abaabcac
第⼀步将模式串写上序号,我们这⾥从1开始(有的从0开始,建议充1开始)
然后计算出maxL值,列出从第⼀个开始的⼦串,找出相等的前缀和后缀的个数
如果2>看不懂的话,看3>,
2>计算maxL值
所以maxL值
如果这个看不懂的话,看下⾯的3>
3>,如果2>看懂了这个就不⽤看了
依次类推4>计算next值
接下来将maxL复制⼀⾏,去掉最后⼀个数,在开头添加⼀个-1,向右平移⼀个格,然后每个值在加1的到next值
5>计算nextVal值,⾸先将第⼀个为0,然后看next和maxL是否相等(先计算不相等的)
当next和maxL不相等时,将next的值填⼊
当next和maxL相等时,填⼊对应序号为next值得nextVal值
所以整个nextVal值为:。
KMP算法(改进的模式匹配算法)——next函数

KMP算法(改进的模式匹配算法)——next函数KMP算法简介KMP算法是在基础的模式匹配算法的基础上进⾏改进得到的算法,改进之处在于:每当匹配过程中出现相⽐较的字符不相等时,不需要回退主串的字符位置指针,⽽是利⽤已经得到的部分匹配结果将模式串向右“滑动”尽可能远的距离,再继续进⾏⽐较。
在KMP算法中,依据模式串的next函数值实现字串的滑动,本随笔介绍next函数值如何求解。
next[ j ]求解将 j-1 对应的串与next[ j-1 ]对应的串进⾏⽐较,若相等,则next[ j ]=next[ j-1 ]+1;若不相等,则将 j-1 对应的串与next[ next[ j-1 ]]对应的串进⾏⽐较,⼀直重复直到相等,若都不相等则为其他情况题1在字符串的KMP模式匹配算法中,需先求解模式串的函数值,期定义如下式所⽰,j表⽰模式串中字符的序号(从1开始)。
若模式串p 为“abaac”,则其next函数值为()。
解:j=1,由式⼦得出next[1]=0;j=2,由式⼦可知1<k<2,不存在k,所以为其他情况即next[2]=1;j=3,j-1=2 对应的串为b,next[2]=1,对应的串为a,b≠a,那么将与next[next[2]]=0对应的串进⾏⽐较,0没有对应的串,所以为其他情况,也即next[3]=1;j=4,j-1=3 对应的串为a,next[3]=1,对应的串为a,a=a,所以next[4]=next[3]+1=2;j=5,j-1=4 对应的串为a,next[4]=2,对应的串为b,a≠b,那么将与next[next[4]]=1对应的串进⾏⽐较,1对应的串为a,a=a,所以next[5]=next[2]+1=2;综上,next函数值为 01122。
题2在字符串的KMP模式匹配算法中,需先求解模式串的函数值,期定义如下式所⽰,j表⽰模式串中字符的序号(从1开始)。
若模式串p为“tttfttt”,则其next函数值为()。
数据结构实验报告 模式匹配算法

return 1; } datatype DeQueue(SeqQueue *q) { datatype x; if(q->front==q->rear) { printf("\nempty!");return 0;} x=q->data[q->front]; q->front=(q->front+1)%max; return x; } void display(SeqQueue *q) { int s; s=q->front; if(q->front==q->rear) printf("empty!"); else while(s!=q->rear) { printf("->%d",q->data[s]); s=(s+1)%max; } printf("\n"); } main() { int a[6]={3,7,4,12,31,15},i; SeqQueue *p; p=InitQueue(); for(i=0;i<6;i++) EnQueue(p,a[i]); printf("output the queue values:"); display(p); printf("\n"); EnQueue(p,100);EnQueue(p,200);
ห้องสมุดไป่ตู้
元素并显示结果为4 ,12, 31, 15 ,100 ,200。
七、具体程序 #include "stdio.h" #include "conio.h" #define max 100 typedef int datatype; typedef struct { datatype data[max]; int front; int rear; }SeqQueue; SeqQueue *InitQueue() { SeqQueue *q; q=(SeqQueue *)malloc(sizeof(SeqQueue)); q->front=q->rear=0; return q; } int QueueEmpty(SeqQueue *q) { if (q->front==q->rear) return 1; else return 0; } int EnQueue(SeqQueue *q,datatype x) { if((q->rear+1)%max==q->front) {printf("\nfull!");return 0;} q->data[q->rear]=x; q->rear=(q->rear+1)%max;
字符串模式匹配

实验7、字符串查找目的掌握字符串模式匹配的经典算法。
问题描述分别用简单方法和KMP方法实现index在文本串中查找指定字符串的功能。
步骤1.定义字符串类型2.实现简单的index操作,从文本串中查找指定字符串。
3.实现KMP方法的index操作,从文本串中查找指定字符串。
4.[选]建立一个文本文件,读入每一行来测试自己完成的练习,观察并理解程序的各个处理。
设备和环境PC计算机、Windows操作系统、C/C++开发环境结论能够理解和掌握字符串模式匹配的典型算法。
思考题1.对KMP算法分别用手工和程序对某个模式串输出next和nextval。
朴素算法:#include<stdio.h>#include<string.h>#define NOTFOUND -1#define ERROR -2#define MAXLEN 100//字符串的最大长度char S[MAXLEN+10],T[MAXLEN+10],st[MAXLEN+10];//串S和串Tint S0,T0; //S0:串S的长度 T0:串T的长度int pos; //pos的起始位置void Init(char *S,int &S0)//读入字符串{int len,i;New_Input:scanf("%s",st);//读入字符串len=strlen(st);if (len>MAXLEN)//如果字符串的长度大于规定的字符串最大长度 {printf("This String is too long,Please Input a new one.nn");goto New_Input;//重新读入字符串}for (i=1;i<=len;i++) S[i]=st[i-1];S[len+1]='';S0=len;}int Index(char *S,char *T,int pos){if (pos<1 || pos>S0) return ERROR; // 输入数据不合法int i=pos,j=1;while (i<=S0 && j<=T0){if (S[i]==T[j]) {i++; j++;}else {i=i-j+2; j=1;}//不匹配时,对应S移到下一位进行匹配}if (j>T0) return i-T0; //返回S中找到的位置else return NOTFOUND;}int main(){int ret;//函数返回值Init(S,S0);Init(T,T0);scanf("%d",&pos);ret=Index(S,T,pos); //在S串中从pos这个位置起,找到第一个与T匹配的子串的起始位置if (ret==NOTFOUND) printf("Not Found.n");else if(ret==ERROR) printf("The Input Data is Error.n");else printf("In S,from %dth is equal to T.n",ret);return 0;}KMP:#include<stdio.h>#include<string.h>#define NOTFOUND -1#define ERROR -2#define MAXLEN 100//字符串的最大长度char S[MAXLEN+10],T[MAXLEN+10],st[MAXLEN+10]; //串S和串Tint S0,T0; //S0:串S的长度 T0:串T的长度int pos; //pos的起始位置int next[MAXLEN+10];void Init(char *S,int &S0)//读入字符串{int len,i;New_Input:scanf("%s",st);//读入字符串len=strlen(st);if (len>MAXLEN)//如果字符串的长度大于规定的字符串最大长度{printf("This String is too long,Please Input a new one.nn");goto New_Input; //重新读入字符串}for (i=1;i<=len;i++) S[i]=st[i-1];S[len+1]='';S0=len;}void Get_next(char *S,int *next){int i=1,j=0;next[1]=0;while (i<T0)if (j==0 || T[i]==T[j]) {i++; j++; next[i]=next[j];}else j=next[j];}int Index_KMP(char *S,char *T,int pos){int i=pos,j=1;while (i<=S0 && j<=T0)if (j==0 || S[i]==T[j]) {i++; j++;}else j=next[j];if (j>T0) return i-T0;else return NOTFOUND;}int main(){int ret;//函数返回值Init(S,S0);Init(T,T0);scanf("%d",&pos);Get_next(T,next);ret=Index_KMP(S,T,pos); //在S串中从pos这个位置起,找到第一个与T匹配的子串的起始位置if (ret==NOTFOUND) printf("Not Found.n");else if (ret==ERROR) printf("The Input Data is Error.n");else printf("In S,from %dth is equal to T.n",ret);return 0;}扩张KMP:#include<stdio.h>#include<string.h>#define NOTFOUND -1#define ERROR -2#define MAXLEN 100 //字符串的最大长度char S[MAXLEN+10],T[MAXLEN+10],st[MAXLEN+10]; //串S和串Tint S0,T0; //S0:串S的长度 T0:串T 的长度int pos; //pos的起始位置int nextval[MAXLEN+10];void Init(char *S,int &S0)//读入字符串{int len,i;New_Input:scanf("%s",st); //读入字符串len=strlen(st);if (len>MAXLEN) //如果字符串的长度大于规定的字符串最大长度{printf("This String is too long,Please Input a new one.nn");goto New_Input; //重新读入字符串}for (i=1;i<=len;i++) S[i]=st[i-1];S[len+1]='';S0=len;}void Get_nextval(char *S,int *nextval){int i=1,j=0;nextval[1]=0;while (i<T0)if (j==0 || T[i]==T[j]){i++; j++;if (T[i]!=T[j]) nextval[i]=j;else nextval[i]=nextval[j];}else j=nextval[j];}int Index_KMP(char *S,char *T,int pos){int i=pos,j=1;while (i<=S0 && j<=T0)if (j==0 || S[i]==T[j]) {i++; j++;}else j=nextval[j];if (j>T0) return i-T0;else return NOTFOUND;}int main(){int ret;//函数返回值Init(S,S0);Init(T,T0);scanf("%d",&pos);Get_nextval(T,nextval);ret=Index_KMP(S,T,pos); //在S串中从pos这个位置起,找到第一个与T匹配的子串的起始位置if (ret==NOTFOUND) printf("Not Found.n");else if (ret==ERROR) printf("The Input Data is Error.n");else printf("In S,from %dth is equal to T.n",ret);return 0;}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、问题描述
模式匹配两个串。
二、设计思想
这种由D.E.Knuth,J.H.Morris和V.R.Pratt同时发现的改进的模式匹配算法简称为KM P算法。
注意到这是一个改进的算法,所以有必要把原来的模式匹配算法拿出来,其实理解的关键就在这里,一般的匹配算法:
int Index(String S,String T,int pos)//参考《数据结构》中的程序
{
i=pos;j=1;//这里的串的第1个元素下标是1
while(i<=S.Length && j<=T.Length)
{
if(S[i]==T[j]){++i;++j;}
else{i=i-j+2;j=1;}//**************(1)
}
if(j>T.Length) return i-T.Length;//匹配成功
else return 0;
}
匹配的过程非常清晰,关键是当‘失配’的时候程序是如何处理的?为什么要回溯,看下面的例子:
S:aaaaabababcaaa T:ababc
aaaaabababcaaa
ababc.(.表示前一个已经失配)
回溯的结果就是
aaaaabababcaaa
a.(babc)
如果不回溯就是
aaaaabababcaaa
aba.bc
这样就漏了一个可能匹配成功的情况
aaaaabababcaaa
ababc
这是由T串本身的性质决定的,是因为T串本身有前后'部分匹配'的性质。
如果T为a bcdef这样的,大没有回溯的必要。
改进的地方也就是这里,我们从T串本身出发,事先就找准了T自身前后部分匹配的位置,那就可以改进算法。
如果不用回溯,那T串下一个位置从哪里开始呢?
还是上面那个例子,T为ababc,如果c失配,那就可以往前移到aba最后一个a的位置,像这样:
...ababd...
ababc
->ababc
这样i不用回溯,j跳到前2个位置,继续匹配的过程,这就是KMP算法所在。
这个当T[j]失配后,j应该往前跳的值就是j的next值,它是由T串本身固有决定的,与S串无关。
《数据结构》上给了next值的定义:
0 如果j=1
next[j]={Max{k|1<k<j且'p1...pk-1'='pj-k+1...pj-1'
1 其它情况
其实它就是描述前面表述的情况,关于next[1]=0是规定的,这样规定可以使程序简单一些,如果非要定为其它的值只要不和后面的值冲突也是可以的;而那个Max是什么意思,举个例子:
T:aaab
...aaaab...
aaab
->aaab
->aaab
->aaab
像这样的T,前面自身部分匹配的部分不止两个,那应该往前跳到第几个呢?最近的一个,也就是说尽可能的向右滑移最短的长度。
到这里,就实现了KMP的大部分内容,然后关键的问题是如何求next值?先看如何用它来进行匹配操作。
将最前面的程序改写成:
int Index_KMP(String S,String T,int pos)
{
i=pos;j=1;//这里的串的第1个元素下标是1
while(i<=S.Length && j<=T.Length)
{
if(j==0 || S[i]==T[j]){++i;++j;} //注意到这里的j==0,和++j的作用就
知道为什么规定next[1]=0的好处了 else j=next[j];//i不变(不回溯),j跳动
}
if(j>T.Length) return i-T.Length;//匹配成功
else return 0;
}
求next值,这也是整个算法成功的关键。
前面说过了,next值表达的就是T串的自身部分匹配的性质,那么,我只要将T串和T串自身来一次匹配就可以求出来了,这里的匹配过程不是从头一个一个匹配,而是从T[1]和T[2]开始匹配,给出算法如下:
void get_next(String T,int &next[])
{
i=1;j=0;next[1]=0;
while(i<=T.Length)
{
if(j==0 || T[i]==T[j]){++i;++j; next[i]=j;/**********(2)*/}
else j=next[j];
}
}
看这个函数非常像KMP匹配的函数!注意到(2)语句逻辑覆盖的时候是T[i]==T[j]以及i前面的、j前面的都匹配的情况下,于是先自增,然后记下来next[i]=j,这样每当i有自增就会求得一个next[i],而j一定会小于等于i,于是对于已经求出来的next,可以继续求后面的next,而next[1]=0是已知,所以整个就这样递推的求出来了,方法非常巧妙。
这样的改进已经是很不错了,但算法还可以改进,注意到下面的匹配情况:
...aaac...
aaaa.
T串中的'a'和S串中的'c'失配,而'a'的next值指的还是'a',那同样的比较还是会失配,而这样的比较是多余的,如果我事先知道,当T[i]==T[j],那next[i]就设为next[j],在求next值的时候就已经比较了,这样就可以去掉这样的多余的比较。
于是稍加改进得到:
void get_nextval(String T,int &next[])
{
i=1;j=0;next[1]=0;
while(i<=T.Length)
{
if(j==0 || T[i]==T[j])
{ ++i;++j;
if(T[i]!=T[j]) next[i]=j;
else next[i]=next[j];//消去多余的可能的比较,next再向前跳 }
else j=next[j];
}
}
三、分析理论时间复杂性
这个程序或许比想像中的要简单,因为对于i值的不断增加,代码用的是for循环。
因此,这个代码可以这样形象地理解:扫描字符串S,并更新可以匹配到T的什么位置。
为什么这个程序是O(n)的? KMP的时间复杂度分析可谓摊还分析的典型。
我们从上述程序的j 值入手。
每一次执行while循环都会使j减小(但不能减成负的),而另外的改变j值的地方只有第五行。
每次执行了这一行,j都只能加1;因此,整个过程中j 最多加了n个1。
于是,j最多只有n次减小的机会(j值减小的次数当然不能超过n,因为j永远是非负整数)。
这告诉我们,while循环总共最多执行了n次。
按照摊还分析的说法,平摊到每次for循环后,一次for循环的复杂度为O(1)。
整个过程显然是O(n)的。
这样的分析对于后面P数组预处理的过程同样有效,同样可以得到预处理过程的复杂度为O(m)。
四、原程序和调试结果
package kmp;
public class kmp {
String s="aaaaaaaa";
String p="aaaab";
int[] next=new int[s.length()];
//主要计算next[]的值
void calnext()
{
int i,j=0;
next[1] = 0;
next[0]=-1;
for(i=2;i<s.length();i++)
{
if(s.charAt(j)==s.charAt(i-1))
{
next[i]=next[i-1]+1;j++;
}
else
{
if(next[j]<0)
next[i]=0;
else
next[i]=next[j];
j=next[i];
}
}
}
//输出实际运算次数
void display()
{
int i=0,j=0,v;
int count=0;
while(i<s.length()&&j<p.length())
{
if(s.charAt(i)==p.charAt(j))
{
i++;j++;
}
else if(j==0)i++;
else j=next[j];
count++;
}
System.out.println(""+count);
}
public static void main(String[] args) {
// TODO code application logic here
kmp k=new kmp();
k.calnext();
k.display();
}
}
五、对结果的分析
进行了12次匹配,匹配成功。
