2大学数学建模(公选课)考核试题2
西安科技大学公选课数学建模试题.
层次分析法建模层次分析法(AHP -Analytic Hierachy process )---- 多目标决策方法70 年代由美国运筹学家T ·L ·Satty 提出的,是一种定性与定量分析相结合的多目标决策分析方法论。
吸收利用行为科学的特点,是将决策者的经验判断给予量化,对目标(因素)结构复杂而且缺乏必要的数据情况下,採用此方法较为实用,是一种系统科学中,常用的一种系统分析方法,因而成为系统分析的数学工具之一。
一、问题举例:A .大学毕业生就业选择问题 获得大学毕业学位的毕业生,“双向选择”时,用人单位与毕业生都有各自的选择标准和要求。
就毕业生来说选择单位的标准和要求是多方面的,例如:① 能发挥自己的才干为国家作出较好贡献(即工作岗位适合发挥专长); ② 工作收入较好(待遇好);③ 生活环境好(大城市、气候等工作条件等); ④ 单位名声好(声誉-Reputation ); ⑤ 工作环境好(人际关系和谐等)⑥ 发展晋升(promote, promotion )机会多(如新单位或单位发展有后劲)等。
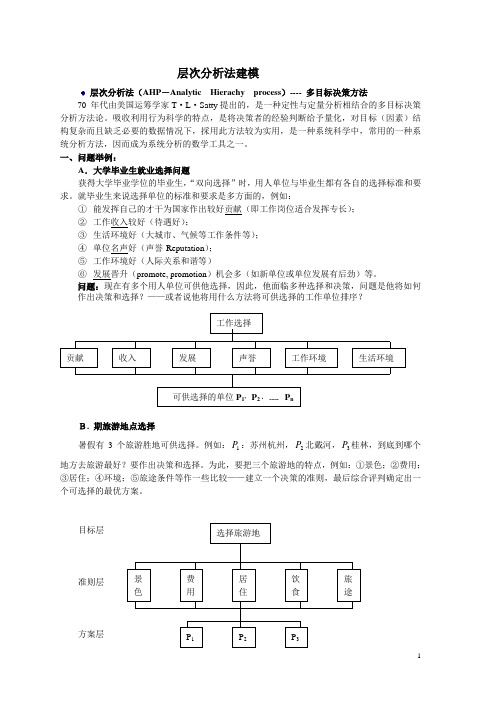
问题:现在有多个用人单位可供他选择,因此,他面临多种选择和决策,问题是他将如何作出决策和选择?——或者说他将用什么方法将可供选择的工作单位排序?B. 期旅游地点选择暑假有3个旅游胜地可供选择。
例如:1P :苏州杭州,2P 北戴河,3P 桂林,到底到哪个地方去旅游最好?要作出决策和选择。
为此,要把三个旅游地的特点,例如:①景色;②费用;③居住;④环境;⑤旅途条件等作一些比较——建立一个决策的准则,最后综合评判确定出一个可选择的最优方案。
目标层准则层方案层C .资源开发的综合判断7种金属可供开发,开发后对国家贡献可以通过两两比较得到,决定对哪种资源先开发,效用最用。
二、问题分析:例如旅游地选择问题:一般说来,此决策问题可按如下步骤进行: (S1)将决策解分解为三个层次,即:目标层:(选择旅游地) 准则层:(景色、费用、居住、饮食、旅途等5个准则)方案层:(有1P ,2P ,3P 三个选择地点)并用直线连接各层次。
2大学数学建模(公选课)考核试题2

2014年6月广东石油化工学院大学数学建模(公选课)考核试题截止时间:2014年6月20日(星期五)晚上21:00,交稿地点二教B703。
请按照附件1的格式要求提交作业,要求:从以下ABC三题选择一题,完成数学建模论文一篇。
论文做封面一张,写上题目、作者、系别、班级、学号、日期论文一律用A4纸打印出来,正文用5号宋体字。
A题经济发展与环境保护建立适当的数学模型说明我国哪些省(直辖市、特别行政区)在发展经济的同时有效地保护了环境资源。
在论文的结尾写一份如何有效发展循环经济的小评论(字数500-1500字,评论中可以对某些省改变经济发展方式提出具体建议)。
几点说明:1.充分利用政府部门公布的各省(直辖市、特别行政区)的历年国民经济和社会发展统计公报中相关数据(如浙江统计局网站)。
2. 可以选择典型的3-10个省的统计数据进行分析。
3. 经济发展水平的衡量可以综合考虑如下指标:GDP、人均GDP、人均收入、进出口外贸总值、人均税收、人均存款、GDP增幅水平等(还有很多衡量经济发展的指标,同学们可以参考各类文献,并自行收集资料,通过建立数学模型(或简单的统计模型)进行综合评定)。
4. 环境资源要考虑到能耗(如水资源、电、煤等耗量),也可考虑主要污染物排放总量(SO2,、COD、废水、废渣、废气等)。
5. 建模中各个省份之间要横向比较,单个省要进行纵向比较(比较历年数据),并得出经济发展和保护环境资源的关系。
6. 查找数据的能力对于本题能否成功求解至关重要,B、汽车售后维修数据统计分析产品质量是企业的生命线,售后服务是产品质量的观测点,如何用好售后服务的数据是现代企业管理的重要问题之一。
现以某小型汽车生产厂家为例考虑这个问题。
假设该厂的保修期是三年,即在售出后三年中对于非人为原因损坏的小型汽车免费维修。
在全国各地的维修站通过网络将保修记录送到统一的数据库里面,原始数据主要包含哪个批次生产的小型汽车(即生产月份)、售出时间、维修时间、维修部位、损坏原因及程度、维修费用等等。
大学数学建模课程真题试卷

大学数学建模课程真题试卷一、选择题(每题 5 分,共 20 分)1、在数学建模中,以下哪种模型常用于预测未来的趋势?()A 线性回归模型B 逻辑回归模型C 聚类分析模型D 决策树模型2、对于一个优化问题,若目标函数为凸函数,约束条件为线性,则该问题属于()A 线性规划问题B 非线性规划问题C 凸规划问题D 整数规划问题3、以下哪个方法常用于求解微分方程?()A 有限差分法B 蒙特卡罗方法C 层次分析法D 主成分分析法4、在建模过程中,数据预处理的主要目的是()A 减少数据量B 提高数据质量C 增加数据多样性D 便于数据存储二、填空题(每题 6 分,共 30 分)1、数学建模的基本步骤包括:问题提出、_____、模型假设、模型建立、模型求解、模型分析与检验、_____。
2、线性规划问题的标准形式中,目标函数为_____,约束条件为_____。
3、常见的概率分布有_____、_____、正态分布等。
4、评价模型优劣的指标通常包括准确性、_____、_____等。
5、一个具有 n 个变量,m 个约束条件的线性规划问题,其可行域是由_____个顶点组成的凸多边形。
三、简答题(每题 10 分,共 30 分)1、请简述层次分析法的基本步骤。
2、解释什么是敏感性分析,并说明其在数学建模中的作用。
3、给出一个实际问题,并简述如何将其转化为数学建模问题。
四、应用题(20 分)某工厂生产 A、B 两种产品,已知生产 A 产品每件需要消耗原材料2 千克,劳动力 3 小时,利润为 5 元;生产 B 产品每件需要消耗原材料 3 千克,劳动力 2 小时,利润为 4 元。
现有原材料 180 千克,劳动力 150 小时,问如何安排生产计划,才能使工厂获得最大利润?(1)建立数学模型(8 分)(2)使用软件求解(给出求解过程和结果)(12 分)接下来,我们对这份试卷进行一下分析。
选择题部分主要考查了学生对数学建模中一些基本概念和常见模型方法的理解。
数学建模试卷及参考答案

数学建模试卷及参考答案一、选择题1. 已知函数 $y = 2x^3 - 5x^2 + 3x - 7$,求导数函数 $y'$ 的值。
A) $6x^2 - 10x + 3$\B) $6x - 10x^2 + 3$\C) $6x - 10x + 3$\D) $6x^2 - 10x^2 + 3$答案:A2. 设矩形的长为 $x$,宽为 $y$,满足 $x^2 + y^2 = 25$。
当矩形的面积最大时,求矩形的长和宽。
A) 长为 4,宽为 3\B) 长为 5,宽为 3\C) 长为 4,宽为 2.5\D) 长为 5,宽为 2.5答案:A3. 一条直线过点 $A(1,2)$ 和点 $B(3,-1)$,与另一条直线 $2x + y - 4 = 0$ 平行。
求该直线的方程。
A) $2x - y + 3 = 0$\B) $2x - y - 3 = 0$\C) $-2x + y - 3 = 0$\D) $2x - y - 5 = 0$答案:B4. 已知函数 $y = e^x$,求 $y$ 的微分值。
A) $e^x$\B) $e^x + C$\C) $e^x - C$\D) $C \cdot e^x$答案:A5. 一辆汽车以每小时 60 公里的速度行驶,途中经过两座相距 60 公里的城市。
假设两座城市间有一辆以每小时90 公里的速度行驶的列车,两车同时出发。
求两辆车首次相遇的时间。
A) 0.5 小时\B) 1 小时\C) 1.5 小时\D) 2 小时答案:A二、填空题6. 已知函数 $f(x) = \sin(x)$,求函数 $g(x) = f^{\prime}(x)$。
答案:$g(x) = \cos(x)$7. 若直线 $3x + ky = 2$ 与直线 $2x - y = 3$ 相垂直,则 $k$ 的值为\_\_\_。
答案:$k = 6$8. 设抛物线 $y = ax^2 - 3x + 2$ 的顶点为 $(2,1)$,则 $a$ 的值为\_\_\_。
武汉理工大学数学建模公共选修课考试试题

武汉理工大学数学建模公共选修课考试试题A题:最低生活保障问题温家宝总理在十届人大三次会议所作的《政府工作报告》中指出,要贯彻落实科学发展观,着力解决与人民群众切身利益相关的突出问题,高度重视解决城乡困难群众基本生活问题,维护社会稳定,努力构建社会主义和谐社会。
1999年国务院颁布《城市居民最低生活保障条例》,规定对持有非农业户口的城市居民,凡共同生活的家庭成员人均收入低于当地城市居民最低生活标准的,均可从当地政府获得基本生活物质帮助。
据民政部统计,截至2004年12月底,全国城市低保对象总人数为2200.8万人,各级财政累计支出低保金172.9亿元,其中中央财政支出102亿元。
低保对象月人均领取低保金65元。
城市居民低保制度的实施,对于巩固社会稳定, 促进社会进步和经济发展起到了极其重大作用。
但是低保制度在实施过程中,也存在一些具体问题。
突出表现在以下两点:一是保障标准的确定问题。
既要能维持保障对象的基本生活需求,又要避免标准设置过高降低工作的积极性;既要随着经济发展逐步提高,又要考虑财政承受力;既要和当地经济社会发展水平相适应,又要防止各地在标准的高低上互相攀比。
二是保障对象的资格问题。
如何实现动态管理下的“应保尽保”,如何合理平衡收入因素和资产、教育、住房、赡养问题等非收入因素,如何制定更为合理有效的“分类施保”政策,避免出现贫困家庭保障不足,相对富裕家庭领取低保的现象。
对这些问题,定性分析较多,定量研究尚不多。
1.分析、确定制定保障标准的主要依据。
2.试就以上一个或两个问题,运用数学工具,建立数学模型,并给出相应的结论。
3.对模型作实证分析,并与当前的有关政策和规定进行比较。
B题房价问题房价问题事关国计民生,对国家经济发展和社会稳定有重大影响,一直是各国政府大力关注的问题。
我国自从取消福利分房制度以来,随着房价的不断飙升,房价问题已经成为全民关注的焦点议题之一,从国家领导人、地方政府官员,到开发商、专家学者、普通百姓通过各种媒体表达各种观点,但对于房价是否合理、未来房价的走势等关键问题,至今尚未形成统一的认识。
《数学建模1》《数学建模2》《数学建模3》《数学建模4》试题及答案

1为调查大学中某一年级学生参加外语考试作弊的比例,用随机问答法进行调查。
设计的两个问题为:问题1:你在这次考试中有作弊行为;问题2:你在这次考试中无作弊行为。
设计的题号卡共100张,其中75张标有数字1,25张标有数字2。
请200名学生根据任意抽得的卡上的标号对问题1或问题2用“是”或“否”回答(抽出的卡再放回),结果有60名回答为“是”,则该年级学生外语考试作弊的比例约为[ 单选题:6 分]A 1%B 5%C 10%D 15%试题解析您的答案:C回答正确2如果原料钢管的长度为19米,当客户的需求为4米、6米、8米有几种合理的切割模式?[ 单选题:6 分]A 6B 7C 8D 不确定试题解析您的答案:B回答正确3原料钢管的长度为19米,客户的需求为4米50根、6米20根、8米15根,则需要的最少原料钢管数为[ 单选题:6 分]A 24B 25C 26D 27试题解析您的答案:D回答正确4在合理切割模式下,余料的长度应该[ 单选题:6 分]A 小于客户需要钢管的最小长度B 小于客户需要钢管的最大长度C 大于客户需要钢管的最小长度D 大于客户需要钢管的大长度试题解析您的答案:A回答正确5在敏感问题调查中,为了减轻被调查者的抵触情绪,瓦纳设计了一种随机问答法,这种方法需要向调查者提几个问题[ 单选题:6 分]A 1B 2C 3D 4试题解析您的答案:B回答正确6钢管下料问题1中,客户需求的钢管米数为[ 多选题:8分 ]A 4B 6C 8D 10试题解析您的答案:ABC回答正确7钢管下料问题2中,在客户增加了需求之后,客户需求的钢管米数为[ 多选题:8分 ]A 4B 5C 6D 8试题解析您的答案:ABCD回答正确8利用瓦纳的随机问答法进行敏感问题调查时,调查结果与下列哪些量有关[ 多选题:8分 ]A 调查的人数B 回答“是”的人数C 标有不同数字的题号卡所占的比例D 进行调查的时间试题解析您的答案:ABC回答正确9钢管下料问题中,对于大规模问题,用模型的约束条件界定合理模式时采用的做法是[ 多选题:8分 ]A 增加约束B 缩小可行域C 减小约束D 增大可行域试题解析您的答案:AB回答正确10钢管下料问题中,在合理切割模式下,余料的米数可以为[ 多选题:8分 ]A 1B 2C 3D 4试题解析您的答案:ABC回答正确11LINGO软件只能求解整数线性规划问题[ 判断题:6分 ]正确错误试题解析您的答案:错误回答正确12敏感问题调查时,直接向被调查者提问该问题就可以得到真实的结果[ 判断题:6分 ]正确错误试题解析您的答案:错误回答正确13钢管下料时,不同的切割标准对应的切割方案也不同[ 判断题:6分 ]正确错误试题解析您的答案:正确回答正确14用户的需求种类越多,对应的合理切割模式也越多[ 判断题:6分 ]正确错误试题解析您的答案:正确回答正确15利用瓦纳的随机问答法进行敏感问题调查时,标有数字1和数字2的题号卡的数量必须相等[ 判断题:6分 ]正确错误试题解析您的答案:错误回答正确1市场经济中,若供大于求,则下阶段会出现?[ 单选题:6 分]A 价格上涨B 价格下降C 没有变化D 供求平衡试题解析您的答案:B回答正确2若有10个工作台,传送带上有40个挂钩,稳态情况下,一个周期内运走的产品数占总产品数的比例为?[ 单选题:6 分]A 25%B 50%C 89.4%D 100%试题解析您的答案:C回答正确3市场经济中,生产者管理水平提高会导致?[ 单选题:6 分]A 平衡点的稳定条件放宽B 平衡点的稳定条件收紧C 没有变化D 市场震荡加剧试题解析您的答案:A回答正确4甲乙丙三系人数分别为103, 63, 34, 总共21个代表席位,按Q值方法进行分配,丙系分得的席位数为?[ 单选题:6 分]A 4B 3C 5D 不确定试题解析您的答案:A回答正确5甲乙丙三系人数分别为103, 63, 34, 总共20个代表席位,按照比例加惯例的方法,甲系分得的席位数为?[ 单选题:6 分]A 9B 10C 11D 不确定试题解析您的答案:B回答正确6若a表示消费者对需求的敏感程度,b表示生产者对价格的敏感程度,则下列说法中正确的是[ 多选题:8分 ]A a越小越有利于经济稳定B a越大越有利于经济稳定C b越小越有利于经济稳定D b越大越有利于经济稳定试题解析您的答案:AC回答正确7市场经济中的蛛网模型主要研究?[ 多选题:8分 ]A 商品数量与价格的变化规律B 商品数量与价格的振荡在什么条件下趋向稳定C 生产者管理水平对平衡点稳定性的影响D 当不稳定时政府能采取什么干预手段使之稳定试题解析您的答案:ABCD回答正确8提高传送带效率的途径有?[ 多选题:8分 ]A 增加工作台数B 减少工作台数C 增加挂钩数D 减少挂钩数试题解析您的答案:BC回答正确9传送系统的效率模型中,主要研究?[ 多选题:8分 ]A 衡量传送带效率的指标B 提高传送带效率的途径C 效率与工作台数量的关系D 效率与挂钩数量的关系试题解析您的答案:ABCD回答正确10席位分配的理想化准则应满足?[ 多选题:8分 ]A 每方分得的席位数介于应得的席位数向上取整和向下取整之间B 当总席位增加时,每方分得的席位数都不会减少C 每方分得的席位数应该四舍五入D 随机分配试题解析您的答案:AB回答正确11席位分配时,Q值方法符合理想化准则的两个条件[ 判断题:6分 ]正确错误试题解析您的答案:错误回答正确12席位分配时,比例加惯例方法符合理想化准则的两个条件[ 判断题:6分 ]正确错误试题解析您的答案:错误回答正确13在市场经济中,供求关系是一直保持平衡的[ 判断题:6分 ]正确错误试题解析您的答案:错误回答正确14挂钩数量越多,传送带的效率就越高[ 判断题:6分 ]正确错误试题解析您的答案:正确回答正确15席位分配时,比例加惯例方法和Q值方法各有优缺点[ 判断题:6分 ]正确错误试题解析您的答案:正确回答正确1A、B两家电视机厂竞争的二人零和纯策略博弈模型中,A厂应生产的电视机型号为?[ 单选题:6 分]A 1B 2C 3D 4试题解析您的答案:B回答正确2二人零和纯策略博弈求解时采用的原则是?[ 单选题:6 分]A 考虑到最坏的可能性的基础上争取最好结果B 考虑到最好的可能性的基础上争取最好结果C 考虑到最坏的可能性的基础上争取最坏结果D 考虑到最好的可能性的基础上争取最坏结果试题解析您的答案:A回答正确3A、B两家电视机厂竞争的二人零和纯策略博弈模型中,B厂应生产的电视机型号为?[ 单选题:6 分]A 1B 2C 3D 不确定试题解析您的答案:B回答正确41981年美国国会表决里根总统年度财政预算时,民主党应该采取的策略是?[ 单选题:6 分]A 大体支持里根B 反对里根C 完全支持里根D 弃权试题解析您的答案:A回答正确51981年美国国会表决里根总统年度财政预算时,共和党应该采取的策略是?[ 单选题:6 分]A 大体支持里根B 反对里根C 完全支持里根D 与民主党妥协试题解析您的答案:C回答正确6二人零和纯策略博弈问题中,利用最大最小原则(最小最大原则)对A的赢利矩阵进行操作,得到的最优解aij满足?[ 多选题:8分 ]A aij是它所在行中的最小值B aij是它所在列中的最小值C aij是它所在行中的最大值D aij是它所在列中的最大值试题解析您的答案:AD回答正确7求纳什均衡点时,采用的方法是[ 多选题:8分 ]A 对赢利表中的赢利对的第一个元素按列求出最大值,将最大元素标上“*”B 对赢利对的第二个元素按行求出最大值,将最大元素标上“*”C 两个元素同时标有“*”号的即为纳什均衡点D 一个元素标有“*”号的即为纳什均衡点试题解析您的答案:ABC回答正确8二人非零和纯策略博弈模型的求解原则有?[ 多选题:8分 ]A 理性原则B 无悔原则C 自由原则D 随机原则试题解析您的答案:AB回答正确9本节讲述的矩阵博弈模型有?[ 多选题:8分 ]A 二人零和纯策略博弈B 二人非零和纯策略博弈C 三人零和纯策略博弈D 三人非零和纯策略博弈试题解析您的答案:AB回答正确10二人零和纯策略博弈的求解时,采用的原则可以称为?[ 多选题:8分 ]A 最大最小原则B 最小最大原则C 最大最大原则D 最小最小原则试题解析您的答案:AB回答正确11二人非零和纯策略博弈模型中,对应任意的赢利矩阵,纳什均衡点必然存在[ 判断题:6分 ]正确错误试题解析您的答案:错误回答正确12二人零和纯策略博弈模型中,鞍点对应的策略符合最小最大原则[ 判断题:6分 ]正确错误试题解析您的答案:正确回答正确13二人非零和纯策略博弈模型中,无悔原则和理性原则是一回事[ 判断题:6分 ]正确错误试题解析您的答案:错误回答正确14二人零和纯策略博弈模型中,一方之所失即为另外一方之所得[ 判断题:6分 ]正确错误试题解析您的答案:正确回答正确15二人非零和纯策略博弈模型中,一方之所失即为另外一方之所得[ 判断题:6分 ]正确错误试题解析您的答案:错误回答正确1多阶段决策时,考虑的原则是?[ 单选题:6 分]A 风险越低越好B 风险越高越好C 期望收益越大越好D 决策过程越简单越好试题解析您的答案:C回答正确2随机事件是?[ 单选题:6 分]A 在一定条件下可能发生也可能不发生的事件B 在一定条件下一定发生的事件C 在一定条件下不可能发生的事件D 从来没发生过的事件试题解析您的答案:A回答正确3有一大批产品,其中15%为一等品,75%为二等品,10%为三等品.一、二、三等产品的单价分别为10元8元和6元.有人要采购一批这种产品,但来不及检验,商品的价格可定为[ 单选题:6 分]A 10元B 8元C 6元D 8.1元试题解析您的答案:D回答正确4口袋中有大小重量相同的红黄球各1个,黑球2个,任摸一球,摸到红球的概率为?[ 单选题:6 分]A 0.25B 0.5C 0.75D 1试题解析您的答案:A回答正确5某船主要对下月渔船是否出海做出决策。
《数学建模》考试试卷与参考答案

《数学建模》试卷 第 1 页 共 4 页《数学建模》试题一、填空题(每题5分,满分20分):1. 设开始时的人口数为0x ,时刻t 的人口数为)(t x ,若人口增长率是常数r ,那麽人口增长问题的马尔萨斯模型应为 .2. 设年利率为0.05,则10年后20万元的现值按照复利计算应为 .3. 所谓数学建模的五步建模法是指下列五个基本步骤,按一般顺序可以写出为 .4. 设某种商品的需求量函数是,1200)(25)(+-=t p t Q 而供给量函数是3600)1(35)(--=t p t G ,其中)(t p 为该商品的价格函数,那麽该商品的均衡价格是 .二、分析判断题(每题10分,满分20分):1. 从下面不太明确的叙述中确定要研究的问题,需要哪些数据资料(至少列举3个),要做些甚麽建模的具体的前期工作(至少列举3个) ,建立何种数学模型:一座高层办公楼有四部电梯,早晨上班时间非常拥挤,该如何解决。
2. 某公司经营的一种产品拥有四个客户,由公司所辖三个工厂生产,每月产量分别为3000,5000和4000件.公司已承诺下月出售4000件给客户1,出售3000件给客户2以及至少1000件给客户3,另外客户3和4都想尽可能多购剩下的件数.已知各厂运销一件产品给客户可得到的净利润如表1所示,问该公司应如何拟订运销方案,才能在履行诺言的前提下获利最多?表1单位:元/件上述问题可否转化为运输模型?若可以则转化之(只需写出其产销平衡运价表即可),否则说明理由。
三、计算题(每题20分,满分40分):1. 有一批货物要从厂家A 运往三个销售地B 、C 、D ,中间可经过9个转运站.,,,,,,,,321321321G G G F F F E E E 从A 到321,,E E E 的运价依次为3、8、7;从1E 到21,F F 的运价为4、3;从2E 到321,,F F F 的运价为2、8、4;从3E 到32,F F 的运价为7、6;从1F 到21,G G 的运价为10、12;从2F 到321,,G G G 的运价为13、5、7;从3F 到32,G G 的运价为6、8;从密线封层次报读学校专业姓名317《数学建模》试卷 第 2 页 共 4 页1G 到C B ,的运价为9、10;从2G 到D C B ,,的运价为5、10、15;从3G 到D C ,的运价为8、7。
数学建模考试试题及答案

数学建模及应用试题汇总1. 假如你站在崖顶且身上带着一只具有跑表功能的计算器, 你也会出于好奇心想用扔下一 块石头听回声的方法来估计山崖的高度,假定你能准确地测定时间,你又怎样来推算山 崖的高度呢,请你分析一下这一问题。
2. 建立理想单摆运动满足的微分方程,并得出理想单摆运动的周期公式。
3. 一根长度为 l 的金属杆被水平地夹在两端垂直的支架上,一端的温度恒为 T1, 另一端温 度恒为 T2, (T1、T2 为常数, T1> T2)。
金属杆横截面积为 A ,截面的边界长度为 B ,它 完全暴露在空气中,空气温度为 T3, (T3< , T3 为常数), 导热系数为α,试求金属杆 上的温度分布 T(x), (设金属杆的导热 2为λ)4. 甲乙两队进行一场抢答竞赛,竞赛规则规定:开始时每队各记 2 分,抢答题开始后,如 甲取胜则甲 加 1 分而乙减 1 分,反之则乙加 1 分甲减 1 分,(每题必需决出胜负 )。
规 则还规定,当其中一方的得分达 到 4 分时,竞赛结束。
现希望知道:(1)甲队获胜的概率有多大?(2)竞赛从开始到结束,平均转移的次数为多少?(3)甲获得 1 、2、3 分的平均次数是多少?5. 由于指派问题的特殊性, 又存在着由匈牙利数学家提出的更为简便的解法——匈牙利算 法。
当系数矩阵为下式,求解指派问题。
「16 15 19 22]C =L17 19 22 16 」6. 在遥远的地方有一位酋长,他想把三个女儿嫁出去。
假定三个女儿为 A 、B 、C , 三位求 婚者为 X 、Y 、Z 。
每位求婚者对 A 、B 、C 愿出的财礼数视其对她们的喜欢程度而定: A B C x 「 3 5 26]问酋长应如何嫁女,才能获得最多的财礼(从总体上讲,他的女婿最喜欢他的女儿。
7. 某工程按正常速度施工时,若无坏天气影响可确保在 30 天内按期完工。
但根据天气预 报, 15 天后天气肯定变坏。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年6月广东石油化工学院大学数学建模(公选课)考核
试题
截止时间:2014年6月20日(星期五)晚上21:00,交稿地点二教B703。
请按照附件1的格式要求提交作业,要求:
从以下ABC三题选择一题,完成数学建模论文一篇。
论文做封面一张,写上题目、作者、系别、班级、学号、日期论文一律用A4纸打印出来,正文用5号宋体字。
A题经济发展与环境保护
建立适当的数学模型说明我国哪些省(直辖市、特别行政区)在发展经济的同时有效地保护了环境资源。
在论文的结尾写一份如何有效发展循环经济的小评论(字数500-1500字,评论中可以对某些省改变经济发展方式提出具体建议)。
几点说明:
1.充分利用政府部门公布的各省(直辖市、特别行政区)的历年国民经济和社会发展统计公报中相关数据(如浙江统计局网站)。
2. 可以选择典型的3-10个省的统计数据进行分析。
3. 经济发展水平的衡量可以综合考虑如下指标:GDP、人均GDP、人均收入、进出口外贸总值、人均税收、人均存款、GDP增幅水平等(还有很多衡量经济发展的指标,同学们可以参考各类文献,并自行收集资料,通过建立数学模型(或简单的统计模型)进行综合评定)。
4. 环境资源要考虑到能耗(如水资源、电、煤等耗量),也可考虑主要污染物排放总量(SO2,、COD、废水、废渣、废气等)。
5. 建模中各个省份之间要横向比较,单个省要进行纵向比较(比较历年数据),并得出经济发展和保护环境资源的关系。
6. 查找数据的能力对于本题能否成功求解至关重要,
B、汽车售后维修数据统计分析
产品质量是企业的生命线,售后服务是产品质量的观测点,如何用好售后服务的数据是现代企业管理的重要问题之一。
现以某小型汽车生产厂家为例考虑这个问题。
假设该厂的保修期是三年,即在售出后三年中对于非人为原因损坏的小型汽车免费维修。
在全国各地的维修站通过网络将保修记录送到统一的数据库里面,原始数据主要包含哪个批次生产的小型汽车(即生产月份)、售出时间、维修时间、维修部位、损坏原因及程度、维修费用等等。
通过这样的数据可以全面了解所有部件的质量情况,若从不同的需求角度出发科学整理数据库中的数据,可得到不同用途的信息,从而实现不同的管理目的。
整车或某个部件的“万车故障数”是一个很重要的指标,常用于描述小型汽车的质量。
首先将小型汽车按生产批次划分成若干个不同的集合(下面表格的同一行数据就来自同一集合),再对每个集合中迄今已售出的全部小型汽车进行统计,由于每个集合中的小型汽车是陆续售出的,因此它们的统计时间的起点即售出时间是不同的。
但在下面表格中,每一列数据的统计时间的长度却是相同的(例如2007年3月底出厂的小型汽车,到2007年8月底;或2008年10月初出厂的小型汽车,到2009年3月初都是最多使用了五个月,显然它们的统计时间的终点也是不同的),在相同使用时间长度(例如下表中第5列都是使用了11
个月的万车故障数)内的整车或某个部件的保修总次数乘以10000再除以迄今已售出的小型汽车数量,即为下面表格中的万车故障数。
数据利用的时效性是很强的,厂方希望知道近期生产中的质量情况,但刚出厂的小型汽车还没有全售出去,已售出的小型汽车也没使用几个月,因此数据显得滞后很多。
当一个批次生产的小型汽车的三年保修期都到时,我们对这批小型汽车的质量情况有了最准确的信息,可惜时间是小型汽车出厂的四、五年后,这些信息已无法指导过去的生产,对现在的生产也没有太大作用。
所以如何更科学地利用少量数据预测未来情况是售后服务数据利用的重要问题。
现有2008年4月1日从数据库中整理出来的某个部件的万车故障数,见下页的表。
其中的使用月数一栏是指售出小型汽车使用了的月份数,使用月数0的列中是已售出的全部小型汽车在用户没使用前统计的万车故障数,1的列中是某一批次已售出的每一辆小型汽车,在它被使用到第一个月结束时统计的,对于该批次售出的全部小型汽车累计的万车故障数(即没使用时和第一个月中万车故障数的和),12列中是每辆车使用到恰好一年结束时的累计万车故障数。
生产月份是生产批次,如0701表示2007年1月份生产的。
随着时间的推移,小型汽车不断地销售出去,已售出小型汽车使用一段时间后的万车故障数也能不断自动更新,再打印出的表中数据也将都有变化。
1. 该表是工厂的真实数据,没有修改,反映的情况很多,请你分析表中是否存在不合理数据,找出不合理数据(不合理数据产生原因可能是统计失误或由于小概率事件产生导致,对指导日后管理工作或预测工作没有太大意义),并给出理由,进一步对数据进行修正。
2.利用这个表的数据预测时请注意区分水平和垂直方向。
请你设计相应的模型与方法,并预测:0701批次使用月数18时的万车故障数;0704批次使用月数15时的万车故障数;0711批次使用月数10时的万车故障数;0801批次使用月数6时的万车故障数。
3.根据表内数据分析,找出汽车售后维修数据中存在的一些规律,写一篇
300-1500字的小评述。
小型汽车某部件万车故障数的数据表使用月数15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0
生产月份制表时销售量
0701 2309 1132.81020.6910.1811.3720.9 670.2 599.7 525.3436.0 349.3272.1229.5168.3 102.280.01 3.2 0702 3108 1319.00 1295.00 1570.00 1322.00 1198.00 972.50 697.20 610.00 440.00 346.60 265.00 225.10 186.10 153.150.6 0703 4506 396.3 340.70 571.60 268.50 226.50 179.50 156.7 133.70 118.889.2 75.367.70 59.70 20.00 0704 4717 预测324.0293.43 238.5201.3116.02 116.02 116.02 116.02 86.82 61.62 41.31 30.5 5.68 0705 3812 498.2390.7302.9 243.7196.99 163.37 132.76 92.45 72.15 61.85 51.54 11.24 0706 4138 90.11 80.87 83.79 78.05 60.65 51.04 37.67 27.88 21.21 17.59 8.09 0707 2111 359.00 289.00 248.70 218.10 167.40 136.40 65.4 63.7 62.79 9.41 0708 3115 599.30 529.00 453.40 367.80 282.10 206.50 136.00 75.60 15.10 0709 2716 846.10 748.80 658.90 520.40 423.10 273.30 112.30 18.70 0710 3117 1844.80 492.90 341.10 243.90 186.80 113.90 28.50 0711 2100 415.90 222.60 138.60 84.40 36.60 7.2 0712 1673 81.62 54.95 41.31 29.53 24.67 0801 1425 0.000.0071.00 29.90 0802 1320 0.00 0.00 0.00 0803 980 0.00 0.00
C、地震问题
下图为四川大地震一截图,主要是地震灾区县(市)公路网示意图,两地距离以实际距离为准(自行收集)。
2008年5月12日发生大地震,该地区遭受地震。
为考察灾情、组织自救,成都领导决定,带领有关部门负责人到受灾地区各县(市)巡视。
巡视路线指从成都所在地出发,走遍各受灾县(市),又回到成都政府所在地的路线。
路上合理考虑阻抗。
问题1、假定巡视人员在各县停留时间t=1.5小时,市停留时间T=2.5小时,汽车行驶一般公路(国道)速度v=60公里/小时,行驶高速速度V=89公里/小时。
若分一组巡视地图上的方框地区,如何设计巡视线路,最短时间为多少?若要在18小时内完成巡视,至少应分几组?请给出这种分组下你认为最佳的巡视路线。
问题2、在上述关于t、v、T 和V的假定下,若分三组(路)巡视方框地区,试设计总路程最短且各组在巡视时间上尽可能均衡的巡视路线。
问题3、考虑更为具体的受灾地区,如附表1所示(与问题1和问题2比较需要巡视的地区数增多),分2组考虑最佳巡视路线。
问题4、进一步考虑通用模型。
已知有M个受灾地点,给定各点之间的距离和路况,在给定t、v、T 和V的假定下,若分2组(路)巡视受灾地点,试设计巡视时间最短的巡视路线。
同学有兴趣的话,可以进一步考虑若分N组(路)巡视受灾地点,试设计巡视时间最短的巡视路线。
要求:问题1和问题2属于基本题,要求必做,问题3和问题4属选做题。
四川大地震一截图
附表1:
四川主要受灾地区
汶川县北川县绵竹市都江堰市
广元市青川县成都什邡市
安县平武县彭州市茂县
江油市理县雅安眉山
巴中南充遂宁乐山
甘孜广安泸州凉山
自贡资阳内江
说明:两地间的距离可以通过INTERNET网查询,路况可做一个大致估计,路上的行驶不需要很精确,但要大致合理。
