破碎岩体强度理论综述
最新岩爆发生的机理分析及防治措施综述

岩爆发生的机理分析及防治措施综述岩爆发生的机理分析及防治措施综述摘要:深部洞室的岩爆已成为水利、隧道、深部采矿工程建设的突出问题。
近年来,我国在深部采矿,隧道开挖等工程领域快速发展,由于工程经验相对较少,且多数理论研究成果很难解释岩爆的发生机理,因此对岩爆的发生机理及防治措施研究显得尤为重要和迫切。
通过介绍已有的岩爆发生机理,比较现有的岩爆发生机理,指出各岩爆机理的优缺点,并提出需要改进的部分,并对相关的隧洞工程总结有效的防治措施。
最后结合当前的研究现状提出几点见解,以期为岩爆区的工程设计、施工建设提供有益参考。
关键词:岩爆;地应力;应变能;隧洞;断裂力学E-mail:ambitiousxjfeng@引言自1738年在英国锡矿坑道中首次发现岩爆现象以来,各国在深部地下工程中的岩爆现象越来越多,这与人类不断向深部开采资源,发展地下空间的活动密切相关。
岩爆作为一种人类地下深部工程活动的产物,其定义众多,目前尚未有统一的认识。
广泛被接受的定义:在高地应力深部地下洞室中,脆性岩石卸荷造成存储的应变能突然释放,使洞室围岩出现崩落,甚至弹射并伴随爆裂声的一种动力失稳现象[1]。
岩爆的发生会给工程造成巨大的损失,严重的情况会造成大型机械设备的损坏以及人员的伤亡,因此对深部岩石的岩爆现象研究显得特别重要。
随着矿山、水利水电、铁路公路交通隧道等工程向深部发展,岩爆作为一种地质灾害现象,其发生越来越频繁。
[2]岩爆作为一种复杂的深部地下工程活动现象,其发生原因受多种因素的影响,因此对岩爆形成的机理研究以及准确预测显得特别困难。
为解决当前我国深部地下工程活动中的地质灾害问题,需要对岩爆发生的力学机理,物理现象做深入的研究,结合室内试验,现场试验以及现场检测对其发生的时间,发生的强度、烈度做进一步精确的预测。
我国自1933年在抚顺胜利煤矿报道岩爆事故以来,已记载了大量的工程岩爆事故,特别近几年来,随着我国不断向深部地下空间发展,岩爆现象发生频繁。
岩石强度破裂准则讲解

2、最大正应变强度理论
岩石强度条件可以表示为:
max m
ε max ——岩石内发生的最大应变值,可用广 义胡克定律求出; ε m—单向压缩或单向拉伸试验时岩石破坏的 极限应变值,由实验求得
试验证明,这种强度理论只适用于脆性岩石, 不适用于岩石的塑性变形。
3、最大剪应力强度理论
最大剪应力张度理论也称为屈瑞斯卡(H.Tresca)强度 准则,是研究塑性材料破坏过程中获得的强度理论。试 验表明,当材料发生屈服时,试件表面将出现大致与轴线 呈45°夹角的斜破面。由于最大剪应力出现在与试件轴 线呈45°夹角的斜面上,所以,这些破裂面即为材料沿 着该斜面发生剪切滑移的结果。一般认为这种剪切滑移 是材料塑性变形的根本原因。因此,最大剪应力强度理 论认为材料的破坏取决于最大剪应力。当岩石承受的最 大剪应力τmax达到其单轴压缩或单轴拉伸极限剪应力 τm时,岩石便被剪切破坏。
1 y 2 3 0
6、八面体应力强度理论
6、八面体应力强度理论
由冯-米塞斯强度条件τOCT=τs,得
1 3
1 2 2 2 3 2 3 1 2
2 3
y
对于塑性材料,这个理论与试验结果很吻合。在塑 性力学中,这个理论称之为冯-米塞斯破坏条件,一直被 广泛应用。
8 软弱面破裂准则
8 软弱面破裂准则
片理
8 软弱面破裂准则
片麻岩
9、格里菲斯强度理论
9、格里菲斯强度理论
三、格里菲斯准则(Griffth 1921)
断裂力学1921年提出,70年代岩石力学领域 (1)实验基础:玻璃材料中的微裂纹张拉扩展,
连接,贯通,导致材料破坏。 (c
σ1e—破坏时最大有效主应力,Mpa; σ3e-破坏时最小有效主应力,Mpa; σc—结构完整的连续介质岩石材料单轴抗压强度,Mpa; m、s—经验系数
第2章 2.6 岩石的强度理论

]
1 = (σ1 − σ 2 )2 + (σ 2 − σ 3 )2 + (σ 3 − σ1 )2 为应力偏量第二不变量; 为应力偏量第二不变量; 6
[
]
α、K为仅与岩石内摩擦角φ和粘结力c有关的试验常数。 为仅与岩石内摩擦角φ和粘结力c有关的试验常数。
α=
2 sin ϕ 3 ( 3 − sin ϕ ) K= 6c cos ϕ 3 ( 3 − sin ϕ )
z
z
τ zx
zy
6个应力分量: 个应力分量: σx,σy,σz, τxy,τyz,τzx
τ yx
τ xz
τ xy
σy τ yz
a
σx τ zy
τ xy
τ xz
b
σx
τ yz τ yx σy
τ zx σz
o
x
y
3、平面问题的简化 、 在实际工程中,可根据不同的受力状态,将三维问题简化 在实际工程中, 可根据不同的受力状态, 为平面问题。 为平面问题。 平面应力问题:其中一个方向的应力为零; (1)平面应力问题:其中一个方向的应力为零; 平面应变问题:其中一个方向的应变为零。 (2)平面应变问题:其中一个方向的应变为零。 4、基本应力公式 以平面应力问题为例,如图, 以平面应力问题为例,如图,任 意角度α截面的应力计算公式如下: 意角度α截面的应力计算公式如下:
tg
σ x −σ y
任一斜面上的正应力和剪应力用主应力表示为: 任一斜面上的正应力和剪应力用主应力表示为:
σn = σ 1 +σ 3
2 2 σ −σ 3 τn = 1 sin 2α 2 +
σ 1 −σ 3
cos 2α
莫尔应力圆的方程: (σ n − 莫尔应力圆的方程:
莫尔-库伦强度理论

03 莫尔-库伦强度理论的实 践应用
在岩土工程中的应用
岩土工程是研究岩体和土体工程的科学,莫尔-库伦强 度理论在岩土工程中有着广泛的应用。
输标02入题
在岩石和土壤的稳定性分析中,莫尔-库伦强度理论可 以用来预测岩石和土壤在受到外力作用时的破坏模式 和失稳情况。
01
03
在边坡工程中,莫尔-库伦强度理论可以用来评估边坡 的稳定性,预测边坡可能出现的滑坡、崩塌等灾害。
对未来研究的展望
随着科技的不断进步,未来对于莫尔-库伦强度理论的研究 可以更加深入,例如通过实验和数值模拟等方法,进一步 揭示岩石和土壤的强度和变形机理。
随着工程实践的不断发展,对于莫尔-库伦强度理论的改进 和完善也是必要的,例如考虑非线性、各向异性等因素对 岩石和土壤强度的影响。
未来研究可以进一步拓展莫尔-库伦强度理论在其他领域的 应用,例如在地质灾害防治、资源开采、环境保护等领域 的应用。
02
在桥梁工程中,莫尔-库伦强度理论可以用来评估桥梁结构的承载能 力和稳定性,预测桥梁可能出现的变形和裂缝。
03
在房屋建筑中,莫尔-库伦强度理论可以用来评估房屋结构的稳定性 和安全性,预测房屋可能出现的墙体开裂、楼板塌陷等问题。
04
在机械工程中,莫尔-库伦强度理论可以用来研究机械零件的强度和 疲劳性能,优化机械零件的材料和结构设计。
和结构设计。
在陶瓷材料中,莫尔-库伦强度 理论可以用来研究陶瓷材料的 脆性和断裂行为,提高陶瓷材 料的强度和韧性。
在金属材料中,莫尔-库伦强度 理论可以用处理工艺。
在结构工程中的应用
01
结构工程是研究结构的分析、设计和施工的科学,莫尔-库伦强度理 论在结构工程中也有着重要的应用。
岩石强度理论解读

5.4.4 Griffith强度理论
1 3 3 0时 3 t ①数学式 ( 1 3 ) 2 8 t 1 3 3 0时 1 3
②最有利破裂的方向角
1 3 1 arccos 2 2( 1 3 )
( 1 3 ) 2 8 t ( 1 3 3 0) 1 3 ( 1 3 3 0) 3 t
5.4.4 Griffith强度理论
1)基本假设(观点): ①物体内随机分布许多裂隙; ②所有裂隙都张开、贯通、独立; ③裂隙断面呈扁平椭圆状态; ④在任何应力状态下,裂隙尖端产生拉应力集 中,导致裂隙沿某个有利方向进一步扩展。 ⑤最终在本质上都是拉应力引起岩石破坏。
剪切面的正应力σ>0,得 出σ1>σc/2
5.4.2 Coulomb强度准则
应用: ①判断岩石在某一应力状态下是否破坏(用应力圆)。 ②预测破坏面的方向:(与最大主平面成 45 0 ); 2 (X 型节理锐角平分线方向为最大主应力方向)。 ③进行岩石强度计算。
评价: ①是最简单的强度准则,是莫尔强度理论的一个特例。 ② 不仅适用于岩石压剪破坏。
2
2
1 3
2
) sin
BD AB sin (c ctg 3
1 sin 1 sin 化简得: 1 2c 3 1 sin 1 sin
(有两种方法推导: 代数、几何 )
5.4.2 Coulomb强度准则
强度准则:
2Ea C
a为裂纹表面单位面积的表面能;E为非破 裂材料的弹性模量。
5.4.4 Griffith强度理论
1924年,Griffith把他的理论推广到用于压缩试验的情 况。在不考虑摩擦对压缩下闭合裂纹的影响和假定椭 圆裂纹将从最大拉应力集中点开始扩展的情况下,如 图所示,获得了双向压缩下裂纹扩展准则,即Griffith 强度准则(σt为单轴抗拉强度):
第二章:岩石破碎基本原理

强度条件:
三向应力时: 3 (1 2 ) t
3
1 E
[ 3
(1
2)]
单向拉伸时: 3 t
3
t
E
单向压缩时: 1 c
3
E
c
适用范围:适合于破坏形式为脆断的材料。
3
2.1 四种常用的强度理论
三、最大剪应力理论(第三强度理论)
莫尔应力圆:
1 3 2 2 1 3 2
2
2
剪切破坏角与内摩擦角的关系:
C
A
2
0 3
1
4 2
12
2.2 岩石破坏准则
三、库伦-莫尔准则(Coulomb-Mohr Criterion)
几个重要关系式推导:
三轴应力状态下的畸变能:
Ud
1
6E
[(
1
2 )2
( 2
3 )2
(3
1 )2 ]
强度条件:
1 2
[(
1
2 )2
( 2
3 )2
(3
1 )2
s
局限性:① 适用于塑性材料; ② 可得出抗拉强度与抗压强度相等的结论,与岩石不符。
8
2.2 岩石破坏准则
二、岩石破坏准则
岩石破坏准则—指岩石在某应力或应变状态下产生破坏的判据。 通常表示为极限应力状态下的主应力间的关系方 程或处于极限平衡状态截面上的剪应力与主应力 的关系方程。
1 f ( 2 , 3 ) 或 f ( )
由于岩石抗压强度与抗拉强度相差较大,所以材料力学中的第一 (最大拉应力理论)、第二(最大拉应变理论)、第三(最大剪应 力理论)、第四强度理论(畸变能理论)都不适用。
岩石的强度理论及破坏判据[详细]
![岩石的强度理论及破坏判据[详细]](https://img.taocdn.com/s3/m/b87c145d5ef7ba0d4b733ba7.png)
依据适合的强度理论,判断岩体的破坏及其破坏形式。 岩体本构关系:指岩体在外力作用下应力或应力速率与其应变 或应变速率的关系。
岩石或岩体的变形性质:弹塑性或粘弹塑性。 本构关系:弹塑性或粘弹塑性本构关系。 本构关系分类:
①弹性本构关系:线性弹性、非线性弹性本构关系。 ②弹塑性本构关系:各向同性、各向异性本构关系。 ③流变本构关系:岩石产生流变时的本构关系。流变
Griffith强度准则只适用于研究脆性岩石的破坏。
Mohr-coulomb强度准则的适用性一般的岩石材料。
0
σ1=σ3
P β
σc / 2
σc
σ1
-σt
A
S
岩石强度理论与破坏判据
三、 莫尔强度理论
莫尔(Mohr,1900年)把库仑准则推广到考虑三向应力状态。最主
要的贡献是认识到材料性质本身乃是应力的函数。他总结指出“到极 限状态时,滑动平面上的剪应力达到一个取决于正 应力与材料性质的最大值”,并可用下列函数关系表示:
σ1 σ
莫尔包络线的具体表达式,可根据试验结果用拟合法求得。
包络线形式有:斜直线型、二次抛物线型、双曲线型等。
斜直线型与库仑准则基本一致,库仑准则是莫尔准则的一个特例。
这里主要介绍二次抛物线和双曲线型的判据表达式。
1、二次抛物线型
τ
岩性较坚硬至较弱的岩石。
2 n t
2
τ=
n(σ
+σt
)
M(σ ,τ)
四、 格里菲斯强度理论
格里菲斯(Griffith ,1920年)认为:脆性材料断 裂的起因是分布在材料中的微小裂纹尖端有拉应力 集中(这种裂纹称之为Griffith裂纹)。
格里菲斯原理认为:当作用力的势能始终保持不 变时,裂纹扩展准则可写为:
东北大学岩石力学讲义第二章 岩石破坏机制及强度理论
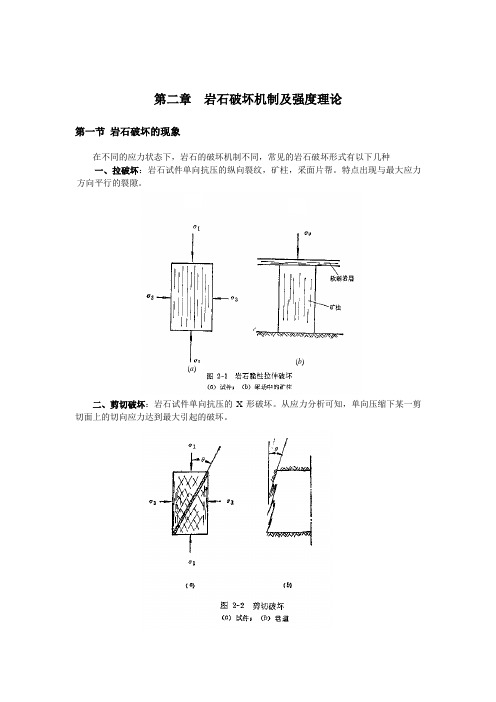
第二章 岩石破坏机制及强度理论第一节 岩石破坏的现象在不同的应力状态下,岩石的破坏机制不同,常见的岩石破坏形式有以下几种一、拉破坏:岩石试件单向抗压的纵向裂纹,矿柱,采面片帮。
特点出现与最大应力方向平行的裂隙。
二、剪切破坏:岩石试件单向抗压的X 形破坏。
从应力分析可知,单向压缩下某一剪切面上的切向应力达到最大引起的破坏。
(a ) (b )三、重剪破坏:即沿原有的结构面的滑动、重剪破坏主要的机制:岩体受剪切作用或者受拉应力的作用、三向受压情况下多数为剪切应力的作用,侧向压力较小时可能是拉神破坏,实际工程中可能是不同机制的组合,但侧向应力较大时,可以认为剪切应力是岩石重剪破坏的主要破坏机制。
从岩石破坏的现象看,从小到几厘米的岩块到大的工程岩体,破坏形式雷同,并可归纳为两种,拉断与剪坏,因此有一定的规律可寻。
对岩石破坏的研究:在单向条件下可以从实验得到破坏的经验关系。
但是三向受力条件下,不同应力的组合有无穷多种,因此无法仅仅依靠实验得到破坏的经验关系,因此在一般应力状态,对岩石破坏的研究需要结合理论分析和试验研究两个方面。
现代关于岩石破坏的理论分析一般归结为、寻求破坏时的主应力之间的关系123(,)f σσσ=研究的方法有:理论分析;2、试验研究;3、理论研究结合试验研究。
第二节 岩石拉伸破坏的强度条件一、最大线应变理论该理论的主要观点是,岩石中某个面上的拉应变达到临界值时破坏,而与所处的应力状态无关。
强度条件为c εε≤ (2-1) c ε—拉应变的极限值,ε—拉应变。
若岩石在破坏之前可看作是弹性体,在受压条件下σ1>σ2>σ3下, 3ε是最小主应力。
按弹性力学有33E Eσμεσσ=-12(+),即33E εσμσσ=-12(+)。
若3ε<0则产生拉应变。
由于E >0,因此产生拉应变的条件是3σμσσ-12(+)<0,3μσσσ12(+)>若3ε=0ε<0则产生拉破坏,此时抗拉强度为0tEσε=⇒0t E σε=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
HOEK -BROWN强度准则及其在破碎岩体强度中的应用摘要:岩石是有大量岩块和结构面组成的不均匀的各向异性材料。
但是因为岩体内部结构的不可预见性和建模、计算能力的限制,很多情况下,只能将岩体作为均匀的宏观复合材料进行研究。
如何准确定义破碎岩体的强度成了一个关系计算准确性和工程安全的重要问题。
本文阐述了岩石力学中破碎岩体的主要强度理论。
并对HOEK -BROWN强度理论的提出、发展、参数的选取与确定及实际应用进行了详细的探讨。
关键词:HOEK -BROWN强度准则,破碎岩体,岩体强度理论1.研究岩体强度理论的重要性人类生活和经济活动越来越离不开以岩体为对象的工程建设,例如水利水电工程、铁道交通工程、工业与民用建筑、隧道工程、矿山建筑与开发工程、国防工程、冶金化工、地震与防护工程等。
总的来说,它们都需要以研究岩体的力学特征为基础。
随着岩体工程的规模、数量及复杂性的增加,所涉及的岩体力学的问题也越来越复杂,以至于经常有重大岩体工程事故发生。
美国的圣弗朗斯西重力坝、法国马尔帕塞大坝、意大利瓦扬水电站、加拿大亚当贝克水电站压力管道及日本关门铁路隧道等工程的失败或失事的惨痛教训,使人们意识必须加强岩体力学理论研究和分析,正确把握岩体在外荷载作用下的强度、变形及破坏规律。
2.研究破碎岩体强度的难点在实际工程中遇到的均质岩体情况很少见,所碰到的岩体绝大多数均被各种结构面切割与破碎。
节理是岩体中发育最广泛的一种结构面,在很多情况下节理面的力学性质很软弱。
节理的存在严重的破坏了岩体的连续性和完整性,大大改变了岩体的力学性质。
节理岩体工程性质的特殊性主要表现在一下三个方面不连续。
节理岩体是由不同规模、不同形态、不同成因、不同方向和不同次序的节理面以及被节理面围限而成的结构体共同组成的综合体,节理岩体在几何上和工程性质上都具有不连续性。
由于发育在岩体中的节理面具有明显方向性,受节理面影响,节理岩体的工程性质呈现显著的各向异性。
另外,实际工程岩体被节理切割程度的大小也与岩体工程规模有关,工程岩体结构也会随着含节理数的多少而发生变化,如图所示,所考虑的岩体范围越小,岩体中所含有的节理数就愈少,因而岩体的结构类型也就会有所不同。
由于节理岩体工程性质的不连续、各向异性以及岩体组成物质的非均质,加之节理面在岩体不同部位发育程度和分布规律的差异,不同工程部位的岩体表现出不同的工程性质。
节理在地壳上部岩石中具有广泛的分布,并且在岩体介质中呈现出强度低、易变形的特征。
节理的发育常常为大坝、边坡和地下硐室等工程带来隐患,并导致工程岩体的失稳与破坏。
地质工程中的岩体强度预测、岩坡稳定性分析、岩基承载力确定、地下硐室围岩稳定性评价及相关的动力学现象围岩垮塌或岩爆均直接或间接与岩体变形及强度特征有关。
鉴于此,普遍认为节理岩体变形及强度特征的研究是一个富有挑战性的基础性课题,开展此方面的研究不仅非常必要,而且有着重要的实用价值和工程意义。
节理的存在不仅大大改变岩体的力学性质,降低岩体的变形模量及强度参数,并使岩体呈现明显的各向异性。
节理岩体变形具有各向异性的特征己为人们所熟知,竖向分布节理岩体的变形模量明显大于水平分布节理岩体的变形模量,这种区别主要在于变形机制不同。
垂直节理面的压缩变形量主要是由岩块和节理面压密综合而成,平行节理面方向的压缩变形量主要是岩块和水平节理面的错动构成,节理岩体各方向的变形性质的差异由此而产生。
与变形特征相类似,节理岩体也具有明显的强度各向异性特征。
通常为了实际的需要将岩石近似地简化为各向同性体,基本上未考虑各向异性的性质,对一种岩石只给出一个确定的强度指标。
在实际的岩石试验过程中发现,即使是同一地点取出的岩石,不同方向上的强度试验结果,往往也具有很大的离散性。
因为本身就已经是各向异性的岩体,在后期构造改造的作用下,其各向异性表现得更加突出。
参照图所示,对不含节理的完整岩体,可认为其在宏观上为均质、各向同性的材料对含有一组、二组或三组节理的岩体,其力学性质通常表现为各向异性若岩体被四组或四组以上的等规模、等间距及强度基本相同的节理面切割,可视此类节理岩体为均质、各向同性的破碎材料但当岩体中包括一条规模相对较大、较长节理时,岩体又在一定程度上表现为各向异性汇。
岩体的各向异性特征在土木、矿业及石油工程中均有着重要的作用,节理岩体各向异性特征的综合研究可以用来指导岩体工程的空间布局、分析计算与设计施工。
[1]鉴于目前的探测手段无法在将岩体内的节理分布详细的描述出来,也没有良好的分析手段可以处理含有大量不规则节理,表现出显著地几何非线性与物理非线性的岩体。
因此,对于含有较少节理的岩体,或某条或某组节理发发育占有明显优势时,可以采用可将节理和岩体作为独立的材料组分,建立二者的力与变形[2]等的协调关系,如采用Goodman[2-3]的独立节理单元技术、离散元技术等对其进行研究。
对于含有大量节理的岩体,应当将其视为整体的宏观复合材料进行研究。
视为整体宏观的复合材料进行研究时需要建立合理的屈服准则和本构关系。
3.常见的岩石强度准则3.1基于力学理论的强度准则库伦于1773年提出了“摩擦”准则[4],库伦认为,岩石的破坏主要是剪切破坏,岩石的强度,即抗摩擦强度等于岩石本身剪切摩擦的的粘结力和剪切面上法向产生的摩擦力。
1900年,摩尔把库伦准则推广到考虑三向应力状态。
最主要的贡献是认识到材料性质本身乃是应力的函数,他指出了“到极限状态时,滑动平面上的剪应力达到一个取决于正应力和材料性质的最大值。
其强度条件为一系列摩尔圆的包络线。
如果应力圆位于包络线的下方,则不会产生破坏。
目前已经提出的摩尔包络线有斜直线型,二次抛物线型和双曲线形等,如图一所示。
考虑到实际工程中破碎岩体节理面中的填充物抗拉强度都很低,实际工程中也经常使用 Mohr-Coulomb 与受拉破坏的破坏复合准则,即爱岩体抗压,抗剪时使用摩尔-库伦准则,而一旦岩体中出现拉应力或拉应力大于某个临界值,即判定为岩体发生破坏。
大多数理论均把岩体材料看作连续的均质介质,实际上,岩体内部存在着许多细微裂隙,在力的作用下,这些细微裂隙周围,特别是裂隙尖端产生较大的应力集中,从而增加裂隙端区域的弹性能。
当由应力集中造成的弹性能积累到能使岩体沿裂纹扩展所作阻力功,岩体材料将沿裂纹开裂。
Griffith 通过对材料及裂隙进行简化,提出了自己的强度准则。
上述Griffith 强度理论是以裂隙张开为前提条件的。
实际上,在压力作用下,材料中的裂隙将趋于闭合,而闭合后的裂隙面上将产生摩擦力,此时的裂隙扩展不同于张开裂隙。
据此,Meclintock 对Griffith 强度理论进行了修正。
近年来,Griffith 强度理论和修正的Griffith 强度理论被引入到断裂力学来解释岩石受力破坏的机理以及破坏的发生、发展过程的。
事实证明,它们对脆性岩石较适用,但不能描述岩体塑形和蠕变破坏的特征。
因而在岩体力学中远不如Mohr-Coulomb 强度理论应用广泛。
西安交通大学俞茂宏[5-6]教授在沙土和破碎岩体承载力的研究中,首次提出并逐渐完善的强度理论,与Mohr-Coulomb 强度理论相比,他认为除了作用于岩体的最大应力摩尔圆τ13对岩体的破坏有影响外,其他2个主剪应力(τ23和τ12)及其作用面上的正应力对岩体破坏有影响。
图1双曲线型破坏准则图2抛物线型破坏准则3.2基于经验的强度准则1980 年E. Hoek 和E. T. Brown 通过对几百组岩石三轴试验资料和大量现场岩体试验成果的统计分析,结合岩石性状方面的理论研究成果和实践检验,提出了迄今为止应用最为广泛、影响最大的岩石强度准则——Hoek-Brown(HOEK -BROWN)强度准则。
HOEK -BROWN强度准则直接来源于大量的实验数据,因此比较接近实际生产中。
易于理解,很受欢迎。
其表达式为:其中m i为反映岩体强度的参数。
取值范围为0.001到25 E Hoke结合工程经验和实验室试验给出的m i的取值范围如表1示。
表1不同岩石的Mi值4.HOEK -BROWN强度理论的完善多年来,经过大量研究人员的不断发展和完善,形成了较为完整的体系。
HOEK -BROWN强度准则可以应用于岩石和岩体,参数可通过常规室内试验、矿物组成和不连续面描述获取。
HOEK -BROWN强度准则可以反映岩石和岩体固有的非线性破坏特点,以及结构面、应力状态对强度的影响,能够解释低应力区、拉应力区和最小主应力对强度的影响,并可适用于各向异性岩体的描述等。
[7]。
HOEK -BROWN强度准则已广泛地应用于大型边坡、长大隧洞、复杂地质条件的地基基础、水电大坝、能源开采等几乎覆盖国计民生的各个方面。
HOEK -BROWN准则在实际应用中也存在比较严重的缺陷。
主要表现在对中间应力考虑不足,对于存在一组主要节理的,表现出明显各向异性的岩体,不能很好地表现出其真实力学特性。
1992 年E. Hoek 等对HOEK -BROWN强度准则进行了改进,使其可同时应用于岩石和岩体,称之为广义HOEK -BROWN岩体强度准则[7]。
其表达式为:其中,m b,a 为针对不同岩体的量纲一的经验参数,s 反映岩体破碎程度,取值范围0.0~1.0,对于完整的岩体(即岩石),s = 1.0。
广义HOEK -BROWN岩体强度准则在原准则的基础上引入参数s,a,以适用于质量较差的岩体,特别是在低应力条件下。
1992 年提出的广义HOEK -BROWN岩体强度准则使得该准则的研究对象从岩石转向具有实际意义的工程岩体。
5.对HOEK -BROWN准则的修正长期以来,大量的国内外学者倾注大量心血,对Hoek-Brown强度准则进行了大量的修正工作。
去的了巨大的进展。
但是经过修正的HOEK -BROWN强度准则仍然假定岩体示各向同性的,这与实际情况中土体,十分完整或十分破碎的岩体比较接近,但当岩体中含有有限组节理。
或者某组节理表现出明显优势是,岩体将会呈现出明显的各向异性,此时岩体的破坏可能将不会沿着最大应力面,而是沿着节理面发生滑动,HOEK -BROWN准则将会发生明显的偏差。
满足各向异性岩体的强度特征,对完善HOEK -BROWN强度理论有着至关重要的作用。
5.1.考虑岩体各向异性的HOEK -BROWN准则修正对于各向异性岩体,通过分别确定岩石和节理面的参数,以反映岩体的各向异性E. Hoek提出基于单弱面理论的解决方法,采用 2 组参数分别反映岩石和节理面,通过试运算确定破坏是由岩石或节理面承担,从而确定各向异性岩体的强度。
宋建波[8]引入经验参数σc,并推导出σ3存在的条件下岩体强度的计算公式,假定节理面滑动破坏遵循Coulomb公式的结构面强度理论,基于简化的Hoek 方法,引用试验数据验证了其可行性。
