中考数学复习专题4-几何小综合多结论选择

初中数学中考复习第3关多结论的几何及二次函数问题为背景的选择填空题(原卷版)

第3关多结论的几何及二次函数问题为背景的选择填空题【考查知识点】以多结论的几何图形为背景的选择填空题题，主要考察了学生对三角形、四边形、圆知识的综合运用能力；以二次函数为背景的选择填空题，主要考察了二次函数的性质及二次函数系数与图象的关系。

【解题思路】1.以多结论的几何图形为背景的选择填空题题中，用“全等法”和“相似法”证题应该是两个基本方法，为了更好掌握这两种方法，应该熟悉一对全等或一对相似三角形的基本图形，下图中是全等三角形的基本图形。

大量积累基本图形，并在此基础上“截长补短”，“能割善补”，是学习几何图形的一个诀窍，每一个重要概念，重要定理都有一个基本图形，三线八角可以算做一个基本图形.2. 以二次函数为背景的选择填空题中，根据图象的位置确定a 、b 、c 的符号，a ＞0开口向上，a ＜0开口向下．抛物线的对称轴为x=2ba-，由图像确定对称轴的位置，由a 的符号确定出b 的符号．由x=0时,y=c ，知c 的符号取决于图像与y 轴的交点纵坐标，与y 轴交点在y 轴的正半轴时，c ＞0，与y 轴交点在y 轴的负半轴时，c ＜0．确定了a 、b 、c 的符号，易确定abc 的符号；根据对称轴确定a 与b 的关系；根据图象还可以确定△的符号，及a+b+c 和a -b+c 的符号。

【典型例题】【例1】（2019·新疆中考真题）如图，正方形ABCD 的边长为2，点E 是BC 的中点，AE 与BD 交于点P ，F 是CD 上的一点，连接AF 分别交BD ，DE 于点M ，N ，且AF ⊥DE ，连接PN ，则下列结论中:①4ABMFDM SS=；②PN =；③tan ∠EAF=34；④.PMN DPE ∽正确的是（）A ．①②③B ．①②④C ．①③④D ．②③④【名师点睛】此题考查三角函数，相似三角形的判定与性质，全等三角形的判定与性质，正方形的性质难度较大，解题关键在于综合掌握各性质【例2】（2019·湖北中考真题）抛物线2y ax bx c =++的对称轴是直线1x =-，且过点（1，0）.顶点位于第二象限，其部分图像如图所示，给出以下判断： ①0ab >且0c <； ②420a b c -+>； ③8>0+a c ； ④33c a b =-；⑤直线22y x =+与抛物线2y ax bx c =++两个交点的横坐标分别为12x x 、，则12125x x x x ++⋅=-.其中正确的个数有( )A ．5个B ．4个C ．3个D ．2个【名师点睛】本题考查了二次函数图象与系数的关系：对于二次函数y=ax 2+bx+c （a≠0），当a>0时，抛物线向上开口；当a<0时，抛物线向下开口；一次项系数b 和二次项系数a 共同决定对称轴的位置：当a 与b 同号时（即ab>0），对称轴在y 轴左侧；当a 与b 异号时（即ab<0），对称轴在y 轴右侧；常数项c 决定抛物线与y 轴交点，抛物线与y 轴交于（0，c ）；抛物线与x 轴交点个数由△决定：△=b 2-4ac>0时，抛物线与x 轴有2个交点；△=b 2-4ac=0时，抛物线与x 轴有1个交点；△=b 2-4ac<0时，抛物线与x 轴没有交点．【例3】（2019·辽宁中考真题）如图，正方形ABCD 和正方形CGFE 的顶点C ，D ，E 在同一条直线上，顶点B ，C ，G 在同一条直线上．O 是EG 的中点，∠EGC 的平分线GH 过点D ，交BE 于点H ，连接FH 交EG 于点M ，连接OH ．以下四个结论：①GH ⊥BE ；②△EHM ∽△GHF；③BCCG =﹣1；④HOM HOGS S ＝2）A．①②③B．①②④C．①③④D．②③④【名师点睛】本题考查了正方形的性质，以及全等三角形的判定与性质，相似三角形的判定与性质，正确求得两个三角形的边长的比是解决本题的关键．【例4】（2018·广西中考真题）如图，抛物线y=14（x+2）（x﹣8）与x轴交于A，B两点，与y轴交于点C，顶点为M，以AB为直径作⊙D．下列结论：①抛物线的对称轴是直线x=3；②⊙D的面积为16π；③抛物线上存在点E，使四边形ACED为平行四边形；④直线CM与⊙D相切．其中正确结论的个数是（）A．1B．2C．3D．4【名师点睛】本题考查了二次函数与圆的综合题，涉及到抛物线的对称轴、圆的面积、平行四边形的判定、待定系数法、两直线垂直、切线的判定等，综合性较强，有一定的难度，运用数形结合的思想灵活应用相关知识是解题的关键.【方法归纳】1.多结论的几何选择填空题考查的知识点较多，如相似三角形的判定与性质、等腰直角三角形的性质、平行线的性质、直角三角形的性质、四边形的知识、圆的知识、等腰三角形的判定与性质以及特殊角三角函数等知识．这类题目的综合性很强，难度较大，解题的关键是注意数形结合思想的应用．2. 多结论的二次函数选择题主要考查了二次函数图象与系数的关系．二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定．数形结合思想贯穿这类题目的始终，解题时应时时注意.【针对练习】1.（2018·四川中考真题）如图，在矩形ABCD 中，E 是AB 边的中点，沿EC 对折矩形ABCD ，使B 点落在点P 处，折痕为EC ，连结AP 并延长AP 交CD 于F 点，连结CP 并延长CP 交AD 于Q 点．给出以下结论：①四边形AECF 为平行四边形； ②∠PBA=∠APQ ； ③△FPC 为等腰三角形； ④△APB ≌△EPC ；其中正确结论的个数为（）A ．1B ．2C ．3D ．42.（2018·辽宁中考真题）已知抛物线y=ax 2+bx+c （0＜2a≤b ）与x 轴最多有一个交点．以下四个结论： ①abc ＞0；②该抛物线的对称轴在x=﹣1的右侧； ③关于x 的方程ax 2+bx+c+1=0无实数根； ④a b cb++≥2．其中，正确结论的个数为（） A ．1个B ．2个C ．3个D ．4个3．（2019·四川中考真题）如图，在正方形ABCD 的对角线AC 上取一点E ．使得15CDE ︒∠=，连接BE 并延长BE 到F ，使CF CB =，BF 与CD 相交于点H ，若1AB =，有下列结论：①BE DE =；②CE DE EF +=；③14DEC S ∆=-；④1DH HC =-．则其中正确的结论有（）A ．①②③B ．①②③④C ．①②④D ．①③④4．（2019·广西中考真题）如图，E 是正方形ABCD 的边AB 的中点，点H 与B 关于CE 对称，EH 的延长线与AD 交于点F ，与CD 的延长线交于点N ，点P 在AD 的延长线上，作正方形DPMN ，连接CP ，记正方形ABCD ，DPMN 的面积分别为1S ，2S ，则下列结论错误的是（）A ．212S S CP +=B ．2AF FD =C ．4CD PD = D ．3cos 5HCD ∠=5．（2019·山东中考真题）如图，在正方形ABCD 中，E 、F 分别是BC 、CD 上的点，且∠EAF ＝45°，AE 、AF 分别交BD 于M 、N ，连按EN 、EF 、有以下结论：①AN ＝EN ，②当AE ＝AF 时，BEEC＝2，③BE+DF ＝EF ，④存在点E 、F ，使得NF ＞DF ，其中正确的个数是（）A ．1B ．2C ．3D ．46．（2019·黑龙江中考真题）如图，在正方形ABCD 中，E F 、是对角线AC 上的两个动点，P 是正方形四边上的任意一点，且42AB EF ＝，＝，设AE x ＝．当PEF 是等腰三角形时，下列关于P 点个数的说法中，一定正确的是（）①当0x ＝（即E A 、两点重合）时，P 点有6个②当02x ＜＜时，P 点最多有9个③当P 点有8个时，x ＝﹣2④当PEF 是等边三角形时，P 点有4个 A ．①③B ．①④C ．②④D ．②③7．（2019·广东中考真题）如图，正方形ABCD 的边长为4，延长CB 至E 使2EB =，以EB 为边在上方作正方形EFGB ，延长FG 交DC 于M ，连接AM 、AF ，H 为AD 的中点，连接FH 分别与AB 、AM 交于点N 、K .则下列结论：①ANH GNF ∆≅∆；②AFN HFG ∠=∠；③2FN NK =；④:1:4AFN ADM S S ∆∆=.其中正确的结论有( )A ．1个B ．2个C ．3个D ．4个8．（2019·湖北中考真题）如图所示，已知二次函数2y ax bx c =++的图象与x 轴交于,A B 两点，与y 轴交于点C ，OA OC =，对称轴为直线1x =，则下列结论：①0abc <；②11024a b c ++=；③10ac b -+=；④2c +是关于x 的一元二次方程20ax bx c ++=的一个根．其中正确的有（）A ．1个B ．2个C ．3个D ．4个9．（2018·黑龙江中考真题）抛物线()2y ax bx c a 0=++≠的部分图象如图所示，与x 轴的一个交点坐标为()4,0，抛物线的对称轴是x 1.=下列结论中：abc 0>①；2a b 0+=②；③方程2ax bx c 3++=有两个不相等的实数根；④抛物线与x 轴的另一个交点坐标为()2,0-；⑤若点()A m,n 在该抛物线上，则2am bm c a b c ++≤++．其中正确的有( )A ．5个B ．4个C ．3个D ．2个10．（2018·黑龙江中考真题）如图，平行四边形ABCD 的对角线AC 、BD 相交于点O ，AE 平分∠BAD ，分别交BC 、BD 于点E 、P ，连接OE ，∠ADC=60°，AB=12BC=1，则下列结论：①∠CAD=30°②③S 平行四边形ABCD =AB•AC ④OE=14AD ⑤S △APO =12，正确的个数是（）A ．2B ．3C ．4D ．511．（2018·山东中考真题）如图，在矩形ABCD 中，∠ADC 的平分线与AB 交于E ，点F 在DE 的延长线上，∠BFE=90°，连接AF 、CF ，CF 与AB 交于G ，有以下结论： ①AE=BC ②AF=CF ③BF 2=FG•FC ④EG•AE=BG•AB其中正确的个数是（）A ．1B ．2C ．3D ．412．（2019·四川中考真题）二次函数2(0)y ax bx c a =++≠的部分图象如图所示，图象过点(1,0)-，对称轴为直线x ＝1，下列结论：①0abc ＜；②b c ＜；③30a c +=；④当0y ＞时，13x -＜＜其中正确的结论有（）A ．1个B ．2个C ．3个D ．4个13．（2019·山东中考真题）如图，正方形ABCD ，点F 在边AB 上，且:1:2AF FB =，CE DF ⊥，垂足为M ，且交AD 于点E ，AC 与DF 交于点N ，延长CB 至G ，使12BG BC =，连接CM ．有如下结论：①DE AF =；②4AN AB =；③ADF GMF ∠=∠；④:1:8ANF CNFB S S ∆=四边形．上述结论中，所有正确结论的序号是（）A ．①②B ．①③C ．①②③D ．②③④14．（2018·湖北中考真题）如图，在四边形ABCD 中，AB=AD=5，BC=CD 且BC ＞AB ，BD=8．给出以下判断：①AC 垂直平分BD ；②四边形ABCD 的面积S=AC•BD ；③顺次连接四边形ABCD 的四边中点得到的四边形可能是正方形； ④当A ，B ，C ，D 四点在同一个圆上时，该圆的半径为256； ⑤将△ABD 沿直线BD 对折，点A 落在点E 处，连接BE 并延长交CD 于点F ，当BF ⊥CD 时，点F 到直线AB 的距离为678125．其中正确的是_____．（写出所有正确判断的序号）15．（2019·广西中考真题）我们定义一种新函数：形如2y ax bx c =++（0a ≠，且240b a ->）的函数叫做“鹊桥”函数．小丽同学画出了“鹊桥”函数y=|x 2-2x -3|223y x x =--的图象（如图所示），并写出下列五个结论：①图象与坐标轴的交点为()1,0-，()3,0和()0,3；②图象具有对称性，对称轴是直线1x =；③当11x -≤≤或3x ≥时，函数值y 随x 值的增大而增大；④当1x =-或3x =时，函数的最小值是0；⑤当1x =时，函数的最大值是4．其中正确结论的个数是______.16．（2018·新疆中考真题）如图，已知抛物线y 1=﹣x 2+4x 和直线y 2=2x ．我们规定：当x 取任意一个值时，x 对应的函数值分别为y 1和y 2，若y 1≠y 2，取y 1和y 2中较小值为M ；若y 1=y 2，记M=y 1=y 2．①当x ＞2时，M=y 2；②当x ＜0时，M 随x 的增大而增大；③使得M 大于4的x 的值不存在；④若M=2，则x=1．上述结论正确的是_____（填写所有正确结论的序号）．17．（2018·黑龙江中考真题）如图，抛物线y=ax 2+bx+c （a≠0）的对称轴为直线x=﹣1，下列结论中： ①abc ＜0；②9a ﹣3b+c ＜0；③b 2﹣4ac ＞0；④a ＞b ，正确的结论是_____（只填序号）18．（2019·湖南中考真题）如图，函数ky x=(k 为常数，k ＞0)的图象与过原点的O 的直线相交于A ，B 两点，点M 是第一象限内双曲线上的动点（点M 在点A 的左侧），直线AM 分别交x 轴，y 轴于C ，D 两点，连接BM 分别交x 轴，y 轴于点E ，F ．现有以下四个结论：①△ODM 与△OCA 的面积相等；②若BM ⊥AM于点M ，则∠MBA ＝30°；③若M 点的横坐标为1，△OAM 为等边三角形，则2k =④若25MF MB =，则MD ＝2MA ．其中正确的结论的序号是_______．19．（2019·辽宁中考真题）如图，点P 是正方形ABCD 的对角线BD 延长线上的一点，连接PA ，过点P 作PE ⊥PA 交BC 的延长线于点E ，过点E 作EF ⊥BP 于点F ，则下列结论中：①PA ＝PE ；②CE PD ；③BF ﹣PD ＝12BD ；④S △PEF ＝S △ADP ，正确的是___（填写所有正确结论的序号）20．（2019·内蒙古中考真题）如图，在Rt ABC ∆中，90,3,ABC BC D ︒∠==为斜边AC 的中点，连接BD ，点F 是BC 边上的动点（不与点B C 、重合），过点B 作BE BD ⊥交DF 延长线交于点E ，连接CE ，下列结论：①若BF CF =，则222CE AD DE +=；②若,4BDE BAC AB ∠=∠=，则158CE =； ③ABD ∆和CBE ∆一定相似；④若30,90A BCE ︒︒∠=∠=，则DE =其中正确的是_____．（填写所有正确结论的序号）21．（2018·湖北中考真题）如图，已知∠MON=120°，点A ，B 分别在OM ，ON 上，且OA=OB=a ，将射线OM 绕点O 逆时针旋转得到OM′，旋转角为α（0°＜α＜120°且α≠60°），作点A 关于直线OM′的对称点C ，画直线BC 交OM′于点D ，连接AC ，AD ，有下列结论：①AD=CD ；②∠ACD 的大小随着α的变化而变化；③当α=30°时，四边形OADC 为菱形；④△ACD a 2；其中正确的是_____．（把你认为正确结论的序号都填上）．。

人教版中考数学中考压轴题突破一、选填题压轴题突破重难点突破六多结论选填题

B．②④
C．③④
D．②③
3．★(2022·广元)二次函数y＝ax2＋bx＋c(a≠0)的部分图象如图所
示，图象过点(－1, 0)，对称轴为直线x＝2，下列结论：①abc<0；② 1
4a＋c>2b；③ 3b－ 2c>0；④若点A(－2，y1)，点B －2，y2 ，点 7
C 2，y3 在该函数图象上，则y1<y3<y2；⑤ 4a＋2b≥m (am＋b) (m为常数)．
2．(2022·临沂)二次函数y＝ax2＋bx＋c (a≠0)的部分图象如图所示，
1 其对称轴为直线x＝－ 2 ，且与x轴的一个交点坐标为(－2，0)．下列结
论：①abc>0；②a＝b；③2a＋c＝0；④关于x的一元二次方程ax2＋bx＋
c－1＝0有两个相等的实数根．其中正确结论的序号是
( D)
A．①③
其中正确的结论有 A．5个 B．4个 C．3个 D．2个
(C)
4．★(2021·荆门)抛物线y＝ax2＋bx＋c(a，b，c为常数)开口向下且过
点A(1，0)，B(m，0)(－2<m<－1)，下列结论：① 2b＋c>0；② 2a＋
c<0；③ a(m＋1)－b＋c>0；④若方程a(x－m)(x－1)－1＝0有两个不等
对称轴x＝－
b 2a
＝1，得b＝－2a，∴y＝ax2－
2ax－1,
确当x＝－1时，
y>0，∴aa＋＋2a2－a－1>0, 1
11 ∴a>33
，故②正正确；当m＝1时，m(am＋b)＝确
aa＋＋b，故③错错误；∵点(－2, y1)到对称轴的距离大大于点(2, y3)到

正方形选择题(中考压轴多结论)

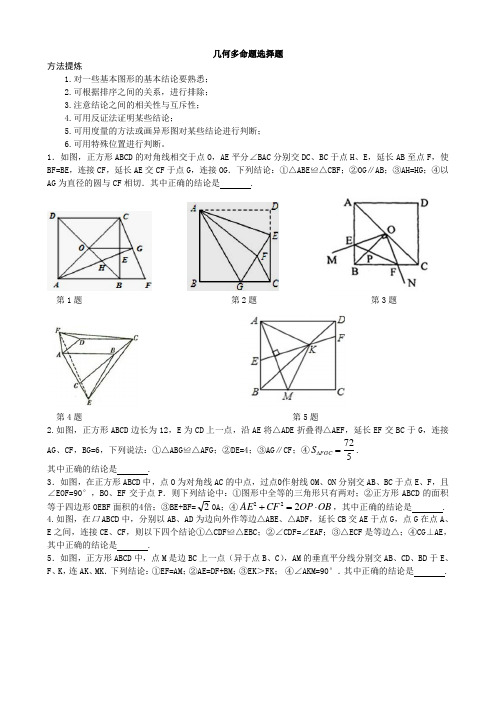
几何多命题选择题方法提炼1.对一些基本图形的基本结论要熟悉；2.可根据排序之间的关系，进行排除；3.注意结论之间的相关性与互斥性；4.可用反证法证明某些结论；5.可用度量的方法或画异形图对某些结论进行判断；6.可用特殊位置进行判断。

1．如图，正方形ABCD 的对角线相交于点O ，AE 平分∠BAC 分别交DC 、BC 于点H 、E ，延长AB 至点F ，使BF=BE ，连接CF ，延长AE 交CF 于点G ，连接OG ．下列结论：①△ABE≌△CBF；②OG∥AB；③AH=HG；④以AG 为直径的圆与CF 相切．其中正确的结论是 .第1题第2题第3题第4题第5题2.如图，正方形ABCD 边长为12，E 为CD 上一点，沿AE 将△ADE 折叠得△AEF，延长EF 交BC 于G ，连接AG 、CF ，BG=6，下列说法：①△ABG≌△AFG；②DE=4；③AG∥CF；④572=∆FGC S . 其中正确的结论是 .3．如图，在正方形ABCD 中，点O 为对角线AC 的中点，过点0作射线OM 、ON 分别交AB 、BC 于点E 、F ，且∠EOF=90°，BO 、EF 交于点P ．则下列结论中：①图形中全等的三角形只有两对；②正方形ABCD 的面积等于四边形OEBF 面积的4倍；③BE+BF=20A ；④OB OP CF AE ⋅=+222，其中正确的结论是 .4.如图，在口ABCD 中，分别以AB 、AD 为边向外作等边△ABE、△ADF，延长CB 交AE 于点G ，点G 在点A 、E 之间，连接CE 、CF ，则以下四个结论①△CDF≌△EBC；②∠CDF=∠EAF；③△ECF 是等边△；④CG⊥AE，其中正确的结论是 .5．如图，正方形ABCD 中，点M 是边BC 上一点（异于点B 、C ），AM 的垂直平分线分别交AB 、CD 、BD 于E 、F 、K ，连AK 、MK ．下列结论：①EF=AM；②AE=DF+BM；③EK＞FK ； ④∠AKM=90°．其中正确的结论是 .第6题第7题第8题6.如图，正方形ABCD 中，P 为对角线上的点，PB=AB ，连PC ，作CE⊥CP 交AP 的延长线于E ，AE 交CD 于F ，交BC 的延长线于G ，则下列结论：①E 为FG 的中点；②CD CF FG ⋅=42；③AD=DE；④CF=2DF．其中正确的结论是 .7.如图，已知四边形ABCD 是四个角都是直角，四条边都相等的正方形，点E 在BC 上，且BC CE 41=，点F 是CD 的中点，延长AF 与BC 的延长线交于点M ．以下结论：①AB=CM；②AE=AB+CE；③ABCF AEF S S 四边形41=∆；④∠AFE=90°，其中正确的结论是 .8.如图，在正方形ABCD 中，对角线AC 、BD 交于点O ，BE 平分∠DBC，交DC 于点E ，延长BC 到点F ，使CF=CE ，连接DF ，交BE 的延长线于点G ，AC 交BG 于点H ，连接OG ，下列结论：①OG∥AD；②△CHE 为等腰三角形；③BH=GH；④tan∠F=2；⑤2:1:=∆∆BDE BCE S S 其中正确的结论是 .9.如图，在边长为1的正方形ABCD 中，E 为AD 边上一点，连接BE ，将ABE 沿BE 对折，A 点恰好落在对角线BD 上的点F 处．延长AF ，与CD 边交于点G ，延长FE ，与BA 的延长线交于点H ，则下列说法：①BFH 为等腰直角三角形；②ADF FHA ≅；③60DFG ∠=︒；④22DE =-；⑤S AEF S DFG =．其中正确的结论是 .第9题第10题10.如图，正方形ABCD 中，M 为BC 上一点，且13BM BC =．△AMN 为等腰直角三角形，斜边AN 与CD 交于点F ，延长AN 与BC 的延长线交于点E ，连接MF 、CN ，作NG⊥BE，垂足为G ，下列结论：①ABM MGN ≅；②△CNG 为等腰直角三角形；③MN=EN；④S ABM S CEN =；⑤BM+DF=MF．其中正确的的结论为 .11.如图，正方形ABCD 中，点E 是对角线BD 上一点，点F 是边BC 上一点，点G 是边CD 上一点，BE=2ED ，CF=2BF ，连接AE 并延长交CD 于G ，连接AF 、EF 、FG ．给出下列五个结论：①DG=GC ；②∠FGC=∠AGF；③S△ABF=S△FCG；④2AF EF =；⑤∠AFB=∠AEB．其中正确结论结论是 . 12.如图，在正方形ABCD 中，E 为AD 的中点，DF ⊥CE 于M ，交AC 于点N ，交AB 于点F ，连接EN 、BM ．有如下结论：①△ADF ≌△DCE ；②MN=FN ；③CN=2AN ；④ADN CNFB SS 25=四边形：：⑤∠ADF=∠BMF ．其中正确的结论为 .第11题第12题第13题14.如图，把矩形纸片ABCD 沿EF 折叠，使点B 落在AD 边上的点B ′处，点A 落在点A ′处．设AE=a ，AB=b ，BF=c ，下列结论：①B ′E=BF ；②四边形B ′CFE 是平行四边形；③a 2+b 2=c 2；④△A ′B ′E ∽△B ′CD ；其中正确的是 .15.如图，在正方形ABCD 中，AB=1，E ，F 分别是边BC ，CD 上的点，连接EF 、AE 、AF ，过A 作AH⊥EF 于点H. 若EF=BE+DF ，那么下列结论：①AE 平分∠BEF；②FH=FD；③∠EAF=45°；④EAF ABE ADF S S S ∆∆∆=+；⑤△CEF 的周长为2.其中正确的结论是 .第14题第15题第16题16.如图，正方形ABCD 中，E 是AD 的中点，连接BE 、CE ，点F 是CE 的中点，连接DF 、BF ，点M 是BF 上一点且21=MF BM ，过点M 做BC MN ⊥于点N ，连接FN .下列结论中①CE BE =；②DFE BEF ∠=∠；③AB MN 61=；④61=∆EBNF FMN S S 四边形其中正确的结论是： .17.如图，正方形ABCD 中，O 为BD 中点，以BC 为边向正方形内作等边△BCE，连接并延长AE 交CD 于F ，连接BD 分别交CE 、AF 于G 、H ，下列结论：①∠CEH=45°；②GF∥DE；③2OH+DH=BD；④2BG DG =；⑤31:BEC BGC S S ∆∆+=．其中正确的结论是 .第17题第18题第19题18.如图，在正方形ABCD中，对角线AC、BD交于点O，BE平分∠DBC，交DC于点E，延长BC到点F，使CF=CE，连接DF，交BE的延长线于点G，AC交BG于点H，连接OG，下列结论：①OG∥AD；②△CHE为等腰三角形；③BH=GH；④tan∠F=2；⑤2BCEBDESS∆∆=其中正确的结论有（）19.如图，将矩形ABCD的一个角翻折，使得点D恰好落在BC边上的点G处，折痕为EF，若EB为∠AEG的平分线，EF和BC的延长线交于点H．下列结论中：①∠BEF=90°；②DE=CH；③BE=EF；④△BEG和△HEG的面积相等；⑤若CD2AD=，则BG5BC6=．以上命题，正确的有的 .20.如图，在正方形ABCD中，E是BC的中点，F是CD上一点，AE⊥EF，有下列结论：①∠BAE=30°；②S△ABE=4S△ECF；③13CF CD=；④△ABE∽△AEF．正确结论的结论为 .第20题第21题21.如图，在正方形ABCD中，对角线AC、BD交于点D，CE平分∠ACD，分别交AD、BD于E、G，EF∥AC交CD于F，连接OE，下列结论：①EF AE=，②AOE AEO∠=∠，③1OG AE2=；④ACE DCES2S∆∆=；⑤AB(21)DG=．其中正确的是 .。

中考数学复习专题：几何综合题（含答案解析）

中考数学复习专题：⼏何综合题（含答案解析）⼏何综合题1.已知△ABC 中，AD 是BAC ∠的平分线，且AD =AB ，过点C 作AD 的垂线，交 AD 的延长线于点H ．（1）如图1，若60BAC ∠=?①直接写出B ∠和ACB ∠的度数；②若AB =2，求AC 和AH 的长；（2）如图2，⽤等式表⽰线段AH 与AB +AC 之间的数量关系，并证明．答案：（1）①75B ∠=?，45ACB ∠=?；②作DE ⊥AC 交AC 于点E .Rt △ADE 中，由30DAC ∠=?，AD=2可得DE =1，AE 3=. Rt △CDE 中，由45ACD ∠=?，DE=1，可得EC =1. ∴AC 31=.Rt △ACH 中，由30DAC ∠=?，可得AH 33+=；（2）线段AH 与AB +AC 之间的数量关系：2AH =AB +AC证明：延长AB 和CH 交于点F ，取BF 中点G ，连接GH .易证△ACH ≌△AFH .∴AC AF =,HC HF =. ∴GH BC ∥. ∵AB AD =，∴ ABD ADB ∠=∠. ∴ AGH AHG ∠=∠ . ∴ AG AH =.∴()2222AB AC AB AF AB BF AB BG AG AH +=+=+=+==.2.正⽅形ABCD 的边长为2，将射线AB 绕点A 顺时针旋转α，所得射线与线段BD 交于点M ，作CE AM ⊥于点E ，点N 与点M 关于直线CE 对称，连接CN ．（1）如图1，当045α?<②⽤等式表⽰NCE ∠与BAM ∠之间的数量关系：__________．（2）当4590α?<CDBA图1备⽤图C DBAM答案：（1）①补全的图形如图7所⽰．（2）当45°<α<90°时，=1802NCE BAM ∠?-∠．证明：如图8，连接CM ，设射线AM 与CD 的交点为H ．∵四边形ABCD 为正⽅形，∴∠BAD=∠ADC=∠BCD=90°，直线BD为正⽅形ABCD的对称轴，点A与点C关于直线BD对称．∵射线AM与线段BD交于点M，∴∠BAM=∠BCM=α．-．∴∠1=∠2=90α∵CE⊥AM，∴∠CEH=90°，∠3+∠5=90°．⼜∵∠1+∠4=90°，∠4=∠5，∴∠1=∠3．-．∴∠3=∠2=90α∵点N与点M关于直线CE对称，-∠．∴∠NCE=∠MCE=∠2+∠3=1802BAM（313. 如图，已知60AOB ∠=?，点P 为射线OA 上的⼀个动点，过点P 作PE OB ⊥，交OB 于点E ，点D 在AOB ∠内，且满⾜DPA OPE ∠=∠，6DP PE +=. （1）当DP PE =时，求DE 的长；（2）在点P 的运动过程中，请判断是否存在⼀个定点M ，证明你的判断.答案：（1）作PF ⊥DE 交DE 于F . ∵PE ⊥BO ，60AOB ∠=o，∴30OPE ∠=o.∴30DPA OPE ∠=∠=o.∴120EPD ∠=o∴cos30DF PD =??=∴2DE DF ==（2）当M 点在射线OA 上且满⾜OM =DMME的值不变，始终为1.理由如下：当点P 与点M 不重合时，延长EP 到K 使得PK PD =.∵,DPA OPE OPE KPA ∠=∠∠=∠,∴KPA DPA ∠=∠. ∴KPMDPM ∠=∠.∵PK PD =,PM 是公共边, ∴KPM △≌DPM △. ∴MKMD =.作ML ⊥OE 于L ,MN ⊥EK 于N . ∵3,60MO MOL =∠=o，∴sin 603ML MO =?=o.∵PE ⊥BO ,ML ⊥OE ,MN ⊥EK ，∴四边形MNEL 为矩形. ∴3EN ML ==.∵6EK PE PK PE PD =+=+=, ∴EN NK =. ∵MN ⊥EK , ∴MKME =.∴ME MKMD ==,即1DMME=. 当点P 与点M 重合时，由上过程可知结论成⽴.4. 如图，在菱形ABCD 中，∠DAB =60°，点E 为AB 边上⼀动点（与点A ，B 不重合），连接CE ，将∠ACE 的两边所在射线CE ，CA 以点C 为中⼼，顺时针旋转120°，分别交射线AD 于点F ，G. （1）依题意补全图形；（2）若∠ACE=α，求∠AFC 的⼤⼩（⽤含α的式⼦表⽰）；（3）⽤等式表⽰线段AE 、AF 与CG 之间的数量关系，并证明．答案：（1）补全的图形如图所⽰.（2）解：由题意可知，∠ECF=∠ACG=120°.∴∠FCG=∠ACE=α.∵四边形ABCD 是菱形，∠DAB=60°，∴∠DAC=∠BAC= 30°. ∴∠AGC=30°. ∴∠AFC =α+30°.证明：作CH ⊥AG 于点H.由（2）可知∠BAC=∠DAC=∠AGC=30°.∴CA=CG. ∴HG =21AG. ∵∠ACE =∠GCF ，∠CAE =∠CGF ，∴△ACE ≌△GCF. ∴AE =FG .在Rt △HCG 中， .23cos CG CGH CG HG =∠?= ∴AG =3CG .即AF+AE =3CG .5.如图，Rt △ABC 中，∠ACB = 90°，CA = CB ，过点C 在△ABC 外作射线CE ，且∠BCE = α，点B 关于CE 的对称点为点D ，连接AD ，BD ，CD ，其中AD ，BD 分别交射线CE 于点M ，N . （1）依题意补全图形；（2）当α= 30°时，直接写出∠CMA 的度数；（3）当0°<α< 45°时，⽤等式表⽰线段AM ，CN 之间的数量关系，并证明．答案：（1）如图；ABCE（2）45°；（3）结论：AM CN．证明：作AG⊥EC的延长线于点G．∵点B与点D关于CE对称，∴CE是BD的垂直平分线．∴CB=CD．∴∠1=∠2=α．∵CA=CB，∴CA=CD．∴∠3=∠CAD．∵∠4=90°，∴∠3=12（180°-∠ACD）=12（180°-90°-α-α）=45°-α．∵∠4=90°，CE是BD的垂直平分线，∴∠1+∠7=90°，∠1+∠6=90°．∴∠6=∠7．∵AG⊥EC，∴∠G=90°=∠8．∴在△BCN和△CAG中，∠8=∠G，∠7=∠6，BC=CA，∴△BCN≌△CAG．∴CN=AG．∵Rt△AMG中，∠G=90°，∠5=45°，∴AM AG．∴AM CN．6.在正⽅形ABCD中，M是BC边上⼀点，点P在射线AM上，将线段AP绕点A顺时针旋转90°得到线段AQ，连接BP，DQ．（1）依题意补全图1；答案：（1）补全图形略（2）①证明：连接BD ，如图2，∵线段AP 绕点A 顺时针旋转90°得到线段AQ ，∴AQ AP =，90QAP ∠=°．∵四边形ABCD 是正⽅形，∴AD AB =，90DAB ∠=°．∴12∠=∠．∴△ADQ ≌△ABP ．∴DQ BP =，3Q ∠=∠．∵在Rt QAP ?中，90Q QPA ∠+∠=°，∴390BPD QPA ∠=∠+∠=°．∵在Rt BPD ?中，222DP BP BD +=，⼜∵DQ BP =，222BD AB =，∴2222DP DQ AB +=．②BP AB =．7.如图，在等腰直⾓△ABC 中，∠CAB=90°，F 是AB 边上⼀点，作射线CF ，过点B 作BG ⊥C F 于点G ，连接AG ．（1）求证：∠ABG =∠ACF ；（2）⽤等式表⽰线段C G ，AG ，BG 之间∵∠CAB=90°. ∵ BG ⊥CF 于点G ，∴∠BGF =∠CAB =90°. ∵∠GFB =∠CFA . ∴∠ABG =∠ACF .（2）CG =2AG +BG .证明：在CG 上截取CH =BG ，连接AH ，∵△ABC 是等腰直⾓三⾓形，∴∠CAB =90°，AB =AC . ∵∠ABG =∠ACH . ∴△ABG ≌△ACH . ∴ AG =AH ,∠GAB =∠HAC . ∴∠GAH =90°. ∴ 222AG AH GH +=. ∴ GH =2AG . ∴ CG =CH +GH =2AG +BG .8.如图，在正⽅形ABCD 中，E 是BC 边上⼀点，连接AE ，延长CB ⾄点F ，使BF=BE ，过点F 作FH ⊥AE 于点H ，射线FH 分别交AB 、CD 于点M 、N ，交对⾓线AC 于点P ，连接AF ．（1）依题意补全图形；（2）求证：∠FAC =∠APF ；（3）判断线段FM 与PN 的数量关系，并加以证明．答案：（1）补全图如图所⽰．（2）证明∵正⽅形ABCD ，∴∠BAC =∠BCA =45°，∠ABC =90°，∴∠PAH =45°-∠BAE ．∵FH ⊥AE ．EDCBAM H PDAC∴∠APF=45°+∠BAE．∵BF=BE，∴AF=AE，∠BAF=∠BAE．∴∠FAC=45°+∠BAF．∴∠FAC=∠APF．（3）判断：FM=PN．证明：过B作BQ∥MN交CD于点Q，∴MN=BQ，BQ⊥AE．∵正⽅形ABCD，∴AB=BC，∠ABC=∠BCD=90°．∴∠BAE=∠CBQ．∴△ABE≌△BCQ．∴AE=BQ．∴AE=MN．∵∠FAC=∠APF，∴FP=MN．∴FM=PN．9.如图所⽰，点P位于等边ABC△的内部，且∠ACP=∠CBP．(1) ∠BPC的度数为________°；(2) 延长BP⾄点D，使得PD=PC，连接AD，CD．①依题意，补全图形；②证明：AD+CD=BD；(3)在(2)的条件下，若BD的长为2，求四边形ABCD的⾯积．M HPD AC解：(1)120°. ----------------------------2分(2)①∵如图1所⽰.②在等边ABC △中，60ACB ∠=?，∴60.ACP BCP ∠+∠=? ∵=ACP CBP ∠∠，∴60.CBP BCP ∠+∠=?∴()180120.BPC CBP BCP ∠=?-∠+∠=?∴18060.CPD BPC ∠=?-∠=? ∵=PD PC ，∴CDP △为等边三⾓形.∵60ACD ACP ACP BCP ∠+∠=∠+∠=?，∴.ACD BCP ∠=∠在ACD △和BCP △中，AC BC ACD BCP CD CP =??∠=∠??=?，，，∴()SAS ACD BCP △≌△. ∴.AD BP =∴.AD CD BP PD BD +=+=-----------------------------------------4分（3）如图2，作BM AD ⊥于点M ，BN DC ⊥延长线于点N .∵=60ADB ADC PDC ∠∠-∠=?，∴=60.ADB CDB ∠∠=?∴=60.ADB CDB ∠∠=?D∴=BM BN BD == ⼜由（2）得，=2AD CD BD +=，ABD BCD ABCD S S S ∴△△四边形=+1122AD BM CD BN =22==-----------------------------------7分10.如图1，在等边三⾓形ABC 中，CD 为中线，点Q 在线段CD 上运动，将线段QA 绕点Q 顺时针旋转，使得点A的对应点E 落在射线BC 上，连接BQ ，设∠DAQ =α（0°＜α＜60°且α≠30°）. （1）当0°＜α＜30°时，①在图1中依题意画出图形，并求∠BQE （⽤含α的式⼦表⽰）；②探究线段CE ，AC ，CQ 之间的数量关系，并加以证明；（2）当30°＜α＜60°时，直接写出线段CE ，AC ，CQ 之间的数量关系.解：（1）①3-． ………………………………………………………………………… 1分② 0≤QL．……………………………………………………………… 2分（2）设直线+33y x =与x 轴，y 轴的交点分别为点A ，点B，可得A ，(0,3)B ．∴OA =3OB =，30OAB ∠=?．由0≤Q①如图13，当⊙D 与x 轴相切时，相应的圆⼼1D 满⾜题意，其横坐标取到最⼤值．作11D E x ⊥轴于点1E ，可得11D E ∥OB ，111D E AE BO AO=．∵⊙D 的半径为1，∴ 111D E =．∴1AE =11OE OA AE =-=．∴1D x =②如图14，当⊙D与直线y =相切时，相应的圆⼼2D 满⾜题意，其横坐标取到最⼩值．作22D E x ⊥轴于点2E ，则22D E ⊥OA ．设直线y =与直线+3y =的交点为F ．可得60AOF ∠=?，OF ⊥AB ．则9cos 2AF OA OAF =?∠==．图13∵⊙D 的半径为1，∴ 21D F =．∴2272AD AF D F =-=．=?∠72==，22OE OA AE =-=．∴2D x =．由①②可得，D x≤D x≤． ………………………………………… 5分（3）画图见图15．．……………………………… 7分11.如图，在等边ABC △中， ,D E 分别是边,AC BC 上的点，且CD CE = ,30DBC ∠对称，连接,AF FE ，FE 交BD 于G .（1）连接,DE DF ，则,DE DF 之间的数量关系是；（2）若DBC α∠=，求FEC ∠的⼤⼩; （⽤α的式⼦表⽰）（3）⽤等式表⽰线段,BG GF 和FA 之间的数量关系，并证明.GFEDCBA图15（1）DE DF =；（2）解：连接DE ，DF ，∵△ABC 是等边三⾓形，∴60C ∠=?. ∵DBC α∠=，∴120BDC α∠=?-.∴120BDF BDC α∠=∠=?-，DF DC =. ∴1202FDC α∠=?+. 由（1）知DE DF =.∴F ，E ，C 在以D 为圆⼼，DC 为半径的圆上.∴1602FEC FDC ∠=∠=?+α.（3）BG GF FA =+.理由如下：连接BF ，延长AF ，BD 交于点H ，∵△ABC 是等边三⾓形，∴60ABC BAC ∠=∠=?，AB BC CA ==. ∵点C 与点F 关于BD 对称，∴BF BC =，FBD CBD ∠=∠.GFEDCBA∴BF BA =. ∴BAF BFA ∠=∠. 设CBD α∠=，则602ABF α∠=?-. ∴60BAF α∠=?+. ∴FAD α∠=.∴FAD DBC ∠=∠.由（2）知60FEC α∠=?+. ∴60BGE FEC DBC ∠=∠-∠=?. ∴120FGB ∠=?，60FGD ∠=?.四边形AFGB 中，360120AFE FAB ABG FGB ∠=?-∠-∠-∠=?. ∴60HFG ∠=?.∴△FGH 是等边三⾓形. ∴FH FG =，60H ∠=?. ∵CD CE =，∴DA EB =.在△AHD 与△BGE 中，,,.AHD BGE HAD GBE AD BE ∠=∠??∠=∠??=?∴△△AHD BGE ?. ∴BG AH =.∵AH HF FA GF FA =+=+，∴BG GF FA =+．HGFEDCBA12.如图，在△ABC中，AB=AC，∠BAC=90°，M是BC的中点，延长AM到点D，AE= AD，∠EAD=90°，CE交AB于点F，CD=DF.（1）∠CAD= 度；（2）求∠CDF的度数；（3）⽤等式表⽰线段CD和CE之间的数量关系，并证明.解：（1）45 ……………………………………………………………1分（2）解：如图，连接DB.∵90，°，M是BC的中点，AB AC BAC=∠=∴∠BAD=∠CAD=45°.∴△BAD≌△CAD. ………………………………2分∴∠DBA=∠DCA，BD = CD.∵CD=DF,∴B D=DF. ………………………………………3分∴∠DBA=∠DFB=∠DCA.∵∠DFB+∠DFA =180°,∴∠DCA+∠DFA =180°.∴∠BAC+∠CDF =180°.∴∠CDF =90°. ………………………………………4分21CD. ……………………………………5分（3）CE=)证明：∵90∠=°，EAD∴∠EAF =∠DAF =45°. ∵AD =AE ，∴△EAF ≌△DAF . …………………………………6分∴DF =EF .由②可知，CF. …………………………7分∴CE=)1C D .13.如图，正⽅形ABCD 中，点E 是BC 边上的⼀个动点，连接AE ，将线段AE 绕点A 逆时针旋转90°，得到AF ，连接EF ，交对⾓线BD 于点G ，连接AG ．（1）根据题意补全图形；（2）判定AG 与EF 的位置关系并证明；（3）当AB = 3，BE = 2时，求线段BG 的长．解：（1）图形补全后如图…………………1分（2）结论：AG ⊥EF ． …………………2分证明：连接FD ，过F 点FM ∥BC ，交BD 的延长线于点M ．∵四边形ABCD 是正⽅形，∴AB=DA=DC=BC ，∠DAB =∠ABE =∠ADC =90°，∠ADB =∠5=45°．∵线段AE 绕点A 逆时针旋转90°，得到AF ，A BC ED∴AE=AF ，∠FAE =90°．∴∠1=∠2．∴△FDA ≌△EBA ． …………………3分∴∠FDA =∠EBA =90°，FD=BE ．∵∠ADC =90°，∴∠FDA +∠ADC =180°。

2019届深圳中考复习《多结论几何综合题》专题试卷含解析

2017届中考复习多结论几何综合题专题试卷一、单选题1、如图，△ABC和△CDE均为等腰直角三角形，点B，C，D在一条直线上，点M是AE的中点，下列结论：①tan∠AEC=；②S△ABC+S△CDE≥S△ACE；③BM⊥DM；④BM=DM．正确结论的个数是（）A、1个B、2个C、3个D、4个2、如图，在Rt△ABC中，AB=AC，D、E是斜边BC上两点，且∠DAE=45°，将△ADC绕点A顺时针旋转90°后，得到△AFB，连接EF，下列结论：①△AED≌△AEF；②=;③△ABC的面积等于四边形AFBD的面积；④BE2+DC2=DE2⑤BE+DC=DE;其中正确的是( )A、①②④B、③④⑤C、①③④D、①③⑤3、如图，将等边△ABC沿射线BC向右平移到△DCE的位置，连接AD、BD ，则下列结论：①AD＝BC；②BD、AC互相平分；③四边形ACED是菱形；④BD⊥DE；其中正确的个数是（）.A、1B、2C、3D、44、如图，把一张长方形纸片ABCD沿对角线BD折叠，使C点落在E处，BE与AD相交于点F，下列结论：①BD=AD2+AB2；②△ABF≌△EDF；③＝④AD=BD•cos45°．其中正确的一组是（）A、①②B、②③C、①④D、③④5、如图，已知正方形ABCD的边长为4，点E、F分别在边AB、BC上，且AE=BF=1，CE、DF交于点O．下列结论：①∠DOC=90°，②OC=OE，③tan∠OCD= ，④S△ODC=S四边形BEOF中，正确的有（）A、1个B、2个C、3个D、4个6、如图，已知正方形ABCD的边长为12，BE=EC，将正方形边CD沿DE折叠到DF，延长EF交AB于G，连接DG，现在有如下4个结论：①△ADG≌△FDG；②GB=2AG；③△GDE∽△BEF；④S△BEF=．在以上4个结论中，正确的有（）A、1B、2C、3D、47、如图，▱ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=60°，AB=BC，连接OE．下列结论：①∠CAD=30°；②S▱ABCD=AB•AC；③OB=AB；④OE=BC，成立的个数有（）A、1个B、2个C、3个D、4个8、如图，AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高，得到下列四个结论：①OA=OD；②AD⊥EF；③当∠A=90°时，四边形AEDF是正方形；④AE+DF=AF+DE．其中正确的是（）A、②③B、②④C、①③④D、②③④9、如图，G，E分别是正方形ABCD的边AB，BC的点，且AG=CE，AE⊥EF，AE=EF，现有如下结论：①BE=GE；②△AGE≌△ECF；③∠FCD=45°；④△GBE∽△ECH，其中，正确的结论有（）A、1个B、2个C、3个D、4个10、如图，PA=PB，OE⊥PA，OF⊥PB，则以下结论：①OP是∠APB的平分线；②PE=PF③CA=BD；④CD∥AB；其中正确的有（）个．A、4B、3C、2D、111、如图，在Rt△ABC中，AB=CB，BO⊥AC，把△ABC折叠，使AB落在AC上，点B与AC上的点E重合，展开后，折痕AD交BO于点F，连接DE、EF．下列结论：①tan∠ADB=2；②图中有4对全等三角形；③若将△DEF沿EF折叠，则点D不一定落在AC上；④BD=BF；⑤S四边形DFOE=S△AOF，上述结论中正确的个数是（）A、1个B、2个C、3个D、4个12、如图，将等边△ABC绕点C顺时针旋转120°得到△EDC，连接AD，BD．则下列结论：①AC=AD；②BD⊥AC；③四边形ACED是菱形．其中正确的个数是（）A、0B、1C、2D、313、如图，CB=CA，∠ACB=90°，点D在边BC上（与B、C不重合），四边形ADEF为正方形，过点F作FG⊥CA，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论：①AC=FG；②S△FAB：S四边形CBFG=1：2；③∠ABC=∠ABF；④AD2=FQ•AC，其中正确的结论的个数是（）A 、1B 、2C 、3D 、414、如图，矩形ABCD 中，O 为AC 中点，过点O 的直线分别与AB 、CD 交于点E 、F ，连结BF 交AC 于点M ，连结DE 、BO ．若∠COB=60°，FO=FC ，则下列结论：①FB 垂直平分OC ；②△EOB ≌△CMB ；③DE=EF ；④S △AOE ：S △BCM =2：3．其中正确结论的个数是（）A 、4个B 、3个C 、2个D 、1个15、（2016•攀枝花）如图，正方形纸片ABCD 中，对角线AC 、BD 交于点O ，折叠正方形纸片ABCD ，使AD 落在BD 上，点A 恰好与BD 上的点F 重合，展开后折痕DE 分别交AB 、AC 于点E 、G ，连结GF ，给出下列结论：①∠ADG=22.5°；②tan ∠AED=2；③S △AGD =S △OGD ；④四边形AEFG 是菱形；⑤BE=2OG ；⑥若S △OGF =1，则正方形ABCD 的面积是6+4 ，其中正确的结论个数为（）A 、2B 、3C 、4D 、516、如图，在正方形ABCD 中，E 、F 分别为BC 、CD 的中点，连接AE ，BF 交于点G ，将△BCF 沿BF 对折，得到△BPF ，延长FP 交BA 延长线于点Q ，下列结论正确的个数是（）①AE=BF ；②AE ⊥BF ；③sin ∠BQP= ；④S四边形ECFG=2S △BGE ．A 、4B 、3C 、2D 、117、如图所示，抛物线y=ax 2+bx+c （a≠0）与x 轴交于点A （﹣2，0）、B （1，0），直线x=﹣0.5与此抛物线交于点C ，与x 轴交于点M ，在直线上取点D ，使MD=MC ，连接AC 、BC 、AD 、BD ，某同学根据图象写出下列结论： ①a ﹣b=0；②当﹣2＜x ＜1时，y ＞0； ③四边形ACBD 是菱形； ④9a ﹣3b+c ＞你认为其中正确的是（）A、②③④B、①②④C、①③④D、①②③18、如图，正方形ABCD中，AB=6，点E在边CD上，且CE=2DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．下列结论：①△ABG≌△AFG；②BG=GC；③EG=DE+BG；④AG∥CF；⑤S△FGC=3.6．其中正确结论的个数是（）A、2B、3C、4D、519、如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足= ，连接AF并延长交⊙O于点E，连接AD，DE，若CF=2，AF=3，给出下列结论：①△ADF∽△AED；②FG=2；③tanE= ；④S△DEF=4 ，其中正确的是（）A、①②③B、②③④C、①②④D、①③④20、如图，在⊙O中，AB是直径，点D是⊙O上一点，点C是弧AD的中点，弦CE⊥AB于点E，过点D的切线交EC的延长线于点G，连接AD，分别交CE、CB 于点P、Q，连接AC，给出下列结论：①∠DAC=∠ABC；②AD=CB；③点P是△ACQ的外心；④AC2=AE•AB；⑤CB∥GD，其中正确的结论是（）A、①③⑤B、②④⑤C、①②⑤D、①③④答案解析部分一、单选题1、【答案】D【考点】等腰三角形的性质，梯形中位线定理，锐角三角函数的定义【解析】【分析】①根据等腰直角三角形的性质及△ABC∽△CDE的对应边成比例知，；然后由直角三角形中的正切函数，得tan∠AEC=，再由等量代换求得tan∠AEC=；②由三角形的面积公式、梯形的面积公式及不等式的基本性质a2+b2≥2ab（a=b时取等号)解答；③、④通过作辅助线MN，构建直角梯形的中位线，根据梯形的中位线定理及等腰直角三角形的判定定理解答．【解答】解：∵△ABC和△CDE均为等腰直角三角形，∴AB=BC，CD=DE，∴∠BAC=∠BCA=∠DCE=∠DEC=45°，∴∠ACE=90°；∵△ABC∽△CDE∴①∴tan∠AEC=，∴tan∠AEC=；故本选项正确；②∵S△ABC=a2，S△CDE=b2，S梯形ABDE=（a+b)2，∴S△ACE=S梯形ABDE-S△ABC-S△CDE=ab，S△ABC+S△CDE=（a2+b2)≥ab（a=b时取等号)，∴S△ABC+S△CDE≥S△ACE；故本选项正确；④过点M作MN垂直于BD，垂足为N．∵点M是AE的中点，则MN为梯形中位线，∴N为中点，∴△BMD为等腰三角形，∴BM=DM；故本选项正确；③又MN=（AB+ED)=（BC+CD)，∴∠BMD=90°，即BM⊥DM；故本选项正确．故选D．【点评】本题综合考查了等腰直角三角形的判定与性质、梯形的中位线定理、锐角三角函数的定义等知识点．在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．2、【答案】C【考点】全等三角形的判定，勾股定理，相似三角形的判定，旋转的性质【解析】【分析】①根据旋转的性质知∠CAD=∠BAF，AD=AF，因为∠BAC=90°，∠DAE=45°，所以∠CAD+∠BAE=45°，可得∠EAF=45°=∠DAE，由此即可证明△AEF≌△AED；②当△ABE∽△ACD时，该比例式成立；③根据旋转的性质，△ADC≌△ABF，进而得出△ABC的面积等于四边形AFBD 的面积；④据①知BF=CD，EF=DE，∠FBE=90°，根据勾股定理判断．⑤根据①知道△AEF≌△AED，得CD=BF，DE=EF；由此即可确定该说法是否正确；【解答】①根据旋转的性质知∠CAD=∠BAF，AD=AF，∵∠BAC=90°，∠DAE=45°，∴∠CAD+∠BAE=45°．∴∠EAF=45°，∴△AED≌△AEF；故本选项正确；②∵AB=AC，∴∠ABE=∠ACD；∴当∠BAE=∠CAD时，△ABE∽△ACD，∴=；当∠BAE≠∠CAD时，△ABE与△ACD不相似，即≠；∴此比例式不一定成立；故本选项错误；③根据旋转的性质知△ADC≌△AFB，∴S△ABC=S△ABD+S△ABF=S四边形AFBD，即三角形ABC的面积等于四边形AFBD的面积；故本选项正确；④∵∠FBE=45°+45°=90°，∴BE2+BF2=EF2，∵△ADC绕点A顺时针旋转90°后，得到△AFB，∴△AFB≌△ADC，∴BF=CD，又∵EF=DE，∴BE2+DC2=DE2，故本选项正确；⑤根据①知道△AEF≌△AED，得CD=BF，DE=EF，∴BE+DC=BE+BF＞DE=EF，即BE+DC＞DE，故本选项错误；综上所述，正确的说法是①③④；故选C．【点评】此题主要考查了图形的旋转变换以及全等三角形的判定等知识，解题时注意旋转前后对应的相等关系．3、【答案】D【考点】等边三角形的性质，菱形的判定与性质，平移的性质【解析】【解答】∵△ABC、△DCE是等边三角形，∴∠ACB＝∠DCE＝60°，AC ＝CD ，∴∠ACD＝180°－∠ACB－∠DCE＝60°，∴△ACD是等边三角形，∴AD＝AC＝BC ，故①正确；由①可得AD＝BC ，∵AB＝CD ，∴四边形ABCD是平行四边形，∴BD、AC互相平分，故②正确；由①可得AD＝AC＝CE＝DE ，故四边形ACED是菱形，即③正确；∵四边形ACED是菱形，∴AC⊥BD ，∵AC∥DE ，∴∠BDE＝∠COD＝90°，∴BD⊥DE ，故④正确；综上可得①②③④正确，共4个，故选D．【分析】先求出∠ACD＝60°，继而可判断△ACD是等边三角形，从而可判断①是正确的；根据①的结论，可判断四边形ABCD是平行四边形，从而可判断②是正确的；根据①的结论，可判断③正确；根据菱形的对角线互相垂直可得AC⊥BD ，再根据平移后对应线段互相平行可得∠BDE＝∠COD＝90°，进而判断④正确．4、【答案】B【考点】勾股定理，翻折变换（折叠问题），相似三角形的判定与性质，特殊角的三角函数值【解析】【解答】①∵△ABD为直角三角形，∴BD2=AD2+AB2，不是BD=AD2+AB2，故说法错误；②根据折叠可知：DE=CD=AB，∠A=∠E，∠AFB=∠EFD，∴△ABF≌△EDF，故说法正确；③根据②可以得到△ABF∽△EDF，∴＝，故说法正确；④在Rt△ABD中，∠ADB≠45°，∴AD≠BD•cos45°，故说法错误．所以正确的是②③．故选B．【分析】①直接根据勾股定理即可判定是否正确；②利用折叠可以得到全等条件证明△ABF≌△EDF；③利用全等三角形的性质即可解决问题；④在Rt△ABD中利用三角函数的定义即可判定是否正确．此题主要考查了折叠问题，也考查了勾股定理、相似三角形的性质、全等三角形的性质及三角函数的定义，它们的综合性比较强，对于学生的综合能力要求比较高，平时加强训练．5、【答案】C【考点】全等三角形的判定与性质，勾股定理，正方形的性质，锐角三角函数的定义【解析】【解答】解：∵正方形ABCD的边长为4，∴BC=CD=4，∠B=∠DCF=90°，∵AE=BF=1，∴BE=CF=4﹣1=3，在△EBC和△FCD中，∴△EBC≌△FCD（SAS），∴∠CFD=∠BEC，∴∠BCE+∠BEC=∠BCE+∠CFD=90°，∴∠DOC=90°；故①正确；若OC=OE，∵DF⊥EC，∴CD=DE，∵CD=AD＜DE（矛盾），故②错误；∵∠OCD+∠CDF=90°，∠CDF+∠DFC=90°，∴∠OCD=∠DFC，∴tan∠OCD=tan∠DFC= = ，故③正确；∵△EBC≌△FCD，∴S△EBC=S△FCD，∴S△EBC﹣S△FOC=S△FCD﹣S△FOC，即S△ODC=S四边形BEOF．故④正确．故选C．【分析】由正方形ABCD的边长为4，AE=BF=1，利用SAS易证得△EBC≌△FCD，然后全等三角形的对应角相等，易证得①∠DOC=90°正确；②由线段垂直平分线的性质与正方形的性质，可得②错误；易证得∠OCD=∠DFC，即可求得③正确；由①易证得④正确．6、【答案】C【考点】全等三角形的判定与性质，正方形的性质，翻折变换（折叠问题），相似三角形的判定与性质【解析】【解答】由折叠可知，DF=DC=DA，∠DFE=∠C=90°，∴∠DFG=∠A=90°，∴△ADG≌△FDG，①正确；∵正方形边长是12，∴BE=EC=EF=6，设AG=FG=x，则EG=x+6，BG=12﹣x，由勾股定理得：EG2=BE2+BG2，即：（x+6）2=62+（12﹣x）2，解得：x=4∴AG=GF=4，BG=8，BG=2AG，②正确；BE=EF=6，△BEF是等腰三角形，易知△GED不是等腰三角形，③错误；S△GBE=×6×8=24，S△BEF=•S△GBE==，④正确．故选：C．【分析】根据正方形的性质和折叠的性质可得AD=DF，∠A=∠GFD=90°，于是根据“HL”判定△ADG≌△FDG，再由GF+GB=GA+GB=12，EB=EF，△BGE为直角三角形，可通过勾股定理列方程求出AG=4，BG=8，进而求出△BEF的面积，再抓住△BEF是等腰三角形，而△GED显然不是等腰三角形，判断③是错误的．7、【答案】C【考点】等边三角形的判定与性质，含30度角的直角三角形，平行四边形的性质【解析】【解答】∵四边形ABCD是平行四边形，∴∠ABC=∠ADC=60°，∠BAD=120°，∵AE平分∠BAD，∴∠BAE=∠EAD=60°∴△ABE是等边三角形，∴AE=AB=BE，∵AB=BC，∴AE=BC，∴∠BAC=90°，∴∠CAD=30°，故①正确；∵AC⊥AB，∴S▱ABCD=AB•AC，故②正确，∵AB=BC，OB=BD，∵BD＞BC，∴AB≠OB，故③错误；∵CE=BE，CO=OA，∴OE=AB，∴OE=BC，故④正确．故选：C．【分析】由四边形ABCD是平行四边形，得到∠ABC=∠ADC=60°，∠BAD=120°，根据AE平分∠BAD，得到∠BAE=∠EAD=60°推出△ABE是等边三角形，由于AB=BC，得到AE=BC，得到△ABC是直角三角形，于是得到∠CAD=30°，故①正确；由于AC⊥AB，得到S▱ABCD=AB•AC，故②正确，根据AB=BC，OB=BD，且BD＞BC，得到AB≠OB，故③错误；根据三角形的中位线定理得到OE=AB，于是得到OE=BC，故④正确．8、【答案】D【考点】全等三角形的判定与性质，角平分线的性质，正方形的判定【解析】【解答】如果OA=OD，则四边形AEDF是矩形，∠A=90°，不符合题意，∴①不正确；∵AD是△ABC的角平分线，∴∠EAD∠FAD，在△AED和△AFD 中，∴△AED≌△AFD（AAS），∴AE=AF，DE=DF，∴AE+DF=AF+DE，∴④正确；在△AEO和△AFO中，，∴△AE0≌△AF0（SAS），∴EO=FO，又∵AE=AF，∴AO是EF的中垂线，∴AD⊥EF，∴②正确；∵当∠A=90°时，四边形AEDF的四个角都是直角，∴四边形AEDF是矩形，又∵DE=DF，∴四边形AEDF是正方形，∴③正确．综上，可得正确的是：②③④．故选：D．【分析】①如果OA=OD，则四边形AEDF是矩形，∠A=90°，不符合题意，所以①不正确．②首先根据全等三角形的判定方法，判断出△AED≌△AFD，AE=AF，DE=DF；然后根据全等三角形的判定方法，判断出△AE0≌△AFO，即可判断出AD⊥EF．③首先判断出当∠A=90°时，四边形AEDF的四个角都是直角，四边形AEDF是矩形，然后根据DE=DF，判断出四边形AEDF是正方形即可．④根据△AED≌△AFD，判断出AE=AF，DE=DF，即可判断出AE+DF=AF+DE成立，据此解答即可．9、【答案】B【考点】全等三角形的判定与性质，正方形的性质，相似三角形的判定与性质【解析】【解答】∵四边形ABCD是正方形，∴∠B=∠DCB=90°，AB=BC，∵AG=CE，∴BG=BE，由勾股定理得：BE=GE，∴①错误；∵BG=BE，∠B=90°，∴∠BGE=∠BEG=45°，∴∠AGE=135°，∴∠GAE+∠AEG=45°，∵AE⊥EF，∴∠AEF=90°，∵∠BEG=45°，∴∠AEG+∠FEC=45°，∴∠GAE=∠FEC，在△GAE和△CEF中∴△GAE≌△CEF，∴②正确；∴∠AGE=∠ECF=135°，∴∠FCD=135°﹣90°=45°，∴③正确；∵∠BGE=∠BEG=45°，∠AEG+∠FEC=45°，∴∠FEC＜45°，∴△GBE和△ECH不相似，∴④错误；即正确的有2个．故选B．【分析】根据正方形的性质得出∠B=∠DCB=90°，AB=BC，求出BG=BE ，根据勾股定理得出BE=GE，即可判断①；求出∠GAE+∠AEG=45°，推出∠GAE=∠FEC，根据SAS推出△GAE≌△CEF，即可判断②；求出∠AGE=∠ECF=135°，即可判断③；求出∠FEC＜45°，根据相似三角形的判定得出△GBE和△ECH不相似，即可判断④．10、【答案】A【考点】全等三角形的判定与性质，圆心角、弧、弦的关系，相似三角形的判定与性质【解析】【解答】连接OP、OC、OA、OD、OB、CD、AB．∵PC•PA=PD•PB（相交弦定理），PA=PB（已知），∴PC=PD，∴AC=BD；在△AOC和△BOD中，∵∠AOC=∠BOD（等弦对等角），OA=OB（半径），OD=OC（半径），∴△AOC≌△BOD，∴③CA=BD；OE=OF；又∵OE⊥PA，OF⊥PB，∴①OP是∠APB的平分线；∴②PE=PF；在△PCD和△PAB中，PC：PA=PD：PB，∠DPC=∠BPA，∴△PCD∽△PAB，∴∠PDC=PBA，∴④CD∥AB；综上所述，①②③④均正确，故答案选A．【分析】①通过证明△AOC≌△BOD，再根据全等三角形的对应高相等求得OE=OF；再根据角平分线的性质证明OP是∠APB的平分线；②由角平分线的性质证明PE=PF；③通过证明△AOC≌△BOD，再根据全等三角形的对应边相等求得CA=BD；④通过证明△PCD∽△PAB，再根据相似三角形的性质对应角相等证得∠PDC=PBA；然后由平行线的判定得出结论CD∥AB．11、【答案】C【考点】全等三角形的判定与性质，翻折变换（折叠问题），锐角三角函数的定义【解析】【解答】①由折叠可得BD=DE，而DC＞DE，∴DC＞BD，∴tan∠ADB≠2，故①错误；②图中的全等三角形有△ABF≌△AEF，△ABD≌△AED，△FBD≌△FED，（由折叠可知) ∵OB⊥AC，∴∠AOB=∠COB=90°，在Rt△AOB和Rt△COB中，AB="CB" ,BO=BO ，∴Rt△AOB≌Rt△COB（HL)，则全等三角形共有4对，故②正确；③∵AB=CB，BO⊥AC，把△ABC折叠，∴∠ABO=∠CBO=45°，∠FBD=∠DEF，∴∠AEF=∠DEF=45°，∴将△DEF沿EF折叠，可得点D一定在AC上，故③错误；④∵OB⊥AC，且AB=CB，∴BO为∠ABC的平分线，即∠ABO=∠OBC=45°，由折叠可知，AD是∠BAC的平分线，即∠BAF=22.5°，又∵∠BFD为三角形ABF的外角，∴∠BFD=∠ABO+∠BAF=67.5°，易得∠BDF=180°-45°-67.5°=67.5°，∴∠BFD=∠BDF，∴BD=BF，故④正确；⑤连接CF，∵△AOF和△COF等底同高，∴S△AOF=S△COF，∵∠AEF=∠ACD=45°，∴EF∥CD，∴S△EFD=S△EFC，∴S四边形DFOE=S△COF，∴S四边形DFOE=S△AOF，故⑤正确；故正确的有3个．故选C．12、【答案】D【考点】等边三角形的性质，菱形的判定，旋转的性质【解析】【解答】解：∵将等边△ABC绕点C顺时针旋转120°得到△EDC，∴∠ACE=120°，∠DCE=∠BCA=60°，AC=CD=DE=CE，∴∠ACD=120°﹣60°=60°，∴△ACD是等边三角形，∴AC=AD，AC=AD=DE=CE，∴四边形ACED是菱形，∵将等边△ABC绕点C顺时针旋转120°得到△EDC，AC=AD，∴AB=BC=CD=AD，∴四边形ABCD是菱形，∴BD⊥AC，∴①②③都正确，故选D．【分析】根据旋转和等边三角形的性质得出∠ACE=120°，∠DCE=∠BCA=60°，AC=CD=DE=CE，求出△ACD是等边三角形，求出AD=AC，根据菱形的判定得出四边形ABCD和ACED都是菱形，根据菱形的判定推出AC⊥BD．本题考查了旋转的性质，菱形的性质和判定，等边三角形的性质和判定的应用，能灵活运用知识点进行推理是解此题的关键．13、【答案】D【考点】全等三角形的判定与性质，矩形的判定与性质，正方形的性质，相似三角形的判定与性质，等腰直角三角形【解析】【解答】解：∵四边形ADEF为正方形，∴∠FAD=90°，AD=AF=EF，∴∠CAD+∠FAG=90°，∵FG⊥CA，∴∠C=90°=∠ACB，∴∠CAD=∠AFG，在△FGA和△ACD中，，∴△FGA≌△ACD（AAS），∴AC=FG，①正确；∵BC=AC，∴FG=BC，∵∠ACB=90°，FG⊥CA，∴FG∥BC，∴四边形CBFG是矩形，∴∠CBF=90°，S△FAB= FB•FG= S四边形CBFG，②正确；∵CA=CB，∠C=∠CBF=90°，∴∠ABC=∠ABF=45°，③正确；∵∠FQE=∠DQB=∠ADC，∠E=∠C=90°，∴△ACD∽△FEQ，∴AC：AD=FE：FQ，∴AD•FE=AD2=FQ•AC，④正确；故选：D．【分析】本题考查了相似三角形的判定与性质、全等三角形的判定与性质、正方形的性质、矩形的判定与性质、等腰直角三角形的性质；熟练掌握正方形的性质，证明三角形全等和三角形相似是解决问题的关键．由正方形的性质得出∠FAD=90°，AD=AF=EF，证出∠CAD=∠AFG，由AAS证明△FGA≌△ACD，得出AC=FG，①正确；证明四边形CBFG是矩形，得出S△FAB= FB•FG= S四边形CEFG，②正确；由等腰直角三角形的性质和矩形的性质得出∠ABC=∠ABF=45°，③正确；证出△ACD∽△FEQ，得出对应边成比例，得出D•FE=AD2=FQ•AC，④正确．14、【答案】B【考点】全等三角形的判定与性质，线段垂直平分线的性质，等腰三角形的性质，矩形的性质【解析】【解答】解：①∵矩形ABCD中，O为AC中点，∴OB=OC，∵∠COB=60°，∴△OBC是等边三角形，∴OB=BC，∵FO=FC，∴FB垂直平分OC，故①正确；②∵FB垂直平分OC，∴△CMB≌△OMB，∵OA=OC，∠FOC=∠EOA，∠DCO=∠BAO，∴△FOC≌△EOA，∴FO=EO，易得OB⊥EF，∴△OMB≌△OEB，∴△EOB≌△CMB，故②正确；③由△OMB≌△OEB≌△CMB得∠1=∠2=∠3=30°，BF=BE，∴△BEF是等边三角形，∴BF=EF，∵DF∥BE且DF=BE，∴四边形DEBF是平行四边形，∴DE=BF，∴DE=EF，故③正确；④在直角△BOE中∵∠3=30°，∴BE=2OE，∵∠OAE=∠AOE=30°，∴AE=OE，∴BE=2AE，∴S△AOE：S△BCM=S△AOE：S△BOE=1：2，故④错误；所以其中正确结论的个数为3个；故选B【分析】①利用线段垂直平分线的性质的逆定理可得结论；②证△OMB≌△OEB得△EOB≌△CMB；③先证△BEF是等边三角形得出BF=EF，再证▱DEBF得出DE=BF，所以得DE=EF；④由②可知△BCM≌△BEO，则面积相等，△AOE和△BEO属于等高的两个三角形，其面积比就等于两底的比，即S△AOE：S△BOE=AE：BE，由直角三角形30°角所对的直角边是斜边的一半得出BE=2OE=2AE，得出结论S△AOE：S△BOE=AE：BE=1：2．本题综合性比较强，既考查了矩形的性质、等腰三角形的性质，又考查了全等三角形的性质和判定，及线段垂直平分线的性质，内容虽多，但不复杂；看似一个选择题，其实相当于四个证明题，属于常考题型．15、【答案】B【考点】菱形的判定与性质，翻折变换（折叠问题），等腰直角三角形【解析】【解答】解：∵四边形ABCD是正方形，∴∠GAD=∠ADO=45°，由折叠的性质可得：∠ADG= ∠ADO=22.5°，故①正确．∵由折叠的性质可得：AE=EF，∠EFD=∠EAD=90°，∴AE=EF＜BE，∴AE＜AB，∴＞2，故②错误．∵∠AOB=90°，∴AG=FG＞OG，△AGD与△OGD同高，∴S△AGD＞S△OGD，故③错误．∵∠EFD=∠AOF=90°，∴EF∥AC，∴∠FEG=∠AGE，∵∠AGE=∠FGE，∴∠FEG=∠FGE，∴EF=GF，∵AE=EF，∴AE=GF，故④正确．∵AE=EF=GF，AG=GF，∴AE=EF=GF=AG，∴四边形AEFG是菱形，∴∠OGF=∠OAB=45°，∴EF=GF= OG，∴BE= EF= ×OG=2OG．故⑤正确．∵四边形AEFG是菱形，∴AB∥GF，AB=GF．∵∠BAO=45°，∠GOF=90°，∴△OGF时等腰直角三角形．∵S△OGF=1，∴OG2=1，解得OG= ，∴BE=2OG=2 ，GF= ==2，∴AE=GF=2，∴AB=BE+AE=2 +2，∴S正方形ABCD=AB2=（2 +2）2=12+8 ，故⑥错误．∴其中正确结论的序号是：①④⑤．故选B．【分析】①由四边形ABCD是正方形，可得∠GAD=∠ADO=45°，又由折叠的性质，可求得∠ADG的度数；②由AE=EF＜BE，可得AD＞2AE；③由AG=GF＞OG，可得△AGD的面积＞△OGD的面积；④由折叠的性质与平行线的性质，易得△EFG是等腰三角形，即可证得AE=GF；⑤易证得四边形AEFG是菱形，由等腰直角三角形的性质，即可得BE=2OG；⑥根据四边形AEFG是菱形可知AB∥GF，AB=GF，再由∠BAO=45°，∠GOF=90°可得出△OGF时等腰直角三角形，由S△OGF=1求出GF的长，进而可得出BE及AE的长，利用正方形的面积公式可得出结论．此题考查的是四边形综合题，涉及到正方形的性质、折叠的性质、等腰直角三角形的性质以及菱形的判定与性质等知识．此题综合性较强，难度较大，注意掌握折叠前后图形的对应关系，注意数形结合思想的应用．16、【答案】B【考点】全等三角形的判定与性质，正方形的性质，翻折变换（折叠问题），相似三角形的判定与性质【解析】【解答】解：∵E，F分别是正方形ABCD边BC，CD的中点，∴CF=BE，在△ABE和△BCF中，，∴Rt△ABE≌Rt△BCF（SAS），∴∠BAE=∠CBF，AE=BF，故①正确；又∵∠BAE+∠BEA=90°，∴∠CBF+∠BEA=90°，∴∠BGE=90°，∴AE⊥BF，故②正确；根据题意得，FP=FC，∠PFB=∠BFC，∠FPB=90°∵CD∥AB，∴∠CFB=∠ABF，∴∠ABF=∠PFB，∴QF=QB，令PF=k（k＞0），则PB=2k在Rt△BPQ中，设QB=x，∴x2=（x﹣k）2+4k2，∴x= ，∴sin=∠BQP= = ，故③正确；∵∠BGE=∠BCF，∠GBE=∠CBF，∴△BGE∽△BCF，∵BE= BC，BF= BC，∴BE：BF=1：，∴△BGE的面积：△BCF的面积=1：5，∴S四边形ECFG=4S△BGE，故④错误．故选：B．【分析】首先证明△ABE≌△BCF，再利用角的关系求得∠BGE=90°，即可得到①AE=BF；②AE⊥BF；△BCF沿BF对折，得到△BPF，利用角的关系求出QF=QB，解出BP，QB，根据正弦的定义即可求解；根据AA可证△BGE与△BCF相似，进一步得到相似比，再根据相似三角形的性质即可求解．本题主要考查了四边形的综合题，涉及正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质以及折叠的性质的知识点，解决的关键是明确三角形翻转后边的大小不变，找准对应边，角的关系求解．17、【答案】D【考点】二次函数的图象，二次函数的性质，菱形的判定【解析】【解答】解：①∵抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣2，0）、B（1，0），∴该抛物线的对称轴为x=﹣=﹣0.5，∴a=b，a﹣b=0，①正确；②∵抛物线开口向下，且抛物线与x轴交于点A（﹣2，0）、B（1，0），∴当﹣2＜x＜1时，y＞0，②正确；③∵点A、B关于x=0.5对称，∴AM=BM，又∵MC=MD，且CD⊥AB，∴四边形ACBD是菱形，③正确；④当x=﹣3时，y＜0，即y=9a﹣3b+c＜0，④错误．综上可知：正确的结论为①②③．故选D．【分析】①由抛物线与x轴的两交点坐标即可得出抛物线的对称轴为x=﹣=﹣0.5，由此即可得出a=b，①正确；②根据抛物线的开口向下以及抛物线与x轴的两交点坐标，即可得出当﹣2＜x＜1时，y＞0，②正确；③由AB关于x=0.5对称，即可得出AM=BM，再结合MC=MD以及CD⊥AB，即可得出四边形ACBD是菱形，③正确；④根据当x=﹣3时，y＜0，即可得出9a﹣3b+c＜0，④错误．综上即可得出结论．本题考查了二次函数的图象、二次函数的性质以及菱形的判定，解题的关键是逐条分析四条结论是否正确．本题属于中档题，难度不大，解决该题型题目时，根据给定的函数图象结合二次函数的性质逐条分析给定的结论是关键．18、【答案】D【考点】全等三角形的判定与性质，正方形的性质，翻折变换（折叠问题）【解析】【解答】解：∵正方形ABCD的边长为6，CE=2DE，∴DE=2，EC=4，∵把△ADE沿AE折叠使△ADE落在△AFE的位置，∴AF=AD=6，EF=ED=2，∠AFE=∠D=90°，∠FAE=∠DAE，在Rt△ABG和Rt△AFG中，∴Rt△ABG≌Rt△AFG（HL），∴GB=GF，∠BAG=∠FAG，∴∠GAE=∠FAE+∠FAG= ∠BAD=45°，所以①正确；设BG=x，则GF=x，C=BC﹣BG=6﹣x，在Rt△CGE中，GE=x+2，EC=4，CG=6﹣x，∵CG2+CE2=GE2，∴（6﹣x）2+42=（x+2）2，解得x=3，∴BG=3，CG=6﹣3=3∴BG=CG，所以②正确；∵EF=ED，GB=GF，∴GE=GF+EF=BG+DE，所以③正确；∵GF=GC，∴∠GFC=∠GCF，又∵Rt△ABG≌Rt△AFG，∴∠AGB=∠AGF，而∠BGF=∠GFC+∠GCF，∴∠AGB+∠AGF=∠GFC+∠GCF，∴∠AGB=∠GCF，∴CF∥AG，所以④正确；过F作FH⊥DC∵BC⊥DH，∴FH∥GC，∴△EFH∽△EGC，∴，EF=DE=2，GF=3，∴EG=5，∴△EFH∽△EGC，∴相似比为：= ，∴S△FGC=S△GCE﹣S△FEC= ×3×4﹣×4×（×3）= =3.6，所以⑤正确．故正确的有①②③④⑤，故选：D．【分析】先计算出DE=2，EC=4，再根据折叠的性质AF=AD=6，EF=ED=2，∠AFE=∠D=90°，∠FAE=∠DAE，然后根据“HL”可证明Rt△ABG≌Rt△AFG，则GB=GF，∠BAG=∠FAG，所以∠GAE= ∠BAD=45°；GE=GF+EF=BG+DE；设BG=x，则GF=x，CG=BC﹣BG=6﹣x，在Rt△CGE中，根据勾股定理得（6﹣x）2+42=（x+2）2，解得x=3，则BG=CG=3，则点G为BC的中点；同时得到GF=GC，根据等腰三角形的性质得∠GFC=∠GCF，再由Rt△ABG≌Rt△AFG得到∠AGB=∠AGF，然后根据三角形外角性质得∠BGF=∠GFC+∠GCF，易得∠AGB=∠GCF，根据平行线的判定方法得到CF∥AG；过F作FH⊥DC，则△EFH∽△EGC，△EFH∽△EGC，由相似比为，可计算S△FGC．本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了三角形全等的判定与性质、勾股定理和正方形的性质．19、【答案】C【考点】垂径定理，圆周角定理，相似三角形的判定与性质，解直角三角形【解析】【解答】解：①∵AB是⊙O的直径，弦CD⊥AB，∴，DG=CG，∴∠ADF=∠AED，∵∠FAD=∠DAE（公共角），∴△ADF∽△AED；故①正确；②∵= ，CF=2，∴FD=6，∴CD=DF+CF=8，∴CG=DG=4，∴FG=CG﹣CF=2；故②正确；③∵AF=3，FG=2，∴AG= = ，∴在Rt△AGD中，tan∠ADG= = ，∴tan∠E= ；故③错误；④∵DF=DG+FG=6，AD= = ，∴S△ADF= DF•AG= ×6×=3 ，∵△ADF∽△AED，∴=（）2，∴= ，∴S△AED=7 ，∴S△DEF=S△AED﹣S△ADF=4 ；故④正确．故选C．【分析】①正确．由AB是⊙O的直径，弦CD⊥AB，根据垂径定理可得：，DG=CG，继而证得△ADF∽△AED；②正确．由= ，CF=2，可求得DF的长，继而求得CG=DG=4，则可求得FG=2；③错误．由勾股定理可求得AG的长，即可求得tan∠ADF的值，继而求得tan∠E=．④首先求得△ADF的面积，由相似三角形面积的比等于相似比的平方，即可求得△ADE的面积，继而求得S△DEF=4 ．20、【答案】D【考点】垂径定理，圆周角定理，相似三角形的判定与性质【解析】【解答】解：∵在⊙O中，点C是的中点，∴= ，∴∠CAD=∠ABC，故①正确；∵≠ ，∴≠ ，∴AD≠BC，故②错误；∵AB是⊙O的直径，∴∠ACB=90°，又∵CE⊥AB，∴∠ACE+∠CAE=∠ABC+∠CAE=90°，∴∠ACE=∠ABC，又∵C为的中点，∴= ，∴∠CAP=∠ABC，∴∠ACE=∠CAP，∴AP=CP，∵∠ACQ=90°，∴∠ACP+∠PCQ=∠CAP+∠PQC=90°，∴∠PCQ=∠PQC，∴PC=PQ，∴AP=PQ，即P为Rt△ACQ斜边AQ的中点，∴P为Rt△ACQ的外心，故③正确；∵AB是⊙O的直径，∴∠ACB=90°，又∵CE⊥AB∴根据射影定理，可得AC2=AE•AB，故④正确；如图，连接BD，则∠ADG=∠ABD，∵≠ ，∴≠ ，∴∠ABD≠∠BAC，∴∠ADG≠∠BAC，又∵∠BAC=∠BCE=∠PQC，∴∠ADG≠∠PQC，∴CB与GD不平行，故⑤错误．故答案为：D．【分析】在同圆或等圆中，同弧或等弧所对的圆周角相等，据此推理可得①正确，②错误；通过推理可得∠ACE=∠CAP，得出AP=CP，再根据∠PCQ=∠PQC，可得出PC=PQ，进而得到AP=PQ，即P为Rt△ACQ斜边AQ的中点，故P为Rt△ACQ 的外心，即可得出③正确；连接BD，则∠ADG=∠ABD，根据∠ADG≠∠BAC，∠BAC=∠BCE=∠PQC，可得出∠ADG≠∠PQC，进而得到CB与GD不平行，可得⑤错误．。

2022年中考数学复习专题几何压轴题题型分类整理

专题训练一平移问题基本模型经过平移，对应线段平行（或共线）且相等，对应角相等，对应点所连接的线段平行（或共线）且相等，因此可以通过平移构造平行四边形，转移线段和角.（基本模型图1）（基本模型图2）如图1，将线段CD 进行平移可得到线段EA ，连接EC ，AD. 根据平移的性质，得CD ∥EA.∴四边形CDAE 是平行四边形.∴EC ∥AD.同理，四边形CDFA 、四边形CDBG 和四边形CDHB 均为平行四边形. 如图2，平移线段AB ，即可得到▱ABCP 、▱ABDM 、▱ABND 和▱ABQC. 典型题在Rt △BAC 中，∠A=90°，D,E 分别为AB ，AC 上的点.（1）如图1，CE=AB ，BD=AE ，过点C 作CF ∥EB ，且CF=EB ，连接DF 交EB 于点G ，连接BF ，求EBDC 的值; （2）如图2,若CE=kAB ，BD=kAE ，EB DC =12，求k 的值.（典型题图1）（典型题图2）拓展题1.如图，在四边形ABCD中，AD∥BC，∠BAC=90°－1∠CAD，AC与BD相交于点E，且∠BEC=60°,若AD=5，2BD=15，求AC的长.（1题图）2.如图,在△ABC中，点D在AB的延长线上，点E在BC上，AC=BC=AD=DE，BE=BD，求∠BAC的度数.（2题图）3.阅读下面材料:数学课上，老师出示了下列问题:（1）如图1，过点B作AB的垂线BD，延长AB到点C,使AC=BD，延长BD到点E，使ED=CB，连接AE，CD，且CD的延长线交AE于点F，求∠AFC的度数;（2）如图2,在△ABC中,AB=AC=5m，D是边BC上一点，连接AD，延长CB到点E，使BE=kAD，过点E作EF，求EF的长.(用含m，k的式子表示)⊥AD，交AD的延长线于点F.若AF=kCD,tanC= 34（3题图1）（3题图2）同学们经过思考后，交流了自己的想法:小明:“通过观察和度量，发现∠AFC的度数等于45°”小伟:“通过平移线段AC，BD，ED，BC中的一条线段，可以构造两个全等三角形，进而可以获得等腰直角三角形,那么∠AFC的度数等于45°这一结论也就显而易见了.”……老师:“只要类比小伟平移线段构造全等三角形的思路与方法，那么（2）的问题就能迎刃而解.”请你根据上面的材料，完成上面的两个问题的解答过程.4.如图，在四边形ABCD中，AD∥BC，AD+BC=BD,AC与BD 相交于点F。

新课标九年级数学中考复习强效提升分数精华版中考数学复习专题代数、三角、几何综合问题

中考数学复习专题代数、三角、几何综合问题概述：代数、三角与几何综合题是较复杂与难度较大的问题，其中包括方程、函数、三角与几何等，内容基本上包含所有的初中数学知识，必须把以前的函数观念、方程思想、数形结合思想、转化与化归思想进行综合来解题．典型例题精析例1．有一根直尺的短边长2cm ，长边长10cm ，还有一块锐角为45°的直角三角形纸板，它的斜边长12cm ，如图1，将直尺的矩边DE 放置与直角三角形纸板的斜边AB 重合，且点D 与点A 重合，将直尺沿AB 方向平移如图2，设平移的长度为xcm （•0≤x ≤10），直尺和三角形纸板的重叠部分（图中阴影部分）的面积为Scm 2．（1）当x=0时（如图），S=________；当x=10时，S=___________；（2）当0<x ≤4时（如图2），求S 关于x 的函数关系式；（3）当4<x<10时，求S 关于x 的函数关系式，并求出S 的最大值（同学可在图3、•图4中画草图）解析：（1）2；2．（2）在Rt △ADG 中，∠A=45°， ∴DG=AD=x ．同理EF=AE=x+2，∴S 梯形DEGF =12（x+x+2）×2=2x+2， ∴S=2x+2．（3）①当4<x<6时，（如图5） GD=AD=x ，EF=EB=12-（x+2）=10-x ，则S △ADG =12x -2，S △BEF =12（10-x ）2，而S △ABC =12×12×6=36，∴S=36-12x 2-12（10-x ）2=-x 2+10x-14，S=-x 2+10x-14=-（x-5）2+11，∴当x=5（4<5<6）时，S 最大值=11．②当6≤x<10时（如图6）， BD=BG=12-x ，BE=EF=10-x ，S=12（12-x+10-x ）×2=22-2x ， S 随x 的增大而减小，所以S ≤10．由①、②可得，当4<x<10时，S 最大值=11．例2．如图所示，点O 2是⊙O 1上一点，⊙O 2与⊙O 1相交于A 、D 两点，BC⊥AD，垂足为D ，分别交⊙O 1、⊙O 2于B 、C 两点，延长DO 2交⊙O 2于E ，交BA 的延长线于F ，BO 2交AD 于G ，连结AG ．•（1）求证：∠BGD=∠C ；（2）若∠DO 2C=45°，求证：AD=AF ；（3）若BF=6CD ，且线段BD 、BF 的长是关于x 的方程x 2-（4m+2）x+4m 2+8=0•的两个实数根，求BD 、BF 的长．解析：（1）∵BC ⊥AD 于D ， ∴∠BDA=∠CDA=90°，∴AB 、AC 分别为⊙O 1、⊙O 2的直径．∵∠2=∠3，∠BGD+∠2=90°，∠C+∠3=90°， ∴∠BGD=∠C ．（2）∵∠DO 2C=45°，∴∠ABD=45°，∵O 2D=O 2C ，∴∠C=∠O 2DC=12（180°-∠DO 2C ）=67.5°， ∴∠4=22.5°， ∵∠O 2DC=∠ABD+∠F ， ∴∠F=∠4=22.5°，∴AD=AF ．（3）∵BF=6CD ，∴设CD=k ，则BF=6k ．连结AE ，则AE ⊥AD ，∴AE ∥BC ，∴AE AFBD BF∴AE ·BF=BD ·AF ．又∵在△AO 2E 和△DO 2C 中，AO 2=DO 2 ∠AO 2E=∠DO 2C ， O 2E=O 2C ，∴△AO 2E≌△DO 2C ，∴AE=CD=k，∴6k2=BD·AF=（BC-CD）（BF-AB）．∵∠BO2A=90°，O2A=O2C，∴BC=AB．∴6k2=（BC-k）（6k-BC）．∴BC2-7kBC+12k2=0，解得：BC=3k或BC=4k．当BC=3k，BD=2k．∵BD、BF的长是关于x的方程x2-（4m+2）x+4m2+8=0的两个实数根．∴由根与系数的关系知：BD+BF=2k+6k=8k=4m+2．整理，得：4m2-12m+29=0．∵△=（-12）2-4×4×29=-320<0，此方程无实数根．∴BC=3k（舍）．当BC=4k时，BD=3k．∴3k+6k=4m+2，18k2=4m2+8，整理，得：m2-8m+16=0，解得：m1=m2=4，∴原方程可化为x2-18x+72=0，解得：x1=6，x2=12，∴BD=6，BF=12．中考样题训练1．已知抛物线y=-x2+（k+1）x+3，当x<1时，y随着x的增大而增大，当x>1时，y 随x的增大而减小．（1）求k的值及抛物线的解析式；（2）设抛物线与x轴交于A、B两点（A在B的左边），抛物线的顶点为P，试求出A、•B、P三点的坐标，并在直角坐标系中画出这条抛物线；（3）求经过P、A、B三点的圆的圆心O′的坐标；（4）设点G（0，m）是y轴上的动点．①当点G运动到何处时，直线BG是⊙O′的切线？并求出此时直线BG的解析式．②若直线BG与⊙O相交，且另一个交点为D，当m满足什么条件时，点D在x轴的下方？2．如图，已知圆心A（0，3），⊙A与x轴相切，⊙B的圆心在x轴的正半轴上，且⊙B与⊙A外切于点P，两圆的公切线MP交y轴于点M，交x轴于点N．（1）若sin ∠OAB=45，求直线MP 的解析式及经过M 、N 、B 三点的抛物线的解析式；（2）若⊙A 的位置大小不变，⊙B 的圆心在x 轴的正半轴上移动，并使⊙B 与⊙A 始终外切，过M 作⊙B 的切线MC ，切点为C ，在此变化过程中探究： ①四边形OMCB 是什么四边形，对你的结论加以证明；②经过M 、N 、B 三点的抛物线内是否存在以BN 为腰的等腰三角形？若存在，•表示出来；若不存在，说明理由．3．如图，已知直线L 与⊙O 相交于点A ，直径AB=6，点P 在L•上移动，连结OP 交⊙O 于点C ，连结BC 并延长BC 交直线L 于点D ．（1）若AP=4，求线段PC 的长；（2）若△PAO 与△BAD 相似，求∠APO 的度数和四边形OADC 的面积．（•答案要求保留根号）LyM CBA xPO N考前热身训练1．如图，已知A 为∠POQ 的边OQ 上一点，以A 为顶点的∠MAN 的两边分别交射线OP 于M 、N 两点，且∠MAN=∠POQ=α（α为锐角），当∠MAN 为以点A 为旋转中心，AM 边从与AO•重合的位置开始，按逆时针方向旋转（∠MAN 保持不变）时，M 、N 两点在射线OP•上同时以不同的速度向右平行移动．设OM=x ，ON=y （y>x ≥0），△AOM 的面积为S ，若cos α、OA•是方程2z 2-5z+2=0的两个根．（1）当∠MAN 旋转30°（即∠OAM=30°）时，求点N 移动的距离；（2）求证：AN 2=ON ·MN ；（3）求y 与x 之间的函数关系式及自变量量x 的取值范围；（4）试写出S 随x 变化的函数关系式，并确定S 的取值范围．2．如图，已知P 、A 、B 是x 轴上的三点，点A 的坐标为（-1，0），点B 的坐标为（3，0），•且PA ：AB=1：2，以AB 为直径画⊙M 交y 轴的正半轴于点C ．（1）求证：PC 是⊙M 的切线；（2）在x 轴上是否存在这样的点Q ，使得直线QC 与过A 、C 、B•三点的抛物线只有一个交点？若存在，求点Q 的坐标，若不存在，请说明理由；（3）画⊙N ，使得圆心N 在x 轴的负半轴上，⊙N 与⊙M 外切，且与直线PC 相切于D ，•问将过A 、C 、B 三点的抛物线平移后，能否同时经过P 、D 、A 三点？为什么？M A Q P O N答案:中考样题看台1．（1）k=1，抛物线解析式y=-x2+2x+3（2）A（-1，0），B（3，0），C（1，4）（3）∵⊙O′过A、B两点，∴O′在AB的垂直平分线上，即在抛物线的对称轴上，设抛物线的对称轴交x轴于M，交⊙O′于N，则有MP×MN=MA×MB，4MN=2×2，∴MN=1，•PN=5，O′P=52<PM，∴O′点在x轴上方，∴O′M=32，∴O′（1，32）．（4）①过B点作⊙O′的切线交y轴于点G，直线BO′交y轴于点E，可求出直线BO•′的解析式为，y=-34x+94，∴E（0，94），∵BG是⊙O′的切线，BO⊥EG，∴BO=OE×OG，∴OG=4，•∴G（0，-4），求出直线BG的解析式为y=43x-4．②-4<m<0．2．（1）在Rt△AOB中，∵OA=3，sin∠OAB=45，cos∠OAB=35，∴AB=5，OB=4，BP=5-3=2．•在Rt△APM中，APAM=cos∠OAB=35，∴AM=5，OM=2，∴点M（0，-2），又△NPB∽△AOB，∴BN AB BP OB，∴BN=52，•∴ON=32，∴点B（32，0），设MP的解析式为y=kx+b，∵MP经过M、N两点，∴MP的解析式为y=43x-2，设过M、N、B的抛物线解析式为y=a（x-32）（x-4）且点M（0，-2）在其上，可得a=-13，即y=-13x2+116x-2．（2）①四边形OMCB是矩形．证明：在⊙A不动，⊙B运动变化过程中，恒有∠BAO=∠MAP，OA=AP，∠AOB=∠APM=90°，∴△AOB≌△APM，∴OB=PM，AB=AM，∴PB=OM ，而PB=BC ，∴OM=BC ，由切线长定理知MC=MP ，∴MC=OB ， ∴四边形MOBC 是平行四边形，又∵∠MOB=90°，∴四边形MOBC 是矩形．②存在，由上证明可知，Rt △MON ≌Rt △BPN ， ∴BN=MN ．因此在过M 、N 、B 三点的抛物线内有以BN 为腰的等腰三角形MNB 存在，• 由抛物线的轴对称性可知，在抛物线上必有一点M ′与M 关于其对称轴对称， ∴BN=BM ′，这样得到满足条件的三角形有两个，△MNB 和△M ′NB ． 3．（1）∵L 与⊙O 相切于点A ，∴∠4=90°，∴OP 2=OA 2+AP 2， ∵OB=OC=12AB=3，AP=4， ∴OP 2=32+42，∴OP=5， ∴PC=5-3=2．（2）∵△PAO ∽△BAD ，且∠1>∠2，∠4=90°， ∴∠2=∠APO ，∴OB=OC ，∴∠2=∠3 ∵∠1=∠2+∠3，∴∠2=2∠2=2∠APO ∴∠4=90°，∴∠1+∠APO=90° ∴3∠APO=90°，∴∠APO=30°．在Rt △BAD 中，∠2=∠APO=30°．∴AD=6sin30°=6×3．过点O 作OE ⊥BC 于点E ∵∠2=30°，BO=3，∴OE=32，BE=3×cos30°=2，∴∴S 四边形OADC =S △BAD -S △BOC =12AB ·AD=12BC ·OE=12×6×12×3294154．考前热身训练1．（1）易知OA=2，cos α=12，∠POQ=∠MAN=60°， ∴初始状态时，△AON 为等边三角形，•∴ON=OA=2，当AM 旋转到AM ′时，点N 移动到N ′， ∵∠OAM ′=30°，∠POQ=∠M ′AN•′=60°，∴∠M ′N ′A=30°，在Rt △OAN 中，ON ′=2AO=4， ∴NN ′=ON ′-ON=2，∴点N 移动的距离为2．（2）易知△OAN ∽△AMN ，∴AN 2=ON ·MN ．（3）∵MN=y-x ，∴AN 2=y 2-xy ，过A 点作AD ⊥OP ，垂足为D ，可得OD=1， ∴DN=ON-OD=y-1，在Rt △AND 中，AN 2=AD 2+DN 2=y 2-2y+4， ∴y 2-xy=y 2-2y+4，即y=42x-． ∴y>0，∴2-x>0，即x<2，又∵x ≥0，∴x 的取值范围是：0≤x<2．（4）S=12·OM ·x ，∵S 是x 的正比例函数，且比例系数2>0，∴0≤S<2·2．即0≤ 2．（1）易知⊙M 半径为2，设PA=x ，则x ：4=1：2⇒x=2，由相交弦定理推论得OC=OA ．OB=1×3，2=PO 2+OC 2=32+2=12，PM 2=42=16，MC 2=22=4，∴PM 2=PC 2+MC 2，∴∠PCM=90°．（2）易知过A 、C 、B 三点的抛物线的解析式为（x+1）（x-3），•假设满足条件的Q 点存在，坐标为（m ，0），直线QC 的解析式为y=-m， ∵直线QC 与抛物线只有一个公共点，∴方程（x+1）（x-3）∴（2+3m）2=0，∴m=-32，即满足条件的Q 点存在，•坐标为（-32，0）；（3）连结DN ，作DH ⊥PN ，垂足为H ，设⊙N 的半径为r ，则∵ND ⊥PC ， ∴ND ∥MC ，∴DN PN MC PM =，∴224r r -=， ∴r=23，∵DN 2=NH ·NP ，∴（23）2=NH·（2-23），∴NH=13，∴，∴D（-2）．∵抛物线y=-3（x+1）（x-3）平移，使其经过P、A两点的抛物线的解析式为y=-3（x+•1）（x+3）又经验证D是该抛物线上的点，∴将过A、C、B三点的抛物线平移后能同时经过P、D、A三点．。

四川省2017中考数学拓展题型突破拓展题型五多结论判断题试题

拓展题型(五) 多结论判断题在四川省的中考中，多结论判断题一般位于选择题或填空题的最后一题，综合性较强，难度较大，且考查频率较高，属于拉分题，复习时要注意这类题型的练习．类型1 代数类多结论判断题1．下列说法：①一个角的两边分别垂直于另一个角的两边，则这两个角相等；②数据5，2，7，1，2，4的中位数是3，众数是2；③平行四边形既是中心对称图形，又是轴对称图形；④命题“若x ＝1，则x 2＝1”的逆命题是真命题；⑤已知方程ax 2＋bx ＋c ＝0，当b 2－4ac ＞0时，方程一定有两个不相等的实数根．其中正确的说法有(A)A ．1个B ．2个C ．3个D ．5个2．(2016·眉山仁寿县二模)已知二次函数y ＝ax 2＋bx ＋c(a ＞0，b ＞0，c ＜0)，关于这个二次函数的图象有如下说法：①图象的开口一定向上；②图象的顶点一定在第四象限；③图象与x 轴的交点至少有一个在y 轴的右侧；④方程ax 2＋bx ＝0一定有两个不相等的实数根．以上说法正确的个数为(B)A ．1B ．2C ．3D ．43．(2014·南充)二次函数y ＝ax 2＋bx ＋c(a≠0)图象如图，下列结论：①abc＞0；②2a＋b ＝0；③当m≠1时，a ＋b ＞am 2＋bm ；④a－b ＋c ＞0；⑤若ax 21＋bx 1＝ax 22＋bx 2，且x 1≠x 2，x 1＋x 2＝2.其中正确的有(D)A ．①②③B ．②④C ．②⑤D ．②③⑤提示：由题意，得a ＜0，b ＝－2a ＞0，c ＞0，∴abc ＜0，b ＋2a ＝0.故①错误，②正确；当x ＝1时，函数有最大值a ＋b ＋c ，则当m≠1时，a ＋b ＋c ＞am 2＋bm ＋c ，即a ＋b ＞am 2＋bm.故③正确；当x ＝－1时，y ＜0，∴a －b ＋c ＜0.故④错误；由ax 21＋bx 1＝ax 22＋bx 2，得(x 1－x 2)[a(x 1＋x 2)＋b]＝0，而x 1≠x 2，则x 1＋x 2＝－b a，然后把b ＝－2a 代入，得x 1＋x 2＝2.4．(2015·南充)关于x 的一元二次方程x 2＋2mx ＋2n ＝0有两个整数根且乘积为正，关于y 的一元二次方程y 2＋2ny＋2m ＝0同样也有两个整数根且乘积为正．给出四个结论：①这两个方程的根都是负根；②(m －1)2＋(n －1)2≥2；③－1≤2m－2n≤1.其中正确结论的个数是(D)A ．0B ．1C ．2D ．3提示：①两个整数根且乘积为正，两个根同号，由韦达定理有，x 1x 2＝2n ＞0，y 1y 2＝2m ＞0，y 1＋y 2＝－2n ＜0，x 1＋x 2＝－2m ＜0，这两个方程的根都为负根，①正确；②由根判别式有：Δ＝b 2－4ac ＝4m 2－8n≥0，Δ＝b 2－4ac ＝4n2－8m≥0，∵4m 2－8n≥0，4n 2－8m≥0，∴m 2－2n≥0，n 2－2m≥0，m 2－2m ＋1＋n 2－2n ＋1＝m 2－2n ＋n 2－2m ＋2≥2，(m －1)2＋(n －1)2≥2，②正确；③由根与系数关系可得2m －2n ＝y 1y 2＋y 1＋y 2＝(y 1＋1)(y 2＋1)－1，由y 1，y 2均为负整数，故(y 1＋1)(y 2＋1)≥0，故2m －2n≥－1.同理可得：2n －2m ＝x 1x 2＋x 1＋x 2＝(x 1＋1)(x 2＋1)－1，得2n －2m≥－1，即2m －2n≤1，故③正确．5．(2016·成都高新区一诊)如图，已知二次函数y ＝ax 2＋bx ＋c(a≠0)的图象经过点(1，2)，且与x 轴交点的横坐标分别为x 1，x 2，其中－1＜x 1＜0，1＜x 2＜2，下列结论：①abc＜0；②a＜b ＜－2a ；③b 2＋8a ＜4ac ；④－1＜a ＜0.其中正确结论的序号是①②．提示：由题意，得a ＜0，c ＞0，b ＞0，∴abc ＜0.故①正确；∵0＜－b 2a ＜1，∴a ＜b ＜－2a.故②正确；∵4ac －b 24a＞2，∴4ac －b 2＜8a ，即b 2＋8a ＞4ac.故③错误；∵当x ＝1时，y ＝a ＋b ＋c ＝2(1)，当x ＝－1时，a －b ＋c ＜0(2)，当x ＝2时，4a ＋2b ＋c ＜0(3)，把(1)代入(3)，得4a ＋b ＋2－a ＜0，则a ＜－b －23.把(1)代入(2)，得b ＞1.则a ＜－1.故④错误． 6．(2016·绵阳南山模拟)已知函数y ＝k(x ＋1)(x －3k )，下列说法：①方程k(x ＋1)(x －3k)＝－3必有实数根；②若移动函数图象使其经过原点，则只能将图象向右平移1个单位；③当k>3时，抛物线顶点在第三象限；④若k<0，则当x<－1时，y 随着x 的增大而增大，其中正确的序号是①③．提示：方程k(x ＋1)(x －3k )＝－3，解得x 1＝0，x 2＝3k －1.∴①正确；∵函数y ＝k(x ＋1)(x －3k)的图象与x 轴交于(－1，0)，(3k ，0)，∴移动函数图象使其经过原点，则将图象向右平移1个单位或向右平移－3k单位；∴②错误，当k ＞3时，3k＜1，∴对称轴在y 轴的左侧，开口向上，与x 轴有两个交点，∴③正确，若k ＜0，开口向下，在对称轴的左侧，y 随着x 的增大而增大，∵函数y ＝k(x ＋1)(x －3k )的对称轴方程是x ＝3－k 2k＜0，∴④错误． 7．(2014·泸州)如图，矩形AOBC 的顶点坐标分别为A(0，3)，O(0，0)，B(4，0)，C(4，3)，动点F 在边BC 上(不与B ，C 重合)，过点F 的反比例函数y ＝k x的图象与边AC 交于点E ，直线EF 分别与y 轴和x 轴相交于点D 和G ，给出下列命题：①若k ＝4，则△OEF 的面积为83； ②若k ＝218，则点C 关于直线EF 的对称点在x 轴上； ③满足题设的k 的取值范围是0<k≤12；④若DE·EG＝2512，则k ＝1. 其中正确的命题的序号是②④(写出所有正确命题的序号)．类型2 几何类多结论判断题8．(2016·中江模拟六)如图，在半径为6 cm 的⊙O 中，点A 是劣弧BC ︵的中点，点D 是优弧BC ︵上一点，且∠D＝30°，下列四个结论：①OA⊥BC；②BC＝6 3 cm ；③sin ∠AOB ＝32；④四边形ABOC 是菱形．其中正确结论的序号是(B)A ．①③B ．①②③④C ．②③④D ．①③④9．(2016·攀枝花)如图，正方形纸片ABCD 中，对角线AC ，BD 交于点O ，折叠正方形纸片ABCD ，使AD 落在BD 上，点A 恰好与BD 上的点F 重合，展开后折痕DE 分别交AB ，AC 于点E ，G ，连接GF ，给出下列结论：①∠ADG＝22.5°；②tan ∠AED ＝2；③S △AGD ＝S △OGD ；④四边形AEFG 是菱形；⑤BE＝2OG ；⑥若S △OGF ＝1，则正方形ABCD 的面积是6＋42，其中正确的结论个数为(B)A ．2B ．3C ．4D ．5提示：①④⑤正确．∵四边形ABCD 是正方形，∴∠GAD ＝∠ADO＝45°，由折叠的性质可得，∠ADG ＝12∠ADO＝22.5°，故①正确；由折叠的性质可得AE ＝EF ，∠EFD ＝∠EAD＝90°，∴AE ＝EF 22BE ＜BE ，∴AE ＜12AB ，∴AD AE＞2，故②错误．∵∠AOB＝90°，∴AG ＝FG ＞OG ，△AGD 与△OGD 同高，∴S △AGD ＞S △OGD ，故③错误．∵∠EFD＝∠AOF＝90°，∴EF ∥AC ，∴∠FEG ＝∠AGE，∵∠AEG ＝∠FEG，∴∠AEG ＝∠AGE，∴AE ＝AG ，∵AE ＝EF ，∴AE ＝GF ，故④正确．∵四边形AEFG 是菱形，∴∠OGF ＝∠OAB＝45°，∴EF ＝GF ＝2OG ，∴BE ＝2EF ＝2×2OG ＝2OG.故⑤正确．∵四边形AEFG 是菱形，易证△OGF 是等腰直角三角形．∵S △OGF ＝1，∴OG 2＝2，解得OG ＝2.∴BE＝2OG ＝22，GF ＝2，∴AE ＝GF ＝2，∴AB ＝BE ＋AE ＝22＋2，∴S 正方形ABCD ＝AB 2＝(22＋2)2＝12＋82，故⑥错误．10．(2016·南充二诊)如图，正方形ABCD 中，P 为AB 中点，BE ⊥DP 交DP 延长线于E ，连接AE ，AF ⊥AE 交DP 于F ，连接BF ，CF.下列结论：①EF＝2AF ；②AB＝FB ；③CF∥BE；④EF＝CF.其中正确的结论有(D)A ．1个B ．2个C ．3个D ．4个提示：∵∠EAB＋∠BAF＝90°，∠FAD ＋∠BAF＝90°，∴∠EAB ＝∠DAF.∵∠EBA＋∠EPB＝∠APD＋∠FDA＝90°，∠EPB ＝∠APD，∴∠EBA ＝∠ADF.又AB ＝AD ，∴△ABE ≌△ADF ，∴AE ＝AF ，∴EF ＝2AF.故①正确；取EF 得中点M ，连接AM ，BM ，则AM ＝EM ＝MF.∵∠PEB＝∠APM＝90°，AP ＝BP ，∠EPB ＝∠MPA，∴△EPB≌△MPA，∴AM ＝BE.∴AM ＝BE ＝EM ＝MF.∴∠AMB＝∠AME＋∠EMB＝135°，∠BMF ＝180°－∠EMB＝135°.∴△ABM ≌△FBM ，∴AB ＝FB.故②正确；由①得，BE ＝DF ，∠ADF ＝∠EBP.又∠EBP＝∠PAM，∠PAM ＝∠MFB，∴∠ADF ＝∠MFB.又∠ADF＋∠FDC＝∠MFB ＋∠EBF＝90°，∴∠FDC ＝∠EBF.∴△BEF≌△DFC，∴EF ＝CF ，∠BEF ＝∠DFC＝90°.∴CF ∥BE.故③④正确．11．(2015·南充)如图，正方形ABCD 边长为1，以AB 为直径作半圆，点P 是CD 中点，BP 与半圆交于点Q ，连接DQ.给出如下结论：①DQ＝1；②PQ BQ ＝32；③S △PDQ ＝18；④cos ∠ADQ ＝35.其中正确结论是①②④．(填写序号)12．(2015·内江)如图，正方形ABCD 的边CD 在正方形ECGF 的边CE 上，O 是EG 的中点，∠EGC 的平分线GH 过点D ，交BE 于点H ，连接OH ，FH ，EG 与FH 交于点M ，对于下面四个结论：①CH⊥BE；②HO12BG ；③S 正方形ABCD ∶S 正方形ECGF ＝1∶2；④EM∶MG＝1∶(1＋2)，其中正确结论的序号为②④．6．(2015·广元)如图，在⊙O 中，AB 是直径，点D 是⊙O 上一点，点C 是AD ︵的中点，CE ⊥AB 于点E ，过点D 的切线交EC 的延长线于点G ，连接AD ，分别交CE ，CB 于点P ，Q ，连接AC ，关于下列结论：①∠BAD ＝∠ABC；②GP＝GD ；③点P 是△ACQ 的外心，其中正确结论是②③．(只需填写序号)．提示：由题意，得AC ︵＝CD ︵≠BD ︵，∴∠BAD ≠∠ABC.故①错误；连接OD ，则OD⊥GD，∠OAD ＝∠ODA.∵∠ODA＋∠GDP＝90°，∠EPA ＋∠EAP＝∠EAP＋∠GPD＝90°，∴∠GPD ＝∠GDP.∴GP＝GD.故②正确；∵CE⊥AB，∠ACB ＝90°，∴∠CAE ＋∠ACE＝∠CAB＋∠CBA＝90°.∴∠CAE ＝∠CBA.∵AC ︵＝AD ︵，∴∠CAD ＝∠CBA.∴∠CAP＝∠ACP.∴PA＝PC.∵∠ACP＋∠PCQ＝∠CAP＋∠CQP＝90°，∴∠PCQ ＝∠PQC.∴PC＝P Q.∴P 为Rt △ACQ 斜边AQ 的中点，∴P 为Rt △ACQ 的外心．故③正确．14．(2016·营山县一模)如图1，正方形纸片ABCD 的边长为2，翻折∠B，∠D ，使两个直角的顶点重合于对角线BD 上一点P ，EF 、GH 分别是折痕(如图2)．设AE ＝x(0＜x ＜2)，给出下列判断：①当x ＝1时，点P 是正方形ABCD 的中心；②当x ＝12时，EF ＋GH ＞AC ； ③当0＜x ＜2时，六边形AEFCHG 面积的最大值是114； ④当0＜x ＜2时，六边形AEFCHG 周长的值不变．其中正确的是①④(写出所有正确判断的序号)．提示：由翻折易得，△BEF 和△DGH 是等腰直角三角形．∴当AE ＝1时，重合点P 是BD 的中点，∴点P 是正方形ABCD的中心．故①正确；易得△BEF∽△BAC，∵x ＝12，∴BE ＝2－12＝32，∴BE BA ＝EF AC ，即322＝EF AC ，∴EF ＝34AC.同理，GH ＝14AC ，∴EF ＋GH ＝AC.故②错误；S 六边形AEFCHG ＝S 正方形ABCD －S △EBF －S △GDH .∵AE ＝x ，∴S 六边形AEFCHG ＝22－12BE·BF－12GD·HD＝4－12(2－x)2－12x 2＝－x 2＋2x ＋2＝－(x －1)2＋3，∴S 六边形AEFCHG 的最大值是3.故③错误；当0＜x ＜2时，∵EF ＋GH ＝AC ，C六边形AEFCHG＝AE＋EF＋FC＋CH＋HG＋AG＝(AE＋CH)＋(FC＋AG)＋(EF＋GH)＝2＋2＋22＝4＋2 2.故C六边形AEFCHG的值不变，故④正确．15．(2016·青羊区二诊)如图，菱形ABCD中，AB＝AC，点E，F分别为边AB，BC上的点，且AE＝BF，连接CE，AF 交于点H，连接DH交AG于点O.则下列结论：①△ABF≌△CAE，②∠AHC＝120°，③AH＋CH＝DH，④AD2＝OD·DH 中，正确的是①②③④．提示：由题意，易得△ABC是等边三角形．同理：△ADC是等边三角形，∴∠B＝∠EAC＝60°.易证△ABF≌△CAE(SAS)．故①正确；由①得，∠BAF＝∠ACE.∵∠AEH＝∠B＋∠BCE，∴∠AHC＝∠BAF＋∠AEH＝∠BAF ＋∠B＋∠BCE＝∠B＋∠ACE＋∠BCE＝∠B＋∠ACB＝60°＋60°＝120°；故②正确；在HD上截取HK＝AH，连接AK，∵∠AHC＋∠ADC＝120°＋60°＝180°，∴点A，H，C，D四点共圆，∴∠AHD＝∠ACD＝60°，∠AC H＝∠ADH，∴△AHK是等边三角形，∴AK＝AH，∠AKH＝60°，∴∠AKD＝∠AHC＝120°.证△AKD≌△AHC(AAS)，∴CH＝DK，∴DH ＝HK＋DK＝AH＋CH.故③正确；∵∠OAD＝∠AHD＝60°，∠ODA＝∠ADH，∴△OAD∽△AHD，∴AD∶DH＝OD∶AD，∴AD2＝OD·DH.故④正确．16．(2016·资阳)如图，在等腰直角△ABC中，∠ACB＝90°，CO⊥AB于点O，点D，E分别在边AC，BC上，且AD ＝CE，连接DE交CO于点P，给出以下结论：①△DOE是等腰直角三角形②∠CDE＝∠COE；③若AC＝1，则四边形CEOD的面积为；④AD2＋BE2－2OP2＝2DP·PE，其中所有正确结论的序号是①②③④．。

2019年中考数学复习专题《代数综合、代数几何综合》(有答案)

代数综合题一：对于实数a，b，我们用符号min{a，b}表示a，b两数中较小的数，如min{3，5}=3，因此，min{－1，－2}=________；若{}22min(1),4+=，则x=___________．x x题二：对于实数c，d，我们用符号max{c，d}表示c，d两数中较大的数，如max{3，5}=5，因此，题四：在平面直角坐标系中，点P(0，m2)(m>0)在y轴正半轴上，过点P作平行于x轴的直线，分别交抛物线C1：y A、B，交抛物线C2：y于点C、D．(1)如图①，原点O关于直线AB的对称点为点Q，分别连接OA，OB，QC 和QD，求△AOB与△CQD面积比为_______．(2)如图②过点A作y轴的平行线交抛物线C2于点E，过点D作y轴的平行线交抛物线C1于点F，在y轴上任取一点M，连接MA、ME、MD和MF，则△MAE与△MDF面积的比值为_______．题七：设函数y =⎩⎨⎧<+≥+-0130242x x x x x ，　，，若互不相等的实数x 1，x 2，x 3，满足y 1=y 2=y 3，求x 1+x 2+x 3的取值范围．题八：在平面直角坐标系xOy 中，抛物线y =243x x ++与x 轴交于点A 、B (点A 在点B 的左侧)，与y 轴交于点C ． (1)求直线AC 的表达式；(2)在x 轴下方且垂直于y 轴的直线l 与抛物线交于点P (x 1，y 1)，Q (x 2，y 2)，与直线AC 交于点N (x 3，y 3)，若x 1>x 2>x 3，结合函数的图象，求x 1+x 2+x 3的取值范围．参考答案题一：－2，－3或2．详解：∵－2<－1，∴min{－1，－2}=－2，∵{}22+=，x xmin(1),4当(x+1)2=x2时，解得：x=－0.5，(x+1)2=x2=0.25，这时不可能得出最小值为4，当x>－0.5，(x+1)2>x2，则x2=4，解得x1=2或x2=－2(舍去)，当x<－0.5，(x+1)2<x2，则(x+1)2=4，解得x1=－3或x2=1(舍去)，∴x=－3或x=2．题二：∵{}22++=，max22,2x x x当x2+2x+2=x2时，解得：x=－1，x2+2x+2=x2=1，这时不可能得出最大值为2，当x>－1，x2+2x+2>x2，则x2+2x+2=2，解得x1=0或x2=－2(舍去)，∴x=0．题三：∴C (－3m ，m 2)，D (3m ，m 2)，∴CD =6m ，∵O 、Q 关于直线CD 对称， ∴PQ =OP ，∵CD ∥x 轴，∴∠DPQ =∠DPO =90°，∴△AOB 与△CQD 的高相等， PQ CD PO AB ⋅⋅2121=mm 64=32．AEM DFMS S=∵S △OEF +S △OFD =S △OEC +S 梯形ECDF ，而S △OFD =S △OEC =2， 2详解：先作出函数y =⎩⎨⎧<+≥+-0130242x x x x x ，　，的图象，如图，不妨设x 1<x 2<x 3，∵y =242x x -+(x ≥0)的对称轴为x =2，y 1=y 2，∴x 2+x 3=4， ∵y =242x x -+(x ≥0)的顶点坐标为(2，－2)，令y =－2，代入y =3x +1，解得：x =－1，∴－1<x 1<0，则x 1+x 2+x 3的取值范围是：－1+4<x 1+x 2+x 3<0+4，∴3<x 1+x 2+x 3<4．题八： (1)y =x +3；(2)－8<x 1+x 2+x 3<－7．详解：(1)由y =243x x ++得到：y =(x +3)(x +1)，C，∴A (－3，0)，B (－1，0)，设直线AC 的表达式为：y =kx +b (k ≠0)， ∴⎩⎨⎧==+303-b b k ，解得:⎩⎨⎧==31b k ，所以直线AC 的表达式为y =x +3，(2)由y =243x x ++得到：y =(x +2)2－1，∴抛物线y =243x x ++的对称轴是x =－2，顶点坐标是(－2，－1)，∵y 1=y 2，∴x 1+x 2=－4，令y =－1，代入y =x +3，解得：x =－4，∵x 1>x 2>x 3，∴－4<x 3<－3，∴－4－4<x 1+x 2+x 3<－3－4，∴－8<x 1+x 2+x 3<－7．代数几何综合题一：如图，已知抛物线y=ax2+bx+c（a≠0）与x轴交于A（-1，0）、B（3，0）两点，与y轴交于点C（0，3）．（1）求抛物线的解析式及顶点M坐标；（2）在抛物线的对称轴上找到点P，使得△P AC的周长最小，并求出点P 的坐标.题二：如图，已知抛物线y=ax2+bx+c（a≠0）与x轴交于点A（-4，0），B（1，0），与y轴交于点D（0，4），点C（-2，n）也在此抛物线上．（1）求此抛物线的解析式及点C的坐标；（2）设BC交y轴于点E，连接AE，AC请判断△ACE的形状，并说明理由.题三：在平面直角坐标系xOy中，给出如下定义：若点P在图形M上，点Q在图形N上，称线段PQ长度的最小值为图形M，N的密距，记为d（M，N）．特别地，若图形M，N有公共点，规定d（M，N）=0．（1）如图1，⊙O的半径为2，①点A（0，1），B（4，3），则d（A，⊙O）=，d（B，⊙O）=.是⊙O的关联点，求m的取值范围；（2）若线段EF上的所有点都是某个圆的关联点，求这个圆的半径r的取值范围．参考答案题一：（1）y =214x --+（），M （1，4）；（2）P （1，2）. 详解：（1）∵抛物线y =ax 2+bx +c （a ≠0）过A （-1，0）、B （3，0），C （0，3）三点，∴93003a b c a b c c ++=⎧⎪-+=⎨⎪=⎩，解得12c=3a b =-⎧⎪=⎨⎪⎩.故抛物线的解析式为222314y x x x =-++=--+（），故顶点M 为（1，4）；（2）如图1，∵点A 、B 关于抛物线的对称轴对称，∴连接BC与抛物线对称轴交于一点，即为所求点P ．设对称轴与x 轴交于点H ，题二：（1）y =-x 2-3x +4，C （-2，6）；（2）△ACE 为等腰直角三角形.详解：（1）∵抛物线经过A 、B 、D 三点，∴代入抛物线解析式可得164004a b c a b c c -+⎧⎪++⎨⎪⎩＝＝＝，解得134a b c -⎧⎪-⎨⎪⎩＝＝＝，∴抛物线的解析式为 y =-x 2-3x +4， ∵点C （-2，n ）也在此抛物线上，∴n =-4+6+4=6，∴C 点坐标为（-2，6）；∴AE2+CE2=20+20=40=AC2，且AE=CE，∴△ACE为等腰直角三角形.。

多命题结论几何选择题(一)

多命题结论几何选择题（一）一、例题讲解：例1、如图1，已知△ABC 中，AB ＝AC ，∠BAC ＝90°，直角∠EPF 的顶点P 是BC 中点，两边PE 、PF 分别交AB 、AC 于点E 、F ，给出以下四个结论：①AE ＝CF ；②△EPF 是等腰直角三角形；③S 四边形AEPF ＝21S △ABC ；④EF ＝AP 。

当∠EPF 在△ABC 内绕顶点P 旋转时（点E 不与A 、B 重合），上述结论中始终正确的有( )A ①②③④B ①②③C ②③④D ①③④例2、如图2，AB 是⊙O 的直径，点P 在BA 的延长线上，弦CD 交AB 与E ，连结OD 、PC 、BC ，∠AOD=2∠ABC ，∠P=∠D ，过E 作弦GF ⊥BC 交圆于G 、F 两点，连结CF 、BG 。

则下列结论其中正确的是（）①CD ⊥AB ； ②PC 是⊙O 的切线；③OD ∥GF ④弦CF 的弦心距等于12BG 。

A ．①②④ B ．③④ C ．①②③ D ．①②③④例3、如图3，PA 、PB 是⊙O 的切线，A 、B 为切点，AC 为⊙O 的直径，弦BD ⊥AC.下列结论：①∠P+2∠D ＝180°； ②∠BOC ＝∠BAD ；③∠DBO ＝∠ABP ； ④∠ABP ＝∠ABD其中正确结论有（）个（A ）1；（B ）2；（C ）3；（D ）4二、课堂练习：1、如图4，⊙O 的弦AB ⊥CD 于H ，D 、E 关于AB 对称，BE 延长线交⊙O 于F ，连接FC ，作OG ⊥AB 于G ，则下列结论：①FC =CE ；②AF =AD =21CF ；④E 点关于BC 的对称点必在⊙O 上，正确的是（）A ．①②③④B ．①②③C ．②③④D ．①②④2、如图5，AB 是⊙O 的直径，弧AC=弧CE ，弦AE 交CD 于F ，交BC 于M ，下列结论：①AE=CD ；②AF=CF ；③AF=ME ；④∠EAB =∠HDO 。

2023年中考数学综合模拟试题四(含答案)

2023年中考数学综合模拟试题四一、选择题（每题3分，共30分） 1、－2 023的相反数等于( ) A ．2 023 B ．－2 023C. 12023D ．－120232、下列图形中,既可以看作是轴对称图形,又可以看作是中心对称图形的为( )3、下列运算正确的是( )A ．(－m 2n)3＝－m 6n 3B ．m 5－m 3＝m 2C ．(m ＋2)2＝m 2＋4D ．(12m 4－3m)÷3m＝4m 34、由一些大小相同的小正方体搭成的几何体的主视图和俯视图,如图所示,则搭成该几何体的小正方体最多是（）个. A.4 B.5 C.6 D.75、关于x 的一元二次方程(a ＋2)x 2－3x ＋1＝0有实数根，则a 的取值范围是( )A ．a ＜14且a≠－2B ．a≤14C ．a≤14且a≠－2D ．a ＜146、我国古代某数学著作中有“多人共车”问题:“今有三人共车,二车空;二人共车,九人步.问:人与车各几何?”其大意如下:有若干人要坐车,如果每3人坐一辆车,那么有2辆空车;如果每2人坐一辆车,那么有9人需要步行,问人与车各多少?设共有x 人,y 辆车,则可列方程组为( )A.{3(y −2)=x 2y −9=x B.{3(y +2)=x 2y +9=x C.{3(y −2)=x 2y +9=x D.{3(y +2)=x2y −9=x7、如图，D ，E ，F 分别是△ABC 各边中点，则以下说法错误的是( ) A ．△BDE 和△DCF 的面积相等 B ．四边形AEDF 是平行四边形 C ．若AB ＝BC ，则四边形AEDF 是菱形D ．若∠A＝90°，则四边形AEDF 是矩形（第7题图）8、关于x 的不等式组{x −m <0,3x −1>2(x −1)无解,那么m 的取值范围为( )A. m ≤-1B.m<-1C.-1<m ≤0D.-1≤m<09、如图所示,已知点A,B 分别在反比例函数y= 1x (x>0), y=- 4x (x>0）)的图象上,且OA ⊥OB,则OBOA 的值为( ) A.√2 B.4 C.√3 D.2（第9题图）10、如图所示,△ABC 是等腰直角三角形,∠A=90°,BC=4,点P 是 △ABC 边上一动点,沿B →A →C 的路径移动,过点P 作PD ⊥BC 于点D,设 BD=x,△BDP 的面积为y,则下列能大致反映y 与x 函数关系图象的是( )二、填空题（每题3分，共24分）11、我国某探测器距离地球约3.2亿千米.数据3.2亿千米用科学记数法可以表示为 km.12、一组数据5,2,x,6,4的平均数是4,这组数据的方差_____.13、动物学家通过大量的调查，估计某种动物活到20岁的概率为0.8，活到25岁的概率为0.5，据此若设刚出生的这种动物共有a 只，则现年20岁的这种动物活到25岁的概率是 ________．14、如图所示,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于12MN的长为半径作弧,两弧相交于点P;③作射线AP,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD的周长为. （第14题图）15、某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到敬老院慰问老人.如果分给每位老人 4盒牛奶,那么剩下28盒牛奶;如果分给每位老人 5盒牛奶,那么最后一位老人分得的牛奶不足4盒,但至少1盒.则这个敬老院的老人最少有__________人.16、如图，在矩形ABCD中，AB＝3，AD＝4，E，F分别是边BC，CD上一点，EF⊥AE，将△ECF沿EF翻折得△EC′F，连接AC′，当BE＝________时，△AEC′是以AE 为腰的等腰三角形．（第16题图）（第17题图）（第18题图）17、如图，已知正方形ABCD的边长为6，点F是正方形内一点，连接CF，DF，且∠ADF＝∠DCF，点E是AD边上一动点，连接EB，EF，则EB＋EF长度的最小值为 ________________．18、如图，△ABC是边长为2的等边三角形，AD是BC边上的高，CE是AB边上的高．将△ADC绕点D顺时针旋转得到，其中点A的对应点为点，点C的对应点为点．在旋转过程中，当点落在直线EC上时，的长为______．三、解答题（共9小题，计66分）19、（5分）(12)-1-√−83+|√3-2|+2sin 60°.A DC''A'C'A'A C'20、（5分）先化简,再求值:(3a+1-a+1)÷a 2−4a 2+2a+1,其中a 从-1,2,3中取一个你认为合适的数代入求值.21、（6分）将正面分别写着数字1，2，3的三张卡片(注：这三张卡片的形状、大小、质地、颜色等其他方面完全相同，若背面朝上放在桌面上，这三张卡片看上去无任何差别)洗匀后，背面朝上放在桌面上，甲从中随机抽取一张卡片，记该卡片上的数字为m ，然后放回洗匀，背面朝上放在桌面上，再由乙从中随机抽取一张卡片，记该卡片上的数字为n ，组成一数对(m ，n)． (1)请写出(m ，n)所有可能出现的结果；(2)甲、乙两人玩游戏，规则如下：按上述要求，两人各抽一次卡片，卡片上数字之和为奇数则甲赢，数字之和为偶数则乙赢．你认为这个游戏公平吗？请说明理由．22、（6分）如图所示，某测量小组为了测量山BC 的高度，在地面A 处测得山顶B 的仰角为45°，然后沿着坡度为1∶3的坡面AD 走了200 m 达到D 处，此时在D 处测得山顶B 的仰角为60°，求山BC 的高度．(结果保留根号)23、（6分）)某校从全体学生中随机抽取部分学生,调查他们平均每周的劳动时间t(单位:h),按劳动时间分为四组:A 组“t<5”,B 组“5≤t<7”,C 组“7≤t<9”,D 组“t ≥9”.将收集的数据整理后,绘制成如图所示的两幅尚不完整的统计图.根据以上信息,解答下列问题:(1)这次抽样调查的样本容量是,C组所在扇形的圆心角的大小是;(2)将条形统计图补充完整;(3)该校共有1 500名学生,请估计该校平均每周劳动时间不少于7 h的学生人数.24、(8分)某乡镇对河道进行整治,由甲乙两工程队合做 20天可完成.已知甲工程队单独整治需60天完成.(1)乙工程队单独完成河道整治需多少天?(2)若甲乙两工程队合做a天后,再由甲工程队单独做天(用含a 的代数式表示)可完成河道整治任务;(3)如果甲工程队每天施工费为5 000元,乙工程队每天施工费为1.5万元,先由甲乙两工程队合做,剩余工程由甲工程队单独完成,要使支付两工程队费用最少,并且确保河道在40天内(含 40天)整治完毕,问需支付两工程队费用最少多少万元?25、(8分)如图所示，在Rt△ABC中，∠ABC＝90°，以AB 为直径作⊙O，点D 为⊙O上一点，且CD＝CB，连接DO并延长交CB的延长线于点E.(1)判断直线CD与⊙O的位置关系，并说明理由；(2)若BE＝2，DE＝4，求圆的半径及AC的长．26.（10分）已知在△ABC中，O为BC边的中点，连接AO，将△AOC绕点O顺时针方向旋转（旋转角为钝角），得到△EOF，连接AE，CF．（1）如图1，当∠BAC＝90°且AB＝AC时，则AE与CF满足的数量关系是；（2）如图2，当∠BAC＝90°且AB≠AC时，（1）中的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由．（3）如图3，延长AO到点D，使OD＝OA，连接DE，当AO＝CF＝5，BC ＝6时，求DE的长．27.（12分）已知，抛物线y＝x2+bx+c与x轴交点为A（﹣1，0）和点B，与y轴交点为C（0，﹣3），直线L：y＝kx﹣1与抛物线的交点为点A和点D．（1）求抛物线和直线L的解析式；（2）如图，点M为抛物线上一动点（不与A、D重合），当点M在直线L下方时，过点M作MN∥x轴交L于点N，求MN的最大值；（3）点M为抛物线上一动点（不与A、D重合），M'为直线AD上一动点，是否存在点M，使得以C、D、M、M′为顶点的四边形是平行四边形？如果存在，请直接写出点M的坐标，如果不存在，请说明理由．参考答案二．填空题第11题：3.2×108 第12题：2 第13题： 58第14题：15 第15题：30 第16题：78 或 43第17题：3√13−3 第18题：√11−√32或√11+√32三．解答题第19题：原式=8第20题：化简，可得，原式=−a −1，因为a ≠−1且a ≠2，所以，当a =3时，原式=−4第21题：（1）所有可能出现的结果为：(1，1) 、(1，2) 、(1，3) 、(2，1) 、(2，2) 、(2，3) 、(3，1) 、(3，2) 、(3，3) 。

中考数学复习专题练习：投影与视图(解析版)

中考数学复习专题练习：投影与视图一、单选题（共19题；共38分）1、如图所示，该几何体的俯视图是（）A 、B 、C 、D 、2、如图，是一圆锥的左视图，根据图中所标数据，圆锥侧面展开图的扇形圆心角的大小为（）A、90°B、120°C、135°D、150°3、把一个正六棱柱如图1摆放，光线由上向下照射此正六棱柱时的正投影是（）A 、B 、C 、D 、4、一个几何体的三视图如图所示，则这个几何体是（）A、球体B、圆锥C、棱柱D、圆柱5、下列几何体中，主视图和俯视图都为矩形的是（）A 、B 、C 、D 、6、圆桌面（桌面中间有一个直径为0.4m的圆洞）正上方的灯泡（看作一个点）发出的光线照射平行于地面的桌面后，在地面上形成如图所示的圆环形阴影．已知桌面直径为1.2m，桌面离地面1m，若灯泡离地面3m，则地面圆环形阴影的面积是（）A、0.324πm2B、0.288πm2C、1.08πm2D、0.72πm27、一个几何体的三视图如图所示，则该几何体的表面积为（）A、4πB、3πC、2π+4D、3π+48、三本相同的书本叠成如图所示的几何体，它的主视图是（）A 、B 、C 、D 、9、如图所示正三棱柱的主视图是（）A 、B 、C 、D 、10、下列四个几何体中，左视图为圆的是（）A 、B 、C 、D 、11、由六个相同的立方体搭成的几何体如图所示，则它的主视图是（）A 、B 、C 、D 、12、将如图绕AB边旋转一周，所得几何体的俯视图为（）A 、B 、C 、D 、13、如图是一个由4个相同的正方体组成的立体图形，它的主视图是（）A 、B 、C 、D 、14、如图，是由两个相同的小正方体和一个圆锥体组成的立体图形，其俯视图是（）A 、B 、C 、D 、15、如图，一个正方体切去一个三棱锥后所得几何体的俯视图是（）A 、B 、C 、D 、16、如图是由5个相同的小正方体构成的几何体，其左视图是（）A 、B 、C 、D 、17、如图，小明同学将一个圆锥和一个三棱柱组成组合图形，观察其三视图，其俯视图是（）A 、B 、C 、D 、18、如图是某工件的三视图，则此工件的表面积为（）A、15πcm2B、51πcm2C、66πcm2D、24πcm219、如图，按照三视图确定该几何体的全面积是（图中尺寸单位：cm）（）A、40πcm2B、65πcm2C、80πcm2D、105πcm2二、填空题（共4题；共4分）20、如图，小军、小珠之间的距离为2.7m，他们在同一盏路灯下的影长分别为1.8m，1.5m，已知小军、小珠的身高分别为1.8m，1.5m，则路灯的高为________m．21、一个侧面积为16 πcm2的圆锥，其主视图为等腰直角三角形，则这个圆锥的高为________cm．22、如果一个圆锥的主视图是等边三角形，俯视图是面积为4π的圆，那么它的左视图的高是________．23、如图是一个圆柱体的三视图，由图中数据计算此圆柱体的侧面积为________．（结果保留π）三、作图题（共1题；共5分）24、由一些相同的小正方体搭成的几何体的左视图和俯视图如图所示，请在网格中涂出一种该几何体的主视图，且使该主视图是轴对称图形．四、解答题（共1题；共5分）25、如图，是由若干个完全相同的小正方体组成的一个几何体．（1）请画出这个几何体的左视图和俯视图；（用阴影表示）（2）如果在这个几何体上再添加一些相同的小正方体，并保持这个几何体的俯视图和左视图不变，那么最多可以再添加几个小正方体？五、综合题（共1题；共15分）26、如图，在矩形纸片ABCD中，AB=4，AD=12，将矩形纸片折叠，使点C落在AD边上的点M 处，折痕为PE，此时PD=3．(1)求MP的值(2)在AB边上有一个动点F，且不与点A，B重合．当AF等于多少时，△MEF的周长最小？(3)若点G，Q是AB边上的两个动点，且不与点A，B重合，GQ=2．当四边形MEQG的周长最小时，求最小周长值．（计算结果保留根号）答案解析一、单选题【答案】C【考点】简单组合体的三视图【解析】【解答】解：从上往下看，可以看到C选项所示的图形．故选：C．【分析】根据俯视图是从物体的上面看得到的视图进行解答即可．本题考查了三视图的知识，掌握俯视图是从物体的上面看得到的视图是解题的关键．【答案】B【考点】圆锥的计算，由三视图判断几何体【解析】【解答】解：∵圆锥的底面半径为3，∴圆锥的底面周长为6π，∵圆锥的高是6 ，∴圆锥的母线长为=9，设扇形的圆心角为n°，∴=6π，解得n=120．答：圆锥的侧面展开图中扇形的圆心角为120°．故选B．【分析】根据圆锥的底面半径得到圆锥的底面周长，也就是圆锥的侧面展开图的弧长，根据勾股定理得到圆锥的母线长，利用弧长公式可求得圆锥的侧面展开图中扇形的圆心角．本题考查了圆锥的计算，圆锥的侧面展开图是一个扇形，此扇形的弧长等于圆锥底面周长，扇形的半径等于圆锥的母线长．本题就是把的扇形的弧长等于圆锥底面周长作为相等关系，列方程求解．【答案】A【考点】平行投影【解析】【解答】解：把一个正六棱柱如图摆放，光线由上向下照射此正六棱柱时的正投影是正六边形．故选A．【分析】根据平行投影特点以及图中正六棱柱的摆放位置即可求解．本题考查了平行投影特点，不同位置，不同时间，影子的大小、形状可能不同，具体形状应按照物体的外形即光线情况而定．【答案】D【考点】由三视图判断几何体【解析】【解答】解：由于主视图和左视图为长方形可得此几何体为柱体，由俯视图为圆可得为圆柱体．故选D．【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形．本题考查了由三视图来判断几何体，还考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力．【答案】B【考点】简单几何体的三视图【解析】【解答】解：A、圆锥的主视图是三角形，俯视图是带圆心的圆，故本选项错误；B、圆柱的主视图是矩形、俯视图是矩形，故本选项正确；C、球的主视图、俯视图都是圆，故本选项错误；D、三棱柱的主视图为矩形和俯视图为三角形，故本选项错误．故选：B．【分析】分别分析四个选项中圆锥、圆柱、球体、三棱柱的主视图、俯视图，从而得出都为矩形的几何体．本题考查了简单几何体的三视图，关键是培养学生的思考能力和对几何体三种视图的空间想象能力．【答案】D【考点】相似三角形的应用，中心投影【解析】【解答】解：如图所示：∵AC⊥OB，BD⊥OB，∴△AOC∽△BOC，∴= ，即= ，解得：BD=0.9m，同理可得：AC′=0.2m，则BD′=0.3m，∴S圆环形阴影=0.92π﹣0.32π=0.72π（m2）．故选：D．【分析】先根据AC⊥OB，BD⊥OB可得出△AOC∽△BOD，由相似三角形的对应边成比例可求出BD的长，进而得出BD′=0.3m，再由圆环的面积公式即可得出结论．本题考查的是相似三角形的应用以及中心投影，利用相似三角形的对应边成比例得出阴影部分的半径是解题关键．【答案】D【考点】由三视图判断几何体【解析】【解答】解：观察该几何体的三视图发现其为半个圆柱放在一个长方体的上面组成的一个几何体，半圆柱的直径为2，长方体的长为2，宽为1，高为1，故其表面积为：π×12+（π+2）×2=3π+4，故选D．【分析】首先根据三视图判断几何体的形状，然后计算其表面积即可．本题考查了由三视图判断几何体的知识，解题的关键是首先根据三视图得到几何体的形状，难度不大．【答案】B【考点】简单组合体的三视图【解析】【解答】解：观察图形可知，三本相同的书本叠成如图所示的几何体，它的主视图是．故选：B．【分析】主视图是分别从物体正面看，所得到的图形．本题考查了几何体的三种视图，掌握定义是关键．注意所有的看到的棱都应表现在三视图中．【答案】C【考点】简单几何体的三视图【解析】【解答】解：如图所示正三棱柱的主视图是平行排列的两个矩形，故选B．【分析】找到从正面看所得到的图形即可．本题考查了三视图的知识，主视图是从物体的正面看得到的视图．注意本题不要误选C．【答案】C【考点】简单几何体的三视图【解析】【解答】解：因为圆柱的左视图是矩形，圆锥的左视图是等腰三角形，球的左视图是圆，正方体的左视图是正方形，所以，左视图是圆的几何体是球．故选：C.【分析】四个几何体的左视图：圆柱是矩形，圆锥是等腰三角形，球是圆，正方体是正方形，由此可确定答案．主要考查立体图形的左视图，关键根据圆柱是矩形，圆锥是等腰三角形，球是圆，正方体是正方形解答．【答案】A【考点】简单组合体的三视图【解析】【解答】解：结合几何体发现：从主视方向看到上面有一个正方形，下面有3个正方形，故选A．【分析】根据主视方向确定看到的平面图形即可．本题考查了简单组合体的三视图的知识，解题的关键是了解主视图是由主视方向看到的平面图形，属于基础题，难度不大．2、【答案】B【考点】点、线、面、体，简单组合体的三视图【解析】【解答】解：将该图形绕AB旋转一周后是由上面一个圆锥体、下面一个圆柱体的组合而成的几何体，从上往下看其俯视图是外面一个实线的大圆（包括圆心），里面一个虚线的小圆，故选：B．【分析】本题考查了简单组合体的三视图，从上面看得到的视图是俯视图．根据旋转抽象出该几何体，俯视图即从上向下看，看到的棱用实线表示；实际存在，没有被其他棱挡住，看不到的棱用虚线表示．【答案】A【考点】简单组合体的三视图【解析】【解答】解：从正面看易得第一层有2个正方形，第二层左边有一个正方形，第三层左边有一个正方形．故选A．【分析】本题考查了简单组合体的三视图的知识，主视图是从物体的正面看得到的视图．找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．2、【答案】C【考点】简单组合体的三视图【解析】【解答】解：从上面看，圆锥看见的是：圆和点，两个正方体看见的是两个正方形．故答案为：C．【分析】此题主要考查了三视图的知识，关键是掌握三视图的几种看法．找到从上面看所得到的图形即可，注意所有的看到的棱都应表现在俯视图中．【答案】D【考点】简单组合体的三视图【解析】【解答】解：所给图形的俯视图是D选项所给的图形．故选D．【分析】俯视图是从上向下看得到的视图，结合选项即可作出判断．本题考查了简单组合体的三视图，属于基础题，关键掌握俯视图是从上向下看得到的视图．2、【答案】C【考点】简单组合体的三视图【解析】【解答】解：观察图形可知，如图是由5个相同的小正方体构成的几何体，其左视图是．故选：C．【分析】几何体的左视图有2列，每列小正方形数目分别为2，1；据此画出图形即可求解．此题考查了简单组合体的三视图，主视图、左视图、俯视图是分别从物体正面、侧面和上面看所得到的图形．2、【答案】B【考点】简单组合体的三视图【解析】【解答】解：由题意得：俯视图与选项B中图形一致．故选B．【分析】根据组合图形的俯视图，对照四个选项即可得出结论．本题考查了简单组合体的三视图，解题的关键是会画简单组合图形的三视图．本题属于基础题，难度不大，解决该题型题目时，掌握简单组合体三视图的画法是关键．【答案】D【考点】由三视图判断几何体【解析】【解答】解：由三视图，得，OB=3cm，0A=4cm，由勾股定理，得AB= =5cm，圆锥的侧面积×6π×5=15πcm2，圆锥的底面积π×（）2=9πcm，圆锥的表面积15π+9π=24π（cm2），故选：D．【分析】根据三视图，可得几何体是圆锥，根据勾股定理，可得圆锥的母线长，根据扇形的面积公式，可得圆锥的侧面积，根据圆的面积公式，可得圆锥的底面积，可得答案．本题考查了由三视图判断几何体，利用三视图得出圆锥是解题关键，注意圆锥的侧面积等于圆锥的底面周长与母线长乘积的一半．【答案】B【考点】由三视图判断几何体【解析】【解答】解：由主视图和左视图为三角形判断出是锥体，由俯视图是圆形可判断出这个几何体应该是圆锥；根据三视图知：该圆锥的母线长为8cm，底面半径为10÷2=5cm，故表面积=πrl+πr2=π×5×8+π×52=65πcm2．故选：B．【分析】由主视图和左视图确定是柱体，锥体还是球体，再由俯视图确定具体形状，确定圆锥的母线长和底面半径，从而确定其表面积．考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．二、填空题2、【答案】3【考点】中心投影【解析】【解答】解：如图，∵CD∥AB∥MN，∴△ABE∽△CDE，△ABF∽△MNF，∴，，即，，解得：AB=3m，答：路灯的高为3m．【分析】根据CD∥AB∥MN，得到△ABE∽△CDE，△ABF∽△MNF，根据相似三角形的想知道的，，即可得到结论．本题考查了中心投影，相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键．2、【答案】4【考点】圆锥的计算，由三视图判断几何体，等腰直角三角形【解析】【解答】解：设底面半径为r，母线为l，∵主视图为等腰直角三角形，∴2r= l，∴侧面积S侧=πrl=2πr2=16 πcm2，解得r=4，l=4 ，∴圆锥的高h=4cm，故答案为：4．【分析】设底面半径为r，母线为l，由轴截面是等腰直角三角形，得出2r= l，代入S侧=πrl，求出r，l，从而求得圆锥的高．本题考查了圆锥的计算，解题的关键是能够熟练掌握有关的计算公式，难度不大．2、【答案】2【考点】圆锥的计算，由三视图判断几何体【解析】【解答】解：设圆锥的底面圆的半径为r，则πr2=4π，解得r=2，因为圆锥的主视图是等边三角形，所以圆锥的母线长为4，所以它的左视图的高= =2 ．故答案为2 ．【分析】先利用圆的面积公式得到圆锥的底面圆的半径为2，再利用等边三角形的性质得母线长，然后根据勾股定理计算圆锥的高．本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．【答案】24π【考点】由三视图判断几何体【解析】【解答】解：由图可知，圆柱体的底面直径为4，高为6，所以，侧面积=π（×4）2×6=24π．故答案为：24π．【分析】根据主视图确定出圆柱体的底面直径与高，然后根据圆柱体的侧面积公式列式计算即可得解．本题考查了立体图形的三视图和学生的空间想象能力，圆柱体的侧面积公式，根据主视图判断出圆柱体的底面直径与高是解题的关键．三、作图题【答案】解：如图所示，【考点】轴对称图形，由三视图判断几何体，作图-三视图【解析】【分析】根据俯视图和左视图可知，该几何体共两层，底层有9个正方体，上层中间一行有正方体，若使主视图为轴对称图形可使中间一行、中间一列有一个小正方体即可．本题主要考查三视图还原几何体及轴对称图形，解题的关键是根据俯视图和左视图抽象出几何体的大概轮廓．四、解答题【答案】解：（1）画图如下：（2）在第二层第二列第二行和第三行各加一个；第三层第二列第三行加一个，第三列第三行加1个，2+1+1=4（个）．故最多可再添加4个小正方体．【考点】作图-三视图【解析】【分析】（1）由已知条件可知，左视图有3列，每列小正方形数目分别为3，2，1；俯视图有3列，每列小正方数形数目分别为3，2，1，据此可画出图形．（2）可在第二层第二列第二行和第三行各加一个；第三层第二列第三行加一个，第三列第三行加1个，相加即可求解．五、综合题【答案】（1）解：∵四边形ABCD为矩形，∴CD=AB=4，∠D=90°，∵矩形ABCD折叠，使点C落在AD边上的点M处，折痕为PE，∴PD=PH=3，CD=MH=4，∠H=∠D=90°，∴MP==5；（2）解：如图1，作点M关于AB的对称点M′，连接M′E交AB于点F，则点F即为所求，过点E作EN⊥AD，垂足为N，∵AM=AD﹣MP﹣PD=12﹣5﹣3=4，∴AM=AM′=4，∵矩形ABCD折叠，使点C落在AD边上的点M处，折痕为PE，∴∠CEP=∠MEP，而∠CEP=∠MPE，∴∠MEP=∠MPE，∴ME=MP=5，在Rt△ENM中，MN===3，∴NM′=11，∵AF∥ME，∴△AFM′∽△NEM′，∴=，即=，解得AF=，即AF=时，△MEF的周长最小.（3）解：如图2，由（2）知点M′是点M关于AB的对称点，在EN上截取ER=2，连接M′R交AB于点G，再过点E作EQ∥RG，交AB于点Q，∵ER=GQ，ER∥GQ，∴四边形ERGQ是平行四边形，∴QE=GR，∵GM=GM′，∴MG+QE=GM′+GR=M′R，此时MG+EQ最小，四边形MEQG的周长最小，在Rt△M′RN中，NR=4﹣2=2，M′R==5，∵ME=5，GQ=2，∴四边形MEQG的最小周长值是7+5．【考点】翻折变换（折叠问题），简单几何体的三视图【解析】【解答】（1）根据折叠的性质和矩形性质以得PD=PH=3，CD=MH=4，∠H=∠D=90°，然后利用勾股定理可计算出MP=5；（2）如图1，作点M关于AB的对称点M′，连接M′E交AB于点F，利用两点之间线段最短可得点F即为所求，过点E作EN⊥AD，垂足为N，则AM=AD﹣MP﹣PD=4，所以AM=AM′=4，再证明ME=MP=5，接着利用勾股定理计算出MN=3，所以NM′=11，然后证明△AFM′∽△NEM′，则可利用相似比计算出AF；（3）如图2，由（2）知点M′是点M关于AB的对称点，在EN上截取ER=2，连接M′R交AB于点G，再过点E作EQ∥RG，交AB于点Q，易得QE=GR，而GM=GM′，于是MG+QE=M′R，利用两点之间线段最短可得此时MG+EQ最小，于是四边形MEQG的周长最小，在Rt△M′RN中，利用勾股定理计算出M′R=5，易得四边形MEQG的最小周长值是7+5．【分析】此题考查了几何图形中的折叠问题，涉及勾股定理，三角形相似以及最值问题。

2020年中考数学复习专题练：《四边形综合》(包含答案)

2020年中考数学复习专题练：《四边形综合》1．如图①所示，已知正方形ABCD 和正方形AEFG ，连接DG ，BE ．（1）发现：当正方形AEFG 绕点A 旋转，如图②所示．①线段DG 与BE 之间的数量关系是；②直线DG 与直线BE 之间的位置关系是；（2）探究：如图③所示，若四边形ABCD 与四边形AEFG 都为矩形，且AD ＝2AB ，AG ＝2AE 时，上述结论是否成立，并说明理由．（3）应用：在（2）的情况下，连接BG 、DE ，若AE ＝1，AB ＝2，求BG 2+DE 2的值（直接写出结果）．2．如图1，在正方形ABCD 中，点E 是CD 上一点（不与C ，D 两点重合），连接BE ，过点C 作CH ⊥BE 于点F ，交对角线BD 于点G ，交AD 边于点H ，连接GE ，（1）求证：△DHC ≌△CEB ；（2）如图2，若点E 是CD 的中点，当BE ＝8时，求线段GH 的长；（3）设正方形ABCD 的面积为S 1，四边形DEGH 的面积为S 2，当的值为时，的值为．3．在平面直角坐标系中，四边形AOBC是矩形，点O（0，0），点A（6，0），点B（0，8）．以点A为中心，顺时针旋转矩形AOBC，得到矩形ADEF，点O，B，C的对应点分别为D，E，F，记旋转角为α（0°＜α＜90°）．（I）如图①，当α＝30°时，求点D的坐标；（Ⅱ）如图②，当点E落在AC的延长线上时，求点D的坐标；（Ⅲ）当点D落在线段OC上时，求点E的坐标（直接写出结果即可）．4．如图，BD是平行四边形ABCD的对角线，DE⊥AB于点E，过点E的直线交BC于点G，且BG＝CG．（1）求证：GD＝EG．（2）若BD⊥EG垂足为O，BO＝2，DO＝4，画出图形并求出四边形ABCD的面积．（3）在（2）的条件下，以O为旋转中心顺时针旋转△GDO，得到△G′D'O，点G′落在BC上时，请直接写出G′E的长．5．（1）【探索发现】如图1，在正方形ABCD中，点M，N分别是边BC，CD上的点，∠MAN＝45°，若将△DAN 绕点A顺时针旋转90°到△BAG位置，可得△MAN≌△MAG，若△MCN的周长为8，则正方形ABCD的边长为．（2）【类比延伸】如图2，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B+∠D＝180°，点M，N分别在边BC，CD上的点，∠MAN＝60°，请判断线段BM，DN，MN之间的数量关系，并说明理由．（3）【拓展应用】如图3，在四边形ABCD中，AB＝AD＝2，∠ADC＝120°，点M，N分别在边BC，CD上，连接AM，MN，AN，△ABM是等边三角形，AM⊥AD于点A，∠DAN＝15°，请直接写出△CMN 的周长．6．（1）如图1，在△ABC中，AB＞AC，点D，E分别在边AB，AC上，且DE∥BC，若AD＝2，AE＝，则的值是；（2）如图2，在（1）的条件下，将△ADE绕点A逆时针方向旋转一定的角度，连接CE 和BD，的值变化吗？若变化，请说明理由；若不变化，请求出不变的值；（3）如图3，在四边形ABCD中，AC⊥BC于点C，∠BAC＝∠ADC＝θ，且tanθ＝，当CD＝6，AD＝3时，请直接写出线段BD的长度．7．如图1，长方形ABCD中，∠DAB＝∠B＝∠DCB＝∠D＝90°，AD＝BC＝6，AB＝CD＝10．点E为射线DC上的一个动点，把△ADE沿直线AE翻折得△AD′E．（1）当D′点落在AB边上时，∠DAE＝°；（2）如图2，当E点与C点重合时，D′C与AB交点F，①求证：AF＝FC；②求AF长．（3）连接D′B，当∠AD′B＝90°时，求DE的长．8．在平面直角坐标系中，点O是坐标原点，A（0，m），B（n，O），AC∥OB，且AC＝OB，连接BC交x轴于点F，其中m、n满足方程+n2+8n+16＝0．（1）求A、B两点坐标；（2）过A做AE⊥BC于E，延长AE交x轴于点D，动点P从点B出发以每秒2个单位的速度向x轴正半轴方向运动，设△PFD的面积为S，请用含t的式子表示S，并直接写出t的取值范围；（3）在（2）的条件下，连接PE，将△PED沿PE翻折到△PEG的位置（点D与点G对应），当四边形PDEG为菱形时，求点P和点G的坐标．9．已知四边形ABCD和四边形CEFG都是正方形，且AB＞CE．（1）如图1，连接BG、DE．求证：BG＝DE；（2）如图2，如果正方形CEFG绕点C旋转到某一位置恰好使得CG∥BD，BG＝BD．①求∠BDE的度数；②若正方形ABCD的边长是，请求出△BCG的面积．10．【综合与实践】如图①，在正方形ABCD中，点E、F分别在射线CD、BC上，且BF＝CE，将线段FA绕点F顺时针旋转90°得到线段FG，连接EG，试探究线段EG和BF的数量关系和位置关系．【观察与猜想】任务一：“智慧小组”首先考虑点E、F的特殊位置如图②，当点E与点D重合，点F与点C重合时，易知：EG与BF的数量关系是，EG与BF的位置关系是．【探究与证明】任务二：“博学小组”同学认为E、F不一定必须在特殊位置，他们分两种情况，一种是点E、F分别在CD、BC边上任意位置时（如图③）；一种是点E、F在CD、BC边的延长线上的任意位置时（如图④），线段EG与BF的数量关系与位置关系仍然成立．请你选择其中一种情况给出证明．【拓展与延伸】“创新小组”同学认为，若将“正方形ABCD”改为“矩形ABCD，且＝k（k≠1）”，点E、F分别在射线CD、BC上任意位置时，仍将线段FA绕点F顺时针旋转90°，并适当延长得到线段FG，连接EG（如图⑤），则当线段BF、CE、AF、FG满足一个条件时，线段EG与BF的数量关系与位置关系仍然成立．（请你在横线上直接写出这个条件，无需证明）11．在平面直角坐标系xOy中，四边形OADC为正方形，点D的坐标为（4，4），动点E沿边AO从A向O以每秒1cm的速度运动，同时动点F沿边OC从O向C以同样的速度运动，连接AF、DE交于点G．（1）试探索线段AF、DE的关系，写出你的结论并说明理由；（2）连接EF、DF，分别取AE、EF、FD、DA的中点H、I、J、K，则四边形HIJK是什么特殊平行四边形？请在图①中补全图形，并说明理由．（3）如图②当点E运动到AO中点时，点M是直线EC上任意一点，点N是平面内任意一点，是否存在点N使以O，C、M、N为顶点的四边形是菱形？若存在，请直接写出点N的坐标；若不存在，请说明理由．12．综合与实践动手操作：第一步：在矩形纸片ABCD的边BC，AD上分别取两点E，F，使CE＝AF；第二步：分别以DE，BF为对称轴将△CDE与△ABF翻折得到△C'DE与△A'BF，且边C'E 与A'B交于点G，边A'F与C'D交于一点H．问题解决：（1）求证：△BEG≌△DFH；（2）请判断四边形A'HC'G的形状，并证明你发现的结论；（3）已知tan∠EBG＝，A'G＝6，C'G＝1，求矩形纸片ABCD的面积．13．如图1，矩形ABCD中，∠ACB＝30°，将△ACD绕C点顺时针旋转α（0°＜α＜360°）至△A'CD'位置．（1）如图2，若AB＝2，α＝30°，求S△BCD′．（2）如图3，取AA′中点O，连OB、OD′、BD′．若△OBD′存在，试判定△OBD′的形状．（3）当α＝α1时，OB＝OD′，则α1＝°；当α＝α2时，△OBD′不存在，则α2＝°．14．已知矩形ABCD 中，AB ＝2，BC ＝m ，点E 是边BC 上一点，BE ＝1，连接AE ．（1）沿AE 翻折△ABE 使点B 落在点F 处，①连接CF ，若CF ∥AE ，求m 的值；②连接DF ，若≤DF ≤，求m 的取值范围．（2）△ABE 绕点A 顺时针旋转得△AB 1E 1，点E 1落在边AD 上时旋转停止．若点B 1落在矩形对角线AC 上，且点B 1到AD 的距离小于时，求m 的取值范围．15．如图1，正方形ABCD 的边CD 在正方形ECGF 的边CE 上，连接BE 、DG ．（1）BE 和DG 的数量关系是，BE 和DG 的位置关系是；（2）把正方形ECGF 绕点C 旋转，如图2，（1）中的结论是否还成立？若成立，写出证明过程，若不成立，请说明理由；（3）设正方形ABCD 的边长为4，正方形ECGF 的边长为3，正方形ECGF 绕点C 旋转过程中，若A 、C 、E 三点共线，直接写出DG 的长．16．如图，正方形ABCD的边长为a，射线AM是∠BAD外角的平分线，点E在边AB上运动（不与点A、B重合），点F在射线AM上，且AF＝BE，CF与AD相交于点G，连结EC、EF、EG．（1）求证：CE＝EF；（2）求△AEG的周长（用含a的代数式表示）；（3）试探索：点E在边AB上运动至什么位置时，△EAF的面积最大．17．问题情境：矩形ABCD中，∠ACB＝30°，将一块直角三角板的直角顶点P放在两对角线的交点处，以点P为旋转中心转动三角板，并保证三角板的两直角边分别与边AB、BC所在的直线相交，交点为E、F．探究1：如图1，当PE⊥AB，PF⊥BC时，则＝．探究2：如图2，在（1）的基础上，将三角板绕点P逆时针旋转，旋转角为α，（0°＜α＜60°），试求的值．探究3：在（2）的基础上继续旋转，当60°＜α＜90°时，将顶点P在AC上移动且使＝时，如图3，试求的值．18．在Rt△ABC中，∠B＝90°，AB＝6，BC＝8，点D从点B出发，以每秒3个单位的速度沿B→A→C运动，到点C停止．在点D运动的过程中，过点D作DE⊥BC，垂足为E，以DE为一边在右侧作矩形DEFG，点F在BC边上，且EF：DE＝4：3，连结AG，CG，设运动时间为t（秒），矩形DEFG与△ABC重叠部分面积为S．（1）当AG＝CG时，求t的值．（2）当点D在边AB上运动时，求S与t的函数关系式．（3）当△ACG的面积为6时，直接写出t的值．19．如图，在四边形ABCD中，AD∥BC，∠C＝90°，BC＝32，DC＝24，AD＝42，动点P从点D出发，沿射线DA的方向以每秒4个单位长的速度运动，动点Q从点C出发，在线段CB 上以每秒2个单位长的速度向点B运动，点P，Q分别从点D，C同时出发，当点Q运动到点B时，点P随之停止运动．设运动的时间为t（秒）．（1）设△BPQ的面积为S，求S与t之间的函数关系式；（2）当t为何值时，以B，P，Q三点为顶点的三角形是等腰三角形？（3）是否存在时刻t，使得PQ⊥BD？若存在，求出t的值；若不存在，请说明理由．20．（1）【发现证明】如图1，在正方形ABCD中，点E，F分别是BC，CD边上的动点，且∠EAF＝45°，求证：EF＝DF+BE．小明发现，当把△ABE绕点A顺时针旋转90°至△ADG，使AB与AD重合时能够证明，请你给出证明过程．（2）【类比引申】①如图2，在正方形ABCD中，如果点E，F分别是CB，DC延长线上的动点，且∠EAF＝45°，则（1）中的结论还成立吗？请写出证明过程．②如图3，如果点E，F分别是BC，CD延长线上的动点，且∠EAF＝45°，则EF，BE，DF之间的数量关系是（不要求证明）（3）【联想拓展】如图1，若正方形ABCD的边长为6，AE＝3，求AF的长．参考答案1．解：（1）①如图②中，∵四边形ABCD和四边形AEFG是正方形，∴AE＝AG，AB＝AD，∠BAD＝∠EAG＝90°，∴∠BAE＝∠DAG，在△ABE和△DAG中，，∴△ABE≌△ADG（SAS），∴BE＝DG；②如图2，延长BE交AD于T，交DG于H．由①知，△ABE≌△DAG，∴∠ABE＝∠ADG，∵∠ATB+∠ABE＝90°，∴∠ATB+∠ADG＝90°，∵∠ATB＝∠DTH，∴∠DTH+∠ADG＝90°，∴∠DHB＝90°，∴BE⊥DG，故答案为：BE＝DG，BE⊥DG；（2）数量关系不成立，DG＝2BE，位置关系成立．如图③中，延长BE交AD于T，交DG于H．∵四边形ABCD与四边形AEFG都为矩形，∴∠BAD＝∠EAG，∴∠BAE＝∠DAG，∵AD＝2AB，AG＝2AE，∴＝＝，∴△ABE∽△ADG，∴∠ABE＝∠ADG，＝，∴DG＝2BE，∵∠ATB+∠ABE＝90°，∴∠ATB+∠ADG＝90°，∵∠ATB＝∠DTH，∴∠DTH+∠ADG＝90°，∴∠DHB＝90°，∴BE⊥DG；（3）如图④中，作ET⊥AD于T，GH⊥BA交BA的延长线于H．设ET＝x，AT＝y．∵△AHG∽△ATE，∴＝＝＝2，∴GH＝2x，AH＝2y，∴4x2+4y2＝4，∴x2+y2＝1，∴BG2+DE2＝（2x）2+（2y+2）2+x2+（4﹣y）2＝5x2+5y2+20＝25．2．证明（1）∵四边形ABCD是正方形，∴CD＝BC，∠HDC＝∠BCE＝90°，∴∠DHC+∠DCH＝90°，∵CH⊥BE，∴∠EFC＝90°，∴∠ECF+∠BEC＝90°，∴∠CHD＝∠BEC，∴△DHC≌△CEB（AAS）．（2）解：∵△DHC≌△CEB，∴CH＝BE，DH＝CE，∵CE＝DE＝CD，CD＝CB，∴DH＝BC，∵DH∥BC，∴．∴GC＝2GH，设GH＝x，则，则CG＝2x，∴3x＝8，∴x＝．即GH＝．（3）解：∵，∴，∵DH＝CE，DC＝BC，∴，∵DH∥BC，∴，∴，，设S△DGH ＝9a，则S△BCG＝49a，S△DCG＝21a，∴S△BCD＝49a+21a＝70a，∴S1＝2S△BCD＝140a，∵S△DEG ：S△CEG＝4：3，∴S△DEG＝12a，∴S2＝12a+9a＝21a．∴．故答案为：．3．解：（I）过点D作DG⊥x轴于G，如图①所示：∵点A（6，0），点B（0，8）．∴OA＝6，OB＝8，∵以点A为中心，顺时针旋转矩形AOBC，得到矩形ADEF，∴AD＝AO＝6，α＝∠OAD＝30°，DE＝OB＝8，在Rt△ADG中，DG＝AD＝3，AG＝DG＝3，∴OG＝OA﹣AG＝6﹣3，∴点D的坐标为（6﹣3，3）；（Ⅱ）过点D作DG⊥x轴于G，DH⊥AE于H，如图②所示：则GA＝DH，HA＝DG，∵DE＝OB＝8，∠ADE＝∠AOB＝90°，∴AE＝＝＝10，∵AE×DH＝AD×DE，∴DH＝＝＝，∴OG＝OA﹣GA＝OA﹣DH＝6﹣＝，DG＝＝＝，∴点D的坐标为（，）；（Ⅲ）连接AE，作EG⊥x轴于G，如图③所示：由旋转的性质得：∠DAE＝∠AOC，AD＝AO，∴∠OAC＝∠ADO，∴∠DAE＝∠ADO，∴AE∥OC，∴∠GAE＝∠AOD，∴∠DAE＝∠GAE，在△AEG和△AED中，，∴△AEG≌△AED（AAS），∴AG＝AD＝6，EG＝ED＝8，∴OG＝OA+AG＝12，∴点E的坐标为（12，8）．4．证明：（1）如图1，延长EG交DC的延长线于点H，∵四边形ABCD是平行四边形，∴AD＝BC，AD∥BC，AB＝CD，AB∥CD，∵AB∥CD，∴∠H＝GEB，且BG＝CG，∠BGE＝∠CGH，∴△CGH≌△BGE（AAS）∴GE＝GH，∵DE⊥AB，DC∥AB，∴DC⊥DE，且GE＝GH，∴DG＝EG＝GH；（2）如图1：∵DB⊥EG，∴∠DOE＝∠DEB＝90°，且∠EDB＝∠EDO，∴△DEO∽△DBO，∴∴DE×DE＝4×（2+4）＝24，∴DE＝2，∴EO＝＝＝2，∵AB∥CD，∴， ∴HO ＝2EO ＝4， ∴EH ＝6，且EG ＝GH ， ∴EG ＝3，GO ＝EG ﹣EO ＝， ∴GB ＝＝＝，∴BC ＝2＝AD ， ∴AD ＝DE ，∴点E 与点A 重合，如图2：∵S 四边形ABCD ＝2S △ABD ，∴S 四边形ABCD ＝2××BD ×AO ＝6×2＝12；（3）如图3，过点O 作OF ⊥BC ，∵旋转△GDO ，得到△G ′D 'O ，∴OG ＝OG '，且OF ⊥BC ，∴GF ＝G 'F ，∵OF ∥AB ，∴＝＝，∴GF＝BG＝，∴GG'＝2GF＝，∴BG'＝BG﹣GG'＝，∵AB2＝AO2+BO2＝12，∵EG'＝AG'＝＝，＝．5．解：（1）如图1中，∵△MAN≌△MAG，∴MN＝GM，∵DN＝BG，GM＝BG+BM，∴MN＝BM+DN，∵△CMN的周长为：MN+CM+CN＝8，∴BM+CM+CN+DN＝8，∴BC+CD＝8，∴BC＝CD＝4，故答案为4；（2）如图2中，结论：MN＝NM+DN．延长CB至E，使BE＝DN，连接AE，∵∠ABC+∠D＝180°，∠ABC+∠ABE＝180°，∴∠D＝∠ABE，在△ABE和△ADN中，，∴△ABE≌△ADN（SAS），∴AN＝AE，∠DAN＝∠BAE，∵∠BAD＝2∠MAN，∴∠DAN+∠BAM＝∠MAN，∴∠MAN＝∠EAM，在△MAN和△MAE中，，∴△MAN≌△MAE（SAS），∴MN＝EM＝BE+BM＝BM+DN，即MN＝BM+DN；（3）如图3，延长BA，CD交于G，∵∠BAM＝60°，∠MAD＝90°，∴∠BAD＝150°，∴∠GAD＝30°，∵AD＝2，∴DG＝1，AG＝，∵∠DAN＝15°，∴∠GAN＝45°，∴AG＝GN＝，∴BG＝2+，∴BC＝2BG＝4+2，CG＝BG＝2+3，∴CD＝CG﹣DG＝2+2，由（2）得，MN＝BM+DN，∴△CMN的周长＝CM+CN+MN＝CN+DN+CM+BM＝BC+CD＝4+2+2+2＝6+4．6．解：（1）∵DE∥BC，∴＝＝＝；故答案为：；（2）的值不变化，值为；理由如下：由（1）得：DE∥B，∴△ADE∽△ABC，∴＝，由旋转的性质得：∠BAD＝∠CAE，∴△ABD∽△ACE，∴＝＝；（3）在AB上截取AM＝AD＝3，过M作MN∥BC交AC于N，把△AMN绕A逆时针旋转得△ADE，连接CE，如图所示：则MN⊥AC，DE＝MN，∠DAE＝∠BAC，∴∠AED＝∠ANM＝90°，∵AC⊥BC于点C，∠BAC＝∠ADC＝θ，且tanθ＝＝，∴BC：AC：AB＝3：4：5，同（2）得：△ABD∽△ACE，∴＝＝，∵MN∥BC，∴△AMN∽△ABC，∴＝，∴MN＝×AM＝×3＝，∵∠BAC＝∠ADC＝θ，∴∠DAE＝∠ADC＝θ，∴AE∥CD，∴∠CDE+∠AED＝180°，∴∠CDE＝90°，∴CE＝＝＝，∴BD＝CE＝×＝．7．解：（1）由题意知△ADE≌△AD′E，∴∠DAE＝∠D′AE，∵D′点落在AB边上时，∠DAE+∠D′AE＝90°，∴∠DAE＝∠D′AE＝45°，故答案为：45；（2）①如图2，由题意知∠ACD＝∠ACD′，∵四边形ABCD是矩形，∴AB∥CD，∴∠ACD＝∠BAC，∴∠ACD′＝∠BAC，∴AF＝FC；②设AF＝FC＝x，则BF＝10﹣x，在Rt△BCF中，由BF2+BC2＝CF2得（10﹣x）2+62＝x2，解得x＝6.8，即AF＝6.8；（3）如图3，∵△AD′E≌△ADE，∴∠AD′E＝∠D＝90°，∵∠AD′B＝90°，∴B、D′、E三点共线，又∵△ABD′∽△BEC，AD′＝BC，∴△ABD′≌△BEC，∴BE＝AB＝10，∵BD′＝＝＝8，∴DE＝D′E＝10﹣8＝2；如图4，∵∠ABD″+∠CBE＝∠ABD″+∠BAD″＝90°，∴∠CBE＝∠BAD″，在△ABD″和△BEC中，∵，∴△ABD″≌△BEC，∴BE＝AB＝10，∴DE＝D″E＝8+10＝18．综上所知，DE＝2或18．8．解：（1）∵，，（n+4）2≥0，∴m﹣4＝0，n+4＝0，∴m＝4，n＝﹣4，∴A（0，4），B（﹣4，0）；（2）∵AC∥OB，∴∠C＝∠CBO，∠CAF＝∠BOF，∵AC＝OB，∴△ACF≌△OBF（ASA），∴AF＝OF＝2，∵OA＝OB，∠OAD＝∠OBF，∠BOF＝∠AOD，∴△BOF≌△AOD（ASA），∴OF＝OD＝2，∴BD＝6，①当0≤t＜3时，S＝PD•OF＝（6﹣2t）×2＝6﹣2t；②当t＞3时，S＝PD•OF＝（2t﹣6）×2＝2t﹣6；（3）①当0≤t＜3，如图2，∵AO＝4，OD＝2，∴AD＝，∵BD×OA＝AD×BE，∴BE＝，∴DE＝，∵四边形PDEG为菱形，∴DP＝DE＝EG＝，∵D（2，0），∴P（2﹣，0），作EH⊥BD于H，∵BE×DE＝BD×EH，∴EH＝，∴HD＝，∴OH＝，∴E（，），∵EG∥OB，∴G与E的纵坐标相同，∴G（﹣，）②当t＞3时，如图3，同理求得P（2+，0），G（+，）．9．（1）证明：∵四边形ABCD和四边形CEFG为正方形，∴BC＝DC，CG＝CE，∠BCD＝∠GCE＝90°．∴∠BCD+∠DCG＝∠GCE+∠DCG，∴∠BCG＝∠DCE．在△BCG和△DCE中，，∴△BCG≌△DCE（SAS）．∴BG＝DE；（2）解：①连接BE，如图2所示：由（1）可知：BG＝DE，∵CG∥BD，∴∠DCG＝∠BDC＝45°，∴∠BCG＝∠BCD+∠DCG＝90°+45°＝135°，∵∠GCE＝90°，∴∠BCE＝360°﹣∠BCG﹣∠GCE＝360°﹣135°﹣90°＝135°，∴∠BCG＝∠BCE，在△BCG和△BCE中，，∴△BCG≌△BCE（SAS），∴BG＝BE，∵BG＝BD＝DE，∴BD＝BE＝DE，∴△BDE为等边三角形，∴∠BDE＝60°；②延长EC交BD于点H，过点G作GN⊥BC于N，如图3所示：在△BCE和△DCE中，，∴△BCE≌△BCG（SSS），∴∠BEC＝∠DEC，∴EH⊥BD，BH＝BD，∵BC＝CD＝，∴BD＝BC＝2，∴BE＝2，BH＝1，∴CH＝1，在Rt△BHE中，由勾股定理得：EH＝＝＝，∴CE＝﹣1，∵∠BCG＝135°，∴∠GCN＝45°，∴△GCN是等腰直角三角形，∴GN＝CG＝（﹣1），＝BC•GN＝××（﹣1）＝．∴S△BCG10．【观察与猜想】解：∵四边形ABCD是正方形，∴∠B＝∠BCD＝∠ADC＝90°，AB＝BC＝CD＝AD，∠ACB＝∠ACD＝45°，由旋转的性质得：GC＝AC，∠ACG＝90°，∴∠ACB＝∠GCD＝45°，在△ABC和△GDC中，，∴△ABC≌△GDC（SAS），∴AB＝GD，∠GDC＝∠B＝90°，∴DG∥BC，△CDG是等腰直角三角形，∴DG＝CD＝BC，∵点E与点D重合，点F与点C重合，∴EG＝BF，EG∥BF；故答案为：EG＝BF，EG∥BF；【探究与证明】证明：点E、F分别在CD、BC边上任意位置时，如图③所示：作GM⊥BC，交BC延长线于M，则∠GMF＝90°，MG∥DC，∵四边形ABCD是正方形，∴AB＝BC，∠BCD＝∠B＝90°，∴∠BAF+∠BFA＝90°，由旋转的性质得：GF＝AF，∠AFG＝90°，∴∠BFA+∠MFG＝90°，∴∠BAF＝∠MFG，在△ABF和△FMG中，，∴△ABF≌△FMG（AAS），∴AB＝FM，BF＝MG，∵AB＝BC，∴BF＝CM，∵BF＝CE，∴MG＝CE，∵MG∥CE，∴四边形CEGM是平行四边形，又∵∠GMF＝90°，∴四边形CEGM是矩形，∴EG＝CM，EG∥CM，∴EG＝BF，EG∥BF；点E、F在CD、BC边的延长线上的任意位置时，如图④所示：作GM⊥BC，交BC延长线于M，则∠GMF＝90°，MG∥DC，∵四边形ABCD是正方形，∴AB＝BC，∠BCD＝∠B＝90°，∴∠BAF+∠BFA＝90°，由旋转的性质得：GF＝AF，∠AFG＝90°，∴∠BFA+∠MFG＝90°，∴∠BAF＝∠MFG，在△ABF和△FMG中，，∴△ABF≌△FMG（AAS），∴AB＝FM，BF＝MG，∵AB＝BC，∴BF＝CM，∵BF＝CE，∴MG＝CE，∵MG∥CE，∴四边形CEGM是平行四边形，又∵∠GMF＝90°，∴四边形CEGM是矩形，∴EG＝CM，EG∥CM，∴EG＝BF，EG∥BF；【拓展与延伸】解：＝＝k（k≠1）时，线段EG与BF的数量关系与位置关系仍然成立；理由如下：作GM⊥BC，交BC延长线于M，如图⑤所示：则∠GMF＝90°，MG∥DC，∵四边形ABCD是正方形，∴AB＝BC，∠BCD＝∠B＝90°，∴∠BAF+∠BFA＝90°，∠B＝∠GMF，由旋转的性质得：∠AFG＝90°，∴∠BFA+∠MFG＝90°，∴∠BAF＝∠MFG，∴△ABF∽△FMG，∴＝＝，∵＝＝k，∴＝＝k，＝＝k，∴FM＝BC，GM＝CE，∴BF＝CM，∵MG∥CE，∴四边形CEGM是平行四边形，又∵∠GMF＝90°，∴四边形CEGM是矩形，∴EG＝CM，EG∥CM，∴EG＝BF，EG∥BF；故答案为：＝＝k（k≠1）．11．解：（1）AF＝DE．理由如下：∵四边形OADC是正方形，∴OA＝AD，∠DAE＝∠AOF＝90°，由题意得：AE＝OF，在△AOF和△DAE中，，∴△AOF≌△DAE（SAS），∴AF＝DE．（2）四边形HIJK是正方形．理由如下：如图①所示：∵H、I、J、K分别是AE、EF、FD、DA的中点，∴HI＝KJ＝AF，HK＝IJ＝ED，HI∥AF，HK∥ED，∵AF＝DE，∴HI＝KJ＝HK＝IJ，∴四边形HIJK是菱形，∵△AOF≌△DAE，∴∠ADE＝∠OAF，∵∠ADE+∠AED＝90°，∴∠OAF+∠AED＝90°，∴∠AGE＝90°，∴AF⊥ED，∵HI∥AF，HK∥ED，∴HI⊥HK，∴∠KHI＝90°，∴四边形HIJK是正方形．（3）存在，理由如下：∵四边形OADC为正方形，点D的坐标为（4，4），∴OA＝AD＝OC＝4，∴C（4，0），∵点E为AO的中点，∴OE＝2，E（0，2）；分情况讨论：如图②所示，①当OC是以O，C、M、N为顶点的菱形的对角线时，OC与MN互相垂直平分，则M为CE 的中点，∴点M的坐标为（2，1），∵点M和N关于OC对称，∴N（2，﹣1）；②当OC是以O，C、M、N为顶点的菱形的边时，若M在y轴的左侧时，∵四边形OCM'N'是菱形，∴OM'＝OC＝4，M'N'∥OC，∴△M'FE∽△COE，∴＝＝2，设EF＝x，则M'F＝2x，OF＝x+2，在Rt△OM'F中，由勾股定理得：（2x）2+（x+2）2＝42，解得：x＝，或x＝﹣2（舍去），∴M'F＝，FN＝4﹣M'F＝，OF＝2+＝，∴N'（，）；若M在y轴的右侧时，作N''P⊥OC于P，∵ON''∥CM''，∴∠PON''＝∠OCE，∴tan∠PON''＝＝tan∠OCE＝＝，设PN''＝y，则OP＝2y，在Rt△OPN''中，由勾股定理得：y2+（2y）2＝42，解得：y＝，∴PN''＝，OP＝，∴N''（，﹣）；综上所述，存在点N使以O，C、M、N为顶点的四边形是菱形，点N的坐标为（2，﹣1）或（，）或（，﹣）．12．（1）证明：∵四边形ABCD为矩形，∴BC＝AD，CD＝AB，∠C＝∠ABC＝∠A＝∠ADC＝90°，∵CE＝AF，∴BC﹣CE＝AD﹣AF，即BE＝DF，在△DCE和△BAF中，，∴△DCE≌△BAF（SAS），∴∠CDE＝∠ABF，∠CED＝∠AFB，由折叠的性质得：∠CDE＝∠C′DE，∠ABF＝∠A′BF，∠CED＝∠C′ED，∠AFB＝∠A′FB，∵∠CDE+∠C′DE+∠HDF＝90°，∠ABF+∠A′BF+∠GBE＝90°，∠CED+∠C′ED+∠GEB＝180°，∠AFB+∠A′FB+∠HFD＝180°，∴∠HDF＝∠GBE，∠GEB＝∠HFD，在△BEG和△DFH中，，∴△BEG≌△DFH（ASA）；（2）解：四边形A'HC'G的形状是矩形；理由如下：由折叠的性质得：∠C＝∠DC′E＝∠A＝∠BA′F＝90°，由（1）得：△BEG≌△DFH，∴∠BGE＝∠DHF，∵∠BGE＝∠A′GC′，∠DHF＝∠A′HC′，∴∠A′GC′＝∠A′HC′，∵∠DC′E+∠BA′F+∠A′GC′+∠A′HC′＝90°+90°+∠A′GC′+∠A′HC′＝360°，∴∠A′GC′+∠A′HC′＝180°，∴∠A′GC′＝∠A′HC′＝90°，∴∠DC′E＝∠BA′F＝∠A′GC′＝∠A′HC′＝90°，∴四边形A'HC'G是矩形；（3）解：由（2）知：∠BGE＝∠A′GC′＝90°，∵tan∠EBG＝，∴设EG＝3x，则BG＝4x，BE＝＝5x，由折叠的性质得：CE＝C′E＝EG+C′G＝3x+1，CD＝AB＝A′B＝BG+A′G＝4x+6，∴BC＝CE+BE＝3x+1+5x＝8x+1，S矩形ABCD＝CD•BC＝4×CD•CE+2×EG•BG﹣A'G•C'G，即（4x+6）（8x+1）＝4×（3x+1）（4x+6）+2×3x•4x﹣6×1，整理得：x2﹣2x＝0，解得：x1＝2，x2＝0（不合题意舍去），∴CD＝4×2+6＝14，CB＝8×2+1＝17，∴S矩形ABCD＝CD•BC＝14×17＝238．13．解：（1）作D'E⊥BC交BC的延长线于E，如图2所示：则∠E＝90°，∵四边形ABCD是矩形，∴∠ABC＝90°，AB∥CD，AD∥BC，CD＝AB＝2，∴∠ACD＝∠BAC，∠DAC＝∠ACB＝30°，∵∠ACB＝30°，∴BC＝AB＝2，∠ACD＝∠BAC＝60°，由旋转的性质得：CD'＝CD＝2，∠ACA'＝30°，∴∠D'CE＝180°﹣30°﹣30°﹣60°＝60°，∴∠CD'E＝30°，∴CE＝CD'＝1，D'E＝CE＝，∴S＝BC×D'E＝×2×＝3；△BCD′（2）△OBD′是直角三角形，理由如下：连接OC，如图3所示：由旋转的性质得：CA'＝CA，∠AD'C＝∠ADC＝90°，∠D'A'C＝∠DAC＝30°，∵O是AA′的中点，∴OC⊥AA'，∴∠AOC＝∠AOC＝90°＝∠ABC＝∠AD'C，∴∠ABC+∠AOC＝180°，∴A、B、C、O四点共圆，∴∠BOC＝∠BAC＝60°，同理；A、D'、C、O四点共圆，∴∠D'OC＝∠D'A'C＝30°，∴∠BOD'＝90°，∴△BOD'是直角三角形；（3）若B、C、D'三点不共线，如图3所示：由（2）得：∠OBC＝∠OAC，∠OD'C＝∠OA'C，∠OAC＝∠OA'C，∴∠OBC＝∠OD'C，∵OB＝OD，∴∠OBD'＝∠OD'B，∴∠CBD'＝∠CD'B，∴CB＝CD'，∵CD'＝CD，∴BC＝CD，这与已知相矛盾，∴B、C、D'三点共线；分两种情况：当点D'在BC的延长线上时，如图4所示：＝90°；α＝α1当点D'在边BC上时，如图5所示：＝360°﹣90°＝270°；α＝α1故答案为：90°或270；时，△OBD′不存在时，分两种情况：当α＝α2当O与D'重合时，如图6所示：∵CA'＝CA，∠CAD'＝∠CA'D'＝30°，∴∠ACA'＝120°，＝360°﹣120°＝240°；∴α＝α2当O与B重合时，如图7所示：则AA'＝2AB＝4，∵CA＝CA'＝2AB＝4＝AA'，∴△ACA'是等边三角形，∴∠A'CA＝60°，＝360°﹣60°＝300°；∴α＝α2故答案为：240°或300．14．解：（1）①如图1，∵CF∥AE ∴∠FCE＝∠AEB，∠CFE＝∠AEF∵△ABE翻折得到△AFE∴EF＝BE＝1，∠AEF＝∠AEB∴∠FCE＝∠CFE∴CE＝EF＝1∴m＝BC＝BE+CE＝2∴m的值是2．②如图2，过点F作GH⊥AD于点G，交BC于点H ∴GH⊥BC∴∠AGF＝∠FHE＝90°∵四边形ABCD是矩形∴∠BAD＝∠B＝90°∴四边形ABHG是矩形∴GH＝AB＝2，AG＝BH∵△ABE翻折得到△AFE∴EF＝BE＝1，AF＝AB＝2，∠AFE＝∠B＝90°∴∠AFG+∠EFH＝∠AFG+∠FAG＝90°∴∠EFH＝∠FAG∴△EFH∽△FAG∴设EH＝x，则AG＝BH＝x+1∴FG＝2EH＝2x∴FH＝GH﹣FG＝2﹣2x∴解得：x＝∴AG＝，FG＝∵AD＝BC＝m∴DG＝|AD﹣AG|＝|m﹣|∴DF 2＝DG 2+FG 2＝（m ﹣）2+2≥，即可把DF 2看作关于m 的二次函数，抛物线开口向上，最小值为∵∴∵（m ﹣）2+2＝解得：m 1＝，m 2＝1 ∴根据二次函数图象可知，1≤m（2）如图3，过点B 1作MN ⊥AD 于点M ，交BC 于点N ∴MN ∥AB ，MN ＝AB ＝2∵AC ＝ ∴sin ∠ACB ＝∵AD ∥BC ，点B 1在AC 上∴∠MAB 1＝∠ACB∴sin ∠MAB 1＝ ∴∵点B 1到AD 的距离小于∴MB 1＝解得：∵m＞0 ∴m＞如图4，当E1落在边AD上，且B1在AC上时，m最大，此时，∠ACB＝∠B1AE1＝∠BAE∴tan∠ACB＝tan∠BAE∴∴m＝BC＝2AB＝4∴m的取值范围是＜m≤415．解：（1）BE＝DG．BE⊥DG；理由如下：∵四边形ABCD和四边形CEFG为正方形，∴CD＝BC，CE＝CG，∠BCE＝∠DCG＝90°，在△BEC和△DGC中，，∴△BEC≌△DGC（SAS），∴BE＝DG；如图1，延长GD交BE于点H，∵△BEC≌△DGC，∴∠DGC＝∠BEC，∴∠DGC+∠EBC＝∠BEC+∠EBC＝90°，∴∠BHG＝90°，即BE⊥DG；故答案为：BE＝DG，BE⊥DG．（2）成立，理由如下：如图2所示：同（1）得：△DCG≌△BCE（SAS），∴BE＝DG，∠CDG＝∠CBE，∵∠DME＝∠BMC，∠CBE+∠BMC＝90°，∴∠CDG+∠DME＝90°，∴∠DOB＝90°，∴BE⊥DG；（3）由（2）得：DG＝EB，分两种情况：①如图3所示：∵正方形ABCD的边长为4，正方形ECGF的边长为3，∴AC⊥BD，BD＝AC＝AB＝4，OA＝OC＝OB＝AC＝2，CE＝3，∴AE＝AC﹣CE＝，∴OE＝OA﹣AE＝，在Rt△BOE中，由勾股定理得：DG＝BE＝＝；②如图4所示：OE＝CE+OC＝2+3＝5，在Rt△BOE中，由勾股定理得：DG＝BE＝＝；综上所述，若A、C、E三点共线，DG的长为或．16．（1）证明：过点F作FH⊥AB于H，如图1所示：则∠AHF＝90°，∵AM平分∠DAH，∴∠FAH＝45°，∴△AFH是等腰直角三角形，∴FH＝AH，AF＝AH＝FH，∵AF＝BE，∴FH＝AH＝BE，∴AH+AE＝BE+AE，∴HE＝AB＝BC，在△FEH和△ECB中，，∴△FEH≌△ECB（SAS），∴CE＝EF；（2）解：∵△FEH≌△ECB，∴∠FEH＝∠ECB，∵在Rt△BCE中，∠ECB+∠CEB＝90°，∴∠FEH+∠CEB＝90°，∴∠CEF＝90°，由（1）知，CE＝EF，∴△CEF是等腰直角三角形，∠ECF＝∠EFC＝45°，把Rt△CDG绕点C逆时针旋转90°至Rt△CBN位置，如图2所示：则∠GCN＝90°，CG＝CN，DG＝BN，∴∠NCE＝∠GCN﹣∠GCE＝45°，∴∠NCE＝∠GCE，在△CEG和△CEN中，，∴△CEG≌△CEN（SAS），∴GE＝NE＝EB+BN＝EB+DG，∴△AEG的周长＝AE+GE+AG＝AE+EB+DG+AG＝AB+AD＝2a；（3）解：设AE＝x，由（1）得：FH＝BE＝a﹣x，则△EAF的面积＝AE×FH＝x（a﹣x）＝﹣（x﹣）2+，∴当x＝，即点E在AB边中点时，△EAF的面积最大，最大值为．17．解：（1）∵矩形ABCD，∴AB⊥BC，PA＝PC；∵PE⊥AB，BC⊥AB，∴PE∥BC，∴∠APE＝∠PCF；∵PF⊥BC，AB⊥BC，∴PF∥AB，∴∠PAE＝∠CPF．∵在△APE与△PCF中，，∴△APE≌△PCF（ASA），∴PE＝CF．在Rt△PCF中，＝tan30°＝，∴＝，故答案为：．（2）如答图1，过点P作PM⊥AB于点M，PN⊥BC于点N，则PM⊥PN．0°～30°时∵PM⊥PN，PE⊥PF，∴∠EPM＝∠FPN，又∵∠PME＝∠PNF＝90°，∴△PME∽△PNF，∴＝，由（1）知，＝，∴＝．同理30°～60°时，＝；（3）当60°＜α＜90°时，将顶点P在AC上移动且使＝时，如答图2，过点P作PM⊥AB于点M，PN⊥BC于点N，则PM⊥PN，PM∥BC，PN∥AB．∵PM∥BC，PN∥AB，∴∠APM＝∠PCN，∠PAM＝∠CPN，∴△APM∽△PCN，∴＝＝，得CN＝2PM．在Rt△PCN中，＝＝tan30°＝，∴＝．∵PM⊥PN，PE⊥PF，∴∠EPM＝∠FPN，又∵∠PME＝∠PNF＝90°，∴△PME∽△PNF，∴＝＝．18．解：（1）∵四边形DEFG是矩形，∴DG＝BF，GF＝BD，∠BDG＝∠BFG＝90°，∴∠ADG＝∠CFG＝90°，由题意得：BD＝3t，则AD＝6﹣3t，DG＝4t，CF＝8﹣4t，FG＝BD＝3t，当AG＝CG时，由勾股定理得：AG2＝AD2+DG2，CG2＝FG2+FC2，∴AD2+DG2＝FG2+FC2，即（6﹣3t）2+（4t）2＝（3t）2+（8﹣4t）2，解得：t＝1，即当AG＝CG时，t＝1秒；（2）分两种情况：①当0＜t≤1时，如图1所示：S＝矩形DEFG的面积＝3t×4t＝12t2；即S＝12t2（0＜t≤1）；②当1＜t≤2时，如图2所示：∵∠ADH＝∠B＝90°，∠A＝∠A，∴△ADH∽△ABC，∴＝，即＝，解得：DH＝8﹣4t，同理得：FM＝6﹣3t，∴S＝×6×8﹣×2×（6﹣3t）（8﹣4t）＝﹣12t2+48t﹣24；即S＝﹣12t2+48t﹣24（1＜t≤2）；（3）分三种情况：①如图1所示：由题意得：×6×8﹣12t2﹣×4t×（6﹣3t）﹣×3t×（8﹣4t）＝6，解得：t＝；②如图3所示：由题意得：×4t×（6﹣3t）+×3t×（8﹣4t）+3t×4t﹣×6×8＝6，解得：t＝；③如图4所示：由勾股定理得：AC＝＝＝10，∴CD＝6+10﹣3t＝16﹣3t，同（2）得：△CDE∽△CAB，∴＝＝，即＝＝，解得：DE＝（16﹣3t），CE＝（16﹣3t），由题意得EF＝（16﹣3t），∴C与F重合，∴×8×（16﹣3t）＝6，解得：t＝；综上所述，当△ACG的面积为6时，t的值为秒或秒或秒．19．解：（1）如图1，过点P作PM⊥BC，垂足为M，则四边形PDCM为矩形．∴PM＝DC＝24．∵QB＝32﹣t，∴S＝×24×（32﹣2t）＝384﹣24t（0≤t＜16）；（2）由图可知：CM＝PD＝4t，CQ＝2t．以B、P、Q三点为顶点的三角形是等腰三角形，可以分三种情况：①若PQ＝BQ．在Rt△PMQ中，PQ2＝4t2+242，由PQ2＝BQ2得4t2+242＝（32﹣2t）2，解得t＝；②若BP＝BQ．在Rt△PMB中，BP2＝（32﹣4t）2+242．由BP2＝BQ2得：（32﹣4t）2+242＝（32﹣2t）2即3t2﹣32t+144＝0．由于△＝﹣704＜0，∴3t2﹣32t+144＝0无解，∴PB≠BQ．③若PB＝PQ．由PB2＝PQ2，得4t2+242＝（32﹣4t）2+242整理，得3t 2﹣64t +256＝0．解得t 1＝，t 2＝16（舍去）综合上面的讨论可知：当t ＝秒或t ＝秒时，以B 、P 、Q 三点为顶点的三角形是等腰三角形．（3）设存在时刻t ，使得PQ ⊥BD ．如图2，过点Q 作QE ⊥AD 于E ，垂足为E ．∵AD ∥BC∴∠BQF ＝∠EPQ ，又∵在△BFQ 和△BCD 中∠BFQ ＝∠C ＝90°，∴∠BQF ＝∠BDC ，∴∠BDC ＝∠EPQ ，又∵∠C ＝∠PEQ ＝90°，∴Rt △BDC ∽Rt △QPE ， ∴＝，即＝，解得t ＝9．所以，当t ＝9秒时，PQ ⊥BD ．20．（1）【发现证明】证明：把△ABE 绕点A 顺时针旋转90°至△ADG ，如图1，∴∠BAE＝∠DAG，AE＝AG，∵∠EAF＝45°，∴∠BAE+∠FAD＝45°，∴∠DAG+∠FAD＝45°，∴∠EAF＝∠FAG，∵AF＝AF，∴△EAF≌△GAF（SAS），∴EF＝FG＝DF+DG，∴EF＝DF+BE；（2）【类比引申】①不成立，结论：EF＝DF﹣BE；证明：如图2，将△ABE绕点A顺时针旋转90°至△ADM，∴∠EAB＝∠MAD，AE＝AM，∠EAM＝90°，BE＝DM，∴∠FAM＝45°＝∠EAF，∵AF＝AF，∴△EAF≌△MAF（SAS），。

2022年九年级数学中考专题十一几何多结论题

专题11 几何多结论选择题一．试题（共14小题）1．如图，矩形ABCD中，AC，BD相交于点O，过点B作BF⊥AC交CD于点F，交AC于点M，过点D作DE ∥BF交AB于点E，交AC于点N，连接FN，EM．则下列结论：①DN＝BM；②EM∥FN；③AE＝FC；④当AO＝AD时，四边形DEBF是菱形．其中，正确的结论是（）A．①③B．①②③C．①③④D．①②③④2．如图，四边形ABCD是平行四边形，点E是边CD上一点，且BC＝EC，CF⊥BE交AB于点F，P是EB延长线上一点，下列结论：①BE平分∠CBF；②CF平分∠DCB；③BC＝FB；④PF＝PC．其中正确结论的个数为（）A．1B．2C．3D．43．如图，在△AOB和△COD中，OA＝OB，OC＝OD，OA＜OC，∠AOB＝∠COD＝36°．连接AC，BD交于点M，连接OM．下列结论：①∠AMB＝36°，②AC＝BD，③OM平分∠AOD，④MO平分∠AMD．其中正确的结论个数有（）个．A．4B．3C．2D．14．如图，在△ABC中，AB＝AC，AD和CE是高，∠ACE＝45°，点F是AC的中点，AD与FE，CE分别交于点G、H，∠BCE＝∠CAD，有下列结论：①图中存在两个等腰直角三角形；②△AHE≌△CBE；③BC•AD=√2AE2；④S△ABC＝4S△ADF．其中正确的个数有（）A ．1B ．2C ．3D ．45．已知如图等腰△ABC ，AB ＝AC ，∠BAC ＝120°，AD ⊥BC 于点D ．点P 是BA 延长线上一点，O 点是线段AD 上一点，OP ＝OC ，下面的结论：①AC 平分∠P AD ；②∠APO ＝∠DCO ；③△OPC 是等边三角形；④AC ＝AO +AP ；⑤S △ABC ＝S 四边形AOCP ．其中正确的序号是．6．如图，分别以Rt △ABC 的斜边AB ，直角边AC 为边向外作等边△ABD 和等边△ACE ，F 为AB 的中点，DE ，AB 相交于点G ，若∠BAC ＝30°，下列结论：①EF ⊥AC ；②四边形ADFE 为菱形；③AD ＝4AG ；④△DBF ≌△EF A ．其中正确结论的个数有（）A ．1B ．2C ．3D ．47．如图，在矩形ABCD 中，AD =√2AB ，AE 平分∠BAD ，DF ⊥AE 于F ，BF 交DE 、CD 于O 、H ，下列结论：①∠DEA ＝∠DEC ；②BF ＝FH ；③OE ＝OD ；④BC ﹣CH ＝2EF ；⑤AB ＝HF ，其中正确结论的个数是（）A ．2个B ．3个C ．4个D ．5个 8．如图，平行四边形ABCD 的对角线AC ，BD 相交于点O ，AE 平分∠BAD ，分别交BC ，BD 于点E ，P ，连接OE ，∠ADC ＝60°，AB =12BC ＝2，下列结论：①∠CAD ＝30°；②BD ＝2√7；③S 四边形ABCD ＝AB •AC ；④OE =14AD ；⑤S △BOE =√32．其中正确的个数有（）个A．2B．3C．4D．59．如图，在等腰Rt△ABC中，AB＝AC，过A作直线交BC于G，BG＜GC，BD⊥AG于D，CE⊥AD于E，F 为BC边中点，则下列结论中：①∠BAD＝∠ACE；②BD＝CE﹣ED；③FE＝FD；④EF⊥DF，其中正确结论的个数为（）A．1个B．2个C．3个D．4个10．如图，已知△ABC和△ADE都是等腰三角形，∠BAC＝∠DAE＝90°，BD，CE交于点F，连接AF．下列结论：①BD＝CE；②BF⊥CF；③AF平分∠CAD；④∠AFE＝45°．其中正确结论的个数有（）A．1个B．2个C．3个D．4个11．如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB、CD交于点E、F，连接BF交AC于点M，连接DE、BO．若∠COB＝60°，FO＝FC，则下列结论：①FB垂直平分OC；②△EOB≌△CMB；③DE＝EF；④S△AOE：S△BCM＝3：2．其中正确结论的个数是（）A．4个B．3个C．2个D．1个12．如图，在平行四边形ABCD中，AD＝2AB，CE⊥AB于点E，点F、G分别是AD、BC的中点，连接CF、EF、FG，下列结论：①CE⊥FG；②四边形ABGF是菱形；③EF＝CF；④∠EFC＝2∠CFD．其中正确的个数是（）A．1个B．2个C．3个D．4个13．如图，AB是⊙O的直径，C，D是⊙O上的点，且OC∥BD，AD分别与BC，OC相交于点E，F，则下列结论：①AD⊥BD；②∠AOC＝∠AEC；③BC平分∠ABD；④AF＝DF；⑤BD＝2OF．其中正确结论的个数是（）A．2B．3C．4D．514．如图，△ABC中，AB＝AC，以AB为直径的⊙O交AC于E，交BC于D，DF⊥AC于F．给出以下五个结论：①BD＝DC；②CF＝EF；③弧AE＝弧DE；④∠A＝2∠FDC；⑤DF是⊙O的切线．其中正确的有（）A．5个B．4个C．3个D．2个专题11 几何多结论选择题参考答案与试题解析一．试题（共14小题）1．【解答】解：∵四边形ABCD 是矩形，∴AB ＝CD ，AB ∥CD ，∠DAE ＝∠BCF ＝90°，OD ＝OB ＝OA ＝OC ，AD ＝BC ，AD ∥BC ， ∴∠DAN ＝∠BCM ，∵BF ⊥AC ，DE ∥BF ，∴DE ⊥AC ，∴∠DNA ＝∠BMC ＝90°，在△DNA 和△BMC 中，{∠DAN =∠BCM ∠DNA =∠BMC AD =BC，∴△DNA ≌△BMC （AAS ），∴DN ＝BM ，∠ADE ＝∠CBF ，故①正确；在△ADE 和△CBF 中，{∠ADE =∠CBF AD =BC ∠DAE =∠BCF，∴△ADE ≌△CBF （ASA ），∴AE ＝FC ，DE ＝BF ，故③正确；∴DE ﹣DN ＝BF ﹣BM ，即NE ＝MF ，∵DE ∥BF ，∴四边形NEMF 是平行四边形，∴EM ∥FN ，故②正确；∵AB ＝CD ，AE ＝CF ，∴BE ＝DF ，∵BE ∥DF ，∴四边形DEBF 是平行四边形，∵AO ＝AD ，∴AO ＝AD ＝OD ，∴△AOD 是等边三角形，∴∠ADO ＝∠DAN ＝60°，∴∠ABD ＝90°﹣∠ADO ＝30°，∵DE ⊥AC ，∴∠ADN ＝∠ODN ＝30°，∴∠ODN ＝∠ABD ，∴DE ＝BE ，∴四边形DEBF 是菱形；故④正确；故选：D ．2．【解答】证明：∵BC ＝EC ，∴∠CEB ＝∠CBE ，∵四边形ABCD 是平行四边形，∴DC ∥AB ，∴∠CEB＝∠EBF，∴∠CBE＝∠EBF，∴①BE平分∠CBF，正确；∵BC＝EC，CF⊥BE，∴∠ECF＝∠BCF，∴②CF平分∠DCB，正确；∵DC∥AB，∴∠DCF＝∠CFB，∵∠ECF＝∠BCF，∴∠CFB＝∠BCF，∴BF＝BC，∴③正确；∵FB＝BC，CF⊥BE，∴B点一定在FC的垂直平分线上，即PB垂直平分FC，∴PF＝PC，故④正确．故选：D．3．【解答】解：∵∠AOB＝∠COD＝36°，∴∠AOB+∠BOC＝∠COD+∠BOC，即∠AOC＝∠BOD，在△AOC和△BOD中，{OA=OB∠AOC=∠BOD OC=OD∴△AOC≌△BOD（SAS），∴∠OCA＝∠ODB，AC＝BD，故②正确；∵∠OAC＝∠OBD，由三角形的外角性质得：∠AMB+∠OBD＝∠OAC+∠AOB，∴∠AMB＝∠AOB＝36°，故①正确；法一：作OG⊥AM于G，OH⊥DM于H，如图所示，则∠OGA＝∠OHB＝90°，∵△AOC≌△BOD，∴OG ＝OH ，∴MO 平分∠AMD ，故④正确；法二：∵△AOC ≌△BOD ，∴∠OAC ＝∠OBD ，∴A 、B 、M 、O 四点共圆，∴∠AMO ＝∠ABO ＝72°，同理可得：D 、C 、M 、O 四点共圆，∴∠DMO ＝∠DCO ＝72°＝∠AMO ，∴MO 平分∠AMD ，故④正确；假设MO 平分∠AOD ，则∠DOM ＝∠AOM ，在△AMO 与△DMO 中，{∠AOM =∠DOMOM =OM ∠AMO =∠DMO，∴△AMO ≌△DMO （ASA ），∴AO ＝OD ，∵OC ＝OD ，∴OA ＝OC ，而OA ＜OC ，故③错误；正确的个数有3个；故选：B ．4．【解答】解：∵CE ⊥AB ，∠ACE ＝45°，∴△ACE 是等腰直角三角形，∵AF ＝CF ，∴EF ＝AF ＝CF ，∴△AEF ，△EFC 都是等腰直角三角形，∴图中共有3个等腰直角三角形，故①错误，∵∠AHE +∠EAH ＝90°，∠DHC +∠BCE ＝90°，∠AHE ＝∠DHC ，∴∠EAH ＝∠BCE ，∵AE ＝EC ，∠AEH ＝∠CEB ＝90°，∴△AHE ≌△CBE ，故②正确，∵S △ABC =12BC •AD =12AB •CE ，AB ＝AC =√2AE ，AE ＝CE ，∴BC •AD =√2CE 2，故③正确，∵AB ＝AC ，AD ⊥BC ，∴BD ＝DC ，∴S △ABC ＝2S △ADC ，∵AF ＝FC ，∴S △ADC ＝2S △ADF ，∴S △ABC ＝4S △ADF ．故选：C ．5．【解答】解：①∵AB＝AC，∠BAC＝120°，AD⊥BC；∴∠CAD=12∠BAC＝60°，∠P AC＝180°﹣∠CAB＝60°，∴∠P AC＝∠DAC，∴AC平分∠P AD故①正确；②由①知：∠APO＝∠ABO，∠DCO＝∠DBO，∵点O是线段AD上一点，∴∠ABO与∠DBO不一定相等，则∠APO与∠DCO不一定相等，故②不正确；③∵∠APC+∠DCP+∠PBC＝180°，∴∠APC+∠DCP＝150°，∵∠APO+∠DCO＝30°，∴∠OPC+∠OCP＝120°，∴∠POC＝180°﹣（∠OPC+∠OCP）＝60°，∵OP＝OC，∴△OPC是等边三角形；故③正确；④如图2，在AC上截取AE＝P A，连接PB，∵∠P AE＝180°﹣∠BAC＝60°，∴△APE是等边三角形，∴∠PEA＝∠APE＝60°，PE＝P A，∴∠APO+∠OPE＝60°，∵∠OPE+∠CPE＝∠CPO＝60°，∴∠APO＝∠CPE，∵OP＝CP，在△OP A和△CPE中，{PA=PE∠APO=∠CPE OP=CP，∴△OP A≌△CPE（SAS），∴AO＝CE，∴AC＝AE+CE＝AO+AP；故④正确；如图3，过点C作CH⊥AB于H，∵∠P AC＝∠DAC＝60°，AD⊥BC，∴CH＝CD，∴S△ABC=12AB•CH，S 四边形AOCP ＝S △ACP +S △AOC =12AP •CH +12OA •CD =12AP •CH +12OA •CH =12H •（AP +OA ）=12CH •AC ， ∴S △ABC ＝S 四边形AOCP ；故⑤正确．本题正确的结论有：①③④⑤故答案为：①③④⑤．6．【解答】解：连接FC ，如图所示：∵∠ACB ＝90°，F 为AB 的中点，∴F A ＝FB ＝FC ，∵△ACE 是等边三角形，∴EA ＝EC ，∵F A ＝FC ，EA ＝EC ，∴点F 、点E 都在线段AC 的垂直平分线上，∴EF 垂直平分AC ，即EF ⊥AC ；∵△ABD 和△ACE 都是等边三角形，F 为AB 的中点，∴DF ⊥AB 即∠DF A ＝90°，BD ＝DA ＝AB ＝2AF ，∠DBA ＝∠DAB ＝∠EAC ＝∠ACE ＝60°． ∵∠BAC ＝30°，∴∠DAC ＝∠EAF ＝90°，∴∠DF A ＝∠EAF ＝90°，DA ⊥AC ，∴DF ∥AE ，DA ∥EF ，∴四边形ADFE 为平行四边形而不是菱形；∵四边形ADFE 为平行四边形，∴DA ＝EF ，AF ＝2AG ，∴BD ＝DA ＝EF ，DA ＝AB ＝2AF ＝4AG ；在△DBF 和△EF A 中，{BD =FE ∠DBF =∠EFA BF =FA，∴△DBF ≌△EF A ；综上所述：①③④正确，故选：C ．7．【解答】解：∵四边形ABCD为矩形，AE平分∠BAD，∴∠BAE＝∠DAE＝∠AEB＝45°，∵∠AFD＝∠ABE＝90°，∴△AFD与△ABE都为等腰直角三角形，即AF＝DF，AB＝BE，∴AE=√2AB，又∵AD=√2AB，∴AD＝AE，∴∠AED＝∠ADE＝67.5°，∴∠DEC＝180°﹣45°﹣67.5°＝67.5°，∴∠DEA＝∠DEC，选项①正确；过F作GM⊥AD，与AD交于G点，与BC交于M点，利用三线合一得到G为AD中点，∴F为BH中点，M为BC中点，∴BF＝FH，选项②正确；∵AD=√2AF，AD=√2AB，∴AF＝AB，∴∠AFB＝67.5°，∴∠OFE＝∠OEF＝67.5°，∴OE＝OF，∴∠ODF＝∠OFD＝22.5°，∴OF＝OD，∴OD＝OE，选项③正确；∴∠DEF＝67.5°﹣45°＝22.5°，∠EDC＝90°﹣67.5°＝22.5°，∴∠EDF＝∠DEC，∵EF⊥DF，EC⊥CD，∴EF＝EC，∵△EFM为等腰直角三角形，∴FM＝ME，∴BC﹣CH＝2CM﹣2FM＝2CM﹣2ME＝2EF，选项④正确；∵AB＝AF，∠BAE＝45°，∴△ABF不是等边三角形，∴AB≠BF，∴即AB≠HF，故⑤错误；综上所述，结论正确的是①②③④．则正确的序号有4个．故选：C．8．【解答】解：①∵AE平分∠BAD，∴∠BAE＝∠DAE，∵四边形ABCD是平行四边形，∴AD∥BC，∠ABC＝∠ADC＝60°，∴∠DAE＝∠BEA，∴∠BAE＝∠BEA，∴AB＝BE＝2，∴△ABE是等边三角形，∴AE＝BE＝2，∵BC＝4，∴EC＝2，∴AE＝EC，∴∠EAC＝∠ACE，∵∠AEB＝∠EAC+∠ACE＝60°，∴∠ACE＝30°，∵AD∥BC，∴∠CAD＝∠ACE＝30°，故①正确；②∵BE＝EC，OA＝OC，∴OE=12AB＝1，OE∥AB，∴∠EOC＝∠BAC＝60°+30°＝90°，Rt△EOC中，OC=√EC2−OE2=√3，∵四边形ABCD是平行四边形，∴∠BCD＝∠BAD＝120°，∴∠ACB＝30°，∴∠ACD＝90°，Rt△OCD中，OD=√OC2+CD2=√7 BD＝2OD＝2√7故②正确③由②知：∠BAC＝90°，∴S▱ABCD＝AB•AC，故③正确；④由②知：OE是△ABC的中位线，∴OE=12AB，∵AB=12BC，∴OE=14BC=14AD，故④正确；⑤∵BE＝EC＝2∴S△BOE＝S△EOC=12OE•OC=√32故⑤正确故选：D．9．【解答】解：如图连接AF．∵AB＝AC，BF＝FC，∴AF⊥BC，∵BD⊥AD，CE⊥AD，∴∠ADB＝∠AEC＝∠BAC＝90°，∵∠CAE+∠BAD＝90°，∠BAD+∠ABD＝90°，∴∠CAE＝∠ABD，故①正确，∴△ABD≌△CAE（AAS），∴BD＝AE，AD＝CE，∴CE﹣ED＝AD﹣DE＝AE＝BD，故②正确，∵∠BAC＝90°，BF＝FC，∴AF＝BF＝FC，∵∠AGF＝∠BGF，∠BDG＝∠AFG＝90°，∴∠DBG＝∠GAF，∵AE＝BD，∴△FBD≌△FEA（SAS），∴EF＝DF，∠AFE＝∠BFD，∴∠AFB＝∠EFD＝90°，∴EF⊥DF，故③④正确．故选：D．10．【解答】解：如图，作AM⊥BD于M，AN⊥EC于N，设AD交EF于O．∵∠BAC＝∠DAE＝90°，∴∠BAD＝∠CAE，∵AB＝AC，AD＝AE，∴△BAD≌△CAE（SAS），∴EC＝BD，∠BDA＝∠AEC，故①正确∵∠DOF＝∠AOE，∴∠DFO＝∠EAO＝90°，∴BD⊥EC，故②正确，∵△BAD≌△CAE，AM⊥BD，AN⊥EC，∴AM＝AN，∴F A平分∠EFB，∴∠AFE＝45°，故④正确，若③成立，则∠EAF＝∠BAF，∵∠AFE＝∠AFB，∴∠AEF＝∠ABD＝∠ADB，推出AB＝AD，由题意知，AB不一定等于AD，所以AF不一定平分∠CAD，故③错误，故选：C．11．【解答】解：①∵矩形ABCD中，O为AC中点，∴OB＝OC，∵∠COB＝60°，∴△OBC是等边三角形，∴OB＝BC，∵FO＝FC，∴FB垂直平分OC，故①正确；②∵△BOC为等边三角形，FO＝FC，∴BO⊥EF，BF⊥OC，∴∠CMB＝∠EOB＝90°，∴BO≠BM，∴△EOB与△CMB不全等；故②错误；③易知△ADE≌△CBF，∠1＝∠2＝∠3＝30°，∴∠ADE＝∠CBF＝30°，∠BEO＝60°，∴∠CDE＝60°，∠DFE＝∠BEO＝60°，∴∠CDE＝∠DFE，∴DE＝EF，故③正确；④易知△AOE≌△COF，∴S△AOE＝S△COF，∵S△COF＝2S△CMF，∴S△AOE：S△BCM＝2S△CMF：S△BCM=2FMBM，∵∠FCO＝30°，∴FM=CM√3，BM=√3CM，∴FMBM=13，∴S△AOE：S△BCM＝2：3，故④错误；所以其中正确结论的个数为2个；故选：C．12．【解答】解：∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，∵点F、G分别是AD、BC的中点，∴AF=12AD，BG=12BC，∴AF＝BG，∵AF∥BG，∴四边形ABGF是平行四边形，∴AB∥FG，∵CE⊥AB，∴CE⊥FG；故①正确；∵AD＝2AB，AD＝2AF，∴AB＝AF，∴四边形ABGF是菱形，故②正确；延长EF，交CD延长线于M，∵四边形ABCD是平行四边形，∴AB∥CD，∴∠A＝∠MDF，∵F为AD中点，∴AF＝FD，在△AEF和△DFM中，{∠A=∠FDM AF=DF∠AFE=∠DFM，∴△AEF≌△DMF（ASA），∴FE＝MF，∠AEF＝∠M，∵CE⊥AB，∴∠AEC＝90°，∴∠AEC＝∠ECD＝90°，∵FM＝EF，∴FC＝EF＝FM，故③正确；∴∠FCD＝∠M，∵四边形ABCD是平行四边形，∴AB＝CD，AD∥BC，∵AF＝DF，AD＝2AB，∴DF＝DC，∴∠DCF＝∠DFC，∴∠M＝∠FCD＝∠CFD，∵∠EFC＝∠M+∠FCD＝2∠CFD；故④正确，故选：D．13．【解答】解：∵AB是⊙O的直径，∴∠ADB＝90°，即AD⊥BD，故①正确；∵∠AEC＝∠DAB+∠EBA，∠AOC＝2∠EBA，∴∠AOC≠∠AEC，故②不正确；∵OC∥BD，∴∠OCB＝∠CBD，∵OC＝OB，∴∠OCB＝∠OBC，∴∠OBC＝∠CBD，即BC平分∠ABD，故③正确；∴OC⊥AD，∴AF＝FD，故④正确；∴OF为△ABD的中位线，∴BD＝2OF，故⑤正确，综上可知正确的有4个，故选：C．14．【解答】解：连接OD，AD．∵AB是⊙O的直径，∴∠ADB＝90°（直径所对的圆周角是直角），∴AD⊥BC；而在△ABC中，AB＝AC，∴AD是边BC上的中线，∴BD＝DC（正确）；∵AB是⊙O的直径，∴AD⊥BC，∵AB＝AC，∴DB＝DC，∵OA＝OB，∴OD是△ABC的中位线，即：OD∥AC，∵DF⊥AC，∴DF⊥OD．∴DF是⊙O的切线（正确）；∵DF⊥AC，AD⊥BC，∴∠FDC+∠C＝∠CAD+∠C＝90°，∴∠FDC＝∠CAD，又AB＝AC，∴∠BAD＝∠CAD，∴∠A＝2∠CAD＝2∠FDC（正确）；∵DF是⊙O的切线，∴∠FDE＝∠CAD＝∠FDC，∴∠C＝∠DEC，∴DC＝DE，又DF⊥AC，∴CF＝EF（正确）；̂=DÊ，此时△ABC为等边三角形，当∠EAD＝∠EDA时，AE当△ABC不是等边三角形时，∠EAD≠∠EDA，̂≠DÊ，则AÊ=DÊ（不正确）；∴AE综上，正确结论的序号是①②④⑤，故选：B．。

中考数学几何模型复习专题手拉手模型(学生版+解析版)

中考数学几何模型复习手拉手模型一、方法突破问题一：构成手拉手的必要条件．当对一个几何图形记忆并不深刻的时候，可以尝试用文字取总结要点，比如手拉手：四线共点，两两相等，夹角相等．条件：如图，OA=OB，OC=OD（四线共点，两两相等），∠AOB=∠COD（夹角相等）结论：△OAC≌△OBD（SAS）证明无需赘述，关于条件中的OA=OB，OC=OD，有时候会直接以特殊几何图形的形式给出，比如我们都很熟悉的等边三角形和正方形．1．等边三角形手拉手（1）如图，B、C、D三点共线，△ABC和△CDE是等边三角形，连接AD、BE，交于点P：结论一：△ACD≌△BCE证明：AC BCACD BCECD CE=⎧⎪∠=∠⎨⎪=⎩→ △ACD≌△BCE（SAS）ABCDOD（2）记AC 、BE 交点为M ，AD 、CE 交点为N ：结论二：△ACN ≌△BCM ；△MCE ≌△NCD证明：MBC NAC BC AC BCM ACN ∠=∠⎧⎪=⎨⎪∠=∠⎩→ △ACN ≌△BCM （SAS ）；MCE NCD CE CDCEM CDN ∠=∠⎧⎪=⎨⎪∠=∠⎩→ △MCE ≌△NCD （ASA ）（3）连接MN ：结论三：△MNC 是等边三角形．证明：60CM CNMCN =⎧⎨∠=︒⎩→△MCN 是等边三角形．（4）记AD 、BE 交点为P ，连接PC ：结论四：PC 平分∠BPD证明：△BCE ≌△ACD → CG =CH → PC 平分∠BPD ．DDHG ααEDCBAP（5）结论五：∠APB =∠BPC =∠CPD =∠DPE =60°．（6）连接AE ：结论六：P 点是△ACE 的费马点（P A +PC +PE 值最小）2．正方形手拉手如图，四边形ABCD 和四边形CEFG 均为正方形，连接BE 、DG ：结论一：△BCE ≌△DCG证明：CB CD BCE DCG CE CG =⎧⎪∠=∠⎨⎪=⎩→ △BCE ≌△DCG （SAS ）结论二：BE =DG ，BE ⊥DG证明：△BCE ≌△DCG → BE =DG ；∠CBE ＝∠CDG → ∠DHB =∠BCD =90°（旋转角都相等）【重点概述】手拉手模型是一种基本的旋转型全等，与其说看图找模型，不如是“找条件、定模型”．60°60°60°60°PABCDEEDCBAPF问题二：条件与结论如何设计？设计一：我们可以给出手拉手模型条件，得到一组全等来解决问题，就像问题一中所得出的结论那样；设计二：如果题目已知△ABC ≌△ADE 外，则还可得△ABD 和△ACE 均为等腰三角形，且有△ABD ∽△ACE ，AB AD BDAC AE CE==．问题三：如何构造手拉手？如何构造手拉手？换句话说，如何构造旋转？当我们在思考这个问题的时候，不妨先问一句，旋转能带来什么？图形位置的改变，这一点就够了，因为，若有数量关系，则先有位置关系．二、典例精析例一：如图，等边三角形ABC 的边长为4，点O 是ABC ∆的中心，120FOG ∠=︒，绕点O 旋转FOG ∠，分别交线段AB 、BC 于D 、E 两点，连接DE ，给出下列四个结论：①OD OE =；②ODE BDE S S ∆∆=；③四边形ODBEBDE ∆周长的最小值为6．上述结论中正确的个数是( )A ．1B ．2C ．3D ．4例二：如图，点P 在等边ABC ∆的内部，且6PC =，8PA =，10PB =，将线段PC 绕点C 顺时针旋转60︒得到P C '，连接AP '，则sin PAP '∠的值为．EDCBAC例三：如图，P 是等边三角形ABC 内一点，将线段AP 绕点A 顺时针旋转60︒得到线段AQ ，连接BQ ．若6PA =，8PB =，10PC =，则四边形APBQ 的面积为．例四：如图，等边三角形ABC 内有一点P ，分別连结AP 、BP 、CP ，若6AP =，8BP =，10CP =．则ABP BPC S S ∆∆+= ．例五：如图，P 为等边三角形ABC 内的一点，且P 到三个顶点A ，B ，C 的距离分别为3，4，5，则ABC∆的面积为( )A．9 B．9 C．18+D．18 例六：在Rt △ABC 中，AB =AC ，点P 是三角形内一点且∠APB =135°，PC =AC 的最大值为_________．QPABCPABCPABCABCP三、中考真题演练1．（2021•日照）问题背景：如图1，在矩形ABCD中，AB=30ABD∠=︒，点E是边AB的中点，过点E作EF AB⊥交BD于点F．实验探究：（1）在一次数学活动中，小王同学将图1中的BEF∆绕点B按逆时针方向旋转90︒，如图2所示，得到结论：①AEDF=；②直线AE与DF所夹锐角的度数为．（2）小王同学继续将BEF∆绕点B按逆时针方向旋转，旋转至如图3所示位置．请问探究（1）中的结论是否仍然成立？并说明理由．拓展延伸：在以上探究中，当BEF∆旋转至D、E、F三点共线时，则ADE∆的面积为．2．（2021•贵港）已知在ABC∆中，O为BC边的中点，连接AO，将AOC∆绕点O顺时针方向旋转（旋转角为钝角），得到EOF∆，连接AE，CF．（1）如图1，当90=；=时，则AE与CF满足的数量关系是AE CF∠=︒且AB ACBAC（2）如图2，当90≠时，（1）中的结论是否仍然成立？若成立，请写出证明过程；若∠=︒且AB ACBAC不成立，请说明理由．（3）如图3，延长AO到点D，使OD OABC=时，求DE的长．=，连接DE，当5==，6AO CF3．（2021•黑龙江）在等腰ADE ∆中，AE DE =，ABC ∆是直角三角形，90CAB ∠=︒，12ABC AED ∠=∠，连接CD 、BD ，点F 是BD 的中点，连接EF ．（1）当45EAD ∠=︒，点B 在边AE 上时，如图①所示，求证：12EF CD =；（2）当45EAD ∠=︒，把ABC ∆绕点A 逆时针旋转，顶点B 落在边AD 上时，如图②所示，当60EAD ∠=︒，点B 在边AE 上时，如图③所示，猜想图②、图③中线段EF 和CD 又有怎样的数量关系？请直接写出你的猜想，不需证明．4．（2021•通辽）已知AOB ∆和MON ∆都是等腰直角三角形)OM OA <<，90AOB MON ∠=∠=︒．（1）如图1，连接AM ，BN ，求证：AM BN =；（2）将MON ∆绕点O 顺时针旋转．①如图2，当点M 恰好在AB 边上时，求证：2222AM BM OM +=；②当点A ，M ，N 在同一条直线上时，若4OA =，3OM =，请直接写出线段AM 的长．5．（2021•十堰）已知等边三角形ABC，过A点作AC的垂线l，点P为l上一动点（不与点A重合），连接CP，把线段CP绕点C逆时针方向旋转60︒得到CQ，连QB．（1）如图1，直接写出线段AP与BQ的数量关系；（2）如图2，当点P、B在AC同侧且AP AC=时，求证：直线PB垂直平分线段CQ；∆，（3）如图3，若等边三角形ABC的边长为4，点P、B分别位于直线AC异侧，且APQ求线段AP的长度．6．（2020•沈阳）在ABC ∆中，AB AC =，BAC α∠=，点P 为线段CA 延长线上一动点，连接PB ，将线段PB 绕点P 逆时针旋转，旋转角为α，得到线段PD ，连接DB ，DC ．（1）如图1，当60α=︒时， ①求证：PA DC =； ②求DCP ∠的度数；（2）如图2，当120α=︒时，请直接写出PA 和DC 的数量关系．（3）当120α=︒时，若6AB =，BP D 到CP 的距离为．中考数学几何模型复习手拉手模型一、方法突破问题一：构成手拉手的必要条件．当对一个几何图形记忆并不深刻的时候，可以尝试用文字取总结要点，比如手拉手：四线共点，两两相等，夹角相等．条件：如图，OA=OB，OC=OD（四线共点，两两相等），∠AOB=∠COD（夹角相等）结论：△OAC≌△OBD（SAS）证明无需赘述，关于条件中的OA=OB，OC=OD，有时候会直接以特殊几何图形的形式给出，比如我们都很熟悉的等边三角形和正方形．3．等边三角形手拉手（1）如图，B、C、D三点共线，△ABC和△CDE是等边三角形，连接AD、BE，交于点P：结论一：△ACD≌△BCE证明：AC BCACD BCECD CE=⎧⎪∠=∠⎨⎪=⎩→ △ACD≌△BCE（SAS）ABCDOD（2）记AC 、BE 交点为M ，AD 、CE 交点为N ：结论二：△ACN ≌△BCM ；△MCE ≌△NCD证明：MBC NAC BC AC BCM ACN ∠=∠⎧⎪=⎨⎪∠=∠⎩→ △ACN ≌△BCM （SAS ）；MCE NCD CE CDCEM CDN ∠=∠⎧⎪=⎨⎪∠=∠⎩→ △MCE ≌△NCD （ASA ）（3）连接MN ：结论三：△MNC 是等边三角形．证明：60CM CNMCN =⎧⎨∠=︒⎩→△MCN 是等边三角形．（4）记AD 、BE 交点为P ，连接PC ：结论四：PC 平分∠BPD证明：△BCE ≌△ACD → CG =CH → PC 平分∠BPD ．DDDHG ααEDCBAP（5）结论五：∠APB =∠BPC =∠CPD =∠DPE =60°．（6）连接AE ：结论六：P 点是△ACE 的费马点（P A +PC +PE 值最小）4．正方形手拉手如图，四边形ABCD 和四边形CEFG 均为正方形，连接BE 、DG ：结论一：△BCE ≌△DCG证明：CB CD BCE DCG CE CG =⎧⎪∠=∠⎨⎪=⎩→ △BCE ≌△DCG （SAS ）结论二：BE =DG ，BE ⊥DG证明：△BCE ≌△DCG → BE =DG ；∠CBE ＝∠CDG → ∠DHB =∠BCD =90°（旋转角都相等）【重点概述】手拉手模型是一种基本的旋转型全等，与其说看图找模型，不如是“找条件、定模型”．60°60°60°60°PAB CDEEDCBAPF问题二：条件与结论如何设计？设计一：我们可以给出手拉手模型条件，得到一组全等来解决问题，就像问题一中所得出的结论那样；设计二：如果题目已知△ABC ≌△ADE 外，则还可得△ABD 和△ACE 均为等腰三角形，且有△ABD ∽△ACE ，AB AD BDAC AE CE==．问题三：如何构造手拉手？如何构造手拉手？换句话说，如何构造旋转？当我们在思考这个问题的时候，不妨先问一句，旋转能带来什么？图形位置的改变，这一点就够了，因为，若有数量关系，则先有位置关系．二、典例精析例一：如图，等边三角形ABC 的边长为4，点O 是ABC ∆的中心，120FOG ∠=︒，绕点O 旋转FOG ∠，分别交线段AB 、BC 于D 、E 两点，连接DE ，给出下列四个结论：①OD OE =；②ODE BDE S S ∆∆=；③四边形ODBEBDE ∆周长的最小值为6．上述结论中正确的个数是( )A ．1B ．2C ．3D ．4 【分析】等边三角形中的旋转型全等连接OB 、OC ，易证△OBD ≌△OCE ，∴OD =OE ，结论①正确；考虑∠FOG 是可以旋转的，△ODE 面积和△BDE 面积并非始终相等，故结论②错误；ECBACC∵△OBD ≌△OCE ，∴四边形ODBE 的面积等于△OBC的面积，142OBCS=⨯=，故结论③正确；考虑BD =CE ，∴BD +BE =CE +BE =4，只要DE 最小，△BDE 周长就最小，△ODE 是顶角为120°的等腰三角形，故OD 最小，DE 便最小，当OD ⊥AB 时，OD此时2DE ==，∴周长最小值为6，故结论④正确．综上，选C ，正确的有①③④．【小结】所谓全等，实际就是将△ODB 绕点O 旋转到△OEC 的位置．等等，好像和某个图有点神似，如下：当然这个图形还可以简化一下，毕竟和D 点及F 点并没有什么关系．结论与证明不多赘述，题型可以换，但旋转是一样的旋转．例二：如图，点P 在等边ABC ∆的内部，且6PC =，8PA =，10PB =，将线段PC 绕点C 顺时针旋转60︒得到P C '，连接AP '，则sin PAP '∠的值为．【分析】连接PP '，则CPP '△是等边三角形，故6PP PC '==，易证△CPB ≌CP A '△，∴10AP BP '==，又AP =8，∴APP '△是直角三角形，∴3sin 5PAP '∠=．D例三：如图，P 是等边三角形ABC 内一点，将线段AP 绕点A 顺时针旋转60︒得到线段AQ ，连接BQ ．若6PA =，8PB =，10PC =，则四边形APBQ 的面积为．【分析】分四边形为三角形．连接PQ ，易证△APQ 是等边三角形，△BPQ 是直角三角形，26APQS=168242BPQS =⨯⨯=， ∴四边形APBQ的面积为(．例四：如图，等边三角形ABC 内有一点P ，分別连结AP 、BP 、CP ，若6AP =，8BP =，10CP =．则ABP BPC S S ∆∆+= ．【分析】构造旋转．如图，将△BPC 绕点B 逆时针旋转60°得△BEA ，连接EP ，可得△AEP 是直角三角形，△BEP 是等边三角形，21688242APBBPCAEPBEPSSSS+=+=⨯⨯+=+ 所以本题答案为24+QPABCQPABCPABCC搭配一：若222PA PB PC+=，则可任意旋转，得等边+直角．且两条较短边夹角（∠APB）为150°．搭配二：若∠APB=150°，则有222PA PB PC+=．例五：如图，P为等边三角形ABC内的一点，且P到三个顶点A，B，C的距离分别为3，4，5，则ABC∆的面积为()A．9B．9C．18+D．18【分析】（3，4，5）是一组勾股数，通过旋转构造直角三角形．法一：如图，将三个小三角形面积分别123S S S、、考虑到△ABC是等边三角形，可将△APB 旋转到△ADC位置，可得：21331334642ADP PCDS S S S+=+=+⨯⨯=，同理可得：212143462S S++⨯⨯=，223153462S S+=+⨯⨯=，∴()123218S S S++，∴1239S S S++，故选A．CC CPABCS3S2S1PAB CC法二：如图，易证∠APB =150°，过点A 作BP 的垂线交BP 延长线于点H ，则1322AH AP ==，PH，4BH =)2229271625944S AH BH ==+=+++=+=⎝．【思考】如果放在正方形里，条件与结论又该如何搭配？作旋转之后，可得△AEP 是等腰直角三角形，若使△PEB 也为直角三角形，则原∠APD =135°，而线段PA 、PB 、PD 之间的关系为：2222PA PD PB +=．搭配一：若∠APD =135°，则2222PA PD PB +=；搭配二：若2222PA PD PB +=，则∠APD =135°．另外，其实这个图和点C 并没有什么关系，所以也可以将正方形换成等腰直角三角形．大概如下图：抓主要条件，舍弃无用条件，也是理解几何图形的一种方式．例六：在Rt △ABC 中，AB =AC ，点P 是三角形内一点且∠APB =135°，PC =AC 的最大值为_________．【分析】显然根据∠APB =135，构造旋转．可得：△APQ 是等腰直角三角形，△PQC 是直角三角形，且∠PQC =90°，另外还有条件PC =HPABC EAB CDEPABCPC重新梳理下条件，（1）有一条线段PC =（2）∠PQC =90°，则Q 点轨迹是个圆弧，（3）以PQ 为斜边在PC 异侧作等腰直角三角形，点A 是直角顶点．∴A 点轨迹是什么？瓜豆原理啦，也是个圆弧：∴AC22=．三、中考真题演练1．（2021•日照）问题背景：如图1，在矩形ABCD 中，AB =30ABD ∠=︒，点E 是边AB 的中点，过点E 作EF AB ⊥交BD 于点F ．实验探究：（1）在一次数学活动中，小王同学将图1中的BEF ∆绕点B 按逆时针方向旋转90︒，如图2所示，得到结论：①AEDF= ；②直线AE 与DF 所夹锐角的度数为．（2）小王同学继续将BEF ∆绕点B 按逆时针方向旋转，旋转至如图3所示位置．请问探究（1）中的结论是否仍然成立？并说明理由．拓展延伸：在以上探究中，当BEF ∆旋转至D 、E 、F 三点共线时，则ADE ∆的面积为．CPP PCCC【解答】解：（1）如图1，30ABD ∠=︒，90DAB ∠=︒，EF BA ⊥，cos BE AB ABD BF DB ∴∠==，如图2，设AB 与DF 交于点O ，AE 与DF 交于点H ，BEF ∆绕点B 按逆时针方向旋转90︒，90DBF ABE ∴∠=∠=︒，FBD EBA ∴∆∆∽，∴AE BE DF BF ==，BDF BAE ∠=∠，又DOB AOF ∠=∠，30DBA AHD ∴∠=∠=︒，∴直线AE 与DF 所夹锐角的度数为30︒，，30︒；（2）结论仍然成立，理由如下：如图3，设AE 与BD 交于点O ，AE 与DF 交于点H ，将BEF ∆绕点B 按逆时针方向旋转，ABE DBF ∴∠=∠，又BE AB BF DB ==， ABE DBF ∴∆∆∽，∴AE BE DF BF ==，BDF BAE ∠=∠，又DOH AOB ∠=∠，30ABD AHD ∴∠=∠=︒，∴直线AE 与DF 所夹锐角的度数为30︒．拓展延伸：如图4，当点E 在AB 的上方时，过点D 作DG AE ⊥于G ，2AB =30ABD ∠=︒，点E 是边AB 的中点，90DAB ∠=︒，BE ∴2AD =，4DB =，30EBF ∠=︒，EF BE ⊥，1EF ∴=，D 、E 、F 三点共线，90DEB BEF ∴∠=∠=︒，DE ∴30DEA ∠=︒，12DG DE ∴==由（2）可得：AE BE DF BF ==，∴=AE ∴，ADE ∴∆的面积1122AE DG =⨯⨯==；如图5，当点E 在AB 的下方时，过点D 作DG AE ⊥，交EA 的延长线于G ，同理可求：ADE ∆的面积1122AE DG =⨯⨯==2．（2021•贵港）已知在ABC ∆中，O 为BC 边的中点，连接AO ，将AOC ∆绕点O 顺时针方向旋转（旋转角为钝角），得到EOF ∆，连接AE ，CF ．（1）如图1，当90BAC ∠=︒且AB AC =时，则AE 与CF 满足的数量关系是；（2）如图2，当90BAC ∠=︒且AB AC ≠时，（1）中的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由．（3）如图3，延长AO 到点D ，使OD OA =，连接DE ，当5AO CF ==，6BC =时，求DE 的长．【解答】解：（1）结论：AE CF=．理由：如图1中，=，∠=︒，OC OB AB ACBAC=，90⊥，∴==，AO BCOA OC OB∠=∠=︒，AOC EOF90∴∠=∠，AOE COF=，=，OE OFOA OCAOE COF SAS∴∆≅∆，()∴=．AE CF（2）结论成立．理由：如图2中，=，∠=︒，OC OBBAC90∴==，OA OC OB∠=∠，AOC EOF∴∠=∠，AOE COF=，=，OE OFOA OC∴∆≅∆，AOE COF SAS()∴=．AE CF（3）如图3中，由旋转的性质可知OE OA=，OA OD=，5OE OA OD∴===，90AED∴∠=︒，OA OE=，OC OF=，AOE COF∠=∠，∴OA OEOC OF=，AOE COF∴∆∆∽，∴AE OACF OC=，5 CF OA==，∴5 53 AE=，253 AE∴=，DE∴=．3．（2021•黑龙江）在等腰ADE ∆中，AE DE =，ABC ∆是直角三角形，90CAB ∠=︒，12ABC AED ∠=∠，连接CD 、BD ，点F 是BD 的中点，连接EF ．（1）当45EAD ∠=︒，点B 在边AE 上时，如图①所示，求证：12EF CD =；（2）当45EAD ∠=︒，把ABC ∆绕点A 逆时针旋转，顶点B 落在边AD 上时，如图②所示，当60EAD ∠=︒，点B 在边AE 上时，如图③所示，猜想图②、图③中线段EF 和CD 又有怎样的数量关系？请直接写出你的猜想，不需证明．【解答】（1）证明：如图①中，EA ED =，45EAD ∠=︒，45EAD EDA ∴∠=∠=︒，90AED ∴∠=︒，BF FD =，12EF DB ∴=， 90CAB ∠=︒，45CAD BAD ∴∠=∠=︒，1452ABC AED ∠=∠=︒， 45ACB ABC ∴∠=∠=︒，AC AB ∴=，AD ∴垂直平分线段BC ，DC DB ∴=，12EF CD ∴=．（2）解：如图②中，结论：12EF CD =．理由：取CD 的中点T ，连接AT ，TF ，ET ，TE 交AD 于点O ． 90CAD ∠=︒，CT DT =，AT CT DT ∴==，EA ED =，ET ∴垂直平分线段AD ，AO OD ∴=，90AED ∠=︒，OE OA OD ∴==，CT TD =，BF DF =，//BC FT ∴，45ABC OFT ∴∠=∠=︒，90TOF ∠=︒，45OTF OFT ∴∠=∠=︒，OT OF ∴=，AF ET ∴=，FT TF =，AFT ETF ∠=∠，FA TE =，()AFT ETF SAS ∴∆≅∆，EF AT ∴=，12EF CD ∴=．如图③中，结论：EF =．理由：取AD 的中点O ，连接OF ，OE ．EA ED =，60AED ∠=︒，ADE ∴∆是等边三角形，AO OD =，OE AD ∴⊥，30AEO OED ∠=∠=︒，tan AO AEO OE ∴∠==∴OEAD =1302ABC AED ∠=∠=︒，90BAC ∠=︒，AB ∴，AO OD =，BF FD =，12OF AB ∴=，∴OF AC =， ∴OE OFAD AC =，//OF AB ，DOF DAB ∴∠=∠，90DOF EOF ∠+∠=︒，90DAB DAC ∠+∠=︒，EOF DAC ∴∠=∠，EOF DAC ∴∆∆∽，∴EFOECD AD =，EF ∴．4．（2021•通辽）已知AOB ∆和MON ∆都是等腰直角三角形)OM OA <<，90AOB MON ∠=∠=︒．（1）如图1，连接AM ，BN ，求证：AM BN =；（2）将MON ∆绕点O 顺时针旋转． ①如图2，当点M 恰好在AB 边上时，求证：2222AM BM OM +=； ②当点A ，M ，N 在同一条直线上时，若4OA =，3OM =，请直接写出线段AM 的长．【解答】（1）证明：90AOB MON ∠=∠=︒， AOB AON MON AON ∴∠+∠=∠+∠，即AOM BON ∠=∠，AOB ∆和MON ∆都是等腰直角三角形，OA OB ∴=，OM ON =，()AOM BON SAS ∴∆≅∆，AM BN ∴=；（2）①证明：连接BN ，90AOB MON ∠=∠=︒，AOB BOM MON BOM ∴∠-∠=∠-∠，即AOM BON ∠=∠，AOB ∆和MON ∆都是等腰直角三角形，OA OB ∴=，OM ON =，()AOM BON SAS ∴∆≅∆，45MAO NBO ∴∠=∠=︒，AM BN =，90MBN ∴∠=︒，222MB BN MN ∴+=，MON ∆都是等腰直角三角形，222MN ON ∴=，2222AM BM OM ∴+=；②解：如图3，当点N 在线段AM 上时，连接BN ，设BN x =，由（1）可知AOM BON ∆≅∆，可得AM BN =且AM BN ⊥，在Rt ABN ∆中，222AN BN AB +=，AOB ∆和MON ∆都是等腰直角三角形，4OA =，3OM =，MN ∴=，AB =222(x x ∴-+=，解得：x =，AM BN ∴= 如图4，当点M 在线段AN 上时，连接BN ，设BN x =，由（1）可知AOM BON ∆≅∆，可得AM BN =且AM BN ⊥，在Rt ABN ∆中，222AN BN AB +=，AOB ∆和MON ∆都是等腰直角三角形，4OA =，3OM =，MN ∴=，AB =222(x x ∴++=，解得：x =，AM BN ∴=，综上所述，线段AM ． 5．（2021•十堰）已知等边三角形ABC ，过A 点作AC 的垂线l ，点P 为l 上一动点（不与点A 重合），连接CP ，把线段CP 绕点C 逆时针方向旋转60︒得到CQ ，连QB ．（1）如图1，直接写出线段AP 与BQ 的数量关系；（2）如图2，当点P 、B 在AC 同侧且AP AC =时，求证：直线PB 垂直平分线段CQ ；（3）如图3，若等边三角形ABC 的边长为4，点P 、B 分别位于直线AC 异侧，且APQ ∆，求线段AP 的长度．【解答】解：（1）在等边ABC ∆中，AC BC =，60ACB ∠=︒，由旋转可得，CP CQ =，60PCQ ∠=︒， ACB PCQ ∴∠=∠，ACB PCB PCQ PCB ∴∠-∠=∠-∠，即ACP BCQ ∠=∠， ()ACP BCQ SAS ∴∆≅∆，AP BQ ∴=．（2）在等边ABC ∆中，AC BC =，60ACB ∠=︒，由旋转可得，CP CQ =，60PCQ ∠=︒，ACB PCQ ∴∠=∠，ACB PCB PCQ PCB ∴∠-∠=∠-∠，即ACP BCQ ∠=∠， ()ACP BCQ SAS ∴∆≅∆，AP BQ ∴=，90CBQ CAP ∠=∠=︒；BQ AP AC BC ∴===，AP AC =，90CAP ∠=︒，30BAP ∴∠=︒，75ABP APB ∠=∠=︒，135CBP ABC ABP ∴∠=∠+∠=︒，45CBD ∴∠=︒，45QBD ∴∠=︒，CBD QBD ∴∠=∠，即BD 平分CBQ ∠，BD CQ ∴⊥且点D 是CQ 的中点，即直线PB 垂直平分线段CQ ．（3）①当点Q 在直线l 上方时，如图所示，延长BQ 交l 于点E ，过点Q 作QF l ⊥于点F ，由题意可得AC BC =，PC CQ =，60PCQ ACB ∠=∠=︒， ACP BCQ ∴∠=∠，()APC BCQ SAS ∴∆≅∆，AP BQ ∴=，90CBQ CAP ∠=∠=︒，60CAB ABC ∠=∠=︒，30BAE ABE ∴∠=∠=︒，4AB AC ==，AE BE ∴=， 60BEF ∴∠=︒，设AP t =，则BQ t =，EQ t ∴=-，在Rt EFQ ∆中，)QF t =-，12APQ S AP QF ∆∴=⋅=，即1)2t ⋅-=，解得t =t ．即AP ． ②当点Q 在直线l 下方时，如图所示，设BQ 交l 于点E ，过点Q 作QF l ⊥于点F ，由题意可得AC BC =，PC CQ =，60PCQ ACB ∠=∠=︒，ACP BCQ ∴∠=∠，()APC BCQ SAS ∴∆≅∆，AP BQ ∴=，90CBQ CAP ∠=∠=︒，60CAB ABC ∠=∠=︒，30BAE ABE ∴∠=∠=︒，120BEF ∴∠=︒，60QEF ∠=︒，4AB AC ==，AE BE ∴=，设AP m =，则BQ m =，EQ m ∴=-，在Rt EFQ ∆中，QF m =，12APQ S AP QF ∆∴=⋅=，即12m m ⋅-解得m m ==．综上可得，AP 6．（2020•沈阳）在ABC ∆中，AB AC =，BAC α∠=，点P 为线段CA 延长线上一动点，连接PB ，将线段PB 绕点P 逆时针旋转，旋转角为α，得到线段PD ，连接DB ，DC ．（1）如图1，当60α=︒时，①求证：PA DC =；②求DCP ∠的度数；（2）如图2，当120α=︒时，请直接写出PA 和DC 的数量关系．（3）当120α=︒时，若6AB =，BP D 到CP 的距离为．【解答】（1）①证明：如图1中，将线段PB 绕点P 逆时针旋转，旋转角为α，得到线段PD ， PB PD ∴=，AB AC =，PB PD =，60BAC BPD ∠=∠=︒， ABC ∴∆，PBD ∆是等边三角形，60ABC PBD ∴∠=∠=︒，PBA DBC ∴∠=∠，BP BD =，BA BC =，()PBA DBC SAS ∴∆≅∆，PA DC ∴=．②解：如图1中，设BD 交PC 于点O ．PBA DBC ∆≅∆，BPA BDC ∴∠=∠，BOP COD ∠=∠，60OBP OCD ∴∠=∠=︒，即60DCP ∠=︒．（2）解：结论：CD =．理由：如图2中，AB AC =，PB PD =，120BAC BPD ∠=∠=︒，2cos30BC AB ∴=⋅⋅︒，2cos30BD BP =⋅︒=，∴BC BD BA BP= 30ABC PBD ∠=∠=︒，ABP CBD ∴∠=∠，CBD ABP ∴∆∆∽，∴CD BC PA AB=CD ∴=．（3）过点D 作DM PC ⊥于M ，过点B 作BN CP ⊥交CP 的延长线于N ．如图31-中，当PBA ∆是钝角三角形时，在Rt ABN ∆中，90N ∠=︒，6AB =，60BAN ∠=︒，cos603AN AB ∴=⋅︒=，sin 60BN AB =⋅︒=2PN PB ==， 321PA ∴=-=，由（2）可知，CD = BPA BDC ∠=∠，30DCA PBD ∴∠=∠=︒， DM PC ⊥，12DM CD ∴=如图32-中，当ABP ∆是锐角三角形时，同法可得235PA =+=，CD =12DM CD ==综上所述，满足条件的DM ．．。

2020年中考数学复习专题练：《四边形综合》(含答案)

2020年中考数学复习专题练：《四边形综合》1．如图①所示，已知正方形ABCD 和正方形AEFG ，连接DG ，BE ．（1）发现：当正方形AEFG 绕点A 旋转，如图②所示．①线段DG 与BE 之间的数量关系是；②直线DG 与直线BE 之间的位置关系是；（2）探究：如图③所示，若四边形ABCD 与四边形AEFG 都为矩形，且AD ＝2AB ，AG ＝2AE 时，上述结论是否成立，并说明理由．（3）应用：在（2）的情况下，连接BG 、DE ，若AE ＝1，AB ＝2，求BG 2+DE 2的值（直接写出结果）．2．如图1，在正方形ABCD 中，点E 是CD 上一点（不与C ，D 两点重合），连接BE ，过点C 作CH ⊥BE 于点F ，交对角线BD 于点G ，交AD 边于点H ，连接GE ，（1）求证：△DHC ≌△CEB ；（2）如图2，若点E 是CD 的中点，当BE ＝8时，求线段GH 的长；（3）设正方形ABCD 的面积为S 1，四边形DEGH 的面积为S 2，当的值为时，的值为．3．在平面直角坐标系中，四边形AOBC是矩形，点O（0，0），点A（6，0），点B（0，8）．以点A为中心，顺时针旋转矩形AOBC，得到矩形ADEF，点O，B，C的对应点分别为D，E，F，记旋转角为α（0°＜α＜90°）．（I）如图①，当α＝30°时，求点D的坐标；（Ⅱ）如图②，当点E落在AC的延长线上时，求点D的坐标；（Ⅲ）当点D落在线段OC上时，求点E的坐标（直接写出结果即可）．4．如图，BD是平行四边形ABCD的对角线，DE⊥AB于点E，过点E的直线交BC于点G，且BG＝CG．（1）求证：GD＝EG．（2）若BD⊥EG垂足为O，BO＝2，DO＝4，画出图形并求出四边形ABCD的面积．（3）在（2）的条件下，以O为旋转中心顺时针旋转△GDO，得到△G′D'O，点G′落在BC上时，请直接写出G′E的长．5．（1）【探索发现】如图1，在正方形ABCD中，点M，N分别是边BC，CD上的点，∠MAN＝45°，若将△DAN 绕点A顺时针旋转90°到△BAG位置，可得△MAN≌△MAG，若△MCN的周长为8，则正方形ABCD的边长为．（2）【类比延伸】如图2，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B+∠D＝180°，点M，N分别在边BC，CD上的点，∠MAN＝60°，请判断线段BM，DN，MN之间的数量关系，并说明理由．（3）【拓展应用】如图3，在四边形ABCD中，AB＝AD＝2，∠ADC＝120°，点M，N分别在边BC，CD上，连接AM，MN，AN，△ABM是等边三角形，AM⊥AD于点A，∠DAN＝15°，请直接写出△CMN 的周长．6．（1）如图1，在△ABC中，AB＞AC，点D，E分别在边AB，AC上，且DE∥BC，若AD＝2，AE＝，则的值是；（2）如图2，在（1）的条件下，将△ADE绕点A逆时针方向旋转一定的角度，连接CE 和BD，的值变化吗？若变化，请说明理由；若不变化，请求出不变的值；（3）如图3，在四边形ABCD中，AC⊥BC于点C，∠BAC＝∠ADC＝θ，且tanθ＝，当CD＝6，AD＝3时，请直接写出线段BD的长度．7．如图1，长方形ABCD中，∠DAB＝∠B＝∠DCB＝∠D＝90°，AD＝BC＝6，AB＝CD＝10．点E为射线DC上的一个动点，把△ADE沿直线AE翻折得△AD′E．（1）当D′点落在AB边上时，∠DAE＝°；（2）如图2，当E点与C点重合时，D′C与AB交点F，①求证：AF＝FC；②求AF长．（3）连接D′B，当∠AD′B＝90°时，求DE的长．8．在平面直角坐标系中，点O是坐标原点，A（0，m），B（n，O），AC∥OB，且AC＝OB，连接BC交x轴于点F，其中m、n满足方程+n2+8n+16＝0．（1）求A、B两点坐标；（2）过A做AE⊥BC于E，延长AE交x轴于点D，动点P从点B出发以每秒2个单位的速度向x轴正半轴方向运动，设△PFD的面积为S，请用含t的式子表示S，并直接写出t的取值范围；（3）在（2）的条件下，连接PE，将△PED沿PE翻折到△PEG的位置（点D与点G对应），当四边形PDEG为菱形时，求点P和点G的坐标．9．已知四边形ABCD和四边形CEFG都是正方形，且AB＞CE．（1）如图1，连接BG、DE．求证：BG＝DE；（2）如图2，如果正方形CEFG绕点C旋转到某一位置恰好使得CG∥BD，BG＝BD．①求∠BDE的度数；②若正方形ABCD的边长是，请求出△BCG的面积．10．【综合与实践】如图①，在正方形ABCD中，点E、F分别在射线CD、BC上，且BF＝CE，将线段FA绕点F顺时针旋转90°得到线段FG，连接EG，试探究线段EG和BF的数量关系和位置关系．【观察与猜想】任务一：“智慧小组”首先考虑点E、F的特殊位置如图②，当点E与点D重合，点F与点C重合时，易知：EG与BF的数量关系是，EG与BF的位置关系是．【探究与证明】任务二：“博学小组”同学认为E、F不一定必须在特殊位置，他们分两种情况，一种是点E、F分别在CD、BC边上任意位置时（如图③）；一种是点E、F在CD、BC边的延长线上的任意位置时（如图④），线段EG与BF的数量关系与位置关系仍然成立．请你选择其中一种情况给出证明．【拓展与延伸】“创新小组”同学认为，若将“正方形ABCD”改为“矩形ABCD，且＝k（k≠1）”，点E、F分别在射线CD、BC上任意位置时，仍将线段FA绕点F顺时针旋转90°，并适当延长得到线段FG，连接EG（如图⑤），则当线段BF、CE、AF、FG满足一个条件时，线段EG与BF的数量关系与位置关系仍然成立．（请你在横线上直接写出这个条件，无需证明）11．在平面直角坐标系xOy中，四边形OADC为正方形，点D的坐标为（4，4），动点E沿边AO从A向O以每秒1cm的速度运动，同时动点F沿边OC从O向C以同样的速度运动，连接AF、DE交于点G．（1）试探索线段AF、DE的关系，写出你的结论并说明理由；（2）连接EF、DF，分别取AE、EF、FD、DA的中点H、I、J、K，则四边形HIJK是什么特殊平行四边形？请在图①中补全图形，并说明理由．（3）如图②当点E运动到AO中点时，点M是直线EC上任意一点，点N是平面内任意一点，是否存在点N使以O，C、M、N为顶点的四边形是菱形？若存在，请直接写出点N的坐标；若不存在，请说明理由．12．综合与实践动手操作：第一步：在矩形纸片ABCD的边BC，AD上分别取两点E，F，使CE＝AF；第二步：分别以DE，BF为对称轴将△CDE与△ABF翻折得到△C'DE与△A'BF，且边C'E 与A'B交于点G，边A'F与C'D交于一点H．问题解决：（1）求证：△BEG≌△DFH；（2）请判断四边形A'HC'G的形状，并证明你发现的结论；（3）已知tan∠EBG＝，A'G＝6，C'G＝1，求矩形纸片ABCD的面积．13．如图1，矩形ABCD中，∠ACB＝30°，将△ACD绕C点顺时针旋转α（0°＜α＜360°）至△A'CD'位置．（1）如图2，若AB＝2，α＝30°，求S△BCD′．（2）如图3，取AA′中点O，连OB、OD′、BD′．若△OBD′存在，试判定△OBD′的形状．（3）当α＝α1时，OB＝OD′，则α1＝°；当α＝α2时，△OBD′不存在，则α2＝°．14．已知矩形ABCD 中，AB ＝2，BC ＝m ，点E 是边BC 上一点，BE ＝1，连接AE ．（1）沿AE 翻折△ABE 使点B 落在点F 处，①连接CF ，若CF ∥AE ，求m 的值；②连接DF ，若≤DF ≤，求m 的取值范围．（2）△ABE 绕点A 顺时针旋转得△AB 1E 1，点E 1落在边AD 上时旋转停止．若点B 1落在矩形对角线AC 上，且点B 1到AD 的距离小于时，求m 的取值范围．15．如图1，正方形ABCD 的边CD 在正方形ECGF 的边CE 上，连接BE 、DG ．（1）BE 和DG 的数量关系是，BE 和DG 的位置关系是；（2）把正方形ECGF 绕点C 旋转，如图2，（1）中的结论是否还成立？若成立，写出证明过程，若不成立，请说明理由；（3）设正方形ABCD 的边长为4，正方形ECGF 的边长为3，正方形ECGF 绕点C 旋转过程中，若A 、C 、E 三点共线，直接写出DG 的长．16．如图，正方形ABCD的边长为a，射线AM是∠BAD外角的平分线，点E在边AB上运动（不与点A、B重合），点F在射线AM上，且AF＝BE，CF与AD相交于点G，连结EC、EF、EG．（1）求证：CE＝EF；（2）求△AEG的周长（用含a的代数式表示）；（3）试探索：点E在边AB上运动至什么位置时，△EAF的面积最大．17．问题情境：矩形ABCD中，∠ACB＝30°，将一块直角三角板的直角顶点P放在两对角线的交点处，以点P为旋转中心转动三角板，并保证三角板的两直角边分别与边AB、BC所在的直线相交，交点为E、F．探究1：如图1，当PE⊥AB，PF⊥BC时，则＝．探究2：如图2，在（1）的基础上，将三角板绕点P逆时针旋转，旋转角为α，（0°＜α＜60°），试求的值．探究3：在（2）的基础上继续旋转，当60°＜α＜90°时，将顶点P在AC上移动且使＝时，如图3，试求的值．18．在Rt△ABC中，∠B＝90°，AB＝6，BC＝8，点D从点B出发，以每秒3个单位的速度沿B→A→C运动，到点C停止．在点D运动的过程中，过点D作DE⊥BC，垂足为E，以DE为一边在右侧作矩形DEFG，点F在BC边上，且EF：DE＝4：3，连结AG，CG，设运动时间为t（秒），矩形DEFG与△ABC重叠部分面积为S．（1）当AG＝CG时，求t的值．（2）当点D在边AB上运动时，求S与t的函数关系式．（3）当△ACG的面积为6时，直接写出t的值．19．如图，在四边形ABCD中，AD∥BC，∠C＝90°，BC＝32，DC＝24，AD＝42，动点P从点D出发，沿射线DA的方向以每秒4个单位长的速度运动，动点Q从点C出发，在线段CB 上以每秒2个单位长的速度向点B运动，点P，Q分别从点D，C同时出发，当点Q运动到点B时，点P随之停止运动．设运动的时间为t（秒）．（1）设△BPQ的面积为S，求S与t之间的函数关系式；（2）当t为何值时，以B，P，Q三点为顶点的三角形是等腰三角形？（3）是否存在时刻t，使得PQ⊥BD？若存在，求出t的值；若不存在，请说明理由．20．（1）【发现证明】如图1，在正方形ABCD中，点E，F分别是BC，CD边上的动点，且∠EAF＝45°，求证：EF＝DF+BE．小明发现，当把△ABE绕点A顺时针旋转90°至△ADG，使AB与AD重合时能够证明，请你给出证明过程．（2）【类比引申】①如图2，在正方形ABCD中，如果点E，F分别是CB，DC延长线上的动点，且∠EAF＝45°，则（1）中的结论还成立吗？请写出证明过程．②如图3，如果点E，F分别是BC，CD延长线上的动点，且∠EAF＝45°，则EF，BE，DF之间的数量关系是（不要求证明）（3）【联想拓展】如图1，若正方形ABCD的边长为6，AE＝3，求AF的长．参考答案1．解：（1）①如图②中，∵四边形ABCD和四边形AEFG是正方形，∴AE＝AG，AB＝AD，∠BAD＝∠EAG＝90°，∴∠BAE＝∠DAG，在△ABE和△DAG中，，∴△ABE≌△ADG（SAS），∴BE＝DG；②如图2，延长BE交AD于T，交DG于H．由①知，△ABE≌△DAG，∴∠ABE＝∠ADG，∵∠ATB+∠ABE＝90°，∴∠ATB+∠ADG＝90°，∵∠ATB＝∠DTH，∴∠DTH+∠ADG＝90°，∴∠DHB＝90°，∴BE⊥DG，故答案为：BE＝DG，BE⊥DG；（2）数量关系不成立，DG＝2BE，位置关系成立．如图③中，延长BE交AD于T，交DG于H．∵四边形ABCD与四边形AEFG都为矩形，∴∠BAD＝∠EAG，∴∠BAE＝∠DAG，∵AD＝2AB，AG＝2AE，∴＝＝，∴△ABE∽△ADG，∴∠ABE＝∠ADG，＝，∴DG＝2BE，∵∠ATB+∠ABE＝90°，∴∠ATB+∠ADG＝90°，∵∠ATB＝∠DTH，∴∠DTH+∠ADG＝90°，∴∠DHB＝90°，∴BE⊥DG；（3）如图④中，作ET⊥AD于T，GH⊥BA交BA的延长线于H．设ET＝x，AT＝y．∵△AHG∽△ATE，∴＝＝＝2，∴GH＝2x，AH＝2y，∴4x2+4y2＝4，∴x2+y2＝1，∴BG2+DE2＝（2x）2+（2y+2）2+x2+（4﹣y）2＝5x2+5y2+20＝25．2．证明（1）∵四边形ABCD是正方形，∴CD＝BC，∠HDC＝∠BCE＝90°，∴∠DHC+∠DCH＝90°，∵CH⊥BE，∴∠EFC＝90°，∴∠ECF+∠BEC＝90°，∴∠CHD＝∠BEC，∴△DHC≌△CEB（AAS）．（2）解：∵△DHC≌△CEB，∴CH＝BE，DH＝CE，∵CE＝DE＝CD，CD＝CB，∴DH＝BC，∵DH∥BC，∴．∴GC＝2GH，设GH＝x，则，则CG＝2x，∴3x＝8，∴x＝．即GH＝．（3）解：∵，∴，∵DH＝CE，DC＝BC，∴，∵DH∥BC，∴，∴，，设S△DGH ＝9a，则S△BCG＝49a，S△DCG＝21a，∴S△BCD＝49a+21a＝70a，∴S1＝2S△BCD＝140a，∵S△DEG ：S△CEG＝4：3，∴S△DEG＝12a，∴S2＝12a+9a＝21a．∴．故答案为：．3．解：（I）过点D作DG⊥x轴于G，如图①所示：∵点A（6，0），点B（0，8）．∴OA＝6，OB＝8，∵以点A为中心，顺时针旋转矩形AOBC，得到矩形ADEF，∴AD＝AO＝6，α＝∠OAD＝30°，DE＝OB＝8，在Rt△ADG中，DG＝AD＝3，AG＝DG＝3，∴OG＝OA﹣AG＝6﹣3，∴点D的坐标为（6﹣3，3）；（Ⅱ）过点D作DG⊥x轴于G，DH⊥AE于H，如图②所示：则GA＝DH，HA＝DG，∵DE＝OB＝8，∠ADE＝∠AOB＝90°，∴AE＝＝＝10，∵AE×DH＝AD×DE，∴DH＝＝＝，∴OG＝OA﹣GA＝OA﹣DH＝6﹣＝，DG＝＝＝，∴点D的坐标为（，）；（Ⅲ）连接AE，作EG⊥x轴于G，如图③所示：由旋转的性质得：∠DAE＝∠AOC，AD＝AO，∴∠OAC＝∠ADO，∴∠DAE＝∠ADO，∴AE∥OC，∴∠GAE＝∠AOD，∴∠DAE＝∠GAE，在△AEG和△AED中，，∴△AEG≌△AED（AAS），∴AG＝AD＝6，EG＝ED＝8，∴OG＝OA+AG＝12，∴点E的坐标为（12，8）．4．证明：（1）如图1，延长EG交DC的延长线于点H，∵四边形ABCD是平行四边形，∴AD＝BC，AD∥BC，AB＝CD，AB∥CD，∵AB∥CD，∴∠H＝GEB，且BG＝CG，∠BGE＝∠CGH，∴△CGH≌△BGE（AAS）∴GE＝GH，∵DE⊥AB，DC∥AB，∴DC⊥DE，且GE＝GH，∴DG＝EG＝GH；（2）如图1：∵DB⊥EG，∴∠DOE＝∠DEB＝90°，且∠EDB＝∠EDO，∴△DEO∽△DBO，∴∴DE×DE＝4×（2+4）＝24，∴DE＝2，∴EO＝＝＝2，∵AB∥CD，∴， ∴HO ＝2EO ＝4， ∴EH ＝6，且EG ＝GH ， ∴EG ＝3，GO ＝EG ﹣EO ＝， ∴GB ＝＝＝，∴BC ＝2＝AD ， ∴AD ＝DE ，∴点E 与点A 重合，如图2：∵S 四边形ABCD ＝2S △ABD ，∴S 四边形ABCD ＝2××BD ×AO ＝6×2＝12；（3）如图3，过点O 作OF ⊥BC ，∵旋转△GDO ，得到△G ′D 'O ，∴OG ＝OG '，且OF ⊥BC ，∴GF ＝G 'F ，∵OF ∥AB ，∴＝＝，∴GF＝BG＝，∴GG'＝2GF＝，∴BG'＝BG﹣GG'＝，∵AB2＝AO2+BO2＝12，∵EG'＝AG'＝＝，＝．5．解：（1）如图1中，∵△MAN≌△MAG，∴MN＝GM，∵DN＝BG，GM＝BG+BM，∴MN＝BM+DN，∵△CMN的周长为：MN+CM+CN＝8，∴BM+CM+CN+DN＝8，∴BC+CD＝8，∴BC＝CD＝4，故答案为4；（2）如图2中，结论：MN＝NM+DN．延长CB至E，使BE＝DN，连接AE，∵∠ABC+∠D＝180°，∠ABC+∠ABE＝180°，∴∠D＝∠ABE，在△ABE和△ADN中，，∴△ABE≌△ADN（SAS），∴AN＝AE，∠DAN＝∠BAE，∵∠BAD＝2∠MAN，∴∠DAN+∠BAM＝∠MAN，∴∠MAN＝∠EAM，在△MAN和△MAE中，，∴△MAN≌△MAE（SAS），∴MN＝EM＝BE+BM＝BM+DN，即MN＝BM+DN；（3）如图3，延长BA，CD交于G，∵∠BAM＝60°，∠MAD＝90°，∴∠BAD＝150°，∴∠GAD＝30°，∵AD＝2，∴DG＝1，AG＝，∵∠DAN＝15°，∴∠GAN＝45°，∴AG＝GN＝，∴BG＝2+，∴BC＝2BG＝4+2，CG＝BG＝2+3，∴CD＝CG﹣DG＝2+2，由（2）得，MN＝BM+DN，∴△CMN的周长＝CM+CN+MN＝CN+DN+CM+BM＝BC+CD＝4+2+2+2＝6+4．6．解：（1）∵DE∥BC，∴＝＝＝；故答案为：；（2）的值不变化，值为；理由如下：由（1）得：DE∥B，∴△ADE∽△ABC，∴＝，由旋转的性质得：∠BAD＝∠CAE，∴△ABD∽△ACE，∴＝＝；（3）在AB上截取AM＝AD＝3，过M作MN∥BC交AC于N，把△AMN绕A逆时针旋转得△ADE，连接CE，如图所示：则MN⊥AC，DE＝MN，∠DAE＝∠BAC，∴∠AED＝∠ANM＝90°，∵AC⊥BC于点C，∠BAC＝∠ADC＝θ，且tanθ＝＝，∴BC：AC：AB＝3：4：5，同（2）得：△ABD∽△ACE，∴＝＝，∵MN∥BC，∴△AMN∽△ABC，∴＝，∴MN＝×AM＝×3＝，∵∠BAC＝∠ADC＝θ，∴∠DAE＝∠ADC＝θ，∴AE∥CD，∴∠CDE+∠AED＝180°，∴∠CDE＝90°，∴CE＝＝＝，∴BD＝CE＝×＝．7．解：（1）由题意知△ADE≌△AD′E，∴∠DAE＝∠D′AE，∵D′点落在AB边上时，∠DAE+∠D′AE＝90°，∴∠DAE＝∠D′AE＝45°，故答案为：45；（2）①如图2，由题意知∠ACD＝∠ACD′，∵四边形ABCD是矩形，∴AB∥CD，∴∠ACD＝∠BAC，∴∠ACD′＝∠BAC，∴AF＝FC；②设AF＝FC＝x，则BF＝10﹣x，在Rt△BCF中，由BF2+BC2＝CF2得（10﹣x）2+62＝x2，解得x＝6.8，即AF＝6.8；（3）如图3，∵△AD′E≌△ADE，∴∠AD′E＝∠D＝90°，∵∠AD′B＝90°，∴B、D′、E三点共线，又∵△ABD′∽△BEC，AD′＝BC，∴△ABD′≌△BEC，∴BE＝AB＝10，∵BD′＝＝＝8，∴DE＝D′E＝10﹣8＝2；如图4，∵∠ABD″+∠CBE＝∠ABD″+∠BAD″＝90°，∴∠CBE＝∠BAD″，在△ABD″和△BEC中，∵，∴△ABD″≌△BEC，∴BE＝AB＝10，∴DE＝D″E＝8+10＝18．综上所知，DE＝2或18．8．解：（1）∵，，（n+4）2≥0，∴m﹣4＝0，n+4＝0，∴m＝4，n＝﹣4，∴A（0，4），B（﹣4，0）；（2）∵AC∥OB，∴∠C＝∠CBO，∠CAF＝∠BOF，∵AC＝OB，∴△ACF≌△OBF（ASA），∴AF＝OF＝2，∵OA＝OB，∠OAD＝∠OBF，∠BOF＝∠AOD，∴△BOF≌△AOD（ASA），∴OF＝OD＝2，∴BD＝6，①当0≤t＜3时，S＝PD•OF＝（6﹣2t）×2＝6﹣2t；②当t＞3时，S＝PD•OF＝（2t﹣6）×2＝2t﹣6；（3）①当0≤t＜3，如图2，∵AO＝4，OD＝2，∴AD＝，∵BD×OA＝AD×BE，∴BE＝，∴DE＝，∵四边形PDEG为菱形，∴DP＝DE＝EG＝，∵D（2，0），∴P（2﹣，0），作EH⊥BD于H，∵BE×DE＝BD×EH，∴EH＝，∴HD＝，∴OH＝，∴E（，），∵EG∥OB，∴G与E的纵坐标相同，∴G（﹣，）②当t＞3时，如图3，同理求得P（2+，0），G（+，）．9．（1）证明：∵四边形ABCD和四边形CEFG为正方形，∴BC＝DC，CG＝CE，∠BCD＝∠GCE＝90°．∴∠BCD+∠DCG＝∠GCE+∠DCG，∴∠BCG＝∠DCE．在△BCG和△DCE中，，∴△BCG≌△DCE（SAS）．∴BG＝DE；（2）解：①连接BE，如图2所示：由（1）可知：BG＝DE，∵CG∥BD，∴∠DCG＝∠BDC＝45°，∴∠BCG＝∠BCD+∠DCG＝90°+45°＝135°，∵∠GCE＝90°，∴∠BCE＝360°﹣∠BCG﹣∠GCE＝360°﹣135°﹣90°＝135°，∴∠BCG＝∠BCE，在△BCG和△BCE中，，∴△BCG≌△BCE（SAS），∴BG＝BE，∵BG＝BD＝DE，∴BD＝BE＝DE，∴△BDE为等边三角形，∴∠BDE＝60°；②延长EC交BD于点H，过点G作GN⊥BC于N，如图3所示：在△BCE和△DCE中，，∴△BCE≌△BCG（SSS），∴∠BEC＝∠DEC，∴EH⊥BD，BH＝BD，∵BC＝CD＝，∴BD＝BC＝2，∴BE＝2，BH＝1，∴CH＝1，在Rt△BHE中，由勾股定理得：EH＝＝＝，∴CE＝﹣1，∵∠BCG＝135°，∴∠GCN＝45°，∴△GCN是等腰直角三角形，∴GN＝CG＝（﹣1），＝BC•GN＝××（﹣1）＝．∴S△BCG10．【观察与猜想】解：∵四边形ABCD是正方形，∴∠B＝∠BCD＝∠ADC＝90°，AB＝BC＝CD＝AD，∠ACB＝∠ACD＝45°，由旋转的性质得：GC＝AC，∠ACG＝90°，∴∠ACB＝∠GCD＝45°，在△ABC和△GDC中，，∴△ABC≌△GDC（SAS），∴AB＝GD，∠GDC＝∠B＝90°，∴DG∥BC，△CDG是等腰直角三角形，∴DG＝CD＝BC，∵点E与点D重合，点F与点C重合，∴EG＝BF，EG∥BF；故答案为：EG＝BF，EG∥BF；【探究与证明】证明：点E、F分别在CD、BC边上任意位置时，如图③所示：作GM⊥BC，交BC延长线于M，则∠GMF＝90°，MG∥DC，∵四边形ABCD是正方形，∴AB＝BC，∠BCD＝∠B＝90°，∴∠BAF+∠BFA＝90°，由旋转的性质得：GF＝AF，∠AFG＝90°，∴∠BFA+∠MFG＝90°，∴∠BAF＝∠MFG，在△ABF和△FMG中，，∴△ABF≌△FMG（AAS），∴AB＝FM，BF＝MG，∵AB＝BC，∴BF＝CM，∵BF＝CE，∴MG＝CE，∵MG∥CE，∴四边形CEGM是平行四边形，又∵∠GMF＝90°，∴四边形CEGM是矩形，∴EG＝CM，EG∥CM，∴EG＝BF，EG∥BF；点E、F在CD、BC边的延长线上的任意位置时，如图④所示：作GM⊥BC，交BC延长线于M，则∠GMF＝90°，MG∥DC，∵四边形ABCD是正方形，∴AB＝BC，∠BCD＝∠B＝90°，∴∠BAF+∠BFA＝90°，由旋转的性质得：GF＝AF，∠AFG＝90°，∴∠BFA+∠MFG＝90°，∴∠BAF＝∠MFG，在△ABF和△FMG中，，∴△ABF≌△FMG（AAS），∴AB＝FM，BF＝MG，∵AB＝BC，∴BF＝CM，∵BF＝CE，∴MG＝CE，∵MG∥CE，∴四边形CEGM是平行四边形，又∵∠GMF＝90°，∴四边形CEGM是矩形，∴EG＝CM，EG∥CM，∴EG＝BF，EG∥BF；【拓展与延伸】解：＝＝k（k≠1）时，线段EG与BF的数量关系与位置关系仍然成立；理由如下：作GM⊥BC，交BC延长线于M，如图⑤所示：则∠GMF＝90°，MG∥DC，∵四边形ABCD是正方形，∴AB＝BC，∠BCD＝∠B＝90°，∴∠BAF+∠BFA＝90°，∠B＝∠GMF，由旋转的性质得：∠AFG＝90°，∴∠BFA+∠MFG＝90°，∴∠BAF＝∠MFG，∴△ABF∽△FMG，∴＝＝，∵＝＝k，∴＝＝k，＝＝k，∴FM＝BC，GM＝CE，∴BF＝CM，∵MG∥CE，∴四边形CEGM是平行四边形，又∵∠GMF＝90°，∴四边形CEGM是矩形，∴EG＝CM，EG∥CM，∴EG＝BF，EG∥BF；故答案为：＝＝k（k≠1）．11．解：（1）AF＝DE．理由如下：∵四边形OADC是正方形，∴OA＝AD，∠DAE＝∠AOF＝90°，由题意得：AE＝OF，在△AOF和△DAE中，，∴△AOF≌△DAE（SAS），∴AF＝DE．（2）四边形HIJK是正方形．理由如下：如图①所示：∵H、I、J、K分别是AE、EF、FD、DA的中点，∴HI＝KJ＝AF，HK＝IJ＝ED，HI∥AF，HK∥ED，∵AF＝DE，∴HI＝KJ＝HK＝IJ，∴四边形HIJK是菱形，∵△AOF≌△DAE，∴∠ADE＝∠OAF，∵∠ADE+∠AED＝90°，∴∠OAF+∠AED＝90°，∴∠AGE＝90°，∴AF⊥ED，∵HI∥AF，HK∥ED，∴HI⊥HK，∴∠KHI＝90°，∴四边形HIJK是正方形．（3）存在，理由如下：∵四边形OADC为正方形，点D的坐标为（4，4），∴OA＝AD＝OC＝4，∴C（4，0），∵点E为AO的中点，∴OE＝2，E（0，2）；分情况讨论：如图②所示，①当OC是以O，C、M、N为顶点的菱形的对角线时，OC与MN互相垂直平分，则M为CE 的中点，∴点M的坐标为（2，1），∵点M和N关于OC对称，∴N（2，﹣1）；②当OC是以O，C、M、N为顶点的菱形的边时，若M在y轴的左侧时，∵四边形OCM'N'是菱形，∴OM'＝OC＝4，M'N'∥OC，∴△M'FE∽△COE，∴＝＝2，设EF＝x，则M'F＝2x，OF＝x+2，在Rt△OM'F中，由勾股定理得：（2x）2+（x+2）2＝42，解得：x＝，或x＝﹣2（舍去），∴M'F＝，FN＝4﹣M'F＝，OF＝2+＝，∴N'（，）；若M在y轴的右侧时，作N''P⊥OC于P，∵ON''∥CM''，∴∠PON''＝∠OCE，∴tan∠PON''＝＝tan∠OCE＝＝，设PN''＝y，则OP＝2y，在Rt△OPN''中，由勾股定理得：y2+（2y）2＝42，解得：y＝，∴PN''＝，OP＝，∴N''（，﹣）；综上所述，存在点N使以O，C、M、N为顶点的四边形是菱形，点N的坐标为（2，﹣1）或（，）或（，﹣）．12．（1）证明：∵四边形ABCD为矩形，∴BC＝AD，CD＝AB，∠C＝∠ABC＝∠A＝∠ADC＝90°，∵CE＝AF，∴BC﹣CE＝AD﹣AF，即BE＝DF，在△DCE和△BAF中，，∴△DCE≌△BAF（SAS），∴∠CDE＝∠ABF，∠CED＝∠AFB，由折叠的性质得：∠CDE＝∠C′DE，∠ABF＝∠A′BF，∠CED＝∠C′ED，∠AFB＝∠A′FB，∵∠CDE+∠C′DE+∠HDF＝90°，∠ABF+∠A′BF+∠GBE＝90°，∠CED+∠C′ED+∠GEB＝180°，∠AFB+∠A′FB+∠HFD＝180°，∴∠HDF＝∠GBE，∠GEB＝∠HFD，在△BEG和△DFH中，，∴△BEG≌△DFH（ASA）；（2）解：四边形A'HC'G的形状是矩形；理由如下：由折叠的性质得：∠C＝∠DC′E＝∠A＝∠BA′F＝90°，由（1）得：△BEG≌△DFH，∴∠BGE＝∠DHF，∵∠BGE＝∠A′GC′，∠DHF＝∠A′HC′，∴∠A′GC′＝∠A′HC′，∵∠DC′E+∠BA′F+∠A′GC′+∠A′HC′＝90°+90°+∠A′GC′+∠A′HC′＝360°，∴∠A′GC′+∠A′HC′＝180°，∴∠A′GC′＝∠A′HC′＝90°，∴∠DC′E＝∠BA′F＝∠A′GC′＝∠A′HC′＝90°，∴四边形A'HC'G是矩形；（3）解：由（2）知：∠BGE＝∠A′GC′＝90°，∵tan∠EBG＝，∴设EG＝3x，则BG＝4x，BE＝＝5x，由折叠的性质得：CE＝C′E＝EG+C′G＝3x+1，CD＝AB＝A′B＝BG+A′G＝4x+6，∴BC＝CE+BE＝3x+1+5x＝8x+1，S矩形ABCD＝CD•BC＝4×CD•CE+2×EG•BG﹣A'G•C'G，即（4x+6）（8x+1）＝4×（3x+1）（4x+6）+2×3x•4x﹣6×1，整理得：x2﹣2x＝0，解得：x1＝2，x2＝0（不合题意舍去），∴CD＝4×2+6＝14，CB＝8×2+1＝17，∴S矩形ABCD＝CD•BC＝14×17＝238．13．解：（1）作D'E⊥BC交BC的延长线于E，如图2所示：则∠E＝90°，∵四边形ABCD是矩形，∴∠ABC＝90°，AB∥CD，AD∥BC，CD＝AB＝2，∴∠ACD＝∠BAC，∠DAC＝∠ACB＝30°，∵∠ACB＝30°，∴BC＝AB＝2，∠ACD＝∠BAC＝60°，由旋转的性质得：CD'＝CD＝2，∠ACA'＝30°，∴∠D'CE＝180°﹣30°﹣30°﹣60°＝60°，∴∠CD'E＝30°，∴CE＝CD'＝1，D'E＝CE＝，∴S＝BC×D'E＝×2×＝3；△BCD′（2）△OBD′是直角三角形，理由如下：连接OC，如图3所示：由旋转的性质得：CA'＝CA，∠AD'C＝∠ADC＝90°，∠D'A'C＝∠DAC＝30°，∵O是AA′的中点，∴OC⊥AA'，∴∠AOC＝∠AOC＝90°＝∠ABC＝∠AD'C，∴∠ABC+∠AOC＝180°，∴A、B、C、O四点共圆，∴∠BOC＝∠BAC＝60°，同理；A、D'、C、O四点共圆，∴∠D'OC＝∠D'A'C＝30°，∴∠BOD'＝90°，∴△BOD'是直角三角形；（3）若B、C、D'三点不共线，如图3所示：由（2）得：∠OBC＝∠OAC，∠OD'C＝∠OA'C，∠OAC＝∠OA'C，∴∠OBC＝∠OD'C，∵OB＝OD，∴∠OBD'＝∠OD'B，∴∠CBD'＝∠CD'B，∴CB＝CD'，∵CD'＝CD，∴BC＝CD，这与已知相矛盾，∴B、C、D'三点共线；分两种情况：当点D'在BC的延长线上时，如图4所示：＝90°；α＝α1当点D'在边BC上时，如图5所示：＝360°﹣90°＝270°；α＝α1故答案为：90°或270；时，△OBD′不存在时，分两种情况：当α＝α2当O与D'重合时，如图6所示：∵CA'＝CA，∠CAD'＝∠CA'D'＝30°，∴∠ACA'＝120°，＝360°﹣120°＝240°；∴α＝α2当O与B重合时，如图7所示：则AA'＝2AB＝4，∵CA＝CA'＝2AB＝4＝AA'，∴△ACA'是等边三角形，∴∠A'CA＝60°，＝360°﹣60°＝300°；∴α＝α2故答案为：240°或300．14．解：（1）①如图1，∵CF∥AE ∴∠FCE＝∠AEB，∠CFE＝∠AEF∵△ABE翻折得到△AFE∴EF＝BE＝1，∠AEF＝∠AEB∴∠FCE＝∠CFE∴CE＝EF＝1∴m＝BC＝BE+CE＝2∴m的值是2．②如图2，过点F作GH⊥AD于点G，交BC于点H ∴GH⊥BC∴∠AGF＝∠FHE＝90°∵四边形ABCD是矩形∴∠BAD＝∠B＝90°∴四边形ABHG是矩形∴GH＝AB＝2，AG＝BH∵△ABE翻折得到△AFE∴EF＝BE＝1，AF＝AB＝2，∠AFE＝∠B＝90°∴∠AFG+∠EFH＝∠AFG+∠FAG＝90°∴∠EFH＝∠FAG∴△EFH∽△FAG∴设EH＝x，则AG＝BH＝x+1∴FG＝2EH＝2x∴FH＝GH﹣FG＝2﹣2x∴解得：x＝∴AG＝，FG＝∵AD＝BC＝m∴DG＝|AD﹣AG|＝|m﹣|∴DF 2＝DG 2+FG 2＝（m ﹣）2+2≥，即可把DF 2看作关于m 的二次函数，抛物线开口向上，最小值为∵∴∵（m ﹣）2+2＝解得：m 1＝，m 2＝1 ∴根据二次函数图象可知，1≤m（2）如图3，过点B 1作MN ⊥AD 于点M ，交BC 于点N ∴MN ∥AB ，MN ＝AB ＝2∵AC ＝ ∴sin ∠ACB ＝∵AD ∥BC ，点B 1在AC 上∴∠MAB 1＝∠ACB∴sin ∠MAB 1＝ ∴∵点B 1到AD 的距离小于∴MB 1＝解得：∵m＞0 ∴m＞如图4，当E1落在边AD上，且B1在AC上时，m最大，此时，∠ACB＝∠B1AE1＝∠BAE∴tan∠ACB＝tan∠BAE∴∴m＝BC＝2AB＝4∴m的取值范围是＜m≤415．解：（1）BE＝DG．BE⊥DG；理由如下：∵四边形ABCD和四边形CEFG为正方形，∴CD＝BC，CE＝CG，∠BCE＝∠DCG＝90°，在△BEC和△DGC中，，∴△BEC≌△DGC（SAS），∴BE＝DG；如图1，延长GD交BE于点H，∵△BEC≌△DGC，∴∠DGC＝∠BEC，∴∠DGC+∠EBC＝∠BEC+∠EBC＝90°，∴∠BHG＝90°，即BE⊥DG；故答案为：BE＝DG，BE⊥DG．（2）成立，理由如下：如图2所示：同（1）得：△DCG≌△BCE（SAS），∴BE＝DG，∠CDG＝∠CBE，∵∠DME＝∠BMC，∠CBE+∠BMC＝90°，∴∠CDG+∠DME＝90°，∴∠DOB＝90°，∴BE⊥DG；（3）由（2）得：DG＝EB，分两种情况：①如图3所示：∵正方形ABCD的边长为4，正方形ECGF的边长为3，∴AC⊥BD，BD＝AC＝AB＝4，OA＝OC＝OB＝AC＝2，CE＝3，∴AE＝AC﹣CE＝，∴OE＝OA﹣AE＝，在Rt△BOE中，由勾股定理得：DG＝BE＝＝；②如图4所示：OE＝CE+OC＝2+3＝5，在Rt△BOE中，由勾股定理得：DG＝BE＝＝；综上所述，若A、C、E三点共线，DG的长为或．16．（1）证明：过点F作FH⊥AB于H，如图1所示：则∠AHF＝90°，∵AM平分∠DAH，∴∠FAH＝45°，∴△AFH是等腰直角三角形，∴FH＝AH，AF＝AH＝FH，∵AF＝BE，∴FH＝AH＝BE，∴AH+AE＝BE+AE，∴HE＝AB＝BC，在△FEH和△ECB中，，∴△FEH≌△ECB（SAS），∴CE＝EF；（2）解：∵△FEH≌△ECB，∴∠FEH＝∠ECB，∵在Rt△BCE中，∠ECB+∠CEB＝90°，∴∠FEH+∠CEB＝90°，∴∠CEF＝90°，由（1）知，CE＝EF，∴△CEF是等腰直角三角形，∠ECF＝∠EFC＝45°，把Rt△CDG绕点C逆时针旋转90°至Rt△CBN位置，如图2所示：则∠GCN＝90°，CG＝CN，DG＝BN，∴∠NCE＝∠GCN﹣∠GCE＝45°，∴∠NCE＝∠GCE，在△CEG和△CEN中，，∴△CEG≌△CEN（SAS），∴GE＝NE＝EB+BN＝EB+DG，∴△AEG的周长＝AE+GE+AG＝AE+EB+DG+AG＝AB+AD＝2a；（3）解：设AE＝x，由（1）得：FH＝BE＝a﹣x，则△EAF的面积＝AE×FH＝x（a﹣x）＝﹣（x﹣）2+，∴当x＝，即点E在AB边中点时，△EAF的面积最大，最大值为．17．解：（1）∵矩形ABCD，∴AB⊥BC，PA＝PC；∵PE⊥AB，BC⊥AB，∴PE∥BC，∴∠APE＝∠PCF；∵PF⊥BC，AB⊥BC，∴PF∥AB，∴∠PAE＝∠CPF．∵在△APE与△PCF中，，∴△APE≌△PCF（ASA），∴PE＝CF．在Rt△PCF中，＝tan30°＝，∴＝，故答案为：．（2）如答图1，过点P作PM⊥AB于点M，PN⊥BC于点N，则PM⊥PN．0°～30°时∵PM⊥PN，PE⊥PF，∴∠EPM＝∠FPN，又∵∠PME＝∠PNF＝90°，∴△PME∽△PNF，∴＝，由（1）知，＝，∴＝．同理30°～60°时，＝；（3）当60°＜α＜90°时，将顶点P在AC上移动且使＝时，如答图2，过点P作PM⊥AB于点M，PN⊥BC于点N，则PM⊥PN，PM∥BC，PN∥AB．∵PM∥BC，PN∥AB，∴∠APM＝∠PCN，∠PAM＝∠CPN，∴△APM∽△PCN，∴＝＝，得CN＝2PM．在Rt△PCN中，＝＝tan30°＝，∴＝．∵PM⊥PN，PE⊥PF，∴∠EPM＝∠FPN，又∵∠PME＝∠PNF＝90°，∴△PME∽△PNF，∴＝＝．18．解：（1）∵四边形DEFG是矩形，∴DG＝BF，GF＝BD，∠BDG＝∠BFG＝90°，∴∠ADG＝∠CFG＝90°，由题意得：BD＝3t，则AD＝6﹣3t，DG＝4t，CF＝8﹣4t，FG＝BD＝3t，当AG＝CG时，由勾股定理得：AG2＝AD2+DG2，CG2＝FG2+FC2，∴AD2+DG2＝FG2+FC2，即（6﹣3t）2+（4t）2＝（3t）2+（8﹣4t）2，解得：t＝1，即当AG＝CG时，t＝1秒；（2）分两种情况：①当0＜t≤1时，如图1所示：S＝矩形DEFG的面积＝3t×4t＝12t2；即S＝12t2（0＜t≤1）；②当1＜t≤2时，如图2所示：∵∠ADH＝∠B＝90°，∠A＝∠A，∴△ADH∽△ABC，∴＝，即＝，解得：DH＝8﹣4t，同理得：FM＝6﹣3t，∴S＝×6×8﹣×2×（6﹣3t）（8﹣4t）＝﹣12t2+48t﹣24；即S＝﹣12t2+48t﹣24（1＜t≤2）；（3）分三种情况：①如图1所示：由题意得：×6×8﹣12t2﹣×4t×（6﹣3t）﹣×3t×（8﹣4t）＝6，解得：t＝；②如图3所示：由题意得：×4t×（6﹣3t）+×3t×（8﹣4t）+3t×4t﹣×6×8＝6，解得：t＝；③如图4所示：由勾股定理得：AC＝＝＝10，∴CD＝6+10﹣3t＝16﹣3t，同（2）得：△CDE∽△CAB，∴＝＝，即＝＝，解得：DE＝（16﹣3t），CE＝（16﹣3t），由题意得EF＝（16﹣3t），∴C与F重合，∴×8×（16﹣3t）＝6，解得：t＝；综上所述，当△ACG的面积为6时，t的值为秒或秒或秒．19．解：（1）如图1，过点P作PM⊥BC，垂足为M，则四边形PDCM为矩形．∴PM＝DC＝24．∵QB＝32﹣t，∴S＝×24×（32﹣2t）＝384﹣24t（0≤t＜16）；（2）由图可知：CM＝PD＝4t，CQ＝2t．以B、P、Q三点为顶点的三角形是等腰三角形，可以分三种情况：①若PQ＝BQ．在Rt△PMQ中，PQ2＝4t2+242，由PQ2＝BQ2得4t2+242＝（32﹣2t）2，解得t＝；②若BP＝BQ．在Rt△PMB中，BP2＝（32﹣4t）2+242．由BP2＝BQ2得：（32﹣4t）2+242＝（32﹣2t）2即3t2﹣32t+144＝0．由于△＝﹣704＜0，∴3t2﹣32t+144＝0无解，∴PB≠BQ．③若PB＝PQ．由PB2＝PQ2，得4t2+242＝（32﹣4t）2+242整理，得3t 2﹣64t +256＝0．解得t 1＝，t 2＝16（舍去）综合上面的讨论可知：当t ＝秒或t ＝秒时，以B 、P 、Q 三点为顶点的三角形是等腰三角形．（3）设存在时刻t ，使得PQ ⊥BD ．如图2，过点Q 作QE ⊥AD 于E ，垂足为E ．∵AD ∥BC∴∠BQF ＝∠EPQ ，又∵在△BFQ 和△BCD 中∠BFQ ＝∠C ＝90°，∴∠BQF ＝∠BDC ，∴∠BDC ＝∠EPQ ，又∵∠C ＝∠PEQ ＝90°，∴Rt △BDC ∽Rt △QPE ， ∴＝，即＝，解得t ＝9．所以，当t ＝9秒时，PQ ⊥BD ．20．（1）【发现证明】证明：把△ABE 绕点A 顺时针旋转90°至△ADG ，如图1，∴∠BAE＝∠DAG，AE＝AG，∵∠EAF＝45°，∴∠BAE+∠FAD＝45°，∴∠DAG+∠FAD＝45°，∴∠EAF＝∠FAG，∵AF＝AF，∴△EAF≌△GAF（SAS），∴EF＝FG＝DF+DG，∴EF＝DF+BE；（2）【类比引申】①不成立，结论：EF＝DF﹣BE；证明：如图2，将△ABE绕点A顺时针旋转90°至△ADM，∴∠EAB＝∠MAD，AE＝AM，∠EAM＝90°，BE＝DM，∴∠FAM＝45°＝∠EAF，∵AF＝AF，∴△EAF≌△MAF（SAS），。

广东省深圳市中考数学复习多结论几何综合题专题-人教版初中九年级全册数学试题

多结论几何综合题专题试卷一、单选题1、如图，△ABC和△CDE均为等腰直角三角形，点B，C，D在一条直线上，点M是AE的中点，下列结论：①tan∠AEC=；②S△ABC+S△CDE≥S△ACE；③BM⊥DM；④BM=DM．正确结论的个数是（）A、1个B、2个C、3个D、4个2、如图，在Rt△ABC中，AB=AC，D、E是斜边BC上两点，且∠DAE=45°，将△ADC 绕点A 顺时针旋转90°后，得到△AFB，连接EF，下列结论：①△AED≌△AEF；②=;③△ABC的面积等于四边形AFBD的面积；④BE2+DC2=DE2⑤BE+DC=DE;其中正确的是( )A、①②④B、③④⑤C、①③④D、①③⑤3、如图，将等边△ABC沿射线BC向右平移到△DCE的位置，连接AD、BD ，则下列结论：①AD＝BC；②BD、AC互相平分；③四边形ACED是菱形；④BD⊥DE；其中正确的个数是（）.A、1B、2C、3D、4 4、如图，把一X长方形纸片ABCD沿对角线BD折叠，使C点落在E处，BE与AD相交于点F，下列结论：①BD=AD 2+AB2；②△ABF≌△EDF；③＝④AD=BD•cos45°．其中正确的一组是（）A、①②B、②③C、①④D、③④5、如图，已知正方形ABCD的边长为4，点E、F分别在边AB、BC上，且AE=BF=1，CE 、DF交于点O．下列结论：①∠DOC=90°，②OC=OE，③tan∠OCD= ，④S△ODC=S 四边形BEOF中，正确的有（）A、1个B、2个C、3个D、4个6、如图，已知正方形ABCD的边长为12，BE=EC，将正方形边CD沿DE折叠到DF，延长EF交AB于G，连接DG，现在有如下4个结论：①△ADG≌△FDG；②GB=2AG；③△GDE∽△BEF；④S△BEF=．在以上4个结论中，正确的有（）A、1B、2C、3D、47、如图，▱ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC 于点E，且∠ADC=60°，AB=BC，连接OE．下列结论：①∠CAD=30°；②S ▱ABCD=AB•AC；③OB=AB；④OE=BC，成立的个数有（）A、1个B、2个C、3个D、4个8、如图，AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高，得到下列四个结论：①OA=OD；②AD⊥EF；③当∠A=90°时，四边形AEDF是正方形；④AE+DF=AF+DE．其中正确的是（）A、②③B、②④C、①③④D、②③④9、如图，G，E分别是正方形ABCD的边AB，BC的点，且AG=CE ，AE⊥EF，AE=EF，现有如下结论：①BE=GE；②△AGE≌△ECF；③∠FCD=45°；④△GBE∽△ECH，其中，正确的结论有（）A、1个B、2个C、3个D、4个10、如图，PA=PB，OE⊥PA，OF⊥PB，则以下结论：①OP是∠APB的平分线；②PE=PF③CA=BD；④CD∥AB；其中正确的有（）个．A、4B、3C、2D、1 11、如图，在Rt△ABC中，AB=CB，BO⊥AC，把△ABC折叠，使AB落在AC上，点B 与AC上的点E重合，展开后，折痕AD交BO于点F，连接DE、EF．下列结论：①tan∠ADB=2；②图中有4对全等三角形；③若将△DEF沿EF折叠，则点D不一定落在AC上；④BD=BF；⑤S四边形DFOE=S△AOF，上述结论中正确的个数是（）A、1个B、2个C、3个D、4个12、如图，将等边△ABC绕点C顺时针旋转120°得到△EDC，连接AD，BD．则下列结论：①AC=AD；②BD⊥AC；③四边形ACED是菱形．其中正确的个数是（）A、0B、1C、2D、313、如图，CB=CA，∠ACB=90°，点D在边BC上（与B、C不重合），四边形ADEF 为正方形，过点F作FG⊥CA，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论：①AC=FG；②S△FAB：S四边形CBFG=1：2；③∠ABC=∠ABF；④AD2=FQ•AC，其中正确的结论的个数是（）A、1B、2C、3D、414、如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB、CD交于点E、F，连结BF交AC于点M，连结DE、BO．若∠COB=60°，FO=FC，则下列结论：①FB垂直平分OC；②△EOB≌△CMB；③DE=EF；④S△AOE：S△BCM=2：3．其中正确结论的个数是（）A、4个B、3个C、2个D、1个15、（2016•某某）如图，正方形纸片ABCD中，对角线AC、BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，点A恰好与BD上的点F重合，展开后折痕DE分别交AB、AC于点E、G，连结GF，给出下列结论：①∠ADG=22.5°；②tan∠AED=2；③S△AGD=S△OGD；④四边形AEFG是菱形；⑤BE=2OG；⑥若S△OGF=1，则正方形ABCD的面积是6+4 ，其中正确的结论个数为（）A、2B、3C、4D、516、如图，在正方形ABCD中，E、F分别为BC、CD的中点，连接AE，BF交于点G，将△BCF沿BF对折，得到△BPF，延长FP交BA延长线于点Q，下列结论正确的个数是（）①AE=BF；②AE⊥BF；③sin∠B QP= ；④S四边形ECFG=2S△BGE．A、4B、3C、2D、1 17、如图所示，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣2，0）、B（1，0），直线x=﹣0.5与此抛物线交于点C，与x轴交于点M，在直线上取点D，使MD=MC，连接AC、BC、AD、BD，某同学根据图象写出下列结论：①a﹣b=0；②当﹣2＜x＜1时，y＞0；③四边形ACBD是菱形；④9a﹣3b+c＞0你认为其中正确的是（）A、②③④B、①②④C、①③④D、①②③18、如图，正方形ABCD中，AB=6，点E在边CD上，且CE=2DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．下列结论：①△ABG≌△AFG；②BG=GC；③EG=DE+BG；④AG∥CF；⑤S△FGC=3.6．其中正确结论的个数是（）A、2B、3C、4D、519、如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足=，连接AF并延长交⊙O于点E，连接AD ，DE，若CF=2，AF=3，给出下列结论：①△ADF∽△AED；②FG=2；③tanE= ；④S△DEF=4 ，其中正确的是（）A、①②③B、②③④C、①②④D、①③④20、如图，在⊙O中，AB是直径，点D是⊙O上一点，点C是弧AD的中点，弦CE⊥AB 于点E，过点D的切线交EC的延长线于点G，连接AD，分别交CE、CB 于点P、Q，连接AC，给出下列结论：①∠DAC=∠ABC；②AD=CB；③点P是△ACQ的外心；④AC2=AE•AB；⑤CB∥GD，其中正确的结论是（）A、①③⑤B、②④⑤C、①②⑤D、①③④答案解析部分一、单选题1、【答案】D 【考点】等腰三角形的性质，梯形中位线定理，锐角三角函数的定义【解析】【分析】①根据等腰直角三角形的性质及△ABC∽△CDE的对应边成比例知，；然后由直角三角形中的正切函数，得tan∠AEC=，再由等量代换求得tan∠AEC=；②由三角形的面积公式、梯形的面积公式及不等式的基本性质a2+b2≥2ab（a=b 时取等号)解答；③、④通过作辅助线MN，构建直角梯形的中位线，根据梯形的中位线定理及等腰直角三角形的判定定理解答．【解答】解：∵△ABC和△CDE均为等腰直角三角形，∴AB=BC，CD=DE，∴∠BAC=∠BCA=∠DCE=∠DEC=45°，∴∠ACE=90°；∵△ABC∽△CDE∴①∴tan∠AEC=，∴tan∠AEC=；故本选项正确；②∵S△ABC =a2， S△CDE=b2， S梯形ABDE=（a+b)2，∴S△ACE=S 梯形ABDE-S△ABC-S△CDE=ab ，S△ABC+S△CDE=（a2+b2)≥ab（a=b时取等号)，∴S△ABC+S△CDE≥S△ACE；故本选项正确；④过点M作MN垂直于BD，垂足为N．∵点M是AE的中点，则MN为梯形中位线，∴N 为中点，∴△BMD 为等腰三角形，∴BM=DM；故本选项正确；③又MN=（AB+ED)=（BC+CD)，∴∠BMD=90°，即BM⊥DM；故本选项正确．故选D．【点评】本题综合考查了等腰直角三角形的判定与性质、梯形的中位线定理、锐角三角函数的定义等知识点．在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．2、【答案】C 【考点】全等三角形的判定，勾股定理，相似三角形的判定，旋转的性质【解析】【分析】①根据旋转的性质知∠CAD=∠BAF，AD=AF，因为∠BAC=90°，∠DAE=45°，所以∠CAD+∠BAE=45°，可得∠EAF=45°=∠DAE，由此即可证明△AEF≌△AED；②当△ABE∽△ACD时，该比例式成立；③根据旋转的性质，△ADC≌△ABF，进而得出△ABC的面积等于四边形AFBD的面积；④据①知BF=CD，EF=DE，∠FBE=90°，根据勾股定理判断．⑤根据①知道△AEF≌△AED，得CD=BF，DE=EF；由此即可确定该说法是否正确；【解答】①根据旋转的性质知∠CAD=∠BAF，AD=AF，∵∠BAC=90°，∠DAE=45°，∴∠CAD+∠BAE=45°．∴∠EAF=45°，∴△AED≌△AEF；故本选项正确；②∵AB=AC，∴∠ABE=∠ACD；∴当∠BAE=∠CAD时，△ABE∽△ACD，∴=；当∠BAE≠∠CAD 时，△ABE与△ACD不相似，即≠；∴此比例式不一定成立；故本选项错误；③根据旋转的性质知△ADC≌△AFB，∴S△ABC=S△ABD+S△ABF=S四边形AFBD，即三角形ABC的面积等于四边形AFBD的面积；故本选项正确；④∵∠FBE=45°+45°=90°，∴BE2+BF2=EF2，∵△ADC绕点A顺时针旋转90°后，得到△AFB，∴△AFB≌△ADC，∴BF=CD，又∵EF=DE，∴BE2+DC2=DE2，故本选项正确；⑤根据①知道△AEF≌△AED，得CD=BF，DE=EF，∴BE+DC=BE+BF＞DE=EF，即BE+DC＞DE，故本选项错误；综上所述，正确的说法是①③④；故选C．【点评】此题主要考查了图形的旋转变换以及全等三角形的判定等知识，解题时注意旋转前后对应的相等关系．3、【答案】D 【考点】等边三角形的性质，菱形的判定与性质，平移的性质【解析】【解答】∵△ABC、△DCE是等边三角形，∴∠ACB＝∠DCE＝60°，AC＝CD ，∴∠ACD＝180°－∠ACB－∠DCE＝60°，∴△ACD是等边三角形，∴AD＝AC＝BC ，故①正确；由①可得AD＝BC ，∵AB ＝CD ，∴四边形ABCD是平行四边形，∴BD、AC互相平分，故②正确；由①可得AD＝AC＝CE＝DE ，故四边形ACED是菱形，即③正确；∵四边形ACED是菱形，∴AC⊥BD ，∵AC∥DE ，∴∠BDE＝∠COD＝90°，∴BD⊥DE ，故④正确；综上可得①②③④正确，共4个，故选D．【分析】先求出∠ACD＝60°，继而可判断△ACD是等边三角形，从而可判断①是正确的；根据①的结论，可判断四边形ABCD是平行四边形，从而可判断②是正确的；根据①的结论，可判断③正确；根据菱形的对角线互相垂直可得AC⊥BD ，再根据平移后对应线段互相平行可得∠BDE＝∠COD＝90°，进而判断④正确．4、【答案】B 【考点】勾股定理，翻折变换（折叠问题），相似三角形的判定与性质，特殊角的三角函数值【解析】【解答】①∵△ABD为直角三角形，∴BD2=AD2+AB2，不是BD=AD2+AB2，故说法错误；②根据折叠可知：DE=CD=AB，∠A=∠E，∠AFB=∠EFD，∴△ABF≌△EDF，故说法正确；③根据②可以得到△ABF∽△EDF，∴＝，故说法正确；④在Rt△ABD 中，∠ADB≠45°，∴AD≠BD•cos45°，故说法错误．所以正确的是②③．故选B．【分析】①直接根据勾股定理即可判定是否正确；②利用折叠可以得到全等条件证明△ABF≌△EDF；③利用全等三角形的性质即可解决问题；④在Rt△ABD中利用三角函数的定义即可判定是否正确．此题主要考查了折叠问题，也考查了勾股定理、相似三角形的性质、全等三角形的性质及三角函数的定义，它们的综合性比较强，对于学生的综合能力要求比较高，平时加强训练．5、【答案】C 【考点】全等三角形的判定与性质，勾股定理，正方形的性质，锐角三角函数的定义【解析】【解答】解：∵正方形ABCD的边长为4，∴BC=CD=4，∠B=∠DCF=90°，∵AE=BF=1，∴BE=CF=4﹣1=3，在△EBC和△FCD中，∴△EBC≌△FCD（SAS），∴∠CFD=∠BEC，∴∠BCE+∠BEC=∠BCE+∠CFD=90°，∴∠DOC=90°；故①正确；若OC=OE，∵DF⊥EC，∴CD=DE，∵CD=AD＜DE（矛盾），故②错误；∵∠OCD+∠CDF=90°，∠CDF+∠DFC=90°，∴∠OCD=∠DFC，∴tan∠OCD=tan∠D FC= = ，故③正确；∵△EBC≌△FCD，∴S△EBC=S△FCD，∴S△EBC﹣S△FOC=S△FCD﹣S△FOC，即S△ODC=S四边形BEOF．故④正确．故选C．【分析】由正方形ABCD的边长为4，AE=BF=1，利用SAS易证得△EBC≌△FCD，然后全等三角形的对应角相等，易证得①∠DOC=90°正确；②由线段垂直平分线的性质与正方形的性质，可得②错误；易证得∠OCD=∠DFC，即可求得③正确；由①易证得④正确．6、【答案】C 【考点】全等三角形的判定与性质，正方形的性质，翻折变换（折叠问题），相似三角形的判定与性质【解析】【解答】由折叠可知，DF=DC=DA，∠DFE=∠C=90°，∴∠DFG=∠A=90°，∴△ADG≌△FDG，①正确；∵正方形边长是12，∴BE=EC=EF=6，设AG=FG=x，则EG=x+6，BG=12﹣x，由勾股定理得：EG2=BE2+BG2，即：（x+6）2=62+（12﹣x）2，解得：x=4∴AG=GF=4，BG=8，BG=2AG，②正确；BE=EF=6，△BEF是等腰三角形，易知△GED不是等腰三角形，③错误；S△GBE=×6×8=24，S△BEF=•S△GBE==，④正确．故选：C．【分析】根据正方形的性质和折叠的性质可得AD=DF，∠A=∠GFD=90°，于是根据“HL”判定△ADG≌△FDG，再由GF+GB=GA+GB=12，EB=EF，△BGE为直角三角形，可通过勾股定理列方程求出AG=4，BG=8，进而求出△BEF的面积，再抓住△BEF是等腰三角形，而△GED显然不是等腰三角形，判断③是错误的．7、【答案】C 【考点】等边三角形的判定与性质，含30度角的直角三角形，平行四边形的性质【解析】【解答】∵四边形ABCD 是平行四边形，∴∠ABC=∠ADC=60°，∠BAD=120°，∵AE平分∠BAD，∴∠BAE=∠EAD=60°∴△ABE是等边三角形，∴AE=AB=BE，∵AB=BC，∴AE=BC，∴∠BAC=90°，∴∠CAD=30°，故①正确；∵AC⊥AB，∴S ▱ABCD=AB•AC，故②正确，∵AB=BC，OB=BD，∵BD＞BC，∴AB≠OB，故③错误；∵CE=BE，CO=OA ，∴OE=AB ，∴OE=BC，故④正确．故选：C．【分析】由四边形ABCD是平行四边形，得到∠ABC=∠ADC=60°，∠BAD=120°，根据AE 平分∠BAD，得到∠BAE=∠EAD=60°推出△ABE是等边三角形，由于AB=BC，得到AE=BC，得到△ABC是直角三角形，于是得到∠CAD=30°，故①正确；由于AC⊥AB，得到S▱ABCD=AB•AC，故②正确，根据AB=BC，OB=BD，且BD＞BC，得到AB≠OB，故③错误；根据三角形的中位线定理得到OE=AB，于是得到OE=BC，故④正确．8、【答案】D 【考点】全等三角形的判定与性质，角平分线的性质，正方形的判定【解析】【解答】如果OA=OD，则四边形AEDF是矩形，∠A=90°，不符合题意，∴①不正确；∵AD是△ABC的角平分线，∴∠EAD∠FAD，在△AED和△AFD中，∴△AED≌△AFD （AAS），∴AE=AF，DE=DF，∴AE+DF=AF+DE，∴④正确；在△AEO和△AFO中，，∴△AE0≌△AF0（SAS），∴EO=FO，又∵AE=AF，∴AO是EF的中垂线，∴AD⊥EF，∴②正确；∵当∠A=90°时，四边形AEDF的四个角都是直角，∴四边形AEDF是矩形，又∵DE=DF，∴四边形AEDF是正方形，∴③正确．综上，可得正确的是：②③④．故选：D．【分析】①如果OA=OD，则四边形AEDF是矩形，∠A=90°，不符合题意，所以①不正确．②首先根据全等三角形的判定方法，判断出△AED≌△AFD，AE=AF，DE=DF；然后根据全等三角形的判定方法，判断出△AE0≌△AFO，即可判断出AD⊥EF．③首先判断出当∠A=90°时，四边形AEDF的四个角都是直角，四边形AEDF是矩形，然后根据DE=DF，判断出四边形AEDF是正方形即可．④根据△AED≌△AFD，判断出AE=AF，DE=DF，即可判断出AE+DF=AF+DE 成立，据此解答即可．9、【答案】B 【考点】全等三角形的判定与性质，正方形的性质，相似三角形的判定与性质【解析】【解答】∵四边形ABCD 是正方形，∴∠B=∠DCB=90°，AB=BC，∵AG=CE，∴BG=BE，由勾股定理得：BE=GE，∴①错误；∵BG=BE，∠B=90°，∴∠BGE=∠BEG=45°，∴∠AGE=135°，∴∠GAE+∠AEG=45°，∵AE⊥EF，∴∠AEF=90°，∵∠BEG=45°，∴∠AEG+∠FEC=45°，∴∠GAE=∠FEC，在△GAE和△CEF中∴△GAE≌△CEF，∴②正确；∴∠AGE=∠ECF=135°，∴∠FCD=135°﹣90°=45°，∴③正确；∵∠BGE=∠BEG=45°，∠AEG+∠FEC=45°，∴∠FEC＜45°，∴△GBE和△ECH不相似，∴④错误；即正确的有2个．故选B．【分析】根据正方形的性质得出∠B=∠DCB=90°，AB=BC，求出BG=BE，根据勾股定理得出BE=GE，即可判断①；求出∠GAE+∠AEG=45°，推出∠GAE=∠FEC，根据SAS推出△GAE≌△CEF，即可判断②；求出∠AGE=∠ECF=135°，即可判断③；求出∠FEC＜45°，根据相似三角形的判定得出△GBE和△ECH不相似，即可判断④．10、【答案】A 【考点】全等三角形的判定与性质，圆心角、弧、弦的关系，相似三角形的判定与性质【解析】【解答】连接OP、OC、OA、OD、OB、CD、AB．∵PC•PA=PD•PB（相交弦定理），PA=PB（已知），∴PC=PD，∴AC=BD；在△AOC和△BOD中，∵∠AOC=∠BOD（等弦对等角），OA=OB （半径），OD=OC （半径），∴△AOC≌△BOD，∴③CA=BD；OE=OF；又∵OE⊥PA，OF⊥PB，∴①OP是∠APB的平分线；∴②PE=PF；在△PCD和△PAB中，PC：PA=PD：PB，∠DPC=∠BPA，∴△PCD∽△PAB，∴∠PDC=PBA，∴④CD∥AB；综上所述，①②③④均正确，故答案选A．【分析】①通过证明△AOC≌△BOD，再根据全等三角形的对应高相等求得OE=OF；再根据角平分线的性质证明OP是∠APB的平分线；②由角平分线的性质证明PE=PF；③通过证明△AOC≌△BOD，再根据全等三角形的对应边相等求得CA=BD；④通过证明△PCD∽△PAB，再根据相似三角形的性质对应角相等证得∠PDC=PBA；然后由平行线的判定得出结论CD∥AB．11、【答案】C 【考点】全等三角形的判定与性质，翻折变换（折叠问题），锐角三角函数的定义【解析】【解答】①由折叠可得BD=DE，而DC＞DE，∴DC＞BD，∴tan∠ADB≠2，故①错误；②图中的全等三角形有△ABF≌△AEF，△ABD≌△AED，△FBD≌△FED，（由折叠可知)∵OB⊥AC，∴∠AOB=∠COB=90°，在Rt△AOB和Rt△COB中，AB="CB" ,BO=BO ，∴Rt△AOB≌Rt△COB（HL)，则全等三角形共有4对，故②正确；③∵AB=CB，BO⊥AC，把△ABC折叠，∴∠ABO=∠CBO=45°，∠FBD=∠DEF，∴∠AEF=∠DEF=45°，∴将△DEF沿EF折叠，可得点D一定在AC上，故③错误；④∵OB⊥AC，且AB=CB，∴BO 为∠ABC的平分线，即∠ABO=∠OBC=45°，由折叠可知，AD是∠BAC的平分线，即∠BAF=22.5°，又∵∠BFD为三角形ABF的外角，∴∠BFD=∠ABO+∠BAF=67.5°，易得∠BDF=180°-45°-67.5°=67.5°，∴∠BFD=∠BDF，∴BD=BF，故④正确；⑤连接CF，∵△AOF和△COF等底同高，∴S△AOF=S△COF，∵∠AEF=∠ACD=45°，∴EF∥CD，∴S△EFD=S△EFC，∴S四边形DFOE=S△COF，∴S四边形DFOE=S△AOF，故⑤正确；故正确的有3个．故选C．12、【答案】D 【考点】等边三角形的性质，菱形的判定，旋转的性质【解析】【解答】解：∵将等边△ABC绕点C顺时针旋转120°得到△EDC，∴∠ACE=120°，∠DCE=∠BCA=60°，AC=CD=DE=CE，∴∠ACD=120°﹣60°=60°，∴△ACD是等边三角形，∴AC=AD，AC=AD=DE=CE，∴四边形ACED是菱形，∵将等边△ABC绕点C顺时针旋转120°得到△EDC，AC=AD，∴AB=BC=CD=AD，∴四边形ABCD是菱形，∴BD⊥AC，∴①②③都正确，故选D．【分析】根据旋转和等边三角形的性质得出∠ACE=120°，∠DCE=∠BCA=60°，AC=CD=DE=CE，求出△ACD是等边三角形，求出AD=AC，根据菱形的判定得出四边形ABCD和ACED都是菱形，根据菱形的判定推出AC⊥BD．本题考查了旋转的性质，菱形的性质和判定，等边三角形的性质和判定的应用，能灵活运用知识点进行推理是解此题的关键．13、【答案】D 【考点】全等三角形的判定与性质，矩形的判定与性质，正方形的性质，相似三角形的判定与性质，等腰直角三角形【解析】【解答】解：∵四边形ADEF为正方形，∴∠FAD=90°，AD=AF=EF，∴∠CAD+∠FAG=90°，∵FG⊥CA，∴∠C=90°=∠ACB，∴∠CAD=∠AFG，在△FGA 和△ACD中，，∴△FGA≌△ACD（AAS），∴AC=FG，①正确；∵BC=AC，∴FG=BC，∵∠ACB=90°，FG⊥CA，∴FG∥BC，∴四边形CBFG 是矩形，∴∠CBF=90°，S△FAB= FB•FG= S四边形CBFG，②正确；∵CA=CB，∠C=∠CBF=90°，∴∠ABC=∠ABF=45°，③正确；∵∠FQE=∠DQB=∠ADC，∠E=∠C=90°，∴△ACD∽△FEQ，∴AC：AD=FE：FQ，∴AD•FE=AD2=FQ•AC，④正确；故选：D．【分析】本题考查了相似三角形的判定与性质、全等三角形的判定与性质、正方形的性质、矩形的判定与性质、等腰直角三角形的性质；熟练掌握正方形的性质，证明三角形全等和三角形相似是解决问题的关键．由正方形的性质得出∠FAD=90°，AD=AF=EF，证出∠CAD=∠AFG，由AAS证明△FGA≌△ACD，得出AC=FG，①正确；证明四边形CBFG是矩形，得出S△FAB= FB•FG= S四边形CEFG，②正确；由等腰直角三角形的性质和矩形的性质得出∠ABC=∠ABF=45°，③正确；证出△ACD∽△FEQ，得出对应边成比例，得出D•FE=AD2=FQ•AC，④正确．14、【答案】B 【考点】全等三角形的判定与性质，线段垂直平分线的性质，等腰三角形的性质，矩形的性质【解析】【解答】解：①∵矩形ABCD中，O为AC中点，∴OB=OC，∵∠COB=60°，∴△OBC是等边三角形，∴OB=BC，∵FO=FC，∴FB垂直平分OC，故①正确；②∵FB垂直平分OC，∴△CMB≌△OMB，∵OA=OC，∠FOC=∠EOA，∠DCO=∠BAO，∴△FOC≌△EOA，∴FO=EO，易得OB⊥EF，∴△OMB≌△OEB，∴△EOB≌△CMB，故②正确；③由△OMB≌△OEB≌△CMB得∠1=∠2=∠3=30°，BF=BE，∴△BEF是等边三角形，∴BF=EF，∵DF∥BE且DF=BE，∴四边形DEBF是平行四边形，∴DE=BF，∴DE=EF，故③正确；④在直角△BOE中∵∠3=30°，∴BE=2OE，∵∠OAE=∠AOE=30°，∴AE=OE，∴BE=2AE，∴S△AOE：S△BCM=S△AOE：S△BOE=1：2，故④错误；所以其中正确结论的个数为3个；故选B【分析】①利用线段垂直平分线的性质的逆定理可得结论；②证△OMB≌△OE B得△EOB≌△CMB；③先证△BEF是等边三角形得出BF=EF，再证▱DEBF得出DE=BF，所以得DE=EF；④由②可知△BCM≌△BEO，则面积相等，△AOE和△BEO属于等高的两个三角形，其面积比就等于两底的比，即S△AOE：S△BOE=AE：BE，由直角三角形30°角所对的直角边是斜边的一半得出BE=2OE=2AE，得出结论S：S=AE：BE=1：2．本题综合性比较强，既考查了矩形的性质、等腰三角形的性质，又考查了全等三角形的性质和判定，及线段垂直平分线的性质，内容虽多，但不复杂；看似一个选择题，其实相当于四个证明题，属于常考题型．15、【答案】B 【考点】菱形的判定与性质，翻折变换（折叠问题），等腰直角三角形【解析】【解答】解：∵四边形ABCD 是正方形，∴∠GAD=∠ADO=45°，由折叠的性质可得：∠ADG= ∠ADO=22.5°，故①正确．∵由折叠的性质可得：AE=EF，∠EFD=∠EAD=90°，∴AE=EF＜BE，∴AE ＜AB，∴ ＞2，故②错误．∵∠AOB=90°，∴AG=FG＞OG ，△AGD与△OGD 同高，∴S △AGD＞S△OGD，故③错误．∵∠EFD=∠AOF=90°，∴EF∥AC，∴∠FEG=∠AGE，∵∠AGE=∠FGE，∴∠FEG=∠FGE，∴EF=GF，∵AE=EF，∴AE=GF，故④正确．∵AE=EF=GF，AG=GF，∴AE=EF=GF=AG，∴四边形AEFG是菱形，∴∠OGF=∠OAB=45°，∴EF=GF= OG ，∴BE= EF= × OG=2OG ．故⑤正确．∵四边形AEFG是菱形，∴AB∥GF，AB=GF．∵∠BAO=45°，∠GOF=90°，∴△OG F 时等腰直角三角形．∵S△OGF=1，∴ OG2=1，解得OG= ，∴BE=2OG=2 ，GF= = =2，∴AE=GF=2，∴AB=BE+AE=2 +2，∴S正方形ABCD=AB2=（2 +2）2=12+8 ，故⑥错误．∴其中正确结论的序号是：①④⑤．故选B．【分析】①由四边形ABCD是正方形，可得∠GAD=∠ADO=45°，又由折叠的性质，可求得∠ADG的度数；②由AE=EF＜BE，可得AD＞2AE；③由AG=GF＞OG，可得△AGD的面积＞△OGD的是等腰三角形，即可证得AE=GF；⑤易证得四边形AEFG 是菱形，由等腰直角三角形的性质，即可得BE=2OG；⑥根据四边形AEFG是菱形可知AB∥GF，AB=GF，再由∠BAO=45°，∠GOF=90°可得出△OGF时等腰直角三角形，由S△OGF=1求出GF的长，进而可得出BE及AE的长，利用正方形的面积公式可得出结论．此题考查的是四边形综合题，涉及到正方形的性质、折叠的性质、等腰直角三角形的性质以及菱形的判定与性质等知识．此题综合性较强，难度较大，注意掌握折叠前后图形的对应关系，注意数形结合思想的应用．16、【答案】B 【考点】全等三角形的判定与性质，正方形的性质，翻折变换（折叠问题），相似三角形的判定与性质【解析】【解答】解：∵E，F分别是正方形ABCD边BC，CD的中点，∴CF=BE，在△ABE和△BCF中，，∴Rt△ABE≌Rt△BCF（SAS），∴∠BAE=∠CBF，AE=BF，故①正确；又∵∠BAE+∠BEA=90°，∴∠CBF+∠BEA=90°，∴∠BGE=90°，∴AE⊥BF，故②正确；根据题意得，FP=FC，∠PFB=∠BFC，∠FPB=90°∵CD∥AB，∴∠CFB=∠ABF，∴∠ABF=∠PFB，∴QF=QB，令PF=k（k＞0），则PB=2k在Rt△BPQ 中，设QB=x ，∴x2=（x ﹣k）2+4k2，∴x= ，∴sin=∠BQP= = ，故③正确；∵∠BGE=∠BCF，∠GBE=∠CBF，∴△BGE∽△BCF，∵BE= BC，BF= BC，∴BE：BF=1：，∴△BGE的面积：△BCF的面积=1：5，∴S四边形ECFG=4S△BGE，故④错误．故选：B．【分析】首先证明△ABE≌△BCF，再利用角的关系求得∠BGE=90°，QF=QB，解出BP，QB，根据正弦的定义即可求解；根据AA可证△BGE与△BCF相似，进一步得到相似比，再根据相似三角形的性质即可求解．本题主要考查了四边形的综合题，涉及正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质以及折叠的性质的知识点，解决的关键是明确三角形翻转后边的大小不变，找准对应边，角的关系求解．17、【答案】D 【考点】二次函数的图象，二次函数的性质，菱形的判定【解析】【解答】解：①∵抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣2，0）、B（1，0），∴该抛物线的对称轴为x=﹣=﹣0.5，∴a=b，a ﹣b=0，①正确；②∵抛物线开口向下，且抛物线与x轴交于点A（﹣2，0）、B（1，0），∴当﹣2＜x＜1时，y＞0，②正确；③∵点A、B关于x=0.5对称，∴AM=BM，又∵MC=MD，且CD⊥AB，∴四边形ACBD是菱形，③正确；④当x=﹣3时，y＜0，即y=9a﹣3b+c＜0，④错误．综上可知：正确的结论为①②③．故选D．【分析】①由抛物线与x轴的两交点坐标即可得出抛物线的对称轴为x=﹣=﹣0.5，由此即可得出a=b，①正确；②根据抛物线的开口向下以及抛物线与x轴的两交点坐标，即可得出当﹣2＜x＜1时，y＞0，②正确；③由AB关于x=0.5对称，即可得出AM=BM，再结合MC=MD以及CD⊥AB，即可得出四边形ACBD 是菱形，③正确；④根据当x=﹣3时，y＜0，即可得出9a﹣3b+c＜0，④错误．综上即可得出结论．本题考查了二次函数的图象、二次函数的性质以及菱形的判定，解题的关键是逐条分析四条结论是否正确．本题属于中档题，难度不大，解决该题型题目时，根据给定的函数图象结合二次函数的性质逐条分析给定的结论是关键．18、【答案】D 【考点】全等三角形的判定与性质，正方形的性质，翻折变换（折叠问题）【解析】【解答】解：∵正方形ABCD的边长为6，CE=2DE，∴DE=2，EC=4，∵把△ADE沿AE折叠使△ADE落在△AFE的位置，∴AF=AD=6，EF=ED=2，∠AFE=∠D=90°，∠FAE=∠DAE，在Rt△ABG和Rt△AFG中，∴Rt△ABG≌Rt△AFG（HL ），∴GB=GF，∠BAG=∠FAG，∴∠GAE=∠FAE+∠FAG= ∠BAD=45°，所以①正确；设BG=x，则GF=x ，C=BC﹣BG=6﹣x，在Rt△CGE中，GE=x+2，EC=4，CG=6﹣x，∵CG2+CE2=GE2，∴（6﹣x）2+42=（x+2）2，解得x=3，∴BG=3，CG=6﹣3=3∴BG=CG，所以②正确；∵EF=ED，GB=GF，∴GE=GF+EF=BG+DE，所以③正确；∵GF=GC，∴∠GFC=∠GCF，又∵Rt△ABG≌Rt△AFG，∴∠AGB=∠AGF，而∠BGF=∠GFC+∠GCF，∴∠AGB+∠AGF=∠GFC+∠GCF，∴∠AGB=∠GCF，∴CF∥AG，所以④正确；过F作FH⊥DC∵BC⊥DH，∴FH∥GC，∴△EFH∽△EGC，∴，EF=DE=2，GF=3，∴EG=5，∴△EFH∽△EGC，∴相似比为：= ，∴S△FGC=S△GCE﹣S△FEC= ×3×4﹣×4×（×3）= =3.6，所以⑤正确．故正确的有①②③④⑤，故选：D．【分析】先计算出DE=2，EC=4，再根据折叠的性质AF=AD=6，EF=ED=2，∠AFE=∠D=90°，∠FAE=∠DAE，然后根据“HL”可证明Rt△ABG≌Rt△AFG，则GB=GF，∠BAG=∠FAG，所以∠GAE= ∠BAD=45°；GE=GF+EF=BG+DE；设BG=x，则GF=x，CG=BC﹣BG=6﹣x，在Rt△CGE中，根据勾股定理得（6﹣x）2+42=（x+2）2，解得x=3，则BG=CG=3，则点G为BC的中点；同时得到GF=GC，根据等腰三角形的性质得∠GFC=∠GCF，再由Rt△ABG≌Rt△AFG得到∠AGB=∠AGF，然后根据三角形外角性质得∠BGF=∠GFC+∠GCF，易得∠AGB=∠GCF，根据平行线的判定方法得到CF∥AG；过F 作FH⊥DC，则△EFH∽△EGC，△EFH∽△EGC，由相似比为，可计算S△FGC．本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了三角形全等的判定与性质、勾股定理和正方形的性质．19、【答案】C 【考点】垂径定理，圆周角定理，相似三角形的判定与性质，解直角三角形【解析】【解答】解：①∵AB是⊙O的直径，弦CD⊥AB，∴ ，DG=CG ，∴∠ADF=∠AED，∵∠FAD=∠DAE（公共角），∴△ADF∽△AED；故①正确；②∵ = ，CF=2，∴FD=6，∴CD=DF+CF=8，∴CG=DG=4，∴FG=CG﹣CF=2；故②正确；③∵AF=3，FG=2，∴AG= = ，∴在Rt△AGD 中，tan∠ADG= = ，∴tan∠E= ；故③错误；④∵DF=DG+FG=6，AD= = ，∴S △ADF= DF•AG= ×6× =3 ，∵△ADF∽△AED，∴ =（）2，∴ = ，∴S△AED=7 ，∴S △DEF=S△AED ﹣S△ADF=4 ；故④正确．故选C．【分析】①正确．由AB是⊙O的直径，弦CD⊥AB，根据垂径定理可得：，DG=CG，继而证得△ADF∽△AED；②正确．由= ，CF=2，可求得DF的长，继而求得CG=DG=4，则可求得FG=2；③错误．由勾股定理可求得AG的长，即可求得tan∠ADF的值，继而求得tan∠E= ．④首先求得△ADF的面积，由相似三角形面积的比等于相似比的平方，即可求得△ADE 的面积，继而求得S△DEF =4 ．20、【答案】D 【考点】垂径定理，圆周角定理，相似三角形的判定与性质【解析】【解答】解：∵在⊙O中，点C是的中点，∴ = ，∴∠CAD=∠ABC，故①正确；∵ ≠ ，∴ ≠ ，∴AD≠BC，故②错误；∵AB是⊙O的直径，∴∠ACB=90°，又∵CE⊥AB，∴∠ACE+∠CAE=∠ABC+∠CAE=90°，∴∠ACE=∠ABC，又∵C为的中点，∴ = ，∴∠CAP=∠ABC，∴∠ACE=∠CAP，∴AP=CP，∵∠ACQ=90°，∴∠ACP+∠PCQ=∠CAP+∠PQC=90°，∴∠PCQ=∠PQC，∴PC=PQ，∴AP=PQ，即P 为Rt△ACQ斜边AQ的中点，∴P为Rt△ACQ的外心，故③正确；∵AB是⊙O的直径，∴∠ACB=90°，又∵CE⊥AB∴根据射影定理，可得AC2=AE•AB，故④正确；如图，连接BD，则∠ADG=∠ABD，∵ ≠ ，∴ ≠ ，∴∠ABD≠∠BAC，∴∠ADG≠∠BAC，又∵∠BAC=∠BCE=∠PQC，∴∠ADG≠∠PQC，∴CB与GD不平行，故⑤错误．故答案为：D．【分析】在同圆或等圆中，同弧或等弧所对的圆周角相等，据此推理可得①正确，②错误；通过推理可得∠ACE=∠CAP，得出AP=CP，再根据∠PCQ=∠PQC，可得出PC=PQ，进而得到AP=PQ，即P为Rt△ACQ斜边AQ的中点，故P为Rt△A CQ的外心，即可得出③正确；连接BD，则∠ADG=∠ABD，根据∠ADG≠∠BAC，∠BAC=∠BCE=∠PQC，可得出∠ADG≠∠PQC，进而得到CB与GD不平行，可得⑤错误．。

中考数学复习专题训练精选试题及答案

中考数学复习专题训练精选试题及答案目录实数专题训练 (2)实数专题训练答案 (4)代数式、整式及因式分解专题训练 (5)代数式、整式及因式分解专题训练答案 (6)分式和二次根式专题训练 (7)分式和二次根式专题训练答案 (8)一次方程及方程组专题训练 (9)一次方程及方程组专题训练答案 (11)一元二次方程及分式方程专题训练 (11)一元二次方程及分式方程专题训练答案 (13)一元一次不等式及不等式组专题训练 (13)一元一次不等式及不等式组专题训练答案 (15)一次函数及反比例函数专题训练 (15)一次函数及反比例函数专题训练答案 (17)二次函数及其应用专题训练 (18)二次函数及其应用专题训练答案 (20)立体图形的认识及角、相交线与平行线专题训练 (20)立体图形的认识及角、相交线与平行线专题训练答案 (22)三角形专题训练 (23)三角形专题训练答案 (25)多边形及四边形专题训练 (25)多边形及四边形专题训练答案 (27)圆及尺规作图专题训练 (28)圆及尺规作图专题训练答案 (30)轴对称专题训练 (30)轴对称专题训练答案 (32)平移与旋转专题训练 (33)平移与旋转专题训练答案 (35)相似图形专题训练 (35)相似图形专题训练答案 (37)图形与坐标专题训练 (38)图形与坐标专题训练答案 (40)图形与证明专题训练 (40)图形与证明专题训练答案 (42)概率专题训练 (42)概率专题训练答案 (44)统计专题训练 (45)统计专题训练答案 (47)实数专题训练一、填空题:（每题 3 分，共 36 分)１、－2 的倒数是＿＿＿＿。

２、4 的平方根是＿＿＿＿.３、－27 的立方根是＿＿＿＿。

４、－2 的绝对值是＿＿＿＿。

５、2004年我国外汇储备3275。

34亿美元，用科学记数法表示为＿＿＿＿亿美元。

６、比较大小：－＿＿＿＿－。

７、近似数0。

020精确到＿＿＿＿位,它有＿＿＿＿个有效数字.８、若 n 为自然数，那么(－1）2n＋（－1）2n＋1＝＿＿＿＿.９、若实数 a、b 满足｜a－2｜＋（ b＋）2＝0，则 ab＝＿＿＿＿.10、在数轴上表示 a 的点到原点的距离为 3,则 a－3＝＿＿＿＿。

初中几何多结论问题

专题—几何多结论问题【考题研究】以函数/几何为背景多结论问题自13年以来深圳广州等地每年必考，出现的位置是选择题或者填空题的压轴题.其难度不言自于，对学生综合分析问题的能力要求比较高.【解题策略】常见类型有：(1)代数中的多结论题;特别是有关二次函数中的多结论选填题是综合性比较强的题目，解决此类题目不仅要掌握二次函数的图象与性质、抛物线位置与字母系数的关系、二次函数与方程、不等式的关系等知识，还要学会代入特殊值的方法并结合二次函数的图象去验证一些不等式的正误;(2)几何中的多结论题;几何中的多结论选填题则结合了三角形、四边形、圆的有关性质和判定，是几何中综合性很强的题目，掌握三角形、四边形、圆的有关性质并能熟练的运用才能解决此类问题.具体求解时，一是从题干出发考虑，探求结果;二是题干和选择支联合考虑或从选择支出发探求是否满足题干条件. 事实上，后者在解答选择题时更常用、更有效.常用方法有以下几种：1.直接法从题设条件出发，通过正确的运算、推理或判断，直接得出结论再与选择支对照，从而作出选择的一种方法。

运用此种方法解题需要扎实的数学基础.2.特例法运用满足题设条件的某些特殊数值、特殊位置、特殊关系、特殊图形、特殊数列、特殊函数等对各选择支进行检验或推理，利用问题在某一特殊情况下不真，则它在一般情况下也不真的原理，由此判明选项真伪的方法。

用特例法解选择题时，特例取得愈简单、愈特殊愈好.3.筛选法(也叫排除法、淘汰法)运用选择题中单选题的特征，即有且只有一个正确选择支这一信息，从选择支入手，根据题设条件和各选项之间的关系，通过分析、推理、计算、判断，对选择项进行筛选，将其中与题设相矛盾的干扰逐一排除从而获得正确结论的方法。

使用筛选法的前提是“答案唯一”，即四个选项中有且只有一个答案正确.4.逆推代入法将选择项中给出的答案或其特殊值，代入题干逐一去验证是否满足题设条件，然后选择符合题设条件的择题项的一种方法. 在运用验证法解题时，若能据题意确定代入顺序，则能较大提高解题速度. 5.直观选择法利用函数图像或数学结果的几何意义，将数的问题(如解方程、解不等式、求最值，求取值范围等)与某些图形结合起来，利用直观几性，再辅以简单计算，确定正确答案的方法。