007第七章 水文频率计算1110
水文频率计算方法 依据实测系列计算三个统计参数
1972
1973 1974
27500
7620 23900
1975
12100
2 3 4 5 6 7 8 9 10 11
23900 18600 17400 15400 15200 12700 12600 12100 12000 11400
2.101
1.635 1.ቤተ መጻሕፍቲ ባይዱ29
1.101
0.635 0.53
1.2119
经验频率及统计参数计算表 m (序号/频数) X (实测值) 递 减 排 序 合计 n 0.00
理论线 表
Kp
(Kp -1)
(Kp -1)2
P = m / (n+1)
(%)
理论频率曲线计算表
项 P%
Cv/Cs
目 Xp= x (1+Cvφp)
0.01
0.1 1 5 10 … 95 99 99.9
1 2 3
二. 适线法
以经验频率点数据为基础,给它选配一条拟合最 佳的频率曲线[理论曲线]。 1 目估适线法 2 优化适线法
1
1. 目估适线法
绘制经验累积频率点据
确定样本统计参数的初值 选定线型, 绘制理论曲线 适线,调参 推求设计频率对应的设计值 误差计算
步骤— 表格
√ 实际计算水文频率时,通过制表完成上述的步骤 。
0.4032 0.2803
1.353
1.336 1.116
0.354
0.336 0.116
0.1251
0.1129 0.0135
1.108
1.063 1.055
0.108
0.064 0.055
0.0115
0.0040 0.0030
《水文频率计算》课件

计算方法分类
参数法
基于概率分布函数(如正态分布、皮 尔逊分布等)拟合水文数据,通过参 数估计和检验确定分布参数。
非参数法
不假定水文数据的概率分布,而是通 过数据驱动的方法(如核密度估计、 最近邻插值等)对水文数据进行概率 密度估计。
计算步骤与流程
数据收集与整理
收集历史水文数据,并进行数据清洗和整理 ,确保数据质量和完整性。
雨量站
通过雨量站收集降雨数据,包 括降雨量、降雨强度等。
水文站
水文站监测河流、湖泊等水体 的水位、流量、流速等数据。
地下水观测井
观测地下水位和水质数据。
遥感技术
利用卫星遥感技术获取大范围 的水文数据。
数据整理与预处理
01
数据筛选
剔除异常值和不合理数据,确保数 据质量。
数据插值
对缺失数据进行插值处理,以获得 完整的时间序列数据。
水资源管理
02
利用软件对水文数据进行处理和分析,为水资源管理提供科学
依据。
农业灌溉
03
利用软件对农田灌溉用水量进行监测和分析,合理安排灌溉计
划,提高灌溉效率。
THANKS 感谢观看
确定概率分布
根据数据特征选择合适的概率分布函数。
参数估计
利用历史数据估计概率分布函数的参数。
拟合检验
对拟合的分布进行统计检验,确保符合所选概率分 布。
计算频率
根据拟合的分布计算不同重现期(或概率)下的 水文值。
结果应用
将计算结果应用于实际工作,如洪水预警、水资源规划 等。
02 水文数据收集与整理
数据来源与采集
通过比较不同频率曲线,可以分析不同地区或不同时间尺度下水 文数据的统计特征和变化规律,为水资源管理和决策提供依据。
007第七章 水文频率计算1110-精品文档

p ~ xP 则可以画出频率曲线。但这样求解工作量太大,
太复杂了,因此,必须想办法简化计算。
为了简化,可以对X作标准化变换,即 标准化后的变量
X EX
也是随机变量,常数为离均系数,若X的数字特征为
Cs ,方差为1, Cs EX , ,Cs , 则 的均值为 0
(2)P-III型分布频率曲线 (xp~p的关系) X的超过累积概率为
P
1 x a P P X x x a e dx P x , Cv , Cs 给定后 , 可唯一确定 , , a , 因此 , 只要 EX , Cv , C 在 EX
X 2 2 Cs Cs
当
,此时
为标准化正体分布∴结论是对的
x EX ,由于 x 与 是严格单调函数,故 dx 1 EX a EX a e f f x x d 2
第 七 章
水文频率计算
水文频率计算
§7-1
§7-2
概述
几种理论分布的频率计算与分析
§7-3
§7-4
参数点估计的数理统计法
参数点估计的水文统计法
§7-5
§7-6
估计量好坏的评判标准
参数的区间估计
§7-1 概 述
问题的提出(堤防高度,历史洪水加成,频率计算,设计标准) 基本问题: 线型选择, 参数估计 线型选择: 理论导出 (中心极限定理,极值分布,物理机制) 因其不同程度假定往往不能满足,一般通过线型与实测数 据拟合作出判断)。不同国家洪水特性不同,结果不一样。
水文频率计算方法

x
2
x (1 C v 2 )
x 3 x (1 C v 3 )
(3-22)
三点的取法: 1~59% 或 3~50~97% 或 5~50~95% 或 10~50~90%
参数计算公式
x 1x3 3x1 1 3
Cv
x1 1x3
x3 3x1
(3-23) (3-24)
x1x32x2 1322 =S 偏度系数
水文频率计算方法
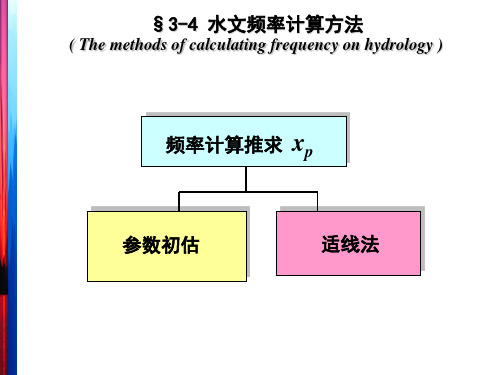
频率计算推求 xp
参数初估
适线法
一. 统计参数初估方法 1 矩法 2 经验关系法 3 三点法 4 权函数法 5 概率权重矩法
矩法
1.矩法
依据实测系列计算三个统计参数:x,Cv ,Cs
经验法
2. 经验关系法
x
1 n
n
xi
i1
Cv
(K i 1) 2
n 1
Cs初值:
设C 计s 暴 雨量( n
2. 优化适线法
最小二乘估计法:
n
S(){ [xi f(Pi,)]2} i1
S(ˆ)minS()
S 0
(3-26) (3-27) (3-28)
End
计算表 题 P66
p m 100% n 1
年最大洪峰流量 Q(m3/s)
28000
24000
Q5%
20000
16000
经验点 经验矩法法配线
三点法配线
12000 8000 4000
0.1 1
Q50%
Q95%
5 10 20 30 40 50 60 70 80 90 95 99 频率P(%)
优化法
(K
i
3
)C
1
v
《水文频率计算 》课件

参数方法
讨论参数统计方法,如极大 似然估计和最大似然估计。
比较与选择
对比非参数方法和参数方法 的优缺点,为选择合适的方 法提供指导。
常见参数分布的介绍
正态分布
详细介绍正态分布及其在水文 频率计算中的应用。
对数正态分布
解释对数正态分布的特点和使 用场景。
威布尔分布
探讨威布尔分布和极值分布之 间的联系。
次大洪水和常年洪水的频率分析方法
1
次大洪水
解释次大洪水的概念,并介绍常用的分析方法。
2
常年洪水
探讨常年洪水的频率分析方法,如平均流量法和频率分析图。
3
工程设计
讨论次大洪水和常年洪水在工程设计中的应用,如排水系统和河道改造。
非参数方法与参数方法的比较
非参数方法
介绍非参数统计方法,如经 验分布函数和核密度估计。
频率分析
学习如何进行频率分析,从极 值分布中估计流域的洪水频率。
案例分析
通过实际案例演示极值分布和 频率分析的应用。
设计洪水的频率分析方法
雨量观测
介绍设计洪水频率分析的基本数 据要求,包括雨量观测和水文站 数据。
水工结构
探讨设计洪水频率分析与水工结 构设计的关系,如水坝和排水系 统。
水文模型
使用水文模型进行设计洪水频率 分析,并预测极端气候事件。
结合实际的水文频率计算方法
案例分析
结合实际案例,演示如何进行 水文频率计算,并解读分析结 果。
工程设计
探讨如何将水文频率计算方法 应用于工程设计,确保工程的 安全可靠性。
效果评估
评估水文频率计算方法的准确 性和可靠性,及其在实际工程 中的实际应用成效。
水文频率计算
007水文频率计算

关于国内采用的分布线型:我国水利水电设计洪水设计规范推荐使用P-III型 分布,特殊情况可以使用其他线型,如对数正态分布,GUMBEL分布等。
参数估计:已知实测资料,分布线型推求总体参数(适线 法,概率权重矩法,线性矩法,权函数法)
不同国家采用总体分布线型
参数估计有两种常用的形式,即点估计和区间估计
点估计
所谓点估计就是用一个具体的数值去估计一个 未知的参数。
参数的区间估计
所谓区间估计就是估计参数所在的区间,也就是说用 一 个区间估计未知参数。
§7-2 几种理论分布的频率计算和分析
1,P-III型分布 (重点) 2,对数正态分布 3,耿贝尔分布
a0
EX (1
2CV CS
)
2
EXCV CS
4 C S2
f(x)
1<α<2
α=2
α>2
0
a0
当0<α<1时,2<CS <∞, 密度曲线呈乙型,以x轴
0<α<1
和当x=αa=0为1时渐,近C线S =2,密度曲 线仍呈乙型,但左端截止
α=1
在曲当线1<的α起<2点时,,右2端1/以2 <xC轴S <2 为渐,近密线度曲线呈铃型,左端截
4.9 14.04 12.54 10.58 9.128 7.705 5.88 4.557 3.301 2.608 …
5 14.22 12.69 10.7 9.22 7.771 5.917 4.573 3.301 2.598 …
值表
99.9 -3.09 -3.061 -3.033 -3.005 -2.976 -2.948 -2.92
水文频率计算
《水文频率计算》根据某水文现象的统计特性,利用现有水文资料,分析水文变量设计值与出现频率(或重现期)之间的定量关系的工作过程称为水文频率计算。
自然界的现象按发生情况可分成:必然事件,即在一定条件下必然会发生的事情,如降雨以后就要涨水是必然发生的;不可能事件,即在各条件实现之下永远不会发生的事情,如只在重力作用下的水由低处向高处流是不可能的;随机事件(也称偶然事件),即在一定条件下可能发生也可能不发生的事件,如每条河流每年出现一个流量的年最大值是必然的,但这个最大值可能是这个值也可能是那个值,它在数量上的出现是一种随机事件。
频率计算中是以1来表示必然事件出现的可能性(即百分之百出现),以0表示不可能事件出现的可能性,随机事件出现的可能性介于0与1之间。
水文要素。
如降雨、流量等在量的出现方面都有随机性的特点,水文变量如年雨量、年最大洪峰流量、枯季最小流量等都属于随机事件,均可用频率分析方法来分析计算。
水文频率分析主要包括:利用现有水文资料组成样本系列,选择合适的频率曲线线型和估计它的统计参数,根据所绘制的频率曲线推求相应于各种频率(或重现期)的水文设计值。
样本系列。
无限个成因相同、相互独立的同类水文变量的集合称为该水文变量的总体。
这个总体是未知的,现有水文资料只是过去发生过的和今后可能发生的整个总体中的一个样本。
把现有水文资料的水文变量按大小次序排列组成一个系列,称为样本系列,其中所含水文变量的项数(系列长度)叫做样本容量。
系列愈长,样本容量愈大。
水文频率分析就是通过样本系列的统计特征来估计其总体的统计特征,如各种统计参数、某水文变量的频率等。
因此,样本系列是水文频率分析的基础。
用样本系列去推估容量很大或无限的总体的情况,会产生因抽样而引起的误差,这就是抽样误差。
水文统计分析中所估计出的各种数值(如频率、分析中的各个参数、相关系数等)都有抽样误差。
样本的容量越大误差越小,否则误差越大。
抽样误差分析方法有两种:①解析法。
007第七章 水文频率计算1110.ppt
在x近=曲线当度在为a0线α曲曲β相当密点2=的线 线切,2α度处时起呈的>,右曲与2,点铃起右端时线x并轴型点端以C,呈在S相,,以x铃=C轴该切左起x2S型轴为1点<,端点/,2为渐2处右,截斜在1渐近与/端密止率2起线,
以x轴为渐近线
x
4 CS 2
铃形比较符合实际
结合水文随机变量物理性质,从理论上讲,在水文中应用 P-Ⅲ型分布时,三参数应满足以下二个关系:
0.04 3.807 3.619 3.357 3.148 2.927 2.613 2.356 2.075 1.898 …
0.06 3.849 3.657 3.389 3.176 2.951 2.632 2.37 2.086 1.906 …
0.08 3.892 3.695 3.422 3.205 2.976 2.651 2.385 2.096 1.914 …
1, P-Ⅲ型分布频率计算
(1) P-Ⅲ型分布的密度曲线形状
f
(x)
(
)
(x
a0 )
1e
( x a0
)
x a0
式中a0,, 0为参数。
E(X )
a0,
D( X
)
2
2
。
CV
a0
CS
2。
由此,三个原始参数,,a0可以用
基本参数E(X ),CV ,CS表示如下
a0
EX
(1
2CV CS
当 Cs 0, ,此时 为标准化正体分布∴结论是对的
x EX,由于x与是严格单调函数,故
f
f
x
x
dx
d
EX a e 1 EX a
2
EX
a
水文频率计算方法
x1x3
13
(3-25)
Sf(Cs,P)
S表
附录C P-III曲线三点法 S 与 Cs 关系表
P368
P = 5 ~ 50 ~ 95%
求参步骤
√ 三点法:
① 据(3-25)式左端计算得S值,且已知P1,P2,P3,查 附录C,求得参数Cs;
② 据Cs查附录B
(3-24)式,求得
。
x,Cv ,Cs
2. 优化适线法
最小二乘估计法:
n
S(){ [xi f(Pi,)]2} i1
S(ˆ)minS()
S 0
(3-26) (3-27) (3-28)
End
水文频率计算方法
频率计算推求 xp
参数初估
适线法
一. 统计参数初估方法 1 矩法 2 经验关系法 3 三点法 4 权函数法 5 概率权重矩法
矩法
1.矩法
依据实测系列计算三个统计参数:x,Cv ,Cs
经验法
2. 经验关系法
x
1 n
n
xi
i1
Cv
(K i 1) 2
n 1
Cs初值:
设C 计s 暴 雨量( n
x
2
x (1 C v 2 )
x 3 x (1 C v 3 )
(3-22)
三点的取法: 1~59% 或 3~50~97% 或 5~50~95% 或 10~50~90%
参数计算公式
x 1x3 3x1 1 3
Cv
x1 1x3
x3 3x1
(3-23) (3-24)
x1x32x2 1322 =S 偏度系数
计算表 题 P66
p m 100% n 1
年最大洪峰流量 Q(m3/s)
水文统计频率分布与计算
Pmnm 1 mlห้องสมุดไป่ตู้,l2,...,n
当实测系列中含有特大洪水时,把这些特大洪水与历史特大洪水 一起排序,但仍然在实测系列中排序,即实测系列的排序为m=l+1 ,l+2,...,n。特大洪水系列的经验频率计算公式为:
洪峰 m3/s
年份
4010 2940 4520 5290 1962 1963 1964 1965
3500 1966
5250 3910 3620 6780 7780 1967 1968 1969 1970 1971
2590 5200 1972 1973
洪峰 5420 6980 4620 3440 10000 5840 4380 5200 3880 4860 6640 5800 m3/s
2. p.198 7-17 3. 根据历史调查知从1920年以来发生过两次特大洪水,分别是1920 年和1934年,经推算得到洪峰流量分别为12000m3/s和9000m3/s。已 知某坝址断面24年的洪峰流量实测值如下表,试计算各洪峰流量的经验频 率。
年份 1950 1951 1952 1953 1954 1955 1956 1957 1958 1959 1960 1961
3/51
Q(m3/s)
a项特大洪水 M=1,2,...,a
实测期内特大洪水,l项
实测一般洪水,n – l项 m = l + 1, l + 2, ..., n
... ...
缺测 ...
...
T
n
N
关键:确定a,l ,N。
4/51
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于国内采用的分布线型:我国水利水电设计洪水设计规范推荐使用P-III型
分布,特殊情况可以使用其他线型,如对数正态分布,GUMBEL分布等。
参数估计:已知实测资料,分布线型推求总体参数(适线
法,概率权重矩法,线性矩法,权函数法)
参数估计有两种常用的形式,即点估计和区间估计
点估计
所谓点估计就是用一个具体的数值去估计一个 未知的参数。
太复杂了,因此,必须想办法简化计算。
为了简化,可以对X作标准化变换,即 标准化后的变量
X EX
也是随机变量,常数为离均系数,若X的数字特征为 ,方差为1, Cs Cs EX , , Cs, 则的均值为0
的最小值为:
0
a EX
2 2 Cs Cs
2500 1000 ② p 3.00 0.50 1000
查 p值表,当CS 2.00时, 如p 1%, 则 P 3.605
如p 2%, 则 P 2.912
线性内插得出相对应 P 3.00时的p值为1.87%, 即P ( X 2500) 0.0187.
从方程组
可解出
以后在不造成混淆的情况下,随机变量与普通变 量不再严格按大小写作区分。
例 题
例:设(X1,X2 , … , Xn )为总体X的一个样本,求总 体的均值a , 及方差σ2的矩估计。 解:
1 n EX a 1 X i 样本平均值 n i 1
D X EX EX 2 1
求未知参数点估计的方法很多,
一般 可以分成两类:一是数理统计中使用 方法,如矩法和极大似然法;另一类 是水文统计中使用方法,包括我国水 文计算中广泛使用的适线法,权函数 法、概率权重矩法,线性矩法等。下 面主要介绍矩法和极大似然法,适线 法,还要简要介绍水文统计中新方法。
二、参数点估计的矩法
当
Cs 0,
,此时
为标准化正体分布∴结论是对的
x EX ,由于x与是严格单调函数,故 dx 1 EX a EX a e f f x x d 2
例:设X服从P–Ⅲ型分布,且 E ( X ) 1000, CV 0.50, CS 2.00 求 ① p 0.2%的x p的值, ② P ( X 2500)。 解 ① 查 p值表,对于CS 2.00, p 0.2%, P 5.215
故 x p E ( X )( pCV 1) 1000(5.215 0.50 1) 3607
②
2Cv Cs 1 k min
K min
xmin x
2Cv 实测最小值x min a EX 1 Cs 2Cv 1 k min Cs 2Cv Cs 1 K min 2Cv 综上所述 2Cv Cs 1 k min
(2)P-III型分布频率曲线 (xp~p的关系) X的超过累积概率为
0
样本的函数,是随机变量,估计值是一个具体数值,它是 估计量U的一个取值。这就是点估计的思想方法。
具体问题: 随机变量X ,F(x)已知,并已有 x1 , x2 ,, xn
1 , 2 , l 样本,但其中
l
,
l 个参数未知,
一般为3个。点估计基本步骤: A:把实测样本( x1 , x2 ,, xn )当作随机样本(
100
0
0.1
1
10
50
90
99
99.9 P(%)
模 比 5 系 数 K 4
3 2
1 0 0
0.1 1 2
10 30 50 70 90 95 98
99.9 P(%)
模 比 系 数 K
1.5 1.4 1.3 1.2 1.1 1.0 0.9 0.8 0.7 0.1 0.5 1 2 10 30 50 70 90 95 98 99.9 P(%)
2 2 2 2
2
1 1 2 1 X i X i Xi X n n n
第 七 章
水文频率计算
水文频率计算
§7-1
§7-2
概述
几种理论分布的频率计算与分析
§7-3
§7-4
参数点估计的数理统计法
参数点估计的水文统计法
§7-5
§7-6
估计量好坏的评判标准
参数的区间估计
§7-1 概 述
问题的提出(堤防高度,历史洪水加成,频率计算,设计标准) 基本问题: 线型选择, 参数估计 线型选择: 理论导出 (中心极限定理,极值分布,物理机制) 因其不同程度假定往往不能满足,一般通过线型与实测数 据拟合作出判断)。不同国家洪水特性不同,结果不一样。
P P X x P
xP
1 x a x a e dx
在 EX , Cv, Cs给定后, 可唯一确定 , , a ,因此, 只要EX , Cv, Cs 已知,可通过积分求出不同 xP 对应的P值。有于不同
p ~ x P 则可以画出频率曲线。但这样求解工作量太大,
求p=0.01的情况下的设计值xp =?
另求Cs=2.05,p=0.2%时的设计值 xp
=
(3)P-III型频率曲线绘制
海森几率格纸,横坐标是频率,纵坐标水文变量,
正态分布成直线,偏态分布曲线(p163,例子)
分布参数对
Cs
300
Cv=0.5 Cs=1.0 200
参数的区间估计
所谓区间估计就是估计参数所在的区间,也就是说用 一 个区间估计未知参数。
§7-2 几种理论分布的频率计算和分析
1,P-III型分布 (重点) 2,对数正态分布
3,耿贝尔分布
1, P-Ⅲ型分布频率计算
(1) P-Ⅲ型分布的密度曲线形状
f ( x) ( x a0 ) 1 e ( xa0 ) x a0 式中a0 , , 0为参数。 ( )
Cs 4
2
有关,那么只要给
p 可通过积分求得p 即
2 p p p
p
1
e d
Cs ~ P ~ p
由于上式右边只是Cs的函数,故可以编制
关系数值表,这方面工作已有人做好;本书在附表4列出了
0<α<1 α=1
1<α<2 α=2 α>2 0
a0
x
4 CS 2
铃形比较符合实际
结合水文随机变量物理性质,从理论上讲,在水文中应用 P-Ⅲ型分布时,三参数应满足以下二个关系:
①
, Cs 2Cv原因是水文变量最小值
a 0, 而EX a 0
2Cv a EX 1 0 Cs 2Cv Cs
假设X 的分布函数为F ( x; u ),u 为未知参数其取值范围
0 0
称为参数空间( X 1 , X 2 , , X n )为X 的样本,构造一个估计 u 的统计量U U ( X 1 , X 2 , , X n ),作为待估参数u 的估
0 0
计,并称U 为u 0的估计量,当有了一个具体样本 ( x1 , x2 , , xn )时,把它代入U的表达式,就得到U的一个观 测值u u ( x1 , x2 , , xn )并称此u值为u 的估计值。估计量是
EX a
1
2
e
1
e
从以上所推导出离均系数分布密度可知,该分布密度仅与
当0<α<1时,2<CS <∞, 密度曲线呈乙型,以x轴 和当α=1时,CS =2,密度曲 x=a0为渐近线 线仍呈乙型,但左端截止 当1<α<2时, 21/2 <CS 在曲线的起点,右端以x轴 <2 , 密度曲线呈铃型,左端截止 为渐近线 在曲线的起点并在该点处与 当α=2时, CS =21/2,密 x=a0相切,右端以x轴为渐 度曲线呈铃型,左端截止 近线 当α>2时, CS < 21/2 , 在曲线的起点,起点斜率 密度曲线呈铃型,在起 为β2,右端以x轴为渐近线 点处与x轴相切,右端 以x轴为渐近线
E ( X ) a0,
CV a0
D( X ) 2 。
2
CS
2
。
由此,三个原始参数,,a0可以用 基本参数E ( X ), CV , CS 表示如下
2CV a0 EX (1 ) CS
2 EXCV CS
4 CS 2
f(x)
X 1 , X 2 ,, X n )一次观测值。
作为总体参数 i0 B:构造统计量 i X 1 , X 2 ,, X n i
^
的估计量。
确定估计方法
C:分析 i 的统计性能(抽样误差大小)。
D:以 x i 代替 X i 所得的估计量 i 作为总体参数的估计值。
Cs ~ P ~ p
关系表,表中 Cs
取值0~5.0,取86数位,P取值0.01%~99.9%共26位,表格形式。
皮尔逊Ⅲ型分布 p 值表
p% Cs 0 0.02 0.04 0.06 0.08 0.1 0.12 1.95 2 4.9 5 0.01 3.719 3.768 3.807 3.849 3.892 3.935 3.978 8.1 8.21 14.04 14.22 0.02 3.54 3.582 3.619 3.657 3.695 3.734 3.773 7.42 7.517 12.54 12.69 0.05 3.291 3.325 3.357 3.389 3.422 3.455 3.488 6.522 6.601 10.58 10.7 0.1 3.09 3.119 3.148 3.176 3.205 3.233 3.262 5.842 5.908 9.128 9.22 0.2 2.878 2.903 2.927 2.951 2.976 3 3.024 5.161 5.215 7.705 7.771 0.5 2.576 2.595 2.613 2.632 2.651 2.67 2.688 4.261 4.298 5.88 5.917 1 2.326 2.341 2.356 2.37 2.385 2.4 2.414 3.579 3.605 4.557 4.573 2 2.054 2.064 2.075 2.086 2.096 2.107 2.118 2.897 2.912 3.301 3.301 3 1.881 1.889 1.898 1.906 1.914 1.923 1.931 2.497 2.507 2.608 2.598 „ „ „ „ „ „ „ „ „ „ „ „ „ 99.9 -3.09 -3.061 -3.033 -3.005 -2.976 -2.948 -2.92 -1.024 -0.999 -0.408 -0.4
