Properties of Fuzzy Implications obtained via the Interval Constructor
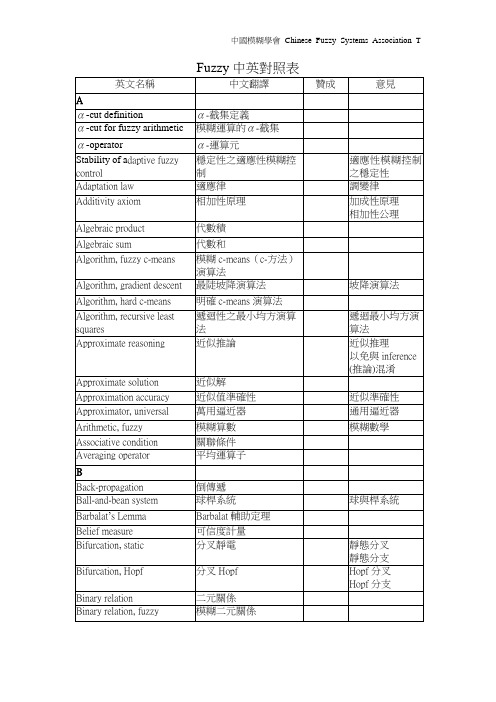
Fuzzy中英对照表
Composition of fuzzy relations
模糊關係之合成
Compositional rule of inference
推論之合成規則
合成規則推論法
Computing, soft
軟性運算
柔性運算或
柔性解算
Conditional possibility distribution
工業流程控制
Inference, composition based
組合式推論
Inference, individual-rule based
個別規則基礎的推論
個別規則式推論
Inference engine, Dienes-Rescher
Dienes-Rescher推論機制
Inference engine, Lukasiewicz
模糊關係方程式
Equilibrium
均衡
平衡
Extension principle
擴展法則
Feedforward network
前饋網路
Fuzzifier, Gaussian
高斯模糊化
高斯模糊化器
Fuzzifier, singleton
單點模糊化
單點模糊化器
Fuzzifier, triangular
Dombi類型之模糊交集
Intersection, fuzzy Dubois-Prade class
Dubois-Prade類型之模糊交集
Intersection Yager class
Yager類型之交集
Interval analysis
區間分析
Interval-valued function
r语言的p.adjust函数 -回复

r语言的p.adjust函数-回复"P.adjust function in R: A Comprehensive Guide"Introduction:R is a statistical programming language widely used by researchers and data scientists for data analysis and visualization. One of the key functions in R is the p.adjust function, which is used for adjusting p-values in multiple hypothesis testing scenarios. This article aims to provide a step-by-step guide on how to use the p.adjust function in R, explaining its significance and various adjustment methods available.What is p.adjust function?The p.adjust function in R helps correct for multiple hypothesis testing by adjusting the p-values obtained from statistical tests. In a typical scenario, when several hypothesis tests are conducted simultaneously, the probability of obtaining a false positive result increases. Therefore, adjusting the p-values is essential to control the overall false discovery rate (FDR) or family-wise error rate (FWER). The p.adjust function automates this adjustment process, saving time and effort for the user.Step 1: Understanding p-valuesBefore diving into the p.adjust function, it is essential to understand the concept of p-values. A p-value represents the probability of obtaining the observed data (or more extreme) if the null hypothesis is true. The lower the p-value, the stronger the evidence against the null hypothesis. In multiple testing scenarios, p-values need to be adjusted to account for the inflation of false positives.Step 2: Basic usage of p.adjust functionThe basic syntax of the p.adjust function in R is as follows:p.adjust(p, method = "BY")Here, 'p' denotes the vector of p-values obtained from multiple hypothesis tests, and 'method' specifies the adjustment method to be applied. The default adjustment method in R is the Benjamini-Hochberg (BH) method, known as the "BY" method, which controls the false discovery rate. Other available methods include "holm", "hochberg", "hommel", "bonferroni", "BH", "BY", "fdr", and "none".Step 3: Adjustment methods and their implicationsAs mentioned earlier, different adjustment methods are available in R's p.adjust function. These methods have varying control properties and are suited for different scenarios. A brief overview of some commonly used methods is as follows:- Holm method: This method is a step-down procedure that provides strong control over the family-wise error rate (FWER). It is suitable when dependent tests or strong control over FWER are required.- Hochberg method: Similar to the Holm method, the Hochberg method also offers strong control over FWER. However, it is slightly more powerful and often preferred when dealing with independent tests.- Bonferroni method: The Bonferroni method is a conservative approach that controls the FWER by dividing the significance level by the number of tests. This method is useful when precision is crucial, but it may become overly conservative for a large number of comparisons.- Benjamini-Hochberg (BH) method: The BH method controls thefalse discovery rate (FDR), which is usually less stringent than the FWER. It is widely used for exploratory analysis and can be used when the FDR control is desirable.Step 4: Examples and practical considerationsTo better understand the application of the p.adjust function, let's consider an example. Suppose we have conducted 20 independent hypothesis tests and obtained a vector of raw p-values. We can use the p.adjust function to adjust these p-values using the desired method. For instance, to use the BH method, we can write:adjusted_p <- p.adjust(raw_p, method = "BH")Once adjusted, the vector 'adjusted_p' will contain the adjusted p-values corresponding to each hypothesis test. These adjusted p-values can be used for further analysis or comparison while controlling for the desired error rate.It is important to note that appropriate adjustment method selection depends on the nature of the data and research goals. Considering the trade-off between statistical power and controlover errors is crucial. Additionally, it is recommended to explore sensitivity analyses and adjust methods accordingly.Conclusion:The p.adjust function in R is a powerful tool for adjusting p-values in multiple hypothesis testing scenarios. By controlling for the overall false discovery rate or family-wise error rate, it ensures more robust and reliable statistical inferences. This comprehensive guide discussed the significance of the p.adjust function, its usage, available adjustment methods, and practical considerations. By following these steps, R users can effectively utilize the p.adjust function for their data analysis needs.。
Optimization of fuzzy rules design using genetic algorithm

Optimization of fuzzy rules design using genetic algorithmS.V.Wong,A.M.S.Hamouda*Department of Mechanical and Manufacturing Engineering,Universiti Putra Malaysia,43400Serdang,MalaysiaReceived1March1999;received in revised form11May1999;accepted17October1999AbstractFuzzy rules optimization is a crucial step in the development of a fuzzy model.A simple two inputs fuzzy model will have more than ten thousand possible combinations of fuzzy rules.A fuzzy designer normally uses intuition and trial and error method for the rules assignment. This paper is devoted to the development and implementation of genetic optimization library(GOL)to obtain the optimum set of fuzzy rules. In this context,afitness calculation to handle maximization and minimization problem is employed.A newfitness-scaling mechanism named as Fitness Mapping is also developed.The developed GOL is applied to a case study involving fuzzy expert system for machinability data selection(Wong SV,Hamouda AMS,Baradie M.Int J Flexi Automat Integr Manuf1997;5(1/2):79–104).The main characteristics of genetic optimization in fuzzy rule design are presented and discussed.The effect of constraint(rules violation)application is also presented and discussed.Finally,the developed GOL replaces the tedious process of trial and error for better combination of fuzzy rules.᭧2000Elsevier Science Ltd.All rights reserved.Keywords:Fuzzy-rules optimization;Genetic algorithms;Genetic optimization;Fitness mapping1.IntroductionFuzzy logic,initially introduced in Zadeh’s pioneering work in mid-1960s[2],and later explored by Mamdani to control a simple laboratory steam engine[3],has established itself as a suitable solution to a range of challenging indus-trial problems[4].Fuzzy logic is a mathematical theory of inexact reasoning that allows us to model the reasoning process of humans in linguistic terms.It is suitable in defin-ing the relationship between the system inputs and the desired system outputs.Fuzzy logic is one of the most successful of today’s technologies for developing sophisti-cated control systems.It is also popular,as its capability for developing rule-based expert systems.Fuzzy controllers and fuzzy reasoning have found particular applications in indus-trial systems that are very complex and cannot be modeled precisely even under various assumptions and approxima-tions[1].The control of such systems by experienced human operators was proven to be in many cases more successful and efficient than by classical automatic control-lers.The human controllers employ experiential rules that can be cast into the fuzzy logic framework.These observa-tions inspired many investigators to work in this area with result being the development of the so-called fuzzy logic and fuzzy rule-based control.Munakata and Jani reported in Ref.[5]that over a thousand commercial and industrial fuzzy systems have been successfully developed in the last few years.The main reason behind this lies on the unique characteristics of fuzzy logic.There are two general methodologies for generating fuzzy model.Thefirst one requires expert information to construct the model,whereas the second lets the system adjust the fuzzy components from representative numerical samples.Thefirst approach requires a prior expert knowledge about the system.It has been a good form to collect expert information from experi-enced experts,as it is much nearer to human normal communication.The main drawbacks of this approach are subjectivity and dependence on expert’s knowledge,which might not be the best at most of the time.The second method has been applied to construct a fuzzy model from the available input–output results.A lot of works has been carried out to adjust and/or to generate input membership functions,output membership functions, and/or fuzzy rule sets[6–9].Tang et al.suggested hierarch-ical genetic algorithms to minimize the number of fuzzy memberships and fuzzy rules in Ref.[10].The main draw-back of this approach is that the representative data is not really representative in an overall manner.Besides that, almost all the systems in reality are non-linear and subjected to many unknown variables,which are normally ignoredAdvances in Engineering Software31(2000)251–262 0965-9978/00/$-see front matter᭧2000Elsevier Science Ltd.All rights reserved.PII:S0965-9978(99)00054-X /locate/advengsoft*Corresponding author.Tel.:ϩ603-948-6101;fax:ϩ603-948-8939. E-mail address:hamouda@.my(A.M.S.Hamouda).during idealization of the problem.Thus,the so-called representative data is not always representative.Fuzzy rules design is never an easy task especially subjected to complex real world problems.Fuzzy if-then rules were derived from human experts in most fuzzy-based systems.Each fuzzy model described in Ref.[1] will have more than2×1029possible sets of fuzzy rules.A simple two-inputs-one-output fuzzy model normally has more than ten thousand possible combinations.Although applying common sense and expert knowledge would normally narrow down the scope,but the selected fuzzy rules are normally not the bestfitted.Recently,several approaches were suggested for generat-ing the fuzzy rules from the numerical data automatically. Wang and Mendel have described a general method to generate fuzzy rules from the numerical data in Ref.[11]. Jang[12]and Berenji and Khedkar[13]have proposed self-learning methods for adjusting membership functions of fuzzy sets in fuzzy if-then rules.According to the authors’opinion,automatically generating fuzzy rules will lose one of the most important features in fuzzy logic.One of the main features of fuzzy logic is its ability of describing the system in a linguistics term.This enables the design of such system with more human-like reasoning,especially with the fuzzy if-then rules.Genetic algorithm(GA)is now a very popular tool for solving optimization problems.It has been used to effec-tivelyfind optimal solutions for a variety of problems(e.g. operations research,hybrid techniques,image processing, etc.).Genetic algorithms are based on the mechanics of natural selection and natural genetics.With GA’s capabil-ities,it has been extended to be a novel optimization algo-rithm.GA has been applied in solving mathematical problems,medical problems,engineering problems and even political science problems[14–17].Genetic algo-rithms have been employed for generating and/or adjusting membership functions of fuzzy sets.Karr[6]adjusted fuzzy membership functions and Nomura et al.[18]determined fuzzy partition of input spaces by genetic algorithms.In this paper,the authors use the genetic algorithm approach in fuzzy rules design.The genetic optimization replaces the tedious process of trial and error for better combination of fuzzy rules.Representative data are used from real world or reliable resources for genetic optimiza-tion.Studies are carried out based on fuzzy models from Refs.[1,19].Both newly suggested algorithms,chromo-some-length independent mutation operation and Fitness Mapping mechanism,are described and discussed.2.Development of GOLThere are two main classes in GOL.Thefirst one is named as Chrom,containing all the necessary information about a chromosome that belongs to an individual member of a population.The second class is called“Population”, consists of all individuals as its members.2.1.Chrom classIn microbiological world,chromosomes are composed of genes,which may take on some number of values called alleles.The Chrom class only stores a series of such coded information,in reality.Designation of allele has to be carried out before hand by the designer.In natural world, the data or information mentioned is referring to the feature carried with the particular value of the allele,such as brown eyes.The definition of the alleles is not provided in the Chrom class,as it is common for the entire population(simi-lar individual or member of the population).All the infor-mation carried by an individual is collected in the chromosome in a standard sequence,which can be defined freely by the user of the GOL.All the information stored in the chromosome is in bit form,means a series of‘1’and‘0’are used for representa-tion of an individual’s characteristics or features.The data has been arranged in such a way as to cope up with different types of information representation.It could be a Boolean, an integer or even a real number.The user of the GOL has all theflexibility to define his/her own definitions for every single allele.In the present work,the authors have chosen binary numbering,as it is the most fundamental in comput-ing world.It can represent any kind of information,ranging from its own binary data to real number.In addition,it will gain more efficient computer resources utilization.The user has to define the length of every single allele for the chro-mosome.The user has to bear in mind that,all the indivi-duals in the population are similar,thus share similar chromosome pattern.In addition,the user has to decide the length of every individual allele in advance.The calcu-latedfitness and penalty factors are stored as member vari-ables in Chrom class as well.A series of member functions are created to abstract and to store allele information from and into the chromosome.The implementation of these functions requires providence of predetermined initial posi-tion and ending position of the allele in a chromosome. 2.2.Population classPopulation class consists of two generations,new genera-tion and present generation.Each generation consists of corresponding individuals(chromosomes)of same kind and each individual carries a series of genes.New genera-tion is breed from the present generation.All the chromo-somes belong to Chrom class,thus carrying all the Chrom class features and functions.Population class carries a number of member variables. They can be divided into two main groups,which are static and dynamic,respectively.The static variables are pre-determined or calculated at the initialization stage and used for the rest of the following processes.While on the contrary,dynamic variables are altered in every generation.S.V.Wong,A.M.S.Hamouda/Advances in Engineering Software31(2000)251–262 252Table1shows crucial static and dynamic member variables of the Population class.Several member functions are included in the Population class.These member functions are used to implement what is shown in Fig.1.Some of them are standard and are used within the GOL.The inheritance and polymorphism of OOP enable overriding and customizing of the member functions to cope with different needs.Some of the common functions are reproduction,select,mutation,crossover,fitness calcu-lation,etc.Common genetic operations are crossover and mutation. They are handled by crossover function and mutation func-tion in Population class.The user can select single bit point crossover or double bit point crossover.Whole allele instead of bit crossover is available.While for mutation operation,a user can choose bit mutation or allele mutation,a single bit of the whole chromosome will be altered to its reverse in bit mutation.While,the whole allele will be altered arbitrary to any possible value within the allele length in terms of bits in allele er of GOL can even override the opera-tions to have his/her custom made genetic crossover and mutation operation.Fitness calculation is a problem-oriented process.It has to be overridden by the user according to the requirement of the system.Fitness of an individual is calculated in terms of real number.Fitness calculation is generally grouped into two main purposes,maximizing and minimizing the solu-tion.The nature of GOL is for maximizationfitness,means, the evolution of generations tends towards maximizing the fitness of the entire population.Minimizing problems can be solved with the following general equationFitness Final KϪFitness Trial 1 Fitness Trial is calculated before hand based on a minimiz-ing problem consideration.Thefinalfitness,Fitness Final, is calculated with Eq.(1)with a constant value K.The value of K must be greater than the worst predicted value of Fitness Trial.In solving a maximizing problem, Fitness Final is equal to Fitness Trial.Constraints(or penalty for rules violation)can be applied in the process of genetic optimization.Penalty factor of each individual is stored in respective object,an instance of Chrom class.When a constraint or a rule is violated,a certain amount of penalty is applied towards thefinalfitness calculation.Penalty treatments are carried out either with single collection or accumulative collection.In single collection,the penalty factor is applied once only,no matter how many constraints is violated.Thus,penalty will be the same regardless the violating degree.On the contrary,with accumulative collection,each violation will cause a certain amount of penalty.At the end,all the penalties are summed up for thefinalfitness calculation.Eq.(2)shows thefitness calculation for minimizing problem with accumulative penalty collection.Fitness Final KϪFitness TrialϪPF i 2 PF i is the penalty factor of an individual i.Constraint(s)or rules violation implementation is usefulS.V.Wong,A.M.S.Hamouda/Advances in Engineering Software31(2000)251–262253 Table1Important member variables of Population classStatic variable Description Dynamic variable DescriptionImember Number of individuals/chromosomes in a generationAvgFitness Averagefitness of the present generationIallele Number of allele in a chromosome MaxFitness Maximumfitness of the present generation LengthAllele Length of a particular allele in achromosome,in term of binary unitFitChrom Chromosome which has the highestfitnesspCross Probability of occurring cross over Ncross Number of cross over occurrencepMutation Probability of occurring mutation NMutation Number of mutationoccurrenceFig.1.Genetic optimizationflow chart.especially in fuzzy rules design.It incorporates expert knowledge into the optimization process.Penalty factor calculation should be overridden for customization purpose.The penalty value must not be too small,which will not cause significant effect.It must not be too large as well,which will cause the whole optimization process inefficient.The summation of all penalty values ( PF i in Eq.(2))must not be greater than the difference between the value of K and the mean of all absolute error percentages.To reduce the unwanted effects from value K ,Eq.(3)is suggested AdjFitness i Fitness Final i Ϫmin Fitness Final 0…Fitness Final n Ϫ13 AdjFitness i is the adjusted final fitness value for a parti-cular member i of the population.Fitness i is the value calcu-lated from Eq.(2)for member i .min(Fitness Final 0…Fitness Finaln Ϫ1)is a function which will yield the minimum value from Fitness Final 0to Fitness Final n Ϫ1:The value n is the size of the population.2.3.Implementation of GOLFig.1shows a flow chart of a typical genetic optimization algorithm.It starts with static variable initialization.All the static and dynamic variables are initialized in the GOL constructor.The GOL uses bit-wise interpretation,whichmeans,the length of a particular allele is expressed in terms of bit.If an allele carries a possible value from 0to 7(or 8possible features),the length of the allele is then three.Calculations are then being carried out for some other static variables,such as the length of a chromosome.Initial individuals or chromosome of the members in a population have to be defined.They can be generated randomly,supplied by the user or partially generated randomly with partial user input.Fitness of initial chromosomes is calcu-lated with the overridden fitness calculation function,including the penalty factor calculation.The Reproduction’s main function is to generate the new generation from the present generation.It consists of selec-tion,mutation and crossover operations.With analogy to the biological world,stronger individual stands higher chance in natural selection for breeding.Thus,individual with better fitness will stand higher chance to be selected in the selection operation.Stochastic sampling with replacement method is used.Crossover and mutation may happen while breeding.The success of crossover and mutation process is depending on the pre-defined mutation probability and crossover probability,respectively.The breeding of new generation is continuing until the population size reaches its limit.All the new generation will replace the present generation in the generation change process.Then the global population information is updated.The whole processes are repeated for the desired number of generation.3.GOL applicationGOL has successfully optimized the fuzzy models used in Refs.[1,19].Tables 2and 3show the fuzzy expressions for the inputs and output memberships,respectively.While Table 4shows the minimum–maximum range of the fuzzy membership functions for four different tool types.The fuzzy models are common in inputs and output membership pattern,but different in range.The inputs and output memberships are equal-sided triangle in shape and well distributed.Different set of fuzzy rule is assigned for each respective tool.Table 5shows fuzzy rules for high-speed tool fuzzy model.The fuzzy rules design was based on intuition with trial and error for fine-tuning.S.V.Wong,A.M.S.Hamouda /Advances in Engineering Software 31(2000)251–262254Table 2Inputs fuzzy expression First input (material hardness)Second input (depth of cut)Index representation for both inputs Abbreviation Expression Abbreviation Expression VS Very soft VS Very shallow 0S Soft S Shallow 1MD Medium MD Medium 2H HardD Deep3VHVery hardVDVery deep4Table 3Output fuzzy expression for cutting speed fuzzy model (cutting speed)Abbreviation ExpressionIndex representation EVS Extremely very slow 0ES Extremely slow 1VVS Very very slow 2VS Very slow 3S Slow4QS Quite slow 5AS A bit slow 6MD Medium 7AF A bit fast 8QF Quite fast 9F Fast10VF Very fast11VVF Very very fast 12EF Extremely fast13EVFExtremely very fast143.1.Fuzzy set handling classA simplified fuzzy set handling class(FSH class)has been developed and incorporated into the optimization process described in this paper.The FSH class is developed using Cϩϩprogramming language.The members of the FSH store the properties of a fuzzy membership.The simpli-fied FSH class can only handle triangle and truncated trian-gle fuzzy shapes.Some common operations like truncation and truth degree calculation are also included.All the calculations described in this paper are based on Max–Min Inference Method.In order to save processing time,Weighted Centroid Output Defuzzification method has been used.The use of Weighted Centroid Output Defuz-zification compared to Union Centroid Output Defuzzificai-ton has proven to cause an insignificantly small difference as reported in Ref.[19].3.2.GOL initializationThe fuzzy models consist offive fuzzy memberships in the input andfifteen in the output.The system required25 fuzzy rules with15possibilities each.Thus,the total number of possible fuzzy rules combination will be1525 2:525×1029:For initialization,25alleles were required andthe length of each allele is4bits in order to cope with15 possible values.Index representations in Tables2and3are used.In addition,the initialization of the alleles,the prob-ability of crossover,the probability of mutation,and the size of the population are needed.The proper size of the popula-tion and probabilities will yield better optimization results. In this study,the population consists of80individuals(sets of fuzzy rule),the crossover probability and the mutation probability are set as0.6and0.009,respectively.Single bit point crossover operation and allele mutation operation are used.The fuzzy rules from Ref.[1]are assigned as one of the initial members.The rest of the rules are generated automatically and randomly.Basically,the size of a popula-tion isfixed.Each individual has its own chromosome, which consists of certainfixed-number of alleles.The genetic optimization processes are repeated for10000 generations.3.3.Fitness calculationCalculation of an individual’sfitness involves extracting data from the individual’s chromosome,translating the value of all the alleles and assigning the represented fuzzy rules into the FSH class.Then fuzzy operations are performed with the predetermined inputs(work piece mate-rial and depth of cut)to yield the output(cutting speed).The number of predetermined sets of inputs is80.Forty sets of representative data are extracted from Machining Data Handbook[20].Additional40sets for uncovered region are obtained through linear interpolation.Calculation of absolute error percentage compared to the result from the above mentioned80sets of data is carried out.The opera-tions iterate untilfinished assessing all the predetermined sets of inputs.The mean of all the individual absolute error percentage is calculated.The mean of absolute error percen-tage is a suitablefitness representation of the particular member(chromosome)in the population.Orientation of fitness consideration in the developed GOL is,higher the value offitness the better.To cope with this scenario,the fitness is obtained through Eq.(4)Fitness KϪni 0abs_error% inϩ1Ϫpenalty_factor where0ՅiՅn4Penalty factor is for rules violation(or constraints).The value K is an arbitrary selected positive value.K is defined as1000for the purpose of this application.Generally,lower mean absolute error percentage,higherfitness value and nearer to K.For thefinal consideration of thefitness in the competition of reproduction selection,Eq.(4)is employed.S.V.Wong,A.M.S.Hamouda/Advances in Engineering Software31(2000)251–262255 Table4Min–max range of fuzzy membership functions for cutting speed fuzzy modelTool type First inputmaterial hardness(BHN)Second input depth of cut(mm)Output cutting speed(m/min)Min Max Min Max Min Max High-speed steel852********* Uncoated brazed carbide8527501660172 Uncaoted indexable carbide8527501663225 Coated carbide85275016105336Table5Fuzzy rules for high-speed steel fuzzy model(with abbreviation indication)Material hardness Depth of cutVS S MD D VDVS EVF MD AS QS VSS F QS S VS VVSMD F S S VVS VVSH QF S VS VVS ESVH MD ES ES ES EVS3.4.Pattern violation (constraint)penaltiesThe genetic optimization class allows the control of fuzzy rules pattern,means,the designer can provide his/her expert knowledge in specifying the relationship between the inputs and the outputs.For the purpose of this paper,the authors have included four general constraints for the fuzzy rules,which are:•harder the workpiece material,faster cutting speed;•softer the workpiece material,slower cutting speed;•shallower the depth of cut,faster cutting speed;•deeper the depth of cut,slower cutting speed.Constraints are applied with accumulative penalty collec-tion.Each violation will cause a penalty value of 25in the summation of error factor in Eq.(4).Thus,more number of violations will cause lower fitness.Pattern validation is carried out during the assignment of fuzzy rules into the FHS class from the value of alleles.The penalty value must not be too small,which will not cause any significant effect.It must not be too large as well,which will make the whole optimization process inefficient.The summation of all penalty values must not be greater than the difference between the value of K and the mean of all absolute error percentages.3.5.Results of GOL implementationBetter results from the trial and error fuzzy rules with genetic optimization are achieved.Table 7shows the summary of validation results,comparing the genetic opti-mized fuzzy model from the literature [1,19].Note that all the fuzzy models in the literatures were fine-tuned through trial and error.Significantly improved fuzzy rules are suggested after genetic optimization for each fuzzy model.4.GOL characteristics and operations discussion General characterization of fuzzy rules genetic optimiza-tion is carried out with the high-speed steel fuzzy model from literature [1]as test media.As a typical situation,a genetic model with relatively huge chromosome is involved.The example fuzzy model requires 25alleles in a chromo-some,and each allele consists of 4bits.As for characteriza-tion tests,no constraint (penalty)is applied.Initial individuals in the initial population are generated randomly.4.1.Efficiency and repeatabilityTen independent runs are carried out to verify genetic optimization’s performance in fuzzy rules design.The number of generation is set to be 200.All the runs share the same genetic parameters,such as the number of indivi-duals in the population and mutation probability,but have different random seeds.The random seed is used to generate random number.Fig.2shows a chart based on the mean absolute error percentage,which is (abs_error%)/(n ϩ1)in Eq.(4).Generation average,generation the best and over-all the best are shown in terms of mean absolute error percentage.They are calculated as the mean value from the ten independent runs.Trend-lines are inserted in Fig.2assuming negative power relationship between mean abso-lute error percentage with the number of generation.Randomly generated initial fuzzy rules have an average value of 40%in mean absolute error percentage with stan-dard deviation of 1.5.The algorithms have significantly narrowed down the search and led to a reduction in the average mean absolute error percentage to around 20%in the first 10generations.The performance of the genetic optimization reduces when evolving for finer solution.The value only improved 1.26%in the second 100genera-tions.Smaller improvement degree is experienced when theS.V.Wong,A.M.S.Hamouda /Advances in Engineering Software 31(2000)251–262256Fig.2.Mean absolute error percentage versus generation with power trend-lines.whole population evolves further.This shows that genetic optimization is performing with excellent phase initially,and the improvement deteriorates from generation to generation till it reaches its optimum point.4.2.Importance of initial populationA good initial population will improve the optimization process.A strong individual in fitness is placed in the initial population,which consists of 79other individuals that generated randomly.The strong individual is selected from the corresponding sets of fuzzy rules from Ref.[1].Averages of generation,average mean absolute error percentage,and the best mean absolute error percentage are calculated from three independent runs under the same parison has been made with 80randomly generated individuals.Fig.3shows that there is a significant improvement in performance by having a single strong indi-vidual in the initial population.The points shown in Fig.3are the average value of mean absolute error in the respec-tive generation.The optimization reduced in mean absolute error percentage from more than 40–8%in the first 10generations,whilst comparing the randomly selected model,only reduced to 20%.Fig.3shows that the single individual-selected population starts staggering from the 50th generation.In the 200th generation,random model achieved 4.3%in mean absolute error percentage while 3.2%with the other model.4.3.Crossover,mutation and population sizeGood genetic algorithm performance requires the choice of a high crossover probability,a low mutation probability (inversely proportional to the population size),and a moder-ate population size.De Jong [21]suggested crossover prob-ability of ter,Grefenstette [22]proved that higherS.V.Wong,A.M.S.Hamouda /Advances in Engineering Software 31(2000)251–262257Fig.3.Performance comparison between random generated population and single strongindividual.Fig.4.Performance comparison with different crossover probabilities.。
Construction of fuzzy automata from fuzzy regular expressions

Available online at Fuzzy Sets and Systems199(2012)1–27/locate/fss Construction of fuzzy automata from fuzzy regular expressionsଁAleksandar Stamenkovi´c,Miroslav´Ciri´c∗University of Niš,Faculty of Sciences and Mathematics,Višegradska33,18000Niš,SerbiaReceived31May2011;received in revised form7January2012;accepted13January2012Available online4February2012AbstractLi and Pedrycz have proved fundamental results that provide different equivalent ways to represent fuzzy languages with mem-bership values in a lattice-ordered monoid,and generalize the well-known results of the classical theory of formal languages.In particular,they have shown that a fuzzy language over an integral lattice-ordered monoid can be represented by a fuzzy regular expression if and only if it can be recognized by a fuzzyfinite automaton.However,they did not give any efficient method for constructing an equivalent fuzzyfinite automaton from a given fuzzy regular expression.In this paper we provide such an efficient method.Transforming scalars appearing in a fuzzy regular expression into letters of the new extended alphabet,we convert the fuzzy regular expression to an ordinary regular expression R.Then,starting from an arbitrary nondeterministicfinite automaton A that recognizes the language R represented by the regular expression R,we construct fuzzyfinite automata A and A r with the same or even less number of states than the automaton A,which recognize the fuzzy language represented by the fuzzy regular expression .The starting nondeterministicfinite automaton A can be obtained from R using any of the well-known constructions for converting regular expressions to nondeterministicfinite automata,such as Glushkov–McNaughton–Yamada’s position automaton,Brzozowski’s derivative automaton,Antimirov’s partial derivative automaton,or Ilie–Yu’s follow automaton.©2012Elsevier B.V.All rights reserved.Keywords:Fuzzy automata;Fuzzy regular expressions;Nondeterministic automata;Regular expressions;Position automata;State reduction;Right invariant equivalences;Lattice-ordered monoids1.IntroductionStudy of fuzzy automata and languages was initiated in1960s by Santos[66–68],Wee[73],Wee and Fu[74], and Lee and Zadeh[45].From late1960s until early2000s mainly fuzzy automata and languages with membership values in the Gödel structure have been considered(see for example[25,28,54]).The idea of studying fuzzy automata with membership values in some structured abstract set comes back to Wechler[72],and in recent years researcher’s attention has been aimed mostly to fuzzy automata with membership values in complete residuated lattices,lattice-ordered moinoids,and other kinds of lattices.Fuzzy automata taking membership values in a complete residuated lattice werefirst studied in[61,62],where some basic concepts have been discussed,and later,extensive research of these fuzzy automata has been carried out in[63,64,75–79].From a different point of view,fuzzy automata with membershipଁResearch supported by Ministry of Education and Science,Republic of Serbia,Grant no.174013.∗Corresponding author.Tel.:+38118224492;fax:+38118533014.E-mail addresses:aca@pmf.ni.ac.rs(A.Stamenkovi´c),miroslav.ciric@.rs,mciric@pmf.ni.ac.rs(M.´Ciri´c).0165-0114/$-see front matter©2012Elsevier B.V.All rights reserved.doi:10.1016/j.fss.2012.01.0072 A.Stamenkovi´c,M.´Ciri´c/Fuzzy Sets and Systems199(2012)1–27values in a complete residuated lattice were studied in[20,21,31–34,70].Fuzzy automata with membership values ina lattice-ordered monoid have been investigated in[46,47,50,52],fuzzy automata over other types of lattices were thesubject of[24,42,43,49,51,56–59],and automata which generalize fuzzy automata over any type of lattices,as well asweighted automata over semirings,have been studied recently in[15,23,41].It is worth noting that fuzzy automata andlanguages are widely used in lexical analysis,description of natural and programming languages,learning systems,control systems,neural networks,clinical monitoring,pattern recognition,databases,discrete event systems,and manyother areas.Li and Pedrycz[50]have proved fundamental results that provide different equivalent ways to represent fuzzylanguages with membership values in a lattice-ordered monoid,e.g.,by fuzzyfinite automata,crisp-deterministicfuzzyfinite automata,fuzzy regular expressions,and fuzzy regular grammars.These results generalize the well-knownresults of the classical theory of formal languages.In particular,they have shown that a fuzzy language over an integrallattice-ordered monoid can be represented by a fuzzy regular expression if and only if it can be recognized by a fuzzyfinite automaton.However,Li and Pedrycz did not give any efficient method for constructing an equivalent fuzzyfiniteautomaton from a given fuzzy regular expression.The purpose of the present paper is to provide such an efficientmethod.Our basic idea is to convert a fuzzy regular expression into an ordinary regular expression R,transforming scalarsappearing in the fuzzy regular expression into letters of the new extended alphabet.Then,starting from an arbitrarynondeterministicfinite automaton A that recognizes the language R represented by the regular expression R,we construct a fuzzyfinite automaton A with the same number of states as the automaton A,which recognizes thefuzzy language represented by the fuzzy regular expression .Moreover,we construct a reduced version A r ofthe fuzzy automaton A ,a fuzzyfinite automaton which also recognizes the fuzzy language and can have evensmaller number of states than A .The method is generic,which means that it can be used in combination with anymethod for constructing a nondeterministicfinite automaton from an ordinary regular expression.In the past,manydifferent techniques for constructing nondeterministicfinite automata from regular expressions have been proposed.Besides Thompson’s construction[71],which builds nondeterministicfinite automata with -transitions,other well-known constructions build nondeterministicfinite automata without -transitions.The best known and most used suchconstructions are the position automaton,discovered independently by Glushkov[27]and McNaughton and Yamada[55],Brzozowski’s derivative automaton[6],Antimirov’s partial derivative automaton[1],and Ilie and Yu’s followautomaton[35–38].Each of these constructions can serve as a basis for the construction of our fuzzyfinite automata. More information on the algorithms for building small nondeterministicfinite automata from regular expressions can be found in[37].It should be noted that the same idea of treating scalars appearing in a fuzzy regular expression as the letters of a newextended alphabet,and then treating a fuzzy regular expression as an ordinary regular expression over a larger alphabet,has been recently used by Kuske[44]in the context of weighted regular expressions and weightedfinite automataover semirings.However,there are some significant differences between his and our approach.First,Kuske consideredonly weighted regular expressions that define proper power series,i.e.,power series with zero as the coefficient of theempty word.In terms of the theory of fuzzy languages,these are fuzzy languages which(absolutely)do not containthe empty word.There is one even more important difference.In the mentioned paper[44],Kuske gave a new proofof the famous Schützenberger’s theorem[26,65]which asserts that the behaviors of weightedfinite automata over anarbitrary semiring are precisely the rational formal power series,i.e.,formal power series defined by weighted regularexpressions.In his proof,Kuskefirst converts a weighted regular expression E to a regular expression E ,then he startsfrom an arbitrary deterministicfinite automaton that recognizes the language defined by E ,and from this automaton heconstructs a weightedfinite automaton whose behavior is the formal power series defined by E.However,the number ofstates of deterministicfinite automata obtained from regular expressions can be exponentially larger than the lengths ofthe corresponding regular expressions.For this reason,regular expressions are more often converted to nondeterministicfinite automata,and the above-mentioned constructions output nondeterministicfinite automata whose number of statesis equal to the length of the regular expression plus one,or even less than that number.In addition,our constructionsoutput fuzzyfinite automata with the same or even smaller number of states than the original nondeterministicfiniteautomaton.As we have said,the size of an automaton obtained from a regular expression plays a very important role,and for thatreason regular expressions are mostly converted to nondeterministicfinite automata.On the other hand,for practicalapplications deterministicfinite automata are usually needed,but determinization of a nondeterministicfinite automatonA.Stamenkovi´c,M.´Ciri´c/Fuzzy Sets and Systems199(2012)1–273 can cause an exponential blow up in the number of states.That is why the number of states of a nondeterministicfiniteautomaton has to be reduced prior to determinization.As the minimization of nondeterministicfinite automata iscomputationally hard,we must be satisfied with the methods for reducing the number of states that do not necessarilygive a minimal automaton,but rather provide a reasonably small automaton that can be efficiently computed.Suchreduction methods have been recently investigated in[8,10,36–40],in the context of nondeterministicfinite automata,and in[20,21,70],in the context of fuzzyfinite automata(see also[16,18,19]).A key role in the state reduction ofnondeterministicfinite automata is played by the right and left invariant equivalences,which have been generalizedin the fuzzy framework as right and left invariant fuzzy equivalences(cf.[20,21,70]).It is worth noting that the rightand left invariant(fuzzy)equivalences are also known as the forward and backward bisimulation(fuzzy)equivalences(cf.[16,18,19]).In particular,it has been proved in[11–13,35–38]that both the partial derivative automaton and thefollow automaton are factor automata of the position automaton with respect to certain right invariant equivalences.Thestate reduction of fuzzyfinite automata by means of right invariant fuzzy and crisp equivalences will be also consideredin this paper.Let us also note that the above-mentioned determinization problem has been recently investigated in thefuzzy framework in[3,15,32,41,50].Our main results are the following.We start from a given fuzzy regular expression over an alphabet X and alattice-ordered monoid L=(L,∧,∨,⊗,0,1,e),and we define an ordinary regular expression R over a newalphabet X∪Y,where Y consists of the letters associated with different scalars appearing in .The mapping of X∪Y to L,which maps all letters from X to e,and letters from Y to related scalars appearing in ,can be extended in a natural way to a homomorphism ∗ of the free monoid(X∪Y)∗to the monoid(L,⊗,e).In the casewhen L is an integral lattice-ordered monoid,using this homomorphism we establish a relationship between the fuzzylanguage represented by and the language R represented by R(cf.Theorem3.6),and starting from any nondeterministicfinite automaton A that recognizes the language R we define the fuzzy automaton A associated with A and ,and we prove that A recognizes the fuzzy language represented by the fuzzy regular expression (cf.Theorem3.7).However,the aforementioned definition of the fuzzy automaton A is not sufficiently constructive,because thecomputation of the fuzzy transition relation and the fuzzy set of terminal states of A requires the computation ofminimal words in certain infinite languages with respect to the embedding order,which might be a problem.We solvethis problem introducing a reflexive and transitive fuzzy relation R A on the set of states of the starting nondeterministicfinite automaton A,which can be efficiently computed as the n-th power of an easily computable fuzzy relation,wheren is the number of states of A.We express the fuzzy relation R A in terms of the homomorphism ∗ and the transitionrelation of A(cf.Theorem4.3),and then we express the fuzzy transition relation and the fuzzy set of terminal states of A in terms of the fuzzy relation R A,the transition relation of A,and the set of terminal states of A(cf.Theorem4.4). This result provides an efficient construction of the fuzzyfinite automaton A associated with A and the fuzzy regular expression .Using the fuzzy relation R A we also construct a version A r of the fuzzyfinite automaton A which can have evensmaller number of states than the fuzzy automaton A and the automaton A,and recognizes the same fuzzy language (cf.Theorem5.1).We show by an example that the number of states of A r can be strictly smaller than the number of states of A and A .We also discuss the state reduction of the fuzzy automaton A by means of right invariant crisp equivalences,and we show that even if the starting automaton A is a minimal deterministic automaton,the number of states of the fuzzy automaton A could be reduced.Finally,we describe certain properties of fuzzy automata obtained from the position and follow automaton.The structure of the paper is as follows.In Section2we recall some basic definitions and results concerning fuzzysets and relations over lattice ordered monoids,nondeterministic and fuzzy automata,and regular and fuzzy regularexpressions.In Section3we give the basic construction of a fuzzyfinite automaton A associated with a fuzzy regularexpression and a nondeterministicfinite automaton A recognizing the language R .Section4addresses the issue of the efficient construction of the fuzzy automaton A ,and in Section5we deal with the version of this construction that gives a fuzzy automaton with a reduced number of states with respect to the original construction.Finally,in Section6we discuss the problem of the reduction of the number of states of fuzzyfinite automata constructed from fuzzy regular expressions.Finally,note that our main results are proven under the assumption that the underlying -monoid is integral.Thisassumption is crucial in the proof Lemma3.5,and consequently,it is necessary in all the theorems that are based onLemma3.5and Theorem3.6(which also uses Lemma3.5).4 A.Stamenkovi´c ,M.´Ciri´c /Fuzzy Sets and Systems 199(2012)1–272.PreliminariesIn this section we recall some basic definitions and results concerning fuzzy sets and relations over lattice ordered monoids,nondeterministic and fuzzy automata,and regular and fuzzy regular expressions.ttice-ordered monoidsA lattice-ordered monoid or an -monoid [47,48,50,69]is an algebra L =(L ,∧,∨,⊗,0,1,e )such that(L1)(L ,∧,∨,0,1)is a lattice with the least element 0and the greatest element 1,(L2)(L ,⊗,e )is a monoid with the unit e ,(L3)x ⊗0=0⊗x =0,for every x ∈L ,(L4)x ⊗(y ∨z )=x ⊗y ∨x ⊗z ,(x ∨y )⊗z =x ⊗z ∨y ⊗z ,for all x ,y ,z ∈L .The operation ⊗is called the multiplication .In addition,if (L ,∧,∨,0,1)is a complete lattice and satisfies the following infinite distributive laws x ⊗ i ∈I x i = i ∈I (x ⊗x i ), i ∈I x i ⊗x = i ∈I(x i ⊗x ),(1)then L is called a quantale .In the general case,in an -monoid L =(L ,∧,∨,⊗,0,1,e )the greatest element 1of the lattice (L ,∧,∨,0,1)and the unit element e of the monoid (L ,⊗,e )are different.If 1and e coincide,then L is called an integral -monoid .Note that some authors understand the notion of a lattice-ordered monoid as having the multiplication distributive over the meet as well,i.e.,not only over the join,as we have in our definition.These concepts are different because the distributivity over the meet does not follow from the one over the join.It can be easily verified that with respect to ≤,the multiplication ⊗in an -monoid is isotone in both arguments,i.e.,for all x ,y ,z ∈L we havex ≤y implies x ⊗z ≤y ⊗z and z ⊗x ≤z ⊗y .(2)An integral quantale with commutative multiplication is known as a complete residuated lattice (cf.[4,5]).The most studied and applied kinds of complete residuated lattices,with the support [0,1],x ∧y =min(x ,y )and x ∨y =max(x ,y ),are the Lukasiewicz structure ,with the multiplication defined by x ⊗y =max(x +y −1,0),the Goguen or product structure ,with x ⊗y =x ·y ,and the Gödel structure ,with x ⊗y =min(x ,y ).The fourth important type of complete residuated lattices is the two-element Boolean algebra of classical logic with the support {0,1},called the Boolean structure .In the further text,if not noted otherwise,L will be an -monoid.A fuzzy subset of a set A is defined as any mapping from A into L .Ordinary crisp subsets of A are considered as fuzzy subsets of A taking membership values in the set {0,e }⊆L .Let f and g be two fuzzy subsets of A .The equality of f and g is defined as the usual equality of functions,i.e.,f =g if and only if f (x )=g (x ),for every x ∈A .The inclusion f ≤g is also defined pointwise:f ≤g if and only if f (x )≤g (x ),for every x ∈A .Endowed with this partial order the set L A of all fuzzy subsets of A forms a lattice,in which the meet (intersection)f ∧g and the join (union)f ∨g of any fuzzy subsets f ,g of A are also fuzzy subsets of A over L defined by(f ∧g )(x )=f (x )∧g (x ),(f ∨g )(x )=f (x )∨g (x ).(3)for each x ∈L .The crisp part of a fuzzy subset f ∈L A is a crisp subset f ={a ∈A |f (a )=e }of A .We will also consider f as a mapping f :A →L defined by f (a )=e ,if f (a )=e ,and f (a )=0,otherwise.A fuzzy relation on A is any fuzzy subset of A ×A .The equality,inclusion and ordering of fuzzy relations are defined as for fuzzy sets.For fuzzy relations R and S on a set A ,their composition R ◦S is the fuzzy relation on A defined by(R ◦S )(a ,b )=c ∈AR (a ,c )⊗S (c ,b ),(4)A.Stamenkovi´c,M.´Ciri´c/Fuzzy Sets and Systems199(2012)1–275 for all a,b∈A,and for a fuzzy subset f of A and a fuzzy relation R on A,the compositions f◦R and R◦f are fuzzy subsets of A defined,for any a∈A,by(f◦R)(a)=b∈A f(b)⊗R(b,a),(R◦f)(a)=b∈AR(a,b)⊗f(b).(5)For fuzzy subsets f and g we writef◦g=a∈Af(a)⊗g(a).(6) It is well known that the composition of fuzzy relations is associative.Moreover(f◦R)◦S=f◦(R◦S),(R◦S)◦f=R◦(S◦f),(f◦R)◦g=f◦(R◦g),(7) for all fuzzy subsets f and g of A,and fuzzy relations R and S on A.If A is afinite set with n elements,then R and S can be treated as n×n matrices over L,and R◦S is their matrix product,whereas f◦R can be treated as the product of the1×n matrix f and the n×n matrix R,and R◦f as the product of the n×n matrix R and the n×1matrix f t (the transpose of f).For afinite set A and an fuzzy relation R on A,a fuzzy relation R n is defined inductively as follows:R0is the crisp equality on A,and R n+1=R n◦R,for n∈N∪{0}.A fuzzy relation R on A is said to be(R)reflexive if R(a,a)=e,for every a∈A;(S)symmetric if R(a,b)=R(b,a),for all a,b∈A;(T)transitive if for all a,b,c∈A we have R(a,b)⊗R(b,c)≤R(a,c).It is easy to check that a reflexive fuzzy relation R is transitive if and only if R2=R,and then R n=R,for every n∈N.A reflexive,symmetric and transitive fuzzy relation is called a fuzzy equivalence.For a fuzzy equivalence E on A and a∈A we define a fuzzy subset E a of A by E a(x)=E(a,x),for every x∈A.We call E a the equivalence class of E determined by a.The set A/E={E a|a∈A}is called the factor set of A with respect to E(cf.[4,5,17]).We use the same notation for crisp equivalences,i.e.,for an equivalence on A,the related factor set is denoted by A/ ,the equivalence class of an element a∈A is denoted by a.A fuzzy equivalence E on a set A is called a fuzzy equality if for all x,y∈A,E(x,y)=e implies x=y.In other words,E is a fuzzy equality if and only if its crisp part E is a crisp equality.2.2.Fuzzy regular expressionsLet X be a non-empty set,which is called an alphabet and whose elements are called letters,and let X∗be the free monoid over X,i.e.,the set of allfinite sequences of letters from X,including the empty sequence,equipped with the concatenation operation.Elements of X∗are called words,and the empty sequence is denoted by and called the empty word.A fuzzy language in X∗is defined as any fuzzy subset of X∗.A language in X∗is a fuzzy language in X∗taking membership values in the set{0,e}.For a fuzzy language f and a scalar ∈L,the scalar multiplication ⊗f is the fuzzy language in X∗defined by( ⊗f)(u)= ⊗f(u),for any u∈X∗.The union(join)f∨g of fuzzy languages f and g is defined as the union of fuzzy subsets f and g. The concatenation(product)fg of fuzzy languages f and g is defined by(f g)(u)=u=vwf(v)⊗g(w).6 A.Stamenkovi´c ,M.´Ciri´c /Fuzzy Sets and Systems 199(2012)1–27The concatenation of fuzzy languages is an associative operation,and for n ∈N ,the n-th power of a fuzzy language f is defined inductively by f 0=f ,where f is a characteristic function of the empty word ,i.e.,f (u )= e if u = ,0otherwise ,(8)and f n +1=f n f ,for each n ∈N ∪{0}.The Kleene closure of a fuzzy language f ,denoted by f ∗,is defined byf =n ∈N ∪{0}f n .Recall the following result proved in [50].Proposition 2.1.If L is an integral -monoid ,then for any fuzzy language f ,the Kleene closure is well defined .The family LR of fuzzy regular expressions over a finite alphabet X is defined inductively in the following way (cf.[47,50]):(i)∅∈LR ;(ii)∈LR ;(iii)x ∈LR ,for all x ∈X ;(iv)( )∈LR ,for all ∈L and ∈LR (scalar multiplication );(v)( 1+ 2)∈LR ,for all 1, 2∈LR (addition );(vi)( 1 2)∈LR ,for all 1, 2∈LR (concatenation );(vii)( ∗)∈LR ,for all ∈LR (star operation );(viii)There are no other fuzzy regular expressions than those given in steps (i)–(viii).In order to avoid parentheses it is assumed that the star operation has the highest priority,then concatenation and then addition.For any fuzzy regular expression ∈LR ,the fuzzy language determined by is defined inductively as follows (cf.[47,50]):(i) ∅ (u )=0,for every u ∈X ∗;(ii)For ∈X ∪{ }, =f ,where f is the characteristic function of defined byf (u )= e if u = ,0otherwise ;(iii)= ⊗ for all ∈L and ∈LR ;(iv)( 1+ 2) = 1 ∨ 2 ,for all 1, 2∈LR ;(v)( 1 2) = 1 2 ,for all 1, 2∈LR ;(v) ∗ = ∗,for all ∈LR .For a fuzzy regular expression over X ,by | |X we denote the number of occurrences of letters from X in .The length of ,denoted by | |,is the sum | |=| |X +| |L ,where | |L is the number of scalars appearing in .A fuzzy regular expression which does not contain any occurrence of an element of L is called a regular expression over an alphabet X .In other words,regular expressions are fuzzy regular expressions without scalar multiplication.Consequently,the length of a regular expression is equal to | |X .Note also that the fuzzy language defined by a regular expression takes membership values in the set {0,e },and thus,it can be considered as an ordinary subset of X ∗.For the free monoid X ∗we set X +=X ∗\{ }.The length of a word u ∈X ∗,in notation |u |,is the number of appearances of the letters from X in u .The embedding order relation ≤em is defined on X ∗byu ≤em v ⇔u =u 1u 2···u n and v =v 0u 1v 1u 2···v n −1u n v n ,(9)where n ∈N and u ,v,u 1,u 2,...,u n ,v 0,v 1,...,v n ∈X ∗.A.Stamenkovi´c ,M.´Ciri´c /Fuzzy Sets and Systems 199(2012)1–277Proposition 2.2(Haines [29],Higman [30]).For any finite alphabet X ,≤em is a partial order on X ∗.Any set of pairwise incomparable words in the partially ordered set (X ∗,≤em )is finite .Consequently,for any U ⊆X ∗,the set M (U )of all minimal words from U with respect to ≤em is finite.Throughout the paper,the set of all minimal words from U ⊆X ∗with respect to the embedding order ≤em will be denoted by M (U ),as in the previous proposition.2.3.Fuzzy automataLet L be an -monoid.A fuzzy automaton (over L )is defined as a five-tuple A =(A ,X , A , A , A ),where A and X are non-empty sets,called respectively the set of states and the input alphabet , A :A ×X ×A →L is a fuzzy subset of A ×X ×A ,called the fuzzy transition relation , A ∈L A is the fuzzy set of initial states ,and A ∈L A is the fuzzy set of terminal states .We will assume that the input alphabet X is always finite.A fuzzy automaton whose set of states is finite is called a fuzzy finite automaton .Since all fuzzy automata considered in this paper will be finite,we will speak simply fuzzy automaton instead of fuzzy finite automaton.Cardinality of a fuzzy automaton A ,in notation |A |,is defined as the cardinality |A |of its set of states A .The fuzzy transition relation A can be extended up to a mapping A ∗:A ×X ∗×A →L in the following way:If a ,b ∈A and ∈X ∗is the empty word,then A ∗(a , ,b )= e if a =b ,0otherwise ,(10)and if a ,b ∈A ,u ∈X ∗and x ∈X ,then A ∗(a ,ux ,b )= c ∈AA ∗(a ,u ,c )⊗ A (c ,x ,b ).(11)Without danger of confusion we shall write just A instead of A ∗.By (L4)and Theorem 3.1in [50]we have that A (a ,u v,b )=c ∈A A (a ,u ,c )⊗ A (c ,v,b ),(12)for all a ,b ∈A and u ,v ∈X ∗.For any u ∈X ∗we define a fuzzy relation A u ∈L A ×A ,called the fuzzy transition relation determined by u ,by A u (a ,b )= A (a ,u ,b ),for all a ,b ∈A .Then for all u ,v ∈X ∗,the equality (12)can be written as A u v = A u ◦ A v .The fuzzy language recognized by a fuzzy automaton A =(A ,X , A , A , A ),denoted by L (A ),is the fuzzy language in X ∗defined by L (A )(u )=a ,b ∈AA (a )⊗ A (a ,u ,b )⊗ A (b ),(13)or equivalently,L (A )(u )= A ◦ A u ◦ A = A ◦ A x 1◦ A x 2◦···◦ A x n ◦ A ,(14)for any u =x 1x 2...x n ∈X ∗with x 1,x 2,...,x n ∈X .In particular,if A =(A ,X , A ,a 0, A )is a fuzzy automaton having a single crisp initial state a 0,then the fuzzy language L (A )recognized by A is given by L (A )(u )=a ∈AA (a 0,u ,a )⊗ A (a ),(15)or equivalently,L (A )(u )=( A u ◦ A )(a 0)=( A x 1◦ A x 2◦···◦ A x n ◦ A )(a 0),(16)for any u =x 1x 2...x n ∈X ∗with x 1,x 2,...,x n ∈X .8 A.Stamenkovi´c,M.´Ciri´c/Fuzzy Sets and Systems199(2012)1–27In the further text,ordinary nondeterministic automata will be considered as fuzzy ly,by a nonde-terministic automaton we mean a fuzzy automaton A=(A,X, A, A, A)such that A x is a fuzzy relation taking values in the set{0,e},for each x∈X,and A and A are fuzzy sets also taking values in{0,e}.In this case,the fuzzy language recognized by A is a crisp language,and it is exactly the language recognized by a nondeterministic automaton in the sense of the well-known definition from the classical theory of nondeterministic automata.Let A=(A,X, A, A, A)be a fuzzy automaton and let E be a fuzzy equivalence on A.Without any restriction on the fuzzy equivalence E,we define a fuzzy transition relation A/E:A/E×X×A/E→L by A/E(E a,x,E b)=a ,b ∈AE(a,a )⊗ (a ,x,b )⊗E(b ,b)=(E◦ x◦E)(a,b)=E a◦ x◦E b,(17) and fuzzy sets A/E∈L A/E and E∈L A/E of initial and terminal states byA/E(E a)=a ∈AA(a )⊗E(a ,a)=( A◦E)(a)= A◦E a,(18)A/E(E a)=a ∈AA(a )⊗E(a ,a)=( A◦E)(a)= A◦E a,(19)for any a∈A.Evidently, A/E, A/E and A/E are well-defined,and A/E=(A/E,X, A/E, A/E, A/E)is a fuzzy automaton,called the factor fuzzy automaton of A with respect to E.2.4.Position automataIn this section we recall the construction of the position automaton from a regular expression[27,55].Let be a regular expression over an alphabet X.Denote by the expression obtained from by marking each letter in with its position.For example,if =x+xy∗,then =x1+x2y∗3.The same notation will be used for removing indices,that is,for a regular expression we put = .We define the following sets:(i)pos0( )={0,1,...,| |X},(ii)f irst( )={i|x i u∈ },(iii)last( )={i|ux i∈ },(iv)f ollo w( ,i)={j|ux i x j v∈ },i>0,(v)f ollo w( ,0)=f irst( ),(vi)last0( )=last( ), /∈ , last( )∪{0}, ∈ .Define pos⊆pos0( )×X×pos0( )by(i,x,j)∈ pos⇔x j=x and j∈f ollo w( ,i).Then A pos( )=(pos0( ),X, pos,0,last0( ))is a nondeterministic automaton called the position automaton of . It was shown by Glushkov[27]and McNaughton and Yamada[55]that L(A pos( ))= .For the sake of simplicity,instead of A pos( )=(pos0( ),X, pos,0,last0( )),in the further text we will write A p( )=(A p,X, A p,0, A p).Let us illustrate the construction of the position automaton by the following simple example.Consider again the regular expression =x+xy∗.The marked version of this expression is =x1+x2y∗3. Next,we have the following:(i)A p=pos0( )={0,1,2,3}is the set of states of A p( ),(ii)f irst( )=f ollo w( ,0)={1,2},(iii)last( )=last0( )={1,2,3},(iv)f ollo w( ,1)=∅,f ollo w( ,2)=f ollo w( ,3)={3}.The transition set pos in this example is pos={(0,x,1),(0,x,2),(2,y,3),(3,y,3)}.。
On interval fuzzy S-implications

On interval fuzzy S-implicationsB.C.Bedregal a,*,G.P.Dimuro b ,R.H.N.Santiago a ,R.H.S.Reiser ca Universidade Federal do Rio Grande do Norte,Departamento de Informática e Matemática Aplicada,Campus Universitário,59072-970Natal,BrazilbUniversidade Federal do Rio Grande,Programa de Pós-Graduação em Modelagem Computacional,Campus Carreiros,96201-090Rio Grande,Brazilc Universidade Católica de Pelotas,Programa de Pós-Graduação em Informática,Rua Felix da Cunha 412,96010-000Pelotas,Brazil a r t i c l e i n f o Article history:Received 6March 2008Received in revised form 21August 2009Accepted 21November 2009Keywords:Fuzzy logic Interval mathematicsInterval representationInterval fuzzy implicationInterval S-implicationInterval automorphisma b s t r a c tThis paper presents an analysis of interval-valued S-implications and interval-valued auto-morphisms,showing a way to obtain an interval-valued S-implication from two S-implica-tions,such that the resulting interval-valued S-implication is said to be obtainable .Someconsequences of that are:(1)the resulting interval-valued S-implication satisfies the cor-rectness property,and (2)some important properties of usual S-implications are preservedby such interval representations.A relation between S-implications and interval-valued S-implications is outlined,showing that the action of an interval-valued automorphism on aninterval-valued S-implication produces another interval-valued S-implication.Ó2009Elsevier Inc.All rights reserved.1.IntroductionFuzzy set theory was introduced by Zadeh [76],allowing the development of soft computing techniques centered on the idea that computation,reasoning and decision making should exploit,whenever possible,the tolerance for imprecision and uncertainty [78].Like classical set theory,the corresponding fuzzy logic has been developed as formal deductive systems,but with a com-parative notion of truth that formalizes deduction under vagueness.It provides tools for approximate reasoning and decision making together with a framework to deal with imprecision,uncertainty,incompleteness of information,conflicting infor-mation,partiality of truth and partiality of possibility [79],improving the design of flexible information processing systems[51].It has been applied in several areas,such as control systems [18],decision making [17],expert systems [67],pattern recognition [19,50],etc.On the other hand,fuzzy logic may be viewed as an attempt to formalize/mechanize the human capability to perform a wide variety of physical and mental tasks without any measurements or computations [79].Fuzzy sets were originally defined by membership functions of the form l A :X !½0;1 ,where any membership degree l A ðx Þwas a precise number.However,in some situations,we do not have precise knowledge about the membership function (or the membership degree)that should be taken into account.This consideration has led to some extensions of fuzzy sets,giving rise to type-n fuzzy sets [77],which incorporated uncertainty about membership functions and membership degrees into fuzzy set theory,where the ‘‘precise number”representing a membership degree was generalized to a value carrying its uncertainty.0020-0255/$-see front matter Ó2009Elsevier Inc.All rights reserved.doi:10.1016/j.ins.2009.11.035*Corresponding author.Tel.:+558432153814;fax:+558432153813.E-mail addresses:bedregal@dimap.ufrn.br (B.C.Bedregal),gracaliz@ (G.P.Dimuro),regivan@dimap.ufrn.br (R.H.N.Santiago),reiser@ucpel.tche.br (R.H.S.Reiser).Information Sciences 180(2010)1373–1389Contents lists available at ScienceDirectInformation Sciencesj o u r n a l ho m e p a g e :w w w.e l s e vier.c om/loc ate/ins1374 B.C.Bedregal et al./Information Sciences180(2010)1373–1389Type-2fuzzy sets have been largely applied since the works of Jerry Mendel[48]in the90s,with the increase of the the-oretical research on their properties[49,71].Interval-valued fuzzy sets are a particular case of type-2fuzzy sets with a rich structure provided by Interval Mathematics[52].Interval Mathematics is a mathematical theory that aims at the representation of uncertain input data and parameters, originally interested in the automatic and rigorous control of the errors that arise in numerical computations[37].It has been applied to deal with the uncertainties in the results of numerical algorithms in Engineering and Scientific Computing,with contributions1/interval-comp/.in several areas[40,41],such as electrical power systems[8],mechan-ical engineering[54],chemical engineering[68],artificial intelligence[38],multiagent systems[26]and geophysics[2].Interval mathematics is another form of information theory which is related to,but independent from,fuzzy logic.In one hand,intervals can be considered to be a particular type of fuzzy set.On the other hand,interval membership degrees can be used to represent the uncertainty and the difficulty of an expert to precisely determine the fairest membership degree of an element with respect to a linguistic term,as considered in interval-valued fuzzy sets.In this case,the radius of an interval is used as an error measure[57],providing an estimation of the uncertainty during membership assignment.Interval degrees can also be viewed as summarizing the opinions of several experts about the exact membership degree for an element with respect to a linguistic term.In this case,the left and right interval endpoints are,respectively,the least and the greatest de-grees provided by a group of experts[29,57,70].In both cases,the richness of interval structures provides tools to deal with such notions of uncertainty.Interval-valued fuzzy sets were introduced independently by Zadeh[77]and other authors in the70s(e.g.,[36,39,63]), allowing to deal not only with vagueness(lack of sharp class boundaries),but also with uncertainty(lack of information) [29,45].Since then,the integration of fuzzy theory with interval mathematics has been studied from different viewpoints, as properly pointed out by Lodwick[45],generating several different approaches(as in[21,27–29,33,44,45,53,56,57,71,75]).In this paper,we follow the approachfirst introduced in Bedregal and Takahashi’s works[12,13],which has already been applied in our previous papers,where we provided interval extensions for some fuzzy connectives(see[9,15,25,59])by con-sidering both correctness(accuracy)and optimality aspects of interval methods[37,64].In particular,we are interested in the investigations of interval extensions of the various types of fuzzy implications and their related properties.Fuzzy implications[4–7,11,31,46,47,58,61,62,66,65,74]play an important role in fuzzy logic.In a broad sense,fuzzy implications are important not only because they are used to formalize‘‘If...then”rules in fuzzy systems,but also because they have different meanings(e.g.,S-implications,R-implications,QL-implications,D-implications etc.)to be used in per-forming inferences in approximate reasoning and fuzzy control[46].The role of fuzzy implications on the development of applications also motivates the research in the narrow sense through the investigation of related logical aspects[47].The aim of this work is to introduce an interval generalization for a particular meaning of fuzzy implications,namely,S-implications[5,6,16,47,61,30,31].This generalization,which we call interval S-implication,satisfies the correctness property mentioned above.We present an analysis of interval S-implications and interval automorphisms,showing a way to obtain an interval S-implication from two S-implications,so that the resulting interval S-implication is said to be obtainable.We prove that interval S-implications are closed under the action of the interval-valued automorphisms introduced in[33,34].We also prove that several analogous important properties of S-implications are also valid for interval S-implications,showing their applicability on interval-based fuzzy systems.Thus,this work is an important step towards the fundamentals for the devel-opment of such interval-based fuzzy systems.The paper is organized as follows:Section2discusses the notions of interval representations of real functions providing the related definitions and results.The main results related to the interval extensions of fuzzy t-conorms introduced in pre-vious works[12–14]are presented in Section3.In Section4,we discuss the interval extensions of fuzzy negations.A brief review about fuzzy implications,and,in particular,S-implications,is presented in Section5,where the main properties of S-implications are presented.Section6introduces interval fuzzy implications and the definition of interval S-implications, showing that several analogous properties of S-implications also hold for interval S-implications.The action of an interval automorphism on an interval S-implication is analyzed in Section7.Section8concludes this paper,summarizing its main results,presenting somefinal remarks and pointing out future works.2.Interval representationsConsider the real unit interval U¼½0;1 #R and the set U¼f½a;b j06a6b61g of subintervals of U.The left and right projections of an interval½a;b 2U are given by the functions l;r:U!U,defined,respectively,bylð½a;b Þ¼a and rð½a;b Þ¼b:ð1ÞFor a given interval X2U;lðXÞand rðXÞare also denoted,respectively,by X and X.The following partial orders play important roles in this paper:(i)The product order(also called component-wise order or Kulisch-Miranker order),defined,for all X;Y2U,by:X6Y()X6Y^X6Y;ð2Þ1For a survey on applications of Interval Mathematics,see,e.g.,/interval-comp/.(ii)The inclusion order,defined,for all X ;Y 2U ,by:X #Y ()X P Y ^X 6Y :ð3ÞThese partial orders can be naturally extended to U n .For example,considering the product order defined in Eq.(2),forany ~X ¼ðX 1;...;X n Þ;~Y ¼ðY 1;...;Y n Þ2U n ,one has that ~X 6~Y ()X 16Y 1^ÁÁÁ^X n 6Y n :ð4ÞAn interval function F :U n !U is said to be strictly increasing if,for each ~X ;~Y 2U n ,whenever ~X <~Y (that is,~X 6~Y and ~X –~Y )it holds that F ð~X Þ<F ð~Y Þ.The notion of interval correctness plays a very important role in numerical computations [64].A correct interval method can always guarantee that if x 2X then f ðx Þ2F ðX Þ,where F is the interval method that evaluates a real function f .In [64],the notion of correctness is formalized by the so-called Interval Representation ,considering that interval methods are represen-tations of punctual methods.In what follows,we reproduce such definition,but,instead of considering the set of real num-bers R ,we consider the set U ¼½0;1 #R .Definition 1[64].An interval X 2U is said to be a representation for a real number a if a 2X .Considering two interval representations X and Y for a real number a ;X is said to be a better interval representation of a than Y ,denoted by Y v X ,if X #Y .The notion of better interval representation can also be easily extended for n -tuples of intervals.Definition 2[64].A function F :U n !U is said to be an interval representation of a real function f :U n !U if,for each ~X 2U n and ~x 2~X ;f ð~x Þ2F ð~X Þ.F is also said to be correct with respect to f .An interval function F :U n !U is said to be a better interval representation of a real function f :U n !U than an intervalfunction G :U n !U ,denoted by G v F ,if F ð~X Þ#G ð~X Þ,for each ~X 2U n [64].In [64],the notion of optimality of interval methods was formalized by the so-called canonical interval representations of real functions,also known by the best interval representations [12]of real functions:Definition 3[64].The best interval representation of a real function f :U n !U is the interval function b f :U n !U ,defined byb f ð~X Þ¼½inf f f ð~x Þj ~x 2~X g ;sup f f ð~x Þj ~x 2~X g :ð5ÞNotice that the interval function b f is well defined and it is clearly an interval representation of f .Moreover,for any other interval representation F of f ,F v b f .This means that b f always returns a narrower interval than the intervals produced by any other interval representation of f .Thus,b f has the optimality property of interval algorithms mentioned by Hickey et al.[37],when it is seen as an algorithm to compute a real function f .Observe that if the real function f is continuous in the usual sense then,for each ~X 2U n ,one has thatb f ð~X Þ¼f f ð~x Þj ~x 2~X g ¼f ð~X Þ;ð6Þthat is,the best interval representation b f of a real function f coincides with its range [64].Definition 4.An interval function F :U n !U is obtainable if there exist projections P 1;...;P 2n :U !U ,where P i 2f l ;r g ,for i ¼1;...;2n ,and functions f 1;f 2:U n !U such that,for each X 1;...;X n 2U ,it holds thatF ðX 1;...;X n Þ¼½f 1ðP 1ðX 1Þ;...;P n ðX n ÞÞ;f 2ðP n þ1ðX 1Þ;...;P 2n ðX n ÞÞ :ð7ÞThe concept of obtainable function generalizes the notion of representable function,as proposed by Deschrijver et al.[22–24,32]in the context of interval t-norms.On the other hand,observe that every obtainable interval function F is an interval representation of some real function f (at least f 1and f 2).However,the converse is not true.For example,the interval functionF :U n !U ,defined by F ðX Þ¼½max ð0;X ÀX Þ;min ð1;X þX 10Þ ,is an interval representation of the identity on U ,id U ðx Þ¼x ,but F is not obtainable.An interval function F :U n !U preserves degenerate intervals ,if it maps degenerate intervals into degenerate intervals,that is,if,for each x 1;...;x n 2U ,there exists y 2U such that F ð½x 1;x 1 ;...;½x n ;x n Þ¼½y ;y .Notice that the best interval representation of any real function is #-monotonic (inclusion-monotonic),obtainable and preserves degenerate intervals.In this paper,we adopt the following notions of continuity defined on the set U of subintervals of ½0;1 :(i)Moore continuity [52]:is defined as an extension of the continuity on the set of the real numbers by considering themetric given by the distance between two intervals X ;Y 2U ,which is defined by:d ðX ;Y Þ¼max fj X ÀY j ;j X ÀY jg .(ii)Scott continuity:is defined as an extension of the continuity on the set of the real numbers,considering the quasi-met-ric q ðX ;Y Þ¼max f Y ÀX ;X ÀY ;0g defined over U ,introduced in [1,64].An alternative way to define the Scott continu-ity on U is to consider the set U with the reverse inclusion order as a continuous domain [35],and a function B.C.Bedregal et al./Information Sciences 180(2010)1373–138913751376 B.C.Bedregal et al./Information Sciences180(2010)1373–1389f:ðU; Þ!ðU; Þis said to be Scott-continuous if it is monotonic and preserves the least upper bound of directed sets[35].2The main result in[64]can be adapted to our context,considering the set U instead of R,as shown in the following: Theorem5.Let f:U n!U be a real function.The following statements are equivalent:(i)f is continuous;(ii)b f is Scott-continuous;(iii)b f is Moore-continuous.3.Interval t-conormsA triangular conorm(t-conorm for short)is a function S:U2!U that is commutative,associative,monotonic and has an identity‘‘0”,generalizing the classical disjunction.Among several t-conorms,in this paper,we consider the maximum t-con-orm S M:U!U,defined asS Mðx;yÞ¼max f x;y g:ð8ÞAn interval generalization of t-conorms was introduced in[13],applying the principles discussed in Section2.The so-called interval t-conorm is defined as an interval representation of a t-conorm.This generalizationfits the idea of interval member-ship degrees as approximations of exact degrees.Definition6[13].A function S:U2!U is an interval t-conorm,whenever it is commutative,associative,monotonic with respect to the product and inclusion orders,and½0;0 is the identity element.In the following,the main results related to interval t-conorms are presented.Proposition7[13,Theorems5.1and5.2].If S is a t-conorm,then its best interval representation b S:U2!U is an interval t-conorm.For example,the supremum interval t-conorm S M:U2!U,defined byS MðX;YÞ¼sup f X;Y g;ð9Þis the best interval representation of the maximum t-conorm S Mðx;yÞ,given in Eq.(8),that is,S M¼c S M.3Proposition8[14,Corollary 5.3].The function S:U2!U is an interval t-conorm if,and only if,the real functions S;S:U2!U,defined bySðx;yÞ¼lðSð½x;x ;½y;y ÞÞand Sðx;yÞ¼rðSð½x;x ;½y;y ÞÞ;ð10Þare t-conorms andSðX;YÞ¼½SðX;YÞ;ð;;ð11Þwhere l and r are,respectively,the left and right projections defined in Eq.(1).Therefore,one has that interval t-conorms are obtainable.The following result is immediate:Corollary9.Let S:U2!U be an interval t-conorm and S:U2!U be a t-conorm.If S represents S then S6S6S. Given a t-conorm S,the interval t-conorm b S can be expressed by:b SðX;YÞ¼½SðX;YÞ;SðX;YÞ :ð12Þ4.Interval fuzzy negationsLike t-conorms,fuzzy negations generalize the classical negations.A function N:U!U is a fuzzy negation ifN1:Nð0Þ¼1and Nð1Þ¼0;N2:If x P y then NðxÞ6NðyÞ;8x;y2U.Fuzzy negations satisfying the involutive property N3are called strong fuzzy nega-tions[16,43]:N3:NðNðxÞÞ¼x;8x2U.In addition,a continuous fuzzy negation is strict whenN4:If x>y then NðxÞ<NðyÞ;8x;y2U.2A directed set ofðU; Þis a non-empty subset S#U such that every pair of intervals in S has an upper bound in S.3sup denotes the supremum related to the Kulisch-Miranker or product order.B.C.Bedregal et al./Information Sciences180(2010)1373–13891377As is well known,all strong fuzzy negations are strict.An element e2U is said to be an equilibrium point of a fuzzy negation N whenever NðeÞ¼e.If N is a strict fuzzy negation, then there exists a unique equilibrium point e N2U and it holds that NðxÞP e N,for all x6e N.Conversely,one has that NðxÞ6e N,for all x P e N.Definition10.An interval function N:U!U is an interval fuzzy negation if,for all X;Y in U,the following properties hold: N1:Nð½0;0 Þ¼½1;1 and Nð½1;1 Þ¼½0;0 ;N2a If X P Y then NðXÞ6NðYÞ;N2b If X#Y then NðXÞ#NðYÞ.If N also satisfies the involutive property N3,then it is said to be a strong interval fuzzy negation:N3:NðNðXÞÞ¼X;8X2U.A Moore and Scott-continuous interval fuzzy negation N is strict if it also satisfies the following properties:N4a If X<Y then NðYÞ<NðXÞ;N4b If X&Y then NðXÞ&NðYÞ.The concepts of interval representation and obtainability show their strength on the context of fuzzy negations in the fol-lowing results.We show that those concepts guarantee that punctual properties are preserved by the interval generalization of fuzzy negations.Let N:U!U be a fuzzy negation.The interval function b N can be expressed as:b NðXÞ¼½NðXÞ;NðXÞ :ð13ÞThe proofs of the next propositions in this section can be found in[10].Proposition11.A function N:U!U is a(strict)interval fuzzy negation if,and only if,the functions N;N:U!U,defined, respectively,byNðxÞ¼lðNð½x;x ÞÞand NðxÞ¼rðNð½x;x ÞÞ;ð14Þare(strict)fuzzy negations andNðXÞ¼½NðXÞ;NðXÞ ;ð15Þwhere l and r are,respectively,the left and right projections defined in Eq.(1).Remark12.If N¼N,then NðXÞ¼b NðXÞ¼b NðXÞ.Therefore,one has that(strict)interval fuzzy negations are obtainable.Proposition13.A function N:U!U is a strong interval fuzzy negation if,and only if,there exists a strong fuzzy negation N such that N¼b N.From Eq.(13)and Remark12,if the conditions of Proposition13hold,then it follows that N¼N¼N.From Propositions11and13,it is immediate that:Corollary14.Let N:U!U be a fuzzy negation.Then b N is an interval fuzzy negation.In addition,if N is a strong(strict)fuzzy negation then b N is a strong(strict)interval fuzzy negation.An interval E2U is an equilibrium point of an interval fuzzy negation N if NðEÞ¼E.Trivially,½0;1 is an equilibrium point of any interval fuzzy negation.Thus,if an equilibrium interval E is such that E–½0;1 then E is said to be a non-trivial equi-librium point.Proposition15.If N is a strong interval fuzzy negation,then N has a degenerate equilibrium.Moreover,it is the unique non-trivial equilibrium point.5.Fuzzy implications and S-implicationsSeveral definitions for fuzzy implications together with related properties have been given(see, e.g.,[4–7,16,30,31,46,47,58,61,60,62,66,65,72–74]).However,there is just one consensus on what a fuzzy implication should be, namely:‘‘a fuzzy implication should present the behavior of the classical implication when the crisp case is considered”[47].In other words,a function I:U2!U is a fuzzy implication whenever it satisfies the minimal boundary conditions:Ið1;1Þ¼Ið0;1Þ¼Ið0;0Þ¼1and Ið1;0Þ¼0:ð16ÞSeveral reasonable properties may be required for fuzzy implications,among them we consider the following: I1:If x6z then Iðx;yÞP Iðz;yÞ(first place antitonicity);I2:If y6z then Iðx;yÞ6Iðx;zÞ(second place isotonicity);I3:Ið1;xÞ¼x(left neutrality principle);I4:Iðx;Iðy;zÞÞ¼Iðy;Iðx;zÞÞ(exchange principle);I5:Iðx;yÞ¼Iðx;Iðx;yÞÞ(iterative boolean-like law);I6:Iðx;NðxÞÞ¼NðxÞ,where N is a strong fuzzy negation;I7:NðxÞ¼Iðx;0Þis a strong fuzzy negation;I8:Iðx;1Þ¼1(dominance of truth of consequent);I9:Iðx;yÞP y;I10:Iðx;yÞ¼IðNðyÞ;NðxÞÞ,where N is a strong fuzzy negation(contra-positive);I11:Ið0;xÞ¼1(dominance falsity).Some relations between classical implications and negations can be recovered for the fuzzy case.For example,if I:U2!U is a fuzzy implication satisfying the Property I1,then there is a fuzzy negation N I:U!U that can be defined by[6,Lemma2.1]:N IðxÞ¼Iðx;0Þ:ð17ÞAnother relation between negation and implication follows the opposite direction,showing that it is possible to define a fuz-zy implication from a fuzzy negation.Let S be a t-conorm and N be a fuzzy negation.An S-implication[5,6,16,30,31,47,61]is a fuzzy implication I S;N:U2!U defined byI S;Nðx;yÞ¼SðNðxÞ;yÞ:ð18ÞIn some texts(e.g.,[16,30,31]),the definition of an S-implication requires a strong fuzzy negation.Such S-implications are called here strong S-implications.Similar definitions can be introduced for continuous S-implications and strict S-implications.Trillas and Valverde[69,Theorem3.2](see also[30,Theorem1.13]and[6,Theorem1.6])provided the following char-acterization for strong S-implications:a function I:U2!U is a strong S-implication if,and only if,it satisfies the Properties I1–I4,and tely,Baczynsky and Jayaram[6,Theorem2.6])introduced a new characterization of strong S-implications, considering properties I1,I4and I7.Strong S-implications also satisfy the properties I8–I11and the following two extra properties below:I12:Iðx;yÞP N IðxÞ;I13:Iðx;yÞ¼0if,and only if,x¼1and y¼0.Notice that any S-implication I S;N satisfies the properties I1–I3,I8,I9,and I11.If a fuzzy implication I is an S-implication then N I,as given in Eq.(17),is the underlying negation of I,that is: N IS;NðxÞ¼I S;Nðx;0Þ¼SðNðxÞ;0Þ¼NðxÞ:ð19ÞTherefore,N I is a strict fuzzy negation if,and only if,I is a strict S-implication.Baczynsky and Jayaram[6,Theorem5.2]provided a characterization for strict S-implications,where an S-implication I S;N is strict if and only if N IS;Nis strict and the properties I1and I10also hold.If a fuzzy implication I:U2!U is a strong S-implication,then I satisfies I6if,and only if,the underlying t-conorm of I isthe maximum t-conorm S M,given in Eq.(8),and,therefore,one has I¼I SM;N ,where N is a strong fuzzy negation.The strong S-implication I SM ;Nalso satisfies the properties I1–I11.Moreover,it is the only S-implication satisfying I6.Given an equilibriumpoint e N,if x2U and x P e N then one has that I SM;Nðx;xÞ¼x.6.Interval fuzzy implicationsSince real numbers may be identified with degenerate intervals in the context of interval mathematics,the boundary con-ditions that must be satisfied by the classical fuzzy implications can be naturally extended to interval fuzzy degrees,when-ever degenerate intervals are considered.Then,a function I:U2!U is said to be an interval fuzzy implication if the following interval-based boundary conditions hold:(i)Ið½1;1 ;½1;1 Þ¼Ið½0;0 ;½0;0 Þ¼Ið½0;0 ;½1;1 Þ¼½1;1 ;(ii)Ið½1;1 ;½0;0 Þ¼½0;0 .The properties presented in Section5can then also be naturally extended to an interval-based approach:I1:If X6Z then IðX;YÞP IðZ;YÞ(first place antitonicity);I2:If Y6Z then IðX;YÞ6IðX;ZÞ(second place isotonicity);1378 B.C.Bedregal et al./Information Sciences180(2010)1373–1389I 3:I ð½1;1 ;X Þ¼X (left neutrality principle);I 4:I ðX ;I ðY ;Z ÞÞ¼I ðY ;I ðX ;Z ÞÞ(exchange principle);I 5:I ðX ;Y Þ¼I ðX ;I ðX ;Y ÞÞ(iterative boolean-like law);I 6:N ðX Þ¼I ðX ;N ðX ÞÞ,where N is a strong interval fuzzy negation;I 7:N ðX Þ¼I ðX ;½0;0 Þis a strong interval fuzzy negation;I 8:I ðX ;½1;1 Þ¼½1;1 (dominance of truth of consequent);I 9:I ðX ;Y ÞP Y ;I 10:I ðX ;Y Þ¼I ðN ðY Þ;N ðX ÞÞ,where N is a strong interval fuzzy negation (contra-positive);I 11:I ð½0;0 ;X Þ¼½1;1 (dominance falsity).It is always possible to canonically obtain an interval fuzzy implication from any fuzzy implication.The interval fuzzy implication satisfies the optimality property and preserves the properties satisfied by the corresponding fuzzy implication.Proposition 16.If I is a fuzzy implication then b I is an interval fuzzy implication.Proof.It is straightforward.hIn the next results,we adopt a canonical way to construct,under some conditions,interval fuzzy implication from fuzzy implication and vice-versa.The properties of fuzzy implications presented in Section 5are related with the respective prop-erties of interval fuzzy implications enrolled above.Theorem 17.Let I 1and I 2be fuzzy implications satisfying the Properties I1and I2and such that I 16I 2.If I 1and I 2satisfy a Property Ik ,for k ¼1;...;6;8;...;11,then I :U 2!U ,defined byI ðX ;Y Þ¼½I 1ðX ;Y Þ;I 2ðX ;Y Þ ;ð20Þsatisfies the Property I k .Proof.Since I 16I 2and by the Properties I1and I2,one has that I 1ð;Y Þ6I 1ðX ;Y Þ6I 2ðX ;Y Þ6I 2ðX ;,and,therefore,I is well defined.It follows that:I 1:Let X ;Y ;Z 2U such that X 6Z .Since X 6Z ;X 6Z ,and I 1and I 2satisfy Property I1,then it holds that I 1ðZ ;Y Þ6I 1ðX ;Y Þand I 2ðZ ;6I 2ðX ;Þ.So,by Eq.(20),it follows that I ðZ ;Y Þ6I ðX ;Y Þ.I 2:Let X ;Y ;Z 2U such that Y 6Z .Since Y 6Z ;Y 6Z ,and I 1and I 2satisfy Property I2,then it holds that I 1ðX ;Y Þ6I 1ðX ;Z Þand I 2ðX ;Y Þ6I 2ðX ;Z Þ.Then,by Eq.(20),it follows that I ðX ;Y Þ6I ðX ;Z Þ.I 3:It holds that I ð½1;1 ;X Þ¼½I 1ð1;X Þ;I 2ð1;¼½X ; ¼X .I 4:By Property I4,it follows that:I ðX ;I ðY ;Z ÞÞ¼I ðX ;½I 1ð;Z Þ;I 2ðY ;Þ Þ¼½I 1ðI 1ðZ ÞÞ;I 2ðX ;I 2ðY ;¼½I 1ð;I 1ð;Z ÞÞ;I 2ðY ;I 2ðX ;ÞÞ ¼I ðY ;I ðX ;Z ÞÞ:I 5:By Property I5,it follows that:I ðX ;Y Þ¼½I 1ðX ;Y Þ;I 2ðX ;Y Þ ¼½I 1ðX ;I 1ðX ;Y ÞÞ;I 2ðX ;I 2ðX ;Y ÞÞ ¼I ðX ;½I 1ðX ;Y Þ;I 2ðX ;Y Þ Þ¼I ðX ;I ðX ;Y ÞÞ:I 6:Let N be a strong interval fuzzy negation.By Proposition 13,there exists a strong fuzzy negation N such thatN ðX Þ¼½N ðX Þ;N ðX Þ .It follows that:I ðX ;N ðX ÞÞ¼I ðX ;½N ð;N ðX Þ Þ¼½I 1ðN ðÞÞ;I 2ðX ;N ðX ÞÞ ¼½N ð;N ðX Þ ðby Property I6Þ¼N ðX Þ:I 8:One has that I ðX ;½1;1 Þ¼½I 1ðX ;1Þ;I 2ðX ;1Þ ¼½1;1 .I 9:By Property I9,it holds that I 1ðX ;Y ÞP Y and I 2ðX ;Y ÞP Y .Then,it follows that I ðX ;Y Þ¼½I 1ðX ;Y Þ;I 2ðX ;Y Þ P Y .I 10:Let N be a strong interval fuzzy negation.By Proposition 13,there exists a strong fuzzy negation N such thatN ðX Þ¼½N ðX Þ;N ðX Þ .So,by Property I10,it follows that:I ðX ;Y Þ¼½I 1ðY Þ;I 2ðX ;Þ ¼½I 1ðN ðY Þ;N ðÞÞ;I 2ðN ð;N ðX ÞÞ ¼I ð½N ð;N ðY Þ ;½N ðÞ;N ðX Þ Þ¼I ðN ðY Þ;N ðX ÞÞ:I 11:One has that I ð½0;0 ;X Þ¼½I 1ð0;X Þ;I 2ð0;Þ ¼½1;1 .hRemark 18.According to the conditions stated by Theorem 17,the Property I 7does not hold even if both I 1and I 2satisfy the Property I7.For example,considering I 1ðx ;y Þ¼min f 1Àx þy ;1g and I 2ðx ;y Þ¼min f ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi1Àx 2þy p ;1g ,it is immediate that I 1and I 2are fuzzy implications,as they satisfy Eq.(16),and it holds that I 16I 2.Moreover,considering N I 1ðx Þ¼I 1ðx ;0Þ¼1Àx and N I 2ðx Þ¼I 2ðx ;0Þ¼ffiffiffiffiffiffiffiffiffiffiffiffiffiffi1Àx 2p ,it is immediate that N I 1is a strong fuzzy negation,and,sinceB.C.Bedregal et al./Information Sciences 180(2010)1373–13891379。
Fuzzy Identity-Based Encryption

Fuzzy Identity-Based EncryptionAmit Sahai1, and Brent Waters21University of California,Los Angelessahai@2Stanford Universitybwaters@Abstract.We introduce a new type of Identity-Based Encryption(IBE)scheme that we call Fuzzy Identity-Based Encryption.In Fuzzy IBE weview an identity as set of descriptive attributes.A Fuzzy IBE schemeallows for a private key for an identity,ω,to decrypt a ciphertext en-crypted with an identity,ω ,if and only if the identitiesωandω areclose to each other as measured by the“set overlap”distance metric.AFuzzy IBE scheme can be applied to enable encryption using biometricinputs as identities;the error-tolerance property of a Fuzzy IBE schemeis precisely what allows for the use of biometric identities,which inher-ently will have some noise each time they are sampled.Additionally,weshow that Fuzzy-IBE can be used for a type of application that we term“attribute-based encryption”.In this paper we present two constructions of Fuzzy IBE schemes.Our constructions can be viewed as an Identity-Based Encryption of amessage under several attributes that compose a(fuzzy)identity.OurIBE schemes are both error-tolerant and secure against collusion attacks.Additionally,our basic construction does not use random oracles.Weprove the security of our schemes under the Selective-ID security model.1IntroductionIdentity-Based Encryption[15](IBE)allows for a sender to encrypt a message to an identity without access to a public key certificate.The ability to do public key encryption without certificates has many practical applications.For example, a user can send an encrypted mail to a recipient,e.g.bobsmith@, without the requiring either the existence of a Public-Key Infrastructure or that the recipient be on-line at the time of creation.One common feature of all previous Identity-Based Encryption systems is that they view identities as a string of characters.In this paper we propose a new type of Identity-Based Encryption that we call Fuzzy Identity-Based Encryption in which we view identities as a set of descriptive attributes.In a Fuzzy Identity-Based Encryption scheme,a user with the secret key for the identityωis ableAmit Sahai’s research was supported by generous grant s from the NSF ITR program, as well as a Sloan Foundation Fellowship.R.Cramer(Ed.):EUROCRYPT2005,LNCS3494,pp.457–473,2005.c International Association for Cryptologic Research2005458 A.Sahai and B.Watersto decrypt a ciphertext encrypted with the public keyω if and only ifωandωare within a certain distance of each other as judged by some metric.Therefore,our system allows for a certain amount of error-tolerance in the identities.Fuzzy-IBE gives rise to two interesting new applications.Thefirst is anIdentity-Based Encryption system that uses biometric identities.That is we canview a user’s biometric,for example an iris scan,as that user’s identity describedby several attributes and then encrypt to the user using their biometric identity.Since biometric measurements are noisy,we cannot use existing IBE systems.However,the error-tolerance property of Fuzzy-IBE allows for a private key(de-rived from a measurement of a biometric)to decrypt a ciphertext encrypted witha slightly different measurement of the same biometric.Secondly,Fuzzy IBE can be used for an application that we call“attribute-based encryption”.In this application a party will wish to encrypt a document toall users that have a certain set of attributes.For example,in a computer sciencedepartment,the chairperson might want to encrypt a document to all of its sys-tems faculty on a hiring committee.In this case it would encrypt to the identity {“hiring-committee”,“faculty”,“systems”}.Any user who has an identity that contains all of these attributes could decrypt the document.The advantage tousing Fuzzy IBE is that the document can be stored on an simple untrusted stor-age server instead of relying on trusted server to perform authentication checksbefore delivering a document.We further discuss the usefulness of using biometrics in Identity-Based andthen discuss our contributions.Using biometrics in Identity-Based Encryption.In many situations,usingbiometric-based identity in an IBE system has a number of important advan-tages over“standard”IBE.We argue that the use of biometric identitiesfitsthe framework of Identity-Based Encryption very well and is a very valuableapplication of it.First,the process of obtaining a secret key from an authority is very naturaland straightforward.In standard Identity-Based Encryption schemes a user witha certain identity,for example,“Bob Smith”,will need to go to an authority toobtain the private key corresponding to the identity.In this process the user willneed to“prove”to the authority that he is indeed entitled to this identity.Thiswill typically involve presenting supplementary documents or credentials.Thetype of authentication that is necessary is not always clear and robustness ofthis process is questionable(the supplementary documents themselves could besubject to forgery).Typically,there will exist a tradeoffbetween a system thatis expensive in this step and one that is less reliable.In contrast,if a biometric is used as an identity then the verification pro-cess for an identity is very clear.The user must demonstrate ownership of thebiometric under the supervision of a well trained operator.If the operator isable to detect imitation attacks,for example playing the recording of a voice,then the security of this phase is only limited by the quality of the biometrictechnique itself.We emphasize that the biometric measurement for an individualneed not be kept secret.Indeed,it is not if it is used as a public key.We mustFuzzy Identity-Based Encryption459 only guarantee that an attacker cannot fool the key authority into believing that an attacker owns a biometric identity that he does not.Also,a biometric identity is an inherent trait and will always with a person. Using biometrics in Identity-Based Encryption will mean that the person will always have their public key handy.In several situations a user will want to present an encryption key to someone when they are physically present.For example,consider the case when a user is traveling and another party encrypts an ad-hoc meeting between them.Finally,using a biometric as an identity has the advantage that identities are unique if the underlying biometric is of a good quality.Some types of standard identities,such as the name“Bob Smith”will clearly not be unique or change owners over time.Security Against Collusion Attacks.In addition to providing error-tolerance in the set of attributes composing the identity any IBE scheme that encrypts to multiple attributes must provide security against collusion attacks.In particular, no group of users should be able to combine their keys in such a way that they can decrypt a ciphertext that none of them alone could.This property is important for security in both biometric applications and“attribute-based encryption”. Our Contributions.We formalize the notion of Fuzzy Identity-Based Encryption and provide a construction for a Fuzzy Identity-Based Encryption scheme.Our construction uses groups for which an efficient bilinear map exists,but for which the Computational Diffie-Hellman problem is assumed to be hard.Our primary technique is that we construct a user’s private key as a set of private key components,one for each attribute in the user’s identity.We share use Shamir’s method of secret sharing[14]to distribute shares of a master secret in the exponents of the user’s private key components.Shamir’s secret sharing within the exponent gives our scheme the crucial property of being error-tolerant since only a subset of the private key components are needed to decrypt a mes-sage.Additionally,our scheme is resistant to collusion attacks.Different users have their private key components generated with different random polynomi-als.If multiple users collude they will be unable to combine their private key components in any useful way.In thefirst version of our scheme,the public key size grows linearly with the number of potential attributes in the universe.The public parameter growth is manageable for a biometric system where all the possible attributes are defined at the system creation time.However,this becomes a limitation in a more general system where we might like an attribute to be defined by an arbitrary string.To accommodate these more general requirements we additionally provide a Fuzzy-IBE system for large universes,where attributes are defined by arbitrary strings.We prove our scheme secure under an adapted version of the Selective-ID security modelfirst proposed by Canetti et al.[5].Additionally,our construc-tion does not use random oracles.We reduce the security of our scheme to an assumption that is similar to the Decisional Bilinear Diffie-Hellman assumption.460 A.Sahai and B.Waters1.1Related WorkIdentity-Based Encryption.Shamir[15]first proposed the concept of Identity-Based Encryption.However,it wasn’t until much later that Boneh and Franklin [3]presented thefirst Identity-Based Encryption scheme that was both practical and secure.Their solution made novel use of groups for which there was an efficiently computable bilinear map.Canetti et al.[5]proposed thefirst construction for IBE that was provably secure outside the random oracle model.To prove security they described a slightly weaker model of security known as the Selective-ID model,in which the adversary declares which identity he will attack before the global public parameters are generated.Boneh and Boyen[2]give two schemes with improved efficiency and prove security in the Selective-ID model without random oracles. Biometrics.Other work in applying biometrics to cryptography has focused on the derivation of a secret from a biometric[12,11,10,6,9,7,4].This secret can be then used for operations such as symmetric encryption or UNIX style password authentication.The distinguishing feature of our work from the above related work on bio-metrics above is that we view the biometric input as potentially public infor-mation instead of a secret.Our only physical requirement is that the biometric cannot be imitated such that a trained human operator would be fooled.We stress the importance of this,since it is much easier to capture a digital reading of someone’s biometric,than to fool someone into believing that someone else’s biometric is one’s own.Simply capturing a digital reading of someone’s biometric would(forever)invalidate approaches where symmetric keys are systematically derived from biometric readings.Attribute-based encryption.Yao et al.[17]show how an IBE system that en-crypts to multiple hierarchical-identities in a collusion-resistant manner implies a forward secure Hierarchical IBE scheme.They also note how their techniques for resisting collusion attacks are useful in attribute-based encryption.However, the cost of their scheme in terms of computation,private key size,and ciphertext size increases exponentially with the number of attributes.1.2OrganizationThe rest of the paper is organized as follows.In Section2we formally define a Fuzzy Identity-Based Encryption scheme including the Selective-ID security model for one.Then,we describe our security assumptions.In Section3we show why two naive approaches do not work.We follow with a description of our construction in Section4and in Section5we prove the security of our scheme.We describe our second construction in Section6.Finally,we conclude in Section7.Fuzzy Identity-Based Encryption461 2PreliminariesWe begin by presenting our definition of security.We follow with a brief review of bilinear maps,and then state the complexity assumptions we use for our proofs of security.2.1DefinitionsIn this section we define our Selective-ID models of security for Fuzzy Identity Based Encryption.The Fuzzy Selective-ID game is very similar to the standard Selective-ID model for Identity-Based Encryption with the exception that the adversary is only allowed to query for secret keys for identities which have less than d overlap with the target identity.Fuzzy Selective-ID.Init.The adversary declares the identity,α,that he wishes to be challenged upon.Setup.The challenger runs the setup phase of the algorithm and tells the ad-versary the public parameters.Phase1.The adversary is allowed to issue queries for private keys for many identities,γj,where|γj∩α|<d for all j.Challenge.The adversary submits two equal length messages M0,M1.The challengerflips a random coin,b,and encrypts M b withα.The ciphertext is passed to the adversary.Phase2.Phase1is repeated.Guess.The adversary outputs a guess b of b..The advantage of an adversary A in this game is defined as Pr[b =b]−12 Definition1(Fuzzy Selective-ID).A scheme is secure in the Fuzzy Selective-ID model of security if all polynomial-time adversaries have at most a negligible advantage in the above game.2.2Bilinear MapsWe briefly review the facts about groups with efficiently computable bilinear maps.We refer the reader to previous literature[3]for more details.Let G1,G2be groups of prime order p,and let g be a generator of G1.We say G1has an admissible bilinear map,e:G1×G1→G2,into G2if the following two conditions hold.The map is bilinear;for all a,b we have e(g a,g b)=e(g,g)ab. The map is non-degenerate;we must have that e(g,g)=1.2.3Complexity AssumptionsWe state our complexity assumptions below.Definition2(Decisional Bilinear Diffie-Hellman(BDH)Assumption). Suppose a challenger chooses a,b,c,z∈Z p at random.The Decisional BDH462 A.Sahai and B.Watersassumption is that no polynomial-time adversary is to be able to distinguish the tuple(A=g a,B=g b,C=g c,Z=e(g,g)abc)from the tuple(A=g a,B= g b,C=g c,Z=e(g,g)z)with more than a negligible advantage.Definition3(Decisional Modified Bilinear Diffie-Hellman(MBDH) Assumption).Suppose a challenger chooses a,b,c,z∈Z p at random.The Decisional MBDH assumption is that no polynomial-time adversary is to be able to distinguish the tuple(A=g a,B=g b,C=g c,Z=e(g,g)ab c)from (A=g a,B=g b,C=g c,Z=e(g,g)z)with more than a negligible advantage. 3Other ApproachesBefore describing our scheme wefirst show three potential approaches to building a Fuzzy Identity-Based Encryption scheme and show why they fall short.This discussion additionally motivates our approach to the problem.Correcting the error.We consider the feasibility of“correcting”the errors of a biometric measurement and then use standard Identity-Based Encryption to encrypt a message under the corrected input.However,this approach relies upon the faulty assumption that each biometric input measurement is slightly devi-ated from some“true”value and that the set of possible“true”values are well known.In practice,the only reasonable assumption is that two measurements sampled from the same person will be within a certain distance of each other. This intuition is captured by previous work.Dodis,Rezyin,and Smith[7]use what they call a fuzzy sketch that contains information of afirst sampling of a biometric which allows subsequent measurements to be corrected to it.If the cor-rection could be done without any additional information then we could simply do away with the fuzzy sketch.Key per Attribute.The second naive approach we consider is for an authority to give a user a different private key for each of the attributes that describe the user. Such a system easily falls prey to simple collusion attacks where multiple users combine their keys to form identities that are a combination of their attributes. The colluders are then able to decrypt ciphertexts that none of them individually were able to decrypt.Several Keys.Suppose a key authority measures an inputωfor a particular party.The authority could create a separate standard IBE private key for every ω such that|ω∩ω |≥d,for some error-tolerance parameter d.However,the pri-vate key storage will grow exponentially in d and the system will be impracticalfor even modest values of d.4Our ConstructionRecall that we view identities as sets of attributes and we let the value d represent the error-tolerance in terms of minimal set overlap.When an authority is creatingFuzzy Identity-Based Encryption463 a private key for a user he will associate a random d−1degree polynomial,q(x), with each user with the restriction that each polynomial have the same valuation at point0,that is q(0)=y.For each of the attributes associated with a user’s identity the key generation algorithm will issue a private key component that is tied to the user’s random polynomial q(x).If the user is able to“match”at least d components of the ciphertext with their private key components,then they will be able to perform decryption.However,since the private key components are tied to random poly-nomials,multiple user’s are unable to combine them in anyway that allows for collusion attacks.A detailed description of our scheme follows.4.1DescriptionRecall that we wish to create an IBE scheme in which a ciphertext created using identityωcan be decrypted only by a secret keyω where|ω∩ω |≥d.Let G1be bilinear group of prime order p,and let g be a generator of G1. Additionally,let e:G1×G1→G2denote the bilinear map.A security parameter,κ,will determine the size of the groups.We also define the Lagrange coefficient∆i,S for i∈Z p and a set,S,of elements in Z p:∆i,S(x)=j∈S,j=i x−j i−j.Identities will be element subsets of some universe,U,of size|U|.We will associate each element with a unique integer in Z p∗.(In practice an attribute will be associated with each element so that identities will have some semantics.) Our construction follows:Setup(d).First,define the universe,U of elements.For simplicity,we can take thefirst|U|elements of Z p∗to be the ly,the integers1,...,|U| (mod p).Next,choose t1,...,t|U|uniformly at random from Z p.Finally,choose y uni-formly at random in Z p.The published public parameters are:T1=g t1,...,T|U|=g t|U|,Y=e(g,g)y.The master key is:t1,...,t|U|,y.Key Generation.To generate a private key for identityω⊆U the following steps are taken.A d−1degree polynomial q is randomly chosen such that q(0)=y. The private key consists of components,(D i)i∈ω,where D i=g q(i)t i for every i∈ω.464 A.Sahai and B.WatersEncryption.Encryption with the public key ω and message M ∈G 2proceeds as follows.First,a random value s ∈Z p is chosen.The ciphertext is then published as:E =(ω ,E =MY s ,{E i =T s i }i ∈ω ).Note that the identity,ω ,is included in the ciphertext.Decryption.Suppose that a ciphertext,E ,is encrypted with a key for identity ω and we have a private key for identity ω,where |ω∩ω |≥d .Choose an arbitrary d -element subset,S ,of ω∩ω .Then,the ciphertext can be decrypted as:E /i ∈S(e (D i ,E i ))∆i,S (0)=Me (g,g )sy /i ∈S e (g q (i )t i ,g st i ) ∆i,S (0)=Me (g,g )sy /i ∈Se (g,g )sq (i ) ∆i,S (0)=M.The last equality is derived from using polynomial interpolation in the expo-nents.Since,the polynomial sq (x )is of degree d −1it can be interpolated using d points.4.2Efficiency and Key SizesThe number of exponentiations in the group G 1to encrypt to an identity will be linear in the number of elements in the identity’s description.The cost of decryption will be dominated by d bilinear map computations.The number of group elements in the public parameters grows linearly with the number attributes in the system (elements in the defined universe).The number of group elements that compose a user’s private key grow linearly with the number of attributes associated with her identity.Finally,the number of group elements in a ciphertext grows linearly with the size of the identity we are encrypting to.4.3Flexible Error-ToleranceIn this construction the error-tolerance is set to a fixed value d .However,in prac-tice a party constructing a ciphertext might want more flexibility.For example,if a biometric input device happens to be less reliable it might be desirable to relax the set overlap parameters.In the example of attribute-based encryption we would like to have flexibility in the number of attributes required to access a document.Fuzzy Identity-Based Encryption465 There are two simple methods for achievingflexible error-tolerance.First,we can create multiple systems with different values of d and the party encrypting a message can choose the appropriate one.For m different systems the size of the public parameters and private keys both increase by a factor of m.In the second method the authority will reserve some attributes that it will issue to every key-holder as part of their identity.The party encrypting the message can increase the error-tolerance by increasing the number of these“default”attributes it includes in the encryption identity.In this approach ciphertexts must be at least as long as the maximum number of attributes that can be required in an encryption. Additionally,we can combine the above two techniques and explore tradeoffs between ciphertext size and public parameter and private key size.5Proof of SecurityWe prove that the security of our scheme in the Selective-ID model reduces to the hardness of the Decisional MBDH assumption.Theorem1.If an adversary can break our scheme in the Fuzzy Selective ID Model,then a simulator can be constructed to play the Decisional MBDH game with a non-negligible advantage.Proof.Suppose there exists a polynomial-time adversary,A,that can attack our scheme in the Selective-ID model with advantage .We build a simulator B thatcan play the Decisional MBDH game with advantage2.The simulation proceedsas follows:Wefirst let the challenger set the groups G1and G2with an efficient bilinear map,e and generator g.The challengerflips a fair binary coin,µ,outside of B’s view.Ifµ=0,the challenger sets(A,B,C,Z)=(g a,g b,g c,e(g,g)ab c);otherwise it sets(A,B,C,Z)=(g a,g b,g c,e(g,g)z)for random a,b,c,z.We assume the universe,U is defined.Init.The simulator B runs A and receives the challenge identity,α.Setup.The simulator assigns the public key parameters as follows.It sets the parameter Y=e(g,A)=e(g,g)a.For all i∈αit chooses randomβi∈Z p and sets T i=Cβi=g cβi.For all i∈U−αit chooses random w i∈Z p and sets T i=g w i.It then gives the public parameters to A.Notice that from the view A all parameters are chosen at random as in the construction.Phase1.A makes requests for private keys where the identity set overlap be-tween the identities for each requested key andαis less than d.Suppose A requests a private keyγwhere|γ∩α|<d.Wefirst define three setsΓ,Γ ,S in the following manner:Γ=γ∩α,466 A.Sahai and B.WatersΓ be any set such thatΓ⊆Γ ⊆γand|Γ |=d−1,andS=Γ ∪{0}.Next,we define the decryption key components,D i,for i∈Γ as:If i∈Γ:D i=g s i where s i is chosen randomly in Z p.If i∈Γ −Γ:D i=gλi w i whereλi is chosen randomly in Z p.The intuition behind these assignments is that we are implicitly choosing a random d−1degree polynomial q(x)by choosing its value for the d−1points randomly in addition to having q(0)=a.For i∈Γwe have q(i)=cβi s i and for i∈Γ −Γwe have q(i)=λi.The simulator can calculate the other D i values where i/∈Γ since the simulator knows the discrete log of T i for all i/∈α.The simulator makes the assignments as follows:If i/∈Γ :D i=(j∈ΓCβj s j∆j,S(i)w i)(j∈Γ −Γgλj∆j,S(i)w i)Y∆0,S(i)w iUsing interpolation the simulator is able to calculate D i=g q(i)t i for i/∈Γ where q(x)was implicitly defined by the random assignment of the other d−1 variables D i∈Γ and the variable Y.Therefore,the simulator is able to construct a private key for the identityγ. Furthermore,the distribution of the private key forγis identical to that of the original scheme.Challenge.The adversary,A,will submit two challenge messages M1and M0to the simulator.The simulatorflips a fair binary coin,ν,and returns an encryption of Mν.The ciphertext is output as:E=(α,E =MνZ,{E i=Bβi}i∈α).Ifµ=0,then Z=e(g,g)ab c.If we let r =bc ,then we have E0=MνZ=Mνe(g,g)ab c=Mνe(g,g)ar =MνY r and E i=Bβi=g bβi=g b c cβi=g r cβi= (T i)r .Therefore,the ciphertext is a random encryption of the message mνunder the public keyα.Otherwise,ifµ=1,then Z=g z.We then have E =Mνe(g,g)z.Since z is random,E will be a random element of G2from the adversaries view and the message contains no information about Mν.Phase2.The simulator acts exactly as it did in Phase1.Guess.A will submit a guessν ofν.Ifν=ν the simulator will outputµ =0 to indicate that it was given a MBDH-tuple otherwise it will outputµ =1to indicate it was given a random4-tuple.As shown in the construction the simulator’s generation of public parameters and private keys is identical to that of the actual scheme.In the case where µ=1the adversary gains no information about ν.There-fore,we have Pr[ν=ν |µ=1]=12.Since the simulator guesses µ =1when ν=ν ,we have Pr[µ =µ|µ=1]=12.If µ=0then the adversary sees an encryption of m ν.The adversary’s advan-tage in this situation is by definition.Therefore,we have Pr[ν=ν |µ=0]=12+ .Since the simulator guesses µ =0when ν=ν ,we have Pr[µ =µ|µ=0]=12+ .The overall advantage of the simulator in the Decisional MBDH game is 12Pr[µ =µ|µ=0]+12Pr[µ =µ|µ=1]−12=12(12+ )+1212−12=12 .5.1Chosen-Ciphertext SecurityOur security definitions and proofs have been in the chosen-plaintext model.Our scheme can be extended to the chosen-ciphertext model by applying the technique of using simulation-sound NIZK proofs to achieve chosen-ciphertext security [13].Alternatively,if we are willing to use random oracles,then the we can use standard techniques such as the Fujisaki-Okamoto transformation [8].5.2Security in Full IBE ModelSuppose all identities are composed of n attributes and we have a universe of attributes,U .We make the observation [2]that our scheme is secure in the full model with a factor of |U|n in the reduction.The original IBE scheme of Boneh and Franklin [3]and a later schemes of Boneh and Boyen [2]and Waters [16]achieve IBE in the full model with non-exponential reductions.However,all methods achieve this by essentially remov-ing the relationships between nearby identities.In Fuzzy-IBE it is essential that there exists a relationship between nearby identities.Therefore,we conjecture that a scheme that has a non-exponential loss of security in the full model will require significantly different methods than those seen in prior work.6Large Universe ConstructionIn the previous construction the size of the public parameters grows linearly with the number of possible attributes in the universe.We describe a second scheme which uses all elements of Z p ∗as the universe,yet the public parameters only grow linearly in a parameter n ,which we fix as the maximum size identity we can encrypt to.In addition to decreasing the public parameter size,having a large universe allows us to apply a collision-resistant hash function H :{0,1}∗→Z p ∗and use arbitrary strings as attributes.We can now use attributes that were not necessarily considered during the public key setup.For example,we can add any verifiable attribute,such as “Ran in N.Y.Marathon 2005”,to a user’s private key.Our large universe construction is built using similar concepts to the previous scheme and uses an algebraic technique of Boneh and Boyen[2].Additionally, we reduce the security of this scheme to the Decisional BDH problem.We now describe our construction and give our proof of security.6.1DescriptionLet G1be bilinear group of prime order p,and let g be a generator of G1.Addi-tionally,let e:G1×G1→G2denote the bilinear map.We restrict encryption identities to be of length n for somefixed n.We define the Lagrange coefficient∆i,S for i∈Z p and a set,S,of elementsin Z p:∆i,S(x)=j∈S,j=i x−j i−j.Identities will be sets of n elements of Z p∗.1Alternatively,we can describe an identity as a collection of n strings of arbitrary length and use a collision resistant hash function,H,to hash strings into members of Z p∗.Our construction follows: Setup(n,d).First,choose g1=g y,g2∈G1.Next,choose t1,...,t n+1uniformly at random from G1.Let N be the set {1,...,n+1}and we define a function,T,as:T(x)=g x n2n+1i=1t∆i,N(x)i.We can view T as the function g x n2g h(x)for some n degree polynomial h.Thepublic key is published as:g1,g2,t1,...,t n+1and the private key is y.Key Generation.To generate a private key for identityωthe following steps aretaken.A d−1degree polynomial q is randomly chosen such that q(0)=y.Theprivate key will consist of two sets.Thefirst set,{D i}i∈ω,where the elements are constructed asD i=g q(i)2T(i)r i,where r i is a random member of Z p defined for all i∈ω.The other set is{d i}i∈ωwhere the elements are constructed asd i=g r i.Encryption.Encryption with the public keyω and message M∈G2proceedsas follows.First,a random value s∈Z p is chosen.The ciphertext is then published as: E=(ω ,E =Me(g1,g2)s,E =g s,{E i=T(i)s}i∈ω ).1With some minor modifications to our scheme,which we omit for simplicity,we can encrypt to all identities of size≤n.。
A Framework for Evaluating Fusion Operators Based on the Theory of Generalized Quantifiers

A Framework for Evaluating Fusion Operators Based on the Theory ofGeneralized QuantifiersIngo Gl¨o ckner and Alois KnollTechnical Computer Science,Faculty of Technology,University of Bielefeld,33501Bielefeld,GermanyAbstractFuzzy linguistic quantifiers–operators intended to model vague quantifying expressions in natural language like“almost all”or“few”–have gained importance as operators for information combination and the fusion of gradual evaluations.They are particularly appealing because of their ease-of-use:people are familiar with these operators,which can be applied for technical fusion purposes in the same way as in everyday language. Because of the irregular and rather intangible phenomena it tries to model–viz,those of imprecision and uncertainty –fuzzy logic should be particularly specific about its foundations.However,work on mathematical foundations and linguistic justification of fuzzy linguistic quantifiers is scarce.In the paper,we propose a framework for evaluating approaches to fuzzy quantification which relates these to the logico-linguistic theory of generalized quantifiers(TGQ).By reformulating these approaches as fuzzification mechanisms,we can investigate properties of the fuzzification mappings which express important aspects of the meaning of natural language quantifiers.1IntroductionNatural language(NL)is pervaded by quantifiers.It is virtually impossible to express a natural language sen-tence which does not involve quantification because every nominal phrase(“most people”,“almost all men”)has a quantificational aspect(typically expressed by a“deter-miner”or“generalized quantifier”such as“most”,“the”,“a”,etc.).In addition,aggregational modes of temporal or local description such as“almost always”,“everywhere”are naturally modelled through quantification.In order to handle such cases,Zadeh[17,18]has initi-ated research which tries to model natural language quan-tifiers by operators called“fuzzy linguistic quantifiers”. Several classes of operators have been proposed as prop-erly representing the phenomenon of“vague”or fuzzy NL quantification(a survey is provided in[11]),but there is no consensus about the proper choice,and notes on implau-sible behavior of these approaches are scattered over the literature[12,13,16,5].These foundational problems notwithstanding,the areas of application have been so obvious and auspicious that a broad span of systems in a variety offields and for a vari-ety of purposes have been implemented.Fuzzy linguistic quantifiers have been utilized for fusion tasks inmulti-criteria decision making[15];data summarisation[14];information retrieval[3];fuzzy databases[9].In our view,fuzzy quantifying operators will unfold their full potential for information aggregation and data fusion only if these operators are linguistically adequate,i.e.able to capture the meaning of corresponding NL quantifiers. For example,if an operator is labelled“most”,it is essen-tial that this operator behave like the NL quantifier“most”. 2(Two-Valued)Generalized QuantifiersWe will start our presentation from the viewpoint of the Theory of Generalized Quantifiers(TGQ[1,2]).By an-ary generalized quantifier(sometimes dubbed“de-terminer”)on a base set we denote a mappingwhich to each-tuple of crisp subsets of assigns a two-valued quantification result.Examples areallsomeatleast mall except mWhenever the base set(domain)is clear from the context, we will drop the subscript;denotes cardinality.Let us remark that might be infinite in the general case.For finite,we can define proportional quantifiersrateratefor,.TGQ has classified the wealth of quantificational phe-nomena in natural languages in order to unveil universal properties shared by quantifiers in all natural languages, or single out classes of quantifiers with specific properties (we shall describe some of these properties below).Anextension to the continuous-valued case,in order to better capture the meaning of vague quantifying expressions like almost all,has not been an issue to TGQ.3Fuzzy Generalized QuantifiersIn[5],we have proposed a straightforward generalisa-tion of generalized quantifiers to the fuzzy case.A fuzzy subset of a set assigns to each a membership degree;we denote bythe set of all fuzzy subsets(fuzzy powerset)of .An-ary fuzzy quantifier on a base set is a mapping which to each-tuple of fuzzy subsets of assigns a gradual result.1An example isFuzzy quantifiers catch a broad class of fusion operators. For example,if is a set of criteria(e.g.multiple sensors,experts),expresses the“weight”or“relevance”of the criterion,and expresses the degree to which is satisfied,then every fusion operator which combines the criteria as a function of and,is a fuzzy quantifier by definition.Let us give an example.In developing a system for the content-based retrieval of meteorological(weather information)documents[7],we have faced the problem of ranking satellite images according to accumulative criteria such as“almost all of Southern Germany is cloudy”. In this case,is the set of pixel coordinates, expresses the degree to which pixel belongs to Southern Germany,and expresses the degree to which the pixel is classified as cloudy(see Fig.1).The desired fusion operator to combine the criteria can then be modeled by a fuzzy quantifiersuited for interpreting“almost all”.The example indicates some problems inherent to fuzzygermany(Pixels with depicted white).(b)cloudy(Pixels clas-sified as cloudy depicted white.The contours of Germany, split in southern,intermediate and northern part,have been added to facilitate interpretation.)quantifiers:Which fuzzy quantifier corresponds to a given (possibly vague)NL quantifier,e.g.“almost all”?How can we describe characteristics of fuzzy quantifiers and how can we locate a fuzzy quantifier based on a description of desired properties?Fuzzy quantifiers are possibly too rich a set of operators to investigate these questions directly, and all approaches to fuzzy quantification have therefore introduced some kind of simplified representation.4Fuzzy Linguistic QuantifiersFollowing Zadeh[17,18,19],most existing approaches to fuzzy quantification have chosen to define fuzzy linguis-tic quantifiers as fuzzy subsets of the non-negative reals (absolute quantifiers like some,with membership functions ),or of the unit interval(proportional quanti-fiers like most,with membership functions).2 These“fuzzy numbers”3provide the desired simplified rep-resentation.For example,we could define a proportional fuzzy linguistic quantifier almost all by almost allforall,using Zadeh’s-function(see Fig.2).The are not directly applicable to fuzzy sets for the purpose of quantification.What is needed is a mechanism which maps each to a fuzzy quantifier(monadic or unrestricted use,relative to), or(two-place or restricted use,relative tofirst argument):4unrestricted:,“elements(of)are”restricted:,“’s are”.00.20.40.60.8100.20.40.60.81Figure 2:A possible definition of almost all Zadeh has also formulated the idea that in order to evalu-ate a statement “are ”(in our notation:to compute),one should instead evaluate the statement“is ”,where is a scalar or fuzzy measure ofthe cardinality of the fuzzy setassociated with the linguistic variable .5The approaches described in the literature mainly differ in the measure of fuzzy cardinality used and in the way that the required comparison of fuzzy cardinalities is accomplished:Zadeh proposes the use of -counts or FG-counts,and Ralescu’s [12]possibilistic ap-proach is based on FE-counts.6Yager [15]proposes the use of Ordered Weighted Averaging (OW A)operators.Before discussing particular approaches,let us con-sider some general implications of using fuzzy linguistic quantifiers.Due to these approaches’direct relying on the computation of (some “fuzzified”notion of)cardinality and proportion,they are unable to provide a uniform account of absolute and proportional quantifiers,which must be represented (and hence evaluated)differently.An extension to other types of quantifiers (e.g.,quantifiers of exception like all except m ,and ternary quantifiers likemorethan are ,would require the introduction of further descriptions for each considered quantifier type,and corresponding evaluation formulas.The notions of cardinality and proportion (ratio)are not sufficient to evaluate all quantifiers of interest even in the crisp case.Apart from quantitative type,there is a variety of non-quantitative (qualitative)quantifiers.78From an information fusion perspective,non-quantitative quanti-fiers are of interest when the criteria cannot be viewed aselseSemi-fuzzy quantifiers are not subject to the restrictions offuzzy linguistic quantifiers:they can express genuine mul-tiplace quantification (arbitrary );they are not restricted to the absolute and proportional types;they are not nec-essarily quantitative (again in the sense of automorphism-invariance);and there is no a priori restriction to finite do-mains.In addition,it is relatively easy to understand the input-output behavior of a semi-fuzzy quantifier because it is stated in terms of crisp argument sets.However,being half-way between two-valued gen-eralized quantifiers and fuzzy quantifiers,semi-fuzzy quantifiers do not accept fuzzy input,and we have to make use of a fuzzification mechanism which transports these to fuzzy quantifiers.6Quantifier Fuzzification MechanismsA quantifier fuzzification mechanism assigns to each semi-fuzzy quantifier a correspondingfuzzy quantifierof the same arity and on the same base set .By viewing approaches to fuzzy quantification as in-stances of quantifier fuzzification mechanisms(QFM),we are able to explore the mathematical well-behavedness of these approaches by investigating preservation and ho-momorphism properties of the corresponding fuzzification mappings.A comprehensive account of such adequacy conditions is given in[5,6].For lack of space,we shall re-strict attention to some special cases required for the proofs to follow.The most basic requirement on a QFM is that of cor-rect generalisation,i.e.for all,(1)i.e.coincides with on all crisp arguments.A semi-fuzzy quantifier is said to be non-increasing in its-th argument(,) iff for all such that,. The definitions for nondecreasing monotonicity,and the adaptation of these concepts to the fuzzy case are straight-forward.We say that preserves monotonicity in argu-ments if nonincreasing or nondecreasing monotonicity of a semi-fuzzy quantifier in its arguments are preserved when applying.is said to have extension if for each choice of base sets and all,(2)This is a very important property possessed by virtually all NL quantifiers,which expresses some kind of context insensitivity:we can add an arbitrary number of irrelevant objects to our original domain without altering the quan-tification result.A QFM is said to preserve extension if each pair,,of semi-fuzzy quantifiers satisfying(2)is mapped to a pair of fuzzy quan-tifiers with the same property(adapted to fuzzy arguments).7The Evaluation FrameworkExisting approaches to fuzzification cannot be directly viewed as quantifier fuzzification mechanisms because they are not applicable to semi-fuzzy quantifiers.We have to bridge the gap between semi-fuzzy quantifiers and fuzzy linguistic quantifiers in a systematical way.Suppose is one of the approaches based on fuzzy lin-guistic quantifiers.Because the quantificational phenom-ena addresses are too limited(see above),it does not give rise to a“full”(totally defined)quantifier fuzzification mechanism.However,we can reconstruct a partially de-fined quantifier fuzzification mechanism in a post-hoc fashion as follows.Let us define the underlying semi-fuzzy quantifierof a given fuzzy quantifier by.Given the membership function of a fuzzy linguistic quantifier,we thenfirst obtain the cor-responding semi-fuzzy quantifier(relative to)as,and use this to define.Obvi-ously,the construction of succeeds only ifis functional,but this is a reasonable adequacy con-dition anyway.10We shall call it the quantifier framework assumption(QFA).In case the QFA holds uncondition-ally for,we can use the constructed partial fuzzifica-tion mechanism to establish or reject the preservation and homomorphism properties of interest.In case the QFA is violated by,it can always be enforced by restricting attention to smaller subsets of considered fuzzy linguis-tic quantifiers,which comply with the QFA.It there-fore makes sense to say that can represent a semi-fuzzy quantifier if there exists some such that.We can then refute a property of inter-est by proving that cannot represent without violating the property.We will now present examples of the framework in action.We will focus on one of the most prominent approaches to fuzzy quantification,namely the-count approach(Zadeh[17,18]).However,the evaluation framework can also be applied to other approaches such as Zadeh’s FG-count approach,Ralescu’s FE-count approach and Yager’s OW A approach,as shown in[6].8Evaluation of the Sigma-Count ApproachThe-count of a fuzzy set(finite),is defined as the sum of its membership values,i.e.-CountIt is claimed to provide a(coarse)summary of the cardi-nality of the fuzzy set,expressed as a non-negative real number.A corresponding scalar definition of fuzzy proportion,the relative-count,is defined by-Count-Count-CountIn the-count approach[17,18],fuzzy linguistic quanti-fiers of the absolute and proportional kinds are treated dif-ferently.Hence,in order to obtain both the unrestricted and restricted versions of absolute and proportional quantifiers,a total of four different evaluation formulae are required.11SC-CountSC SCSC SCSC-CountLet us now recast Yager’s example[16,p.257]on counter-intuitive behaviour of the-count approach in our setting.Suppose hans maria tom is a set of persons,andusing Zadeh’s notation,blond maria.Let us nowevaluate one blond,where one denotes the two-valued quantifier exactly one in its monadic use(i.e.thestatement expresses“there is exactly one blond(person)”).Then,assuming that correct generalisation be respected,we are forced to have.It follows that theabove statement evaluates to(fully true),although there isclearly not exactly one blond person in the base set(whichone should that be?)but rather a total amount of blondnessof one,as Yager puts it.Now let us address some novelaspects.Question1:Does the-count approach comply withthe QFA?Answer:No.12This is most apparent with absolutefuzzy linguistic quantifiers:Any pairsuch that violates the assumption.The trouble is that with absolute quantifiers,the-countapproach requires a decision on which quantification re-sults to assign in the case that the computed-count is nota cardinal number.But intuitions are scarce in this unfa-miliar case.“Trivial”or“degenerate”cases often require particularattention.One such case is that of a quantifier supplied withan argument tuple of empty sets.Question2:Does the-count approach treat consis-tently the case of empty argument sets?Answer:No.As an example,let us chooseand consider the two-valued proportionalquantifiers rate rate(see p.1),which have,but.The problem is that Zadeh does not spec-ify the denotation of-Count.So let us assume that-Count.Correct generalization demandsthat,i.e.,but also that,i.e.,which contradicts our assumption.In addition,the-count approach yields potentially sat-isfying results only if is genuinely fuzzy,because a two-13This problem has been obscured by Zadeh’s use of the quantifiermost,which he views as being genuinely fuzzy.Lemma.If SC is nondecreasing(nonin-creasing)in itsfirst argument and,then.Proof.Suppose that is nondecreasing in itsfirst argument.a.Suppose,choose someand let,。
fuzzy control 外文翻译

C H A P T E R2Fuzzy Control:The BasicsA few strong instincts and a few plain rules sufficeus.–Ralph Waldo Emerson2.1OverviewThe primary goal of control engineering is to distill and apply knowledge about how to control a process so that the resulting control system will reliably and safely achieve high-performance operation.In this chapter we show how fuzzy logic provides a methodology for representing and implementing our knowledge about how best to control a process.We begin in Section2.2with a“gentle”(tutorial)introduction,where we focus on the construction and basic mechanics of operation of a two-input one-output fuzzy controller with the most commonly used fuzzy operations.Building on our understanding of the two-input one-output fuzzy controller,in Section2.3we pro-vide a mathematical characterization of general fuzzy systems with many inputs and outputs,and general fuzzification,inference,and defuzzification strategies.In Section2.4we illustrate some typical steps in the fuzzy control design process via a simple inverted pendulum control problem.We explain how to write a computer program that will simulate the actions of a fuzzy controller in Section2.5.More-over,we discuss various issues encountered in implementing fuzzy controllers in Section2.6.Then,in Chapter3,after providing an overview of some design methodologies for fuzzy controllers and computer-aided design(CAD)packages for fuzzy system construction,we present several design case studies for fuzzy control systems.It is these case studies that the reader willfind most useful in learning thefiner2324Chapter2/Fuzzy Control:The Basicspoints about the fuzzy controller’s operation and design.Indeed,the best way toreally learn fuzzy control is to design your own fuzzy controller for one of theplants studied in this or the next chapter,and simulate the fuzzy control system toevaluate its performance.Initially,we recommend coding this fuzzy controller in ahigh-level language such as C,Matlab,or ter,after you have acquiredafirm understanding of the fuzzy controller’s operation,you can take shortcuts byusing a(or designing your own)CAD package for fuzzy control systems.After completing this chapter,the reader should be able to design and simulatea fuzzy control system.This will move the reader a long way toward implementationof fuzzy controllers since we provide pointers on how to overcome certain practicalproblems encountered in fuzzy control system design and implementation(e.g.,coding the fuzzy controller to operate in real-time,even with large rule-bases).This chapter provides a foundation on which the remainder of the book rests.After our case studies in direct fuzzy controller design in Chapter3,we will usethe basic definition of the fuzzy control system and study its fundamental dynamicproperties,including stability,in Chapter 4.We will use the same plants,andothers,to illustrate the techniques for fuzzy identification,fuzzy adaptive control,and fuzzy supervisory control in Chapters5,6,and7,respectively.It is thereforeimportant for the reader to have afirm grasp of the concepts in this and the nextchapter before moving on to these more advanced chapters.Before skipping any sections or chapters of this book,we recommend that the reader study the chapter summaries at the end of each chapter.In these summarieswe will highlight all the major concepts,approaches,and techniques that are coveredin the chapter.These summaries also serve to remind the reader what should belearned in each chapter.2.2Fuzzy Control:A Tutorial IntroductionA block diagram of a fuzzy control system is shown in Figure2.1.The fuzzy con-troller1is composed of the following four elements:1.A rule-base(a set of If-Then rules),which contains a fuzzy logic quantificationof the expert’s linguistic description of how to achieve good control.2.An inference mechanism(also called an“inference engine”or“fuzzy inference”module),which emulates the expert’s decision making in interpreting and ap-plying knowledge about how best to control the plant.3.A fuzzification interface,which converts controller inputs into information thatthe inference mechanism can easily use to activate and apply rules.4.A defuzzification interface,which converts the conclusions of the inferencemechanism into actual inputs for the process.1.Sometimes a fuzzy controller is called a“fuzzy logic controller”(FLC)or even a“fuzzylinguistic controller”since,as we will see,it uses fuzzy logic in the quantification of linguisticdescriptions.In this book we will avoid these phrases and simply use“fuzzy controller.”2.2Fuzzy Control:A Tutorial Introduction 25FIGURE 2.1Fuzzy controller.We introduce each of the components of the fuzzy controller for a simple prob-lem of balancing an inverted pendulum on a cart,as shown in Figure 2.2.Here,y denotes the angle that the pendulum makes with the vertical (in radians),l is the half-pendulum length (in meters),and u is the force input that moves the cart (in Newtons).We will use r to denote the desired angular position of the pendulum.The goal is to balance the pendulum in the upright position (i.e.,r =0)when it initially starts with some nonzero angle offthe vertical (i.e.,y =0).This is a very simple and academic nonlinear control problem,and many good techniques already existfor its solution.Indeed,for this standard configuration,a simple PID controller works well even in implementation.In the remainder of this section,we will use the inverted pendulum as a con-venient problem to illustrate the design and basic mechanics of the operation of a fuzzy control system.We will also use this problem in Section 2.4to discuss much more general issues in fuzzy control system design that the reader will find useful for more challenging applications (e.g.,the ones in the next chapter).FIGURE 2.2Inverted pendulumon a cart.26Chapter2/Fuzzy Control:The Basics2.2.1Choosing Fuzzy Controller Inputs and OutputsConsider a human-in-the-loop whose responsibility is to control the pendulum,asshown in Figure2.3.The fuzzy controller is to be designed to automate how ahuman expert who is successful at this task would control the system.First,theexpert tells us(the designers of the fuzzy controller)what information she or hewill use as inputs to the decision-making process.Suppose that for the invertedpendulum,the expert(this could be you!)says that she or he will usee(t)=r(t)−y(t)andde(t)dtas the variables on which to base decisions.Certainly,there are many other choices(e.g.,the integral of the error e could also be used)but this choice makes goodintuitive sense.Next,we must identify the controlled variable.For the invertedpendulum,we are allowed to control only the force that moves the cart,so thechoice here is simple.FIGURE2.3Human controlling aninverted pendulum on a cart.For more complex applications,the choice of the inputs to the controller and outputs of the controller(inputs to the plant)can be more difficult.Essentially,youwant to make sure that the controller will have the proper information availableto be able to make good decisions and have proper control inputs to be able tosteer the system in the directions needed to be able to achieve high-performanceoperation.Practically speaking,access to information and the ability to effectivelycontrol the system often cost money.If the designer believes that proper informationis not available for making control decisions,he or she may have to invest in anothersensor that can provide a measurement of another system variable.Alternatively,the designer may implement somefiltering or other processing of the plant outputs.In addition,if the designer determines that the current actuators will not allowfor the precise control of the process,he or she may need to invest in designingand implementing an actuator that can properly affect the process.Hence,while insome academic problems you may be given the plant inputs and outputs,in manypractical situations you may have someflexibility in their choice.These choices2.2Fuzzy Control:A Tutorial Introduction27 affect what information is available for making on-line decisions about the controlof a process and hence affect how we design a fuzzy controller.Once the fuzzy controller inputs and outputs are chosen,you must determinewhat the reference inputs are.For the inverted pendulum,the choice of the referenceinput r=0is clear.In some situations,however,you may want to choose r assome nonzero constant to balance the pendulum in the off-vertical position.To dothis,the controller must maintain the cart at a constant acceleration so that the pendulum will not fall.After all the inputs and outputs are defined for the fuzzy controller,we canspecify the fuzzy control system.The fuzzy control system for the inverted pendu-lum,with our choice of inputs and outputs,is shown in Figure2.4.Now,within this framework we seek to obtain a description of how to control the process.We see thenthat the choice of the inputs and outputs of the controller places certain constraintson the remainder of the fuzzy control design process.If the proper information isnot provided to the fuzzy controller,there will be little hope for being able to designa good rule-base or inference mechanism.Moreover,even if the proper informationis available to make control decisions,this will be of little use if the controller isnot able to properly affect the process variables via the process inputs.It must be understood that the choice of the controller inputs and outputs is a fundamentally important part of the control design process.We will revisit this issue several times throughout the remainder of this chapter(and book).FIGURE2.4Fuzzy controller for an inverted pendulum on a cart.2.2.2Putting Control Knowledge into Rule-BasesSuppose that the human expert shown in Figure2.3provides a description of howbest to control the plant in some natural language(e.g.,English).We seek to takethis“linguistic”description and load it into the fuzzy controller,as indicated bythe arrow in Figure2.4.28Chapter2/Fuzzy Control:The BasicsLinguistic DescriptionsThe linguistic description provided by the expert can generally be broken intoseveral parts.There will be“linguistic variables”that describe each of the time-varying fuzzy controller inputs and outputs.For the inverted pendulum,“error”describes e(t)“change-in-error”describes ddt e(t)“force”describes u(t)Note that we use quotes to emphasize that certain words or phrases are linguistic descriptions,and that we have added the time index to,for example,e(t),to em-phasize that generally e varies with time.There are many possible choices for the linguistic descriptions for variables.Some designers like to choose them so that they are quite descriptive for documentation purposes.However,this can sometimes lead to long descriptions.Others seek to keep the linguistic descriptions as short as pos-sible(e.g.,using“e(t)”as the linguistic variable for e(t)),yet accurate enough so that they adequately represent the variables.Regardless,the choice of the linguistic variable has no impact on the way that the fuzzy controller operates;it is simply a notation that helps to facilitate the construction of the fuzzy controller via fuzzy logic.Just as e(t)takes on a value of,for example,0.1at t=2(e(2)=0.1),linguistic variables assume“linguistic values.”That is,the values that linguistic variables take on over time change dynamically.Suppose for the pendulum example that “error,”“change-in-error,”and“force”take on the following values:“neglarge”“negsmall”“zero”“possmall”“poslarge”Note that we are using“negsmall”as an abbreviation for“negative small in size”and so on for the other variables.Such abbreviations help keep the linguistic de-scriptions short yet precise.For an even shorter description we could use integers:“−2”to represent“neglarge”“−1”to represent“negsmall”“0”to represent“zero”“1”to represent“possmall”“2”to represent“poslarge”This is a particularly appealing choice for the linguistic values since the descriptions are short and nicely represent that the variable we are concerned with has a numeric quality.We are not,for example,associating“−1”with any particular number of radians of error;the use of the numbers for linguistic descriptions simply quantifies the sign of the error(in the usual way)and indicates the size in relation to the2.2Fuzzy Control:A Tutorial Introduction29 other linguistic values.We shallfind the use of this type of linguistic value quite convenient and hence will give it the special name,“linguistic-numeric value.”The linguistic variables and values provide a language for the expert to expressher or his ideas about the control decision-making process in the context of the framework established by our choice of fuzzy controller inputs and outputs.Recallthat for the inverted pendulum r=0and e=r−y so thate=−yandd dt e=−ddtysince ddt r=0.First,we will study how we can quantify certain dynamic behaviorswith linguistics.In the next subsection we will study how to quantify knowledge about how to control the pendulum using linguistic descriptions.For the inverted pendulum each of the following statements quantifies a different configuration of the pendulum(refer back to Figure2.2on page25):•The statement“error is poslarge”can represent the situation where the pendulum is at a significant angle to the left of the vertical.•The statement“error is negsmall”can represent the situation where the pendulum is just slightly to the right of the vertical,but not too close to the vertical to justify quantifying it as“zero”and not too far away to justify quantifying it as “neglarge.”•The statement“error is zero”can represent the situation where the pendulum is very near the vertical position(a linguistic quantification is not precise,hence we are willing to accept any value of the error around e(t)=0as being quantified linguistically by“zero”since this can be considered a better quantification than “possmall”or“negsmall”).•The statement“error is poslarge and change-in-error is possmall”can representthe situation where the pendulum is to the left of the vertical and,since ddt y<0,the pendulum is moving away from the upright position(note that in this case the pendulum is moving counterclockwise).•The statement“error is negsmall and change-in-error is possmall”can represent the situation where the pendulum is slightly to the right of the vertical and,sinced dt y<0,the pendulum is moving toward the upright position(note that in thiscase the pendulum is also moving counterclockwise).It is important for the reader to study each of the cases above to understand how the expert’s linguistics quantify the dynamics of the pendulum(actually,each partially quantifies the pendulum’s state).30Chapter2/Fuzzy Control:The BasicsOverall,we see that to quantify the dynamics of the process we need to have a good understanding of the physics of the underlying process we are trying to control.While for the pendulum problem,the task of coming to a good understanding ofthe dynamics is relatively easy,this is not the case for many physical processes.Quantifying the process dynamics with linguistics is not always easy,and certainlya better understanding of the process dynamics generally leads to a better linguisticquantification.Often,this will naturally lead to a better fuzzy controller providedthat you can adequately measure the system dynamics so that the fuzzy controllercan make the right decisions at the proper time.RulesNext,we will use the above linguistic quantification to specify a set of rules(arule-base)that captures the expert’s knowledge about how to control the plant.Inparticular,for the inverted pendulum in the three positions shown in Figure2.5,we have the following rules(notice that we drop the quotes since the whole rule islinguistic):1.If error is neglarge and change-in-error is neglarge Then force is poslargeThis rule quantifies the situation in Figure2.5(a)where the pendulum has alarge positive angle and is moving clockwise;hence it is clear that we shouldapply a strong positive force(to the right)so that we can try to start thependulum moving in the proper direction.2.If error is zero and change-in-error is possmall Then force is negsmallThis rule quantifies the situation in Figure2.5(b)where the pendulum hasnearly a zero angle with the vertical(a linguistic quantification of zero does notimply that e(t)=0exactly)and is moving counterclockwise;hence we shouldapply a small negative force(to the left)to counteract the movement so that itmoves toward zero(a positive force could result in the pendulum overshootingthe desired position).3.If error is poslarge and change-in-error is negsmall Then force is negsmallThis rule quantifies the situation in Figure2.5(c)where the pendulum is far tothe left of the vertical and is moving clockwise;hence we should apply a smallnegative force(to the left)to assist the movement,but not a big one since thependulum is already moving in the proper direction.Each of the three rules listed above is a“linguistic rule”since it is formed solely from linguistic variables and values.Since linguistic values are not preciserepresentations of the underlying quantities that they describe,linguistic rules arenot precise either.They are simply abstract ideas about how to achieve good controlthat could mean somewhat different things to different people.They are,however,at2.2Fuzzy Control:A Tutorial Introduction31(a)(b)(c)FIGURE2.5Inverted pendulum in various positions.a level of abstraction that humans are often comfortable with in terms of specifyinghow to control a process.The general form of the linguistic rules listed above isIf premise Then consequentAs you can see from the three rules listed above,the premises(which are sometimescalled“antecedents”)are associated with the fuzzy controller inputs and are onthe left-hand-side of the rules.The consequents(sometimes called“actions”)are associated with the fuzzy controller outputs and are on the right-hand-side of therules.Notice that each premise(or consequent)can be composed of the conjunctionof several“terms”(e.g.,in rule3above“error is poslarge and change-in-error is negsmall”is a premise that is the conjunction of two terms).The number of fuzzy controller inputs and outputs places an upper limit on the number of elementsin the premises and consequents.Note that there does not need to be a premise (consequent)term for each input(output)in each rule,although often there is.Rule-BasesUsing the above approach,we could continue to write down rules for the pendulumproblem for all possible cases(the reader should do this for practice,at least fora few more rules).Note that since we only specify afinite number of linguisticvariables and linguistic values,there is only afinite number of possible rules.Forthe pendulum problem,with two inputs andfive linguistic values for each of these,there are at most52=25possible rules(all possible combinations of premiselinguistic values for two inputs).A convenient way to list all possible rules for the case where there are not toomany inputs to the fuzzy controller(less than or equal to two or three)is to use atabular representation.A tabular representation of one possible set of rules for theinverted pendulum is shown in Table2.1.Notice that the body of the table lists thelinguistic-numeric consequents of the rules,and the left column and top row of thetable contain the linguistic-numeric premise terms.Then,for instance,the(2,−1)position(where the“2”represents the row having“2”for a numeric-linguistic valueand the“−1”represents the column having“−1”for a numeric-linguistic value)has a−1(“negsmall”)in the body of the table and represents the rule32Chapter2/Fuzzy Control:The BasicsIf error is poslarge and change-in-error is negsmall Then force is negsmall which is rule3above.Table2.1represents abstract knowledge that the expert hasabout how to control the pendulum given the error and its derivative as inputs.TABLE2.1Rule Table for the Inverted Pendulum“force”“change-in-error”˙eu−2−1012−222210“error”−12210−1e0210−1−2110−1−2−220−1−2−2−2The reader should convince him-or herself that the other rules are also valid and take special note of the pattern of rule consequents that appears in the body of thetable:Notice the diagonal of zeros and viewing the body of the table as a matrixwe see that it has a certain symmetry to it.This symmetry that emerges whenthe rules are tabulated is no accident and is actually a representation of abstractknowledge about how to control the pendulum;it arises due to a symmetry in thesystem’s dynamics.We will actually see later that similar patterns will be foundwhen constructing rule-bases for more challenging applications,and we will showhow to exploit this symmetry in implementing fuzzy controllers.2.2.3Fuzzy Quantification of KnowledgeUp to this point we have only quantified,in an abstract way,the knowledge thatthe human expert has about how to control the plant.Next,we will show how touse fuzzy logic to fully quantify the meaning of linguistic descriptions so that wemay automate,in the fuzzy controller,the control rules specified by the expert.Membership FunctionsFirst,we quantify the meaning of the linguistic values using“membership func-tions.”Consider,for example,Figure2.6.This is a plot of a functionμversus e(t)that takes on special meaning.The functionμquantifies the certainty2that e(t)can be classified linguistically as“possmall.”To understand the way that a mem-bership function works,it is best to perform a case analysis where we show how tointerpret it for various values of e(t):2.The reader should not confuse the term“certainty”with“probability”or“likelihood.”Themembership function is not a probability density function,and there is no underlying probabilityspace.By“certainty”we mean“degree of truth.”The membership function does not quantifyrandom behavior;it simply makes more accurate(less fuzzy)the meaning of linguisticdescriptions.2.2Fuzzy Control:A Tutorial Introduction33•If e(t)=−π/2thenμ(−π/2)=0,indicating that we are certain that e(t)=−π/2is not“possmall.”•If e(t)=π/8thenμ(π/8)=0.5,indicating that we are halfway certain thate(t)=π/8is“possmall”(we are only halfway certain since it could also be“zero”with some degree of certainty—this value is in a“gray area”in terms oflinguistic interpretation).•If e(t)=π/4thenμ(π/4)=1.0,indicating that we are absolutely certain thate(t)=π/4is what we mean by“possmall.”•If e(t)=πthenμ(π)=0,indicating that we are certain that e(t)=πis not “possmall”(actually,it is“poslarge”).FIGURE2.6Membership function forlinguistic value“possmall.”The membership function quantifies,in a continuous manner,whether values ofe(t)belong to(are members of)the set of values that are“possmall,”and hence itquantifies the meaning of the linguistic statement“error is possmall.”This is why itis called a membership function.It is important to recognize that the membershipfunction in Figure2.6is only one possible definition of the meaning of“error is possmall”;you could use a bell-shaped function,a trapezoid,or many others.For instance,consider the membership functions shown in Figure2.7.For some application someone may be able to argue that we are absolutely certain that anyvalue of e(t)nearπ4is still“possmall”and only when you get sufficiently far fromπ4do we lose our confidence that it is“possmall.”One way to characterize this un-derstanding of the meaning of“possmall”is via the trapezoid-shaped membership function in Figure2.7(a).For other applications you may think of membership in the set of“possmall”values as being dictated by the Gaussian-shaped member-ship function(not to be confused with the Gaussian probability density function) shown in Figure2.7(b).For still other applications you may not readily acceptvalues far away fromπ4as being“possmall,”so you may use the membership func-tion in Figure2.7(c)to represent this.Finally,while we often think of symmetric characterizations of the meaning of linguistic values,we are not restricted to these34Chapter 2/Fuzzy Control:The Basicssymmetric representations.For instance,in Figure 2.7(d)we represent that we be-lieve that as e (t )moves to the left of π4we are very quick to reduce our confidencethat it is “possmall,”but if we move to the right of π4our confidence that e (t )is“possmall,”diminishes at a slower rate.(a) Trapezoid.(b) Gaussian.(c) Sharp peak.(d) Skewed triangle.FIGURE 2.7A few membership function choices for representing “error ispossmall.”In summary,we see that depending on the application and the designer (ex-pert),many different choices of membership functions are possible.We will further discuss other ways to define membership functions in Section 2.3.2on page 55.It is important to note here,however,that for the most part the definition of a member-ship function is subjective rather than objective.That is,we simply quantify it in a manner that makes sense to us,but others may quantify it in a different manner.The set of values that is described by μas being “positive small”is called a “fuzzy set.”Let A denote this fuzzy set.Notice that from Figure 2.6we are absolutely certain that e (t )=π4is an element of A ,but we are less certain thate (t )=π16is an element of A .Membership in the set,as specified by the membership function,is fuzzy;hence we use the term “fuzzy set.”We will give a more precise description of a fuzzy set in Section 2.3.2on page 55.A “crisp”(as contrasted to “fuzzy”)quantification of “possmall”can also be specified,but via the membership function shown in Figure 2.8.This membership function is simply an alternative representation for the interval on the real line π/8≤e (t )≤3π/8,and it indicates that this interval of numbers represents “poss-mall.”Clearly,this characterization of crisp sets is simply another way to represent a normal interval (set)of real numbers.While the vertical axis in Figure 2.6represents certainty,the horizontal axis is also given a special name.It is called the “universe of discourse”for the input e (t )since it provides the range of values of e (t )that can be quantified with linguistics2.2Fuzzy Control:A Tutorial Introduction35FIGURE2.8Membership function for acrisp set.and fuzzy sets.In conventional terminology,a universe of discourse for an input oroutput of a fuzzy system is simply the range of values the inputs and outputs cantake on.Now that we know how to specify the meaning of a linguistic value via a mem-bership function(and hence a fuzzy set),we can easily specify the membershipfunctions for all15linguistic values(five for each input andfive for the output)of our inverted pendulum example.See Figure2.9for one choice of membership functions.Notice that(for our later convenience)we list both the linguistic values andthe linguistic-numeric values associated with each membership function.Hence,we see that the membership function in Figure2.6for“possmall”is embeddedamong several others that describe other sizes of values(so that,for instance,the membership function to the right of the one for“possmall”is the one that represents“error is poslarge”).Note that other similarly shaped membership functions makesense(e.g.,bell-shaped membership functions).We will discuss the multitude ofchoices that are possible for membership functions in Section2.3.2on page55.The membership functions at the outer edges in Figure2.9deserve specialattention.For the inputs e(t)and ddt e(t)we see that the outermost membershipfunctions“saturate”at a value of one.This makes intuitive sense as at some point the human expert would just group all large values together in a linguistic de-scription such as“poslarge.”The membership functions at the outermost edges appropriately characterize this phenomenon since they characterize“greater than”(for the right side)and“less than”(for the left side).Study Figure2.9and convince yourself of this.For the output u,the membership functions at the outermost edges cannot be saturated for the fuzzy system to be properly defined(more details on this point will be provided in Section2.2.6on page44and Section2.3.5on page65).The basic reason for this is that in decision-making processes of the type we study,we seek to take actions that specify an exact value for the process input.We do not generally indicate to a process actuator,“any value bigger than,say,10,is acceptable.”It is important to have a clear picture in your mind of how the values of the membership functions change as,for example,e(t)changes its value over time. For instance,as e(t)changes from−π/2toπ/2we see that various membership。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
TEMA put.,8,No.1(2007),33-42.c Uma Publica¸c˜a o da Sociedade Brasileira de Matem´a tica Aplicada e Computacional.Properties of Fuzzy Implications obtainedvia the Interval ConstructorB.R.C.BEDREGAL1,R.H.SANTIAGO2,Departamento de Inform´a tica e Matem´a tica Aplicada,UFRN,Natal,BrazilR.H.S.REISER3,G.P.DIMURO4,Programa de P´o s-Gradua¸c˜a o em Inform´a tica, ESIN,UCPEL,Pelotas,Brasil.Abstract.This work considers an interval extension of fuzzy implication based on the best interval representation of continuous t-norms.Some related properties can be naturally extended and that extension preserves the behaviors of the implications in the interval endpoints.1.IntroductionFuzzy logic is a new form of information theory that is related to but independent of interval mathematics.However,when intervals can be thought as a particular type of fuzzy set,or when interval degrees of membership are used to deal with the uncertainties of the belief degrees of a specialist,it is natural and interesting to consider an interval fuzzy approach[8,9,16,17].Based on this approach,in this work we consider the comparative analysis started with the work of Bedregal and Takahashi[5]integrating both areas:(1)fuzzy logic,as a formal mathematical theory for the representation of uncertainty concerned with fuzzy set theory,which is crucial for the management and control of real systems;and(2)interval mathe-matics,providing the correctness criteria and the optimality properties of numerical computations,and offering a more reliable modelling of real systems.Emerging from the fuzzy set theory,a fuzzy logic can be understood as a superset of classical logic to handle the concept of partial truth and considers the extension principle,from a crisp(discrete)to a continuous(fuzzy)form.This means that truth values are distributed as degrees between completely true and completely false,both represented by the endpoints0and1of the real unity interval[0,1].In addition, continuous t-norms are modelled as standard truth functions of conjunction,and residue as standard truth functions of implication.Thus,the extension of classical logic connectives to the real unit interval is fundamental for the studies on fuzzy logic and,therefore,it is essential for the development of fuzzy systems.This extension 1bedregal@dimap.ufrn.br2regivan@dimap.ufrn.br3reiser@ucpel.tche.br4liz@ucpel.tche.br34Bedregal,Santiago,Reiser and Dimuro must preserve the behaviors of the connectives at the interval endpoints,i.e.,for the crisp values.Moreover,it has been a consensus in this research area that,for the case of the connectives conjunction and disjunction,this extension must also preserve other important properties,such as commutative and associative properties,which result in the notions of triangular norms and triangular conorms.Fuzzy implications play an important role in fuzzy logic,both in the broad sense(heavily applied to fuzzy control,analysis of vagueness in natural language and techniques of soft-computing)and in the narrow sense(developed as a branch of many-valued logic which are able to investigate deep logical questions).How-ever,there is not a consensus among researchers which extra properties fuzzy im-plications must satisfy.In the literature,several fuzzy implication properties have already been proved and their interrelationship with the other kinds of connec-tives were presented.Recently,Bedregal and Takahashi[5,6],working towards the connection between fuzzy logic and interval mathematics,have provided inter-val extensions for the fuzzy connectives considering both correctness(accuracy)and optimality aspects,as properly shown in[20].In a categorical approach,the interval generalization related to both t-norms and automorphisms can be seen as interval representation satisfying the correctness principle of interval computations.In this work,for the case of fuzzy implication,the authors only considered the properties proposed by Fodor and Roubens and the class of R-implications[10].In this present work,the interval constructor introduced by Bedregal and Taka-hashi in[5,6]is used in order to show that most of the properties considered nowadays for fuzzy implication in the literature are also preserved.Then,we focus attention in the interval extension of fuzzy t-norm and fuzzy negation in Sections3 and4,respectively.Further analysis of properties met by interval fuzzy implications are focused in Section4.Finally,our main results are summarized in Section5. 2.Best Interval RepresentationsConsider the real unit interval U=[0,1].Let U be the set of subintervals of U, i.e.,U={[a,b]|0≤a≤b≤1}.The interval set has two projections l:U−→U and r:U−→U defined by l([a,b])=a and r([a,b])=b.As a convention,for each X∈U the projections l(X)and r(X)will also be denoted by X and X,respectively.Several natural partial orders can be defined on U[4].The most used orders in the context of interval mathematics and considered in this work,are the following.1.Product:X≤Y if and only if X≤Y and X≤Y,2.Inclusion order:X⊆Y if and only if X≥Y and X≤Y.A function F:U n−→U is an interval representation of a function f:U n−→U if,for each X∈U n and x∈ X,f( x)∈F( X)[20].An interval can be seen as a representation of a subset of real numbers.In this case we can say that an interval X is a better representation of a real r than an interval Y if X is narrower than Y, i.e.,if X⊆Y.Trivially,this notion could be extended for tuples on intervals.Analogously,an interval function F:U n−→U is a better representation of the function f:U n−→U than G:U n−→U,denoted by G⊑F,if for each X∈U n, F( X)⊆G( X).For each function f:U n−→U, f:U n−→U defined byInterval Fuzzy Implications35f( X)=[inf{f( x)| x∈ X},sup{f( x)| x∈ X}]is well defined and for any other interval representation F of f,F⊑ f.In other words, f returns a narrower interval than any other interval representation of f and is therefore its best interval representation[20].Thus, f has the optimality property of interval algorithms mentioned by Hickey et al.[12],when seen as an algorithm to compute f.Notice that if f is continuous in the usual sense,then for each X∈U n, f( X)={f( x)| x∈ X}=f( X).In the interval analysis,the continuity of interval functions can be obtained as an extension of the real ones.5Moore and Scott continuities are the two most common continuity notions used in interval mathematics.The former is concerned with the metric distance d(X,Y)=max(|X−Y|,|X−Y|)defined over the space of Moore intervals,with intervals seen as a subspace of the real plane emphasizing the related notion of proximity.In the latter,the set of real intervals with reverse inclusion order can be defined as a continuous domain(consistently complete continuous dcpo)[1] whose objects are intervals interpreting partial information of real numbers.Let E=(E,≤E)and D=(D,≤D)be directed complete partially ordered set(dcpo’s).A function f:E→D is called Scott continuous if it is monotonic(i.e.,x≤E y⇒f(x)≤D f(y))and preserves the least upper bound(supremum)of directed setsX)= f(X)).The main result in[20](p.(i.e.,for each directed set A⊆D,f(240)involving Scott and Moore continuities is the following:Theorem2.1.Let f:ℜ−→ℜbe a real function.f is continuous iff f is Scott continuous iff f is Moore continuous.Clearly,the theorem2.1can be adapted to our context,i.e.,for U n instead ofℜ.3.Interval T-NormsGiven a t-norm based propositional fuzzy calculus,one can construct the corre-sponding predicate calculus,which is axiomatizable w.r.t.the general algebraic semantics[11].A triangular norm,t-norm for short,is a function T:U2→U that is commutative,associative,monotonic and has1as neutral element.Following the approach introduced in[5],an extension of the t-norm notion for U is considered: Definition3.1.A function T:U2→U is an interval t-norm if it is commu-tative,associative,monotonic w.r.t.the product and inclusion order and[1,1]is a neutral element.Proposition3.1.If T is a t-norm then T:U2→U is an interval t-norm. Proof.See[5].5A survey relating continuity notions can be found in[19].36Bedregal,Santiago,Reiser and Dimuro 4.Interval Fuzzy NegationRecall that a function N:U→U is a fuzzy negation ifN1:N(0)=1and N(1)=0.N2:If x≥y then N(x)≤N(y),∀x,y∈U.Fuzzy negations satisfying the involutive property:N3:N(N(x))=x,∀x∈U,are called strong fuzzy negations[14,7].Definition4.1.An interval function N:U−→U is an interval fuzzy negation if, for any X,Y in U,the following properties holdN1:N([0,0])=[1,1]and N([1,1])=[0,0].N2:If X≥Y then N(X)≤N(Y).N3:If X⊆Y then N(X)⊇N(Y).If N is also meets the involutive property,it is a strong interval fuzzy negation: N4:N(N(X))=X,∀X∈U.Theorem4.1.Let N:U−→U be a fuzzy negation.Then N is an interval fuzzy negation.If N is a strong fuzzy negation then N is a strong interval fuzzy negation. Proof.N1:Trivially,N1is satisfied.N2:If X≥Y then Y≤X and Y≤X therefore,by N2property, N(X)= [N(X),N(X)]≤[N(Y),N(Y)]= N(Y).N3:If X⊆Y then X≤Y and Y≤X therefore,by N2property, N(X)= [N(X),N(X)]⊆[N(Y),N(Y)]= N(Y).N4:If N is strong, N( N(X))= N([N(X),N(X)])=[N(N(X)),N(N(X))]=X.5.Fuzzy ImplicationsSeveral definitions for fuzzy implication have been given,see for example [2,3,7,11,10,13,15,18,21,22,23].The unique consensus in these defini-tions is that the fuzzy implication should have the same behavior as the classical implication for the crisp case.Thus,I:U2−→U is a fuzzy implication ifI(1,1)=I(0,1)=I(0,0)=1and I(1,0)=0.In the following several reasonable extra properties that can be required for fuzzy implications are listed.In fact,each one of these properties can be found in most of the following papers:[2,7,11,10,13,15,18,21,22,23].I1:If x≤z then I(x,y)≥I(z,y).I2:If y≤z then I(x,y)≤I(x,z).Interval Fuzzy Implications37I3:I(0,y)=1,(falsity principle).I4:I(x,1)=1,(neutrality principle).I5:I(x,I(y,z))=I(y,I(x,z)),(exchange principle).I6:If x≤y then I(x,y)=1,(boundary condition).I7:I(x,x)=1,(identity property).I8:I(x,y)≥y.I9:I is a continuous function,(continuity condition).I10:I(x,y)=I(x,I(x,y)).Other two properties related to fuzzy implications with strong negation[7].I11:If N is a strong negation,I(x,y)=I(N(y),N(x)),(contrapositive w.r.t.N). I12:Let N:U−→U.If N(x)=I(x,0)then N is a strong fuzzy negation. Proposition5.1.Let I be a fuzzy implication.If I satisfies I11and I12then for each x,y∈U,I(x,y)=I(I(y,0),I(x,0)).Proof.See[2].The law of importation relates some fuzzy implications with some t-norms[3]: I13:Let T be a t-norm,I(T(x,y),z)=I(x,I(y,z)).5.1.Interval Fuzzy ImplicationsSince real values in interval mathematics are identified with degenerate intervals, the minimal properties of fuzzy implications can be naturally extended for interval fuzzy degrees,considering the respective degenerate intervals.Thus,a function I:U2−→U is a fuzzy interval implication ifI([1,1],[1,1])=I([0,0],[0,0])=I([0,0],[1,1])=[1,1]and I([1,1],[0,0])=[0,0]. Notice that,by having two natural partial orders on U and two continuity notions, some extra properties can have two natural versions.Extra properties of interval fuzzy implicationsI1:If X≤Z then I(X,Y)≥I(Z,Y).I2:If Y≤Z then I(X,Y)≤I(X,Z).I3:I([0,0],Y)=[1,1].I4:I(X,[1,1])=[1,1].38Bedregal,Santiago,Reiser and DimuroI5:I(X,I(Y,Z))=I(Y,I(X,Z)).I6a:If X≤Y then1∈I(X,Y).I6b:If X⊆Y then1∈I(X,Y).I6c:If[x,x]≤Y then I([x,x],Y)=[1,1].I6d:If X≤[y,y]then I(X,Y[y,y])=[1,1].I7:1∈I(X,X).I8:I(X,Y)≥Y.I9a:I is a Moore continuous function.I9b:I is a Scott continuous function.I10a:I(X,Y)⊆I(X,I(X,Y)).I10b:I([x,x],Y)=I([x,x],I([x,x],Y)).I11:Let N be a strong fuzzy negation.If I(X,Y)=I(N(Y),N(X))then I is contrapositive w.r.t.N.I12:If N:U−→U,N(X)=I(X,[0,0])then N is a strong interval fuzzy negation. I13:Let T be an interval t-norm.I(T(X,Y),Z)=I(X,I(Y,Z)).Starting from any fuzzy implication it is always possible to obtain canonically an interval fuzzy implication.Then,the interval fuzzy implication also meets the optimality property and preserves the same properties satisfied by the fuzzy im-plication.In the next two propositions,the best interval representation of fuzzy implication is shown to be an inclusion-monotonic function in both arguments,and the proofs are straightforward,following from the definition of I. Proposition5.2.If I is a fuzzy implication then I is an interval fuzzy implication. Proposition5.3.Let I be a fuzzy implication.For each X1,X2,Y1,Y2∈U,if X1⊆X2and Y1⊆Y2then I(X1,Y1)⊆ I(X2,Y2).Theorem5.1.Let I be a fuzzy implication.If I satisfies a property Ik,for some k=1,...,10then I satisfies the property I k.Proof.I1:If u∈ I(X,Y),then there exist x∈X and y∈Y such that I(x,y)=u.If X≤Z,then there exists z∈Z such that x≤z.So,by I1,it holds that u=I(x,y)≥I(z,y).On the other hand,if v∈ I(Z,Y),then there exist z∈Z and y∈Y such that I(z,y)=v.If X≤Z then x≤z for some x∈X.So,by I1,it holds that I(x,y)≥I(z,y)=v.Therefore,for each u∈ I(X,Y), there is v∈ I(Z,Y)such that u≥v,and,for each v∈ I(Z,Y),there is u∈ I(X,Y)such that u≥v.Hence,it holds that I(X,Y)≥ I(Z,Y).Interval Fuzzy Implications39I2:If u∈ I(X,Y),then there exist x∈X and y∈Y such that I(x,y)=u.If Y≤Z,then there exists z∈Z such that y≤z.So,by I2,it holds that u=I(x,y)≤I(x,z).On the other hand,if v∈ I(X,Z),then there exist z∈Z and x∈X such that I(x,z)=v.If Y≤Z then y≤z,for some y∈Y.So,by I2,it holds that I(x,y)≥I(x,z)=v.Thus,for each u∈ I(X,Y), there is v∈ I(X,Z)such that u≤v,and for each v∈ I(X,Z),there is u∈ I(X,Y)such that u≤v.Then,it holds that I(X,Y)≤ I(X,Z).I3:Trivially,by I3,for each y∈Y,I(0,y)=1,and so{I(0,y):y∈Y}=[1,1].Thus,since I([0,0],Y)is the narrowest interval containing{I(0,y):y∈Y}, then I([0,0],Y)=[1,1].I4:Trivially,by I4,for each x∈X,I(x,1)=1and so{I(x,1):x∈X}=[1,1].Thus,since I(X,[1,1])is the narrowest interval containing{I(x,1):x∈X}, then I(X,[1,1])=[1,1].I5:If u∈ I(X, I(Y,Z)),then there exist x∈X,y∈Y and z∈Z such that I(x,I(y,z))=u.But,by I5,one has that u=I(y,I(x,z)).So, u∈ I(Y, I(X,Z)),and,therefore, I(X, I(Y,Z))⊆ I(Y, I(X,Z)).Analo-gously,if u∈ I(Y, I(X,Z)),then there exist x∈X,y∈Y and z∈Z such that I(y,I(yx,z))=u.But,by I5,onde has that u=I(x,I(y,z)).So, u∈ I(X, I(XY,Z)),and,therefore, I(Y, I(X,Z))⊆ I(X, I(Y,Z)).Hence,it holds that I(X, I(Y,Z))= I(Y, I(X,Z)).I6a:If X≤Y,then there exist x∈X and y∈Y such that x≤y,and so,by I6, I(x,y)=1.Therefore,it holds that1∈ I(X,Y).I6b:If X⊆Y,then there exist x∈X and y∈Y such that x≤y,and so,by I6, I(x,y)=1.Therefore,it holds that1∈ I(X,Y).I6c:If[x,x]≤Y,then,for each y∈Y,x≤y.So,by I6,for each y∈Y, I(x,y)=1and,therefore,it holds that I([x,x],Y)=[1,1].I6d:If X≤[y,y],then for each x∈X,x≤y.So,by I6,for each x∈X, I(x,y)=1and,therefore,it holds that I(X,[y,y])=[1,1].I7:If x∈X,then I(x,x)=1,and so1∈ I(X,X).I8:By I8,for each x∈X and y∈Y,I(x,y)≥y.So, I(X,Y)≥Y.I9a and I9b:it is straightforward,following from Theorem2.1.I10a:If u∈ I(X,Y),then there exist x∈X and y∈Y such that I(x,y)=u.So, by I10,u=I(x,I(x,y)),and,therefore,u∈ I(X, I(X,Y)).Hence,it holds that I(X,Y)⊆ I(X, I(X,Y)).I10b:By I10a, I([x,x],Y)⊆ I([x,x], I([x,x],Y)).So,it only remains to prove that I([x,x],Y)⊇ I([x,x], I([x,x],Y)).Conisdering u∈ I([x,x], I([x,x],Y)), then there exists y∈Y such that u=I(x,I(x,y)).But,by I10,onde has that I(x,I(x,y))=I(x,y).So,u∈ I([x,x],Y),and,therefore,it holds that I([x,x],Y)⊇ I([x,x], I([x,x],Y)).40Bedregal,Santiago,Reiser and Dimuro The preservation of properties I11,I12and I13will be proved separately,because another connective will be considered.Proposition5.4.Let I be a fuzzy implication and N be a fuzzy strong negation, such that I is contrapositive w.r.t.N,i.e.,it satisfies I11.Then I is contrapositive w.r.t. N,i.e.,it satisfies I11.Proof.If u∈ I(X,Y),then there exist x∈X and y∈Y such that I(x,y)=u. But,by I11,one has that I(x,y)=I(N(y),N(x)).Since N(y)∈ N(Y)and N(x)∈ N(X),then u∈ I( N(Y), N(X)).So,it holds that I(X,Y)⊆ I( N(Y), N(X)).On the other hand,if u∈ I( N(Y), N(X)),then there exist v∈ N(Y)and w∈ N(X) such that I(v,w)=u.But,since v∈ N(Y)and w∈ N(X),there exist y∈Y and x∈X such that N(y)=v and N(x)=w.So,it holds that I(N(y),N(x))=u. But,by I11,onde has that I(N(y),N(x))=I(x,y).Then,it holds that u∈ I(X,Y) and I(X,Y)= I( N(Y), N(X)).Proposition5.5.Let I be a fuzzy implication.If I satisfies a property I12,then the interval function N:U−→U,defined by N(X)= I(X,[0,0])is a strong interval fuzzy negation,i.e.satisfy the property I12.Proof.By I12,N:U−→U defined by N(x)=I(x,0)is a strong fuzzy implication, and,therefore,by Theorem4.1, N is a strong interval fuzzy negation.We will prove that N= N.Consider X∈U.If u∈N(X),then there exists x∈X such that I(x,0)=u,and,therefore,such that N(x)=u.So,u∈ N(X).Conversely,if u∈ N(X)then there exist x∈X such that N(x)=u.But,by I12,onde has that I(x,0)=u.So,it holds that u∈ I(X,[0,0]),i.e.,u∈N(X).Therefore,one concludes that N= N.Proposition5.6.Let I be a fuzzy implication and T be a t-norm,such that I satisfy the law of importation w.r.t.T,i.e.,it satisfies I13.Then I satisfy the property I13w.r.t. T.Proof.If u∈ I( T(X,Y),Z),then there exist v∈ T(X,Y)and z∈Z such that u= I(v,z).But,if v∈ T(X,Y),then there exist x∈X and y∈Y such that v=T(x,y). So,u=I(T(x,y),z),and,therefore,by property I13,u=I(x,I(y,z)).Thus,since x∈X and I(y,z)∈ I(Y,Z),one has that u∈ I(X, I(Y,Z)).Therefore,it holds that I( (T)(X,Y),Z)⊆ I(X, I(Y,Z)).On the other hand,if u∈ I(X, I(Y,Z)), then there exist x∈X and v∈ I(Y,Z)such that u=I(x,v).But,if v∈ I(Y,Z), then there exist y∈Y and z∈Z such that v=I(y,z).So,u=I(x,I(y,z)),and, therefore,by property I13,onde has that u=I(T(x,y),z).Thus,since T(x,y)∈ T(X,Y)and z∈Z,it holds that u∈ I( T(X,Y),Z).Therefore,one concludes that I( T(X,Y),Z)= I(X, I(Y,Z)).6.Final RemarksIn this paper,we mainly discussed under which conditions generalized fuzzy impli-cations applied to interval values preserve properties of canonical forms generatedInterval Fuzzy Implications41 by interval t-norms.It was shown that properties of fuzzy logic can be naturally extended for interval fuzzy degrees considering the respective degenerate intervals. The results are important not only for analyzing deductive systems in mathematical depth but also as foundations of methods of fuzzy logic in broad sense.AcknowledgementsThis work is partially supported by CNPq(Proc.470871/2004-0).The authors are grateful to the referees for their valuable suggestions.Resumo.Este trabalho considera a extens˜a o intervalar da implica¸c˜a o fuzzy baseada no conceito de melhor representa¸c˜a o intervalar de t-normas cont´ınuas,previamente introduzido por Bedregal e Takahashi.As correspondentes propriedades foram analisadas e verificou-se que o comportamento das implica¸c˜o es nos extremos do intervalo unit´a rio pode ser preservado e naturalmente estendido. References[1]S.Abramsky,A.Jung,“Domain Theory.Handbook of Logic in ComputerScience”,Clarendon Press,1994.[2]M.Baczynski,Residual implications revisited.Notes on the Smets-Magrez,Fuzzy Sets and Systems,145,No.2(2004),267-277.[3]J.Balasubramaniam,Yager’s new class of implications J f and some classicaltautologies,Information Sciences,(2006).[4]R.Bedregal,B.Bedregal,Intervals as a domain constructor,in“Seleta doXXIII CNMAC”(E.X.L.de Andrade,J.M.Balthazar,S.M.Gomes,G.N.Silvae A.Sri Ranga,eds.),TEMA-Tendˆe ncias em Matem´a tica Aplicada e Com-putacional,Vol.2,pp.43-52,SBMAC,2001.[5]B.Bedregal,A.Takahashi,The Best interval representation of T-norms andautomorphisms,Fuzzy Sets and Systems157,No.24(2006),3220–3230. [6]B.Bedregal,A.Takahashi,Interval valued versions of T-conorms,fuzzy nega-tions and fuzzy implications,in“2006IEEE Intl.Conf.on Fuzzy Systems (Fuzz-IEEE2006)”,July16-21,2006,Vancouver-Canada,pp.1981–1987,2006.[7]H.Bustince,P.Burilo,F.Soria,Automorphism,negations and implicationoperators,Fuzzy Sets and Systems,134(2003),209-229.[8]D.Dubois,H.Prade,“Fuzzy Sets and Systems”,Academic Press,New York,1996.[9]D.Dubois,H.Prade,Interval-valued fuzzy sets,possibility theory and im-precise probability,in“Proc.Intl.Conf.Fuzzy Logic and Technology”,pp.314–319,Barcelona,2005.[10]J.Fodor,M.Roubens,“Fuzzy Preference Modelling and Multicriteria DecisionSupport”,Kluwer Academic Publisher,Dordrecht,1994.42Bedregal,Santiago,Reiser and Dimuro [11]J.Fodor,On fuzzy implication operators,Fuzzy Sets and Systems,42(1991),293-300.[12]T.Hickey,Q.Ju,M.Emdem,Interval arithmetic:from principles to imple-mentation,Journal of the ACM,48,No.5(2001),1038-1068.[13]R.Horcik,M.Navara,Validation sets in fuzzy logics,Kybernetika,38,No.2(2002),319-326.[14]E.Klement,R.Mesiar,E.Pap,“Triangular Norms”,Kluwer Academic Pub-lisher,Dordrecht,2000.[15]J.Leski,ε-Insensitive learning techniques for approximate reasoning system,Int.Jour.of Computational Cognition,1,No.1(2003),21–77.[16]R.Moore,W.Lodwick,Interval analysis and fuzzy set theory,Fuzzy Sets andSystems,135,No.1(2003),5–9.[17]H.Nguyen,V.Kreinovich,Q.Zuo,Interval-valued degrees of belief:applica-tions of interval computations to expert systems and intelligent control,Intl.J.Uncertainty,Fuzziness,Knowledge-Based Syst.,5,No.3(1997),317–358.[18]D.Ruan,E.Kerre,Fuzzy implication operators and generalized fuzzy methodsof cases,Fuzzy Sets and Systems,54,(1993),23–37.[19]R.Santiago,B.Bedregal,B.Aci´o ly,Comparing continuity of interval functionbased on Moore and Scott continuity,EJMC,2,No.1(2005),1–14.[20]R.Santiago,B.Bedregal,B.Aci´o ly,Formal aspects of correctness and optimal-ity in interval computations,Formal Aspects of Computing,18,No.2(2006), 231-243.[21]R.Yager,On the implication operator in fuzzy logic,Information Sciences,31(1983),141-164.[22]R.Yager,On global requirements for implication operators in fuzzy modusponens,Fuzzy Sets and Systems,106(1999),3-10.[23]R.Yager,On some new classes of implication operators and their role in ap-proximate reasoning,Information Sciences,167(2004),193-216.。
