高中数学 第二章 解三角形 2.3 解三角形的实际应用举例 全方位聚焦正余弦定理的应用素材 北师大版5 精
高中数学 第二章 解三角形 2.3 解三角形的实际应用举例课件高二必修5数学课件

们的关键是根据题意和图形及有关概念,确定所求的角在哪个三角形中,该
三角形中已知哪些量,需要求哪些量.通常是首先根据题意,从实际问题中抽
象出一个或几个三角形,然后通过解这些三角形,得到所求的量,从而得到
实际问题的解.
2.对于本例还要注意相遇时两船航行的时间相等这一条件,应用余弦定
理构建出方程是关键所在.
首页
探究(tànjiū)
一
探究(tànjiū)
二
探究(tànjiū)
三
合作学习
当堂检测
规范解答
解:如图,若设甲、乙两船在 B 处相遇,所需时间为 t h,这样由题
设知,AC=10 n mile,AB=20 3t n mile,BC=20t n mile,
∠ACB=45°+75°=120°.
设甲船沿方位角(45°+θ)方向航行.
§3
解三角形的实际应用(yìngyòng)举例
12/8/2021
第一页,共三十页。
-1-
首页
自主预习
学 习 目 标
合作学习
思 维 脉 络
1.能运用正弦定理、余弦定理等知识解决
测量中的距离问题、高度问题、角度问题.
2.通过解三角形实际应用的学习,提高解
决实际问题的能力.
12/8/2021
第二页,共三十页。
一
探究(tànjiū)
二
探究(tànjiū)
三
探究二
自主预习
合作学习
当堂检测
规范解答
测量高度问题
【例2】 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的
两个测点C与D.现测得∠BCD=α,∠BDC=β,CD=s,并在点C测得塔顶A的仰角
正弦定理和余弦定理的应用举例(解析版)

正弦定理和余弦定理的应用举例考点梳理1.用正弦定理和余弦定理解三角形的常见题型测量距离问题、高度问题、角度问题、计算面积问题、航海问题、物理问题等.2.实际问题中的常用角(1)仰角和俯角与目标线在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线上方的角叫仰角,目标视线在水平视线下方的角叫俯角(如图①).(2)方向角:相对于某正方向的水平角,如南偏东30°,北偏西45°,西偏北60°等;(3)方位角指从正北方向顺时针转到目标方向线的水平角,如B点的方位角为α(如图②).(4)坡度:坡面与水平面所成的二面角的度数.【助学·微博】解三角形应用题的一般步骤(1)阅读理解题意,弄清问题的实际背景,明确已知与未知,理清量与量之间的关系.侧重考查从实际问题中提炼数学问题的能力.(2)根据题意画出示意图,将实际问题抽象成解三角形问题的模型.(3)根据题意选择正弦定理或余弦定理求解.(4)将三角形问题还原为实际问题,注意实际问题中的有关单位问题、近似计算的要求等.解三角形应用题常有以下两种情形(1)实际问题经抽象概括后,已知量与未知量全部集中在一个三角形中,可用正弦定理或余弦定理求解.(2)实际问题经抽象概括后,已知量与未知量涉及到两个或两个以上的三角形,这时需作出这些三角形,先解够条件的三角形,然后逐步求解其他三角形,有时需设出未知量,从几个三角形中列出方程(组),解方程(组)得出所要求的解.考点自测1.(2012·江苏金陵中学)已知△ABC的一个内角为120°,并且三边长构成公差为4的等差数列,则三角形的面积等于________.解析记三角形三边长为a-4,a,a+4,则(a+4)2=(a-4)2+a2-2a(a-4)cos120°,解得a=10,故S=12×10×6×sin 120°=15 3.答案15 32.若海上有A,B,C三个小岛,测得A,B两岛相距10海里,∠BAC=60°,∠ABC=75°,则B,C间的距离是________海里.解析由正弦定理,知BCsin 60°=ABsin(180°-60°-75°).解得BC=56(海里).答案5 63.(2013·日照调研)如图,一船自西向东匀速航行,上午10时到达一座灯塔P 的南偏西75°距塔68海里的M处,下午2时到达这座灯塔的东南方向的N处,则这只船的航行速度为________海里/时.解析由正弦定理,得MN=68sin 120°sin 45°=346(海里),船的航行速度为3464=1762(海里/时).答案176 24.在△ABC中,若23ab sin C=a2+b2+c2,则△ABC的形状是________.解析由23ab sin C=a2+b2+c2,a2+b2-c2=2ab cos C相加,得a2+b2=2ab sin ⎝ ⎛⎭⎪⎫C +π6.又a 2+b 2≥2ab ,所以 sin ⎝ ⎛⎭⎪⎫C +π6≥1,从而sin ⎝ ⎛⎭⎪⎫C +π6=1,且a =b ,C =π3时等号成立,所以△ABC 是等边三角形.答案 等边三角形5.(2010·江苏卷)在锐角△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .若b a +a b=6cos C ,则tan C tan A +tan C tan B 的值是________.解析 利用正、余弦定理将角化为边来运算,因为b a +a b =6cos C ,由余弦定理得a 2+b 2ab =6·a 2+b 2-c 22ab ,即a 2+b 2=32c 2.而tan C tan A +tan C tan B =sin C cos C ⎝ ⎛⎭⎪⎫cos A sin A +cos B sin B =sin C cos C ·sin Csin A sin B =c 2ab ·a 2+b 2-c 22ab=2c 2a 2+b 2-c 2=2c 232c 2-c 2=4. 答案 4考向一 测量距离问题【例1】 如图所示,A 、B 、C 、D 都在同一个与水平面垂直的平面内,B 、D 为两岛上的两座灯塔的塔顶.测量船于水面A 处测得B 点和D 点的仰角分别为75°,30°,于水面C 处测得B 点和D 点的仰角均为60°,AC =0.1 km.(1)求证:AB =BD ;(2)求BD .(1)证明 在△ACD 中,∠DAC =30°,∠ADC =60°-∠DAC =30°,所以CD =AC =0.1.又∠BCD =180°-60°-60°=60°,故CB 是△CAD 底边AD 的中垂线,所以BD =BA .(2)解 在△ABC 中,AB sin ∠BCA =AC sin ∠ABC, 即AB =AC sin 60°sin 15°=32+620(km),因此,BD =32+620(km)故B 、D 的距离约为32+620 km.[方法总结] (1)利用示意图把已知量和待求量尽量集中在有关的三角形中,建立一个解三角形的模型.(2)利用正、余弦定理解出所需要的边和角,求得该数学模型的解.(3)应用题要注意作答.【训练1】 隔河看两目标A 与B ,但不能到达,在岸边先选取相距3千米的C ,D 两点,同时测得∠ACB =75°,∠BCD =45°,∠ADC =30°,∠ADB =45°(A ,B ,C ,D 在同一平面内),求两目标A ,B 之间的距离.解 如题图所示,在△ACD 中,∵∠ADC =30°,∠ACD =120°,∴∠CAD =30°,AC =CD =3(千米).在△BDC 中,∠CBD =180°-45°-75°=60°.由正弦定理,可得BC =3sin 75°sin 60°=6+22(千米).在△ABC 中,由余弦定理,可得AB 2=AC 2+BC 2-2AC ·BC cos ∠BCA ,即AB 2=(3)2+⎝ ⎛⎭⎪⎫6+222-23·6+22cos 75°=5, ∴AB =5(千米).所以两目标A ,B 间的距离为5千米.考向二 测量高度问题【例2】 (2010·江苏)某兴趣小组要测量电视塔AE 的高度H (单位:m)如图所示,垂直放置的标杆BC 的高度h =4 m ,仰角∠ABE =α,∠ADE =β.(1)该小组已测得一组α、β的值,算出了tan α=1.24,tan β=1.20,请据此算出H 的值;(2)该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d (单位:m),使α与β之差较大,可以提高测量精度.若电视塔的实际高度为125 m ,试问d 为多少时,α-β最大?解 (1)由AB =H tan α,BD =h tan β,AD =H tan β及AB +BD =AD 得H tan α+h tan β=H tan β解得H =h tan αtan α-tan β=4×1.241.24-1.20=124. 因此,算出的电视塔的高度H 是124 m.(2)由题设知d =AB ,得tan α=H d .由AB =AD -BD =H tan β-h tan β,得tan β=H -h d ,所以tan(α-β)=tan α-tan β1+tan αtan β=h d +H (H -h )d ≤h 2H (H -h ), 当且仅当d =H (H -h )d,即d =H (H -h )=125×(125-4)=555时,上式取等号.所以当d =555时,tan(α-β)最大.因为0<β<α<π2,则0<α-β<π2,所以当d =555时,α-β最大.故所求的d 是55 5 m.[方法总结] (1)测量高度时,要准确理解仰、俯角的概念.(2)分清已知和待求,分析(画出)示意图,明确在哪个三角形应用正、余弦定理.(3)注意竖直线垂直于地面构成的直角三角形.【训练2】如图所示,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,现测得∠BCD=α,∠BDC=β,CD=s,并在点C测得塔顶A 的仰角为θ,求塔高AB.解在△BCD中,∠CBD=π-α-β,由正弦定理得BCsin∠BDC=CDsin∠CBD,所以BC=CD sin∠BDCsin∠CBD=s·sin βsin(α+β)在Rt△ABC中,AB=BC tan∠ACB=s tan θsin βsin(α+β).考向三运用正、余弦定理解决航海应用问题【例3】我国海军在东海举行大规模演习.在海岸A处,发现北偏东45°方向,距离A(3-1)km的B处有一艘“敌舰”.在A处北偏西75°的方向,距离A 2 km的C处的“大连号”驱逐舰奉命以10 3 km/h的速度追截“敌舰”.此时,“敌舰”正以10 km/h的速度从B处向北偏东30°方向逃窜,问“大连号”沿什么方向能最快追上“敌舰”?解设“大连号”用t h在D处追上“敌舰”,则有CD=103t,BD=10t,如图在△ABC中,∵AB=3-1,AC=2,∠BAC=120°,∴由余弦定理,得BC2=AB2+AC2-2AB·AC·cos∠BAC=(3-1)2+22-2·(3-1)·2·cos 120°=6∴BC=6,且sin∠ABC=ACBC·sin∠BAC=26·32=22.∴∠ABC=45°,∴BC与正北方向垂直.∴∠CBD=90°+30°=120°,在△BCD中,由正弦定理,得sin∠BCD=BD·sin∠CBDCD=10t sin 120°103t=12,∴∠BCD=30°.即“大连号”沿东偏北30°方向能最快追上“敌舰”.[方法总结] 用解三角形知识解决实际问题的步骤:第一步:将实际问题转化为解三角形问题;第二步:将有关条件和求解的结论归结到某一个或两个三角形中.第三步:用正弦定理和余弦定理解这个三角形.第四步:将所得结果转化为实际问题的结果.【训练3】(2013·广州二测)如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B 处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上,此时到达C处.(1)求渔船甲的速度;(2)求sin α的值.解(1)依题意知,∠BAC=120°,AB=12(海里),AC=10×2=20(海里),∠BCA=α,在△ABC中,由余弦定理,得BC2=AB2+AC2-2AB·AC·cos∠BAC=122+202-2×12×20×cos 120°=784.解得BC=28(海里).所以渔船甲的速度为BC2=14海里/时.(2)在△ABC中,因为AB=12(海里),∠BAC=120°,BC=28(海里),∠BCA=α,由正弦定理,得ABsin α=BCsin 120°.即sin α=AB sin 120°BC=12×3228=3314.高考经典题组训练1.(四川卷改编)如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连结EC、ED,则sin∠CED=________.解析在Rt△EAD和Rt△EBC中,易知ED=2,EC=5,在△DEC中,由余弦定理得cos∠CED=ED2+EC2-CD22ED·EC=2+5-12×2×5=31010.∴sin∠CED=1010.答案10 102.(2011·新课标卷)在△ABC中,B=60°,AC=3,则AB+2BC的最大值为________.解析由正弦定理知ABsin C=3sin 60°=BCsin A,∴AB=2sin C,BC=2sin A.又A+C=120°,∴AB+2BC=2sin C+4sin(120°-C)=2(sin C+2sin 120°cos C -2cos 120°sin C)=2(sin C+3cos C+sin C)=2(2sin C+3cos C)=27sin(C +α),其中tan α=32,α是第一象限角.由于0°<C <120°,且α是第一象限角,因此AB +2BC 有最大值27.答案 273.(湖北卷改编)若△ABC 的三边长为连续三个正整数,且A >B >C,3b =20a cos A ,则sin A ∶sin B ∶sin C =________.解析 由A >B >C ,得a >b >c .设a =c +2,b =c +1,则由3b =20a cos A ,得3(c+1)=20(c +2)·(c +1)2+c 2-(c +2)22(c +1)c,即3(c +1)2c =10(c +1)(c +2)(c -3),解得c =4,所以a =6,b =5.答案 6∶5∶44.(2·陕西卷)如图,A ,B 是海面上位于东西方向相距5(3+3)海里的两个观测点,现位于A 点北偏东45°,B 点北偏西60°的D 点有一艘轮船发出求救信号,位于B 点南偏西60°且与B 点相距203海里的C 点的救援船立即前往营救,其航行速度为30海里/时,该救援船达到D 点需要多长时间?解 由题意知AB =5(3+3)海里,∠DBA =90°-60°=30°,∠DAB =90°-45°=45°,所以∠ADB =180°-(45°+30°)=105°,在△ADB 中,由正弦定理得DB sin ∠DAB =AB sin ∠ADB, 所以DB =AB ·sin ∠DAB sin ∠ADB =5(3+3)·sin 45°sin 105°=5(3+3)·sin 45°sin 45°cos 60°+cos 45°sin 60°=103(海里), 又∠DBC =∠DBA +∠ABC =30°+(90°-60°)=60°, BC =203(海里),在△DBC 中,由余弦定理得 CD 2=BD 2+BC 2-2BD ·BC ·cos ∠DBC=300+1 200-2×103×203×12=900,所以CD =30(海里),则需要的时间t =3030=1(小时).所以救援船到达D 点需要1小时.(江苏省2013届高三高考压轴数学试题)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知a =5,b =4,cos(A -B )=3231. (Ⅰ) 求sin B 的值;(Ⅱ) 求cos C 的值.分层训练A 级 基础达标演练(时间:30分钟 满分:60分)一、填空题(每小题5分,共30分)1.若渡轮以15 km/h 的速度沿与水流方向成120°角的方向行驶,水流速度为4km/h ,则渡轮实际航行的速度为(精确到0.1 km/h)________.答案 13.5 km/h2.江岸边有一炮台高30 m ,江中有两条船,船与炮台底部在同一水面上,由炮台顶部测得俯角分别为45°和60°,而且两条船与炮台底部连线成30°角,则两条船相距________m.解析 如图,OM =AO tan 45°=30 (m),ON =AO tan 30°=33×30=10 3 (m),由余弦定理得,MN = 900+300-2×30×103×32=300=10 3 (m). 答案 10 33.某人向正东方向走x km 后,他向右转150°,然后朝新方向走3 km ,结果他离出发点恰好 3 km ,那么x 的值为________.解析 如图,在△ABC 中,AB =x ,BC =3,AC =3,∠ABC =30°,由余弦定理得(3)2=32+x 2-2×3x ×cos 30°,即x 2-33x +6=0,解得x 1=3,x 2=23,经检测均合题意.答案 3或2 34.如图所示,为了测量河对岸A ,B 两点间的距离,在这一岸定一基线CD ,现已测出CD =a 和∠ACD =60°,∠BCD =30°,∠BDC=105°,∠ADC =60°,则AB 的长为________.解析 在△ACD 中,已知CD =a ,∠ACD =60°,∠ADC=60°,所以AC =a .①在△BCD 中,由正弦定理可得BC =a sin 105°sin 45°=3+12a .②在△ABC 中,已经求得AC 和BC ,又因为∠ACB =30°,所以利用余弦定理可以求得A ,B 两点之间的距离为AB =AC 2+BC 2-2AC ·BC ·cos 30°=22a .答案 22a5.(2010·新课标全国卷)在△ABC 中,D 为边BC 上一点,BD =12CD ,∠ADB =120°,AD =2,若△ADC 的面积为3-3,则∠BAC =________.解析 由A 作垂线AH ⊥BC 于H .因为S △ADC =12DA ·DC ·sin 60°=12×2×DC ·32=3-3,所以DC =2(3-1),又因为AH ⊥BC ,∠ADH =60°,所以DH =AD cos 60°=1,∴HC =2(3-1)-DH =23-3.又BD =12CD ,∴BD =3-1,∴BH =BD +DH = 3.又AH =AD ·sin 60°=3,所以在Rt △ABH 中AH =BH ,∴∠BAH =45°.又在Rt △AHC 中tan ∠HAC =HC AH =23-33=2-3, 所以∠HAC =15°.又∠BAC =∠BAH +∠CAH =60°,故所求角为60°.答案 60°6.如图,为测得河对岸塔AB 的高,先在河岸上选一点C ,使C 在塔底B 的正东方向上,测得点A 的仰角为60°,再由点C 沿北偏东15°方向走10米到位置D ,测得∠BDC =45°,则塔AB 的高是________米.解析 在△BCD 中,CD =10(米),∠BDC =45°,∠BCD =15°+90°=105°,∠DBC =30°,BC sin 45°=CD sin 30°,BC =CD sin 45°sin 30°=102(米).在Rt △ABC 中,tan 60°=AB BC ,AB =BC tan 60°=106(米).答案 10 6二、解答题(每小题15分,共30分)7.(2011·常州七校联考)如图,在半径为3、圆心角为60°的扇形的弧上任取一点P ,作扇形的内接矩形PNMQ ,使点Q 在OA 上,点N 、M 在OB 上,设矩形PNMQ 的面积为y ,(1)按下列要求写出函数的关系式:①设PN =x ,将y 表示成x 的函数关系式;②设∠POB =θ,将y 表示成θ的函数关系式;(2)请你选用(1)中的一个函数关系式,求出y 的最大值.解 (1)①∵ON =OP 2-PN 2=3-x 2,OM =33x ,∴MN =3-x 2-33x ,∴y =x ⎝⎛⎭⎪⎫3-x 2-33x ,x ∈⎝ ⎛⎭⎪⎫0,32. ②∵PN =3sin θ,ON =3cos θ,OM =33×3sin θ=sin θ,∴MN =ON -OM =3cos θ-sin θ,∴y =3sin θ(3cos θ-sin θ),即y =3sin θcos θ-3sin 2θ,θ∈⎝ ⎛⎭⎪⎫0,π3. (2)选择y =3sin θcos θ-3sin 2θ=3sin ⎝ ⎛⎭⎪⎫2θ+π6-32, ∵θ∈⎝ ⎛⎭⎪⎫0,π3,∴2θ+π6∈⎝ ⎛⎭⎪⎫π6,5π6,∴y max =32. 8.某港口O 要将一件重要物品用小艇送到一艘正在航行的轮船上.在小艇出发时,轮船位于港口O 北偏西30°且与该港口相距20海里的A 处,并正以30海里/时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v 海里/时的航行速度匀速行驶,经过t 小时与轮船相遇.(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?(2)假设小艇的最高航行速度只能达到30海里/时,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由. 解 (1)设相遇时小艇航行的距离为S 海里,则 S =900t 2+400-2·30t ·20·cos (90°-30°)=900t 2-600t +400= 900⎝ ⎛⎭⎪⎫t -132+300. 故当t =13时,S min =103(海里),此时v =10313=303(海里/时).即,小艇以303海里/时的速度航行,相遇时小艇的航行距离最小.(2)设小艇与轮船在B 处相遇,则v 2t 2=400+900t 2-2·20·30t ·cos(90°-30°),故v 2=900-600t +400t 2,∵0<v ≤30,∴900-600t +400t 2≤900,即2t 2-3t ≤0,解得t ≥23.又t =23时,v =30海里/时.故v=30海里/时时,t取得最小值,且最小值等于2 3.此时,在△OAB中,有OA=OB=AB=20海里,故可设计航行方案如下:航行方向为北偏东30°,航行速度为30海里/时,小艇能以最短时间与轮船相遇.。
高考数学考点专题:三角函数与解三角形:正弦定理和余弦定理应用举例

正弦定理和余弦定理应用举例【考点梳理】1.应用正弦定理和余弦定理解三角形的常见题型主要有测量距离问题、高度问题、角度问题、计算面积问题、航海问题、物理问题等.2.实际问题中的常用角(1)仰角和俯角与目标线在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线上方叫仰角,目标视线在水平视线下方叫俯角(如图①).图①图②(2)方向角:相对于某正方向的水平角,如南偏东30°,北偏西45°等.(3)方位角指从正北方向顺时针转到目标方向线的水平角,如B点的方位角为α(如图②).(4)坡度:坡面与水平面所成的二面角的正切值.【教材改编】1.(必修5 P19A组T7改编)如图,飞机的航线和山顶在同一个铅垂面内,若飞机的高度为海拔18 km,速度为1 000 km/h,飞行员先看到山顶的俯角为30°,经过1 min后又看到山顶的俯角为75°,则山顶的海拔高度为(精确到0.1 km)()A.11.4 km B.6.6 kmC.6.5 km D.5.6 km[答案] B[解析] ∵AB =1 000×1 000×160=50 0003 m , ∴BC =AB sin 45°·sin 30°=50 00032m. ∴航线离山顶h =50 00032×sin 75°≈11.4 km. ∴山高为18-11.4=6.6 km.2.(必修5 P 19A 组T 1改编)一艘船以每小时15 km 的速度向东航行,船在A 处看到一个灯塔M 在北偏东60°方向,行驶4 h 后,船到达B 处,看到这个灯塔在北偏东15°方向,这时船与灯塔的距离为( )A .15 2 kmB .30 2 kmC .45 2 kmD .60 2 km[答案] B[解析] 如图所示,依题意有AB =15×4=60,∠DAC =60°,∠CBM =15°, ∴∠MAB =30°,∠AMB =45°.在△AMB 中,由正弦定理,得60sin 45°=BM sin 30°,解得BM =302,故选B.3.(必修5 P 14例5改编)如图,测量河对岸的塔高AB 时可以选与塔底B 在同一水平面内的两个测点C 与D ,测得∠BCD =15°,∠BDC =30°,CD =30 m ,并在点C 测得塔顶A 的仰角为60°,则塔高AB 等于( )A .5 6 mB .15 3 mC .5 2 mD .15 6 m[答案] D[解析] 在△BCD 中,∠CBD =180°-15°-30°=135°.由正弦定理得BC sin 30°=30sin 135°,解得BC =152(m).在Rt △ABC 中,AB =BC tan ∠ACB =152×3=156(m).4.(必修5 P 24A 组T 5改编)如图,从气球A 上测得正前方的河流的两岸B ,C 的俯角分别为75°,30°,此时气球的高是60 m ,则河流的宽度BC 等于( )A .240(3-1)mB .180(2-1)mC .120(3-1)mD .30(3+1)m[答案] C[解析] 如图,在△ACD 中,∠CAD =90°-30°=60°,AD =60 m ,所以CD =AD ·tan 60°=603(m).在△ABD 中,∠BAD =90°-75°=15°,所以BD =AD ·tan 15°=60(2-3)(m). 所以BC =CD -BD =603-60(2-3)=120(3-1)(m).5.(必修5 P 13练习T 1改编)如图,一艘船上午9:30在A 处测得灯塔S 在它的北偏东30°的方向,之后它继续沿正北方向匀速航行,上午10:00到达B 处,此时又测得灯塔S 在它的北偏东75°的方向,且与它相距8 2 n mile.此船的航速是________n mile/h.[答案] 32[解析] 设航速为v n mile/h ,在△ABS 中AB =12v ,BS =82,∠BSA =45°,由正弦定理得82sin 30°=12v sin 45°,则v =32.6.(必修5 P 15练习T 1改编)如图,在山脚A 测得山顶P 的仰角为α,沿倾斜角为β的斜坡向上走a 米到达B ,在B 测得山顶P 的仰角为γ,则山高PQ =________米.[答案] a sin αsin (γ-β)sin (γ-α)[解析] 在△APB 中,∠P AB =α-β,∠APB =γ-α,∠ABP =180°-(γ-β),由正弦定理得AP sin ∠ABP =AB sin ∠APB, ∴AP =a sin [180°-(γ-β)]sin (γ-α) =a sin (γ-β)sin (γ-α),∴PQ =AP sin α=a sin αsin (γ-β)sin (γ-α).7.(必修5 P 13例3改编)如图所示,为测量一树的高度,在地面上选取A ,B 两点,从A ,B 两点分别测得树尖的仰角为30°,45°,且A ,B 两点间的距离为60 m ,则树的高度为________m.[答案] 30+30 3[解析] 在△P AB 中,∠P AB =30°,∠APB =15°,AB =60,sin 15°=sin(45°-30°)=sin 45°cos 30°-cos 45°sin 30°=22×32-22×12=6-24,由正弦定理得PB sin 30°=AB sin 15°, ∴BP =12×606-24=30(6+2),∴树的高度为PB ·sin 45°=30(6+2)×22=(30+303)m.8.(必修5 P 15例6改编)某渔轮在航行中不幸遇险,发出呼救信号,我海军舰艇在A 处获悉后,立即测出该渔轮在方位角为45°,距离为10 n mile 的C 处,并测得渔轮正沿方位角为105°的方向,以9 n mile/h 的速度向某小岛靠拢,我海军舰艇立即以21 n mile/h 的速度前去营救,求舰艇的航向和靠近渔轮所需的时间.⎝ ⎛⎭⎪⎫注:sin 22°≈3314 [解析] 如图所示,根据题意可知AC =10,∠ACB =120°,设舰艇靠近渔轮所需的时间为t h ,并在B 处与渔轮相遇,则AB =21t ,BC =9t ,在△ABC 中,根据余弦定理得AB 2=AC 2+BC 2-2AC ·BC ·cos 120°,所以212t 2=102+81t 2+2×10×9t ×12,即360t 2-90t -100=0,解得t =23或t =-512(舍去).所以舰艇靠近渔轮所需的时间为23 h.此时AB =14,BC =6.在△ABC 中,根据正弦定理,得BC sin ∠CAB=AB sin 120°,所以sin ∠CAB =6×3214=3314,即∠CAB ≈22°或∠CAB ≈158 °(舍去),即舰艇航行的方位角为45°+22°=67°. 所以舰艇以67°的方位角航行,需23 h 才能靠近渔轮.9.(必修5 P 11例2改编)如图,隔河看两目标A 与B ,但不能到达,在岸边先选取相距3千米的C ,D 两点,同时,测得∠ACB =75°,∠BCD =45°,∠ADC =30°,∠ADB =45°(A ,B ,C ,D 在同一平面内),求两目标A ,B 之间的距离.[解析] 在△ACD 中,∠ACD =120°,∠CAD =∠ADC =30°,∴AC =CD = 3 km.在△BCD 中,∠BCD =45°,∠BDC =75°,∠CBD =60°.∴BC =3sin 75°sin 60°=6+22.在△ABC 中,由余弦定理,得AB 2=(3)2+⎝ ⎛⎭⎪⎫6+222-2×3×6+22×cos 75°=3+2+3-3=5, ∴AB =5(km),∴A ,B 之间的距离为 5 km.。
高中数学-解三角形及其应用
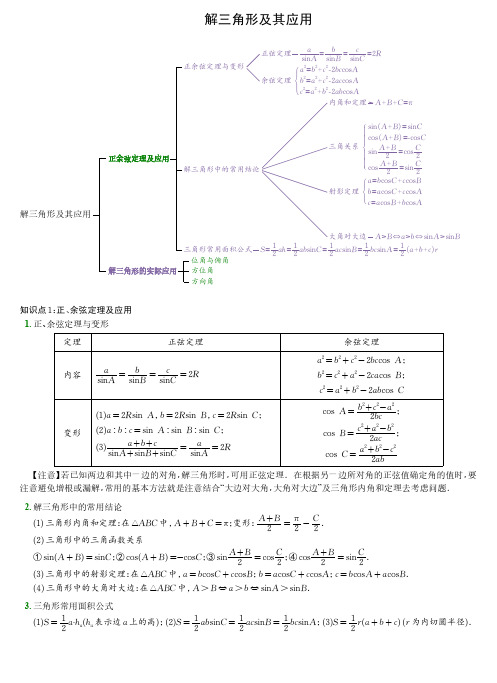
解三角形及其应用解三角形及其应用正余弦定理及应用正余弦定理与变形正弦定理aAsin=bBsin=cCsin=2R余弦定理a2=b2+c2-2bc Acosb2=a2+c2-2ac Acosc2=a2+b2-2ab Acos解三角形中的常用结论内角和定理A+B+C=π三角关系A+Bsin=CsinA+Bcos=-CcosA+B2sin=C2cosA+B2cos=C2sin射影定理a=b Ccos+c Bcosb=a Ccos+c Acosc=a Bcos+b Acos大角对大边A>B⇔a>b⇔Asin>Bsin 三角形常用面积公式S=12ah=12ab Csin=12ac Bsin=12bc Asin=12a+b+cr解三角形的实际应用位角与俯角方位角方向角知识点1:正、余弦定理及应用1.正、余弦定理与变形定理正弦定理余弦定理内容asin A=bsin B=csin C=2Ra2=b2+c2-2bc cos A;b2=c2+a2-2ca cos B;c2=a2+b2-2ab cos C变形(1)a=2R sin A,b=2R sin B,c=2R sin C;(2)a∶b∶c=sin A∶sin B∶sin C;(3)a+b+csin A+sin B+sin C=asin A=2Rcos A=b2+c2-a22bc;cos B=c2+a2-b22ac;cos C=a2+b2-c22ab【注意】若已知两边和其中一边的对角,解三角形时,可用正弦定理.在根据另一边所对角的正弦值确定角的值时,要注意避免增根或漏解,常用的基本方法就是注意结合“大边对大角,大角对大边”及三角形内角和定理去考虑问题.2.解三角形中的常用结论(1)三角形内角和定理:在△ABC中,A+B+C=π;变形:A+B2=π2-C2.(2)三角形中的三角函数关系①sin(A+B)=sin C;②cos(A+B)=-cos C;③sin A+B2=cos C2;④cosA+B2=sin C2.(3)三角形中的射影定理:在△ABC中,a=b cos C+c cos B;b=a cos C+c cos A;c=b cos A+a cos B.(4)三角形中的大角对大边:在△ABC中,A>B⇔a>b⇔sin A>sin B.3.三角形常用面积公式(1)S=12a·h a(h a表示边a上的高);(2)S=12ab sin C=12ac sin B=12bc sin A;(3)S=12r(a+b+c)(r为内切圆半径).知识点2:解三角形的实际应用名称意义图形表示仰角与俯角在目标视线与水平视线所成的角中,目标视线在水平视线上方的叫做仰角,目标视线在水平视线下方的叫做俯角铅垂线目标视线水平视线目标视线仰角俯角方位角从某点的指北方向线起按顺时针方向到目标方向线之间的夹角叫做方位角,方位角θ的范围是0°≤θ<360°O东北135°方向角正北或正南方向线与目标方向线所成的锐角,通常表达为北(南)偏东(西)例:(1)北偏东α:(2)南偏西α:东北α东北α一、正(余)弦定理解三角形解三角时,正余弦定理的选择:(1)已知两角及一边,求其余的边或角,利用正弦定理;(2)已知两边及其一边的对角,求另一边所对的角,利用正弦定理;(3)已知两边及其夹角,求第三边,利用余弦定理;(4)已知三边求角或角的余弦值,利用余弦定理的推论;(5)已知两边及其一边的对角,求另一边,利用余弦定理;1.在△ABC中,角A,B,C所对的边分别为a,b,c.若a=2,b=4,cos C=14,则c=()A.2B.4C.16D.262.在△ABC中,A=60°,AC=4,BC=23,则角B的值为()A.45°B.45°或135°C.90°D.135°3.△ABC中,角A,B,C所对的边分别为a,b,c,已知b=2,B=π6,cos A=-35,则a=()A.252 B.852 C.8156 D.21564.△ABC的内角A,B,C所对边分别为a,b,c,若a2+b2-c2=-ab,则角C的大小()A.π6B.π3C.π2D.2π3二、边角互化的应用边化角是正弦定理齐次比例关系非常重要的应用,其主要特点是将混有边角关系的条件问题转化为三角恒等变换问题,并从角的角度来审视三角形的特征,要熟练掌握边化角的三角形考题的特征,一般来说,当条件中含有特殊数,如3(往往和特殊角有关)或者齐次特征明显时,常进行边化角处理对于正弦定理与三角恒等变换的综合问题,大多是基于三角形内角和定理展开的,故一般有两种类型:一是利用相应半角的互余关系、角的互补关系研究三角恒等变换,进而达到减元的目的,也就可以盯着目标进行三角恒等变换:二是利用正弦定理求得相应的角或者寻找相应的边角关系,进而运用三角恒等变换转化为一个角的三角函数问题.5.在△ABC中,角A,B,C所对的边分别为a,b,c,且2a cos B=c-2a,b=2a,则()A.2a=3cB.3a=2cC.b=2cD.2b=c6.已知△ABC的内角A,B,C的对边分别为a,b,c,且cb +2bc=3cos A,1tan A+1tan C=2tan B,则sin B=()A.64B.105C.156D.2177.在△ABC中,角A,B,C所对的边分别为a,b,c,已知c sin C-a sin A=4b sin B,且cos C=-15,则sin Asin B=()A.215B.265C.5612D.1528.设△ABC的内角A,B,C的对边分别为a,b,c,若△ABC的周长为a sin Bsin A+sin B-sin C,则()A.C=2π3B.B=2π3C.C=π3D.B=π3三、判断三角形解的个数1、从代数上来说,可由“大边对大角”来判断;2、从几何上来说,已知两边及一边对角,解三角形(三角形多解问题)在△ABC中,已知a,b和A时,解的情况如下:当A为锐角时:AH C a b ca <CH =b Asin 无解A H C abc a =CH =b A sin 仅有一个解AHC ab cCH =b A sin <a <b有两个解AHC ab ca ≥b 仅有一个解当A 为钝角时ABC ab A B Cab仅有一个解仅有一个解9.根据下列情况,判断三角形解的情况,其中有唯一解的是()A.a =20,b =11,B =30°B.a =6,c =4,C =60°C.b =18,c =20,B =120°D.a =30,b =25,A =150°10.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,则下列判断正确的是()A.B =30°,c =4,b =5,有两解B.B =30°,c =4,b =3.9,有一解C.B =30°,c =4,b =3,有一解D.B =30°,c =4,b =1,无解11.在△ABC 中,a =x ,b =2,B =45°,若满足条件的△ABC 有且仅有一个,则x 的取值范围是()A.0,2 ∪22B.2,22C.0,2 ∪22D.0,2212.在△ABC 中,∠A =30°,AC =23,满足此条件△ABC 有两解,则BC 边长度的取值范围为()A.(23,4)B.(3,23)C.(23,+∞)D.(3,23)四、判断三角形的形状判断三角形形状的两种途径1、角化边:利用正弦定理、余弦定理化角为边,通过代数恒等变换,求出边与边之间的关系进行判断;2、边化角:通过正弦定理和余弦定理,化边为角,利用三角变换得出三角形内角之间的关系进行判断.13.在△ABC 中,内角A ,B ,C 所对边分别为a ,b ,c ,若b cos A +a cos B =b ,则△ABC 的形状是()A.直角三角形B.等腰三角形C.等腰直角三角形D.等腰或直角三角形14.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,若满足2a cos B =c ,则该三角形为()A.直角三角形B.等腰三角形C.等边三角形D.不能确定15.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若sin 2A 2=c -b2c ,则△ABC 的形状为()A.正三角形B.直角三角形C.等腰三角形D.钝角三角形16.(多选)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,下列四个命题中正确的是()A.若b cos C +c cos B =b ,则△ABC 是等腰三角形B.若a sin A +b sin B >c sin C ,则△ABC 为锐角三角形C.若a cos A =b cos B =ccos C ,则△ABC 一定是等边三角形D.若a cos A =b cos B ,则△ABC 一定是等腰三角形五、三角形的周长与面积1、三角形面积公式的使用原则:对于面积公式S=12ab sin C=12ac sin B=12bc sin A,一般是使用哪一个角就使用哪一个公式;2、与面积有关的问题:一般要用到正弦定理和余弦定理进行边角互化;3、三角形的周长问题:一般是利用余弦定理和公式a2+b2=(a+b)2-2ab将问题转化为求两边之和的问题.17.在△ABC中,角A,B,C的对边分别是a,b,c,且三边满足a+b+ca-b+c=42,B=π4,则△ABC的面积为()A.2-2B.4-22C.2+2D.4+2218.在△ABC中,已知b=2,B=30°,sin A=3sin C,则△ABC的面积为()A.4B.3C.2D.119.已知a,b,c分别是△ABC的内角A,B,C的对边,且ab =cos A2-cos B.(1)求ac;(2)若cos C=14,△ABC的面积为15,求△ABC的周长.20.在△ABC中,角A,B,C所对的边分别为a,b,c,已知23ac sin B=a2-b2-c2(1)求A;(2)若a=7,且△ABC的周长为1+3+7,求△ABC的面积六、三角形的外接圆问题利用正弦定理:asin A =bsin B=csin C=2R可求解三角形外接圆的半径.若要求三角形外接圆半径的范围,一般将R用含角的式子表示,再通过三角函数的范围来求半径的范围.21.在△ABC中,已知a=42,b=1,C=π4,则△ABC的外接圆的直径为()A.43B.5C.52D.6222.在△ABC中,角A、B、C所对的边分别为a、b、c,且c cos B+b cos C=a2,若B+C=2A,则△ABC外接圆半径为.23.在△ABC中,角A,B,C所对的边分别为a,b,c,c cos A=(2b-a)cos C.若A=π12,点D在边AB上,AD=BC =1,则△BCD的外接圆的面积是()A.2+33π B.4+33π C.6+33π D.8+33π24.现给出两个条件:①2b sin A =a tan B ,②a sin A -sin C =b sin B -c sin C ,从中选出一个条件补充在下面的问题中,并以此为依据求解问题.(选出一种可行的条件解答,若两个都选则按第一个解答计分)在△ABC 中,a ,b ,c 分别为内角A ,B ,C 所对的边,若.(1)求B ;(2)若△ABC 的面积为43,求△ABC 外接圆半径的最小值.七、三角形的中线问题1、中线长定理:在ΔABC 中,AD 是边BC 上的中线,则AB 2+AC 2=2(BD 2+AD 2).2、中线向量化:由2AD =AB +AC (核心技巧)得AD 2=14(b 2+c 2+2bc cos A )(结论).3、邻角互补应用:核心技巧:∠ADB +∠ADC =π⇒cos ∠ADB +cos ∠ADC =0在ΔADB 中有:cos ∠ADB =DA 2+DB 2-AB 22DA ×DB ;在ΔADC 中有:cos ∠ADC =DA 2+DC 2-AC 22DA ×DC.25.已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若a =8,b =9,c =7.则BC 边上的中线AM 的长为.26.如图,在△ABC 中,已知AB =4,AC =10,∠BAC =60°,M ,N 分别为BC ,AC 边上的中点,AM ,BN 相交于点P .ABCMNP(1)求BC ;(2)求cos ∠MPN 的值.27.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且2a sin C =3b sin A ,cos A =13.(1)证明:△ABC 为等腰三角形.(2)若D 是边BC 的中点,AD =34,求△ABC 的面积.28.在△ABC中,角A,B,C所对的边分别为a,b,c,27b cos A sin B+a cos2B-a=0.(1)求tan A的值;(2)若a=2,点M是AB的中点,且CM=1,求△ABC的面积.八、三角形的角平分线问题如图,在ΔABC中,AD平分∠BAC,角A,B,C所对的边分别为a,b,c,(1)利用角度的倍数关系:∠BAC=2∠BAD=2∠CAD(2)内角平分线定理:AD为ΔABC的内角∠BAC的平分线,则ABAC =BDDC.说明:三角形内角平分线性质定理将分对边所成的线段比转化为对应的两边之比,再结合抓星结构,就可以转化为向量了,一般的,涉及到三角形中“定比”类问题,运用向量知识解决起来都较为简捷。
正余弦定理在解三角形中的应用

2023年6月上半月㊀解法探究㊀㊀㊀㊀正余弦定理在解三角形中的应用◉甘肃省平凉市静宁县第二中学㊀杜春雯㊀㊀摘要:三角形是几何中的基础图形,解三角形是从已知三角形的某些元素(边或角)出发,利用正弦定理㊁余弦定理求这个三角形其他元素的过程.本文中主要介绍三角形中求边长(或角度)㊁判断三角形形状㊁三角形的面积(周长)的最值㊁三角形中范围问题等常见题型的解题策略,帮助学生提升数学运算能力和转化应用能力.关键词:解三角形;正弦定理;余弦定理㊀㊀三角形是生活中最常见的数学几何模型.解三角形问题在高考中经常出现,常见题型涉及边角运算㊁判断三角形形状㊁最值㊁范围等,常常利用正弦定理㊁余弦定理,结合三角形的性质㊁三角函数㊁平面向量㊁基本不等式等知识进行考查.下面举例说明正弦定理㊁余弦定理在解三角形中的应用.1题型一:边角运算从已知两角一边(或两边一角)的可解三角形入手,通过公共边(或等角㊁补角)作为桥梁转化到另一个需解三角形中[1],利用正弦定理㊁余弦定理求需解三角形中的某一边(或角),常见于实际问题中边角的求解.例1㊀在梯形A B C D 中,A D ʊB C ,且A B =5,A C =9,øB C A =30ʎ,øA D B =45ʎ,求B D 的长.分析:在可解әA B C 中已知两边一角,想要转化到әA B D 中求B D 的长,必须求得边B D 所对角øB A D 的正弦值.由梯形中øA B C +øB A D =180ʎ,可得øA B C ,øB A D 的正弦值相等,以A B 为桥梁,由可解三角形向需解三角形转化,即可求得边长B D .解:在әA B C 中,根据正弦定理,得A Cs i n øA B C =A B s i n øB C A ,则s i n øA B C =910.由A D ʊB C ,得øA B C +øB A D =180ʎ.所以s i n øB A D =s i n øA B C =910.在әA B D 中,根据正弦定理,得B Ds i n øB A D=A B s i n øA D B ,解得B D =922.点评:在解三角形中求边(角)的常见情况有以下三种.①两边一夹角,用余弦定理的夹角对边公式(例:A ңa 2);②两边和其中一边的对角,求边用余弦定理,求角选用正弦定理;③两角一边,利用三角形内角和等于180ʎ先求第三角(注意诱导公式的应用),再利用正弦定理求边.2题型二:判断三角形的形状例2㊀在әA B C 中,a ,b ,c 分别是内角A ,B ,C所对的边,且2a s i n A =(2b +c )s i n B +(2c +b )s i n C ,若s i n C +s i n B =1,试判断әA B C 的形状.分析:本题中第一个条件的左右两边都含有边和角,而且次数相同,所以既可以角化边,也可以边化角,但边化角复杂点,所以选择正弦定理将角化边,利用余弦定理求得角A .在用已知中的第二个条件时,要充分挖掘三角形内角和等于180ʎ,把角B 用角C 来表示,从而求得角B 和角C ,故而得出三角形的形状.解:根据正弦定理,将2a s i n A =(2b +c )s i n B +(2c +b )s i n C 角化边,得2a 2=(2b +c )b +(2c +b )c ,即a 2=b 2+c 2+b c .由余弦定理a 2=b 2+c 2-2b c c o s A ,得c o s A =-12.又因为A 是三角形的内角,所以0<A <π,故A =2π3.又B =π-A -C =π3-C ,由s i n C +s i n B =1,得s i n C +s i n(π3-C )=1.化简,得s i n (π3+C )=1.因为0<C <π2,所以C =π6,从而B =π6.17Copyright ©博看网. All Rights Reserved.解法探究2023年6月上半月㊀㊀㊀故әA B C 是等腰钝角三角形.点评:在利用正弦定理进行边角互化的过程中,一定要注意等式的每一项中都含有齐次的边或角的正弦项[2],本题的第二个条件中等号右边没有角的正弦项,所以不适合角化边.在边化角的过程中要注意对角的范围的讨论.3题型三:求取值范围利用正弦定理㊁余弦定理进行边角互化,结合三角函数来解三角形中的范围问题.例3㊀在әA B C 中,a ,b ,c 分别是内角A ,B ,C所对的边,若a 2+b 2+a b =4,c =2,试求2a +b 的取值范围.解:由a 2+b 2+a b =4,c =2,c 2=a 2+b 2-2a bc o s C ,得c o s C =-12.因为0<C <π,所以C =2π3.又A +B +C =π,所以B =π3-A .由正弦定理,得c s i n C =2R =433=a s i n A =bs i n B (R 为әA B C 的外接圆半径),则㊀㊀2a +b =2R (2s i n A +s i n B )=433[2s i n A +s i n (π3-A)]=4s i n (A +π6).因为0<A <π3,所以π6<A +π6<π2.故2<2a +b <4.点评:本题是正弦定理和余弦定理的综合应用,求边长代数式范围的关键是把边换成角的正弦值,减少未知元,再利用三角函数的值域确定范围.4题型四:求最值利用余弦定理转化两边的和(或积)为定值,结合基本不等式求三角形的面积(或周长)的最值.例4㊀在锐角三角形A B C 中,已知m ʊn ,且m =(2s i n (A +C ),3),n =(c o s2B ,2c o s2B2-1),若A C =1,求әA B C 面积的最大值.分析:本题根据向量平行,结合向量坐标运算建立等式,求得B =π6;再利用余弦定理和基本不等式,求得әA B C 面积的最值.解:由m ʊn ,得2s i n (A +C ) (2c o s2B2-1)=3c o s 2B .在әA B C 中,因为有A +C =π-B ,所以可得2s i n B c o s B =3c o s 2B ,则t a n 2B =3.又因为在锐角三角形A B C 中,0<B <π2,所以B =π6.根据b 2=a 2+c 2-2a c c o s B ,得1=a 2+c 2-3a c ,则1+3a c =a 2+c 2ȡ2a c .所以a c ɤ12-3=2+3.故S әA B C =12a c s i n B ɤ12(2+3)ˑ12=2+34,当且仅当a =c 时等号成立.故әA B C 为等腰三角形时面积最大,且最大值为2+34.点评:三角形的面积计算公式中S әA B C =12a c s i n B ,当B 为定值时,两条边的乘积a c 的最大值可根据基本不等式a c ɤ12a 2+c2()来求,从而确定三角形面积的最大值.在求周长的最值时,b 为定值,可用基本不等式a c ɤ(a +c 2)2确定a +c 的范围,从而求得周长的最小值.正弦定理和余弦定理是解三角形的基本工具,在此基础上结合向量㊁三角函数等知识综合考查学生的运算能力.在解题教学过程中,应引导学生注意总结,以提高其分析和解决问题的能力,同时灵活处理知识点之间的联系.参考文献:[1]汤文兵,陈萍.快解斜三角形的一种有效策略[J ].数学之友,2017(2):71G73.[2]方敏洁.解三角形的一般方法与策略分析[J ].数学大世界(下旬),2017(7):75.Z 27Copyright ©博看网. All Rights Reserved.。
第二章用余弦定理正弦定理解三角形【新教材】北师大版高中数学必修第二册课件

答案B
激趣诱思
知识点拨
微练习2
已知目标A的方位角为135°,请画出其图示.
解如图所示:
激趣诱思
知识点拨
微练习3
请分别画出北偏东30°,南偏东45°的方向角.
解如图所示:
探究一
探究二
当堂检测
解三角形与三角形有关的几何计算
角度1 三角形中线段长度的计算
例1
在四边形ABCD中,已知AD⊥CD,AD=10,AB=14,∠BDA=60°,∠BCD=135°,
当堂检测
反思感悟 1.测量从一个可到达的点与一个不可到达的点之间的距离问题,
一般可转化为已知两个角和一条边解三角形的问题,从而运用正弦定理解
决.
2.如图,点B为不可到达点,求A,B的距离的
具体解题步骤:
(1)取基线AC(尽量长),且使AB,AC不共线;
(2)测量AC,∠BAC,∠BCA;
sin
B之间的
m,达到点B.
距离.
又因为AB=10,BC=20,∠ABC=120°,
南偏西44°50'方向上
例6地图测绘人员在点A测得某一目标参照物P在他的北偏东30°的方向,且距离他40
若P在Q的北偏东44°50'方向上,则Q在P的(
)
答案(1)C (2)等腰直角三角形
第3课时 用余弦定理、正弦定理解三角形
冬奥会上,有两个滑冰者甲和乙位于冰面上A、B两点,A与B相距100 m.
如果甲从A出发,以8 m/s速度沿着一条与AB成60°角的直线滑行,同时乙
从B出发,以7 m/s 的速度沿着与甲相遇的最短直线滑行.
那么相遇时,甲滑行了多远呢?
激趣诱思
解三角形在现实生活中的应用——正、余弦定理

解三角形在现实生活中的应用——正、余弦定理解三角形在现实生活中的应用——正、余弦定理一、引言在数学领域中,三角形是一个非常重要的图形。
它不仅有着丰富的理论内涵,更有着广泛的实际应用。
本文将重点探讨三角形中的正、余弦定理在现实生活中的应用。
正、余弦定理是三角形中的重要定理,它们不仅是解决三角形问题的基础,更是许多实际问题的关键。
二、正、余弦定理的概念和原理在介绍正、余弦定理在现实生活中的应用之前,我们有必要回顾一下这两个定理的概念和原理。
正、余弦定理是三角形中用来描述边与角之间关系的重要定理。
正定理指出:在任意三角形中,边的平方等于其他两边平方和减去这两边与它们夹角的余弦之积的两倍。
余弦定理则指出:在任意三角形中,边的平方等于其他两边平方和减去这两边之积与它们夹角的余弦积的两倍。
通过正、余弦定理,我们可以推导出许多三角形的性质和关系,从而在实际问题中得到应用。
三、海上测距中的应用在海上航行中,船舶需要不断地确定自己的位置,以避免发生碰撞或迷失方向。
正、余弦定理就被广泛应用在海上测距中。
通过观测两个不同方向上的地标并测量它们的夹角,船舶可以利用余弦定理计算出自己与地标的距离。
在实际操作中,船舶的船长和船员们可以根据余弦定理的公式,精确计算出自己与地标的距离,并及时调整航线,确保航行安全。
四、建筑工程中的应用在建筑工程中,正、余弦定理也扮演着重要的角色。
在设计斜拉桥、悬索桥等大型桥梁时,工程师们需要精确计算桥墩与桥塔的高度和跨度,以确保桥梁的稳定性和安全性。
正、余弦定理可以帮助他们在实际建设过程中,精确计算各个零部件的尺寸和位置,从而保证桥梁的结构稳固。
五、航天工程中的应用在航天工程领域,正、余弦定理也被广泛应用。
在设计和控制航天器的轨道时,科学家们需要精确计算航天器与地球、月球或其他天体之间的距离和角度。
通过应用正、余弦定理,他们可以准确地计算出航天器的轨道曲线和飞行路径,确保航天器能够按照预定计划完成任务。
高中数学第二章解三角形2.3解三角形的实际应用举例全方位聚焦正余弦定理的应用素材北师大版必修

全方位聚焦正余弦定理的应用正、余弦定理是研究三角形的边和角之间的关系,是解决三角形问题的有力工具和重要手段,下面将对正余弦定理的应用进行全方位扫描.一、合理选用定理解三角形:求解三角形是典型问题,问题涉及三角形的若干几何量,解题时要注意边与角的互化.一般地,已知三角形的三个独立条件(不含已知三个角的情况),应用两定理,可以解三角形,具体可以解决的类型如下:例1.在三角形ABC 中,已知︒===45,2,3B b a ,解此三角形.分析:本题是一类已知两边一对角的解三角形问题,可用正弦定理,也可用余弦定理. 解法一:利用正弦定理,得︒=45sin 2sin 3A ,则23sin =A . 由于b a >,根据大边对大角,得︒=60A 或︒120.当︒=60A 时,得︒=75C ,22645sin 75sin 2sin sin +=︒︒==B C b c ; 当︒=120A 时,得︒=15C ,22645sin 15sin 2sin sin -=︒︒==B C b c . 解法二:利用余弦定理,得◊⋅⋅-+=45cos 32)3()2(222c c ,整理得0162=+-c c ,得226±=c . 当226+=c 时,212cos 222=-+=bc a c b A ,所以︒=60A ,则︒=75C ; 当226-=c 时,212cos 222-=-+=bc a c b A ,所以︒=120A ,则︒=15C . 点评:已知三角形的两边一对角这一类型,是同学们在学习过程中感到最困难的一种类型,这种类型的题,正弦和余弦定理都可以解决.(1)用正弦定理解,往往通过大边对大角这个性质,来判断解的个数;(2)用余弦定理解,一般转化为关于某条边的一元二次方程,利用∆或根的正负性来判断解的个数.二 判断三角形的形状解此类问题时,往往利用正弦或余弦定理转化到边或角,再通过边来判断或角来判断此三角形的形状.例2在△ABC 中已知acosB=bcosA,试判断△ABC 的形状.分析:利用正弦定理或余弦定理判断三角形形状,可以将三角形中的边用角表示,也可将角用边来表示.从中找到三角形中的边角关系,判断出三角形的形状.解1:由扩充的正弦定理:代入已知式2RsinAcosB=2RsinBcosA ,sinAcosB-cosAsinB=0 , sin(A-B)=0, 则A-B=0,∴A=B,即△ABC 为等腰三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全方位聚焦正余弦定理的应用
正、余弦定理是研究三角形的边和角之间的关系,是解决三角形问题的有力工具和重要手段,下面将对正余弦定理的应用进行全方位扫描.
一、合理选用定理解三角形:
求解三角形是典型问题,问题涉及三角形的若干几何量,解题时要注意边与角的互化.一般地,已知三角形的三个独立条件(不含已知三个角的情况),应用两定理,可以解三角形,具体可以解决的类型如下:
例1.在三角形ABC 中,已知︒===45,2,3B b a ,解此三角形.
分析:本题是一类已知两边一对角的解三角形问题,可用正弦定理,也可用余弦定理. 解法一:利用正弦定理,得︒=45sin 2sin 3A ,则2
3sin =A . 由于b a >,根据大边对大角,得︒=60A 或︒120.
当︒=60A 时,得︒=75C ,2
2645sin 75sin 2sin sin +=︒︒==B C b c ; 当︒=120A 时,得︒=15C ,22645sin 15sin 2sin sin -=︒︒==
B C b c . 解法二:利用余弦定理,得◊⋅⋅-+=45cos 32)3()2(222c c ,
整理得0162=+-c c ,得2
26±=c . 当2
26+=c 时,212cos 222=-+=bc a c b A ,所以︒=60A ,则︒=75C ; 当2
26-=c 时,212cos 222-=-+=bc a c b A ,所以︒=120A ,则︒=15C . 点评:已知三角形的两边一对角这一类型,是同学们在学习过程中感到最困难的一种类型,这种类型的题,正弦和余弦定理都可以解决.
(1)用正弦定理解,往往通过大边对大角这个性质,来判断解的个数;
(2)用余弦定理解,一般转化为关于某条边的一元二次方程,利用∆或根的正负性来判断解的个数.
二 判断三角形的形状
解此类问题时,往往利用正弦或余弦定理转化到边或角,再通过边来判断或角来判断此三角形的形状.
例2在△ABC 中已知acosB=bcosA,试判断△ABC 的形状.
分析:利用正弦定理或余弦定理判断三角形形状,可以将三角形中的边用角表示,也可将角用边来表示.从中找到三角形中的边角关系,判断出三角形的形状.
解1:由扩充的正弦定理:代入已知式2RsinAcosB=2RsinBcosA ,
sinAcosB-cosAsinB=0 , sin(A-B)=0, 则A-B=0,∴A=B,即△ABC 为等腰三角形。
解2:由余弦定理:
2
2222222bc a c b b ac b c a a -+⋅=-+⋅22b a = ∴ b a =, 即△ABC 为等腰三角形.
点评:法一将已知条件全部转化成角的关系,法二则将已知条件全部转化成边的关系,这样更有利于寻求到角与角或边与边存在的内在联系,这种方法在解其它有关三角形的问题中也是常用的,不同的思维有助于学生建立属于自己的良好的认知结构.
三 解决与面积有关的问题 例3.在A B C ∆中,若B A B A c b a tan tan 33tan tan ,5,4=++=+=,求A
B C ∆的面积.
解析:由已知得3tan tan 1)1tan (tan 3tan tan 1tan tan )tan(-=--=-+=+B
A B A B A B A B A
0120=+∴B A ,得060=C
由余弦定理得022260cos 2ab b a c -+=,又5=+c b 因此2
7)5(4)5(1622=⇒---+=c c c c ,从而23=b 因此,ABC ∆的面积2
332323421sin 21=⨯⨯⨯==C ab 点评:本题有一定的难度,首先要用和角的正切公式产生B A +的值,进一步产生角C ;其次要灵活运用条件及余弦定理产生b ,然后再求三角形的面积,可以说是一道小型综合题,不能全面把握基础知识是难以完成求解的.
四、求值
例4 在ABC ∆中,求
A C c A b a C b sin sin cos cos ---的值 解一:原式A C A
B A B
C B C B A C C R A B R A R C B R sin sin )sin(cos sin )sin(cos sin sin sin sin 2cos sin 2sin 2cos sin 2-+-+-=---= 0sin sin sin cos sin cos =-=A
C A B C B 解二:原式=---+⋅--+⋅=R a R c c bc a c b b a ab c b a b 2222222222022222222=-----=a c c
a c
b a a
c b 点评:本题是一个“纸老虎”,看模样,有点吓人,但真正动手求解,也很顺利,正弦定理与余弦定理均可达到目的.
五、证明恒等式
例5 在ABC ∆中,求证:C B A c
b a sin )sin(222-=- 证明:右边⋅=⋅-⋅=-=c
a A C B B C A C B A B A cos sin sin cos sin sin sin sin cos cos sin =-+⋅--+bc a c
b
c b ac b c a 22222222=-22
2c
b a 左边,故等式成立 点评:本题特点很突出,左边是边的式子、右边是角的式子,要完成这二者的统一(即都是边的式子或都是角的式子)可以用正弦定理,也可以用余弦定理或两个定理联合使用.这里的求解是两个定理联合使用.
六、求解平面几何问题
例6 已知圆内接四边形ABCD 的边长4,6,2====DA CD BC AB ,求四边形
ABCD 的面积.
解:连结BD ,则A AD AB S S S BCD ABD ABCD sin 2
1⋅⋅=+=∆∆ C CD BC sin 2
1⋅⋅+
,由0180=+C A ,得C A sin sin = 那么A A CD BC AD AB S ABCD sin 16sin )(21=⋅+⋅= 由于C A BD cos 46246cos 4224222222⨯⨯-+=⨯⨯-+=,又C
A cos cos -=得2
1cos -=A ,因此0120=A 故四边形ABCD 的面积为382
316sin 16=⨯==A S ABCD . 点评:平几中涉及长度与面积问题往往需要用正弦或余弦定理进行求解.由于平几的图形不一定是几条单纯的线或三角形,求解时,一定要认真分析图形,努力使已知量转化为三角形中的边与角,促使正弦定理与余弦定理得以顺利应用.。
