梁受压区高度的计算公式
相对受压区高度
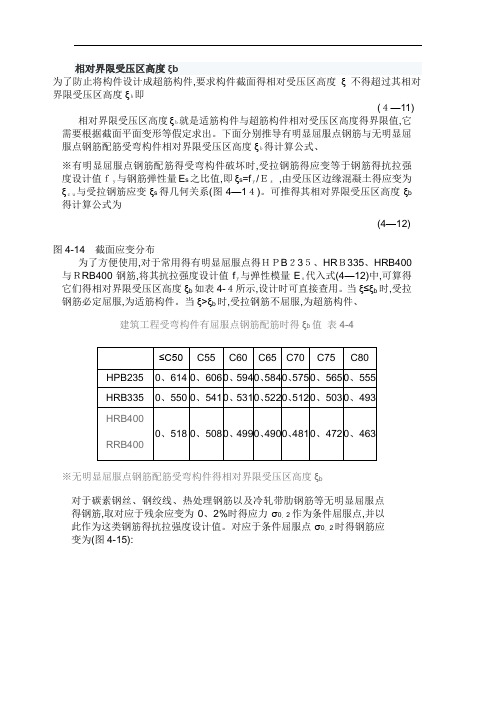
相对界限受压区高度ξb为了防止将构件设计成超筋构件,要求构件截面得相对受压区高度ξ不得超过其相对界限受压区高度ξb即(4—11) 相对界限受压区高度ξb就是适筋构件与超筋构件相对受压区高度得界限值,它需要根据截面平面变形等假定求出。
下面分别推导有明显屈服点钢筋与无明显屈服点钢筋配筋受弯构件相对界限受压区高度ξb得计算公式、※有明显屈服点钢筋配筋得受弯构件破坏时,受拉钢筋得应变等于钢筋得抗拉强度设计值fy与钢筋弹性量E s之比值,即ξs=fy/Es,由受压区边缘混凝土得应变为ξcu与受拉钢筋应变ξs得几何关系(图4—14)。
可推得其相对界限受压区高度ξb 得计算公式为(4—12)图4-14截面应变分布为了方便使用,对于常用得有明显屈服点得HPB235、HRB335、HRB400与RRB400钢筋,将其抗拉强度设计值fy与弹性模量Es代入式(4—12)中,可算得它们得相对界限受压区高度ξb如表4-4所示,设计时可直接查用。
当ξ≤ξb时,受拉钢筋必定屈服,为适筋构件。
当ξ>ξb时,受拉钢筋不屈服,为超筋构件、建筑工程受弯构件有屈服点钢筋配筋时得ξb值表4-4※无明显屈服点钢筋配筋受弯构件得相对界限受压区高度ξb对于碳素钢丝、钢绞线、热处理钢筋以及冷轧带肋钢筋等无明显屈服点得钢筋,取对应于残余应变为0、2%时得应力σ0、2作为条件屈服点,并以此作为这类钢筋得抗拉强度设计值。
对应于条件屈服点σ0、2时得钢筋应变为(图4-15):图4-15 无明显屈服点钢筋得应力—应变曲线(4-13)式中 f y ——无明显屈服点钢筋得抗拉强度设计值;E s ——无明显屈服点钢筋得弹性模量。
根据截面平面变形等假设,可以求得无明显屈服点钢筋受弯构件相对界限受压区高度ξb 得计算公式为:(4-14)截面相对受压区高度ξ与截面配筋率ρ之间存在对应关系。
ξb 求出后,可以求出适筋受弯构件截面最大配筋率得计算公式。
由式(4-8)可写出: (4-15)(4-16)式(4-16)即为受弯构件最大配筋率得计算公式。
梁受压区高度与有效高度比

梁端受压区高度与有效高度之比(强条)
《抗规》6.3.3.1:梁端计入受压钢筋的混凝土受压区高度和有效高度之比,一级不应>0.25,二、
1. 混凝土:混凝土强度等级采用 C fc =
MPa α1·fc =×=MPa ft =MPa ftk =MPa MPa β1 =εcu=2. 非预应力普通钢筋:采用
级钢(HRB400)Es =Mpa
fy=fy ´=Mpa ξb =β1/[1+fy/(Es×εcu)]=A. 截面参数计算
mm 梁纵筋排数:n=mm 梁纵筋排距:d2=mm (当n≥2时)mm 抗震等级为:级mm As=mm²(顶筋)mm As´=mm²(底筋)梁截面有效高度:h0=
mm
B. 计算公式受压区高度x=(fy*As-fy´*As´)/(α1*fc*b)<
h0x/h0=顶筋配筋率:ρ=As/(b*h0)=
%1800.3512724620.407
40018334.50.51765梁截面宽度:b =
梁截面高度:h=
梁顶筋直径:d=
梁保护层厚度:c =
梁箍筋直径:d1=
225325 1.271.78Ec = 2.80E+040.800.00330
2.11325
11.9 1.0011.911.90Ⅲ2.0E+0536010
不应>0.25,二、三级不应>0.35。
c30混凝土相对受压区高度

C30混凝土相对受压区高度1. 引言C30混凝土是一种常用的建筑材料,其强度等级表示了其抗压能力。
在设计和施工过程中,我们需要确定混凝土梁或柱的相对受压区高度,以确保结构的稳定性和安全性。
本文将介绍C30混凝土相对受压区高度的计算方法和影响因素。
2. C30混凝土相对受压区高度计算方法C30混凝土相对受压区高度与钢筋的位置有关。
根据相关规范,我们可以使用以下公式计算C30混凝土梁或柱的相对受压区高度:h = a - As/(b*d)其中, - h为相对受压区高度 - a为截面高度 - As为钢筋面积 - b为截面宽度- d为有效截面尺寸(即截面最外层钢筋至中和轴的距离)3. 影响C30混凝土相对受压区高度的因素3.1 混凝土强度等级C30表示混凝土的标称抗压强度为30MPa,该强度等级的混凝土相对受压区高度一般较大,因为其抗压能力较强。
如果使用更高的强度等级,例如C40或C50,相对受压区高度可能会进一步减小。
3.2 钢筋面积和布置方式钢筋在混凝土中起到了增加结构的抗拉能力的作用。
钢筋面积越大,相对受压区高度越小。
此外,钢筋的布置方式也会影响相对受压区高度。
常见的布置方式有矩形网格、斜向网格和环形箍筋等。
3.3 截面尺寸和形状截面尺寸和形状对C30混凝土相对受压区高度有重要影响。
一般来说,截面尺寸越大,相对受压区高度越小。
此外,在设计过程中还需要考虑截面形状是否合理,以满足结构强度和稳定性的要求。
4. 实例分析为了更好地理解C30混凝土相对受压区高度的计算方法和影响因素,我们将通过一个实例进行分析。
假设我们需要设计一根C30混凝土矩形梁,其截面尺寸为300mm×500mm,钢筋采用矩形网格布置,钢筋面积为1000mm²。
根据上述公式,我们可以计算得到相对受压区高度为:h = 300 - 1000/(500*300) = 0.6333 mm因此,该C30混凝土矩形梁的相对受压区高度为0.6333 mm。
混凝土相对受压区高度

混凝土相对受压区高度1. 引言嘿,大家好,今天咱们聊聊一个挺有趣的主题,混凝土的相对受压区高度。
听起来很复杂对吧?其实它就像你在做一道数学题,里边藏着一些“玄机”。
混凝土在建筑中可是个重要角色,就像小猫咪在你生活中的地位一样,离不开,但又常常被忽视。
今天我们就来揭开它的神秘面纱,看看它到底有什么“不得了”的地方。
2. 什么是混凝土的相对受压区高度?2.1 定义简单来说,混凝土的相对受压区高度,就是在受压情况下,混凝土内部那些被压得“喘不过气”的区域有多高。
你可以把它想象成一个海洋,水越深压力越大,混凝土也是一样,随着受力的增加,内部的压缩区域就像是海底的深渊,越来越深。
2.2 重要性那么,这个高度为什么这么重要呢?想象一下,如果你盖了栋大楼,但没考虑到混凝土的受压区高度,结果就像是买了个大西瓜却不知道怎么切,最后还是一团乱。
建筑物的安全性、稳定性、甚至美观性都和这个高度息息相关。
如果计算错了,可能会引发一系列问题,严重的甚至可能导致倒塌,真是让人心惊肉跳啊。
3. 如何计算相对受压区高度?3.1 公式推导当然,光说不练假把式。
计算这个高度可不复杂,主要用到一些公式。
先说简单的,受压区的高度h可以通过几何和材料的性质来推导出来。
有时候就像炒菜,配料搭配得当,才能做出美味的佳肴。
不同的混凝土配比、不同的受力情况都会影响到这个高度的计算,真是“变幻莫测”。
3.2 实际应用接下来说说实际应用。
在建筑工地上,工程师们每天都在使用这些公式,确保每一块混凝土都能承受住它应承担的重任。
有时他们甚至需要调配混凝土的配比,就像调制一杯完美的咖啡,太浓或太淡都不好,得找到一个平衡点。
记住,建筑可不是随便盖盖的,事关性命的大事可得谨慎啊。
4. 常见问题和误区4.1 误解说到这里,可能有朋友会想,“这不就是个数字吗?有什么了不起?”其实,误解可多了,尤其是在一些小工程里。
有的工人可能觉得只要混凝土浇上去就行,哪管它的受压区多高。
混凝土受压区高度

混凝土受压区高度混凝土受压区高度是混凝土结构设计的主要参数,它是混凝土结构的一项基础性能指标,对建筑物的耐久性、安全性、美观性等有着重要影响。
因此,选择恰当的混凝土受压区高度对混凝土结构的设计和建造有重要意义。
本文主要介绍混凝土受压区高度计算及其设计原则,旨在为设计者提供参考。
一、混凝土受压区高度的计算混凝土受压区高度的计算是混凝土结构设计中的基础工作。
混凝土受压区高度的计算公式如下:H=1/2*δ+S1+S2+─+Sn其中,H混凝土受压区高度;δ是混凝土梁或柱的厚度;S1,S2,…,Sn是混凝土梁或柱上部构件的厚度,例如横梁、楔形筋、控制拉筋等。
二、混凝土受压区高度的设计原则对于不同结构类型,混凝土受压区高度的设计原则也有所不同。
1、墙体结构混凝土受压区高度的设计应尽量保证墙体的稳定性,提高抗震性能,以及合理利用受压构件的节约原则。
墙体结构的混凝土受压区高度一般不小于400mm,应设置足够的横梁、角梁和楔形筋,以支撑墙体受压区域。
2、梁结构梁结构的混凝土受压区高度,除了考虑结构安全稳定以外,也应考虑梁的最佳截面尺寸。
梁结构的混凝土受压区高度应保证梁的截面尺寸合理,以免构成结构火山口,影响结构性能。
3、柱结构对于柱结构,混凝土受压区高度的设计也应考虑结构的安全稳定性和最佳结构尺寸问题。
一般来说,混凝土受压区高度应大于300mm,以保证土坯的牢固性,防止滑移和错位等现象的发生。
三、结论根据以上探讨可知,混凝土受压区高度的设计是混凝土结构设计中的重要环节,对于不同结构类型,其设计原则也不尽相同,因此设计者应根据工程实际情况来进行合理选择和计算。
钢筋混凝土梁的受压区高度计算的统一公式

在设计和结构工程中,钢筋混凝土梁的受压区高度计算一直是一个重要且具有挑战性的问题。
设计师和工程师需要通过科学的方法来确定梁的受压区高度,以确保结构的安全和稳定。
在本文中,我将就钢筋混凝土梁受压区高度计算的统一公式进行探讨,并共享我的个人观点和理解。
1. 钢筋混凝土梁受压区高度计算的重要性钢筋混凝土梁是建筑结构中常见的承载构件,其受压区高度的计算对梁的受力性能和承载能力具有重要影响。
合理的受压区高度计算能够确保梁的受压区受力均匀,避免发生局部破坏和失稳现象,从而保证整个梁的受力性能和安全性。
统一公式的提出对于工程设计和实际应用具有重要的意义。
2. 目前钢筋混凝土梁受压区高度计算存在的问题目前,钢筋混凝土梁受压区高度的计算方法存在着多样性和分散性。
不同的设计规范和国家标准对于受压区高度的计算方法各有不同,而且很多国家或地区都没有专门的统一公式。
这就给工程师和设计师在实际工程设计中造成了困扰,因为需要根据不同的规范和标准来确定受压区高度,增加了工作的复杂性和不确定性。
3. 钢筋混凝土梁受压区高度计算的统一公式的重要性针对目前存在的问题,提出一个统一的、科学的公式来计算钢筋混凝土梁的受压区高度至关重要。
这样的公式应该能够兼顾结构的受力性能和承载能力,适用于不同的设计规范和不同的设计要求,能够简化受压区高度的计算方法,提高工作效率,同时有效地确保梁结构的安全性和稳定性。
4. 钢筋混凝土梁受压区高度计算的统一公式的探讨在实际工程设计中,如何确定钢筋混凝土梁的受压区高度一直是一个具有挑战性的问题。
目前,关于受压区高度计算的统一公式还在不断的探讨和研究之中。
一些学者和专家提出了一些基于经验和试验数据的公式,但尚未形成广泛的共识和应用。
需要在更深入的理论研究和实际工程经验的基础上,不断完善和提升这样的统一公式,以满足工程实际应用的需求。
5. 我的个人观点和理解作为一名结构工程师,我深刻理解钢筋混凝土梁受压区高度计算的重要性和挑战性。
受弯构件双筋截面计算基本公式

受弯构件是工程结构中常见的一种构件类型,受弯构件在承受外力时,其截面会发生弯曲变形,因此需要进行合理的设计和计算。
双筋截面是一种常用的受弯构件截面形式,在计算受弯构件双筋截面时,需要应用基本公式进行计算。
一、受弯构件双筋截面的定义受弯构件双筋截面是指在构件受弯矩作用下,构件的两侧均设置有受拉和受压钢筋的构件截面形式。
通过设置双筋,可以提高构件的受弯承载能力,并且能够延缓构件发生破坏的过程,提高构件的抗震性能和延性。
二、受弯构件双筋截面计算基本公式在进行受弯构件双筋截面计算时,需要应用以下基本公式进行计算:1. 构件受压区高度的计算公式构件受压区高度h为:h = α_1 * x_u其中,α_1为受压区高度系数,x_u为截面受压区的核心深度。
构件受压钢筋面积A_s为:A_s = α * f_yk * A_s1其中,α为钢筋截面系数,f_yk为钢筋的屈服强度设计值,A_s1为截面内受拉钢筋面积。
3. 构件受压区混凝土承压应力的计算公式构件受压区混凝土承压应力f_cd为:f_cd = \f rac{α_1 * x_u * f_ck}{γ_c}其中,α_1为受压区高度系数,x_u为截面受压区的核心深度,f_ck 为混凝土立方体抗压强度设计值,γ_c为混凝土的材料安全系数。
4. 构件受拉区承受弯矩的计算公式构件受拉区的抗弯承载力M_rd为:M_rd = A_s * f_yd * (d - \frac{α_1 * x_u}{2})其中,A_s为受拉钢筋面积,f_yd为钢筋的设计弯曲强度,d为截面的有效高度。
5. 构件抗弯承载力的计算公式构件的抗弯承载力为:M_rd = M_sd其中,M_rd为构件受拉区的抗弯承载力,M_sd为设计弯矩。
三、受弯构件双筋截面计算实例以某一具体受弯构件为例,假设构件的混凝土强度等级为C30,钢筋的强度等级为HRB400,构件的设计受压区高度系数为0.8,设计受拉区高度系数为0.9。
钢筋混凝土相对受压区高度ξb

相对界限受压区高度ξb为了防止将构件设计成超筋构件,要求构件截面的相对受压区高度ξ不得超过其相对界限受压区高度ξb即(4-11)相对界限受压区高度ξb是适筋构件与超筋构件相对受压区高度的界限值,它需要根据截面平面变形等假定求出。
下面分别推导有明显屈服点钢筋和无明显屈服点钢筋配筋受弯构件相对界限受压区高度ξb的计算公式。
※有明显屈服点钢筋配筋的受弯构件破坏时,受拉钢筋的应变等于钢筋的抗拉强度设计值f y与钢筋弹性量E s之比值,即ξs=f y/E s,由受压区边缘混凝土的应变为ξcu与受拉钢筋应变ξs的几何关系(图4-14)。
可推得其相对界限受压区高度ξb的计算公式为(4-12)为了方便使用,对于常用的有明显屈服点的HPB235、HRB335、HRB400和RRB400钢筋,将其抗拉强度设计值f y和弹性模量E s代入式(4-12)中,可算得它们的相对界限受压区高度ξb 如表4-4所示,设计时可直接查用。
当ξ≤ξb时,受拉钢筋必定屈服,为适筋构件。
当ξ>ξb时,受拉钢筋不屈服,为超筋构件。
建筑工程受弯构件有屈服点钢筋配筋时的ξb值表4-4※无明显屈服点钢筋配筋受弯构件的相对界限受压区高度ξb对于碳素钢丝、钢绞线、热处理钢筋以及冷轧带肋钢筋等无明显屈服点的钢筋,取对应于残余应变为0.2%时的应力σ0.2作为条件屈服点,并以此作为这类钢筋的抗拉强度设计值。
对应于条件屈服点σ0.2时的钢筋应变为(图4-15):图4-15 无明显屈服点钢筋的应力—应变曲线(4-13)式中f y——无明显屈服点钢筋的抗拉强度设计值;E s——无明显屈服点钢筋的弹性模量。
根据截面平面变形等假设,可以求得无明显屈服点钢筋受弯构件相对界限受压区高度ξb的计算公式为:(4-14)截面相对受压区高度ξ与截面配筋率ρ之间存在对应关系。
ξb求出后,可以求出适筋受弯构件截面最大配筋率的计算公式。
由式(4-8)可写出:(4-15)(4-16)式(4-16)即为受弯构件最大配筋率的计算公式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
梁受压区高度的计算公式
在结构力学中,计算梁受压区高度的常用方法是根据弯矩和梁截面的性能参数进行求解。
以下是一般情况下计算梁受压区高度的常用公式:
1. 矩形梁:
假设梁截面为矩形,梁的宽度为b,混凝土的强度为f_c,弯矩为M,则梁受压区高度h_c可以用以下公式计算:
h_c >= (M / (0.85 * b * f_c))
2. T形梁:
假设梁截面为T形,梁的腿部宽度为b_f,腿部混凝土的强度为f_cf,梁的翼缘宽度为b_w,翼缘混凝土的强度为f_cw,弯矩为M,则梁
受压区高度h_c可以用以下公式计算:
h_c >= (M / (0.85 * (b_f * f_cf + b_w * f_cw)))
上述公式中,0.85是梁截面系数,考虑了混凝土的荷载偏心率和不均匀承载的情况。
同时,这些公式均为粗略的估算,实际设计中还需要考虑其他因素,如梁的几何形状、截面形态、混凝土的拉压强度差异等。
在进行梁设计时,建议参考相关结构设计规范和标准,以确保梁的设计满足安全和可靠性要求。
具体的计算方法可能会根据国家或地区的不同而有所差异,因此,建议与结构工程师或相关专业人员合作,以确保正确应用适用于您所在地区的设计准则和规范。
