结构力学位移法表格
结构力学-位移法的典型方程及计算步骤
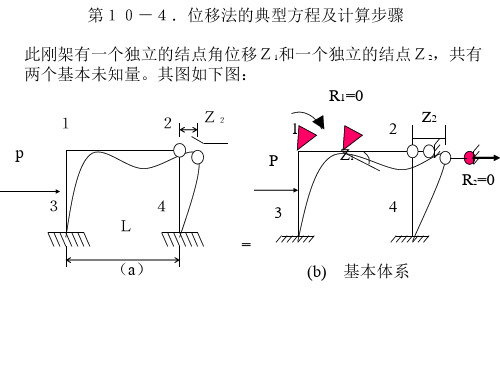
(e)
依题意可知并根据叠加原理上述条件可写为:
R1=R11+R12+R1P=r11 Z1+r12 Z2+R1P=0 R2=R21+R22+R2P=r21 Z1+r22 Z2+R2P=0
上述方程称为位移法基本方程,也称为位移法的典型方程。
为了求出典型方程的系数和自由项,可借助于表10-1,绘出基本
结构图,如下图10-7a,b, 和c所示。然后求出各系数和自由项。
r11 1 3i 4i
r12 6i1 0
R1P PL1 0
l
8
Z1=1
4i 1
2
6i 1l
2
Z2=1 1
2
3i M
3 2i 4
(a)
6i 3 l
3i 4 l
(b)
p
MP
PL 3
4
8
(C)
T10-7
1
2
r21 1
2
r22 1
6i l
0
12i
L2
3i
P
L2
2
2
R2P
0
系数和自由项可分为两类,分别由力矩平衡方程 M1=O求得为:
0
6 2 6 9 12 2 11 l Z1 l 2 Z2 16 P 0
Z1 0.02218 Pl Z2 0.02859 Pl 2
M M1Z1 M 2Z2 M P
转到下一节
者的原理有所不同。
§10-7 有侧移的斜柱刚架
B
B’
C’ C
C”
C
A
D
O A,D
B 结点位移图
O为极点,各结点位移前的位置
结构力学第8章位移法(f).

9 Fl 22 Fl 2 Z1 , Z2 552 i 552 i
结构的最后弯矩图可由叠加法绘制: M
M1Z1 M 2 Z 2 M P
内力图校核同力法,略。
§8-4 位移法的典型方程及计算步骤
位移法计算步骤
(1)确定基本未知量:独立的结点角位移和线位移,加入附加
一个附加联系上的附加反力矩和附加反力都应等于零。
原结构的静力平衡条件
§8-4 位移法的典型方程及计算步骤
为求系数和自由项,绘弯矩图如图a、b、c。
r11 7i
6i r12 l
Fl R1P 8
6i r21 l
15i r22 2 l
F R2 P 2
§8-4 位移法的典型方程及计算步骤
§8-3 位移法的基本未知量和基本结构
确定独立的结点线位移另种一方法
把原结构的所有刚结点和固定支座均改为铰结点→铰结体系,如图b。 此铰结体系为几何不变,原结构无结点线位移。 此铰结体系为几何可变或瞬变,添加最少的支座链杆保证其几何不变, 添加的链杆数目既是原结构独立的结点线位移数目。如图b,加一个水 平支座链杆,体系成为几何不变的。
自由项 作
位移法基本方程
Z1 1 及荷载作用下的弯矩图,如图a、b。
由a图,取结点B为隔离体,由∑MB=0,可得r11=3i+3i=6i 由b图,取结点B为隔离体,由∑MB=0,可得R1P=-24kN· m
i
EI 8m
§8-4 位移法的典型方程及计算步骤
将 r11和R1P代入方程求出
R1P 4kN m Z1 r11 i
r11Z1 r1i Z i r1n Z n R1P 0 ri1Z1 rii Z i rin Z n RiP 0 rn1Z1 rni Z i rnn Z n RnP 0
结构力学 位移法典型方程、计算举例
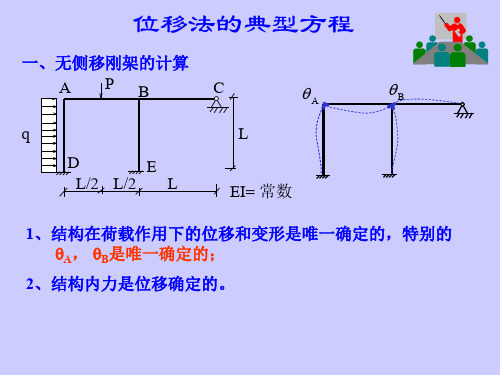
r21 B r22 CH R2
满足此方程,就消去了施加的2个约束
即,
r11 B r12 CH R1P 0 r21 B r22 CH R2 P 0
4)弯矩图的作法----消去最先附加的刚臂 P R1P R2P + MP图 R2
r
j 1
n
ij
Zj
,为消去该处的约束力,令: R iP
r
j 1
n
ij
Z j =0 即可。写成方程组的形式为:
r11 Z1 r12 Z 2 r1n Z n R1P 0 r Z r Z r Z R 0 21 1 22 2 2n n 2P rn1 Z1 rn 2 Z 2 rnn Z n RnP 0
R1P
R2P
+ +
r11 R A
1
r21R 2A
MP图 +
r12 B
r22 B
或
P
qL2/12
PL/8
4i
2i
q
R1P
R2P
+ A•
r11 8i r21 2i
2i
M 1图
MP图
4i
+
B•
4i r22 11i 2i r12 2i 3i 2i
M 2图
M M P M 1 A M 2 B
叠加右侧2个图,意味着结点B转动 及结点C侧移都发生。
叠加后B处的转角和C处的位移
分别为:B CH 则两处的约 束力必为R1,R2
r12 CH
结构力学-7 位移法2
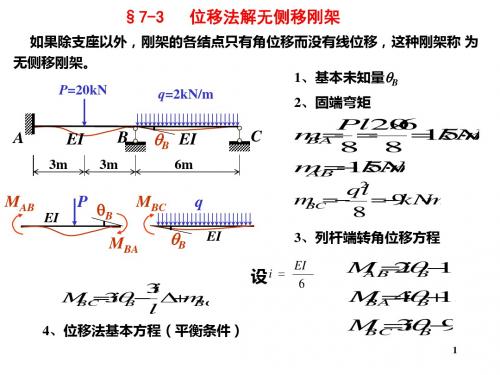
4iB 153iB 90
B
6 7i
16.72
11.57
M AB 2i7 6i1 51.7 6k2N m
M BA 4i7 6i1 51.5 1k7N m M BC 3i7 6i91.5 1k7N m
3.21
M图 kNm
梁 MBC4B2C41.741.1524.8941.746.9kNm
..............................................
柱 MBE443B3B31.153.45kNm
MCF412C2C2(4.89)9.8kNm
MBC
q
mBCq82l 9kNm
MBA
B EI
3、列杆பைடு நூலகம்转角位移方程
MBC3iB3limBC
设i
EI 6
4、位移法基本方程(平衡条件)
MAB2iB15 MBA4iB15
MBC3iB9
1
M超AB静EI定结P构分B 析M必B须C 满足q的三个条件:3、列杆端转角位移方程
2
C
D
1
C
D
A
B
7
线位移数也可以用几何构造分析方法确定。 将结构中所有刚结点和固定支座,代之以铰结点和铰支座,分析新体系的几 何构造性质,若为几何可变体系,则通过增加支座链杆使其变为无多余联系的 几何不变体系,所需增加的链杆数,即为原结构位移法计算时的线位移数。
1
4
0
8
BA EID
MEB
F
MCB
C
MCF
MCD
C
C MC 0
MFC
15
基本未知量为: C
结构力学1之位移法

用条件是什么?
3.组合结构
ip
M P M i d s N P N il
EI
EI
h
28
例. 试求图示梁B端转角.
A
P B B
EI
l/2
l/2
MP
Pl/ 4
解: B MEMIPds
yc
EI
1 1 l Pl 1 EI 2 4 2
M1
A
B
1
Mi
为什么弯矩图在 杆件同侧图乘结
果为正?
1 Pl 2 ( ) 16 EI
Z1
R1 位移法
基本体系
11Pl/32
EA
R1=0
位移法方程
P
R1P
r R1= 11 Z1+ R1P =0
3Pl/16 3i/l
MP
5P/16 EAZ1=1
r 3i / l2 11
R1P
r11
3i / l2
M1
Z1
3i/l
MM 1Z1M P
Z1---位移法
基本未知量
R1P5P/16 r116i/l2 Z15P2l/9i6
作业:11.1 11.2 11.6
h
27
11.1 荷载作用产生的位移计算
一.单位荷载法
二.位移计算公轴式力、剪力、弯矩
1.梁与刚架
4.拱
ip
MPMi ds EI
ip
[MPM i NPNi]d EI EA
s
2.桁结架构受外力作用时
会i产p生内N 力EPN A ,i d都s 产生这些哪公式的适
些NP内Nil力? EA
h
29
例. 试求图示结构B点竖向位移.
P
结构力学位移法01

位移法的概念 位移法基本体系的确定 位移法计算荷载引起的超静定结构内力 位移法计算温度改变引起的超静定结构内力 位移法计算支座位移引起的超静定结构内力 混合法
位移法是计算超静定结构的基本方法之一. 主要用于超静定梁和刚架的内力计算。
FP
力法计算,9个基本未知量
位移法计算, 1个基本未知量
§6-2 位移法基本概念
1
1
B EA D
FP
EI
EI
A
C
1
D
C
1
B
FP
FP
=
A
1
+
3i/l
3i/l 2
3FPl /16
3i/l 2 FP
内力计算的关键是
求结点位移Δ1
11FP /16 5FP /16
l/2 l/2
1
1
B EA D
FP
EI
EI
A
C
F1 0 F1 F11 F1P 0
k111 F1P 0
§6-1 单跨超静定梁的形常数与载常数
一.等截面梁的形常数 杆端位移引起的杆端内力称为形常数.
6i/l
6i/l
1
1
1
12i/l 2
12i/l 2
i=EI/l----线刚度
1
2i
4i
6i/l
6i/l
3i 3i/l
3i/l
3i/l 2
3i/l
3i/l 2
1
1
i
0
0
0
二.等截面梁的载常数
荷载引起的杆端内力称为载常数.
FPl
5 32 FPl
M图
Δ1
F1
07★结构力学A上★第七章★位移法

例:作图示刚架弯矩图。忽略横梁的 轴向变形。 解:(1)基本未知量:各柱顶水平 位移相等,只有一个独立线位移Δ。 (2)各柱的杆端弯矩和剪力为:
EI1 i1 h1 EI 2 i2 h2 EI 3 i3 h3
32
M BA 3i1 M DC 3i2 M FE 3i3
FP i1 i2 i3 3 2 2 2 h1 h2 h3 FP 3 i h2
列出水平投影方程:
X 0
33
(4)各柱最终杆端弯矩,画弯矩图:
i1 2 h1 FP i 2 h i3 2 h3 FP i 2 h i2 2 h2 i 2 h
转角位移方程。因此,不能利用刚性杆两端的刚结点力矩平
衡条件。应建立弹性杆端的剪力平衡方程。 刚性杆虽然没有变形,但是可存在内力。
30
2. 基本方程的建立
B= 0.737/ i (1) 基本未知量 B = 7.58/i
(2) 杆端弯矩
1 AB:M AB 2i B 6i 3 42 4 12 1 M BA 4iB 6i 3 42 4 12
M E 0, FQBE
M F 0, FQCF
1 (M EB M BE ) 4
1 M FC M CF 6
1 1 (M EB M BE ) M FC M CF 0 4 6
(4)解方程组
1.125 B 0.5C 0.728 0
得 B= 0.94 C= -4.94 = -1.94
10 B 2C 1.125 1.7 0 2 B 9C 0.5 41.7 0 1.125 B 0.5C 0.728 0
结构力学 第七章 位移法

表示等截面直杆杆端力与杆端位移及杆上荷载间关系的表达式
B A
Δ
6i F M AB l 6i F M BA 2i A 4i B M BA l 6i 6i 12i F F QAB A B 2 FAB l l l M AB 4i A 2i B
B
4i
1
2i
6i l
12i
l
6i
3i
l
6i
0
l2
θ =1
B B
3i
3i l
l
2
1 θ =1
B
3i
i
l
0
A
-i
0
三 等截面直杆的载常数 由荷载作用所引起的杆端力(固端力)
单跨超静定梁简图
q A
↓↓↓↓↓↓ ↓↓↓↓↓↓ ↓↓
mAB
B
mBA
ql 2 12
Pl 8
ql 2 12
Pl 8
位移法方程实质上平衡方程
Z1
D i A 2i E
Z2
C 2i
i EI l
4m
EI
i B
A
B
4m
2m
2m
位移法基本体系
解:1 确定位移法基本体系 2 列位移法方程 k11Z1+ k12Z2+ F1P=0 k21Z1+ k22Z2+ F2P=0
3 计算系数和自由项 Z1=1
4i 4i D i8i A 2i 8i 2i E 2i i B C
M AB 2i B
M BC ql 2 4i B 12
ql 2 ql 2 ql 2 4i 96i 12 24
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结构力学位移法表格
篇一:结构力学位移法解析
第十章位移法
10-1 概述
位移法——以结点位移(线位移,转角)为基本未知量的方法。
基本概念:以刚架为例(图10-1)
基本思路:以角位移Z1为基本未知量
平衡条件——结点1的力矩平衡
位移法要点:一分一合
①确定基本未知量(变形协调)基本体系-独立受力变形的杆件
②将结构拆成杆件-杆件分析(刚度方程-位移产生内力、荷载产生内力)③将结构杆件合成结构:整体分析——平衡条件——建立方程
10-2 等截面直杆的转角位移方程
单跨超静定梁——由杆端位移求杆端力——转角位移方程
矩阵形式
一、端(B端)有不同支座时的刚度方程
(1)B端固定支座
(2)B端饺支座
(3)B端滑动支座
二、由荷载求固端力(3*,4,11*,12,19,20)
(1)两端固定
(2)一端固定,一端简支
(3)一端固定,一端滑动(可由两端固定导出)
三、一般公式
叠加原理杆端位移与荷载共同作用
杆端弯矩:(10-1)
位移法意义(对于静定、超静定解法相同)
基本未知量-被动(由荷载等因素引起)
→按主动计算——位移引起杆端力+荷载的固端力
→结点满足平衡
正负号规则——结点转角(杆端转角)
弦转角——顺时针为正杆端弯矩
位移法三要素:
1.基本未知量-独立的结点位移
2.基本体系-原结构附加约束,分隔成独立变力变形的杆件体系。
3.基本方程-基本体系在附加约束上的约束力(矩)与原结构一致(平衡条件)
10-3基本未知量的确定
角位移数=刚结点数(不计固定端)
线位移数=独立的结点线位移
观察
几何构造分析方法——结点包括固定支座)变铰结点
铰结体系的自由度数=线位移数
――即使其成为几何不变所需添加的链杆数。
10-4典型方程及计算步骤
典型方程(10-5、6)
无侧移刚架的计算
无侧移刚架-只有未知结点角位移的刚架(包括连续梁)(△=0)有侧移刚架计算
有侧移刚架――除结点有位移外还有结点线位移
求解步骤:
(1)确定基本未知量:Zi (按正方向设基本未知量)——基本体系,
(2)作荷载、Zi = 1 —— MP??i=0?、Mi??i?1?图
(3)求结点约束力矩:荷载——自由项RIp,及ΔJ = 1 ——刚度系数 kIJ
(4)建立基本方程:[kIJ]{ Zi } + { RIp } = {0} ——附加约束的平衡条件求解Zi (Δi)
(5) 叠加法作M?MP??MiZi
10-5 直接建立位移法方程
求解步骤:
(1)确定基本未知量:Zi (按正方向设基本未知量)——基本体系,
(2)写杆端弯矩(转角位移方程)
(3)建立位移法方程——附加约束的平衡,求解Zi
(4) 叠加法作M?MP??MiZi
10-6 对称性利用
对称结构
对称荷载作用——变形对称,内力对称
(M、N图对称,Q图反对称——Q对称)
反对称荷载作用——变形反对称,内力反对称
(M、N图反对称,Q图对称——Q反对称)
——取半跨
对称结构上的任意荷载——对称荷载+反对称荷载
10-7支座位移和温度改变时的计算
一、支座位移的计算
超静定结构:支座有已知位移——引起内力
位移法计算:基本未知量、(基本体系)、基本方程及解题步骤与荷载作用时一样区别在于固端力——自由项:R1P——荷载引起
R1C ——支座位移引起
二、温度改变时的计算
与支座位移相同,超静定结构:温度改变——内力
固端力(相当荷(来自: 小龙文档网:结构力学位移法表格)载作用)(表11—1,5、11、15)
Δt = t1 — t2 ——M图,受拉面在温度铰低一侧。
同时还有轴向变形(不能忽略):t0=(t1+t2)/2(平均温度变化)
t0l ——本杆不产生M,但产生结点位移,使其它杆产生侧移——固端弯矩
10-8小结
一、位移法的基本概念
二、基本公式
三、解题步骤
四、对称结构
五、支座移动与温度变化的计算
六、超静定(静定)结构位移的计算
对偶:
位移法力法
1.基本未知量结点转角,线位移多余未知力
2.基本体系加约束撤除约束
位移:被动→主动多余约束力:被动→主动在原作用(荷载,支座,温度等)
和约束位移(基本未知量)和多余约束力(基本未知量)
共同作用下,与原结构的受力、变形相同
3.基本方程附加约束处、约束力撤除约束处位移与原结构相同
平衡条件位移变形条件
篇二:结构力学位移法题及答案
超静定结构计算——位移法
一、判断题:
1、判断下列结构用位移法计算时基本未知量的数目。
(1)(2)(3)
(4)(5)(6)
EI
2EI
2EIEAa
4EI
EIEA
bEI=
2EI4EI
4EI
2、位移法求解结构内力时如果MP图为零,则自由项R1P一定为零。
3、位移法未知量的数目与结构的超静定次数有关。
4、位移法的基本结构可以是静定的,也可以是超静定的。
5、位移法典型方程的物理意义反映了原结构的位移协调条件。
二、计算题: 12、
1、(1)、4;(6)、7。
2、(X)
3、(X)
4、(O)
5、(X)
(2)、4;
(3)、9;
(4)、5;
(5)、7;
篇三:结构力学位移法题及答案
超静定结构计算——位移法
一、判断题:
1、判断下列结构用位移法计算时基本未知量的数目。
(1)(2)(3)
(4)(5)(6)
EIEI
EI2EI
2EIEAa
4EI
4EI
EAbEIEI
2EI
4EI
2、位移法求解结构内力时如果MP图为零,则自由项R1P一定为零。
3、位移法未知量的数目与结构的超静定次数有关。
4、位移法的基本结构可以是静定的,也可以是超静定的。
5、位移法典型方程的物理意义反映了原结构的位移协调条件。
二、计算题:
12、用位移法计算图示结构并作M图,横梁刚度EA →∞,两柱线刚度 i 相同。
2
13、用位移法计算图示结构并作M图。
E I =常数。
14、求对应的荷载集度q。
图示结构横梁刚度无限大。
已知柱顶的水平位移为 512/(3EI)。
q
8m
15、用位移法计算图示结构并作M图。
EI =常数。
l
16、用位移法计算图示结构,求出未知量,各杆EI相同。
19、用位移法计算图示结构并作M图。
q
20、用位移法计算图示结构并作M图。
各杆EI =常数,q = 20kN/m。
23、用位移法计算图示结构并作M图。
EI =常数。
2
24、用位移法计算图示结构并作M图。
EI =常数。
q
29、用位移法计算图示结构并作M图。
设各杆的EI相同。
q
q
32、用位移法作图示结构M图。
E I =常数。
l/2
l/2
q
36、用位移法计算图示对称刚架并作M图。
各杆EI =常数。
l
l
38、用位移法计算图示结构并作M图。
EI =常数。
q
1.5
42、用位移法计算图示结构并作M图。
P
43、用位移法计算图示结构并作M图。
EI =常数。
ql
l
48、已知B点的位移?,求P。
A
/2
/2
51、用位移法计算图示结构并作M图。
q
超静定结构计算——位移法(参考答案)
1、(1)、4;(6)、7。
2、(X)
3、(X)
4、(O)
5、(X)
12、 13、
pl69/104
(2)、4;(3)、9;(4)、5;(5)、7;15104
3.517
21/1014/104
6
2
(×qh/40) ??Pl?。
