小学数学最难的13种典型题
较难的典型分数应用题(四)(答案加习题)

较难的典型分数应用题混合练习1. 六年级一班有学生55人,二班有学生57人,从一班调多少人到二班,才能使一、二班人数的比是7:9?答:一、二班总人数为55+57=112人,一、二班人数比如果为7:9,可以认为把总人数分为7+9=16份,则每一份人数为112÷16=7人,一班人数为7×7=49人,因此从一班调55-49=6人,可以使一、二班人数的比是7:9。
2. 一个直角梯形,上底与下底的比是3:5,如果把上底增加7厘米,下底增加1厘米,就变成了一个正方形。
求梯形面积是多少平方厘米? 答:设梯形下底为xcm ,则上底为53xcm ,根据题意可得x+1=53x+7,x=15cm 上底为15×53=9cm根据题意还可以知1,梯形的高h=x+1=15+1=16cm 因此,梯形的面积S=21(9+15)×16=192cm 2。
3. 五个连续自然数中最小的一个等于这五个数的和的61,这五个数分别是多少? 答:设最小自然数为x ,则其余四个自然数分别为x+1,x+2,x+3,x+4,根据题意可得 x=61(x+ x+1+x+2+x+3+x+4)4. 甲仓库存粮比乙仓库多25吨,从甲仓库调出40吨后,剩下的存粮是乙仓库的87。
乙仓库存粮多少吨? 答:甲仓库调出25T 存粮后,甲乙仓库存粮数相等,再调出15T ,剩下的存粮是乙仓库的87,相当于乙仓库存粮的81为15T ,因此,可以得到乙仓库存粮数量为15÷81=120T 。
5. 甲乙两车间人数比为3:5,如果从甲车间调150人到乙车间,甲乙车间人数比为3:7,原来甲乙车间各多少人? 答:设乙车间人数为x 人,则甲车间人数为53x 人,根据题意可得x-150=73(53x+150)6. 美术小组女生占103,后来又有5名女生参加,这时女生占美术小组人数的52。
现在美术小组有多少名学生?答:设美术小组原有学生x 人,则女生原有3x 人,根据题意可得103x+5=52(x+5)7. 甲乙两个车间,如果从甲车间调12人到乙车间,这时乙车间的人数就是甲车间的87。
关于六年级下数学第二单元最难的应用题

关于六年级下数学第二单元最难的应用题小学数学小升初应用题专项练习在数学中最重要的占分值比重最大的应该还是属于数学应用题。
许多同学在小学成绩上不去,考试成绩不理想,多半的都是在应用题上栽了跟头。
六年级1、一个长方形的周长是24厘米,长与宽的比是2:1,这个长方形的面积是多少平方厘米?2、一个长方体棱长总和为96厘米,长、宽、高的比是3∶2∶1,这个长方体的体积是多少?3、学校参加电脑兴趣小组的有42人,其中男、女生人数的比是4∶3,男生有多少人?4、有两筐水果,甲筐水果重32千克,从乙筐取出20%后,甲乙两筐水果的重量比是4:3,原来两筐水果共有多少千克?5、做一个600克豆沙包,需要面粉、红豆和糖的比是3:2:1,面粉、红豆和糖各需多少克6、两桶油共重27千克,大桶的油用去2千克后,剩下的油与小桶内油的重量比是3:2。
求大桶里原来装有多少千克油?7、一个长方体的棱长和是144厘米,它的长、宽、高之比是4:3:2,长方体的体积是多少?8、小红有邮票60张,小明有邮票40张,小红给多少张小明,两人的邮票张数比为1:4?9、两个城市相距225千米,一辆客车和一辆货车同时从这两城市相对开出,2、5小时后相遇,已知货车与客车速度比是4︰5,客车和货车每小时各行多少千米?10、用一根长282、6厘米的铁条焊接成一个圆形铁环,它的半径是多少厘米?参考答案1、24÷2÷(2+1)=4(cm)(42)(41)=32(cm²)2、96÷4÷(3+2+1)=4(cm)(43)(42)(41)=384(cm³)3、42÷(4+3)4=24(人)4、解:设原来两筐水果共有千克32:[(-32)(1-20%)]=4:3=625、600÷(3+2+1)=100(克)面粉:1003=300(克)红豆:1002=200(克)糖:1001=100(克)6。
小学数学中的13种典型例题口诀及解析
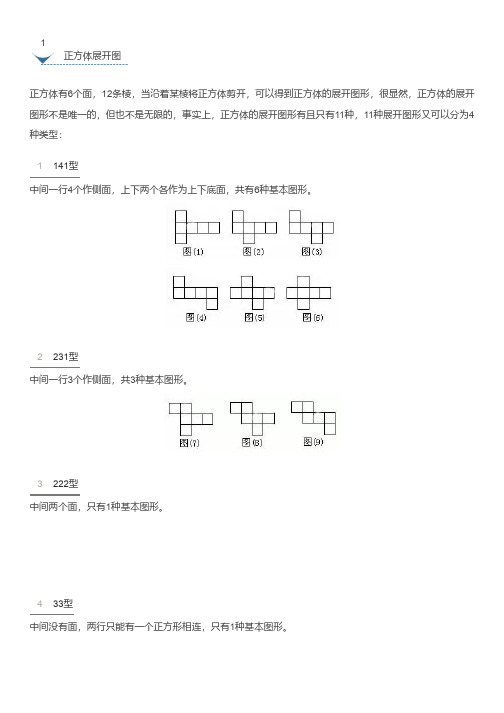
1正方体展开图正方体有6个面,12条棱,当沿着某棱将正方体剪开,可以得到正方体的展开图形,很显然,正方体的展开图形不是唯一的,但也不是无限的,事实上,正方体的展开图形有且只有11种,11种展开图形又可以分为4种类型:1141型中间一行4个作侧面,上下两个各作为上下底面,共有6种基本图形。
2231型中间一行3个作侧面,共3种基本图形。
3222型中间两个面,只有1种基本图形。
433型中间没有面,两行只能有一个正方形相连,只有1种基本图形。
2和差问题已知两数的和与差,求这两个数。
【口诀】: 和加上差,越加越大; 除以2,便是大的; 和减去差,越减越小; 除以2,便是小的。
例:已知两数和是10,差是2,求这两个数。
按口诀,则大数=(10+2)÷2=6,小数=(10-2)÷2=4。
3鸡兔同笼问题【口诀】: 假设全是鸡,假设全是兔。
多了几只脚,少了几只足? 除以脚的差,便是鸡兔数。
例:鸡免同笼,有头36 ,有脚120,求鸡兔数。
求兔时,假设全是鸡,则免子数=(120-36X2)÷(4-2)=24求鸡时,假设全是兔,则鸡数 =(4X36-120)÷(4-2)=124浓度问题(1)加水稀释【口诀】: 加水先求糖,糖完求糖水。
糖水减糖水,便是加糖量。
例:有20千克浓度为15%的糖水,加水多少千克后,浓度变为10%?加水先求糖,原来含糖为:20X15%=3(千克)糖完求糖水,含3千克糖在10%浓度下应有多少糖水,3÷10%=30(千克)糖水减糖水,后的糖水量减去原来的糖水量,30-20=10(千克)(2)加糖浓化【口诀】: 加糖先求水,水完求糖水。
糖水减糖水,求出便解题。
例:有20千克浓度为15%的糖水,加糖多少千克后,浓度变为20%?加糖先求水,原来含水为:20X(1-15%)=17(千克)水完求糖水,含17千克水在20%浓度下应有多少糖水,17÷(1-20%)=21.25(千克)糖水减糖水,后的糖水量减去原来的糖水量,21.25-20=1.25(千克)5路程问题(1)相遇问题【口诀】: 相遇那一刻,路程全走过。
典型分数应用题(较难)

较难的典型分数应用题 用不变的量作“桥”1. 把含糖10110%的葡萄糖溶液500毫升,稀释成含糖252的葡萄糖溶液,需要加蒸馏水多少毫升?2. 某班原有54名学生,男生占95,转来几名女生后,女生占全班的199,转来了几名女生?3. 甲乙两桶水,甲桶有28千克,甲桶喝了41,乙桶喝了52后,剩下的水一样重。
乙桶原有水多少千克?4. 食堂运来大米和面粉共360袋,其中大米占43,后来用了一些大米后,面粉的袋数恰好是大米的53。
用了多少袋大米?5. 书店有故事书和科技书共300本,故事书和科技书的比是3:2,后来又运来一些科技书,这时故事书和科技书的比是9:8,求又运来科技书多少本?6. 图书馆原有文艺书和连环画630本,其中文艺书与连环画之比是1:4,后来又买进些文艺书,这时文艺书与连环画之比是3:7,问买进文艺书有多少本?7. 二班原有学生42人,其中女生占73,后来又转来女生若干名,这时女生与男生人数之比是5:6,现在全班有学生多少人?8. 两筐水果共重130千克,如将甲筐水果的61装入乙筐后,甲乙两筐水果的重量之比是7:6,求甲乙两筐原各有水果多少千克?9. 有两堆煤,第一堆运走41,第二堆运走一部分后还剩53,余下的第一堆和第二堆的重量比是3:5,第一堆原有煤120吨,第二堆原有煤多少吨?用不变的量作“单位一”1. 某校六年级数学兴趣小组中,女生人数占83,后来又增加了4个女同学,这时,女生人数正好占全组的94,现在小组共有多少人?2. 某小学组织手工比赛,开始入选的学生中有53的男生,后来作了调整,用1名女生替换了一名男生,这时女生人数占总人数的53,现在参加比赛的同学中有几名男生?3. 甲乙两车间原有人数的比是3:2,甲车间调48人到乙车间后与乙车间人数的比是2:3,两车间原来各有多少人?4. 甲乙二人共有人民币若干元,其中甲占53。
若甲给乙8元,则甲乙二人钱数相等。
甲乙二人共有人民币多少元?5. 一辆长途客车只有32的座位上坐了乘客。
小学数学难题解法大全 第五部分 典型难题讲析(七~一) 数的计算

小学数学难题解法大全第五部分典型难题讲析(七之一)数的计算(一)数的计算1.四则计算【基本题】例1 计算7142.85÷3.7÷2.7×1.7×0.7(1991年全国小学数学奥林匹克初赛试题)讲析:本题的两个除数和乘数依次是3.7,2.7,1.7,0.7。
从数字上分析,不能运用简便运算。
所以,只能从左至右依次计算。
结果是850.85。
(1990年江西省“八一杯”小学数学竞赛试题)成假分数之后,分子都含有22的约数,于是可采用分配律计算。
(1994年全国小学数学奥林匹克决赛试题)讲析:两个分数的分母都是3,所以,可把小数化成分数计算。
【巧算题】(全国第三届“华杯赛”初赛试题)讲析:括号中的三个数如果直接通分,则比较繁琐。
经观察,可将三个分母分解质因数,求出公分母;在求公分母的过程中,不必急于求出具体的数,而可边算边约分,能使计算简便一些。
(1993年全国小学数学奥林匹克决赛试题)讲析:当把两个带分数化成假分数时,分子都是65。
于是,第一个括号中可提出一个65,第二个括号中可提出一个5,能使计算变得比较简便。
例3 计算:(全国第四届“华杯赛”复赛试题)讲析:经观察发现,可将整数部分与分数部分分开计算。
这时,每个带分数的分数部分,都可以拆分成两个单位分数之差,然后互相抵消。
计算就很简便了例4 计算:(1990年《小学生数学报》小学数学竞赛试题)除以两数之积,就等于分别除以这两个数。
然后可将它们重新组合计算为法分配律计算。
于是可将10.375分开,然后重新组合。
(1990年小学数学奥林匹克初赛试题)用字母代替去计算。
(长沙市小学数学奥林匹克集训队选拔赛试题)26.3乘以2.5。
这样计算,可较为简便。
原式=2.5×24.7+29×2.5+26.3×2.5=2.5×(24.7+29+26.3)=200。
例8 已知11×13×17×19=46189计算:3.8×8.5×11×39(广州市小学数学竞赛试题)讲析:根据已知条件来计算另一个算式的结果,应尽量将计算式化成与已知条件式相同或相似的式子。
小学六年级奥数试题及答案解析(中高难度)

小学六年级中高难度奥数题及答案解析(1)“奥数”是奥林匹克数学竞赛的简称。
学习奥数可以锻炼思维,是大有好处的。
学习奥数的年龄根据学生自身特点而定。
小学频道在这里精选了一些典型的小学六年级中高难度的奥数试题,并附有答案解析,大家来做做看吧!题1:(中等难度)做少年广播体操时,某年级的学生站成一个实心方阵时(正方形队列)时,还多10人,如果站成一个每边多1人的实心方阵,则还缺少15人.问:原有多少人?【答案解析】当扩大方阵时,需补充10+15人,这25人应站在扩充的方阵的两条邻边处,形成一层人构成的直角拐角成的直角拐角..补充人后,扩大的方阵每边上有扩大的方阵每边上有((10+15+110+15+1))÷2=13人.因此扩大方阵共有13×13=169人,去掉15人,就是原来的人数169-15=154人.题2:(中等难度)桌上有9只杯子,全部口朝上,每次将其中6只同时“翻转”只同时“翻转”..请说明:无论经过多少次这样的“翻转”,都不能使9只杯子全部口朝下。
【答案解析】要使一只杯子口朝下,必须经过奇数次要使一只杯子口朝下,必须经过奇数次""翻转翻转".".".要使要使9只杯子口全朝下,必须经过9个奇数之和次之和次""翻转翻转".".".即即"翻转翻转""的总次数为奇数但是,按规定每次翻转6只杯子,无论经过多少次"翻转翻转"",翻转的总次数只能是偶数次,翻转的总次数只能是偶数次..因此无论经过多少次因此无论经过多少次""翻转翻转"",都不能使9只杯子全部口朝下。
∴被除数口朝下。
∴被除数=21=21=21××40+16=85640+16=856。
答:被除数是856856,除数是,除数是2121。
小学较难的典型分数应用80道

小学较难的典型分数应用题1、某班原有54名学生,男生占5/9,转来几名女生后,女生占全班的9/19,转来了几名女生?2、甲乙两桶水,甲桶有28千克,甲桶喝了1/4,乙桶喝了2/5后,剩下的水一样重。
乙桶原有水多少千克?3、食堂运来大米和面粉共360袋,其中大米占3/4,后来用了一些大米后,面粉的袋数恰好是大米的3/5。
用了多少袋大米?4、书店有故事书和科技书共300本,故事书和科技书的比是3:2,后来又运来一些科技书,这时故事书和科技书的比是9:8,求又运来科技书多少本?5、图书馆原有文艺书和连环画630本,其中文艺书与连环画之比是1:4,后来又买进些文艺书,这时文艺书与连环画之比是3:7,问买进文艺书有多少本?6、二班原有学生42人,其中女生占3/7,后来又转来女生若干名,这时女生与男生人数之比是5:6,现在全班有学生多少人?7、两筐水果共重130千克,如将甲筐水果的1/6装入乙筐后,甲乙两筐水果的重量之比是7:6,求甲乙两筐原各有水果多少千克?8、某校六年级数学兴趣小组中,女生人数占3/8,后来又增加了4个女同学,这时,女生人数正好占全组的4/9,现在小组共有多少人?9、甲乙两车间原有人数的比是3:2,甲车间调48人到乙车间后与乙车间人数的比是2:3,两车间原来各有多少人?10、一辆长途客车只有2/3的座位上坐了乘客。
如果乘客再增加6人,则已坐的座位和空座位的比是4:1,这辆车共有多少个座位?11、甲乙重量比是4:1,如果从甲中取出13千克放入乙中,甲乙重量比是7:5,甲原有多少千克?12、书店新进一批书籍,已知科技书是文艺书的3/5,是故事书的2/3,文艺书比故事书多24本。
这三种书各买回了多少本?13、甲乙两们同学参加英语听力测试,他们的分数比是5:4,如果甲少得17.5分,乙多得17.5分,则他们的分数比是5:7,甲乙各得多少分?14、甲乙丙三人共加工了480个零件,已知甲加工的个数是其他两人加工总数的7/9,乙加工的个数是其他两人加工总数的1/3。
小学数学13种典型例题

小学数学13种典型例题正方体展开图正方体有6个面,12条棱,当沿着某棱将正方体剪开,可以得到正方体的展开图形,很显然,正方体的展开图形不是唯一的,但也不是无限的,事实上,正方体的展开图形有且只有11种,11种展开图形又可以分为4种类型:01 1141型中间一行4个作侧面,上下两个各作为上下底面,共有6种基本图形。
02 231型中间一行3个作侧面,共3种基本图形。
03 222型中间两个面,只有1种基本图形。
04 33型中间没有面,两行只能有一个正方形相连,只有1种基本图形。
02和差问题已知两数的和与差,求这两个数。
【口诀】和加上差,越加越大;除以2,便是大的;和减去差,越减越小;除以2,便是小的。
例:已知两数和是10,差是2,求这两个数。
按口诀,则大数=(10+2)/2=6,小数=(10-2)/2=4。
03鸡兔同笼问题【口诀】假设全是鸡,假设全是兔。
多了几只脚,少了几只足?除以脚的差,便是鸡兔数。
例:鸡免同笼,有头36 ,有脚120,求鸡兔数。
求兔时,假设全是鸡,则免子数=(120-36X2)/(4-2)=24求鸡时,假设全是兔,则鸡数 =(4X36-120)/(4-2)=1204浓度问题(1)加水稀释【口诀】加水先求糖,糖完求糖水。
糖水减糖水,便是加糖量。
例:有20千克浓度为15%的糖水,加水多少千克后,浓度变为10%?加水先求糖,原来含糖为:20X15%=3(千克)糖完求糖水,含3千克糖在10%浓度下应有多少糖水,3/10%=30(千克)糖水减糖水,后的糖水量减去原来的糖水量,30-20=10(千克)(2)加糖浓化【口诀】加糖先求水,水完求糖水。
糖水减糖水,求出便解题。
例:有20千克浓度为15%的糖水,加糖多少千克后,浓度变为20%?加糖先求水,原来含水为:20X(1-15%)=17(千克)水完求糖水,含17千克水在20%浓度下应有多少糖水,17/(1-20%)=21.25(千克)糖水减糖水,后的糖水量减去原来的糖水量,21.25-20=1.25(千克)05路程问题(1)相遇问题【口诀】相遇那一刻,路程全走过。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学数学最难的13种典型题
小学数学满分是一件特别简单的情况。
今天给大伙儿分享小学最重要的13种典型应用题,这些不掌握,小孩以后数学都不太容易学好。
正方体展开图
正方体有6个面,12条棱,当沿着某棱将正方体剪开,能够得到正方体的展开图形,特别显然,正方体的展开图形不是唯一的,但也不是无限的,事实上,正方体的展开图形有且只有11种,11种展开图形又能够分为4种类型: 141型
中间一行4个作侧面,上下两个各作为上下底面,共有6种基本图形。
231型
中间一行3个作侧面,共3种基本图形。
222型
中间两个面,只有1种基本图形、
33型
中间没有面,两行只能有一个正方形相连,只有1种基本图形、
和差问题
已知两数的和与差,求这两个数、
【口诀】:
和加上差,越加越大;
除以2,便是大的;
和减去差,越减越小;
除以2,便是小的、
例:已知两数和是10,差是2,求这两个数。
按口诀,则大数=(10+2)/2=6,小数=(10-2)/2=4。
鸡兔同笼问题
【口诀】:
假设全是鸡,假设全是兔、
多了几只脚,少了几只足?
除以脚的差,便是鸡兔数。
例:鸡免同笼,有头36 ,有脚120,求鸡兔数。
求兔时,假设全是鸡,则免子数=(120-36X2)/(4-2)=24
求鸡时,假设全是兔,则鸡数 =(4X36-120)/(4-
2)=12
浓度问题
(1)加水稀释
【口诀】:
加水先求糖,糖完求糖水、
糖水减糖水,便是加糖量、
例:有20千克浓度为15%的糖水,加水多少千克后,浓度
变为10%?加水先求糖,原来含糖为:20X15%=3(千克)。
糖完求糖水,含3千克糖在10%浓度下应有多少糖水,3/10%=30(千克)、糖水减糖水,后的糖水量减去原来的糖水量,30—20=10(千克)。
(2)加糖浓化
【口诀】:
加糖先求水,水完求糖水、
糖水减糖水,求出便解题。
例:有20千克浓度为15%的糖水,加糖多少千克后,浓度变为20%?。
加糖先求水,原来含水为:20X(1—15%)=17(千克)。
水完求糖水,含17千克水在20%浓度下应有多少糖水,17/(1—20%)=21、25(千克)。
糖水减糖水,后的糖水量减去原来的糖水量,21、25-20=1。
25(千克) 。
路程问题
(1)相遇问题
【口诀】:
相遇那一刻,路程全走过。
除以速度和,就把时间得、
例:甲乙两人从相距120千米的两地相向而行,甲的速度为40千米/小时,乙的速度为20千米/小时,多少时间相遇?
相遇那一刻,路程全走过。
即甲乙走过的路程和恰好是两地的距离120千米。
除以速度和,就把时间得。
即甲乙两人的总速度为两人的速度之和40+20=60(千米/小时),因此相遇的时间就为120/60=2(小时)
(2)追及问题
【口诀】:
慢鸟要先飞,快的随后追、
先走的路程,除以速度差,
时间就求对。
例:姐弟二人从家里去镇上,姐姐步行速度为3千米/小时,先走2小时后,弟弟骑自行车出发速度6千米/小时,几时追上?
先走的路程,为3X2=6(千米)
速度的差,为6—3=3(千米/小时)。
因此追上的时间为:6/3=2(小时)。
和比问题
已知整体求部分。
【口诀】:
家要众人合,分家有原则。
分母比数和,分子自己的。
和乘以比例,就是该得的。
例:甲乙丙三数和为27,甲;乙:丙=2:3:4,求甲乙丙三数、
分母比数和,即分母为:2+3+4=9;
分子自己的,则甲乙丙三数占和的比例分别为2/9,3/9,4/9。
和乘以比例,因此甲数为27X2/9=6,乙数
为:27X3/9=9,丙数为:27X4/9=12、
差比问题(差倍问题)
【口诀】:
我的比您多,倍数是因果。
分子实际差,分母倍数差。
商是一倍的,
乘以各自的倍数,两数便可求得、
例:甲数比乙数大12,甲:乙=7:4,求两数。
先求一倍的量,12/(7-4)=4,
因此甲数为:4X7=28,乙数为:4X4=16。
工程问题
【口诀】:
工程总量设为1,
1除以时间就是工作效率、
单独做时工作效率是自己的,
一齐做时工作效率是众人的效率和、
1减去差不多做的便是没有做的,
没有做的除以工作效率就是结果。
例:一项工程,甲单独做4天完成,乙单独做6天完成。
甲乙同时做2天后,由乙单独做,几天完成?
[1-(1/6+1/4)X2]/(1/6)=1(天)
植树问题
【口诀】:
植树多少颗,
要问路如何?
直的减去1,
圆的是结果。
例1:在一条长为120米的马路上植树,间距为4米,植树多少颗?
路是直的。
因此植树120/4-1=29(颗)。
例2:在一条长为120米的圆形花坛边植树,间距为4米,植树多少颗?路是圆的,因此植树120/4=30(颗)。
盈亏问题
【口诀】:
全盈全亏,大的减去小的;
一盈一亏,盈亏加在一起。
除以分配的差,
结果就是分配的东西或者是人。
例1:小朋友分桃子,每人10个少9个;每人8个多7个。
求有多少小朋友多少桃子?
一盈一亏,则公式为:(9+7)/(10—8)=8(人),相应桃子为8X10-9=71(个)
例2:士兵背子弹。
每人45发则多680发;每人50发则多200发,多少士兵多少子弹?
全盈问题。
大的减去小的,则公式为:(680-200)/(50-45)=96(人)则子弹为96X50+200=5000(发)。
例3:学生发书。
每人10本则差90本;每人8 本则差8本,多少学生多少书?
全亏问题。
大的减去小的。
则公式为:(90—8)/(10-8)=41(人),相应书为41X10—90=320(本)
牛吃草问题
【口诀】:
每牛每天的吃草量假设是份数1,
A头B天的吃草量算出是几?
M头N天的吃草量又是几?
大的减去小的,除以二者对应的天数的差值,
结果就是草的生长速率。
原有的草量依此反推、
公式就是A头B天的吃草量减去B天乘以草的生长速率。
将未知吃草量的牛分为两个部分:
一小部分先吃新草,个数就是草的比率;
有的草量除以剩余的牛数就将需要的天数求知。
例:整个牧场上草长得一样密,一样快。
27头牛6天能够把草吃完;23头牛9天也能够把草吃完、问21头多少天把草吃完、
每牛每天的吃草量假设是1,则27头牛6天的吃草量是27X6=162,23头牛9天的吃草量是23X9=207;
大的减去小的,207-162=45;二者对应的天数的差值,是9-6=3(天)、结果就是草的生长速率。
因此草的生长速率是45/3=15(牛/天);原有的草量依此反推、
公式就是A头B天的吃草量减去B天乘以草的生长速率、因此原有的草量=27X6—6X15=72(牛/天)。
将未知吃草量的牛分为两个部分:一小部分先吃新草,个数就是草的比率;这就是说将要求的21头牛分为两部分,一部分15头牛吃新生的草;剩下的21—15=6去吃原有的草,因此所求的天数为:原有的草量/分配剩下的牛=72/6=1
2(天)
年龄问题
【口诀】:
岁差可不能变,同时相加减、
岁数一改变,倍数也改变。
抓住这三点,一切都简单。
例1:小军今年8 岁,爸爸今年34岁,几年后,爸爸的年龄的小军的3倍?
岁差可不能变,今年的岁数差点34-8=26,到几年后仍然可不能变。
已知差及倍数,转化为差比问题、
26/(3-1)=13,几年后爸爸的年龄是13X3=39岁,小军的年龄是13X1=13岁,因此应该是5年后。
例2:姐姐今年13岁,弟弟今年9岁,当姐弟俩岁数的和是40岁时,两人各应该是多少岁?
岁差可不能变,今年的岁数差13—9=4几年后也可不能改变。
几年后岁数和是40,岁数差是4,转化为和差问题。
则几年后,姐姐的岁数:(40+4)/2=22,弟弟的岁
数:(40—4)/2=18,因此答案是9年后。
余数问题
【口诀】:
余数有(N—1)个,
最小的是1,最大的是(N-1)。
周期性变化时,
不要看商,
只要看余、
例:假如时钟现在表示的时间是18点整,那么分针旋转
1990圈后是几点钟?
分针旋转一圈是1小时,旋转24圈就是时针转1圈,也就是时针回到原位、1980/24的余数是22,因此相当于分针向前旋转22个圈,分针向前旋转22个圈相当于时针向前走22个小时,时针向前走22小时,也相当于向后24—22=2个小时,即相当于时针向后拔了2小时。
即时针相当因此18—2=16(点)。
