等边三角形PPT教学课件
合集下载
等边三角形优秀PPT课件

数学研究中
等边三角形是数学研究中的重要对 象之一,与三角函数、数列等领域 有密切联系。
03
等边三角形面积与周长计算
面积计算公式推导
等边三角形面积公式
S = (a^2 * sqrt(3)) / 4,其中a为等边三角形的边长。
公式推导
等边三角形可以划分成两个等腰直角三角形,每个直角三角形的面积为(1/2) * a * (a * sqrt(3) / 2),因此等边三角形面积为2 * (1/2) * a * (a * sqrt(3) / 2) = (a^2 * sqrt(3)) / 4。
05
等边三角形相关数学问题探讨
等腰直角三角形与等边三角形关系探讨
定义与性质 等腰直角三角形是两边相等的直角三角形,等边三角形则 是三边都相等的三角形。两者都属于特殊三角形,具有一 些独特的性质。
关联与转化 等腰直角三角形可以通过添加辅助线转化为等边三角形, 从而利用等边三角形的性质解决问题。反之,等边三角形 也可以转化为等腰直角三角形进行求解。
三边相等判定法
定义
判定方法
三边长度相等的三角形称为等边三角 形。
通过测量三角形的三边长度,判断是 否相等来确定是否为等边三角形。
判定定理
若三角形三边长度分别为a、b、c, 且满足a=b=c,则该三角形为等边三 角形。
两角相等判定法
定义
有两个内角相等的三角形 称为等腰三角形,若这两 个内角均为60度,则为等 边三角形。
特点
等边三角形的三个内角均为60°, 具有对称性。
与其他三角形关系
01
02
03
与等腰三角形关系
等边三角形是特殊的等腰 三角形,其中两腰长度相 等且等于第三边。
与直角三角形关系
等边三角形是数学研究中的重要对 象之一,与三角函数、数列等领域 有密切联系。
03
等边三角形面积与周长计算
面积计算公式推导
等边三角形面积公式
S = (a^2 * sqrt(3)) / 4,其中a为等边三角形的边长。
公式推导
等边三角形可以划分成两个等腰直角三角形,每个直角三角形的面积为(1/2) * a * (a * sqrt(3) / 2),因此等边三角形面积为2 * (1/2) * a * (a * sqrt(3) / 2) = (a^2 * sqrt(3)) / 4。
05
等边三角形相关数学问题探讨
等腰直角三角形与等边三角形关系探讨
定义与性质 等腰直角三角形是两边相等的直角三角形,等边三角形则 是三边都相等的三角形。两者都属于特殊三角形,具有一 些独特的性质。
关联与转化 等腰直角三角形可以通过添加辅助线转化为等边三角形, 从而利用等边三角形的性质解决问题。反之,等边三角形 也可以转化为等腰直角三角形进行求解。
三边相等判定法
定义
判定方法
三边长度相等的三角形称为等边三角 形。
通过测量三角形的三边长度,判断是 否相等来确定是否为等边三角形。
判定定理
若三角形三边长度分别为a、b、c, 且满足a=b=c,则该三角形为等边三 角形。
两角相等判定法
定义
有两个内角相等的三角形 称为等腰三角形,若这两 个内角均为60度,则为等 边三角形。
特点
等边三角形的三个内角均为60°, 具有对称性。
与其他三角形关系
01
02
03
与等腰三角形关系
等边三角形是特殊的等腰 三角形,其中两腰长度相 等且等于第三边。
与直角三角形关系
等边三角形的性质和判定PPT教学课件

1.5
5140 9766
1.5
6130
1164 7
2.2
7070
1343 3
2.2
8010
1521 9
28
2.2
8950
1700 5
30
2.2
9890
1879 1
➢ 上图采用周边传动刮泥机结构 主要由中心支座、桁架、传动装置、刮板等部分组成,
该机为全桥(或半桥)周边传动刮泥,传动是由电机经行 星摆线针轮减速机直接或通过链条驱动滚轮,以中心支座 为圆心在池壁顶做圆周运行。 ------结构简单,耗电省,运行可靠,目前已广泛推广
3.在△ABC中,∠A=∠B=∠C,你能得到AB=BC=CA 吗?为什么? 你从中能得到什么结论? 三个角都相等的三角形是等边三角形. 4.在△ABC中,AB=AC,∠A=60°.(1)求证:△ABC是 等边三角形; (2)如果把∠A=60°改为∠B=60°或∠C=60°,那么结论 还成立吗? (3)由上你可以得到什么结论? 有一个角是60°的等腰三角形是等边三角形.
将污泥与3-4倍污泥量的水混合而进行沉降分离 (仅适用于消化污泥)
目的:降低污泥中的碱度和粘度,以节省混凝 剂的用量,提高浓缩效果,缩短浓缩时间。
过程:泥水混合—淘洗—沉淀
三、加热加压调理
可使部分有机物分解,亲水性有机胶体物质水解,颗粒 结构改变,从而改善污泥的浓缩与脱水性能
(一)高温加压调理 流程 图5-6
第五章 污泥的浓缩与脱水
第一节 概述 一、污泥的种类
按来源分: 生活污水污泥、工业废水污泥、给水污泥
按污泥从水中的分离过程分: 沉淀污泥(初沉池污泥、混凝沉淀污泥、化学沉
淀污泥)及生物污泥(包括腐殖污泥、剩余活性污泥 )
等边三角形的判定PPT教学课件

a2=b2+c2-bc,b2=c2+a2-ca,c2=a2+b2-ab,
则△ABC是( D )
A.钝角三角形
B.直角三角形
C.等腰直角三角形 D.等边三角形
2020/12/10
13
3.如图,点D是等边△ABC的边BC上一点, ∠ADE=60°,则∠BAD与∠CDE的大小关系
是( B )
A. ∠BAD>∠CDE B. ∠BAD=∠CDE C. ∠BAD<∠CDE D. 无法确定
定理:有两个角等于60度的三角形 是等边三角形。
2020/12/10
5
练习:如图,△ABC,
(1)如果AB=AC,∠A=60°, △ABC是等边三角形吗?
A
(2)如果AB=AC,∠B=60°,
△ABC是等边三角形吗?
(3)如果AB=AC,∠C=60°,
△ABC是等边三角形吗? B
C
你能用一句话概括上面得到的结论吗?
在△ABE和△DBC中, 在△ABM和△DBN中,
AB=DB
∠BAE=∠BDC
∠ABE=∠DBC BE=BC ∴△ABE≌△DBC
∴∠BAE=∠BDC
2020/12/10
AB=DB ∠ABM=∠DBN=60° ∴△ABM≌△DBN ∴BM=BN ∵∠MBN=60°
∴△BMN是等边三角形。 9
例2:如图,△ABC中,D、E是BC上的点, 且BD=DE=EC=AD=AE,求∠BAC的度数。
2020/12/10
14
4.如图,△ABC中,AB=AC,D、E在BC、 AC上,且AD=AE,∠1=40°,
则∠2=____2_0__°.
此题的一般结论: ∠1=2∠2
《等边三角形的判定》证明课件ppt文档

在△ABC中,∵∠ACB=900,∠A=300(已知),B
CD
∴∠B=600(直角三角形两锐角互余).
又∵ ∠ACB=900, (已知),
∴∠ACD=900(平角意义).
在△ABC与△ADC中
∵BC=DC(作图),
∠ACB=∠ACD(已证),
AC=AC(公共边), ∴△ABC≌△ADC(SAS).
驶向胜利 的彼岸
具体做法.
600
C
我能行 1
命题的证明
定理:有一个角是600的等腰三角形是等边三角形.
已知:如图,在△ABC中AB=AC,∠B=600. A 求证:△ABC是等边三角形.
证明:∵AB=AC, ∠B=600(已知), 600
∴∠C=∠B=600.(等边对等角). B
C
∴∠A=600(三角形内角和定理).
等的三角形是等边三角形).
600
C
这又是一个判定靠边三角形的根据之一.
驶向胜利 的彼岸
我能行 3
命题的猜想
1 操作:用两个含有300角的三角
尺,你能拼成一个怎样的三角形?
300
300 300 300
300
300
能拼出一个等边三角形吗?说说你的理由.
由此你想到,在直角三角形中, 300角所对的 直角边与斜边有怎样的大小关系?
∴∠A=∠B(等式性质).
∴ AC=CB(等角对等边).
∴AB=BC=AC(等式性质).
∴ △ABC是等边三角形(等边三角形 意义).
驶向胜利 的彼岸
回顾反思 1
几何的三种语言
定理:有一个角是600的等腰三角形是等边三角形.
在△ABC中,
A
∵AB=AC,∠B=600(已知).
等边三角形PPT优秀课件

∵ DE∥BC
B
图13.3-7
C
∴∠ADE=∠B,∠AED=∠C
∴∠A=∠ADE=∠AED
∴⊿ADE是等边三角形
试一试
课本的证明是用判定方法二证明的,你能用判 定方法三来证明例4吗?(提示:先证明有一个 角是60 °,再证明它是等腰三角形)
巩固练习
1.等边三角形是轴对称图形吗?如果是,指
出它的对称轴.
等边三角形PPT优秀课件
☻等边三角形的定义:
三边都相等的三角形叫等边三角 形(也叫正三角形) 。
☻等边三角形的性质
等腰三角形是有两边相等的三角形,而 等边三角形是一种三边都相等的特殊的等 腰三角形。
等边三角形性质与等腰三角形性质有紧 密的联系,可以从中类比而得出。采用类 比这种方法学习新知识,可以进一步了解 新旧知识的联系,更加方便于理解、记忆 和应用。
B
等边 三角形
C
求证:有一个角是60 °的等腰三角形是等边三角形。
假若AB=AC.则∠ B= ∠ C (1)当顶角∠A=60 °时,∠ B= ∠ C= 60 ° ∴ ∠A= ∠ B= ∠ C=60 ° ∴ △ABC是等边三角形.(判定方法2)
(2)当底角∠ B= 60°时,∠ C=60 °, ∠A=180 -60 °x2=60 ° ∴ ∠A= ∠ B= ∠ C=60 ° ∴ △ABC是等边三角形. (判定方法2)
归纳:怎样判断一个三角形是等边三角形?
A
方法一:三角形的三边相等;
方法二:三角形的三角相等;
B
C
方法三:有一个角等于60°的等腰三角形 是等边三角形。
例4:如图,⊿ABC是等边三角形,DE∥BC,
交AB、AC于D、E,
A
人教版等边三角形 (2) PPT

等边三角形的对称轴是各边高线(中线,或 者所对角的角平分线)所在的直线。
大家有疑问的,可以询问和交流
可以互相讨论下,但要小声点
总结: 等边三角形的性质
1 . 等边三角形三边相等
2. 等边三角形的内角都相等,且等于60 °
3. 各边上的三线互相重合.(三线合一) 4. 等边三角形是轴对称图形,且有三条 对称轴.
思考
一个三角形满足什 么条件就是等边三 角形?
判定1: 三个角都相等的三角 形是等边三角形。
A
已知: ∠A=∠B=∠C
求证: AB=AC=BC
证明:
B
C
判定2: 有一个角是60。的等腰三角 形是等边三角形
A
已知: AB=AC,∠A=60。
求证: AB=AC=BC
证明:
B
C
一般三角形
等边三角形
人教版 八年级上册
等腰三角形
性质1 等腰三角形是轴对称图形,它有一条对称轴
性质2 等腰三角形的两个底角相等 (等边对等角) 性质3 等腰三角形的顶角平分线与底边上的中线,
底边上的高互相重合 (三线合一)
我们一起学习
用数学画图软件---玲珑画板演示 等腰三角形的性质
腰
腰
一般三角形
等腰三角形
等边三角形
⒈ 三个角都相等的三角形是等边三角形.
等腰三角形
等边三角形
⒉ 有一个角是60°的等腰三角形是等边 三角形.
讨 等边三角形是一种特殊的等腰三角 论 形,你能述说等边三角形与等腰三角
形在定义,性质和判定的异同吗?
有二条边 相等
有三条边 相等
1、两个底角相等 2、三线合一 3、对称轴一条
1、根据定义 2、等角对等边
等边三角形课件共14张PPT
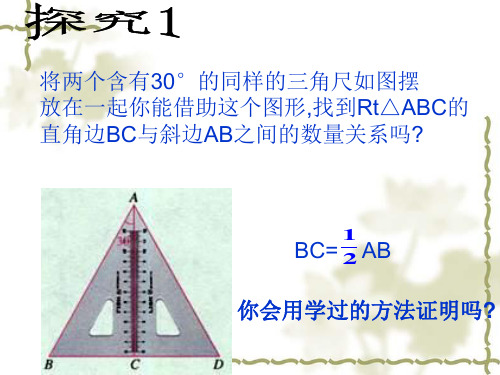
2
你能用一句话来
A
描述你的结论吗?
B
C
D
定理
在直角三角形中,如果一个锐角等于30° 那么它所对的直角边等于斜边的一半。
数学式:
A
30°
∵∴B∠CA=C12B=ARBt ∠ ,∠A=30°
C ┓ B 你还能用其它方法证明吗?
“在直角三角形中,如果一个锐角等于30° 那么它所对的直角边等于斜边的一半。”
C D
B
E
A
5、 如图,在△ABC中, ∠ACB= 90°,
∠B= 15°,AB的垂直平分线分别交BC、AB 于D、E。求证:DB=2AC
小结:
❖ 等边三角形的性质: 三边相等,三个角都是600,”三线合一”,三条对 称轴. ❖ 等边三角形的判定: 定义:有三边相等的三角形是等边三角形. 定理:有一个角是600的等腰三角形是等边三角形. 定理:三个角都相等的三角形是等边三角形. ❖ 特殊的直角三角形的性质: 定理:在直角三角形中, 如果有一个锐角等于300, 那么它所对的直角边等于斜边的一半. 定理:在直角三角形中, 如果一条直角边等于斜 边的一半,那么它所对的锐角等于300.
C D
B
E
A
4、 如图,上午9时,一条渔船从A出发,
以12海里/时的速度向正北航行,11时到达
B处,从A、B两处望小岛C,测得
∠NAC=150内有暗礁,问该渔船继续向正北
航行有无触礁的危险?
N
C
D
B
A
4、如图,在△ABC中, AB=AC, ∠BAC= 120°,AC的垂直平分线EF交AC 于点E,交BC于点F。求证:BF=2CF。
练习: 已知:等腰三角形的底角为150,腰长为2a. 求:腰上的高.
你能用一句话来
A
描述你的结论吗?
B
C
D
定理
在直角三角形中,如果一个锐角等于30° 那么它所对的直角边等于斜边的一半。
数学式:
A
30°
∵∴B∠CA=C12B=ARBt ∠ ,∠A=30°
C ┓ B 你还能用其它方法证明吗?
“在直角三角形中,如果一个锐角等于30° 那么它所对的直角边等于斜边的一半。”
C D
B
E
A
5、 如图,在△ABC中, ∠ACB= 90°,
∠B= 15°,AB的垂直平分线分别交BC、AB 于D、E。求证:DB=2AC
小结:
❖ 等边三角形的性质: 三边相等,三个角都是600,”三线合一”,三条对 称轴. ❖ 等边三角形的判定: 定义:有三边相等的三角形是等边三角形. 定理:有一个角是600的等腰三角形是等边三角形. 定理:三个角都相等的三角形是等边三角形. ❖ 特殊的直角三角形的性质: 定理:在直角三角形中, 如果有一个锐角等于300, 那么它所对的直角边等于斜边的一半. 定理:在直角三角形中, 如果一条直角边等于斜 边的一半,那么它所对的锐角等于300.
C D
B
E
A
4、 如图,上午9时,一条渔船从A出发,
以12海里/时的速度向正北航行,11时到达
B处,从A、B两处望小岛C,测得
∠NAC=150内有暗礁,问该渔船继续向正北
航行有无触礁的危险?
N
C
D
B
A
4、如图,在△ABC中, AB=AC, ∠BAC= 120°,AC的垂直平分线EF交AC 于点E,交BC于点F。求证:BF=2CF。
练习: 已知:等腰三角形的底角为150,腰长为2a. 求:腰上的高.
等边三角形PPT课件

2.请同学用一句话来概括大家找到的结论.
等边三角形的各个角都相等,并且每一个 内角都等于60°.
3.若在等边三角形ABC中,AD⊥BC,
你能找到新的结论吗?
A
∠BAD=∠CAD =30°;
┓
AB=2BD=2DC.
B
D
C
4.如果将图中右边部分中的AC、CD擦掉,你
有新的想法吗?
A
┓
B
D
C
在直角三角形ABD中,30°角所 对的直角边等于斜边的一半.
三等分点, △AED是等边三角形,则
∠BAC为(
)度?
A
B
D
E
C
A
因为 ∠A+∠B+∠C=180°,
所以∠A=∠B=∠C=60°.
B
C
试用推理格式写出整个推理过程
推理过程:
∵ AB=AC (已知)
A
∴∠B=∠C (等边对等角)
同理 ∠A=∠B
∴ ∠A=∠B=∠C
B
C
∵ ∠A+∠B+∠C=180°
(三角形内角和为180°) ∴ ∠A=∠B=∠C = 1830°= 60°.
1、等边三角形是_______对称图形,它有 _______条对称轴,是_________________。
2、已知△ABC中,∠A=∠B=60°,AB=3cm 则△ABC的周长________
3、 △ABC是等腰三角形,周长为15cm且 ∠A=60°,则BC=_______
4、如图, △ABC中,D、E是BC边上的
一、创设情境 1.有两边相等的三角形是等腰三角形,有 三边相等的三角形是等边三角形也称正三 角形.(如图)
2.①等腰三角形是轴对称图形. ②等腰三角形平分线,底边上的 中线和底边上的高互相重合.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
已知:△ABC , AB=AC, ∠A=60°( ∠B=60°
或 ∠C=60°)
求证: △ABC是等边三角形
证明:
B
C
2020/12/12
9
课外活动小组在一次测量活动中,测得
∠APB=60°AP=BP=200cm,他们
便得到了一个结论:池塘最长处不小
于200cm.他们的结论对吗?
A
P )60°
2020/12/12
❖ 2、等边三角形的对称轴有( ) ❖ (A)1条(B)2条(C)3条(D)4条
2020/12/12
14
3、已知△ABC中,∠A=∠B=60°,AB=3cm
则△ABC的周长________
4、 △ABC是等腰三角形,周长为15cm且∠A=60°, 则BC=_______
5、如图, △ABC中,D、E是BC边上的三等分点,
谢谢观看
Thank You For Watching
23
2020/12/12
5
A
B )60° 60(° C
⑴等边三角形的三边都相等
⑵等边三角形的三个内角都相等,并且
每一个角都等于60°你能证明吗?
(3)等边三角形各边上中线,高和所对角的平分线
都三线合一.
(4)等边三角形是轴对称图形,有3条对称轴
2020/12/12
6
?
思考题
一个三角形满足什么条件 就是等边三角形?
A OP
C B
Q
2020/12/12
12
例2:如图,已知△ABC 是等边三角形,BD 是中线,延长BC至E,使CE=CD, 求证:DB=DE
A
D
B
C
E
课堂练习:教材P54练习
2020/12/12
13
❖ 1、下列四个说法中,不正确的有( ) ❖ ①、三个角都相等的三角形是等边三角形。 ❖ ②、有两个角等于60°的三角形是等边三角形。 ❖ ③、有一个角是60°的等腰三角形是等边三角形。 ❖ ④、有两个角相等的等腰三角形是等边三角形。 ❖ (A)0个(B)1个(C)2个(D)3个
2020/12/12
19
我们这节课学习了哪些知识? 谈谈你的体会.
作业:书57页:第11题, 65页:第12题
2020/12/12
20
2020/12/12
21
这是两个等边三角形,那么请移动三根火柴 ,将此图变成四个等边三角形.
随堂练习
2020/12/12 (一)课本P145练习 1、2.
22
PPT教学课件
B 10
例4 如图,△ABC是等边三角 形,DE∥BC交AB,AC于D,E 求证: △ADE是等边三角形
A
分析:判定等边三角形方法几种?已知给我们创
造了什么条件?应该选择什么方法,你能证明吗?
D
E
B
C
2020/12/12
11
在等边ΔABC中,P,Q分别为AC,B C上的点,且AP=CQ,BP交AQ于 O,试求∠BOQ的度数.
C
17
7.已知:如图,P,Q是△ABC边上BC上的 两点,且BP=PQ=QC=AP=AQ,求∠BAC的 度数.
A
2020/12/12
BP
QC
18
E D
F
G
A
C
B
如图,点C是AB上一点,三角形ACD 和三角形BCE均为等边三角形,连接AE交 CD于F,连接BD交CE于G,图中有几对 全等三角形?判断FG与的AB的位置关系。
A
B
C
2020/12/12
1
观察下列图片,你有 什么印象?
2020/12/12
2
你发现了什么?
这就是今天我们要学的
2020/12/12
3
什么样的三角形是等边三角形?
三条边都相等的三角形叫等边三角形
2020/12/12
4
想想看,等边三角形
A
有什么性质?
B
C
⑴三边之间 AB_=AC_=BC
⑵三角之间 ∠A_=∠B_=∠C= _6度0
△AED是等边三角形,则∠BAC为(
)度?
A
2020/12/12
B
D
E
C
15
(1)△ ABD≌ △ACD ≌ △CAF ≌ △CBF ≌ △BAE ≌ △ BCE
等边三角形三条中线相交于一
点,画出图形,讨论找出图中
所有的全等三角形,证明它们
全等
A
(2)△AOF≌ △AOE ≌ △BOF ≌ △BOD ≌ △COD ≌ △COE
2020/12/12
7
一般三角形
等边三角形
1.三条边都相等的三角形是等边三角形(定义)
2. 三个角都相等的三角形是等边三角形.(猜 想、画图、写出已知、求证、请证明)
已知:△ABC, ∠A= ∠B= ∠C
A
求证: △ABC是等边三角形
证明:
B
C
2020/12/12
8
等腰三角形
等边三角形
3.有一个角是60°的等腰三角形是等边三角形. (猜想、画图,写出已知、求证、请证明)
(3)△ AOB≌ △ BOC≌ △COA
F
E
O
你能证明三 角形全等吗?
B
D
C
2020/12/12
16
练习
1. 如图,等边△ABC中,AD是BC上的高 , ∠ BDE= ∠ CDF=600,图中有哪些与BD 相等的线段?
BD=CD=CF=AF=DF
A
=AE =BE=DE
E
F
2020/12/12
B D
