学×思面授班初三数学春季目标班讲义第15讲.目标班期末复习之知识点睛及模拟测试.目标班.教师版

合集下载

[中考]初三数学复习讲义

4 3 2 1
2
2 - 3 与3 � 0 1 )3( , 7
� 31
与5
� 5 1 ) 2 ( , 1 1 2 与5
3 ) 1( :小大较比.3
0
)1 � ( , 7 2
,
2
�
, 2� ,
4
3
1
, 4 :差的积的数理无与和的数理有算计,中数实个
2
6 列下在请.2
. 值的a 数实求 , y � x 3 � y x a 若 , 0 � 9 � y 6 � y � 4 � x 3
。
则.
a 1
�值对绝�6� 为数倒的�0≠a�a 若。数倒为互数个两的积乘�数倒�5�
。
。轴数做叫线直的和、则�数反相为互 b、a 若。数反相为互数个两的同不
) (� �) (�
了定规�轴数�4� 有只�数反相�3�
) )
(� �) (�
� ) � (� ) � 0 � 数理有� ) � � (� � )
2
】析剖题考典经【 �二
④和③�D ④和①�C � �是的式根次二类同是
5. 0 . D 21 . C
5
③和②�B ③和①�A
, 21
3
和72
④�
3 2
③
3
2
②
①�式根次二在 .5
y x .B
2
1+ x
2
�A � �是的式根次二简最于属式各列下 .4
x- 2 = ) 2- x(
2
2�x .D 2≥ x .C 2� x .B
�数负非的要重个三.5
�区校道大城新�
义讲课授化性个育教文龙
-5-
�39213836 �话电询咨�校学导辅化性个业专的赖信得值您——育教文龙

学而思九年级数学教材

第一讲一次函数和反比例函数知识点、重点、难点函数(0)y kx b k =+≠称为一次函数，其函数图像是一条直线。

若0b =时，则称函数y kx =为正比例函数，故正比例函数是一次函数的特殊情况。

当0k >时，函数y kx b =+是单调递增函数，即函数值y 随x 增大（减小）而增大（减小）；当0k <，y kx b =+是递减函数，即函数值y 随x 增大（减小）而减小（增大）。

函数(0)ky k x =≠称为反比例函数，其函数图像是双曲线。

当0k >且0x >时，函数值y 随x 增大（减小）而减小（增大）；当0k >且0x <，函数值y 随x 增大（减小）而减小（增大），也就是说：当0k >时，反比例函数k y x =分别在第一或第三象限内是单调递减函数；当0k <时，函数k y x =分别在第二或第四象限内是单调递增函数。

若111222(0),(0).y k x b k y k x b k =+≠=+≠当12k k =时，12b b ≠时，两面直线平行。

当12k k =时，12b b =时，两面直线重合。

当12k k ≠时，两直线相交。

当121k k =-时，两直线互相垂直。

求一次函数、反比例函数解析式，关键是要待定解析式中的未知数的系数；其次，在解题过程中要重视数形相结合。

例题精讲例1：在直角坐标平面上有点(1,2)A --、(4,2)B 、(1,)C c ，求c 为何值时AC BC +取最小值。

解显然，当点C 在线段AB 内时，AC BC +最短。

设直线AB 方程为y kx b =+，代入(1,2)A --、(4,2)B得242,k b k b -+=-⎧⎨+=⎩解得456,5k b ⎧=⎪⎪⎨⎪=-⎪⎩ 所以线段AB 为46(14),55y x x =--≤≤ 代入(1,)C c ，得4621.555c =⨯-=- 例2：求证：一次函数211022k k y x k k --=-++的图像对一切有意义的k 恒过一定点，并求这个定点。

【初数】中考一轮复习课程(共15讲)_第05讲_反比例函数

一、反比例函数的概念一、反比例函数的定义函数ky x=(k 为常数，0k ≠)叫做反比例函数，其中k 叫做比例系数，x 是自变量，y 是函数，自变量x 的取值范围是不等于0的一切实数．二、反比例函数的图象和性质二、反比例函数的图象反比例函数ky x=(k 为常数，0k ≠)的图象由两条曲线组成，每条曲线随着x 的不断增大(或减小)越来越接近坐标轴，反比例函数的图象属于双曲线．反比例函数k y x =与ky x=-(0k ≠)的图象关于x 轴对称，也关于y 轴对称．三、反比例函数图象的性质反比例函数ky x=(k 为常数，0k ≠)的图象是双曲线；当0k >时，函数图象的两个分支分别位于第一、三象限内，它们关于原点对称，在每一个象限内，y 随x 的增大而减小；当0k <时，函数图象的两个分支分别位于第二、四象限内，它们关于原点对称，在每一个象限内，y 随x 的增大而增大．三、反比例函数综合应用反比例函数与方程、不等式综合如图双曲线与直线相交，则方程12k k x b x =+的解为交点的横坐标12x x 、；不等式12kk x b x+>的解为120x x x x ><<或．反比例函数知识点四、反比例函数实际应用把实际问题抽象成反比例函数的问题来解决．一、反比例函数的图像和性质1、下面的函数是反比例函数的是（） A ．31y x =+ B ．22y x x =+ C ．2xy = D ．2y x=【答案】 D【解析】该题考查的是反比例函数定义．反比例函数形如()0ky k x=≠，本题中，A 为一次函数；B 为二次函数；C 为一次函数；D 为反比例函数，故本题选D ．2、下列四个点中，在反比例函数2y x=-上的点是（）A ．()1,1k 1x例题B ．()1,2-C ．()1,2--D ．()1,2【答案】 B 【解析】该题考查的是反比例函数的性质．将选项中各个点坐标代入函数中，若等式成立，则点在反比例函数上，经验证，只有()1,2-点满足，故该题答案为B ．3、（2014初三上期末大兴区）若反比例函数1k y x-=的图象在各自象限内，y 随x 的增大而减小，则k 的值可能是（） A ．4- B ．5 C ．0 D ．2-【答案】 B【解析】该题考察的是反比例函数的性质．因为反比例函数1k y x-=的图象在各自象限内，y 随x 的增大而减小，所以10k ->，解得1k >，只有B 选项符合，故答案是B ．4、（2012初二下期末西城区北区）如图，矩形ABCD 的边分别与两坐标轴平行，对角线AC 经过坐标原点，点D 在反比例函数2510k k y x-+=（0x >）的图象上．若点B 的坐标D ．1-或6【答案】 D【解析】该题考查的是反比例函数的性质． ∵点B 的坐标为()4,4--， ∴点D 坐标为()4,4，将点D 坐标代入反比例函数中， 251016k k -+=，解得16k =，21k =-，故该题答案为D ．5、（2010初二下期中101中学）已知()111,P x y ，()222,P x y ，()333,P x y 是反比例函数2y x=的图象上的三点，且1230x x x <<<，则1y 、2y 、3y 的大小关系是（） A ．321y y y << B ．123y y y << C ．213y y y << D ．231y y y <<【答案】 C【解析】该题考察的是反比例的单调性．∵反比例函数2y x=中，20>， ∴此函数的图象在一、三象限，在每一象限内y 随x 的增大而减小，∵()111,P x y ，()222,P x y ，()333,P x y 是反比例函数2y x=的图象上的三点，且120x x <<， ∴1P ，2P 在第三象限且120y y <<，又∵30x <， ∴213y y y <<，故答案是C ．6、（2014北京中考）如图，在平面直角坐标系xOy 中，正方形OABC 的边长为2．写出一个函数()0ky k x=≠，使它的图象与正方形OABC 有公共点，这个函数的表达式为________【答案】 4y x=【解析】该题考查的是反比例函数解析式求法．由题可知()22B ，∵反比例函数的图象与正方形OABC 有公共点∴将()22B ，代入ky x=，解得4k =．7、（2014中考怀柔二模）如图，四边形ABCD 为菱形，已知()0,4A ，()3,0B -．（1）求点D 的坐标；（2）求经过点C 的反比例函数表达式．【答案】（1）()1,0- (2) 15y x=【解析】该题考查的是反比例函数综合．（1）根据题意得4AO =，3BO =，90AOB ∠=︒，∴5AB =． …………………1分 ∵四边形ABCD 为菱形， ∴5AD AB ==，∴1OD AD AO =-=， ∵点D 在y 轴负半轴，∴点D 的坐标为()1,0-． ………………………………3分（2）设反比例函数表达式为()0ky k x=≠． ∵5BC AC ==，3OB =，∴点C 的坐标为()3,5-．………………………………4分 ∵反比例函数表达式ky x=经过点C ， ∴反比例函数表达式为15y x=．………………………..5分8、（2014初二下期末北达资源中学）已知()4,A a ()2,4B --，是一次函数y kx b =+的图象与反比例函数my x=的图象的交点．（1）求反比例函数和一次函数的解析式；（2）求△AOB 的面积；（3）结合图象，直接写出不等式mkx b x+≥的解集．【答案】（1）8y x=；2y x =-（2）6（3）20x -≤<或4x ≥【解析】该题考查的是一次函数与反比例函数综合．（1）将()2,4B --代入my x=中得8m = 反比例函数的解析式为8y x= 将()4,A a 代入8y x=中得2a = 一次函数y kx b =+过()2,4B --，()4,2A 得42k b -=-+，24k b =+ 得1k =，2b =-所以一次函数的解析式为2y x =-（2）直线2y x =-同x 轴的交点()2,0，y 轴的交点()0,2- 1112222226222S AOB =⨯⨯+⨯⨯+⨯⨯=（3）由图象可知，mkx b x+≥的解集是20x -≤<或4x ≥9、（2013初二下期末东城区南区）下图是反比例函数1k y x =和2ky x=（12k k <）在第一象限的图象，直线AB x ∥轴，并分别交两条曲线于A 、B 两点，若2AOB S ∆=，则21k k -的值为___________【答案】4【解析】该题考查的是反比例函数．设A ，B 的纵坐标为y ，∴1A kx y =，2B k x y =，∴21k k AB y y=-， ∴122△AOB S AB y =⋅=， ∴21122kk y y y ⎛⎫-= ⎪⎝⎭，解得214k k -=．10、（2012初三上期末门头沟）如图，已知反比例函数ky x=与一次函数2y x =-+的图象交于A 、B 两点，且点A 的横坐标是2-．（1）求出反比例函数的解析式；（2）求AOB ∆的面积．【答案】（1）8y x=-（2）6【解析】该题考查的是反比例函数（1）由题意，得，()224--+=A 点坐标()2,4-…………………………………………．．1分 42k=-，8k =-反比例函数解析式为8y x=- ………………………………．．2分（2）由题意，得B 点坐标()4,2-………………………………3分一次函数2y x =-+与x 轴的交点坐标()2,0M ，与y 轴的交点()0,2N ………4分 6AOB OMB OMN AON S S S S =++== …………………5分11、点P 在反比例函数1y x=（0x >）的图象上，且横坐标为2．若将点P 先向右平移两个单位，再向上平移一个单位后得到点P '．则在第一象限内，经过点P '的反比例函数图象的解析式是（）A ．5(0)y x x =->B ．5(0)y x x =>C ．6(0)y x x=->D ．6(0)y x x=>【答案】 D【解析】由题意得12,2P ⎛⎫ ⎪⎝⎭，平移后得到3'4,2P ⎛⎫⎪⎝⎭，设经过点P '的反比例函数的解析式为k y x =（0k >），则3462k =⨯=，所以6y x=（0x >），故答案为D 选项．12、如图，将一块直角三角板OAB 放在平面直角坐标系中，(2,0)B ，o 60AOB ∠=，点A 在第一象限，过点A 的双曲线为ky x=．在x 轴上取一点P ，过点P 作直线OA 的垂线l ，以直线l 为对称轴，线段OB 经轴对称变换后的像是O B ''．当点O '与点A 重合时，点P 的坐标是_______．【答案】()4,0【解析】点'O 与点A 重合时，直线l 垂直平分OA ，如图，连接PA ，则PA PO =，因为()2,0B ，60AOB ︒∠=，所以2OB =，AB =设(),0P x ，则P A P O x ==，2PB x =-，在Rt P A B ∆中，由勾股定理可得()(2222x x =-+，解得4x =，所以()4,0P ．二、反比例函数综合13、（2014中考大兴一模）在平面直角坐标系xOy 中，直线l 与直线2y x =-关于y 轴对称，直线l 与反比例函数xky =的图象的一个交点为()2,A m ． (1) 试确定反比例函数的表达式；(2) 若过点A 的直线与x 轴交于点B ，且45ABO ∠=︒，直接写出点B 的坐标．【答案】（1）8y x=（2）()6,0或()2,0-【解析】该题考查的是反比例函数与一次函数的交点问题．由题意，直线l 与直线2y x =-关于y 轴对称，∴直线l 的解析式为2y x = …………………………………………………1分 ∵点()2,A m 在直线l 上, ∴224m =⨯=.∴点A 的坐标为()2,4………………………………………………………2分又∵点()2,4A 在反比例函数ky x=的图象上, ∴42k =， ∴8k =∴反比例函数的解析式为8y x=……………………………………………3分（2）∵45ABO ∠=︒∴A 的纵坐标值等于A 点、B 点横坐标差的绝对值， ∴B 点横坐标246x =+=或242x =-=- 又∵B 点在x 轴上，故B 点纵坐标为0∴B 点的坐标为()6,0或()2,0-…………………………………………5分14、（2013中考海淀一模）如图，在平面直角坐标系xOy 中，反比例函数2y x=-的图象与一次函数y kx k =-的图象的一个交点为()1,A n -．（1）求这个一次函数的解析式；（2）若P 是x 轴上一点，且满足45APO ∠=︒，直接写出点P 的坐标．【答案】（1）1y x =-+（2）()3,0-或()1,0【解析】该题考查的是反比例函数和一次函数综合．（1）∵点()1,A n -在反比例函数2y x=-的图象上， ∴2n = ………………………1分 ∴点A 的坐标为()1,2-∵点A 在一次函数y kx k =-的图象上，∴2k k =--∴1k =-………………………2分∴一次函数的解析式为1y x =-+………………………3分（2）点P 的坐标为()3,0-或()1,0………………………5分（写对一个给1分）15、（2013中考海淀二模）如图，在平面直角坐标系xOy 中，反比例函数ky x=的图象与一次函数2y x =+的图象的一个交点为(),1A m -．（1）求反比例函数的解析式；（2）设一次函数2y x =+的图象与轴交于点B ，若P 是y 轴上一点，且满足PAB ∆ 的面积是3，直接写出点P 的坐标．【答案】（1）3y x=（2）()0,0或()0,4【解析】该题考查的是一次函数和反比例函数的综合．（1）∵点(),1A m -在一次函数2y x =+的图象上，∴3m =- -------------------------1分 ∴A 点的坐标为()3,1-- ∵点()3,1A --在反比例函数ky x=的图象上， ∴3k =-------------------------2分 ∴反比例函数的解析式为3y x=．-------------------------3分（2）点P 的坐标为()0,0或()0,4．-------------------------5分（写对一个给1分）16、（2012中考东城二模）如图，在平面直角坐标系xOy 中，直线AB 与反比例函数k y x=的图像交于点()3,4A -，AC x ⊥轴于点C ． (1)求此反比例函数的解析式；(2)当直线AB 绕着点A 转动时，与x 轴的交点为(),0B a ，并与反比例函数ky x=图象的另一支还有一个交点的情形下，求ABC ∆的面积S 与a 之间的y函数关系式，并写出自变量a 的取值范围．【答案】（1）12y x=-（2）()263S a a =+>-【解析】该题考查的是一次函数和反比例函数的综合题．（1）∵43k=-∴12k =- ∴12y x=-……2分（2）∵()33BC a a =--=+，4AC = ∴()1432ACB S a ∆=⨯⨯+……4分()2 6 3a a =+>-……5分17、（2012中考朝阳二模）如图，点()3,0P -是反比例函数my x=的图象上的一点．（1）求该反比例函数的解析式；（2）设直线y kx =与双曲线m y x =的两个交点分别为P 和P′，当mkx x<时，直接写出x 的取值范围．【答案】（1）3y x=-（2）3x <-或03x <<该题考查的是反比例函数和一次函数的综合．（1）∵点()3,1P -在反比例函数ky x=的图象上，由13k =-得3k =-.∴反比例函数的解析式为3y x=-. …………………………………………3分（2）3x <-或03x <<. …………………………………………………………5分18、（2014中考石景山一模）如图，一次函数12y kx =+的图象与x 轴交于点()2,0B -，与函数()20my x x=>的图象交于点()1,A a ．（1）求k 和m 的值；（2）将函数()20my x x=>的图象沿y 轴向下平移3个单位后交x 轴于点C ．若点D 是平移后函数图象上一点，且△BCD 的面积是3，直接写出点D 的坐标．【答案】（1）3m =（2）3,25⎛⎫⎪⎝⎭或()3,2-【解析】该题考查的是一次函数与反比例函数．（1）根据题意，将点代入12y kx =+， ∴022k =-+．∴1k = ∴()1,3A 将其代入2my x=，可得3m =．（2）函数()230y x x =>的图象沿y 轴向下平移3个单位后解析式为()330y x x=->，与交x 轴于点C ，令0y =代入上解析式中得1x =．∴C 点坐标为()1,0．∵()2,0B -，∴3BC =．∵△BCD 的面积是3，∴D 到x 轴的距离为2．当点D 在x 轴上方时，2y =，则横坐标为35x =，故坐标为3,25⎛⎫⎪⎝⎭当点D 在x 轴下方时，2y =-，则横坐标为3x =，故坐标为()3,2-19、（2014中考西城二模）经过点()1,1的直线l ：()2 0y kx k =+≠与反比例函数1G ：()10my m x=≠的图象交于点()1,A a -，(),1B b -，与y 轴交于点D ．（1）求直线l 对应的函数表达式及反比例函数G 1的表达式；（2）反比例函数G 2：()2 0ty t x=≠，①若点E 在第一象限内，且在反比例函数G 2的图象上，若EA EB =，且△AEB 的面积为8，求点E 的坐标及t 值；②反比例函数G 2的图象与直线l 有两个公共点M ，N （点M 在点N 的左侧），若DM DN +<t 的取值范围．【答案】（1）2y x =-+；3y x=-（2）()3,3E ；504t -<<或01t <<【解析】该题考查的是一次函数和反比例函数．（1）∵直线l : 2 (0)y kx k =+≠经过()1,1-，∴1k =-，∴直线l 对应的函数表达式2y x =-+． 1分 ∵直线l 与反比例函数G 1:1 (0)my m x=≠的图象交于点(1,)A a -，(),1B b -， ∴3a b ==．∴(1,3)A -，()3,1B - ∴3m =-．∴反比例函数G 1函数表达式为3y x=-． ······················································· 2分（2）∵EA EB =，(1,3)A -，()3,1B -， ∴点E 在直线y x =上．∵△AEB 的面积为8，AB =，∴EH =∴△AEB 是等腰直角三角形．∴()3,3E 5分 ②分两种情况：（ⅰ）当0t >时，则01t <<； 6分（ⅱ）当0t <时，则504t -<<．综上，当504t -<<或01t <<时，反比例函数2G 的图象与直线l 有两个公共点M ，N ，且DM DN +< 7分20、（2013初二下期末东城区南区）在直角坐标平面内，反比例函数my x=的图象经过点()1,4A 、()B a b ，过点A 作x 轴垂线，垂足为C ，过点B 作y 轴垂线，垂足为D（1）求反比例函数的解析式；为顶点的四边形是等腰梯形，点B 的坐标是______；（3）ABD ∆的面积为4，求点B 的坐标。

学而思中考数学第10讲.点睛班之一模考前知识梳理与易错题赏析.尖子1班.教师版

`【例1】 ⑴已知抛物线过()10A -，和()30B ，点，与y 轴交于点C ，且32BC =，则这条抛物线的解析式为_________________________________．⑵如图所示，在梯形ABCD 中，AD BC ∥，90ABC ∠=︒， 6AD AB ==，14BC =，点M 是线段BC 上一定点，且 8MC =．动点P 从C 点出发沿C D A B →→→的路线运动，运动到点B 停止．在点P 的运动过程中，使PMC △为等腰三角形的点P 有______个．⑶已知四边形ABCD 中，23AB BC ==，60ABC ∠=︒，90BAD ∠=︒，且ACD △是一个直角三角形，那么AD 的长等于__________________．⑷当k 为何值时，方程230x kx +-=和方程230x x k +-=有公共根？并求出公共根．【解析】 ⑴223y x x =--或223y x x =-++⑵4⑶3或4⑷令两方程的公共根是m ，则223030m km m m k ⎧+-=⎪⎨+-=⎪⎩，两式相减得()()131k m k -=--， ①若10k -=，即1k =，两个方程都是230x x +-=，则公共根是113x -±=；典题精练10第二轮复习之一模考前知识梳理与易错赏析题型一：分类讨论精选题MDCA②若10k -≠，即1k ≠，则3m =-，此时2k =．综上所述，1k =时，公共根是1132-±；2k =时，公共根是3-．一、旋转精选题【例2】 ⑴（2012四川绵阳）如图，P 是等腰直角△ABC 外一点，把BP 绕点B 顺时针旋转90°到BP ′，已知∠AP ′B =135°，P′A ：P ′C =1：3，则P ′A ：PB =（）P 'PCBAA ．1：2B ．1：2C ．3：2D ．1：3【答案】B.【解析】如图，连接AP ，∵BP 绕点B 顺时针旋转90°到BP ′， ∴BP=BP ′，∠ABP +∠ABP ′=90° 又∵△ABC 是等腰直角三角形，∴AB=BC ，∠CBP ′+∠ABP ′=90°，∴∠ABP =∠CBP ′在△ABP 和△CBP ′中，∵ BP=BP ′，∠ABP=∠CBP ′，AB=BC ，∴△ABP ≌△CBP ′（SAS ） ∴AP =P ′C∵P ′A ：P ′C =1：3，∴P ′C=AP =3P ′A连接PP ′，则△PBP ′是等腰直角三角形.∴∠BP ′P =45°，PP 2PB ∵∠AP ′B =135°，∴∠AP ′P =135°-45°=90°，∴△APP ′是直角三角形. 设P ′A =x ，则AP =3x ，在Rt △APP ′中，2222''(3)22PP AP P A x x x =--=题型二：几何小题精选在Rt △APP ′中，'2PP PB = ∴222PB x =，解得PB =2x ∴P ′A ：PB =x ：2x =1：2⑵(2012广西)如图，在平面直角坐标系中，矩形OEFG 的顶点F 的坐标为(4，2)，将矩形OEFG 绕点O 逆时针旋转，使点F 落在y 轴上，得到矩形OMNP ，OM 与GF 相交于点A ．若经过点A 的反比例函数(0)ky x x =>的图象交EF 于点B ，则点B 的坐标为 .OEF NMG Py xBA【答案】（4，12）【解析】 ∵矩形OEFG 绕点O 逆时针旋转，使点F 落在y 轴的点N 处，得到矩形OMNP ，∴∠P =∠POM =∠OGF =90°,∵PNO NOM ∠=∠ ∴△OGA ∽△NPO∵E 点坐标为（4，0），G 点坐标为（0，2），∴OE =4，OG =2 ∴OP=OG=2，PN=GF=OE =4∵△OGA ∽△NPO ，∴OG ：NP =GA ：OP ，即2：4=GA ：2 ∴GA=1 ∴A 点坐标为（1，2）把A （1，2）代入ky x=得k =1×2=2 ∴过点A 的反比例函数解析式为2y x= 把x =4代入2y x =得12y =1 2）∴B点坐标为（4，D30°A 1B 1CBA ⑶（2012广东佛山）如图，把一个斜边长为2且含有30°的直角三角板ABC 绕直角顶点C 顺时针旋转90°到△A 1B 1C ，则在旋转过程中这个三角板扫过的图形的面积是（）30°A 1B 1CB AA 3 C ．334π D ．11312π 【答案】D【解析】因为旋转过程中这个三角板扫过的图形的面积分为三部分扇形ACA 1、 BCD 和△ACD计算即可：在△ABC 中，∠ACB=90°，∠BAC =30°，AB =2， ∴BC =12AB =1，∠B =90°－∠BAC =60°。

学×思面授班初三数学秋季提高班讲义第3讲.第二轮复习之代数综合.提高班.学生版

在北京中考试卷中，代数综合题出现在第23题左右，分值为7分，主要以方程、函数这两部分为考查重点，会涉及到四大数学思想：转化（化归）思想、分类讨论思想、方程（函数）思想、数形结合思想．也会考查代数式的恒等变形，比如代入法、待定系数法、降次法、配方法等．【例1】 ⑴ 已知：24510x x +-=，则代数式()()()()221122x x x x x +--++- ．⑵ 已知223n m =-和223m n =-，且m n ≠，则代数式33222m mn n -+的值．⑶ 已知1mn =-，23320m m ++=，则22332015n n ++= ． ⑷ 已知4a b +=，226210a b b +-+=，则ab = ．【例2】抛物线2(3)3(0)y mx m x m =+-->与x 轴交于A 、B 两点，且点A 在点B 的左侧，与y 轴交于点C ，OB=OC ．⑴ 求这条抛物线的解析式；⑵ 若点P 1(,)x b 与点Q 2(,)x b 在（1）中的抛物线上，且12x x <，PQ=n .① 求2124263x x n n -++的值；② 将抛物线在PQ 下方的部分沿PQ 翻折，抛物线的其它部分保持不变，得到一个新图象.当这个新图象与x 轴恰好只有两个公共点时，b 的取值范围是 .（2013海淀期末）典题精练3第二轮复习之代数综合【例3】已知：关于x 的一元二次方程()()21210m x m x -+--=（m 为实数）. ⑴ 若方程有两个不相等的实数根，求m 的取值范围； ⑵ 求证：抛物线()()2121y m x m x =-+--总过轴上的一个定点；⑶ 若m 是整数，且关于x 的一元二次方程()()21210m x m x -+--=有两个不相等的整数根时，把抛物线()()2121y m x m x =-+--向右平移3个单位长度，求平移后的解析式．(2013东城二模)【例4】已知点A （a ，）、B （2a ，y ）、C （3a ，y ）都在抛物线21122y x x =-上.⑴ 求抛物线与x 轴的交点坐标； ⑵ 当a =1时，求△ABC 的面积；⑶ 是否存在含有、y 、y ，且与a 无关的等式？如果存在，试给出一个，并加以证明；如果不存在，请说明理由.（2013昌平二模）x 1y 231y 23【例5】二次函数，其顶点坐标为M (1，4-)．⑴ 求二次函数的解析式；⑵ 将二次函数的图象在轴下方的部分沿轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合新图象回答：当直线与这个新图象有两个公共点时，求的取值范围．(2013丰台一模)【例6】已知关于m 的一元二次方程221x mx +-=0. ⑴ 判定方程根的情况；⑵ 设m 为整数，方程的两个根都大于1-且小于32，当方程的两个根均为有理数时，求m 的值．(2013平谷一模)2y x bx c =++x x y x n =+n【例7】已知二次函数在和时的函数值相等。

初中数学九年级上册讲义第15讲-反比例函数与反比例函数图像(提高)-学案

初中数学九年级上册讲义第15讲-反比例函数与反比例函数图像（提高）-学案学科教师辅导讲义学员编号_________年级九年级课时数3学员姓名辅导科目数学学科教师授课主题第15讲---反比例函数与反比例函数图像授课类型T同步课堂P实战演练S归纳总结教学目标理解反比例函数的概念，能判断两个变量之间的关系是否是反比例函数关系；能根据已知条件确定反比例函数的表达式及作出函数图像；掌握函数图像的性质与系数k的几何意义。

授课日期及时段T（Textbook-Based）同步课堂体系搭建一.知识框架二.知识概念（一）反比例与反比例函数1.反比例如果两个变量的每一组对应值的乘积是一个非零常数，那么这两个变量成反比例，用数学符号语言记为xyk，或k0）。

成反比例的关系式不一定是反比例函数,但是反比例函数中的两个变量必成反比例关系。

2.反比例函数（1）定义一般地，形如（为常数，）的函数称为反比例函数。

还可以写成。

也可以写成xyk,它表明在反比例函数中自变量x与其对应函数值y之积，总等于已知常数k.（2）反比例函数解析式的特征等号左边是函数，等号右边是一个分式。

分子是不为零的常数（也叫做比例系数），分母中含有自变量，且指数为1.比例系数自变量的取值为一切非零实数。

函数的取值是一切非零实数。

（3）待定系数法反比例函数解析式的确定利用待定系数法（只需一对对应值或图像上一个点的坐标即可求出）。

（二）反比例函数的图像与性质1.图像的画法描点法列表（应以O为中心，沿O的两边分别取三对或以上互为相反的数）描点（有小到大的顺序）连线（从左到右光滑的曲线）2.图像特征（1）反比例函数的图像是双曲线，（为常数，）中自变量，函数值，所以双曲线是不经过原点，断开的两个分支，延伸部分逐渐靠近坐标轴，但是永远不与坐标轴相交。

（2）反比例函数的图像是是轴对称图形（对称轴是或），也是中心对称图形。

（3）系数的几何意义过双曲线（）上任意引轴轴的垂线，所得矩形面积为。

初三数学教案-第15课时反比例函数( 精品

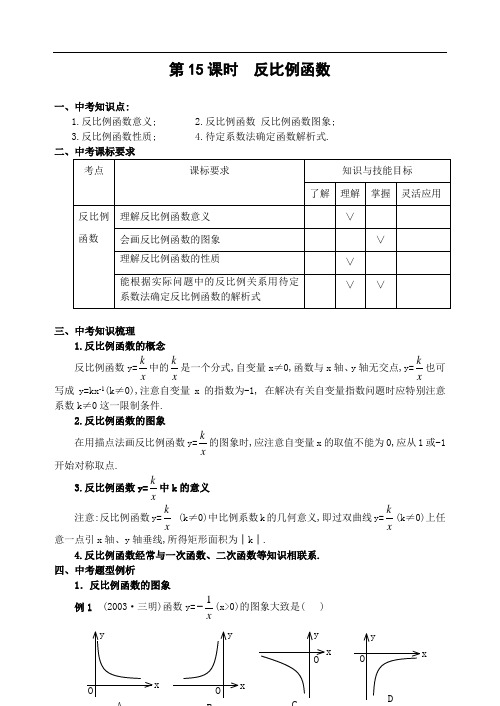
第15课时反比例函数一、中考知识点:1.反比例函数意义;2.反比例函数反比例函数图象;3.反比例函数性质;4.待定系数法确定函数解析式.三、中考知识梳理1.反比例函数的概念反比例函数y=kx中的kx是一个分式,自变量x≠0,函数与x轴、y轴无交点,y=kx也可写成y=kx-1(k≠0),注意自变量x的指数为-1, 在解决有关自变量指数问题时应特别注意系数k≠0这一限制条件.2.反比例函数的图象在用描点法画反比例函数y=kx的图象时,应注意自变量x的取值不能为0,应从1或-1开始对称取点.3.反比例函数y=kx中k的意义注意:反比例函数y=kx(k≠0)中比例系数k的几何意义,即过双曲线y=kx(k≠0)上任意一点引x轴、y轴垂线,所得矩形面积为│k│.4.反比例函数经常与一次函数、二次函数等知识相联系.四、中考题型例析1．反比例函数的图象例1 (2003·三明)函数y=1x(x>0)的图象大致是( )y y y y解析:函数y=kx的图象是双曲线,当k<0时双曲线两分支分别在第二、四象限内, 而已知中(x>0)表明横坐标为正,故双曲线位于第四象限.答案:D.点评:本题主要考查反比例函数的图象.但需注意的是y=1x- 中的限制条件(x>0), 即双曲线的横坐标为正.例2 (2003·宜昌)函数y=kx+1与函数y=kx在同一坐标系中的大致图象是( )分析:明确一次函数y=kx+1中的k 的含义与函数y=kx中k 的含义是解题的关键. 解:可用排除法,假设y=kx中k>0,双曲线过第一、三象限,则直线y=kx+1 也应过第一、第三象限且与y 轴交于正半轴,故排除B 、D.同理可排除C,故答案为A.点评:解决同一坐标系中两种函数共存问题,首先明确同一字母系数在不同函数解析式中的含义,切勿出现“张冠李戴”的错误.2.待定系数法确定函数解析式例3 (2003·南充)已知y 与x 2成反比例,并且当x=-1时,y=2,那么当x=4时,y 等于( )A.-2B.2C.12D.-4 分析:已知y 与x 2成反比例,∴y=2k x (k ≠0).将x=-2,y=2代入y=2kx可求得k,从而确定双曲线解析式.解:∵y 与x 2成反比例,∴y=2kx (k ≠0). 当x=-2时,y=2,∴2=2(2)k-,k=8 y O xAy OxBy O xCy O xD∴y=28x ,把x=4代入y=28x 得y=12. 故答案为C.点评:此题主要考查反比例函数概念及待定系数法确定函数解析式. 3.反比例函数的应用例 4 (2003·天津)如图所示,已知一次函数y=kx+b(k ≠0)的图象与x 轴、y 轴分别交于A 、B 两点,且与反比例函数y=mx(m ≠0)的图象在第一象限交于C 点, CD 垂直于x 轴,垂足为D.若OA=OB=OD=1,(1)求点A 、B 、D 的坐标; (2)求一次函数和反比例函数的解析式. 分析:(1)由OA=OB=OD=1可确定A 、B 、D 三点坐标. (2)将A 、B 两点坐标分别代入y=kx+b,可用待定系数法确定一次函数的解析式, 由C 点在一次函数的图象上可确定C 点坐标,将C 点坐标代入y=kx可确定反比例函数的解析式. 解:(1)∵OA=OB=OD=1,∴点A 、B 、D 的坐标分别为A(-1,0),B(0,1),C(1,0). (2)∵点A 、B 在一次函数y=kx+b(k ≠0)的图象上, ∴01k b b -+=⎧⎨=⎩,解得11k b =⎧⎨=⎩,∴一次函数的解析式为y=x+1.∵点C 在一次函数y=x+1的图象上,且CD ⊥x 轴, ∴点C 的坐标为(1,2) .又∵点C 在反比例函数y=mx (m ≠0)的图象上,m=2. ∴反比例函数的解析式为y=2x.基础达标验收卷一、选择题:(第5题为多项选择题)1.(2004·沈阳)经过点(2,-3)的双曲线是( ) A.y=-6x B.6xC.y=32xD.-32xyO x DCB A2.(2003·江西)反比例函数y=-1x的图象大致是( )3.(2003·广东)如图,某个反比例函数的图象经过点P,则它的解析式为( )A.y=1x (x>0); B.y=-1x (x>0)C.y=1x (x<0); D.y=-1x(x<0) 4.(2004·徐州)如图,点P 是x 轴上的一个动点,过点P 作x 轴的垂线PQ 交双曲线于点Q,连结OQ,当点P 沿x 轴正半方向运动时,Rt △QOP 的面积( )A.逐渐增大;B.逐渐减小;C.保持不变;D.无法确定 5.(2004·上海)在函数y=kx(k>0)的图象上有三点A 1(x 1,y 1),A 2(x 2,y 2),A 3( x 3.y 3),已知x 1<x 2<0<x 3,则下列各式中,正确的是( )A.y 1<0<y 3B.y 3<0<y 1;C.y 2<y 1<y 3D.y 3<y 1<y 2 6.(2004·武汉)已知直线y=kx+b 与双曲线y=kx交于A(x 1,y 1),B(x 2,y 2) 两点, 则x 1·x 2的值( )A.与k 有关、与b 无关;B.与k 无关、与b 无关;C.与k 、b 都有关;D.与k 、b 都无关 7.(2002.青岛)已知关于x 的函数y=k(x-1)和y=-kx (k ≠0),它们在同一坐标系内的图象大致是下图中的( )二、填空题:1.(2004.福州)如果反比例函数图象过点A(1,2),那么这个反比例函数的图象在第_______象限.2.(2004.哈尔滨)反比例函数y=kx(k 是常数,k ≠0)的图象经过点(a,- a) , 那么k_____0(填“>”或“<”).y O x A y O x B yO x C y O xD1-1y OxPy Q OxPyO x A yO x B yO x C y Ox3.(2004.陕西)若反比例函数y=kx经过点(-1,2),则一次函数y=-kx+2的图象一定不经过第_____象限.4.(2004.北京)我们学习过反比例函数.例如,当矩形面积S一定时,长a是宽b 的反比例函数,其函数关系式可以写为a=sb(S为常数,S≠0).请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例,并写出它的函数关系式.实例:_______________________________________________________________;函数关系式:_______________________.5.(2003.安徽)近视眼镜的度数y(度)与镜片焦距x(米)成反比例.已知400 度近视眼镜镜片的焦距为0.25米,则眼镜度数y与镜片焦距x之间的函数关系式是____.三、解答题:1.(2004·天津)已知一次函数y=x+m与反比例函数y=1mx(m≠-1)的图象在第一象限内的交点为P(x0,3).(1)求x0的值;(2)求一次函数和反比例函数的解析式.2.(2004·呼和浩特)如图,一次函数y=kx+b的图象与反比例函数y=mx的图象交于A、B两点:A(-2,1),B(1,n).(1)求反比例函数和一次函数的解析式;(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.3.(2003·海南)如科,已知反比例函数y=12x的图象与一次函数y=kx+4的图象相交于P、Q两点,并且P点的纵坐标是6.(1)求这个一次函数的解析式;(2)求△POQ的面积.yOxBAyOxP能力提高练习一、学科内综合题 1.(2002·潍坊)如图,△OPQ 是边长为2的等边三角形,若反比例函数的图象过点P,则它的解析式是_________. 2.(2002·南宁)如图,Rt △ABO 的顶点A 是双曲线y=kx 与直线y=-x-(k+1)在第二象限的交点.AB ⊥x 轴于B,且S △ABO =32.(1)求这两个函数的解析式;(2)求直线与双曲线的两个交点A 、C 的坐标和△AOC 的面积.二、学科间综合题3.(2004·南京)在压力不变的情况下,某物体承受的压强p(Pa) 是它的受力面积S(m2)的反比例函数,其图象如图所示.(1)求p 与S 之间的函数关系式; (2)求当S=0.5m 2时,物体承受的压强p.y QO xPy O x C B AS(m 2)三、实际应用题 4.(2002·吉林)某单位为响应政府发出的全民健身的号召,打算在长和宽分别为20m 和11m 的矩形大厅内修建一个60m2的矩形健身房ABCD. 该健身房的四面墙壁中有两侧沿用大厅的旧墙壁(如图为平面示意图),已知装修旧墙壁的费用为20元/m 2,新建(含装修)墙壁的费用为80元/m 2.设健身房的高为3m,一面旧墙壁AB 的长为xm,修建健身房墙壁的总投入为y 元.(1)求y 与x 的函数关系式;(2)为了合理利用大厅,要求自变量x 必须满足条件:8≤x ≤12, 当投入的资金为4800元时,问利用旧墙壁的总长度为多少?11m20mDCB A5.(2003.金华)为了预防“非典”,某学校对教室采用药薰消毒法进行消毒. 已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧完后,y 与x 成反比例(如图所示),现测得药物8分钟燃毕, 此时室内空气中每立方米的含药量为6毫克.请根据题中所提供的信息,解答下列问题:(1)药物燃烧时y 关于x 的函数关系式为: _____________, 自变量x 的取值范围是:________________;药物燃烧后y 关于x 的函数关系式为:___________________.(2)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过_______分钟后,学生才能回到教室;(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10 分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?x(分钟)y(豪克)86O答案:一、1.A 2.D 3.D 4.C 5.A,C 6.D 7.B二、1.一、三 2.< 3.四 4.如当路程s 一定时,速度v 是时间t 的反比例函数;函数关系式为v=s t (s 是常数) 5.y=100x三、(1)∵点P(x 0,3)在一次函数y=x+m 的图象上.∴3=x 0+m,即m=3-x 0.又点P(x 0,3)在反比例函数y=1m x+ 的图象上. ∴3=1m x +,即m=3x 0-1. ∴3-x 0=3x 0-1,解得x 0=1. (2)由(1),得m=3-x 0=3-1=2, ∴一次函数的解析式为y=x+2,反比例函数的解析式为y=3x2.解:(1)点A(-2,1)在反比例函数y=mx的图象上, ∴m=(-2)×1=-2. ∴反比例函数解析式y=2x点B(1,n)也在反比例函数的图象上, ∴n=-2.点A 、B 均在一次函数y=kx+b 的图象上 ∴21121k b k k b b -+==-⎧⎧⇒⎨⎨+=-=-⎩⎩∴一次函数的解析式为y=-x-1. (2)根据图象可知,满足要求的x 取值范围为x<-2或0<x<1. 3.解:(1)因点P 在反比例函数y=12x 的图象上,且其纵坐标为6,于是,得12x=6,解得x=2, ∴P(2,6).又∵点P 在函数y=kx+4的图象上, ∴6=2k+4,解得k=1. ∴所求一次函数解析式为y=x+4.(2)解方程组412y x y x =+⎧⎪⎨=⎪⎩得121262,26x x y y =-=⎧⎧⎨⎨=-=⎩⎩ ∴Q(-6,-2) 令y=0,代入y=x+4, 解得x=-4,∴函数y=x+4的图象与x 轴的交点是A(-4,0).∴△AOP 和△AOQ 的公共边OA=4,OA 边上的高分别为PM=6,QN=2. ∴S △POQ =S △AOP +S △AOQ =12×4×6+12×4×2=16. 能力提高练习1.y=x(x>0) 2.解:(1)设A 点坐标为(x,y),且x<0,y>0则S △ABO =12·│BO │·│BA │=12·(-x)·y=32。

九年级数学第15讲.目标班期末复习之知识点睛及模拟测试.目标班.学生版

学而思学校秋季第五级（下）初三数学测试卷（目标班）一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个．．是符合题意的． 1. 下列运算错误的是（） A 235 B ．236= C 623= D ．2(2)2-=2.抛物线24(3)1y x =-+-的顶点坐标是（） A ． ()31-， B ．()31--， C ． ()31， D ．()31-，3.如图，O ⊙的直径4AB =，点C 在O ⊙上，30ABC =︒∠，则AC 的长是（） A ．1B 2C 3D ．24. 在ABC △中，点D 、E 分别在边AB 、AC 上，若DE BC ∥，12AD BD =，4cm DE =，则BC 的长为（） A ．8cm B ．12cm C ．11cm D ．10cm5.已知方程2540x x -+=的两根分别为1O ⊙与2O ⊙的半径，且123O O =，那么两圆的位置关系是（）A ．相交B ．外切C ．内切D ．相离6.如图，在小正方形组成的网格中，点A 、B 、C 、D 、E 都在小正方形的顶点上，则tan ADC ∠的值为（）A ．14B ．13C ．12D ．17.已知三角形的三边长分别为345，，（） A ．01234，，，， B ．01245，，，， C ．012345，，，，， D ．0123456，，，，，， 8.如图，在平面直角坐标系xOy 中，P 是反比例函数xy 1=（x > 0）图象上的一个动点，点A 在x 轴上，且PO =P A ，EDCBAOCBAAB 是PAO △中OP 边上的高．设m OA =，n AB =，则下列图象中，能表示n 与m 的函数关系的图象大致是( )A B C D二、填空题（本题共16分，每小题4分） 9. 2x -x 的取值范围是．10. 如图，O ⊙的直径CD AB ⊥，60AOC =︒∠，则CDB ∠为度．个11. 将二次函数22y x =+的图象向左平移1个单位，再向下平移3单位，则平移后抛物线的表达式为． 12.如图，在平面直角坐标系xOy 中，点1A ，2A ，3A ，… 都在y 轴上，对应的纵坐标分别为1，2，3，…．直线1l ，2l ，3l ，…分别经过点1A ，2A ，3A ，…，且都平行于x轴．以点O 为圆心，半径为2的圆与直线1l 在第一象限交于点1B ，以点O 为圆心，半径为3的圆与直线2l 在第一象限交于点2B ，…，依此规律得到一系列点n B （n 为正整数），则点1B 的坐标为，点n B 的坐标为．三、解答题（本题共30分，每小题5分）13. 计算：118122sin 60tan 602-骣÷ç+--白?÷ç÷ç桫14. 已知：0162=-+x x ，求代数式()()()()3312122+-+--+x x x x x 的值．15. 先化简，再求值：23111xx x x x x -⎛⎫-⋅⎪-+⎝⎭，其中22x =．OBAmn O16. 在Rt ABC △中，AD 为斜边上的高，若4AD =,3BD =，求AC 的长．x 轴交17.如图，二次函数2y x bx c =-++的图象经过坐标原点，且与于()20A -，．⑴求此二次函数解析式及顶点的坐标；⑵在抛物线上有一点P ，满足3AOP S =△，直接写出点P 的坐标．18.如图，AB 是O ⊙的直径，点D 在O ⊙上，45DAB =︒∠，BC AD ∥，CD AB ∥．⑴判断直线CD 与O ⊙的位置关系，并说明理由； ⑵若O ⊙的半径为1，求图中阴影部分的面积（结果保留π）．DB AOAyxODB四、解答题（本题共20分，每小题5分） 19.阅读并回答问题：小亮是一位刻苦学习、勤于思考、勇于创新的同学．一天他在解方程21x =-时，突发奇想：21x =-在实数范围内无解，如果存在一个数i ，使21i =-，那么当21x =-时，有x =±i ，从而x =±i 是方程21x =-的两个根．据此可知：(1) i 可以运算，例如：321i i i i i =⋅=-⨯=-，则i 4= ， i 2011=______________，i 2017=__________________；(2)方程2220x x -+=的两根为（根用i 表示）．20.如图，正方形网格中的每一个小正方形的边长都是1，四边形ABCD 的四个顶点都在格点上，O 为AD 边的中点，若把四边形ABCD 绕着点O 顺时针旋转180︒，试解决下列问题：⑴画出四边形ABCD 旋转后的图形； ⑵求点C 旋转过程时所经过的路径长；⑶设点B 旋转后的对应点为B '，求t a n D A B '∠的值．21.吸烟有害健康！你知道吗，即使被动吸烟也大大危害健康．有消息称，我国准备从2011年元月一日起在公众场所实行“禁烟”，为配合“禁烟”行动，某校组织同学们在某社区开展了“你支持哪种戒烟方式”的问卷调查，征求市民的意见，并将调查结果整理后制成了如下统计图：根据统计图解答：戒烟戒烟戒烟戒烟人数120603015%10%强制戒烟警示戒烟替代品戒烟药物戒烟A BCDO图2图1A'PPA ABCBC⑴同学们一共随机调查了多少人？ ⑵请你把统计图补充完整；⑶如果在该社区随机咨询一位市民，那么该市民支持“强制戒烟”的概率是多少？假定该社区有1万人，请估计该地区大约有多少人支持“警示戒烟”这种方式．22.阅读下面材料：小伟遇到这样一个问题：如图1，在ABC △（其中BAC ∠是一个可以变化的角）中，2AB =，4AC =，以BC 为边在BC 的下方作等边PBC △，求AP 的最大值。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

学而思学校秋季第五级（下）初三数学测试卷（目标班）一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个．．是符合题意的． 1. 下列运算错误的是（）A=B ．= C = D ．2(2=2.抛物线24(3)1y x =-+-的顶点坐标是（） A ． ()31-， B ．()31--， C ． ()31，D ．()31-， 3.如图，O ⊙的直径4AB =，点C 在O ⊙上，30ABC =︒∠，则AC 的长是（） A ．1B CD ．24. 在ABC △中，点D 、E 分别在边AB 、AC 上，若DE BC ∥，12AD BD =，4cm DE =，则BC 的长为（） A ．8cm B ．12cm C ．11cm D ．10cm5.已知方程2540x x -+=的两根分别为1O ⊙与2O ⊙的半径，且123O O =，那么两圆的位置关系是（）A ．相交B ．外切C ．内切D ．相离6.如图，在小正方形组成的网格中，点A 、B 、C 、E 都在小正方形的顶点上，则tan ADC ∠的值为（A ．14B ．13C ．12D ．17.已知三角形的三边长分别为345，，有可能情况是（） A ．01234，，，， B ．01245，，，， C ．012345，，，，， D ．0123456，，，，，，BA8. 如图，在平面直角坐标系xOy 中，P 是反比例函数xy 1=（x > 0）图象上的一个动点，点A 在x 轴上，且PO =P A ， AB 是PAO △中OP 边上的高．设m OA =，n AB =，则下列图象中，能表示n 与m 的函数关系的图象大致是( )A B C D二、填空题（本题共16分，每小题4分） 9. 使2x -有意义的x 的取值范围是．10. 如图，O ⊙的直径CD AB ⊥，60AOC =︒∠，则CDB ∠为度．11. 将二次函数22y x =+的图象向左平移1个单位，再向下平移3个单位，则平移后抛物线的表达式为． 12.如图，在平面直角坐标系xOy 中，点1A ，2A ，3A ，… 都在y 轴上，对应的纵坐标分别为1，2，3，…．直线1l ，2l ，3l ，…分别经过点1A ，2A ，3A ，…，且都平行于x轴．以点O 为圆心，半径为2的圆与直线1l 在第一象限交于点1B ，以点O 为圆心，半径为3的圆与直线2l 在第一象限交于点2B ，…，依此规律得到一系列点n B （n 为正整数），则点1B 的坐标为，点n B 的坐标为．三、解答题（本题共30分，每小题5分）13.计算：118122sin 60tan 602-骣÷ç++--白?÷ç÷ç桫14. 已知：0162=-+x x ，求代数式()()()()3312122+-+--+x x x x x 的值．15. 先化简，再求值：23111x x x x x x -⎛⎫-⋅ ⎪-+⎝⎭，其中22x =-．16.在Rt ABC △中，AD 为斜边上的高，若4AD =,3BD =，求AC 的长．17.如图，二次函数2y x bx c =-++的图象经过坐标原点，且与x 轴交于()20A -，． ⑴求此二次函数解析式及顶点的坐标；⑵在抛物线上有一点P ，满足3AOP S =△，直接写出点P 的坐标．ODCBADC B A OAy xmn O18. 如图，AB 是O ⊙的直径，点D 在O ⊙上，45DAB =︒∠，BC AD ∥，CD AB ∥．⑴判断直线CD 与O ⊙的位置关系，并说明理由； ⑵若O ⊙的半径为1，求图中阴影部分的面积（结果保留π）．四、解答题（本题共20分，每小题5分） 19.阅读并回答问题：小亮是一位刻苦学习、勤于思考、勇于创新的同学．一天他在解方程21x =-时，突发奇想：21x =-在实数范围内无解，如果存在一个数i ，使21i =-，那么当21x =-时，有x =±i ，从而x =±i 是方程21x =-的两个根．据此可知：(1) i 可以运算，例如：321i i i i i =⋅=-⨯=-，则i 4= ， i 2011=______________，i 2012=__________________；(2)方程2220x x -+=的两根为（根用i 表示）．20.如图，正方形网格中的每一个小正方形的边长都是1，四边形ABCD 的四个顶点都在格点上，O 为AD 边的中点，若把四边形ABCD 绕着点O 顺时针旋转180︒，试解决下列问题： ⑴画出四边形ABCD 旋转后的图形； ⑵求点C 旋转过程时所经过的路径长；⑶设点B 旋转后的对应点为B '，求tan DAB '∠的值．21.吸烟有害健康！你知道吗，即使被动吸烟也大大危害健康．有消息称，我国准备从2011年元月一日起在公众场所实行“禁烟”，为配合“禁烟”行动，某校组织同学们在某社区开展了“你支持哪种戒烟方式”的问卷调查，征求市民的意见，并将调查结果整理后制成了如下统计图：根据统计图解答：⑴同学们一共随机调查了多少人？ ⑵请你把统计图补充完整；⑶如果在该社区随机咨询一位市民，那么该市民支持“强制戒烟”的概率是多少？假定该社区有1万人，请估计该地区大约有多少人支持“警示戒烟”这种方式．戒烟戒烟戒烟戒烟15%10%强制戒烟警示戒烟替代品戒烟药物戒烟A BCDO图2图1A'PPA ABCBC22.阅读下面材料：小伟遇到这样一个问题：如图1，在ABC △（其中BAC ∠是一个可以变化的角）中，2AB =，4AC =，以BC 为边在BC 的下方作等边PBC △，求AP 的最大值。

小伟是这样思考的：利用变换和等边三角形将边的位置重新组合．他的方法是以点B 为旋转中心将ABP △逆时针旋转60︒得到'A BC △,连接'A A ,当点A 落在'A C 上时,此题可解（如图2）．请你回答：AP 的最大值是．参考小伟同学思考问题的方法，解决下列问题：如图3，等腰Rt ABC △．边4AB =,P 为ABC △内部一点，则AP BP CP ++的最小值是 .（结果可以不化简）五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）23. 已知关于x 的一元二次方程242(1)0x x k -+-=有两个不相等的实数根．⑴ 求k 的取值范围；⑵ 如果抛物线242(1)y x x k =-+-与x 轴的两个交点的横坐标为整数，求正整数k 的值；⑶ 直线y x =与⑵中的抛物线在第一象限内的交点为点C ，点P 是射线OC 上的一个动点（点P 不与点O 、点C重合），过点P 作垂直于x 轴的直线，交抛物线于点M ，点Q 在直线PC 上，距离点P 为个单位长度，设点P 的横坐标为t ，△PMQ 的面积为S ，求出S 与t 之间的函数关系式．图3CABP24.如图，在平面直角坐标系xOy 中，点()2A m ，第一象限，满足tan AOx =∠点P 是y 动点，点()0Q n ，()0n >是x 轴上的动点． ⑴求m 的值；⑵若APQ △是以PAQ ∠为顶角的等腰三角形，n 的取值范围．⑶抛物线222ay x x a =-+经过点Q ，若APQ △等腰直角三角形，则4165a a +-= ．25.⑴如图1，四边形ABCD 是菱形，60BAD BCD ==︒∠∠，当12AC =时，则BCD △的周长为． ⑵如图2，若四边形ABCD 不是菱形，2260BAD ACB ACD ===︒∠∠∠，12AC =，判断BCD △的周长是否变化，并说明理由．⑶如图3，在四边形ABCD 中，45BAD ACB ACD ===︒∠∠∠，12AC =，直接写出BCD △的周长为．ABC D图3ABC D图2图1DC BA参考答案及评分标准一、选择题（本题共32分，每小题4分）三、解答题（本题共30分，每小题5分）13.解：原式212=+-…………………………………………4分33=+-=…………………………………………………………………5分14.解：原式222922144xxxxx-++-++=…………………………………2分1062++=xx…………………………………3分当0162=-+xx时，162=+xx…………………………………4分原式11=．…………………………………5分15.解：()()2113131111x xx x x x xx x x x x x+--⎛⎫⎛⎫-⋅=-⋅⎪ ⎪-+-+⎝⎭⎝⎭()()()()1111311x x x xx xx x x x+-+-=⋅-⋅-+()()31124x x x=+--=+………………………………………………………3分当2x=时，原式=………………………………………………5分16.解：在Rt ABD△中，90ADB=︒∠，4AD=，3BD=由勾股定理得222AB BD AD=+∴5AB==90B BAD CAD BAD+=+=︒∠∠∠∠∴B CAD=∠∠……………………………………1分在ABD△和CAD△中ABD CADADB CDA=⎧⎨=⎩∠∠∠∠∴ABD CAD△∽△……………………………………3分DBA∴AB BDCA AD =……………………………………………4分即534AC = ∴203AC =（其它方法同样给分）……………………5分17.解：⑴()00，和()20-，代入2y x bx c =-++得 0420c b c =⎧⎨--+=⎩………………………………………1分解得20b c =-⎧⎨=⎩此二次函数解析式为22y x x =--． ………………2分写成顶点式()211y x =-++∴顶点坐标为()11-，． ………………………………3分 ⑵()33--，和()13-，． …………………………5分 18.解：连接OD ．⑴直线CD 为O ⊙的切线．……………………………1分 ∵AO DO =∴45ADO DAB ==︒∠∠∴90BOD =︒∠……………………………………………2分又∵CD AB ∥∴90CDO =︒∠……………………………………………3分 ∴CD 为O ⊙的切线．…………………………………………4分 ⑵阴影部分的面积为¼3π24ABCD AOD BOD S S S --=-Y 扇形△．………………………5分四、解答题（本题共20分，每小题5分） 19.解： (1)41i =，2011ii =- 20121i = ……3分(2)方程2220x x -+=的两根为1+i 和1i - ……5分20.解：⑴如图所示：…………………………1分⑵易知点C 的旋转路径是以为O 圆心，OC 为半径的半圆，因为OC ==…………………………3分⑶B D AB ''=，AD = 所以22'2AD B D AB '=+所以ADB '∆是直角三角形，且90AB D '∠=︒…………………4分所以1tan 3DB DAB AB ''∠=='．…………………………5分 21.解：设调查的人数为x ，则根据题意： 10%30x ⋅=，∴300x =∴一共调查了300人…………………………1分O(A')B'C'D CBA4510535%40% 戒烟戒烟戒烟戒烟人数1206030O15%10%强制戒烟警示戒烟替代品戒烟药物戒烟⑵由⑴可知，完整的统计图如图所示．…………………………3分 ⑶设该市发支持“强制戒烟”的概率为P ，由⑴可知，40%0.4P ==支持“警示戒烟”这种方式的人有1000035%3500⨯=…………………………5分22.⑴ AP 的最大值是：6………………………………..2分⑵ AP BP CP ++的最小值是：2226+（或不化简为32163+）……5分五、解答题（本题共22分，第23题7分，第24题7分，第25题8分） 23. ⑴由题意得0∆>．∴2(4)4[2(1)]8240k k ∆=---=-+>．……1分 ∴解得3k <．……2分⑵∵3k <且k 为正整数，∴1k =或2．……3分当1k =时，24y x x =-，与x 轴交于点（0，0）、（4，0），符合题意；当2k =时，242y x x =-+，与x 轴的交点不是整数点，故舍去．综上所述，1k =．……4分⑶∵2,4y x y x x =⎧⎨=-⎩，∴点C 的坐标是（5，5）．∴OC 与x 轴的夹角为45°．过点Q 作QN ⊥PM 于点N ，（注：点Q 在射线PC 上时，结果一样，所以只写一种情况即可） ∴∠NQP =45°，12S PM NQ =⋅． ∵PQ =2，∴NQ =1． ∵P （,t t ），则M （2,4t t t -）， ∴PM =22(4)5t t t t t --=-+．……5分 ∴2152S t t =-+． ∴当05t <<时，21522S t t =-+；……6分当5t >时，21522S t t =-．……7分24.解：⑴过点A作AH x⊥轴于H．（如图）∴在Rt AOH△中，2AH=，∴2 tanAHAOxOH OH==∠∴OH=，∴m=⑵∵APQ△是以PAQ∠其实就是以点A为圆心作圆A⊙，∵点P是y轴上的动点，点()0Q n，(n轴上的动点．就是要使A⊙与y轴相交，与x交．………3分当A⊙与y轴相切时，半径为点ACE==OD=∴n的取值范围为0n<≤n≥．……5分⑶7．……………………………7分提示：情况一：点A为直角顶点的直角三角形，如图①，图②：可推Rt RtAPM AQN△∽△，∴AP AMAQ AN==，∴AP AQ≠．情况二：点P为直角顶点的直角三角形，如图③，图④，图⑤，显然，图③④不符合情况，图⑤用相似可证AP PQ≠．情况三：点Q为直角顶点的直角三角形，如图⑥，图⑦．图⑥用相似可证AP PQ ≠．图⑦若满足条件，ANQ QOP △≌△，∴2OQ AN ==， ∴()20Q ，，∴2220a a -+=，即222a a =- ∴()2416522165a a a a +-=-+- 2484165a a a =-++- 2481a a =+-()42281a a =-+-=7．25.解：⑴；……………………………1分 ⑵不变．以AB 为对称轴，画出ABC △的轴对称图形ABC '，以AD 为对称轴，画出ACD △的轴对称图形ADC ''，连接C C '''．''12AC AC AC '===，30AC B ACB ACD AC D '''====︒∠∠∠∠，BAC BAC '=∠∠，CAD C AD ''=∠∠………3分 AC C '''△是等腰三角形， ∵60BAD =︒∠，∴120C AC '''=︒∠∴30AC C AC C ''''''==︒∠∠∴点B 、D 在线段C C '''上…………5分 ∴BCD △的周长等于CC '''的长度∴C C ''''==∴BCD △的周长不变． (6)分（旋转方法也能操作，不过比较复杂） ⑶8分C''C'DCBA。