系统的瞬态响应与误差分析
合集下载
机械控制工程基础第4章系统的瞬态响应与误差分析
C(t)
n 1
2
exp(nt) sin(d t).
(4 34)
(2) 临界阻尼 1
响应函数 C(s) G(s)R(s)
2 n
(s n )2
拉氏逆变换 c(t) n2t exp(nt)
(4 35) (4 36)
（3） 过阻尼 1
C(s)
2 n
(s n n 2 1)(s n n 2 1)
M
p
C(t p ) C() C()
100%
C(t p ) 1
exp( ) 1 2
可见，超调量仅与阻尼比有关。
（4）调整时间ts
对欠阻尼二阶系统，瞬态响应为
C
(t
)
1
exp(n2t 1 2
)
sin(d
t
arctan
1 2
), t 0.
(4 28)
其包络线方程为 f (t) 1 exp(nt) / 1 2
s
2 n
)(s
)
a1 y a0 y b0 x （2）对应方程 a2 y a1 y a0 y b0 x
a3y a2 y a1 y a0 y b0 x
(4 39)
（3）单位阶跃响应
C(s) G(s)R(s)
2 n
1,
(s 2
2n s
2 n
)(s
)
s
令 ，作拉氏逆变换，得 n
B 2 4mk 2m
n2
k m
,
2 n
B m
G(s) 1
n2
k
s
2
n
s
2 n
(4)二阶系统的标准形式及方块图
G(s)
Xo(s) Xi(s)
瞬态响应及误差分析(时域分析法)
10K O 10K O K OG ( S ) 10K O 1 10K H ( s) 0.2s 1 0.2 1 K H G ( s) 1 10K H 0.2s 1 10K H s 1 0.2s 1 1 10K H 10K O 1 10K K * 10 K O 10 0.2 H T * 0.02 K H 0.9 1 10K H
12
3. 选取试验输入信号的原则：
选取的输入信号应反映系统工作的大部分实际情况； 形式简单，便于用数学式表达及分析处理，实际中可 以实现或近似实现； 应选取那些能够使系统工作在最不利的情形下的输入 信号作为典型试验信号；
•如控制系统的输入量是突变的，采用阶跃信号。如室温 调节系统 。 •如控制系统的输入量是随时间等速变化，采用斜坡信号 作为实验信号 •如控制系统的输入量是随时间等加速变化，采用抛物线 信号； 宇宙飞船控制系统 •如控制系统为冲击输入量，则采用脉冲信号
特征点： 1 A点 : xo (T ) 0.368 xo (0) ） 2）零时刻点： xo (t )
1 T
2e
t T t 0
1 2 ; x o ( 0) T T
24
1
一阶系统单位脉冲响应的特点： 1. 瞬态响应：(1/T )e –t/T；稳态响应0； 2. 瞬态响应的特性反映系统本身的特性，时间常数大的 系统，其响应速度慢于时间常数小的系统。 3. 输入试验信号仅是为了识别系统特性，系统特性只取 决于组成系统的参数，不取决于外作用的形式。 4. xo(0)=1/T,随时间的推移，xo(t)指数衰减。 5.
量从初始状态到稳定状态的响应过程。
稳态响应：当某一输入信号的作用下，系统的响应
控制工程基础实验指导书(答案) 2讲解
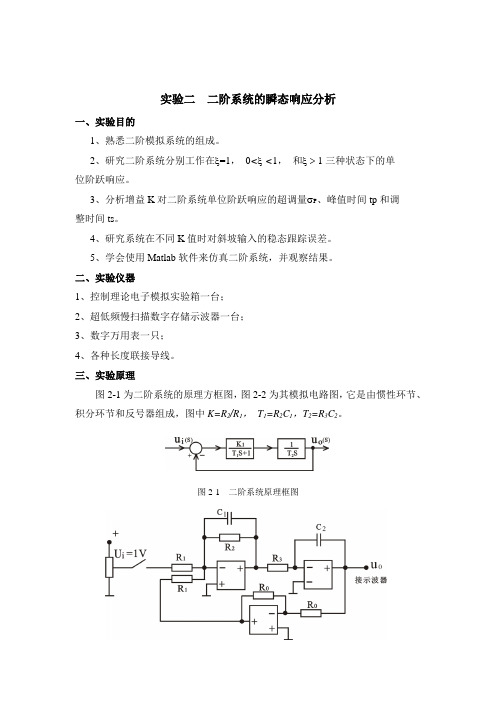
实验二二阶系统的瞬态响应分析一、实验目的1、熟悉二阶模拟系统的组成。
2、研究二阶系统分别工作在ξ=1，0<ξ<1，和ξ> 1三种状态下的单位阶跃响应。
3、分析增益K对二阶系统单位阶跃响应的超调量σP、峰值时间tp和调整时间ts。
4、研究系统在不同K值时对斜坡输入的稳态跟踪误差。
5、学会使用Matlab软件来仿真二阶系统，并观察结果。
二、实验仪器1、控制理论电子模拟实验箱一台；2、超低频慢扫描数字存储示波器一台；3、数字万用表一只；4、各种长度联接导线。
三、实验原理图2-1为二阶系统的原理方框图，图2-2为其模拟电路图，它是由惯性环节、积分环节和反号器组成，图中K=R2/R1，T1=R2C1，T2=R3C2。
图2-1 二阶系统原理框图图2-1 二阶系统的模拟电路由图2-2求得二阶系统的闭环传递函1222122112/() (1)()/O i K TT U S K U S TT S T S K S T S K TT ==++++ :而二阶系统标准传递函数为(1)(2), 对比式和式得n ωξ==12 T 0.2 , T 0.5 , n S S ωξ====若令则。
调节开环增益K 值，不仅能改变系统无阻尼自然振荡频率ωn 和ξ的值，可以得到过阻尼(ξ>1)、临界阻尼（ξ=1）和欠阻尼（ξ<1）三种情况下的阶跃响应曲线。
（1）当K >0.625， 0 < ξ < 1，系统处在欠阻尼状态，它的单位阶跃响应表达式为：图2-3 0 < ξ < 1时的阶跃响应曲线（2）当K =0.625时，ξ=1，系统处在临界阻尼状态，它的单位阶跃响应表达式为：如图2-4为二阶系统工作临界阻尼时的单位响应曲线。
(2) +2+=222nn nS S )S (G ωξωω1()1sin( 2-3n to d d u t t tgξωωωω--=+=式中图为二阶系统在欠阻尼状态下的单位阶跃响应曲线etn o n t t u ωω-+-=)1(1)(图2-4 ξ=1时的阶跃响应曲线（3）当K < 0.625时，ξ> 1，系统工作在过阻尼状态，它的单位阶跃响应曲线和临界阻尼时的单位阶跃响应一样为单调的指数上升曲线，但后者的上升速度比前者缓慢。
第3章_时域瞬态响应分析_3.2一阶系统的瞬态响应
(t ≥ 0)
1 斜率 − 2 T
1 0.368 T
1 − t /T xo (t ) = e T
T
一阶系统三种典型输入信号及响应关系： 一阶系统三种典型输入信号及响应关系：
xi (t ) = t
输 入
xt (t ) = t − T + Te x1 (t ) = 1 − e 1 1 −T t xδ (t ) = e T
x0(t) 1
1/T
xo(t)=1-e-t/T
86.5%
0
63.2%
95.0%
98.2%
T
2T
3T
4T
t
特点 一阶惯性系统总是稳定的，无振荡。 （1）一阶惯性系统总是稳定的，无振荡。 曲线上升到0.632的高度 。 反过来 ， 的高度。 （ 2 ） 经过时间 T ， 曲线上升到 的高度 反过来， 如果用实验的方法测出响应曲线达到0.632的时间 ， 的时间， 如果用实验的方法测出响应曲线达到 的时间 即是惯性环节的时间常数。 即是惯性环节的时间常数。 经过时间3 响应曲线达稳定值的95 95％ （3）经过时间 3T～ 4T，响应曲线达稳定值的95％～ 98％ 可以认为其调整过程已经完成， 98 ％ ， 可以认为其调整过程已经完成 ， 故一般取调 整时间( 整时间(3～4)T。 响应曲线的切线斜率为1/T。 （4）在t＝0处，响应曲线的切线斜率为 。
注意： 该性质只适用于线性定常系统， 注意 ： 该性质只适用于线性定常系统 ， 不适用于 线性时变系统和非线性系统。 线性时变系统和非线性系统。
1 T T = 2− + s s s+ 1 T
单位斜坡响应为 x0 (t ) = t − T + Te
控制工程基础—第7章控制系统的误差分析与计算
稳态误差 ：
ss 0
(3)Ⅱ型系统（N=2）
静态位置误差系数为Kp=∞，稳态误差ss=0。 图7-4 所示为单位反馈控制系统的单位阶跃响应 曲线，其中图7-4a为0型系统；图7-4b为Ⅰ型或 高于Ⅰ型系统。
图7-4 单位阶跃响应曲线
2. 静态速度误差系数Kv 系统对斜坡输入X(s)= R/s2的稳态误差称为速度误 差，即
图7-6 单位加速度输入的响应曲线
表7-1 单位反馈系统稳态误差 ss 输入信号 系统 类型 阶跃 x(t)=R
R 1 K
斜坡 x(t)=Rt
R K
加速度
R 2 x( t ) t 2
0型 Ｉ型 Ⅱ型
R K
0 0
0
三、其它输入信号时的误差
如果系统承受除三种典型信号之外的某一信号x(t) 输入，此信号x(t)在t=0点附近可以展开成泰勒级 数为 ：
1 R R ss lim s . 3 2 s0 1 G( s ) s lim s G ( s )
s0
（ 7-20 ）
静态加速度误差系数Ka定义为：
K a lim s G( s )
2 s 0
（ 7-21 ） （ 7-22 ）
所以
R ss Ka
(1) 0 型系统（N=0）
稳态误差 对式（7-5）进行拉氏反变换，可求得系统的误差 (t) 。对于稳定的系统，在瞬态过程结束后，瞬 态分量基本消失，而(t)的稳态分量就是系统的 稳态误差。应用拉氏变换的终值定理，很容易求 出稳态误差：
E ( s) ss lim ( t ) lim s ( s ) lim s t s0 s0 H ( s)
K v lim sG ( s )
ss 0
(3)Ⅱ型系统（N=2）
静态位置误差系数为Kp=∞，稳态误差ss=0。 图7-4 所示为单位反馈控制系统的单位阶跃响应 曲线，其中图7-4a为0型系统；图7-4b为Ⅰ型或 高于Ⅰ型系统。
图7-4 单位阶跃响应曲线
2. 静态速度误差系数Kv 系统对斜坡输入X(s)= R/s2的稳态误差称为速度误 差，即
图7-6 单位加速度输入的响应曲线
表7-1 单位反馈系统稳态误差 ss 输入信号 系统 类型 阶跃 x(t)=R
R 1 K
斜坡 x(t)=Rt
R K
加速度
R 2 x( t ) t 2
0型 Ｉ型 Ⅱ型
R K
0 0
0
三、其它输入信号时的误差
如果系统承受除三种典型信号之外的某一信号x(t) 输入，此信号x(t)在t=0点附近可以展开成泰勒级 数为 ：
1 R R ss lim s . 3 2 s0 1 G( s ) s lim s G ( s )
s0
（ 7-20 ）
静态加速度误差系数Ka定义为：
K a lim s G( s )
2 s 0
（ 7-21 ） （ 7-22 ）
所以
R ss Ka
(1) 0 型系统（N=0）
稳态误差 对式（7-5）进行拉氏反变换，可求得系统的误差 (t) 。对于稳定的系统，在瞬态过程结束后，瞬 态分量基本消失，而(t)的稳态分量就是系统的 稳态误差。应用拉氏变换的终值定理，很容易求 出稳态误差：
E ( s) ss lim ( t ) lim s ( s ) lim s t s0 s0 H ( s)
K v lim sG ( s )
控制工程第4章_系统的瞬态响应与误差分析
➢对稳定的线性定常系统来说，稳态响应只是由输入信号 引起，而与系统初始状态无关。因为初始状态由于能量 有限，所以它引起的响应总要衰减到0，因此，初始状 态引起的响应属于瞬态响应（但不等于瞬态响应，因为 输入量也能引起瞬态响应）。稳态响应反映了系统响应的
准确性。
*
17
4-1 时间响应
➢ 求系统时间响应的方法：
➢系统的快速性
快速性是指输出量和输入量产生偏差时，系统消除 这种偏差的快慢程度。
*
4
引言
➢ 二阶系统G(s)=ωn2/(s2+2ζωns+ωn2)的单位阶跃响应曲线
二阶系统 G (s) n 2/(s2 2 n s n 2)的单位阶跃响应曲线
2
=0
1.8
1.6
1.4
允 差
=0.4 =0.7 =1
y(t) 输出 Y(s)
Y (s)G (s)X (s)
系统对任意输入的响应
y ( t) L 1 [ Y ( s ) ] L 1 [ G ( s ) X ( s ) ]
*
零状态响应
18
4-2 一阶系统的时间响应
1. 一阶系统的数学模型 2. 一阶系统（惯性环节）的单位阶跃响应 3. 一阶系统（惯性环节）的单位脉冲响应 4. 一阶系统（惯性环节）的单位斜坡响应
*
14
4-1 时间响应
➢瞬态响应ctr(t)：对稳定的系统，瞬态响应是指时 间响应中随着时间的增加而逐渐减小，最终趋于0 的那部分响应。
➢教材中的定义：系统受到外加作用激励后，从初 始状态到最终状态的响应过程称为瞬态响应。指 的是稳定状态之前的整个时间响应过程。
➢稳态响应css(t)：是指当时间趋于无穷大时系统的 输出状态。
准确性。
*
17
4-1 时间响应
➢ 求系统时间响应的方法：
➢系统的快速性
快速性是指输出量和输入量产生偏差时，系统消除 这种偏差的快慢程度。
*
4
引言
➢ 二阶系统G(s)=ωn2/(s2+2ζωns+ωn2)的单位阶跃响应曲线
二阶系统 G (s) n 2/(s2 2 n s n 2)的单位阶跃响应曲线
2
=0
1.8
1.6
1.4
允 差
=0.4 =0.7 =1
y(t) 输出 Y(s)
Y (s)G (s)X (s)
系统对任意输入的响应
y ( t) L 1 [ Y ( s ) ] L 1 [ G ( s ) X ( s ) ]
*
零状态响应
18
4-2 一阶系统的时间响应
1. 一阶系统的数学模型 2. 一阶系统（惯性环节）的单位阶跃响应 3. 一阶系统（惯性环节）的单位脉冲响应 4. 一阶系统（惯性环节）的单位斜坡响应
*
14
4-1 时间响应
➢瞬态响应ctr(t)：对稳定的系统，瞬态响应是指时 间响应中随着时间的增加而逐渐减小，最终趋于0 的那部分响应。
➢教材中的定义：系统受到外加作用激励后，从初 始状态到最终状态的响应过程称为瞬态响应。指 的是稳定状态之前的整个时间响应过程。
➢稳态响应css(t)：是指当时间趋于无穷大时系统的 输出状态。
第六讲(3) 3瞬态响应及误差分析
sX i ( s ) = = = ess lim e(t ) lim sE ( s ) lim t →∞ s →0 s → 0 H ( s ) [1 + G ( s ) H ( s ) ]
H(s)、G(s)分别为系统的反馈传递函数和前向通路传递函数， G(s)H(s)为系统的开环传递函数。 偏差对输入信号的传递函数为
考虑单位反馈系统，H(s)=1，有
上海大学 机电工程与自动化学院
3.5.4 静态误差系数与稳态误差
静态加速度误差系数 对于0型或Ⅰ型系统（ν =0或ν =1）：
对于Ⅱ型系统（ν =2）：
对于Ⅲ型系统或高于Ⅲ型的系统（ν ≥3）：
上海大学 机电工程与自动化学院
3.5.4 静态误差系数与稳态误差
加速度信号输入时的系统稳态误差 对于0型或Ⅰ型系统（ν =0或ν =1 ）： 对于Ⅱ型系统（ν =2）：
ε N (s) −G2 ( s ) EN ( s ) = N (s) 1 + G1 ( s )G2 ( s ) H ( s ) H (s)
由扰动引起的稳态误差：
essN
G2 ( s ) = lim sEN ( s ) = − lim s N (s) s →0 s → 0 1 + G ( s )G ( s ) H ( s ) 1 2
Xi(s) +
-
K (0.5s + 1) s ( s + 1)(2 s + 1)
Xo(s)
解：对于输入信号 xi(t)=t，其拉氏变换为Xi(s)=1/s2 。将传递
函数、输入信号代入稳态误差计算公式，得
s ⋅1/ s 2 ess = lim s →0 K (0.5s + 1) 1+ s ( s + 1)(2 s + 1)
系统的瞬态响应与误差分析PPT共71页
谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路，那么，任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远，吾将上下而求索。——屈原 75、内外相应，言行相称。——韩非
系统的瞬态响应与误差分析
16、自己选择的路、跪着也要把它走 完。 17、一般情况下)不想三年以后的事， 只想现 在的事 。现在 有成就 ，以后 才能更 辉煌。
18、敢于向黑暗宣战的人，心里必须 充满光 明。 19、学习的关键--重复。
2ห้องสมุดไป่ตู้、懦弱的人只会裹足不前，莽撞的 人只能 引为烧 身，只 有真正 勇敢的 人才能 所向披 靡。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
稳态响应：t T 瞬态响应：Tet T
xi (t) t
➢ 一阶系统单位速度响应的特点
t
x0 (t)
xo (t) t T Te T , t 0
xi (t)
T T
经过足够长的时间(稳态时，
如：t 4T)，输出增长速率近似 0 与输入相同，此时输出为：t –
t t 4T
T，即输出相对于输入滞后时
Xi (s) G(s) X0(s)
凡是能够用一阶微分方程描述的系统。
典型形式：G(s) 1 Ts 1
极点（特征根）：-1/T
一、一阶系统的单位阶跃响应
1
X
i
(s)
1 s
s 1 T
X
o
(s)
G(s)
X
i
(s)
1 Ts 1
1 s
1 s
T Ts
1
t
xo (t) 1 e T , t 0
t
xo (t) 1 e T , t 0
间T；
系统响应误差为： e(t) xi (t) xo (t) T (1 et T ) e() T
三、 一阶系统的单位脉冲响应
x0 (t)
1 T
斜率： 1 T2
0.368 1 T
Xi (s) 1
X o (s)
G(s)
1 T
s
1
1 T
xo
(t)
1 T
t
eT
,
t0
t
0T
➢ 一阶系统单位脉冲响应的特点
重点：二阶系统的时域响应及其性能指标。 难点：二阶系统时域响应的数学表达式。
时间响应
任一系统的时间响应都是由瞬态响应或 稳态响应两部分组成。
瞬态响应：系统受到外加作用力激励后， 从初始状态到最终状态的响应过程。
稳态响应：时间趋于无穷大时，系统的 输出状态。
瞬态响应反映了系统动态性能，而稳态 响应偏离系统希望值的程度可用来衡量系统 的精确程度。
时域分析的目的
在时间域，研究在一定的输入信号作用下，系统 输出随时间变化的情况，以分析和研究系统的控制 性能。
优点：直观、简便
§4.1 典型输入信号
在时间域进行分析时，为了比较不同系统的控制 性能，需要规定一些具有典型意义的输入信号建立 分析比较的基础。这些信号称为控制系统的典型输 入信号。
一、典型输入信号
ln[1-xo(t)]
该性质可用于判别系统是否为
惯性环节，以及测量惯性环节的时
0
t
间常数。
二、一阶系统的单位速度响应
G(s) 1 ， Ts 1
xi (t) t
x0 (t)
Xi
(s)
1 s2
Xo(s) G(s)Xi(s)
0
1 1 1T T
Ts 1
s2
s2
s
s
1 T
t
xo (t) t T Te T , t 0
保证典型输入信号与实际输入信号有着良好的对应关系， 且代表最恶劣的输入情况，因此，当系统的设计基于典型信 号来进行时，那么在实际输入的情况下，系统响应特性一般 是能够满足要求的。
注意：对于同一系统，无论采用哪种输入信号，由时域分 析法所表示的系统本身的性能不会改变。
§4.2 一阶系统的时间响应
一阶系统：
稳态响应：1
表示t时，系统的输出状态。
e(t) xi (t) xo (t) et T
xo(0) = 0，xo() = 1
e() 0
无稳态误差；随时间的推移， xo(t) 指数增大，且无振荡。
xo(T) = 1 - e-1 = 0.632，即经过时间T，系统响应达到其稳 态输出值的63.2%，从而可以通过实验测量惯性环节的时间 常数T；
瞬态响应：(1/T )e – t /T ；稳态响应：0；
xo(0)=1/T,随时间的推移，xo(t)指数衰减；
dxo (t) dt
t0
1 T2
对于实际系统，通常应用具有较小脉冲宽 度（脉冲宽度小于0.1T）和有限幅值的脉 冲代替理想脉冲信号。
一阶系统的时间响应
时间响应：系统在典型输入信号的作用下之输出。
1.单位阶跃响应
t
xo (t) 1 e T , t 0
xo (t)
1
2.单位速度响应
t
xo (t) t T Te T , t 0
x0 (t)
xi (t)
T T
3.单位脉冲响应
xo
(t
)
1 T
t
eT
,
t0
x0 (t) 1 T
t
t
t
0
0
t 4T
0
四、线性定常系统时间响应的性质 ➢ 系统时域响应通常由稳态分量和瞬态分量共同组成，前者
xo(t) 斜率=1/T 1
0.632
B A
xo (t) 1 et / T
63.2% 86.5% 95% 98.2% 99.3% 99.8%
0 1T 2T 3T 4T 5T 6T
t
➢ 一阶系统单位阶跃响应的特点
响应分为两部分
瞬态响应： et T
t
xo (t) 1 e T , t 0
表示系统输出量从初态到终态的变化过程（动态/过渡过程）
1 xi (t)
xi (t)
xi (t)
1
t
t
t
0
0
0
xi (t)
xi (t)
t
t
0
0
二、对典型输入信号的要求
能够反映系统工作在最不利的情形； 形式简单，便于解析分析； 实际中可以实现或近似实现。
➢ 常用的典型输入信号的数学表达
名
称
时域表达式
单位阶跃信号
1(t)，t0
单位速度(斜坡)信号 单位加速度信号 单位t 0 T
时间常数T反映了系统响应的快慢。通常工程中当响应曲线 达到并保持在稳态值的95%～98%时，认为系统响应过程基本 结束。从而惯性环节的过渡过程时间为3T~4T。
将一阶系统的单位阶跃响应式改写为：
t
e T 1 xo (t)
1 T
t
ln
1
xo
(t)
即ln[1-xo(t)]与时间t成线性关系。
第四章 系统的瞬态响应与误差分析
本章主要内容 一、典型输入信号 二、一阶系统的时间响应 三、二阶系统的时间响应
※ 四、高阶系统的时间响应 五、误差分析和计算 六、稳定性分析
教学目的： 1.掌握一阶、二阶系统在典型输入信号作用下的时域响 应和时域性能指标。 2.了解高阶系统时域响应的特点。 3.掌握系统误差的概念和计算稳态误差的方法。 4.掌握系统稳定的概念和分析、判别系统稳定的方法。
t， t0
1 t2, t 0 2
(t)，t=0
正弦信号
Asint
复数域表达式
1 s 1 s2 1 s3
1
A s2 2
三、典型输入信号的选择原则
脉冲信号：模拟系统突遭脉动电压、机械碰撞、敲打冲击等； 阶跃信号：实际系统的输入具有突变性质，例：模拟电源突然
接通、负荷突然变化、指令突然转换等； 速度信号：实际系统的输入随时间逐渐变化（匀速变化）。
反映系统的稳态特性，后者反映系统的动态特性。