第四章 控制系统的传递函数(2)
现代控制理论-4-控制系统的稳定性分析
外部稳定性只适用于线性系统，内部稳定性不但适用于线性系 统，而且也适用于非线性系统。对于同一个线性系统，只有在 满足一定的条件下两种定义才具有等价性。
不管哪一种稳定性，稳定性是系统本身的一种特性，只和系统 本身的结构和参数有关，与输入－输出无关。
V ( x)半负定
同时有
& V
(
x
)
-
2
x22
不可能恒为零。
由判据2可知，系统在原点处的平衡状态是渐近稳定的。
27
4.5 李雅普诺夫方法 在线性系统中的应用
28
一、线性定常连续系统的稳定性分析
目的：将李氏第二法定理来分析线性定常系统 x& Ax 的稳定性
讨论：V选&(x择) 二(x次T P型x)函 x&数T PVx +(xx)TPxx& TP(xAx为)T P李x +氏x函T PA数x。
如果d 与初始时刻 t0无关，则称平衡状态xe为一致渐近稳定。
渐近稳定几何表示法：
10
3、大范围渐近稳定
如果对状态空间的任意点，不管初始偏差有多大，都有渐
近稳定特性，即：lim x t
- xe
0
对所有点都成立，称平衡状态xe为大范围渐近稳定的。其
渐近稳定的最大范围是整个状态空间。
必要性：整个状态空间中，只有一个平衡状态。 （假设有2个平衡状态，则每个都有自己的稳定范 围，其稳定范围不可能是整个状态空间。）
（2） 求系统的特征方程：
det(lI
-
A)
l
- 1
求得： l1 2，l2 -3
2-4 线性系统的传递函数
0
T
t
11
惯性环节的实例如下图所示。
R C uc
ur
(a)
在图(a)所示的电路中，输出电压uc与输入电 压ur间的微分方程为
du c T + uc = ur dt
式中T=RC，为电路的时间常数。
12
if uf
Rf
Lf
(b)
在图(b)所示的直流电机的激磁电路中，当 以激磁电压uf为输入量、以激磁电流if为输出量 时，其电路方程为
G (s) = R(s) =
m m −1 1 0
a n s + a n −1 s
n
n −1
+ …… + a1 s + a 0
( 2 − 50 )
可见，传递函数是由系统微分方程经拉氏变换而引出 的。 系统输入、输出及传递函数之间的相互关系可用 下图表示，输出是由输入经过G(s)的传递而得到的， 因此称G(s)为传递函数。因为传递函数是在零初始条 件下定义的，故在初始条件为零时，它才能完全表征 系统的动态性能。
+ (a)
C ic uc
ur n θ
(b)
ur 在图(a)中，因为 i c = i = R
容两端电压，所以有
uc = 1 c
而输出电压uc近似等于电
∫ i c dt =
在图(b)中，以电动机的转速n(转/分)为输入量， 以减速齿轮带动负载运动的轴的角位移θ为输出量， 可得微分方程 1
θ (t ) =
§2-4 线性系统的传递函数
控制系统的微分方程，是时域中描述系统动态性 能的数学模型，求解微分方程可以得到在给定外界作 用及初始条件下系统的输出响应，并可通过响应曲线 直观地反映出系统的动态过程。但系统的参数或结构 形式有变化，微分方程及其解都会同时变化，不便于 对系统进行分析与研究。 根据求解微分方程的拉氏变换法，可以得到系统 的另一种数学模型——传递函数。它不仅可以表征系 统的动态特性，而且可以方便地研究系统的参数或结 构的变化对系统性能所产生的影响。在经典控制理论 中广泛应用的根轨迹法和频率法，就是在传递函数基 础上建立起来的。
自动控制原理第四章习题解答
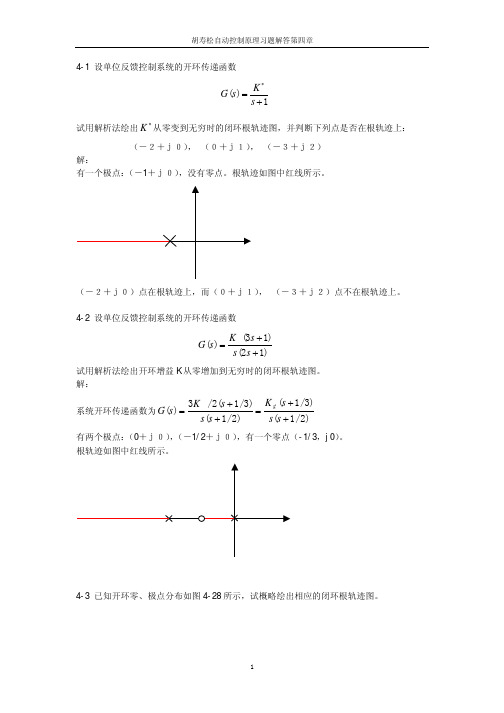
4
胡寿松自动控制原理习题解答第四章
（２） G(s) =
K ∗ (s + 20)
。
s(s + 10 + j10)(s + 10 − j10)
解：
系统开环传递函数为 G(s) =
K ∗ (s + 20)
s(s + 10 + j10)(s + 10 − j10)
有三个极点：p1 =（0，j0），p2 =（-10＋ｊ10），p3 =（－10-ｊ10），有一个零点 z1 =（－
(2) 确定 G(s) = K ∗ (s + z)
产生纯虚根为±ｊ1 的ｚ值和 K ∗ 值。
s 2 (s + 10)(s + 20)
解：系统特征方程为 s4 + 30s3 + 200s2 + K *s + K *z = 0 令 s = j1代入特征方程中得：
20，ｊ０）。 起始角：
∑ ∑ θ pi
= (2k
+ 1)π
+
m
ϕ z j pi
j =1
n
−
θ pi pi
j =1
( j≠i)
k = 0,±1,±2,L
θ p1 = 1800
θ p2 = 1800 ϕ + z1p2 θ − p1p2 θ − p3p2 = 1800 + 450 − 1350 − 900 = 00
有两个极点：（0＋ｊ０），（－0.5＋ｊ０），有一个零点（－1＋ｊ０）。
分离点坐标计算如下：
1+ 1 = 1 d d + 0.5 d + 1
d 2 + 2d + 0.5 = 0 解方程的 d1 = −1.7 ， d2 = −0.29
自动控制原理第二版第四章课后答案
自动控制原理第二版第四章课后答案【篇一：《自动控制原理》第四章习题答案】4-1 系统的开环传递函数为g(s)h(s)?k*(s?1)(s?2)(s?4) 试证明点s1??1?j3在根轨迹上，并求出相应的根轨迹增益k*和开环增益k。
解若点s1在根轨迹上，则点s1应满足相角条件?g(s)h(s)??(2k?1)?，如图解4-1所示。
对于s1= -1+j3，由相角条件?g(s1)h(s1)?0??(?1?j3?1)??(?1?j3?2)??(?1?j3?4)? 0??2??3??6???满足相角条件，因此s1= -1+j3在根轨迹上。
将s1代入幅值条件： g(s1)h（s1?k*?1?1?j3?1??1?j3?2??1?j3?4k8*解出： k=12 ，k=*?324-2 已知开环零、极点如图4-2 所示，试绘制相应的根轨迹。
解根轨如图解4-2所示：4-3 单位反馈系统的开环传递函数如下，试概略绘出系统根轨迹。
⑴ g(s)?ks(0.2s?1)(0.5s?1)k(s?5)s(s?2)(s?3)* ⑵ g(s)?⑶ g(s)?k(s?1)s(2s?1)解⑴ g(s)?ks(0.2s?1)(0.5s?1)=10ks(s?5)(s?2)系统有三个开环极点：p1?0,p2= -2,p3 = -5①实轴上的根轨迹：???,?5?, ??2,0?0?2?57?????a??33②渐近线： ????(2k?1)????,?a?33?③分离点：1d?1d?5?1d?2?0解之得：d1??0.88，d2?3.7863(舍去)。
④与虚轴的交点：特征方程为 d(s)=s3?7s2?10s?10k?0?re[d(j?)]??7?2?10k?0令 ? 3im[d(j?)]????10??0?解得?????k?7。
根轨迹如图解4-3(a)所j）与虚轴的交点（0，?示。
⑵根轨迹绘制如下：①实轴上的根轨迹：??5,?3?, ??2,0?0?2?3?(?5)????0a??2②渐近线： ????(2k?1)????a?22?③分离点： 1d?1d?2?1d?3?1d?5用试探法可得 d??0.886。
第四章 控制系统的传递函数(2)
Ub(s) R2
ቤተ መጻሕፍቲ ባይዱ
Uo(s) I(s)
C1
C2
I f ( s)
U b ( s) 1 R1 c1s
R c s 1 1 1 1 1 I ( s ) U ( s ) I ( s ) R // b 1 2 c c s c s c s c s s 1 1 2 2 1 1 2 c R
2 d dx o o ⑤ 二阶环节和振荡环节 T x T x Kx o o i 2 dt dt
G(s)
2 K n 2 2 s 2 s n n
⑥ 延时环节
xo (t) = xi (t-τ)
G (s) es
求右图油缸-阻尼-弹簧 系统的传递函数.其中， p为输入，xo为输出。
试画出人工控制的恒温箱原理框图
脑
① 比例环节
xo(t)=kxi(t)
G(s)
Xo (s) Xi (s)
k
小 节
② 微分环节
③ 积分环节
dx i (t) xo(t) T G(s)=TS dt
x ( t) T t) dt G(s)=T/S o i( x
dx K G ( s ) ④ 惯性环节 T o xo Kx i Ts1 dt
第四章 控制系统的传递函数
第二节 复合环节传递函数
一般来说，采用调节器的控制系统，既能获得较高的 静态精度，又具有较快的动态响应。
2014.10.13
1. 复合环节概念
在自动控制技术中，常用到一些被称为调节器（校正器）的 动态元件。他们就是由一些典型环节组成的复合环节。不同 环节的组合，构成各种性能不同的调节器。了解这些调节器 的传递函数，会方便以后的设计。 单一典型环节组合 复合环节，如PI调节器、PD调节器
第四章控制系统的传递函数
其中，
n
1 T
——环节的 固有频率
To 2
1 T
——环节的 阻尼比
如果0≤ξ<1，二阶环节称为振荡环节
例7 图示是由质量m、阻尼c、弹簧k组成的动力系统. 求G(s)
依动力平衡原理有 Xi(t) k m c
Xo(t)
d 2 xo dxo m 2 c kxo kxi dt dt
因此，系统的传递函数就是系统单位脉冲响应 的拉氏变换。
一般地,传递函数的表达式为
X o ( s) ao s n a1s n1 a2 s n2 an G( s ) X i ( s) bo s m b1s m1 b2 s m2 bm
2. 传递函数的性质
k
k为比例环节的增益或称为放大系数
例1
解
ni(t)
z1
求一对齿轮传动的传递函数 no z1 k ∴G(s)=k ni z2
最基本的运算放大器
no(t)
z2
例2
i 1= i 2
ei ea ea eo R1 R2
ei eo R1 R2
ei
R2 R1 e i2 a Ko a i3 i1 +
ZL=Ls
3.电容元件
dUC iC C dt
ZC(s) = 1/sC
例5
下图是一个由运算放大器组成的积分器， 求G(s)。 C R i + uc 取拉氏变换 uo Ui(s) R
Zc
i
+ Uo(s)
ui
解：
1 uc idt c
I ( s) U c ( s) cs
K s
1 Zc cs
ms2 X o ( s) csX o (s) kXo ( s) kXi (sG( s) 2 ms cs k
自动控制原理第四章2
开、闭环零极点与根轨迹设计
给F(s)增加零点(续)
F(s) =
K
,
s(s + a)(s + b)
C
a > 0, b > a.
z 给F(s)增加零点： s = – c， c > b .
原系统根轨迹的共轭复 根部分向左弯曲
增加零点可以改善系统 的相对稳定程度
12
开、闭环零极点与根轨迹设计
增加开环零点对根轨迹的影响
渐近中心: ？ C
有两条复根根轨迹，向右弯曲得更厉害
D
给F(s)增加极点将使根轨迹的 主导部分向右半s平面移动 9
开、闭环零极点与根轨迹设计
给F(s)增加零点
z增加一个实零点：
F (s)
=
K(s + b) ,
s(s + a)
a > 0, b > a.
z增加一对共轭复零点： B
σ
A
原系统根轨迹的共轭复根部分向
F(s)
=
K(s + s2(s +
b) a)
.
图C a = 8.
图D a = 3.
图E
a = b = 1.
极点 s = – a 和 零点 s = – b 相互抵消
分离点式子
s1,2
=
−
a
+ 4
3
± 1 a 2 − 10 a + 9 4
对于 a < 9 无意义
系统退化为二 阶情形，根轨 迹为整个虚轴
17
分离点式子
s1,2
=
−
a
+ 4
3
±
1 4
a2 − 10a + 9
《控制工程基础》第四章习题解题过程和参考答案
《控制工程基础》第四章习题解题过程和参考答案4-1 设单位反馈系统的开环传递函数为：10()1G s s =+。
当系统作用有下列输入信号时：()sin(30)r t t =+︒，试求系统的稳态输出。
解：系统的闭环传递函数为：10()()11()()1()111C s G s s s R s G s Φ===++这是一个一阶系统。
系统增益为：1011K =，时间常数为：111T =其幅频特性为：()A ω=其相频特性为：()arctan T ϕωω=- 当输入为()sin(30)r t t =+︒，即信号幅值为：1A =，信号频率为：1ω=，初始相角为：030ϕ=︒。
代入幅频特性和相频特性，有：1(1)A ====11(1)arctan arctan5.1911T ωϕω==-=-=-︒所以，系统的稳态输出为：[]()(1)sin 30(1)24.81)c t A A t t ϕ=⋅⋅+︒+=+︒4-2 已知系统的单位阶跃响应为：49()1 1.80.8(0)ttc t e e t --=-+≥。
试求系统的幅频特性和相频特性。
解：对输出表达式两边拉氏变换：1 1.80.8361()49(4)(9)(1)(1)49C s s s s s s s s s s =-+==++++++由于()()()C s s R s =Φ，且有1()R s s =（单位阶跃）。
所以系统的闭环传递函数为：1()(1)(1)49s s sΦ=++ 可知，这是由两个一阶环节构成的系统，时间常数分别为：1211,49T T == 系统的幅频特性为二个一阶环节幅频特性之积，相频特性为二个一阶环节相频特性之和：12()()()A A A ωωω===1212()()()arctan arctan arctanarctan49T T ωωϕωϕωϕωωω=+=--=--4-3 已知系统开环传递函数如下，试概略绘出奈氏图。
（1）1()10.01G s s =+ （2）1()(10.1)G s s s =+（3）)1008()1(1000)(2+++=s s s s s G （4）250(0.61)()(41)s G s s s +=+ 解：手工绘制奈氏图，只能做到概略绘制，很难做到精确。
控制系统的传递函数
第二章 控制系统的传递函数
借助表达系统输入、输出之间动态关系的微分方程：
a x (n) no
(t)
...
a x (1) 1o
(t)
a0
xo(t)
b x (m) mi
(t)
...
b x (1) 1i
(t)
b0
xi(t)
可对系统进行描述。
i=0,1…n j=0,1,…m
1、线性定常系统 ai,bj 都不是xo(t)和xi(t)及它们导数的函数，也不 是时间的函数；
第二章 控制系统的传递函数
3、同一控制系统可以有不同的数学模型 同一控制系统具有各种物质运动形式（机械传动、电磁量运动、热
变形等），而不同的物质运动形式又分别受不同的物理规律约束，因而 建立的数学模型可能不同。 因此，建立数学模型时，一定要搞清输入 t
b1s m1 a1s n 1
bm1s bm an1s an
(n>m)
2.3.2 几点说明（性质） （1）传递函数是系统数学模型的又一种形式，也是一种表示输入输出
的模型形式。
它表示了系统本身的特性而与输入信号无关。
它仅能表示输入输出关系，而无法表示出系统的内部结构。
传递函数的分母和分子分别反映系统本身与外界无关的固有特性 和系统同外界之间的联系。
（b）图给出了一种大为简化的悬浮系统，设 p 点的运动 为系统的输入，车体的垂直运
动 为系统的输出，只考虑车体在垂直方向的运动时，求
。
（a）汽车悬浮系统
（b）减化悬浮系统
第二章 控制系统的传递函数
2.3.4 反馈控制系统的传递函数
（解释一下方框图----将系统中各元件的名称或功用写在框图单元中，并标 明它们之间的连接顺序和信号流向。主要用来说明系统的构成和工作原理）
课件：控制系统的传递函数
s
Rs
如果H(s)=1，则下图所示的系统为单位反馈系统，它的闭环 传递函数为
CR s Rs
1
G1 s G2 s G1sG2s
Gs 1 Gs
(2 - 50)
5
如果H(s)=1
CR s Rs
1
G1 s G2 s G1sG2 s
1
Gs Gs
(2 - 50)
其中Gs
G1
s
G2
s
,
若令Gs
U V
s s
CR s R(s)
CR s Rs
1
G1 s G2 s G1 s G2 s H
s
pp58:练习2-3 15
2.7 控制系统的反馈特性
闭环控制系统又名反馈控制系统。这类系统之所以被人们 广泛应用，其原理是它有着下列开环系统所没有的特性。
一: 反馈能减小参数变化对系统的影响
图(a)和(b)分别为开环和闭环系统的方框图。开环系统的输出
s
H
s
Rs
1
G2 sHs G1sG2 sH
s
Ds
（2-57）
当满足|G1(s)H(s) |>>1和|G1(s)G2(s)H(s) |>>1时，可得出如下 的结论：
13
CR s Rs
1
G1 s G2 s G1 s G2 s H
s
(2- 49)
1）当 | G1(s) G2(s ) H(s) |>>1时，由式（2-49）得
20
图2-41 扰动作用下系统的框图
10
求得扰动误差的传递函数为：
ED s Ds
1
G2sH s G1 s G2 s H
2.4传递函数及典型环节传递函数
输出量不失真、无惯性地跟随输入量， 两者成比例关系。
传递函数及典型环节的传递函数
比例环节的传递函数为：
传递函数及典型环节的传递函数
2 惯性环节： 凡运动方程为一阶微分方程
形式的环节称为惯性环节。其传递函数为：
K—环节增益（放大系数） T—时间常数，表征环节的惯性，和 环节结构参数有关
传递函数及典型环节的传递函数
如：有源积分网络
传递函数及典型环节的传递函数
液压缸
传递函数及典型环节的传递函数
5 二阶振荡环节 含有两个独立的储能元件，且所存储的 能量能够相互转换，从而导致输出带有 振荡的性质，运动方程为：
传递函数：
传递函数及典型环节的传递函数
振荡环节传递函数的另一常用标准形式为 （K=1）
无源微分网络
无源网络
显然，无源微分网络包括有惯性环节和微 分环节，称之为惯性微分环节，只有当 |Ts|<<1时，才近似为微分环节。
传递函数及典型环节的传递函数
除了上述微分环节外，还有一类一阶微分环 节，其传递函数为：
微分环节的输出是输入的导数，即输出反 映了输入信号的变化趋势，从而给系统以 有关输入变化趋势的预告。因此，微分环 节常用来改善控制系统的动态性能。
2) 传递函数是s 的复变函数。传递函数中的 各项系数和相应微分方程中的各项系数对应 相等，完全取决于系统结构参数；
传递函数及典型环节的传递函数
3) 传递函数是在零初始条件下定义的，即在零时 刻之前，系统对所给定的平衡工作点处于相对静 止状态。因此，传递函数原则上不能反映系统在 非零初始条件下的全部运动规律； 4) 传递函数只能表示系统输入与输出的关系,无 法描述系统内部中间变量的变化情况。
3控制系统方框图的化简及传递函数
-
1 R1
A
A
1 sC1
-
1 R2
B
1 sC2
U 2 ( s)
U1 ( s )
-
1 R1
-
1 sC1
sC2
1 R2
1 sC2
B
U 2 ( s)
19
第二个小回路化简
U1 ( s )
-
1 R1
A
-
1 sC1
sC2
1 R2
1 sC2
B
U 2 ( s)
1 R2C2 s 1 1 R2C2 s
12
结论
下( s )
具有相同的特征多项式
13
闭环特征多项式：
1 G1 (s)G2 (s) H (s)
14
G1 (s)G2 (s) (s) 1 G1 (s)G2 (s) H (s)
输出对输入 对 比
G2 (s) F ( s) 1 G1 (s)G2 (s) H (s)
3
Y (s) (s) R( s)
G1 (s)G2 (s) 1 G1 (s)G2 (s) H (s)
当 H ( s) 1 时 ， 单位负反馈
G1 (s)G2 (s) ( s ) 1 G1 (s)G2 (s)
4
（3） 输出对于扰动输入的闭环传递函数
Y (s) 令 R( s ) 0 ， F (s) F (s)
+
G1 ( s )
Y ( s)
B( s )
F (s)
H (s)
+
G2 (s)
H (s)
1
( s)
G1 ( s )
10
F (s)
自动控制原理第四章
4.1 根轨迹法的基本概念
幅值条件： 幅值条件：
N (s) = D (s)
∏ (s + z ) ∏ (s + p )
j =1 j i =1 n i
m
∏l = ∏L
i =1 j =1
i
j
开环有限零点到s点的矢量长度之积 1 = = 开环极点到s点的矢量长度之积 Kg
东北大学《自动控制原理》课程组
l
1 ，即把它等效成为 1+τ s
25
4.2 根轨迹的绘制法则
例4-7 试绘制下图示系统的根轨迹。 试绘制下图示系统的根轨迹。
解
− （1）二个开环极点：p0 = 0 ， p1 = − 二个开环极点： 二个开环极点
− 一个有限零点： 一个有限零点： z1 = −
1 Ta
把以上诸值代入辐角条件，即得起点（ 把以上诸值代入辐角条件，即得起点（-1+j1）的出射角为 ）
β 4 = −26.6
东北大学《自动控制原理》课程组 15
4.2 根轨迹的绘制法则
通过这个例子，可以得到计算出射角的公式为 通过这个例子，可以得到计算出射角的公式为 出射角
m n −1 β sc = 180 − ∑ β j − ∑ α i i =1 j =1
s3
s
2
1
3
2
2K K
s
1
2K K 2− 3
2K K
19
s0
东北大学《自动控制原理》课程组
4.2 根轨迹的绘制法则
在第一列中， 行等于零， 在第一列中，令 s1 行等于零，则得临界放大系数 K K = Kl = 3 根轨迹与虚轴的交点可根据 s 2 行的辅助方程求得，即 行的辅助方程求得，
自动控制原理传递函数
自动控制原理传递函数
自动控制原理是指使用控制器对系统进行控制的一种方法。
在控制系统中，常常使用传递函数来描述系统的动态特性。
传递函数可以理解为输入与输出之间的数学关系，它可以表示为：
G(s) = Y(s) / U(s)
其中，G(s)表示传递函数，Y(s)表示输出信号的 Laplace 变换, U(s)表示输入信号的 Laplace 变换，s表示复变量。
为了进行系统的分析与设计，可以从传递函数的特性出发，了解系统的频率响应、稳态误差、稳定性等重要信息。
在传递函数的分析中，常常需要考虑传递函数的零点和极点。
零点是使得传递函数为零的点，而极点是使得传递函数为无穷大的点。
零点与极点的位置对于系统的稳定性和动态特性有着重要的影响。
当进行控制系统的设计时，可以通过调整传递函数的参数来实现期望的控制效果。
常见的控制方法包括比例控制、积分控制和微分控制，通过调整这些控制参数，可以实现系统的稳定性和响应速度的要求。
总之，传递函数是自动控制原理中的重要工具，通过分析传递函数的特性，可以更好地理解和设计控制系统。
自动控制原理答案(黄坚)第四章
第四章 根轨迹分析法习题4-2 单位回馈控制系统的开环传递函数1)(+=s K s G r，试用解析法绘出r K 从零变化到无穷时的死循环根轨迹图，并判断-2, j1, (-3+j2)是否在根轨迹上。
解：1-s 01s 0r=⇒=+=时，K2-s 02s 1r=⇒=+=时，K3-s 03s 2r=⇒=+=时，K……-2 在根轨迹上，（-3+j2），j1不在根轨迹上。
4-3 回馈控制系统的开环传递函数如下，0≥r K ，试画出各系统的根轨迹图。
(2) )4)(1()5.1()(+++=s s s s K s G r (3) 2)1()(+=s s K s G r ，解：（2）1）开环零、极点：p 1=0，p 2=-1,p 3=-4,z=-1.0，n=3，m=1 2）实轴上根轨迹段：（0，-1），（-1.5，-4） 3）根轨迹的渐近线：︒±=±=-+±=-=----=902)12(,75.12)5.1(410)2( ππϕσm n k aa夹角交点条渐近线4）分离点和会合点6.05.1141111-=+=++++d d d d d 试探法求得（3）1）开环零、极点：p 1=0，p 2,3=-1，n=32）实轴上根轨迹段：（0，-1），（-1，-∞） 3）根轨迹的渐近线：±=-+±=-=--=3)12(,323110)3( ππϕσm n k aa夹角交点条渐近线4）分离点和会合点310121-=⇒=++d d d 5）与虚轴交点：223++s s4-5 系统的开环传递函数为)1()2()(++=s s s K s G r ，(1) 画出系统的根轨迹，标出分离点和会合点；(2) 当增益r K 为何值时，复数特征根的实部为-2？求出此根。
解： （1）1）开环零、极点：p 1=0，p 22）实轴上根轨迹段：（0，-13）分离点和会合点.3,586.02111121-=-=⇒+=++d d d d d123s s s s r2K -r21 1K rKj,202rr±==⇒=-s K K（2）系统特征方程为02)1(rr2=+++K s K s2j 2322122,1rr±-==-=+-=-s K Ka b ，，得：由4-6 单位回馈系统的前向信道函数为)3)(1()(++=s s s K s G r，为使死循环主导极点具有阻尼比5.0=ξ，试确定r K 的值。
控制工程基础4-第2章 (数学模型-2：传递函数)
拉氏变换可以简化线性微分方 程的求解。还可将线性定常微分方 程转换为复数S域内的数学模型— 传递函数。
一、传递函数的概念
二、典型环节的传递函数
一、 传递函数概念
输入
输入拉氏 变换
设一控制系统 r(t) c(t) 系统 G(S)
R(S)
输出 输出拉氏 变换
C(S)
传递函数的定义：
零初始条件下，系统输出量拉氏变换与系 统输入量拉氏变换之比。
R(s)
G1(s)+G2(s)
C(s)
+ G2(s) C2(s)
n C1(s)=R(s)G1(s) C2(s)=R(s)G2(s) G (s)=Σ Gi (s) n个环节的并联 i=1 C(s)=C1(s)+C2(s) =R(s)G1(s)+R(s)G2(s) C(s) =G (s)+G (s) G(s)= R(s) 1 等效 2
2） 传递函数取决于系统的结构和参数， 与外施信号的大小和形式无关。
3） 传递函数为复变量S 的有理分式。
4） 传递函数是在零初始条件下定义 的，不能反映非零初始条件下系统的运 动过程。
二、 基本环节的传递函数
不同的物理系统，其结构差别很 大。但若从系统的数学模型来看，一 般可将自动控制系统的数学模型看作 由若干个典型环节所组成。研究和掌 握这些典型环节的特性将有助于对系 统性能的了解。
结构图特点
• 结构图是方块图与微分方程（传函）的结合。一方面它直观反映了整 个系统的原理结构（方块图优点），另一方面对系统进行了精确的定 量描述（每个信号线上的信号函数均可确定地计算出来） • 能描述整个系统各元部件之间的内在联系和零初始条件下的动态性能， 但不能反映非零条件下的动态性能 • 结构图最重要的作用：计算整个系统的传函 • 对同一系统，其结构图具有非唯一性；简化也具有非唯一性。但得到 的系统传函是确定唯一的. • 结构图中方块≠实际元部件，因为方框可代表多个元件的组合，甚至 整个系统
计算机控制系统 数学描述及脉冲传递函数
i 0
bi x (k i ) a i y(k i )
i 1
m
n
3. 由微分导出差分dy( t ) y (t ) y( kT ) y( kT T ) y (t ) (1)一阶差分： t dt T
例：一阶微分方程： T0 y ( t ) y( t ) ax( t ) 对应的一阶差分方程：
y(k ) a1 y(k 1) an y(k n)
b0 x(k ) b1 x(k 1) bm x(k m)
y (k )
2. 离散系统差分方程形式
注意：n 阶； n-m=d,输出相对于输入有d拍延迟。 后向差分与前向差分。 物理意义：采样系统某时刻的输出值， 由当前与过去时刻的输入值及过去时刻的 输出值共同决定。
C ( z) G( z) R( z )
1 ai z i
i 0
n
C ( z ) ai z C ( z ) b j z j R( z )
i i 1 j 0
n
m
Z反变换
c(k ) ai c(k i) b j r (k j )
i 1 j 0
2. 迭代法 已知x(kT)和初值y(0)，令k=1,2,3…,逐步求出 各采样时刻的输出序列y(T), y(2T)，… . 例：教材例4.2
y (k ) y (k 1) x (k ) x (k 1) 1 x( k ) 0 k 为偶数 k 为奇数
y(-1)=x(-1)=0
复习：1.Z变换的定义
2.滞后定理： 3. 超前定理
Y ( z ) Z[ y ( t )]
k y ( kT ) z k 0
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Rcs 1 Ts 1
例2
ui
Ri
a
R1 if
ub R2
C i Ui(s) Ri a
Zm If (s) Uo (s)
uo
U b ( s) I f ( s) R1
1 R1 R1 cs U b ( s) I ( s) I ( s) 1 R1cs 1 R1 cs U ( s) Ub ( s) I ( s) o R2
设 X1(s)=Xi(s)· G1(s), Xo(s)=X1(s) · G2(s)
则用框图表示如下 Xi(s)
G1(s)
X1(s)
G2(s)
Xo(s)
对于串连的传递函数
Xo(s)=X1(s) · G2(s) = G1(s) · G2(s) · Xi(s)
∴G(s)= G1(s) · G2(s)
如一个系统由n各环节串联而成，则系统的传递函数为
G( s ) Gi ( s)
i 1
n
② 并联
设 X1(s)=Xi(s)· G1(s), X2(s)=Xi(s)· G2(s), Xo(s)=X1(s)± X2(s) 对于并连的传递函数 Xo(s) ± Xo(s) = X1(s)± X2(s) = Xi(s)· G1(s) ± Xi(s)· G2(s) = [G1(s) ± G2(s)] Xi(s) 则用框图表示如下
Xi(s) + A
E(s)
±
B(s)
G(s)
Xo(s)
H(s)
如果在点 A 处将反馈回路切断，则得到以E(s)为输入，B(s) 为输出的传递函数Gk(s)，称之为闭环系统的开环传递函数。 Gk(s) = H(s)G(s) Xi(s)
Gb(s)
Xo(s)
作业：
求由运算放大器组成的复合环节的传递函数
2
令
A2 R T K
G( s)
Ts Ts 1
求下图的传递函数,并计算ωn 、ξ
L i ZL
ui
R
C
uo
I ( s) Ui(S) Z Uo(S)
ZL=Ls
Z=R//1/cs
2 U o ( s) Z n R G( s) 2 2 2 U i ( s ) Z L Z LRCs Ls R s 2n s n
G(s)
H(s)
所以对于该闭环系统，传递函数为：
G( s) Gb ( s ) 1 G( s) H ( s)
“-”表示正反馈，“+”表示负反馈
G( s) 控制系统中主要采用负反馈，则 Gb ( s ) 1 G( s) H ( s) G( s) 单位负反馈 Gb ( s ) 1 G( s)
Xi(s)
G(s)
Xo(s)
2. 绘制框图的要点
a. b. c. d. 方框内只允许填写传递函数G(s)； 框图中的全部变量 都是取了拉氏变换后的变量，要求大写； 变量一般置于箭头的上方，箭头的指向表示信号的流向； 框图的联接是按信号流向进行的，有串联、并联和反馈联接 三种。
3. 框图的联接
① 串联
dxo xo Kxi ④ 惯性环节 T dt
⑤ 二阶环节和振荡环节
d 2 xo dxo T To xo Kxi 2 dt dt
2 Kn G( s) 2 2 s 2n s n
⑥ 延时环节
xo (t) = xi (t-τ)
G( s) es
求右图油缸-阻尼-弹簧 系统的传递函数.其中， p为输入，xo为输出。
试画出人工控制的恒温箱原理框图
脑
① 比例环节
xo(t)=kxi(t)
dxi (t ) xo (t ) T dt
G( s)
X o ( s) X i ( s)
k
小 节
② 微分环节
③ 积分环节
G(s)=TS
xo (t ) T xi (t )dt G(s)=T/S
G( s) K Ts 1
G( s)
Zm Ri
Байду номын сангаас
例4
请先行练习
下图是由放大电路组成的PI调节器，求G(s)
在反馈电路中并联了一个积分电路的放大器，各变量已取 拉氏变换。其中，Uf(s)为反馈电压，E(s)为偏差电压。
解
K
Uo ( s) KE( s)
Ui(s)
E(s)
UO(s) R
K (Ui (s) U f (s))
xo
K A
解
p
dx o c kx o pA dt
csX o ( s) kX o ( s) AP( s)
X o ( s) A P( s ) cs K
c
G( s)
G( s)
K Ts 1
求图示液压阻尼器的 传递函数,并判断属于 什么环节
q
R
xo(t)
K
解
A( p2 p1 ) Kxo (t )
C
R R1 3 ui Ri if
+
R2 i uo
证明下面两个系统是相似系统
C1 R1
C2
K2 C1
xi
ui
R2
C2
uo
K1
xo
Uo ( s) Ub ( s) I ( s) R2
R1 R2 c1c2 s 2 ( R1c1 R2 c2 R2 c1 ) s 1 Zm c1s
Zm G( s) Ri
PID控制的原理和特点
在工程实际中，应用最为广泛的调节器控制规律为比例、积分、 微分控制，简称PID控制，又称PID调节。PID控制器问世至今 已有近70年历史，它以其结构简单、稳定性好、工作可靠、调 整方便而成为工业控制 的主要技术之一。当被控对象的结构 和参数不能完全掌握，或得不到精确的数学模型时，控制理论 的其它技术难以采用时，系统控制器的结构和参数必须依靠经 验和现场调试来确定，这时应用PID控制技术最为方便。即当 我们不完全了解一个系统和被控对象﹐或不能通过有效的测量 手段来获得系统参数时，最适合用PID控制技术。PID控制，实 际中也有PI和PD控制。PID控制器就是根据系统的误差，利用 比例、积分、微分计算出控制量进行控制的。
U f ( s)
R R 1 cs U o ( s)
Uf (s) C
Rcs U o (s) Rcs 1
K Rcs 1 G( s ) 1 Rcs Rcs 1 1 K Rcs Rcs 1 K
1 1 1 Rcs Ts
③ PI D调节器 比例、积分、微分环节组成的调节器。
Ui(s)
K
E(s)
UO(s) R
K (Ui (s) U f (s))
Uf (s)
C
1 1 cs U ( s ) U f ( s) Uo ( s) 1 o Rcs 1 R cs
K ( Rcs 1) Rcs 1 G( s ) Rcs 1 k Rcs 1 1 K
dxi dxo q A dt dt
p 2 p1 q R
G( s) s K s 2 A R
p1
A
p2
xi(t)
K X o ( s) s 2 sX i ( s) A R
dx dx A R i o Kxo dt dt
第四章 控制系统的传递函数
第二节 复合环节传递函数
一般来说，采用调节器的控制系统，既能获得较高的 静态精度，又具有较快的动态响应。
2014.10.13
1. 复合环节概念
在自动控制技术中，常用到一些被称为调节器（校正器）的 动态元件。他们就是由一些典型环节组成的复合环节。不同 环节的组合，构成各种性能不同的调节器。了解这些调节器 的传递函数，会方便以后的设计。 单一典型环节组合 复合环节，如PI调节器、PD调节器
Ub(s) R2
Uo(s) I(s)
C1
C2
I f ( s)
U b ( s) 1 R1 c1s
R1c1 s 1 1 1 U b ( s ) I ( s ) R1 c s // c s R c c s 2 c s c s I ( s ) 1 2 1 1 2 2 1
比例积分环节组成的调节器。
T——时间常数，K——比例系数
1 G( s ) K 1 Ts
例3
解
ui(t)
下图是由放大电路组成的PI调节器，求G(s)
R2 Zm Ui(s) R1 C a
Ri
uo (t)
Ri
a
Uo (s)
1 R 1 R2 ( R1cs 1) R2 cs Zm=(R1+1/cs)∥R2 1 ( R1cs R2 cs 1) R R 1 2 cs
Xi(s)
G1(s) G2(s)
X1(s)
X2(s)
∴G(s)= G1(s) ± G2(s)
如一个系统由n个环节并联而成，则系统的传递函数为
各环节传递函数的代数和。若把并联处都看成相加，则
G ( s ) Gi ( s )
i 1
n
③ 反馈联接
反馈联接框图如下图所示 Xi(s) + A E(s) ± B(s) Xo(s) 由图可知 E(s) = Xi(s)± B(s) Xo(s)= G(s) E(s) B(s)= H(s) Xo(s)
1 G( s) K T1 s T s 1 2
例4
下图是由放大电路组成的PID调节器，求G(s)
R1
C2
C1
R2
i Ui(s) Ri a