哈工大理论力学考研《理论力学Ⅱ》考研2021考研真题库
理论力学考研试题合集及答案

理论力学考研试题合集及答案# 理论力学考研试题合集及答案一、选择题1. 一个物体在水平面上以匀速直线运动,其受力情况是()。
A. 只受重力B. 只受支持力C. 水平方向上受力平衡D. 竖直方向上受力平衡答案: D2. 根据牛顿第二定律,物体的加速度与作用在物体上的合力成正比,与物体的质量成反比。
这一定律的数学表达式是()。
A. \( F = ma \)B. \( F = \frac{m}{a} \)C. \( a = \frac{F}{m} \)D. \( a = \frac{m}{F} \)答案: C3. 一个质点做匀速圆周运动时,其向心力的来源是()。
A. 质点自身的惯性力B. 外界提供的约束力C. 质点的重力D. 质点的离心力答案: B二、简答题1. 简述达朗贝尔原理及其在解决动力学问题中的应用。
答案:达朗贝尔原理,也称为动静法或虚位移原理,是分析力学中的一个基本原理。
它指出,一个处于平衡状态的物体,如果受到一个额外的力,那么物体就会发生一个虚拟的位移,而这个位移与力的方向相反。
在动力学问题中,达朗贝尔原理常用于求解约束力,特别是在复杂约束条件下的动力学分析中非常有用。
2. 什么是科里奥利力?它在哪些领域有应用?答案:科里奥利力是一种在旋转参考系中观察到的惯性力,它作用于运动物体,使其轨迹相对于旋转参考系发生偏移。
科里奥利力的方向垂直于物体的速度和旋转轴,其大小与物体的速度、物体与旋转轴的距离以及旋转的角速度成正比。
科里奥利力在气象学、海洋学、航空航天以及旋转机械等领域有广泛的应用,例如在解释地球上的风向和洋流模式时就非常重要。
三、计算题1. 一个质量为 \( m \) 的物体,从静止开始沿着一个倾角为\( \theta \) 的斜面下滑,假设斜面是光滑的,没有摩擦力。
求物体下滑的加速度。
答案:物体下滑的加速度可以通过自由体受力分析得到。
物体受到两个主要力的作用:重力 \( mg \) 和斜面的支持力 \( N \)。
理论力学复习题及答案(哈工大版)汇总

理论力学复习题及答案(哈工大版)汇总一、是非题1、力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
(√)2、在理论力学中只研究力的外效应。
(√) 3、两端用光滑铰链连接的构件是二力构件。
(× ) 4、作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
(√ ) 5、作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
(× ) 6、三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
(× ) 7、平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
(√ )8、约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
(× ) 9、在有摩擦的情况下,全约束力与法向约束力之间的(应是最大)夹角称为摩擦角。
(× ) 10、用解析法求平面汇交力系的平衡问题时,所建立的坐标系x,y轴一定要相互垂直。
(× )11、一空间任意力系,若各力的作用线均平行于某一固定平面,则其独立的平衡方程最多只有3个。
(× )12、静摩擦因数等于摩擦角的正切值。
(√ ) 13、一个质点只要运动,就一定受有力的作用,而且运动的方向就是它受力方向。
(× ) 14、已知质点的质量和作用于质点的力,质点的运动规律就完全确定。
(× ) 15、质点系中各质点都处于静止时,质点系的动量为零。
于是可知如果质点系的动量为零,则质点系中各质点必都静止。
(× )16、作用在一个物体上有三个力,当这三个力的作用线汇交于一点时,则此力系必然平衡。
(× )17、力对于一点的矩不因力沿其作用线移动而改变。
(√ )18、在自然坐标系中,如果速度υ = 常数,则加速度α = 0应是切线方向加速度为零。
(× )19、设一质点的质量为m,其速度?与x轴的夹角为α,则其动量在x轴上的投影为mvx =mvcosa。
哈工大理论力学教研室《理论力学》(第7版)笔记和课后习题(含考研真题)详解(第16~17章)【圣才出

第16章非惯性系中的质点动力学16.1复习笔记一、基本方程1.非惯性系中的质点动力学基本方程(或称为质点相对运动动力学基本方程),其表达式为r Ie ICma F F F =++v v v v 式中,e Ie F ma =-v v ,表示牵连惯性力;C C I F ma =-v v ,表示科氏惯性力。
2.在动参考系内,把非惯性系质点动力学基本方程写成微分形式22Ie IC d d r m F F F t'=++v v v v 3.几种特殊情况(1)当动参考系相对于定参考系作平移时,则C 0a = ,0F =IC ,于是相对运动动力学基本方程为r Iema F F =+v v v (2)当动参考系相对于定参考系作匀速直线平移时,则C 0a = ,e 0a = ,Ie 0F F ==IC,于是相对运动动力学基本方程与相对于惯性参考系的基本方程形式一样,其表达式为r ma F= ①相对于惯性参考系做匀速直线平移的参考系都是惯性参考系。
②发生在惯性参考系本身的任何力学现象,都无助于发现该参考系本身的运动状况,这称为经典力学的相对性原理。
(3)当质点相对于动参考系静止时,则r r 00a υ==v v ,,0F =IC ,所以质点相对静止的平衡方程为F F +=Ie 上式称为质点相对静止的平衡方程,即当质点在非惯性参考系中保持相对静止时,作用在质点上的力与质点的牵连惯性力相互平衡。
(4)当质点相对于动参考系作等速直线运动时,有r 0a =,质点相对平衡方程为0Ie IC F F F ++=v v v 上式称为质点相对平衡方程。
可见在非惯性参考系中,质点相对静止和作等速直线运动时,其平衡条件是不相同的。
二、非惯性系中质点的动能定理1.质点相对运动动能定理的微分形式质点在非惯性系中相对动能的增量,等于作用于质点上的力与牵连惯性力在相对运动中所作的元功之和。
即2r 1d()δδ2F mv W W ''=+Ie 2.质点相对运动动能定理的积分形式质点在非惯性参考系中相对动能的变化,等于作用在质点上的力与牵连惯性力在相对路程上所作的功之和。
哈工大理论力学历年考研真题——静力学题经典题目
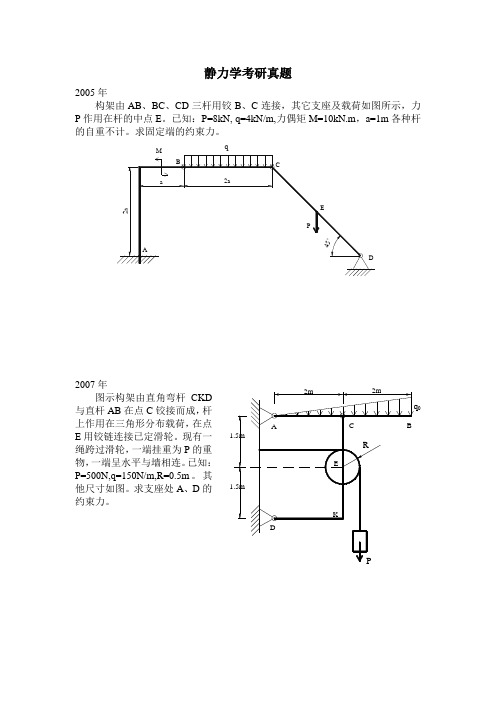
静力学考研真题2005年构架由AB、BC、CD三杆用铰B、C连接,其它支座及载荷如图所示,力P作用在杆的中点E。
已知:P=8kN, q=4kN/m,力偶矩M=10kN.m,a=1m各种杆的自重不计。
求固定端的约束力。
q2007年图示构架由直角弯杆CKD与直杆AB在点C铰接而成,杆上作用在三角形分布载荷,在点E用铰链连接已定滑轮。
现有一绳跨过滑轮,一端挂重为P的重物,一端呈水平与墙相连。
已知:P=500N,q=150N/m,R=0.5m。
其他尺寸如图。
求支座处A、D的约束力。
2002年 图示构架,A 为固定铰链,B 处为光滑平面,各杆件自重不计。
已知:P1=P2=100kN ,L=5m,试求A 、D 、E 、H 各铰链处的约束力。
00年如图所示,平面构架的各杆自重不计 ,已知:q=1kN/m,L=1m,a=0.6m,EH=0.3m;在DE 杆上作用已力偶,其矩M=kN.m 。
试求铰链B 、D 、H 、A 的约束力。
L1999 年构架如图所示,各杆自重不计。
皆为铰链。
已知:q=50kN/m,M=80kN.m,L=1m 。
试求固定端A 和支座B 的约束力。
1994年图示平面结构,尺寸如图所示,AC 、BC 及DF 三杆重量不计,A 、D 、C 、E 均为光滑铰链连接,B 为滚动支座。
C 处作用有已知水平力P ,F 处受力偶作用,力偶矩为M 。
试求水平杆DE 与D 、E 处所收的约束力。
图示平面结构,其中水平梁由AB 与BD 组成,图中各杆件的自重不计。
C 、BK 、E 、G 、H 均为光滑的铰链。
已知:集中载荷P=qaN 均布载荷qN/m ;力偶矩M=qa.a 。
AC=CB=BK=KD=GH=AE=CG=BH=am 。
求插入端A 的约束力1990年图示构架,各杆的自重不计,A 、B 、C 、D 、E 、F 处均为光滑铰链连接。
已知M=50kN.m ,P=,45,θ=各尺寸如图所示。
CD 、BF 杆水平,ABC 杆铅垂。
哈工大力学基础考研真题

哈工大力学基础考研真题哈尔滨工业大学力学基础考研真题一、引言力学基础是力学学科的基础和核心,对于力学学科的理论研究和工程应用都具有重要意义。
哈尔滨工业大学作为国内一流的工科院校,力学基础考研真题也一直备受关注。
本文将分享一道哈尔滨工业大学力学基础考研真题,并根据题目的要求来详细讨论解答方法。
二、力学基础考研真题**题目:**已知一质点在二维坐标系中运动,其位置由位矢r(t) = x(t) i + y(t) j 表示,其中i、j为单位基矢量。
(a) 求质点的速度v(t);(b) 求质点的加速度a(t);(c) 若质点的运动满足v(t) = t^2 i + 2t j,求质点的位矢r(t)。
三、解答方法(a) 求质点的速度v(t)根据速度的定义,速度v(t)是位矢r(t)对时间t的导数。
根据题目给出的位矢r(t),可以得到质点的速度v(t)如下:v(t) = dr(t)/dt = (dx(t)/dt) i + (dy(t)/dt) j(b) 求质点的加速度a(t)加速度a(t)是速度v(t)对时间t的导数,即速度的导数。
根据题目给出的速度v(t),可以得到质点的加速度a(t)如下:a(t) = dv(t)/dt = d^2x(t)/dt^2 i + d^2y(t)/dt^2 j(c) 求质点的位矢r(t)根据速度v(t)等于t^2 i + 2t j,可以进行速度的积分,得到位矢r(t)如下:r(t) = ∫v(t)dt = ∫(t^2 i + 2t j)dt = (t^3/3) i + (t^2) j + C四、解答过程(a) 求质点的速度v(t)根据速度的定义,速度v(t)是位矢r(t)对时间t的导数。
由题意得到位矢r(t) = x(t) i + y(t) j ,所以质点的速度v(t)可以表示为:v(t) = dr(t)/dt = (dx(t)/dt) i + (dy(t)/dt) j(b) 求质点的加速度a(t)加速度a(t)是速度v(t)对时间t的导数,即速度的导数。
哈工大理论力学考研《理论力学Ⅱ》考研2021考研真题库

哈工大理论力学考研《理论力学口》考研2021考研真题库第一部分名校考研真题1 .如图15-1所示,物块A的质量为mi, B轮的质量为m2,半径为R ,在水平面做无滑动滚动。
轮心用刚度为k长度为I的弹簧与物块A相连,物块A与水平面间为光滑接触。
试以Xi, X2为广义坐标,(1)写出系统的动能及势能及拉格朗日函数;(2)写出系统的第二类拉格朗日方程;(3 )求系统的第二类拉格朗日方程的首次积分。
[中山大学2011研]—WWXWv\\\\\\\\\\图15-1解:(1)系统的动能为:r = -W, X +-w, X X2 1 4 . 2 ・系统势能为:展兴优十月2其中分为处于平衡位置弹簧的伸长量。
拉格朗日函数1 .L a .1 \L = T-V=-m lX +-^x--^+x)2(2)第二类拉格朗日方程代入上一步的表达式,得3 -Wj x+ — rn2x— M 认 +工)=0(3 )求其首次积分。
因拉格朗日函数中不显含时间t,故存在能量积分,系统机械]・ 3 ・ 1 、-m.x + 二阳、x 一一左(房+力’2 । 4 • 2 ' 二c C为常数2.质量为m的重物悬挂在刚度系数为k的弹壁上,且在光滑的铅垂滑道中运动°在重物的中心处钱接一个质量为M、长为21的匀质杆,杆在铅垂平面内运动,如图15-2所示。
(1)试确定系统的自由度并选择广义坐标;(2)写出系统的动能及势能及拉格朗日函数;(3)写出系统的第二类拉格朗日方程;(4 )求系统的第二类拉格朗日方程的首次积分。
[中山大学2010研]解:(1 )以整个系统为研究对象,物块和杆均做平面运动,该系统具有两个自由度。
故系统的拉格朗日函数为图 15-4选重物A 的中心的垂直坐标y 和杆的偏角隼为广义坐标,如下图所示。
因为作用在 系统上的主动力即重力和弹性力均为有势力,所以可用拉格朗日方程式主动力有势 形式求解。
(2 )以A 的中心C 点为基点分析AB 杆质心D 的速度,如图15-3所示。
理论力学考研真题答案

理论力学考研真题答案1. (a) 根据题意,物体在重力场中做简谐振动,受到的驱动力是常数倍于受力恢复力的力。
设物体的质量为m,振幅为A,重力加速度为g,则物体受到的恢复力为F = -mgx,其中x为物体离开平衡位置的距离。
由动力学方程F = ma,将上式代入可得:ma = -mgxa = -gx物体的加速度与位移x成线性关系,所以物体在重力场中做简谐振动。
(b) 物体的周期T与物体的振动频率f满足以下关系:f = 1/T物体的周期T由以下公式给出:T = 2π√(m/k)其中m为物体的质量,k为恢复力常数。
将恢复力公式F = -mgx代入可得:k = mg代入周期公式可得:T = 2π√(m/mg)T = 2π√(1/g)所以,物体在重力场中的简谐振动周期只与重力加速度有关,与物体的质量无关。
2. (a) 根据波动方程的一般形式:∂^2Ψ/∂t^2 = v^2∂^2Ψ/∂x^2其中Ψ为波函数,t为时间,x为位置,v为波速。
将Ψ(x,t)拆解为X(x)T(t)的乘积形式:Ψ(x,t) = X(x)T(t)代入波动方程可得:X''(x)T(t) = (1/v^2)X(x)T''(t)T''(t)/T(t) = v^2X''(x)/X(x)等式两边为常数,分别记为-ω^2,即:T''(t)/T(t) = -ω^2X''(x)/X(x) = -ω^2求解T''(t)/T(t) = -ω^2,可得:T(t) = Acos(ωt+φ)求解X''(x)/X(x) = -ω^2,可得:X(x) = Asin(kx+φ)其中A、k和φ为常数,分别为振幅、波数和相位常数。
将Ψ(x,t) = X(x)T(t)代入Ψ(x,t) = Acos(ωt+φ)sin(kx+φ)可得:Ψ(x,t) = Acos(ωt+φ)sin(kx+φ)(b) 波函数Ψ(x,t) = Acos(ωt+φ)sin(kx+φ)表示横波的传播,振动方向垂直于传播方向。
(NEW)哈工大理论力学教研室《理论力学》(第7版)笔记和课后习题(含考研真题)详解

目 录第1章 静力学公理和物体的受力分析1.1 复习笔记
1.2 课后习题详解
1.3 名校考研真题详解
第2章 平面力系
2.1 复习笔记
2.2 课后习题详解
2.3 名校考研真题详解
第3章 空间力系
3.1 复习笔记
3.2 课后习题详解
3.3 名校考研真题详解
第4章 摩 擦
4.1 复习笔记
4.2 课后习题详解
4.3 名校考研真题详解第5章 点的运动学
5.1 复习笔记
5.2 课后习题详解
5.3 名校考研真题详解第6章 刚体的简单运动
6.1 复习笔记
6.2 课后习题详解
6.3 名校考研真题详解第7章 点的合成运动
7.1 复习笔记
7.2 课后习题详解
7.3 名校考研真题详解第8章 刚体的平面运动8.1 复习笔记
8.2 课后习题详解
8.3 名校考研真题详解
第9章 质点动力学的基本方程9.1 复习笔记
9.2 课后习题详解
9.3 名校考研真题详解
第10章 动量定理
10.1 复习笔记
10.2 课后习题详解
10.3 名校考研真题详解
第11章 动量矩定理
11.1 复习笔记
11.2 课后习题详解
11.3 名校考研真题详解
第12章 动能定理
12.1 复习笔记
12.2 课后习题详解
12.3 名校考研真题详解
第13章 达朗贝尔原理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
哈工大理论力学考研《理论力学Ⅱ》考研
2021考研真题库
第一部分名校考研真题
1.如图15-1所示,物块A的质量为m1,B轮的质量为m2,半径为R,在水平面做无滑动滚动。
轮心用刚度为k长度为l的弹簧与物块A相连,物块A与水平面间为光滑接触。
试以X1,X2为广义坐标,
(1)写出系统的动能及势能及拉格朗日函数;
(2)写出系统的第二类拉格朗日方程;
(3)求系统的第二类拉格朗日方程的首次积分。
[中山大学2011研]
图15-1
解:(1)系统的动能为:
系统势能为:
其中为处于平衡位置弹簧的伸长量。
拉格朗日函数
(2)第二类拉格朗日方程
代入上一步的表达式,得
(3)求其首次积分。
因拉格朗日函数中不显含时间t,故存在能量积分,系统机械能守恒,即
=C C为常数
2.质量为m的重物悬挂在刚度系数为k的弹簧上,且在光滑的铅垂滑道中运动。
在重物的中心处铰接一个质量为M、长为21的匀质杆,杆在铅垂平面内运动,如图15-2所示。
(1)试确定系统的自由度并选择广义坐标;
(2)写出系统的动能及势能及拉格朗日函数;
(3)写出系统的第二类拉格朗日方程;
(4)求系统的第二类拉格朗日方程的首次积分。
[中山大学2010研]
图15-2
解:(1)以整个系统为研究对象,物块和杆均做平面运动,该系统具有两个自由度。
选重物A的中心的垂直坐标y和杆的偏角为广义坐标,如下图所示。
因为作用在系统上的主动力即重力和弹性力均为有势力,所以可用拉格朗日方程式主动力有势形式求解。
(2)以A的中心C点为基点分析AB杆质心D的速度,如图15-3所示。
图15-3
根据速度合成公式有
其中。
系统动能为
选O为零势能点,设弹簧的原长为l0,则系统的势能为
故系统的拉格朗日函数为
(3)求各偏导数
将以上各式代入第二类拉格朗日方程
(4)求其首次积分
因拉格朗日函数中不显含时间t,故存在能量积分,系统机械能守恒,即
3.如图15-4所示。
重为P的板搁在两个半径为r、重为W的磙子上,磙子可视为均质圆柱。
设接触面足够粗糙,磙子与板和水平面之间均无相对滑动。
在板上作用一水平拉力F,求板的加速度。
[北京邮电大学2010研]
图15-4
解:拉格朗日方程
该系统只有一个自由度,取板的水平位移x为广义坐标,列出每部分的动能
总动能为
代入拉格朗日方程
解得。
