人教版七年级上册数学代数式求值(整体代入三)天天练
七年级数学上册 综合训练 代数式求值(含字母的代数式化简、数位表示)天天练新人教版

代数式求值学生做题前请先回答以下问题问题1:①若关于x的代数式mx+1的值不受x取什么值的影响,即与x无关,只需m_______,理由是__________________;②若关于x的代数式(m+1)x+1的值不受x取什么值的影响,即与x无关,只需m_______;③若关于x的代数式(2m-1)x+1的值不受x取什么值的影响,即与x无关,只需m_______.问题2:数位表示要先画_________,再乘以对应的_________.代数式求值(含字母的代数式化简、数位表示)(人教版)一、单选题(共11道,每道9分)1.若关于x的多项式ax+4的值与x无关,则下列说法正确的是( )A.a=1B.a=0C.x=1D.x=02.若关于x的多项式的值与x无关,则m的值为( )A.0B.1C.6D.-63.若关于x,y的多项式的值与y无关,则a的值为( )A.-1B.5C.0D.-54.若关于x的多项式的值与x无关,则( )A.m=1,n=3B.m=-1,n=3C.m=1,n=-3D.m=0,n=05.已知代数式的值与x无关,则的值为( )A.12B.-12C.24D.-246.若关于x,y的多项式的值与y无关,则的值为( )A.-46B.8C.26D.277.一个三位数,百位上的数字为,十位上的数字是百位上的数字的2倍,个位上的数字是5,用代数式表示这个三位数为( )A. B.C. D.8.若表示一个两位数,表示一个一位数,把放在的左边,则组成的三位数应表示为( )A. B.C.D.9.若表示一个三位数,表示一个一位数,把放在的左边,则组成的四位数应表示为( )A. B.C. D.10.若表示一个两位数,也表示一个两位数,把放在的右边,则组成的四位数应表示为( )A. B.C. D.11.若表示一个两位数,表示一个三位数,把放在的右边,则组成的五位数应表示为( )A. B.C. D.如有侵权请联系告知删除,感谢你们的配合!。
3.2代数式的值++同步练习2024—2025学年人教版数学七年级数学上册

3.2代数式的值课时 1 代数式的值刷基础知识点1 直接代入求值1 当x=-1时,代数式x²−3x的值是 ( )A.4B.2C.-4D.-22在-1,0,1,2,3,4这六个数中,能使代数式x(x+1)(x-2)(x-6)的值为零的有 ( )A.2个B.3个C.4个D.5个3 如图所示是一个运算程序示意图.若第1 次输入k的值为125,则第2 024次输出的结果是 .4 已知有下列两个代数式:①a²-b²;②(a+b)(a-b).(1)当a=5,b=4时,代数式①的值是 ,代数式②的值是 .(2)当a=-2,b=3时,代数式①的值是 ,代数式②的值是 .(3)观察(1)和(2)中代数式的值,你发现代数式a²−b²和(a+b)(a-b)的关系为 .(4)利用你发现的规律,求2022²−2021².知识点2 先确定字母值的情况,再代入求值5 如果|a+2|+(b-1)²=0,那么代数式(a+b)²⁰²⁴的值是 ( )A.1B.-1C.±1D.2 0216 当x=1时,代数式ax³+bx+1的值为2023,当x=-1时,代数式.ax³+bx+1的值为 .7 已知代数式3(13−m)的值为p.(1)当m=2时,求p的值;(2)若m的取值为小于0且不小于-2的整数,求p的值.刷易错易错点代入数值时,因忘加括号和符号错误而致错8嘉嘉在解决问题“当x=32,y=−6时,求代数式x²−2xy+y²的值.”时,他的解题过程如下:解:当x=32,y=−6时,x2−2xy+y2=322−2×32×(−6)−62=92+18−36=−1312.你认为他的计算正确吗?若不正确,请写出正确答案.课时2 求代数式的值的应用刷基础知识点1在实际应用问题中求代数式的值1一辆汽车在一段平直的公路上行驶,若汽车行驶的路程s(m)与时间t(s)的关系式为s=5t²+2t,则t =4时,这辆汽车行驶的路程为 ( )A.28 mB.48 mC.68 mD.88 m2某种型号的巡航导弹的速度v(km/h)与时间t(h)的关系是v=1 000+50t,现导弹发出1h时击中目标,此2时该导弹的速度应为 .3 某城市大剧院地面的一部分为扇形,观众席的座位按下列方式设置:(1)第5,6排分别有多少个座位?(2)写出用n表示 m 的式子.(3)当n=28时,求m的值.知识点2在几何图形问题中求代数式的值4 如图,在一块长为a,宽为2b的长方形铁皮中,以2b为直径分别剪掉两个半圆,若a=4,b=1,则剩下的铁皮的面积为(π取3) ( )A.5B.7C.8D.125 如图,一个长方形推拉窗,窗高1.4m,当活动窗扇沿图中所示的方向移动时,随着窗扇拉开长度b(m)的变化,窗户的通风面积A(m²)也发生了变化.在这个变化过程中,当拉开长度b从0.1m变化到0.4m时,通风面积A 从m²变化到m².下列选项正确的是 ( )A.0.14 5.6B.0.24 0.48C.0.14 0.56D.2.4 5.66 如图,在一个底为a,高之h的三角形铁皮上剪去一个半径为r的半圆.当a=8,h=6,r=3时,剩余铁皮的面积S的值为 .(结果保留π)7 教材拓展[2024辽宁沈阳期末]如图是一幢公寓窗户的形状,其上部是半圆形,下部是边长相同的四个小正方形,已知下部的小正方形的边长为 a m.(1)窗户的总面积是多少?(窗框面积忽略不计)(2)窗框的总长是多少?(3)如果窗户上安装的是玻璃,购买玻璃的费用是40元/m²,购买窗框的费用是24元/m,当a=0.5 时,制作一扇窗户需要的费用是多少元? (取π=3).刷提升1 某班数学活动小组的同学用纸板制作长方体包装盒,其平面展开图和相关尺寸如图(1)所示.(单位:cm)(1)求该长方体的表面积(用含x,y的代数式表示).(2)当x=20cm,y=10cm时,数学活动小组的同学准备用边长为a的正方形纸板(如图(2))裁剪成六块,作为长方体的六个面,粘合成如图(1)所示的长方体包装盒.①求a的值;②在图(2)中画出裁剪线的示意图,并标注相关的数据.2 某公园出售的一次性使用门票,每张10元,为了吸引更多游客,最近推出购买“个人年票”的售票活动(从购买日起,可供持票者使用一年).年票分 A、B两类:A类年票每张 100 元,持票者每次进入公园无需再购买门票;B类年票每张50元,持票者进入公园时需再购买每次2元的门票.(1)某游客一年进入该公园共有n次,若不购买年票,则一年的费用为元;若购买 A类年票,则一年的费用为元;若购买 B类年票,则一年的费用为元.(用含 n的代数式表示) (2)假如某游客一年中进入该公园共有 12次,选择哪种购买方式比较合算?请通过计算说明理由.3 如图是某校田径运动场的平面图,最中间是长方形,长为a 米,两端为两个半圆,半径为r 米,每条跑道的宽为1.2米,共四个跑道.若每个跑道按内侧边线的总长度计算路程,请.解答下列问题: (1)第2跑道的总长度为 米. (2)第3跑道的总长度为 米.(3)若a=50,且要求第1跑道的总长度为200米.(以下问题结果精确到个位,π取3.1) ①求r 的值;②操场中心(阴影部分)铺设地砖,跑道及两端的半圆铺设塑胶和人工草,若铺设地砖需要50元/平方米,铺设塑胶和人工草需要100元/平方米,则学校共需付多少铺设费用?。
2024-2025学年人教版七年级数学上册《第3章代数式》单元同步练习题(附答案)

2024-2025学年人教版七年级数学上册《第3章代数式》单元同步练习题(附答案)一、单选题1.下列式子,符合代数式书写格式的是()A.2B.283C.×7D.+人2.下列各式中是代数式的是()A.2−2=0B.6C.4>3D.5−2≠0 3.“4与x的平方的积”可表示为()A.4B.42C.16D.1624.一本笔记本原价a元,降价后比原来便宜了b元,小玲买了3本这样的笔记本,比原来便宜了()A.3−元B.3−元C.3元D.3元5.若=5,=2,且B<0,则−的值为()A.7B.3或−3C.3D.7或36.(代数式应用)一个两位数,十位上的数字是a,个位上的数字是6,表示这个两位数的式子是()A.6B.60+C.6+D.6+107.已知式子−3的值是3,则式子1−3+9的值是().A.−8B.−6C.6D.88.把三角形按如图所示的规律拼图案,其中第①个图案中有1个三角形,第②个图案中有4个三角形,第③个图案中有8个三角形,…,按此规律排列下去,则第⑦个图案中三角形的个数为()A.15B.17C.19D.24二、填空题9.试写出一个含x的代数式:当=3时,它的值为−5.这个代数式可以是.10.若s互为相反数,是最大的负整数,则3+3−4=.11.学校买来6个足球,每个元,又买来个篮球,每个58元,6+58表示.12.当=2时,整式B3+B−1的值等于−19,那么当=−2时,整式B3+B−1的值为.13.小强购买绿、橙两种颜色的珠子串成一条手链,已知绿色珠子m个,每个2元,橙色珠子n个,每个5元,那么小强购买珠子需花费元.14.一组按规律排列的代数式:+2,2−23,3+25,4−27,…,则第10个式子是.15.观察下列各式:22−2×1=1+1,32−2×2=4+1,42−2×3=9+1,52−2×4= 16+1,…,第n个等式是.16.在如图所示的运算程序中,若开始输入的x的值为36,我们发现第1次输出的结果为18,第2次输出的结果为9,……,则第2023次输出的结果为.三、解答题17.当=−2,=3时,求下列代数式的值:(1)3(−p;;(3)(−p2;(4)(B)2;(5)2+2.18.回答下列问题:(1)小明每季度有零花钱a元,拿出b元捐给爱心基金,平均每月剩余的零花钱是多少?(2)七年级(1)班共有a名学生,其中有b名男生,男生的三分之一去参加篮球比赛了,班级剩余多少人?(3)某种汽车油箱装满后有油Y,每小时耗油Y,行驶了3h,油箱剩余油量是多少?(4)某商品原价每件a元,商场打折,现价每件b元,现买3件可以省多少元?19.已知,如图,某长方形广场的四角都有一块边长为米的正方形草地,若长方形的长为米,宽为米.(1)请用代数式表示阴影部分的面积;(2)若长方形广场的长为20米,宽为10米,正方形的边长为1米,求阴影部分的面积.20.如图,两摞规格完全相同的课本整齐叠放在讲台上.请根据图中所给出的数据信息,回答下列问题:(1)每本课本的厚度为cm ;(2)若有一摞上述规格的课本x 本,整齐叠放在讲台上,请用含x 的代数式表示出这一摞数学课本的顶部距离地面的高度;(3)当=55时,若从中取走13本,求余下的课本的顶部距离地面的高度.21.11×2=1−12,12×3=12−13,13×4=13−14,14×5=14−15=⋯(1)第5个式子是_______;第个式子是_______.(2)从计算结果中找规律,利用规律计算:11×2+12×3+13×4+14×5+⋯+12020×2021=_______;(3)计算:(由此拓展写出具体过程):①11×3+13×5+15×7+⋯+199×101;②1−12−16−112−⋯−19900.22.【实践与应用】学校举办诗歌颂祖国活动,需要定制一批奖品颁发给表现突出的同学,每份奖品包含纪念徽章与纪念品各一个,现有两家供应商可以提供纪念徽章设计、制作和纪念品制作业务,报价如下:纪念徽章设计费纪念徽章制作费纪念品费用甲供应商300元3元/个18元/个乙供应商免设计费6元/个不超过100个时,20元/个;超过100个时,其中100个单价仍是20元/个,超出部分打九折(1)若学校需要定制20份奖品,则选甲供应商需要支付____________元,选乙供应商需要支付____________元;(2)现学校需要定制>100份奖品.若选择甲供应商,需要支付的费用为元;(用含的代数式表示,结果需化简)若选择乙供应商,需要支付的费用为元;(用含的代数式表示,结果需化简)(3)如果学校需要定制150份奖品,请你通过计算说明选择哪家供应商比较省钱.参考答案:题号12345678答案A B B D A D A D1.解:A、2符合代数式书写格式,故此选项符合题意;B、的系数应该为假分数,故此选项不符合题意;C、数字7应该在字母的前面,乘号省略,故此选项不符合题意;D、+应该加上括号,故此选项不符合题意;故选:A.2.解:、2−2=0不是代数式,不符合题意;B、6为代数式,符合题意;C、4>3不是代数式,不符合题意D、5−2≠0不是代数式,不符合题意.故选:B.3.解:的平方可以写成2,再与4的积,可以写成42,故选:B.4.解:一本笔记本原价元,降价后比原来便宜了元,则三本便宜了3元,故选:D.5.解:∵=5,=2,∴=±5,=±2,∵B<0,∴、异号,∴=5,=−2或=−5,=2,①当=5,=−2时,−=5−−2=5+2=7;②当=−5,=2时,−=−5−2=−7=7,综上所述,−的值为7.故选:A.6.解:10×+1×6=10+6;故选:D.7.解:∵式子−3的值是3,∴−3=3,∴1−3+9=1−3−3=1−3×3=1−9=−8.故选:A.8.解:∵第①个图案有三角形1个,第②图案有三角形1+3=4个,第③个图案有三角形1+3+4=8个,…∴第n个图案有三角形4−1个(>1时),则第⑦个图中三角形的个数是4×7−1=24个,故选:D.9.解:依题意,满足题意的代数式可以是−8,故答案为:−8(答案不唯一).10.解:∵s互为相反数,是最大的负整数,∴+=0,=−1,∴3+3−4=3+−4=3×0−4×−1=4,故答案为:4.11.解:6+58表示买来6个足球和个篮球一共花多少钱,故答案为:买来6个足球和个篮球一共花多少钱.12.解:∵当=2时,整式B3+B−1的值为−19,∴8+2−1=−19,即8+2=−18,则当=−2时,原式=−8−2−1=18−1=17,故答案为:1713.解:∵绿色珠子每个2元,橙色珠子每个5元,∴小强购买珠子共需花费2+5元.故答案为:2+5.14.解:∵当n为奇数时,−1r1=1;当n为偶数时,−1r1=−1,∴第n个式子是:+−1r1⋅22K1.当=10时,代数式为:10−219故答案为:10−21915.解:∵22−2×1=1+1=12+1,32−2×2=4+1=22+142−2×3=9+1=32+1,52−2×4=16+1=42+1,…,∴第n个等式为:(+1)2−2=2+1.故答案为:(+1)2−2=2+1.16.解:第1次输出的结果为18,第2次输出的结果为12×18=9,第3次输出的结果为9+3=12,第4次输出的结果为12×12=6,第5次输出的结果为12×6=3,第6次输出的结果为3+3=6,第7次输出的结果为12×6=3,…,如此循环,从第4次开始第偶次输出的是6,第奇次输出的是3.第2023次输出的结果为3.故答案为:3.17.解:(1)3−=3×−2−3=−15(2=−3=49(3)−2=−2−32=25(4)B2=−2×32=36(5)2+2=−22+32=4+9=1318.(1)解:小明每季度有零花钱a元,拿出b元捐给希望工程,一个季度有3个月,则平均每月剩余零花钱K3元;(2)解:七年级(1)班共有a名学生,其中有b名男同学,男生的三分之一去参加篮球比赛,则班里还有−13人;(3)解:某种汽车油箱装满后有油Y,每小时耗油Y,行驶了3h,油箱剩余油量−3L;(4)解:某商品原价每件a元,商场打折,现价每件b元,现买3件可以省3−元.19.(1)解:∵某长方形广场的四角都有一块边长为米的正方形草地,若长方形的长为米,宽为米.∴由图可得,阴影部分的面积是(B−42)平方米;(2)解:当=20,=10,=1时,B−42=20×10−4×12=200−4=196(平方米),即阴影部分的面积是196平方米.20.(1)解:根据题意,得三本书的高度为88−86.5=1.5cm,故每本课本的厚度为1.5÷3=0.5cm,故答案为:0.5.(2)解:∵三本书的高度为88−86.5=1.5cm,∴桌子距离地面的高度为86.5−1.5=85cm,∵每本课本的厚度为0.5cm,∴x本的高度为0.5vm,∴距离地面的高度为0.5+85cm.(3)解:根据题意,得x本书顶部距离地面的高度为0.5+85cm,故当=55−13=42时,0.5+85=106cm.21.(1)解:∵11×2=1−12,12×3=12−13,13×4=13−14,14×5=14−15,∴第5个式子是:15×6=15−16;=11r1;第故答案为:15×6=15−16;=1−1r1;(2)解:1111+⋯1=1−2+23++ (2020)=1−12+12−13+13−14+…+12020−12021=1−12021=20202021;(3)解:①11×3+13×5+15×7+1=1313−15+…+199=2=50101.②1−12−16−112−⋯−19900=1−11×212×3−13×4−⋯−199×100=1−212×3+13×4+⋯+99=1−1−1212−13+13−14+⋯+199=1−1−100=1−1+1100=1100.22.(1)解:学校需要定制20份奖品,则选甲供应商需要支付:300+20×3+20×18=720(元),学校需要定制20份奖品,则选乙供应商需要支付:20×6+20×20=520(元).故答案为:720,520.(2)解:选择甲需要支付费用:300+3+18=21+300元;选择乙需要支付费用:当不超过100个时,4.5+20=24.5(元),当超过100个时,6+20×100+20×90%−100=24+200元.故答案为:21+300,24+200.(3)解:当=150时,甲供应商:21+300=21×150+300=3450(元)乙供应商:24+200=24×150+200=3800(元)∵3450<3800∴选择甲供应商比较省钱.。
3.2+代数式的值同步练习2024—2025学年人教版数学七年级上册
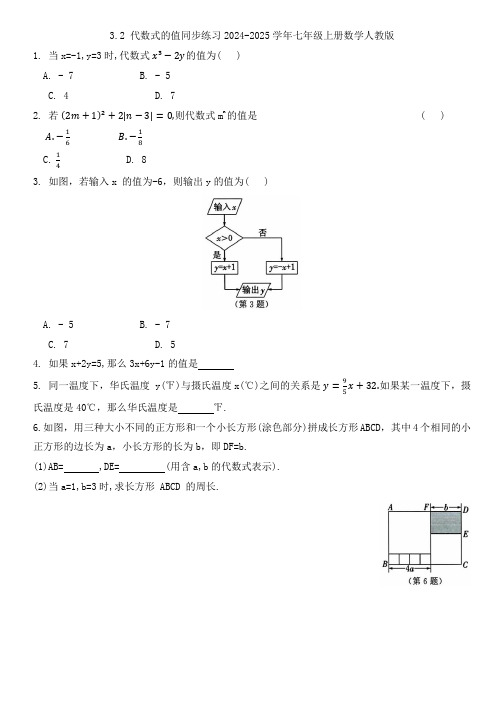
3.2 代数式的值同步练习2024-2025学年七年级上册数学人教版1. 当x=-1,y=3时,代数式x³−2y的值为( )A. - 7B. - 5C. 4D. 72. 若(2m+1)²+2|n−3|=0,则代数式m n的值是 ( )A.−16B.−18C.14D. 83. 如图,若输入x 的值为-6,则输出y的值为( )A. - 5B. - 7C. 7D. 54. 如果x+2y=5,那么3x+6y-1的值是5. 同一温度下,华氏温度y(℉)与摄氏温度x(℃)之间的关系是y=95x+32.如果某一温度下,摄氏温度是40℃,那么华氏温度是℉.6.如图,用三种大小不同的正方形和一个小长方形(涂色部分)拼成长方形ABCD,其中4个相同的小正方形的边长为a,小长方形的长为b,即DF=b.(1)AB= ,DE= (用含a,b的代数式表示).(2)当a=1,b=3时,求长方形 ABCD 的周长.7. 关于代数式1-m² 的值,下列说法中一定正确的是( )A. 比1小B. 比-1大C. 比m²小D. 比-m² 大8. 当x=1时,2ax²−bx的值为-4.当x=-2时,ax²+bx的值为 ( )A. 2B. - 2C. 8D. - 89.设(x−1)³=ax³+bx²+cx+d,则a-b+c-d的值为()A. 2B. 8C. - 2D. - 810. 已知当x=a时,代数式-x+m与代数式x+n 的值都为 8,则代数式 m+n=11. 定义:若a-b=0,则称a 与b 互为“代换数”.若3x²−5与-x+4互为“代换数”,则代数式6x²+2x−5=.12. 火车站、机场等场所都有为旅客提供打包服务的项目.现有一个长、宽、高分别为a cm,b c m,30cm的箱子(其中a>b),准备采用如图①②所示的两种打包方式,所用打包带的总长(不计接头处的长)分别记为l₁,l₂.(1) 求图①中打包带的总长l₁、图②中打包带的总长l₂分别是多少(用含a,b的代数式表示).(2)当a=70,b=50时,计算两种打包方式所用的打包带总长各是多少,并判断哪一种打包方式更节省打包带.13. (1) 根据表中所给a,b的值,分别填写下表中a²−b²和(a+b)(a-b)的值.(3) 请根据你的发现计算:78.35²−21.65².。
七年级数学上册 综合训练 代数式求值(整体代入一)天天练(新版)新人教版

代数式求值学生做题前请先回答以下问题问题1:整体代入的思考方向①求值困难,考虑_____________;②化简________________,对比确定________;③整体代入,化简.问题2:已知代数式2a2+3b=6,求代数式4a2+6b+8的值.①根据2a2+3b=6无法求出a和b的具体值,考虑_____________;②对比已知及所求,考虑把________作为整体;③整体代入,化简,最后结果为______.代数式求值(整体代入一)(人教版)一、单选题(共13道,每道7分)1.把看成一个整体,合并同类项的结果为( )A. B.C. D.2.把看成一个整体,合并同类项的结果为( )A. B.C.D.3.设,把用含的代数式表示并化简的结果为( )A. B.C. D.4.设,把用含的代数式表示并化简的结果为( )A. B.C. D.5.若,则代数式的值为( )A.0B.4C.6D.26.已知,则的值为( )A.-1B.0C.1D.37.若,则代数式的值为( )A.-1B.1C.-5D.58.已知代数式的值是4,则的值为( )A.1B.5C.9D.109.若代数式的值为5,则代数式的值为( )A.1B.9C.11D.2110.已知代数式的值为6,则的值为( )A.24B.18C.12D.911.若,则的值为( )A.0B.2C.5D.812.若,则的值为( )A.7B.-7C.1D.-113.若,则的值为( )A.-59B.-31C.41D.61感谢您的支持,我们会努力把内容做得更好!。
人教版七年级上册数学代数式求值(整体代入一)天天练

人教版七年级上册数学代数式求值(整体代入一)天天练学生做题前请先回答以下问题:问题1:整体代入的思考方向①求值困难,考虑整体代入;②化简代数式,对比确定要代入的整体;③整体代入后化简。
问题2:已知代数式2a²+3b=6,求代数式4a²+6b+8的值。
①根据2a²+3b=6无法求出a和b的具体值,考虑整体代入;②对比已知及所求,把4a²+6b+8作为整体;③整体代入后化简,最后结果为28.代数式求值(整体代入一)(人教版)一、单选题(共13道,每道7分)1.把(a+b)²看成一个整体,合并同类项的结果为() A。
a²+2ab+b²B。
a²-b²C。
2a²+2ab+2b²D。
a²+2b2.把(a-b)²看成一个整体,合并同类项的结果为() A。
a²+2ab+b²B。
a²-b²C。
2a²-2ab+2b²D。
a²-2b3.设a=2,b=3,把2a²-3b化简的结果为()A。
6B。
0C。
3D。
-64.设a=-2,b=1,把2a²+3b化简的结果为()A。
-7B。
11C。
-5D。
75.若a=1,b=2,则2a²+3b的值为() A。
0B。
4C。
6D。
26.已知2a²+3b=6,求a的值。
A。
-1B。
0C。
1D。
37.若2a²+3b=5,则4a²+6b+8的值为() A。
-1B。
1C。
-5D。
58.已知2a²+3b=4,则4a²+6b+8的值为()A。
1B。
5C。
9D。
109.若4a²+6b+8的值为5,则2a²+3b的值为() A。
1B。
9C。
11D。
2110.已知4a²+6b+8的值为6,则2a²+3b的值为() A。
3.2代数式的值拓展练习:代数式的化简求值问题人教版2024—2025学年七年级上册

3.2代数式的值拓展练习:代数式的化简求值问题人教版2024—2025学年七年级上册一、问题引入与归纳1.用具体的数值代替代数式中的字母所得的数值,叫做这个代数式的值。
注:一般来说,代数式的值随着字母的取值的变化而变化。
2.代数式的求值(整体代入法):整体思想就是从问题的整体性质出发,突出对问题的整体结构的分析和改造,发现问题的整体结构特征,善于用“集成”的眼光,把某些式子或图形看成一个整体,把握它们之间的关联,进行有目的、有意识的整体处理。
二、典型例题解析例1.若多项式()x y x x x mx 537852222+--++-的值与x 无关,求])45(2[22m m m m +---的值.变式1.已知多项式(m ﹣3)x |m |﹣2y 3+x 2y ﹣2xy 2是关于x ,y 的四次三项式.(1)求m 的值;(2)当x =,y =﹣1时,求此多项式的值.例2.当代数式532++x x 的值为7时,求代数式2932-+x x 的值.变式2.已知x ﹣2y =3,则代数式6﹣2x +4y 的值为( )A .0B .﹣1C .﹣3D .3变式3.当x =1时,代数式ax 3﹣3bx +4的值是7,则当x =﹣1时,这个代数式的值是( )A .7B .3C .1D .﹣7变式4.若m ﹣n =﹣1,则(m ﹣n )2﹣2m +2n 的值为( )A .﹣1B .1C .2D .3变式5.已知2a +3b =4,则整式﹣4a ﹣6b +1的值是( )A .5B .3C .﹣7D .﹣10变式6.当x =﹣2时,式子3x 2+ax +8的值为16,当x =﹣1时,这个式子的值为( )A .2B .9C .21D .3变式7.如果a 和﹣4b 互为相反数,那么多项式2(b ﹣2a +10)+7(a ﹣2b ﹣3)的值是( )A .﹣3B .﹣1C .1D .3变式8.若x 2﹣4x ﹣1=0,则2x 2﹣8x ﹣(x 2﹣4x )+2020的值为( )A .2021B .2022C .2023D .2024变式9.已知m +n =﹣2,mn =﹣4,则整式2(mn ﹣3m )﹣3(2n ﹣mn )的值为( )A .8B .﹣8C .16D .﹣16变式10.已知a +2b =3,则代数式2(2a ﹣3b )﹣3(a ﹣3b )﹣b 的值为( )A .﹣3B .3C .﹣6D .6变式11.已知代数式m 2+m ﹣1=0,那么代数式2023﹣2m 2﹣2m 的值是( )A .2021B .﹣2021C .2025D .﹣2025 例3.x=-2时,代数式635-++cx bx ax 的值为8,求当x=2时,代数式635-++cx bx ax 的值。
七上数学每日一练:代数式求值练习题及答案_2020年解答题版

七上数学每日一练:代数式求值练习题及答案_2020年解答题版
答案解析答案解析答案解析答案解析答案解析2020年七上数学:数与式_代数式_代数式求值练习题
1.
(2019长春.七上期末) 已知a -2b =3.求9-2a +4b 的值.
考点: 代数式求值;2.
(2019长春.七上期末) 已知,a
、b 互为相反数,c 、d 互为倒数,求
的值.考点: 相反数及有理数的相反数;代数式求值;3.(2019
大庆.七上期中) 如图所示的是用四块完全相同的小长方形拼成的一个“回形”正方形.
(1) 用两个不同的代数式表示图中的阴影部分的面积,你能得到怎样的等式?
(2) 请用乘法公式说明你所得等式是正确的;
(3) 利用(1)中所得等式计算:已知(a+b )=4,ab= ,求a-b .
考点: 列式表示数量关系;代数式求值;4.
(2020.七上期中)
已知a+2是1的平方根,3是b-3的立方根,
的整数部分为c ,求a+b+c 的值考点: 平方根;立方根及开立方;代数式求值;5.
(2019滨州.七上期中) (2017七上·信阳期中) 已知a 、
b 互为相反数,
c 、
d 互为倒数,|m|=3,求
的值.
考点: 相反数及有理数的相反数;绝对值及有理数的绝对值;代数式求值;2020
年七上数学:数与式_代数式_
代数式求值练习题答案
1.
答案:2.
答案:
3.答案:
4.答案:2
5.答案:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学生做题前请先回答以下问题
问题1:整体代入的思考方向:
①求值困难,考虑_____________;
②化简________________,对比确定________;
③整体代入,化简.
问题2:当时,代数式的值是 2 015;则当时,计算代数式
的值.
①根据题意可得,化简得,无法求出p和q的具体值,考虑_____________;
②所求是,化简得,对比已知及所求,考虑把________作为整体;
③整体代入,化简,最后结果为______.
代数式求值(整体代入三)(人教版)
一、单选题(共12道,每道8分)
1.当x=1时,代数式的值为100,则当x=-1时,这个代数式的值为( )
A.-98
B.-99
C.-100
D.98
2.当x=-3时,代数式的值为7,则当x=3时,这个代数式的值为( )
A.-3
B.-7
C.7
D.-17
3.当x=2时,代数式的值为3,则当x=-2时,代数式的值为( )
A.-5
B.0
C.-3
D.-6
4.当时,代数式的值为6,则当时,代数式
的值为( )
A.6
B.-22
C.-14
D.-2
5.当x=1时,代数式的值为3,则当x=-1时,代数式的值为( )
A.2
B.1
C.9
D.7
6.当x=1时,代数式的值为7,则当x=-1时,这个代数式的值为( )
A.7
B.1
C.3
D.-7
7.当x=-1时,代数式的值为5,则当x=1时,代数式的值为( )
A.2
B.-2
C.10
D.-10
8.若,则的值为( )
A.1
B.-1
C.5
D.-5
9.若,则的值为( )
A.5
B.6
C.11
D.12
10.若,则的值为( )
A. B.1
C. D.
11.若,,则代数式的值为( )
A.-3
B.
C. D.
12.若,,则代数式的值为( )
A.11
B.4
C.9
D.6。
