巧借Excel在AutoCAD中设计凸轮轮廓曲线
巧借Excel在AutoCAD中设计凸轮轮廓曲线

巧借Excel在AutoCAD中设计凸轮轮廓曲线摘要:本文介绍一种借用EXCEL应用程序来计算并保存数据,并与CAD精确绘图巧妙地结合,设计凸轮轮廓曲线的方法,该方法也可用于其它二维或三维曲线的绘制中。
论文毕业论文关键词:凸轮轮廓曲线 AutoCAD 图解法1.问题的提出本文以设计二维凸轮轮廓曲线为例,介绍一种一般操作者就能方便做到的,借用EXCEL应用程序来计算并保存数据,并与AutoCAD精确绘图巧妙地结合,绘制二维或三维非规则曲线的方法,以供大家参考。
2.概述在凸轮机构中,最常用的就是平面凸轮机构,要设计平面凸轮的轮廓曲线。
设计方法通常有图解法和解析法两种。
作图法简便易行、直观,作图误差较大,精度较低,适用于低速对从动件运动规律要求不高的一般精度凸轮设计;对于精度要求高的高速凸轮、靠模凸轮等,必须用解析法列出凸轮的轮廓曲线方程,用计算机辅助设计精确地设计凸轮机构。
我们沿用原有的图解法思路,使用CAD作为工具,两者的联合运用,能产生意想不到的更简单、直接、方便的处理方法。
在这种基于AutoCAD的图解法基础上,利用AutoCAD与其它文档交换信息和数据的功能,对于一些计算量较大输入点较多的图形,与EXCEL应用程序相结合,使作图更加简便快捷。
如设计下面的偏置滚子从动件盘形凸轮轮廓曲线,已知偏距e=10㎜,基圆半径r0=40㎜,行程h=25㎜,滚子半径rT=10㎜。
凸轮以角速度ω顺时针转动,从动件的运动规律为:运动阶段1,推程Φ=180°、凸轮转角φ(°)为0~180,运动形式:等加速-等减速运动,运动方程方程:s=(2h/Φ2)φ2=(2*25/1802)φ(0≤φ≤90)或s=h-2h(Φ-φ)2/Φ2=25-2*25*(180-φ)2/1802(90≤φ≤180)运动阶段2,远休止ΦS=30°、凸轮转角φ(°)为180~210,运动形式:静止不动,运动方程方程: s=h=25(180≤φ≤210)运动阶段3,回程Φ=90°、凸轮转角φ(°)为210~300,运动形式:等加速-等减速运动,运动方程方程: s= h-(2h/Φ’2)/φ’2=25-(2*25/180)2/(φ-210)2(180≤φ≤210)或s=2h(Φ’-φ’)2/Φ’2=2*25*(90-(φ-210))2/902(180≤φ≤210)运动阶段4,远休止ΦS=60°、凸轮转角φ(°)为300~360,运动形式:静止不动,运动方程方程: s=0(300≤φ≤360)3、解题思路要使基于CAD技术的图解法充分发挥软件精确、高效绘图的作用,就要首先改进原来的作图方法。
巧用Excel在AutoCAD中精确绘制公式曲线曲面

图 1 渐开线形成果原理图 图 2 AutoCAD 中得到的渐开线齿轮轮廓
第二步打开 AutoCAD ,绘制齿轮的齿顶圆 、分度圆 、齿根圆 ,并点击工具栏“Spline”样条曲线 ,把 Excel 电 子表格中极坐标列数据复制到 AutoCAD 命令行中 ,即可生成一条齿轮渐开线 ,再经过镜像 、旋转 、阵列等命 令得到一个完整的渐开线齿轮轮廓如图 2 所示. 此渐开线齿轮齿廓可在 AutoCAD 环境下对它进行拉伸形成齿轮三维立体模型[324 ] . 也可对它进行其它 的分析和计算等.
向径/ mm 46. 984 6 46. 985 1 46. 986 6 46. 988 9 46. 992 4 46. 996 8 47. 002 1 47. 008 4 47. 015 6 47. 023 8 47. 033 1 47. 043 2 47. 054 4 47. 066 5 47. 079 6 47. 093 7
顶圆半径
ra
=
m(z
+
2
h
3 a
)
/
2
=
52
,
基圆半径
rb =
rcosα =
m zcosα/ 2 = 46. 98 ( r 为分度圆半径) ,齿顶圆压力角αa = arc2
cos ( rb/ ra) = 25. 37°. 为了得到足够长度的渐开线 , 这里取最
大压力角 αmax = 26°;根据精度要求在渐开线上取分段数 ,这
第 20 卷 第 2 期 2009 年 6 月
广 西 工 学 院 学 报
Vol120 No12
J OU RNAL OF GUAN GXI UN IV ERSIT Y OF TECHNOLO GY
利用CAD画凸轮机构
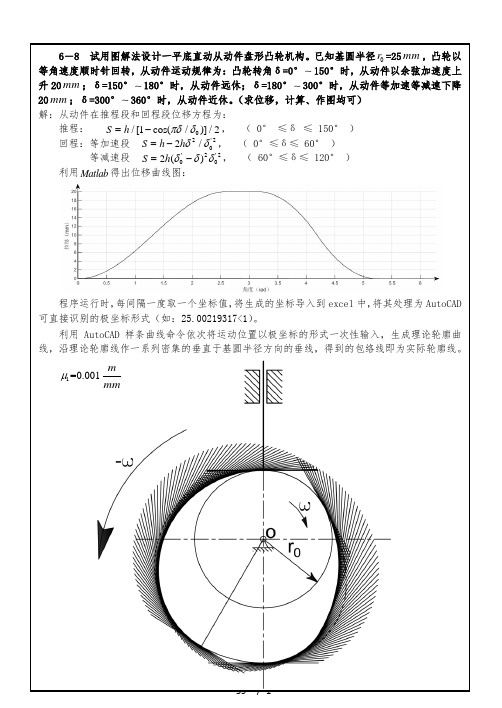
利用CAD 画凸轮机构 - 59 - / 1
6-8 试用图解法设计一平底直动从动件盘形凸轮机构。
已知基圆半径0r =25mm ,凸轮以等角速度顺时针回转,从动件运动规律为:凸轮转角δ=0°150°时,从动件以余弦加速度上升20mm ;δ=150°180°时,从动件远休;δ=180°300°时,从动件等加速等减速下降20mm ;δ=300°360°时,从动件近休。
(求位移,计算、作图均可) 解:从动件在推程段和回程段位移方程为: 推程: 0/[1cos(/)]/2S h πδδ=-, ( 0° ≤δ ≤ 150° ) 回程:等加速段 2'202/S h h δδ=-, ( 0°≤δ≤ 60° ) 等减速段 '2'2002()S h δδδ=-, ( 60°≤δ≤ 120° ) 利用Matlab 得出位移曲线图: 程序运行时,每间隔一度取一个坐标值,将生成的坐标导入到excel 中,将其处理为AutoCAD 可直接识别的极坐标形式(如:25.00219317<1)。
利用AutoCAD 样条曲线命令依次将运动位置以极坐标的形式一次性输入,生成理论轮廓曲线,沿理论轮廓线作一系列密集的垂直于基圆半径方向的垂线,得到的包络线即为实际轮廓线。
1=0.001μm mm。
EXCEL和CAD结合自动生成曲线的简单方法

可能很多人都困惑如何能方便地在CAD中划曲线。
下面这个方法是本人毕业设计时琢磨出来了,划型线非常方便。
希望大家广泛传播,减轻大家划曲线的工作量。
假如3个点的坐标为 1,2 3,4 5,6
在excel 单元格中
A B C D E
spline 1,2 3,4 5,6 ( 输入2个空格)
复制整行,粘贴到CAD命令栏内,曲线就自动生成了。
(spline 也可以换成_spline)
多个曲线时,如上所示,下一行在EXCEL中也这样排列,然后把几行一起复制粘贴到CAD 命令栏中,几条曲线就自动生成了。
单元格中的点,比如"1,2" 可以用 EXCEL 文字结合命令组合,如下所示:
A B C
1 1
2 (=A1&","&B1)
这样可以结合成点坐标,然后按照上面提到的spline 输入格式可以自动生成曲线。
这个原理其实就是利用CAD本身的输入规则,在EXCEL中排列好,粘贴到CAD命令栏,就相当于输入数据,最后的空格也是和在CAD中
画曲线后两端的自动取曲率是一样的。
一种凸轮廓线的设计方法

一种凸轮廓线的设计方法
方法一:使用CAD软件来设计凸轮廓线
1、选择CAD软件,打开新的工程,创建一个新的图形;
2、根据规定的要求,在图形中绘制凸轮廓线,可以直接使用绘图工具进行绘制,也可以使用数学函数来生成凸轮廓线;
3、如果需要对凸轮廓线进行修改,可以使用CAD软件中的编辑工具来修改;
4、保存凸轮廓线,并将其导出为可以使用的文件格式。
方法二:使用绘图工具来设计凸轮廓线
1、选择一款绘图工具,打开新的工程,创建一个新的图形;
2、根据规定的要求,使用绘图工具在图形中绘制凸轮廓线;
3、如果需要对凸轮廓线进行修改,可以使用绘图工具中的编辑工具来修改;
4、保存凸轮廓线,并将其导出为可以使用的文件格式。
CAD精确绘制盘形凸轮曲线的方法

CAD精确绘制盘形凸轮曲线的方法2003年6月第16卷第2期十堰职业技术学院JournalofShiyanTechnicalInstituteJune,2003V oI.16NO.2CAD精确绘制盘形凸轮曲线的方法鲁春发,莫足琴(十堰职业技术学院计算机工程系,湖北十堰442000)[摘要]通过对凸轮轮廓曲线的几何分析,运用应用程序Excel和AutoCAD精确地绘制出了凸轮的轮廓曲线,解决了AutoCAD2000中不能画凸轮的问题,使AutoCAD2000的功能得到了扩展.[关键词]Excel;CAD;凸轮;轮廓曲线[中图分类号]TH122[文献标识码]A[文章编号]1008-4738(2003)02-0060-02l引言我们在设计盘形凸轮机构时,通常采用图解法或解析法进行凸轮轮廓曲线的设计,图解法作图误差较大,精度低,而传统的解析法又比较繁琐,现在,计算机的普及为我们精确地绘制盘形凸轮机构凸轮的轮廓曲线提供了便捷工具.我们可采用常用的应用程序Excel和AutoCAD绘制出盘形凸轮的轮廓曲线.2尖顶从动件盘形凸轮轮廓曲线上点的直角坐标的确定方法如图1所示,当凸轮逆时针转动,从动件的尖顶从岛点转到B点转过角度时,尖顶从动件盘形凸轮轮廓曲线上B点的直角坐标,y^可根据盘形凸轮的回转中心0点的坐标(,),基圆的半径凡,偏心距e(右偏,图中OA的长度)及从动杆的运动规律F()来确定(=Bo0C).由图中我们可知:珈._,x图1=Xo+c+BC×sin(BCE)y^=yd+YC+BC×c∞(LBCE)其中:BC=F(),LBCE=LDCE—LDCB=一arcsin(e/Rb)(如从动杆为左偏,则将式中的"一"号改为"+"号即可),Xc=凡×sin(),Yc=R6×C05().所以.尖顶从动件盘形凸轮轮廓曲线上曰点的直角坐标可表示为:五=+R^×sin()+F()×sin(一arcsin(e/Rb))Yb=y0+R^×C05()+F()×C05(一arcsin(e/Rb))3软件应用3.1用Excel计算出尖顶从动件盘形凸轮轮廓曲线上B点的直角坐标打开一张Excel工作表将A列置为凸轮转动的角度,可每5.算一个值(此值设置得愈小,算出的坐标值愈多,则描绘出的凸轮轮廓曲线愈精确,当然花的时间也相应多些),共72个值,Al输人标题,A2,A3分别输入0,5二值后同时选中A2,A3两单元格,将鼠标指向选中的单元格右下角的十字光标,按住鼠标左键往下拖动到A73单元格后松开鼠标即输入完所需的数据;将B列置为F(),B1输入标题F(),从JB2开始按从动杆的运动规律分段输人运动规律函数,将鼠标指向输人函数的单元格右下角的十字光标,按住鼠标左键分段往下拖动即计算完并显示出所需的数据(下面各列数据的计算和显示均用此法);将C列置为,将D列置为,为了坐标值不出现负值以方便绘图时点的输人,可将坐标,yD设置得稍微大些;将E列置为基圆半径R,将F列置为偏心距e;将G列置为偏角LBCD,LBCD=arcsin(e/Rb)=arcsin(F/E);将H列置为偏心距以=Xo+R^×sin()+F()×sin(一arcsin(e/瞄))=C+E×sin(3.1415926×A/180)+B×sin(3.1415926×A/180一G)将,列置为偏心距y^y^=ro+R^×cos()+F()×C05(一arcsin(e/瞄))=D+E×C05(3.1415926×A/180)+B×C05(3.1415926×A/180一G)直接用已知条件给出的数值代替表中的符号.Excel工作表就能快速准确地显示出尖顶从动件盘形凸轮轮廓曲线[收稿日期]2002—11-30[作者简介]鲁春发(1964一),男,十堰职业技术学院计算机工程系党总支书记,高级实验师;莫足琴(1973一),女,十堰职业技术学院计算机工程系助理实验师.一6o一CAD精确绘制盘形凸轮曲线的方法上各点的直角坐标.此方法还有一个好处是在设计不同的凸轮轮廓曲线时只需将从动杆的运动规律函数F('p)改变一下,其它地方均无需改动,即可得出另一个尖顶从动件盘形凸轮轮廓曲线上各点的直角坐标值.3.2用AutoCAD绘制凸轮轮廓曲线打开AutoCAD应用程序,输人"样条曲线"命令,在命令行中输人用Excel工作表算出的值,输完后即得到了尖顶从动件盘形凸轮轮廓曲线.如果是滚子从动件盘形凸轮,则先按上述方法绘制出尖顶从动件盘形凸轮轮廓曲线后,利用AutoCAD应用程序中的偏移工具进行绘制,方法是:1)输人"偏移"命令;2)给出偏移的距离(即滚子的半径);3)选择要偏移的实体(即尖顶从动件盘形凸轮轮廓曲线);4)指定偏移的方位(用鼠标点击尖顶从动件盘形凸轮轮廓曲线的内侧即可).此时CAD自动绘出滚子从动件盘形凸轮的轮廓曲线.4应用举例例如:设计一偏置滚子移动从动件盘形凸轮机构.已知凸轮的基圆半径为r5:40rata,滚子半径I"t=12mm,从动件偏在凸轮转动中心0的右边,其偏距e=18mm.凸轮以逆时针方向回转,当凸轮转过.=180.时,从动件按余弦加速度规律上升36ram;当凸轮再转过=20.时,从动件停留在最高位置不动;当凸轮又转过,=120.时,从动件按等加速等减速运动规律退回原处;当凸轮再转过轨=4o.时,从动件停留在最低位置不动.设计这一凸轮轮廓曲线时,首先列出凸轮理论轮廓各段曲线上点的坐标方程:0.~180.:F()=36/2×(1一cos~o)180.一200.:,(p)=36200.一320.:分等加速和等减速两部分等加速部分(200.~260.):F(p)=36—36X2/120X(p一200)等减速部分(260.一320.):F(p)=36X2/120X(320一妒)320.一360.:F(p)=0将上述函数表达式分段代人设计好的F~eel工作表,同时用已知条件代替表格中的符号,Excel工作表即显示出各点的直角坐标(见图2,此处仅显示部分坐标点的值).为方便点的输人,可用"格式"菜单中的"单元格"选项将H列和I 列单元格数值的小数位设置成一位,使坐标值保留一位小数.打开AutoCAD应用程序,输人"样条曲线"命令,在命令行分别输人72个点的直角坐标值,即得出凸轮的理论轮廓曲线.强萄需麓甏%鐾…墼糊黼瞄圄鲴..一1.2蠲镕目目嘲r(由)-x?'Y●,Rb'B,膏轴Yho0.0O0.8o80.408O.'','58O,0.t2O.O:50.06880804OI8O.4''7'S83.5l19.9O.273808o40I80.4''々'586.9ll9.70.6l3808O40I8O.4''7'590.2lI9.21.0868O8o哇0I8O.4''7'S93.6ll8.7251.6e080曩0l8O.4667'S96.7.嘉蠹囊02.4l0o8O哇0l8O.4''76510o.1l7.353,.8O.4''76S1O3.4ll6.0404.2O.6'7'SlO6.7lI4.7鬓.27280I0.06'7'5lo9.9ll3.3糍5o6.8t)_辱o,l80.4''7'SllS.2ll1.6 墨嚣s5y.6r,6808ol18O.'67'Sll6.tlO9.76().18O.66了'5ll9.6lO7.S651.39380l8O.4''7'5I22.7lO5.1图输人"偏移"命令,在命令行输人滚子的半径l2,然后用鼠标点击理论轮廓曲线的内侧,即得到了要设计的偏置滚子移动从动件盘形凸轮机构凸轮的实际轮廓曲线(见图3).5小结目前中还没有画凸轮轮廓曲线的功能,采用绘制机械图时还不能准确地画出凸轮轮廓曲线,用上述方法不仅可绘制出凸轮轮廓曲线,而且非常准确,特别是对滚子从动件,直接运用图中的"偏移"命令,快速准确,省去了手工绘图时必须画圆的包络线的麻烦.另外用计算尖顶从动件盘形凸轮轮廓曲线上点的直角坐标时,一旦设置好后可保存在电脑中,以后再设计凸轮轮廓曲线时只需将其调出,将运动规律函数及其它参数修改一下即可,对经常从事机械设计者非常适用.咖CADLU一.一(..,,,)c鲫applyap.c舢●:;;curve一6l一¨一秘-.|断一。
基于AutoCAD的凸轮外形轮廓曲线设计

0
1
00 ■
【
s :
“ 3 0 ・0
_ ; 々
.
} } ’ 0… ∞
一
…
{ ∞
) 0
。
一 0
0, ∞…
c
L
t:
¨
∞
… {
】 J
《
j , ‘ 1
0
s 4 ∞
l
≯
0{ 0 i
‘ e { } i … { …
1 々
-
“ 。 ”
一 ^ … 1^ 一 } £ ∞
0
L_ ' f
, } , l
{ ’ 0 I J 0 【
§
《
’ 【
{
“0 0 0 ∞
t
-
L
1_ _ …
f
一
…Leabharlann n ,_
~ … %
1引言
’
凸轮 机 构 是 机 械 传 动 中 的一 种 常 用机 根 据 凸轮 精 度 要 求 可 将 凸轮 转 角 分 成 构 , 自动 化 和 半 自动 化 机 械 中 应 用 非 常 , 分 , 取 值越 大 , 廓 曲线越 精 确 。 本例 在 l 等 n 轮 广 泛 。 根据 使 用 要 求 确 定 了 凸轮 机 构 的类 中取 , 1 0 利 用 E c l l O, = x e 的快 速 制表 和 数据 型 、基 本 参 数 以 及 从 动件 运 动 规 律 后 , 即 计 算 功 能 完 成坐 标 的 计 算 , 体 如 下 : 具 可 进 行 凸轮 外 形 轮 廓 曲线 的 设 计 , 计 凸 设 () E c l A 列第 一 行 A1 1在 x e 中 中输 入 轮 外 形 轮 廓 曲 线 的 方 法 有 作 图 法 和 解 析 “ 角 ( ” A2中输 入 “ ” 由于 推 程 角 转 p , 0, 法 , 者 所 依 据 的 设 计 原 理 基 本 相 同 。 作 两 9 。 ,=10所 以 A 0 / 0 I 2中输 入 “ .” 利用 09 , 图法 简便 、直 观 , 作 图误 差 较 大 , 以 获 但 难 E cl x e 的等差数 列 快速 输入 法 , 可以快 速在 得 凸轮 外 形 轮 廓 曲线 上 各 点 的 精 确 坐 标 , A 列 依次 生 成 0 0 , 长 为 0 9 等差 ~9 。 步 .的 所 以 按 照 作 图法 所 得 轮 廓 数 据 加 工 的 凸轮
应用EXCEL在CAD中绘制曲线

应用EXCEL在CAD中绘制曲线随着计算机技术的不断发展和CAD软件的不断完善,现在在CAD中绘制曲线已经不再像是几十年前那样需要手动勾画了。
使用软件可以完成绘制所有类型的曲线,让绘制曲线的过程更加快速简便。
本文将从应用EXCEL在CAD中绘制曲线入手,为大家详细介绍如何利用软件这一工具在CAD中绘制高质量的曲线。
一、前置知识在学习如何利用EXCEL绘制曲线前,我们需要先了解一些基本的CAD曲线绘制知识,以便更好地运用EXCEL工具。
1.1 CAD中的曲线类型1.1.1 直线直线是CAD中最简单的曲线,可以通过给定两个点来绘制。
直线子命令可以通过选择“直线”工具栏上的图标或输入“line”来启动。
在CAD中,直线通常是由图形的边缘或边缘之间组成的。
1.1.2 圆圆是CAD中最基本的弧线。
绘制圆时,可以将其中心点和半径指定到指定的位置,也可以使用两个点定义其直径。
圆子命令可以通过选择“圆”工具栏上的图标或输入“circle”来启动。
1.1.3 椭圆椭圆是由半长轴和半短轴决定的圆形变体。
与圆不同,椭圆在CAD中无法通过设置半径来确定。
可以使用两个点或关键点、与两个轴线相交的点、中心点和两个轴线的长度来创建椭圆。
椭圆子命令可以通过选择“椭圆”工具栏上的图标或输入“ellipse”来启动。
1.1.4 弧弧是由圆弧的圆心、半径和起始和结束角度定义的。
可以通过向圆弧添加关键点来创建更复杂的弧。
弧度量采用角度制方式,可以通过键入一个角度度数、长度或一个关键点位置来创建。
圆弧子命令可以通过选择“圆弧”工具栏上的图标或输入“arc”来启动。
1.1.5 曲线CAD中的曲线通常是由控制点定义的NURBS曲线。
控制点是影响曲线形状的点,曲线从一个控制点移动到另一个控制点。
曲线的精度通常通过指定控制点的数量来控制。
例如,如果只有少量控制点,则曲线将是基本的弧线。
如果有非常多的控制点,曲线可以非常复杂。
在CAD中,曲线子命令可以通过选择“曲线”工具栏上的图标或输入“spline”来启动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
巧借Excel在AutoCAD中设计凸轮轮廓
曲线
摘要:本文介绍一种借用EXCEL应用程序来计算并保存数据,并与CAD精确绘图巧妙地结合,设计凸轮轮廓曲线的方法,该方法也可用于其它二
维或三维曲线的绘制中。
论文毕业论文关键词:凸轮轮廓曲
线 AutoCAD 图解法1.问题的提出本文以设计二维凸轮轮廓曲线为例,
介绍一种一般操作者就能方便做到的,借用EXCEL应用程序来计算并保存数据,并与AutoCAD精确绘图巧妙地结合,绘制二维或三维非规则曲线的方法,以供大家参考。
2.概述在凸轮机构中,最常用的就是平面凸轮机构,要设计平面凸轮的轮廓曲线。
设计方法通常有图解法和解析法两种。
作图法简便易行、直观,作图误差较大,精度较低,适用于低速对从动件运动规律要求不高的一般精度凸轮设计;对于精度要求高的高速凸轮、靠模凸轮等,必须用解析法列出凸轮的轮廓曲线方程,用计算机辅助设计精确地设计凸轮机构。
我们沿用原有的图解法思路,使用CAD作为工具,两者的联合运用,能产生意想不到的更简单、直接、方便的处理方法。
在这种基于AutoCAD的图解法基础上,利用AutoCAD与其它文档交换信息和数据的功能,对于一些计算量较大输入点较多的图形,与EXCEL应用程序相结合,使作图更加简便快捷。
如设计下面的偏置滚子从动件盘形凸轮轮廓曲线,已知偏距e=10㎜,基圆半径r0=40㎜,行程h=25㎜,滚子半径rT=10㎜。
凸轮以角速度ω顺时针转动,从动件的运动规
律为:运动阶段1,推程Φ=180°、凸轮转角φ(°)为0~180,运动形式:等加速-等减速运动,运动方程方程:s=(2h/Φ2)φ2=(2*25/1802)φ
(0≤φ≤90)或s=h-2h(Φ-φ)2/Φ2=25-2*25*(180-
φ)2/1802(90≤φ≤180)运动阶段2,远休止ΦS=30°、凸轮转角φ(°)为180~210,运动形式:静止不动,运动方程方程: s=h=25
(180≤φ≤210)运动阶段3,回程Φ=90°、凸轮转角φ(°)为210~300,运动形式:等加速-等减速运动,运动方程方程: s= h-(2h/Φ’2)/φ’2=25-(2*25/180)2/(φ-210)2(180≤φ≤210)或s=2h(Φ’-
φ’)2/Φ’2=2*25*(90-(φ-210))2/902(180≤φ≤210)运动阶段4,远休
止ΦS=60°、凸轮转角φ(°)为300~360,运动形式:静止不动,运动方程
方程: s=0(300≤φ≤360)3、解题思路要使基于CAD技术的图解法充分发挥软件精确、高效绘图的作用,就要首先改进原来的作图方法。
图解法和解析法其本质完全相同,只是求解手段、求解过程不同,这里我们不用作图法确定曲线上点的方法,而是直接利用解析法里凸轮轮廓曲线的极坐标方程,求出凸轮轮廓曲线上若干个点(越多曲线越准确)的极坐标值(ρ,θ),再用spline (绘制样条曲线)命令,输入各点坐标值,作出凸轮的轮廓曲线。
如果是滚子从动件,得到理论轮廓线后,直接用offset(偏移)命令,输入滚子半径即可得到凸轮的实际轮廓曲线。
这里有两个问题需要解决。
首先是计算,为了得到更为准确的曲线,取点要尽量多,求这些点的极坐标值是一个很大的计算量,如何计算,计算后数据保存在哪里?其次是绘制曲线时点的坐标的输入,如果一个个
输入要输二十多次,非常费时而且很容易出错。
4、解决办法4.1数据的计算EXCEL是我们大家比较熟悉的应用程序,可以执行计算、分析信息并管理表格等,我们就用它来进行计算和保存数据。
按从动件的运动规律所给数据,由于凸轮轮廓曲线要对应推程运动角(Φ)、远休止角(ΦS)、回程运动角(Φ’)、近休止角(Φ’S)四个部分。
根据运动规律,推程运动角(Φ)和回程运动角(Φ’)对应的是不规则的二维曲线,远休止角(ΦS)和近休止角(Φ’S)对应的是正圆弧,我们都用SPLINE命令绘制。
为使曲线尽量准确,各段都要均分为若干份。
推程运动角(Φ)和回程运动角(Φ’)因为对应角都较大各分成8分共16个点;远休止角(ΦS)较小分成2份共,近休止角(Φ’S)分成4份共6个点,合计共取22个点。
先把这些数据输入EXCEL表格,按从动件的运动规律所给数据计算各点对应于基圆的位移值S、运动过程中通过各分点的导路方向与基圆半径的夹角β及起始位置点B0对应的夹角β0,凸轮轮廓曲线上各点对应极半径ρ和夹角θ等,最后才能合成各点的极坐标值。
这个过程计算量比较大,但无论采用何种方法设计,初始数据的取得都要经过计算,计算过程中所用公式及各参数的含义请参阅相关资料,因篇幅有限,这里不多作说明。
4.2极坐标的合成如图2所示,经过计算得到极半径ρ和夹角θ的值后,要合并成极坐标(ρ<θ)的形式。
使用连接运算符即“与”号(&)连接F列和G列两个数字串,两数字串中间还要用表示角度的符号“<”连接,操作方法如下:在H2单元格内输入公式“=A2&“<”&B2”,并按下Enter键,H2中就出现了一对极坐标值,再用鼠标拖动的方法将H2的的公式进行复制,就可以得到一组极坐标值。
这就是我们需要的凸轮轮廓曲线上各点的极坐标,将数据保存备用。
如果引号中间括起的是“,”号,就可以得到直角坐标的形式,在以直角坐标绘制曲线时可用。
以此类推开去,这样合并或连接,可得到任何你需要的数据。
4.3数据的输入,理论轮廓曲线的形成选出凸轮轮廓曲线上的点的极坐标值,即图中H列数据,将其复制到剪贴板上,可用Excel中的复制按钮或者直接按下
Ctrl+C键来完成此工作。
打开AutoCAD,在命令行处键入spline(绘制样条曲线)命令,出现提示:"输入第一点或[对象(O)]",在此位置处点击鼠标右键,从弹出的菜单中选择“粘贴”菜单项,这样在Excel中的极坐标值就传送到了AutoCAD中,并自动连接成曲线,单击鼠标右键或按下Enter键,取消继续画线状态,你需要的曲线就立刻出现在你面前,既简捷又不会出错,比一次次输入点的坐标值不知要快上了多少倍。
4.4实际轮廓曲线的形成如果是尖顶从动件,上面的曲线即为所求凸轮的轮廓曲线。
对于滚子从动件,我们得到理论轮廓线后,直接用offset(偏移)命令,出现提示:“指定偏移距离或[通过(T)]<通过>:”,输入滚子半径rT=10㎜,选择轮廓曲线作为偏移对象,指定内侧为偏移方向,即可得到凸轮的实际轮廓曲线。
4.5其它需要解决的问题如果需要表示曲线及基圆上各分点等,可以依照上述方法推广,在EXCEL表格中得出各分点的极坐标,在CAD中设置点样式用绘制点的命令一次输入各点坐标值即可。
凸轮的基圆、偏距圆等,用相应命令绘制,非常简单,不必多说。
该方法还可推广到绘制其它二维或三维曲线。
如渐开线、阿基米德螺旋线、摆线等二维曲线。
三维曲线如绘制三维螺旋线也属此类问题,可以先在EXCEL表格中得到螺旋线的柱面坐标值如图3所示,这用上面的方法也不难得到,然后再用spline命令将在EXCEL表格中得到的各分点坐标值粘贴过来就可完成三维螺旋线的绘制,如果需要多圈,再复制或阵列即可。
上述方法方便快捷,简单易行,不需任何编程,对.于不太熟悉CAD二次开发的用户是一种快速绘制二维或
三维曲线的好办法。
参考文献:[1]陈立德机械设计基础 (第2版) 北京高等教育出版社[M] 2004.7 62-72[2]张帆等 AutoCAD辅助设计专家北京清华大学出版社[M] 2005.2 366-369[3]王有良、唐跃
刚 AutoCAD开发与应用[J] 山东大学学报 2005,。
