神奇的数字--从数字赏数学之美共36页
浅谈数学之美

浅谈数学之美【摘要】数学美是自然美的客观反映,是科学美的核心。
“那里有数学,哪里就有美”,数学美不是什么虚无缥缈、不可捉摸的东西,而是有其确定的客观内容.数学美的内容是丰富的,如数学概念的简单性、统一性,结构系统的协调性、对称性,数学命题与数学模型的概括性、典型性和普遍性,还有数学中的奇异性等,都是数学美的具体内容。
本文主要围绕数学美的三个特征:简洁性、和谐性和奇异性进行阐述。
【关键词】数学,数学美,美学特征数学美的表现形式是多种多样的,从外在形象上看:她有体系之美、概念之美、公式之美;从思维方式上看:她有简约之美、无限之美、抽象之美、类比之美;从美学原理上看:她有对称之美、和谐之美、奇异之美等.此外,数学还有着完美的符号语言、特有的抽象艺术、严密的逻辑体系、永恒的创新动力等特点。
但这些都离不开数学美的三大特征,即:简洁性、和谐性和奇异性。
1简洁性是数学美的首要特点爱因斯坦说:“美,本质上终究是简单性",“只有既朴实清秀,又底蕴深厚,才称得上至美”。
简洁本身就是一种美,而数学的首要特点在于它的简洁性.数学中的基本概念、理论和公式所呈现的简单性就是一种实实在在的简洁美。
数学家莫德尔说过:“在数学里美的各个属性中,首先要推崇的大概是简单性了”.数学的简洁性在人们生活中屡见不鲜:钱币只须有一分、二分、五分、一角、二角、五角、一元、二元、五元、十元……就可简单的构成任何数目的款项;圆的周长公式:C=2πR,就是“简洁美”的典范,它概括了所有圆形的共同特性;把一亿写成l08,把千万分之一写成10—7;二进制在计算机领域的应用……化繁为简,化难为易,力求简洁、直观。
数学不仅仅是在运算上要求这样,论证说明也更是如此。
显然,数学的公式与公理就是简洁美的最佳证据之一.1.1简洁性之一:符号美实现数学的简洁性的重要手段是使用了数学符号.符号对于数学的发展来讲是极为重要的,它可使人们摆脱数学自身的抽象与约束,集中精力于主要环节,没有符号去表示数及其运算,数学的发展是不可想象的。
数学之美论文2000数学之美论文

数学之美论文2000数学之美论文数学之美论文篇一人类对数学的认识最早是从自然数开始的。
这看似极普通的自然数里面,其实就埋藏着数不尽的奇珍异宝。
古希腊的毕达哥拉斯学派对自然数很有研究,当他们将这数不尽的奇珍异宝的一部分挖掘出来并呈现于人类面前时,人们就为这数的美震撼了。
其实,“哪里有数学,哪里就有美”,这是古代哲学家对数学美的一个高度评价。
一、简洁美数学中的概念许许多多,但每个概念都是以最精炼、最概括的语言给出的。
如在《图的初步知识》教学中,可以先让学生去探究过两点的直线有多少条然后再让学生用自己的语言来概括这个结论,最后教师再给出“两点确定一条直线”,短短的一句话,简练严谨,内涵丰富,充分让学生体会了数学定理的简洁之美;又如九年级上圆的定义“圆是到定点的距离等于定长的点的集合”,若无“集合”则形成了点,构不成圆,一字之差则情况相差万里,充分体现了数学概念的简洁美。
欧拉给出的公式:V-E+F=2堪称“简单美”的典范。
世间的多面体有多少没有人能说清楚。
但它们的顶点数V、棱数E、面数F,都必须服从欧拉给出的公式,一个如此简单的公式,概括了无数种多面体的共同特性,能不令人惊叹不已在数学中,像欧拉公式这样形式简洁、内容深刻、作用很大的定理还有许多。
二、和谐美古希腊数学家毕达哥拉斯有一句至理名言:“凡是美的东西都具有共同的特性,这就是部分与部分、部分与整体之间的和谐性。
”三、对称美毕达哥拉斯学派认为,一切空间图形中,最美的是球形;一切平面图形中,最美的是圆形。
圆是中心对称图形――圆心是它的对称中心,圆也是轴对称图形――任何一条直径都是它的对称轴。
对称美的形式很多,对称的这种美也不只是数学家独自欣赏的,人们对于对称美的追求是自然的、朴素的。
如我们喜爱的对数螺线、雪花,知道它的一部分,就可以知道它的全部。
数学美学中的对称美并不局限于客观事物外形的对称。
它着重追求的是数学对象乃至整个数学体系的合理,匀称与协调。
数学概念,数学公式,数学运算,数学方程式,数学结论甚至数学方法中,都蕴含着奇妙的对称性。
数学中的美

数学中美的欣赏数学美是一种蕴涵的美,它需要从深处去挖掘。
关于数学美的内容很多,本文是为了从浅层阐述数学的美,让学生初步感受数学中美的存在,所以本文就主要从数学美的概念、数学美与其它美的区别、数学美的内容和它在数学教育中的体现这几个方面作以下的阐述。
一、数学美的概念美是人类创造性实践活动的产物,是人类本质力量的感性显现。
通常我们所说的美以自然美、社会美以及在此基础上的艺术美、科学美的形式存在。
数学美是自然美的客观反映,是科学美的核心。
简言之数学美就是数学中奇妙的有规律的让人愉悦的美的东西。
历史上许多学者、数学家对数学美从不同的侧面作过生动的阐述。
普洛克拉斯早就断言:“哪里有数,哪里就有美。
”亚里士多德也曾讲过:“虽然数学没有明显地提到善和美,但善和美也不能和数学完全分离。
因为美的主要形式家是“秩序、匀称和确定性”,这些正是数学研究的原则。
”徐利治教授说:“作为科学语言的数学,具有一般语言文字与艺术所共有的美的特点,即数学在其内容结构上和方法上也都具有自身的某种美,既所谓数学美。
数学美的含义是丰富的,如数学概念的简单性、统一性,结构关系的协调性,对称性,数学命题与数学模型的概括性、典型性和普遍性,还有数学中的奇异性等等都是数学美的具体内容。
以上的论述可见,数学中充满着美的因素,数学美是数学科学的本质力量的感性和理性的呈现,它不是什么虚无飘渺、不可捉摸的东西,而是有其确定的客观内容。
二、数学美与其它美的区别数学美有别与其它的美,它没有鲜艳的色彩,没有美妙的声音,没有动感的画面,它却是一种独特的美。
美国数学家克莱因曾对数学美作过这样的描述:“音乐能激发或抚慰情怀,绘画使人赏心悦目,诗歌能动人心弦,哲学使人获得智慧,科技可以改善物质生活,但数学却能提供以上一切。
”数学美与其它美的区别还在于它是蕴涵在其中的美。
打个比方来说,大家一定都有这种感觉,绝大部分同学对音体美容易产生兴趣,而对数学感兴趣的不多。
我认为,这主要有两个方面的原因:一是音体美中所表现出来的美是外显的,这种美同学们比较容易感受、认识和理解;而数学中的美虽然也有一些表现在数学对象的外表,如精美的图形、优美的公式、巧妙的解法等等,但总的来说数学中的美还是深深地蕴藏在它的基本结构之中,这种内在的理性美学生往往难以感受、认识和理解,这也是数学区别于其它学科的主要特征之一。
探寻神奇的幻方

淄博第五中学 雷建环
背景分析
如果将抽象、枯燥的数字,按一定规律摆 成一个整齐的数字方阵,则会出现奇特的现象, 使人绞尽脑汁,而又感到妙趣横生,其乐无穷。 你可知道这图充满了许许多多的数学学问,并
且有着广泛的应用。这就是数学中的一个珍品——幻方。
本节课从最简单的三阶幻方入手,感受数学的神奇与魅力, 开发学生的计算能力,提高学生的思维推理能力,使枯燥无味的 数学变得有味。幻方人人都懂,但是研究起来困难重重。因此, 我对幻方这节的内容进行了如下处理,把两个“议一议”的内容 整合,再完成“想一想”的内容。通过设计一系列由易到难的问 题串,引导学生在轻松愉悦的氛围中积极主动的投入到本节综合 实践活动课中来。
(2)如果把和相等的每一组数分别连线,这些连线段会构成一个怎样 的图形?描述你得到的图形有什么特点?
图形均衡对称,和谐美丽
展示交流
(3)你能否改变上述幻方中数字的位置,使它们仍然满足你发现的那 些相等关系?
834 159 672
618 753 294
276 951 438
816 357 492
672 159 834
将9个数填在3×3(三行三列)的方格中, 如果满足每个横行、每个竖行和每条对角 线上的三个数之和都相等,这样的图为广 义的三阶幻方。
合作探究(2)
你能用-4,-3,-2,-1,0,1, 2, 3, 4这九个数构造一个 广义的三阶幻方吗?
(1)在这九个数中,三个不同的数相加,和等于0 的算式有哪些?(经过运用加法交换律后相同的 式子视为同一个算式)
把每列数字看成一个三位数则这个三位数之和等于它们的逆转数之和2769514386721598341665把中间一行中间一列每条对角线上的数字看成一个三位数则每个三位数与它的逆转数之和都等于111035775395115925885245665411101中心方格中的数是每行每列和每条对角线上的三个数之和的13或者是另两个数的和的12
数学文化之旅------神奇的斐波那契数列与黄金分割

神奇的斐波那契数列与黄金分割石家庄二中南校区孟柳比萨的列奥纳多,又称斐波那契(Leonardo Pisano ,Fibonacci, Leonardo Bigollo,1175年-1250年),中世纪意大利数学家,是西方第一个研究斐波那契数的人,并将现代书写数和乘数的位值表示法系统引入欧洲。
列奥纳多的父亲Guilielmo(威廉),外号Bonacci.因此列奥纳多就得到了外号斐波那契(Fibonacci,意即filius Bonacci,Bonacci之子)。
1202年,他撰写了《算盘全书》(Liber Abacci)一书。
他是第一个研究了印度和阿拉伯数学理论的欧洲人。
他的父亲被比萨的一家商业团体聘任为外交领事,派驻地点相当于今日的阿尔及利亚地区,当时仍是小伙子的列奥纳多已经开始协助父亲工作,因此得以在一个阿拉伯老师的指导下研究数学。
他还曾在埃及、叙利亚、希腊、西西里和普罗旺斯等地研究数学。
于是他就学会了阿拉伯数字。
他是西方第一个研究斐波那契数的人,并将现代书写数和乘数的位值表示法系统引入欧洲。
主要著作有《算盘书》《几何实践》《花朵》《平方数书》斐波那契在《算盘书》中提出了一个有趣的兔子问题:一般而言,兔子在出生两个月后就具有了繁殖能力,一对兔子每个月能生出一对兔子,如果兔子都不死,那么一年后能有多少对兔子?拿新出生的一对兔子研究:第一个月兔子没有繁殖能力,两个月后生下一对小兔总数共有两对;三个月后,老兔子生下又一对,因为上一轮的小兔没有繁殖能力,所以总数是三对;…………..1,1,2,3,5,8,13,21,34,55,89,144……依次类推下去,你会发现,它后一个数等于前面两个数的和。
在这个数列中的数字,就被称为斐波那契数。
2是第3个斐波那契数。
斐波那契数列还满足一下特点:1.任一项的平方数都等于与它相邻的两项乘积相差12.相邻的4个数,内积与外积相差13.前一项与后一项的比大约是0.6184.后一项比前一项大约是1.618经研究发现,相邻两个斐波那契数的比值是随序号的增加而逐渐趋于黄金分割比的。
神奇的数字

西西弗斯串在古希腊神话中,科林斯国王西西弗斯被罚将一块巨石推到一座山上,但是无论他怎么努力,这块巨石总是在到达山顶之前不可避免地滚下来,于是他只好重新再推,永无休止。
著名的西西弗斯串就是根据这个故事而得名的。
什么是西西弗斯串呢?也就是任取一个数,例如35962,数出这数中的偶数个数、奇数个数及所有数字的个数,就可得到2(2个偶数)、3(3个奇数)、5(总共五位数),用这3个数组成下一个数字串235。
对235重复上述程序,就会得到1、2、3,将数串123再重复进行,仍得123。
对这个程序和数的"宇宙"来说,123就是一个数字黑洞。
是否每一个数最后都能得到123呢?用一个大数试试看。
例如:88883337777444992222,在这个数中偶数、奇数及全部数字个数分别为11、9、20,将这3个数合起来得到11920,对11920这个数串重复这个程序得到235,再重复这个程序得到123,于是便进入"黑洞"了。
这就是数学黑洞"西西弗斯串"。
孔雀开屏数:(20+25)的平方=2025类似的数还有两个:(30+25)的平方=3025(98+01)的平方=9801 与此相类似的还有:(2+4+0+1)的4次方=2401(5+1+2)的立方=512(8+1)的平方=81回归数英国大数学家哈代(G.H.Hardy,1877-1947)曾经发现过一种有趣的现象:153=1^3+5^3+3^3371=3^3+7^3+1^3370=3^3+7^3+0^3407=4^3+0^3+7^3他们都是三位数且等于各位数字的三次幂之和,这种巧合不能不令人感到惊讶.更为称奇的是,一位读者看过哈代的有趣发现后,竟然构造出其值等于各位数字四(五,六)次幂之和的四(五,六)位数:1634=1^4+6^4+3^4+4^454748=5^5+4^5+7^5+4^5+8^5548834=5^6+4^6+8^6+8^6+3^6+4^6注:3位3次幂回归数又称位“水仙花数”像这种其值等于各位数字的n 次幂之和的n 位数,称为n 位n 次幂回归数.本文只讨论这种回归数,故简称为回归数,人们自然要问:对于什么样的自然数n 有回归数?这样的n 是有限个还是无穷多个?对于已经给定的n ,如果有回归数,那么有多少个回归数?1986年美国的一位数学教师安东尼.迪拉那(Anthony Diluna)巧妙地证明了使n 位数成为回归数的n 只有有限个.设An 是这样的回归数,即:An=a1a2a3...an=a1^n+a2^n+...+an^n (其中0<=a1,a2,...an<=9)从而10^n-1<=An<=n9^n 即n 必须满足n9^n>10^n-1 也就是(10/9)^n<10n (1)随着自然数n 的不断增大,(10/9)^n 值的增加越来越快,很快就会使得(1)式不成立,因此,满足(1)的n 不能无限增大,即n 只能取有限多个.进一步的计算表明:(10/9)^60=556.4798...<10*60=600 (10/9)^61=618.3109...>10*61=610对于n>=61,便有(10/9)^n>10n由此可知,使(1)式成立的自然数n<=60.故这种回归数最多是60位数.迪拉那说,他的学生们早在1975年借助于哥伦比亚大学的计算机得到下列回归数:一位回归数:1,2,3,4,5,6,7,8,9二位回归数:不存在三位回归数:153,370,371,407四位回归数:1634,8208,9474五位回归数:54748,92727,93084六位回归数:548834七位回归数:1741725,4210818,9800817八位回归数:24678050,24678051但是此后对于哪一个自然数n (<=60)还有回归数?对于已经给定的n ,能有多少个回归数?最大的回归数是多少?3 153 370 371 4074 1634 8208 94745 54748 92727 930846 5488347 1741725 4210818 9800817 99263158 24678050 24678051 885934779 146511208 472335975 534494836 91298515310 467930777411 82693916578 44708635679 94204591914 32164049651 42678290603 40028394225 32164049650 4938855060612 无解13 无解0564240140138(只有广义解一组)14 2811644033596715 无解16 4338281769391371 433828176939137017 35641594208964132 21897142587612075 35875699062250035 233411150132317(广义解)18 无解19 4498128791164624869 4929273885928088826 3289582984443187032 151784154330750503920 14543398311484532713 6310542598859969391621 128468643043731391252 44917739914603869730722 无解23 21887696841122916288858 28361281321319229463398、27879694893054074471405 35452590104031691935943 27907865009977052567814数学黑洞6174数学黑洞是古希腊的一个国王偶然发现的。
神奇的数字数学

• 完全数的全部因子的倒数和都等于2,如:
• 逻辑美,思辨美
3.14159926
• 至1999年,已经算到小数点后2061亿位. • 从小数点后第71,0100位起连续出现6个3;小数点后一 千万位中,连续出现6个同一数字的有87次: • 前六位有效数字314159是个素数,把它反过来 (951413)还是素数;314159恰好是三个素数31、41、 59连写而成,这三个素数的和,它们的立方和,以及五 次方和也都是素数. • (奇异美)
………………
如此循环, 18个9除以7等于多少呢? 等于57142857142857 —三组“142857” 24个9除以7呢? 是142857142857142857142857— 组“142857”....... 不信的按按计算器
—四
亲和数
• 亲和数——正整数M(N)的全部正因子(去掉其 本身)之和,恰为N(M),则称M和N为一对亲 和数.(奇异美) • 毕达哥拉斯时代就知道220和284是一对亲和数
• 1636年皮勒发现并公布了第二对亲和数 17296和18416, • 阿拉伯数学家本· 科拉建立了一个亲和数公 式:设
其中n是大于1的正整数,如果 全是 素数,那么 与 便是一对亲 和数. (统一美)
142857x142857=20408122449
• 再把20408122449分解两组数字,20408和 122449 ,它们之和是:
20408+122449=142857
• 它发现于埃及金字塔内 • 它是一组神奇的数字 • 它证明一星期有7天 • 它自我累加一次,就由它的6个数字,依顺序轮值 一次,到了第7天,他们就放假,由999999去代 班,数字越加越大,每超过一星期轮回,每个数 字需要分身一次,你不需要计算机,只要知道它 的分身方法,就可以知道继续累加的答案 • 它还有更神奇的地方等待你去发掘! • 也许,它就是宇宙的密码
神奇数字与股市预测——斐波纳契数
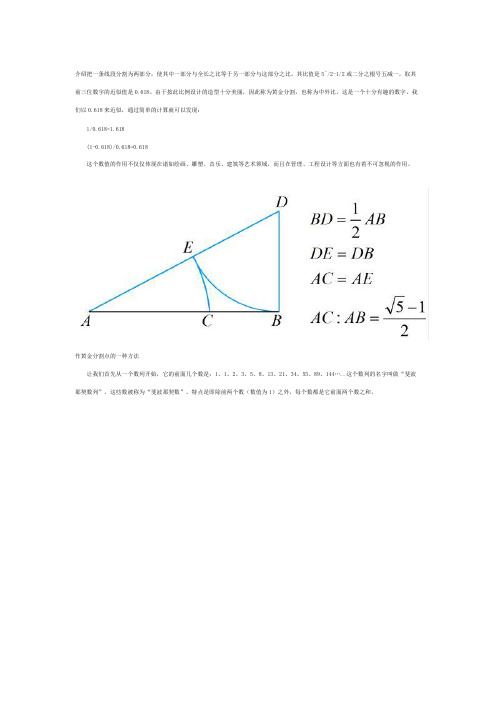
介绍把一条线段分割为两部分,使其中一部分与全长之比等于另一部分与这部分之比。
其比值是5^/2-1/2或二分之根号五减一,取其前三位数字的近似值是0.618。
由于按此比例设计的造型十分美丽,因此称为黄金分割,也称为中外比。
这是一个十分有趣的数字,我们以0.618来近似,通过简单的计算就可以发现: 1/0.618=1.618 (1-0.618)/0.618=0.618 这个数值的作用不仅仅体现在诸如绘画、雕塑、音乐、建筑等艺术领域,而且在管理、工程设计等方面也有着不可忽视的作用。
作黄金分割点的一种方法 让我们首先从一个数列开始,它的前面几个数是:1、1、2、3、5、8、13、21、34、55、89、144…..这个数列的名字叫做“斐波那契数列”,这些数被称为“斐波那契数”。
特点是即除前两个数(数值为1)之外,每个数都是它前面两个数之和。
作黄金分割点的一种方法 斐波那契数列与黄金分割有什么关系呢?经研究发现,相邻两个菲波那契数的比值是随序号的增加而逐渐趋于黄金分割比的。
即f(n)/f(n-1)-→0.618…。
由于斐波那契数都是整数,两个整数相除之商是有理数,所以只是逐渐逼近黄金分割比这个无理数。
但是当我们继续计算出后面更大的斐波那契数时,就会发现相邻两数之比确实是非常接近黄金分割比的。
一个很能说明问题的例子是五角星/正五边形。
五角星是非常美丽的,我国的国旗上就有五颗,还有不少国家的国旗也用五角星,这是为什么?因为在五角星中可以找到的所有线段之间的长度关系都是符合黄金分割比的。
正五边形对角线连满后出现的所有三角形,都是黄金分割三角形。
黄金分割三角形还有一个特殊性,所有的三角形都可以用四个与其本身全等的三角形来生成与其本身相似的三角形,但黄金分割三角形是唯一一种可以用5个而不是4个与其本身全等的三角形来生成与其本身相似的三角形的三角形。
由于五角星的顶角是36度,这样也可以得出黄金分割的数值为2Sin18 。
