北师大版九年级数学上册课时练：第六章《反比例函数》 (培优篇)

合集下载

北师大版九年级数学上册第六章反比例函数教材同步培优、拔高复习(无答案)

北师大版九年级数学上册第六章反比例函数教材同步培优、拔高复习一、反比例函数的概念：知识要点：1、一般地，形如 y =xk( k 是常数, k = 0 ) 的函数叫做反比例函数。

注意：（1）常数 k 称为比例系数，k 是非零常数；（2）解析式有三种常见的表达形式：（A ）y =xk（k ≠ 0）；（B ）xy = k （k ≠ 0）；（C ）y=kx -1（k ≠0）典型例题精选：有关反比例函数的解析式一、填空题1．一般的，形如____________的函数称为反比例函数，其中x 是______，y 是______．自变量x 的取值范围是______． 2．写出下列各题中所要求的两个相关量之间的函数关系式，并指出函数的类别．(1)商场推出分期付款购电脑活动，每台电脑12000元，首付4000元，以后每月付y 元，x 个月全部付清，则y 与x 的关系式为____________，是______函数．(2)某种灯的使用寿命为1000小时，它的使用天数y 与平均每天使用的小时数x 之间的关系式为__________________，是______函数．(3)设三角形的底边、对应高、面积分别为a 、h 、S ．当a ＝10时，S 与h 的关系式为____________，是____________函数；当S ＝18时，a 与h 的关系式为____________，是____________函数．(4)某工人承包运输粮食的总数是w 吨，每天运x 吨，共运了y 天，则y 与x 的关系式为______，是______函数．3．下列各函数①x k y =、②x k y 12+=、③x y 53=、④14+=x y 、⑤x y 21-=、⑥31-=x y 、⑦24xy =和⑧y ＝3x －1中，是y 关于x 的反比例函数的有：____________(填序号)． 4．若函数11-=m x y (m 是常数)是反比例函数，则m ＝____________，解析式为____________．5．近视眼镜的度数y (度)与镜片焦距x (m)成反比例，已知400度近视眼镜片的焦距为0.25m ，则y 与x 的函数关系式为____________．二、选择题 6．已知函数xky =，当x ＝1时，y ＝－3，那么这个函数的解析式是( )． (A)x y 3=(B)xy 3-= (C)xy 31=(D)xy 31-= 7．已知y 与x 成反比例，当x ＝3时，y ＝4，那么y ＝3时，x 的值等于( )． (A)4 (B)－4 (C)3 (D)－3三、解答题8．已知y 与x 成反比例，当x ＝2时，y ＝3． (1)求y 与x 的函数关系式； (2)当y ＝－23时，求x 的值．综合、运用、诊断一、填空题9．若函数522)(--=k xk y (k 为常数)是反比例函数，则k 的值是______，解析式为_________________________．10．已知y 是x 的反比例函数，x 是z 的正比例函数，那么y 是z 的______函数．二、选择题11．某工厂现有材料100吨，若平均每天用去x 吨，这批原材料能用y 天，则y 与x 之间的函数关系式为( )．(A)y ＝100x(B)xy 100=(C)xy 100100-= (D)y ＝100－x 12．下列数表中分别给出了变量y 与变量x 之间的对应关系，其中是反比例函数关系的是( )．三、解答题13．已知圆柱的体积公式V ＝S ·h ．(1)若圆柱体积V 一定，则圆柱的高h (cm)与底面积S (cm 2)之间是______函数关系； (2)如果S ＝3cm 2时，h ＝16cm ，求： ①h (cm)与S (cm 2)之间的函数关系式； ②S ＝4cm 2时h 的值以及h ＝4cm 时S 的值．拓展、探究、思考14．已知y 与2x －3成反比例，且41=x 时，y ＝－2，求y 与x 的函数关系式．15．已知函数y ＝y 1－y 2，且y 1为x 的反比例函数，y 2为x 的正比例函数，且23-=x 和x ＝1时，y 的值都是1．求y 关于x 的函数关系式．二、反比例函数的图象和性质：知识要点：1、形状：图象是双曲线。

【完整版】北师大版九年级上册数学第六章反比例函数含答案

北师大版九年级上册数学第六章反比例函数含答案一、单选题(共15题，共计45分)1、已知点P（a，b）是反比例函数y=象上异于点（﹣1，﹣1）的一个动点，则+=（）A.2B.1C.D.2、函数y=与y=x﹣1图象的一个交点的横、纵坐标分别为a、b，则﹣的值为（）A.-B.C.3D.1﹣33、如图，反比例函数y＝（x＞0）的图象与一次函数y=ax+b的图象交于点A（1，6）和点B（3，2）．当ax+b＜时，则x的取值范围是（）A.1＜x＜3B.x＜1或x＞3C.0＜x＜1D.0＜x＜1或x＞34、如图，△AOB是直角三角形，∠AOB=90°，OB=2OA，点A在反比例函数y= 的图象上．若点B在反比例函数y= 的图象上，则k的值为（）A.﹣4B.4C.﹣2D.25、关于反比例函数y＝﹣，下列说法不正确的是（）A.函数图象分别位于第二、四象限B.函数图象关于原点成中心对称 C.函数图象经过点（﹣6，﹣2） D.当x＜0时，y随x的增大而增大6、如图，正比例函数y＝x与反比例函数y＝的图象相交于A，C两点．AB⊥x轴于B，CD⊥x轴于D，当四边形ABCD的面积为6时，则k的值是（）A.6B.3C.2D.7、如图，已知A，B是反比例函数y= （k＞0，x＞0）图象上的两点，BC∥x轴，交y轴于点C，动点P从坐标原点O出发，沿O→A→B→C（图中“→”所示路线）匀速运动，终点为C，过P作PM⊥x轴，垂足为M．设三角形OMP的面积为S，P点运动时间为t，则S关于x的函数图象大致为（）A. B. C. D.8、若点（3，4）是反比例函数图象上一点，则此函数图象必经过点（）A.（2，6）B.（2，-6）C.（4，-3）D.（3，-4）9、在反比例函数图象的每一支曲线上，y都随x的增大而减小，则k 的取值范围是A.k＞3B.k＞0C.k＜3D.k＜010、已知直线y=kx（k＞0）与双曲线y=交于点A（x1， y1），B（x2，y 2）两点，则x1y2+x2y1的值为（）A.﹣6B.﹣9C.0D.911、已知点A（x1， y1）、B（x2， y2）是反比例函数y=﹣图象上的两点，若x2＜0＜x1，则有（）A.0＜y1＜y2B.0＜y2＜y1C.y2＜0＜y1D.y1＜0＜y212、在反比例函数的每一条曲线上，y都随着x的增大而减小，则k 的值可以是（）A.﹣1B.1C.2D.313、如图，在平面直角坐标系中，▱OABC的对角线OB在y轴正半轴上，点A，C 分别在函数y＝（x＞0），y＝（x＜0）的图象上，分别过点A，C作AD⊥x轴于点D，CE⊥x轴于点E，若|k1|：|k2|＝9：4，则AD：CE的值为（）A.2：3B.3：2C.4：9D.9：414、已知点（﹣2，a），（2，b），（3，c）在函数y＝（k＞0）的图象上，则下列判断正确的是（）A. a＜b＜cB. b＜a＜cC. a＜c＜bD. c＜b＜a15、如果y是z的反比例函数，z是x的反比例函数，那么y是x的（）函数．A.正比例B.反比例C.一次函数D.二次函数二、填空题(共10题，共计30分)16、如图，一次函数y=x+m的图象与反比例函数y= 的图象交于A，B两点，且与x轴交于点C，点A的坐标为（2，1），结合图象写出不等式组0＜x+m≤ 的解集为________．17、在反比例函数的图象的每一条曲线上，y随着x的增大而增大，则k的取值范围是________．18、长方形的面积为60cm2，如果它的长是ycm，宽是xcm，那么y是x的________ 函数关系，y写成x的关系式是________ ．19、反比例函数与一次函数的图象有一个交点是，则它们的另一个交点的坐标是________.20、如图，点A是双曲线y=﹣在第二象限分支上的一个动点，连接AO并延长交另一分支于点B，以AB为底作等腰△ABC，且∠ACB=120°，随着点A的运动，点C的位置也不断变化，但点C始终在双曲线y= 上运动，则k=________．21、如图，点A（m，6），B（n，1）在反比例函数图象上，AD⊥x轴于点D，BC⊥x轴于点C，DC=5．线段DC上有一点E，当△ABE的面积等于5时，点E的坐标为________．22、图1所示矩形ABCD中，BC=x，CD=y，y与x满足的反比例函数关系如图2所示，等腰直角三角形AEF的斜边EF过C点，M为EF的中点，则下列结论正确的序号是________.①当x=3时，EC<EM；②当y=9时，EC>EM③当x增大时，EC⋅CF的值增大；④当y增大时，BE⋅DF的值不变。

北师大版九年级数学上册第六章反比例函数第2节反比例函数的图像和性质课堂练习

第六章反比例函数第2节反比例函数的图像和性质课堂练习学校:___________姓名：___________班级：___________考生__________ 评卷人得分一、单选题1．反比例函数y ＝1x（x ＜0）的图象位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．对于反比例函数3y x=，下列说法错误的是（） A ．图象经过点()1,3B ．图象在第一、三象限C ．0x >时，y 随x 的增大而增大D ．x 0<时，y 随x 增大而减小3．若点A(x 1，y 1），B(x 2，y 2)在反比例函数3y -x=的图象上，且x 1<0<x 2．则（）A ．12y 0y <<B ．12y 0y >>C ．12y 0y >>D ．12y 0y <<4．反比例函数y ＝mx的图象如图所示，以下结论：①常数m ＞0；①在每个象限内，y 随x 的增大而增大；①若A （﹣1，h ），B （2，k ）在图象上，则h ＜k ；①若P （x ，y ）在图象上，则P '（﹣x ，﹣y ）也一定在图象上．其中正确的是（）A ．①①B ．①①C ．①①①D ．①①①5．如图，P （x ，y ）是反比例函数3y x=的图象在第一象限分支上的一个动点，P A ①x 轴于点A ，PB ①y 轴于点B ，随着自变量x 的逐渐增大，矩形OAPB 的面积（）A ．保持不变B ．逐渐增大C ．逐渐减小D ．无法确定6．已知正比例函数1y k x=和反比例函数2kyx=，在同一直角坐标系下的图象如图所示，其中符合120k k⋅>的是（）A．①①B．①①C．①①D．①①7．若反比例函数()110ay a xx-=><，图象上有两个点()()1122,,x y x y，，设()1212()m x x y y=--，则y mx m=-不经过第()象限．A．一B．二C．三D．四8．如图，过x轴正半轴上的任意一点P，作y轴的平行线，分别与反比例函数y3=x （x＞0）和y6=x-（x＞0）的图象交于B、A两点．若点C是y轴上任意一点，则①ABC的面积为（）A．3B．6C．9D．92评卷人得分二、填空题9．已知反比例函数6yx=，当x＞3时，y的取值范围是_____．10．如图，直线y=kx与双曲线y=2x交于A，B两点，BC①y轴于点C，则△ABC的面积为_____．11．如果点（﹣1，y1）、B（1，y2）、C（2，y3）是反比例函数y＝1x图象上的三个点，则y1、y2、y3的大小关系是_____．12．若点A（-2，a），B（1，b），C（4，c）都在反比例函数8yx=-的图象上，则a、b、c大小关系是________．13．若点A（﹣5，y1），B（1，y2），C（2，y3）在反比例函数21ayx+=（a为常数）的图象上，则y1，y2，y3的大小关系是_____．（用“＜”连接）14．如图，点A是反比例函数y＝kx图象上的一个动点，过点A作AB①x轴，AC①y 轴，垂足点分别为B、C，矩形ABOC的面积为4，则k＝________．15．如图，点A在双曲线y＝kx的第一象限的那一支上，AB①y轴于点B，点C在x 轴正半轴上，且OC＝2AB，点E在线段AC上，且AE＝3EC，点D为OB的中点，若①ADE的面积为32，则k的值为______．评卷人得分三、解答题16．如图，()A4,3是反比例函数kyx=在第一象限图象上一点，连接OA，过A作AB//x轴，截取AB OA(B=在A右侧)，连接OB，交反比例函数kyx=的图象于点P．（1）求反比例函数kyx=的表达式；（2）求点B的坐标及OB所在直线解析式；（3）求OAP的面积．17．如图，反比例函数kyx=与一次函数y x b=-+的图象交于点A（1，3）和点B．（1）求k的值和点B的坐标．（2）结合图象，直接写出当不等式kx bx<-+成立时x的取值范围．（3）若点C是反比例函数kyx=第三象限图象上的一个动点，当CA CB=时，求点C的坐标．18．如图，Rt AOB ∆的直角边OB 在x 轴的正半轴上，反比例函数(0)k y x x=>的图象经过斜边OA的中点D ,与直角边AB 相交于点C . ①若点(4,6)A ，求点C 的坐标： ①若9S OCD ∆=，求k 的值.19．如图，已知一次函数y ＝kx ＋b 的图象与反比例函数8y x＝－的图象交于A 、B 两点，且点A 的横坐标和点B 的纵坐标都是－2．求：（1）一次函数的解析式；（2）△AOB 的面积．20．已知：如图，∆ABC是等腰直角三角形，①B=90°，点B的坐标为(1,2)．反比例函数kyx的图象经过点C，一次函数y=ax+b的图象经A,C两点．（1）求反比例函数和一次函数的关系式；（2）直接写出不等式组0<ax+b≤kx的解集．参考答案：1．C 【解析】【分析】根据题目中的函数解析式和x 的取值范围，可以解答本题．【详解】解：①反比例函数y ＝1x（x ＜0）中，k ＝1＞0，①该函数图象在第三象限，故选：C ．【点睛】本题考查反比例函数的图象,关键在于熟记反比例函数图象的性质. 2．C 【解析】【分析】根据反比例函数的性质得出函数的增减性以及所在象限和经过的点的特点分别分析得出即可．【详解】解：A ，因为133⨯=，所以图象经过点(1)3，，A 选项正确，故不选A ； B ，因为30k =>，图象在第一、三象限，B 选项正确，故不选B ；C ，因为30k =>，图象在第一、三象限，所以0x >时，y 随x 的增大而减小，C 选项错误，故选C ；D ，因为30k =>，图象在第一、三象限，所以0x <时，y 随x 的增大而减小，D 选项正确，故不选D ．故选：C ．【点睛】此题主要考查了反比例函数的性质，根据解析式确定函数的性质是解题的关键． 3．B 【解析】【分析】根据题意和反比例函数的性质可以解答本题．①反比例函数3y -x=，①该函数图像在第二、四象限，在每个象限y 随x 的增大而增大， ①A(x 1，y 1），B(x 2，y 2)在反比例函数3y -x=的图象上，且x 1<0<x 2，①12y 0y >>，故选B. 【点睛】本题考查反比例函数图象上点的坐标特征，解答本题的关键是明确题意，利用反比例函数的性质解答． 4．D 【解析】【分析】根据反比例函数的图象的位置确定其比例系数的符号，利用反比例函数的性质进行判断即可．【详解】解：①反比例函数的图象可知，m ＞0，故①正确；当反比例函数的图象位于一、三象限时，在每一象限内，y 随x 的增大而减小，故①错误；将A （-1，h ），B （2，k ）代入y ＝mx得到h=-m ，2k=m ， ①m ＞0，①h ＜k ，故①正确；将P （x ，y ）代入y ＝m x 得到m=xy ，将P′（-x ，-y ）代入y ＝mx得到m=xy ，若P （x ，y ）在图象上，则P′（-x ，-y ）也在图象上故①正确，故选：D ．【点睛】本题考查了反比例函数图象上点的坐标特征，反比例函数的性质，熟练掌握反比例函数的图象和性质是解题的关键． 5．A【分析】因为过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S 是个定值，即S=12|k|，所以随着x 的逐渐增大，矩形OAPB 的面积将不变．【详解】解：依题意有矩形OAPB 的面积=2×12|k|=3，所以随着x 的逐渐增大，矩形OAPB 的面积将不变．故选：A ．【点睛】本题考查了反比例函数 y ＝kx中k 的几何意义，即过双曲线上任意一点引x 轴、y 轴垂线，所得矩形面积为|k|，解题的关键是掌握图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S 的关系即S=12|k|． 6．B 【解析】【分析】根据正比例函数和反比例函数的图象逐一判断即可．【详解】解：观察图像①可得120,0k k >>，所以120k k >，①符合题意；观察图像①可得120,0k k <>，所以120k k <，①不符合题意；观察图像①可得120,0k k ><，所以120k k <，①不符合题意；观察图像①可得120,0k k <<，所以120k k >，①符合题意；综上，其中符合120k k ⋅>的是①①，故答案为：B ．【点睛】本题考查的是正比例函数和反比例函数的图像，当k ＞0时，正比例函数和反比例函数经过一、三象限，当k ＜0时，正比例函数和反比例函数经过二、四象限． 7．C【分析】利用反比例函数的性质判断出m 的正负，再根据一次函数的性质即可判断．【详解】解：①()110a y a x x-=><，， ①a-1＞0， ①()110a y a x x-=><，图象在三象限，且y 随x 的增大而减小， ①图象上有两个点（x 1，y 1），（x 2，y 2），x 1与y 1同负，x 2与y 2同负， ①m=（x 1-x 2）（y 1-y 2）＜0，①y=mx-m 的图象经过一，二、四象限，不经过三象限，故选：C ．【点睛】本题考查反比例函数的性质，一次函数的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型． 8．D 【解析】【分析】设P （a ，0），由直线APB 与y 轴平行，得到A 和B 的横坐标都为a ，将x ＝a 代入反比例函数y 6x-＝和y 3x ＝中，分别表示出A 和B 的纵坐标，进而由AP ＋BP 表示出AB ，三角形ABC 的面积12⨯＝AB ×P 的横坐标，求出即可．【详解】解：设P （a ，0），a ＞0，则A 和B 的横坐标都为a ，将x ＝a 代入反比例函数y 6x =-中得：y 6a=-，故A （a ，6a -）；将x＝a代入反比例函数y3x＝中得：y3a=，故B（a，3a），①AB＝AP＋BP639a a a+＝＝，则S△ABC12=AB•xP19922aa=⨯⨯=，故选D．【点睛】本题主要考查反比例函数图象k的几何意义，解决本题的关键是要熟练掌握反比例函数k 的几何意义.9．0＜y＜2【解析】【分析】根据反比例函数的性质可以得到反比例函数y＝6x，当x＞3时，即可得到y的取值范围．【详解】①y＝6x，6＞0，①当x＞0时，y随x的增大而减小，当x＝3时，y＝2，①当x＞3时，y的取值范围是0＜y＜2，故答案为0＜y＜2【点睛】本题考查反比例函数的性质，解答本题的关键是明确题意，利用反比例函数的性质解答．10．2【解析】【分析】根据直线y=kx与双曲线y=2x交于A，B两点，可得A、B关于原点对称，从而得到S△BOC=S△AOC，然后根据反比例函数的系数k的几何意义求出的S△BOC面积即可.【详解】①直线y=kx与双曲线y=2x交于A，B两点，①点A与点B关于原点对称，①S△BOC=S△AOC，而S△BOC=12×2=1，①S△ABC=2S△BOC=2．故答案为2．【点睛】反比例函数中比例系数k的几何意义是初中数学的重点，贯穿于整个初中数学的学习，是中考中比较常见的知识点，一般难度不大，需熟练掌握.11．y2＞y3＞y1【解析】【分析】先根据反比例函数的解析式判断出函数图象所在的象限,再根据各点横坐标的特点进行解答即可.【详解】解：①1＞0,反比例函数y=1x图象在一、三象限,并且在每一象限内y随x的增大而减小,因为-1＜0,①A点在第三象限,①y1＜0,①2＞1＞0,①B、C两点在第一象限,①y2＞y3＞0,①y2＞y3＞y1.故答案是:y2＞y3＞y1.【点睛】本题主要考查的是反比例函数图象上点的坐标特点,解决本题的关键是要熟练掌握反比例函数图象性质.12．a＞c＞b【解析】【分析】根据题意，分别求出a 、b 、c 的值，然后进行判断，即可得到答案．【详解】解：①点A 、B 、C 都在反比例函数8y x =-的图象上，则当2x =-时，则842a =-=-；当1x =时，则881b =-=-；当4x =时，则824c =-=-； ①a c b >>；故答案为：a c b >>．【点睛】本题考查的是反比例函数图象上点的坐标特点，熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．13．y 1＜y 3＜y 2．【解析】【分析】先计算出自变量为﹣5、1、2对应的函数值，从而得到y 1，y 2，y 3的大小关系．【详解】当x =﹣5时，y 1=﹣15(a 2+1)；当x =1时，y 2=a 2+1；当x =2时，y 3=12(a 2+1)，所以y 1＜y 3＜y 2．故答案为：y 1＜y 3＜y 2．【点睛】本题考查的是反比例函数图象上点的坐标特点，熟知反比例函数函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．14．-4【解析】【详解】试题分析：由于点A是反比例函数y=kx上一点，矩形ABOC的面积S=|k|=4，则k的值为-4．考点：反比例函数15．83【解析】【分析】如下图，连接CD，由AE＝3EC，①ADE的面积为32，得到①CDE的面积为12，则①ADC 的面积为2，设A点坐标为（a，b），则k＝ab，AB＝a，OC＝2AB＝2a，BD＝OD＝b，利用S梯形OBAC＝S△ABD+S△ADC+S△ODC即可得出ab的值进而得出结论．【详解】如下图，连CD①AE＝3EC，①ADE的面积为32，①①CDE的面积为12，①①ADC的面积为2，设A点坐标为（a，b），则AB＝a，OC＝2AB＝2a，①点D为OB的中点，①BD＝OD＝12b，①S梯形OBAC＝S△ABD+S△ADC+S△ODC，①12（a+2a）×b＝12a×12b+2+12×2a×12b，①ab＝83，把A（a，b）代入双曲线y＝kx得，k ＝ab ＝83．故答案为：83．【点睛】本题考查利用几何图形的面积求解反比例函数的解析式，解题关键是将几何图形的面积和点的坐标结合起来，然后利用待定系数法求得解析式.16．（1）12y x =（2）（9，3）；13y x = （3）5 【解析】【分析】（1）直接代入A 点坐标课的k 的值，进而可得函数解析式；（2）过点A 作AC①x 轴于点C ，利用勾股定理计算出AO 的长，进而可得AB 长，然后可得B 点坐标．设OB 所在直线解析式为y=mx （m≠0）利用待定系数法可求出BO 的解析式；（3）首先联立两个函数解析式，求出P 点坐标，过点P 作PD①x 轴，延长DP 交AB 于点E ，连接AP ，再确定E 点坐标，最后求面积即可．【详解】解：()1将点()A 4,3代入()k y k 0x=≠，得：12k =，则反比例函数解析式为：12y x =； () 2如图，过点A 作AC x ⊥轴于点C ，则OC 4=、AC 3=，22OA 435∴=+=，AB//x 轴，且AB OA 5==，∴点B的坐标为()9,3；设OB所在直线解析式为()y mx m0=≠，将点()B9,3代入得13=m，OB∴所在直线解析式为1y x3=；()3联立解析式：1y x312yx⎧=⎪⎪⎨⎪=⎪⎩，解得：x6,y2=⎧⎨=⎩可得点P坐标为()6,2，过点P作PD x⊥轴，延长DP交AB于点E，连接AP，则点E坐标为()6,3，AE2∴=，PE1=，PD2=，则OAP的面积()11126362215222=⨯+⨯-⨯⨯-⨯⨯=．【点睛】此题主要考查了待定系数法求反比例函数和正比例函数解析式，关键是掌握凡是函数图象经过的点，必能满足解析式．17．（1）3k=，B（3，1）；（2）1x3<<或x0<；（3）C（33--，）【解析】【分析】（1）分别把()1,3A代入一次函数与反比例函数，可得,k b的值，联立两个解析式，解方程组可得B的坐标；（2）由k x＜x b -+，则反比例函数值小于一次函数值，所以反比例函数的图像在一次函数的图像的下方，从而可得答案；（3）由,CA CB = 则C 在AB 的垂直平分线上，利用直线AB 与坐标轴构成的三角形是等腰直角三角形，证明AB 的垂直平分线经过原点，再求解垂直平分线的解析式，联立两个解析式解方程组即可得到答案．【详解】解：（1）把()1,3A 代入y x b =-+，13,b ∴-+=4,b ∴=所以：一次函数为：4,y x =-+把()1,3A 代入k y x=， 133,k ∴=⨯= 3,y x∴= 3,4y x y x ⎧=⎪∴⎨⎪=-+⎩ 34,x x∴=-+ 2430,x x ∴-+=121,3,x x ∴== 把11x =代入4,y x =-+13,y ∴=把23x =代入4,y x =-+21,y ∴=121213,,31x x y y ==⎧⎧∴⎨⎨==⎩⎩ 经检验：方程的解符合题意，()3,1.B ∴（2）由kx＜x b-+，则反比例函数值小于一次函数值，所以反比例函数的图像在一次函数的图像的下方，结合图像可得：1x3<<或0x<．（3）,CA CB=C∴在AB的垂直平分线上，记AB的中点为D，()()1,3,3,1,A B∴()2,2,D∴记AB与,x y轴的交点分别为,F EAB为4,y x=-+()()4,0,0,4,F E∴4,OE OF∴==OD∴为AB的垂直平分线，设OD为,y mx=把()2,2D代入：22,m=1,m∴=AB∴的垂直平分线为：,y x=,3y xyx=⎧⎪∴⎨=⎪⎩解得：121233,,33x x y y ⎧⎧==-⎪⎪⎨⎨==-⎪⎪⎩⎩ 经检验：方程的解符合题意，C 在第三象限，()3,3.C ∴--【点睛】本题考查的是利用待定系数法求解一次函数与反比例函数中的字母参数，同时考查利用图像判断一次函数值与反比例函数值的大小，还考查线段的垂直平分线的性质，函数的交点坐标问题，一元二次方程的解法，掌握以上知识是解题的关键．18．①（4，32）；①k=12 【解析】【分析】①根据点D 是OA 的中点即可求出D 点坐标，再将D 的坐标代入解析式求出解析式，从而得到C 的坐标；①连接OC, 设A(a,b),先用代数式表示出三角形OAB,OBC,OCD 的面积，再根据条件列出方程求k 的值即可．【详解】解：①①D 是OA 的中点，点A 的坐标为（4，6），①D （42，62），即（2，3） ①k=2×3=6①解析式为6y x= ①A 的坐标为（4，6），AB①x 轴①把x=4代入6y x=得y=32 ①C 的坐标为（4，32） ①连接OC,设A(a,b),则D(2a , 2b ) 可得k=4ab ，ab=4k ①解析式为4ab y x= ①B(a,0),C(a, 4b ) ①11222OAB SOB AB ab k === 1122OBC S OB BC k =•= 11()22OCD OAC OAB OBC S S S S ∴==- ①11(2)922k k -= 解得：k=12【点睛】本题考查了一次函数的性质，要正确理解参数k 的几何意义，能用代数式表达三角形OCD 的面积是解题的关键．19．（1）y ＝－x ＋2；（2）6【解析】【分析】（1）把点A 的横坐标代入8y x＝－，可得4y =，即可求出A 点的坐标，把B 点的纵坐标代入8y x＝－，可得4x =，即可求出B 点的坐标，把A B 、两点的坐标代入一次函数的解析式即可求解；（2）首先求出直线AB 与x 轴的交点坐标M ，然后根据AOB AOM BOM S S S ∆∆∆＝＋进行求解即可；【详解】解：（1）把2A x =-代入8y x＝－中，得4A y = ① 点()2,4A -把2B y =-代入8y x＝－中，得4B x = ① 点()4,2B -把AB 、两点的坐标代入y kx b ＝＋中，得 42,24.k b k b ⎧⎨-⎩＝－＋＝＋解得1,2.k b ⎧⎨⎩＝－＝ ① 所求一次函数的解析式为2y x ＝－＋（2）当0y ＝时，2x ＝, ①2y x ＝－＋与x 轴的交点为()2,0M ,即2OM =①AOB AOM BOM S S S ∆∆∆＝＋ B A y OM y OM ⋅⋅⋅⋅2121＋＝11242222⨯⨯⨯⨯＝＋＝6【点睛】本题主要考查反比例函数与一次函数的综合，熟练掌握一次函数的解析式求法以及图中的面积求法是求解本题的关键.20．（1）反比例函数关系式为y =6x，一次函数函数关系式为y =x-1；（2）1<x ≤3 【解析】【分析】①根据等腰三角形的性质求出A,C 点的坐标，即可求出反比例和一次函数关系式 ①观察图像即可找出x 的解集【详解】解：（1）①∆ABC 是等腰直角三角形且点B 的坐标为(1,2)①AB =BC =2①点C 的坐标为(3,2)，点A 的坐标为(1,0)把点C 的坐标代入y =k x，解得k =6 ①反比例函数关系式为y =6x 把点C(3,2)，点A(1,0)代入一次函数y=ax+b320a b a b +=⎧⎨+=⎩解得11a b =⎧⎨=-⎩①一次函数函数关系式为y =x-1（2）由函数图像及A ，C 两点坐标可得不等式组的解集为：1<x ≤3【点睛】本题解题的关键是根据等腰直角三角形的性质求出A,C 点的坐标，写x 的范围时可以先用笔画出符合要求的线段不易出错。

北师大版数学九年级上册第六章反比例函数-课时练试题及答案

北师大版数学九年级上册第六章反比例函数课时作业6.1反比例函数【基础练习】一、填空题：1.A、B两地相距120千米，一辆汽车从A地去B地，则其速度v（千米/时）与行驶时间t（小时）之间的函数关系可表示为；2.有一面积为60的梯形，其上底长是下底长的13，设下底长为x，高为y，则y与x的函数关系式是；3.已知y与x成反比例，并且当x=2时，y=-1，则当x=-4时，y=.二、选择题：1.下列各问题中的两个变量成反比例的是（）；A.某人的体重与年龄B.时间不变时，工作量与工作效率C.矩形的长一定时，它的周长与宽D.被除数不变时，除数与商2.已知y与x成反比例，当x=3时，y=4，那么当y=3时，x的值为（）；A.4B.-4C.3D.-33.下列函数中，不是反比例函数的是（）A.xy=2B.y=-k3x (k≠0) C.y=3x-1D.x=5y-1三、解答题：1.一水池内有污水60m3，设放净全池污水所需的时间为t(小时），每小时的放水量为w m3，（1）试写出t与w之间的函数关系式，t是w反比例函数吗？（2）求当w=15时，t的值.2.已知y 是x 的反比例函数，下表给出了x 与y 的一些值：（1）写出这个反比例函数表达式；（2）将表中空缺的x 、y 值补全.【综合练习】举出几个日常生活中反比例函数的实例.【探究练习】已知函数y =y 1+y 2，y 1与x 成正比例，y 2与x 成反比例，且当x =1时，y =4,当x =2时，y =5.求y 关于x 的函数解析式.答案:【基础练习】一、1.v =120t ； 2.y =90x ； 3.12.二、1.D ；2.A ；3.C.三、1.（1）t =60w，（2）t =4. 2.（1）y =3x ；（2）从左至右：x =-4，-1，2，3；y =-35，-32，3，34，35.【综合练习】略.x -5-3-2145y-34-1-3321【探究练习】y =2x +2x. 6.1反比例函数一．判断题1．如果y 是x 的反比例函数，那么当x 增大时，y 就减小（）2．当x 与y 乘积一定时，y 就是x 的反比例函数，x 也是y 的反比例函数（）3．如果一个函数不是正比例函数，就是反比例函数（）4．y 与x 2成反比例时y 与x 并不成反比例（）5．y 与2x 成反比例时，y 与x 也成反比例（）6．已知y 与x 成反比例，又知当2=x 时，3=y ，则y 与x 的函数关系式是6xy =（）二．填空题7．)0(≠=k xky 叫__________函数，x 的取值范围是__________；8．已知三角形的面积是定值S ，则三角形的高h 与底a 的函数关系式是_________=h ，这时h 是a 的__________；9．如果y 与x 成反比例，z 与y 成正比例，则z 与x 成__________；10．如果函数y =222-+k k kx是反比例函数，那么k =________，此函数的解析式是；11．下列函数表达式中，x 均表示自变量，那么哪些是反比例函数，如果是请在括号内填上k 的值，如果不是请填上“不是”①x y 5=；（）②x y 4.0=；（）③2x y =；（）④2=xy ；（）⑤πx y =；（）⑥xy 5-=（）⑦12-=x y （）12．判断下面哪些式子表示y 是x 的反比例函数？①31-=xy ；②x y -=5；③x y 52-=；④)0(2≠=a a xay 为常数且；解：其中是反比例函数，而不是；13．计划修建铁路1200km ，那么铺轨天数y （天）是每日铺轨量x 的反比例函数吗？解：因为，所以y 是x 的反比例函数；14．一块长方形花圃，长为a 米，宽为b 米，面积为8平方米，那么a 与b 成函数关系，列出a 关于b 的函数关系式为；三．选择题：15．若nxm y ++=2)5(是反比例函数，则m 、n 的取值是（）（A ）3,5-=-=n m （B ）3,5-=-≠n m （C ）3,5=-≠n m （D ）4,5-=-≠n m 16．附城二中到联安镇为5公里，某同学骑车到达，那么时间t 与速度（平均速度）v 之间的函数关系式是（）（A ）stv =（B ）st v +=（C ）ts v =（D ）st v =17．已知A （2-，a ）在满足函数xy 2=，则___=a （）（A ）1-（B ）1（C ）2-（D ）218．下列函数中，是反比例函数的是（）（A ）1)1(=-y x （B ）11+=x y （C ）21xy =（D ）x y 31=19．下列关系式中，哪个等式表示y 是x 的反比例函数（）（A ）x k y =（B ）2xB y =（C ）121+=x y （D ）12=-xy 20．函数y m x mm =+--()2229是反比例函数，则m 的值是（）（A ）m =4或m =-2（B ）m =4（C ）m =-2（D ）m =-1四．解答题：21．在某一电路中，保持电压V （伏特）不变，电流I （安培）与电阻R （欧姆）成反比例，当电阻R=5时，电流I=2安培。

新北师大版九年级数学上册：第六章反比例函数同步练习(含答案)

第六章反比例函数 1 反比例函数01 基础题知识点1 反比例函数的概念1．下列函数是y 关于x 的反比例函数的是(C)A ．y ＝xB ．y ＝kxC ．y ＝－8xD ．y ＝8x 22．在函数y ＝1x中，自变量x 的取值范围是(A)A ．x ≠0B ．x>0C ．x<0D ．一切实数3．反比例函数y ＝－25x中，k 的值是(C)A ．2B ．－2C ．－25D ．－524．若函数y ＝x 2m ＋1为反比例函数，则m 的值是(D)A ．1B ．0 C.12D ．－1 知识点2 判断反比例函数关系5．如果直角三角形的面积一定，那么下列关于这个直角三角形边的关系中，正确的是(B)A ．两条直角边成正比例B ．两条直角边成反比例C ．一条直角边与斜边成正比例D ．一条直角边与斜边成反比例6．用电器的输出功率P 与通过的电流I 、用电器的电阻R 之间的关系是P ＝I 2R ，下面说法正确的是(B)A ．P 为定值，I 与R 成反比例B ．P 为定值，I 2与R 成反比例C ．P 为定值，I 与R 成正比例D ．P 为定值，I 2与R 成正比例知识点3 反比例函数的表达式7．已知y 是x 的反比例函数，且当x ＝2时，y ＝3，则该反比例函数的表达式是(C)A ．y ＝6xB ．y ＝16xC ．y ＝6xD ．y ＝6x－18．某工厂现有原材料100吨，每天平均用去x 吨，这批原材料能用y 天，则y 与x 之间的函数关系式为(B)A ．y ＝100xB ．y ＝100xC ．y ＝12x ＋100 D ．y ＝100－x9．已知近视眼镜的度数y(度)与镜片焦距x(m)成反比例．若200度近视眼镜的镜片焦距为0.5 m ，则y 与x 之间的函数关系式是y ＝100x.10．(教材P150“做一做”T3变式)已知变量y 与变量x 之间的对应值如下表：则变量y 与x 之间的函数关系式为y ＝6x ，当x ＝－12时，y ＝－12.11．列出下列问题中的函数关系式，并判断它们是否为反比例函数．(1)某农场的粮食总产量为1 500 t ，则该农场人数y(人)与平均每人占有粮食量x(t)之间的函数关系；(2)在加油站，加油机显示器上显示的某一种油的单价为每升6.85元，总价从0元开始随着加油量的变化而变化，则总价y(元)与加油量x(L)之间的函数关系．解：(1)y ＝1 500x，是反比例函数． (2)y ＝6.85x ，不是反比例函数．易错点忽视反比例函数中k ≠0的条件而致错12．若函数y ＝m －1x|m|是反比例函数，则m ＝－1．【变式】已知函数y ＝(m ＋1)xm 2－2是反比例函数，则m 的值为1． 02 中档题13．下列函数：①y ＝2x ；②y ＝－x ＋1；③xy ＝5；④y ＝x －1；⑤y ＝1x ＋1；⑥y ＝3x ＋7；⑦y ＝2x 2.其中是y 是x 的反比例函数的有(C)A ．0个B ．1个C ．2个D ．3个14．下列关系中，两个变量之间为反比例函数关系的是(D)A ．长40米的绳子用去x 米，还剩y 米B ．买单价3元的笔记本x 本，花了y 元C ．正方形的面积为S ，边长为aD ．菱形的面积为20，对角线的长分别为x ，y15．函数y ＝m （m ＋1）x是反比例函数，则m 必须满足(D)A ．m ≠0B ．m ≠－1C ．m ≠－1或m ≠0D ．m ≠－1且m ≠016．【关注整体思想】已知y 与2x ＋1成反比例函数关系，且当x ＝1时，y ＝2，那么当x ＝0时，y ＝6． 17．水池中有水若干吨，若单开一个出水口，出水速度v 与全池水放光所用时间t 如表：(1)(2)这是一个反比例函数吗？解：(1)t ＝10v.(2)是一个反比例函数．18．设面积为20 cm 2的平行四边形的一边长为a cm ，这条边上的高为h cm. (1)求h 关于a 的函数表达式及自变量a 的取值范围；(2)h 关于a 的函数是不是反比例函数？如果是，请说出它的比例系数； (3)当a ＝25时，求这条边上的高．解：(1)h ＝20a(a>0)．(2)是反比例函数，它的比例系数是20.(3)当a ＝25时，h ＝2025＝45.∴这条边上的高为45cm.03 综合题19．将x ＝23代入函数y ＝－1x 中，所得函数值记为y 1；又将x ＝y 1＋1代入函数y ＝－1x 中，所得函数值记为y 2；再将x ＝y 2＋1代入函数y ＝－1x 中，所得函数值记为y 3；…；继续下去，则y 1＝－32，y 2＝2，y 3＝－13，y 2 019＝－13．20．已知函数y ＝y 1＋y 2，y 1与x 成正比例，y 2与x 成反比例，且当x ＝1时，y ＝4；当x ＝2时，y ＝5. (1)求y 与x 之间的函数关系式； (2)当x ＝4时，求y 的值．解：(1)设y 1＝k 1x ，y 2＝k 2x ，则y ＝y 1＋y 2＝k 1x ＋k 2x.∵当x ＝1时，y ＝4；当x ＝2时，y ＝5，∴⎩⎪⎨⎪⎧4＝k 1＋k 2，5＝2k 1＋k 22.解得⎩⎪⎨⎪⎧k 1＝2，k 2＝2. ∴y ＝2x ＋2x.(2)当x ＝4时，y ＝2×4＋24＝812.2 反比例函数的图象与性质第1课时反比例函数的图象01 基础题知识点1 反比函数图象的画法1．请在如图所示的平面直角坐标系中画出反比例函数y ＝4x 和y ＝－4x的图象．解：如图所示．知识点2 反比例函数的图象与系数k 的关系2．反比例函数y ＝kx(k>0)的大致图象是(A)3．反比例函数y ＝－1x的图象位于第二、四象限．4．(新疆中考)如图，它是反比例函数y ＝m －5x图象的一支，根据图象可知常数m 的取值范围是m ＞5. 知识点3 反比例函数图象上点的坐标5．下列各点在反比例函数y ＝2x图象上的是(C)A ．(1，0.5)B ．(2，－1)C ．(－1，－2)D ．(－2，1)6．(海南中考)已知反比例函数y ＝kx的图象经过点(－1，2)，则这个函数的图象位于(D)A ．第二、三象限B ．第一、三象限C ．第三、四象限D ．第二、四象限 7．如图，已知OA ＝6，∠AOB ＝30°，则经过点A 的反比例函数的表达式为(B)A ．y ＝－93xB ．y ＝93xC ．y ＝9xD ．y ＝－9x8．(哈尔滨中考改编)已知反比例函数y ＝2k －3x的图象经过点(1，1)，则k 的值为2．9．已知点A(2，4)与点B(－3，m)在同一反比例函数的图象上，则m 的值是－83．知识点4 反比例函数图象的对称性10．对于反比例函数y ＝6x图象的对称性，下列叙述错误的是(D)A ．关于原点中心对称B ．关于直线y ＝x 对称C ．关于直线y ＝－x 对称D ．关于x 轴对称11．如图，在平面直角坐标系中，正方形的中心在原点O ，且正方形的一组对边与x 轴平行．若正方形的边长是2，则图中阴影部分的面积等于1．易错点分析问题不全面而致错12．已知反比例函数y ＝(m ＋1)xm 2－5的图象在第二、四象限内，则m 的值是－2． 02 中档题13．(教材P161复习题T6变式)(娄底中考)如图，在同一平面直角坐标系中，反比例函数y ＝kx与一次函数y ＝kx －1(k 为常数，且k ＞0)的图象可能是(B)14．如图是三个反比例函数y 1＝k 1x ，y 2＝k 2x ，y 3＝k 3x在x 轴上方的图象，由此观察得到k 1，k 2，k 3的大小关系为(C)A ．k 1＞k 2＞k 3B ．k 3＞k 1＞k 2C ．k 2＞k 3＞k 1D ．k 3＞k 2＞k 115．(绍兴中考)如图，Rt △ABC 的两个锐角顶点A ，B 在函数y ＝kx(x ＞0)的图象上，AC ∥x 轴，AC ＝2.若点A 的坐标为(2，2)，则点B 的坐标为(4，1)．16．已知反比例函数y ＝kx(k 为常数，k ≠0)的图象经过点A(2，3)．(1)求这个函数的表达式；(2)判断点B(－1，6)，C(3，2)是否在这个函数的图象上，并说明理由．解：(1)∵反比例函数y ＝kx的图象经过点A(2，3)，把点A 的坐标(2，3)代入表达式，得3＝k2.解得k ＝6.∴这个函数的表达式为y ＝6x.(2)分别把点B ，C 的坐标代入y ＝6x，可知点B 的坐标不满足函数表达式，点C 的坐标满足函数表达式． ∴点B 不在这个函数的图象上，点C 在这个函数的图象上．17．已知反比例函数y 1＝kx的图象与一次函数y 2＝kx ＋m 的图象相交于点A(2，1)，分别求出这两个函数的表达式，并在同一坐标系内画出它们的大致图象．解：∵反比例函数y 1＝kx的图象与一次函数y 2＝kx ＋m 的图象相交于点A(2，1)，∴⎩⎪⎨⎪⎧2×1＝k ，2k ＋m ＝1，解得⎩⎪⎨⎪⎧k ＝2，m ＝－3.∴y 1＝2x，y 2＝2x －3.它们的图象如图所示．03 综合题18．已知反比例函数y ＝1－2mx(m 为常数)的图象在第一、三象限．(1)求m 的取值范围；(2)如图，若该反比例函数的图象经过▱ABOD 的顶点D ，点A ，B 的坐标分别为(0，3)，(－2，0)． ①求出函数表达式；②【分类讨论思想】设点P 是该反比例函数图象上的一点，若OD ＝OP ，则P 点的坐标为(3，2)或(－2，－3)或(－3，－2)；若以D ，O ，P 为顶点的三角形是等腰三角形，则满足条件的点P 的个数为4个．解：(1)由题意知1－2m ＞0，解得m ＜12.(2)∵四边形ABOD 是平行四边形， ∴AD ∥BO 且AD ＝BO.∵A(0，3)，B(－2，0)，O(0，0)， ∴点D 的坐标是(2，3)． ∴1－2m 2＝3，1－2m ＝6.∴函数表达式为y ＝6x.第2课时反比例函数的性质01 基础题知识点1 反比例函数的性质1．反比例函数y ＝1x(x ＞0)的图象如图所示，随着x 值的增大，y 值(A)A ．减小B ．增大C ．不变D ．先减小，后不变2．(赤峰中考)点A(1，y 1)，B(3，y 2)是反比例函数y ＝9x图象上的两点，则y 1，y 2的大小关系是(A)A ．y 1＞y 2B ．y 1＝y 2C ．y 1＜y 2D ．不能确定3．反比例函数y ＝m ＋1x的图象在每个象限内，函数值y 随x 的增大而增大，则m 的取值范围是(D)A ．m ＜0B ．m ＞0C ．m ＞－1D ．m ＜－14．关于反比例函数y ＝－2x的图象，下列说法正确的是(D)A ．图象经过点(1，1)B ．两个分支分布在第一、三象限C ．两个分支关于x 轴成轴对称D ．当x ＜0时，y 随x 的增大而增大5．(本课时T2变式)(抚顺中考)已知A(x 1，y 1)，B(x 2，y 2)是反比例函数y ＝－3x图象上的两点，且x 1＞x 2＞0，则y 1＞y 2(填“＞”或“＜”)．6．已知反比例函数y ＝(2m －1)xm 2－2，当x ＞0时，函数值y 随x 的增大而增大，求m 的值．解：根据题意，得m 2－2＝－1，解得m ＝±1. ∵当x ＞0时，y 随x 的增大而增大，∴2m －1＜0.解得m ＜12.∴m ＝－1.知识点2 反比例函数中k 的几何意义7．如图，在平面直角坐标系中，点P 是反比例函数y ＝kx(x ＞0)图象上的一点，分别过点P 作PA ⊥x 轴于点A ，PB ⊥y轴于点B.若四边形OAPB 的面积为3，则k 的值为(A)A ．3B ．－3 C.32 D ．－328．(娄底中考)如图，在平面直角坐标系中，O 为坐标原点，点P 是反比例函数y ＝2x(x>0)图象上的一点，PA ⊥x 轴于点A ，则△POA 的面积为1．易错点1 忽视了函数增减性的前提条件9．(教材P157习题T4变式)若点A(a ，m)和点B(b ，n)在反比例函数y ＝7x的图象上，且a ＜b ，则(D)A ．m ＞nB ．m ＜nC ．m ＝nD ．m ，n 的大小无法确定易错点2 确定自变量的取值范围时漏解10．已知反比例函数y ＝10x，当y ＜5时，x 的取值范围是x ＞2或x ＜0.易错点3 忽视了反比例函数中k 的符号11．如图，A 为反比例函数y ＝kx图象上一点，AB ⊥x 轴于点B.若S △AOB ＝3，则k 的值为－6.02 中档题12．(遂宁中考)若点A(－6，y 1)，B(－2，y 2)，C(3，y 3)在反比例函数y ＝a 2＋1x(a 为常数)的图象上，则y 1，y 2，y 3大小关系为(D)A ．y 1＞y 2＞y 3B ．y 2＞y 3＞y 1C ．y 3＞y 2＞y 1D ．y 3＞y 1＞y 213．已知A(x 1，y 1)，B(x 2，y 2)是反比例函数y ＝kx(k ≠0)图象上的两个点，当x 1＜x 2＜0时，y 1＞y 2，那么一次函数y＝－kx ＋k 的图象不经过(C)A ．第一象限B ．第二象限C ．第三象限D ．第四象限14．(本课时T7变式)如图，反比例函数y ＝2x的图象经过矩形OABC 的边AB 的中点D ，则矩形OABC 的面积为4.15．(贵阳中考)如图，过x 轴上任意一点P 作y 轴的平行线，分别与反比例函数y ＝3x (x ＞0)，y ＝－6x(x ＞0)的图象交于A 点和B 点．若C 为y 轴任意一点，连接AC ，BC ，则△ABC 的面积为92．16．已知反比例函数y ＝k －1x(k 为常数，k ≠1)． (1)若在这个函数图象的每一分支上，y 随x 的增大而减小，求k 的取值范围； (2)若k ＝13，试判断点C(2，5)是否在这个函数的图象上，并说明理由．解：(1)∵在这个函数图象的每一分支上，y 随x 的增大而减小， ∴k －1＞0.解得k ＞1.(2)点C(2，5)不在这个函数的图象上．理由：∵当k ＝13时，k －1＝12， ∴反比例函数的表达式为y ＝12x. 当x ＝2时，y ＝6≠5，∴点C(2，5)不在这个函数的图象上．17．(河南中考)如图，反比例函数y ＝kx(x ＞0)的图象过格点(网格线的交点)P.(1)求反比例函数的表达式；(2)在图中画出两个矩形(不写画法)，要求每个矩形均满足下列两个条件： ①四个顶点均在格点上，且其中两个顶点分别是点O ，点P ； ②矩形的面积等于k 的值．解：(1)∵反比例函数y ＝kx(x ＞0)的图象过格点P(2，2)，∴k ＝2×2＝4.∴反比例函数的表达式为y ＝4x.(2)如图所示，矩形OAPB ，矩形OCDP 即为所求作的图形．03 综合题 18．如图，在平面直角坐标系中，△ABC 的顶点A 和C 分别在x 轴、y 轴的正半轴上，且AB ∥y 轴，AB ＝3，△ABC 的面积为2 3.(1)求点B 的坐标；(2)将△ABC 以点B 为旋转中心顺时针方向旋转90°得到△DBE ，反比例函数图象恰好过点D 时，求反比例函数的表达式．解：(1)过点C 作CH ⊥AB 于点H ，BD 交y 轴于点G ，∵S △ABC ＝12AB·CH ，∴12×3·CH ＝2 3. ∴CH ＝433.∵AB ∥y 轴，∴点B 的坐标为(433，3)．(2)∵△ABC 以点B 为旋转中心顺时针方向旋转90°得到△DBE ， ∴BD ＝BA ＝3，∠DBA ＝90°. ∴BD ∥x 轴．∵DG ＝BD －BG ＝3－433，设反比例函数表达式为y ＝kx，∴k ＝(433－3)×3＝43－9.∴反比例函数表达式为y ＝43－9x.3 反比例函数的应用01 基础题知识点1 反比例函数的实际应用1．某电子商城推出分期付款购买电脑的活动，一台电脑的售价为1.2万元，前期付款4 000元，后期每个月分期付相等数额，则每个月的付款额y(元)与付款月数x 之间的函数关系式是(A)A ．y ＝8 000x (x 取正整数)B ．y ＝8xC ．y ＝8 000xD ．y ＝8 000x2．(沈阳铁西区期末)小明乘车从广州到北京，行车的平均速度y(km/h)和行车时间x(h)之间的函数图象是(B)3．把一个长、宽、高分别为3 cm 、2 cm 、1 cm 的长方体铜块铸成一个圆柱体铜块，则该圆柱体铜块的底面积S(cm 2)与高h(cm)之间的函数关系式为S ＝6h．4．如图所示是某一蓄水池的排水速度v(m 3/h)与排完水池中的水所用时间t(h)之间的函数关系图象，则排水速度v(m 3/h)与时间t(h)之间的函数关系式是v ＝48t.若要5 h 排完水池中的水，则排水速度应为9.6__m 3/h.知识点2 反比例函数跨学科的应用5．水平地面上重1 500 N 的物体，与地面的接触面积为x m 2，那么该物体对地面的压强y(单位：N/m 2)与地面的接触面积x(m 2)之间的函数关系可以表示为y ＝1 500x．6．实验表明，当导线的长度一定时，导线的电阻与它的横截面积成反比例．一条长为100 cm 的导线的电阻R(Ω)与它的横截面积S(cm 2)的函数图象如图所示，那么当S ＝2 cm 2时，R ＝14.5Ω.知识点3 反比例函数与一次函数的综合7．(广东中考)如图，在同一平面直角坐标系中，直线y ＝k 1x(k 1≠0)与双曲线y ＝k 2x(k 2≠0)相交于A ，B 两点，已知点A 的坐标为(1，2)，则点B 的坐标为(A)A ．(－1，－2)B ．(－2，－1)C ．(－1，－1)D ．(－2，－2)8．(鸡西中考)如图是反比例函数y 1＝kx(x>0)和一次函数y 2＝mx ＋n 的图象．若y 1＜y 2，则相应的x 的取值范围是1＜x ＜6．9．(贵港中考)如图，一次函数y ＝2x －4的图象与反比例函数y ＝kx(k ≠0)的图象交于A ，B 两点，且点A 的横坐标为3.(1)求反比例函数的表达式； (2)求点B 的坐标．解：(1)把x ＝3代入y ＝2x －4，得y ＝6－4＝2. 则点A 的坐标是(3，2)．把(3，2)代入y ＝kx，得k ＝6.则反比例函数的表达式是y ＝6x .(2)根据题意，得2x －4＝6x，解得x ＝3或－1.把x ＝－1代入y ＝2x －4，得y ＝－6，则点B 的坐标是(－1，－6)．易错点1 确定自变量的取值范围时漏解10．【数形结合思想】如图，已知一次函数y ＝ax ＋b 和反比例函数y ＝kx(k ≠0)的图象相交于A(－2，y 1)，B(1，y 2)两点，则不等式ax ＋b ＜kx的解集为－2＜x ＜0或x ＞1．易错点2 忽略反比例函数中自变量的取值范围致错11．(宜昌中考)某学校要种植一块面积为100 m 2的长方形草坪，要求两边长均不小于5 m ，则草坪的一边长为y(单位：m)随另一边长x(单位：m)的变化而变化的图象可能是(C)02 中档题12．(牡丹江中考)如图，直线y ＝－12x ＋b 与x 轴交于点A ，与双曲线y ＝－4x(x ＜0)交于点B.若S △AOB ＝2，则b 的值是(D)A ．4B ．3C ．2D ．113．(安徽中考)如图，正比例函数y ＝kx 与反比例函数y ＝6x的图象有一个交点A(2，m)，AB ⊥x 轴于点B.平移直线y ＝kx ，使其经过点B 得到直线l ，则直线l 对应的函数表达式是y ＝32x －3．14．(内江中考)已知A(－4，2)，B(n ，－4)两点是一次函数y ＝kx ＋b 和反比例函数y ＝mx图象的两个交点．(1)求一次函数和反比例函数的表达式； (2)求△AOB 的面积；(3)观察图象，直接写出不等式kx ＋b －mx＞0的解集．解：(1)把A(－4，2)代入y ＝mx ，得m ＝2×(－4)＝－8.∴反比例函数的表达式为y ＝－8x.把B(n ，－4)代入y ＝－8x ，得－4＝－8n.解得n ＝2.把A(－4，2)和B(2，－4)代入y ＝kx ＋b ，得 ⎩⎪⎨⎪⎧－4k ＋b ＝2，2k ＋b ＝－4.解得⎩⎪⎨⎪⎧k ＝－1，b ＝－2. ∴一次函数的表达式为y ＝－x －2.(2)y ＝－x －2中，令y ＝0，则x ＝－2， ∴点C 的坐标为(－2，0)． ∴S △AOB ＝S △AOC ＋S △BOC ＝12×2×2＋12×2×4 ＝6.(3)由图可得，不等式kx ＋b －mx>0的解集为x<－4或0<x<2.15．【关注数学建模】(丽水中考)丽水某公司将“丽水山耕”农副产品运往杭州市场进行销售，记汽车行驶时间为t 小时，平均速度为v(1)(2)汽车上午7：30从丽水出发，能否在上午10：00之前到达杭州市场？请说明理由； (3)若汽车到达杭州市场的行驶时间t 满足3.5≤t ≤4，求平均速度v 的取值范围．解：(1)根据表格中数据，可知v ＝kt.∵v ＝75时，t ＝4，∴k ＝75×4＝300.∴v ＝300t.(2)∵10－7.5＝2.5，∴当t ＝2.5时，v ＝3002.5＝120＞100.∴汽车上午7：30从丽水出发，不能在上午10：00之前到达杭州市场．(3)∵3.5≤t ≤4，∴75≤v ≤6007.答：平均速度v 的取值范围是75≤v ≤6007.求反比例函数与一次函数图象的交点问题【方法指导】求反比例函数与一次函数图象的交点问题，应联立反比例函数与一次函数表达式，构造关于自变量的一元二次方程，根据一元二次方程根的判别式判断交点情况，具体如下：①当Δ＞0时，反比例函数与一次函数图象有两个交点；②当Δ＝0时，反比例函数与一次函数图象有且只有一个交点；③当Δ＜0时，反比例函数与一次函数图象没有交点．1．已知一次函数y ＝－x ＋4与反比例函数y ＝kx的图象在同一平面直角坐标系中有两个交点，则k 的取值范围是(D)A ．k ＜4B ．k ≤4C ．k ≤4且k ≠0D ．k ＜4且k ≠02．已知反比例函数y ＝－2x 和一次函数y ＝kx ＋1的图象只有一个交点，那么k 的值为18．3．如图，过点C(2，1)作AC ∥x 轴，BC ∥y 轴，点A ，B 都在直线y ＝－x ＋6上．若双曲线y ＝kx(x ＞0)与△ABC总有交点，则k 的取值范围是2≤k ≤9．小专题15 反比例函数与一次函数综合类型1 在平面直角坐标系中判断函数图象1．已知函数y ＝kx(k ≠0)中，在每个象限内，y 随x 的增大而增大，那么它和函数y ＝kx(k ≠0)在同一直角坐标系内的大致图象是(B)2．(日照中考)反比例函数y ＝kbx的图象如图所示，则一次函数y ＝kx ＋b(k ≠0)的图象大致是(D)3．(广元中考)如图为一次函数y ＝ax －2a 与反比例函数y ＝－ax(a ≠0)在同一平面直角坐标系中的大致图象，其中较准确的是(B)4．(潍坊中考)一次函数y ＝ax ＋b 与反比例函数y ＝a －bx，其中ab ＜0，a ，b 为常数，它们在同一平面直角坐标系中的图象可以是(C)类型2 反比例函数与一次函数的交点问题5．如图，反比例函数y ＝k x 的图象与一次函数y ＝－12x 的图象交于点A(－2，m)和点B ，则点B 的坐标是(A)A ．(2，－1)B ．(1，－2)C ．(12，－1)D ．(1，－12)6．(自贡中考)一次函数y 1＝k 1x ＋b 和反比例函数y 2＝k 2x(k 1·k 2≠0)的图象如图所示．若y 1＞y 2，则x 的取值范围是(D)A ．－2＜x ＜0或x ＞1B ．－2＜x ＜1C ．x ＜－2或x ＞1D ．x ＜－2或0＜x ＜17．如图，已知一次函数y ＝－x ＋b 与反比例函数y ＝1x的图象有2个公共点，则b 的取值范围是(C)A ．b ＞2B ．－2＜b ＜2C ．b ＞2或b ＜－2D ．b ＜－28．(烟台中考)如图，直线y ＝x ＋2与反比例函数y ＝kx(k>0)的图象在第一象限交于点P.若OP ＝10，则k 的值为3.9．(连云港中考)设函数y ＝3x 与y ＝－2x －6的图象的交点坐标为(a ，b)，则1a ＋2b的值是－2.10．(仙桃中考)如图，在平面直角坐标系中，直线y ＝－12x 与反比例函数y ＝kx(k ≠0)在第二象限内的图象相交于点A(m ，1)．(1)求反比例函数的表达式；(2)将直线y ＝－12x 向上平移后与反比例函数图象在第二象限内交于点B ，与y 轴交于点C ，且△ABO 的面积为32，求直线BC 的表达式．解：(1)∵直线y ＝－12x 过点A(m ，1)，∴－12m ＝1，解得m ＝－2. ∴A(－2，1)．∵反比例函数y ＝kx(k ≠0)的图象过点A(－2，1)，∴k ＝(－2)×1＝－2.∴反比例函数的表达式为y ＝－2x .(2)设直线BC 的表达式为y ＝－12x ＋b ，∵△ACO 与△ABO 面积相等，且△ABO 的面积为32，∴S △ACO ＝12OC·2＝32.∴OC ＝32，即b ＝32.∴直线BC 的表达式为y ＝－12x ＋32.11．(菏泽中考)如图，已知点D 在反比例函数y ＝ax(a ≠0)的图象上，过点D 作DB ⊥y 轴，垂足为B(0，3)，直线y＝kx ＋b 经过点A(5，0)，与y 轴交于点C ，且BD ＝OC ，OC ∶OA ＝2∶5.(1)求反比例函数y ＝ax和一次函数y ＝kx ＋b 的表达式；(2)直接写出关于x 的不等式ax＞kx ＋b 的解集．解：(1)∵BD ＝OC ，OC ∶OA ＝2∶5，点A(5，0)，点B(0，3)， ∴OA ＝5，OC ＝BD ＝2，OB ＝3.又∵点C 在y 轴负半轴，点D 在第二象限，∴点C 的坐标为(0，－2)，点D 的坐标为(－2，3)．∵点D(－2，3)在反比例函数y ＝ax的图象上，∴a ＝(－2)×3＝－6.∴反比例函数的表达式为y ＝－6x.将A(5，0)，C(0，－2)代入y ＝kx ＋b ，得⎩⎪⎨⎪⎧5k ＋b ＝0，b ＝－2.解得⎩⎪⎨⎪⎧k ＝25，b ＝－2.∴一次函数的表达式为y ＝25x －2.(2)将y ＝25x －2代入y ＝－6x ，得25x －2＝－6x. 整理，得25x 2－2x ＋6＝0.∵Δ＝(－2)2－4×25×6＝－285＜0，∴一次函数图象与反比例函数图象无交点．观察图象，可知：当x ＜0时，反比例函数图象在一次函数图象上方，∴不等式ax＞kx ＋b 的解集为x ＜0.12．(绵阳中考)如图，一次函数y ＝－12x ＋52的图象与反比例函数y ＝kx(k ＞0)的图象交于A ，B 两点，过A 点作x 轴的垂线，垂足为M ，△AOM 的面积为1. (1)求反比例函数的表达式；(2)在y 轴上求一点P ，使PA ＋PB 的值最小，并求出其最小值和点P 的坐标．解：(1)∵△AOM 面积的为1， ∴12|k|＝1. ∵k ＞0，∴k ＝2.故反比例函数的表达式为y ＝2x.(2)作点A 关于y 轴的对称点A′，连接A′B ，交y 轴于点P ，则PA ＋PB 的值最小．由⎩⎨⎧y ＝－12x ＋52，y ＝2x，解得⎩⎪⎨⎪⎧x ＝1，y ＝2或⎩⎪⎨⎪⎧x ＝4，y ＝12.∴A(1，2)，B(4，12)．∴A′(－1，2)，最小值A′B ＝（4＋1）2＋（12－2）2＝1092.设直线A′B 的表达式为y ＝mx ＋n ，则⎩⎪⎨⎪⎧－m ＋n ＝2，4m ＋n ＝12.解得⎩⎨⎧m ＝－310，n ＝1710. ∴直线A′B 的表达式为y ＝－310x ＋1710.∴x ＝0时，y ＝1710.∴点P 的坐标为(0，1710)．小专题16 反比例函数中k 的几何意义类型1 同一象限内运用k 的几何意义S 矩形PAOB ＝|k| S △AOP ＝|k|2 S △ACP ＝|k|21．如图，过反比例函数y ＝2x(x ＞0)图象上任意两点A ，B 分别作x 轴的垂线，垂足分别为C ，D ，连接OA ，OB ，设AC 与OB 的交点为E ，△AOE 与梯形ECDB 的面积分别为S 1，S 2，比较它们的大小，可得(C)A ．S 1＞S 2B ．S 1＜S 2C ．S 1＝S 2D ．S 1，S 2的大小关系不能确定2．如图，已知双曲线y ＝kx(k ＜0)的图象经过Rt △OAB 斜边OA 的中点D ，且与直角边AB 相交于点C.若点A 的坐标为(－8，4)，则△AOC 的面积为12．3．(烟台中考)如图，反比例函数y ＝kx(k ≠0)的图象经过▱ABCD 对角线的交点P ，已知点A ，C ，D 在坐标轴上，BD ⊥DC ，▱ABCD 的面积为6，则k ＝－3．4．如图，过点P(2，3)分别作PC ⊥x 轴于点C ，PD ⊥y 轴于点D ，PC ，PD 分别交反比例函数y ＝kx(x ＞0)的图象于点A ，B ，△OAB 的面积为83，则k 的值是2．类型2 两个象限内运用k 的几何意义S △ABC ＝|k| S △APP 1＝2|k|5．如图，在平面直角坐标系中，直线y ＝kx(k ≠0)与双曲线y ＝3x相交于A ，B 两点，过点A 作AM ⊥x 轴，过点B 作BN ⊥y 轴，则图中阴影部分的面积为3．6．如图，直线y ＝mx 与双曲线y ＝kx(k ≠0)交于A ，B 两点，过点A 作AM ⊥x 轴，垂足为M ，连接BM.若S △ABM＝4，则k 的值为－4．7．(陕西中考)如图，在平面直角坐标系中，过点M(－3，2)分别作x 轴、y 轴的垂线与反比例函数y ＝4x的图象交于A ，B 两点，则四边形MAOB 的面积为10．类型3 双反比例函数中运用k 的几何意义S 矩形ABCD ＝|k 1|－|k 2| S △ABO ＝|k 1|－|k 2|2 S △ABC ＝S △ABO ＝|k 1|＋|k 2|28．(龙东中考)如图，平面直角坐标系中，点A 是x 轴上任意一点，BC 平行于x 轴，分别交y ＝3x (x ＞0)，y ＝kx(x ＜0)的图象于B ，C 两点．若△ABC 的面积为2，则k 的值为－1．9．如图，点A 在反比例函数y ＝2x (x ＞0)的图象上，点B 在反比例函数y ＝4x(x ＞0)的图象上，且AB ∥x 轴，BC ⊥x轴于点C ，则四边形ABCO 的面积为3．10．反比例函数y 1＝－3x ，y 2＝k x 的图象如图所示，点A 为y 1＝－3x的图象上任意一点，过点A 作x 轴的平行线交y 2＝kx的图象于点C ，交y 轴于点B.点D 在x 轴的正半轴上，CD ∥OA.若四边形AODC 的面积为2，则k 的值为－1．小专题17 反比例函数与几何图形综合类型1 反比例函数与特殊三角形1．(仙桃中考)如图，P(m ，m)是反比例函数y ＝9x在第一象限内的图象上一点，以P 为顶点作等边△PAB ，使AB 落在x 轴上，则△POB 的面积为(D)A.92B ．3 3 C.9＋1234 D.9＋3322．(遵义中考)如图，直角三角形的直角顶点在坐标原点，∠OAB ＝30°，若点A 在反比例函数y ＝6x(x ＞0)的图象上，则经过点B 的反比例函数表达式为(C)A ．y ＝－6xB ．y ＝－4xC ．y ＝－2xD ．y ＝2x3．如图，点A 为函数y ＝16x (x ＞0)图象上一点，连接OA ，交函数y ＝4x(x ＞0)的图象于点B ，点C 是x 轴上一点，且AO ＝AC ，则△ABC 的面积为(B)A ．6B ．8C ．10D ．12类型2 反比例函数与特殊四边形4．(重庆中考)如图，在平面直角坐标系中，菱形ABCD 的顶点A ，B 在反比例函数y ＝kx(k ＞0，x ＞0)的图象上，横坐标分别为1，4，对角线BD ∥x 轴．若菱形ABCD 的面积为452，则k 的值为(D)A.54B.154C ．4D ．55．如图，正方形OABC 和正方形ADEF 的顶点A ，D ，C 在坐标轴上，点F 在AB 上，点B ，E 在函数y ＝1x的图象上，则点E 的坐标是(A)A.⎝ ⎛⎭⎪⎫5＋12，5－12B.⎝ ⎛⎭⎪⎫3＋52，3－52C.⎝ ⎛⎭⎪⎫5－12，5＋12D.⎝ ⎛⎭⎪⎫3－52，3＋526．(荆门中考)如图，在平面直角坐标系xOy 中，函数y ＝kx(k ＞0，x ＞0)的图象经过菱形OACD 的顶点D 和边AC的中点E.若菱形OACD 的边长为3，则k 的值为7．(广西中考)如图，矩形ABCD 的顶点A ，B 在x 轴上，且关于y 轴对称，反比例函数y ＝k 1x(x ＞0)的图象经过点C ，反比例函数y ＝k 2x(x ＜0)的图象分别与AD ，CD 交于点E ，F.若S △BEF ＝7，k 1＋3k 2＝0，则k 1等于9．类型3 反比例函数与图形变换8．如图，在平面直角坐标系中，菱形ABCD 的顶点A 的坐标为(1，0)，顶点B ，C 在第一象限，顶点D 在y 轴的正半轴上，∠BAD ＝60°，将菱形ABCD 沿AB 翻折得到菱形ABC′D′，点D′恰好落在x 轴上．若函数y ＝kx(x ＞0)的图象经过点C′，则k 的值为(D)A. 3 B ．2 3 C ．3 3 D ．4 39.如图，在平面直角坐标系中，矩形OABC 的顶点AC 分别在x 轴的负半轴、y 轴的正半轴上，点B 在第二象限．将矩形OABC 绕点O 顺时针旋转，使点B 落在y 轴上，得到矩形ODEF ，BC 与OD 相交于点M.若经过点M 的反比例函数y ＝k x (x ＜0)的图象交AB 于点N ，OA ＝4，OC ＝2，则BN 的长为32．回顾与思考(六) 反比例函数01 分点突破知识点1 反比例函数的图象与性质1．(柳州中考)已知反比例函数的表达式为y ＝|a|－2x，则a 的取值范围是(C) A ．a ≠2 B ．a ≠－2 C ．a ≠±2 D ．a ＝±22．(徐州中考)如果点(3，－4)在反比例函数y ＝kx的图象上，那么下列各点中，在此图象上的是(C)A ．(3，4)B ．(－2，－6)C ．(－2，6)D ．(－3，－4)3．(衡阳中考)对于反比例函数y ＝－2x，下列说法不正确的是(D)A ．图象分布在第二、四象限B ．当x>0时，y 随x 的增大而增大C ．图象经过点(1，－2)D ．若点A(x 1，y 1)，B(x 2，y 2)都在图象上，且x 1<x 2，则y 1<y 24．(齐齐哈尔中考)已知反比例函数y ＝2－kx的图象在第一、三象限内，则k 的值可以是1(答案不唯一)．(写出满足条件的一个k 的值即可)知识点2 反比例函数与一次函数综合5．(徐州中考)如图，在平面直角坐标系xOy 中，函数y ＝kx ＋b(k ≠0)与y ＝mx(m ≠0)的图象相交于点A(2，3)，B(－6，－1)，则不等式kx ＋b ＞mx 的解集为(B)A ．x ＜－6B ．－6＜x ＜0或x ＞2C ．x ＞2D ．x ＜－6或0＜x ＜26．(大庆中考)在同一平面直角坐标系中，函数y ＝kx(k ≠0)和y ＝kx －3的图象大致是(B)知识点3 反比例函数与几何图形综合7．如图，在△AOB 中，AO ＝AB ，点A 在第一象限，点B 在x 轴上，△AOB 的面积为4，反比例函数y ＝kx(x ＞0)的图象经过点A ，则k 的值等于(C)A ．1B ．2C ．4D ．8知识点4 反比例函数的应用8．(台州中考)已知电流I(安培)、电压U(伏特)、电阻R(欧姆)之间的关系为I ＝UR，当电压U 为定值时，I 关于R 的函数图象是(C)9.码头工人往一艘轮船上装载货物，装完货物所需时间y(min)与装载速度x(t/min)之间的函数关系如图(双曲线y ＝kx的一支)．如果以5 t/min 的速度卸货，那么卸完货物需要的时间是120min.02 易错题集训10．已知函数y ＝(m －2)xm 2－10是反比例函数，且当x ＜0时，y 随x 的增大而减小，则m 的值是3．11.如图，点A 是反比例函数y ＝kx(k ≠0)的图象上的一点，过点A 作AB ⊥x 轴，垂足为B.点C 为y 轴上的一点，连接AC ，BC.若△ABC 的面积为4，则k 的值是－8．12．正比例函数y ＝x 的图象与反比例函数y ＝4x 的图象在第一象限内交于点B ，点C 是反比例函数y ＝4x在第一象限图象上的一个动点．当△OBC 的面积为3时，点C 的横坐标是1或4． 03 中考题型演练13．(威海中考)若点(－2，y 1)，(－1，y 2)，(3，y 3)在双曲线y ＝kx(k ＜0)上，则y 1，y 2，y 3的大小关系是(D)A ．y 1＜y 2＜y 3B ．y 3＜y 2＜y 1C ．y 2＜y 1＜y 3D ．y 3＜y 1＜y 214．(郴州中考)如图，A ，B 是反比例函数y ＝4x在第一象限内的图象上的两点，且A ，B 两点的横坐标分别是2和4，则△OAB 的面积是(B)A ．4B ．3C ．2D ．115．(陕西中考)已知A ，B 两点分别在反比例函数y ＝3m x (m ≠0)和y ＝2m －5x (m ≠52)的图象上．若点A 与点B 关于x 轴对称，则m 的值为1.16．(淄博中考)如图，在平面直角坐标系中，Rt △ABC 的直角边AC 在x 轴上，∠ACB ＝90°，AC ＝1，反比例函数y ＝kx(k ＞0)的图象经过BC 边的中点D(3，1)． (1)求这个反比例函数的表达式；(2)若△ABC 与△EFG 成中心对称，且△EFG 的边FG 在y 轴的正半轴上，点E 在这个函数的图象上． ①求OF 的长；②连接AF ，BE ，求证：四边形ABEF 为正方形．解：(1)∵反比例函数y ＝kx(k>0)的图象经过点D(3，1)，∴k ＝3×1＝3.∴反比例函数的表达式为y ＝3x.(2)①∵D 为BC 的中点， ∴BC ＝2.∵△ABC 与△EFG 成中心对称， ∴△ABC ≌△EFG .∴GF ＝BC ＝2，GE ＝AC ＝1. ∵点E 在反比例函数的图象上， ∴E(1，3)，即OG ＝3. ∴OF ＝OG －FG ＝1.②证明：∵AC ＝1，OC ＝3， ∴OA ＝GF ＝2.在△AOF 和△FGE 中，⎩⎪⎨⎪⎧AO ＝FG ，∠AOF ＝∠FGE ，OF ＝GE ，∴△AOF ≌△FGE(SAS)．∴AF ＝EF.∴∠GFE ＝∠FAO ＝∠ABC.∴∠GFE ＋∠AFO ＝∠FAO ＋∠BAC ＝90°. ∴∠EFA ＝∠FAB ＝90°. ∴EF ∥AB. 又∵EF ＝AB ，∴四边形ABEF 为矩形． ∵AF ＝EF ，∴四边形ABEF 为正方形． 04 核心素养专练17．【注重实践探究】(乌鲁木齐中考)小明根据学习函数的经验，对函数y ＝x ＋1x的图象与性质进行了探究．下面是小明的探究过程，请补充完整：(1)函数y ＝x ＋1x的自变量x 的取值范围是x ≠0；(2)下表列出了y 与x 的几组对应值，请写出m ，n 的值：m ＝103，n ＝103；(3)(4)结合函数图象，请完成：①当y ＝－174时，x ＝－4或－14；②写出该函数的一条性质答案不唯一，如：①图象在第一、三象限且关于原点对称；②当－1≤x<0，0<x ≤1时，y 随x 增大而减小；当x<－1，x>1时，y 随x 的增大而增大；③若方程x ＋1x＝t 有两个不相等的实数根，则t 的取值范围是t>2或t<－2．。

北师大版数学九年级上册第六章反比例函数课时练试题及答案

北师大版数学九年级上册第六章反比例函数课时作业6.1 反比例函数【基础练习】一、填空题：1.A、B两地相距120千米，一辆汽车从A地去B地，则其速度v（千米/时）与行驶时间t（小时）之间的函数关系可表示为；2.有一面积为60的梯形，其上底长是下底长的13，设下底长为x，高为y，则y与x的函数关系式是；3.已知y与x成反比例，并且当x = 2时，y = -1，则当x = -4时，y = .二、选择题：1.下列各问题中的两个变量成反比例的是（）；A.某人的体重与年龄B.时间不变时，工作量与工作效率C.矩形的长一定时，它的周长与宽D.被除数不变时，除数与商2.已知y与x成反比例，当x = 3时，y = 4，那么当y = 3时，x的值为（）；A. 4B. -4C. 3D. -33.下列函数中，不是反比例函数的是（）A. xy = 2B. y = - k3x(k≠0) C. y =3x-1 D. x = 5y-1三、解答题：1.一水池内有污水60m3，设放净全池污水所需的时间为t (小时），每小时的放水量为w m3，（1）试写出t与w之间的函数关系式，t是w反比例函数吗？（2）求当w = 15时，t的值.2.已知y 是x 的反比例函数，下表给出了x 与y 的一些值：（1）写出这个反比例函数表达式；（2）将表中空缺的x 、y 值补全.【综合练习】举出几个日常生活中反比例函数的实例.【探究练习】已知函数y = y 1 +y 2，y 1与x 成正比例，y 2与x 成反比例，且当x = 1时，y = 4,当x = 2时，y = 5. 求y 关于x 的函数解析式.答案:【基础练习】一、1. v = 120t ； 2. y = 90x ； 3. 12. 二、1. D ； 2. A ； 3. C. 三、1. （1）t =60w ，（2）t = 4. 2. （1）y = 3x ；（2）从左至右：x = -4，-1，2，3；y = - 35 ，- 32 ，3，34，35. 【综合练习】略.x -5-3-2 1 4 5 y-34-1-3321]【探究练习】y = 2x + 2x .6.1 反比例函数一．判断题1．如果y 是x 的反比例函数，那么当x 增大时，y 就减小（） 2．当x 与y 乘积一定时，y 就是x 的反比例函数，x 也是y 的反比例函数（） 3．如果一个函数不是正比例函数，就是反比例函数（） 4．y 与x 2成反比例时y 与x 并不成反比例（） 5．y 与2x 成反比例时，y 与x 也成反比例（） 6．已知y 与x 成反比例，又知当2=x 时，3=y ，则y 与x 的函数关系式是6xy =（）二．填空题 7．)0(≠=k xky 叫__________函数，x 的取值范围是__________； 8．已知三角形的面积是定值S ，则三角形的高h 与底a 的函数关系式是_________=h ，这时h 是a 的__________；9．如果y 与x 成反比例，z 与y 成正比例，则z 与x 成__________； 10．如果函数y =222-+k k kx是反比例函数，那么k =________，此函数的解析式是；11．下列函数表达式中，x 均表示自变量，那么哪些是反比例函数，如果是请在括号内填上k 的值，如果不是请填上“不是”①x y 5=；（） ②x y 4.0=；（） ③2xy =；（） ④2=xy ；（）⑤πx y =；（）⑥xy 5-=（）⑦12-=x y （）12．判断下面哪些式子表示y 是x 的反比例函数？①31-=xy ； ②x y -=5； ③x y 52-=； ④)0(2≠=a a xay 为常数且；解：其中是反比例函数，而不是；13．计划修建铁路1200km ，那么铺轨天数y （天）是每日铺轨量x 的反比例函数吗？解：因为，所以y 是x 的反比例函数；14．一块长方形花圃，长为a 米，宽为b 米，面积为8平方米，那么a 与b 成函数关系，列出a 关于b 的函数关系式为；三．选择题： 15．若nxm y ++=2)5(是反比例函数，则m 、n 的取值是（）（A ）3,5-=-=n m （B ）3,5-=-≠n m （C ） 3,5=-≠n m （D ）4,5-=-≠n m 16．附城二中到联安镇为5公里，某同学骑车到达，那么时间t 与速度（平均速度）v 之间的函数关系式是（）（A ） st v = （B ） s t v += （C ） t s v = （D ） stv = 17．已知A （2-，a ）在满足函数xy 2=，则___=a （）（A ） 1- （B ） 1 （C ） 2- （D ） 218．下列函数中，是反比例函数的是（）（A ） 1)1(=-y x （B ） 11+=x y （C ） 21xy = （D ） x y 31= 19．下列关系式中，哪个等式表示y 是x 的反比例函数（）（A ） x ky = （B ） 2xB y = （C ） 121+=x y （D ） 12=-xy20．函数y m xm m =+--()2229是反比例函数，则m 的值是（）（A ）m =4或m =-2（B ） m =4 （C ） m =-2 （D ） m =-1四．解答题：21．在某一电路中，保持电压V （伏特）不变，电流I （安培）与电阻R （欧姆）成反比例，当电阻R=5时，电流I=2安培。

(含答案)九年级数学北师大版上册课时练第6章《6.2反比例函数的图像与性质》(2)

答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读题，结合平时课堂上所学的知识，解答难题；一定要镇定，不能因此慌了手脚，影响下面的答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的小朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！课时练6.2反比例函数的图象与性质一、选择题1.反比例函数5n y x+=的图象经过点()2,3,则n 的值是()A.-2B.-1C.0D.12.若0ab <，则正比例函数y ax =与反比例函数by x=在同一平面直角坐标系中的大致图像可能是()A. B.C. D.3.如图，点A 是反比例函数(0)ky x x=<图象上的一点，过点A 作ABCD ，使点B 、C 在x 轴上，点D 在y 轴上.已知ABCD 的面积为8，则k 的值为()A.8B.-8C.4D.-44．点A （x 1，y 1），B （x 2，y 2）都在反比例函数y ＝的图象上，且x 1＜x 2＜0，则y 1，y 2的大小关系是（）A ．y 2＞y 1＞0B ．y 1＞y 2＞0C ．0＞y 2＞y 1D ．0＞y 1＞y 25．反比例函数y ＝（a 为常数）的图象上有三个点（﹣1，y 1），（2，y 2），（3，y 3），则y 1，y 2，y 3的大小关系是（）A ．y 2＜y 3＜y 1B ．y 3＜y 2＜y 1C ．y 1＜y 2＜y 3D ．y 1＜y 3＜y 26．在同一直角坐标系中反比例函数y ＝与一次函数y ＝x +a （a ≠0）的图象大致是（）A ．B ．C ．D ．7.如图,在平面直角坐标系中,点P 是反比例函数y=（x＞0）图象上的一点,分别过点P 作PA ⊥x 轴于点A，PB⊥y 轴于点B.若四边形OAPB 的面积为3,则k 的值为（）A.3B.﹣3C. D.﹣8.如图，过点O 作直线与双曲线y=kx -1（k≠0）交于A、B 两点，过点B 作BC⊥x 轴于点C，作BD⊥y 轴于点D．在x 轴，y 轴上分别取点E、F，使点A、E、F 在同一条直线上，且AE=AF．设图中矩形ODBC 的面积为S 1，△EOF 的面积为S 2，则S 1、S 2的数量关系是（）A.S 1=S 2B.2S 1=S 2C.3S 1=S 2D.4S 1=S 2二、填空题9．在函数4y x=-的图象上有三点(﹣3，y 1)、(﹣2，y 2)、(1，y 3)，则函数值y 1、y 2、y 3的大小关系为______．10．在平面直角坐标系内，过反比例函数(0)ky k x=>的图象上的一点分别作x 轴、y 轴的垂线段，与x 轴、y 轴所围成的矩形面积是6，则函数解析式为_________．11．如图，反比例函数ky x=与⊙O 的一个交点为P （2，1），则图中阴影部分的面积是_____．12．已知反比例函数y=2k x-的图象如图，则一元二次方程x 2﹣（2k ﹣1）x+k 2﹣1=0根的情况是__．13.已知点(m－1，y 1)，(m－3，y 2)是反比例函数y=mx (m<0)的图象上的两点，则y 1______y 2(填“>”“=”或“<”)14.如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F 在AB上,点B、E在反比例函数y=的图象上,OA=1,OC=6,则正方形ADEF的边长为．三、解答题15．如图，反比例函数y 1＝（x ＞0）的图象与一次函数y 2＝kx +b 的图象交于A ，B 两点，点A 的坐标为（2，6），点B 的坐标为（n ，1）．（1）求反比例函数与一次函数的表达式；（2）当y1＞y2时，请直接写出x的取值范围；＝5，求点E的坐标．（3）点E为y轴上一个动点，若S△AEB16．如图，一次函数y＝﹣x+b的图象与x轴交于A点，与y轴交于B点，与反比例函数y＝的图象交于点E（1，5）和点F．（1）求k，b的值以及点F的坐标；（2）求△EOF的面积；（3）请根据函数图象直接写出反比例函数值大于一次函数值时x的范围．参考答案1.D2.B3B.4.A.5.A6.C7.A8.B9．y3＜y1＜y210．6 yx =11．5 4 p12．无实数根13.>14.2．15．解：（1）把点A（2，6）代入y＝，得m＝12，则y＝，把点B（n，1）代入y＝，得n＝12，则点B的坐标为（12，1），由直线y＝kx+b过点4（2，6），点B（12，1）得，解得，则所求一次函数表达式为y＝﹣x+7；（2）由图象得：当y1＞y2时，0＜x＜2或x＞12，故答案为0＜x＜2或x＞12；（3）如图，设直线AB与y轴的交点为P，点的坐标为（0，a），连接AE，BE，则点P的坐标为（0，7），∴PE＝|a﹣7|．∴S△AEB ＝S△BPE﹣S△APE＝5，∴×|a﹣7|×（12﹣2）＝5，∴|a﹣7|＝1，∴a＝6或8，∴点E的坐标为（0，6）或（0，8）．16．解：（1）将点E（1，5）代入y＝﹣x+b和y＝，得b＝6，k＝5，由题意，联立方程组得，，解得或，∴点F的坐标为（5，1）；（2）∵一次函数y＝﹣x+b的图象与x轴交于A点，与y轴交于B点，∴A（6，0），B（0，6），∴S△EOF ＝S△AOB﹣S△AOF﹣S△BOE＝6×6﹣×1﹣6×1＝18﹣6＝12；（3）观察函数图象可知：反比例函数值大于一次函数值时x的范围为：0＜x＜1或x＞5．。

北师大版九年级数学上册第六章反比例函数提高培优讲义：反比例函数和一次函数综合(含答案)

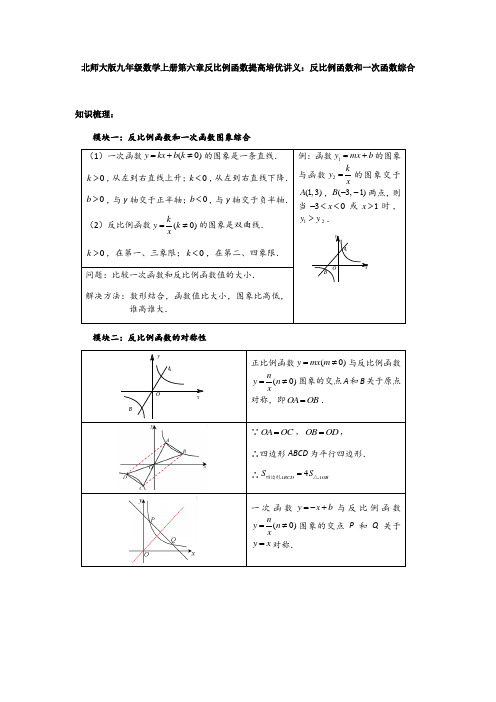
北师大版九年级数学上册第六章反比例函数提高培优讲义：反比例函数和一次函数综合知识梳理：模块一：反比例函数和一次函数图象综合模块二：反比例函数的对称性(第14题)模块三：平行和相等模型AM BN =AM BN =模块四、例题讲解:例1、（1）函数y kx k =+与()ky k x=≠0在同一直角坐标系中的图象大致是（）A ．B ．C ．D ．（2）在同一坐标系内，表示函数y kx b =+与kby x=（k ≠0，b ≠0）的图像只可能是下图中的（）D C B AD C BD CDA ．B ．C ．D ．（1）C ；（2）B ．例2、如图，反比例函数ky x=与一次函数y mx b =+的图象交于(,)A 13，(,)B n -1两点．（1）求反比例函数与一次函数的解析式；（2）据图象回答：当x 取何值时，反比例函数的值小于一次函数的值．（1）y x3=，y x =+2；（2）x -3<<0或x >1．例3、（1）如图3-1，直线()y kx k =>0与双曲线y x2=交于A 、B 两点，坐标分别为(,)A x y 11，(,)B x y 22，则x y x y 1221+的值为_________．（2）如图3-2，已知直线y x 1=2与双曲线()ky k x=>0交于A 、B 两点，且点A 的横坐标为4．过原点O 的另一条直线l 交双曲线()ky k x=>0于P 、Q 两点（P 点在第一象限），若由点P 、Q 、A 、B 为顶点组成的四边形面积为24，则点P 的坐标为____________．图3-1 图3-2（1）-4；（提示：x x 21=-，y y 21=-）（2）由对称性可得，OP OQ =，OA OB =，则四边形APBQ 是平行四边形，∴△POA APBQ S S 11==⨯24=644，设P 点坐标为,p p x x 8⎛⎫ ⎪⎝⎭，若p x 0<<4，则()p p x x 18⎛⎫2+4-=6 ⎪2⎝⎭，解得p x =2（舍负），∴(,)P 24；若p x >4，则()p p x x 18⎛⎫2+-4=6 ⎪2⎝⎭，解得p x =8（舍负），∴(,)P 81，故P 点坐标为(,)24或(,)81．例4、（1）已知一次函数y x b =-+的图象与反比例函数()ky k x=>0的图象的一个交点坐标是(,)26，则另一个交点的坐标是_________．（2）已知一次函数y x b =+的图象与反比例函数()ky k x=<0的图象的一个交点坐标是(,)-15，则另一个交点的坐标是_________．（1）(,)62；（2）(,)-51．例5、（1）如图5-1，直线y x =-+1与x 轴交于点A ，与y 轴交于点B ，与反比例函数ky x=在第一象限内的图象交于C 、D 两点，已知C 点的横坐标为14．则△OCD 的面积为______________．（2）如图5-2，已知直线y x m n =-++与双曲线y x1=交于两个不同的点(,)A m n (≥m 2)和(,)B p q ．直线y x m n =-++与y 轴交于点C ，则△OBC 的面积S 和m 的函数关系式为_________________．（3）如图5-3，等腰直角三角形ABC 位于第一象限，AB AC ==2，直角顶点A 直线y x =上，其中A 点的横坐标为1，且两条直角边AB 、AC 分别平行于x 轴、y 轴，若双曲线()ky k x=≠0与△ABC 有交点，则k 的取值范围是．图5-1 图5-2 图5-3（1）由题意，C 点的坐标为,13⎛⎫ ⎪44⎝⎭，∴D 点的坐标为31⎛⎫⎪44⎝⎭，，∴△OCD S 13111⎛⎫=+⨯⨯= ⎪44224⎝⎭．（2）由题意，点A 与点B 关于直线y x =对称，则B 点坐标为(,)n m ，∴(△)OBC S S m n n mn n 2111==+⋅=+222，又n m 1=，∴S m 211=+22．（3）≤≤k 14．例6、在平面直角坐标系中，函数my x=（x >0，m 是常数）的图象经过点(,)A 14，点(,)B a b ，其中a >1，过点A 作x 轴的垂线，垂足为C ，过点B 作y 轴的垂线，垂足为D ，AC 与BD 相交于点M ，连接AD ，DC ，CB 与AB ．（1）求m 的值；（2）求证：DC//AB ；（3）当AD BC =时，求直线AB 的函数解析式．（1）m =4；（2）略；（3）当四边形ABCD 为平行四边形或为等腰梯形时，对应的直线AB 的解的式为y x =-2+6或y x =-+5．例7、（1）如图7-1，一次函数y ax b =+的图象与x 轴，y 轴交于A ，B 两点，与反比例函数ky x=的图象相交于C ，D 两点，分别过C ，D 两点作y 轴，x 轴的垂线，垂足为E ，F ，连接CF ，DE ．有以下四个结论：①△CEF 与△DEF 的面积相等；②△≌△AOB FOE ；③△≌△DCE CDF ；④AC BD =．其中正确的结论是________（把你认为正确结论的序号都填上）．（2）如图7-2，在平面直角坐标系xOy 中，直线y x 3=2与双曲线y x6=相交于A ，B 两点，C 是第一象限内双曲线上一点，连接CA 并延长交y 轴于点P ，连接BP ，BC ．若△PBC 的面积是20，则点C 的坐标为___________．（3）如图7-3，在平面直角坐标系xOy 中，△OAB 的顶点A 在x 轴正半轴上，OC 是△OAB的中线，点B ，C 在反比例函数()y x x3=>0的图象上，则△OAB 的面积等于________．图7-1 图7-2 图7-3（1）①④（2）,149⎛⎫⎪37⎝⎭；（3）92．模块五、课后作业：1、（1）已知关于x 的函数()y k x =+1和()≠ky k x=-0，它们在同一坐标系中的图象可能是（）A ．B ．C ．D ．（2）已知a ≠0，b ≠0，a b +≠0，则函数y ax b =+与a by x+=在同一坐标系中的图象不可能是（）A ．B ．C ．D ．（1）A ；（2）B ．2、（1）若一次函数y x b =3+和反比例函数b y x-3=的图像有两个交点，当b =______时，有一个交点的纵坐标为6．（2）如图是一次函数y kx b 1=+和反比例函数my x2=的图象，观察图象写出y y 12>时，x 的取值范围为____________．（1）由题意可得y =6，代入y x b =3+，b y x-3=可得b =5．（2）观察图象得3x >或20x -<<．3、如图，双曲线my x=在第一象限的一支上有一点(,)C 15，经过点C 的直线()y kx b k =-+>0与x 轴交于点(,)A a 0．（1）求点A 的横坐标a 与k 之间的函数关系式；（2）当这条直线与双曲线的另一交点D 的横坐标为9时，求△COA 的面积．（1）由(,)A a 0、(,)C 15两点在直线y kx b =-+上，有,.k b ka b -+=5⎧⎨-+=0⎩消去b 得a k 5=1+．（2）容易求得双曲线解析式5y x =，从而交点59,9D ⎛⎫⎪⎝⎭，可得，解得由（1）的结论，可得，故． 4、（1）如图4-1，直线()y ax a =>0与双曲线y x3=交于(,)A x y 11，(,)B x y 22两点，则x y x y 12214-3=_______．（2）如图4-2，已知反比例函数y x4=与直线y x b =-+交于P 、Q 两点，其中点Q 为(4, m )，则△OPQ 的面积为________．5599k b k b -+=⎧⎪⎨-+=⎪⎩，5950.9k b ⎧=⎪⎪⎨⎪=⎪⎩，51a k =+10a =1105252COA S ∆=⨯⨯=图4-1 图4-2（1）-3；（提示：x x 21=-，y y 21=-）；（2）152． 5、一次函数y ax b =+的图象分别于x 轴、y 轴交于点M 、N ，与反比例函数ky x=的图象相交于A 、B ，过点A 分别作AC x ⊥轴，AE y ⊥轴，垂足分别为C 、E ；过点B 分别作BF x ⊥轴，BD y ⊥轴，垂足分别为F 、D ；AC 与BD 交于点K ，连结CD ．（1）若点A 、B 在反比例函数ky x=的图象的同一分支上，如图5-1，试证明：①AEDK CFBK S S =四边形四边形；②AN BM =．（2）若点A 、B 分别在反比例函数ky x=的图象的不同分支上，如图5-2，则AN 与BM 还相等吗？试证明你的结论．图5-1 图5-2（1）①AEOC BDOF S S k ==矩形矩形，AEOC DOCK BDOF DOCK S S S S ∴-=-矩形矩形矩形矩形，即AEDK CFBK S S =四边形四边形．②如图①，连AD 、BC ，得△△ADK BCK S S =， △△ADC BDC S S ∴=，得BC//AB ．AC //y 轴，∴四边形ACDN 是平行四边形，AN CD ∴=，同理BM CD =，故AN BM =；（2）AN 与BM 仍然相等，证法同①．6、平行四边形AOBC 中，对角线交于点E ，双曲线()k y k x=>0经过A ，E 两点，若平行四边形AOBC 的面积为18，则k =________．k=6．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

课时练：第六章《反比例函数》（培优篇）一．选择题1．下列各点中，在反比例函数y ＝图象上的是（） A ．（﹣1，8）B ．（﹣2，4）C ．（1，7）D ．（2，4） 2．如果点A （﹣1，y 1）、B （1，y 2）、C （2，y 3）是反比例函数图象上的三个点，则下列结论正确的是（） A ．y 1＞y 3＞y 2 B ．y 3＞y 2＞y 1C ．y 2＞y 1＞y 3D ．y 3＞y 1＞y 23．函数图象的大致形状是（）A ．B ．C ．D ．4．如图，过点A （4，5）分别作x 轴、y 轴的平行线，交直线y ＝﹣x +6于B 、C 两点，若函数y ＝（x ＞0）的图象△ABC 的边有公共点，则k 的取值范围是（）A ．5≤k ≤20B ．8≤k ≤20C ．5≤k ≤8D ．9≤k ≤205．如图，在直角坐标系中，正方形的中心在原点O ，且正方形的一组对边与x 轴平行，点P （4a ，a ）是反比例函数y ＝（k ＞0）的图象上与正方形的一个交点，若图中阴影部分的面积等于16，则k 的值为（）A ．16B ．1C ．4D ．﹣166．如图，在平面直角坐标系中，矩形ABOC 的两边在坐标轴上，OB ＝1，点A 在函数y ＝﹣（x ＜0）的图象上，将此矩形向右平移3个单位长度到A 1B 1O 1C 1的位置，此时点A 1在函数y ＝（x ＞0）的图象上，C 1O 1与此图象交于点P ，则点P 的纵坐标是（）A ．B ．C ．D ．7．函数y ＝ax ﹣a 与y ＝（a ≠0）在同一直角坐标系中的图象可能是（）A ．B ．C ．D ．8．如图，A 、C 分别是x 轴、y 轴上的点，双曲线y ＝（x ＞0）与矩形OABC 的边BC 、AB 分别交于E 、F ，若AF ：BF ＝1：2，则△OEF 的面积为（）A．2 B．C．3 D．9．如图，矩形OABC的顶点A在y轴上，C在x轴上，双曲线y＝与AB交于点D，与BC 交于点E，DF⊥x轴于点F，EG⊥y轴于点G，交DF于点H．若矩形OGHF和矩形HDBE的面积分别是1和2，则k的值为（）A．B．+1 C．D．210．如图，点A是反比例函数y＝（x＞0）的图象上任意一点，AB∥x轴交反比例函数y＝﹣的图象于点B，以AB为边作平行四边形ABCD，其中C、D在x轴上，则S平行四边形ABCD 为（）A．2 B．3 C．4 D．511．如图，平面直角坐标系中，点A（1，2），将AO绕点A逆时针旋转90°，点O的对应B点恰好落在双曲线y＝（x＞0）上，则k的值为（）A．2 B．3 C．4 D．612．如图，一次函数与反比例函数的图象交于A（1，12）和B（6，2）两点．点P是线段AB上一动点（不与点A和B重合），过P点分别作x、y轴的垂线PC、PD交反比例函数图象于点M、N，则四边形PMON面积的最大值是（）A．B．C．6 D．12二．填空题13．反比例函数的图象在一、三象限，则k应满足．14．如图，点A是双曲线y＝在第一象限上的一动点，连接AO并延长交另一分支于点B，以AB为斜边作等腰Rt△ABC，点C在第二象限，随着点A的运动，点C的位置也不断的变化，但始终在一函数图象上运动，则这个函数的解析式为．15．如图，点A是反比例函数的图象上的一点，过点A作▱ABCD，使点B、C 在x轴上，点D在y轴上，则▱ABCD的面积为．16．如图，两个反比例函数y＝和y＝﹣的图象分别是l1和l2．设点P在l1上，PC⊥x轴，垂足为C，交l2于点A，PD⊥y轴，垂足为D，交l2于点B，则△PAB的面积为．17．如图，等腰直角三角形ABC 位于第一象限，AB ＝AC ＝2，直角顶点A 在直线y ＝x 上，其中A 点的横坐标为1，且两条直角边AB 、AC 分别平行于x 轴、y 轴，若双曲线y ＝（k ≠0）与△ABC 有交点，则k 的取值范围是．18．如图所示，P 1（x 1，y 1）、P 2（x 2，y 2），…P n （x n ，y n ）在函数y ＝（x ＞0）的图象上，△OP 1A 1，△P 2A 1A 2，△P 3A 2A 3…△P n A n ﹣1A n …都是等腰直角三角形，斜边OA 1，A 1A 2…A n ﹣1A n ，都在x 轴上，则y 1+y 2+…y n ＝．三．解答题19．如图，已知一次函数y ＝kx +b 的图象与反比例函数的图象交于A ，B 两点，且点A的横坐标和点B 的纵坐标都是﹣2，求：（1）一次函数的解析式；（2）△AOB 的面积；（3）直接写出一次函数的函数值大于反比例函数的函数值时x 的取值范围．20．制作一种产品，需先将材料加热达到60℃后，再进行操作．设该材料温度为y（℃），从加热开始计算的时间为x（min）．据了解，当该材料加热时，温度y与时间x成一次函数关系；停止加热进行操作时，温度y与时间x成反比例关系（如图所示）．已知该材料在操作加热前的温度为15℃，加热5min后温度达到60℃．（1）分别求出将材料加热和停止加热进行操作时，y与x的函数解析式；（2）根据工艺要求，当材料的温度低于15℃时，须停止操作，那么从开始加热到停止操作，共经历了多少时间？21．如图，一次函数y＝kx+b的图象与反比例函数y＝的图象交于A、B两点．（1）利用图中的条件，求反比例函数和一次函数的解析式．（2）求△AOB的面积．（3）根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围．22．如图，在矩形OABC中，OA＝3，OC＝2，点F是AB上的一个动点（F不与A，B重合），过点F的反比例函数y＝的图象与BC边交于点E．（1）当F为AB的中点时，求该函数的解析式；（2）当k为何值时，△EFA的面积最大，最大面积是多少？23．如图，在平面直角坐标系xOy中，△OAB如图放置，点P是AB边上的一点，过点P的反比例函数y＝与OA边交于点E，连接OP．（1）如图1，若点A的坐标为（3，4），点B的坐标为（5，0），且△OPB的面积为5，求直线AB和反比例函数y＝的解析式；（2）如图2，若∠AOB＝60°，过P作PC∥OA，与OB交于点C，若OE＝4，并且△OPC 的面积为，求反比例函数y＝的解析式及点P的坐标．参考答案一．选择题1．解：A、∵﹣1×8＝﹣8≠8，∴该点不在函数图象上，故本选项错不合题意；B、∵﹣2×4＝﹣8≠8，∴该点不在函数图象上，故本选项不合题意；C、∵1×7＝7≠8，∴该点不在函数图象上，故本选项不合题意；D、2×4＝8，∴该点在函数图象上，故本选项符合题意．故选：D．2．解：∵反比例函数的比例系数为﹣1，∴图象的两个分支在二、四象限；∵第四象限的点的纵坐标总小于在第二象限的纵坐标，点A在第二象限，点B、C在第四象限，∴y1最大，∵1＜2，y随x的增大而增大，∴y2＜y3，∴y1＞y3＞y2．故选：A．3．解：由函数解析式可得x可取正数，也可取负数，但函数值只能是负数；所以函数图象应在x轴下方，并且x，y均不为0．故选：D．4．解：∵过点A（4，5）分别作x轴、y轴的平行线，交直线y＝﹣x+6于B、C两点，∴点B的纵坐标为5，点C的横坐标为4，将y＝5代入y＝﹣x+6，得x＝1；将x＝4代入y＝﹣x+6得，y＝2，∴点B的坐标为（1，5），点C的坐标为（4，2），∵函数y＝（x＞0）的图象与△ABC的边有公共点，点A（4，5），点B（1，5），∴1×5≤k≤4×5即5≤k≤20，故选：A．5．解：∵图中阴影部分的面积等于16，∴正方形OABC 的面积＝16， ∵P 点坐标为（4a ，a ）， ∴4a ×4a ＝16，∴a ＝1（a ＝﹣1舍去）， ∴P 点坐标为（4，1），把P （4，1）代入y ＝，得k ＝4×1＝4．故选：C ．6．解：∵OB ＝1，AB ⊥OB ，点A 在函数y ＝﹣（x ＜0）的图象上， ∴当x ＝﹣1时，y ＝2， ∴A （﹣1，2）．∵此矩形向右平移3个单位长度到A 1B 1O 1C 1的位置， ∴B 1（2，0）， ∴A 1（2，2）．∵点A 1在函数y ＝（x ＞0）的图象上， ∴k ＝4，∴反比例函数的解析式为y ＝，O 1（3，0）， ∵C 1O 1⊥x 轴， ∴当x ＝3时，y ＝， ∴P （3，）．故选：C ．7．解：A 、从反比例函数图象得a ＞0，则对应的一次函数y ＝ax ﹣a 图象经过第一、三、四象限，所以A 选项错误；B 、从反比例函数图象得a ＞0，则对应的一次函数y ＝ax ﹣a 图象经过第一、三、四象限，所以B 选项错误；C 、从反比例函数图象得a ＜0，则对应的一次函数y ＝ax ﹣a 图象经过第一、二、四象限，所以C 选项错误；D 、从反比例函数图象得a ＜0，则对应的一次函数y ＝ax ﹣a 图象经过第一、二、四象限，所以D 选项正确．故选：D ．8．解：设F 点的坐标为（t ，）， ∵AF ：BF ＝1：2， ∴AB ＝3AF ，∴B 点坐标为（t ，），把y ＝代入y ＝得x ＝， ∴E 点坐标为（，），∴△OEF 的面积＝S 矩形ABCO ﹣S △OEC ﹣S △OAF ﹣S △BEF ＝t •﹣×2﹣×2﹣•（﹣）•（t ﹣）＝．故选：B ．9．解：设D （t ，），∵矩形OGHF 的面积为1，DF ⊥x 轴于点F ， ∴HF ＝，而EG ⊥y 轴于点G ， ∴E 点的纵坐标为，当y ＝时，＝，解得x ＝kt ， ∴E （kt ，）， ∵矩形HDBE 的面积为2，∴（kt ﹣t ）•（﹣）＝2，整理得（k ﹣1）2＝2，而k ＞0， ∴k ＝+1．故选：B ．10．解：连结OA 、OB ，AB 交y 轴于E ，如图， ∵AB ∥x 轴， ∴AB ⊥y 轴，∴S △OEA ＝×3＝，S △OBE ＝×2＝1， ∴S △OAB ＝1+＝，∵四边形ABCD 为平行四边形， ∴S 平行四边形ABCD ＝2S △OAB ＝5．故选：D ．11．解：作AC ⊥y 轴于C ，AD ⊥x 轴，BD ⊥y 轴，它们相交于D ，如图， ∵A 点坐标为（1，2）， ∴AC ＝1，OC ＝2，∵AO 绕点A 逆时针旋转90°，点O 的对应B 点，即把△AOC 绕点A 逆时针旋转90°得到△ABD ， ∴AD ＝AC ＝1，BD ＝OC ＝2，∴B 点坐标为（3，1）， ∴k ＝3×1＝3．故选：B ．12．解：设反比例函数解析式为y ＝，一次函数解析式为y ＝ax +b ，将点A （1，12）代入y ＝中，得k ＝12， ∴反比例函数解析式为y ＝，将点A （1，12）、B （6，2）代入y ＝ax +b 中，得，解得，∴一次函数解析式为y ＝﹣2x +14．设点P 的坐标为（m ，14﹣2m ），则S 四边形PMON ＝S 矩形OCPD ﹣S △OCM ﹣S △ODN ＝S 矩形OCPD ﹣|k |＝m （14﹣2m ）﹣12＝﹣2m 2+14m ﹣12＝﹣2+，∴四边形PMON 面积的最大值是．故选：A ．二．填空题（共6小题） 13．解：由题意得，反比例函数的图象在二、四象限内，则k +2＞0，解得k ＞﹣2．故答案为k ＞﹣2．14．解：连结OC ，作CD ⊥x 轴于D ，AE ⊥x 轴于E ，如图，设A 点坐标为（a ，），∵A 点、B 点是正比例函数图象与双曲线y ＝的交点，∴点A与点B关于原点对称，∴OA＝OB∵△ABC为等腰直角三角形，∴OC＝OA，OC⊥OA，∴∠DOC+∠AOE＝90°，∵∠DOC+∠DCO＝90°，∴∠DCO＝∠AOE，∵在△COD和△OAE中∴△COD≌△OAE（AAS），∴OD＝AE＝，CD＝OE＝a，∴C点坐标为（﹣，a），∵﹣•a＝﹣4，∴点C在反比例函数y＝﹣图象上．故答案为y＝﹣（x＜0）．15．解：连结OA、CA，如图，则S△OAD＝|k|＝×6＝3，∵四边形ABCD为平行四边形，∴BC∥AD，∴S△CAD ＝S△OAD＝3，∴▱ABCD的面积＝2S△CAD＝6．故答案为6．16．解：∵点P在y＝上，∴|x p|×|y p|＝|k|＝1，∴设P的坐标是（a，）（a为正数），∵PA⊥x轴，∴A的横坐标是a，∵A在y＝﹣上，∴A的坐标是（a，﹣），∵PB⊥y轴，∴B的纵坐标是，∵B在y＝﹣上，∴代入得：＝﹣，解得：x＝﹣2a，∴B的坐标是（﹣2a，），∴PA＝|﹣（﹣）|＝，PB＝|a﹣（﹣2a）|＝3a，∵PA⊥x轴，PB⊥y轴，x轴⊥y轴，∴PA⊥PB，∴△PAB的面积是：PA×PB＝××3a＝故答案为：．17．解：如图，设直线y＝x与BC交于E点，分别过A、E两点作x轴的垂线，垂足为D、F，EF交AB于M，∵A点的横坐标为1，A点在直线y＝x上，∴A（1，1），又∵AB ＝AC ＝2，AB ∥x 轴，AC ∥y 轴，∴B （3，1），C （1，3），且△ABC 为等腰直角三角形，BC 的中点坐标为（，），即为（2，2），∵点（2，2）满足直线y ＝x ，∴点（2，2）即为E 点坐标，E 点坐标为（2，2）， ∴k ＝OD ×AD ＝1，或k ＝OF ×EF ＝4，当双曲线与△ABC 有唯一交点时，1≤k ≤4．故答案为：1≤k ≤4．18．解：（方法一）如图，过点P 1作P 1M ⊥x 轴， ∵△OP 1A 1是等腰直角三角形， ∴P 1M ＝OM ＝MA 1，设P 1的坐标是（a ，a ），把（a ，a ）代入解析式y ＝（x ＞0）中，得a ＝3， ∴A 1的坐标是（6，0），又∵△P 2A 1A 2是等腰直角三角形，设P 2的纵坐标是b ，则P 2的横坐标是6+b ，把（6+b ，b ）代入函数解析式得b ＝，解得b ＝3﹣3，∴A 2的横坐标是6+2b ＝6+6﹣6＝6，同理可以得到A 3的横坐标是6，A n 的横坐标是6，根据等腰三角形的性质得到y 1+y 2+…y n 等于A n 点横坐标的一半， ∴y 1+y 2+…y n ＝．故答案为：．（方法二）设OA 1＝2a 1，A 1A 2＝2a 2，A 2A 3＝2a 3，…，A n ﹣1A n ＝2a n ，∴A 1（2a 1，0），A 2（2a 1+2a 2，0），…，A n （2a 1+2a 2+…+2a n ，0）． ∵△OP 1A 1，△P 2A 1A 2，△P 3A 2A 3，…，△P n A n ﹣1A n ，…，都是等腰直角三角形，∴y 1＝a 1，y 2＝a 2，y 3＝a 3，…，y n ＝a n ，x 1＝a 1，x 2＝2a 1+a 2，x 3＝2a 1+2a 2+a 3，…，x n ＝2a 1+2a 2+…+a n ，∴y 1+y 2+…y n ＝OA n ．∵P 1（x 1，y 1）、P 2（x 2，y 2），…P n （x n ，y n ）在函数y ＝（x ＞0）的图象上， ∴a 12＝9，（2a 1+a 2）a 2＝9，（2a 1+2a 2+a 3）a 3＝9，…，（2a 1+2a 2+…+a n ）a n ＝9， ∴a 1＝3，a 2＝3﹣3，a 3＝3﹣3，…，a n ＝3﹣3，∴y 1+y 2+…y n ＝a 1+a 2+…+a n ＝3+3﹣3+3﹣3+…+3﹣3＝3．故答案为：．三．解答题（共5小题）19．解：（1）由题意A （﹣2，4），B （4，﹣2）， ∵一次函数过A 、B 两点， ∴，解得，∴一次函数的解析式为y ＝﹣x +2；（2）设直线AB 与y 轴交于C ，则C （0，2）， ∵S △AOC ＝×OC ×|A x |，S △BOC ＝×OC ×|B x | ∴S △AOB ＝S △AOC +S △BOC ＝•OC •|A x |+•OC •|B x |＝＝6；（3）由图象可知：一次函数的函数值大于反比例函数的函数值时x 的取值范围是x ＜﹣2或0＜x ＜4．20．解：（1）材料加热时，设y＝ax+15（a≠0），由题意得60＝5a+15，解得a＝9．则材料加热时，y与x的函数关系式为y＝9x+15（0≤x≤5）．停止加热时，设y＝（k≠0），由题意得60＝，解得k＝300．则停止加热进行操作时y与x的函数关系式为y＝（x≥5）；（2）把y＝15代入y＝，得x＝20，因此从开始加热到停止操作，共经历了20分钟．答：从开始加热到停止操作，共经历了20分钟．21．解：（1）把A（2，1）代入y＝，得：m＝2，∴反比例函数的解析式为y＝，把B（﹣1，n）代入y＝，得：n＝﹣2，即B（﹣1，﹣2），将点A（2，1）、B（﹣1，﹣2）代入y＝kx+b，得：，解得：，∴一次函数的解析式为y＝x﹣1；（2）在一次函数y＝x﹣1中，令y＝0，得：x﹣1＝0，解得：x＝1，则S＝×1×1+×1×2＝；△AOB（3）由图象可知，当x＞2或﹣1＜x＜0时，一次函数的值大于反比例函数的值．22．解：（1）∵在矩形OABC中，OA＝3，OC＝2，∴B（3，2），∵F为AB的中点，∴F（3，1），∵点F在反比例函数y＝的图象上，∴k＝3，∴该函数的解析式为y＝；（2）由题意知E，F两点坐标分别为E（，2），F（3，），＝AF•BE＝×k（3﹣k），∴S△EFA＝k﹣k2＝﹣（k2﹣6k+9﹣9）＝﹣（k﹣3）2+当k＝3时，S有最大值．S＝．最大值23．解：（1）如图1，过点P作PQ⊥x轴交x轴于点Q，∵点A的坐标为（3，4），点B的坐标为（5，0），∴设直线AB的解析式为y＝kx+b（k≠0），∴，解得，∴直线AB的解析式为：y＝﹣2x+10．∵点B的坐标为（5，0），且△OPB的面积为5，∴PQ＝2，点P纵坐标为2．∵点P在直线AB上﹣2x+10＝2，解得x＝4，∴点P坐标为（4，2）∴此反比例函数的解析式为y＝；（2）如图2，过点E作EF⊥x轴交x轴于点F，过点P作PS⊥x轴交x轴于点S，∵∠AOB＝60°，∠EFO＝90°，OE＝4，∴OF＝2，EF＝2，∴此反比例函数的解析式为y＝．＝＝OC•PS，∵S△OCP∴OC•PS＝3．∵OS•PS＝4，∴CS•PS＝．∵∠AOB＝60°PC∥OA，∴∠PCS＝60°，∴PS＝CS，∴CS＝1．∴点P坐标为（4，）．。

北师大版九年级数学上册课时练：第六章 《反比例函数》 (培优篇)

北师大版九年级数学上册 第六章 反比例函数 教材同步培优、拔高复习(无答案)

【完整版】北师大版九年级上册数学第六章 反比例函数含答案