第4章习题解答
第4章课后习题及答案

返 回
第 4 章 供 电 与 用 电
练习题解答
4.1.1 某三相同步发电机,三相绕组联结成星形时的线电压为 10.5kV,若将它联结成三角形,则线电压是多少?若联结成星形 时,L2相绕组的首末端接反了,则三个线电压的有效值U12 , U23 和U31各是多少? · · · · U31= U3 -U1 · -U2 解: 星形联结时UlY = 10.5kV U3 · U 3 UlY 10.5 = kV = 6.06kV ∴UpY = · · U 1=U23 √ 3 √3 · ·-U =U 三角形联结时相电压不变, 2 3 · UlY = UpY =6.06kV L2首末端接反的相量图如图所示:
· · · 0 0 0 IL2 = I2 - I1 ( 8 . 8 30 8 . 8 0 ) A 4 . 56 105 A · · · 0 0 0 IL3 = I3 - I2 ( 8 . 8 30 8 . 8 30 ) A 8 . 8 90 A
XL= Z sin = 77.1×0.6 Ω = 46.3 Ω
返 回 上一题 下一题
第 4 章 供 电 与 用 电
4.3.2 某三相负载,额定相电压为220V,每相负载的电阻为4Ω,感 抗为3Ω,接于线电压为380V的对称三相电源上,试问该负载应
采用什么联结方式?负载的有功功率、无功功率和视在功率?
· I
l2
· I
l3
· I
2
· I
3
-jXC
解: 负载为不对称三相负载
· · 0 U U 220 120 2 23 · 0 I2 = Z = -jX = 8 . 8 30 A -j25 2 C
返 回 上一题 下一题
第4章 习题解答

第4章 习题与答案4-1作简谐振动的物体,每次通过同一位置时,不一定相同的量是 [ ] (A) 位移 ; (B) 速度 ; (C) 加速度; (D) 能量。
[答案:B ]4-2 把单摆摆球从平衡位置向位移正方向拉开,使摆线与竖直方向成一微小角度θ ,然后由静止放手任其振动,从放手时开始计时。
若用余弦函数表示其运动方程,则该单摆振动的初相为 [ ](A) π; (B) π/2; (C) 0; (D) θ [答案:C ]4-3 谐振动的振动曲线如题4-3图所示,则有[ ] (A )A 超前π/2; (B )A 落后π/2; (C )A 超前π; (D )A 落后π。
[答案:A ]4-4 一个质点作简谐振动,振辐为A ,在起始时刻质点的位移为A /2,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为题4-4图 中哪一个? [ ][答案:B ]4-5 两个质点各自作简谐振动,它们的振幅相同、周期相同。
第一个质点的振动方程为x 1 = A cos(ωt + α)。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点恰在最大负位移处。
则第二个质点的振动方程为 [ ] (A) )π21cos(2++=αωt A x ; (B) )π21cos(2-+=αωt A x ; (C) )π23cos(2-+=αωt A x ; (D) )cos(2π++=αωt A x 。
[答案:A ]4-6 已知某简谐振动的振动曲线如题4-6图所示。
则此简谐振动的振动方程(SI )为 [ ](A) 题4-4图题4-3图(A )220.02cos()33x t =π+π;(B )220.02cos()33x t =π-π;(C )420.02cos()33x t =π+π;(D )420.02cos()33x t =π-π。
[答案:C ]4-7 弹簧振子作简谐振动,先后以相同的速度依次通过A 、B 两点,历时1秒,质点通过B 点后再经过1秒又第二次通过B 点,在这2秒内质点通过的总路程为12cm ,则质点的振动周期和振幅分别为 [ ](A )3s 、12cm ; (B )4s 、6cm ; (C )4s 、9cm ; (D )2s 、8cm 。
习题参考答案(第4章)
a' V XH
a
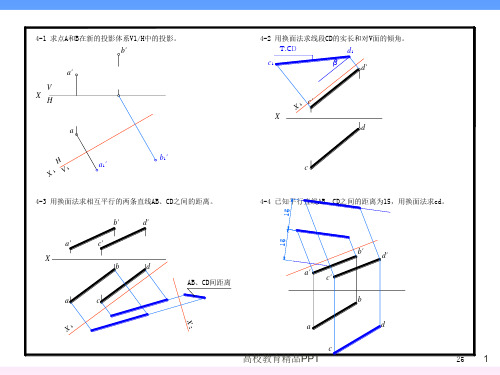
4-2 用换面法求线段CD的实长和对V面的倾角。
T.CD
d1
c1 d'
X 1 c' X
d
H X1 V1
a1'
b1'
c
4-3 用换面法求相互平行的两条直线AB、CD之间的距离。
b'
d'
a'
c'
X
b
d
a
c
AB、CD间距离
4-4 已知平行直线AB、CD之间的距离为15,用换面法求cd。
15
15
a' c'
b'
d'
b
X2
பைடு நூலகம்X1
a
d
c
高校教育精品PPT
25 1
4-5 已知直线AB与CD垂直相交,用换面法求c'd'。 b'
a'
c a
b d
4-6 用换面法求点到直线BC距离,并求垂足。
a'
c'
b'
c a
A到BC距离 b
O2
4-7 已知点A到直线BC的距离为15,求a。 a1
R15
b1
c1
O1
a b
c a'1
c'1 c2
a2
b1' b2
高校教育精品PPT
27 3
4-11 已知直线AB与 CDE的距离为10,用换面法求ab。
c' e'
b'
a' X
第4章 习题及答案
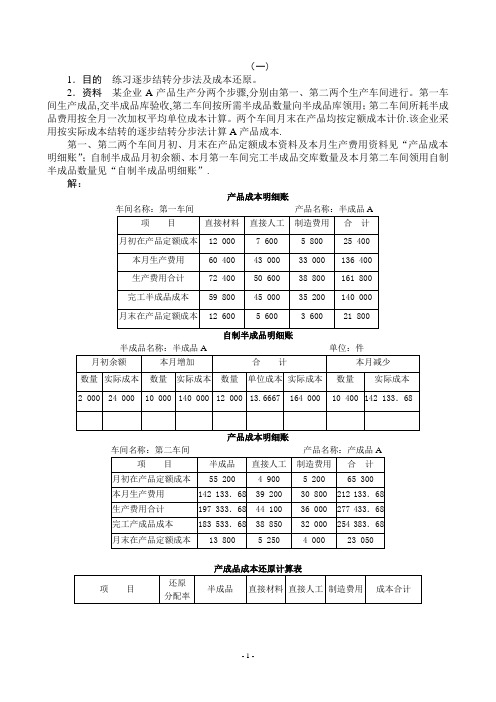
(一)1.目的练习逐步结转分步法及成本还原。
2.资料某企业A产品生产分两个步骤,分别由第一、第二两个生产车间进行。
第一车间生产成品,交半成品库验收,第二车间按所需半成品数量向半成品库领用;第二车间所耗半成品费用按全月一次加权平均单位成本计算。
两个车间月末在产品均按定额成本计价.该企业采用按实际成本结转的逐步结转分步法计算A产品成本.第一、第二两个车间月初、月末在产品定额成本资料及本月生产费用资料见“产品成本明细账”;自制半成品月初余额、本月第一车间完工半成品交库数量及本月第二车间领用自制半成品数量见“自制半成品明细账”.解:产品成本明细账车间名称:第一车间产品名称:半成品A自制半成品明细账半成品名称:半成品A 单位:件产品成本明细账产成品成本还原计算表(二)1.目的练习产品成本计算的综合结转分步法.2.资料某企业生产甲产品,分三个生产步骤进行生产。
该企业设有第一、第二、第三三个基本生产车间,甲产品由这三个车间顺序加工而成。
成本计算采用综合结转法。
原材料在第一车间开始加工时一次投入,半成品不通过中间仓库收发,上一步骤完工后全部交由下一步骤继续加工。
月末在产品按约当产量法计算,各车间月末在产品完工程度均为50%。
该企业本年5月份有关成本计算资料如表1、表2所示。
表1产量记录表2月初在产品成本和本月发生费用表3产品成本计算单135070÷(88+16)=1298。
75 24960÷(88+16×50%)=260 19200÷(88+16×50%)=200表4产品成本计算单173890÷(8050%)=326。
6表5产品成本计算单244450÷(96+4)=2444.5 34300÷(96+4×50%)=350 23520÷(96+4×50%)=240表6(三)1.目的练习产品成本计算的平行结转分步法.2.资料某厂设有三个基本生产车间,第一车间生产甲半成品,交第二车间继续加工,第二车间生产乙半成品,交第三车间生产丙产成品。
第4章 习题解答
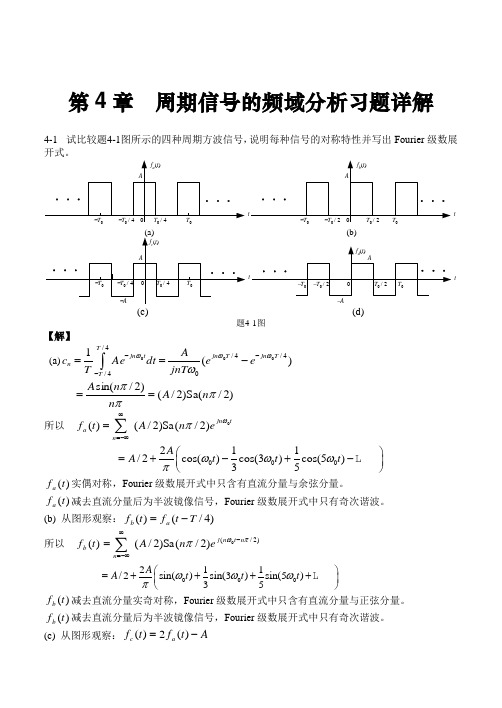
第4章 周期信号的频域分析习题详解4-1 试比较题4-1图所示的四种周期方波信号,说明每种信号的对称特性并写出Fourier 级数展开式。
tt(b)tt-A(c) (d)题4-1图【解】 (a))(14/4/04/4/000T jn T jn tjn T T n eejnT A dt AeTc ωωωω----==⎰)2/(Sa )2/()2/sin(πππn A n n A ==所以 tjn n a e n A t f 0)2/(Sa )2/()(ωπ∑∞-∞==000211/2cos()cos(3)cos(5)35A A t t t ωωωπ⎛⎫=+-+- ⎪⎝⎭)(t f a 实偶对称,Fourier 级数展开式中只含有直流分量与余弦分量。
)(t f a 减去直流分量后为半波镜像信号,Fourier 级数展开式中只有奇次谐波。
(b) 从图形观察:)4/()(T t f t f a b -=所以 )(t f b )2/(0)2/(Sa )2/(πωπn t n j n en A -∞-∞=∑=000211/2sin()sin(3)sin(5)35A A t t t ωωωπ⎛⎫=++++ ⎪⎝⎭)(t f b 减去直流分量实奇对称,Fourier 级数展开式中只含有直流分量与正弦分量。
)(t f b 减去直流分量后为半波镜像信号,Fourier 级数展开式中只有奇次谐波。
(c) 从图形观察:A t f t f a c -=)(2)(第4章 周期信号的频域分析 83所以 tjn n n c en A t f 0)2/(Sa )(0,ωπ∑∞≠-∞==000411c o s ()c o s (3)c o s (5)35A t t t ωωωπ⎛⎫=-+- ⎪⎝⎭)(t f c 实偶对称,且是半波镜像信号,Fourier 级数展开式中只含有奇次谐波的余弦分量。
(d) 从图形观察:)4/()(T t f t f c d -=所以 )2/(0,0)2/(Sa )(πωπn t n j n n d en A t f -∞≠-∞=∑=000411sin()sin(3)sin(5)35A t t t ωωωπ⎛⎫=++- ⎪⎝⎭)(t f d 实奇对称,且是半波镜像信号,Fourier 级数展开式中只含有奇次谐波的正弦分量。
第4章 习题答案

50������-2 = 0
������������������������ = -0.5 +
������������
解得 L=10(已舍去负值)
且
������2������������������ ������������2
=
-100������-3<0
所以,当劳动投入量 L=10 时,劳动的
第四章 生产论 3. 已知生产函数 Q=f(L,K)=2KL-0.5L2 -0.5K2, 假定厂商目前处于短期生产,且 K =10。
(1)写出在短期生产中该厂商关于劳动的 总产量 TPL 函数、劳动的平均产量 APL 函数 和劳动的边际产量 MPL 函数。
(2)分别计算当劳动的总产量 TPL、劳动 的平均产量 APL 和劳动的边际产量 MPL 各自 达到最大值时的厂商的劳动投入量。
有 MP=0,于是,有 35+16L-3L2=0。
解得������ = − 5
3
和
L=7。������
=
-
5 3
不合
理,舍去,故取 L=7。
由此可得,生产要素 L 投入量的合理区 间为[4,7]。因此,企业对生产要素 L 的使用 量为 6 是处于短期生产的合理区间的。
11. 已知生产函数 Q=AL1/3K2/3。 判断:(1)在长期生产中,该生产函数的规模 报酬属于哪一种类型?
50 劳动的平均产量函数:
APL=
TPL =20-0.5L- 50
������
������
劳动的边际产量函数:
MPL=
������������������������ ������������
=20-L
(2)关于总产量的最大值:
第4章习题参考解答

p3()
{
P(s);
…
}
参考解答:
因p1和p2进程是p3进程开始执行的先决条件,即当p1和p2进程均执行完毕时,p3才能执行,则p3需有两个信号量,分别表示p1进程执行完毕的信号量s1,以及p2进程执行完毕的信号量s2。则同步算法描述如下:
main()
{
int s1=0,s2=0;
cobegin
p1();
p4();
coend
}
p1()
{
p1 execute;
V(s12);
V(s13);
V(s14);
}
p2()
{
P(s12);
p2 execute;
}
p3()
{
P(s13);
p3 execute;
}
p4()
{
P(s14);
p4 execute;
}
4-15
解:
main()
{
int sa=1,sb=0;// sa表示缓冲区S是否为空,sb表示是否为满。
(3)设a、b两并发进程,它们共享一临界资源。其执行临界区的算法框图如下图,
进程A和进程B为互斥进程,则需一个互斥信号量s,初值为1,表示临界资源初始情况下无进程使用。
main()
{
int s=1;
cobegin
pa();
pb();
coend
}
pa()
{
P(s);
进入csa…
V(s);
}
pb()
{
P(s);
进入csb…
V(s);
}
4-21
答:线程有时也称为轻量级进程,它是比进程更小的活动单位,它是进程中的一个执行路径。一个进程可以有多个执行路径即线程。
第4章 习题解答

根据采样定理,可实时处理的最高频率:
2 2 注:具体应用时 f m ax 还应再小一些 f m ax FS 15625 7 8 1 2 .5 Hz
第4章 快速傅里叶变换(FFT)
3.已知X(k)和Y(k)是两个N点实序列x(n)和y(n)的DFT,
希望从X(k)和Y(k)求x(n)和y(n), 为提高运算效率,试设计用
一次N点IFFT来完成的算法。 解:根据DFT的对称性质,实序列x(n)和y(n)的DFT X(k)和
Y(k)均为共轭对称,即X(k) =X*(N-k),Y(k) =Y*(N-k),则 (jY(k))*= -jY(N-k),所以jY(k)为共轭反对称。
解: (1) 直接计算: 复数乘法:4*N2=4*10242=4194304μs=4194.304ms 复数加法:1*N(N-1)=1024*1023=1047552μs=1047.552ms 1024点DFT直接计算时:4194.304+1047.552=5241.856ms
(2) 用FFT计算: 复数乘法:4* (N/2)*lbN= 4* 512*10=20480μs=20.48ms 复数加法:1*N*lbN= 1*1024*10=10240μs=10.24ms 1024点DFT采用FFT算法时:20.48+10.24=30.72ms
设: A(k) = X(k)+ jY(k) ,计算A(k)的N点快速IDFT,即 a(n)= IFFT(A(k)) = Re(a(n)) + jIm(a(n)),
其中,Re(a(n)) = IDFT(X(k)) = x(n) ,
jIm(a(n)) = IDFT(jY(k))= jy(n) 所以:x(n) = Re(a(n)) = 1/2(a(n)+a*(n)) y(n) = Im(a(n)) = -j/2(a(n)-a*(n))
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4章习题解答4.1.1 测得某放大电路中BJT的三个电极A、B、C的对地电位分别为V A=-9 V,V B =一6 V,Vc=6.2 V,试分析A、B、C中哪个是基极b、发射极e、集电极c,并说明此BJT是NPN管还是PNP管。
解:由于锗BJT的|V BE|≈0.2V,硅BJT的|V BE|≈0.7V,已知用BJT的电极B的V B=一6 V,电极C的Vc=–6.2 V,电极A的V A=-9 V,故电极A是集电极。
又根据BJT工作在放大区时,必须保证发射结正偏、集电结反偏的条件可知,电极B是发射极,电极C是基极,且此BJT为PNP管。
4.2.1试分析图题4.2.1所示各电路对正弦交流信号有无放大作用。
并简述理由。
(设各电容的容抗可忽略)解:图题4.2.1a无放大作用。
因R b=0,一方面使发射结所加电压太高,易烧坏管子;另一方面使输人信号v i被短路。
图题4.2.1b有交流放大作用,电路偏置正常,且交流信号能够传输。
图题4.2.1c无交流放大作用,因电容C bl隔断了基极的直流通路。
图题4.2.1d无交流放大作用,因电源V cc的极性接反。
4.3.2 测量某硅BJT各电极对地的电压值如下,试判别管子工作在什么区域。
(a)V C=6 V V B=0.7 V V E=0 V(b)V C=6 V V B=2 V V E=1.3 V(c)V C=6 V V B=6V V E=5.4 V(d)V C=6 V V B=4V V E=3.6 V(。
)V C=3.6 V V B=4 V V E=3. 4 V解(a)放大区,因发射结正偏,集电结反偏。
(b)放大区,V BE=(2—l.3)V=0.7 V,V CB=(6-2)V=4 V,发射结正偏,集电结反偏。
(C)饱和区。
(d)截止区。
(e)饱和区。
4.3.5 电路如图所示,画出了某固定偏流放大电路中BJT的输出特性及交、直流负载线,试求:(1)电源电压V CC ,静态电流I B 、I C 和管压降V CE 的值; (2)电阻R b 、R C 的值;(3)输出电压的最大不失真幅度;(4)要使该电路能不失真地放大,基极正弦电流的最大幅值是多少?解 (1)由图可知,直流负载线与横坐标轴的交点即Vcc 值的大小,故Vcc= 6 V 。
由Q 点的位置可知,I B =20µA ,I C =1 mA ,V CE =3 V 。
(2)由基极回路得: Ω=≈k I V R BCCb 300 由集-射极回路得 Ω=−==k I V V R CCECC C 3 (3)求输出电压的最大不失真幅度由交流负载线与输出特性的交点可知,在输人信号的正半周,输出电压v CE 从3V到0.8V ,变化范围为2.2V ;在输入信号的负半周,输出电压v CE 从3V 到4.6V ,变化范围为1.6V 。
综合起来考虑,输出电压的最大不失真幅度为1.6V 。
(4)基极正弦电流的最大幅值是20 µA 。
4.3.8 画出图题4.3.8所示电路的小信号等效电路,设电路中各电容容抗均可忽略,并注意标出电压、电流的正方向。
解图题4.3.8所示各电路的小信号等效电路如下图所示。
4.3.9单管放大电路如图题4.3.9所示,已知BJT的电流放大系数β=50。
(1)估算Q点;(2)画出简化H参数小信号等效电路;(3)估算 BJT 的朝人电阻 r be ;(4)如输出端接入 4 k Ω的电阻负载,计算i O V V V A =及SO VS V V A =。
解(1)估算Q 点A R V I bCCB µ40=≈mA I I B C 2==β V R I V V C C CC CE 4=−= (2)简化的H 参数小信号等效电路如上图所示。
(3)求r beΩ=++Ω=++Ω=863226)501(20026)1(200mAmVI mV r E bc β (4)116)||('0−≈−=−==be L C be L iV r R R r R V V A ββ 73||||00−≈+=+=⋅==be b s be b V s i i V si i s VS r R R r R A R R R A V V V V V V A 4.3.11 电路如图题4.3.11所示,已知BJT 的β=100,V BE =-0.7V。
(1)试估算该电路的Q 点;(2)画出简化的H 参数小信号等效电路;(3)求该电路的电压增益vA ,输入电阻R i 、输出电阻R o ; (4)若v o 中的交流成分出现图题4.3.11b 所示的失真现象,问是截止失真还是饱和失真?为消除此失真,应调整电路中的哪个元件?如何调整?图题4.3.11解(1)估算Q 点4044CCB C B CE CC c c bV I AI I mA V V I R V R µβ≈====−=−(2)简化的H参数小信号等效电路如下图所示。
(3)求vA 、R i 、R o 。
BJT 的输入电阻 Ω≈++Ω=857426)1001(200mAmVr be (||)155.6||8572c L v i b be be o c beR R A R R r r R R k r β=−≈−=≈=Ω≈=Ω(4)因图题4.3.11a 中的BJT 是PNP 管,故图题4.3.11b 中出现的v o 失真是截止失真;应调整R b ,使之减小,可消除此失真。
4.3.12 在图题4.3.12所示电路中设电容C 1、C 2、C 3对交流信号可视为短路。
(1)写出静态电流Ic 及电压V CE 的表达式;(2)写出电压增益VA 、输人电或Ri .和输出电阻Ro 的表达式; (3)若将电容C 3开路,对电路将会产生什么影响? 解(1)I C 及V CE 的表达式1R V I I CCB C ββ≈= )(32R R I V V C CC CE +−=(2)VA 、Ri .和Ro 的表达式 beL V r R R A )||(2β−=be i r R R ||1= 2R R O ≈(3)C 3开路后,将使电压增益的大小增加beL V r R R R A ]||)[(32+−=β同时R o 也将增加,32R R R O+≈。
4.4.3 射极偏置电路和BJT 的输出特性曲线如图题4.4.3所示,已知β=60。
(1)分别用估算公式和图解法求Q 点; (2)求输入电阻r be ;(3)用小信号模型分析法求电压增益VA ; (4)若电路其他参数不变,如果要使V CE =4V ,问上偏流电阻为多大?解(1)估算法求Q 点:V V V B 41610)6020(102033=×Ω×+Ω×= 1.6528(23)7.75C B BEC B eCE CC C I V V I mA I A R V V I k k Vµβ−===≈=−Ω+Ω= (2)Ω≈++=k I mVr r Ebb be 2.126)1(β(3)100−=′−=beL vr R A β ,其中Ω=Ω+×==′k k R R R L c L26363|| (4)当V CE =4V 时mA R R V V I ec CECC C 4.2=+−=V V R I V V V BE e C BE E B 5.5=+=+=上偏流电阻Ω≈⋅−=k R V V V R b BBCC b 2.3821 4.5.3 电路如图4.5.3所示,设β=100,试求:(1)Q 点;(2)电压增益s o V V V A 11=和so V V V A 22=; (3)输入电阻R i ; (4)输出电阻R O1和R O2解 (1)求Q 点:V V R R R V CC b b b B 3.4212≈+=mA R V V I I eBEB EC 8.1=−=≈V R R I V V e c C CC CE 8.2)(=+−=A I I CB µβ18==(2)求r be 及RiΩ≈++=k I mVr r Ebb be 66.126)1('βΩ≈++=k R r R R R e be b b i 2.8])1([||||21β (3) 求A vs1,A Vs2010110.79(1)i c i Vs s i s be e i sV V V R R A V V V r R R R ββ==⋅=−⋅≈−+++020220.8(1)i e i Vs s i s be e i sV V V R R A V V V r R R R ββ==⋅=−⋅≈+++ (4)求R O1和R O2、Ω=≈k R R C O 21 Ω≈++=311)||||(||2102βs b b be e R R R r R R4.5.5 电路如图题4.5.5a 所示。
BJT 的电流放大系数为β,输入电阻为r be ,略去了偏置电路。
试求下列三种情况下的电压增益vA 、输入电阻R i 和输出电阻R o : ①v s2=0,从集电极输出; ②v s1=0,从集电极输出; ③v s2=0,从发射极输出。
并指出上述①、②两种情况的相位关系能否用图b 来表示?符号“+”表示同相输入端,即v c 与v e 同相。
而符号“-”表示反相输入端,即v c 与v b反相。
解 ①c o ebe i ebe v R R R r R R r RA C≈++=++−=)1()1(βββ ②c o bee i be cvR R r R R r R A ≈++=++=βββ1Re)1(③ ebe evR r R A )1()1(ββ+++=ββ+=++=1||)1(bee o e be i r R R R r R ①、②两种情况的相位关系能用图b 表示,即将v s1加于“-”端,v s2加于“+”端。
4.6.2:电路如图4.6.3所示。
设两管的特性一致,β1=β2=50,V BEQ1=V BEQ2=0.7V 。
(1)试画出该电路的交流通路,说明T 1、T 2各为什么组态; (2)估算I CQ1、V CEQ1、I CQ2、V CEQ2; (3)求A V 、Ri 和Ro 。
解:(1)估算两管的Q 点21121111111111117.515 2.78337.5()/(2.780.7)/2 1.041.04/10010.4()15 1.047.17.6b BQ CC b b EQ CQ BQ BEQ e CQ BQ CEQ CC CQ e c R V V R R I I V V R mA I I mA AV V I R R Vµβ≈=×≈++≈=−=−=====−+=−×≈2221122222222222(15 1.04 5.10.7)9/9/3.3 2.72.7/1002715 2.7 3.36EQ BQ BEQ CC CQ e BEQ CQ EQ EQ e CQ BQ CEQ CC CQ e V V V V I R V V I I V R mA I I mA AV V I R Vµβ=−=−−=−×−≈≈==≈====−=−×≈(2)求A V 、Ri、Ro求得:122.73 1.2be be r K r K ≈Ω≈Ω11 ()(){}111211122211//1//182Lv v v be e be e L be R A A A r R r R R r βββ′=≈−×++⎡⎤⎣⎦=−≈− 1121222//// 1.88//611i be b b e be o e R r R R K R r R R β=≈Ω+=≈Ω+4.7.1某放大电路中A V 的数幅频特性如图题4.7.1所示。
