数值分析课件第四章
合集下载
数值分析课程课件 直接三角分解方法
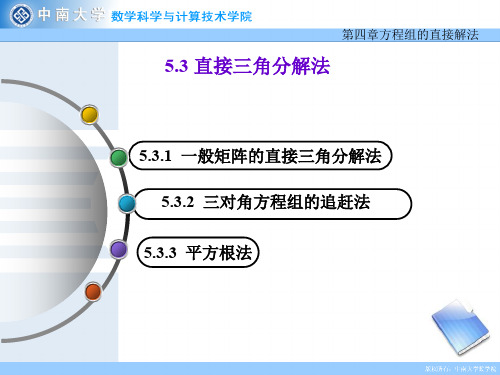
u22
u11
u2n
l n1 l n2
1
unn
即
a11 a12 a 21 a22
a1n
a2n
u11 l21u11
u12 l21u12 u22
u1n
l21u1n
u2n
a n1 a n2
ann
ln1u 11
由(5.3.1)- (5.3.4)求得L和U后,解方程组Ax=b 化为求解LUx=b,若记Ux=y,则有Ly=b。于是可分两部解 方程组LUx=b,只要逐次向前代入的方法即可求得y。第
二步求解Ux=y,只要逐次用向后回代的方法即可求得x。 设 x=(x1 ,x2, ···xn) T, y=(y1, y2, ···yn) T,
n
i1
lniuin
unn
第四章方程组的直接解法
由A的第1行和第1列可计算出U的第1行和L的第1列,即
u1 j a1 j , j 1, 2, , n,
(5.3.1)
lk1
ak1 u11
,k
2, 3,
, n.
(5.3.2)
如果U的第1至k-1列和L的第1至k-1列已经算出,则由
解 设 A=LU,即
l11 a11 1, l21 a21 2, l31 a31 0
u12
a12 l11
2, u13
a13 l11
1,
l22 a22 l21u12 3, l32 a32 l31u12 1
数值分析第四章课件

xk
1.25 1.375 1.3125 1.3438 1.3281 1.3203 1.3242
f (xk)的符号
+ + + -
14
f ( x0 ) f ( x0 h ) 0
那么所求的根x*必在x0与x0+h之间,这里可取x0或x0+h作为根 的初始近似。
4
例1:考察方程 f ( x) x3 x 1 0 注意到f (0)< 0, f (+)>0,知f (x)至少有一个 正的实根。 设从x = 0出发,取h = 0.5为步长向右进行 根的扫描,下表记录各个结点上函数值的符号, 我们发现,在区间(1, 1.5)内必有实根,因此可 取x0 = 1或x0 = 1.5作为根的初始近似值。
第四章 方程求根
§4.1 二分法 §4.2 迭代法 §4.3牛顿法 §4.4弦截法
1
我们很熟悉一次、二次代数方程以及某些特殊的高 次方程或超越方程的解法。这些方法都是代数解法, 也是精确法。但在实际中,有许多方程问题无法求出 公式解。例如超越方程
tgx x 0 0.25 tgx 4.8889 sin x 0
9
由于
1 xk x (bk a k ) bk 1 a k 1 2
*
(1)
只要有根区间[ak+1, bk+1]的长度小于预先给定的误差, 那么就可以取
xk 1 1 ( ak bk ) 2
作为所求根x*的第k+1次近似值。其误差估计为: 1 * x xk 1 k 1 ( b a ) 2 综上所述,设f (x)在[a, b]上存在一阶导数且不变号, 如果f (a)f (b)<0,则由(1)所知,当k时, x* - xk0,即xkx*。
清华第五版数值分析第4章课件

3! 0
3
3
6
72
R[ f ] 1 f ''' ()
72
收敛性定义
在 b
n
f (x)dx
a
Ak f (xk )
k 0
中,若
n
b
limn,h0 Ak f (xk ) a f (x)dx
k 0
则称求积公式是收敛的。
稳定性定义
• 设 f (xk ) %fk k
a (x xk ) dx k0
xk
x0 jh,
x x0 th R[ f ] hn2
n 0
n
(t k)dt
k0
n even, n/2 integer, let t u n / 2, we have
R[ f ] hn2 n/2 n (u n / 2 k) du 0 n/2 k0
第四章 数值积分和数值微分
为什么要数值积分?
Newton-Leibniz 公式:
b a
f
(x)dx
F ( x)
b a
F (b)
F (a)
其中, F (x)是被积函数 f (x)的原函数。
要求被积函数f(x) ☞ 有解析表达式;
☞ f(x)的原函数F(x)为初等函数.
问题
1) f(x)没有解析表达式,只有数表形式 e.g. x 1 2 3 4 5
若求积公式代数精度为 m ,则可设
R( f )
b
f (x)dx
a
n
Ak f (xk ) Kf (m1) ()
k 0
求出K即可。K不依赖于函数f。令 f (x) xm1
数值分析第四章4-1

2011-10-31
2
引例与问题综述(续)
表4.1.1 函数表
x f(x)
x0 f(x0)
x1 f(x1)
… …
xn f(xn)
2011-10-31
3
引例与问题综述(续)
• • •
需要通过这组实验观测数据 (xi , yi ) (i =0, 1,2,…, n) 揭示自变量x与因变量y之间的关系。 一般地,可以用一个近似的函数关系式y = f(x)来表示 自变量x与因变量y之间的关系。 函数 f(x) 的产生办法因观测数据与要求的不同而异, 通常可采用两种方法:插值与数据拟合。
2011-10-31
20
2.如果给定的数据是大量的测试或统计的结果,并不是 必须严格遵守的,而是起定性地控制作用的,那么宜选用数据 拟合的方法。这是因为,一方面测试或统计数据本身往往带有 测量误差,如果要求所得的函数与所给数据完全吻合,就会使 所求函数保留着原有的测量误差;另一方面,测试或统计数据 通常很多,如果采用插值方法,不仅计算麻烦,而且逼近效果 往往较差。
2011-10-31
4
一、引例 引例1 海水温度问题 已经测得在北纬 32.3° 海洋不同深度处的温度如下表:
表4.1.2 海水温度表
深度x (m) 水温y (C°)
466 7.04
714 4.28
950 3.40
1422 2.54
1634 2.13
根据这些数据,我们希望能合理地估计出其它深度(如 500米、 600米、1000米…)处的水温。 解决这个问题,可以通过构造一个与给定数据相适应的函数来 解决,这是一个被称为插值的问题。
2011-10-31
21
问题综述(续)
数值分析第四版第四章数值积分与数值微分精品PPT课件

b
n
b
R( f ) f (x)dx a
在a,b内存在一点 ,使得
b
I ( f ) f (x)dx (b a) f ( )
a
f ?
称 f 为 f x 在区间 a,b上的平均高度.
3、求积公式的构造
➢ 若简单选取区间端点或中点的函数值作为平均高度,则 可得一点求积公式如下:
左矩形公式: I f f ab a
中矩形公式:Biblioteka nAk b ak 0
n
k 0
Ak xk
1 2
b2 a2
n
k 0
Ak
xk m
1 m 1
bm1 am1
§2 插值型求积公式
一、定义
在积分区间 a,b上,取 n 1个节点 xi , i 0,1, 2,..., n
作f x 的 n 次代数插值多项式(拉格朗日插值公式):
2 式(两点求积公式)
I f f a f b b a
2
y
f b
f a Oa
f x
bx
➢
若取三点,a,b, c
ab 2
并令 f
f
a4 f
c
f
b
6
则可得Simpson公式(三点求积公式)
I f b a f a 4 f c f b
6
➢ 一般地 ,取区间 a,b 内 n 1 个点xi,i 0,1, 2,..., n
2. 有些被积函数其原函数虽然可以用初等函数表示,但表达 式相当复杂,计算极不方便.
例如函数:
x2 2x2 3
并不复杂,但它的原函数却十分复杂:
1 x 2 2x 2 3 3 x 2x 2 3 9 ln( 2 x 2x 2 3 )
数值分析第五版李庆扬王能超课件第4章(1)

1.483240 1.549193 1.612452 1.673320 1.732051
y1
yi 1 yi h f ( xi , yi ) ( i 0, ... , n 1)
亦称为欧拉折线法
/* Euler’s polygonal arc method*/
2.1
欧拉方法
定义 在假设 yi = y(xi),即第 i 步计算是精确的前提下,考 虑的截断误差 Ri = y(xi+1) yi+1 称为局部截断误差 /* local
1.264911 1.341641
0.5
0.6 0.7 0.8 0.9 1.0
1.435133
1.508966 1.580338 1.649783 1.717779 1.784770
1.416402
1.485956 1.552514 1.616475 1.678166 1.737867
1.414214
隐式欧拉公式
y i 1 y i h f ( x i 1 , yi 1 ) ( i 0, ... , n 1)
2.1
欧拉方法
注:
由于未知数 yi+1 同时出现在等式的两边,不能直接得
到,故称为隐式(后退) /* implicit */ 欧拉公式,而前 者称为显式 /* explicit */ 欧拉公式。
truncation error */。
定义 若某算法的局部截断误差为 O(hp+1),则称该算法有 pding term */
欧拉法的局部截断误差:
Ri y( xi 1 ) yi 1 [ y( xi ) hy( xi ) h2 y( xi ) O( h3 )] [ yi hf ( xi , yi )]
y1
yi 1 yi h f ( xi , yi ) ( i 0, ... , n 1)
亦称为欧拉折线法
/* Euler’s polygonal arc method*/
2.1
欧拉方法
定义 在假设 yi = y(xi),即第 i 步计算是精确的前提下,考 虑的截断误差 Ri = y(xi+1) yi+1 称为局部截断误差 /* local
1.264911 1.341641
0.5
0.6 0.7 0.8 0.9 1.0
1.435133
1.508966 1.580338 1.649783 1.717779 1.784770
1.416402
1.485956 1.552514 1.616475 1.678166 1.737867
1.414214
隐式欧拉公式
y i 1 y i h f ( x i 1 , yi 1 ) ( i 0, ... , n 1)
2.1
欧拉方法
注:
由于未知数 yi+1 同时出现在等式的两边,不能直接得
到,故称为隐式(后退) /* implicit */ 欧拉公式,而前 者称为显式 /* explicit */ 欧拉公式。
truncation error */。
定义 若某算法的局部截断误差为 O(hp+1),则称该算法有 pding term */
欧拉法的局部截断误差:
Ri y( xi 1 ) yi 1 [ y( xi ) hy( xi ) h2 y( xi ) O( h3 )] [ yi hf ( xi , yi )]
数值分析课件第4章

数值分析课件第4章
数值分析课件第4章:插值与拟合。从插值与拟合的概念和区别开始,详细介 绍线性插值、非线性插值、最小二乘法、数据拟合、插值误差和拟合误差等 内容,以及在图像处理和实际问题中的应用。
插值与拟合的概念及区别
插值与拟合是数值分析中常用的数据处理方法。插值通过已知数据点之间的 函数曲线拟合,以在未知点上估计函数值。拟合则是找到最适合数据的函数 曲线,可能不通过已知数据点。
最小二乘法:原理与应用
最小二乘法是一种通过最小化数据与拟合函数之间的误差来拟合数据的方法。它可以应用于线性和非线 性拟合问题,适用于存在噪音和不完美数据的情况。
数据拟合:多项式拟合、指数拟合、对 数拟合等
数据拟合是根据数据的特点选择合适的函数形式进行拟合。多项式拟合在一定范围内适用于大多数问题, 而指数拟合和对数拟合则适合呈指数或对数关系的数据。
插值误差与拟合误差
插值误差是指插值函数与真实函数之间的差距,取决于插值方法和数据分布。 拟合误差则是指拟合函数与真实数据之间的偏差,受拟合口卷积法等
数据平滑是通过降低噪音和突变来减少数据中的波动。移动平均法和窗口卷积法是常用的数据平滑方法, 可以平滑曲线并减少噪音的影响。
线性插值:拉格朗日与牛顿法
线性插值可以用拉格朗日或牛顿法实现。拉格朗日插值使用多个已知数据点 构建一个多项式函数,适用于等间距的数据。牛顿插值则通过分段差商构造 一个插值多项式。
非线性插值:样条插值
非线性插值中,样条插值是常用的方法。它使用分段多项式函数拟合数据, 每个区间内都有一个多项式来逼近数据的行为,从而实现更加平滑的插值效 果。
数值分析第五版李庆扬王能超课件第4章(2)

30 x
1.0000 2.0000 4.0000 8.0000 1.6000101 3.2000101
1.0000 2.5000101 6.2500102 1.5625102 3.9063103 9.7656104
1.0000 2.5000 6.2500 1.5626101 3.9063101 9.7656101
稳定性 /* Stability */
例:考察初值问题
2.2 单步法的稳定性
y( x ) 30 y( x ) 在区间[0, 0.5]上的解。 y ( 0) 1
分别用欧拉显、隐式格式和改进的欧拉格式计算数值解。
节点 xi 0.0 0.1 0.2 0.3 0.4 0.5 欧拉显式 欧拉隐式 改进欧拉法 精确解 小扰动引起了质的改变 ! ye
其中2阶方法
yi 1 yi hK 1 K f (x h , y h K ) 1 i i 1 2 2
Img
的绝对稳定区域为
而显式 1~ 4 阶方法的绝对稳定 Img 区域为
k=4 - 3
0
Re
k=1
k=3 k=2
-2 -1
-3
-2
-1
Re
无条件阶经典龙格-库塔法 /* Classical Runge-Kutta Method */ :
y i 1 K1 K2 K3 K4
yi h ( K1 2K 2 2K 3 K 4 ) 6 f ( xi , yi )
h f ( xi h , y K1 ) i 2 2 h f ( xi h , y K2 ) i 2 2
1.0000 4.9787102 2.4788103 1.2341104 6.1442106 3.0590107
1.0000 2.0000 4.0000 8.0000 1.6000101 3.2000101
1.0000 2.5000101 6.2500102 1.5625102 3.9063103 9.7656104
1.0000 2.5000 6.2500 1.5626101 3.9063101 9.7656101
稳定性 /* Stability */
例:考察初值问题
2.2 单步法的稳定性
y( x ) 30 y( x ) 在区间[0, 0.5]上的解。 y ( 0) 1
分别用欧拉显、隐式格式和改进的欧拉格式计算数值解。
节点 xi 0.0 0.1 0.2 0.3 0.4 0.5 欧拉显式 欧拉隐式 改进欧拉法 精确解 小扰动引起了质的改变 ! ye
其中2阶方法
yi 1 yi hK 1 K f (x h , y h K ) 1 i i 1 2 2
Img
的绝对稳定区域为
而显式 1~ 4 阶方法的绝对稳定 Img 区域为
k=4 - 3
0
Re
k=1
k=3 k=2
-2 -1
-3
-2
-1
Re
无条件阶经典龙格-库塔法 /* Classical Runge-Kutta Method */ :
y i 1 K1 K2 K3 K4
yi h ( K1 2K 2 2K 3 K 4 ) 6 f ( xi , yi )
h f ( xi h , y K1 ) i 2 2 h f ( xi h , y K2 ) i 2 2
1.0000 4.9787102 2.4788103 1.2341104 6.1442106 3.0590107
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n
b
lim
n h0
k 0
Ak
f
( xk
)
a
f (x)dx,
其中h max(xi xi1),则称求积公式(1.3)是收敛的.
1in
设计算f
(xk )有误差k ,
即f
(xk )
~ fk
k
(k
0,1,, n)。
定义3 若
n t j
(b a)(1)nk n n
Ak
h 0
j0
dt k j
nk!(n k)!
(t j)dt.
0 j0
jk
jk
(2.1)
记C(kn)
(1)nk nk!(n k)!
n 0
n j0
(t
j)dt
jk
有
b f (x)dx (b a)
11 f (x)dx w0 f (1) w1 f (0) w2 f (1)
试确定系数w0, w1, w2, 使上述求积公式的代数精度尽量高.
三、插值型求积公式
已知在n 1个互异节点a x0 x1 xn b上函数值f0,
f1,,
f
,构造拉格
n
朗日插值多项式
a
n
C(n) k
fk
,
k 0
(2.2)
称为Newton- Cotes公 式,C(kn)称为Cotes系 数,可事先求出,
见书上柯特斯系数表.
当n 1时, 得到梯形公式
ab
f
( x)dx
T
b a[ 2
f
(a)
f
(b)],
当n 2时, 得到抛物线公式, 也称为辛普森(Simpson)公式
R4[ f
]
I
C
2(b a) 945
b a 6 4
f
(6) (),
[a,b].
(2.6)
§3 复合求积公式
问题的提出和解决办法. 一、复合梯形公式
把 区 间[a, b] n等 分 为n个 小 区间[xi , xi1],其 中
xi
a ih,
(h
ba ,i n
)
~ fk
(k 0,, n), 就有
~
| In ( f ) In ( f ) |
n Ak [ f (xk ) ~f (xk )] ,
k 0
则称求积公式(1.3)是稳定的.
定 理 2 若求积公式 (1.3)中系数Ak (0 0,1,, n), 则求积公式 是稳定的.
n 8时C(kn)出现负值 , N C公式不稳定.
二、 Newton-Cotes公式的代数精度
由定理1知,n阶N C公式至少n次代数精度.
例:考察辛普森公式
S b a [ f (a) 4 f ( a b) f (b)].
6
2
定理3 若n为偶数,则n阶N C公式至少有n 1次代数精度.
它的余项为
R[
f
]
ab
f
(
x)
Ln
(
x)dx
ab
f (n1) ( )
(n 1)!
n
(
j0
x
x
j
)dx.
(1.7)
定理1
求积公式
b
f (x)dx
a
n
Ak fk至少具有n次代数精度
k 0
它是插值型求积公式.
四、求积公式的收敛性和稳定性
定义2 在求积公式(1.3)中, 若
三、几种低阶Newton-Cotes求积公式的余项
1. 梯形公式的余项 若f (x)在[a,b]上连续,则梯形公式的余项为
R1[ f ] I T
(b a)3
12
f (),
[a,b].
(1.10)
2. 辛普森公式的余项
若f (4) (x)在[a,b]上连续, 则辛普森公式的余项为
b
n
f (x)dx
a
Ak f (xk ),
(1.3)
k 0
称为机 械 求 积 公 式. Ak称为求积系数,xk称为求积节点。
二、代数精度的概念
定义1 若一个求积公式对于所有次数不超过m的多项式 都准确成立,而对于某一个m 1次的多项式等式不准确成 立, 则称该求积公式具有m次代数精度. 练习 设有求积公式
这是因为, 当 f (xk ) ~fk (k 0,, n)时, 有
| In ( f ) In ( ~f ) |
n
Ak
f (xk )
~ f (xk )
n
Ak
(b a) .
k 0
k 0
§2 牛顿—柯特斯公式
一、Newton-Cotes公式(等距节点的插值型求积公式)
ab
f
( x)dx
S
b
6
a[
f
(a)
4
f
(a
2
b)
f
(b)],
(2.3)
当n 4时,得到柯特斯(cotes)公式
C
b a[7 90
f
( x0
)
32
f
( x1 )
12
f
( x2
)
32
f
(
x3 )
7
f
( x4
)],
其中xk
a
kh,h
b a. 4
( 2.4)
将求积区间[a, b] n等分,步长 h b a , 推导等距节点 n
xk a kh上的插值型求积公式
b
n
f (x)dx
a
Ak fk
k 0
Ak
b
a lk (x)dx
bn a
j0
x x j dx xk x j
jk
作变换x a th,则有
得到
即得求积公式
n
f (x) Ln (x) lk (x) fk
k 0
b
f (x)dx
a
b a
Ln (x)dx
n k 0
b a
lk
(
x)dx
fk ,
b
a
f
( x)dx
n
Ak
fk ,
其中Ak
b
a lk (x)dx.
k 0
(1.5)
称为插值型求积公式.
第4章 数值积分和数值微分
§1 数值积分概论
一、数值积分的基本思想
问题的提出和解决办法:
I ab f (x)dx. ab f (x)dx F (b) F (a).
当原函数不能求出时怎么办?由定积分的定义:
b
n
a
f (x)dx
lim
x 0 k 0
f (k )xk
构造求积公式
b
ba
ab
R2[ f ] I S a f (x)dx 6 [ f (a) 4 f ( 2 ) f (b)]
b a b a 4 f (4) (), [a,b].
(2.5)
180 2
3. 柯特斯公式的余项
若f (6) (x)在[a,b]上连续, 则柯特斯公式的余项为
