2018年秋浙教版八年级数学上第2章自我评价试卷含答案
2018秋浙教版八年级数学上册(浙江专版)试卷含答案

C ������ 猴子是动物 ㊀㊀㊀D ������ 2 0 1 6 年奥运会在巴西的里约热内卢举行
线段最短 A ������ 同位角相等 ㊀㊀㊀B ������ 两点之间 ,
(A )
则a > 正确的反例是 4 ������ 对假命题 若 a> b, b 举反例 ,
2 2
如图 , 若 5 ������ ( 2 0 1 7 年陕西省 ) A BʊC D, A E 平分 øC A B 交C D 于点 E . A ������ 6 5 ʎ , 则 øA øC=5 0 ʎ E D= B ������ 1 1 5 ʎ C ������ 1 2 5 ʎ D ������ 1 3 0 ʎ
二 ㊁ 填空题 ( 每小题 4 分 , 共2 4 分)
给出下列五个论断 : 1 3 ������ 对于平面内三条直线 a㊁ b㊁ c, 以其中两个论断为条件 , 一个论断为结论组成一个你认为正确的 命题 : ①②→④ ( 用序号写出一个即可 ) .
第1 1 题图
㊀㊀
第1 2 题图
㊀㊀
第1 4 题图
A ������ 1 5 ʎ
B ������ 2 5 ʎ
C ������ 3 0 ʎ
D ������ 1 0 ʎ
A ����第 9 题图
㊀㊀
第1 0 题图
如图 , 已知 钝 角 三 角 形 A 依下列步骤尺规作 1 0 ������ ( 2 0 1 7 年河北省 ) B C, 以 B 为 圆 心, 交 弧 ① 于 点 D; 步 骤 3: 连接 2: B A 为 半 径 画 弧 ②, 交B 下列叙述正确的是 AD, C 的延长线于点 H . C ������ SәABC =B C������AH A ������ BH 垂直平分线段 AD D ������ A B=AD B ������ A C 平分 øB AD 图, 并保留作图痕迹 : 步骤 1: 以 C 为圆心 , 步骤 C A 为半径画弧 ① ; (A )
【教育专用】2018年秋八年级数学上册期末综合自我评价练习新版浙教版

期末综合自我评价一、选择题(每小题2分,共20分)1.下面四个标志中,是轴对称图形的是(D)2.在平面直角坐标系中,点P(3,-2)关于y轴的对称点在(C)A. 第一象限B. 第二象限C. 第三象限D. 第四象限3.使不等式x-2≥-3与2x+3<5同时成立的x的整数值是(C)A. -2,-1,0B. 0,1C. -1,0D. 不存在4.一个三角形的两边长分别为3 cm和7 cm,则此三角形第三边长可能是(C)A.3 cm B.4 cmC.7 cm D.11 cm5.为了举行班级晚会,小张同学准备去商店购买20个乒乓球做道具,并买一些乒乓球拍做奖品.已知乒乓球每个1.5元,球拍每个25元.如果购买金额不超过200元,且要求买的球拍尽可能多,那么小张同学应该买的球拍的个数是(B)A. 5B. 6C. 7D. 86.如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P是BD的中点.若AD=6,则CP的长为(A)A. 3B. 3.5C. 4D. 4.5(第6题)(第7题)7.如图,把一张长方形纸片ABCD 沿EF 折叠后,点A 落在CD 边上的点A′处,点B 落在点B′处.若∠2=40°,则图中∠1的度数为(A )A. 115°B. 120°C. 130°D. 140°【解】 由折叠可得∠1=∠EFB ′,∠B ′=∠B =90°. ∵∠2=40°,∴∠CFB ′=90°-40°=50°. ∵∠1+∠EFB ′-∠CFB ′=180°, ∴∠1+∠1-50°=180°,解得∠1=115°.8.在平面直角坐标系中,将直线l 1:y =-2x -2平移后,得到直线l 2:y =-2x +4,则下列平移作法中,正确的是(A )A. 将直线l 1向右平移3个单位B. 将直线l 1向右平移6个单位C. 将直线l 1向上平移2个单位D. 将直线l 1向上平移4个单位【解】 ∵将直线l 1:y =-2x -2平移后,得到直线l 2:y =-2x +4, ∴-2(x +a )-2=-2x +4或-2x -2+b =-2x +4,解得a =-3,b =6. ∴应将直线l 1向右平移3个单位或向上平移6个单位.故选A.9.已知A(x 1,y 1),B(x 2,y 2)为一次函数y =2x +1的图象上的两个不同的点,且x 1x 2≠0.若M =y 1-1x 1,N =y 2-1x 2,则M 与N 的大小关系是(C )A .M >NB .M <NC .M =ND .不确定【解】 将y 1=2x 1+1,y 2=2x 2+1分别代入M ,N ,得M =2x 1+1-1x 1=2,N =2x 2+1-1x 2=2,∴M =N .10.如图,在等边三角形ABC 中,AB =10,BD =4,BE =2,点P 从点E 出发沿EA 方向运动,连结PD ,以PD 为边,在PD 右侧按如图方式作等边三角形DPF ,当点P 从点E 运动到点A 时,点F 运动的路径长是(A )A. 8B. 10C. 3πD. 5π导学号:91354037(第10题)(第10题解)【解】 如解图,连结DE ,过点F 作FH⊥BC 于点H. ∵△ABC 为等边三角形,∴∠B =60°. 过点D 作DE′⊥AB,则∠BDE′=30°, ∴BE ′=12BD =2,∴点E′与点E 重合,∴∠BDE =30°,DE =BD 2-BE 2=2 3. ∵△DPF 为等边三角形, ∴∠PDF =60°,DP =DF. ∴∠EDP +∠HDF=90°. ∵∠HDF +∠HFD=90°, ∴∠EDP =∠HFD.在△DPE 和△FDH 中,∵⎩⎪⎨⎪⎧∠PED=∠DHF,∠EDP =∠HFD,DP =FD ,∴△DPE ≌△FDH(AAS),∴FH =DE =2 3.∴点P 从点E 运动到点A 时,点F 运动的路径为一条线段,此线段到BC 的距离为2 3. 当点P 在点E 处时,作等边三角形DEF 1,∠BDF 1=30°+60°=90°,则DF 1⊥BC. 当点P 在点A 处时,作等边三角形DAF 2,过点F 2作F 2Q ⊥BC ,交BC 的延长线于点Q ,易得△DF 2Q ≌△ADE ,∴DQ =AE =10-2=8,∴F 1F 2=DQ =8.∴当点P 从点E 运动到点A 时,点F 运动的路径长是8.二、填空题(每小题3分,共30分)11.已知点A(x,4-y)与点B(1-y,2x)关于y轴对称,则点(x,y)的坐标为(1,2).12.如果关于x的不等式(a+1)x>a+1(a≠-1)可以变形为x<1,那么a的取值范围是a<-1.13.在△ABC中,AB=15,AC=13,高AD=12,则BC的长为14或4.【解】如解图①.由勾股定理,得BD=AB2-AD2=9,CD=AC2-AD2=5,∴BC=BD+CD=14.(第13题解)如解图②,同理可得BD=9,CD=5,∴BC=BD-CD=4.(第14题)14.如图,△ABC和△DCE都是边长为4的等边三角形,点B,C,E在同一条直线上,连结BD,则BD的长为4_【解】∵△ABC和△DCE都是边长为4的等边三角形,∴CB=CD,∴∠BDC=∠DBC=30°.又∵∠CDE=60°,∴∠BDE=90°.在Rt△BDE中,DE=4,BE=8,∴BD=BE2-DE2=82-42=4 3.15.有学生若干人,住若干间宿舍.若每间住4人,则有20人无法安排住宿;若每间住8人,则最后有一间宿舍不满也不空,则学生有__44__人.【解】设共有x间宿舍,则学生有(4x+20)人.由题意,得0<4x +20-8(x -1)<8, 解得5<x<7.∵x 为整数,∴x =6,即学生有4x +20=44(人).16.若关于x 的不等式组⎩⎪⎨⎪⎧x -a>3,1-2x>x -2无解,则a 的取值范围是a ≥-2.【解】 解不等式①,得x>3+a 。
2018年秋浙教版八年级数学上第1章自我评价试卷含答案

第1章自我评价一、选择题(每小题3分,共30分)(第1题)1.如图,已知MB=ND,∠MBA=∠NDC,则下列条件中不能判定△ABM≌△CDN 的是(B)A.∠M=∠NB.AM=CNC.AB=CDD.AM∥CN2.若一个三角形的两边长分别是2和4,则该三角形的周长可能是(C)A.6B.7C.11 D.123.如图,在△ABC中,∠BAC=x,∠B=2x,∠C=3x,则∠BAD的度数为(B)A.145°B.150°C.155°D.160°(第3题)(第4题)4.如图,把一块含有45°角的直角三角尺的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数为(C )A . 15°B . 20°C . 25°D . 30°(第5题)5.如图,在△ABC 中,分别以点A 和点B 为圆心,大于12AB 长为半径画弧,两弧分别相交于点M ,N ,作直线MN ,交BC 于点D ,连结AD .若△ADC 的周长为10,AB =7,则△ABC 的周长为(C )A . 27B . 14C . 17D . 206.如图,已知∠1=∠2,AE ⊥OB 于点E ,BD ⊥OA 于点D ,AE ,BD 的交点为C ,则图中的全等三角形共有(C )A . 2对B . 3对C . 4对D . 5对, (第6题)),(第7题)) 7.如图,BE ⊥AC 于点D ,且AD =CD ,BD =ED .若∠ABC =72°,则∠E 等于(B )A .18°B .36°C .54°D .72°【解】 可证△ADB ≌△CDE ,△ABD ≌△CBD ,∴∠E =∠ABD =12∠ABC =36°. 8.如图,△ABC 的三边AB ,BC ,CA 的长分别是100,110,120,其三条角平分线将△ABC 分为三个三角形,则S △ABO ∶S △BCO ∶S △CAO =(C )。
浙教版八年级上册数学第二章-测试卷及答案

浙教版八年级上册数学第二章测试卷一、选择题(每题3分,共30分)1.下列四个图形分别是低碳、节水、节能和绿色食品标志,在这四个标志中,是轴对称图形的是( )2.如图,在△ABC 中,AB =AC ,∠A =36°,BD 是AC 边上的高,则∠DBC 的度数是( ) A .18°B .24°C .30°D .36°(第2题) (第4题) (第8题)3.在直角三角形ABC 中,∠C =90°,AC =9,BC =12,则点C 到AB 的距离是( ) A.365B.1225C.94D.3344.如图,已知∠C =∠D =90°,添加一个条件,可使用“HL”判定Rt △ABC ≌Rt △ABD ,以下给出的条件合适的是( ) A .AC =ADB .BC =ADC .∠ABC =∠ABD D .∠BAC =∠BAD5.已知一个等腰三角形的两个内角度数之比为1:4,则这个等腰三角形顶角的度数为( ) A .20°B .120°C .20°或120°D .36°6.在△ABC 中,AB 2=(a +b )2,AC 2=(a -b )2,BC 2=4ab ,且a >b >0,则下列结论中正确的是( ) A .∠A =90°B .∠B =90°C.∠C=90°D.△ABC不一定是直角三角形7.直角三角形两条直角边长分别是5和12,则第三条边上的中线长是() A.5 B.6 C.6.5 D.128.如图,在△ABC中,AD,CE分别是△ABC的中线和角平分线,若AB=AC,∠CAD=20°,则∠ACE的度数是()A.20°B.35°C.40°D.70°9.如图,在直线l上依次摆放着七个正方形.已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积从左往右依次是S1,S2,S3,S4,则S1+S2+S3+S4等于()A.3 B.4 C.5 D.6(第9题)(第10题)10.如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连结AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连结PQ,BM,下面结论:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形.其中正确的有()A.0个B.1个C.2个D.3个二、填空题(每题3分,共24分)11.请写出“三个角都相等的三角形是等边三角形”的逆命题:______________________.12.若等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的底角为____________.13.已知实数x,y满足(x-4)2+(y-8)2=0,则以x,y的值为两边长的等腰三角形的周长是________.14.已知a,b,c是△ABC的三边长,且满足关系式(c2-a2-b2)2+|a-b|=0,则△ABC的形状为____________.15.如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中有________对全等三角形.(第15题)(第16题)(第17题)(第18题)16.如图,由四个边长为1的小正方形构成一个大正方形,连结小正方形的三个顶点,可得到△ABC,则△ABC中BC边上的高是________.17.如图,在正方形网格中,阴影部分是涂黑7个小正方形所形成的图案,再将网格内一个空白小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有________种.18.如图,在等腰三角形ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,沿EF折叠后,点C与点O重合,则∠OEC的度数是________.三、解答题(19,20题每题6分,21,22,23题每题8分,24题10分,共46分)19.已知命题“等腰三角形两腰上的高相等”.(1)写出该命题的逆命题.(2)该逆命题是真命题还是假命题?如果是真命题,请画出“图形”,写出“已知”“求证”,再进行“证明”;如果是假命题,请举反例说明.20.如图,点E,F在△ABC的边BC上.若AE=AF,BE=CF,则AB=AC,并说明理由.(第20题)21.如图,AB∥CD,EG,FG分别是∠BEF和∠DFE的平分线.求证:△EGF 是直角三角形.(第21题)22.如图,∠ABC的平分线BF与△ABC中∠ACB的邻补角的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E,则:(1)图中有哪几个等腰三角形?为什么?(2)BD,DE,CE之间存在着什么数量关系?并说明理由.(第22题)23.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB交AB于E,F在AC上,BD=DF.求证:(1)CF=EB;(2)AB=AF+2EB.(第23题)24.如图,等腰直角三角形DBC中,∠BDC=90°,BF平分∠DBC,与CD相交于点F,延长BD到A,使DA=DF,连结AC.(1)求证:△FBD≌△ACD;(2)如图,延长BF交AC于点E,且BE⊥AC,求证:CE=12BF.(3)在(2)的条件下,H是BC边的中点,连结DH,与BE相交于点G.试探索CE,GE,BG之间的数量关系,并证明你的结论.(第24题)参考答案一、1.D 2.A 3.A 4.A 5.C 6.C 7.C 8.B 9.B 10.D 二、11.等边三角形的三个角都相等 12.75°或15° 13.20 14.等腰直角三角形 15.3 16.322 17.3 18.100° 三、19.解:(1)两边上的高相等的三角形是等腰三角形.(2)真命题.已知:如图,在△ABC 中,BE ⊥AC 于E , CD ⊥AB 于D ,且CD =BE . 求证:AB =AC .证明:∵BE ⊥AC ,CD ⊥AB , ∴∠BEA =∠CDA =90°, 又∵∠A =∠A ,BE =CD , ∴△ABE ≌△ACD ,∴AB =AC .(第19题)20.解:∵AE =AF ,∴∠AEF =∠AFE .∵BE =CF ,∴BE +EF =CF +EF ,∴BF =CE .在△ACE 和△ABF 中,⎩⎨⎧AE =AF ,∠AEC =∠AFB ,CE =BF ,∴△ACE ≌△ABF (SAS), ∴AB =AC .21.证明:∵AB ∥CD ,∴∠BEF +∠DFE =180°(两直线平行,同旁内角互补). ∵EG ,FG 分别是∠BEF 和∠DFE 的平分线, ∴∠GEF =12∠BEF ,∠GFE =12∠DFE ,∴∠GEF +∠GFE =12(∠BEF +∠DFE )=12×180°=90°, ∴△EGF 是直角三角形. 22.解:(1)△BDF 和△CEF .∵BF 平分∠ABC , ∴∠ABF =∠FBC ,∵DF ∥BC ,∴∠FBC =∠DFB , ∴∠DFB =∠DBF ,∴DB =DF , ∴△BDF 是等腰三角形. 同理,△CEF 也是等腰三角形.(2)BD =DE +CE .由(1)知△CEF 是等腰三角形,且EC =EF ,∵BD =DF =DE +EF ,∴BD =DE +CE .点拨:“平行线+角平分线”是等腰三角形中常见的基本图形之一,应注意在其他图形中的发掘与应用.23.证明:(1)∵AD 是∠BAC 的平分线,DE ⊥AB ,DC ⊥AC ,∴DE =DC .又∵BD =DF ,∴Rt △CDF ≌Rt △EDB (HL). ∴CF =EB .(2)由(1)可知DE =DC ,又∵AD =AD , ∴Rt △ADC ≌Rt △ADE .∴AC =AE .∴AB =AE +BE =AC +EB =AF +CF +EB =AF +2EB .点拨:(1)根据角平分线的性质“角平分线上的点到角的两边的距离相等”,可得点D 到AB 的距离等于点D 到AC 的距离,即CD =DE ,再根据Rt △CDF ≌Rt △EDB ,得CF =EB .(2)利用(1)中结论证明Rt △ADC ≌R t △ADE ,∴AC =AE ,再将线段AB 进行转化.24.(1)证明:∵△BCD 是等腰直角三角形,且∠BDC =90°,∴BD =CD ,∠BDC =∠CDA =90°. 在△FBD 和△ACD 中,⎩⎨⎧BD =CD ,∠BDF =∠CDA ,DF =DA ,∴△FBD ≌△ACD (SAS). (2)证明:∵BE ⊥AC ,∴∠BEA=∠BEC=90°.∵BF平分∠DBC,∴∠ABE=∠CBE,又∵BE=BE,∴△ABE≌△CBE(ASA),∴AE=CE.∴CE=12AC.由(1)知△FBD≌△ACD,∴BF=AC,∴CE=12BF.(3)解:BG2=GE2+CE2.证明:连结CG,∵H是BC边的中点,BD=CD,∴DH垂直平分BC,∴BG=CG(线段垂直平分线上的点到这条线段两个端点的距离相等).∵BE⊥AC,∴CG2=GE2+CE2,∴BG2=GE2+CE2.点拨:本题综合考查全等三角形的判定与性质,以及通过添加辅助线利用勾股定理解决问题.。
浙教版八年级上《第2章特殊三角形》自我评价测试含答案

第2章自我评价一、选择题(每小题3分,共30分)1.下列轴对称图形中,对称轴条数最多的是(D)A. 线段B. 角C. 等腰三角形D. 等边三角形2.以下列各组数为边长的三角形中,能组成直角三角形的是(B)A.3,4,6 B.15,20,25C.5,12,15 D.10,16,253.一个等腰三角形的两边长分别为5,6,则它的周长为(D)A.16 B.17C.18 D.16或174.若等腰三角形有一个角为40°,则它的顶角为(C)A.40°B.100°C.40°或100°D.无法确定5.如图,将直角边AC=6 cm,BC=8 cm的直角△ABC纸片折叠,使点B与点A重合,折痕为DE,则CD的长为(C)A. 254 B.223C. 74 D.53(第5题)(第6题)6.如图,在△ABC中,AC=DC=DB,∠ACD=88°,则∠B等于(C)A.46°B.44°C.23°D.22°7.在直线l上依次摆放着七个正方形(如图所示),已知斜放置的三个正方形的面积分别为a,b,c,正放置的四个正方形的面积依次是S1,S2,S3,S4,则S1+S2+S3+S4=(C)(第7题)A.a+b B.b+cC.a+c D.a+b+c【解】∵∠ACB+∠BAC=90°,∠ACB+∠DCE=90°,∴∠BAC=∠DCE,故可证得△ABC≌△CDE,∴AB=CD.同理可证得△PQM≌△MFN,∴PQ=MF.∵CD2+DE2=AB2+DE2=a,MF2+FN2=PQ2+FN2=c,又∵S1=AB2,S2=DE2,S3=PQ2,S4=FN2,∴S1+S2+S3+S4=AB2+DE2+PQ2+FN2=a+c.8.如图,所有的四边形都是正方形,其中最大的正方形的边长为15 cm,正方形A的边长为11 cm,B的边长为8 cm,C的边长为5 cm,则正方形D的边长为(C)A.14 cm B.4 cmC.15 cm D.3 c m【解】设正方形D的边长为x.据勾股定理,得S A+S B+S C+S D=S大正方形,∴112+82+52+x2=152,解得x=±15(负的舍去),∴正方形D的边长为15.(第8题)(第9题)9.用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案如图所示,已知大正方形的面积为49,小正方形的面积为9,若用x,y表示直角三角形的两直角边(x>y),请观察图案,指出以下关系式中不正确的是(D)A.x2+y2=49 B.x-y=3C.2xy+9=49 D.x+y=13【解】在Rt△ACB中,x2+y2=AB2=49.∵CD2=9,∴CD=3(-3舍去),∴x-y=3,∴(x-y)2=9,∴x2+y2-2xy=9,∴2xy+9=x2+y2=49,∴2xy=40,∴x2+y2+2xy=89,(x+y)2=89,∴x+y=89≠13,故选D.10.如图,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是(D)(第10题)A.①②③B.①②④C .②③④D .①③④【解】 ①中,作∠ABC 的平分线与AC 交于点D ,则△ABD 和△BCD 为等腰三角形; ②不能分成两个小的等腰三角形;③作∠BAC 的平分线AD ,则△ABD 和△ACD 为等腰三角形;④过点A 作∠BAD =36°交BC 于点D ,则△ABD 和△ACD 为等腰三角形. 二、填空题(每小题3分,共30分)11.在Rt △ABC 中,∠C =90°,∠A =37°,则∠B =__53°__.12. 已知直角三角形的斜边长是6,则以斜边的中点为圆心,斜边上的中线为半径的圆的面积是__9π__.13. 若直角三角形的两直角边长分别为a ,b ,且满足a 2-6a +9+|b -4|=0,则该直角三角形的斜边长为__5__.14.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条路,他们仅仅少走了__4__步路(假设2步为1 m),却踩伤了花草.(第14题) (第15题)15.如图,已知D 为等边三角形ABC 内的一点,DB =DA ,BF =AB ,∠1=∠2,则∠BFD =30°. 【解】 连结CD ,可证明△BCD ≌△BFD ≌△ACD ,故可得∠BFD =∠BCD =∠ACD =12×60°=30°.16. 命题“等腰三角形两腰上的高相等”的逆命题是如果一个三角形两边上的高相等,那么这个三角形是等腰三角形,这个逆命题是__真__命题.(第17题)17.如图,在△ABC 中,AB =6,AC =9,AD ⊥BC 于点D ,M 为AD 上任意一点,则MC 2-MB 2等于45.18.如图,在Rt △ABC 中,∠ACB =90°,∠BAC 的平分线AD 交BC 于点D ,DE ∥AC ,DE 交AB 于点E ,M 为BE 的中点,连结DM .在不添加任何辅助线和字母的情况下,图中的等腰三角形有△MBD ,△MDE ,△EAD .(第18题) (第19题)19.如图,在Rt △ABC 中,∠ACB =90°,AB =4,分别以AC ,BC 为直径作半圆,面积分别记为S 1,S 2,则S 1+S 2的值等于__2π__.【解】 S 1=12π·⎝⎛⎭⎫AC 22=π8AC 2,S 2=12π·⎝⎛⎭⎫BC 22=π8BC 2,∴S 1+S 2=π8(AC 2+BC 2)=π8AB 2=2π.(第20题)20.如图,已知等腰Rt △ABC 的直角边长为1,以Rt △ABC 的斜边AC 为直角边,画第二个等腰Rt △ACD ,再以Rt △ACD 的斜边AD 为直角边,画第三个等腰Rt △ADE ……依此类推,直到第五个等腰Rt △AFG ,则由这五个等腰直角三角形所构成的图形的面积为__15.5__. 【解】 ∵AB =BC =1,∠ABC =90°, ∴CA =12+12=2=DC .同理,DA =(2)2+(2)2=2=DE ,EA =22+22=2 2=EF ,F A =(2 2)2+(2 2)2=4=FG .∴S △ABC =12AB ·BC =12×1×1=12,S △ACD =12AC ·CD =12×2×2=1,S △ADE =12AD ·DE =12×2×2=2,S △AEF =12AE ·EF =12×2 2×2 2=4,S △AFG =12AF ·FG =12×4×4=8.∴S △A BC +S △ACD +S △ADE +S △AEF +S △AFG =12+1+2+4+8=1512.三、解答题(共40分)(第21题)21.(6分)在一块平地上,张大爷家房屋前9 m 远处有一棵大树.在一次强风中,这棵大树从离地面6 m 处折断倒下,量得倒下部分的长是10 m .大树倒下时会砸到张大爷的房子吗?请你通过计算,分析后给出正确的回答. 【解】 不会.理由如下: 如解图,在(第21题解)Rt △ABC 中,∠C =90°,AB =10 m ,AC =6 m .由勾股定理,得BC =AB 2-AC 2=100-36=8(m). ∵8<9,∴大树不会砸到张大爷的房子.(第22题)22.(6分)如图,在△ABC 中,AB =AC ,D 为BC 边上一点,∠B =30°,∠DAB =45°. (1)求∠DAC 的度数; (2)求证:DC =AB . 【解】 (1)∵AB =AC , ∴∠C =∠B =30°.∵∠C+∠BAC+∠B=180°,∴∠BAC=180°-30°-30°=120°.∵∠DAB=45°,∴∠DAC=∠BAC-∠DAB=120°-45°=75°.(2)∵∠DAB=45°,∠B=30°,∴∠ADC=∠B+∠DAB=75°.∵∠DAC=75°,∴∠DAC=∠ADC,∴DC=AC.∵AB=AC,∴DC=AB.23.(8分)在△ABC中,AB边上的中线CD=3,AB=6,AC+BC=8.求△ABC的面积.(第23题解)【解】如解图,在△ABC中,CD是AB边上的中线.∵CD=3,AB=6,∴AD=DB=3,∴CD=AD=DB,∴∠1=∠2,∠3=∠4.∵∠1+∠2+∠3+∠4=180°,∴∠1+∠3=90°,∴△ABC是直角三角形,∴AC2+BC2=AB2=36.又∵AC+BC=8,∴AC2+2AC·BC+BC2=64,∴2AC·BC=64-(AC2+BC2)=64-36=28.又∵S△ABC=12AC·BC,∴S△ABC =12×282=7.(第24题)24.(8分)一牧童在A处牧马,牧童的家在B处,A,B处距河岸的距离分别是AC=500 m,BD=700 m,且C,D两地间的距离也为500 m,天黑前牧童从点A将马牵到河边去饮水,再赶回家,为了使所走的路程最短.(1)牧童应将马赶到河边的什么地点?请你在图中画出来;(2)问:他至少要走多少路?【解】(1)如解图①,作点A关于河岸的对称点A′,连结BA′交河岸于点P,则PB+P A=PB+P A′=BA′最短,故牧童应将马赶到河边的点P处.(第24题解)(2)如解图②,过点A′作A′B⊥BD交BD的延长线于点B′.易知A′C∥B′D,A′B′∥CD,∴四边形A′B′DC是平行四边形,∴B′A′=CD=500 m,B′D=A′C=AC=500 m.在Rt△BB′A′中,BB′=BD+DB′=1200 m,A′B′=500 m,∴BA′=12002+5002=1300(m).答:他至少要走1300 m路.25.(12分)某数学兴趣小组开展了一次活动,过程记录如下:设∠BAC=θ(0°<θ<90°).现把不同长度的小棒依次摆放在两射线AB,AC之间,并使小棒两端分别落在两射线上.活动一:如图①,从点A1开始,依次向右摆放小棒,使小棒与小棒在两端点处互相垂直,A1A2为第1根小棒.(第25题①)数学思考:(1)小棒能无限摆下去吗?答:__能__(填“能”或“不能”);(2)设AA1=A1A2=A2A3=1.①θ=__22.5__度;②若记小棒A2n-1A2n的长度为a n(n为正整数,如A1A2=a1,A3A4=a2),求此时a2,a3的值,并直接写出a n的值(用含n的式子表示);活动二:如图②,从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第1根小棒,且A1A2=AA1.(第25题②)数学思考:(3)若已经向右摆放了3根小棒,则θ1=__2θ__,θ2=__3θ___,θ3=__4θ___(用含θ的式子表示); (4)若只能摆放4根小棒,求θ的范围.【解】 (2)②∵AA 1=A 1A 2=A 2A 3=1, A 1A 2⊥A 2A 3, ∴A 1A 3=2,AA 3=1+ 2. 又∵A 2A 3⊥A 3A 4,∴A 1A 2∥A 3A 4. 同理,A 3A 4∥A 5A 6,∴∠A =∠AA 2A 1=∠AA 4A 3=∠AA 6A 5, ∴AA 3=A 3A 4,AA 5=A 5A 6, ∴a 2=A 3A 4=AA 3=1+2, a 3=AA 3+A 3A 5=a 2+A 3A 5. ∵A 3A 5=2a 2,∴a 3=A 5A 6=AA 5=a 2+2a 2=(2+1)2. 同理,a n =(2+1)n -1.(4)由题意,得⎩⎪⎨⎪⎧4θ<90°,5θ≥90°,∴18°≤θ<22.5°.。
浙教版八年级数学上第2章单元检测题有答案
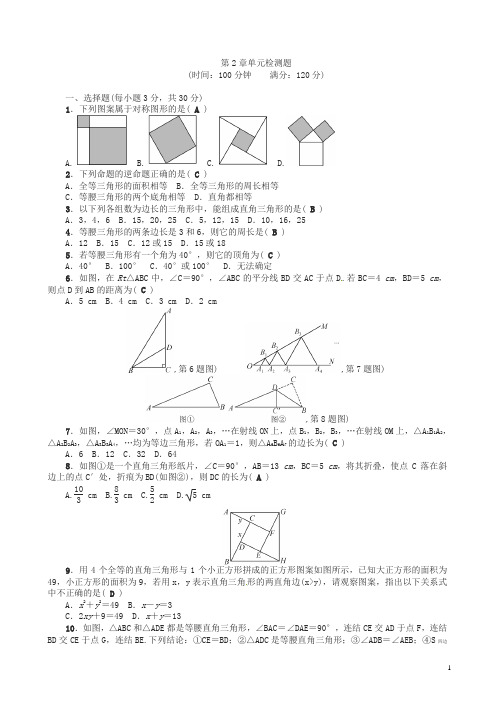
第2章单元检测题(时间:100分钟满分:120分)一、选择题(每小题3分,共30分)1.下列图案属于对称图形的是( A )A. B. C. D.2.下列命题的逆命题正确的是( C )A.全等三角形的面积相等 B.全等三角形的周长相等C.等腰三角形的两个底角相等 D.直角都相等3.以下列各组数为边长的三角形中,能组成直角三角形的是( B )A.3,4,6 B.15,20,25 C.5,12,15 D.10,16,254.等腰三角形的两条边长是3和6,则它的周长是( B )A.12 B.15 C.12或15 D.15或185.若等腰三角形有一个角为40°,则它的顶角为( C )A.40° B.100° C.40°或100° D.无法确定6.如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若BC=4 cm,BD=5 cm,则点D到AB的距离为( C )A.5 cm B.4 cm C.3 cm D.2 cm,第6题图) ,第7题图),第8题图)7.如图,∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=1,则△A6B6A7的边长为( C )A.6 B.12 C.32 D.648.如图①是一个直角三角形纸片,∠C=90°,AB=13 cm,BC=5 cm,将其折叠,使点C落在斜边上的点C′处,折痕为BD(如图②),则DC的长为( A )A.103cm B.83cm C.52cm D. 5 cm9.用4个全等的直角三角形与1个小正方形拼成的正方形图案如图所示,已知大正方形的面积为49,小正方形的面积为9,若用x,y表示直角三角形的两直角边(x>y),请观察图案,指出以下关系式中不正确的是( D )A.x2+y2=49 B.x-y=3C.2xy+9=49 D.x+y=1310.如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,连结CE交AD于点F,连结BD交CE于点G,连结BE.下列结论:①CE=BD;②△ADC是等腰直角三角形;③∠ADB=∠AEB;④S四边形BCDE=12BD·CE;⑤BC 2+DE 2=BE 2+CD 2.其中正确的结论有( C ) A .1个 B .2个 C .3个 D .4个,第10题图) ,第14题图) ,第15题图),第16题图)二、填空题(每小题4分,共24分)11.命题“等腰三角形两腰上的高相等”的逆命题是__两边上的高相等的三角形是等腰三角形__,这个逆命题是__真__命题.12.在△ABC 中,AB =AC ,AD 是中线,若∠B=60°,则∠BAD=.13.在Rt △ABC 中,AB =5,BC =3,则斜边上的中线长为__2.5或2. 14.如图,在△ABC 中,CD ⊥AB 于点D ,E 是AC 的中点.若AD =6,DE =5,则CD 的长等于__8__. 15.如图,BD ,CE 分别是△ABC 两个外角的角平分线,DE 过点A 且DE∥BC.若DE =14,BC =7,则△ABC 的周长为__21__.16.如图,已知D 为等边三角形ABC 内的一点,DB =DA ,BF =AB ,∠1=∠2,则∠BFD=__30°__. 点拨:证△BCD ≌△ACD 得∠BCD =30°,再证△BFD≌△BCD 得∠BFD =∠BCD =30° 三、解答题(共66分)17.(7分)如图,在Rt △ABC 中,∠B =90°,分别以点A ,C 为圆心,大于12AC 为半径画弧,两弧相交于点M ,N ,连结MN ,与AC ,BC 分别交于点D ,E ,连结AE.(1)求∠ADE 的度数;(直接写出结果)(2)当AB =3,AC =5时,求△ABE 的周长.解:(1)由题意可知MN 是线段AC 的垂直平分线,∴∠ADE =90°(2)由勾股定理可求BC =4,∵MN 是线段AC 的垂直平分线,∴AE =CE ,∴△ABE 的周长=AB +(AE +BE )=AB +BC =718.(8分)如图,AD =BC ,AC =BD.求证:△EAB 是等腰三角形.证明:易证△ABD≌△BAC (SSS ),∴∠ABD =∠BAC ,∴AE =BE ,即△EAB 是等腰三角形19.(8分)在等腰三角形ABC 中,AB =AC ,∠C =30°,AB ⊥AD ,AD =2,求BC 的长.解:BC =620.(8分)如图,在△ABC 中,点D 是BC 边上一点,且BA =BD ,∠DAC =12∠B,∠C =50°,求∠BAC的度数.解:设∠DAC =x °,则∠B =2x °,∠BDA =∠C +∠DAC =50°+x °.∵BD =BA ,∴∠BAD =∠BDA =50°+x °.∵∠B +∠BAD +∠BDA =180°,∴2x +50+x +50+x =180,解得x =20,∴∠BAD =∠BDA =70°,∠BAC =∠BAD +∠DAC =90°21.(8分)如图,AD ⊥BC 于点D ,∠B =∠DAC,点E 在BC 上,△EAC 是以EC 为底的等腰三角形,AB =4,AE =3.(1)判断△ABC 的形状,并说明理由; (2)求△ABC 的面积.解:(1)△ABC 是直角三角形.理由:∵AD⊥BC ,∴∠DAC +∠C =90°,∵∠B =∠DAC ,∴∠B +∠C =90°,∴△ABC 是直角三角形 (2)S △ABC =622.(8分)一牧童在A 处牧马,牧童的家在B 处,A ,B 处距河岸的距离分别是AC =500 m ,BD =700 m ,且C ,D 两地间的距离也为500 m ,天黑前牧童从点A 将马牵到河边去饮水,再赶回家,为了使所走的路程最短.(1)牧童应将马赶到河边的什么地点?请你在图中画出来; (2)问:他至少要走多少路?解:(1)如图①,作点A关于河岸的对称点A′,连结BA′交河岸于点P,则PB+PA=PB+PA′=BA′最短,故牧童应将马赶到河边的点P处(2)如图②,过点A′作A′B′⊥BD交BD的延长线于点B′,∴B′A′=CD=500 m,B′D=A′C =AC=500 m.在Rt△BB′A′中,BB′=BD+DB′=1200 m,A′B′=500 m,∴BA′=12002+5002=1300(m),即他至少要走1300 m路23.(9分)如图,△ABC和△CDE均为等边三角形,且点B,C,D在同一直线上,连结AD,BE,分别交CE和AC于点G,H,连结GH.(1)请说出AD=BE的理由;(2)试说出△BCH≌△ACG的理由;(3)试猜想△CGH是什么特殊的三角形,并加以证明.解:(1)∵△ABC和△CDE均为等边三角形,∴AC=BC,EC=DC,∠ACB=∠ECD=60°,∴∠AC D=∠BCE,∴△ACD≌△BCE(SAS),∴AD=BE(2)∵△ACD≌△BCE,∴∠CBH=∠CAG.∵∠ACB=∠ECD=60°,点B,C,D在同一条直线上,∴∠ACB=∠ECD=∠ACG=60°.又∵AC=BC,∴△BCH≌△ACG(ASA) (3)△CGH是等边三角形,理由:∵△ACG≌△BCH,∴CG=CH,又∵∠ACG=60°,∴△CGH是等边三角形24.(10分)(1)如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高线AG与正方形的边长相等,求∠EAF的度数;(2)如图②,在Rt△BAD中,∠BAD=90°,AB=AD,点M,N是BD边上的任意两点,且∠MAN=45°.将△AB M绕点A逆时针旋转90°至△ADH位置,连结NH,试判断MN,ND,DH之间的数量关系,并说明理由.解:(1)易证Rt△ABE≌Rt△AGE(HL),Rt△AGF≌Rt△ADF(HL),∴∠BAE=∠GAE,∠DAF=∠GAF,∵∠BAD=90°,∠EAF=12∠BAD=45°(2)MN2=ND2+DH2.理由:可证△AMN≌△AHN(SAS),∴MN=HN.∵∠BAD=90°,AB=AD,∴∠AB D=∠ADB=45°,∴∠HDN=∠HDA+∠ADB=∠ABD+∠A DB=90°,∴HN2=ND2+DH2.∴MN2=ND2+DH2。
浙教版八年级上册数学第2章 特殊三角形 含答案
浙教版八年级上册数学第2章特殊三角形含答案一、单选题(共15题,共计45分)1、在中,斜边AB=2,则的值是()A.6B.8C.10D.122、若等腰三角形有两条边的长度为2和5,则此等腰三角形的周长为()A.9B.12C.9或12D.103、下面有4个汽车标志图案,其中是轴对称图形的是 ( )①②③④A.②③④B.①②③C.①②④D.①③④4、在下列条件中,不能判定两直角三角形全等的是()A.斜边和一锐角对应相等B.斜边上的中线和一直角边对应相等C.两边分别相等D.直角的平分线和一直角边对应相等5、等腰三角形的一腰长为3a,底角为15°,则另一腰上的高为()A.aB. aC.2aD.3a6、等腰三角形的一个外角是130°,则它的底角等于()A.50°B.65°C.100°D.50°或65°7、如图,△ABC内接于☉O,D为线段AB的中点,延长OD交☉O于点E,连接AE,BE,在以下判断中,不正确的是( )A.AB⊥DEB.AE=BEC.OD=DED. =8、下列定理中逆定理不存在的是()A.全等三角形的对应角相等B.如果在一个三角形中,两边相等,那么它们所对的角也相等C.同位角相等,两直线平行D.角平分线上的点到这个角的两边的距离相等9、在平面直角坐标系中,点A(,),B(3,3),动点C在x轴上,若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数为()A.2B.3C.4D.510、如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,延长AM交BC于点N,连结DM 、 MC 下列结论:①DF=DN;②△ABM≌△BNM;③△CMN是等腰三角形;④AE=CN;其中正确的结论个数是()A.1个B.2个C.3个D.4个11、下列图形中,既是轴对称图形又是中心对称图形的是()A. B. C. D.12、如图,将△ABC放在正方形网格图中(图中每个小正方形的边长均为1),点A,B,C恰好在网格图中的格点上,那么△ABC中BC的高是()A. B. C. D.13、如图,在矩形纸片ABCD中,已知AD=8,折叠纸片,使AB边与对角线AC 重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为()A.3B.4C.5D.614、如图,某建筑物在一个坡度为的山坡上,建筑物底部点到山脚点的距离米,在距山脚点右侧水平距离为60米的点处测得建筑物顶部点的仰角是24°,建筑物和山坡的剖面的同一平面内,则建筑物的高度约为()(参考数据:,,)A.32.4米B.20.4米C.16.4米D.15.4米15、如图,在矩形ABCD中,AB=5,BC=5 ,点P在线段BC上运动(含B、C两点),连接AP,以点A为中心,将线段AP逆时针旋转60°到AQ,连接DQ,则线段DQ的最小值为()A. B. C. D.3二、填空题(共10题,共计30分)16、如图,在边长为4的正方形ABCD中,对角线AC,BD相交于点O,点E是AD边上一点,连接CE,把△CDE沿CE翻折,得到△CPE,EP交AC于点F,CP 交BD于点G,连接PO,若PO∥BC,则四边形OFPG的面积是________.17、在Rt△ABC中,∠B=90°,∠C=30°,AB=2,则BC的长为________.18、如图,已知点,直线与两坐标轴分别交于A,B两点,D,E分别是AB,OB上的动点,则周长的最小值是________.19、在中,边上的高为4,,,则的周长等于________.20、如图,点E在正方形ABCD内,满足∠AEB=90°,AE=3,BE=4,则阴影部分的面积是________.21、如图,在中,为BC上一点,过点D作,垂足为E,连接AD,若,则AB的长为________22、在平面直角坐标系中,A(4,0),直线l:y=6与y轴交于点B,点P是直线l上点B右侧的动点,以AP为边在AP右侧作等腰Rt△APQ,∠APQ=90°,当点P的横坐标满足0≤x≤8,则点Q的运动路径长为________.23、在△ABC中,∠A=40°,∠C=70°,则△ABC是________三角形.24、已知,点在的内部,与关于对称,与关于对称,________ .25、如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移2个单位后,得到△A’B’C’,连接A’C,则△A’B’C的周长为________.三、解答题(共5题,共计25分)26、如图,在中,,点在边上,且,连接,若,求的度数.27、如图△ABC为等边三角形,直线a∥AB,D为直线BC上任一动点,将一60°角的顶点置于点D处,它的一边始终经过点A,另一边与直线a交于点E.(1)若D恰好在BC的中点上(如图1)求证:△ADE是等边三角形;(2)若D为直线BC上任一点(如图2),其他条件不变,上述(1)的结论是否成立?若成立,请给予证明;若不成立,请说明理由.28、如图所示,AB⊥BC,DC⊥AC,垂足分别为B,C,过D点作BC的垂线交BC 于F,交AC于E,AB=EC,试判断AC和ED的长度有什么关系并说明理由.29、如图,在四边形ABCD中,对角线AC=BD,E,F为AB、CD的中点,连接EF交BD、AC于P、Q,取BC中点G,连EG、FG,求证:OP=OQ.30、已知△ABC中,AC=BC,∠C=100°,AD平分∠BAC交BC于D,点E 为AB上一点,且∠EDB=∠B.求证:AB=AD+CD.参考答案一、单选题(共15题,共计45分)1、B2、B3、B4、C5、B6、D7、C9、B10、C11、D12、A13、D14、C15、A二、填空题(共10题,共计30分)16、17、18、19、20、21、22、24、25、三、解答题(共5题,共计25分)26、29、。
浙教版八年级上册数学第2章 特殊三角形含答案(全国通用)
浙教版八年级上册数学第2章特殊三角形含答案一、单选题(共15题,共计45分)1、下列能断定△ABC为等腰三角形的是()A.∠A=30°,∠B=60°B.AB=AC=2,BC=4C.∠A=50°,∠B=80° D.AB=3、BC=7,周长为132、如图,以为直径分别向外作半圆,若,则( )A.2B.6C.D.3、⊿ABC中,AB=AC,D是BC中点,下列结论中不一定正确的是( )A.∠B=∠CB.AD⊥BCC.AD平分∠BACD.AB=2BD4、下列各组数据中,能构成直角三角形三边长的是()A. ,2,B.1,,C.6,7,8D.2,3,45、如图,AC,BD是菱形ABCD的对角线,BH垂直AD于点H,若AC=4,BD=3,则BH的长为()A.2.4B.2.5C.4.8D.56、如图,以O为圆心的两个同心圆中,大圆的弦AB切小圆于点C,若∠AOB=120°,则大圆半径R与小圆半径r之间的关系满足( )A.R=2rB.R=3rC.R= rD.R= r7、如图,正方形ABCD的边长为4,点E在对角线BD上,且,EF⊥AB,垂足为F,则EF的长为()A.1B.C.D.8、如图,AB为⊙O的直径,C为⊙O上一点,其中AB=4,∠AOC=120°,P为⊙O上的动点,连AP,取AP中点Q,连CQ,则线段CQ的最大值为( )A.3B.1+C.1+3D.1+9、如图,AB,BC是⊙O的弦,∠B=60°,点O在∠B内,点D为上的动点,点M,N,P分别是AD,DC,CB的中点.若⊙O的半径为2,则PN+MN的长度的最大值是()A. B. C. D.10、如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线交AB于点D,交AC于点E,连接BE,则∠CBE的度数为()A.80°B.70°C.40°D.30°11、如图,△ABC中,以B为圆心,BC长为半径画弧,分别交AC,AB于D,E两点,并连接BD,DE.若∠A=30°,AB=AC,则∠BDE的度数为何()A.45B.52.5C.67.5D.7512、如果一直角三角形两边的长分别为6、8,则第三边长是()A.10B.4 或2C.10或2D.以上都不对13、如图,正三角形的内切圆半径为1,那么这个正三角形的边长为( )A.2B.3C.D.14、下列各组数是三角形的三边,能组成直角三角形的一组数是()A.2,3,4B.3,4,5C.6,8,12D.15、在△ABC中,∠C=90°,∠B=60°,下列说法中,不一定正确的是()A.BC 2+AC 2=AB 2B.2BC=ABC.若△DEF的边长分别为1,2,,则△DEF和△ABC全等 D.若AB中点为M,连接CM,则△BCM为等边三角形二、填空题(共10题,共计30分)16、已知△ABC中,AC=BC,∠A=80°,则∠B=________°.17、如图,在△ABC中,AB=AC=5,BC=6,点M是BC上一点,且BM=4,点P是边AB上一动点,连接PM,将△BPM沿PM翻折得到△DPM,点D与点B对应,连接AD,则AD的最小值为________.18、在一棵树的10米高的B处有两只猴子为抢吃池塘边水果,一只猴子爬下树跑到A处(离树20米)的池塘边.另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高________米.19、如图,等腰△ABC中,AB=AC,∠BAC=50°,AB的垂直平分线MN交AC于点D,则∠DBC的度数是________.20、如图P是正方形内的一点,将绕点C逆时针方向旋转后与重合,若,则=________.21、如图,Rt△ABC中,∠C=90°,点P为AC边上的一点,延长BP至点D,使得AD=AP,当AD⊥AB时,过D作DE⊥AC于E,AB-BC=4,AC=8,则△ABP面积为________.22、如图,已知∠AOB=60°,点P是OA边上,OP=8cm,点M、N在边OB上,PM=PN,若MN=2cm,则ON=________cm.23、如图,在△ABC中,AC=BC=2,∠C=900, AD是△ABC的角平分线,DE⊥AB,垂足为E,AD的垂直平分线交AB于点F,则DF的长为 ________24、如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为________.25、如图,在△ABC中,∠ACB=90°,CD是AB边上的中线,CE⊥AB于E,AC=8,BC=6,则DE=________.三、解答题(共5题,共计25分)26、如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′•OP=r2,则称点P′是点P关于⊙O的“反演点”.如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A′,B′分别是点A,B关于⊙O的反演点,求A′B′的长.27、已知如图,在四边形ABCD中,AD//BC,∠ABD=30°,AB=AD,DC⊥BC于点C,若BD=4,求CD的长.28、如图,⊙O的直径AB垂直于弦CD,垂足P是OB的中点,CD=6cm,求直径AB的长.29、在平面直角坐标系xOy中,直线为一、三象限角平分线.点P关于y轴的对称点称为P的一次反射点,记作;关于直线的对称点称为点P的二次反射点,记作.若点A在轴左侧,点,分别是点A的一次、二次反射点,△ 是等腰直角三角形,请直接写出点A在平面直角坐标系xOy中的位置.30、如图,点A′在Rt△ABC的边AB上,∠ABC=30°,AC=2,∠ACB=90°,△ACB绕顶点C按逆时针方向旋转与△A′CB′重合,A'B'与BC交于点D,连接BB′,求线段BB′的长度.参考答案一、单选题(共15题,共计45分)1、C2、A3、D5、A6、A7、C8、D9、D10、D11、C12、C13、D14、B15、C二、填空题(共10题,共计30分)16、17、18、19、20、21、22、24、25、三、解答题(共5题,共计25分)26、27、28、。
2017-2018学年浙教版八年级数学上第2章单元检测题有答案AKKHAl
第2章单元检测题(时间:100分钟 满分:120分)一、选择题(每小题3分,共30分) 1.下列图案属于对称图形的是( A )A. B. C. D. 2.下列命题的逆命题正确的是( C )A .全等三角形的面积相等B .全等三角形的周长相等C .等腰三角形的两个底角相等D .直角都相等3.以下列各组数为边长的三角形中,能组成直角三角形的是( B ) A .3,4,6 B .15,20,25 C .5,12,15 D .10,16,25 4.等腰三角形的两条边长是3和6,则它的周长是( B ) A .12 B .15 C .12或15 D .15或185.若等腰三角形有一个角为40°,则它的顶角为( C ) A .40° B .100° C .40°或100° D .无法确定6.如图,在Rt △ABC 中,∠C =90°,∠ABC 的平分线BD 交AC 于点D.若BC =4 cm ,BD =5 cm ,则点D 到AB 的距离为( C )A .5 cmB .4 cmC .3 cmD .2 cm,第6题图) ,第7题图),第8题图)7.如图,∠MON =30°,点A 1,A 2,A 3,…在射线ON 上,点B 1,B 2,B 3,…在射线OM 上,△A 1B 1A 2,△A 2B 2A 3,△A 3B 3A 4,…均为等边三角形,若OA 1=1,则△A 6B 6A 7的边长为( C )A .6B .12C .32D .648.如图①是一个直角三角形纸片,∠C =90°,AB =13 cm ,BC =5 cm ,将其折叠,使点C 落在斜边上的点C′处,折痕为BD(如图②),则DC 的长为( A )A.103 cmB.83 cmC.52cm D. 5 cm9.用4个全等的直角三角形与1个小正方形拼成的正方形图案如图所示,已知大正方形的面积为49,小正方形的面积为9,若用x ,y 表示直角三角形的两直角边(x>y),请观察图案,指出以下关系式中不正确的是( D )A .x 2+y 2=49B .x -y =3C .2xy +9=49D .x +y =1310.如图,△ABC 和△ADE 都是等腰直角三角形,∠BAC =∠DAE =90°,连结CE 交AD 于点F ,连结BD 交CE 于点G ,连结BE.下列结论:①CE =BD ;②△ADC 是等腰直角三角形;③∠ADB =∠AEB ;④S 四边形BCDE =12BD·CE ;⑤BC 2+DE 2=BE 2+CD 2.其中正确的结论有( C )A .1个B .2个C .3个D .4个,第10题图) ,第14题图) ,第15题图),第16题图)二、填空题(每小题4分,共24分)11.命题“等腰三角形两腰上的高相等”的逆命题是__两边上的高相等的三角形是等腰三角形__,这个逆命题是__真__命题.12.在△ABC 中,AB =AC ,AD 是中线,若∠B =60°,则∠BAD =__30°__. 13.在Rt △ABC 中,AB =5,BC =3,则斜边上的中线长为__2.5或2. 14.如图,在△ABC 中,CD ⊥AB 于点D ,E 是AC 的中点.若AD =6,DE =5,则CD 的长等于__8__. 15.如图,BD ,CE 分别是△ABC 两个外角的角平分线,DE 过点A 且DE ∥BC.若DE =14,BC =7,则△ABC 的周长为__21__.16.如图,已知D 为等边三角形ABC 内的一点,DB =DA ,BF =AB ,∠1=∠2,则∠BFD =__30°__.点拨:证△BCD ≌△ACD 得∠BCD =30°,再证△BFD ≌△BCD 得∠BFD =∠BCD =30° 三、解答题(共66分)17.(7分)如图,在Rt △ABC 中,∠B =90°,分别以点A ,C 为圆心,大于12AC 为半径画弧,两弧相交于点M ,N ,连结MN ,与AC ,BC 分别交于点D ,E ,连结AE.(1)求∠ADE 的度数;(直接写出结果)(2)当AB =3,AC =5时,求△ABE 的周长.解:(1)由题意可知MN 是线段AC 的垂直平分线,∴∠ADE =90°(2)由勾股定理可求BC =4,∵MN 是线段AC 的垂直平分线,∴AE =CE ,∴△ABE 的周长=AB +(AE +BE )=AB +BC =718.(8分)如图,AD =BC ,AC =BD.求证:△EAB 是等腰三角形.证明:易证△ABD ≌△BAC (SSS ),∴∠ABD =∠BAC ,∴AE =BE ,即△EAB 是等腰三角形19.(8分)在等腰三角形ABC 中,AB =AC ,∠C =30°,AB ⊥AD ,AD =2,求BC 的长.解:BC =620.(8分)如图,在△ABC 中,点D 是BC 边上一点,且BA =BD ,∠DAC =12∠B ,∠C =50°,求∠BAC的度数.解:设∠DAC =x °,则∠B =2x °,∠BDA =∠C +∠DAC =50°+x °.∵BD =BA ,∴∠BAD =∠BDA =50°+x °.∵∠B +∠BAD +∠BDA =180°,∴2x +50+x +50+x =180,解得x =20,∴∠BAD =∠BDA =70°,∠BAC =∠BAD +∠DAC =90°21.(8分)如图,AD ⊥BC 于点D ,∠B =∠DAC ,点E 在BC 上,△EAC 是以EC 为底的等腰三角形,AB =4,AE =3.(1)判断△ABC 的形状,并说明理由; (2)求△ABC 的面积.解:(1)△ABC 是直角三角形.理由:∵AD ⊥BC ,∴∠DAC +∠C =90°,∵∠B =∠DAC ,∴∠B +∠C =90°,∴△ABC 是直角三角形 (2)S △ABC =622.(8分)一牧童在A 处牧马,牧童的家在B 处,A ,B 处距河岸的距离分别是AC =500 m ,BD =700 m ,且C ,D 两地间的距离也为500 m ,天黑前牧童从点A 将马牵到河边去饮水,再赶回家,为了使所走的路程最短.(1)牧童应将马赶到河边的什么地点?请你在图中画出来; (2)问:他至少要走多少路?解:(1)如图①,作点A 关于河岸的对称点A′,连结BA′交河岸于点P ,则PB +PA =PB +PA ′=BA′最短,故牧童应将马赶到河边的点P 处(2)如图②,过点A′作A′B′⊥BD 交BD 的延长线于点B′,∴B ′A ′=CD =500 m ,B ′D =A′C =AC =500 m .在Rt △BB ′A ′中,BB ′=BD +DB′=1200 m ,A ′B ′=500 m ,∴BA ′=12002+5002=1300(m ),即他至少要走1300 m 路23.(9分)如图,△ABC 和△CDE 均为等边三角形,且点B ,C ,D 在同一直线上,连结AD ,BE ,分别交CE 和AC 于点G ,H ,连结GH.(1)请说出AD =BE 的理由;(2)试说出△BCH ≌△ACG 的理由;(3)试猜想△CGH 是什么特殊的三角形,并加以证明.解:(1)∵△ABC 和△CDE 均为等边三角形,∴AC =BC ,EC =DC ,∠ACB =∠ECD =60°,∴∠AC D =∠BCE ,∴△ACD ≌△BCE (SAS ),∴AD =BE(2)∵△ACD ≌△BCE ,∴∠CBH =∠CAG .∵∠ACB =∠ECD =60°,点B ,C ,D 在同一条直线上,∴∠ACB =∠ECD =∠ACG =60°.又∵AC =BC ,∴△BCH ≌△ACG (ASA ) (3)△CGH 是等边三角形,理由:∵△ACG ≌△BCH ,∴CG =CH ,又∵∠ACG =60°,∴△CGH 是等边三角形24.(10分)(1)如图①,在正方形ABCD 中,△AEF 的顶点E ,F 分别在BC ,CD 边上,高线AG 与正方形的边长相等,求∠EAF 的度数;(2)如图②,在Rt △BAD 中,∠BAD =90°,AB =AD ,点M ,N 是BD 边上的任意两点,且∠MAN =45°.将△AB M 绕点A 逆时针旋转90°至△ADH 位置,连结NH ,试判断MN ,ND ,DH 之间的数量关系,并说明理由.解:(1)易证Rt △ABE ≌Rt △AGE (HL ),Rt △AGF ≌Rt △ADF (HL ),∴∠BAE =∠GAE ,∠DAF =∠GAF ,∵∠BAD =90°,∠EAF =12∠BAD =45° (2)MN 2=ND 2+DH 2.理由:可证△AMN ≌△AHN (SAS ),∴MN=HN.∵∠BAD =90°,AB =AD ,∴∠AB D =∠ADB =45°,∴∠HDN =∠HDA +∠ADB =∠ABD +∠ADB =90°,∴HN 2=ND 2+DH 2.∴MN 2=ND 2+DH 2。
浙教版八年级上册数学第2章 特殊三角形含答案
浙教版八年级上册数学第2章特殊三角形含答案一、单选题(共15题,共计45分)1、下列说法:①有理数和数轴上的点一一对应;②成轴对称的两个图形是全等图形;③- 是17的平方根;④等腰三角形的高线、中线及角平分线重合.其中正确的有()A.0个B.1C.2个D.3个2、如图,中,于点,点为的中点,连接,则的周长是()A.4+2B.7+C.12D.103、正方形ABCD、正方形BEFG,点A,B,E在半圆O的直径上,点D,C,F在半圆O上,若EF=4,则该半圆的半径为()A. B.8 C. D.4、将△ABC的三个顶点的横坐标乘以-1,纵坐标不变,则所得图形()A.与原图形关于y轴对称B.与原图形关于x轴对称C.与原图形关于原点对称D.向x轴的负方向平移了一个单位5、下列图形中是中心对称图形,而不是轴对称图形的是()A.等边三角形B.平行四边形C.矩形D.菱形6、如图,在等边△ABC中,BD=CE,将线段AE沿AC翻折,得到线段AM,连结EM交AC于点N,连结DM、CM.以下说法:①AD=AM ②∠MCA=60°③CM=2CN,④MA=DM其中正确的有()A.1个B.2个C.3个D.4个7、观察下列图形,是轴对称图形的是()A. B. C. D.8、下列设计的图案中,是中心对称图形但不是轴对称图形的是()A. B. C. D.9、如图,在ΔABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N,则MN的长为()A. B. C. D.10、如图,矩形ABCD的边AD长为2,AB长为1,点A在数轴上对应的数是-1,以A点为圆心,对角线AC长为半径画弧,交数轴于点E,则点E表示的实数是()A. +1B. -1C.D.1-11、如图,在△ABC中,∠C=90°,DE⊥AB于D,BC=BD,如果AC=3m,那么AE+DE等于()A.2.5mB.3mC.3.5mD.4m12、如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是()A. 米2B. 米2C. 米2 D. 米213、已知等腰三角形两边长是8cm和4cm,那么它的周长是()A.12cmB.16cmC.16cm或20cmD.20cm14、已知等腰三角形的一边长为8,另一边长为方程x2﹣6x+9=0的根,则该等腰三角形的周长为()A.14B.19C.14或19D.不能确定15、某市在旧城改造中,计划在市内一块如图所示的三角形空地上种植草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要()A.450a元B.225a 元C.150a元D.300a元二、填空题(共10题,共计30分)16、如图,在直角中,,,,、分别为边、上的两个动点,若要使是等腰三角形且是直角三角形,则________.17、如图,AC⊥BC,AD⊥BD,垂足分别是C、D,若要用“HL”得到Rt△ABC≌Rt△BAD,则你添加的条件是________.(写一种即可)18、如图,在△ABC中,AB=AC=5,BC=6,E是BA延长线的一点,P是∠EAC的平分线上一个动点,当△APC是以AC为腰的等腰三角形时,△APC的面积为________.19、如图,AB为⊙O的直径,延长AB至点D,使BD=OB,DC切⊙O于点C,点B 是CF的中点,弦CF交AB于点E.若⊙O的半径为2,则CF=________20、如图,在一张长为7cm,宽为5cm的矩形纸片上,现要剪下一个腰长为4cm 的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为________.21、如图,∠C=∠D=90º,添加一个条件:________ (写出一个条件即可),可使 Rt△ABC 与Rt△ABD 全等.22、如图,在△ABC中,AD⊥BC于D点,BD=CD,若BC=6,AD=5,则图中阴影部分的面积为________.23、如图,在△ABC中,∠BAC=105°,将△ABC绕点A逆时针旋转得到△AB′C′.若点B'恰好落在BC边上,且AB′=CB′,则∠C′的度数为________°.24、如图,已知△ABC是等腰三角形,且AB=AC≠BC,在平面上确定点P,使△PAB、△PAC、△PBC都是等腰三角形,这样的点一共有________个.25、如图,在Rt△ABC中,∠C=30°,以直角顶点A为圆心,AB长为半径画弧交BC于点D,过D作DE⊥AC于点E.若DE=a,则△ABC的周长用含a的代数式表示为________ .三、解答题(共5题,共计25分)26、已知:如图,在△ABC中,AB=AC,点D,E在边BC上,且BD=CE.求证:AD=AE.27、如图,一块四边形草地ABCD,其中∠B=90°,AB=4m,BC=3m , AD=12m, CD =13cm,求这块草地的面积.28、等腰三角形的周长是12,一边长是3,求三边长.29、如图,写出△ABC的各顶点坐标,并画出△ABC关于y轴对称的△A1B1C1,画出△ABC关于x轴对称的△A2B2C2并写出△A2B2C2的顶点坐标.30、如图,在平行四边形ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.求证:四边形ABEF是菱形;参考答案一、单选题(共15题,共计45分)1、C2、D3、A4、A5、B6、D7、A8、9、C10、B11、B12、C13、D14、A15、C二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、28、29、。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2章自我评价一、选择题(每小题3分,共30分)1.在下列标志中,属于轴对称图形的是(B)2.下列四组线段能构成直角三角形的是(D)A.a=1,b=2,c=3 B.a=2,b=3,c=4C.a=2,b=4,c=5 D.a=3,b=4,c=53.有下列命题:①同位角相等,两直线平行;②全等三角形的周长相等;③直角都相等;④等边对等角.其中逆命题是真命题的有(B)A.1个B.2个C.3个D.4个4.如图,AB∥CD,AD=CD,∠1=70°,则∠2的度数是(C)A.20°B.35°C.40°D.70°(第4题)(第5题)5.如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果M是OP的中点,那么DM的长是(C)A.2B. 2C.3D.2 3(第6题)6.如图,在△ABC 中,∠C =90°,∠B =30°,以点A 为圆心,任意长为半径画弧,分别交AB ,AC 于点M 和N ,再分别以点M ,N 为圆心,大于12MN 长为半径画弧,两弧交于点P ,连结AP 并延长,交BC 于点D ,则下列说法中,正确的个数是(D ) ①AD 是∠BAC 的平分线;②∠ADC =60°;③点D 在AB 的中垂线上;④S △DAC ∶S △ABC =1∶3.A . 1B . 2C . 3D . 47.如图,将一把含45°角的三角尺的直角顶点放在一张宽为3 cm 的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角尺的一边与纸带的一边所在的直线成30°角,则三角尺的最大边长为(D )A . 3 cmB . 6 cmC . 18 cmD . 72 cm(第7题)(第7题解)【解】 如解图,过点C 作CD ⊥AD 于点D , 则CD =3 cm . 在Rt △ADC 中,∵∠CAD =30°,∴AC =2CD =2×3=6(cm). ∵该三角尺是含45°角的三角尺, ∴∠BAC =90°,AB =AC =6 cm , ∴BC =AB 2+AC 2=62+62=72(cm).(第8题)8.如图,在△ABC中,AB=AC=BD,DA=DC,则∠B的度数为(C)A.22.5°B.30°C.36°D.45°【解】设∠B=x.∵AB=AC,∴∠C=∠B=x.∵DA=DC,∴∠DAC=∠C=x.∴∠ADB=∠C+∠DAC=2x.∵AB=BD,∴∠BAD=∠ADB=2x.在△ABD中,∵∠B=x,∠ADB=∠BAD=2x,∴x+2x+2x=180°,解得x=36°,即∠B=36°.9.如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是线段AD上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为(C)A.20°B.25°C.30°D.45°(第9题)(第9题解)【解】如解图,过点E作EM∥BC,交AB于点M,则∠AME=∠B,∠AEM=∠ACB.∵△ABC是等边三角形,∴∠B=∠ACB=60°,AB=AC=BC=4.∴∠AME=∠AEM=60°.∴AM=AE=2.∴BM =AB -AM =2.∵AD 是BC 边上的中线,∴AD ⊥BC . ∵EM ∥BC ,∴AD ⊥EM . ∴点E 和点M 关于AD 对称. 连结CM 交AD 于点F ,连结EF , 则此时EF +CF 的值最小. ∵AC =BC ,AM =BM , ∴∠ECF =12∠ACB =30°.10.如图,在四边形ABCD 中,AC 平分∠BAD ,CE ⊥AB 于点E ,∠ADC +∠ABC =180°,有下列结论:①CD =CB ;②AD +AB =2AE ;③∠ACD =∠BCE ;④AB -AD =2BE .其中正确的是(C )A . ②B . ①②③C . ①②④D . ①②③④ 导学号:91354016(第10题)(第10题解)【解】 如解图,在EA 上取点F ,使EF =BE ,连结CF . ∵CE ⊥AB ,EF =BE , ∴CF =CB ,∴∠CFB =∠B .∵∠AFC +∠CFB =180°,∠ADC +∠ABC =180°,∴∠D =∠AFC . ∵AC 平分∠BAD ,∴∠DAC =∠FAC .在△ACD 和△ACF 中,∵⎩⎨⎧∠D =∠AFC ,∠DAC =∠FAC ,AC =AC ,∴△ACD ≌△ACF(AAS).∴AD =AF ,CD =CF .∴CD =CB ,故①正确.AD +AB =AF +(BE +AE)=AF +EF +AE =AE +AE =2AE ,故②正确. 根据已知条件无法证明∠ACD =∠BCE , 故③错误.AB -AD =AB -AF =BF =2BE ,故④正确. 综上所述,正确的是①②④. 二、填空题(每小题3分,共30分)11.如图,在△ABC 中,AB =AC ,AD 是中线.若∠B =60°,则∠BAD =__30°__.,(第11题)) ,(第12题))12.如图,在等腰△ABC 中,AB =AC =10 cm ,BC =12 cm ,则BC 边上的高AD 的长是__8__ cm .13.如图,AB ∥CD ,FE ⊥DB ,垂足为E .若∠1=50°,则∠2的度数为__40°__.,(第13题)) ,(第14题))14.如图,在△ABC 中,BO ,CO 分别是∠ABC ,∠ACB 的平分线,且它们相交于点O ,OE ∥AB ,OF ∥AC ,BC =10,则△OEF 的周长为__10__.【解】 ∵OB ,OC 分别是∠ABC ,∠ACB 的平分线, ∴∠ABO =∠CBO ,∠ACO =∠BCO . ∵OE ∥AB ,OF ∥AC ,∴∠ABO =∠BOE ,∠ACO =∠COF , ∴∠CBO =∠BOE ,∠BCO =∠COF ,∴BE =OE ,OF =FC ,∴△OEF 的周长=OE +EF +OF =BE +EF +FC =BC =10.(第15题)15.如图,在△ABC 中,D 是BC 上一点,AC =AD =DB ,∠BAC =102°,则∠ADC =__52°__.【解】 ∵AC =AD =DB , ∴∠B =∠BAD ,∠ADC =∠C . 设∠ADC =α,则∠B =∠BAD =α2. ∵∠BAC =102°,∴∠DAC =102°-α2. ∵∠ADC +∠C +∠DAC =180°, ∴2α+102°-α2=180°, 解得α=52°,即∠ADC =52°.16.如图,已知△ABC 的周长是21,BO ,CO 分别平分∠ABC 和∠ACB ,OD ⊥BC ,垂足为D ,且OD =3,则△ABC 的面积是__632__., (第16题)) , (第16题解))【解】 如解图,过点O 作OE ⊥AB ,OF ⊥AC ,垂足分别为E ,F ,连结OA . 由角平分线的性质知OD =OE =OF ,∴S △ABC =S △AOB +S △BOC +S △AOC =12AB·OE +12BC·OD +12AC·OF =12(AB +BC +AC)·OD =12×21×3=632.17.如图,在△ABC 中,AB =AC =5,BC =6.若点P 在边AC 上移动,则BP 的最小值是__245__.,(第17题)),(第17题解))【解】 过点A 作AD ⊥BC 于点D ,如解图. ∵AB =AC =5,BC =6,∴BD =12BC =3,∴AD =AB 2-BD 2=4. 易得当BP ⊥AC 时,BP 有最小值. 此时12AD·BC =12BP·AC ,得4×6=5BP ,∴BP =245.18.如图是两把完全一样的含30°角的三角尺,分别记做△ABC 与△A′B′C′,现将两把三角尺重叠在一起,设较长直角边的中点为M ,绕中点M 转动上面的三角尺ABC ,使其直角顶点C 恰好落在三角尺A′B′C′的斜边A′B′上.当∠A =30°,AC =10时,两直角顶点C ,C ′间的距离是__5__.(第18题)(第18题解)【解】 如解图,连结C′C .∵M 是AC ,A ′C ′的中点,AC =A′C′=10, ∴CM =A′M =C′M =12AC =5,∴∠A ′CM =∠A′=30°,∴∠CMC ′=60°. ∴△MCC ′为等边三角形.∴C′C =CM =5.(第19题)19.按如图所示的方式作正方形和等腰直角三角形.若第一个正方形的边长AB =1,第一个正方形与第一个等腰直角三角形的面积和为S 1,第二个正方形与第二个等腰直角三角形的面积和为S 2……则第n 个正方形与第n 个等腰直角三角形的面积和S n =__52__.【解】 易得第一个正方形的面积为1, 第一个等腰直角三角形的面积为14,第二个正方形的面积为12,第二个等腰直角三角形的面积为12×14, ……∴第n 个正方形的面积为⎝⎛⎭⎫12n -1×1=12n -1,第n 个等腰直角三角形的面积为⎝⎛⎭⎫12n -1×14=12n +1,∴第n 个正方形与第n 个等腰直角三角形的面积和S n =⎝⎛⎭⎫12n -1+12n +1=52n +1.(第20题)20.如图,正方形ABDE ,正方形CDFI ,正方形EFGH 的面积分别为25,9,16,△AEH ,△BDC ,△GFI 的面积分别为S 1,S 2,S 3,则S 1+S 2+S 3=__18__.导学号:91354017【解】 过点A 作AK ⊥HE ,交HE 的延长线于点K . 易得DE 2=25,DE 2=9,EF 2=16, ∴DE 2=DF 2+EF 2,∴△DEF 是直角三角形,且∠DFE =90°. 易得∠AEK +∠DEK =∠DEK +∠DEF =90°, ∴∠AEK =∠DEF .又∵AE =DE ,∠K =∠DFE =90°, ∴△AEK ≌△DEF (AAS ), ∴AK =DF . 又∵EH =EF ,∴S △AHE =12EH ·AK =12EF ·DF =S △DEF .同理,S △BDC =S △GFI =S △DEF , ∴S 1+S 2+S 3=3S △DEF . 易得DF =3,EF =4, ∴S △DEF =12×3×4=6, ∴S 1+S 2+S 3=3×6=18. 三、解答题(共40分)21.(6分)如图,AD =BC ,AC =BD .求证:△EAB 是等腰三角形.(第21题)【解】 在△ADB 和△BCA 中,∵⎩⎨⎧AD =BC ,BD =AC ,AB =BA ,∴△ADB ≌△BCA(SSS), ∴∠DBA =∠CAB , ∴△EAB 是等腰三角形.(第22题)22.(6分)如图,△ABC为等边三角形,DE⊥BC,EF⊥AC,FD⊥AB,垂足分别为E,F,D,则△DEF是等边三角形吗?请说明理由.【解】△DEF是等边三角形.理由如下:∵DE⊥BC,EF⊥AC,FD⊥AB,△ABC为等边三角形,∴∠A=60°,∠ADF=∠CFE=90°,∴∠AFD=30°,∴∠DFE=180°-30°-90°=60°.同理,∠FDE=∠DEF=60°.∴△DEF是等边三角形.(第23题)23.(8分)如图,在△ABC中,AB=AC,点E在CA的延长线上,∠E=∠AFE,请判断EF与BC的位置关系,并说明理由.【解】EF⊥BC.理由如下:过点A作AD⊥BC于点D,延长EF交BC于点G.∵AB=AC,AD⊥BC,∴∠BAC=2∠CAD.又∵∠BAC=∠E+∠AFE,∠E=∠AFE,∴∠BAC=2∠E,∴∠CAD=∠E,∴AD∥EF.又∵∠ADC=90°,∴∠EGC=90°,即EF⊥BC.24.(10分)已知△ABC 和△ADE 是等腰直角三角形,∠ACB =∠ADE =90°,F 为BE 的中点,连结DF ,CF .(1)如图①,当点D 在AB 上,点E 在AC 上,请直接写出此时线段DF ,CF 的数量关系和位置关系.(2)如图②,在(1)的条件下将△ADE 绕点A 顺时针旋转45°,请你判断此时(1)中的结论是否仍然成立,并证明你的判断.(3)如图③,在(1)的条件下将△ADE 绕点A 顺时针旋转90°,若AD =1,AC =8,求此时线段CF 的长(直接写出结果).(第24题)【解】 (1)∵∠ACB =∠ADE =90°,F 为BE 的中点,∴DF =BF =12BE ,CF =12BE ,∴DF =CF . ∵△ABC 是等腰直角三角形,∴∠ABC =45°.∵BF =DF ,∴∠DBF =∠BDF .∵∠DFE =∠DBF +∠BDF ,∴∠DFE =2∠DBF .同理,∠CFE =2∠CBF ,∴∠DFE +∠CFE =2∠DBF +2∠CBF =2∠ABC =90°,∴DF ⊥CF .(2)(1)中的结论仍然成立.证明如下:如解图①,延长DF 交BC 于点G .∵∠ADE =∠ACB =90°,∴DE ∥BC ,∴∠DEF =∠GBF ,∠EDF =∠BGF .∵F 为BE 的中点,∴EF =BF ,∴△DEF ≌△GBF(AAS),∴DE =GB ,DF =GF .∵AD=DE,∴AD=GB.∵AC=BC,∴AC-AD=BC-GB,即DC=GC.∵∠ACB=90°,∴△DCG是等腰直角三角形.∵DF=GF,∴DF=CF,DF⊥CF.(第24题解) (3)如解图②,延长DF交BA于点H.∵△ABC和△ADE是等腰直角三角形,∴AC=BC,AD=DE,∠AED=∠ABC=45°.由旋转可知∠CAE=∠BAD=∠ACB=90°,∴AE∥BC,∴∠AEB=∠CBE,∴∠DEF=∠HBF.∵F是BE的中点,∴EF=BF.又∵∠DFE=∠HFB,∴△DEF≌△HBF(ASA),∴ED=BH.∵BC=AC=8,∠ACB=90°,∴AB=4.∵BH=ED=AD=1,∴AH=3.∵∠BAD=90°,∴DH=10,∴DF=102,∴CF=102.25.(10分)问题探究:(1)如图①,在锐角△ABC中,分别以AB,AC为边向外作等腰三角形ABE和等腰三角形ACD,使AE=AB,AD=AC,∠BAE=∠CAD,连结BD,CE,试猜想BD与CE的大小关系,并说明理由.深入探究:(2)如图②,在四边形ABCD 中,AB =7,BC =3,∠ABC =∠ACD =∠ADC =45°,求BD 的长.(3)如图③,在(2)的条件下,当△ACD 在线段AC 的左侧时,求BD 的长.(第25题)导学号:91354018【解】 (1)BD =CE .理由如下:∵∠BAE =∠CAD ,∴∠BAE +∠BAC =∠CAD +∠BAC ,即∠EAC =∠BAD .在△EAC 和△BAD 中,∵⎩⎨⎧AE =AB ,∠EAC =∠BAD ,AC =AD ,∴△EAC ≌△BAD(SAS),∴BD =CE .(2)如解图①,在△ABC 的外部作等腰直角三角形BAE ,使∠BAE =90°,AE =AB ,连结EC .∵∠ACD =∠ADC =45°,∴AC =AD ,∠CAD =90°,∴∠BAE +∠BAC =∠CAD +∠BAC ,即∠EAC =∠BAD .在△EAC 和△BAD 中,∵⎩⎨⎧AE =AB ,∠EAC =∠BAD ,AC =AD ,∴△EAC ≌△BAD(SAS),∴EC =BD .∵AE =AB =7,∴BE =72+72=98.易知∠ABE =45°,又∵∠ABC =45°,∴∠CBE =45°+45°=90°,∴EC =BE 2+BC 2=(98)2+32=107,∴BD =EC =107.(第25题解)(3)如解图②,在线段AC 的右侧过点A 作AE ⊥AB ,交BC 的延长线于点E . ∵AE ⊥AB ,∴∠BAE =90°.又∵∠ABC =45°,∴∠E =∠ABC =45°,∴AE =AB =7,∴BE =72+72=98.∵∠ACD =∠ADC =45°,∴∠DAC =90°=∠BAE ,∴∠BAE -∠BAC =∠DAC -∠BAC ,即∠EAC =∠BAD .在△EAC 和△BAD 中,∵⎩⎨⎧AE =AB ,∠EAC =∠BAD ,AC =AD ,∴△EAC ≌△BAD(SAS),∴EC =BD .又∵BC =3,∴BD =EC =BE -BC =98-3.。
