高中化学竞赛辅导专题讲座三维化学 (3)

合集下载

高中化学竞赛辅导专题讲座——三维化学3-

▁▂▃▄▅▆▇█▉▊▋▌精诚凝聚 =^_^= 成就梦想 ▁▂▃▄▅▆▇█▉▊▋▌▃ ▄ ▅ ▆ ▇ █ █ ■ ▓点亮心灯 ~~~///(^v^)\\\~~~ 照亮人生 ▃ ▄ ▅ ▆ ▇ █ █ ■ ▓ 高中化学竞赛辅导专题讲座——三维化学第三节正八面体与正方体前文我们学习了正方体与正四面体，现在我们来学习另一种空间正多面体——正八面体。

由于在高中立体几何中并未涉及这种立体图形，使同学们【讨论】顾名思义，正八面体应该有八个完全相同的面，如右图3-1所示，每个面都是正三角形；另外正八面体有六个顶点，十二条棱。

让我们与正方体作一对比，它们都有十二条棱，正方体有六个面（正八面体六个顶点）八个顶点（正八面体八个面），与正八面体的面数和顶点数正好相反，它们是否存在内在的空间关系呢？我们连接正方体六个面的面心形成的是什么空间图形呢？它就是正八面体（能理解了吧！我们也可以将空间直角坐标系xyz 轴上与原点等距的六个点连起来构成正八面体）。

正八面体与正方体都是十二条棱，它们的空间位置显然是不一样的，但它们的十二条棱的棱心的空间位置又如何呢？应该是一样的吧。

先让我们看个例题再讨论吧！【例题1】已知[Co(NH 3)6]3＋的立体结构如图3-2所示，其中1~6处的小圆圈表示NH 3分子，且各相邻的NH 3分子间的距离相等（图中虚线长度相同）。

Co 3+位于八面的中心，若其中两个NH 3被Cl －取代，所形成的[Co(NH 3)4Cl 2]+的同分异构体的数目是 ① A 1 B 2 C 3 D 4【分析】正八面体每个顶点在空间是完全等价的，当选定一个顶点后，另五个顶点就在空间形成两种相对的位置，四个是相邻的，一个是相对的，【解答】B 【练习1】SF 6是一种无色气体，具有很强的稳定性，可用于灭火。

SF 6的分子结构如图3-3所示，呈正八面体型。

如果F 元素有两种稳定的同位素，则SF 6的不同分子种数为 ② A 6种 B 7种 C 10种 D 12种【讨论】用同位素考察分子的空间结构是一种新方法，也是一种好方法。

三维化学的-正八面体与正方体

实用标准文案精彩文档高中化学竞赛辅导专题讲座一一三维化学第三节正八面体与正方体前文我们学习了正方体与正四面体，现在我们来学习另一种空间正多面体——正八面体。

由于在高中立体几何中并未涉及这种立体图形，使同学们在理解上存在一定的困难，那么就让我们先来讨论一下正八面体吧!【讨论】顾名思义，正八面体应该有八个完全相同的面，如右图3-1所示，每个面都是正三角形；另外正八面体有六个顶点，十二条棱。

让我们与正方体作一对比，它们都有十二条棱，正方体有六个面（正八面体六个顶点）、八个顶点（正八面体八个面），与正八面体的面数和顶点数正好相反，它们是否存在内在的空间关系呢？我们连接正方体六个面的面心形成的是什么空间图形呢？它就是正八面体（能理解了吧！我们也可以将空间直角坐标系 xyz十二条棱，它们的空间位置显然是不一样的，但它们的十二条棱的棱心的空间位置又如何呢？应该是一样的吧。

先让我们看个例题再讨论吧!【例题1】已知[Co （NH 3）6]3+的立体结构如图3-2所示，其中1~6 处的小圆圈表示NH 3分子，且各相邻的NH 3分子间的距离相等（图中虚线长度相同）。

Co 3+位于八面的中心，若其中两个NH 3被Cl -取代，所形图1-1轴上与原点等距的六个点连起来构成正八面体）正八面体与正方体都是S实用标准文案成的[Co(NH 3)4Cl2]+的同分异构体的数目是A 1B 2C 3D 4【分析】正八面体每个顶点在空间是完全等价的，当选定一个顶点后，另五个顶点就在空间形成两种相对的位置，四个是相邻的，一个是相对的，故二氯取代物是两种，两个氯的距离图3-2 分别是边长和对角线长。

【解答】B【练习1】SF6是一种无色气体，具有很强的稳定性，可用于灭火。

SF6的分子结构如图3-3所示，呈正八面体型。

如果F元素有两种稳定的同位素，贝USF6的不同分子种数为 _______________________ ②A 6种B 7种C 10种D 12种【讨论】用同位素考察分子的空间结构是一种新方法，也是一种好方法。

2020全国高中化学竞赛辅导-有机化学(决赛篇)-有机合成反应：α-卤代酮的合成和杂环的酚羟基或醚的

R
COOCH2CF3
COOCH2CF3
HO R'
R'
R
COOCH2CF3
DEAD, PPh3
COOCH2CF3
NO2
HO R' R
NO2
R
CN
CN
DEAD, PPh3
R'
30
小结
➢ 一般手性醇翻转成其他氧，氮，硫衍生物时需要用 Mitsunobu反应
➢ 反应产物极性与副产物相差较大，效果较好。内部期刊上有一篇怎样除去副产物的文摘。
O H3C
1. i-Pr2NLi, THF
O
2. p-TsCl, 0'C H3C
Cl
O Ph
CH3 COOEt
1. NaH, DMSO 2. CuBr
O CH3
Ph
Br
COOEt
另外，甲基酮可用甲基格式试剂与相应的Weinreb 酰胺来制备，如下例即是先合成甲基酮，后溴化来合成α-溴代酮的。
O
DCC, DMAP, NHMeOMe
33
2. 氯代
杂环的酚羟基的氯代一般用三氯氧磷1,2,3或三氯氧磷与五氯化磷混合 4,5处理。使用五氯化磷的条件更强，用于难以发生的杂环的酚羟基的氯代反应。杂环烷氧基的氯代也可用三氯氧磷直接处理
2.1 杂环的酚羟基的用三氯氧磷氯代反应示例1
O2N
I
N OH
POCl3
O2N
I
N Cl
34
2.2 杂环的酚羟基用三氯氧磷与五氯化磷混合处理氯代反应示例
3.1 应用重氮酮（由酰氯和重氮甲烷反应而来）合成α-溴化酮示例
(COCl)2 COOH
1. CH2N2/Et2O 2. HBr/AcOH COCl

高中化学奥林匹克竞赛辅导讲座第16讲立体化学基础-知识梳理

高中化学奥林匹克竞赛辅导讲座第16讲立体化学基础【竞赛要求】有机立体化学基本概念。

构型与构象。

顺反异构（trans -、cis -和Z -、E -构型）。

手性异构。

endo -和exo -。

D,L 构型。

【知识梳理】从三维空间结构研究分子的立体结构，及其立体结构对其物理性质和化学性质的影响的科学叫立体化学。

一、异构体的分类按结构不同，同分异构现象分为两大类。

一类是由于分子中原子或原子团的连接次序不同而产生的异构，称为构造异构。

构造异构包括碳链异构、官能团异构、位置异构及互变异构等。

另一类是由于分子中原子或原子团在空间的排列位置不同而引起的异构，称为立体异构。

立体异构包括顺反异构、对映异构和构象异构。

二、立体异构（一）顺反异构分子中存在双键或环等限制旋转的因素，使分子中某些原子或基团在空间位置不同，产生顺反异构现象。

双键可以是C=C 、C=N 、N=N 。

双键产生顺反异构体的条件是双键两端每个原子所连二基团或原子不同。

如：顺反异构的构型以前用顺– 和反– 表示。

如：但顺反异构体的两个双键碳原子上没有两个相同的取代基用这种命名法就无能为力。

如：系统命名法规定将双键碳链上连接的取代基按次序规则的顺序比较，高序位基在双键同侧的称Z 型，ab c b cab c dcab c dcH HC = CH 3CH 3C 顺 – 2 – 丁烯H CH 3 C = CH 3HC 反 – 2 – 丁烯H 3CCH 2CH 3 C =H CH(CH 3)2 C反之称E 型。

如上化合物按此规定应为E 型。

命名为E – 4 – 甲基 – 3 – 已基 – 2 – 戊烯。

所谓“次序规则”，就是把各种取代基按先后次序排列的规则。

（1）原子序数大的优先，如I ＞Br ＞Cl ＞S ＞P ＞F ＞O ＞N ＞C ＞H ，未共用电子对为最小；（2）同位素质量数大的优先，如D ＞H ；（3）二个基团中第一个原子相同时，依次比较第二、第三个原子；（4）重键，如：分别可看作：（5）当取代基的结构完全相同，只是构型不同时，则R ＞S ，Z ＞E 。

三维化学-空间正多面体

高中化学竞赛辅导专题讲座——三维化学第八节空间正多面体前面几节我们学习了五种正多面体，以及它们在化学中的应用。

此节我们将继续对这一内容进行讨论、总结与深化。

何为正多面体，顾名思义，正多面体的每个面应为完全相同的正多边形。

对顶点来说，每个顶点也是等价的，即有顶点引出的棱的数目是相同的，相邻棱的夹角也应是一样的。

那么三维空间里的正多面体究竟有多少种呢？【例题1】利用欧拉定理（顶点数－棱边数＋面数＝2），确定三维空间里的正多面体。

【分析】从两个角度考虑：先看每个面，正多边形可以是几边形呢？我们知道三个正六边形共顶点是构成平面图形的。

因此最多只可以是正五边形，当然还有正三角形和正方形；再看顶点，每个顶点至少引出三条棱边，最多也只有五条棱边（六条棱边时每个角应小于60°，不存在这样的正多边形）。

因此，每个面是正五边形时，三棱共顶点；正方形时，也只有三棱共顶点（四个正方形共顶点是平面的）；正三角形时，可三棱、四棱、五棱共顶点（六个正三角形共顶点也是平面的），当然也可以说，一顶点引出三条棱边时可以为正三角形面、正方形面和正五边形面；一顶点引出四条棱边时只可以为正三角形面；一顶点引出五条棱边时也只可以为正三角形面——共计五种情况，是否各种情况都存在呢？（显然是，各种情况前面均已讨论）我们用欧拉定理来计算。

①正三角形，三棱共顶点：设面数为x，则棱边数为3x/2（一面三棱，二面共棱），顶点数为x（一面三顶点，三顶点共面），由欧拉定理得x－3x/2＋x＝2，解得x＝4，即正四面体；②正三角形，四棱共顶点：同理，3x/4－2x＋x＝2，解得x＝8，即正八面体；③正三角形，五棱共顶点：同理，3x/5－3x/2＋x＝2，解得x＝20，即正二十面体；④正方形，三棱共顶点：同理，4x/3－2x＋x＝2，解得x＝6，即正方体；⑤正五边形，三棱共顶点：同理，5x/3－5x/2＋x＝2，解得x＝12，即正十二面体。

【解答】共存在五种正多面体，分别是正四面体、正方体、正八面体、正十二面体、正二十面体。

高中化学竞赛辅导专题讲座——三维化学

高中化学竞赛辅导专题讲座——三维化学第二节规则晶体的密度计算在第一节中，我们学习了空间正方体与正四面体的关系，能把四面体型的碳化硅原子晶体（或金刚石）用正方体模型表示出来。

本节我们将着重讨论如何来计算其密度。

先来了解一下有关密度的问题吧。

【讨论】在初中物理中，我们学习了密度概念。

密度是某一物质单位体积的质量，就是某一物质质量与体积的比值。

密度是物质的一种属性，我们无限分割某一物质，密度是不变的（初中老师说过）。

这儿请注意几个问题：其一，密度受环境因素，如温度、压强的影响。

“热胀冷缩”引起物质体积变化，同时也改变了密度。

在气体问题上，更是显而易见。

其二，从宏观角度上来看，无限分割的确不改变物质的密度；但从微观角度来看呢，当把物质分割到原子级别时，我们拿出一个原子和一块原子间的空隙，或在一个原子中拿出原子核与核外部分，其密度显然都是不一样的。

在化学中有关晶体密度的求算，我们是从微观角度来考虑的。

宏观物质分到何时不应再分了呢？我们只要在微观角度找到一种能代表该宏观物质的密度的重复单位。

一般我们都是选取正方体型的重复单位，它在三维空间里有规则地堆积（未留空隙），就构成宏观物质了，也就是说这个正方体重复单位的密度代表了该物质的密度。

我们只要求出该正方体的质量和体积，不就是可以求出其密度了吗？现在，我们先主要来探讨一下正方体重复单位的质量计算。

【例题1】如图2-1所示为高温超导领域里的一种化合物——钙钛矿的结构。

该结构是具有代表性的最小重复单元。

确定该晶体结构中，元素钙、钛、氧的个数比及该结构单元的质量。

（相对原子质量：Ca 40.1 Ti 47.9 O 16.0；阿佛加德罗常数：6.02×1023）【分析】我们以右图2-1所示的正方体结构单元为研究对象，讨论钙、钛、氧这三种元素属于这个正方体结构单元的原子（或离子）各有几个。

首先看钙原子，它位于正方体的体心，自然是1；再看位于顶点上的钛原子，属于这个正方体是1/8吗？在第一节中，我们曾将一个大正方体分割成八个小正方体，原来在大正方体的一个原子被分割成了八个，成为小正方体的顶点。

简单分子的空间结构

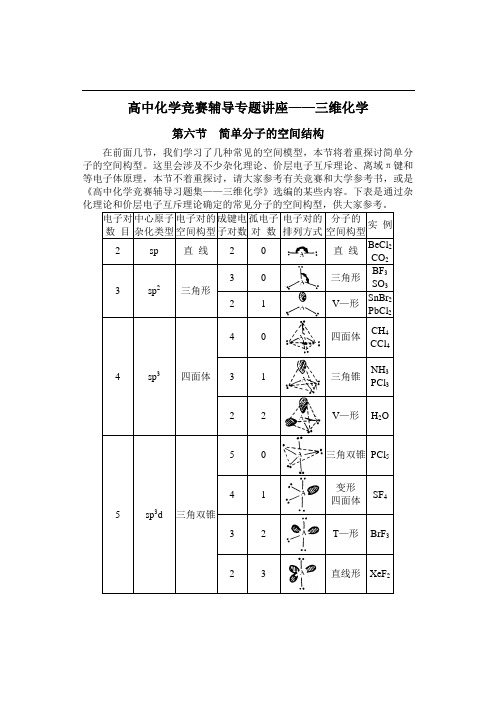
高中化学竞赛辅导专题讲座——三维化学第六节简单分子的空间结构在前面几节，我们学习了几种常见的空间模型，本节将着重探讨简单分子的空间构型。

这里会涉及不少杂化理论、价层电子互斥理论、离域π键和等电子体原理，本节不着重探讨，请大家参考有关竞赛和大学参考书，或是《高中化学竞赛辅导习题集——三维化学》选编的某些内容。

下表是通过杂【讨论】给出一个分子或离子，我们一般先找出中心原子，确定它的成键电子对数和孤电子对数，判断杂化类型和电子对构型，再判断分子或离子的构型。

由于等电子体具有类似的空间结构，我们也可以据此判断复杂的分子或离子的空间构型。

我们结合以下例题具体讨论。

【例题1】磷的氯化物有PCl3和PCl5，氮的氯化物只有NCl3，为什么没有NCl5？白磷在过量氯气（其分子有三种不同的相对分子质量）中燃烧时，其产物共有几种不同分子。

①【分析】PCl5中心原子P有3d轨道，能与3s、3p轨道一起参与杂化，杂化类型为sp3d，构型为三角双锥。

第二问是通过同位素来考察三角双锥的空间构型：“三角”是一个正三角形的三个顶点，等价的三个点；“双锥”是对称的两个锥顶。

P35Cl5的37Cl的一取代物可在角上和锥顶上2种情况；37Cl 的二取代物可在两个角上、两个锥顶上和一个角一个锥顶上3种情况；利用对称性，三取代物、四取代物与二取代物、一取代物是相同的。

共计有(1＋2＋3)×2＝12种。

【解答】N原子最外层无d轨道，不能发生sp3d杂化，故无NCl5。

12种。

【练习1】PCl5是一种白色固体，加热到160℃不经过液态阶段就变成蒸气，测得180℃下的蒸气密度（折合成标准状况）为9.3g/L，极性为零，P－Cl键长为204pm和211pm两种。

继续加热到250℃时测得压力为计算值的两倍。

PCl5在加压下于148℃液化，形成一种能导电的熔体，测得P－Cl的键长为198pm和206pm两种。

（P、Cl相对原子质量为31.0、35.5）回答如下问题：①180℃下，PCl5蒸气中存在什么分子？为什么？写出分子式，画出立体结构。

高中化学竞赛辅导专题讲座——三维化学4-

▁▂▃▄▅▆▇█▉▊▋▌精诚凝聚 =^_^= 成就梦想 ▁▂▃▄▅▆▇█▉▊▋▌▃ ▄ ▅ ▆ ▇ █ █ ■ ▓点亮心灯 ~~~///(^v^)\\\~~~ 照亮人生 ▃ ▄ ▅ ▆ ▇ █ █ ■ ▓高中化学竞赛辅导专题讲座——三维化学第四节正四、六、八面体的组合前文我们学习了正方体、正四面体与正八面体，本节我们将对内容做进一步的巩固复习，并将探讨一下正四、八面体的组合。

【例题1】XeF 8是一种尚未合成的化合物，预测它的空间构型；F 有二种同位素，则XeF 8有种不同分子。

（不计顺反异构和旋光异构）①【分析】八个原子在空间的最对称排列是正方体。

在着重讨论过正四面体与正八面体后，再看这个正方体问题。

不妨设正方体八个顶点全被a F 占据，我们每一次用0，1，2，3……8个b F 去取代，看两个b F ，有3种，分别在棱上，面对角线上，体对角线上；看三个b F ，也有3种，三个b F 构成的三角形边长分别为1，1，2；1，2，3；2，2，2。

关键是看四个b F 时有几种。

如图4-1所示正方体，四个b F 共面时有2种（如面ABCD 与面A 1B 1CD 型），四个b F 构成正三棱锥有2种（如正四面体型的ACB 1D 1与三棱垂直的ABDA 1），另外还各有一个ABCC 1型和ABCD 1型。

因此总数应为(1＋1＋3＋3)×2＋6＝22种。

【解答】正方体 22【练习1】1964年Eaton 合成了一种新奇的烷，叫立方烷，化学式为C 8H 8 (A )。

20年后，在Eaton 研究小组工作的博士后XIONG YUSHENG (译音熊余生)合成了这种烷的四硝基衍生物(B ), 是一种烈性炸药。

最近，有人计划将B 的硝基用19种氨基酸取代，得到立方烷的四酰胺基衍生物(C )，认为极有可能从中筛选出最好的抗癌、抗病毒，甚至抗爱滋病的药物来。

四硝基立方烷理论上可以有多种异构体，但仅只一种是最稳定的，它就是(B )，请画出它的结构式；C 中每个酰胺基是一个氨基酸基团。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

高中化学竞赛辅导专题讲座——三维化学近年来，无论是高考，还是全国竞赛，涉及空间结构的试题日趋增多，成为目前的热点之一。

本文将从最简单的五种空间正多面体开始，与大家一同探讨中学化学竞赛中与空间结构有关的内容。

在小学里，我们就已经系统地学习了正方体，正方体（立方体或正六面体）有六个完全相同的正方形面，八个顶点和十二条棱，每八个完全相同的正方体可构成一个大正方体。

正四面体是我们在高中立体几何中学习的，它有四个完全相同的正三角形面，四个顶点和六条棱。

那么正方体和正四面体间是否有内在的联系呢？请先让我们看下面一个例题吧：【例题1】常见有机分子甲烷的结构是正四面体型的，请计算分子中碳氢键的键角（用反三角函数表示）【分析】在化学中不少分子是正四面体型的，如CH4、CCl4、NH4＋、 SO42－……它们的键角都是109º28’，那么这个值是否能计算出来呢？如果从数学的角度来看，这是一个并不太难的立体几何题，首先我们把它抽象成一个立体几何图形（如图1-1所示），取CD中点E，截取面ABE（如图1-2所示），过A、B做AF⊥BE，BG⊥AE，AF交BG 于O，那么∠AOB就是所求的键角。

我们只要找出AO（=BO）与AB的关系，再用余弦定理，就能圆满地解决例题1。

当然找出AO和AB的关系还是有一定难度的。

先把该题放下，来看一题初中化学竞赛题：【例题2】CH4分子在空间呈四面体形状，1个C原子与4个H原子各共用一对电子对形成4条共价键，如图1-3所示为一个正方体，已画出1个C原子(在正方体中心)、1个H原子(在正方体顶点)和1条共价键(实线表示)，请画出另3个H原子的合适位置和3条共价键，任意两条共价键夹角的余弦值为①【分析】由于碳原子在正方体中心，一个氢原子在顶点，因为碳氢键是等长的，那么另三个氢原子也应在正方体的顶点上，正方体余下的七个顶点可分成三类，三个为棱的对侧，三个为面对角线的对侧，一个为体对角线的对侧。

显然三个在面对角线对侧上的顶点为另三个氢原子的位置。

【解答】答案如图1-4所示。

【小结】从例题2中我们发现：在正四面体中八个顶点中不相邻的四个顶点（不共棱）可构成一个正四面体，正四面体的棱长即为正方体的棱长的倍，它们的中心是互相重合的。

【分析】回到例题1，将正四面体ABCD放入正方体中考虑，设正方体的边长为1，则AB为面对角线长，即，AO为体对角线长的一半，即/2，由余弦定理得cosα＝(AO2＋BO2－AB2)/2AO·BO＝－1/3【解答】甲烷的键角应为π－arccos1/3【练习1】已知正四面体的棱长为，计算它的体积。

【讨论】利用我们上面讲的思想方法，构造一个正方体，那么正四面体就相当于正方体削去四个正三棱锥（侧面为等腰直角三角形），V正四面体＝a3－4×(1/6)×a3。

若四面体相对棱的棱长分别相等，为a、b、c，求其体积。

我们也只需构造一个长方体，问题就迎刃而解了。

【练习2】平面直角坐标系上有三个点（a1，b1）、（a2，b2）、（a3，b3）求这三个点围成的三角形的面积。

【讨论】通过上面的构造思想，你能构造何种图形来解决呢？是矩形吧！怎样表达面积呢？你认为下面的表达式是否写得有道理？S△＝（max{a1，a2，a3}－min{a1，a2，a3}）×（max{b1，b2，b3}－min{b1，b2，b3}）－（＋＋）【练习3】在正四面体中体心到顶点的距离是到底面距离的几倍，能否用物理知识去理解与解释这一问题呢？【讨论】利用物理中力的正交分解来解决这一问题，在平面正三角形中，从中心向顶点构造三个大小相等，夹角为120º的力F1、F2、F3。

设F1在x轴正向，F2、F3进行正交分解在x、y轴上，在x轴上的每一个分力与F1相比就相当于中心到底面与到顶点距离之比，而两个分力之和正好与F1抵消，即大小相等。

显然中心到顶点距离应为到底边距离的2倍。

在空间，构造四个力Fi（i＝1，2，3，4），F1在x轴正向（作用点与坐标原点重合），F2、F3、F4分解在与x轴与yz面上，yz面上三个力正好构成正三角形，而在x轴（负向）上有三个分力，其之和与F1抵消，想想本题答案应为3吗？当然这个问题用体积知识也是易解决的。

让我们再回到正题，从上面的例题1，2中，我们了解了正四面体与正方体的关系，虽然这是一个很浅显易懂的结论，但我们还是应该深刻理解和灵活应用，帮助我们解决一些复杂的问题。

先请再来看一个例题吧：【例题3】SiC是原子晶体，其结构类似金刚石，为C、Si两原子依次相间排列的正四面体型空间网状结构。

如图1-5所示为两个中心重合，各面分别平行的大小两个正方体，其中心为一Si原子，试在小正方体的顶点上画出与该Si最近的C的位置，在大正方体的棱上画出与该Si最近的Si的位置。

两大小正方体的边长之比为_______；Si—C—Si的键角为______(用反三角函数表示)；若Si—C键长为a cm，则大正方体边长为_______cm；SiC晶体的密度为________g/cm3。

（N A为阿佛加德罗常数，相对原子质量 C.12 Si.28）②【分析】正方体中心已给出了一个Si原子，那么与Si相邻的四个C原子则在小正方体不相邻的四个顶点上，那么在大正方体上应画几个Si原子呢？我们知道每个碳原子也应连四个硅原子，而其中一个必为中心的硅原子，另外还剩下4×3＝12个硅原子，这12个点应落在大正方体上。

那么这12个又在大正方体的何处呢？前文介绍正方体时曾说正方体有12条棱，是否每一条棱上各有一个碳原子？利用对称性原则，这12个硅原子就应落在各棱的中点。

让我们来验证一下假设吧。

过大正方体的各棱中心作截面，将大正方体分割成八个小正方体，各棱中点、各面心、顶点、中心构成分割后正方体的顶点。

原来中心的硅原子就在分割后八个正方体的顶点上了，由于与一个碳原子相邻的四个硅原子是构成一个正四面体的。

利用例2的结论，分割后的正方体上另三个硅原子的位置恰为原来大正方体的棱心（好好想一想）。

那么碳原子又在分割后的正方体的哪里呢，毫无疑问，在中心。

那么是否每个分割后的正方体的中心都有碳原子呢？这是不可能的，因为只有四个碳原子，它们应该占据在不相邻的四个正方体的中心。

碳原子占据四个硅原子构成的最小正四面体空隙的几率为1/2，那么反过来碳原子占据碳原子四面体空隙的几率又是多少呢？也1/2吧，因为在空间，碳硅两原子是完全等价的，全部互换它们的位置，晶体是无变化的。

我们可以把大正方体看成SiC晶体的一个基本重复单位，那么小正方体（或分割后的小正方体）能否看成一个基本重复单位呢？这是不行的，因为有的小正方体中心是有原子的，而有些是没有的。

大小两个正方体的边长应是2:1吧，至于键角也就不必再说了。

最后还有一个密度问题，我们将留在第二节中去分析讨论。

●● Si ○ C图1-5【解答】如图1-6所示（碳原子在小正方体不相邻的四个顶点上，硅原子在大正方体的十二条棱的中点上） 2:1 arcos (－1/3)4/3 15/2N A a3【练习4】金刚石晶体是正四面体型的空间网状结构，课本上的金刚石结构图我们很难理解各原子的空间关系，请用我们刚学的知识将金刚石结构模型化。

【练习5】在例题3中，如果在正方体中心不画出Si原子，而在小正方体和大正方体上依旧是分别画上C原子和Si原子，应该怎么画呢？【讨论】还是根据例题3 的分析，在例题3中，将大正方体分割成小正方体后，我们所取的四个点在大正方体上是棱心和体心，那么我们是否可以取另外四个点呢？它们在大正方体中又在何位置呢？与原来的位置（棱心＋体心）有什么关系呢？【练习参考答案】1．；2．该表达式是正确的；3．3倍4．只需将例题3中将Si原子变成C原子，就是我们所需的金刚石结构模型，大正方体就是金刚石的晶胞（下文再详述）。

5．可以取另外四个点，C原子的位置无变化，Si原子在大正方体的面心和顶点上（这不就是山锌矿的晶胞吗？下文再详述）；与原来的位置正好相差了半个单位，即只需将原来的大正方体用一水平面分成两等份，将下面部分平移到上面一部分的上面接上即可。

在第一节中，我们学习了空间正方体与正四面体的关系，能把四面体型的碳化硅原子晶体（或金刚石）用正方体模型表示出来。