地下水污染物迁移数值模拟分析
河湖相沉积区地下污染物运移数值模拟

q s 一一 源 ( 正值 )或汇 ( 负值)的单位流来自 一 一孔隙 度
—
—
源或 汇的 浓度
一
—
—
阶反 应速 率常数
多孔介 质的 比重 c—— 吸 附在 介质上 的污 染物 浓度 R — — 阻滞 因子
— —
纵 向 分 析 Z Kl 、Z K 2 、Z K4 、Z K 8 和 Z K1 2 钻孔 ( 钻 孔 分 布 图 见图 1 )中土样 S O 卜含量主要集中于埋深 0 - 5 m;Z K5 、 Z K6 、Z K7 和Z K9 钻 孔 中土样 S O 卜含 量主 要集 中于 埋深 5 1 0 m;Z K1 5 和Z K1 6 钻 孔 中土样 S O 卜含量 主要 集 中于 埋深 1 0 m以下 ( 见图 3 )。纵 向分 析土 样 中 S O 一 扩 散 及 迁移 范 围示 意 如 图 2 。 横 向分 析 通过 模拟 分析 ,S O 一 的具 体 含量分 布 见 图 4 、5 。 分析土样 中埋深 5 m内的S O 卜的含量 , 大致以 Z K1 ( 泄 漏 点 )为 中心 点外扩 5 0 m 范 围内 S O 一的含 量均 较 高 ,该 范 围内有 Z K1 、Z K2 、Z K3 、Z K4 、Z K4 —1和 Z K7 , 该 平面 范 围 内以 S O 卜含 量较 高 的 Z K1 为 中心 向外 呈递 减 形 式扩 散 ,5 0 m 范 围外 S O 含量 基本 趋 于背景 值 。 通过分析对比埋深 5~ 1 0 m 土样中 S O 的含量,该 层位 的土 样 中 S O 的 含量 最大钻 孔 为 Z K2 和Z K 7 ,大 致 以这 两 个钻 孔 为 中心 ,沿 南东 方 向及 正北 方 向以 递减 方 式 扩散 ,扩 散至 南东 方 向 Z Kl 6范 围内 ( 距离 Z Kl 平 面距 离 约1 3 5 m)的 S O 卜的 含 量 较 背景 值 高 ; 向北 方 向扩 散 至 Z K 9 位置的 S O 4 2含量 较 背景 值高 ,位 置距离 Z K1 平面 位
地下水污染物迁移转化模型及数值解_Parts 3

有限差分与有限元数值解法的 主要差异: 主要差异: (1)网格刨分灵活性方面 (2)质量守恒方面
地下水污染控制与修复——王明玉
地下水模拟建模过程与方法
地下水污染控制与修复——王明玉
Introduction to Modeling Approaches
地下水污染控制与修复——王明玉
地下水污染控制与修复——王明玉
PRIMARY ISSUES OF CONCERN AT LARGE AND COMPLEX SITES
Data availability – How many sampling points are there? For how long? Data spatial distribution – Where are they located relative to the plume / source? Data quality / data management – Where is the data housed? Who uses it? Characterization and conceptualization of Site Conditions - How can they be represented conceptually?
地下水污染控制与修复——王明玉
National Academy of Sciences:
Thus, when models form the basis for decision-making, uncertainty will be an inescapable component of environmental management and regulation. A key consideration in any modeling process is whether the model has undergone sufficient development and testing to address the problem being analyzed in a sufficiently meaningful manner.
地下水数值模拟任务、步骤及常用软件

地下水数值模拟任务、步骤及常用软件展开全文一、地下水模拟任务大多数地下水模拟主要用于预测,其模拟任务主要有4种:1)水流模拟主要模拟地下水的流向及地下水水头与时间的关系。
2)地下水运移模拟主要模拟地下水、热和溶质组分的运移速率。
这种模拟要特别考虑到“优先流”。
所谓“优先流”就是局部具有高和连通性的渗透性,使得水、热、溶质组分在该处的运移速率快于周围地区,即水、热、溶质组分优先在该处流动。
3)反应模拟模拟水中、气-水界面、水-岩界面所发生的物理、化学、生物反应。
4)反应运移模拟模拟地下水运移过程中所发生的各种反应,如溶解与沉淀、吸附与解吸、氧化与还原、配合、中和、生物降解等。
这种模拟将地球化学模拟(包括动力学模拟)和溶质运移模拟(包括非饱和介质二维、三维流)有机结合,是地下水模拟的发展趋势。
要成功地进行这种模拟,还需要研究许多水-岩相互作用的化学机制和动力学模型。
二、模拟步骤对于某一模拟目标而言,模拟一般分为以下步骤:1)建立概念模型根据详细的地形地貌、地质、水文地质、构造地质、水文地球化学、岩石矿物、水文、气象、工农业利用情况等,确定所模拟的区域大小,含水层层数,维数(一维、二维、三维),水流状态(稳定流和非稳定流、饱和流和非饱和流),介质状况(均质和非均质、各向同性和各向异性、孔隙、裂隙和双重介质、流体的密度差),边界条件和初始条件等。
必要时需进行一系列的室内试验与野外试验,以获取有关参数,如渗透系数、弥散系数、分配系数、反应速率常数等。
2)选择数学模型根据概念模型进行选择。
如一维、二维、三维数学模型,水流模型,溶质运移模型,反应模型,水动力-水质耦合模型,水动力-反应耦合模型,水动力-弥散-反应耦合模型。
3)将数学模型进行数值化绝大部分数学模型是无法用解析法求解的。
数值化就是将数学模型转化为可解的数值模型。
常用数值化有有限单元法和有限差分法。
4)模型校正将模拟结果与实测结果比较,进行参数调整,使模拟结果在给定的误差范围内与实测结果吻合。
地下水核素迁移数值模拟简介-2019年文档

地下水核素迁移数值模拟简介1、概述放射性核素在地下水中迁移、吸附和沉积是目前国内核电厂特别是内陆核电厂选址和设计过程中需特别关注的问题。
研究和预测核素在地下水中的迁移扩散,能够为核电厂环境影响评价提供支持。
国内核电厂主要以数模计算的方式开展放射性核素在地下水中的迁移扩散研究。
根据研究介质的不同,主要分为孔隙介质和裂隙介质。
目前,孔隙介质中的溶质运移理论已经较成熟,但裂隙介质由于岩体裂隙的空间几何因素、渗透系数和弥散系数等具有显著的不确定性和方向性,使得裂隙岩体的渗流和溶质运移的研究具有较大的难度。
2、溶质(核素)迁移的基本理论核素在地下水中迁移的基本理论主要是溶质运移的相关理论,其中最基本的是孔隙介质中的溶质运移理论,裂隙介质中的溶质运移主要是以孔隙介质溶质运移理论为基础,考虑裂隙介质的相关特性。
溶质在介质中的迁移机制主要有三方面:对流、分子扩散和机械弥散。
分子扩散和机械弥散统称为水动力弥散。
另外,溶质在介质中迁移的同时,还有可能发生各种反应,包括物理反应、化学反应和生物反应等。
对于放射性核素在地下水中的迁移来说,主要是考虑吸附和放射性衰变。
2.1 裂隙介质中溶质运移基本理论裂隙介质中的地下水数值模拟技术远落后于孔隙介质。
自20世纪60年代以来,人们就开始了对裂隙岩体地下水溶质运移的探索工作,在试验、理论研究和计算模拟方法等方面都取得了一定的进展。
然而,由于裂隙岩体中的渗流具有高度的复杂性,岩体裂隙的空间几何因素、渗透参数、弥散系数等有显著的不确定性,使得裂隙岩体渗流研究具有极大的难度。
3、溶质(核素)迁移数值模拟分析和计算程序根据溶质运移基本方程和边界条件,仅对于较简单情况可得出解析解,多数情况需采用数值计算方法。
国内地下水数值模拟的研究开始于20世纪70年代,经过30多年来的努力,取得了快速进步和发展,但至今国内仍然未见报道具有知识产权的通用地下水模拟软件。
目前,孔隙介质溶质运移数值模拟计算常用的软件有:MODFLOW、MT3D、MT3DMS、GMS、FEMWATER、3DFEMWATER、FEFLOW、PMWIN和GeoStudio等。
北方某城市浅层地下水中有机污染物迁移转化的数值模拟研究

可能是由于该货场和该铁路段在清洗过 (), 标准的 0 !-./。 程中, 常常要使用有机溶剂, 并顺地表直接排放。通过在地下 水流场方向上对该井上下游水井对比取样分析, 该货场和该 铁路段上游井中, 三氯乙烯几乎没有检出, 而在 2 号井下游 井中三氯乙烯很高, 但比 2 号井稍低, 即沿着地下水流向, 污 染物浓度减小。由此基本可以确定货场和铁路段是 2 号井的 主要污染源。 !"$ 地下水中的氯代烃运移影响因素 地下水中有机污染物的迁移转化同时受生物和非生物 过程的影响。地下水的流场方向和流速控制着污染物迁移的 流向和流速; 弥散使有机污染物在流场的横向和纵向方向上 扩散; 吸附和解吸附阻碍着污染物的迁移; 生物降解决定了 地下水中有机物的存在, 或许可以影响降解后最终产物的形 态。 这些作用都和地下水化学性质, 含水层介质性质相关。 如 果不把这些作用综合到数学模型中, 就很难描述污染物在地 下水中的迁移转化规律。 !"% 研究区地下水水化学特征 的对比可以判断, 研 从研究区各指标值与标准值( 表 4) 究区地下水环境是一个好氧与硝酸盐还原的兼性环境。另 外, 在地下水取样的微生物分析测试中已证实研究区地下水 有降解有机物的微生物存在, 这表明研究区中可能存在有机 污染物的生物降解作用。
>
图 9 @# 井四氯乙烯拟合曲线 #$%&9 #$::$;% <)4=+ 324 ’56 /: -$:+ @> 。从图中可以看出, 四氯乙烯的污染羽状体短而圆, 而三氯 7) 乙烯则细而长, 并且中心处三氯乙烯污染羽状体的浓度比四 氯乙烯高。这是因为, 污染羽状体中心的反应过程是厌氧反 应, 而边缘带是好氧和厌氧两种反应。好氧生物降解过程中, 氯代烃的氯原子越少, 降解的越快; 而厌氧生物降解过程中, 氯原子越多, 反应的越快, 并且好氧降解反应速率比厌氧快。 另外四氯乙烯在好氧条件下只有与某些有机物共代谢作用 才能降解, 但在研究区这有机物没有检出, 因此在研究区影 响四氯乙烯浓度变化的主要是厌氧条件下的降解; 而三氯乙 烯在好氧和厌氧条件下都可以降解。这两种作用的结果造成 了两种污染物的污染羽状体在形状和浓度上的差异。另外从
《土默川平原地下水数值模拟及应用》范文

《土默川平原地下水数值模拟及应用》篇一一、引言土默川平原作为我国重要的农业与水资源富集区,其地下水资源的研究与利用对于当地经济发展及生态环境保护具有重要意义。
近年来,随着人口增长和工业化进程的加速,地下水资源的合理开发与管理成为一项紧迫的任务。
本文通过建立土默川平原地下水数值模型,对地下水流动和污染状况进行模拟,并探讨其在实际应用中的价值。
二、研究区域概况土默川平原位于我国某省(市)中部,地势平坦,气候适宜,是典型的农业种植区。
近年来,随着经济的快速发展和城市化进程的推进,该区域的地下水开采量逐渐增加,对地下水资源管理提出了新的挑战。
三、地下水数值模拟方法与模型建立3.1 数值模拟方法概述数值模拟方法通过数学模型来描述地下水的流动、传输及变化规律,具有成本低、效率高、预测准确等优点。
本文采用先进的地下水数值模拟软件,通过构建合理的模型参数和边界条件,实现对土默川平原地下水的模拟。
3.2 模型建立根据土默川平原的地质构造、水文地质条件及历史水文地质资料,建立三维地下水数值模型。
模型包括地层结构、含水层参数、边界条件等要素。
通过率定和验证模型参数,确保模型的准确性和可靠性。
四、地下水流动与污染模拟4.1 地下水流动模拟利用建立的地下水数值模型,模拟土默川平原地下水的流动状况,包括水位变化、流速分布等。
通过分析模拟结果,了解地下水的补给与排泄途径,为合理开发利用提供依据。
4.2 地下水污染模拟结合实际污染情况,模拟不同污染源对地下水的影响范围和程度。
通过分析污染物的迁移、扩散规律,评估污染对地下水水质的影响,为制定污染防治措施提供科学依据。
五、应用实践5.1 地下水开采管理通过地下水数值模拟结果,合理规划开采井位和开采量,避免过度开采导致的地下水位下降和地质灾害。
同时,根据模拟结果调整开采计划,实现地下水的可持续利用。
5.2 污染防治措施制定根据地下水污染模拟结果,制定针对性的污染防治措施。
包括污染源控制、污染物处理、污染区域治理等措施,有效降低污染物对地下水的污染程度。
VM数值模拟、污染物运移
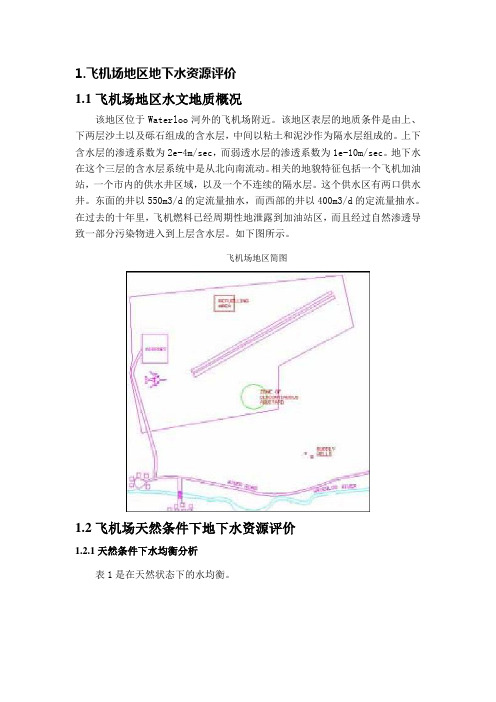
1.飞机场地区地下水资源评价1.1飞机场地区水文地质概况该地区位于Waterloo河外的飞机场附近。
该地区表层的地质条件是由上、下两层沙土以及砾石组成的含水层,中间以粘土和泥沙作为隔水层组成的。
上下含水层的渗透系数为2e-4m/sec,而弱透水层的渗透系数为1e-10m/sec。
地下水在这个三层的含水层系统中是从北向南流动。
相关的地貌特征包括一个飞机加油站,一个市内的供水井区域,以及一个不连续的隔水层。
这个供水区有两口供水井。
东面的井以550m3/d的定流量抽水,而西部的井以400m3/d的定流量抽水。
在过去的十年里,飞机燃料已经周期性地泄露到加油站区,而且经过自然渗透导致一部分污染物进入到上层含水层。
如下图所示。
飞机场地区简图1.2飞机场天然条件下地下水资源评价1.2.1天然条件下水均衡分析表1是在天然状态下的水均衡。
表1 天然状态下的水均衡分析统计表天然条件是指没有人为活动的影响,只受自然因素的制约的条件。
该区天然条件地下水均衡分析是指,没有人为的开采井和注水井,没有农田灌溉等,只在自然条件下进行各个过程的转换和水文循环。
通过模拟得出天然条件下,飞机场地区地下水均衡如表1所示。
从模拟结果我们可以看出,天然条件下,地下水的补给项主要来源于降雨入渗补给,弱透水层的越流补给和边界的流入;而地下水的排泄途径主要为河流排泄、越流和边界上的排泄。
飞机场地区地下水获得的主要补给是降水补给,1077.5m/d,占总补给量的99.99%。
排泄主要是向河流的排泄,863.12 m/d,占总排泄量的80.02%,由均衡表可以发现,在天然状态下,地下水的输入输出项是均衡地。
1.2.2天然条件下流场图及流场分析天然状态下地下水流场图(第一层)天然状态下地下水流场图(第二层)天然状态下地下水流场图(第三层)天然条件下研究区地下水流方向是从北向南,由于各层的渗透性不同,流场在各层的分布也就出现不同。
第一层是由砂砾石组成的透水性较好的含水层,该层中地下水总体流向是自北向南。
地下水污染迁移

污染物在地下水中迁移转化的研究,主要是运用数学模拟方法进行的。
应用数学模型模拟可溶性污染物在地下含水层中迁移时,需要将水流模型和水质模型耦合起来,求出污染物浓度的时空变化规律,以此来预测地下水污染的瞬时动态与扩展范围,为制定合理有效的地下水污染防治措施,选择最佳治理方案提供科学依据。
20世纪60年代后期,为了研究地下水水质,人们把数学模型应用进来。
首先由苏联的Bel对孔隙介质中水动力弥散进行了详细研究,指出了水动力弥散可由纵向弥散和横向弥散系数来表征。
Fried(1972年)进一步研究了经典模型与水动力弥散方程,该方程是建立在宏观孔隙介质连续的前提下的,据此认为:孔隙介质的每个无穷小单元体都是由固体物质与孔隙构成的,并提出了考虑固体物质与孔隙分界面是浓度与浓度梯度跳跃的新水动力弥散模型,导致水动力弥散方程中增加了补充项。
至于可预测含水层中污染浓度的复杂数学模型是由Konikon等人在1978年研制出来。
1977年Wills和Neumman 在系列论文中提出了分散参数系统内地下水质动态管理的通用模型。
近年来,国内外学者在地下水溶质运移理论及试验研究方面又取得了新的进展。
如对污染物迁移的弥散系数提出了与时空有关的表达式;通过大量的试验研究使得迁移方程中的衰减、离子交换、生物、化学反应项的系数取值更为合理,考虑的因素更为全面;对于污染物中固液相浓度的相互转化关系进行了深入的研究,吸附条件由平衡等温模式发展到考虑非平衡吸附模式;边界条件和初始条件的设定也更趋于合理和全面。
随着研究的深入,国外对污染物迁移转化的随机模型也开始广泛的研究,新的成果不断问世。
在迁移载体水分运动方面,又发展到考虑可动和不可动水体等因素。
我国地下水水质模拟研究工作是最近20年来的事情,1980年初首先由山东省地质局等单位在济宁市郊区进行了现场试验研究工作,并建立了我国第一个为预测地下水污染发展趋势的地下水水质模型。
1982年武汉水利电力学院应用伽辽金有限元法求解了在渗流区有抽水井条件下的二维溶质迁移及在自由表面上有入渗补给时二维渗流中的溶质迁移问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Average linear velocity
True velocities
We will assume that dispersion follows Fick’s law, or in other words, that dispersion is “Fickian(费克方程)”. This is an important assumption;it turns out that the Fickian assumption is not strictly valid(有效的) near the source of the contaminant.
How about Fick’s law (见下一张PPT) where D is the effective d of diffusion? diffusion coefficient.
c2 c1 FDiff DdA x
Fick’s law describes diffusion of ions on a molecular scale as ions diffuse from areas of higher to lower concentrations.
3. No density effects
Density-dependent flow requires a different governing equation. See Zheng and Bennett, Chapter 15.
Figures from Freeze & Cherry (1979)
c2 c1 fD Dx x
D is the dispersion coefficient. It includes the effects of dispersion and diffusion. Dx is sometimes written DL and called the longitudinal(纵向的) dispersion coefficient.
Tracer:示踪剂
Advective flux
fA = qxc
c2 c1 fDx Dx ( ) x
Dispersive fluxes
c 2 c1 fDy Dy ( ) y
c2 c1 fDz Dz ( ) z
Dx represents longitudinal dispersion (& diffusion); Dy represents horizontal transverse (水平横波)dispersion (& diffusion); Dz represents vertical transverse dispersion (& diffusion).
(i.e., a medium with connected pore space or a densely fractured medium with a single network of connected fractures)
2. Miscible flow(混相流动)
(i.e., solutes dissolve in water; DNAPL’s(重非轻亲 水相液体) and LNAPL’s (轻非轻亲水相液体) require a different governing equation. See p. 472, note 15.5, in Zheng and Bennett.)
(Zheng & Bennett, Fig. 3.8.)
Transverse:横向
We need to introduce a “law” to describe dispersion, to account for(解释) the deviation (偏差) of velocities from the average linear velocity calculated by Darcy’s law.
Dispersive Transport & Advection-dispersion Equation (ADE)
Advection only
C0
Advection & Dispersion
C0
C (viC ) xi t
v = q/θ
Assuming particles travel at same average linear velocity v=q/θ
Dx Lv* is the effective molecular diffusion coefficient [L2T-1]
is the tortuosity(扭转) factor [-]
1
Assume 1D flow
Case 2
and a point source
In fact, particles travel at different velocities v>q/θ or v<q/θ
Derivation(推导) of the Advection-Dispersion Equation (ADE) Assumptions
1. Equivalent(当量) porous medium (epm)
porosity
c2 c1 fD D x
where D is the dispersion coefficient.
Case 1
Advective flux Assume 1D flow
porosity
h2 h1 fA qxc [K ]c vxc x
Dispersive flux
Adective flux
h1 h2
Darcy’s law:
h2 h1 Q KA s
q = Q/A
advective flux fA = q c f = F/A
How to quantify the dispersive flux?
h1 h2 fA = advective flux = qc f = fA + fD
