【最新】引例零件参数设计
零件的参数设计

零件的参数设计孙连山,洪献,曹奕剑模型是研究产品各零件参数对产品某一性能影响的连续模型,以减少生产产品总费用最小为最终目的,主要用非线性规划化的思想建立,因为零件参数为随机变量,所以建模时要用概率论的方法给出非线性规划化问题目标函数。
模型形式简洁,因零件加工精度的限制,实际参数标定值的选取是离散的,我们可充分利用计算机的数值计算能力,用格种方法搜索最优值,其中虎克—吉福斯直接搜索法效果最好。
零件的参数设计.pdf (362.12 KB)零件参数设计的数学模型黄杲,陈旭东,邵伟本文建立了一个关于零件参数设计的数学模型,本文首先利用概率的理论,假设各零件产品的参数服务从正态分布,推出粒子分离器某参数(y)偏差的分布函数,进而可得一批产品总费用的目标函数,运用龙贝格数值积分将其转化为计算机可求值的函数,然后运用网格搜索法和蒙特卡罗法求出目标函数的全局最优解。
零件参数设计的数学模型.pdf (309.51 KB)零件的参数设计何华海,李江滔,束礼宝本文对零件参数设计问题提出了有效的算法, 零件参数设计可以归结为在一定约束条件下求总费用(成本和质量损失的总和)最小的一个非线性规划问题,我们采用分两步走的策略来简化问题,即首先选定零件参数的标定值,再在此基础上选取零件容差等级。
设计的总费用是由y的具体分布所决定的,我们采用了两种方法来计算y的概率分布:一种是用蒙特卡罗方法来模拟;另一种是将y的经验公式作线性近似,得到y近似服从正态分布,我们又引入了函数E(y-1.5)~2,以此作为新的目标函数对问题进行简化,对模型的求解,我们采用了梯度法来搜索目标函数在限定区域内的最优解,得到相应的总费用(单件产品)为 430元,远低于原设计方案的3150元。
通过检验,我们发现通过线性近似得到y服从正态分布的结论是基本可靠的,分两步走策略也是合理、有效的,最后我们还讨论了当质量损失函数为连续(特例为抛物线)时的情形。
零件的参数设计(1).pdf (333.62 KB)零件参数设计的动态规划模型高洁,郭去疾,康俊海对于本零件参数设计问题,我们建立一个动态规划模型,分阶段以不同的目标搜索求优。
零件的参数设计

零件的参数设计一、模型假设1.零件参数1x ,2x ,...,n x 为相互独立的随机变量,期望值和均方差分别记作0i x 和i σ(i =1,2,...,n )。
绝对容差i 记作3ir =i σ,相对容差记作i i i r t x =,()12,,...,n t t t t =2.产品参数y 由1x ,2x ,...n x 决定,记作()12,,...,n f x x x y=。
由于ix 偏离0i x 很小,可在0x 10200(,,...,)n x x x处对f做Taylor 展开,并略去二阶及二阶以上诸项,有001()ni i i i f x d x x =-∑y=()+0i x i fd x =∂=∂于是随机变量y 的期望值为0()Ey f x =,方差2221nyi i i d σσ==∑2011()9ni i i i d x t ==∑ 3. 由于y 偏离目标值0y 造成的(单件产品)质量损失记作L (y ),由题目所给数据可设L (y )与20()y y -成正比。
即L (y )20()k y y =-,且可得k =310/20.1510=。
4. 成批生产,平均每件产品的损失为0(,)Q x t E =L (y )20()kE y y =- ={}22002k Ey y Ey y -+{}222200()()2k Ey Ey Ey y Ey y =-+-+{}20()k Dy Ey y =+-{}220()y k Ey y σ=-+[]()2200011()9ni i i i k f x y k d x t ==-+∑5. 单件产品的零件成本仅取决于容差(等级)i t ,记作()i i c t 。
于是零件总成本为1()()ni i i c t c t ==∑。
6. 综合考虑y 偏离0y 造成的损失和零件成本,将本问题的目标函数定为成比生产平均每件产品的总费用00(,)(,)()Z z t Q x t c t =+。
Geomagic Studio 12参数化曲面设计案例之机械零件

Geomagic Studio 12参数化曲面设计案例之机械零件Geomagic Studio 12.0参数化曲面模块擅长设计一些规则的机械零件,而不能设计由非倒圆的连续曲面构成的零件,因为没法处理曲面连续问题,不能设置曲面之间的相切连续与曲率连续,曲面之间的衔接只能使用倒圆处理。
以一标准零件为例,介绍Geomagic Studio 12参数化曲面模块的设计流程。
与精确曲面模块相同,网格数据不能有破洞,不能有锯齿的边界,因为设计出的曲面与stl数据会基本一致。
图 1 标准件(尺寸200mm×100mm×35mm)参数化曲面设计流程:探测区域(编辑轮廓线)——区域分类(编辑区域)——拟合曲面(编辑曲面、约束曲面)——拟合连接(分类连接)——裁剪缝合曲面图2 标准件STL数据详细步骤:1.探测轮廓实际就是拆面的过程,UG,PORE,CATIA的逆向设计都是手动拆面,每个设计师设计同一零件拆面的思路可能都一样,杰魔的拆面是根据零件的曲率拆分,自动计算其轮廓,生成轮廓线。
图3 探测轮廓 图4 提取轮廓线轮廓探测轮廓,抽取曲线以后,还需要对曲线进行编辑,补充或删除曲线,光顺曲线。
2.区域分类通过了探测区域,系统会自动拆面,不同的曲面类型赋予不同的颜色,例如平面为绿色,圆柱为黄色,拉伸为桔黄色等。
当然系统自动赋予的曲面类型不一定是我们需要的,因此当系统将一个拉伸面识别为一个自由曲面的时候,需要我们手动去改变该曲面的类型,这里我们把该曲曲由粉红色自由曲面修改为橘红色拉伸曲面。
要识别曲面是什么类型,需要我们有一定的曲面基础知识,还需要猜测设计者的设计意图。
杰魔里面的曲面可分为平面、圆柱、圆锥、拉伸、拉伸拔模、旋转、球、扫略、放样、自由形态。
图5 曲面分类 图6 修改错误的曲面类型3.拟合曲面修改曲面类型以后,便可以拟合主曲面,ctrl+A选取全部曲面,应用确定后还需要编辑曲面,修改圆柱直径,根据点云自动拟合的圆柱,直径数值一般不是相对整的数,如5.012mm,我们最初在设计的时候,不会出现这么多位的小数的,产生的这种误差来源于零件的加工误差以及点云拟合误差,我们可以根据实际情况保留小数点后1位的数值或直接取整。
零件参数设计的数学模型

具体计算程序的流程图如下: 1:固定一组容差(Yi)等级,用7个for循环列出可行域内的xi; 2: 利用软件现成求导函数,求出y在这一组xi下,对xi求偏导的值 g(xi)。
3: 偏导f(xi)与三分之一容差1/3*Yi对应相乘,再求和,得到 y 4: 带入目标函数,求出W. 5: 重复循环,不断比较W,待循环完,得出一优W和xi; 6: 在较优xi基础上,改变Yi,经过循环迭代得出最优值。 当然,这样仍较复杂,我们可队程序作部分优化,如必要的判断 语句提早提前,以减少循环次数和计算量。 经过计算得出下列一组最优值: p1=16.52%,p2=0.01% X T =(0.075,0,375,0.125,0.113,1.1716,20,0.5725) GT =[B,B,B,C,C,B,B] W=42.12万元
由以上可知y由Xi的标定值和容差两方面决定,在此我们可估计 y~N( y x , i ),为更确认一些我们选取1000多个随机点来作出y的直方 图,来观察y的分布:
结合题意我们建立目标函数:
产品总费用=零件总成本+次品损失费+ 废品损失费 即 7 min w Ci 1000* p1 9000* p2
标定植取值范围
X1 X2 X3 X4 X5 X6
[0.075,0.125] [0.225,0.375] [0.075,0.125] [0.075,0.125] [1.125,1.875] [12,20]
x7
[0.5625,0.935]
C 等 / 20 20 50 50 10 /
B等
25 50 50 100 / 25 25
问题分析
要求的问题是使总费用最低,而总费用包括各 零件成本及次,废品损失费,综合考虑两种问 题可归纳为总费用的非线形优化问题。 由于待优化的目标函数复杂,无法利用其解析 性求最优解,故可考虑用直接全局搜索法或随 机试验点法. 从生产实际考虑,本问题对解的精确度要求很 高,但是对求解的实时性无明确要求,我们认为, 只要求解时间不是太长,都是可以接受的.
零件的参数设计

零件的参数设计摘要对于原设计:在各参数标定值范围以及容差等级确定的情况下;然后根据各个参数的分布matlab中normrnd函数可以取出正态分布的随机数据,每个零件随机产生1000个实际值,代入公式算出每一个产品的y值,根据其与目标值的关系判断损失费用。
根据matlab 程序可以得出总的成本为:3028000元对于改进后的设计:类似与原设计的思想,可以直接求解出题目的答案根据模型二的求解;可以得到的答案为:同时可以得到最小成本:426000元;前后可以节省的成本为:2602000元问题重述一件产品由若干零件组装而成,标志产品性能的某个参数取决于这些零件的参数。
零件参数包括标定值和容差两部分。
进行成批生产时,标定值表示一批零件该参数的平均值,容差则给出了参数偏离其标定值的容许范围。
若将零件参数视为随机变量,则标定值代表期望值,在生产部门无特殊要求时,容差通常规定为均方差的3倍。
零件参数的设计,就是要确定其标定值和容差。
这时要考虑两方面因素:一是当各零件组装成产品时,如果产品参数偏离预先设定的目标值,就会造成质量损失,偏离越大,损失越大;二是零件容差的大小决定了其制造成本,容差设计得越小,成本越高。
粒子分离器某参数(记作y )由7个零件的参数(记作x 1,x 2,...,x 7)决定,经验公式为:7616.1242356.02485.01235136.0162.2142.174x x x x x x x x x x x y ⎪⎪⎭⎫ ⎝⎛⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛--⨯⎪⎪⎭⎫ ⎝⎛-⨯⎪⎪⎭⎫ ⎝⎛⨯=-y 的目标值(记作y 0)为1.50。
当y 偏离y 0±0.1时,产品为次品,质量损失为1,000元;当y 偏离y 0±0.3时,产品为废品,损失为9,000元。
零件参数的标定值有一定的容许范围;容差分为A、B、C三个等级,用与标定值的相对值表示,A等为%1±,B等为%5±,C等为%10±。
CAD中的零件参数化设计与批量生成方法

CAD中的零件参数化设计与批量生成方法CAD(Computer-Aided Design)是一种广泛应用于工业设计和工程领域的计算机辅助设计软件。
它通过数字化手段帮助设计师创建、修改和分析各种产品的二维和三维模型。
在设计过程中,参数化设计和批量生成是提高效率和减少工作量的关键方法。
参数化设计是指在CAD软件中使用参数和表达式来定义和控制模型的尺寸、形状和位置。
通过定义参数,设计师可以在任何时候修改模型的尺寸和参数,而不必重新建模或修改复杂的几何构造。
这种灵活性极大地提高了设计师的工作效率。
在CAD软件中,常见的参数化设计方法有两种:直接编辑参数和使用关系创建参数。
直接编辑参数是最简单的方法之一。
设计师可以通过选择和编辑模型的特定尺寸来修改其参数。
例如,设计师可以选择一个线段的长度并将其修改为特定的数值。
这种方法适用于简单的模型或需要快速调整的设计。
但对于较为复杂的模型,这种方法不够灵活和高效。
与直接编辑参数相比,使用关系创建参数可以更灵活地定义模型的参数。
关系是指模型中的几何和尺寸之间的依赖关系。
通过使用关系,设计师可以建立一系列数学公式和条件来定义模型的参数。
这些公式可以基于几何特性、尺寸关系和设计规则等。
例如,对于一个圆,设计师可以定义其直径和半径之间的关系,如直径=2*半径。
当设计师修改半径时,直径会自动更新。
批量生成是另一个使用CAD软件的关键技巧。
它允许设计师快速创建多个相似的模型,而不必一个一个手动操作。
批量生成适用于需要大量相同或类似模型的场景,如零件的多种规格、产品的多个尺寸和构件的批量生产等。
在CAD软件中,常见的批量生成方法有复制、阵列和宏命令。
复制是最基本和常用的方法之一。
设计师可以选择一个模型并进行复制操作,然后将复制的模型放置到新的位置。
阵列是指将一个模型按照特定的规律和方向进行复制生成。
通过定义阵列的数量、间距和方向,设计师可以快速创建一系列相同的模型。
宏命令是指录制和保存一系列CAD操作的过程,并在需要时重复执行。
SolidWorks零件设计表运用参数化设计
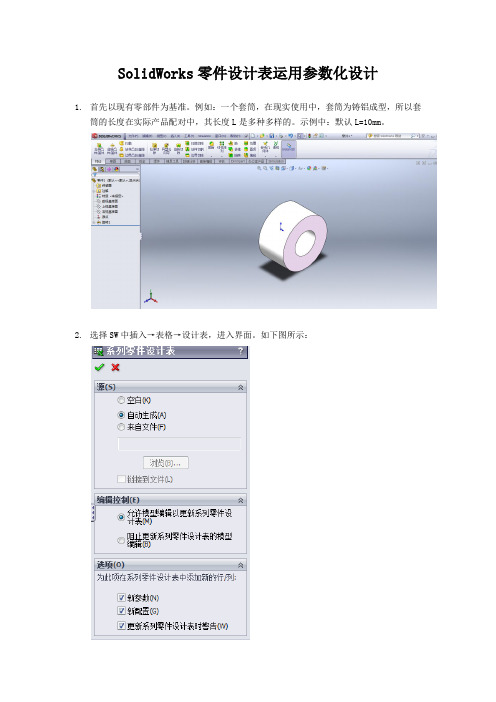
SolidWorks零件设计表运用参数化设计1.首先以现有零部件为基准。
例如:一个套筒,在现实使用中,套筒为铸铝成型,所以套筒的长度在实际产品配对中,其长度L是多种多样的。
示例中:默认L=10mm。
2.选择SW中插入→表格→设计表,进入界面。
如下图所示:3.默认选择自动生成,选择所需草图特征,确认后进入设计表格。
如下图所示:4.选中表格中“普通”右击选择“设置单元格格式”选择“常规”进行确认,将表格中:“普通”转换零件尺寸数值。
(如同Excel表格操作一样)5.在本示例中,我们所关心的只是套筒L长度,所以可以把表格中后面三项“套筒的内径”、“套筒的外径”以及“旋转生成所需的中心轴”草图特征删除。
同时为便于查看表格,可以对表格进行优化(根据个人习惯,无非就是单元格的插入、删除、输入而已)。
如下图所示:6.依次在表格中输入我们所需要的参数值,示例中,我们取套筒五种型号,从P01到P05,长度依次递增10mm,(注:在输入新的L值时,我们输入的是数字但有可能会显示出文字“普通”,只需参照步骤4设置单元格格式即可调节成数值)如下图:7.到此为止,我们设计表中的参数已设置好,只需在SW界面中,鼠标点击设计表以外的操作区域,设计表将会自动保存。
弹出如下对话框,点击确定即可!8.回到SW界面设计树中,选择“配置”界面,如下图所示。
可以清楚的看到我们刚刚在设计表中所输入的参数值。
可以把不需要的配置删除(例如:默认这个配置),保留我们所需。
9. 点击我们所做的配置,可以相应得到套筒的不同规格长度L 。
如下图所示:1)P01,L=10mm2)P02,L=20mm3)P03,L=30mm小结:通过SW中的设计表,我们可以很好的实现产品参数化设计,以本示例中,我们只是单一的配置了套筒的长度L值,其实在设计表中,我们还可以对套筒的内径、外径同时进行参数配置。
说直白点,其实SW设计表就是一个简单的Office 工具Excel输入的过程,只需明白控制表格中零件草图特征所对应的含义,找对草图特征,表格输入相应参数然后在实际使用过程中调用出来,就OK了!以上只是个人在实际工作中SolidWorks2011所运用的内容,现阶段SW 2015版本都发布了,也许相应的内容会更加强大,在产品参数化领域有着更好进步与发展!此文档只为分享一些心得,如有雷同敬请谅解,大家共同学习与进步!。
CAD中的参数化零件设计指南

CAD中的参数化零件设计指南参数化零件设计是现代CAD软件提供的一项重要功能,它允许工程师根据需要快速创建和修改设计。
参数化设计背后的核心理念是通过定义和控制变量,使设计可自由修改,为工程师提供更高的灵活性和效率。
本文将介绍CAD中参数化零件设计的基本概念和一些使用技巧。
首先,我们需要了解CAD软件中的参数化设计基本术语。
参数通常指的是数字变量或公式,它们可以代表尺寸、角度、曲率等与设计相关的要素。
每个参数都可以在设计过程中进行修改,从而影响整个设计。
参数可以用于创建特征、关系,以及控制约束条件。
在CAD软件中,我们可以使用参数化设计来创建二维和三维对象。
对于二维设计,我们可以定义线段的长度、圆的半径、椭圆的轴长度等参数。
通过修改这些参数,我们可以轻松地改变图形形状和尺寸。
对于三维设计,我们可以定义立方体的长度、球体的半径、圆柱体的高度等参数。
同样地,通过修改这些参数,我们能够快速调整设计的外观和尺寸。
在设计参数时,我们需要考虑合理的命名规范和逻辑结构。
为了方便日后的修改与维护,我们可以给每个参数取一个有意义的名称,例如“length”代表长度、“width”代表宽度。
此外,我们还可以使用表达式和公式来定义参数之间的关系。
例如,我们可以定义一个“diameter”的表达式为“2 * radius”,这样当我们修改“radius”参数时,“diameter”参数也会相应更新。
参数化设计还允许我们创建关系和约束条件,以确保设计的准确性和一致性。
关系是指不同参数之间的数学关系,例如等于、大于、小于等等。
通过设定关系,我们可以保证设计的相互依赖性。
约束条件是指限制设计参数取值的规则,例如最小值、最大值、等式或不等式。
通过定义约束条件,我们可以防止设计出现无效或不实际的结果。
在进行参数化设计时,我们还可以使用变量表和参数数值化进行管理。
变量表是一个显示了所有参数和其当前数值的列表。
通过查看变量表,我们可以一目了然地了解设计的参数设置情况,并进行修改。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C的内部,则C的体积约为D的体积乘以
NC/N 2021/2/2
12
✓ 最优化计算Monte Carlo法 求下列函数的最大值:
f(x ) ( 1 x 3 )s in (3 x ), 2 x 2
2021/2/2
13
✓median: 返回中值; ✓std: 返回标准差
✓cov: 返回协方差矩阵; ✓ corrcoef: 返回相关系数矩阵
✓sum: 各元素的和;
✓ cumsum: 元素累计和
✓prod: 各元素的积; ✓ cumprod: 元素累积积
2021/2/2
8
✓ 直方图 ✓ Bar(Y): 作向量Y的直方图 ✓ Bar(X, Y): 作向量Y相对于X的直方图 ✓ Hist(X, k): 将向量X中数据等矩分为k组,并作 出直方图,缺省k=10 ✓ [N, X]=hist(Y, k): 不作图,N返回各组数据个 数,X返回各组的中心位置
设是一个分布已知的随机变量,为了求取 = f()
的概率分布或数字特征,生成N个(N足够大)服从
的分布的随机数x1, x2, …, xN,令yi = f(xi), i=1,2,…,N, 那么
P (
A)
N ( yi
A) ;
N
E ( ) y 1 N
N
yi;
i 1
2021/2/2
D ( )
1 N 1
引例(零件参数设计)
产品性能的评价取决于产品包含零件 的某个参数。由标定值和容差两个 控制指标。
标定值:一批零件该参数的平均值 (期望值)
容差:参数偏离标定值的容许范围
(一般为均方差的3倍)
2021/2/2
2
粒子分离器某个参数(用y表示)由7个零 件的参数(用x1,x2,…,x7表示)决定,经
验公式为
容差 B B B C C B B
2021/2/2
11
✓ Monte Carlo法计算积分
使用随机模拟法可以求解一些复杂的非随机问
题。
使用随机模拟计算二重积分的原理:
假设C被包含在几何体D内,D的体积已知,若
在D内生成1个均匀分布的随机数,则该随机
数落在C中的概率应当是C的体积除以D的体
积。若一共生成N个随机数,其中有NC个在
✓ 随机数的生成
✓R=rand(m,n): 生成(0,1)上均匀分布的m行n列随机矩阵
✓R=randn(m,n):生成标准正态分布的m行n列随机矩阵
2021/2/2
9
✓ R=randperm(N): 生成1,2,…,N的一个随机排列
✓ R=unidrnd(N,m,n):生成1,2,…,N的等概率m行n列随机 矩阵
N
( yi
i 1
y )2
7
数据分析与随机数生成的MATLAB命 令
✓数据分析(注意对向量和矩阵的不同运算方式)
✓a=min(X)(max(X)): 返回向量X的最小(大)向量
✓X=min(A)(max(A)): 返回矩阵A每列最小(大)元素构成 的行向量
✓mean(X),mean(A): 返回向量X的平均值(矩阵A的列向量 的均值构成的向量)
0.85yFra bibliotek174
.42
x 1
x 5
x 2
x 3
x 1
3
1
2.62 1
0.36
x 4
x 2
0.56
2
x 4
x 2
1.16
xx 67
2021/2/2
3
评价标准:
(1)设定y的目标值(记为y0)为1.50; (2)当y偏离目标值0.1时,产品为次品,质
量损失1000元
(3)当y偏离目标值0.3时,产品为废品,质
mu为均值向量,sigma为n阶协方差矩阵(必须正定),
R为m行n列矩阵,每行代表一个随机数
2021/2/2
10
实验例题
零件参数设计 计算下述情况的零件每件产品的平均损失
容差分为A,B,C三个等级,用与标定值的相对值 表示, A等为1%, B等为5%, C等为15%
x1 x2 x3 x4 x5 x6 x7 标定值 0.1 0.3 0.1 0.1 1.5 16 0.75
量损失9000元
要求:
对于给定的零件参数标定值和容差,计算产 品的损失,同时进行零件参数最优化设计。
2021/2/2
4
概率论知识复习
✓ 事件A发生的可能性称为事件A的概率。
✓ 随机现象中,取值不确定的变量称为随 机变量,描述随机变量取各种值的概率 函数称为概率分布。
✓ 数学期望(均值):描述随机变量的平 均值
✓ 方差,标准差(均方差):描述随机变 量分布的差异程度。
2021/2/2
5
概率分布 ✓ 0-1分布 ✓ 二项分布 ✓ 均匀分布 ✓ 正态分布(标准正态分布)
2021/2/2
6
随机模拟原理
大数定理表明,当k 时,样本平均值趋向于总体 平均值,它是数理统计参数估计的理论基础,也 是数字特征随机模拟的理论根据。
✓ R=unifrnd(a,b,m,n): 生成[a,b]区间上的均匀分布的m行 n列矩阵
✓ R=normrnd(mu,sigma,m,n): 生成均值为mu,均方差为 sigma的m行n列随机矩阵
✓ R=binornd(k,p,m,n): 生成参数为k,p的m×n列二项分布 随机矩阵
✓ R=mvnrnd(mu,sigma,m): 生成n维正态分布数据,其中
