1.6 几何光学 薄透镜
薄透镜成像实验报告

薄透镜成像实验报告一、实验目的1、加深对薄透镜成像规律的理解。
2、学会测量薄透镜的焦距。
3、掌握光路的调节方法,提高实验操作能力。
二、实验原理1、薄透镜成像公式当光线通过薄透镜时,会发生折射现象。
根据几何光学的原理,可以得到薄透镜成像公式:1/u + 1/v = 1/f ,其中 u 是物距(物体到透镜的距离),v 是像距(像到透镜的距离),f 是透镜的焦距。
2、凸透镜成像规律当物距 u 大于 2 倍焦距 2f 时,成倒立、缩小的实像;当物距 u 等于2 倍焦距 2f 时,成倒立、等大的实像;当物距 2f > u > f 时,成倒立、放大的实像;当物距 u < f 时,成正立、放大的虚像。
3、凹透镜成像规律凹透镜始终成正立、缩小的虚像。
三、实验仪器光具座、凸透镜、凹透镜、蜡烛、光屏、直尺等。
四、实验步骤1、仪器安装将蜡烛、凸透镜、光屏依次安装在光具座上,使它们的中心大致在同一高度。
2、测量凸透镜的焦距(1)将蜡烛放在距离凸透镜较远的位置,移动光屏,直到光屏上出现清晰的蜡烛火焰的像。
记录此时的物距 u 和像距 v 。
(2)根据薄透镜成像公式 1/u + 1/v = 1/f ,计算出凸透镜的焦距f 。
3、探究凸透镜成像规律(1)将蜡烛放在大于 2 倍焦距的位置,移动光屏,观察并记录像的性质(倒立、缩小、实像)、像距和物距。
(2)将蜡烛放在 2 倍焦距的位置,重复上述操作。
(3)将蜡烛放在 2 倍焦距与 1 倍焦距之间的位置,再次重复上述操作。
(4)将蜡烛放在小于 1 倍焦距的位置,观察像的情况。
4、测量凹透镜的焦距(1)将凸透镜换成凹透镜,将蜡烛放在较近的位置,移动光屏,观察像的情况。
(2)在光具座上插入一个已知焦距的凸透镜,与凹透镜组成透镜组,移动光屏,直到出现清晰的像。
记录此时的物距 u 和像距 v 。
(3)根据成像公式计算出凹透镜的焦距。
5、整理仪器实验结束后,整理好实验仪器,保持实验台整洁。
五、实验数据及处理1、凸透镜焦距的测量实验次数物距 u(cm)像距 v(cm)焦距 f(cm)1 _____ _____ _____2 _____ _____ _____3 _____ _____ _____计算出三次测量的焦距平均值。
薄透镜 厚透镜

1.薄透镜的密接组合
n1
O
L1 L2
n1
密接条件d≈0,
(u = u1 , v = v2 )
u1
v2
d u2 = - v1
对L1
11 1 u1 v1 f1
对L2
11 1 u2 v2 f2
11 1 1 u v f1 f2
11 1 1 1 u v f1 f2 f
)
1 r1
1 r2
透镜置于空气中
1 f
n
1
1 r1
1 r2
透镜两侧介质不同
n1
n2
n
n1 n n2
f1 f2
r1
r2
10.2.3 薄透镜组合
如何求物像关系? 逐次成像法
1.以薄透镜为基本单元,用薄透镜公式列 方程;
2.依透镜顺序逐次成像; 注意:
前一透镜之像( vi)为后一透镜之物 ( ui+1 ), ui+1=d- vi 。
①在透镜前加一光栏. ②在会聚透镜后放置发散透镜
2.色像差
原因:介质对不同波长的光线有不同的折 射率.
纠正的方法:用不同的会聚透镜和发散透 镜组合起来.
(a)
(b)
色像差及其矫正
小结
1.薄透镜成像公式:
1 u
1 v
n
n0 n0
1 r1
1 r2
高斯形式: 1 1 1 uv f
例: 已知f1=20cm 、 f2=-40cm, d=40cm,u=30cm 求:最后成像的位置。 解: 2.作图法
v2
v1
10.3 厚透镜(共轴球面系统的三对基点)
1.两焦点、两主点、两节点 (1)两焦点
1-06 薄透镜
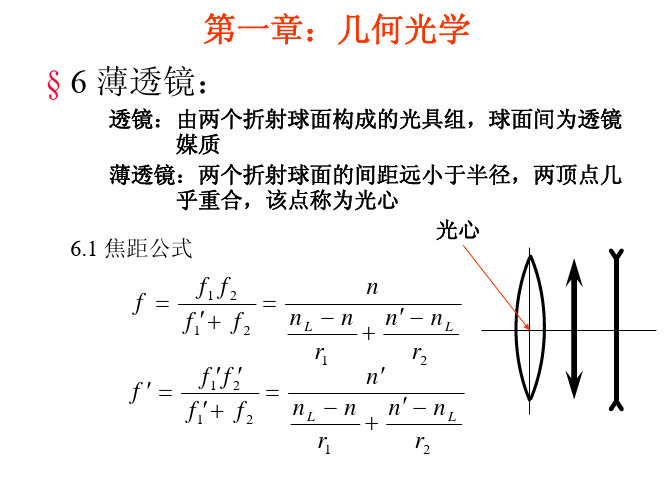
第一章:几何光学 § 6 薄透镜:
6.1 焦距公式 有 若
f n = f ′ n′
n′ = n = 1 f = f′= 1
摩镜者公式 1 1 ( n L − 1)( + ) r1 r2 n′ n nL − n n′ − nL 光焦度 P = = = P1 + P2 = + f′ f r1 r2 正透镜、会聚透镜、凸透镜:f, f’>0, 1 r1 > 1 r2 负透镜、发射透镜、凹透镜:f, f’<0, 1 r1 < 1 r2
第一章:几何光学 § 6 薄透镜:
6.2 成像公式 高斯公式 牛顿公式 符号规则
f′ f + =1 s′ s x x ′ = ff ′
F′
x
o
x′
F
6.3 密接透镜组
P = P1 + P2 1 1 1 = + f f1 f2
第一章:几何光学 § 6 薄透镜:
6.4 焦面 物方焦面:通过物方焦点垂直于光轴的平面,又称第 一焦面、前焦面,记为F 。物方焦面上的点成 像于像方轴外无穷远处(与光轴成一定角度 的平行光束) 像方焦面:通过像方焦点垂直于光轴的平面,又称第 二焦面、后焦面,记为F’ 。物方轴外无穷远 处的物点(与光轴成一定角度的平行光束)成 像于像方焦面上 F’ F
6.6 透镜组成像(逐次成像)
作业
p.69: 2, 3, 8, 9, 11
y
o F
F′
y′
6.6 透镜组成像(逐次成像)
i) 通过物方焦点的光线折射后平行于主轴。
y
o F
ቤተ መጻሕፍቲ ባይዱ
F′
y′
y
o F
F′
1.6薄透镜解读

2019/2/19
f f ',则有:
s' V s
12
6.3 密接薄透镜组
透镜组合的最简单情形是两个薄透镜紧密 接触在一起,成为复合透镜。 密接薄透镜组的焦距:
1 1 1 s '1 s1 f1
1 1 1 s' 2 s 2 f2
,
s 2 s'1 , s s1
1 1 1 1 1 s s' f1 f 2 f
nL
n
P
s '1
P1 P2
d
s2
a、焦距公式的推导(逐次成像)
s2 d s '1
f '1 f1 1 s'1 s1
s '1
s
s1 s '
s '2
过度公式
f '2 f 2 1 s' 2 s 2
物像距公式
消去S1’和S2,可得:
f '1 f ' 2 f1 f 2 f '1 f 2 s' s
2 1 2
F
F
1
3
L
O
Q
3
9
L
Q
3
L
2
Q
2
1
3
F
Q
O
F
3
3
F
Q
1
O
F
1
16
(2)一般光线作图法:利用一条特殊光线和焦面 性质,找到任意入射光线的出射共轭线。 作 图 法 求 出 射 共 轭 线
2019/2/19 17
6.6共轴薄透镜组成像
f f ' 1 nL 1 1 ( 1)( ) n r1 r2
大学物理 几何光学 薄透镜.ppt
n0 ni 1
i
ff
ni
(nL
1 1)( 1
r1
1) r2
O i
Qp
nL
d 0
d
p1 Q2 Q1 p2
薄透镜成像公式
1 1 1 p p f
➢ 符号规则:以薄透镜光心为分界点,入射光线方向 为正向,如入射光线自左向右,则当物点、像点、焦点 和薄透镜两面的曲率中心在光心右侧时,物距、像距、 焦距和曲率半径均为正;反之,在左侧则为负 .
r1 0, r2 0 r1 r2
r2 r1 0
r1 0, r2 0 r2 0 r1
r1 0,r2 0 r1 r2
➢ 凹、凸透镜成像图
1
1
h0
hi
2
F
p
2
1
h0
2 3
f
F
F
hi 3
P
p 1 2
➢ 焦平面 过焦点且垂直于主
光轴的平面,平行光线 (近轴)会聚于焦平面.
焦平面
解:第一种情况时有
第二种情况时有
11 1 p1 p1 f
11 1 p2 p2 f
p1 hi 1 p1 h0 2
p2 1 p2
得 p1 3 f
且 p2 p1 100 3 f 100 得 f 100mm
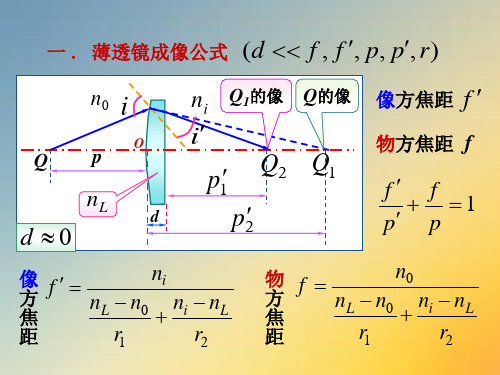
一 . 薄透镜成像公式 (d f , f , p, p, r)
n0 i
O
Qp
nL
d
d 0
ni Q1的像 Q的像
i
p1 Q2 Q1 p2
像方焦距 f
物方焦距 f
f f 1 p p
像 方 焦
f
ni nL n0 ni
nL
《光学教程》第五版 姚启钧 第一章 几何光学

B'
利用 物方焦平面 作图 光心
利用 物方焦点 作图 象方焦平面
利用 象方焦平面 作图 光心
四、 物像之间的等光程性
物点和像点之间各光线的光程相等。
F
F'
例1-3. p36 已知薄透镜 f ' 12cm, 问:
(1) 球面完全对称,折射率n=1.5,求曲率半径R;
(2) n1=4/3, n2=1 r2=R, f ' 12cm求, 曲率半径r1。
A ╭r φ-li''u'╭ n' P′
P -p
O
-y'
p'
笛 卡 儿 符 号 法
则
(3) 角度(以锐角量度)
{ 以主轴转向考虑的光线 顺时针为正 逆时针为负
(4) 全正图形 图中标记的是线段或角度的绝对值(如上)
二、傍轴条件下单球面折射的物象公式
在下图中,当u,u’ 很小时, 称为傍轴条件
n -i
n
P
F’
P’
x'
-p’
-f ’ -p
-x
n′
F
f
六、 傍轴物点成像的放大率 亥姆霍兹-拉格朗日定理
1. 横向放大率
y pi y' p'i'
ni n'i'
n
y -x • P F•
-f i
-p
y' y
n p' n' p
利用-p=-(f+x),p'=(f '+x')
及牛顿公式,得
f x'
第一章几何光学基础11几何光学基本规律12光程费马原理13棱镜和最小偏向角全内反射和光学纤维14同心光束和象散光束物和象15单球面上的傍轴成象内容16薄透镜的成象规律17理想光学系统的基点和基面18共轴球面系统组合的理论19空气中的厚透镜薄透镜组110一般理想光具组的作图求像法和物像公式11几何光学的基本原理11光源
1.7 薄透镜

P
F
F
P
由此可得出轴上物点作图求像法的特征光线: (1)与主轴成一定倾角的光线,折射后通过(或反 向延长线通过)像方焦平面与入射光线平行且通过光 心的光线的交点。
(2)通过(或延长线通过)物方焦平面上一点的光线, 折射后平行于物方焦平面上的该点与光心的连线。
物理科学与信息工程学院 21
例图1
对薄透镜,s1 = s2 ,s2 = s, s1 =s , y1 = y2
y1 ' n1s1 ' 1 y ns1 y ' ns2 ' 2 y2 n2 s2
或
1 2
n1s ' n2 s
f s' f 's
物理科学与信息工程学院 16
若n1=n2 ,则 若采用牛顿公式:
物理科学与信息工程学院
7
当像点在无穷远处时,即
f s
s
n1
n n1 n2 n r1 r2
此时,主轴上的物点即为透镜的物方焦点,由称 第一焦点,用F表示,透镜的光心到物方焦点的距 离既为物方焦距,也称第一焦距,用f表示。 所以,像方焦 距和物方焦距之 比为:
f n2 . f n1
物理科学与信息工程学院 12
Φ >0时,此系统是 会聚系统,此时f>0, F和F 为实焦点。
F
n1
n n2
F'
Φ <0时,此系统是 发散系统,此时f<0, F和F 为虚焦点。
F
n1
n n2
F
物理科学与信息工程学院 13
三、薄透镜成像的高斯公式和牛顿公式 将透镜的焦距公式带入透镜成像公式中,
薄透镜成像的几何光学规律及其傅里叶解释

数, 当不考虑孔径影响时, P (x, y) 恒取 1, 即认为透 径孔径为无限大。
(2. 8) 式就是透镜前物场与透镜后衍射场之间
的傅里叶变换关系的一般表达式, 当 d1 取为物距, d2 取为像距, (2. 8) 式反映的就是物场分布与像场 分布的关系。
3. 薄透镜成像的傅里叶分析与解释
2. 8 式反映了薄透镜成像的物场与像场间的一
如图 (2. 2) , P 点发出的球面波, 到达 P1 面上时
(点 x, y) , 振幅
U 1 (x, y) =
e ikd1 +
ik 2d1
(x2+
y2)
(2. 1)
这里, 表达式中略去了与 x, y 无关的因子A d1。
由于是薄透镜, 故认为光束到达 P2 面时高度不
变, 也在对应的点 (x, y) , 而 P2 面上的光场又可看成 由 P′点发出的球面波产生的, 故
ns11′′-
n1 s1
=
n1′- n1 r1
(1. 1)
ns22′′-
n2 s2
=
n2′- n2 r2
(1. 2)
由于 s1= s, s2′= s′, s1′= s2, n1′= n2= n0, n1= n,
n2′= n′, 故 1. 1 式和 1. 2 式经合并整理后有
ns′′-
n s
简单的形式
S1′-
1 S
=
1 f′
(1. 6)
对于有一定大小的物体, 经薄透镜成像后, 像的
大小发生了变化, 在理想情况下, 垂直主轴放置的大
小为 y 的线状物经透镜成像后, 像也为一垂直主轴
的 线状物, 大小为 y′, 则像的放大率可定义为 (横
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
d << r1 , r2 , | s |, | s ′ |
就是薄透镜,通常可以认为
通常情况下 n=n' ≈ 1
d =0
3
此时,两球面顶点重合,称为光心,记为O。
6.1 薄透镜的成像特性
回顾逐次成像法 ① 成像透镜由两个折射球面组成,透镜使光线经过了两个球 面的折射。 ② 可以用逐次成像法得到透镜的成像公式。 ③ 物Q经第一面折射成像Q'(应用物像关系可确定像)。 ④ Q'无论虚实,总是发出光线的,对第二面来说等效于物。 ⑤ Q'作为第二面的物,经第二面折射成像 像关系可确定像)。 ⑥ 反复应用上述方法,可得到最终的像。 (再次应用物
n f = = n L − n n ′ − nL Φ + r1 r2
f′= nL − n n′ − n L + r1 r2
n′
n
物方焦距
s=∞
n′
=
n′ Φ
像方焦距
n
nL
f
f′
8
6.1 薄透镜的成像特性
空气中的薄透镜
n = n′ = 1
1
磨镜者公式
f = f′=
1 1 (n L − 1)( − ) r1 r2
n L − n n′ − n L Φ= + r1 r2
薄透镜的光焦度,单位是屈光度(diopter,D),对于眼镜,度数为100Φ
6
6.1 薄透镜的成像特性
问题:厚透镜有“光焦度”的概念吗?
n
Q C2
Σ1 Σ 2 − r2 nL
O1 O
r1
n′
Q1′
O2 Q ′ C1
′ s2
s1
− s2
′ s1
d
r2 > 0 ⇒ f = f′<0 r1 < 0 r2 < 0 & r2 > r1 r < 0& r < r ⇒ f = f ′ > 0 2 1 2
f = f ′ > 0 ⇒ 正透镜
f = f ′ < 0 ⇒ 正透镜
13
从Fermat原理看,这也是很自然的结果。
6.1 薄透镜的成像特性
11
6.1 薄透镜的成像特性
正透镜与负透镜
① 焦距为正值的透镜是正透镜;焦距为负值的透镜是负透镜。 ② 正透镜的像方焦点在光线出射方;负透镜的像方焦点在光线入射 方。 ③ 正透镜使入射的平行光汇聚在像方焦点;负透镜使入射的平行光 发散,反向延长线通过像方焦点。 ④ 空气中,中间厚边缘薄的透镜是正透镜;中间薄边缘厚的透镜是 负透镜。
s = x+ f
s′ = x′ + f ′
xf ′ + ff ′ + x′f + f ′ f = x′x + x′f + xf ′ + f ′ f
牛顿公式的符号约定 (1)物点Q 在F 的左边时,x>0;反之,则 x<0。 (2)像点Q' 在F' 的左侧时,x'<0;反之,则 x'>0。
⇒
xx′ = ff ′
s
0 −a
s
0
a
正透镜
f =a
−a
0
a
负透镜
15
6.1 薄透镜的成像特性
薄透镜成像的横向放大率
(1) 总放大率为两次成像的放大率的乘积
n
s
第一次成像,V 1 是实物成像
nL
′ ns1 = (− ) nL s
n′
s′
s1′
nL s ′ = [− ] ′) n′( − s1
V = VV 1 2
(2) Lagrange-Helmhotz恒等式依然成立
从费马原理再看光学成像
• 证明空气中的正透镜必定是中间厚边缘薄;负透镜必定是中 间薄边缘厚 • 所谓正透镜,系指物方焦点在其光线入射方,而像方焦点在 其光线出射方 • 以平行光正入射证明
平行光自左侧入射,汇聚到正透镜右侧焦点 光线愈远离光轴,所经过距离愈长 为使光程相等,则远离光轴的光线,其在透镜中的距离必须较短 所以正透镜的形状,必须愈远离中心轴线,厚度愈薄 正透镜的形状,必定是中间厚边缘薄的结构 同理,负透镜的形状,必定是中间薄边缘厚的结构 光线在透镜中的光程+虚光线的虚光程=定值
n′ = 1
n =1
nL
f = f′
9
6.1 薄透镜的成像特性
Gauss物像公式 - 距离从光心算起
n
Σ1
nL
Σ2
n′
Q
d
′ s2
Q′ s2
Q1
s = s1
n′ n n L − n n′ − n L + = + s′ s r1 r2
nL − n n′ − nL + r1 r2 n′ f′= nL − n n′ − nL + r1 r2 f = n
34
12
6.1 薄透镜的成像特性
正透镜与负透镜
f = f′= 1 (n L − 1)( 1 1 − ) r1 r2
1 1 正透镜 > r1 r2
1 1 负透镜 < r1 r2
r2 < 0 ⇒ f = f′>0 r1 > 0 r2 > 0 & r2 > r1 r > 0&r < r ⇒ f = f ′ < 0 2 1 2
F'
F'
14
6.1 薄透镜的成像特性
o
结论:薄透镜的物 方和像方焦点永远 分处 于 透镜的两 侧 。 并且一般情况下两 个焦点不对称,即 焦距大小不相等。 只有当物像方介质 折射率相等时,透 镜的物像方焦距大 小才相等。
a 0 −a
s′
实 像 虚物 虚 像
−a a
s′
实 像 虚物 虚 像 实物
实物
F F’
o
19
6.3 焦平面
薄透镜的光学参数定义 物方焦平面 像方焦平面
F
F′
光轴
物方焦点
F
f
光心 O
像方焦点
f′
像方焦距
F′
O
物方焦距
特性:极薄的平行玻璃平 板,两侧折射率相等,通 过光心的光线方向不变
副光轴:通过光心的直线。 主光轴:光具组的光轴,简称主轴。
20
6.4 薄透镜作图法
三对共轭的特殊光线
F1
F1′
F2′
F2
28
6.5 透镜组成像
逐次成像法示例2:透镜1所成的像是透镜2的虚物
L1 F1 F2′ F1′
L2 F2
L1的实像,对于L2来说,是虚物
29
6.5 透镜组成像
另一种透镜组的作图解法
L1 F1
L2 F2
F2′ F1′
1. 直接利用第一镜的光线作图; 2. 利用第二镜的物的特殊光线作图。
F
F′
像方焦点
物方焦平面
像方焦平面
23
6.4 薄透镜作图法
正透镜作图法3
物方焦点
F
F ′ 像方焦点
物方焦平面
像方焦平面
24
6.4 薄透镜作图法
负透镜作图法1
像方焦点
F′
F
物方焦点
像方焦平面
物方焦平面
25
6.4 薄透镜作图法
负透镜作图法2
像方焦点
F′
F
物方焦点
像方焦平面
物方焦平面
26
6.4 薄透镜作图法
′ nL s′ ns1 = (− )( ) ′ nL s n′s1
第二次成像, V 2 是虚物成像
ns′ =− n′s
′nLu1 ′ = y ′n′u′ ynu = y1
16
6.1 薄透镜的成像特性
薄透镜的横向放大率
n
nL
n′
f
ns′ V =− n′s x′
F
x
′ F f′ s′
s
f n ′ fs = 用高斯公式表示: 利用 得到 V = − f ′ n′ ′ fs fs′ f ( x′ + f ′) 用牛顿公式表示 V = − =− × 利用 xf = x′f ′ ′ fs f′ x+ f
33
习题
p.70: 2, 3, 8, 11
补充题: 在科研实验中,经常需要将入射的平行光改变为较粗或教细的平行光,这 被称为无焦系统。例如,将激光发出的光束扩展为较宽的光束,这种系统被称 为扩束系统。请根据理想光具组的计算方法,采用两个焦距分别为f1' 和f2' 的薄 透镜,设计一个无焦系统,并给出其横向放大率(光束直径)的分析。
F 物方焦平面
F' 像方焦平面
平行于光轴的入射光线←→经过像方焦点的光线 经过物方焦点的光线←→平行于光轴的像方光线 经过透镜光心的入射光线←→经过透镜光心的像方光线
21
6.4 薄透镜作图法
正透镜作图法1
物方焦点
F
F ′ 像方焦点
物方焦平面
像方焦平面
22
6.4 薄透镜作图法
正透镜作图法2
物方焦点
第一章 几何光学
第六节 薄透镜
1
第六节 薄透镜
6.1 薄透镜的成像特性 6.2 密接薄透镜组 6.3 焦平面 6.4 薄透镜作图法 6.5 透镜组成像
2
6.1 薄透镜的成像特性
透镜 透镜:由两个折射球面构成的 光具组,球面间为透镜媒质。 薄透镜 由两个折射球面组成,过两 球面圆心的直线为光轴,顶 点间距 d。如果满足:
f x′ 得到 V = − = − x f′
若n=n',则
