北京市朝阳2014届高三二模理科数学试卷(带解析)
高考数学 2014-2015朝阳高三二模理答案

北京市朝阳区高三年级第二次综合练习数学试卷答案(理工类)2015.5一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.(15)(本小题满分13分)解:(Ⅰ)在ACDD中, 因为cos14CAD?,所以sin14CAD?,由正弦定理得,sin sinAC CDADC CAD=行,即2sinsin14CD ADCACCAD´仔===Ð……………………………………6分(Ⅱ)在ACDD中, 由余弦定理得,22422cos120AC AD AD=+-⨯⨯o,整理得22240AD AD+-=,解得4AD=(舍负).过点D作DE AB⊥于E,则DE为梯形ABCD的高.因为AB P CD,120ADC?o,所以60BAD?o.在直角ADED中,sin60DE AD==o即梯形ABCD的高为……………………………………………………13分(16)(本小题满分13分) 解:(Ⅰ)由题意可得:4分(Ⅱ)记事件M :被抽取的,,A B C 三种答卷中分别再各任取1份,这3份答卷恰有1份得优,可知只能C 题答卷为优.依题意131()1355P M =⨯⨯=.………………………………………………8分 (Ⅲ)由题意可知,B 题答卷得优的概率是13.显然被抽取的B 题的答卷中得优的份数X的可能取值为0,1,2,3,4,5,且X :1(5,)3B .00551232(0)()()33243P X C ===;11451280(1)()()33243P X C ===; 22351280(2)()()33243P X C ===;33251240(3)()()33243P X C ===;44151210(4)()()33243P X C ===;5505121(5)()()33243P X C ===. 随机变量X 的分布列为所以0123452432432432432432433EX =⨯+⨯+⨯+⨯+⨯+⨯=.…………………………………………………………13分(17)(本小题满分14分)证明:(Ⅰ)由已知得90FAB ∠=︒,所以FA AB ⊥,因为平面ABEF ⊥平面ABCD ,且平面ABEF I 平面ABCD AB =,所以FA⊥平面ABCD ,由于BC ⊂平面ABCD ,所以FA BC ⊥.………………………………………………………………………4分 (Ⅱ)由(Ⅰ)知FA ⊥平面ABCD ,所以,FA AB FA AD ⊥⊥, 由已知DA AB ⊥,所以,,AD AB AF 两两垂直.以A 为原点建立空间直角坐标系(如图). 因为112AD DC AB ===, 则(0,2,0),(1,1,0),(1,0,0),(0,1,1)B C D E ,所以(1,1,0),(0,1,1)BC BE =-=-u u u r u u u r,设平面BCE 的一个法向量为()x,y,z n =.所以0,0,BC BE ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u rn n即0,0.x y y z -=⎧⎨-+=⎩令1x =,则(1,1,1)n =.设直线BD 和平面BCE 所成角为θ,因为(1,2,0)BD =-u u u r,所以sin cos ,BD BD BDθ⋅=〈〉===⋅u u u r u u u r u u u r n n n .所以直线BD 和平面BCE 9分 (Ⅲ)在A 为原点的空间直角坐标系A xyz -中,AD HC BENM(0,0,0)A ,(1,0,0)D ,(0,0,1)F ,(0,2,0)B ,H 1(,1,0)2.设()01DM k k DF =<?, 即DM k DF =uuu u r uuu r .(),0,DM k k =-uuu u r,则(1,0,)M k k -, 1(,1,)2MH k k =--uuu r ,(1,0,1)FD =-u u u r .若FD ^平面MNH ,则FD MH ^.即0FD MH ?uu u r uuu r. 102k k -+=,解得14k =. 则11(,1,)44MH =--uuu r,4MH =uuur .…………………………………………………14分(18)(本小题满分13分)解:(Ⅰ)椭圆C 的方程可化为22143x y +=,则2a =,b =,1c =. 故离心率为12,焦点坐标为(1,0),(1,0)-. ……………………………………4分 (Ⅱ)由题意,直线AB 斜率存在.可设直线AB 的方程为y kx m =+,11(,)A x y ,22(,)B x y ,则11y kx m =+,22y kx m =+.由22,3412y kx m x y =+⎧⎨+=⎩得222(34)84120k x kmx m +++-=. 判别式2222=644(34)(412)k m k m D -+-=2248(43)0k m -+>. 所以122834km x x k -+=+,212241234m x x k -=+,因为直线MA 与直线MB 斜率之积为14, 所以12121224y y x x ⋅=--, 所以12124()()(2)(2)kx m kx m x x ++=--.化简得221212(41)(42)()440k x x km x x m -++++-=, 所以22222412(8)(41)(42)4403434m km k km m k k---+++-=++,化简得22280m km k --=,即4m k =或2m k =-.当4m k =时,直线AB 方程为(4)y k x =+,过定点(4,0)-.4m k =代入判别式大于零中,解得1122k -<<. 当2m k =-时,直线AB 方程为(2)y k x =-,过定点(2,0)M ,不符合题意舍去.故直线AB 过定点(4,0)-.………………………………………………………13分(19)(本小题满分14分)解:(Ⅰ)当0a =时,2()e x f x x =,2()e (2)x f x x x '=+.由2e (2)0x x x +=,解得0x =,2x =-. 当(,2)x ∈-∞-时,f '(x )>0,f (x )单调递增; 当(2,0)x ∈-时,f '(x )<0,f (x )单调递减;当(0,)x ∈+∞时,f '(x )>0,f (x )单调递增.所以函数()f x 的单调增区间为(,2)-∞-,(0,)+∞,单调减区间为(2,0)-.…………4分 (Ⅱ)依题意即求使函数2()e ()xf x x a =-在()1,2上不为单调函数的a 的取值范围.2()e (2)x f x x x a '=+-.设2()2g x x x a =+-,则(1)3g a =-,(2)8g a =-.因为函数()g x 在()1,2上为增函数,当(1)30(2)80g a g a ì=-<ïïíï=->ïî,即当38a <<时,函数()g x 在()1,2上有且只有一个零点,设为0x .当0(1,)x x Î时,()0g x <,即()0f x ¢<,()f x 为减函数; 当0(,2)x x Î时,()0g x >,即()0f x ¢>,()f x 为增函数,满足在()1,2上不为单调函数.当3a £时,(1)0g ³,(2)0g >,所以在()1,2上()g x 0>成立(因()g x 在()1,2上为增函数),所以在()1,2上()0f x '>成立,即()f x 在()1,2上为增函数,不合题意. 同理8a ³时,可判断()f x 在()1,2上为减函数,不合题意.综上38a <<. …………………………………………………………9分(Ⅲ) 2()e (2)x f x x x a '=+-.因为函数()f x 有两个不同的极值点,即()f x ¢有两个不同的零点,即方程220x x a +-=的判别式440a ∆=+>,解得1a >-.由220x x a +-=,解得1211x x =-=- 此时122x x +=-,12x x a =-. 随着x 变化时,()f x 和()f x '的变化情况如下:所以1x 是函数()f x 的极大值点,2x 是函数()f x 的极小值点.所以1()f x 为极大值,2()f x 为极小值.所以12221212()()e ()e ()xxf x f x x a x a =-⨯-因为1a >-,所以224e4e a ---<.所以212()()4e f x f x -<.……………………………………………………………… 14分(20)(本小题满分13分) 解:(Ⅰ)满足条件的数列有两个:3,1,4,2,5;与2,4,1,3,5.…… 3分 (Ⅱ)由(Ⅰ)知数列5A :2,4,1,3,5满足55=a ,把其各项分别加5后,所得各数依次排在后,因为65||2a a -=,所得数列10A 显然满足12--=k k a a 或3,{}2,3,,10k ∈L ,即得H 数列10A :2,4,1,3,5,7,9,6,8,10.其中10,5105==a a .如此下去,即可得一个满足)403,,2,1(55Λ==k k a k 的H 数列2015A 为{}121222222121222221212122222=e [()]=e [()2]=e [(42]=4e .x x x x x x a x x a x x a x x x x a a a a a a )++---++-+-+-++-⎪⎪⎩⎪⎪⎨⎧=-=--=--=+-=+=kn n k n n k n n k n n k n n a n 5,15,125,235,245,1,(其中)403,,3,2,1Λ=k (写出此通项也可以:2,541,531,522,51,5n n n k n n k a n n k n n k n n k+=-⎧-=-⎪⎪=+=-⎨-=-⎪=⎪⎩(其中)403,,3,2,1Λ=k )…… 8分(Ⅲ)不妨设0d >.(1)若6d ≥,则20154031402140262413a b b d ==+≥+⨯=,与20152015≤a 矛盾.(2)若14d ≤≤.(i )若1001≤b ,则1(1)10040241708k b b k d =+-≤+⨯=,403.,2,1⋅⋅⋅=k . 不妨设052015l i a -=,其中0{1,2,,403},{1,2,3,4}l i ∈⋅⋅⋅∈. 于是000000555515(1)5||||||312.l l i l l l i l i a a a a a a i ------≤-+⋅⋅⋅+-≤≤ 即05|2015|12l a -≤,可得2003005≥=l l a b ,与17080≤l b 矛盾. (ii )若1011≥b ,则1011≥≥b b k ,403,,2,1⋅⋅⋅=k . 不妨设051l i a -=,其中0{1,2,,403},{1,2,3,4}l i ∈⋅⋅⋅∈. 于是000000555515(1)5||||||312l l i l l l i l i a a a a a a i ------≤-+⋅⋅⋅+-≤≤ 即05|1|12l a -≤,可得13005≤=l l a b ,与1010≥l b 矛盾.因为d 为整数,所以综上可得5d =.由(Ⅱ)可知存在使55k k b a k ==(其中403,,2,1⋅⋅⋅=k )的H 数列2015A . 把上述H 数列2015A 倒序排列,即有5d =-.所以5d =或5-. …… 13分。
北京市朝阳区2014届高三二模数学(文)试题

北京市朝阳区高三年级第二次综合练习数学学科测试(文史类)2014.5(考试时间120分钟 满分150分)本试卷分为选择题(共40分)和非选择题(共110分)两部分第一部分(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项. (1)若全集{},,,U a b c d =,{},A a b =,{}B c =,则集合{}d 等于 (A )()U AB ð (B )A B (C )A B (D )()U AB ð (2)下列函数中,既是奇函数又在区间0,+∞()上单调递增的函数为(A ) sin y x = (B )ln y x = (C )3y x = (D ) 2x y = (3)已知抛物线22x y =,则它的焦点坐标是(A )1,04⎛⎫⎪⎝⎭ (B )10,2⎛⎫ ⎪⎝⎭ (C )10,4⎛⎫ ⎪⎝⎭ (D )1,02⎛⎫⎪⎝⎭(4)执行如图所示的程序框图.若输入3a =,则输出i 的值是(A )2 (B ) 3 (C ) 4 (D ) 5(5)由直线10x y -+=,50x y +-=和10x -=所围成的三角形区域(包括边界)用不等式组可表示为(A )10,50,1.x y x y x -+≤⎧⎪+-≤⎨⎪≥⎩ (B )10,50,1.x y x y x -+≥⎧⎪+-≤⎨⎪≥⎩ (C )10,50,1.x y x y x -+≥⎧⎪+-≥⎨⎪≤⎩ (D )10,50,1.x y x y x -+≤⎧⎪+-≤⎨⎪≤⎩(6)在区间ππ[-,]上随机取一个实数x ,则事件:“cos 0x ≥”的概率为 (A )14 (B ) 34 (C )23 (D )12(7)设等差数列{}n a 的公差为d ,前n 项和为n S .若11a d ==,则8n nS a +的最小值为(A )10 (B )92 (C )72 (D)12+ ( 8 )已知平面上点{2200(,)()()16,P x y x x y y ∈-+-=其中}22004x y +=,当0x ,0y 变化时,则满足条件的点P 在平面上所组成图形的面积是(A) 4π (B) 16π ( C) 32π (D )36π第二部分(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上. 9.计算12i1i+=- . 10.已知两点()1,1A ,()1,2B -,若12BC BA =,则C 点的坐标是 . 11.圆心在x 轴上,半径长是4,且与直线5x =相切的圆的方程是 .12.由两个四棱锥组合而成的空间几何体的三视图如图所示,则其体积是 ;表面积是 .22俯视图侧视图正视图13.设一列匀速行驶的火车,通过长860m 的隧道时,整个车身都在隧道里的时间是22s .该列车以同样的速度穿过长790m 的铁桥时,从车头上桥,到车尾下桥,共用时33s ,则这列火车的长度为___m .14.在如图所示的棱长为2的正方体1111ABCD A BC D -中,作与平面1ACD 平行的截面,则截得的三角形中,面积最大的值是___; 截得的平面图形中,面积最大的值是___.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题满分13分)在ABC 中,a ,b ,c 分别是角A B C ,,的对边.已知a =π3A =.(Ⅰ)若b =C 的大小; (Ⅱ)若2c =,求边b 的长. 16. (本小题满分13分)某市规定,高中学生在校期间须参加不少于80小时的社区服务才合格.某校随机抽取20位学生参加社区服务的数据,按时间段75,80),80,85),[85,90),[90,95),[95,100][[(单位:小时)进行统计,其频率分布直方图如图所示.(Ⅰ)求抽取的20人中,参加社区服务时间不少于90小时的学生人数; (Ⅱ)从参加社区服务时间不少于90小时的学生中任意选取2人,求所选学生的参加社区服务时间在同一时间段内的概率.A17. (本小题满分14分)如图,在四棱锥P ABCD -中,底面ABCD 是正方形,侧面PAD ⊥底面ABCD . (Ⅰ)若E ,F 分别为PC ,BD 中点,求证:EF ∥平面PAD ; (Ⅱ)求证:PA ⊥CD ;(Ⅲ)若PA PD AD ==, 求证:平面PAB ⊥平面PCD . 18.(本小题满分13分)已知函数e ()xa f x x⋅=(a ∈R ,0a ≠).(Ⅰ)当1a =时,求曲线()y f x =在点()1,(1)f 处切线的方程; (Ⅱ)求函数()f x 的单调区间;(Ⅲ)当()0,x ∈+∞时,()f x 1≥恒成立,求a 的取值范围. 19.(本小题满分14分)已知椭圆C 的中心在原点O ,焦点在x 轴上,离心率为12,右焦点到右顶点的距离为1. (Ⅰ)求椭圆C 的标准方程;(Ⅱ)若直线:l 10mx y ++=与椭圆C 交于,A B 两点,是否存在实数m ,使O A O B O A O B +=-成立?若存在,求m 的值;若不存在,请说明理由.20.(本小题满分13分)已知函数()f x 对任意,x y ∈R 都满足()()()1f x y f x f y +=++,且1()02f =,数列{}n a 满足:()n a f n =,*n ∈N . (Ⅰ)求(0)f 及(1)f 的值; (Ⅱ)求数列{}n a 的通项公式; (Ⅲ)若311()()42n naa nb +=-,试问数列{}n b 是否存在最大项和最小项?若存在,求出最大项和最小项;若不存在,请说明理由.A北京市朝阳区高三年级第二次综合练习数学学科测试文史类答案 2014.5三、解答题(满分80分) 15. (本小题满分13分) (Ⅰ)解:由正弦定理sin sin a bA B=,=,解得sin 2B =. 由于B 为三角形内角,b a <,则4B π=,所以3412C ππ5π=π--=. ………6分 (Ⅱ)依题意,222cos 2b c a A bc+-=,即2141224b b +-=.整理得2280b b --=, 又0b >,所以4b =. ………13分另解:由于sin sin a cA C=2sin C =,解得1sin 2C =. 由于a c >,所以π6C =. 由π3A =,得π2B =. 由勾股定理222b c a =+,解得4b =. ………13分16.(本小题满分13分) 解:(Ⅰ)由题意可知,参加社区服务在时间段[90,95)的学生人数为200.0454⨯⨯=(人), 参加社区服务在时间段[95,100]的学生人数为200.0252⨯⨯=(人). 所以参加社区服务时间不少于90小时的学生人数为 4+26=(人). ………5分 (Ⅱ)设所选学生的参加服务时间在同一时间段内为事件A . 由(Ⅰ)可知,参加社区服务在时间段,95)[90的学生有4人,记为,,,a b c d ; 参加社区服务在时间段5,100[9]的学生有2人,记为,A B .从这6人中任意选取2人有,,,,,,,,,,,,,,ab ac ad aA aB bc bd bA bB cd cA cB dA dB AB共15种情况.事件A 包括,,,,,,ab ac ad bc bd cd AB 共7种情况. 所以所选学生的服务时间在同一时间段内的概率7()15P A =.………13分 17. (本小题满分14分) 证明:(Ⅰ)如图,连结AC .因为底面ABCD 是正方形,所以AC 与BD 互相平分. 又因为F 是BD 中点, 所以F 是AC 中点.在△PAC 中,E 是PC 中点,F 是AC 中点, 所以EF ∥PA .又因为EF ⊄平面PAD ,PA ⊂平面PAD ,所以EF ∥平面PAD . ………4分 (Ⅱ)因为平面PAD ⊥底面ABCD ,且平面PAD 平面=ABCD AD ,又CD AD ⊥,CD ⊂平面ABCD , 所以CD ⊥面PAD .A又因为PA ⊂平面PAD ,所以CD PA ⊥.即PA ⊥CD . ………9分(Ⅲ)在△PAD 中,因为2PA PD AD ==, 所以PA PD ⊥.由(Ⅱ)可知PA ⊥CD ,且=CD PD D ,所以PA ⊥平面PCD . 又因为PA ⊂平面PAB ,所以平面PAB ⊥平面PCD . ………14分 18. (本小题满分13分)(Ⅰ)22e e e (1)()x x x ax a a x f x x x ⋅--'==,0x ≠.当1a =时,2e (1)()x x f x x-'=. 依题意(1)0f '=,即在1x =处切线的斜率为0.把1x =代入e ()xf x x=中,得(1)e f =.则曲线()f x 在1x =处切线的方程为e y =. ………………….4分(Ⅱ)函数()f x 的定义域为{}0x x ≠.22e e e (1)()x x x ax a a x f x x x ⋅--'==.(1)若0a >,当()0f x '>,即1x >时,函数()f x 为增函数;当()0f x '<,即0x <和01x <<时,函数()f x 为减函数. (2)若0a <,当()0f x '>,即0x <和01x <<时,函数()f x 为增函数;当()0f x '<,即1x >时,函数()f x 为减函数.综上所述,0a >时,函数()f x 的单调增区间为()1,+∞;单调减区间为(),0-∞,()0,1.0a <时, 函数()f x 的单调增区间为(),0-∞,()0,1;单调减区间为()1,+∞.………………….9分(Ⅲ)当()0,x ∈+∞时,要使()f x =e 1xa x⋅≥恒成立,即使e x x a ≥在()0,x ∈+∞时恒成立. 设()e x x g x =,则1()e xxg x -'=.可知在01x <<时,()0g x '>,()g x 为增函数;1x >时,()0g x '<,()g x 为减函数.则max 1()(1)e g x g ==.从而1ea ≥.另解:(1)当0a <时,()e 1a f a =<,所以()f x 1≥不恒成立.(2)当0a >且()0,x ∈+∞时,由(Ⅰ)知,函数()f x 的单调增区间为()1,+∞,单调减区间为()0,1.所以函数()f x 的最小值为(1)e f a =,依题意(1)e 1f a =≥,解得1ea ≥. 综上所述,1ea ≥. ………………….13分 19. (本小题满分14分)(Ⅰ)设椭圆C 的方程为22221x y a b+=()0a b >>,半焦距为c .依题意1,21.c e a a c ⎧==⎪⎨⎪-=⎩ 解得1c =,2a =,所以2223b a c =-=.所以椭圆C 的标准方程是22143x y +=. ………………….4分 (Ⅱ)不存在实数m ,使||||OA OB OA OB +=-,证明如下:把1y mx =--代入椭圆C:223412x y +=中,整理得22(34)880m x mx ++-=. 由于直线l 恒过椭圆内定点()0,1-,所以判别式0∆>. 设1122(,),(,)A x y B x y ,则122843m x x m +=-+,122843x x m -⋅=+. 依题意,若||||OA OB OA OB +=-,平方得0OA OB ⋅=. 即12121212(1)(1)0x x y y x x mx mx +=+--⋅--=, 整理得21212(1)()10m x x m x x ++++=,所以2(1)m +2843m -+2281043m m -+=+, 整理得2512m =-,矛盾. 所以不存在实数m ,使||||OA OB OA OB +=-. ………………….14分 20. (本小题满分13分)解:(Ⅰ)在()()()1f x y f x f y +=++中,取0x y ==,得(0)1f =-, 在()()()1f x y f x f y +=++中,取12x y ==,得(1)1f =,…………2分 (Ⅱ)在()()()1f x y f x f y +=++中,令x n =,1y =, 得(1)()2f n f n +=+,即12n n a a +-=.所以{}n a 是等差数列,公差为2,又首项1(1)1a f ==,所以21n a n =-,*n ∈N . …………6分 (Ⅲ)数列{}n b 存在最大项和最小项令2111()()22na n t -==,则22111()816256nb t t t =-=--, 显然102t <≤,又因为N n *∈,所以当12t =,即1n =时,{}n b 的最大项为1316b =. 当132t =,即3n =时,{}n b 的最小项为331024b =-. …………13分。
北京市朝阳区2014届高三上学期期末考试数学理试题含答案

北京市旭日区 2013-2014 学年度高三年级第一学期期末一致考试数学试卷(理工类)2014.1(考试时间120 分钟满分150 分)本试卷分为选择题(共40 分)和非选择题(共110 分)两部分第一部分(选择题共 40分)一、选择题:本大题共8 小题,每题 5 分,共 40 分.在每题给出的四个选项中,选出切合题目要求的一项 .1.函数f ( x)1x 的定义域为x1A.[0,)B.(1,)C.[0,1)(1,)D.[0,1)2.假如点P 2, y0在以点 F 为焦点的抛物线y24x 上,则PFA .1B.2C.3D.43.命题p:x R, x2ax a20 ;命题q:x R ,sin x cos x 2 ,则以下命题中为真命题的是A .p q B.p q开始C.( p) q D.( p) ( q)4.在△ABC中,A30 ,AB3,BC 1 ,i0则△ ABC 的面积等于a a0A .3B.3i i1 24C. 3 或3D. 3 或3a 2 a1224是a<2013?5.履行以下图的程序框图,输出结果是4.若 a01,2,3,则 a0全部可能的取值为否.. 1输出 iA1,2,3BC.2D.1,2结束6.已知正方形的四个极点分别为O (0,0) , A(1,0) , B(1,1),C (0,1) ,点 D , E 分别在线段 OC , AB 上运动,且 OD BE ,设 AD 与 OE 交于点 G ,则点 G 的轨迹方程是A .y x(1x) (0x1)B.x y(1y) (0 y1)C.y x2(0 x 1)D.y 1 x2(0 x 1)7.已知平面向量 a ,b的夹角为120,且 a b 1 ,则 | a b |的最小值为A .6B.3C.2D. 18.已知数列a n知足 a n n k n (n N ,0 k 1) 下边说法正确的选项是①当k 1时,数列 a n为递减数列;2②当1k1时,数列a n不必定有最大项;21③当 0k a为递减数列;时,数列2n④当k为正整数时,数列a n必有两项相等的最大项 .1kA. ①②B. ②④C. ③④D. ②③第二部分(非选择题共 110 分)二、填空题:本大题共 6 小题,每题 5 分,共30 分 . 把答案填在答题卡上.9.某校为认识高一学生寒假时期的阅读状况,频次 /组距抽查并统计了100 名同学的某一周阅读时间,绘制了频次散布直方图(以下图),那么这1000.150.14名学生中阅读时间在 [4,8) 小时内的人数为0.12_____.0.050.042468 10 12小时10.在各项均为正数的等比数列a n中,若 log 2 a2 log2 a81,则 a3 a7.11.直线y kx与圆( x 2)2y 24订交于O,A两点,若OA =2 3 ,则实数k的值是 _____.12.一个三棱锥的三视图以下图,则该三棱锥的体积是;表面积是.2 633正视图俯视图x y 3, 13.实数x, y知足y 若 y k( x 2)2x0,恒成立,则实数k 的最大值是.14.全部真约数(除自己以外的正约数)的和等于它自己的正整数叫做完整数.2 33侧视图如: 6=123;28=124714 ;496=1248163162124248 .已经证明:若2n1是质数,则2n1(2n1) 是完整数,n N .请写出一个四位完整数;又6 23 ,所以 6 的全部正约数之和可表示为(1 2)(13);28227 ,所以 28的全部正约数之和可表示为(1222) (1 7);按此规律,496 的全部正约数之和可表示为.三、解答题:本大题共 6 小题,共80 分 . 解答应写出文字说明,演算步骤或证明过程.15.(此题满分13 分)已知函数 f (x)cos2 x sin x 1 .(Ⅰ)求函数 f ( x) 的最小值;(Ⅱ)若 f ( )5的值.,求 cos 21616.(此题满分13 分)甲、乙两名同学参加“汉字听写大赛”选拔测试,在同样测试条件下,两人5次测试的成绩(单位:分)以下表:第 1 次第 2 次第 3 次第 4 次第 5 次甲5855769288乙6582878595(Ⅰ)请画出甲、乙两人成绩的茎叶图. 你以为选派谁参赛更好?说明原因(不用计算);(Ⅱ)若从甲、乙两人 5 次的成绩中各随机抽取一个成绩进行剖析,设抽到的两个成绩中,90 分以上的个数为 X ,求随机变量X 的散布列和希望 EX .17.(此题满分 14 分)如图,在三棱锥P- ABC 中, PA平面 ABC,AB AC.(Ⅰ)求证: AC PB ;(Ⅱ)设 O, D 分别为 AC, AP 的中点,点 G 为△ OAB 内一点,且知足 OG 1OB),(OA3P求证: DG ∥面 PBC ;(Ⅲ)若 AB = AC = 2, PA= 4,D 求二面角 A PB C 的余弦值.C OAGB18.(此题满分13 分)已知函数 f (x) (x a)ln x , a R .(Ⅰ)当 a 0 时,求函数 f ( x) 的极小值;(Ⅱ)若函数 f ( x) 在 (0,) 上为增函数,求 a 的取值范围.19.已知椭圆C两焦点坐标分别为F1(3,0) , F21 ( 3,0) ,且经过点P( 3, ).2(Ⅰ)求椭圆 C 的标准方程;(Ⅱ)已知点A(0, 1) ,直线 l 与椭圆 C 交于两点 M , N .若△ AMN 是以 A 为直角极点的等腰直角三角形,试求直线l 的方程.20.(此题满分 13 分)已知 a, b, c 是正数,a1lg a , a2 lg b , a3 lg c .(Ⅰ)若 a,b,c 成等差数列,比较a1 a2与 a2 a3的大小;(Ⅱ)若 a1a2a2 a3a3a1,则a,b,c三个数中,哪个数最大,请说明原因;(Ⅲ)若 a t ,b t2, c t 3( t N),且a1,a2,a3的整数部分分别是 m, m21, 2m2 1, 求全部 t 的值.北京市旭日区 2013-2014 学年度高三年级第一学期期末一致考试数学答案(理工类)2014.1一、号 1 2 3 4 5 6 7 8答案CCBDBAAC二、填空91 1112114号 03答542 3 18 236 32 (1 2 222324) (1 31)8128案33三、解答15.解:(Ⅰ)因f (x)cos 2 xsin x 1sin 2 xsin x(sin x 1 )2 1 ,2 4又 sin x1,1 ,所以当 sin x 1f ( x) 的最小1 6 分 ,函数.⋯⋯2 4(Ⅱ)由(Ⅰ)得(sin1 )2 1 5 ,24 16所以 (sin1 )2 9 .2 16于是 sin51(舍)或 sin.44又 cos21 2sin21 2(1)27 .4816.解:(Ⅰ)茎叶 如右 所示,由 可知,乙的平 大于甲的均匀成 ,且乙的方差小于甲的方差,所以参 更好.⋯⋯⋯⋯⋯⋯6 分(Ⅱ)随机 量 X 的全部可能取 0,1,2 .P( XC 41C 41 16 ,0)25C 51C 51P( X 2C 418,1)25C 51C 51⋯⋯⋯⋯⋯⋯13 分均 成甲乙 派 乙585656 78 8 2 75295P( X11,2)25C51C51随机量 X 的散布列是:X012P 1681 252525EX01618212.⋯⋯⋯⋯⋯⋯13 分252525517.明:(Ⅰ)因PA平面 ABC , AC平面 ABC ,所以 PA AC .又因 AB AC ,且 PA AB= A,所以 AC平面 PAB .又因 PB平面 PAB ,所以 AC PB .⋯⋯⋯⋯⋯⋯4 分(Ⅱ)解法 1: 因PA平面ABC,所以PA AB , PA AC .又因 AB AC ,所以成立如所示的空直角坐系 A xyz .AC = 2a , AB = b , PA = 2c ,A(0,0,0) , B(0, b,0) , C (2 a,0,0) ,P(0,0,2 c), D (0,0, c) , O( a,0,0) .1又因 OG(OA OB),3a b所以 G( , ,0).z PD于是 DG( a,b, c) ,x 33BC (2 a,b,0) , PB(0, b, 2c) .平面 PBC 的一个法向量n BC0,n( x0, y0 , z0 ) ,有C O AGB即n PB0.2ax0by00,by02cz00.y不如 z0 1 ,有y02c, x0c,所以 n b a因 n DG (c,2c,1)(a,b,c)c aa b33a3所以 n DG .又因DG平面 PBC ,(c,2c,1) .a b2c b 1 ( c) 0 ,b3所以 DG ∥平面 PBC .⋯⋯⋯⋯⋯⋯ 9 分P解法 2:取 AB 中点 E , OE , OE1(OA OB) .122D由已知 OG(OA OB )可得 OG OE ,33点 G 在OE 上.AG 并延 交 CB 于F , PF .O因 O, E 分 AC , AB 的中点,CAG所以 OE ∥BC ,即G AF 的中点.E又因 D 段 PA 的中点,F所以 DG ∥PF .又 DG平面 PBC , PF平面 PBC ,B所以 DG ∥平面 PBC .⋯⋯⋯⋯⋯⋯ 9 分(Ⅲ)由(Ⅱ)可知平面PBC 的一个法向量 n( c ,2c,1)(2, 2,1) .a b又因 AC 面 PAB ,所以面 PAB 的一个法向量是 AC(2,0,0) .又 cos n , ACn AC 4 2 ,n AC 3 23由 可知,二面角 A PBC 角,所以二面角 A PBC 的余弦2 . ⋯⋯⋯⋯⋯⋯14 分318. 解:(Ⅰ)定 域 (0,) .当 a0 , f (x) xln x , f ( x)ln x 1 .令 f (x)0 ,得 x1.(0, 1) , fe当 x( x) 0 , f ( x) 减函数;e当 x( 1, ) , f ( x)0 , f ( x) 增函数 .e所以函数f (x) 的极小 是 f ( 1)1 . ⋯⋯⋯⋯⋯⋯5 分ee(Ⅱ)由已知得f ( x)ln x xa x .因 函数 f ( x) 在 (0,) 是增函数,所以f (x) 0 , x(0, ) 恒成立.由 f( x) 0 得 ln x a0 ,即 x ln xx a x(0,) 恒成立.xxg( x) x ln x x ,要使“ x ln xxa x (0,) 恒成立”,只需 ag( x)min .因 g ( x)ln x 2 ,令 g ( x) 0得 x12.12 ) , g ( x)e当 x(0,0 , g( x) 减函数;e当 x(12 ,) , g ( x) 0 , g ( x) 增函数 .e11所以 g (x) 在 0,上的最小 是g()2 2.ee故函数 f ( x) 在 (0,) 是增函数 , 数 a 的取 范 是( ,12 ]⋯⋯13 分e19.解:(Ⅰ) 准方程x 2 y 2 1( ab 0) .依 意a2b 22aPF 1PF 212 1 1 4,所以 a 2 .44又 c3 ,所以 b 2 a 2 c 2 1 .于是 C 的 准方程x 2y 2 1 .⋯⋯⋯⋯⋯⋯5 分4(Ⅱ)依 意, 然直l 斜率存在 . 直 l 的方程 y kxm ,x 2 y 21(4k 21)x 28kmx 4m 24 0 .由 4得y kx m因64k 2 m 2 4(4k 2 1)(4m 2 4) 0 ,得 4k 2 m 2 1 0 .⋯⋯⋯⋯⋯⋯ ①x 1 x 28km4k 21M ( x 1 , y 1), N ( x 2 , y 2 ) , 段 MN 中点 Q(x 0 , y 0 ) ,4m24x 1 x 24k21于是 x 04km , y 0kx 0mm .4k 2 14k 2 1因 AM AN , 段 MN 中点 Q ,所以 AQ MN .( 1)当 x0 ,即 k0且 m 0 ,y 01k1,整理得 3m 4k21.⋯⋯⋯⋯⋯⋯②x0因 AM AN,AM(x1, y11), AN( x2 , y21) ,所以AM AN x1 x2( y11)( y2 1) (1 k2 )x1x2k( m 1)( x1x2 ) m22m 1(1k24m24k(m1)(8km)22m 1 0,)214k2m4k1整理得 5m22m30 ,解得 m3或 m1.当 m1,由②不合意舍去.5由①②知,m 35., k55( 2)当x00,(ⅰ)若 k0 ,直 l 的方程 y m ,代入方程中得x 2 1 m2.M (21m2 , m) , N (2 1 m2 , m) ,依意,若△AMN 等腰直角三角形,AQ QN.即2 1m21m ,解得 m1或 m3. m1不合意舍去,35即此直 l 的方程y.5(ⅱ)若k0 且 m0 ,即直 l 原点.依的称性有Q (0, 0), 依意不可以有AQ MN ,即此不足△AMN 等腰直角三角形.上,直 l的方程y 35x 5 y30或5x 5 y30.⋯⋯⋯⋯⋯⋯14分或5a3 ) =lgalgblgac20.解:(Ⅰ)由已知得(a1a2 )( a2.a cb c b2因 a,b,c 成等差数列,所以b2,(a1a2 ) ( a2a3 ) lg4ac,(a c) 2因 a2c22ac ,所以(a c)24ac,即4ac1,(a c) 2(a1a2 )( a2a3 ) 0 ,即 a1a2a2a3,当且当a b c 等号成立.⋯⋯⋯⋯⋯⋯ 4 分(Ⅱ)解法 1:令m a a , n a a , p a a ,122331依意, m n p 且 m n p0 ,所以 m0p .故 a1a20 ,即lg a lg b ;且a1a30 ,即lg a lg c.所以 a b 且a c .故 a, b, c 三个数中,a最大.解法 2:依意lg algblgc,即ab c .b c a b c a因 a0, b0, c0 ,所以 ac b2, a2bc , ab c2.于是,abc b3, a3abc , abc c3,所以 a3b3, a3c3.因 y x3在R上增函数,所以a b 且a c .故 a,b,c 三个数中,a最大.⋯⋯⋯⋯⋯⋯8 分(Ⅲ)依意,lg t ,lg t2,lg t3的整数部分分是m, m21, 2m21,m lg t m 1,所以 2m2lg t2m2.又 lg t 22lg t , lg t2的整数部分是2m或 2m 1 .当 m2 1 2m , m 1;当 m2 1 2m 1 , m 0,2 .( 1)当m0 , lg t ,lg t2,lg t3的整数部分分是 0,1,1 ,1 ,1 lg t2lg t 31212所以 0 lg t 2 ,1 2 .所以lg t,解得 102t 10 3.2312又因 10 23,4 , 1034,5,所以此 t 4 .( 2)当m1,同理可得 1lg t 2 ,2lg t 2 3 , 3lg t3 4 .444所以 1lg t t10 3.又10321,22,此 t 10,11,12,...20,21 .,解得 103( 3)当m 2,同理可得 2 lg t3,5 lg t2 6 , 9lg t 310 ,同足条件的 t 不存在.上所述 t4,10,11,12,...20,21 .⋯⋯⋯⋯⋯⋯13 分。
北京市朝阳2014届高三二模文科数学试卷(带解析)

北京市朝阳2014届高三二模文科数学试卷(带解析)1.若全集{},,,U a b c d =,{},A a b =,{}B c =,则集合{}d 等于( )(A )()U A B ð (B )A B (C )A B (D )()U AB ð 【答案】A 【解析】 试题分析:因为{,,}A B a b c =,所以()U A B ð{}.d =而A B .φ=()U AB ð.U =所以选A.考点:集合运算2.下列函数中,既是奇函数又在区间0,+∞()上单调递增的函数为( )(A )sin y x = (B )ln y x = (C )3y x = (D )2x y = 【答案】C【解析】试题分析:sin y x =是奇函数但在区间0,+∞()上不是单调函数.ln y x =在区间0,+∞()上单调递增但不是奇函数,3y x =既是奇函数又在区间0,+∞()上单调递增的函数,2xy =在区间0,+∞()上单调递增但不是奇函数.考点:函数奇偶性及单调性3.已知抛物线22x y =,则它的焦点坐标是( )(A )1,04⎛⎫ ⎪⎝⎭ (B )10,2⎛⎫ ⎪⎝⎭ (C )10,4⎛⎫ ⎪⎝⎭ (D )1,02⎛⎫ ⎪⎝⎭ 【答案】B【解析】试题分析:因为抛物线22(0)x py p =>的焦点坐标为(0,),2p 所以抛物线22x y =的焦点坐标是10,2⎛⎫⎪⎝⎭.考点:抛物线焦点4.执行如图所示的程序框图.若输入3a =,则输出i 的值是( )(A )2 (B ) 3 (C ) 4 (D ) 5 【答案】C 【解析】试题分析:第一次循环,9,1,a i ==第二次循环,21,2,a i ==第三次循环,45,3,a i ==第四次循环,93,4,a i ==结束循环,输出 4.i = 考点:循环结构流程图5.由直线10x y -+=,50x y +-=和10x -=所围成的三角形区域(包括边界)用不等式组可表示为( ) (A )10,50,1.x y x y x -+≤⎧⎪+-≤⎨⎪≥⎩ (B )10,50,1.x y x y x -+≥⎧⎪+-≤⎨⎪≥⎩ (C )10,50,1.x y x y x -+≥⎧⎪+-≥⎨⎪≤⎩ (D )10,50,1.x y x y x -+≤⎧⎪+-≤⎨⎪≤⎩【答案】A 【解析】试题分析: 由题意得:所围成的三角形区域在直线10x y -+=的上方,直线50x y +-=的下方,及直线10x -=的右侧,所以10x y -+≤,50x y +-≤,10.x -≥ 考点:不等式组表示平面区域6.在区间ππ[-,]上随机取一个实数x ,则事件:“cos 0x ≥”的概率为( )(A )14 (B ) 34 (C )23 (D )12【答案】D 【解析】试题分析:由cos 0x ≥,x ∈ππ[-,]得:[,]22x ππ∈-,所以事件:“cos 0x ≥”的概率为()122.()2ππππ--=-- 考点:几何概型概率7.设等差数列{}n a 的公差为d ,前n 项和为n S .若11a d ==,则8n n S a +的最小值为( ) (A )10 (B )92 (C )72 (D)12+【答案】B 【解析】试题分析:由题意得:(1),2n n n n a n S +==,所以8n n S a+1819.222n n +=+≥+=当且仅当4n =时取等号.因此8n n S a +的最小值为92.考点:基本不等式求最值8.已知平面上点{2200(,)()()16,P x y x x y y ∈-+-=其中}22004x y +=,当0x ,0y 变化时,则满足条件的点P 在平面上所组成图形的面积是( )(A )4π (B )16π ( C )32π (D )36π 【答案】C 【解析】试题分析:圆心00(,)x y 在圆224x y +=上运动 一周,点P 在平面上所组成图形为以坐标原点为圆心,6为半径的实心圆减去以坐标原点为圆心,2为半径的实心圆的一个圆环,面积是226232πππ-=.考点:圆的方程,动点轨迹9.计算12i1i +=- . 【答案】13i 22-+【解析】 试题分析:12i (12i)(1+i)13.1i (1i)(1+i)2i++-+==-- 考点:复数运算10.已知两点()1,1A ,()1,2B -,若12BC BA =,则C 点的坐标是 . 【答案】30,2⎛⎫ ⎪⎝⎭【解析】试题分析:设C 点的坐标是(,)x y ,则由12BC BA =得1(1,2)(11,12),2x y +-=+-即30,.2x y ==C 点的坐标是30,2⎛⎫⎪⎝⎭.考点:向量坐标运算11.圆心在x 轴上,半径长是4,且与直线5x =相切的圆的方程是 .【答案】()22116x y -+=和()22916x y -+=【解析】试题分析:设圆心为(),a b ,因为与直线5x =相切,所以|5|4,1a r a -===或9.a =因此圆的方程是()22116x y -+=和()22916x y -+=考点:圆的标准方程12.由两个四棱锥组合而成的空间几何体的三视图如图所示,则其体积是 ;表面积是 .【答案】3, 【解析】2的正方形.因此体积为21223⨯=表面积为8个全等的边长为2的等边三角形面积之和,即282= 考点:三视图 13.设一列匀速行驶的火车,通过长860m 的隧道时,整个车身都在隧道里的时间是22s .该列车以同样的速度穿过长790m 的铁桥时,从车头上桥,到车尾下桥,共用时33s ,则这列火车的长度为___m . 【答案】200 【解析】试题分析:设这列火车的长度为xm ,则由题意得:860790,200.2233x xx -+==.考点:实际问题应用题14.在如图所示的棱长为2的正方体1111ABCD A BC D -中,作与平面1ACD 平行的截面,则截得的三角形中,面积最大的值是___;截得的平面图形中,面积最大的值是___.AC【答案】【解析】试题分析:截得的三角形中,面积最大的是三角形11ACB ,面积为2=的平面图形中,面积最大的是正六边形,如图,面积为26=考点:空间想象15.在ABC ∆中,a ,b ,c 分别是角A B C ,,的对边.已知a =π3A =. (1)若b =C 的大小; (2)若2c =,求边b 的长. 【答案】(1),125π(2)4b =. 【解析】 试题分析:(1)解三角形问题,一般利用正余弦定理进行边角转化. 由正弦定理由于B 为三角形内角,b a <,则4B π=,所以3412C ππ5π=π--=.(2)由余弦定理222cos 2b c a A bc +-=得2141224b b +-=整理得2280b b --=,又0b >,所以4b =.本题也可由正弦定理sin sin a c A C =2sin C=,解得1sin 2C =.由于a c >,所以π6C =.由π3A =,得π2B =. 由勾股定理222b c a =+,解得4b =.(1由于B 为三角形内角,b a <,则4B π=,所以3412C ππ5π=π--=. 6分(2)依题意,222cos 2b c a A bc+-=,即2141224b b +-=.整理得2280b b --=,又0b >,所以4b =. 13分另解: 由于sin sin a c A C =2sin C=,解得1sin 2C =.由于a c >,所以π6C =. 由π3A =,得π2B =. 由勾股定理222b c a =+,解得4b =. 13分考点:正余弦定理16.某市规定,高中学生在校期间须参加不少于80小时的社区服务才合格.某校随机抽取20位学生参加社区服务的数据,按时间段75,80),80,85),[85,90),[90,95),[95,100][[(单位:小时)进行统计,其频率分布直方图如图所示.(Ⅰ)求抽取的20人中,参加社区服务时间不少于90小时的学生人数;(Ⅱ)从参加社区服务时间不少于90小时的学生中任意选取2人,求所选学生的参加社区服务时间在同一时间段内的概率.【答案】(Ⅰ)6,(Ⅱ)7.15【解析】 试题分析:(Ⅰ)根据频率分布直方图中小长方形面积为频率,而频数为总数与频率之积. 因此参加社区服务在时间段[90,95)的学生人数为200.0454⨯⨯=(人),参加社区服务在时间段[95,100]的学生人数为200.0252⨯⨯=(人).所以参加社区服务时间不少于90小时的学生人数为 4+26=(人).(Ⅱ)解概率应用题,要注意“设、列、解、答”. 设所选学生的参加服务时间在同一时间段内为事件A .由(Ⅰ)可知,参加社区服务在时间段,95)[90的学生有4人,记为,,,a b c d ;参加社区服务在时间段5,100[9]的学生有2人,记为,A B .从这6人中任意选取2人有,,,,,,,,a b ac ad a A a B b c b d b A b B c d共15种情况.事件A 包括,,,,,,a b a c a d b c b d c d AB 共7种情况.所以所选学生的服务时间在同一时间段内的概率7()15P A =. 解:(Ⅰ)由题意可知,参加社区服务在时间段[90,95)的学生人数为200.0454⨯⨯=(人), 参加社区服务在时间段[95,100]的学生人数为200.0252⨯⨯=(人).所以参加社区服务时间不少于90小时的学生人数为 4+26=(人). 5分 (Ⅱ)设所选学生的参加服务时间在同一时间段内为事件A . 由(Ⅰ)可知,参加社区服务在时间段,95)[90的学生有4人,记为,,,a b c d ; 参加社区服务在时间段5,100[9]的学生有2人,记为,A B .从这6人中任意选取2人有,,,,,,,,,,,,,,ab ac ad aA aB bc bd bA bB cd cA cB dA dB AB 共15种情况.事件A 包括,,,,,,ab ac ad bc bd cd AB 共7种情况. 所以所选学生的服务时间在同一时间段内的概率7()15P A =. 13分 考点:频率分布直方图,古典概型概率17.如图,在四棱锥P ABCD -中,底面ABCD 是正方形,侧面PAD ⊥底面ABCD . (Ⅰ)若E ,F 分别为PC ,BD 中点,求证:EF ∥平面PAD ; (Ⅱ)求证:PA ⊥CD ;(Ⅲ)若2PA PD AD ==,求证:平面PAB ⊥平面PCD .A【答案】(Ⅰ)详见解析,(Ⅱ)详见解析,(Ⅲ)详见解析. 【解析】 试题分析:(Ⅰ)证明线面平行,关键在于找出线线平行.本题条件含中点,故从中位线上找线线平行. E ,F 分别为PC ,BD 中点,在△PAC 中,E 是PC 中点,F 是AC 中点,所以EF ∥PA .又因为EF ⊄平面PBC ,PA ⊂平面BC P ,所以EF ∥平面PAD .(Ⅱ)由面面垂直性质定理可得线面垂直,因为平面PAD ⊥底面ABCD ,且平面PAD 平面=ABCD AD ,又CD AD ⊥,CD ⊂平面ABCD , 所以CD ⊥面PAD .又因为PA ⊂平面PAD ,所以CD PA ⊥.即PA ⊥CD .(Ⅲ)证明面面垂直,关键找出线面垂直. 在△PAD中,因为2PA PD AD ==,所以PA PD ⊥.由(Ⅱ)可知PA ⊥CD ,且=C D P D D , 所以PA ⊥平面PCD .又因为PA ⊂平面PAB ,所以平面PAB ⊥平面PCD . 证明:(Ⅰ)如图,连结AC . 因为底面ABCD 是正方形,所以AC 与BD 互相平分. 又因为F 是BD 中点, 所以F 是AC 中点.在△PAC 中,E 是PC 中点,F 是AC 中点, 所以EF ∥PA .又因为EF ⊄平面PAD ,PA ⊂平面PAD ,所以EF ∥平面PAD . 4分 (Ⅱ)因为平面PAD ⊥底面ABCD ,且平面PAD 平面=ABCD AD , 又CD AD ⊥,CD ⊂平面ABCD , 所以CD ⊥面PAD . 又因为PA ⊂平面PAD ,所以CD PA ⊥.即PA ⊥CD . 9分(Ⅲ)在△PAD 中,因为PA PD AD ==, 所以PA PD ⊥. 由(Ⅱ)可知PA ⊥CD ,且=CD PD D ,所以PA ⊥平面PCD . 又因为PA ⊂平面PAB ,所以平面PAB ⊥平面PCD . 14分 考点:线面平行判定定理,面面垂直性质定理与判定定理18.已知函数e ()xa f x x⋅=(a ∈R ,0a ≠).(Ⅰ)当1a =时,求曲线()y f x =在点()1,(1)f 处切线的方程; (Ⅱ)求函数()f x 的单调区间;(Ⅲ)当()0,x ∈+∞时,()f x 1≥恒成立,求a 的取值范围.【答案】(Ⅰ)e y =,(Ⅱ)0a >时,函数()f x 的单调增区间为()1,+∞;单调减区间为(),0-∞,()0,1.0a <时, 函数()f x 的单调增区间为(),0-∞,()0,1;单调减区间为()1,+∞.(Ⅲ)1ea ≥ 【解析】试题分析:(Ⅰ))利用导数的几何意义,在1x =处切线的斜率为0即为(1).f '因为22e e e (1)()x x x ax a a x f x x x ⋅--'==,所以当1a =时,2e (1)()x x f x x -'=.(1)0f '=,又(1)e f =,则曲线()f x 在1x =处切线的方程为e y =. (Ⅱ)利用导数求函数单调区间,需明确定义域{}0x x ≠,再导数值的符号确定单调区间. (1)若0a >,当()0f x '>,即1x >时,函数()f x 为增函数;当()0f x '<,即0x <和01x <<时,函数()f x 为减函数.若0a <,当()0f x '>,即0x <和01x <<时,函数()f x 为增函数;当()0f x '<,即1x >时,函数()f x 为减函数.(Ⅲ)不等式恒成立问题,一般利用变量分离转化为最值问题. 当()0,x ∈+∞时,要使()f x =e 1x a x ⋅≥恒成立,即使e x xa ≥在()0,x ∈+∞时恒成立. 设()e xx g x =,易得max 1()(1)e g x g ==,从而1ea ≥. (Ⅰ)22e e e (1)()x x x ax a a x f x x x ⋅--'==,0x ≠. 当1a =时,2e (1)()x x f x x -'=.依题意(1)0f '=,即在1x =处切线的斜率为0.把1x =代入e ()xf x x=中,得(1)e f =.则曲线()f x 在1x =处切线的方程为e y =. .4分 (Ⅱ)函数()f x 的定义域为{}0x x ≠.22e e e (1)()x x x ax a a x f x x x ⋅--'==.(1)若0a >,当()0f x '>,即1x >时,函数()f x 为增函数;当()0f x '<,即0x <和01x <<时,函数()f x 为减函数. (2)若0a <,当()0f x '>,即0x <和01x <<时,函数()f x 为增函数;当()0f x '<,即1x >时,函数()f x 为减函数.综上所述,0a >时,函数()f x 的单调增区间为()1,+∞;单调减区间为(),0-∞,()0,1. 0a <时, 函数()f x 的单调增区间为(),0-∞,()0,1;单调减区间为()1,+∞. .9分(Ⅲ)当()0,x ∈+∞时,要使()f x =e 1x a x⋅≥恒成立,即使e x x a ≥在()0,x ∈+∞时恒成立. 设()e x x g x =,则1()ex x g x -'=.可知在01x <<时,()0g x '>,()g x 为增函数; 1x >时,()0g x '<,()g x 为减函数.则max 1()(1)e g x g ==.从而1ea ≥. 另解:(1)当0a <时,()e 1a f a =<,所以()f x 1≥不恒成立.(2)当0a >且()0,x ∈+∞时,由(Ⅰ)知,函数()f x 的单调增区间为()1,+∞,单调减区间为()0,1.所以函数()f x 的最小值为(1)e f a =,依题意(1)e 1f a =≥,解得1ea ≥. 综上所述,1ea ≥. .13分 考点:利用导数求切线,利用导数求单调区间,利用导数求最值 19.已知椭圆C 的中心在原点O ,焦点在x 轴上,离心率为12,右焦点到右顶点的距离为1. (Ⅰ)求椭圆C 的标准方程;(Ⅱ)若直线:l 10mx y ++=与椭圆C 交于,A B 两点,是否存在实数m ,使O A O B O A O B +=-成立?若存在,求m 的值;若不存在,请说明理由.【答案】(Ⅰ)22143x y +=,(Ⅱ)不存在. 【解析】试题分析:(Ⅰ)求椭圆标准方程,关键利用待定系数法求出a,b. 由..及1a c -=,解得1c =,2a =.所以2223b a c =-=.所以椭圆C 的标准方程是22143x y +=.(Ⅱ)存在性问题,一般从假设存在出发,建立等量关系,有解就存在,否则不存在. 条件22OA OB OA OB +=-的实质是垂直关系,即0OA OB ⋅=.所以12120x x y y +=.1212()()0x x kx m kx m +++=,221212(1)()0k x x km x x m ++++=把1y mx =--代入椭圆C:223412x y +=中,整理得22(34)880m x mx ++-=.整理得2512m =-,矛盾. (Ⅰ)设椭圆C 的方程为22221x y a b+=()0a b >>,半焦距为c . 依题意1,21.c e a a c ⎧==⎪⎨⎪-=⎩ 解得1c =,2a =,所以2223b a c =-=.所以椭圆C 的标准方程是22143x y +=. .4分 (Ⅱ)不存在实数m ,使||||OA OB OA OB +=-,证明如下:把1y mx =--代入椭圆C:223412x y +=中,整理得22(34)880m x mx ++-=. 由于直线l 恒过椭圆内定点()0,1-,所以判别式0∆>.设1122(,),(,)A x y B x y ,则122843m x x m +=-+,122843x x m -⋅=+. 依题意,若||||OA OB OA OB +=-,平方得0OA OB ⋅=.即12121212(1)(1)0x x y y x x mx mx +=+--⋅--=,整理得21212(1)()10m x x m x x ++++=,所以2(1)m +2843m -+2281043m m -+=+, 整理得2512m =-,矛盾. 所以不存在实数m ,使||||OA OB OA OB +=-. .14分考点:椭圆标准方程,直线与椭圆位置关系20.已知函数()f x 对任意,x y ∈R 都满足()()()1f x y f x f y +=++,且1()02f =,数列{}n a 满足:()n a f n =,*n ∈N .(Ⅰ)求(0)f 及(1)f 的值;(Ⅱ)求数列{}n a 的通项公式;(Ⅲ)若311()()42n n a a n b +=-,试问数列{}n b 是否存在最大项和最小项?若存在,求出最大项和最小项;若不存在,请说明理由.【答案】(Ⅰ)(0)1f =-,(1)1f =,(Ⅱ)21na n =-,(Ⅲ)当12t =,即1n =时,{}nb 的最大项为1316b =.当132t =,即3n =时,{}n b 的最小项为331024b =-.【解析】试题分析:(Ⅰ)对应抽象函数,一般方法为赋值法. 在()()()1f x y f x f y +=++中,取0x y ==,得(0)1f =-,在()()()1f x y f x f y +=++中,取12x y ==,得(1)1f =,(Ⅱ)在()()()1f x y f x f y +=++中,令x n =,1y =,得(1)()2f n f n +=+,即12n n a a +-=.所以{}n a 是等差数列,公差为2,又首项1(1)1a f ==,所以21n a n =-,*n ∈N .(Ⅲ)研究数列{}nb 是否存在最大项和最小项,关键看通项公式的特征.令2111()()22n a n t -==,则22111()816256n b t t t =-=--,显然102t <≤,又因为N n *∈,所以当12t =,即1n =时,{}n b 的最大项为1316b =.当132t =,即3n =时,{}n b 的最小项为331024b =-解:(Ⅰ)在()()()1f x y f x f y +=++中,取0x y ==,得(0)1f =-,在()()()1f x y f x f y +=++中,取12x y ==,得(1)1f =, 2分(Ⅱ)在()()()1f x y f x f y +=++中,令x n =,1y =,得(1)()2f n f n +=+,即12n n a a +-=. 所以{}n a 是等差数列,公差为2,又首项1(1)1a f ==,所以21n a n =-,*n ∈N . 6分(Ⅲ)数列{}n b 存在最大项和最小项令2111()()22na nt-==,则22111()816256nb t t t=-=--,显然12t<≤,又因为Nn*∈,所以当12t=,即1n=时,{}n b的最大项为1316b=.当132t=,即3n=时,{}n b的最小项为331024b=-. 13分考点:等差数列,赋值法研究抽象函数。
北京市2013-2014朝阳高三上续期期末理科数学含答案-含答案
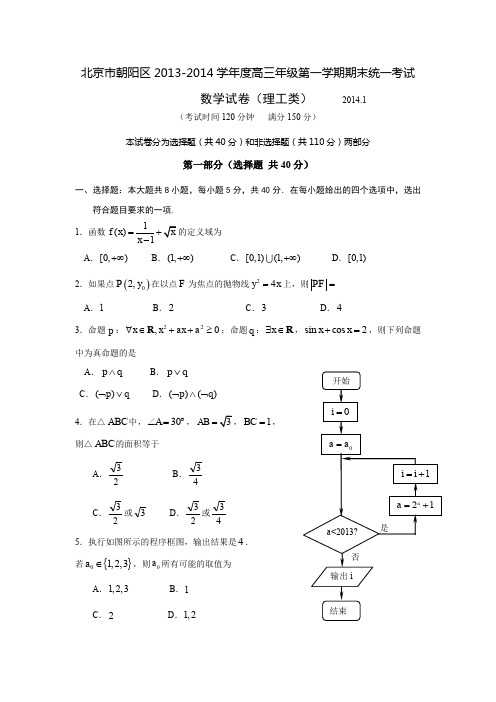
北京市朝阳区2013-2014学年度高三年级第一学期期末统一考试数学试卷(理工类) 2014.1(考试时间120分钟 满分150分)本试卷分为选择题(共40分)和非选择题(共110分)两部分第一部分(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项. 1.函数1()1f x x =+- A .[0,)+∞ B .(1,)+∞ C .[0,1)(1,)+∞ D .[0,1)2.如果点()02,P y 在以点F 为焦点的抛物线24y x =上,则PF = A .1 B .2 C .3 D .43.命题p :22,0x x ax a ∀∈++≥R ;命题q :x ∃∈R ,sin cos 2x x +=,则下列命题中为真命题的是A .p q ∧B .p q ∨C .()p q ⌝∨D .()()p q ⌝∧⌝4.在△ABC 中,︒=∠30A,AB =1BC =, 则△ABC 的面积等于A .23 B .43 C .23或3 D .23或435.执行如图所示的程序框图,输出结果是4. 若{}01,2,3a ∈,则0a 所有可能的取值为A .1,2,3B .1C .2D .1,26.已知正方形的四个顶点分别为(0,0)O ,(1,0)A ,(1,1)B ,(0,1)C ,点,D E 分别在线段,OC AB 上运动,且OD BE =,设AD 与OE 交于点G ,则点G 的轨迹方程是A .(1)(01)y x x x =-≤≤B .(1)(01)x y y y =-≤≤C .2(01)y x x =≤≤ D .21(01)y x x =-≤≤7.已知平面向量a ,b 的夹角为120,且1⋅=-a b ,则||-a b 的最小值为 A .BCD . 18.已知数列{}n a 满足(,01)n n a n k n k *=⋅∈<<N 下面说法正确的是①当12k =时,数列{}n a 为递减数列; ②当112k <<时,数列{}n a 不一定有最大项; ③当102k <<时,数列{}n a 为递减数列;④当1k k-为正整数时,数列{}n a 必有两项相等的最大项.A. ①②B. ②④C. ③④D. ②③第二部分(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上. 9.某校为了解高一学生寒假期间的阅读情况,抽查并统计了100名同学的某一周阅读时间,绘制了频率分布直方图(如图所示),那么这100名学生中阅读时间在[4,8)小时内的人数为_____.10.在各项均为正数的等比数列{}n a 中,若2228log log 1a a +=,则37a a ⋅= . 11.直线y kx =与圆22(2)4x y -+=相交于O ,A两点,若OA k 的值0.040.05 0.12是_____.12.一个三棱锥的三视图如图所示,则该三棱锥的体积是 ;表面积是 .13.实数,x y 满足3,20,x y x y +≥⎧⎨-≤⎩若(2)y k x ≥+恒成立,则实数k 的最大值是 .14.所有真约数(除本身之外的正约数)的和等于它本身的正整数叫做完全数. 如:6=123++;28=124714++++;496=1248163162124248++++++++.已经证明:若21n-是质数,则12(21)n n --是完全数,n *∈N .请写出一个四位完全数 ;又623=⨯,所以6的所有正约数之和可表示为(12)(13)+⋅+;22827=⨯,所以28的所有正约数之和可表示为2(122)(17)++⋅+;按此规律,496的所有正约数之和可表示为 .三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本题满分13分)已知函数2()cos sin 1f x x x =--+. (Ⅰ)求函数)(x f 的最小值; (Ⅱ)若5()16f α=,求cos2α的值.俯视图 侧视图正视图16.(本题满分13分)甲、乙两名同学参加“汉字听写大赛”选拔测试,在相同测试条件下,两人5次测试的成绩(单位:分)如下表:(Ⅰ)请画出甲、乙两人成绩的茎叶图. 你认为选派谁参赛更好?说明理由(不用计算); (Ⅱ)若从甲、乙两人5次的成绩中各随机抽取一个成绩进行分析,设抽到的两个成绩中,90分以上的个数为X ,求随机变量X 的分布列和期望EX .17.(本题满分14分)如图,在三棱锥P -ABC 中,PA ⊥平面ABC ,AB AC ⊥. (Ⅰ)求证:AC ⊥PB ;(Ⅱ)设,O D 分别为,AC AP 的中点,点G 为△OAB 内一点,且满足13OG OA OB =+(), 求证:DG ∥面PBC ;(Ⅲ)若==2AB AC ,=4PA , 求二面角A PB C --的余弦值.18.(本题满分13分)已知函数()()ln f x x a x =-,a ∈R . (Ⅰ)当0a =时,求函数()f x 的极小值;(Ⅱ)若函数()f x 在(0,)+∞上为增函数,求a 的取值范围.PDOACG19.已知椭圆C 两焦点坐标分别为1(F ,2F ,且经过点1)2P . (Ⅰ)求椭圆C 的标准方程;(Ⅱ)已知点(0,1)A -,直线l 与椭圆C 交于两点,M N .若△AMN 是以A 为直角顶点的等腰直角三角形,试求直线l 的方程.20.(本题满分13分)已知,,a b c 是正数, 1lg a a =,2lg a b =,3lg a c =. (Ⅰ)若,,a b c 成等差数列,比较12a a -与23a a -的大小;(Ⅱ)若122331a a a a a a ->->-,则,,a b c 三个数中,哪个数最大,请说明理由;(Ⅲ)若a t =,2b t =,3c t =(t *∈N ),且1a ,2a ,3a 的整数部分分别是,m 21,m +221,m +求所有t 的值.北京市朝阳区2013-2014学年度高三年级第一学期期末统一考试数学答案(理工类) 2014.1三、解答题15.解:(Ⅰ)因为2()cos sin 1f x x x =--+ 2sin sin x x =- 211(sin )24x =--, 又[]sin 1,1x ∈-,所以当1sin 2x =时,函数)(x f 的最小值为14-.…… 6分(Ⅱ)由(Ⅰ)得2115(sin )2416α--=,所以219(sin )216α-=.于是5sin 4α=(舍)或1sin 4α=-.又2217cos 212sin 12()48αα=-=--=. ……………… 13分16.解:(Ⅰ)茎叶图如右图所示,由图可知,乙的平均成绩大于甲的平均成绩,且乙的方差小于甲的方差,因此应选派乙参赛更好. ……………… 6分 (Ⅱ)随机变量X 的所有可能取值为0,1,2.1144115516(0)25C C P X C C ===, 14115528(1)25C P X C C ===, 115511(2)25P X C C ===, 随机变量X 的分布列是:160122525255EX =⨯+⨯+⨯=. ……………… 13分17.证明:(Ⅰ)因为PA ⊥平面ABC ,AC ⊂平面ABC ,所以PA AC ⊥.又因为AB AC ⊥,且PA AB=A ,所以AC ⊥平面PAB . 又因为PB ⊂平面PAB ,所以AC ⊥PB . ……………… 4分(Ⅱ)解法1:因为PA ⊥平面ABC ,所以PA AB ⊥,PA AC ⊥.又因为AB AC ⊥,8 7 5 6 9826 甲 乙5 57 2 58 5所以建立如图所示的空间直角坐标系A xyz -. 设=2AC a ,=AB b ,=2PA c , 则(0,0,0)A ,(0,,0)B b ,(2,0,0)C a ,(0,0,2),(0,0,)P c D c ,(,0,0)O a .又因为13OG OA OB =+(), 所以(,,0)33a b G . 于是(,,)33a b DG c =-,(2,,0)BC a b =-,(0,,2)PB b c =-.设平面PBC 的一个法向量000(,,)x y z =n ,则有0,0BC PB ⎧⋅=⎪⎨⋅=⎪⎩n n .即000020,20.ax by by cz -=⎧⎨-=⎩不妨设01z =,则有002,c c y x b a ==,所以2(,,1)c ca b=n . 因为22(,,1)(,,)1()03333c c a b c a c bDG c c a b a b ⋅=⋅-=⋅+⋅+⋅-=n ,所以DG ⊥n .又因为DG ⊄平面PBC ,所以DG ∥平面PBC . ……………… 9分解法2:取AB 中点E ,连OE ,则1()2OE OA OB =+. 由已知13OG OA OB =+()可得23OG OE =, 则点G 在OE 上.连结AG 并延长交CB 于F ,连PF .因为,O E 分别为,AC AB 的中点, 所以OE ∥BC ,即G 为AF 的中点. 又因为D 为线段PA 的中点, 所以DG ∥PF .又DG ⊄平面PBC ,PF ⊂平面PBC , 所以DG ∥平面PBC .……………… 9分CPDOAGEF(Ⅲ)由(Ⅱ)可知平面PBC 的一个法向量2(,,1)(2,2,1)c ca b==n . 又因为AC ⊥面PAB ,所以面PAB 的一个法向量是(2,0,0)AC =. 又42cos ,323AC AC AC⋅===⨯⋅n n n , 由图可知,二面角A PB C --为锐角,所以二面角A PB C --的余弦值为23. ……………… 14分 18. 解:(Ⅰ)定义域(0,)+∞.当0a =时,()ln f x x x =,()ln 1f x x '=+. 令()0f x '=,得1ex =. 当1(0,)ex ∈时,()0f x '<,()f x 为减函数; 当1(,)ex ∈+∞时,()0f x '>,()f x 为增函数.所以函数()f x 的极小值是11()e e f =-. ……………… 5分(Ⅱ)由已知得()ln x af x x x-'=+.因为函数()f x 在(0,)+∞是增函数,所以()0f x '≥,对(0,)x ∈+∞恒成立. 由()0f x '≥得ln 0x ax x-+≥,即ln x x x a +≥对(0,)x ∈+∞恒成立. 设()ln g x x x x =+,要使“ln x x x a +≥对(0,)x ∈+∞恒成立”,只要min ()a g x ≤. 因为()ln 2g x x '=+,令()0g x '=得21ex =. 当21(0,)ex ∈时,()0g x '<,()g x 为减函数; 当21(,)ex ∈+∞时,()0g x '>,()g x 为增函数. 所以()g x 在()0,+∞上的最小值是2211()e eg =-.故函数()f x 在(0,)+∞是增函数时,实数a 的取值范围是21(,]e -∞-…… 13分 19.解:(Ⅰ)设椭圆标准方程为22221(0)x y a b a b+=>>.依题意1224a PF PF =+==,所以2a =.又c =2221b a c =-=.于是椭圆C 的标准方程为2214x y +=. ……………… 5分 (Ⅱ)依题意,显然直线l 斜率存在.设直线l 的方程为y kx m =+,则由2214x y y kx m ⎧+=⎪⎨⎪=+⎩得222(41)8440k x kmx m +++-=. 因为2222644(41)(44)0k m k m ∆=-+->,得22410k m -+>. ……………… ①设1122(,),(,)M x y N x y ,线段MN 中点为00(,)Q x y ,则12221228414441km x x k m x x k ⎧+=-⎪⎪+⎨-⎪=⎪+⎩于是000224,4141km mx y kx m k k =-=+=++. 因为AM AN =,线段MN 中点为Q ,所以AQ MN ⊥. (1)当00x ≠,即0k ≠且0m ≠时,0011y k x +=-,整理得2341m k =+. ………………② 因为AM AN ⊥,1122(,1),(,1)AM x y AN x y =+=+,所以2212121212(1)(1)(1)(1)()21AM AN x x y y k x x k m x x m m =+++=+++++++22222448(1)(1)()2104141m kmk k m m m k k -=+++-+++=++,整理得25230m m +-=,解得35m =或1m =-. 当1m =-时,由②不合题意舍去. 由①②知,35m =时,k =.(2)当00x =时,(ⅰ)若0k =时,直线l 的方程为y m =,代入椭圆方程中得x =±.设()M m -,)N m ,依题意,若△AMN 为等腰直角三角形,则AQ QN =.即1m =+,解得1m =-或35m =.1m =-不合题意舍去, 即此时直线l 的方程为35y =. (ⅱ)若0k ≠且0m =时,即直线l 过原点.依椭圆的对称性有(0,0)Q ,则依题意不能有AQ MN ⊥,即此时不满足△AMN 为等腰直角三角形.综上,直线l 的方程为35y =530y -+=530y +-=. ………………14分 20.解:(Ⅰ)由已知得1223()()a a a a ---=2lg lg lg a b acb c b-=.因为,,a b c 成等差数列,所以2a cb +=,则1223()()a a a a ---=24lg()aca c +, 因为222a c ac +≥,所以2()4a c ac +≥,即241()aca c ≤+, 则1223()()0a a a a ---≤,即12a a -≤23a a -,当且仅当abc ==时等号成立.……………… 4分(Ⅱ)解法1:令12m a a =-,23n a a =-,31p a a =-,依题意,m n p >>且0m n p ++=,所以0m p >>. 故120a a ->,即lg lg a b >;且130a a ->,即lg lg a c >. 所以a b >且a c >. 故,,a b c 三个数中,a 最大. 解法2:依题意lglg lg a b c b c a >>,即a b c b c a>>. 因为0,0,0a b c >>>,所以2ac b >,2a bc >,2ab c >. 于是,3abc b >,3a abc >,3abc c >, 所以33a b >,33a c >.因为3y x =在R 上为增函数,所以a b >且a c >.故,,a b c 三个数中,a 最大. ……………… 8分(Ⅲ)依题意,lg t ,2lg t ,3lg t 的整数部分分别是,m 21,m +221m +,则l g 1m t m ≤<+, 所以22lg 22m t m ≤<+.又2lg 2lg t t =,则2lg t 的整数部分是2m 或21m +.当212m m +=时,1m =;当2121m m +=+时,0,2m =.(1) 当0m =时,lg t ,2lg t ,3lg t 的整数部分分别是0,1,1,所以0lg 1t ≤<,21lg 2t ≤<,31lg 2t ≤<.所以12lg 23t ≤<,解得21321010t ≤<. 又因为()12103,4∈,()23104,5∈,所以此时4t =.(2)当1m =时,同理可得1lg 2t ≤<,22lg 3t ≤<,33lg 4t ≤<. 所以41lg 3t ≤<,解得431010t ≤<.又()431021,22∈,此时10,11,12,...20,21t =. (3)当2m =时,同理可得2lg 3t ≤<,25lg 6t ≤<,39lg 10t ≤<,同时满足条件的t 不存在.综上所述4,10,11,12,...20,21t =. ……………… 13分。
2014北京各区高考数学二模试题及答案解析

2014北京各区高考数学二模
试题及答案解析
2014年北京市各县区的高考二模对于测验高三考生的复习成果和接下来的高考志愿填报具有非常重要的参考价值。
本人特将一模试题进行整理汇总,以下是2014年北京各城区高考二模试题及答案汇总,供考生
参考!
北京市西城区2014年高三二模试卷
数 学(理科) 2014.5
第Ⅰ卷(选择题 共40分)
一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合
题目要求的一项.
1.已知集合{|20}A x x =-<,{|}B x x a =<,若A B A =,
则实数a 的取值范围是( ) (A )(,2]-∞-
(B )[2,)-+∞
(C )(,2]-∞
(D )[2,)+∞
2.在复平面内,复数2
=(12i)z +对应的点位于( ) (A )第一象限 (B )第二象限 (C )第三象限
(D )第四象限
3.直线2y x =为双曲线22
22 1(0,0)x y C a b a b
-=>>:的一条渐近线,则双曲线C 的离心率是( )
(A (B (C
(D。
2014年北京市朝阳区高三二模数学(理)试题和答案

北京市朝阳区高三年级第二次综合练习数学学科测试(理工类)2014.5(考试时间120分钟 满分150分)本试卷分为选择题(共40分)和非选择题(共110分)两部分第一部分(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项. (1)已知集合{230}A x x =∈-≥R ,集合2{320}B x x x =∈-+<R ,则A B =(A )32x x ⎧⎫≥⎨⎬⎩⎭ (B )322x x ⎧⎫≤<⎨⎬⎩⎭ (C ){}12x x << (D )322x x ⎧⎫<<⎨⎬⎩⎭(2)如果0a b >>,那么下列不等式一定成立的是(A )33log log a b < (B )11()()44a b > (C )11a b< (D )22a b <(3)执行如右图所示的程序框图.若输出的结果为2,则输入的正整数a 的可能取值的集合是 (A ){}1,2,3,4,5(B ){}1,2,3,4,5,6(C ){}2,3,4,5(D ){}2,3,4,5,6(4)已知函数()π()sin (0,0,)2f x A x A ωϕωϕ=+>><的部分图象如图所示,则ϕ= (A )π6- (B )6π(C )π3- (D )π3(5)已知命题p :复数1iiz +=在复平面内所对应的点位于第四象限;命题q :0x ∃>,cos x x =,则下列命题中为真命题的是(A )()()p q ⌝∧⌝ (B )()p q ⌝∧ (C )()p q ∧⌝ (D )p q ∧(6)若双曲线2221(0)y x b b-=>的一条渐近线与圆22(2)1x y +-=至多有一个交点,则双曲线离心率的取值范围是(A )(1,2] (B )[2,)+∞(C) (D))+∞(7)某工厂分别生产甲、乙两种产品1箱时所需要的煤、电以及获得的纯利润如上表所示.若生产甲、乙两种产品可使用的煤不超过120吨,电不超过60千度,则可获得的最大纯利润和是(A )60万元 (B )80万元(C )90万元(D )100万元 (8)如图放置的边长为1的正△PMN 沿边长为3的正方形ABCD动.当△PMN 沿正方形各边滚动一周后,回到初始位置时,点P 的轨迹长度是 (A )83π (B )163π(C )4π (D )5π 第二部分(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上.(9)已知平面向量a ,b 满足1=a ,2=b ,a 与b 的夹角为60︒,则2+=a b ____. (10)5(12)x -的展开式中3x 项的系数为___.(用数字表示)(11)如图,AB 为圆O 的直径,2AB =,过圆O 上一点M 作圆O 的切线,交AB 的延长线于点C ,过点M 作MD AB ⊥于点D ,若D 是OB 中点,则AC BC ⋅=_____. (12)由两个四棱锥组合而成的空间几何体的三视图如图所示, 则其体积是 ;表面积是 .(13)已知数列{}n a 的前n 项和为n S ,且满足24()n n S a n *=-∈N ,则n a = ;数列2{log }n a 的前n 项和为 .(14)若存在正实数M ,对于任意(1,)x ∈+∞,都有()f x M ≤,则称函数()f x 在(1,)+∞ 上是有界函数.下列函数①1()1f x x =-;②2()1x f x x =+;③ln ()xf x x =; 22俯视图侧视图正视图(第12题图)④()sinf x x x=,其中“在(1,)+∞上是有界函数”的序号为.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.(15)(本小题满分13分)在△ABC中,角A,B,C的对边分别是a,b,c,且A2π=,3b=,△ABC的面积.(Ⅰ)求边a的长;(Ⅱ)求cos2B的值.(16)(本小题满分13分)某市规定,高中学生三年在校期间参加不少于80小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段[)75,80,[)80,85,[)85,90,[)90,95,[]95,100(单位:小时)进行统计,其频率分布直方图如图所示.(Ⅰ)求抽取的200位学生中,参加社区服务时间不少于90小时的学生人数,并估计从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的概率;(Ⅱ)从全市高中学生(人数很多)中任意选取3位学生,记ξ为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量ξ的分布列和数学期望Eξ.(17)(本小题满分14分)如图,在四棱锥P ABCD-中,底面ABCD是正方形,侧面PAD⊥底面ABCD,E,F分别为PA,BD中点,2PA PD AD===.(Ⅰ)求证:EF∥平面PBC;(Ⅱ)求二面角E DF A--的余弦值;(Ⅲ)在棱PC上是否存在一点G,使GF⊥平面EDF?若存在,指出点G的位置;若不存在,说明理由.(18)(本小题满分13分)已知函数21()e1xf x ax+=-+,a∈R.(Ⅰ)若曲线()y f x=在点(0,(0))f处的切线与直线e10x y++=垂直,求a的值;(Ⅱ)求函数()f x的单调区间;(Ⅲ)设32ea<,当[0,1]x∈时,都有()f x≥1成立,求实数a的取值范围.(19)(本小题满分14分)已知椭圆C的中心在原点O,焦点在x轴上,离心率为12,右焦点到右顶点的距离为1.(Ⅰ)求椭圆C的标准方程;(Ⅱ)是否存在与椭圆C交于,A B两点的直线l:()y kx m k=+∈R,使得22OA OB OA OB+=-成立?若存在,求出实数m的取值范围,若不存在,请说明理由.(20)(本小题满分13分)已知1x,2x是函数2()f x x mx t=++的两个零点,其中常数m,t∈Z,设12()nn r rnrT x x n-*==∈∑N.(Ⅰ)用m,t表示1T,2T;(Ⅱ)求证:543T mT tT=--;(Ⅲ)求证:对任意的,nn T*∈∈N Z.北京市朝阳区高三年级第二次综合练习数学学科测试(理工类)2014.515.(本小题满分13分)解:(Ⅰ)由1sin2ABCS bc A∆=得,13sin23ABCS c∆2π=⨯⨯=.所以5c=.由2222cosa b c bc A=+-得,22235235cos493a2π=+-⨯⨯⨯=,所以7a=.……………7分(Ⅱ)由sin sina bA B=3sin B=,所以sin14B=.所以271cos212sin98B B=-=.…………13分FABCDPE服务时间/小时16.(本小题满分13分)解:(Ⅰ)根据题意,参加社区服务时间在时间段[)90,95小时的学生人数为2000.060560⨯⨯=(人),参加社区服务时间在时间段[]95,100小时的学生人数为2000.020520⨯⨯=(人).所以抽取的200位学生中,参加社区服务时间不少于90小时的学生人数为80人.所以从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的概率估计为6020802.2002005P +===…………5分(Ⅱ)由(Ⅰ)可知,从全市高中生中任意选取1人,其参加社区服务时间不少于90小时的概率为2.5由已知得,随机变量ξ的可能取值为0,1,2,3.所以0031123323272354(0)()();(1)()()5512555125P C P C ξξ==⋅===⋅=; 221330332336238(2)()();(3)()()5512555125P C P C ξξ==⋅===⋅=.随机变量ξ的分布列如右表。
2014年北京市朝阳区高三二模数学(理)试题及答案

北京市朝阳区高三年级第二次综合练习数学学科测试(理工类)2014.5(考试时间120分钟 满分150分)本试卷分为选择题(共40分)和非选择题(共110分)两部分第一部分(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.(1)已知集合{230}A x x =∈-≥R ,集合2{320}B x x x =∈-+<R ,则AB =(A )32x x ⎧⎫≥⎨⎬⎩⎭ (B )322x x ⎧⎫≤<⎨⎬⎩⎭ (C ){}12x x << (D )322x x ⎧⎫<<⎨⎬⎩⎭(2)如果0a b >>,那么下列不等式一定成立的是(A )33log log a b < (B )11()()44a b > (C )11a b< (D )22a b <(3)执行如右图所示的程序框图.若输出的结果为2,则输入的正整数a 的可能取值的集合是 (A ){}1,2,3,4,5(B ){}1,2,3,4,5,6(C ){}2,3,4,5(D ){}2,3,4,5,6(4)已知函数()π()sin (0,0,)2f x A x A ωϕωϕ=+>><的部分图象如图所示,则ϕ= (A )π6- (B )6π(C )π3- (D )π3(5)已知命题p :复数1i iz +=在复平面内所对应的点位于第四象限;命题q :0x ∃>,cos x x =,则下列命题中为真命题的是(A )()()p q ⌝∧⌝ (B )()p q ⌝∧ (C )()p q ∧⌝ (D )p q ∧(6)若双曲线2221(0)y x b b-=>的一条渐近线与圆22(2)1x y +-=至多有一个交点,则双曲线离心率的取值范围是 (A )(1,2] (B )[2,)+∞(C) (D))+∞(7)某工厂分别生产甲、乙两种产品1箱时所需要的煤、电以及获得的纯利润如上表所示.若生产甲、乙两种产品可使用的煤不超过120吨,电不超过60千度,则可获得的最大纯利润和是(A )60万元 (B )80万元(C )90万元(D )100万元 (8)如图放置的边长为1的正△PMN 沿边长为3的正方形ABCD 的各边内侧逆时针方向滚动.当△PMN 沿正方形各边滚动一周后,回到初始位置时,点P 的轨迹长度是 (A )83π (B )163π(C )4π (D )5π 第二部分(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上.(9)已知平面向量a ,b 满足1=a ,2=b ,a 与b 的夹角为60︒,则2+=a b ____. (10)5(12)x -的展开式中3x 项的系数为___.(用数字表示)(11)如图,AB 为圆O 的直径,2AB =,过圆O 上一点M 作圆O 的切线,交AB 的延长线于点C ,过点M 作MD AB ⊥于点D ,若D 是OB 中点,则AC BC ⋅=_____. (12)由两个四棱锥组合而成的空间几何体的三视图如图所示, 则其体积是 ;表面积是 .(13)已知数列{}n a 的前n 项和为n S ,且满足24()n n S a n *=-∈N ,则n a = ;数列2{log }n a 的前n 项和为 .(14)若存在正实数M ,对于任意(1,)x ∈+∞,都有()f x M ≤,则称函数()f x 在(1,)+∞ 上是有界函数.下列函数①1()1f x x =-;②2()1x f x x =+;③ln ()xf x x =; ④()sin f x x x =,其中“在(1,)+∞上是有界函数”的序号为 .三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.(第11题图)22俯视图侧视图正视图(第12题图)A(15)(本小题满分13分)在△ABC中,角A,B,C的对边分别是a,b,c,且A2π=,3b=,△ABC的面积.(Ⅰ)求边a的长;(Ⅱ)求cos2B的值.(16)(本小题满分13分)某市规定,高中学生三年在校期间参加不少于80小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段[)75,80,[)80,85,[)85,90,[)90,95,[]95,100(单位:小时)进行统计,其频率分布直方图如图所示.(Ⅰ)求抽取的200位学生中,参加社区服务时间不少于90小时的学生人数,并估计从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的概率;(Ⅱ)从全市高中学生(人数很多)中任意选取3位学生,记ξ为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量ξ的分布列和数学期望Eξ.(17)(本小题满分14分)如图,在四棱锥P ABCD-中,底面ABCD是正方形,侧面PAD⊥底面ABCD,E,F分别为PA,BD中点,2PA PD AD===.(Ⅰ)求证:EF∥平面PBC;(Ⅱ)求二面角E DF A--的余弦值;(Ⅲ)在棱PC上是否存在一点G,使GF⊥平面EDF?若存在,指出点G的位置;若不存在,说明理由.(18)(本小题满分13分)已知函数21()e1xf x ax+=-+,a∈R.(Ⅰ)若曲线()y f x=在点(0,(0))f处的切线与直线e10x y++=垂直,求a的值;(Ⅱ)求函数()f x的单调区间;(Ⅲ)设32ea<,当[0,1]x∈时,都有()f x≥1成立,求实数a的取值范围.(19)(本小题满分14分)已知椭圆C的中心在原点O,焦点在x轴上,离心率为12,右焦点到右顶点的距离为1.(Ⅰ)求椭圆C的标准方程;(Ⅱ)是否存在与椭圆C交于,A B两点的直线l:()y kx m k=+∈R,使得22OA OB OA OB+=-成立?若存在,求出实数m的取值范围,若不存在,请说明理由.(20)(本小题满分13分)已知1x,2x是函数2()f x x mx t=++的两个零点,其中常数m,t∈Z,设12()nn r rnrT x x n-*==∈∑N.(Ⅰ)用m,t表示1T,2T;(Ⅱ)求证:543T mT tT=--;(Ⅲ)求证:对任意的,nn T*∈∈N Z.北京市朝阳区高三年级第二次综合练习数学学科测试(理工类)2014.515.(本小题满分13分)解:(Ⅰ)由1sin2ABCS bc A∆=得,13sin23ABCS c∆2π=⨯⨯.所以5c=.由2222cosa b c bc A=+-得,22235235cos493a2π=+-⨯⨯⨯=,所以7a=.……………7分(Ⅱ)由sin sina bA B=3sin B=,所以sin B=271cos212sin98B B=-=.…………13分16.(本小题满分13分)解:(Ⅰ)根据题意,参加社区服务时间在时间段[)90,95小时的学生人数为2000.060560⨯⨯=(人),参加社区服务时间在时间段[]95,100小时的学生人数为2000.020520⨯⨯=(人).所以抽取的200位学生中,参加社区服务时间不少于90小时的学生人数为80人.所以从全市高中学生中任意选取一人,其参加社区服务时间不少于90FABCDPE服务时间/小时小时的概率估计为6020802.2002005P +===…………5分(Ⅱ)由(Ⅰ)可知,从全市高中生中任意选取1人,其参加社区服务时间不少于90小时的概率为2.5由已知得,随机变量ξ的可能取值为0,1,2,3.所以0031123323272354(0)()();(1)()()5512555125P C P C ξξ==⋅===⋅=; 221330332336238(2)()();(3)()()5512555125P C P C ξξ==⋅===⋅=.随机变量ξ的分布列如右表。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京市朝阳2014届高三二模理科数学试卷(带解析)1.已知集合{230}A x x =∈-≥R ,集合2{320}B x x x =∈-+<R ,则AB =( )(A )32x x ⎧⎫≥⎨⎬⎩⎭ (B )322x x ⎧⎫≤<⎨⎬⎩⎭ (C ){}12x x << (D )322x x ⎧⎫<<⎨⎬⎩⎭【答案】B【解析】试题分析:3{230}[,).2A x x =∈-≥=+∞R 2{320}(1,2).B x x x =∈-+<=R 所以A B =322x x ⎧⎫≤<⎨⎬⎩⎭.考点:集合运算2.如果0a b >>,那么下列不等式一定成立的是( )(A )33log log a b < (B )11()()44a b>(C )11a b< (D )22a b < 【答案】C 【解析】试题分析:33log log ,a b a b <⇔<11()(),44a b a b >⇔<110b a a b ab -<⇔<,又0a b >>所以0b aab -<成立,22||||a b a b <⇔<,而0a b >>,所以||||a b <不成立. 考点:不等式恒等变形3.执行如图所示的程序框图.若输出的结果为2,则输入的正整数a 的可能取值的集合是( )(A ){}1,2,3,4,5 (B ){}1,2,3,4,5,6 (C ){}2,3,4,5 (D ){}2,3,4,5,6【答案】C 【解析】试题分析:因为输出的结果为2,所以2313,2(23)313a a +≤++>,即75,4a <≤又a 为正整数,所以a 的可能取值的集合是{}2,3,4,5考点:循环结构流程图4.已知函数()π()sin (0,0,)2f x A x A ωϕωϕ=+>><的部分图象如图所示,则ϕ=( )(A )π6- (B )6π(C )π3- (D )π3【答案】D 【解析】试题分析:由题意得:2,, 2.24312T T A T ππππω=-====,又sin(2)112πϕ⨯+=,π2ϕ<,所以π3ϕ=.考点:三角函数图像与性质 5.已知命题p :复数1iiz +=在复平面内所对应的点位于第四象限;命题q :0x ∃>,cos x x =,则下列命题中为真命题的是( )(A )()()p q ⌝∧⌝ (B )()p q ⌝∧ (C )()p q ∧⌝ (D )p q ∧ 【答案】D 【解析】试题分析:因为1i 1i z i +==-,所以复数1ii z +=在复平面内所对应的点位于第四象限,命题p 为真命题,因为y x =与cos y x =在(0,)2π上有交点,所以0x ∃>,cos x x =,命题q 为真命题,p q ∧为真命题.考点:复合命题真假6.若双曲线2221(0)y x b b-=>的一条渐近线与圆22(2)1x y +-=至多有一个交点,则双曲线离心率的取值范围是( )(A )(1,2] (B )[2,)+∞ (C)(1 (D))+∞ 【答案】A 【解析】试题分析:双曲线2221(0)y x b b -=>的一条渐近线为y bx =,由题意得:圆心到渐近线的2222211,3,4,1 2.1c b b e e a +≥≤==≤<≤考点:双曲线渐近线若生产甲、乙两种产品可使用的煤不超过120吨,电不超过60千度,则可获得的最大纯利润和是( )(A )60万元 (B )80万元 (C )90万元 (D )100万元 【答案】C 【解析】试题分析:设生产甲x 吨、乙y 吨.则312060,0x y x y x y +≤⎧⎪+≤⎨⎪>⎩,利润2z x y =+.可行域为一个四边形OABC 及其内部,其中(60,0),(30,30),(0,40)A B C ,当2z x y =+过点B 时取最大值,为90.考点:线性规划8.如图放置的边长为1的正△PMN 沿边长为3的正方形ABCD 的各边内侧逆时针方向滚动.当△PMN 沿正方形各边滚动一周后,回到初始位置时,点P 的轨迹长度是( ) (A )83π (B )163π (C )4π (D )5πBA【答案】B 【解析】试题分析:由题意得:当△PMN 沿正方形一边滚动时,点P 的轨迹为两个圆弧,其对应圆半径皆为1,圆心角为23π,因此点P 的轨迹长度是21624.33ππ⨯⨯=考点:动点轨迹9.已知平面向量a ,b 满足1=a ,2=b ,a 与b 的夹角为60︒,则2+=a b ____.【答案】【解析】试题分析:因为2221244122+=++⋅⨯⨯=a b a b a b =4+4+42,所以2+=a b考点:向量数量积10.5(12)x -的展开式中3x 项的系数为___.(用数字表示) 【答案】80- 【解析】试题分析:由15(2)r r r T C x +=-得:3x 项的系数为335(2)80.C -=-.考点:二项展开式定理求特定项11.如图,AB 为圆O 的直径,2AB =,过圆O 上一点M 作圆O 的切线,交AB 的延长线于点C ,过点M 作MD AB ⊥于点D ,若D 是OB 中点,则AC BC ⋅=_____.【答案】3 【解析】试题分析:由切割线定理得:2AC BC CM ⋅=,连OM ,则在直角三角形ODM 中,因为OM=2OD,所以60DOM ∠=,因此CM = 3.AC BC ⋅=考点:切割线定理12.由两个四棱锥组合而成的空间几何体的三视图如图所示,则其体积是 ;表面积是 .【解析】2的正方形.因此体积为212233⨯=表面积为8个全等的边长为2的等边三角形面积之和,即282= 考点:三视图13.已知数列{}n a 的前n 项和为n S ,且满足24()n n S a n *=-∈N ,则n a = ; 数列2{log }n a 的前n 项和为 . 【答案】12n +,(3)2n n + 【解析】试题分析:因为24,n n S a =-所以1124(2)n n S a n --=-≥,两式相减得1122,2n n n n n a a a a a --=-=.因此{}n a 为等比数列,又11124,4S a a =-=,所以11422.n n n a -+=⋅=因此2log 1,n a n =+前n 项和为(21)(3)22n n n n +++=.考点:已知n S 求.n a14.若存在正实数M ,对于任意(1,)x ∈+∞,都有()f x M ≤,则称函数()f x 在(1,)+∞ 上是有界函数.下列函数①1()1f x x =-; ②2()1x f x x =+; ③ln ()xf x x=; ④()sin f x x x =,其中“在(1,)+∞上是有界函数”的序号为 . 【答案】②③【解析】试题分析:因为(1,)x ∈+∞时,1()(0,)1f x x =∈+∞-,所以函数①不是有界函数.因为(1,)x ∈+∞时,21|()|122x x f x x x =≤=+,所以函数②是有界函数.因为(1,)x ∈+∞时,2l n 1l n (),()x x f x f x x x-'==,()f x 在(1,)e 单调增,在(,)e +∞上单调减,所以函数10()()f x f e e<≤=,因此③是有界函数.因为(1,)x ∈+∞时,取2()2x k k z ππ=+∈,则()sin f x x x x ==→+∞,所以函数④不是有界函数.考点:函数值域15.在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,且3A 2π=,3b =,△ABC的面积为4. (Ⅰ)求边a 的长; (Ⅱ)求cos 2B 的值. 【答案】(Ⅰ)7a =,(Ⅱ)71.98【解析】试题分析:(Ⅰ)解三角形问题,一般利用正余弦定理进行边角转化. 由1sin 2ABC S bc A ∆=得,13sin 234ABC S c ∆2π=⨯⨯=.所以5c =.由余弦定理2222cos a b c bc A =+-得,22235235cos 493a 2π=+-⨯⨯⨯=,所以7a =.(Ⅱ)由正弦定理得sin sin a bA B =,即3sin B=,所以sin 14B =,根据二倍角公式有271cos 212sin 98B B =-=. 解:(Ⅰ)由1sin 2ABC S bc A ∆=得,13sin 234ABC S c ∆2π=⨯⨯=. 所以5c =.由2222cos a b c bc A =+-得,22235235cos493a 2π=+-⨯⨯⨯=, 所以7a =. 7分(Ⅱ)由sin sin a b A B =得,3sin B=,所以sin B =所以271cos 212sin 98B B =-=. 13分 考点:正余弦定理,二倍角公式16.某市规定,高中学生三年在校期间参加不少于80小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段[)75,80,[)80,85,[)85,90,[)90,95,[]95,100(单位:小时)进行统计,其频率分布直方图如图所示.(Ⅰ)求抽取的200位学生中,参加社区服务时间不少于90小时的学生人数,并估计 从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的概率;(Ⅱ)从全市高中学生(人数很多)中任意选取3位学生,记ξ为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量ξ的分布列和数学期望E ξ.【答案】(Ⅰ)2.(Ⅱ)6.E ξ=【解析】 试题分析:(Ⅰ)根据频率分布直方图中小长方形面积为频率,而频数为总数与频率之积. 因此参加社区服务时间在时间段[)90,95小时的学生人数为2000.060560⨯⨯=(人),参加社区服务时间在时间段[]95,100小时的学生人数为2000.020520⨯⨯=(人).所以抽取的200位学生中,参加社区服务时间不少于90小时的学生人数为80人.概率估计为6020802.2002005P +===(Ⅱ)随机变量ξ的可能取值为0,1,2,3.由(Ⅰ)可知,概率为2.5因为 ξ~2(3)B ,,所以26355E ξ=⨯=.随机变量ξ的分布列为解:(Ⅰ)根据题意,参加社区服务时间在时间段[)90,95小时的学生人数为2000.060560⨯⨯=(人), 参加社区服务时间在时间段[]95,100小时的学生人数为2000.020520⨯⨯=(人). 所以抽取的200位学生中,参加社区服务时间不少于90小时的学生人数为80人. 所以从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的 概率估计为6020802.2002005P +=== 5分 (Ⅱ)由(Ⅰ)可知,从全市高中生中任意选取1人,其参加社区服务时间不少于90小时的概率为2.5由已知得,随机变量ξ的可能取值为0,1,2,3.所以00332327(0)()()55125P C ξ==⋅=;11232354(1)()()55125P C ξ==⋅=;22132336(2)()()55125P C ξ==⋅=;3303238(3)()()55125P C ξ==⋅=.随机变量ξ的分布列为因为 ξ~2(3)5B ,,所以26355E ξ=⨯=. 13分 考点:频率分布直方图17.如图,在四棱锥P ABCD -中,底面ABCD 是正方形,侧面PAD ⊥底面ABCD ,E ,F 分别为A P ,BD 中点,2PA PD AD ===. (Ⅰ)求证:EF ∥平面BC P ;(Ⅱ)求二面角E DF A --的余弦值;(Ⅲ)在棱C P 上是否存在一点G ,使GF ⊥平面EDF ?若存在,指出点G 的位置;若不存在,说明理由.FABCDP E【答案】(Ⅰ)详见解析,(Ⅱ)5(Ⅲ)不存在. 【解析】 试题分析:(Ⅰ)证明线面平行,关键在于找出线线平行.本题条件含中点,故从中位线上找线线平行. E ,F 分别为A P ,BD 中点,在△PAC 中,E 是A P 中点,F 是AC 中点,所以EF ∥PC .又因为EF ⊄平面PBC ,PC ⊂平面BC P ,所以EF ∥平面BC P .(Ⅱ)求二面角的大小,有两个思路,一是作出二面角的平面角,这要用到三垂线定理及其逆定理,利用侧面PAD ⊥底面ABCD ,可得底面ABCD 的垂线,再作DF 的垂线,就可得二面角的平面角,二是利用空间向量求出大小.首先建立空间坐标系. 取AD 中点O .由侧面PAD ⊥底面ABCD 易得PO ⊥面ABCD .以O 为原点,,,OA OF OP 分别为,,x y z 轴建立空间直角坐标系.再利用两平面法向量的夹角与二面角的平面角的关系,求出结果,(Ⅲ)存在性问题,一般从假设存在出发,构造等量关系,将存在是否转化为方程是否有解.E P DCBAF证明:(Ⅰ)如图,连结AC . 因为底面ABCD 是正方形, 所以AC 与BD 互相平分. 又因为F 是BD 中点,所以F 是AC 中点.在△PAC 中,E 是A P 中点,F 是AC 中点, 所以EF ∥PC .又因为EF ⊄平面PBC ,PC ⊂平面BC P ,所以EF ∥平面BC P . 4分 (Ⅱ)取AD 中点O .在△PAD 中,因为PA PD =, 所以PO AD ⊥.因为面PAD ⊥底面ABCD , 且面PAD 面=ABCD AD , 所以PO ⊥面ABCD . 因为OF ⊂平面ABCD 所以PO OF ⊥.又因为F 是AC 中点, 所以OF AD ⊥.如图,以O 为原点,,,OA OF OP 分别为,,x y z 轴建立空间直角坐标系. 因为2PA PD AD ===,所以OP =则(0,0)O ,(1,0,0)A ,(1,2,0)B ,(1,2,0)C -,(1,0,0)D -,P,1(,0,22E ,(0,1,0)F .于是(0,2,0)AB =,3(2DE =,(1,1,0)DF =. 因为OP ⊥面ABCD,所以OP =是平面FAD 的一个法向量. 设平面EFD 的一个法向量是000=(,,)x y z n .因为0,0,DF DE ⎧⋅=⎪⎨⋅=⎪⎩n n所以00000,30,2x y x z +=⎧⎪⎨+=⎪⎩即0000,.y x z =-⎧⎪⎨=⎪⎩ 令01x =则=(1,1,-n .所以cos ,OP OP OP ⋅<>===⋅n n n. 由图可知,二面角E-DF-A 为锐角,所以二面角E-DF-A . 10分 (Ⅲ)假设在棱C P 上存在一点G ,使GF ⊥面EDF .设111G(,,)x y z ,则111FG =(,1,)x y z -. 由(Ⅱ)可知平面EDF 的一个法向量是=(1,1,-n . 因为GF ⊥面EDF ,所以FG =λn .于是,111,1,x y z λλ=-=-=,即111,1,x y z λλ==-=. 又因为点G 在棱C P 上,所以GC 与PC 共线.因为PC (1,2,=-,111CG (+1,2,)x y z =-, 所以111212x y +--=.所以1112λλ+---= 故在棱C P 上不存在一点G ,使GF ⊥面EDF 成立. 14分 考点:线面平行判定定理,利用空间向量求二面角 18.已知函数21()e 1x f x ax +=-+,a ∈R .(Ⅰ)若曲线()y f x =在点(0,(0))f 处的切线与直线e 10x y ++=垂直,求a 的值; (Ⅱ)求函数()f x 的单调区间;(Ⅲ)设32e a <,当[0,1]x ∈时,都有()f x ≥1成立,求实数a 的取值范围.【答案】(Ⅰ)e a =,(Ⅱ)当0a ≤时,)(x f 的单调增区间为(),-∞+∞;当0a >时,()f x 的单调增区间是11(ln,)222a -+∞,()f x 的单调减区间是11(,ln )222a -∞-. (Ⅲ)22(,e ]-∞.【解析】试题分析:(Ⅰ)利用导数的几何意义,曲线()f x 在点(0,(0))f 处的切线斜率为在点(0,(0))f 处的导数值. 由已知得21()2e x f x a +'=-.所以(0)e f '=.(0)2e e f a '=-=,e a =(Ⅱ)利用导数求函数单调区间,需明确定义域(),-∞+∞,再导数值的符号确定单调区间. 当0a ≤时,()0f x '>,所以)(x f 的单调增区间为(),-∞+∞.当0a >时,令()0f x '>,得11ln 222a x >-,所以()f x 的单调增区间是11(ln ,)222a -+∞;令()0f x '<,得11ln 222a x <-,所以()f x 的单调减区间是11(,ln )222a -∞-.(Ⅲ)不等式恒成立问题,一般利用变量分离转化为最值问题. “当(0,1]x ∈时,21()e 11x f x ax +=-+≥恒成立”等价于“当(0,1]x ∈时,21e x a x +≤恒成立.”设21e ()x g x x+=,只要“当(0,1]x ∈时,min ()a g x ≤成立.” 易得函数()g x 在12x =处取得最小值,所以实数a 的取值范围22(,e ]-∞.(Ⅰ)由已知得21()2e x f x a +'=-.因为曲线()f x 在点(0,(0))f 处的切线与直线e 10x y ++=垂直, 所以(0)e f '=.所以(0)2e e f a '=-=.所以e a =. 3分(Ⅱ)函数()f x 的定义域是(),-∞+∞,21()2e x f x a +'=-.(1)当0a ≤时,()0f x '>成立,所以)(x f 的单调增区间为(),-∞+∞. (2)当0a >时,令()0f x '>,得11ln 222a x >-,所以()f x 的单调增区间是11(ln ,)222a -+∞;令()0f x '<,得11ln 222a x <-,所以()f x 的单调减区间是11(,ln )222a -∞-. 综上所述,当0a ≤时,)(x f 的单调增区间为(),-∞+∞;当0a >时,()f x 的单调增区间是11(ln ,)222a -+∞, ()f x 的单调减区间是11(,ln )222a -∞-. 8分(Ⅲ)当0x =时,(0)e 11f =+≥成立,a ∈R . “当(0,1]x ∈时,21()e11x f x ax +=-+≥恒成立”等价于“当(0,1]x ∈时,21e x a x+≤恒成立.” 设21e ()x g x x+=,只要“当(0,1]x ∈时,min ()a g x ≤成立.”212(21)e ()x x g x x +-'=.令()0g x '<得,12x <且0x ≠,又因为(0,1]x ∈,所以函数()g x 在1(0, )2上为减函数;令()0g x '>得,12x >,又因为(0,1]x ∈,所以函数()g x 在1(,1]2上为增函数.所以函数()g x 在12x =处取得最小值,且21()2e 2g =. 所以22e a ≤. 又因为a 32e <,所以实数a 的取值范围22(,e ]-∞. 13分 (Ⅲ)另解:(1)当0a ≤时,由(Ⅱ)可知, ()f x 在[0,1]上单调递增,所以()(0)e 1f x f ≥=+. 所以当0a ≤时,有()1f x ≥成立.(2)当02e a <≤时, 可得11ln 0222a -≤. 由(Ⅱ)可知当0a >时,()f x 的单调增区间是11(ln ,)222a -+∞,所以()f x 在[0,1]上单调递增,又()(0)e 1f x f ≥=+,所以总有()f x ≥1成立.(3)当32e 2e a <<时,可得110ln 1222a <-<. 由(Ⅱ)可知,函数()f x 在11[0,ln )222a -上为减函数,在11(ln ,1]222a -为增函数,所以函数()f x 在11ln 222a x =-处取最小值,且ln 211(ln )e ln 1ln 122222222a a a a a a af a -=-++=-+.当[0,1]x ∈时,要使()f x ≥1成立,只需ln 1122a aa -+≥,解得22e a ≤.所以22e 2e a <≤. 综上所述,实数a 的取值范围22(,e ]-∞.考点:利用导数求切线,利用导数求单调区间,利用导数求最值 19.已知椭圆C 的中心在原点O ,焦点在x 轴上,离心率为12,右焦点到右顶点的距离为1.(Ⅰ)求椭圆C 的标准方程;(Ⅱ)是否存在与椭圆C 交于,A B 两点的直线l :()y kx m k =+∈R ,使得22OA OB OA OB +=-成立?若存在,求出实数m 的取值范围,若不存在,请说明理由.【答案】(Ⅰ)22143x y +=,(Ⅱ)2(,[21,)7-∞+∞. 【解析】试题分析:(Ⅰ)求椭圆标准方程,关键利用待定系数法求出a,b. 由12c e a ==及1a c -=,解得1c =,2a =.所以2223b a c =-=.所以椭圆C 的标准方程是22143x y +=.(Ⅱ)存在性问题,一般从假设存在出发,建立等量关系,有解就存在,否则不存在. 条件22OA OB OA OB +=-的实质是垂直关系,即0OA OB ⋅=.所以12120x x y y +=.1212()()0x x kx m kx m +++=,221212(1)()0k x x km x x m ++++=,由22,1,43y kx m x y =+⎧⎪⎨+=⎪⎩得222(34)84120k x kmx m +++-=.122834kmx x k +=-+,212241234m x x k -=+.代入化简得,2271212m k =+.由222(8)4(34)(412)0k mk m ∆=-+->化简得2234k m +>.解得,234m >. 由227121212m k =+≥,2127m ≥,所以实数m 的取值范围是2(,[21,)7-∞+∞. (Ⅰ)设椭圆C 的方程为22221x y a b +=()0a b >>,半焦距为c .依题意12c e a ==,由右焦点到右顶点的距离为1,得1a c -=. 解得1c =,2a =.所以2223b a c =-=.所以椭圆C 的标准方程是22143x y +=. 4分(Ⅱ)解:存在直线l ,使得22OA OB OA OB +=-成立.理由如下:由22,1,43y kx m x y =+⎧⎪⎨+=⎪⎩得222(34)84120k x kmx m +++-=.222(8)4(34)(412)0km k m ∆=-+->,化简得2234k m +>.设1122(,),(,)A x y B x y ,则122834km x x k +=-+,212241234m x x k-=+. 若22OA OB OA OB +=-成立,即2222OA OB OA OB +=-,等价于0OA OB ⋅=.所以12120x x y y +=.1212()()0x x kx m kx m +++=,221212(1)()0k x x km x x m ++++=, 222224128(1)03434m kmk km m k k-+⋅-⋅+=++, 化简得,2271212m k =+.将227112k m =-代入2234k m +>中,22734(1)12m m +->, 解得,234m >.又由227121212m k =+≥,2127m ≥,从而2127m ≥,m ≥m ≤ 所以实数m 的取值范围是2(,[21,)7-∞+∞. 14分 考点:椭圆标准方程,直线与椭圆位置关系20.已知1x ,2x 是函数2()f x x mx t =++的两个零点,其中常数m ,t ∈Z ,设120()nn r rn r T x x n -*==∈∑N .(Ⅰ)用m ,t 表示1T ,2T ;(Ⅱ)求证:543T mT tT =--; (Ⅲ)求证:对任意的,n n T *∈∈N Z .【答案】(Ⅰ)1,T m =-22.T m t =-(Ⅱ)详见解析,(Ⅲ)详见解析. 【解析】试题分析:(Ⅰ)由题意得:12x x m +=-,12x x t =.因为120nn r r n r T x x -==∑,所以11112120r r r T x x x x m-===+=-∑.222222212112212120()r r r T x x x x x x x x x x m t -===++=+-=-∑.对抽象的求和符号具体化处理,是解答本题的关键.(Ⅱ)555432234551211212121220,r rr T xx x x x x x x x x x x -===+++++∑而4322343212343121121212212112122()()()mT tT x x x x x x x x x x x x x x x x x x --=+++++-+++5432234432234543223411212121212121212212121212()()x x x x x x x x x x x x x x x x x x x x x x x x x x =+++++++++-+++5432234511212121225x x x x x x x x x x T =+++++=,(Ⅲ)用数学归纳法证明有关自然数的命题. (1)当1,2n =时,由(Ⅰ)问知k T 是整数,结论成立.(2)假设当1,n k =-n k =(2k ≥)时结论成立,即1,k k T T -都是整数,由(Ⅱ)问知11k k k T mT tT +-=--.即1n k =+时,结论也成立. 解:(Ⅰ)由12x x m +=-,12x x t =.因为120nn r r n r T xx-==∑,所以11112120r r r T x x x x m-===+=-∑.222222212112212120()r r r T x x x x x x x x x x m t -===++=+-=-∑. 3分(Ⅱ)由12kk r rk r T xx -==∑,得5454555121122142r r r r r r T xx x x x x x T x --====+=+∑∑. 即55142T x T x =+,同理,44132T x T x =+. 所以5241232x T x x T x =+.所以5142412312412343()()T x T x T x x T x x T x x T mT tT =+-=+-=--. 8分 (Ⅲ)用数学归纳法证明.(1)当1,2n =时,由(Ⅰ)问知k T 是整数,结论成立.(2)假设当1,n k =-n k =(2k ≥)时结论成立,即1,k k T T -都是整数. 由12kk r rk r T xx -==∑,得1111121122k kk r rk r r k k r r T xx x x x x ++--++====+∑∑. 即1112k k k T x T x ++=+.所以112k k k T xT x -=+,121212k k k x T x x T x +-=+.所以11212112121()()k k k k k k T x T x T x x T x x T x x T +--=+-=+-. 即11k k k T mT tT +-=--.由1,k k T T -都是整数,且m ,t ∈Z ,所以1k T +也是整数.即1n k =+时,结论也成立.由(1)(2)可知,对于一切n *∈N ,120nn r r r xx-=∑的值都是整数. 13分考点:数学归纳法证明。
