气象统计方法 第四章 一元线性回归分析
《一元线性回归》课件
使用评价指标对模型的性能进行评估。
《一元线性回归》PPT课 件
一元线性回归是一种用于探索变量之间关系的统计方法。本课件将介绍一元 线性回归的基本概念、模型、参数估计、模型评估以及Python实现。
一元线性回归-简介
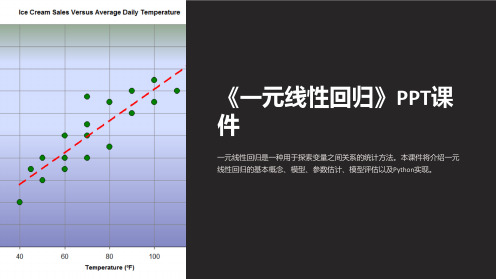
一元线性回归是一种分析两个变量之间线性关系的方法。在这一节中,我们 将介绍一元线性回归的定义、使用场景以及它的重要性。
决定系数
4
方的平均值。
衡量模型对观测值的解释能力,取值范 围从0到1。
一元线性回归-Python实现
导入数据
使用Python的pandas库导入数据集。
划分数据集
将数据集划分为训练集和测试集。
预测结果
使用测试集数据对模型进行预测。
特征工程
选择合适的特征并对其进行处理。
训练模型
使用训练集数据训练线性Байду номын сангаас归模型。
一元线性回归-线性回归模型
1
简单线性回归模型
一个自变量和一个因变量之间的线性关
多元线性回归模型
2
系。
多个自变量和一个因变量之间的线性关
系。
3
线性回归模型的假设
包括线性关系、平均误差为零、误差具 有相同的方差、误差相互独立等。
一元线性回归-模型参数估计
1
最小二乘法
通过最小化观测值和模型预测值之间的平方误差来估计模型参数。
2
矩阵求导
使用矩阵求导的方法来计算模型参数的最优解。
3
梯度下降法
通过迭代的方式逐步优化模型参数,使得模型预测值与观测值之间的差距最小。
一元线性回归-模型评估
1
对模型误差的描述
通过各种指标来描述模型预测值和观测
气象统计分析与预报方法:08-第二章-回归分析4

▪ 感谢阅读
End Of Curve Estimation
➢非线性回归 2
多项式回归
yi 0 1xi 2 xi2 ... p xip ei
可化为线性的曲线回归 初等函数变换
一般的非线性回归
yi f ( xi , ) ei
用Gauss-Newton 法确定系数向量
感谢阅读
▪ 感谢阅读
▪ 感谢阅读
2.20 162.00 5.09
.79
10.00 12.00 2.48 2.30
8.10 19.00 2.94 2.09
Let Y2=ln(Y), X2=ln(X) Then Y2=ln(b)+b1* ln(X)
14.80 7.90 2.07 2.69
5.5
2.80 178.00 5.18 1.03
参数设置 因变量 自变量
Models (Selection)
中文含义
线性 二次曲线 复合函数 生长曲线 对数函数 三次曲线 S--曲线 指数函数 倒数函数 幂函数 逻辑斯谛函数
其它例子: 1)Y=b0+b1t+b2t2 令:X1=t; X2=t2 则化为线性二元回归方程: Y= b0+b1X1+b2X2 2)Y=a X-b exp(-cX) 取对数:ln(Y)=ln(a)-b*ln(X)-c*X
3.00 135.00
200
11.40
8.90
4.80 6.80 10.20
61.60 39.80 10.00
Example 2:power
100
Observed
Cu b i c
0
P ow er
2
4
6
8
气候统计一元线性回归,方差分析,显著性检验

SSR n 2 R xi x yi y / SST i 1
i
i
2 2 2 x x y y r i i xy i 1 i 1 n n
2
可见解释方差反应了两个变量之间的线性关系密切程 度程度。
第二章 回归分析
SST SSR SSE
1 n 2 1 n 2 ˆ s e y y ( x ) 无偏残差平方和: i i i n 2 i 1 n 2 i 1 1 SST SSR n2 n 1 n 2 2 2 2 2 y ny b x nx i i n 2 i 1 i 1
残差方差(MSE),自由度为(n-2):
MSE SST SSR / n 2
第二章
回归分析
回归分析Part I
1. 前言 2. 一元线性回归模型和参数估计 3. 方差分析 4. 相关系数与线性回归 5. 显著性检验
3. 方差分析——方差的无偏估计
第二章
回归分析
回归分析Part I
(4). α,β的最小二乘估计
设 a ,b分别为α,β的估计值,即 ˆ b 则 y a bx e ˆ a,
i i
i
ˆi ˆi a bxi , 残差估计量为 ei yi y 预报量的估计量记为 y
第二章
回归分析
回归分析Part I
1. 前言 2. 一元线性回归模型和参数估计 3. 方差分析 4. 相关系数与线性回归 5. 显著性检验
气象预报业务中最基本的方法之一; 包括一元线性回归、多元回归和非线性回归等。
第二章
回归分析
回归分析Part I
一元线性回归分析

模型评估指标
模型评估指标用于衡量回归模型的拟合优度和预测精度。常用的指标包括均 方误差、决定系数和标准化残差等,可以帮助我们评估模型的有效性和适用 性。
参数估计方法
参数估计是确定回归模型中各个参数的取值的过程。常用的参数估计方法包括最小二乘法、最大似然估 计法和贝叶斯估计法等,可以帮助我们找到最优的参数估计结果。
一元线性回归分析
回归分析是一种用于建立变量之间关系的统计方法。本演示将介绍一元线性 回归模型的构建、参数估计、模型假设检验以及模型预测和应用。
回归分析的概述
回归分析是一种通过建立变量之间的关系来描述和预测现象的统计方法。它 可以帮助我们理解变量之间的因果关系,并从中推断出未知的检验
模型假设检验用于验证回归模型的假设是否成立。常见的假设检验包括检验回归系数的显著性、整体模 型的显著性以及模型的线性关系等,可以帮助我们判断模型是否可靠。
回归诊断和残差分析
回归诊断和残差分析通过检查模型的残差来评估模型的拟合优度和假设的满 足程度。常用的诊断方法包括残差图、QQ图和离群值分析等,可以帮助我们 发现模型的不足和改进方向。
模型预测和应用
回归模型可以用于预测未知观测值,并帮助我们做出决策和制定策略。它在经济学、社会科学、医学等 领域具有广泛的应用,可以为决策者提供有力的数据支持。
气象统计方法气象资料及其表示方法课件

(1)概念 峰度系数与偏度系数是用来衡量随机变量概率
密度分布曲线形状的数字特征,描述了气候变量 的分布特征。
偏度系数:表征曲线峰点对期望值(平均值) 偏离的程度。
峰度系数:表征曲线分布形态顶峰的凸平度 (即渐进于横轴的陡度)。
气象统计方法气象资料及其表示方法
(2)标准偏度系数和峰度系数的计算公式为:
气象统计方法气象资料及其表示方法
气象统计方法气象资料及其表示方法
气象统计方法气象资料及其表示方法
ARGO计划
气象统计方法气象资料及其表示方法
气象监测意义:
1. 记录天气、气候的实际情况 2. 了解气候的基本状况 3. 分析研究气候变化规律 4. 气候预测 (第一张天气图的诞生)
气象统计方法气象资料及其表示方法
气象统计方法气象资料及其表示方法
江苏省气温异常及其标准化
气象统计方法气象资料及其表示方法
降水距平百分率
距平/平均值*100% 1)计算降水距平,即观测值减去平均值 2)1步骤所得结果除以该平均值,乘以100
%,即为降水距平百分比 注意:当观测值序列时间比较长,超过30年,可以
选择1980-2009的平均值,作为步骤1中的平均值
化)。
气象统计方法气象资料及其表示方法
江苏省全年月降水数据分布图
气象统计方法气象资料及其表示方法
第二节 多要素的气象资料
*也可以理解为同一要素多个格点(站点) 的资料,下面慢慢体会。
气象统计方法气象资料及其表示方法
江苏省冬季气温的异常(1958-2007)
气象统计方法气象资料及其表示方法
如何正确计算异常场?
气象统计方法气象资料及其表示方法
从统计学看线性回归(1)——一元线性回归

从统计学看线性回归(1)——⼀元线性回归⽬录1. ⼀元线性回归模型的数学形式2. 回归参数β0 , β1的估计3. 最⼩⼆乘估计的性质 线性性 ⽆偏性 最⼩⽅差性⼀、⼀元线性回归模型的数学形式 ⼀元线性回归是描述两个变量之间相关关系的最简单的回归模型。
⾃变量与因变量间的线性关系的数学结构通常⽤式(1)的形式:y = β0 + β1x + ε (1)其中两个变量y与x之间的关系⽤两部分描述。
⼀部分是由于x的变化引起y线性变化的部分,即β0+ β1x,另⼀部分是由其他⼀切随机因素引起的,记为ε。
该式确切的表达了变量x与y之间密切关系,但密切的程度⼜没有到x唯⼀确定y的这种特殊关系。
式(1)称为变量y对x的⼀元线性回归理论模型。
⼀般称y为被解释变量(因变量),x为解释变量(⾃变量),β0和β1是未知参数,成β0为回归常数,β1为回归系数。
ε表⽰其他随机因素的影响。
⼀般假定ε是不可观测的随机误差,它是⼀个随机变量,通常假定ε满⾜:(2)对式(1)两边求期望,得E(y) = β0 + β1x, (3)称式(3)为回归⽅程。
E(ε) = 0 可以理解为ε对 y 的总体影响期望为 0,也就是说在给定 x 下,由x确定的线性部分β0 + β1x 已经确定,现在只有ε对 y 产⽣影响,在 x = x0,ε = 0即除x以外其他⼀切因素对 y 的影响为0时,设 y = y0,经过多次采样,y 的值在 y0 上下波动(因为采样中ε不恒等于0),若 E(ε) = 0 则说明综合多次采样的结果,ε对 y 的综合影响为0,则可以很好的分析 x 对 y 的影响(因为其他⼀切因素的综合影响为0,但要保证样本量不能太少);若 E(ε) = c ≠ 0,即ε对 y 的综合影响是⼀个不为0的常数,则E(y) = β0 + β1x + E(ε),那么 E(ε) 这个常数可以直接被β0 捕获,从⽽变为公式(3);若 E(ε) = 变量,则说明ε在不同的 x 下对 y 的影响不同,那么说明存在其他变量也对 y 有显著作⽤。
掌握一元线性回归分析-PPT模板

)(y x)2
y
)
a y bx
5
根据表计算
代入回归方程 yc a bx
6
序 号
产品产 生产费 量x 用y(万
(千吨) 元)
1 1.2
62
2 2.0
86
3 3.1
80
4 3.8
110
5 5.0
115
6 6.1
132
7 7.2
135
8 8.0
160
合 计
36.4
880
x2
1.44 4
9.61 14.44
207.54
xy 74.4 172 248 418 575 805.2 972 1 280
4 544.6
yc 66.79 77.11 91.3 100.33 115.81 130 144.19 154.51
880
(y yc)2 22.944 1 79.032 1 127.69 93.508 9 0.656 1
统计学基础
一、理解回归分析的概念
当给出自变量某一数值时,不能根据相 关系数来估计或预测因变量可能发生的数值。 回归分析就是对具有相关关系的变量之间数 量变化的一般关系进行测定,确定一个相关 的数学表达式,以便于进行估计或预测的统 计方法。
相关关系是一种数量关系不严格的相互依存关系。
2
二、掌握一元线性回归分析方法
1
一元线性回归分析的特点
在两个变量之间进行回归分析时,必须根据研究目的,具体确定
(1) 哪个是自变量,哪个是因变量。
在两个现象互为根据的情况下,可以有两个回归方程——y倚x回归方程和x倚y回
(2) 归方程。这和用以说明两个变量之间关系密切程度的相关关系只能计算一个是不相同的。
一元线性回归法linlm

b
x y xy x2 x2
101.8389 ,
a y bx -28.6883
y
[ yi (a bxi )]2 n2
0.931912
利用肖维涅舍弃判据来剔除测量值中带有粗差的数 据,列表如下(n=16时,Cu=2.15):
y'=a+bxi-Cu·σy
y"=a+bxi+Cu·σy
令Y lห้องสมุดไป่ตู้ y, X x,A lna, B b
则方程可化为:Y A BX
可求得,BA
A B
A B
Alna,Bba b
eA eAA B B
线性方程 y a bx
a y bx
xy x y
,
b
x2 x2
a b. x2
b
n(
x
1 2
x
2
)
.
y
r
xy x y
n 14 15 16 17 18 19 20 21 22 Cu 2.10 2.13 2.15 2.17 2.20 2.22 2.24 2.26 2.28
n 23 24 25 30 40 50 75 100 200 Cu 2.30 2.31 2.33 2.39 2.49 2.58 2.71 2.81 3.02
最终得到最佳的拟合直线方程(也称回归方程):
y a bx
• 需要考虑的两个问题
* 经验公式是否合适——相关系数 * 测量列是否存在粗差——肖维涅舍弃判据
附:相关系数表和肖维涅系数表
注意
*相关系数 r
1.只有当x和y之间存在线性关系时,拟合的直线才有
意义。
2.为了检验拟合的直线有无意义,引入一个叫相关系 数r来判别,r的定义为:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.残差平方和(Q)
反映除 x 以外的其它因素对 y 取值的影响,也称为 不可解释的平方和或剩余平方和。
n 2 ( yi a bxi ) 0 i 1 n 2 ( y a bx ) x 0 i i i i 1
5. 相关系数与线性回归---(1)因为回归方差不可能大于预报量的 方差,可以用它们的比值来衡量方程的拟 合效果。即:
上式还可以表示为:
2 Sy ˆ
1 F 2 Se ( n 2)
2 Sy ˆ
r 2 1 r n2
2 2 2 Sy Sy ˆ Se
2
S
2 y
r
2 xy
由于回归系数b已经知道,根据
rxy
Sx b Sy
n 1 2 2 x ( x ) i i n i 1 i 1 n n 1 2 2 y ( y ) i i n i 1 i 1 n
如:为了预报某地某月平均气温 (预报量)未来时刻的变化,选择预报 前期已发生的多个有关的气象要素(预 报因子),利用回归分析方法分析多个 预报因子和预报变量之间的相互关系, 建立统计关系方程式,最后利用其对未 来时刻的气温作出预报估计。
回归模型的类型
回归模型
一元回归 线性回归 非线性回归 多元回归 线性回归 非线性回归
S xx
Q S yy
2 S xy
S xx
b
S xy
2 Sx
回归分析与相关分析的区别
1. 相关分析中,变量 x 变量 y 处于平等的地位; 回归分析中,变量 y 称为因变量,处在被解释 的地位,x 称为自变量,用于预测因变量的变化。 2. 相关分析中所涉及的变量 x 和 y 都是随机变量; 回归分析中,因变量 y 是随机变量,自变量 x 可以是随机变量,也可以是非随机的确定变量。 3. 相关分析主要是描述两个变量之间线性关系的密 切程度;回归分析不仅可以揭示变量 x 对变量 y 的影响大小,还可以由回归方程进行预测和控 制。
或者写为一般的回归方程
ˆ a bx y
a是截距,b是斜率。
ˆ i 与 yi 对所有的 x i ,若 y 的 偏差最小,就认为(1)所确定的直线能最 好地代表所有实测点的散布规律。 为了消除偏差符号的影响,可以用偏差 的平方来反映偏差的绝对值偏离情况。
y
( xn , yn ) ( x2 , y2 ) ( x1 , y1 )
n
n
S yy
(y
i 1
n
i
y)
2
y
i 1
2 i
ny 2
S xx ( xi x ) xi2 nx 2
2 i 1 i 1
n
n
一 组 计 算 公 式
ˆ i y) U (y
i 1
n
2
ˆ)2 Q ( yi y
i 1
n
U
2 S xy
S S
2 ˆ y 2 y
1 2 ˆi y ) (y U n i 1 n 1 S yy 2 ( yi y ) n i 1
n
S S
2 ˆ y 2 y
2 ( a bx a b x ) i i 1 2 ( y y ) i i 1 n
n
2 2 b ( x x ) i i 1 n 2 ( y y ) i i 1
4.回归问题的方差分析 (1)意义 评价回归方程的优劣。 (2)预报量的方差可以表示成回归估计值 的方差(回归方差)和误差方差(残 差方差)之和。
2 2 2 Sy Sy S ˆ e
即:
预报量方差
回归方差
误差方差
n n 1 n 1 1 2 2 2 ˆ ˆ ( yi y ) ( yi y ) ( yi yi ) n i 1 n i 1 n i 1
回归系数也可直接表示为:
a y bx n n n 1 xi yi ( xi )( yi ) n i 1 i 1 i 1 n n b 1 2 2 xi ( xi ) n i 1 i 1
x y
i 1 n i
n
i
nx y nx
ˆ i y) U (y
i 1
n
2
2 ˆ Q ( yi y ) i 1
n
S yy U Q
U和Q分别称为回归平方和及残差平方和, S yy 称为总 离差平方和。
1.总离差平方和( S yy )
反映因变量的 n 个观察值与其均值的总离差。
2.回归平方和(U)
反映自变量 x 的变化对因变量 y 取值变化的影响,或 者说,是由于 x 与 y 之间的线性关系引起的 y 的取 值变化,也称为可解释的平方和。
计算检验统计量F 确定显著性水平,并根据分子自由度1 和分母自由度n-2找出临界值F 作出决策:若F >F ,拒绝H0;若F<F , 不能拒绝H0
7.回归系数的显著性检验
气象中经常使用回归方程的距平形 式,对回归方程的显著性检验可以只对 因子的回归系数进行检验。
b t c
Q n2
c [ ( xi x ) ]
b
计算出x和y的相关系数,然后可以求得F.
注意: 对于一元线性回归来说,因为F的相关 系数表达式开方就是相关系数t检验的表达 式,故回归方程的检验与相关系数的检验一 致。
r F 2 1 r n2
2
t
r 1 r
2
n2
线性关系检验的步骤概括如下:
提出假设
– H0:1=0, 线性关系不显著
因为 yi 可以看成遵从 N (0 xi ; 2 ) 的分
布,所以其95%的置信区间为 E ( yi ) 1.96 。
ˆ
Q n2
n 1 Q 2 2 ˆ ˆi ) ( yi y n 2 i 1 n2
ˆi 1.96 ˆ y
ˆ 是总体均方差(误差均方差)的无偏估计量。
气象统计方法
主讲:温 娜
南京信息工程大学 大气科学学院 2014年9月
本课件主要参考南信大李丽平老师的课件
第四章 一元线性回归(huang28)
主要内容
概述 基本概念 原理 方差分析 相关系数和线性回归 回归方程的显著性检验
1.概述 回归分析是用来寻找若干变量之 间的统计联系一种方法,利用找到 的统计关系对某一变量作出未来时 刻的估计,称为预报值。包括线性 回归和非线性回归,常用的线性回 归。
ˆ ˆx ˆ y 0 1
}
( x i , y i)
ei = yi^ - yi
x
全部观测值与回归估计值的离差平方和记为
ˆi )2 Q ( a , b) ( y i y
t 1 n
它刻画了全部观测值与回归直线偏离程度。 显然,Q值越小越好。a和b是待定系数,根据 微积分学中的极值原理,要求:
2
S xy S
2 x
x
i 1
2 i
上述求回归系数的方法称为最小二乘法
距平形式的回归方程: 即当变量为距平时,回归方程可以不用求 a,因为a=0,回归直线通过原点。
ˆ y b( x x ) y
标准化距平形式的回归方程:
b S xy S
2 x
Sy Sx
rxy
y * rxy x *
2.基本概念 一元回归处理的是两个变量之 间的关系,即一个预报量和一个预 报因子之间的关系。
3.原理
一般来说,对样本量为n的预报量y与预 报因子x的一组样本,如果认为y与x是一种 线性统计关系,预报量的估计量与x有如下 关系: ˆ a bx i 1,2,, n (1) y
i i
:
n 2 ( yi a bxi ) 0 i 1 n 2 ( y a bx ) x 0 i i i i 1
上式称为求回归系数的标准方程组。展 开: n n
na b xi y i i 1 i 1 n n n 2 a x b x xi y i i i i 1 i 1 i 1
(2)回归系数b与相关系数之间的关系
b
r与b同号。
S xy S
2 x
Sy Sx
rxy
6. 回归方程的显著性检验
U 1 F Q ( n 2)
原假设回归系数b为0的条件下,上述统计量遵 从分子自由度为1,分母自由度为(n-2)的F分布, 若线性相关显著,则回归方差较大,因此统计量F 也较大;反之,F较小。对给定的显著性水平 , 查表得到F临界值 F ,如果 F F ,则拒绝原假 设,认为线性相关显著。
方差分析表明,预报量y的变化可以看成由前期 因子x的变化所引起的,同时加上随机因素e变化的 影响,这种前期因子x的变化影响可以归为一种简 单的线性关系,这部分关系的变化可以用回归方差 的大小来衡量。如果回归方差大,表明用线性关系 解释y与x的关系比较符合实际情况,回归模型比较 好。
有时候,两边同时乘以n变成各变量离差平方和的关 系。
例1:
1)计算回归系数,确定方程
X变化一个单 位,气温降低 0.23度。
2)回归方程显著性检验:
3)计算预报值得置信区间,作出预测:
X和y离差积之和 总离差平方和 x离差平方和
S xy ( xi x )( yi y ) xi yi nx y
i 1 i 1
n
作业
利用冬季热带太平洋Nino3.4区平均海 温异常指数,建立与江苏省夏季降水异常 的一元线性回归预测模型。据观测2007年 冬Nino3.4海温异常为 -1.2度,对江苏省夏 季降水异常进行预测。
