模糊聚类案例分析(DOC)
模糊聚类分析模板

模糊聚类分析1.1 模糊聚类分析法的基本原理模糊聚类分析是根据事物间的不同特征、亲疏程度和相似性等关系,通过建立模糊相似关系对客观事物进行分类的一种数学方法。
用模糊聚类分析方法处理带有模糊性的聚类问题更为客观、灵活、直观,计算也更加简捷。
1.2 模糊聚类分析的简要流程1.3 模糊聚类分析的一般步骤Step1:数据标准化(1) 获取数据设论域12{,,,}n X x x x =为被分类对象,每个对象又有m 个指标表示其性状,即:12{,,,}(1,2,,)i i i im x x x x i n ==。
于是,得到原始数据矩阵为:111212122212()m m ij n m n n nm x x x x x x A x x x x ⨯⎛⎫ ⎪ ⎪== ⎪ ⎪⎝⎭ 其中,nm x 表示第n 个分类对象的第m 个指标的原始数据。
(2)数据的标准化处理在实际问题中,不同的数据一般有不同的量纲,为了使不同的量纲也能进行比较,通常需要对数据做适当的变换。
但是,即使这样,得到的数据也不一定在区间[0,1]上。
因此,这里说的数据标准化,就是要根据模糊矩阵的要求,将数据压缩到区间[0,1]上。
通常有以下几种变换:标准差变换与极差变换,本文采用极差变换对原始数据标准化处理,其数学模型模型为:'111min{}max{}min{}ik ik i n ik ik ik i ni n x x x x x ≤≤≤≤≤≤-=-,(1,2,,)k m =显然有01ikx ''≤≤,且消除了量纲的影响,从而可以得到模糊矩阵: ''()ij n m R x ⨯=Step2:建立模糊相似矩阵设论域12{,,,}n X x x x =,12{,,(1,2,..,,)}.i i i im x x x x i n ==,即数据矩阵()ij n m A x ⨯=。
如果i x 与j x 的相似程度(,)ij i j r R x x =,则称之为相似系数。
由模糊相似关系进行聚类分析

1 0 1 1 1
1 0 1 1 1
因此可分为两类,即: { x1, x3 , x4 , x5}和 { x2 } 小结:
用“传递闭包法”把模糊相似矩阵改造成模糊等价矩阵时,往
往 计算工作量很大,需要进行多次自乘。但是我们前面学习的“编网 法”(1979年吴望名曾提出)和“最大树法”(1980年赵汝怀曾提 出) 不需要作矩阵自乘,应用起来更方便。
0.8 0.4 1 0.5 0.5
即 R 4 R 4 R8,故 R 4 即为所求的模糊等价矩阵。于是就可由
模糊等价矩阵进行聚类分析。
例如 取 0.5 ,模糊等价矩阵 R 的 截矩阵为:
4
R0.5
1 0 1 1 1
0 1 0 0 0
1 0 1 1 1
由模糊相似关系进行聚类分析
我们前面学习的十二种标定方法所构成的模糊矩阵,往往只满足自 反
性和对称性,而不一定满足传递性。
当所得到的模糊矩阵是个模糊等价矩阵时,就是我们前面所讲的 “基 于模糊等价关系的聚类分析”。 当所得到的模糊矩阵只是个模糊相似矩阵时,就不能对它直接进行 聚类分析,需要对它进行改造。下面我们就来讨论如何把模糊相似矩阵改 造成模糊等价矩阵,在进行聚类分析。
0.8 0.4 1 0.5 0.5
0.5 0.4 0.5 1 0.6
0.5 0.4 0.5 0.6 1
0 .5 0 .4 0 .5 1 0 .6 .5 0.4 0.5 0.6 1
第三步,求出 R 4 R 4 R8 0.4 1 1 0.4 R 4 R 4 R 8 0 .8 0 . 4 0 .5 0 . 4 0 .5 0 . 4
模糊相似矩阵的改造方法——传递闭包法(平方法)
模糊聚类分析实验报告
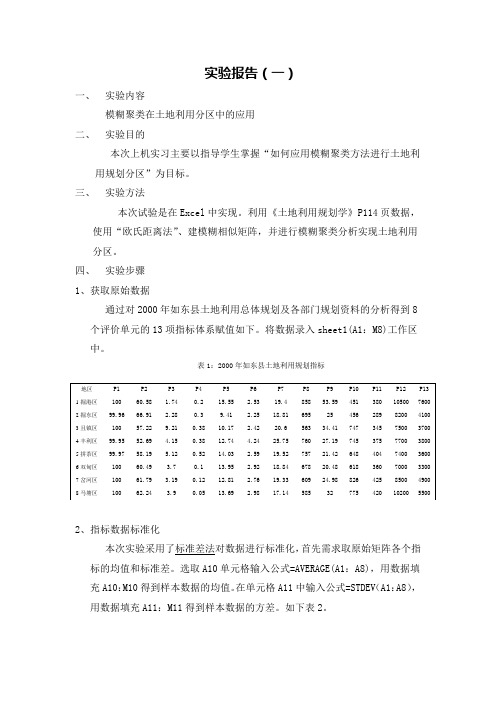
实验报告(一)一、实验内容模糊聚类在土地利用分区中的应用二、实验目的本次上机实习主要以指导学生掌握“如何应用模糊聚类方法进行土地利用规划分区”为目标。
三、实验方法本次试验是在Excel中实现。
利用《土地利用规划学》P114页数据,使用“欧氏距离法”、建模糊相似矩阵,并进行模糊聚类分析实现土地利用分区。
四、实验步骤1、获取原始数据通过对2000年如东县土地利用总体规划及各部门规划资料的分析得到8个评价单元的13项指标体系赋值如下。
将数据录入sheet1(A1:M8)工作区中。
表1:2000年如东县土地利用规划指标2、指标数据标准化本次实验采用了标准差法对数据进行标准化,首先需求取原始矩阵各个指标的均值和标准差。
选取A10单元格输入公式=AVERAGE(A1:A8),用数据填充A10:M10得到样本数据的均值。
在单元格A11中输入公式=STDEV(A1:A8),用数据填充A11:M11得到样本数据的方差。
如下表2。
表2:13个指标值得均值和标准差选取A13单元格输入公式=(A1-A$10)/A$11,并用数据填充A13:M20区域得到标准化矩阵如下表3。
表3:标准化数据矩阵3、求取模糊相似矩阵本次试验是通过欧氏距离法求取模糊相似矩阵。
其数学模型为:mr ij=1−c√∑(x ik−x jk)2k=1选取A23单元格输入公式=SQRT((A$13-A13)^2+(B$13-B13)^2+(C$13-C13)^2+(D$13-D13)^2+(E$13-E13)^2+(F$13-F13)^2+(G$13-G13)^2+(H$13-H13)^2+(I$13-I13)^2+(J$13-J13)^2+(K$13-K13)^2+(L$13-L13)^2+(M$13-M13)^2)求的d11,B23中输入公式=SQRT((A$14-A13)^2+(B$14-B13)^2+(C$14-C13)^2+(D$14-D13)^2+(E$14-E13)^2+(F$14-F13)^2+(G$14-G13)^2+(H$14-H13)^2+(I$14-I13)^2+(J$14-J13)^2+(K$14-K13)^2+(L$14-L13)^2+(M$14-M13)^2)q 求的d12。
模糊聚类分析

1 2 m
x11 x21 xm1
x12 x22 xm 2
x1n x2 n xmn
2 .模糊聚类分析的一般步骤
实际问题中,不同的数据可能有不同的量 纲。为了使不同量纲的数据也能进行比较,需 要对数据进行适当的变换。根据模糊矩阵的要 求将数据压缩到区间 【0,1】。通常使用平移极差标准化: xik min{xik } 1im xik (k 1,2,, n) max{xik } min{xik }
取=0.8,得 :
~ R0.8 1 0 0 0 0 0 1 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1
X分为4类:{X1,,X3},{X2},{X4 }, { X5 }。
2 .模糊聚类分析的一般步骤
取=0.5,得 :
~ R0.5 1 0 0 0 0 0 1 1 0 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1
3 .应用实例
通过聚类分析,该矿决定在房柱法的基础 上增加采矿费用的投入,采用无底柱上向干式 充填采矿法。
谢
谢!
模糊聚类分析步骤可以分为:数据标准化、建立 模糊相似矩阵、聚类
2 .模糊聚类分析的一般步骤
2.1 数据标准化 设论域 X {x , x ,, x } 为被分类的对象,每个对像 又由n个指标表示其性状,即:xi (xi1, xi2 ,, xin ) (i 1,2,, m) 于是,得到原始数据矩阵为:
rij
m in (x
k 1
n
ik
, x jk )
1 2
(x
k 1
n
ik
关于运用模糊聚类分析评价教学质量的研究.doc

关于运用模糊聚类分析评价教学质量的研究作者:周世学邓蓓张静来源:《教育与职业·理论版》2007年第09期[摘要]教育现象的许多因素无法划分到绝对明晰的类别中,任何具体的同一性都是相对的,其中包含着差异和变化,因而呈现出一定的不确定性。
依照模糊数学的观点,被人们视为同一的许多事物,都是一个模糊集合。
据此,我们可以借助模糊聚类分析测量教育因素间的指标值或计算它们的相关值,建立教育研究评判指标,对教师教学质量进行科学的量化评价。
[关键词]模糊综合评判教师教学质量教学评价[作者简介]周世学(1957- ),男,辽宁大连人,天津大学在读博士,天津职业大学副教授,主要从事教育经济与管理等方面的研究。
(天津300700)邓蓓(1962- ),女,天津人,天津中德职业技术学院副教授,主要从事信息管理等方面的研究工作。
(天津300191)张静(1979- ),女,山东德州人,天津职业大学硕士研究生,主要从事计算数学、教学管理等方面的研究工作。
(天津300420)[中图分类号]G40-058.1[文献标识码]A[文章编号]1004-3985(2007)14-0125-01客观事物皆具有两重性,即确定性与模糊性。
所谓模糊性,主要是指客观事物在差异的“中介过程”所呈现的“亦此亦彼”性。
而教育作为一种以人为主要研究对象的社会范畴,是一个远比生物学和物理学更复杂的研究领域。
教育诸种特性构成教育状态的复杂性,与这种复杂性紧紧相伴的便是教育现象的模糊性。
正因如此,对教育问题的量化评价要比物理现象的测量和统计困难得多。
教育评价研究的这一难题随着模糊数学的诞生与移植在很大程度上得到了解决。
学校要提高教育质量,首先就要提高教学质量,教学评价就是判断教学质量是否达到一定要求。
因此,客观、公正、科学、有效地对教师教学质量做出正确评价,对学校的生存与发展至关重要。
一、教学评价量化的模糊数学方法1.聚类分析法。
聚类分析是按照一定的标准对事物进行分类的数学方法。
模糊聚类分析实验报告

专业:信息与计算科学 姓名: 学号:实验一 模糊聚类分析实验目的:掌握数据文件的标准化,模糊相似矩阵的建立方法,会求传递闭包矩阵;会使用数学软件MATLAB 进行模糊矩阵的有关运算实验学时:4学时实验内容:⑴ 根据已知数据进行数据标准化.⑵ 根据已知数据建立模糊相似矩阵,并求出其传递闭包矩阵.⑶ (可选做)根据模糊等价矩阵绘制动态聚类图.⑷ (可选做)根据原始数据或标准化后的数据和⑶的结果确定最佳分类. 实验日期:20017年12月02日实验步骤:1 问题描述:设有8种产品,它们的指标如下:x 1 = (37,38,12,16,13,12)x 2 = (69,73,74,22,64,17)x 3 = (73,86,49,27,68,39)x 4 = (57,58,64,84,63,28)x 5 = (38,56,65,85,62,27)x 6 = (65,55,64,15,26,48)x 7 = (65,56,15,42,65,35)x 8 = (66,45,65,55,34,32)建立相似矩阵,并用传递闭包法进行模糊聚类。
2 解决步骤:2.1 建立原始数据矩阵设论域},,{21n x x x X 为被分类对象,每个对象又有m 个指标表示其性状, im i i i x x x x ,,,21 ,n i ,,2,1 由此可得原始数据矩阵。
于是,得到原始数据矩阵为323455654566356542155665482615645565276285655638286384645857396827498673176422747369121316123837X 其中nm x 表示第n 个分类对象的第m 个指标的原始数据,其中m = 6,n = 8。
2.2 样本数据标准化2.2.1 对上述矩阵进行如下变化,将数据压缩到[0,1],使用方法为平移极差变换和最大值规格化方法。
(1)平移极差变换:111min{}max{}min{}ik ik i n ik ik ik i n i n x x x x x ,(1,2,,)k m L显然有01ikx ,而且也消除了量纲的影响。
聚类分析-模糊聚类分析解析

模糊方阵的幂
定义:若A为 n 阶方阵,定义A2 = A ° A,A3 = A2 ° A,…,Ak = Ak-1 ° A.
0.1 0.4
0.3
3
0.3
0.7 0.4
0.3 0.7
0.1 0.4
00..73
0.3 0.4
模糊矩阵间的关系及并、交、余运算
设A=(aij)m×n,B=(bij)m×n都是模糊矩阵,定义 相等:A = B aij = bij; 包含:A≤B aij≤bij; 并:A∪B = (aij∨bij)m×n; 交:A∩B = (aij∧bij)m×n; 余:Ac = (1- aij)m×n.
模糊关系的矩阵表示
对于有限论域 X = {x1, x2, … , xm}和Y = { y1, y2, … , yn},则X 到Y 模糊关系R可用m×n 阶模糊 矩阵表示,即
R = (rij)m×n, 其中rij = R (xi , yj )∈[0, 1]表示(xi , yj )关于模糊关 系R 的相关程度.
R2≤R ( ∨{(rik∧rkj) | 1≤k≤n} ≤ rij) .
当<时, R的分类是R分类的加细.当由1变
ቤተ መጻሕፍቲ ባይዱ到0时, R的分类由细变粗,由模糊等价关系R确定 的分类所含元素由少变多,逐步归并,最后成一类, 这个过程形成一个动态聚类图,称之为模糊分类.
00..73
模糊矩阵的转置
定义 设A = (aij)m×n, 称AT = (aijT )n×m为A的转置 矩阵,其中aijT = aji.
转置运算的性质:
性质1:( AT )T = A; 性质2:( A∪B )T = AT∪BT,
聚类分析-模糊聚类分析

1 1 A0.3 0 0
1 1 0 1
0 0 1 1
0 1 1 1
模糊聚类分析
模糊关系 模糊等价矩阵
模糊相似矩阵
模糊聚类分析的一般步骤
模糊关系
与模糊子集是经典集合的推广一样,模糊关 系是普通关系的推广.
设有论域X,Y,X Y 的一个模糊子集 R 称 为从 X 到 Y 的模糊关系. 模糊子集 R 的隶属函数为映射 R : X Y [0,1]. 并称隶属度R (x , y ) 为 (x , y )关于模糊关系 R 的 相关程度. 特别地,当 X =Y 时,称之为 X 上各元素之 间的模糊关系.
例设U {u1 , u2 , u3 , u4 , u5 }, 1 0.4 R 0.8 0.5 0.5 0.4 0.8 0.5 0.5 1 0.4 0.4 0.4 0.4 1 0.5 0.5 0.4 0.5 1 0.6 0.4 0.5 0.6 1
又若R为布尔矩阵时,则关系R为普通关系,即xi 与 yj 之间要么有关系(rij = 1),要么没有关系( rij = 0 ).
模糊关系的合成 设 R1 是 X 到 Y 的关系, R2 是 Y 到 Z 的关系, 则R1与 R2的合成 R1 ° R2是 X 到 Z 上的一个关系. (R1 ° R2) (x, z) = ∨{[R1 (x, y)∧R2 (y, z)]| y∈Y } 当论域为有限时,模糊关系的合成化为模糊 矩阵的合成. 设X = {x1, x2, …, xm},Y = { y1 , y2 , … , ys}, Z= {z1, z2, … , zn},且X 到Y 的模糊关系R1 = (aik)m×s , Y 到Z 的模糊关系R2 = (bkj)s×n ,则X 到Z 的模糊 关系可表示为模糊矩阵的合成: R1 ° R2 = (cij)m×n 其中cij = ∨{(aik∧bkj) | 1≤k≤s}.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模糊数学方法及其应用论文题目:模糊聚类方法案例分析小组成员:王季光宋申辉兰洁陈倩芸肖仑杨洋吴云峰2013年10 月27 日模糊聚类分析方法1.1距离和相似系数为了将样品(或指标)进行分类,就需要研究样品之间关系。
目前用得最多的方法有两个:一种方法是用相似系数,性质越接近的样品,它们的相似系数的绝对值越接近1,而彼此无关的样品,它们的相似系数的绝对值越接近于零。
比较相似的样品归为一类,不怎么相似的样品归为不同的类。
另一种方法是将一个样品看作P 维空间的一个点,并在空间定义距离,距离越近的点归为一类,距离较远的点归为不同的类。
但相似系数和距离有各种各样的定义,而这些定义与变量的类型关系极大,因此先介绍变量的类型。
由于实际问题中,遇到的指标有的是定量的(如长度、重量等),有的是定性的(如性别、职业等),因此将变量(指标)的类型按以下三种尺度划分: 间隔尺度:变量是用连续的量来表示的,如长度、重量、压力、速度等等。
在间隔尺度中,如果存在绝对零点,又称比例尺度,本书并不严格区分比例尺度和间隔尺度。
有序尺度:变量度量时没有明确的数量表示,而是划分一些等级,等级之间有次序关系,如某产品分上、中、下三等,此三等有次序关系,但没有数量表示。
名义尺度:变量度量时、既没有数量表示,也没有次序关系,如某物体有红、黄、白三种颜色,又如医学化验中的阴性与阳性,市场供求中的“产”和“销”等。
不同类型的变量,在定义距离和相似系数时,其方法有很大差异,使用时必须注意。
研究比较多的是间隔尺度,因此本章主要给出间隔尺度的距离和相似系数的定义。
设有n 个样品,每个样品测得p 项指标(变量),原始资料阵为px x x np n n p p nx x x x x x x x x X X X X 2122221112112121 ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=其中(1,,;1,,)ij x i n j p ==为第i 个样品的第j 个指标的观测数据。
第i 个样品iX 为矩阵X 的第i 行所描述,所以任何两个样品XK 与XL 之间的相似性,可以通过矩阵X 中的第K 行与第L 行的相似程度来刻划;任何两个变量Kx 与Lx 之间的相似性,可以通过第K 列与第L 列的相似程度来刻划。
1.2 F 相似关系 1.2.1定义设)(U U F R ⨯∈,如果具有自反和对称关系,则称R 为U 上的一个F 相似关系(F 表示模糊)当论域U 为有限时,F 相似关系可以用F 矩阵表示。
具有F 相似关系的矩阵,称为F 相似矩阵。
在实际应用时,通常只能得到自反矩阵和对称举证,即相似矩阵。
现在的问题是对具有相似关系的元素怎样进行分类,也就是如何将相似矩阵改造为等价矩阵。
1.2.2 定理若TR R =,则称R 为对称矩阵。
(1)若R I ⊇(I 是单位矩阵),则称R 为自反矩阵。
(2)若2R R ⊇,则称R 为传递的F 关系。
(3)若满足上面三点则称为等价矩阵。
定理1:相似矩阵n n R u ⨯∈的传递闭包是等价矩阵,且nR R ∧=。
证 只需要证明R ∧是自反的、对称的。
因R 是自反的,故R I ⊇,2R R ⊇。
不难得到n R 不减,因此1nk n k R R R I∧===⊇,即R ∧是自反的。
因为TR R =,()()n T T n nR R R ==,故R ∧是对称的。
有定理1可见,要想将相似矩阵改变为等价矩阵,只需求相似矩阵的传递闭包。
定理2:设n n R u ⨯∈是自反矩阵,则任意自然数m n ≥,都有m R R ∧=证 由R 自反性推得2......n R R R ⊆⊆⊆⊆ 当m n ≥时,有1nmkk R R R R R∞∧∧==⊆⊆=1.3 聚类分析所谓聚类分析,就是用数学的方法对事物进行分类,它有广泛的实际应用。
在模糊数学产生之前,聚类分析已是数理统计多元分析的一个分支,然而现实的分类问题往往伴有模糊性。
例如,环境污染分类、春天连阴雨预报、临床症状资料分类、岩石分类,等等。
对这些伴有模糊性的聚类问题,用模糊数学语言来表达更为自然。
模糊聚类分析的步骤: 第一步:数据标准化 数据矩阵 设论域12{,,}n U x x x =为被分类的对象,每个对象由m 个指标表示其性状,即12(,,...,)m i i i i x x x x =于是得到原始数据矩阵为111212122212m m n n nm x x x x x x x x x ⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭数据标准化 在实际问题中,不同的数据一般有不同的量纲。
为了使有不同的量纲的量也能进行比较,通常需要对数据作适当的变换。
但是,即使这样,得到的数据也不一定在区间[0,1]上。
因此,这里说的数据标准化,就是要根据模糊矩阵的要求,将数据压缩到区间[0,1]上。
通常需要作如下集中变换。
1)平移∙标准差变换 2)平移∙极差变换 3)对数变换第二步 标定(建立模糊相似矩阵)设12{,,,}n U u u u =⋯为待分类的全体。
其中每一待分类对象由一组数据表征如下:12(,,...,)m i i i i u x x x = 现在的问题是如何建立iu 和ju 之间的相似关系。
这有许多方法(这里选一些,列在下面),我们可以按照实际情况,选其中一种来求iu 与ju 的相似关系(,)i j i jR u u r =。
(1)形似系数法 数量积法111.kkmij i j k i jr xx i jM ==⎧⎪=⎨≠⎪⎩∑当当其中M 为一适当选择之正数,满足,1max(.)k k mi j i jk M x x =≥∑夹角余弦法12211mijjkk ij mmik jk k k xx r x x ===⋅=⋅∑∑∑相关系数法12211||||().()kk kkmi i j j k ij mmi i j j k k xx x x r xx xx ===--=--∑∑∑其中11111,k km i i j j k k x x x x m m ====∑∑ 最大最小法11min(,)max(,)kk kk mi j k ij m i j k xx r x x ===∑∑算术平均最小法11min(,)1()2kk k k mi j k ij mi j k xx r x x ===+∑∑几何平均最小法11min(,).kk k kmi j k ij mi j k xx r x x ===∑∑绝对值指数法1||mi j k k k x x ij r e=--∑=绝对值减数法111||k k m ij i j k i j r c x x i j==⎧⎪=⎨--≠⎪⎩∑当当其中,c 适当选取,使01ij r ≤≤。
(2)距离法1)直接距离法 海明距离 欧几里得距离 切比雪夫距离 2)倒数距离法 3)指数距离法选择上述哪一个方法好,要按实际情况而定。
在实际应用时,最好采用多种方法,选取分类最符合实际的结果。
第三步 聚类(求动态聚类图)。
由第一步得到的矩阵R 一般只满足自反性和对称性,即R 是相似矩阵,需将它改造成模糊等价矩阵。
为此,采用平方法求出R 的传递闭包ˆR ,ˆR 便是所求的模糊等价矩阵。
通过ˆR便可对U 进行分类。
实际应用具体问题如下:1x :地区生产总值(当年价格)(亿元);2x :第一产业增加值;3x :第二产业增加值;4x :第三产业增加值;5x :地方财政一般预算内收入;6x :工业企业数(个);7x :工业总产值(当年价格)(万元);8x :从业人员年平均人数(万人);9x :流动资产年平均余额(万元) ;10x :主营业务收入(万元)11x :利润总额(万元);12x :移动电话年末用户数(万户);13x :国际互联网用户数(户);14x :公路里程;15x:普通中学学生数(万人);16x:医院、卫生院数(个);17x:医生数(执业医师+执业助理医师)(个)。
17项指标来描述江西省11各市区经济发展水平情况。
现将11个不同经济发展水平的市区进行聚类。
到的动态聚类图如下:λ1352681147910分类数1110.8573100.685390.6620380.614470.563660.496950.486240.452730.4316201标准差变换下——相关系数法构造相似矩阵R采用传递闭包法进行聚类,得到的动态聚类图如下:λ1924567810311分类数1110.9526100.87290.868480.857270.840860.837350.8273540.7549130.716520.68881动态聚类图如下:λ1235478910116分类数1110.8904100.864490.839480.837670.783860.7733150.771940.720130.6949320.63561极差变换下——相关系数法构造相似矩阵R采用传递闭包法进行聚类,得到的动态聚类图如下:λ1924785103611分类数1110.9563100.936690.8859580.876770.85960.830850.756740.756530.69220.677211。
